Quantifying the Benefits of Link-Tracing Designs for Partnership Network Studies

Abstract

Difficult-to-reach populations are frequently sampled through various link-tracing based designs, which rely on interpersonal networks to identify members of the population. This article examines the substantive returns to one such multiple-link tracing design in the Colorado Springs “Project 90” HIV risk networks study. Cross-links were respondents who were targeted for enrollment because of being named as partners by at least two other respondents in the sample. We compare cross-links to other respondents on sociodemographic characteristics and network properties using bivariate and multivariate adjusted statistics. We evaluate their contributions to observed network structure by creating a set of counterfactual networks deleting the information they provided. Results suggest that the link-tracing techniques led to identifying populations that would have otherwise been missed and that their absence would have underestimated potential HIV risk by distorting epidemiologically relevant measures within the network.

Introduction

Researchers rarely have clear sampling frames from which to recruit study participants from hard-to-reach populations. To address this problem, researchers in numerous substantive areas have developed strategies for finding, enumerating, and enrolling people from hidden populations. Referral-based strategies, including snowball sampling (Frank and Snijders 1994; Johnson et al. 1989), link-tracing (Félix-Medina and Thompson 2004; Thompson and Frank 2000), and respondent-driven sampling (Heckathorn 1997, 2002; Salganik and Heckathorn 2004), provide an important class of approaches for studying such populations. All of these rely on researchers’ ability to identify entry points, from which they uncover additional members of the subpopulation of interest.

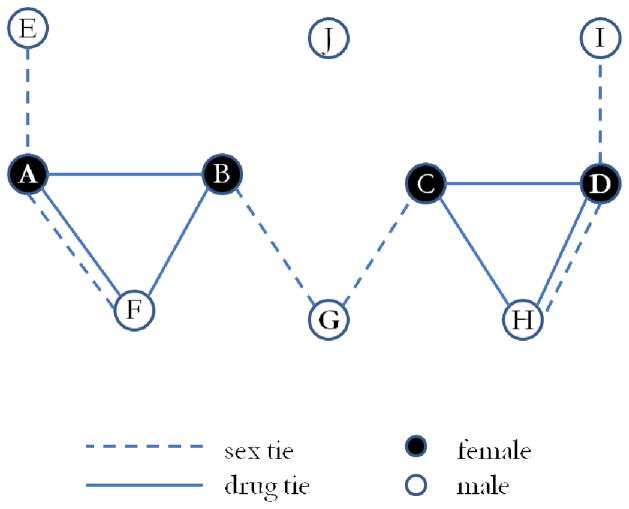
Link-tracing strategies are especially common in studies of sexually transmitted infections (STIs) for following the trajectory of infection spread through a population (De et al. 2004; Friedman et al. 2007; Klovdahl et al. 2001; Potterat et al. 2002) and identifying optimal strategies for preventing further infections (Neaigus 1998). Link tracing often involves clinical interviews regarding an STI or other infectious agent, where infected patients provide information about others with whom they have had contact and could potentially have already transmitted the infection.¹ Respondents generally report on frequency and type of interactions for their own relationships—known as their “direct ties” along with basic demographic attributes about these contacts. If respondents name more than one contact, they can be asked to report on potential relationships among their contacts, here referred to as “indirect ties.” For example, in Figure 1, A could report on “direct ties” with B, E, and F as well as the indirect tie between B and F. Nominated contacts may be used to recruit additional respondents for a particular study. The study we examine here focused on a specific set of nominated contacts—known as “cross-links”—which identify people nominated by at least two respondents. In Figure 1—supposing respondents B and C each nominated G (a nonrespondent) among their direct ties, G would be identified as a cross-link and subsequently targeted for recruitment. Because cross-links were expected to play an important role in connecting the network, they became a focus of the link-tracing recruitment strategy. In this article, we examine the specific gains resulting from recruiting cross-links.

Figure 1.

Exemplar Graph of Network Characteristics

Link tracing is also increasingly being used to study the characteristics of the networks connecting recruited participants (De et al. 2004; Handcock and Gile 2008). While standard link-tracing approaches often focus only on ties through which a pathogen could potentially spread, previous work shows that tracing a variety of ties—both those that are directly STI-diffusion relevant (e.g., sexual or needle-sharing contacts) and those that are not (e.g., sharing meals or housing)—can assist in accurately reconstructing the networks within populations of interest (Rothenberg et al. 1998b). Eliciting networks that represent both “risky” contacts and social context can provide information about the community, and ultimately the risk network itself that would be overlooked when sampling risky contacts alone (Rothenberg et al. 1998b). As such, cross-links are identified based on nominations by any two respondents—regardless of the tie type identified, though most were risk ties.

For any data collection strategy, researchers must carefully consider the tradeoffs inherent in their chosen approach. For referral-based strategies, these tradeoffs frequently involve decreased costs (financial and otherwise) at the expense of reduced representativeness of the derived sample(s) (Heckathorn 1997). Researchers evaluating link-tracing must therefore consider their ability to accurately estimate the size of such populations and match sample characteristics to those of the target population (Goel and Salganik 2010; Heckathorn 2002; Salganik and Heckathorn 2004; Woodhouse et al. 1994).

As described above, researchers using link-tracing based designs are also interested in how network structure promotes or constrains STI spread (Friedman et al. 1997; Potterat et al. 2002; Rothenberg et al. 1995b, 1998a). Thus, an additional consideration important for researchers using link tracing is whether, and how, different classes of respondents might differentially contribute to measures of network structure within a study sample. It is important to note that in this article we do not evaluate how readily the observed network matches the “actual” risk network, since that question has been thoroughly explored elsewhere (Potterat et al. 1999; Woodhouse et al. 1994). Our aim is to determine how respondents recruited via link tracing differentially contributed to the observed sample and network characteristics. In addition to informing future researchers examining disease diffusion within this particular population, we also demonstrate an additional means by which future link-tracing studies should be evaluated and provide a method for making those comparisons.

Data

The Colorado Springs “Project 90” study was a federally funded CDC project focused on HIV transmission in heterosexual and intravenous drug use (IDU) populations. The primary aim of the project was to identify and interview as many people in the target population as possible (IDUs, prostitutes, and their sex partners), and to assess the size, structure, and epidemic potential of the high-risk partnership network. Data were collected from 595 respondents using face-to-face interviews over a 5-year period, using an open cohort design. Detailed overviews of the study and sample design have been published previously (Darrow et al. 1999; Klovdahl et al. 1992; Potterat et al. 2004; Woodhouse et al. 1994).

Respondents were asked about basic risk-taking behaviors, daily activities, and health status. The questionnaire also contained a local network module (Potterat et al. 2004)for collecting data on respondents’ sexual, needle-sharing, drug-using, and personal contacts in the previous 6 months. Respondents provided basic demographic information for each of their contacts and the frequency and type of their interactions. Further, respondents reported about the indirect ties among their contacts—indicating whether each pair shared sexual, drug, or social ties. These data have been used previously to examine the impact of network structure on disease transmission (Darrow et al. 1999; Potterat et al. 1999; Rothenberg et al. 1995a, 1998a).

Recruitment Strategy

Given that one aim of Project 90 was to approximate a census of the at-risk population, the team employed a multi-pronged recruitment strategy. Respondents were recruited through the public HIV testing center, STI clinic, drug clinic, and correctional system. Additional persons were recruited through street outreach and a prior study of street prostitutes (CDC 1987; Khabbaz et al. 1990).

Klovdahl’s modified link-tracing mechanism was adopted as the primary method of chain-referral (Potterat et al. 2004; Woodhouse et al. 1994). Identifying information (name, address, phone number, etc.) on direct ties (sex, needle, drugs, social) was evaluated for possible matches. If two or more respondents were found to have nominated the same partner, identifying a cross-link, this partner was targeted for enrollment. Though considerable effort was expended to identify, find, and interview cross-links, the yield was low.² Of the 341 cross-links identified and targeted for recruitment, only 92 (27%) were successfully interviewed.

Analytic Strategy

We compare the 92 respondents recruited as cross-links across the 5-year study period to all other respondents (N=503). Once enrollment was completed, researchers identified a group of directly recruited respondents who, like cross-links, were also multiply nominated. Because there was no tracing process involved in enrolling this group, they cost no more to enroll than non-cross-linked respondents; however, they share some partner-based characteristics with cross-links. As such, for some analyses we split direct recruits into those who were multiply nominated (“DR2+,” N=172) and those who were not (“DR0 1,” N=331).³ We use bivariate and multivariate statistics to evaluate whether cross-links differ from other respondents on a range of sociodemographic characteristics.

Individual Measures

Demographic Attributes

First, we compare cross-links to other respondents on a range of characteristics: Demographic attributes include sex, age, and race; risk category attributes include recent (within 6 months) IDU, exchanging sex for money or drugs, and sex with persons in either risk category (paid or not).

Network Position

For each node, we calculate a number of standard network-based measures that have direct relevance for STIs regarding individual risk exposure and population transmission dynamics. Unless indicated, formal definitions of network measures are available in Wasserman and Faust (1994). We construct two types of individual position measures from the observed network: Local network measures focus on single respondents and those to whom they are connected, while global network measures describe an individual’s location in the entire observed network. For both local and global network measures, we include direct and indirect tie reports (see adams and Moody 2007) for an evaluation of respondents’ ability to accurately report indirect ties. While cross-links could be identified based on social, sexual, or drug-sharing ties, the analyzed networks include only the HIV epidemiologically relevant ties (i.e., sex and drug-sharing ties).

The local network measures we examine are degree, local network density, and racial heterogeneity. A respondent’s degree is the number of persons they are directly linked to via sex and/or drug sharing. We derive from the aggregate network—constructed across time from all respondents—rather than a personal estimate from a single survey question. Local network density measures the extent to which one’s partners have sex or drug ties among themselves. This measure is normalized by the total number of possible ties, and ranges from 0 (no partners connected to each other—e.g., node G in Figure 1) to 1 (all partners connected to each other—e.g., node F or H in Figure 1). Computed local density is limited to nodes with degree 2 or higher (see Table 1 for N). Degree and density increase the epidemic potential within the local network. Racial heterogeneity reflects the racial diversity within each respondent’s local network. It is calculated as $1-{\displaystyle \sum _k}{(\frac{n_k}{N})}^2$, where k indexes the different racial groups, n_k is the number of people in race k and N is the total number of people in the local network (Blau 1977). Respondents with racially heterogeneous networks often act as bridges between racial groups otherwise separated by patterns of selective mixing (Morris 1993; Youm and Laumann 2002).

Table 1.

Sociodemographic Attributes and Network Characteristics by Recruitment Category

Attribute	Description	Cross-Links	All Direct Recruits (DR)	DR 0-1	DR 2+
Sex	Female	43.48	46.32	35.35	67.44*
Race:	White	47.83	62.82*	65.86	56.98
	Black	30.43	17.29*	14.80*	22.09
	Hispanic	17.39	14.51	14.20	15.12
	Other	4.35	5.37	5.14	5.81
Age	Years	31.38	28.63*	29.10*	27.72*
Risk Group:	IDU	31.52	54.67*	48.64*	66.28*
	Prostitutea	3.26 [7.50]	25.65* [55.38]*	15.11* [42.74]*	45.93* [68.10]*
	Pimpa	15.22 [26.92]	6.56* [12.22]*	6.34* [9.81]*	6.98* [21.43]*
Network Characteristics
Sex/Drug ties:	At least one	96.74	97.82	96.68	100
	Two or more	95.51	88.74	85.00	95.93
	↑Average #	16.80	12.25*	6.12*	24.04*
↑Local net density		0.22	0.15*	0.14*	0.17*
↑Race heterogeneity		0.27	0.30	0.27	0.36*
↑Closeness centrality		0.20	0.19	0.18*	0.21*
Component membership:	In largest component	98.88	64.06*	49.06*	93.02*
	In largest bi-component	88.76	46.50*	26.25*	85.47
N		92	503	331	172

NOTE: All numbers present the percent of members within each category that have the described characteristic, except those noted with (^↑), which present avearage values. Significance calculations are based on a multinomial logistic regression, without controls. An asterisk (*) denotes significant difference from cross-links (Column I). Where Columns III–IV are significantly different from each other, they are bold-underlined.

^aFor “pimps” and “prostitutes,” we also report [in brackets] the gender-specific percentage (i.e., the percent of in-category males who are pimps and of females who are prostitutes).

The global network positional measures we examine include membership in the largest component and bicomponent, closeness centrality, and positional equivalence. A component is defined as a set of persons who are connected by a path of any length. Most large networks, including the observed Project 90 risk network, contain a “giant component” (Palmer 1985) comprising over half of all participants connected through a chain of relations. The measure in largest component indicates whether a node is in the giant component (e.g., in Figure 1, only node J would not be in the connected component). Component membership represents both the personal risk of infection and the potential to infect others due to the large number of reachable persons. In largest bicomponent measures a subgroup within the largest component where every person is connected by at least two completely independent paths (Harary 1969; Moody and White 2003). There are two bi-components in Figure 1—A–B–F and C–D–H. In a risk-contact network, bi-components are subsections of the graph where a higher likelihood of transmission exists because pathogens can follow multiple distinct routes between pairs.

Closeness centrality measures the inverse of the average distance between a person and all other people in the largest connected component.⁴ The standardized index ranges from 0 to 1. High values indicate persons close to many others. Since exposure risk declines with relational distance, persons with higher closeness centrality are at greater risk of disease acquisition. All of the measures described above are computed for each node in the observed network.

Network equivalence measures the extent to which groups of persons have similar patterns of ties. Two persons occupy an equivalent network position if they have the same types of ties to similar types of people, where “types” are defined by tie patterns (White et al. 1989). For example, nodes A and D in Figure 1 are regularly equivalent—they each have one tie that includes only sex (to nodes not connected to anyone else), one tie that includes only drugs (to nodes with one additional sexual partner, G), and one tie that includes both sex and drugs (who also share drugs with their respective drug-only tie). Here, we define equivalence by examining—for all pairs of nodes in the network—the similarity on their triadic census distributions, incorporating drug, sex, or both links for constructed triads.⁵ Two respondents who are strictly “regularly equivalent” across sex and drug tie patterns would have identical distributions across the possible triad configurations.

Results

In the following sections, we present bivariate and multivariate comparisons of cross-links to direct recruits, where appropriate separating the latter into those who were multiply-nominated and those who were not. Table 1 presents comparisons of individual attributes and network measures across the two recruitment strategies (columns I–II) and splitting DR (columns III–IV).

Bivariate Results

Individual Measures

While cross-links and direct recruits are predominantly male, DR2+ are more likely to be female (Column IV). Recruited cross-links yielded respondents who were on average nearly 3 years older than direct recruits, and more likely than direct recruits to be non-white. Cross-links also display distinctive patterns of risk behavior and network position. Virtually all respondents report sexual or drug-sharing partners during the study interval, though cross-links report less IDU. While female cross-links are less likely to participate in prostitution, male cross-links are more likely to be pimps. On average, cross-links have more risk partners than direct recruits, though they have fewer than DR2+. Local network density is highest among cross-links. Average closeness centrality does not differ appreciably by recruitment status and is normally distributed, suggesting an absence of “hubs” in this network who provide between other nodes. Cross-links are more likely to be in the largest component than DR, however this difference is much smaller when compared only to DR2+. Multiply nominated respondents (whether cross-links or direct recruits) are similarly likely to be in the largest bicomponent (89% and 86% respectively).

Network Measures

The largest connected component (see Figure 2) of the risk-partnership network includes 405 respondents and 3,779 total persons (68% of respondents, and all names mentioned respectively).The full study population includes 5,595 named persons, of whom, 595 are respondents. For more details see (Potterat et al. 2004). The layout algorithm in Figure 2 (Fruchterman and Reingold 1991) tends to group nodes with similar patterns of ties closer to each other in the figure (Batagelj and Mrvar 2003). Thus, if cross-links occupy different locations from DR (whether multiply nominated or not), they may appear in different regions of this figure. The absence of such obvious differences suggests that cross-links and DR occupy approximately similar positions and may share similar patterns of ties. Table 2 formally quantifies similarity in network position, comparing the correlation in network equivalence across recruitment strategy. If different recruitment strategies find respondents with different network positions, the result would be high within-group correlations and low between-group correlations. The within-group correlations are generally high (r~0.6). Remarkably, cross-links are similar to all DR (r~0.5), though slightly more similar to DR2+ than DR0 1 (r~0.6, 0.5 respectively). This seems to indicate that all respondents fulfill roughly similar roles in the network, and the similarity between cross-links and DR2+ is virtually indistinguishable from similarity among each.

Figure 2.

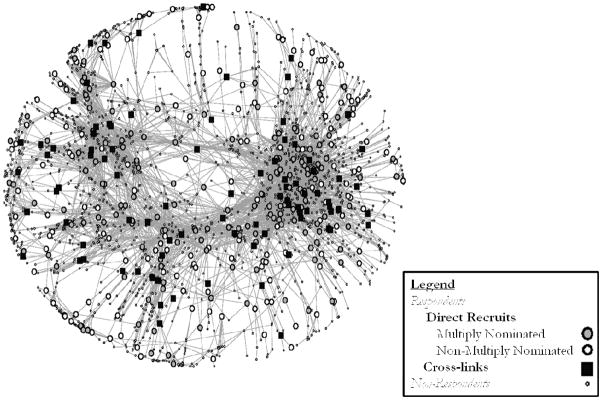
Network Position by Sample Strategy

Largest Component, Pooled Drug or Sex Tie Network

Table 2.

Mean Network Equivalence by Recruitment Category

	A	B	B1	B2
A) Cross links	0.62 (0.38)	0.54 (0.35)	0.49 (0.36)	0.63 (0.33)
B) Direct Recruits		0.59 (0.32)	-	-
1) <2 Nominations			0.66 (0.31)	0.52 (0.33)
2) ≥ 2 Nominations				0.66 (0.31)

NOTE: Numbers presented are the mean correlations across the tie-type specific triad distributions, with standard deviations in parentheses.

Multivariate Results

While cross-links possess unique demographic characteristics, risk-behavior attributes, and network positions (see Table 1), controlling for demographic differences reduces the magnitude and significance of some network-based differences. Table 3 presents these differences between cross-links and DR2+,⁶ with Column 1 including only a recruitment strategy dummy, while Column 2 controls for recruitment strategy plus age, race, sex, and risk category. Net of controls, cross-links lower degree, density and centrality is reduced and insignificant. However, even controlling for demographic attributes, cross-links continue to have more racially homogeneous partners and are more often in the largest component.

Table 3.

Network Position Comparison: Cross-Links and Multiply Nominated Direct Recruits (DR2+)

Dependent Variable	Coefficient for Cross-Linksa
	Unadjustedb	Adjustedc
Average Degree	−7.24 ** (1.99)	−2.94 (1.98)
Race Heterogeneity	−0.10 ** (0.03)	−0.07 * (0.03)
Local Net Density	−0.05 * (0.02)	−0.03 (0.02)
Closeness Centrality	−0.01 * (0.004)	−0.004 (0.004)
In Largest Component	1.89 (1.05)	2.19 * (1.06)
In Largest Bicomponent	0.30 (0.40)	0.49 (0.42)

^aMultiply nominated direct recruits is the reference category

^bUnadjusted includes a recruitment category dummy only

^cAdjusted controls for age, race, sex, and risk group, with a dummy for recruitment category.

^dLogistic regressions were used for modeling membership in the largest component/bicomponent. OLS regressions were used for all other models.

Network Structure Contributions

Cross-links were more likely than DR to provide redundant nominations, naming alters who: were more likely to be respondents themselves (34.5%, compared to 15.5% for DR) and received more nominations on average (2.1 nominations on average, compared to 1.6 for DR). Combined, these suggest they may differentially contribute to the observed network structure. Even combining these observations with the respondent class differences from above, does not sufficiently account for how cross-link recruitment changed estimated epidemic potential of the global network. We estimate this contribution by constructing a version of the risk network that assumes no cross-links were enrolled. This counterfactual network removes all the information uniquely provided by each cross-link: any of their partners who were not nominated by other respondents and any ties that were reported exclusively by the cross-links. Note that this will not result in the removal of cross-links from the network, since, by definition, they were nominated by at least two other respondents. We compare this cross-link reduced network to the observed network and to a series of 100 randomly reduced networks, each of which is created by following a similar procedure for 92 randomly chosen direct recruits and removing the information they uniquely provide. By comparing the observed network to these reduced networks, we can identify how the information obtained from cross-links contributed to the observed network.

For these comparisons, we examine how the reduced and observed networks differ on network size, the number of ties, the size of the largest component, and reachability over short paths (Rothenberg et al. 1995a, 1998a). Network size and number of ties measures network volume as the number of persons and ties in the network, respectively. Giant component size measures the number of persons linked together in the largest component (e.g., in Figure 1, the large component contains nine nodes). Reachability in three steps captures the proportion of dyads in the giant component that are linked by a path no longer than three ties. For example in the giant component in Figure 1 (which excludes only J), there are (N*N 1)/2 = 36 possible dyads. Of those, 25 can be connected in three steps or less (only AD, AH, AI, BI, CE, DE, DF, EH, EI, FH, and FI are longer than three steps). Thus, reachability is 25/36 = 0.694. Intuitively, these are one’s partners’, partners’ partners. Potential disease diffusion between a randomly selected pair of (indirectly) connected nodes rapidly declines with increases in the distance between them. For each of these measures, differences resulting from removals reveal the inverse effects of the contributions provided by the removed group. For example, if cross-links bridge disparate populations, then removing their information will result in greater distances between people, suggesting they provided “shortcuts” for potential disease diffusion across the observed network.

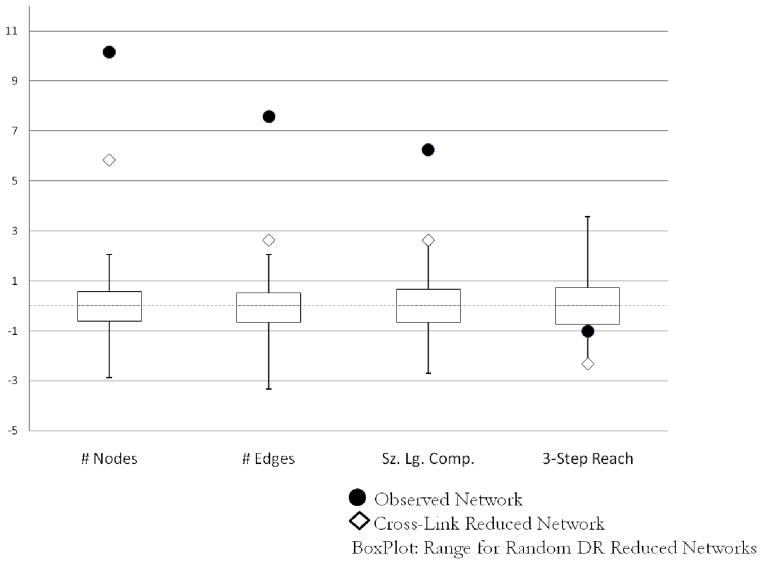
Figure 3 compares these network statistics for the observed network (circle), the counterfactual network with cross-links information deleted (diamond), and the range from the corresponding 100 DR-removed counterfactual networks (boxplot). To be able to compare across these differences, Figure 3 presents them as Z-score standardizations; however, we discuss the absolute differences. Given the extent of redundancy in the nodes nominated by cross-links, removing cross-link information has a comparatively small effect on measures of network volume. Had cross-links not been enrolled, 364 persons would have been missed, about 6.5% of the observed network. We also would have missed 1,243 partnerships, about 10.3% of the total, and found 379 fewer persons in the largest component, a drop of 10.1%. While potentially substantively important, the effect on each of these measures is substantially less than if we had not sampled an equivalent number of DR. Information from cross-links also played a role in reducing the distance between persons (Figure 3, “3-step Reach”). Within the largest component of the observed network, the median person can reach 157 people in three steps; this falls to 123 people without cross-link information, a 21.7% drop. Combined, these findings suggest that while information provided by cross-links did not identify many new people, the ties reported by cross-links were more likely to form bridges in the largest component, shortening overall distance between pairs.

Figure 3.

Network Structure Counterfactuals

Measures with and without Information Provided by Node Types

Discussion

Project 90 sought to identify the potential for HIV transmission among a high-risk population in Colorado Springs by mapping their drug and sex partner network. The study enrolled respondents with a conventional convenience sample and a modified link-tracing design. Here, we use standard bivariate and multivariate statistical comparisons to examine how recruits resulting from these strategies differed on individual demographic and network characteristics, and a new strategy using simulated counterfactual networks to examine their differential contributions to observed network connectivity. Our findings suggest that the cross-links were systematically different, but that their network position differences were largely explained by their demographic attributes. The network information provided by cross-links was largely redundant with respect to the individuals identified, but unique in the pattern of relations identified among these persons. Findings do not provide unqualified support for targeted contact tracing, but they do help clarify three important conditions under which the additional costs associated with link-tracing may be justified.

First, cross-link sampling captured a subpopulation that differed significantly from that obtained using conventional sampling (e.g., more likely to be older, male, pimps, and black). While the specific attributes that marked this population may not apply to other contexts, the first potentially generalizable finding is that cross-link tracing can uncover populations that would otherwise be hidden. Particularly when the target population involves high-risk groups that are hard to reach, a cross-link design can help counteract the limitations of convenience sampling. This was a challenging setting for observing such an effect, as the study team had more than 20 years of experience in STI control in this community. The high levels of trust and local knowledge developed here likely raised the quality of the convenience sample obtained. If, even in this context, the cross-link tracing strategy led to different members of the high-risk network, the value of cross-link strategies for revealing hidden subpopulations is likely quite general. Second, cross-links’ network characteristics differed in important ways from DR (they had lower average degree, lower density, and less racially heterogeneity, and were less central in the global network than DR). These differences in network position largely disappear, if conditioned on demographic attributes and risk group. Thus, in similar contexts, one could combine external information on the demographic profile of the high-risk population with more detailed information from a convenience sample to obtain better estimates of network structure. In Project 90, the tracing sample changed estimates of the profile of the high-risk population, and thus was required to model missing data. However, the results suggest researchers may be able to accomplish this with a relatively small tracing sample.

Finally, while cross-links and DR (especially DR2+) occupied similar network positions and contributed similar kinds of information regarding network connectivity, the cross-links provided a specific epidemiologically relevant capacity for identifying and mapping the community risk network. The fact that partners named by cross-links were often redundant should not be surprising, since (by definition) these people are within the risk circles of at least two other respondents. What makes them valuable is that cross-links identified connections among other respondents that change the overall distance between pairs. To clarify, if B and C (Figure 1) were targeted cross-links, they have similar characteristics to others in their local network (e.g., A and D respectively) regarding number and types of ties. However, without recruiting them, we likely would have missed their ties to G, whose presence connects those on the left and the right of the graph. Because pathogens are more likely to be passed through short relational chains, this finding has direct implications for estimates of the network STI transmission potential. This difference would not have been discoverable from the positions of cross-links in the global network, nor would variations in their local-network or the complete network among cross-links. We were only able to discern this unique characteristic of the information provided by cross-links via our strategy for comparing observed networks to simulated counterfactual networks.

These findings are limited by the relatively low response rate Project 90 staff obtained among targeted cross-links. It is possible that nonenrolled cross-links had different characteristics and networks. This reflects the inherent difficulties of contact tracing. Although it limits our ability to estimate the true population values of cross-links’ attributes, our findings are still likely useful for estimating the practical value that cross-links added to Project 90 network estimates. To quantify the value of the targeted cross-link tracing strategy, we can compare the costs of their recruitment to those with similar characteristics found through the convenience sampling mechanism. Of the 503 enrolled DR, 172 were multiply nominated, so the relative cost per DR2+ is 2.9 times the cost per DR0 1. Roughly speaking, then, if it costs three times more to trace and enroll cross-links, that is about the break-even point. This is likely to be a conservative estimate. The relatively high yield of DR2+ here is due to the effort expended in enrolling as many high-risk persons as possible in a relatively small community and the high levels of connectedness in this network. In a larger community, with less connectivity, any corresponding drop in the yield of convenience strategies would quickly raise the relative gains provided from recruiting cross-links.