Abstract
We propose a beta product confidence procedure (BPCP) that is a non-parametric confidence procedure for the survival curve at a fixed time for right-censored data assuming independent censoring. In such situations, the Kaplan–Meier estimator is typically used with an asymptotic confidence interval (CI) that can have coverage problems when the number of observed failures is not large, and/or when testing the latter parts of the curve where there are few remaining subjects at risk. The BPCP guarantees central coverage (i.e. ensures that both one-sided error rates are no more than half of the total nominal rate) when there is no censoring (in which case it reduces to the Clopper–Pearson interval) or when there is progressive type II censoring (i.e. when censoring only occurs immediately after failures on fixed proportions of the remaining individuals). For general independent censoring, simulations show that the BPCP maintains central coverage in many situations where competing methods can have very substantial error rate inflation for the lower limit. The BPCP gives asymptotically correct coverage and is asymptotically equivalent to the CI on the Kaplan–Meier estimator using Greenwood’s variance. The BPCP may be inverted to create confidence procedures for a quantile of the underlying survival distribution. Because the BPCP is easy to implement, offers protection in settings when other methods fail, and essentially matches other methods when they succeed, it should be the method of choice.
Keywords: Clopper–Pearson confidence interval, Exact confidence interval, Kaplan–Meierestimator, Median survival, Non-parametric methods, Survival analysis
1. Introduction
In this paper, we use products of beta random variables to create a new pointwise confidence procedure for the survival distribution from right-censored data. Our beta product confidence procedure (BPCP) is invariant to monotonic transformations and can be applied to data with tied event times. The BPCP is designed to guarantee central coverage, so that a 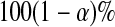 confidence interval (CI) allows one to conclude whether survival at a specific time is higher (or lower) than a reference value, with a type I error rate that is less than or equal to
confidence interval (CI) allows one to conclude whether survival at a specific time is higher (or lower) than a reference value, with a type I error rate that is less than or equal to 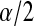 . Theoretically, under progressive type II censoring the BPCP guarantees central coverage. Our simulations show that under independent censoring for small samples the BPCP retains coverage, whereas existing procedures based on the Kaplan–Meier estimator do not. Further asymptotically, both limits of the BPCP are correct and equivalent to the usual confidence limits based on the Kaplan–Meier estimator and Greenwood’s formula.
. Theoretically, under progressive type II censoring the BPCP guarantees central coverage. Our simulations show that under independent censoring for small samples the BPCP retains coverage, whereas existing procedures based on the Kaplan–Meier estimator do not. Further asymptotically, both limits of the BPCP are correct and equivalent to the usual confidence limits based on the Kaplan–Meier estimator and Greenwood’s formula.
A common approach to estimating CIs for the survival distribution is to use a normal approximation with the Greenwood formula for the variance of the Kaplan–Meier estimator and the delta method on a transformation (see, e.g. Kalbfleisch and Prentice, 2002; Meeker and Escobar, 1998; SAS, 2011; Therneau, 2012). Strawderman and others (1997) discuss improving the normal CIs using Edgeworth expansions. Barber and Jennison (1999) review several more complex confidence procedures for survival and identify two CIs that perform quite well, the constrained estimator of Thomas and Grunkemeier (1975) and the constrained bootstrap, the latter of which can be computationally time consuming.
Although many of the previously developed CIs are asymptotically consistent when the censoring is independent with a fixed distribution (Andersen and others, 1993), those CIs can have coverage problems at times before very many events have occurred. For example, consider CIs before the first death at 14 days (0.038 years) in the data from Nash and others (2007) (see Figure 1 and Section 8 for details). The Kaplan–Meier estimator before the first death equals 1 and its estimated variance is 0, so the Greenwood 95% CI is [1,1], which is clearly not correct. Andersen and others (1993, p. 214, 268) discuss adjusting this first interval using exact methods, but our BPCP does this naturally, giving a 95% CI of 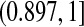 . This interval is the same as the exact Clopper–Pearson interval for 34 out of 34 surviving. The BPCP reduces to this type of exact interval at each time point when there is no censoring.
. This interval is the same as the exact Clopper–Pearson interval for 34 out of 34 surviving. The BPCP reduces to this type of exact interval at each time point when there is no censoring.
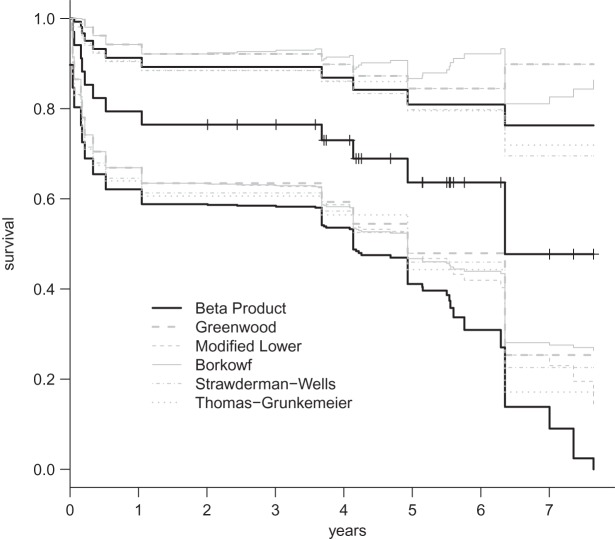
Fig. 1.
The black middle curve is the Kaplan–Meier estimator of survival for 34 patients with 12 observed deaths from Nash and others (2007). Censored values are denoted by small vertical hashes. Gray lines are previously derived CIs and the black CIs are the BPCP intervals developed in this paper.
A second coverage problem with many traditional CIs occurs when the Kaplan–Meier estimate does not change as subjects are censored, and the Greenwood CIs, for example, also do not change. In Figure 1, we would expect that the variance of the Kaplan–Meier estimate would be larger (and hence the CI should be larger) just before the 12th failure time (6.35 years) when there are only 4 subjects at risk, than just after the 11th failure (4.93 years) when there are 13 subjects at risk. Because of the constancy of the Greenwood CIs between failure times, we have oddities such as the following: the 95% lower confidence limit just before the 12th failure is 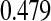 , but immediately after the 12th failure our estimate of the survival distribution is
, but immediately after the 12th failure our estimate of the survival distribution is 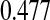 , even lower than the Greenwood lower limit just prior to the failure. There are several additional methods that allow CIs to change in intervals where only censored observations are observed (Peto and others, 1977; Dorey and Korn, 1987; Borkowf, 2005), but they are all based on asymptotic normal approximations, so their coverage for small samples will not be guaranteed. It appears that the Greenwood and other previously developed lower limits just prior to the 12th failure are too high. In fact, we show through simulations in Section 7 that the lower bound can have very poor one-sided coverage for previously developed methods when there are either few observed failures or when there are few subjects at risk.
, even lower than the Greenwood lower limit just prior to the failure. There are several additional methods that allow CIs to change in intervals where only censored observations are observed (Peto and others, 1977; Dorey and Korn, 1987; Borkowf, 2005), but they are all based on asymptotic normal approximations, so their coverage for small samples will not be guaranteed. It appears that the Greenwood and other previously developed lower limits just prior to the 12th failure are too high. In fact, we show through simulations in Section 7 that the lower bound can have very poor one-sided coverage for previously developed methods when there are either few observed failures or when there are few subjects at risk.
A third issue with some previously developed CIs is that the upper limit may increase (see the upper limits in Figure 1), while we know that the survival curve does not increase. Our simulations show that some upper bounds can be needlessly conservative compared with our BPCP.
We can invert the BPCP to obtain confidence procedures for quantiles of the survival distribution (see, e.g. Barber and Jennison, 1999). These BPCP quantile confidence procedures are simpler than the method of Guilbaud (2001), which uses a mixture representation of the order statistics to provide an exact non-parametric confidence procedure for quantiles from progressive type II censoring. The associated median unbiased estimator (MUE) provides estimates of quantiles (e.g. median).
We begin by defining beta product random variables in Section 2, since they are essential in the development of the BPCP. Our development of the BPCP first assumes continuous failure times (Section 3), but then we allow ties through grouping of the failure times (Section 4). The BPCP requires estimation of beta product quantiles described in Section 5. In Section 6, we discuss extensions such as MUEs of survival at t based on the BPCP. We end with simulations, applications, and a discussion.
2. Beta product random variables
Let 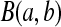 be a beta random variable with parameters a and b, with mean
be a beta random variable with parameters a and b, with mean 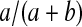 and variance
and variance 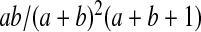 , and let
, and let 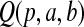 be the pth quantile of that beta distribution. For notational convenience, we extend the definition of beta distribution to include the limits. Specifically,
be the pth quantile of that beta distribution. For notational convenience, we extend the definition of beta distribution to include the limits. Specifically, 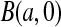 with
with 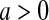 and
and 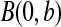 with
with 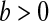 are random variables with point masses at 1 and 0, respectively, so that
are random variables with point masses at 1 and 0, respectively, so that 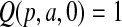 and
and 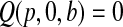 for
for 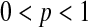 . We leave
. We leave 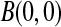 undefined.
undefined.
Let 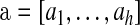 and
and 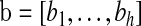 be vectors with all values ≥0
be vectors with all values ≥0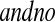 j
j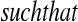 aj = bj = 0
aj = bj = 0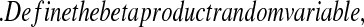 BP(a,b), such that
BP(a,b), such that
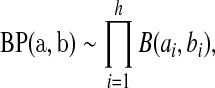 |
where ∼ denotes “is distributed as” and the terms in the product are all independent. Let 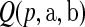 be the pth quantile of
be the pth quantile of 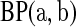 .
.
In some cases, a beta product random variable simplifies to a beta random variable:
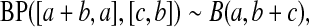 |
for constants 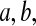 and c where the beta product variables are defined. To see this for cases with
and c where the beta product variables are defined. To see this for cases with 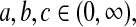 see Casella and Berger (2002, p. 158), and for cases with some parameters equal to 0, we can show the result by inspecting each case. By repeated use of this property, we have
see Casella and Berger (2002, p. 158), and for cases with some parameters equal to 0, we can show the result by inspecting each case. By repeated use of this property, we have
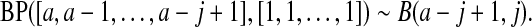 |
(2.1) |
3. Continuous failure with no grouping
3.1. Proposed confidence procedure
We define our procedure first without motivation; in later subsections, we motivate it under various censoring conditions. Throughout Section 3, we assume that the failure time for the ith individual is continuously distributed with random variable Xi and 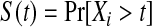 . Suppose that there are n total observations, and we observe the failure time exactly in
. Suppose that there are n total observations, and we observe the failure time exactly in 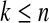 of those observations. Let the k observed failure times be
of those observations. Let the k observed failure times be 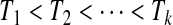 , and define
, and define 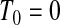 . Let
. Let 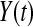 be the number at risk just before time t, and no more individuals are at risk after
be the number at risk just before time t, and no more individuals are at risk after 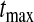 , and let
, and let
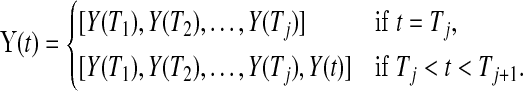 |
Similarly, define
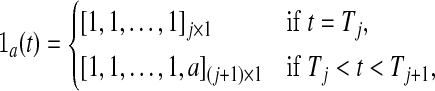 |
where 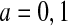 . Let
. Let 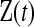 be all the data collected up until time t. We define the
be all the data collected up until time t. We define the 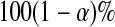 BPCP for
BPCP for 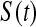 with
with 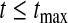 as
as
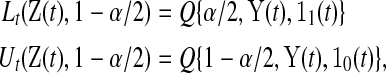 |
(3.1) |
and with 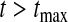 as
as 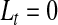 and
and 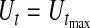 . Note that
. Note that 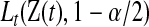 and
and 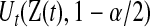 can each be separately interpreted as one-sided
can each be separately interpreted as one-sided 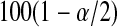 % confidence procedures.
% confidence procedures.
3.2. No censoring
We begin motivating and exploring the properties of the BPCP with the simplest case, when there are no censored observations and no tied event times. Suppose that we observe 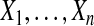 independent observations from the distribution
independent observations from the distribution 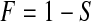 . Then, by the probability integral transformation (see, e.g. Casella and Berger, 2002, p. 54),
. Then, by the probability integral transformation (see, e.g. Casella and Berger, 2002, p. 54), 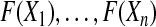 are uniformly distributed. Let
are uniformly distributed. Let 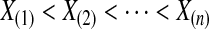 be the order statistics; then
be the order statistics; then 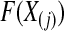 is the jth order statistic from a uniform distribution and is distributed
is the jth order statistic from a uniform distribution and is distributed 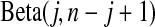 (see, e.g. Casella and Berger, 2002, p. 230). The associated survival distribution,
(see, e.g. Casella and Berger, 2002, p. 230). The associated survival distribution, 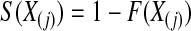 is distributed
is distributed 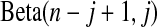 . With no censoring, (2.1) shows that B(n−j+1,j)∼BP{Y(Tj),1(Tj)},
. With no censoring, (2.1) shows that B(n−j+1,j)∼BP{Y(Tj),1(Tj)},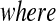 1(Tj) = 10(Tj) = 11(Tj). Thus, the BPCP uses quantiles of that distribution at the observed failures, and in between the observed failures the BPCP just acts conservatively (see Figure 2). A formal proof that the BPCP guarantees central coverage is given in Theorem 1, in which the no censoring setting is just a special case. Note that for t in the intervals between the death times, this confidence procedure is equivalent to performing the Clopper–Pearson interval for a binomial observation based on the fact that the number that survive past t is binomial with parameter
1(Tj) = 10(Tj) = 11(Tj). Thus, the BPCP uses quantiles of that distribution at the observed failures, and in between the observed failures the BPCP just acts conservatively (see Figure 2). A formal proof that the BPCP guarantees central coverage is given in Theorem 1, in which the no censoring setting is just a special case. Note that for t in the intervals between the death times, this confidence procedure is equivalent to performing the Clopper–Pearson interval for a binomial observation based on the fact that the number that survive past t is binomial with parameter 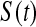 , and the Clopper–Pearson interval for
, and the Clopper–Pearson interval for 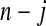 out of n is {Q(α/2,n−j,j+1),Q(1−α/2,n−j+1,j)} (see, e.g. Meeker and Escobar, 1998).
out of n is {Q(α/2,n−j,j+1),Q(1−α/2,n−j+1,j)} (see, e.g. Meeker and Escobar, 1998).
Figure 2.
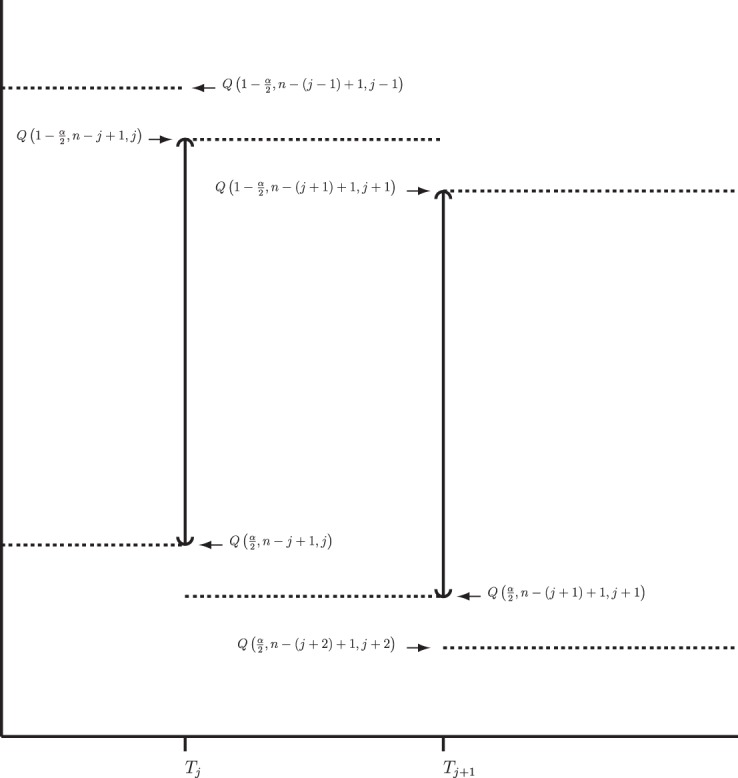
BPCP without censoring. Recall that 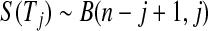 . Note that the upper limits use the
. Note that the upper limits use the 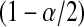 th quantile of
th quantile of 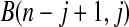 in
in 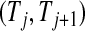 , while the lower limits use the
, while the lower limits use the 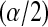 th quantile of
th quantile of 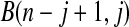 in
in 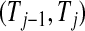 . For any
. For any 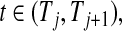 the CI is equivalent to the Clopper–Pearson interval for
the CI is equivalent to the Clopper–Pearson interval for 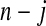 successes out of n trials with probability
successes out of n trials with probability  .
.
3.3. Progressive type II censoring
Now assume progressive type II censoring (see Kalbfleisch and Prentice [2002, p. 54]), and so immediately after each failure a fixed proportion of the remaining individuals are randomly selected to be censored. Under this censoring scheme, no censoring occurs before the first event time, and we know from Section 3.2 that the distribution of S(T1) = S(X(1))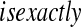 Beta(n,1)
Beta(n,1)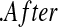 T1
T1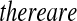 Y (T2) subjects at risk, and the conditional survival distribution, given survival after
Y (T2) subjects at risk, and the conditional survival distribution, given survival after 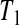 and
and 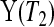 , can be shown to be
, can be shown to be 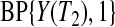 . Using this type of argument, we show formally in supplementary material available at Biostatistics online (Section A) that
. Using this type of argument, we show formally in supplementary material available at Biostatistics online (Section A) that
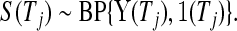 |
This motivates the following theorem.
Theorem 1 —
Under independent progressive type II censoring and assuming a continuous failure time distribution, the
BPCP given by (3.1) guarantees central coverage for
.
Proof —
For the proof, see supplementary material available at Biostatistics online (Section B).
3.4. Independent censoring
Now suppose that the censoring times are independent of the failure times, and allow censoring to happen at any time. Although we do not formally prove guaranteed central coverage of the BPCP under this scenario, we give some motivation to argue that the BPCP is a reasonable confidence procedure.
Consider first the lower BPCP confidence limit. Suppose that there are 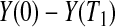 subjects censored before
subjects censored before 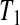 and that the observed censoring times before
and that the observed censoring times before 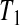 are T01<T02<⋯<T0k0
are T01<T02<⋯<T0k0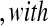 Y (T0j)−Y (T0,j+1)
Y (T0j)−Y (T0,j+1)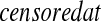 T0j
T0j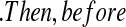 T01 we have
T01 we have 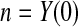 subjects at risk. Consider the lower CI for
subjects at risk. Consider the lower CI for 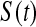 . For
. For 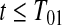 , we know that none of the n at-risk subjects had the event before
, we know that none of the n at-risk subjects had the event before 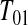 , and if a subject had an event at
, and if a subject had an event at 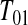 , then the lower interval would have been
, then the lower interval would have been 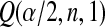 . We let the lower CI be as high as that value, suggesting that we conservatively retain coverage. For the next interval,
. We let the lower CI be as high as that value, suggesting that we conservatively retain coverage. For the next interval, 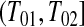 , imagine that
, imagine that 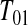 was actually
was actually 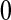 and
and 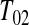 represented a failure time. Then from the previous section a lower CI for
represented a failure time. Then from the previous section a lower CI for 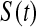 for
for 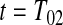 would be
would be 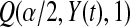 . Each of these modifications (
. Each of these modifications (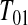 moving to zero and
moving to zero and 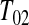 representing a failure) indicate a lower survival, so we treat
representing a failure) indicate a lower survival, so we treat 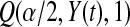 as a conservative lower limit. We continue with this reasoning for intervals up until
as a conservative lower limit. We continue with this reasoning for intervals up until 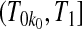 . At
. At 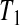 the lower limit matches the limit for the associated progressive type II case (i.e. matches the modification that moves all the censored observations before
the lower limit matches the limit for the associated progressive type II case (i.e. matches the modification that moves all the censored observations before 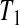 to
to 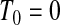 ). Continuing with this type of reasoning throughout the rest of the sample space suggests the one-sided guaranteed coverage of the lower BPCP.
). Continuing with this type of reasoning throughout the rest of the sample space suggests the one-sided guaranteed coverage of the lower BPCP.
Now consider the upper limit of the BPCP. The upper BPCP limit under independent censoring matches the upper limit progressive type II case (i.e. matches the case where all censoring times are moved to immediately following the previous failure time). This fact appears to suggest that the upper BPCP is too low, since knowing that the censoring times did in fact happen later than immediately after the last failure would suggest that the survival curve was larger in that interval. But (3.1) implies that the upper limit is constant between observed failure times, and it does not decrease between failures regardless of the censoring pattern between failures. Although we do not formally prove that the BPCP guarantees central coverage, we show in Theorem 2 the asymptotic equivalence of the BPCP to the usual normal theory confidence procedures, and hence the BPCP has correct coverage asymptotically.
The Nelson–Aalen estimator of the cumulative hazard, 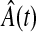 , and its variance estimate,
, and its variance estimate, 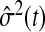 , are, respectively,
, are, respectively,
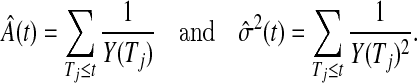 |
By asymptotic normality, a 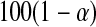 confidence procedure for the cumulative hazard is
confidence procedure for the cumulative hazard is 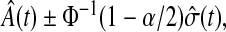 where
where 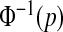 is the pth quantile of the standard normal distribution (see, e.g. Andersen and others, 1993). Since for continuous failure times
is the pth quantile of the standard normal distribution (see, e.g. Andersen and others, 1993). Since for continuous failure times 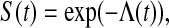 where
where 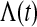 is the cumulative hazard, a confidence procedure for
is the cumulative hazard, a confidence procedure for 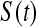 is
is
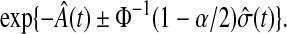 |
(3.2) |
Another asymptotically equivalent confidence procedure is to use the Kaplan–Meier survival estimator
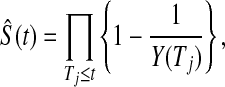 |
and the Greenwood formula for its variance (Kaplan and Meier, 1958),
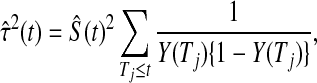 |
yielding the interval
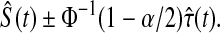 |
(3.3) |
Other asymptotically equivalent confidence procedures may be constructed using transformations and the delta method (see, e.g. Andersen and others, 1993). All of these confidence procedures are all known to give 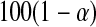 % central coverage asymptotically, so the following theorem shows that the asymptotic coverage of the BPCP approaches the nominal value.
% central coverage asymptotically, so the following theorem shows that the asymptotic coverage of the BPCP approaches the nominal value.
Theorem 2 —
Under independent censoring with continuous failure time where the censoring distribution is the same for all individuals and
for all
, where C represents the censoring random variable, the BPCP for
for
is asymptotically equivalent to the procedures given in (3.2) or (3.3).
Proof —
For the proof, see supplementary material available at Biostatistics online (Section C).
4. Handling ties via grouping
The continuity of the failure times is a vital condition for the motivation of the BPCPs, but ties in failure times are common with real data. Now we formally adjust the BPCP to allow for ties. The basic idea is simple: tied failures can be interpreted as grouped continuous failures, and grouping hides information about the continuous failure time, but we can extend the confidence procedures of (3.1) in a conservative way using the monotonicity of survival distributions.
Under grouping, we only observe the number who are still at risk and the number who were known to have failed at certain assessment times. For full generality, we define those assessment times as 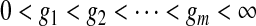 . We consider only conventional grouping for right-censored data, where if failure observations and censored observations occur in the same interval, the censored observations are assumed to occur after the failure observations in that interval. Since we still assume continuous survival, the probability that a failure time would occur exactly at some gj is
. We consider only conventional grouping for right-censored data, where if failure observations and censored observations occur in the same interval, the censored observations are assumed to occur after the failure observations in that interval. Since we still assume continuous survival, the probability that a failure time would occur exactly at some gj is 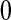 .
.
Let 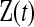 represent the information about survival or censoring as in Section 3, only now
represent the information about survival or censoring as in Section 3, only now 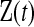 is unobserved. Let
is unobserved. Let 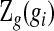 be the observed data up until time gi after grouping,
be the observed data up until time gi after grouping, 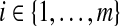 . Although not measured continuously, it is convenient to use
. Although not measured continuously, it is convenient to use 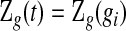 for
for 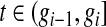 , with
, with 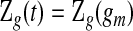 for
for 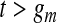 . Let
. Let 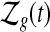 be the set of all
be the set of all 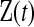 that are consistent with
that are consistent with 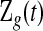 under conventional grouping. Then we extend the BPCP to grouped data. Define the
under conventional grouping. Then we extend the BPCP to grouped data. Define the 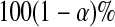 BPCP for
BPCP for 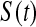 applied to grouped data as
applied to grouped data as
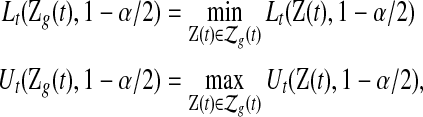 |
(4.1) |
where 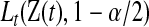 and
and 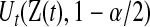 are given in (3.1). Equivalently, for
are given in (3.1). Equivalently, for 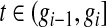 with
with 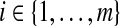 ,
,
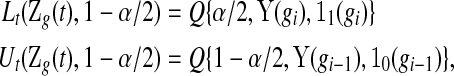 |
(4.2) |
and, for 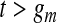 ,
, 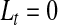 and
and 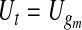 . Expression (4.2) is more straightforward for implementation and is motivated by the monotonicity of both the upper and lower limits of the continuous BPCP. Expression (4.1) clearly shows that if a BPCP under continuity guarantees coverage, then it will continue to guarantee coverage under conventional grouping. If there are intervals with more than one failure, then since we assume all censoring in an interval happens at the end, the beta product vectors may be collapsed using (2.1); see supplementary material available at Biostatistics online (Section D).
. Expression (4.2) is more straightforward for implementation and is motivated by the monotonicity of both the upper and lower limits of the continuous BPCP. Expression (4.1) clearly shows that if a BPCP under continuity guarantees coverage, then it will continue to guarantee coverage under conventional grouping. If there are intervals with more than one failure, then since we assume all censoring in an interval happens at the end, the beta product vectors may be collapsed using (2.1); see supplementary material available at Biostatistics online (Section D).
5. Estimation of the beta product quantiles
The calculation of 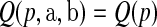 used in the definition of the BPCP is not straightforward (Johnson and others, 1995), so we propose two implementations: the Monte Carlo implementation of the BPCP (
used in the definition of the BPCP is not straightforward (Johnson and others, 1995), so we propose two implementations: the Monte Carlo implementation of the BPCP (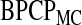 ) and the method of moments implementation of the BPCP (
) and the method of moments implementation of the BPCP (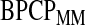 ). To estimate
). To estimate 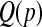 in
in 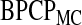 , we take m Monte Carlo replicates, where the ith replicate is
, we take m Monte Carlo replicates, where the ith replicate is 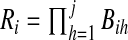 with
with 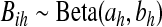 . Then we estimate
. Then we estimate 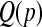 with the empirical quantile of the m Monte Carlo Ri values.
with the empirical quantile of the m Monte Carlo Ri values.
For the method of moments implementation, we estimate 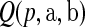 with the pth quantile of a beta distribution with the same mean and variance as
with the pth quantile of a beta distribution with the same mean and variance as 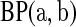 . In particular, when no
. In particular, when no 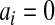 and no
and no 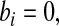 we use the pth quantile of a beta distribution with parameters
we use the pth quantile of a beta distribution with parameters 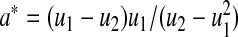 and
and 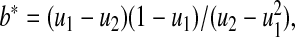 where
where 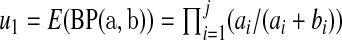 and
and 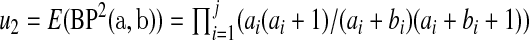 . Fan (1991) has shown that this method works fairly well by comparing the first 10 moments of this beta distribution to the first 10 moments of the true distribution of
. Fan (1991) has shown that this method works fairly well by comparing the first 10 moments of this beta distribution to the first 10 moments of the true distribution of 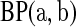 for several examples. Modification of the method to cases with
for several examples. Modification of the method to cases with 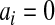 or
or 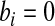 is straightforward.
is straightforward.
06. Extensions
6.1. Confidence procedures on quantiles
Once we have a CI procedure for 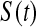 for any t, say
for any t, say 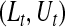 , we can invert that procedure to provide CIs for quantiles (Barber and Jennison, 1999). A
, we can invert that procedure to provide CIs for quantiles (Barber and Jennison, 1999). A 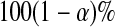 CI for
CI for 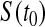 can represent a test of
can represent a test of 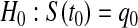 , where we fail to reject the null hypothesis if
, where we fail to reject the null hypothesis if 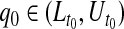 . For most of this paper we have fixed
. For most of this paper we have fixed 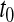 , but we could alternatively have fixed
, but we could alternatively have fixed  . Since
. Since 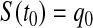 and
and 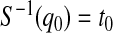 are equivalent, a
are equivalent, a 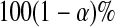 confidence procedure for
confidence procedure for 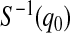 is the set of all t for which
is the set of all t for which 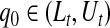 .
.
6.2. MUE of survival
Because we have a confidence procedure that is defined for all confidence levels, we can create an MUE of the survival from the confidence procedure (Read, 1985). Specifically, the MUE of 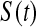 is motivated by letting
is motivated by letting 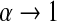 , and is defined as
, and is defined as
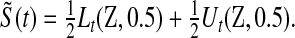 |
We performed a simple simulation. Let 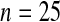 and suppose that the failure times are distributed exponentially with mean 1 and the censoring times are distributed uniformly on
and suppose that the failure times are distributed exponentially with mean 1 and the censoring times are distributed uniformly on 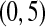 . We simulated this
. We simulated this 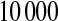 times. Because the Kaplan–Meier is not defined after the largest observation if it is censored, we define it in three ways after the last observation: KML defines it as 0, KMH defines it as the Kaplan–Meier at the last value, and KMM = 0.5*KML+0.5*KMH. The simulated mean squared error (MSE) for
times. Because the Kaplan–Meier is not defined after the largest observation if it is censored, we define it in three ways after the last observation: KML defines it as 0, KMH defines it as the Kaplan–Meier at the last value, and KMM = 0.5*KML+0.5*KMH. The simulated mean squared error (MSE) for 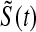 was between
was between 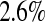 and
and 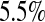 less than the MSE for all three Kaplan–Meier methods for values not at the extremes (when
less than the MSE for all three Kaplan–Meier methods for values not at the extremes (when 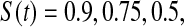 or
or 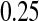 ), and was between
), and was between 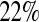 and
and 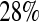 less than the Kaplan–Meier methods at
less than the Kaplan–Meier methods at 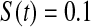 ; however, the MSE for
; however, the MSE for 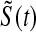 at
at 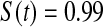 was higher than the three Kaplan–Meier estimators, and at
was higher than the three Kaplan–Meier estimators, and at 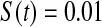 was higher than KML and KMM. Simulated MSE details are in supplementary material available at Biostatistics online (Section E).
was higher than KML and KMM. Simulated MSE details are in supplementary material available at Biostatistics online (Section E).
To gain intuition for this result, we examine the case of no censoring. Let t∈(X(j),X(j+1)) t is
t is 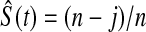 . The survival estimator that is the best invariant one for monotonic transformations under the squared error loss function is
. The survival estimator that is the best invariant one for monotonic transformations under the squared error loss function is 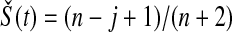 , which pulls the Kaplan–Meier estimator toward
, which pulls the Kaplan–Meier estimator toward 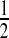 (see, e.g. Ferguson, 1967, Section 4.8). Our MUE is
(see, e.g. Ferguson, 1967, Section 4.8). Our MUE is
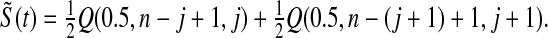 |
For large n, the beta distribution approaches the normal distribution and the median approaches the mean, so our MUE is approximately
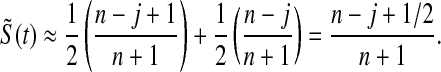 |
In other words, it is approximately halfway between 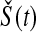 and the Kaplan–Meier estimator
and the Kaplan–Meier estimator 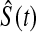 . For small
. For small 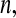 we would expect our estimator to be between those two estimators, and hence
we would expect our estimator to be between those two estimators, and hence 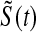 extends this appealing shrinkage to censored data (see also Borkowf, 2005, on shrinkage estimators for Kaplan–Meier).
extends this appealing shrinkage to censored data (see also Borkowf, 2005, on shrinkage estimators for Kaplan–Meier).
For situations with extreme censoring toward the end of follow-up with few additional failures (see, e.g. Figure 3), the MUE will decrease substantially over time, implying that there is real information about a survival decrease at those time points, when in fact the MUE decrease may be caused only by the lack of confidence in the estimator. However, the MUE can be appealing in the middle part of the survival curve as shown by our simulation.
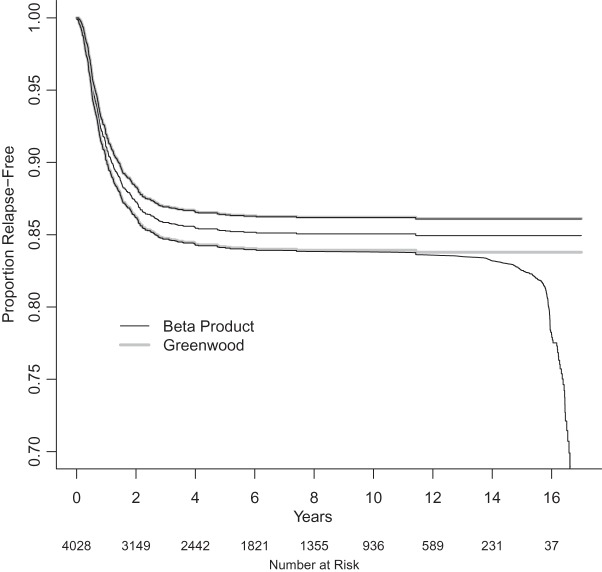
Figure 3.
National Wilms Tumor Study Group, third and fourth clinical trials (Breslow and Chatterjee, 1999). The black middle curve is the Kaplan–Meier estimator for time to relapse for the 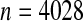 children included in the dataset in the R survival package (Therneau, 2012). Thick gray lines are standard CIs (Greenwood variance using log transformation) and the black CIs are the BPCP intervals.
children included in the dataset in the R survival package (Therneau, 2012). Thick gray lines are standard CIs (Greenwood variance using log transformation) and the black CIs are the BPCP intervals.
7. Simulations
We conducted a simulation study to evaluate coverage of the BPCP compared with competing methods under a range of scenarios. For this simulation, we studied both BPCPMM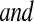 BPCPMC
BPCPMC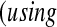 100 000 Monte Carlo samples). The competing asymptotic methods were as follows: Greenwood
100 000 Monte Carlo samples). The competing asymptotic methods were as follows: Greenwood  log
log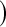 , Greenwood variance assuming normality on
, Greenwood variance assuming normality on 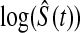 (default in Therneau (2012)); Modified GW
(default in Therneau (2012)); Modified GW  log
log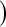 , same as previous but for the lower limit multiply the variance at t by a factor of
, same as previous but for the lower limit multiply the variance at t by a factor of 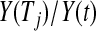 , where Tj is the largest observed survival less than or equal to t (Therneau, 2012, conf. lower option); Borkowf
, where Tj is the largest observed survival less than or equal to t (Therneau, 2012, conf. lower option); Borkowf  log
log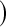 , a different modification that also gives wider intervals with more censoring and assumes normality on
, a different modification that also gives wider intervals with more censoring and assumes normality on 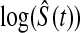 (Borkowf, 2005); Borkowf
(Borkowf, 2005); Borkowf  log,shrink
log,shrink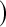 , which uses a shrinkage estimator of the Kaplan–Meier estimator with a hybrid variance estimator (Borkowf, 2005); Strawderman–Wells (see Strawderman and others, 1997, Equation (9)), an Edgeworth expansion method; Thomas–Grunkemeier (Thomas and Grunkemeier, 1975), an empirical likelihood ratio method; Constrained Beta (Barber and Jennison, 1999); Bootstrap, a non-parametric bootstrap method (Efron, 1981; Akritas, 1986); and Constrained Bootstrap (Barber and Jennison, 1999), where the last two methods use 1000 bootstrap samples. Finally, we also considered the inefficient binomial approach which guarantees coverage, but only includes individuals whose censoring times are known to be greater than or equal to the test time (
, which uses a shrinkage estimator of the Kaplan–Meier estimator with a hybrid variance estimator (Borkowf, 2005); Strawderman–Wells (see Strawderman and others, 1997, Equation (9)), an Edgeworth expansion method; Thomas–Grunkemeier (Thomas and Grunkemeier, 1975), an empirical likelihood ratio method; Constrained Beta (Barber and Jennison, 1999); Bootstrap, a non-parametric bootstrap method (Efron, 1981; Akritas, 1986); and Constrained Bootstrap (Barber and Jennison, 1999), where the last two methods use 1000 bootstrap samples. Finally, we also considered the inefficient binomial approach which guarantees coverage, but only includes individuals whose censoring times are known to be greater than or equal to the test time (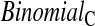 ). Unlike the other methods,
). Unlike the other methods, 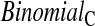 requires knowledge of the censoring times even for individuals with observed failures. However, there are real-life situations where this information would be available. For example, consider a staggered entry trial where all censoring occurs at the end of the trial and we wish to test at four years. To use the
requires knowledge of the censoring times even for individuals with observed failures. However, there are real-life situations where this information would be available. For example, consider a staggered entry trial where all censoring occurs at the end of the trial and we wish to test at four years. To use the 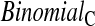 method, we only include patients who began the trial at least 4 years prior to the end, so that censored observations will not be included nor will failures for patients enrolled after 4 years prior to the end. Because all the methods have asymmetric coverage, instead of presenting results in terms of coverage, we present rejection rates for both one-sided tests.
method, we only include patients who began the trial at least 4 years prior to the end, so that censored observations will not be included nor will failures for patients enrolled after 4 years prior to the end. Because all the methods have asymmetric coverage, instead of presenting results in terms of coverage, we present rejection rates for both one-sided tests.
We first simulated the size of the tests. We let 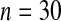 subjects, where the failure times are exponential with a mean of 10 and the independent censoring times are uniform on 0–5. We ran 100 000 replications. We tested at times 1–4 and, for each time, list the survival, the simulated average number of observed failures (which we write as
subjects, where the failure times are exponential with a mean of 10 and the independent censoring times are uniform on 0–5. We ran 100 000 replications. We tested at times 1–4 and, for each time, list the survival, the simulated average number of observed failures (which we write as 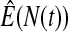 ), and the simulated number at risk (
), and the simulated number at risk (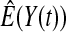 ). The simulation results are given in Table 1 as the percent error on each side of the 95% CI, so guaranteed central coverage would have
). The simulation results are given in Table 1 as the percent error on each side of the 95% CI, so guaranteed central coverage would have 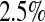 or less. Overall, we see that the asymptotic methods (the first nine rows) have some situations where the lower limit is too high, giving error rates larger than 2.5%. At
or less. Overall, we see that the asymptotic methods (the first nine rows) have some situations where the lower limit is too high, giving error rates larger than 2.5%. At 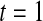 when there are few observed failures, seven of the asymptotic methods have 6.7% error rates for the lower bound. Note the Greenwood
when there are few observed failures, seven of the asymptotic methods have 6.7% error rates for the lower bound. Note the Greenwood  log
log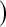 has up to 11.2% simulated lower error rates. Among the asymptotic methods, the Constrained Bootstrap is best (and most computationally time consuming), but it still has a case where the error rate is about twice what it should be (at
has up to 11.2% simulated lower error rates. Among the asymptotic methods, the Constrained Bootstrap is best (and most computationally time consuming), but it still has a case where the error rate is about twice what it should be (at  the simulated lower error rate is
the simulated lower error rate is 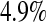 ). None of the upper limits appear much higher than 2.5%. Some of the methods which can have much larger upper intervals than the BCPC (see Figure 1), have much lower simulated size on the high end than the BPCP. Importantly, the BPCP and
). None of the upper limits appear much higher than 2.5%. Some of the methods which can have much larger upper intervals than the BCPC (see Figure 1), have much lower simulated size on the high end than the BPCP. Importantly, the BPCP and 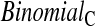 methods are the only ones that retain the proper coverage for both sides.
methods are the only ones that retain the proper coverage for both sides.
Table 1.
Simulated size 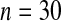 with
with 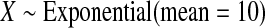 and
and 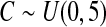
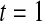 |
 |
 |
 |
|||||
|---|---|---|---|---|---|---|---|---|
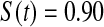 |
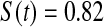 |
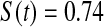 |
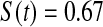 |
|||||
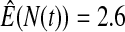 |
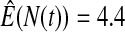 |
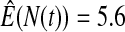 |
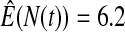 |
|||||
 |
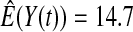 |
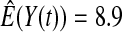 |
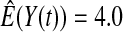 |
|||||
| Low | High | Low | High | Low | High | Low | High | |
Greenwood  log log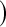
|
6.7 | 0.2 | 10.0 | 0.3 | 9.3 | 0.2 | 11.2 | 0.1 |
| Modified lower | 6.7 | 0.2 | 7.3 | 0.3 | 5.6 | 0.2 | 3.7 | 0.1 |
Borkowf  log log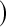
|
6.7 | 0.1 | 6.8 | 0.2 | 5.3 | 0.2 | 3.9 | 0.0 |
Borkowf  log log shrink shrink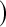
|
6.7 | 0.2 | 4.7 | 0.2 | 3.7 | 0.2 | 2.8 | 0.0 |
| Strawderman–Wells | 6.7 | 2.6 | 4.1 | 2.0 | 4.6 | 1.8 | 6.5 | 1.4 |
| Thomas–Grunkemeier | 6.7 | 2.1 | 3.8 | 2.3 | 4.1 | 2.4 | 5.6 | 2.4 |
| Constrained Beta | 0.0 | 1.4 | 3.6 | 1.9 | 4.6 | 2.1 | 6.0 | 2.5 |
| Bootstrap | 6.7 | 1.2 | 6.4 | 1.3 | 6.2 | 1.5 | 7.5 | 1.3 |
| Constrained Bootstrap | 0.0 | 2.7 | 2.2 | 2.4 | 3.2 | 2.3 | 4.9 | 1.9 |
Binomial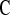
|
0.0 | 1.4 | 0.7 | 1.4 | 0.5 | 1.4 | 0.1 | 1.0 |
| BPCP (MM) | 0.0 | 1.3 | 0.3 | 1.4 | 0.1 | 1.3 | 0.0 | 1.1 |
| BPCP (MC) | 0.0 | 1.3 | 0.3 | 1.4 | 0.1 | 1.5 | 0.0 | 1.3 |
Simulation had 100 000 replications. Percent error on each side of 95% interval (nominal is 2.5%).
We repeated simulations using a mixture of exponentials to mimic the Nash and others (2007) data (see Section 8.1), and the results were similar although slightly less extreme (the maximum lower error rates for the asymptotic methods ranged from 3.8% to 7.0%); see supplementary material available at Biostatistics online (Section F). The problems with a type I error rate are more severe in the exponential simulation than in the mixture of exponentials. This is presumably because the model based on the Nash and others (2007) data has a flatter survival curve during the time when there is much censoring, so that failure to address the censoring between events is less critical than for the simple exponential model.
Since both the BPCP methods and the 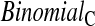 method have proper simulated coverage for both sides, we compare them by checking the power (i.e. testing null hypotheses that are different from the true values). We used the same simulation set-up as in Table 1, except that we test two different false null hypotheses for each time point t, the null that
method have proper simulated coverage for both sides, we compare them by checking the power (i.e. testing null hypotheses that are different from the true values). We used the same simulation set-up as in Table 1, except that we test two different false null hypotheses for each time point t, the null that 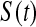 is exponential with mean equal to either 2.5 (lower than the truth) or 100 (higher than the truth). In Table 2, we give the percent rejection rates for the three methods that have at least proper coverage. The results exhibited in Table 2 show that the BPCP typically has better power than
is exponential with mean equal to either 2.5 (lower than the truth) or 100 (higher than the truth). In Table 2, we give the percent rejection rates for the three methods that have at least proper coverage. The results exhibited in Table 2 show that the BPCP typically has better power than 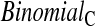 , and, not surprisingly, this advantage improves as censoring increases. We note that when the first year survival is tested against
, and, not surprisingly, this advantage improves as censoring increases. We note that when the first year survival is tested against 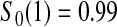 , the binomial has superior power to BPCP methods. This may be a function of luck and due to the fact that the power for exact binomial tests is not monotonically increasing in the sample size due to the discreteness of the tests (see, e.g. Chan and Bohidar, 1998, Table II). Typically, the BPCP methods will have larger power since they will use more of the data.
, the binomial has superior power to BPCP methods. This may be a function of luck and due to the fact that the power for exact binomial tests is not monotonically increasing in the sample size due to the discreteness of the tests (see, e.g. Chan and Bohidar, 1998, Table II). Typically, the BPCP methods will have larger power since they will use more of the data.
Table 2.
Simulated power
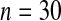 with
with 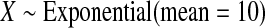 and
and 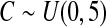
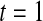 |
 |
 |
 |
|||||
|---|---|---|---|---|---|---|---|---|
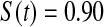 |
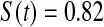 |
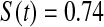 |
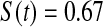 |
|||||
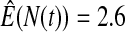 |
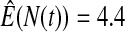 |
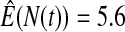 |
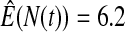 |
|||||
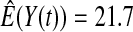 |
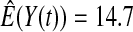 |
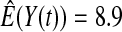 |
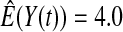 |
|||||
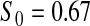 |
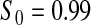 |
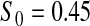 |
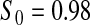 |
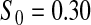 |
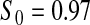 |
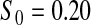 |
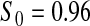 |
|
Binomial
|
73.0 | 56.5 | 86.4 | 65.5 | 81.1 | 64.3 | 53.4 | 49.3 |
| BPCP (MM) | 76.3 | 50.9 | 92.5 | 83.8 | 90.4 | 87.0 | 65.9 | 90.3 |
| BPCP (MC) | 76.1 | 51.6 | 92.2 | 83.7 | 89.2 | 88.0 | 60.6 | 90.9 |
Percent rejected for testing H0 : S(t) = S0(t) = S0.
Finally, note that in both simulation tables the BPCP (MM) and the BPCP (MC) methods generally match quite well. Thus, the MM implementation can be recommended for routine use since it is much faster computationally.
8. Applications
8.1. Pilot study of treatment in severe systemic sclerosis
Between 1997 and 2005, a cohort of 34 patients with severe systemic sclerosis was enrolled in a single-arm pilot study of high-dose immunosuppressive therapy and autologous hetapoietic cell transplantation (Nash and others, 2007). The entry criteria were such that the expected 5-year mortality rate with conventional treatment would be about 0.50. The median follow-up for this study was 4 years.
Figure 1 presents the Kaplan–Meier estimator for all-cause mortality in this cohort, along with pointwise 95% CIs using 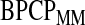 , as well as some of the competing methods. Since the patient population was selected to have approximately 0.50 mortality rate at 5 years with conventional therapy, it would be natural to assess how the results at the same time point with this alternate regimen compare. The survival estimate in the new cohort at 5 years is 0.636, suggesting an improved survival. Nonetheless, all methods include 0.50 in their 5-year 95% CIs, and the BP CI
, as well as some of the competing methods. Since the patient population was selected to have approximately 0.50 mortality rate at 5 years with conventional therapy, it would be natural to assess how the results at the same time point with this alternate regimen compare. The survival estimate in the new cohort at 5 years is 0.636, suggesting an improved survival. Nonetheless, all methods include 0.50 in their 5-year 95% CIs, and the BP CI 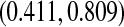 has the lowest lower bound of all the methods. The methods are relatively similar at the 5-year point since there was a death just prior at 4.93 years. The methods are especially divergent at 6.3 years, a point where most patients who were at risk at the prior death have now been censored, so there are only four patients remaining at risk; at this time, the BP CI is
has the lowest lower bound of all the methods. The methods are relatively similar at the 5-year point since there was a death just prior at 4.93 years. The methods are especially divergent at 6.3 years, a point where most patients who were at risk at the prior death have now been censored, so there are only four patients remaining at risk; at this time, the BP CI is 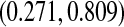 , whereas the Greenwood is
, whereas the Greenwood is 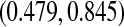 . We know from simulations that only the BPCP is likely to have proper coverage (see, e.g. Table 1). We also note that there is no censoring during the first 2 years, and at any point in that time period the BPCP is a Clopper–Pearson interval. Across time, the upper bound of the BP CI is the lowest of all methods except Strawderman–Wells and Thomas–Grunkemeier, and the lower bound of the BPCP is the lowest throughout.
. We know from simulations that only the BPCP is likely to have proper coverage (see, e.g. Table 1). We also note that there is no censoring during the first 2 years, and at any point in that time period the BPCP is a Clopper–Pearson interval. Across time, the upper bound of the BP CI is the lowest of all methods except Strawderman–Wells and Thomas–Grunkemeier, and the lower bound of the BPCP is the lowest throughout.
As shown in simulations, unlike competing methods, our procedure would allow us to test whether the survival at 5 years is greater than 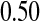 with the type I error rate less than or equal to
with the type I error rate less than or equal to 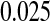 . If we had used the Greenwood CI or other competing CIs, we would not have been assured control of the type I error rate at
. If we had used the Greenwood CI or other competing CIs, we would not have been assured control of the type I error rate at 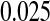 .
.
The median survival time estimated by Kaplan–Meier is 6.35 years and the BPCP 95% CI on the median is 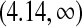 . The upper limit is infinity because there is no value of t for which Ut<0.5.
. The upper limit is infinity because there is no value of t for which Ut<0.5.
8.2. National Wilms Tumor Study
To emphasize that the differences in the 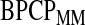 and the Greenwood (log) method are slight when the sample size is large, we plot in Figure 3 the Kaplan–Meier estimator with the two types of CIs for 4028 children in the third and fourth clinical trials of the National Wilms Tumor Study Group (Breslow and Chatterjee, 1999; Therneau, 2012). The event is time until relapse and there were 571 who relapsed, but only 1 who relapsed after 10 years. We see that the two types of CIs match well early in the study when there are a large number of individuals at risk, but at the end of the follow-up, when there are fewer individuals still at risk, we see the substantial differences between the methods. This application points to an undesirable aspect of the MUE as discussed at the end of Section 6.2.
and the Greenwood (log) method are slight when the sample size is large, we plot in Figure 3 the Kaplan–Meier estimator with the two types of CIs for 4028 children in the third and fourth clinical trials of the National Wilms Tumor Study Group (Breslow and Chatterjee, 1999; Therneau, 2012). The event is time until relapse and there were 571 who relapsed, but only 1 who relapsed after 10 years. We see that the two types of CIs match well early in the study when there are a large number of individuals at risk, but at the end of the follow-up, when there are fewer individuals still at risk, we see the substantial differences between the methods. This application points to an undesirable aspect of the MUE as discussed at the end of Section 6.2.
9. Discussion
We have proposed a pointwise CI for right-censored data, and have shown that it guarantees central coverage when the data are uncensored or censored with Progressive Type II censoring. For independent censoring, we have shown that our BPCP is asymptotically correct, and simulations have shown that it maintains proper coverage. The BPCP for survival can be inverted to get CIs for quantiles of the survival distribution, and the good coverage properties of the BPCP for survival are expected to carry over to its inversion as well. The calculations needed to do the BPCP (method of moments implementation) are straightforward and can be done quickly using the bpcp R package. The full range of CIs for the National Wilms Tumor Study  of Figure 3 took less than a second to calculate on a standard PC (1.8 GHz, 3.25 GB RAM).
of Figure 3 took less than a second to calculate on a standard PC (1.8 GHz, 3.25 GB RAM).
The BPCP offers protection in settings where other methods fail, and it essentially matches the other methods when they succeed. Thus, we believe BPCP should be the preferred method for constructing pointwise CIs for the Kaplan–Meier curve.
10. Software
An R package called bpcp is available online at http://cran.r-project.org. The package includes software and documentation to calculate the BPCP methods and most of the competing methods.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Acknowledgements
We thank Dr John Hyde for sparking our interest in this topic and Dr Richard Nash for granting us permission to use the data from the severe systemic sclerosis pilot trial. The simulations were run using the Biowulf Linux cluster at the National Institutes of Health, Bethesda, MD (http://biowulf.nih.gov). Conflict of Interest: None declared.
References
- Akritas M. G. Bootstrapping the Kaplan–Meier estimator. Journal of the American Statistical Association. 1986;81:1032–1038. [Google Scholar]
- Andersen P. K., Borgan O., Gill R. D., Keiding N. Statistical Models Based on Counting Processes. New York: Springer; 1993. [Google Scholar]
- Barber S., Jennison C. Symmetric tests and confidence intervals for survival probabilities and quantiles of censored survival data. Biometrics. 1999;55:430–436. doi: 10.1111/j.0006-341x.1999.00430.x. [DOI] [PubMed] [Google Scholar]
- Borkowf C. B. A simple hybrid variance estimator for the Kaplan–Meier survival function. Statistics in Medicine. 2005;24:827–851. doi: 10.1002/sim.1960. [DOI] [PubMed] [Google Scholar]
- Breslow N. E., Chatterjee N. Design and analysis of two-phase studies with binary outcome applied to Wilms tumour prognosis. Journal of the Royal Statistical Society. 1999;48:457–468. [Google Scholar]
- Casella G., Berger R. L. Statistical Inference. 2nd edition. Pacific Grove, CA: Duxbury Press; 2002. [Google Scholar]
- Chan I. S. F., Bohidar N. R. Exact power and sample size for vaccine efficacy studies. Communications in Statistics-Theory and Methods. 1998;27:1305–1322. [Google Scholar]
- Dorey F. J., Korn E. L. Effective sample sizes for confidence intervals for survival probabilities. Statistics in Medicine. 1987;6:679–687. doi: 10.1002/sim.4780060605. [DOI] [PubMed] [Google Scholar]
- Efron B. Censored data and the bootstrap. Journal of the American Statistical Association. 1981;76:312–319. [Google Scholar]
- Fan D. Y. The distribution of the product of independent beta variables. Communications in Statistics-Theory and Methods. 1991;20:4043–4052. [Google Scholar]
- Ferguson T. S. Mathematical Statistics, A Decision Theoretic Approach. New York: Academic Press; 1967. [Google Scholar]
- Guilbaud O. Exact non-parametric confidence intervals for quantiles with progressive type-ii censoring. Scandinavian Journal of Statistics. 2001;28:699–713. [Google Scholar]
- Johnson N. L., Kotz S., Balakrishnan N., editors. Volume 2. New York: John Wiley & Sons; 1995. Continuous Univariate Distributions. [Google Scholar]
- Kalbfleisch J. D., Prentice R. L. The Statistical Analysis of Failure Time Data. 2nd edition. New York: John Wiley & Sons; 2002. [Google Scholar]
- Kaplan E. L., Meier P. Nonparametric estimation from incomplete observations. Journal of the American Statistical Association. 1958;53:457–481. [Google Scholar]
- Meeker W. Q., Escobar L. A. Statistical Methods for Reliability Data. New York: John Wiley & Sons; 1998. [Google Scholar]
- Nash R. A., McSweeney P. A., Crofford L. J., Abidi M., Chen C. S., Godwin J. D., Gooley T. A., Holmberg L., Henstorf G., LeMaistre C. F. High-dose immunosuppressive therapy and autologous hematopoietic cell transplantation for severe systemic sclerosis: long-term follow-up of the us multicenter pilot study. Blood. 2007;110:1388. doi: 10.1182/blood-2007-02-072389. others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peto R., Pike M. C., Armitage P., Breslow N. E., Cox D. R., Howard S. V., Mantel N., McPherson K., Peto J., Smith P. G. Design and analysis of randomized clinical trials requiring prolonged observation of each patient. ii. analysis and examples. British Journal of Cancer. 1977;35(1):1. doi: 10.1038/bjc.1977.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Read C. B. Median unbiased estimators. Encyclopedia of Statistical Sciences. 1985;5:424–426. [Google Scholar]
- SAS. SAS/STAT 9.3 User’s Guide, Proc LIFETEST. Cary, NC: SAS; 2011. [Google Scholar]
- Strawderman R. L., Parzen M. I., Wells M. T. Accurate confidence limits for quantiles under random censoring. Biometrics. 1997;53:1399–1415. [PubMed] [Google Scholar]
- Therneau T. 2012. A Package for Survival Analysis in S. R package version 2.36-12. http://CRAN.R-project.org/package=survival .
- Thomas D. R., Grunkemeier G. L. Confidence interval estimation of survival probabilities for censored data. Journal of the American Statistical Association. 1975;70:865–871. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.