A state-space model of the burst suppression ratio

Abstract

Burst suppression is an electroencephalogram pattern observed in states of severely reduced brain activity, such as general anesthesia, hypothermia and anoxic brain injuries. The burst suppression ratio (BSR), defined as the fraction of EEG spent in suppression per epoch, is the standard quantitative measure used to characterize burst suppression. We present a state space model to compute a dynamic estimate of the BSR as the instantaneous probability of suppression. We estimate the model using an approximate EM algorithm and illustrate its application in the analysis of rodent burst suppression recordings under general anesthesia. Our approach removes the need to artificially average the ratio over long epochs and allows us to make formal statistical comparisons of burst activity at different time points. Our state-space model suggests a more principled way to analyze this key EEG feature that may offer more informative assessments of its associated brain state.

I. Introduction

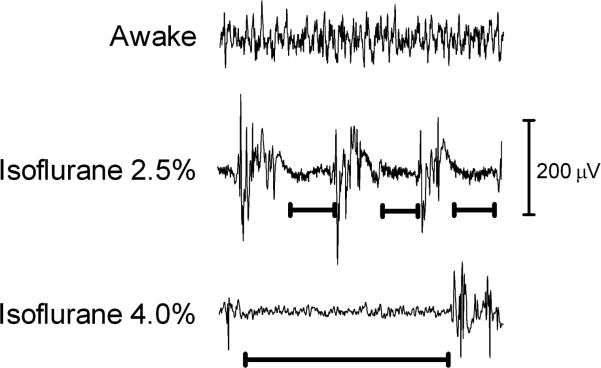
Burst suppression is an electroencephalogram (EEG) pattern consisting of alternating high amplitude bursts and low amplitude or isoelectric periods (see Fig.1). Burst suppression can be observed in deep state of general anesthesia, coma associated with diffuse brain injuries, induced hypothermia, epilepsy due to Ohtahara's syndrome [1], and postasphyctic newborn babies [2]. It is usually caused by physical damage (e.g brain injury, lesions), or reversible general anesthetic effects. In burst suppression less than 5% of the cortical neurons and less than 40% of the thalamic neurons are active during suppression [3].

Fig. 1.

The EEG signals of a rat, awake, under 2.5% and 4 % Isoflurane.

Burst suppression patterns (BSPs) differ in the durations of the alternating periods. For instance, in the case of subacute sclerosing panencephalitis, the duration between bursts tends to shorten with the progression of the disease [4]. In the case of general anesthesia, BSPs produced by different anesthetics show clear differences [5]. The burst suppression ratio (BSR), a measure of the fraction of time spent in suppression per epoch is traditionally used to characterize BSPs. The conventions for computing BSR are chosen empirically. The voltage threshold, which discriminates between low and high amplitude can be set at 15 [6]-[8] or at 5 [9]-[11] μV , and the minimal suppression time that the EEG has to be isoelecric is set at 100 milliseconds in some cases [6]-[8] and 0.5 seconds in others [9]-[11]. Likewise, the length of the epoch over which the fraction of suppression is computed can take values from 4 [9]-[11] to 15 [6]-[8] seconds. Finally the number of epochs that is averaged is typically chosen to span 60 seconds [6]-[11] resulting in only one data point per minute. The ease of computation and its real-time application make this method appealing. However, it offers a coarse characterization of the EEG pattern and limits the information extracted from the data sets. For instance, when analyzing the modulation of the BSP caused by certain drugs and inferring from it the anesthetic state of the brain, important dynamics taking place over several seconds can be hidden by averaging. This approach artificially segments the EEG signal into epochs and averages sequences whereas the signal is continuous and changes dynamically. Also, because different conventions are used to estimate the BSR, comparing results across studies is challenging [12]. The need for a more precise definition of BSR is thus motivated by the interest in inferring the dynamics of brain states from the relevant variations in BSPs. A more rigorous definition also facilitates achieving consistency between results across different studies, opening the door for insightful comparisons.

The BSP can be described by a series of 1s (suppression) and 0s (no suppression). This definition casts the problem in a dynamic Bernoulli process framework. Therefore, we can analyze it using a state-space model to characterize the burst suppression ratio as the probability of suppression as a function of time. A Bernoulli probability model is used to describe the suppression occurrences and a Gaussian state equation describes the unobservable brain state whose evolution we want to track. We estimate the model using an approximate expectation maximization (EM) algorithm [13][14], and compute the dynamic estimate of the BSR. We illustrate our method by computing the BSR before and after the administration of the cholinergic agonist physostigmine. We show how our approach may be used to conduct formal statistical analyses of the BSR.

II. Model Definition

A state space model is completely characterized by two equations: a state equation and an observation equation. The state equation defines the unobservable state process whose evolution we wish to track over time. The state in our case represents the brain state of the subject. We define our state to be positively correlated with the BSR. That is as the state increases the BSR increases and as the state decreases the BSR decreases. The observation equation describes how the observed data are related to the unobservable state. In our case, the observed data are the sequence of 1s and 0s which represent the suppression or not of a burst respectively. We define a burst suppression to be a sequence of low amplitude EEG voltages over at least a 100 milliseconds. Our objective is thus to estimate the states and the parameters of the model from the observed data and use these estimates to compute the dynamic estimate of the BSR with confidence intervals. Our experiment consists of N discrete time steps indexed 1, ..., N. Let b_i be the indicator of the event at time i which is 1 if the event is suppressed and 0 otherwise. Let p_i denote the probability of a suppression at time i. In our state space model we assume that the probability p_i is governed by an unobservable state variable x_i. The observation model can be described by the Bernoulli probability mass function

$$Pr(b_i\mid p_i,x_i)=p_i^{b_i}{(1-p_i)}^{1-b_i},$$ (1)

where p_i is defined by the logistic equation

$$p_i=\frac{exp\left(x_i\right)}{1+exp\left(x_i\right)}.$$ (2)

The logistic function is commonly used to model how the probability of an event is affected by one or many explanatory variables. In our case it ensures that the probability p_i is always between 0 and 1 as the state x_i varies over all real numbers. We define the unobserved state model by a random walk

$$x_i=x_{i-1}+{∊}_i,$$ (3)

where the ε_i are independent Gaussian random variables with mean 0 and variance σ². This definition of the state model provides a stochastic continuity constraint, which insures that states that are close in time are close in value. In our case this guarantees continuity of the burst probabilities. The parameter σ² governs how rapidly changes can occur between adjacent states. To estimate the set of states and σ² we use an expectation maximization (EM) algorithm for point processes and binary time series [13][14].

III. Estimation Algorithm

Our objective is to estimate the state process x_i and the parameter ${\sigma }_e^2$ for i = 1, ..., N. This will allow us to compute the BSR estimate with its confidence intervals. We treat the initial condition x₀ as a parameter. The states and parameter estimates are computed by maximizing the expectation of the complete data log likelihood. The complete data likelihood is

$$\begin{array}{cc}\hfill p(b_{1:N},x\mid {\sigma }_e^2,x_0)& ={\Pi }_{i=1}^N{p}_i^{b_i}{(1-p_i)}^{1-b_i}{\left(\frac{1}{2\pi {\sigma }_e^2}\right)}^{\frac{1}{2}}\times exp(-\frac{1}{2}\frac{{(x_i-x_{i-1})}^2}{{\sigma }_e^2})\hfill \\ \hfill & =p(b_{1:N}\mid x)p(x\mid {\sigma }_e^2,x_0).\hfill \end{array}$$ (4)

The EM algorithm iterates between an expectation or E-step and a maximization or M-step. The expectation step is

A. Expectation Step

At iteration l + 1 we compute in the expectation step the expected value of the complete data log likelihood given the complete data b_1:N and the estimates σ^2(l) and $x_0^{\left(l\right)}$ of the parameters from iteration l:

$$Q({\sigma }_e^2,x_0\mid {\sigma }^{2\left(l\right)},x_0^{\left(l\right)})=E[\text{log}[p(b_{1:N},x\mid b_{1:N},{\sigma }^{2\left(l\right)},x_0^{\left(l\right)})=E({\Sigma }_{i=1}^N{b}_i{x}_i-\text{log}(1+\text{exp}\left(x_i\right)\mid b_{1:N},{\sigma }^{2\left(l\right)},x_0^{\left(l\right)}))+E[{\Sigma }_{i=1}^N-\frac{1}{2}\frac{{(x_i-x_{i-1})}^2}{{\sigma }_e^2}-\frac{N+1}{2}\text{log}\left(2\pi \right)-\frac{N+1}{2}\text{log}\left({\sigma }_e^2\right)-\frac{x_0^2}{2{\sigma }_e^2}\mid b_{1:N},{\sigma }_e^{2\left(l\right)},x_0^{\left(l\right)}].$$ (5)

We can see upon further expanding the right hand side that we need to estimate three quantities for i = 1, ..., N

The expectation of the state variable given the data up to time N,

$$x_{i\mid N}\equiv E[x_i\mid b_{1:N},{\sigma }_e^{2\left(l\right)},x_0^{\left(l\right)}],$$ (6)

and the covariances given the data up to time N,

$$W_{i\mid N}\equiv E[x_i^2\mid b_{1:N},{\sigma }_e^{2\left(l\right)},x_0^{\left(l\right)}]$$ (7)

and,

$$W_{i,i-1\mid N}\equiv E[x_i{x}_{i-1}\mid b_{1:N},{\sigma }_e^{2\left(l\right)},x_0^{\left(l\right)}].$$ (8)

The expectation step consists of three parts. First we compute the estimates of x_i|i and ${\sigma }_{i\mid i}^2$ from the forward filter. Second, we use the backward filter to compute x_i|N and ${\sigma }_{i\mid N}^2$. Finally, we use the state space covariance algorithm to compute the covariances W_i|N and W_i,i–1|N.

1) Forward Filter

Given the parameters estimates from iteration l, this step estimates x_i|i and ${\sigma }_{i\mid i}^2$, meaning that it will estimate the state and the variance at i looking at data from the start of the experiment up to i using a non linear forward filter algorithm [13][14]. The one step prediction mean and variance are given by

$$x_{i\mid i-1}=x_{i-1\mid i-1},$$ (9)

$${\sigma }_{i\mid i-1}^2={\sigma }_{i-1\mid i-1}^2+{\sigma }_e^{2\left(l\right)}.$$ (10)

The posterior mode and variance are given by

$$x_{i\mid i}=x_{i\mid i-1}+{\sigma }_{i\mid i-1}^2(b_i-p_{i\mid i}),$$ (11)

$${\sigma }_{i\mid i}^2={[{\left({\sigma }_{i\mid i-1}^2\right)}^{-1}+p_{i\mid i}(1-p_{i\mid i})]}^{-1}.$$ (12)

The initial conditions are $x_{0\mid 0}=x_0^{\left(l\right)}$ and ${\sigma }_{0\mid 0}^{}={\sigma }^{2\left(l\right)}$. p_i|i corresponds to the mode of the posterior distribution which we estimate recursively. This filter is non-linear because x_i|i appears on both sides of (11).

2) Backward Filter

Using the posterior estimates, a fixed-interval smoothing algorithm (FIS) [13][14] gives us the estimates x_i|N for i = N – 1, ..., 1 , meaning that the estimate at time i is based on all the data up to time N. Our final estimate of the state will be thus a Gaussian distributed variable with mean x_i|N and variance ${\sigma }_{i\mid N}^2$. The FIS is

$$x_{i\mid N}=x_{i\mid i}+A_i(x_{i+1\mid N}-x_{i+1\mid i}),$$ (13)

$$A_i={\sigma }_{i\mid i}^2{\left({\sigma }_{i+1\mid i}^2\right)}^{-1},$$ (14)

$${\sigma }_{i\mid N}^2={\sigma }_{i\mid i}^2+A_i^2({\sigma }_{i+1\mid N}^2-{\sigma }_{i+1\mid i}^2).$$ (15)

The initial conditions are x_N|N and ${\sigma }_{N\mid N}^2$ previously estimated in the filter algorithm.

3) State Space Covariance Algorithm

Finally, the state space covariance algorithm [15] gives σ_i,j|N:

$${\sigma }_{i,j\mid N}=A_i{\sigma }_{i+1,j\mid N},$$ (16)

where 1 < i < j < N. The covariances are thus given by

$$W_{i,i-1\mid N}={\sigma }_{i,i-1\mid N}+x_{i\mid N}{x}_{i-1\mid N}$$ (17)

and,

$$W_{k,k\mid K}={\sigma }_{i\mid N}^2+x_{i\mid N}^2.$$ (18)

The maximization step is

B. Maximization Step

In the maximization step, the complete data log likelihood is maximized with respect to σ² and x₀. This yields the estimates

$${\sigma }^{2(l+1)}={(N+1)}^{-1}(2({\Sigma }_{i=2}^N{W}_{i\mid N}-{\Sigma }_{i=2}^N{W}_{i-1,i\mid N})+\frac{3}{2}{W}_{1\mid N}-W_{N\mid N})$$ (19)

and,

$$x_0^{(l+1)}=\frac{1}{2}{x}_{1\mid N}.$$ (20)

Dynamic BSR Estimate

The algorithm iterates between the Expectation and Maximization steps until convergence. The convergence criteria we use are the same as those developed by [12]. The fixed-interval smoothing algorithm evaluated at the maximum likelihood estimates x₀ and ${\sigma }_2^2$ together with the logistic equation (2) give us the probability of a suppression at time i for i = 1, ..., N. From there we can compute the probability density function which corresponds to the dynamic BSR estimate and is given by:

$$f(p\mid x_{i\mid N},{\sigma }_{i\mid N}^2,{\sigma }_{i\mid N}^2)={\left[{\left(2\pi {\sigma }_{i\mid N}^2\right)}^{0.5}p(1-p)\right]}^{-1}\times exp(-\frac{1}{2{\sigma }_{i\mid N}^2}{[log\left[p{(1-p)}^{-1}\right]-x_{i\mid N}]}^2).$$ (21)

IV. Results

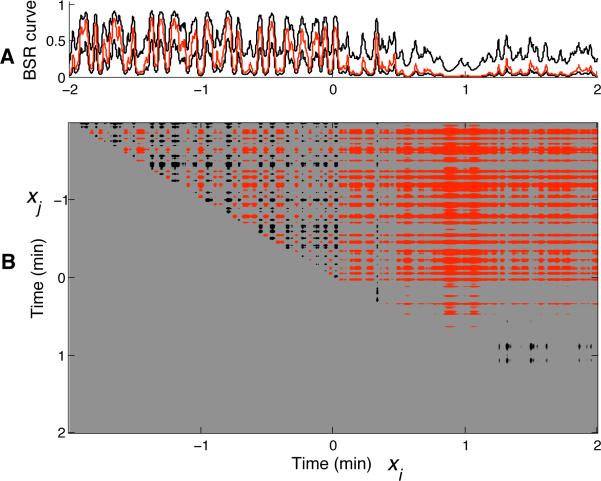
Fig. 2 illustrates the results of our algorithm. The data used were recorded from a rat under stable 2% isoflurane for sixty minutes. A four-minute window centered at the time of physostigmine injection is shown in Fig. 2. We adapted the algorithm of Vijn and colleagues [6] to extract the burst suppression binary sequence by setting the minimum burst suppression window and the epoch size to 100 milliseconds. This binary sequence is the input to our algorithm. The analysis was conducted using the Matlab software (MathWorks, Natick, MA) available at our website (http://neurostat.mgh.harvard.edu/BehavioralLearning/Matlabcode).

Fig. 2.

Panel A shows the estimated BSR (red curve) with its 95% confidence intervals (black curves). The BSR declines appreciably after administration of physostigmine at time 0. Panel B shows a scatter plot of the significant differences (see text) between points in time. Red and black dots indicate that the probability of x_i being significantly smaller and greater than x_j respectively is 0.975.

Panel A in Fig. 2 shows the dynamic BSR curve with its 95% confidence intervals. Prior to the administration of physostigmine at time 0, the BSR oscillates approximately between 0.2 and 0.8 with a median value of approximately 0.6. This suggests that the EEG spent the majority of its time in the suppressed state. After time 0, there is a steep decrease in the BSR. From this point on the BSR oscillates between 0.05 and 0.10. This is consistent with a decrease in suppression or equivalently, an increase in arousal. Because we estimated the joint distribution of the state process we can evaluate Pr(x_i > x_j) for any 0 ≤ i < j ≤ N which is equivalent to the probability that the BSR at time i is greater than the BSR at time j because the transformation between the state variable x_i and the probability of a suppression p_i is monotonic. Panel B in Fig.2 is a scatter plot showing the pairwise significant differences between the BSR across time. The red and black dots correspond to Pr(x_i < x_j) = 0.975 and Pr(x_i > x_j) = 0.975 respectively, where i is the index across the x – axis and j is the index across the y – axis.

To illustrate how to read Fig. 2B, notice that the BSR decreases at time −0.75 min. The red vertical strip at time −0.75 min show that the BSR at all times from −2 min to −0.75 min are significantly greater than the BSR at −0.75 min to −0.80 min. In contrast, the black vertical strip at the −0.5 min shows that all BSR prior to this time are significantly smaller. This observation is consistent with the BSR estimates in Fig. 2A. The red dots clearly show that Pr(x_i < x_j) = 0.975 for i ≥ 0 and j < 0, which means that the BSR after the injection of the physostigmine is significantly smaller than before the injection. This abrupt drop in the BSR is expected because physostigmine is a cholinergic agonist that induces increased arousal.

V. Conclusion

We have presented a state space model in which we define BSR dynamically as the probability of a suppression period as a function of time. We estimated the model using an approximate EM algorithm and illustrated its application in the analysis of rodent burst suppression recordings under general anesthesia. Our approach removes the need to average the ratio over long epochs. It also provides a continuous estimate of the probability of a burst and the joint distribution of the burst suppression states. The latter allows us to make formal statistical comparisons between burst activity at any time points. Our state-space model suggests a more principled way to analyze this key EEG feature that may offer more informative assessment of this important brain state.