Power and sample size calculations for longitudinal studies comparing rates of change with a time-varying exposure

SUMMARY

Existing study design formulas for longitudinal studies have assumed that the exposure is time-invariant. We derived sample size formulas for studies comparing rates of change by exposure when the exposure varies with time within a subject, focusing on observational studies where this variation is not controlled by the investigator. Two scenarios are considered, one assuming the effect of exposure on the response is acute and one assuming it is cumulative. We show that accurate calculations can often be obtained by providing the exposure prevalence at each time point and the intraclass correlation of exposure. When comparing rates of change, studies with a time-varying exposure are, in general, less efficient than studies with a time-invariant one. We provide a public access program to perform the calculations described in the paper (http://www.hsph.harvard.edu/faculty/spiegelman/optitxs.html).

1. INTRODUCTION

Studies involving repeated measurements of a binary exposure typically aim to compare the rate of change in response in the two exposure groups, or equivalently, the interest is in an exposure by time interaction. Study design formulas for such studies have mostly been derived in the context of clinical trials, and therefore assume that the exposure is time-invariant [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]. When the exposure varies within a subject, some methods have been developed when interest is in the main effect of exposure, for example in crossover designs [12, 13] and in multi-center clinical trials with randomization at the patient level [14]. However, these methods do not apply to observational studies, where exposure or treatment is not assigned by the investigator. When the interest is in the exposure by time interaction, no study design formulas have previously been developed for longitudinal studies with time-varying exposure, to the best of our knowledge.

In this paper, we derive study design formulas that are valid when the aim is to compare rates of change in response in relation to a time-varying exposure. Our formulas are derived for a binary exposure and for equidistant time points. The formulas we derive here are motivated by applications in observational studies, where exposure is not assigned by design and many exposure patterns may be observed, with variation in the number of exposed periods per participant and changes in the cross-sectional prevalence of exposure over time. However, all results readily apply to the controlled setting as a simple special case. We then compare the formulas we derive for the time-varying case with the existing ones for the time-invariant case, so that investigators can anticipate when they will need to recruit more or less participants because their exposure is time-varying instead of time-invariant. This paper is structured as follows. In section 2, we introduce notation and several models that extend the rates of change comparison to the time-varying exposure setting. In section 3, we derive expressions for the variance of the coefficient of interest for each model considered, in order to obtain the formula for the test statistic upon which power and sample size calculations are based. In section 4, we assess the effect of changing some of the assumptions, including time-varying vs. time-invariant exposure, on sample size. In section 5, the methods are applied to the design of a real study. In section 6, the results and their implications are discussed. In addition, we provide public access software to perform all the calculations discussed in this paper (http://www.hsph.harvard.edu/faculty/spiegelman/optitxs.html).

2. NOTATION AND MODELS

2.1. Notation

Let Y_ij be the outcome of interest for the measurement taken at the jth (j = 0,…, r) time for the ith (i = 1,…, N) participant, and E_ij represent the exposure for the period between the measurements of Y_i,j−1 and Y_ij. Thus, r is the number of post-baseline measurements of the response per participant, or, equivalently, the total number of measurements per participant is r +1. We consider studies that obtain repeated measures every s time units, as is the usual design in epidemiologic studies. Let t_i0 be the initial time for participant i and V (t₀) be its variance. When V (t₀) = 0, all participants have the same time vector, as when using time since enrollment in the study as the time variable of interest. However, when age is the time metameter of interest, as is often the case in epidemiology, and when, in addition, participants enter the study at different ages, V (t₀) > 0. We base our results on linear models of the form Y_i = X_i Γ (i = 1,…, N), for some covariate matrix X_i ((r +1) × q), where q is the number of variables in the model, and Γ is a vector of unknown regression parameters. The (r+1) × (r+1) residual covariance matrix is V ar (Y_i|X_i) = Σ_i (i = 1,…, N). Note that Σ_i can be any valid covariance matrix, and can include terms associated with between-subjects variability as well as within-subjects variation. We base our development on the generalized least squares (GLS) estimator of Γ, which has the form $\mathbf{\Gamma ̂}={\left(\frac{1}{N}\sum _i{\mathbf{X}\prime }_i{\mathbf{\Sigma }}_i^{-1}{\mathbf{X}}_i\right)}^{-1}\left(\frac{1}{N}\sum _i{\mathbf{X}\prime }_i{\mathbf{\Sigma }}_i^{-1}{\mathbf{Y}}_i\right)$. Since the design matrix is not known a priori, following Whittemore [15] and Shieh [16], study design calculations use $\frac{1}{N}$ Σ_Γ as the variance of Γ̂, where

$${\mathbf{\Sigma }}_{\mathrm{\Gamma }}={({𝔼}_X[{\mathbf{X}\prime }_i{\mathbf{\Sigma }}_i^{-1}{\mathbf{X}}_i])}^{-1}.$$ (1)

As long as Σ_i does not depend on the covariates, (1) can be fully specified by the first and second order moments of the covariate distribution [17].

2.2. Extending the model for time-varying exposure

When the exposure is time-invariant, the usual model is

$$𝔼(Y_{ij}|X_{ij})={\gamma }_0+{\gamma }_t{t}_{ij}+{\gamma }_e{E}_i+{\gamma }_{te}(t_{ij}\times E_i),$$ (2)

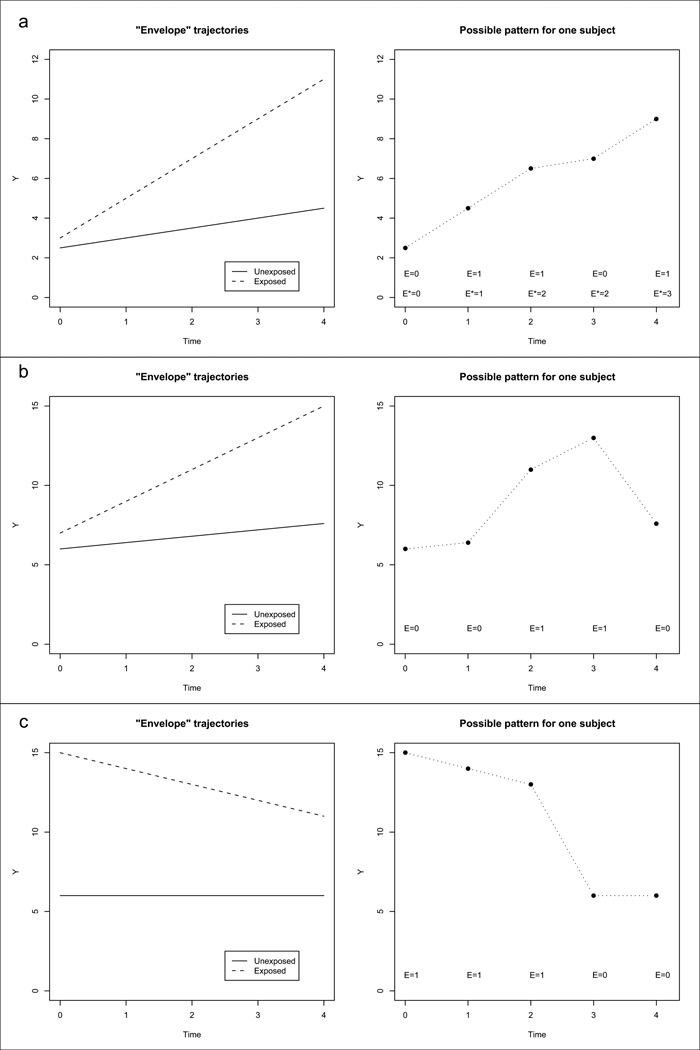
where the interest is in the exposure by time interaction. Figures 1a–1c illustrate some possible trajectories which could occur when the rate of change depends on exposure. The left panels show the trajectories for a time-invariant exposure, which occurs with a linear exposure-by-time interaction as described in (2).

Figure 1.

Envelope trajectories (trajectory for participants with time-invariant exposure) and possible individual patterns according to: a) model (3) and (4); b) and c) models (5) and (6)

The model can be extended to the time-varying exposure case in at least two ways, one that assumes that the effect of exposure on the response is cumulative and the other that assumes it is acute and transient. The new model equations for these two genearalizations will be given below. For both options, the response trajectory of participants whose exposure status does not vary with time will be equal to the trajectories shown in the left panels of Figures 1a–1c, and this trajectory will be the same whether we assume the exposure has a cumulative or an acute effect. The trajectories for participants with changes in exposure over time will be different in the two models. Since all possible trajectories implied by the models will be encompassed by the two extreme trajectories of those with time-invariant exposure, Singer and Willett [18] referred to these as the envelope trajectories.

When the effect of exposure is cumulative, we define a new variable, the cumulative exposure variable, $E_{ij}^{*}$, where $E_{ij}^{*}={\sum }_{k⩾j}{E}_{ik}$, and we assume that Y_ij depends on the exposure only through $E_{ij}^{*}$ (see Checkoway et al. [19] for the motivation for and examples of cumulative exposure). Note that if a participant is exposed for the entire study period, cumulative exposure since entering the study is proportional to time in the study. We denote the cumulative exposure before entering the study for subject i as $E_{i,-1}^{*}$. Then, $E_{ij}^{*}=E_{i,-1}^{*}+\sum _{k=0}^j{E}_{ik}$. Often, $E_{i,-1}^{*}$ is unknown. The right panel of Figure 1a shows a possible trajectory for one participant with $E_{i,-1}^{*}=0$ and exposure E_i = (0, 1, 1, 0, 1), which gives ${\mathbf{E}}_i^{*}=(0,1,2,2,3)$. This pattern is consistent with a cumulative effect of exposure as well as an independent effect of time for both the exposed and the unexposed (e.g. due to ageing), and it can be modeled as

$$𝔼(Y_{ij}|{\mathbf{X}}_i)={\gamma }_0+{\gamma }_t{t}_{ij}+{\gamma }_{e*}{E}_{ij}^{*}.$$ (3)

For example, in a study of the relationship between changes in lung function and smoking status in a cohort followed from 13 to 27 years of age, it was found that the rate of increase in lung function was smaller in periods with active smoking [20, page 118]. Since cumulative exposure is, by definition, the sum of the product of point exposure by exposure duration, model (3) does not need to include an interaction term to be a generalization of model (2) for the time-varying case. A response trajectory is defined for each possible exposure history, E_i, or equivalently, for each cumulative exposure history, ${\mathbf{E}}_i^{*}$. Model (3) assumes that the within-and between-subject effects of cumulative exposure (and time) are equal, that is, there is no confounding by between-subject effects [21]. If this assumption is unreasonable, one may want to fit the following change model,

$$𝔼(Y_{ij}-Y_{i,j-1}|{\mathbf{X}}_i)={\gamma }_t^W+{\gamma }_{e*}^W(E_{ij}^{*}-E_{i,j-1}^{*})={\gamma }_t^W+{\gamma }_{e*}^W{E}_{ij}$$ (4)

This model results from applying the first difference operator

$$\mathbf{\Delta }=\left(\begin{array}{ccccc}\hfill -1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill & \hfill 1\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 1\hfill \end{array}\right)$$

to model (3), so that ΔY_i is the vector with elements Y_i,j+1 − Y_ij, j = 1,…, r, and V ar (ΔY_i) = ΔΣ_iΔ′. For a multivariate normal response with known Σ_i, fitting model (4) by GLS is equivalent to fitting model (3) by conditional linear regression (Web Appendix A). If there is no confounding by between-subjects determinants of response, γ̂_e* will estimate the same parameter as ${\mathrm{\gamma ̂}}_{e*}^W$, otherwise not [21]. In observational studies, model (4) is often preferred, since each participant serves as his or her own control, fully controlling for confounding by all between-subject (time-invariant) effects, including cumulative exposure at entry and age at entry. However, the trade-off is that model (4) is less efficient than (3) [21].

When the effect of exposure is acute, we assume the response depends on exposure only through the exposure in the previous period. The right panel of Figure 1b shows a possible trajectory for one participant with exposure E_i = (0, 0, 1, 1, 0). This situation can be modeled as

$$𝔼(Y_{ij}|{\mathbf{X}}_i)={\gamma }_0+{\gamma }_t{t}_{ij}+{\gamma }_e{E}_{ij}+{\gamma }_{te}(E_{ij}\times t_{ij})$$ (5)

and we are interested in the parameter γ_te. Note that under this model, a participant shifts trajectories when exposure changes, the ”jumps” being larger or smaller as time increases. Although this model is considered in the literature on longitudinal data analysis, the situation it implies may be harder to find in real life, and many times models with only a main effect of exposure may be more appropriate when the effect of exposure is acute. Singer and Willett [18] fit model (5) in a study on the effect of time since unemployment in relation to the occurrence of depression symptoms. The trajectory implied by their analysis is illustrated in Figure 1c. Immediately after layoff (time 0), participants had high depression index values. Over time, they acclimated to their new status and the values for the depression index decreased over time, without reaching the levels of the employed. Once a formerly unemployed individual found a job and kept it, the depression score dropped to the level of the employed and remained constant over time. Like model (3), model (5) assumes that there is no between-subject confounding [21]. As above, the within-subject effects of exposure and time can be estimated by using the model for change that is obtained after applying the first difference operator to model (5),

$$𝔼(Y_{i,j+1}-Y_{ij}|{\mathbf{X}}_i)={\gamma }_t^W+{\gamma }_e^W(E_{i,j+1}-E_{ij})+{\gamma }_{te}^W[(E_{i,j+1}-E_{ij})t_{ij}+E_{i,j+1}].$$ (6)

Again, under multivariate normality, fitting model (6) by GLS is algebraically equivalent to fitting model (3) by conditional likelihood (Web Appendix A).

2.3. Power and sample size formulas

Let γ be the parameter of interest, which is γ_e* for model (3), ${\gamma }_{e*}^W$ for model (4), γ_te for model (5) or ${\gamma }_{te}^W$ for model (6). Let σ̃² be the diagonal element of the matrix Σ_Γ, defined in (1), that is associated with the parameter γ. The Wald test statistic to test if γ̂ is different from zero is $T=\sqrt{N}\mathrm{\gamma ̂}/\mathrm{\sigma ̃}$ [9], and the formula for the power of a study to detect an effect γ is $\mathrm{\Phi }[\sqrt{N}|\gamma |/\mathrm{\sigma ̃}-z_{1-\alpha /2}]$ where α is the significance level, and z_u and Φ (·) are the uth quantile and the cumulative density of a standard normal. The formula for the required sample size to detect an effect γ with power π is N = σ̃² (z_π + z_1−α/2)²/γ². For both power and sample size calculations, we need to derive σ̃² following (1) and the model of choice from (3)–(6). Note that σ̃² will depend on r and on several other parameters associated with the distributions of the response, the exposure and time.

3. DERIVATION OF σ̃²

3.1. Compound symmetry of both the response and the exposure process and other simplifications

We start by deriving formulas for σ̃² when it is assumed that both the response and the exposure process have a CS covariance and the exposure prevalence, p_e, is constant over time, in which case a closed-form formula for σ̃² can be derived. Under CS of the response, Σ_i = Σ has diagonal terms equal to σ², where σ² = V ar (Y_ij|X_ij) is the residual variance of the response given the covariates, and off-diagonal terms equal to σ² ρ, where ρ is the correlation between two measurements from the same participant, known as the reliability coefficient or the intraclass correlation coefficient [11]. Then, assuming CS of exposure, the covariance matrix of exposure has diagonal elements equal to p_e (1 − p_e) and off-diagonal elements equal to ρ_x p_e (1−p_e), where ρ_x is the common correlation between exposure at different time points.

When the prevalence of exposure is constant over time, the correlation ρ_x is equal to the intraclass correlation of exposure, ρ_e, defined as the percentage of variation in exposure that is due to between-subject variation [22]. Otherwise, one can still derive a relationship between the intraclass correlation, ρ_e, and the common correlation under compound symmetry, ρ_x (Web Appendix B). Because of the equality of ρ_e and ρ_x in the constant exposure prevalence case, and the fact that ρ_e has an intuitive interpretation and well-defined properties as detailed below, we will parameterize σ̃² in terms of ρ_e henceforth. The intraclass correlation, ρ_e, is bounded below by −1/r, and for binary variables, as here, there is a correction factor that needs to be added to this bound [22]. The upper bound is one when the exposure prevalence constant over time, and below one otherwise. An expression for the upper bound in the latter case was derived in Web Appendix C. These bounds are calculated by our program and displayed to the user after r and the prevalence at each time point have been provided.

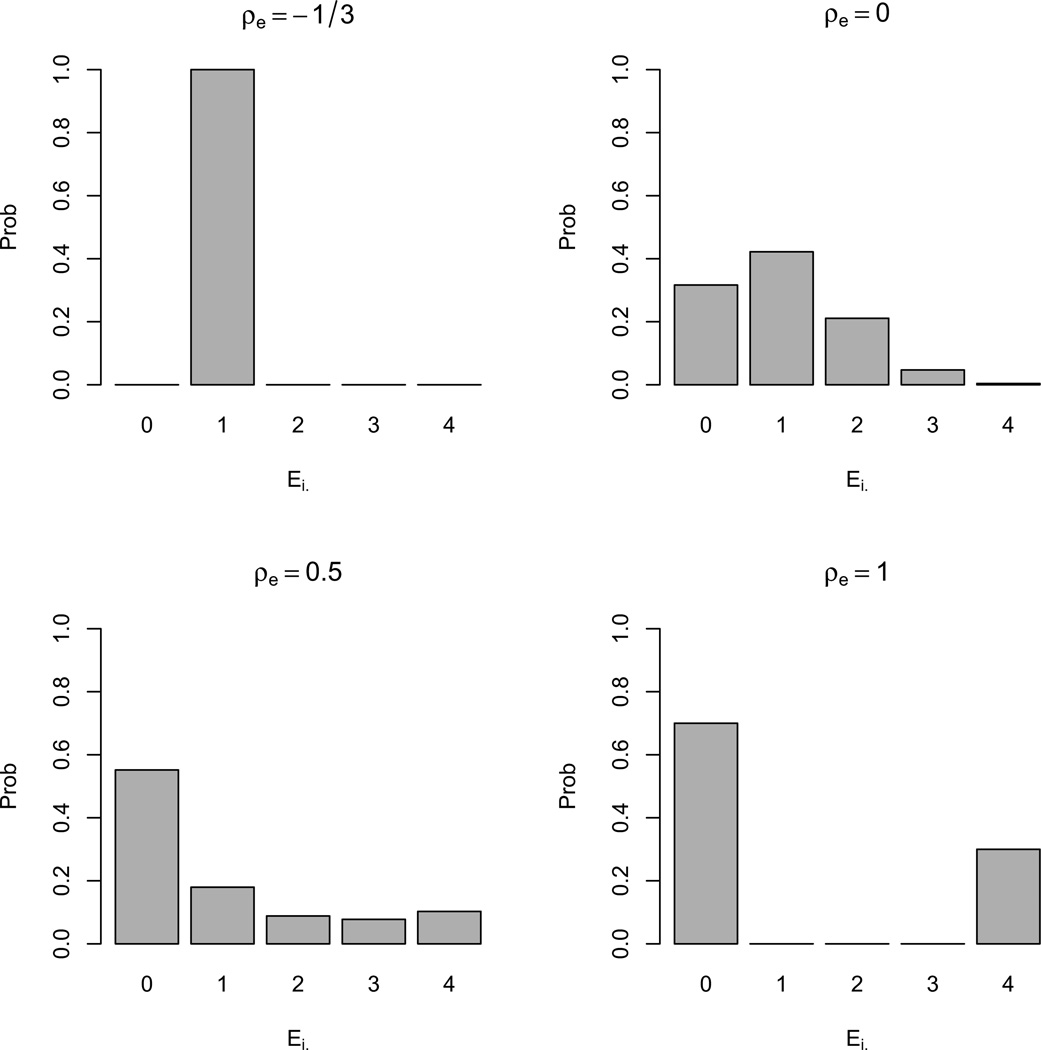
Apart from being the percentage of between-subject variation in exposure and being equal to the common correlation if the exposure prevalence is fixed, the intraclass correlation of exposure can also be regarded as a measure of imbalance in the number of exposed periods per subject, E_i·. When E_i· is balanced across subjects, then everyone is exposed for the same number of periods as, for example, in some crossover studies. Then, ρ_e = −1/r. Conversely, when the exposure is time-invariant, the imbalance is maximal since E_i· is either zero with probability (1 − p_e) or r + 1 with probability p_e, and ρ_e = 1. In observational studies, intermediate values between the bounds ρ_e = −1/r (same number of exposed periods for all participants) and ρ_e = 1 (time-invariant exposure) will often be observed, and when pilot data are not available, the investigator can assess the sensitivity of the study design over a range of plausible values for ρ_e. To help the investigator assess what value of ρ_e is appropriate for his or her exposure, our program provides the distribution of E_i· once r and p_e are fixed and a CS covariance of exposure is assumed. Examples of distributions of E_i· by varying ρ_e are shown in Figure 2.

Figure 2.

Distribution of E_i· for r = 3, p̄_e = 0.25 and different values of ρ_e.

Table I shows the expressions for σ̃² for models (3)–(6). For models (3), (5) and (6), all participants are assumed to enter the study at the same time (V (t₀) = 0). For model (3), all participants are assumed to be unexposed at baseline ($E_{i,-1}^{*}=0$ ∀i). Expressions are derived in Web Appendix D. In section 4, we will assess the effects of departures from the scenarios assumed in this section that were used to derive the expressions in Table I.

Table I.

Power and sample size equations for models (3)–(6) assuming CS covariance of both response and exposure, and constant exposure prevalence. For models (3), (5) and (6), all participants are assumed to enter the study at the same time (V (t₀) = 0). For model (3), all participants are assumed to be unexposed at baseline $(E_{i,-1}^{*}=0\forall i)$.

	Power formula: $\pi =\mathrm{\Phi }[\sqrt{N}|\gamma |/\mathrm{\sigma ̃}-z_{1-\alpha /2}]$
	Sample size formula: N = σ̃2 (zπ + z1−α/2)2/γ2
Model	Parameter of interest	σ̃2
(3)	γe*	$\frac{12{\sigma }^2(1-\rho )(1+r\rho )}{p_e(1-p_e)(r+1)(r+2)[6+2(r-3)\rho +r(4+(r-5)\rho ){\rho }_e]}$
(4)	${\gamma }_{e*}^W$	$\frac{12{\sigma }^2(1-\rho )}{p_e(1-p_e)s^{2}r(r+2)[2+(r-1){\rho }_e]}$
(5)	γte	$\frac{12{\sigma }^2(1-\rho )(1+r\rho )}{p_e(1-p_e)s^{2}r(r+1)(r+2)[1+r\rho -\rho (1-{\rho }_e)]}$
(6)	${\gamma }_{te}^W$	$\frac{12{\sigma }^2(1-\rho )}{p_e(1-p_e)s^{2}r(r+{\rho }_e)(r+2)}$

3.2. General covariance of the response and the exposure process

As shown above, the main difficulty in computing power and sample size for longitudinal studies with time-varying exposures is characterizing σ̃², the diagonal element of the matrix Σ_Γ, defined in (1), that is associated with the parameter γ. Its calculation involves the specification of the matrix ${𝔼}_X[{\mathbf{X}\prime }_i{\mathbf{\Sigma }}_i^{-1}{\mathbf{X}}_i]$ and the computation of its inverse. A simple general expression for σ̃² is difficult to obtain (Web Appendix D), but it can be easily computed with our program once ${𝔼}_X[{\mathbf{X}\prime }_i{\mathbf{\Sigma }}_i^{-1}{\mathbf{X}}_i]$ has been defined. So, in this section, we only state the input parameters needed for each one of models (3)–(6) to perform such calculations.

The parameters defining the covariance of the response need to be provided for all four models. Examples of two common covariance structures different from CS are discussed in section 4.1. In addition, one needs to provide the exposure prevalence at each time point, p_ej, j = 0, …, r, and the correlation between exposure at the jth and j′th measurements, ρe_j, e_j′ ∀j ≠ j′, for all four models.

If a cumulative exposure effect is assumed and model (4) is assumed, no additional parameters apart from those discussed in the previous paragraph are needed (Web Appendix D.2). However, if model (3) is assumed, age is the time metameter for the study and participants enter at different ages, i.e. V (t₀) > 0, and/or if participants enter the study with different values of cumulative exposure, i.e. $V(E_{-1}^{*})>0$, then additional parameters are needed for an exact calculation of σ̃² (Web Appendix D.1). Some of these parameters involve correlations between pairs of variables, or equivalently, expected values of products of variables. These parameters are: the baseline mean and variance of time metameter, 𝔼 (t₀) and V (t₀); the baseline mean and variance of cumulative exposure, $𝔼(E_{-1}^{*})$ and $V(E_{-1}^{*})$; the correlation between the baseline cumulative exposure and the baseline time metameter, or $𝔼[E_{-1}^{*}{t}_0]$; correlation between the time metameter at baseline and the exposure at all times henceforth, or 𝔼 [E_j t₀] ∀j; and the correlation between the baseline cumulative exposure and the exposure at all subsequent measurement times, or 𝔼 [$E_{-1}^{*}{E}_j$] ∀j. These quantities are difficult to provide a priori unless longitudinal pilot data are available, so one option is to base study design on model (4), which estimates only within-subject effects. In that case, none of these additional parameters are needed and a conservative study design will result, i.e. more participants than needed will be recruited. When it is reasonable to assume that all participants are unexposed at baseline, i.e. $E_{i,-1}^{*}=0$ ∀i, and time in the study is the time metameter of interest, i.e. V (t₀) = 0, then only the exposure prevalence at each time point, p_ej ∀j, and the intraclass correlation of exposure, ρe_j, e_j′ ∀j, j′, are needed, even for a study designed to fit model (3) (Web Appendix D.1.1). However, in an observational study, one still may want to base study design calculations on model (4), which estimates the effect of cumulative exposure during the study period but controls for all measured and unmeasured time-invariant confounders.

If a cumulative effect of exposure is assumed, when age is the time metameter of interest and participants enter the study at different ages, i.e. V (t₀) > 0, to exactly compute σ̃², the investigator would need to specify the following additional parameters for both model (5) and (6) (Web Appendix D.3): variance of the time metameter at baseline, V (t₀); correlation between time metameter at baseline and exposure at all time henceforth, or 𝔼 [E_j t₀] ∀j; expected value of the crossproduct of exposure at all pairs of time points and baseline time metameter, 𝔼 [E_jE_j′ t₀] ∀j, j′; and expected value of the crossproduct of exposure at all pairs of time points and baseline time metameter squared $𝔼[E_j{E}_{j\prime }{t}_0^2]$ ∀j, j′. Clearly, these quantities will be impossible to provide a priori in most study settings unless longitudinal pilot data are available, so some simplifications need to be implemented. One option is to perform the calculations for the case V (t₀) = 0, which seemed numerically to always provide conservative estimates, although we were unable to prove this analytically. When V (t₀) = 0 is assumed, only p_ej ∀j and ρ_ej, e_j′ ∀j, j′ need to be provided (Web Appendix D.3.1).

4. EFFICIENCY COMPARISONS

In section 3.1, we obtained formulas for σ̃² under several scenarios likely to be encountered in practice. In this section, we compare the required sample size under those assumptions to the required sample size when those assumptions are not met. We will investigate the direction of the differences to identify under what circumstances incorrect assumptions lead to conservative (overpowered) designs, and under what circumstances incorrect assumptions will lead to underpowered studies. In practice, the investigator can also do these comparisons by performing the calculations under various scenarios using our software.

4.1. Effect of departures from the assumption of CS response covariance

In this section, we consider two response covariance structures that are commonly used and are more general than CS, but that include CS as a particular case: damped exponential (DEX) and random intercepts and slopes (RS). Under the DEX covariance structure [23], the [j, j′] element of Σ_i = Σ has the form σ² ρ^|j−j′|θ, where the correlation between two measurements decays exponentially as the separation between measurements increases, but the parameter θ attenuates this decay. Thus, when θ = 0, the CS covariance structure is obtained, and when θ = 1, the AR(1) covariance structure is given. The RS covariance structure is the one that arises in mixed models, when there is a random effect associated with the intercept and one associated with time. The covariance matrix is typically given as ${\mathbf{\Sigma }}_i={\mathbf{Z}}_i\mathbf{D}{\mathbf{Z}\prime }_i+{\sigma }_w^2\mathbf{I}$, where Z_i contains a column of ones and the column of times for participant i, and D is the 2 × 2 covariance matrix of the random effects, with elements $({\sigma }_{b_0}^2,{\rho }_{b_0{b}_1}{\sigma }_{b_0}{\sigma }_{b_1},{\rho }_{b_0{b}_1}{\sigma }_{b_0}{\sigma }_{b_1},{\sigma }_{b_1}^2)$ [11]. The RS covariance structure is heteroscedastic and non-stationary [11]. When all participants are observed at the same times, Z_i = Z ∀i and, therefore, Σ_i = Σ ∀i. When that is not the case, Σ_i depends on the covariates, and expression (1) can only be calculated if a distribution for the time variable is assumed. We define the total variance at baseline as $V(Y_{i0}|{\mathbf{X}}_i)={\sigma }_{t_0}^2={\sigma }_{b_0}^2+{\sigma }_w^2$, the intraclass correlation at baseline as ${\rho }_{t_0}={\sigma }_{b_0}^2/{\sigma }_{t_0}^2$, and the slope reliability as

$${\rho }_{b_1}={\sigma }_{b_1}^2/(\frac{12(1-{\rho }_{t_0}){\sigma }_{t_0}^2}{s^{2}r(r+1)(r+2)}+{\sigma }_{b_1}^2),$$

which is the percentage of variation in the slopes that is between subjects, it does not depend on the response units and it has a closed range (between zero and one) [18]. Then, the RS covariance can be expressed in terms of $({\sigma }_{t_0}^2,{\rho }_{t_0},{\rho }_{b_1},{\rho }_{b_0{b}_1})$. When ρ_b1 = 0 the CS covariance is obtained. The slope reliability needs to be defined for a particular r. Throughout this paper, values of ρ_b1 will be calculated at the value r = 5. Although this choice was arbitrary, it would be consistent with a typical longitudinal study funded by the U.S. National Institutes of Health. These studies can be funded for no more than five years, and if one measurement was to be taken at the end of each year of funding, r = 5.

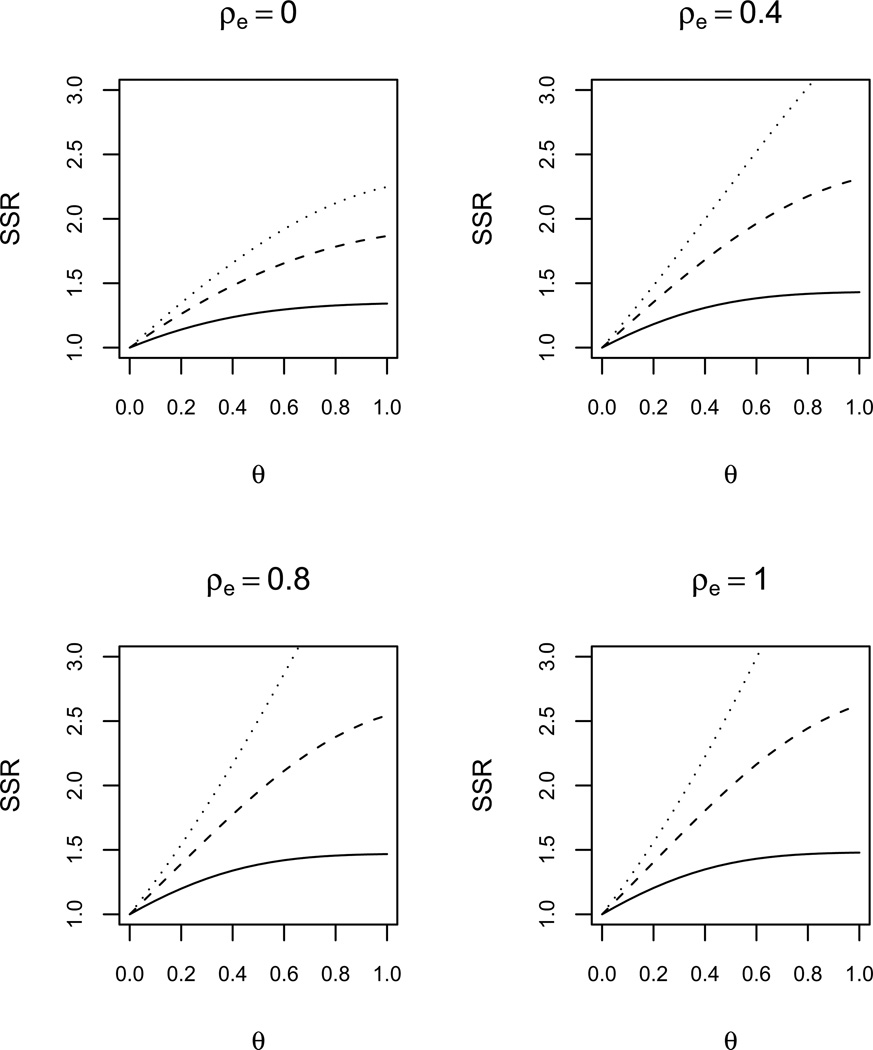
Under the assumption that the effect of exposure is cumulative, we assessed departures from assuming CS response covariance based on model (4) (similar results were obtained using model (3)). The covariance of the exposure is still assumed to be CS. Through a grid search, we found that, for two studies with the same ρ_e, departures from CS in the response, i.e. of θ > 0 if DEX is assumed or ρ_b1 > 0 if RS is assumed, increased σ̃² and therefore increased the required sample size. Figure 3 illustrates this increase when DEX response covariance, CS exposure covariance and constant exposure prevalence are assumed, for several values of ρ, θ, and ρ_e (including independence, i.e. ρ_e = 0, and time-invariant exposure, i.e. ρ_e = 1). The increase in required sample size with θ is larger for larger values of ρ_e and ρ. We performed the same assessment when the effect of exposure is acute based on models (5) and (6), and the effect was similar to that described in Figure 3, but with lower SSRs as the within-subject exposure correlation decreased.

Figure 3.

Sample size ratio (SSR = N_θ/N_θ=0) comparing the required sample size of a study with CS response covariance (i.e. θ = 0) to a study with DEX response covariance (i.e. θ > 0) when the cumulative exposure effect model (4), CS exposure covariance, constant exposure prevalence and r = 5 are assumed, for several values of ρ and ρ_e. Lines indicate: (—) ρ = 0.2, (- - -) ρ = 0.5, (…) ρ = 0.8.

4.2. Effect of departures from the assumption of CS exposure covariance

To assess departures from CS in the exposure covariance, we adopted a slightly different approach than when assessing departures from CS of the response covariance. We performed a numerical analysis to evaluate the accuracy of the CS exposure covariance assumption as an approximation to σ̃² when the exposure process had some other correlation structure, i.e. when the exposure covariance was misspecified. To compute the true and misspecified σ̃², the exposure prevalence vector and the correlation matrix of exposure are needed. For values of r equal to 2, 5 and 10, we generated 10,000 arbitrary prevalence vectors and correlation matrices using a process described in Web Appendix E. Then, the SSR based upon the misspecified and true σ̃² was calculated. The response covariance was assumed to be known here, and the calculations were repeated for CS, DEX and RS response covariance to determine whether the results were dependent upon the assumed response covariance structure. The values of the response covariance parameters were ρ = (0.8, 0.5, 0.2) for CS; the same values of ρ and θ = (0.2, 0.5, 0.8, 1) for DEX; and the same values of ρ_t0 that we used for ρ, and ρ_b1 = (0.05, 0.1, 0.2, 0.5, 0.8) for RS.

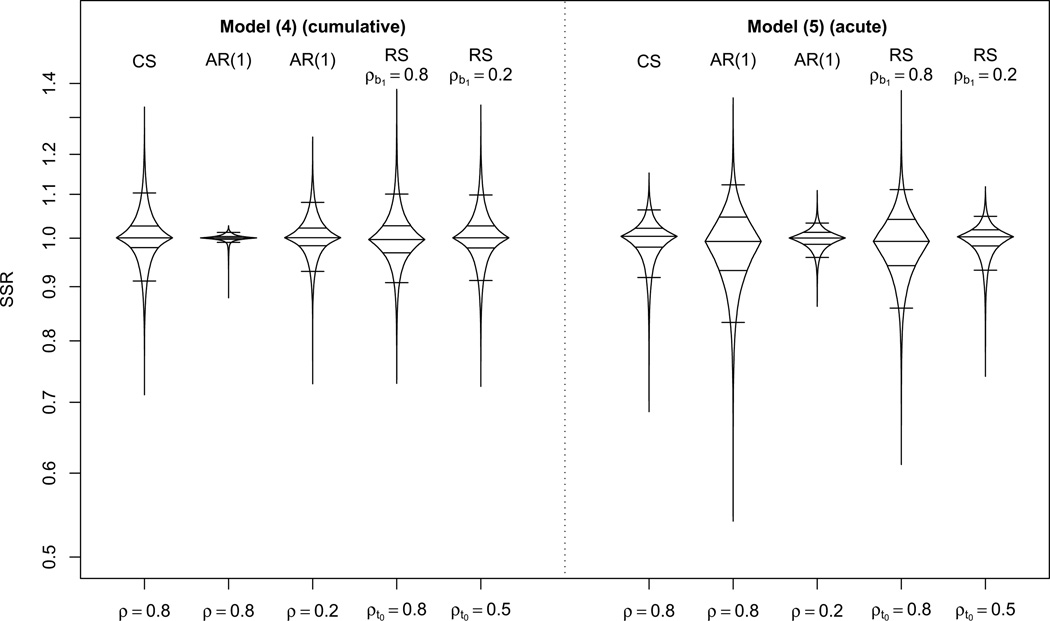
Figure 4 summarizes the results for some values of the response covariance for r = 5. Results for r = 2 and r = 10 were similar. Results from model (3) were very similar to those of model (4), and results from model (6) were similar to those of model (5). For the cumulative exposure effect models (3) and (4), most of the scenarios considered (around 90%) fell into the interval (0.9, 1.1) with CS response. As θ increased, results were better than in the CS case. When RS of the response was assumed, results were similar for all combinations of ρ_t0 and ρ_b1 considered, and less than 5% of scenarios had SSR<0.9. We are particularly concerned with those scenarios with low SSR (<0.9), since when SSR is greater than one, conservative designs are obtained. We observed that the scenarios with lowest SSRs were characterized by small, negative correlations for pairs of exposure close in time, and large, positive correlations for pairs of exposures distant to each other. To confirm this numerically, we regressed all correlation coefficients from each of the 10,000 exposure correlation matrices against time separation, so 10,000 slopes were obtained. A positive slope indicates that the correlations increase with time separation. Then, when the SSRs were regressed against these slopes, a strong linear negative relationship was obtained for all response covariances used in Figure 4, with the higher slopes presenting the smallest SSRs. The R² of these regressions ranged from 0.63 to 0.79.

Figure 4.

Box-percentile plots of the ratio of required sample sizes obtained when incorrectly assuming CS covariance of exposure divided by the required sample size obtained using the true exposure covariance in 10,000 scenarios generated to have an arbitrary exposure covariance, for r = 5 and for several correlation structures of the response. For RS models, ρ_b0,b1 = −0.5 is assumed. At any height, the width of the irregular ”box” is proportional to the percentile of that height. Horizontal lines indicate the 5th, 25th, 50th, 75th and 95th percentiles. Y-axis on logarithmic scale.

For the acute exposure effect model with CS response, the SSR was between 0.9 and 1.1 for more than 95% of the scenarios. For DEX response, the same pattern as with CS response was observed when θ or ρ were small, but when both θ and ρ were large, a higher percentage of scenarios with SSR less than 0.9 were observed. For example, when the response was AR(1) with ρ = 0.8, 15% of the scenarios were below that value. Similarly, for RS covariance, only for high ρ_t0 and ρ_b1 did we find a high percentage of scenarios with SSRs less than 0.9 (12% for ρ_t0 = 0.8, ρ_b1 = 0.5). We observed that the scenarios with the lowest SSRs were characterized by having high correlations for pairs of exposures that were both either at the beginning or at the end of the study, while the remaining correlations were negative. This implied a convex quadratic relationship between correlations and the sum of times of each pair. To numerically confirm this, we regressed the correlation coefficients from each of these 10,000 exposure correlation matrices against the sum of times and the sum of times squared, and obtained 10,000 coefficients associated with the quadratic term. Then, when the SSRs were regressed against these coefficients, a strong linear negative relationship was obtained for all response covariances used in Figure 4, with the higher coefficients presenting the lowest SSRs. The R² of these regressions ranged from 0.54 to 0.77.

In conclusion, both for the cumulative and the acute exposure effect models, the cases with SSR<0.9 had exposure correlation matrices that are unlikely to be found in practice, and assuming CS of exposure resulted in good approximations of the required sample size in most cases considered.

4.3. Effect of ρ_e on sample size

In this section, we assessed the effect of ρ_e on sample size. This will also allow comparing the required sample size obtained in a study with time-invariant exposure (ρ_e = 1) to a study with time-varying exposure (ρ_e < 1). This comparison has never been done, precluding investigators to anticipate whether they will need to recruit more or less participants if they have a time-varying exposure instead of a time-invariant one.

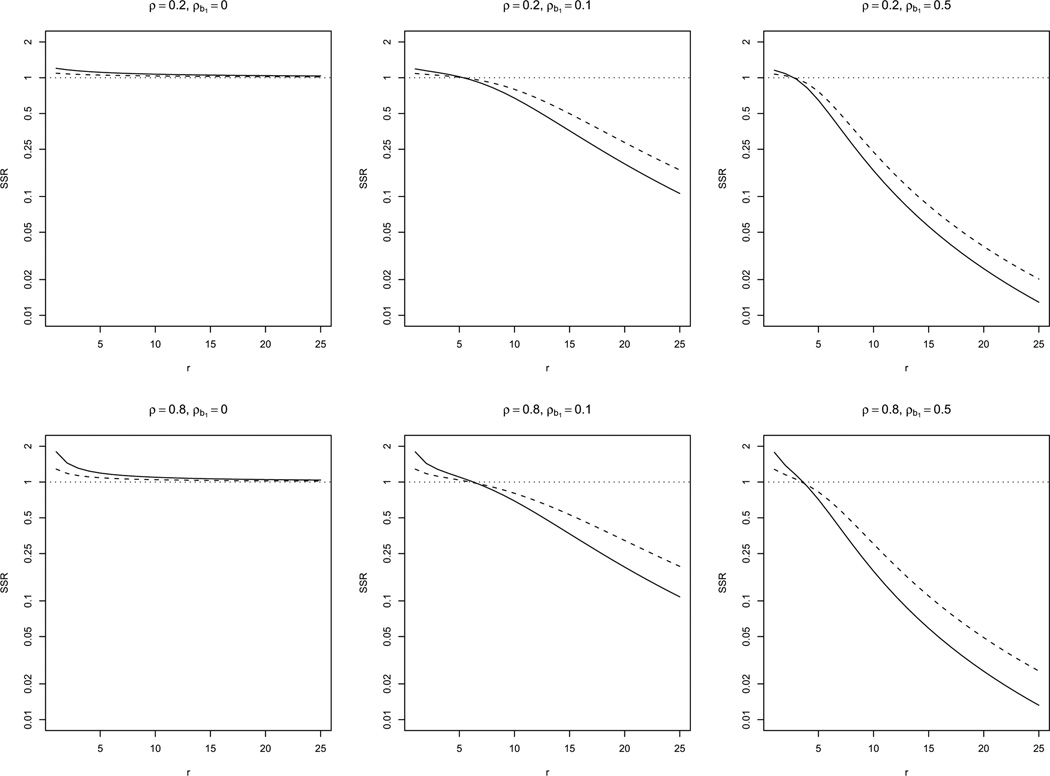
When assuming that the effect of exposure is cumulative, results were based on model (4) (results were verified to be similar using model (3)). For model (4), we show in Web Appendix D.2.2 that, if w^jj′ ⩾ 0 ∀j ≠ j′, where w_jj′ is the [j, j′] element of (ΔΣ_iΔ′)⁻¹, then σ̃² is minimal when ρ_e takes its upper bound (i.e. ρ_e = 1, the time-invariant exposure case, if the prevalence is constant over time) and maximal when ρ_e takes its lower bound, regardless of the form of the covariance of the exposure. The condition w^jj′ ⩾ 0 ∀j ≠ j′ holds when the response has CS or DEX covariance, but it does not necessarily hold for RS (Web Appendix D.2.2). Thus, under CS or DEX covariance of the response, and when w^jj′ ⩾ 0 ∀j ≠ j′ for RS, efficiency is always lost when the exposure varies over time. To illustrate this, Figure 5 shows the ratio of required sample sizes, SSR = N_ρe/N_{ρe = 1}, comparing a study with a time-varying exposure with CS covariance to a study with a time-invariant exposure, for the case where the response variable has RS covariance. It can be seen that, for large r and ρ_b1, a study with a time-varying exposure can end up being more efficient than one a with time-invariant exposure. In contrast, for DEX response, the SSR keeps increasing as r increases, with a slower rate than for CS response, which is shown in the first panel of Figure 5 (ρ_b1 = 0 case). When both the response and the exposure process can be assumed to follow CS and the prevalence of exposure is constant over time, we can derive an explicit formula for the ratio of variances, or equivalently, the ratio of required sample sizes, comparing the time-varying exposure case to the time invariant one, SSR = N_ρe/N_ρe=1 = (r + 1)/(2 + (r − 1)ρ_e). The SSR is always greater or equal than one. So, as discussed above, in this particular case, efficiency is lost when the exposure varies over time.

Figure 5.

Sample size ratio (SSR = N_ρe/N_ρe=1) comparing the required sample size of a study with time-varying exposure to a study with time-invariant exposure when the cumulative exposure effect model (4), RS covariance of the response, CS covariance of exposure, constant exposure prevalence and ρ_b0,b1 = −0.5 are assumed, for several values of r, ρ_t0, ρ_b1 and ρ_e. Y-axis on logarithmic scale. Lines indicate: (—) ρ_e = 0, (- - -) ρ_e = 0.5, (…) ρ_e = 1.

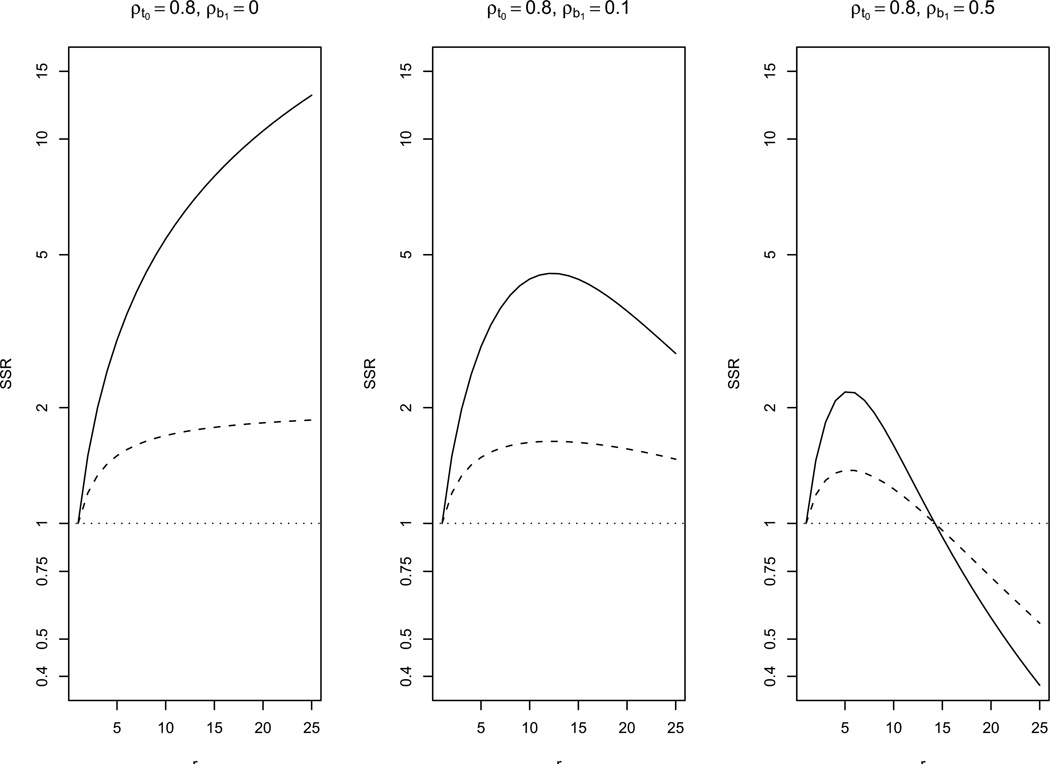
When the exposure is acute, we based our results on model (5) (results were verified to be similar using model (6)). For model (5), Figure 6 shows the ratio of required sample sizes, SSR = Nρ_e/N_ρe=1, comparing a study with a time-varying exposure with CS covariance to a study with a time-invariant exposure, where both studies have a RS covariance of the response. When the response follows CS (ρ_b1 = 0 case), a study with a time-varying exposure is less efficient than a study with a time-varying one, although for large values of r the differences become negligible. For this particular case (ρ_b1 = 0), the SSR has the expression N_ρe/N_ρe=1 = (1+rρ)/(1 + rρ − ρ(1 − ρ_e)) ⩾ 1. Thus, as with the cumulative effect model, in this simplest case, efficiency is lost when the exposure varies over time, and the loss increases as the response correlation increases, as the within-subject exposure correlation decreases, and as r decreases. However, when the response has RS covariance (ρ_b1 > 0), a study with a time-varying exposure can become more efficient than a study with a time-invariant exposure as r increases, and this gain in efficiency can be substantial. If the response follows DEX, results similar to the RS case (Figure 6) are obtained. Thus, it is important to correctly specify the covariance of the response when assessing the effect of a time-varying exposure, since assuming CS vs. RS or DEX can lead to very different study designs, and studies which can be substantially under- or over-powered.

Figure 6.

Sample size ratio (SSR = N_ρe/N_ρe=1) comparing the required sample size of a study with time-varying exposure to a study with time-invariant exposure under the acute exposure effect model (5), RS covariance of the response, CS covariance of exposure, constant exposure prevalence, V (t₀) = 0 and ρ_b0,b1 = −0.5 are assumed, for several values of r,ρ, θ and ρ_e. Y-axis on logarithmic scale. Lines indicate: (—) ρ_e = 0, (- - -) ρ_e = 0.5, (…) ρ_e = 1.

5. EXAMPLE: THE MSCM STUDY [24]

In this section, we applied our methods to the setting of a study of the effects of maternal depression on child health (the MSCM study, dataset available on-line at http://faculty.washington.edu/heagerty/Books/AnalysisLongitudinal/datasets.html [7]), to assess with real data the performance of our formulas. Participants (N = 142 with complete data) were followed for r + 1 = 28 consecutive days. The prevalence of depression fluctuated from a maximum of 0.26 at baseline to a minimum of 0.06 at the second to last day, with a mean of p̄_e = 0.13, and ρ_e was 0.10. Although the response variable in this study (child health) was binary, we considered the planning of a new study where child health is measured continuously. and wants to perform sample size calculations for it. We performed several calculations under the assumption of different scenarios for the response covariance. As in section 4.2, we will illustrate, this time with exposure data from a real study, that by computing sample size under an assumed CS exposure covariance gives a required sample size that closely approximates the result obtained using the observed exposure covariance. In addition, we will show that using the formulas for a time-invariant exposure, poor approximations are obtained.

Table II shows the ratio between the required sample size obtained when CS or time-invariant exposure are used and the required sample size obtained when the observed exposure process is used, i.e. when equation (1) is replaced by ${\left(\frac{1}{N}\sum _i{\mathbf{X}\prime }_i{\mathbf{\Sigma }}_i^{-1}{\mathbf{X}}_i\right)}^{-1}$ using the observed X_i values in the MSCM study. Calculations are done for both the cumulative exposure effect model (4) and the acute exposure effect model (5). Results for models (3) and (6) were almost identical. In this study, under the cumulative exposure effect model, incorrectly using the sample size formula for time-invariant exposure led to a large underestimate of the required sample size, except when RS was assumed and ρ_b1 was large. Assuming CS of exposure led to reasonably accurate estimates of the required sample size except when the response was RS, in which case slight overestimations were obtained. In order to consider the situation where fewer repeated measurements are planned, we repeated these calculations using data only from the first three periods of the study (r = 2). In that case, the approximation of assuming a CS exposure process provided accurate calculations for all response covariances considered.

Table II.

Ratio of required sample sizes obtained by dividing the required sample size assuming CS or time-invariant exposure by the required sample size obtained using the observed exposure distribution for the MSCM study (r = 27, p̄_e = 0.13, ρ_e = 0.1). The cumulative exposure effect model (4) or the acute exposure effect model (5) are assumed. Calculations are reported for different scenarios of the response covariance. The true prevalence of exposure at each time point is used except for the the time-invariant exposure case, where p̄_e is used. For model (5), V (t₀) = 0 is assumed.

Exposure Covariance Assumption	Response Covariance
	ρ = 0.8					ρ = 0.5
	CS	DEX	AR(1)	RS1	RS1	CS	DEX	AR(1)	RS1	RS1
		θ = 0.5		ρb1 = 0.1	ρb1 = 0.5		θ = 0.5		ρb1 = 0.1	ρb1 = 0.5
Cumulative exposure effect (model (4))
Time-invariant	0.16	0.26	0.27	0.53	3.48	0.16	0.20	0.18	0.53	3.48
CS	1.01	1.04	1.01	1.17	1.25	1.01	1.03	1.02	1.17	1.25
Acute exposure effect (model (6))
Time-invariant	0.97	9.09	14.4	10.2	84.5	0.97	4.02	3.31	10.2	85.6
CS	0.98	0.91	0.90	0.97	0.97	0.98	0.93	0.92	0.97	0.97

¹ρ_b0,b1 = −0.5

For the acute exposure effect model (5), as the response covariance departed from CS, the formulas that assumed a time-invariant exposure led to a substantial overestimation of the required sample size, in part due to the large r of the study. Assuming CS covariance of exposure led to reasonably accurate calculations, with underestimation of sample size no less than 10% in all scenarios considered. As before, we repeated the same calculations but only using the first three periods of the study. Then, using the formulas for a time-invariant exposure led to underestimations of 10% to 20%, as opposed to the overestimations obtained when the full study was considered, while assuming CS of exposure still provided good aproximations.

In conclusion, assuming CS covariance of exposure gave very accurate calculations in this example, while the existing formulas for a time-invariant exposure perform led to seriously flawed calculations.

6. DISCUSSION

In this paper, we developed study design formulas that accommodate a time-varying exposure for longitudinal studies designed to compare rates of change in the response according to exposure. The paper is mainly focused on the design of observational studies, where the within-subject variation of exposure is not determined by design. We defined models for acute and cumulative effect of exposure and presented some simplifications so that the only additional parameters needed to calculate the required sample size when the exposure varies with time within a subject are the exposure prevalence and the intraclass correlation of exposure. When studied numerically and applied to a real data example, our methods provided reasonable approximations for the required sample size, which in many cases greatly improved the results that would have been obtained by using the available methods for time-invariant exposure. The formulas presented in this paper are implemented in a public access program that can be downloaded at the link provided in section 1 (Web Appendix F).

We examined whether studies with a time-varying exposure require recruiting more or less participants than a study with a time-invariant exposure. Under the cumulative exposure effect models, a study with a time-varying exposure requires more participants than one with a time-invariant exposure when the response covariance is CS or DEX, and in many cases with RS covariance. Under the acute exposure effect models, the results depend on the covariance of the response. If the response has a CS covariance, we find the same result as in the cumulative exposure case, and the study with a time-varying exposure requires more participants. However, in studies with several repeated measures and a DEX or RS covariance of the response, a significantly lower number of participants may be needed in the time-varying case compared to the time-invariant case.

The influence of dropout in the required sample size has been studied previously in studies with time-invariant exposure [4, 5, 8, 9, 10]. Galbraith and Marschner[8] suggested the method of computing N for 90% power when 80% power is intended and Fitzmaurice et al.[11] suggested inflating N by 1/(1 − f), where f is the anticipated fraction of lost to follow-up. The performance of these approaches in longitudinal studies with time-varying exposures remains to be investigated. Another interesting topic for future research is to generalize the summary measure approach [4, 11] to the analysis of longitudinal studies with a time-varying exposure, and compare the efficiency of that analysis to the GLS approach used here.

We presented methods that provide accurate estimates of the required sample size given information on parameters that can often be obtained or guessed by the investigator a priori. It is advisable to perform sensitivity analysis by assessing the effects of different values of the required parameters before determining the final sample size. We hope that the software we provide, which can be downloaded at the link provided in section 1 and implements all calculations presented in this paper, will be a helpful tool for study planning in these unavoidably complex settings. A demonstration of the program use can be found in Web Appendix F.