Impact of a single base pair substitution on the charge transfer rate along short DNA hairpins

Abstract

Numerical studies of hole migration along short DNA hairpins were performed with a particular emphasis on the variations of the rate and quantum yield of the charge separation process with the location of a single guanine:cytosine (G:C) base pair. Our calculations show that the hole arrival rate increases as the position of the guanine:cytosine base pair shifts from the beginning to the end of the sequence. Although these results are in agreement with recent experimental findings, the mechanism governing the charge migration along these sequences is revisited here. Instead of the phenomenological two-step hopping mechanism via the guanine base, the charge propagation occurs through a delocalization of the hole density along the base pair stack. Furthermore, the variations of the charge transfer with the position of the guanine base are explained by the impact of the base pair substitutions on the delocalized conduction channels.

Despite a rather long history, investigations of excess charge carriers in DNA remain an area of intensive experimental and theoretical research (reviewed in refs. 1–3). This interest is mainly due to the relevance of the charge transfer (CT) phenomenon to the oxidation damage (4, 5) and to the potential application of DNA in nanoelectronics (6, 7). Experimentally, charge migration through DNA can be probed either by steady-state methods based on measurements of the damage ratio (8–10) or by time-resolved spectroscopic techniques (11–14). The latter experimental approach was shown to be particularly efficient for monitoring charge motion in DNA hairpins (13). To carry out time-resolved spectroscopic experiments on these small DNA model systems, the opposite ends of the hairpin are capped with stilbene linkers S_a and S_b, serving as the hole donor and acceptor, respectively. It has been demonstrated that photoexcitation of S_a results in the formation of a bound electron–hole pair initially localized on the hole donor. The separation of this pair occurs via the migration of the hole along the hairpin and the subsequent reaction of the positive charge with the stilbene acceptor. Kinetics of the hole arrival at S_b, monitored by a second pulse, enable one to deduce the hole arrival rate, k_a, and the quantum yield, Φ_a, of the charge separation process.

Hole migration along hairpins with less than three base pairs is discussed in terms of a single-step superexchange (15–18). In contrast, multistep sequential hopping is assumed to be responsible for charge propagation along longer hairpins (19–23). The competition between these two mechanisms leads to a distance dependence of the hole arrival rate given by:

where N is the number of base pairs in the sequence, κ₁ and κ₂ are scaling factors, 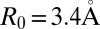is the mean interbase pair distance, 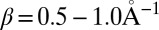is the exponential falloff parameter for the superexchange mechanism (24–29), and 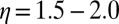is the exponent of the power law characteristic for the incoherent multistep hopping mechanism (13, 14, 15, 23, 30, 31).

Recent experiments have demonstrated that the rates of CT processes in DNA hairpins depend not only on the distance between the donor and the acceptor sites but on the base pair sequence (32–37). In particular, it has been found that sequences containing both guanine:cytosine (G:C) and adenine:thymine (A:T) base pairs exhibit a faster hole transfer between S_a and S_b than sequences involving only A:T base pairs (32, 33). This increase of the arrival rate was attributed to the low ionization potential (IP) of the G base, which is 0.5 eV smaller than the IP reported for adenine molecules (38, 39). Recently, Lewis et al. (32) have also studied the migration of a positive charge along hairpins containing a single G:C base pair incorporated in a poly(A)-poly(T) sequence. Their results show that the substitution of the first A:T base pair of this sequence by a G:C pair results in a significant decrease of the charge separation quantum yield, Φ_a, and a small increase of the k_a value. In contrast, the replacement of the last A:T with a G:C base pair results in little or no change in Φ_a and significantly increases k_a (32).

A phenomenological two-step kinetic scheme was proposed to explain the variations of k_a and Φ_a with the location of the G base in the sequence (32). Initially localized on S_a, the hole is transferred to the G base in a single step using the intermediary A bases as virtual states. The G base then serves as a temporary resting site for the hole density. The hole is thereafter transferred from the G base to the hole acceptor once again using the A bases as virtual states (32). The effect of the position of a single G:C pair on k_a can also be demonstrated by calculating the mean first passage time for a random walk in a finite 1D system (40) or by analyzing the hopping regime of intramolecular electron transfer (23). However, in both cases, this effect can be demonstrated only within the framework of particular random walk models using certain assumptions about the energy landscape. In addition, the lack of information about the rates of elementary steps involved in such stochastic processes does not allow verification of the validity of the models and assumptions used, making a quantitative description of the effect under consideration difficult.

Several theoretical models have been developed to gain deeper insight into the mechanism of CT along DNA hairpins (16, 21, 41–44). Semiclassical approaches, such as the variable range hopping (21) that considers incoherent transfer via a mixture of localized and delocalized channels, generally provide satisfying results for extended oligomers. However, these methods fail to capture the coherent nature of CT along short hairpins. Quantum propagation of the charge density using various model Hamiltonians has been extensively performed to describe the cross-over between superexchange and incoherent hopping (18, 45). These calculations usually give satisfying results for short hairpins, but their predictions for longer sequences are at best qualitative (18). Furthermore, and despite recent efforts (46), a satisfying theoretical explanation for the dependence of k_a and Φ_a on the position of the G base is still missing. It should also be mentioned that the idea of the sharp transition between superexchange and hopping has been questioned (47) and that an intermediary mechanism, such as quantum filling, may play a crucial role during CT along hairpins containing 3–10 base pairs.

We have recently presented numerical simulations of CT in poly(A)-poly(T) hairpins (47). Calculations performed within the framework of our model yield values of k_a that are in good agreement with experimental data for hairpins containing one to six A:T base pairs. Our simulations also demonstrate the existence of a CT mechanism intermediate between superexchange and multistep hopping. As previously suggested (48, 49), this intermediate CT mechanism is mediated by a fluctuation-gated delocalization of the charge density along the base pair stack. Such delocalization can be expected for homopurine systems, where all the base pairs are identical. However, the incorporation of a G:C base pair in a poly(A)-poly(T) sequence is expected to cause localization of the hole density on G (i.e., on the nucleobase with the lowest oxidation potential).

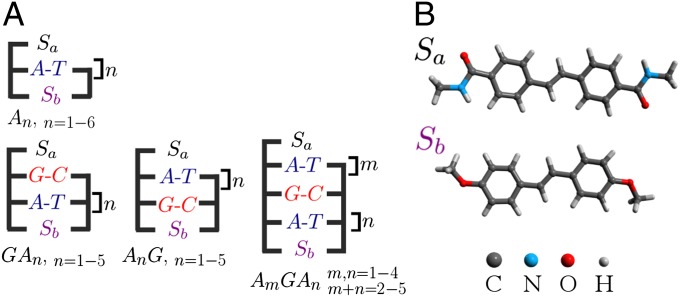
In the present paper, we study CT along the sequences shown in Fig. 1. With the exception of the A_n series, each of these sequences contains a single G:C base pair. A tight-binding Hamiltonian (47) was used to simulate the charge propagation along these sequences. The site energy of individual base pairs and the electronic coupling between neighboring pairs have been previously evaluated from density functional theory (DFT) electronic structure calculations coupled to molecular dynamics (MD) simulations (18, 46). This MD/DFT procedure revealed large temporal fluctuations of the electronic couplings and site energies induced by conformational changes of the hairpin (50). As demonstrated earlier (18), this dynamic disorder helps the hole density to overcome the potential barrier created by the electrostatic interactions between the propagating positive charge and the anion . To simulate the dissipative dynamics of the propagating hole, a stochastic surrogate Hamiltonian (SSH) scheme was used (47, 51–54). The SSH approach is based on the numerical propagation of a multiparticle density matrix that accounts for the degrees of freedom associated with the propagating charge and a few phonon modes (47) (details are provided in SI Text). Note that the methodology developed here is rather general and would be suitable to study CT in a large variety of materials, such as molecular wires (55) or discotic liquid crystals (56).

Fig. 1.

Structures of DNA hairpins (A) and stilbene linkers S_a and S_b (B) serving as the hole donor and the hole acceptor, respectively.

Results

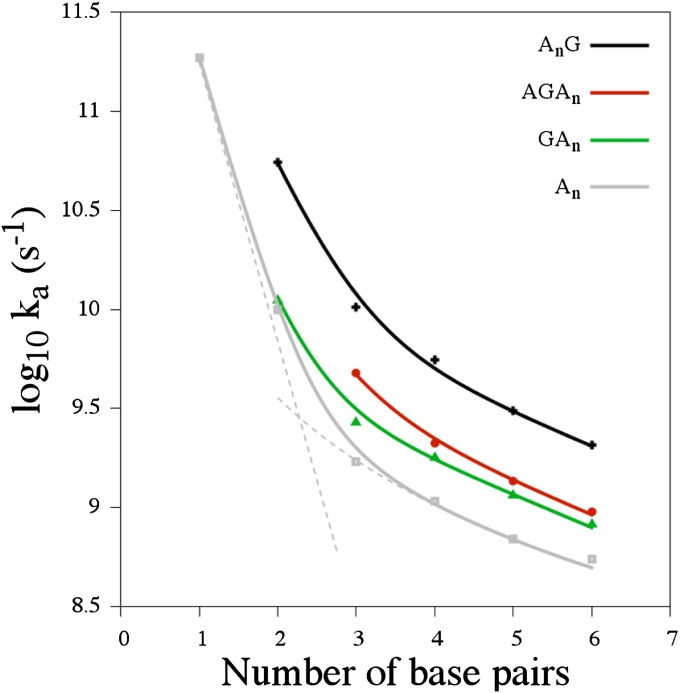
Characteristic time-dependent dynamics of the site populations obtained within the framework of our model for different hairpins are reported in SI Text. The hole arrival rate, k_a, and the quantum yield of the charge separation process, Φ_a, were directly deduced from the hole dynamics by fitting the population of the hole acceptor site with a rising exponential function (47) (details are provided in Tables S1 and S2). These values are shown in Fig. 2 and compared with experimental results in Table 1. As seen in this table, theoretical and experimental results for k_a were found to be in satisfactory agreement. As explained in our previous study (47), such a satisfying agreement is only possible if trap states are included in our model. Fig. 2 shows that the distance dependence of the arrival rate obtained with our model is well described by Eq. 1 for each series. The fitting of our numerical results with this equation yields values of the falloff parameter β ranging from 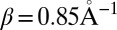for the A_n series to 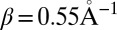for the A_nG series. The exponent η of the power law was found to be independent of the base pair sequence and was equal to 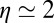for all the series. The scaling factor κ₁ was found to be equal to a few picoseconds for each series, whereas κ₂ was found to vary from 1.6 ns⁻¹ for the A_n series to 20 ns⁻¹ for the A_nG series. This important increase of κ₂ suggests that the introduction of a G:C base pair in the sequence facilitates CT via neighboring sites (47).

Fig. 2.

Arrival rate k_a calculated for different hairpin lengths and sequences (dots) and fit of these values according to Eq. 1 (solid line). The results obtained for four different series are represented: A_n (gray), GA_n (green), AGA_n (red), and A_nG (black). Large (small) values of k_a are obtained when the G:C base pair is located next to S_b (S_a).

Table 1.

Experimental and theoretical values of the arrival rate (k_a) and the charge separation quantum yield (Φ_a)

	Experiment (32)		Theory
Sequence	ka, ns−1	Φa	ka, ns−1	Φa
AG	30.90	0.70	54.95	0.61
A2G	8.31	0.52	10.23	0.15
GA	11.32	0.20	11.5	0.27
GA2	4.67	0.07	2.69	0.18
AGA	5.24	0.16	4.78	0.12
A2GA	2.18	0.29	2.29	0.13
A3GA	1.00	0.30	1.54	0.10
A4GA	0.16	0.12	0.97	0.09

Our calculations show that the position of the G:C base pair along the sequence modifies the value of the arrival rate significantly. Performing the A:T/G:C substitution on the first site of the sequence, (i.e., the base pair next to S_a) yields small changes in the value of k_a. Differently, an A:T/G:C substitution performed on the site next to S_b increases k_a significantly. This modification of the arrival rate on base pair substitution is clearly visible in Figs. S1–S3. The hole density localized on S_b significantly increases when placing the G:C base pair near S_b. These theoretical results are consistent with experimental findings (33) and suggest that hairpin A₅G is a promising candidate to obtain fast and efficient charge separation over long distances. These results may remain valid for longer sequences. However, CT along longer hairpins is expected to be less sensitive to sequence modifications. Hence, the CT rate along A₉G and GA₉, for example, may be very similar.

Discussion

As mentioned in the Introduction, it is usually assumed that the introduction of a G:C base pair in the sequence allows the hole density to bypass several A:T bases during its propagation along the hairpin (32). In this picture, the hole directly hops from the hole donor to the G base and/or from the G base to the hole acceptor.

CT Mechanism.

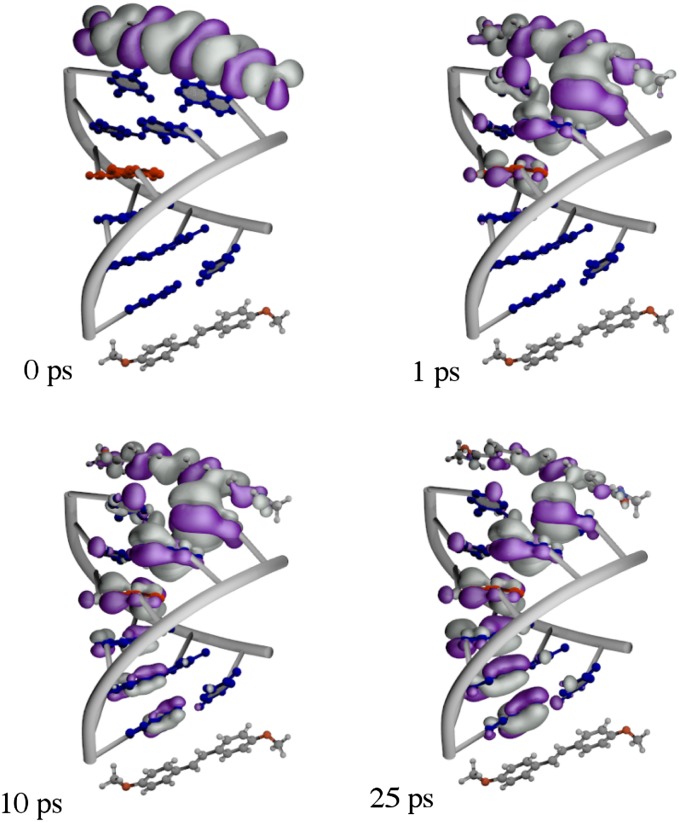
The CT mechanism obtained from our simulations is very different from the two-step mechanism described above. This difference becomes evident from the example depicted in Fig. 3. Initially localized on S_a, the hole density is rapidly transferred to the first A base pair, where 60% of the total charge is localized after 1 ps. The charge density is then slowly transferred to the subsequent base pairs, asymptotically tending to a nearly uniform distribution along the base pair stack. The hole density is thereafter transferred to the hole acceptor. However, due to the large energy difference between the base pairs and the hole acceptor, this last transfer step is slower than the interbase pair transfer and should be considered as the limiting step of the charge propagation (47). As shown in Table S3, an A:T/G:C substitution at a given position along the hairpin always increases the charge density localized on that site. However, this increase is weak, and a strong localization of the hole density on the G base, typical for the familiar model of sequential hopping, has never been reproduced in our calculations.

Fig. 3.

Snapshots of the hole propagation along the A₂GA₃ hairpin. The hole density is depicted in gray and purple. The two colors correspond to a positive phase and a negative phase of the wave function. The G:C and A:T base pairs are shown in red and blue, respectively.

A similar CT mechanism without localization of the charge density has been reported for hairpins with poly(A)-poly(T) sequences (47). This CT mechanism is intermediary between superexchange and hopping (47), and it is characterized by a progressive filling of the molecular orbitals of the base pairs. This quantum filling asymptotically yields a nearly uniform distribution of the charge density along the hairpins. This uniform charge distribution is in contrast to the one obtained with the phonon-assisted polaron hopping mechanism (42). Charge delocalization within small CT-active domains formed by 5–10 strongly interacting base pairs has been proposed previously to explain charge propagation along extended hairpins (17, 48). CT then occurs via conformationally gated hopping between neighboring domains. Such a propagation mechanism could, in principle, be included in our calculations by considering several tightly packed base pair stacks that are weakly coupled with each other. The method presented in this article may then be suitable to study how the charge density is transferred between neighboring domains. Note, however, that our model ignores the reorganization of the solvent around the hairpin. Therefore, this model may not be valid for long hairpins, where the time required for hole delocalization is comparable to or greater than the solvent reorganization time (57, 58).

Effect of the G Position.

A simple explanation for the variations of k_a with the position of the G:C base pair along the sequence can be obtained via the analysis of the delocalized conduction channels (DCCs). As originally proposed in the framework of the variable range hopping model (21), CT can be described in terms of localized channels (i.e., transfer between neighboring sites, see Table S4 for details) or DCCs. The two representations are equivalent, and calculations performed using either of them lead to the same values of the arrival rate and quantum yield. However, when considering the DCCs, the charge propagation is described in terms of transfer from S_a to S_b via the eigenstates of the base pair stack: In this representation, a series of noninteracting parallel quantum states (i.e., the DCCs) bridge the hole acceptor and the hole donor. Due to the weak coupling between S_a, S_b, and the DCCs, the effective transfer rate via the ith DCC can be approximated by:

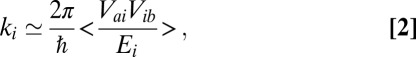where V_ai and V_bi are the coupling between the ith channel and S_a and S_b, respectively, and E_i is the energy of the ith channel. The < > symbol indicates the average over the dynamic disorder. Due to the low IP of the G base, an A:T/G:C substitution decreases substantially one or several E_is. Such substitution also modifies the delocalization of the DCCs along the hairpin, and therefore increases or decreases the couplings V_ai and V_ib.

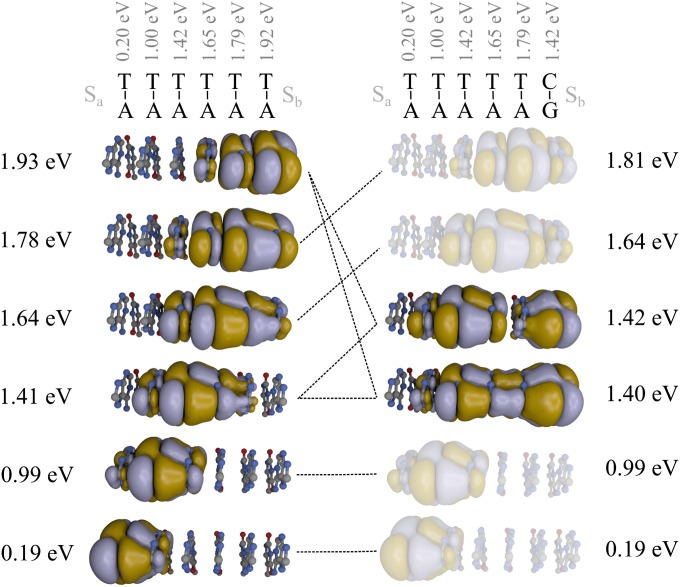
To understand the variations of k_a with the position of a single G:C base pair in the sequence, we analyze the modifications of the DCCs of a six-base pair hairpin induced by an A:T/G:C substitution performed at different locations along the sequence. The details of this analysis can be found in Table S5. The DCCs of hairpins A₆ and A₅G are shown in Fig. 4 as examples. Due to the energy profile along the base pair stack, the low energy DCCs of A₆ are strongly localized near the hole donor, whereas the high energy channels are delocalized over several base pairs near S_b. Therefore, an A:T/G:C substitution on the first base pair modifies only the two lowest DCCs. Due to their strong localization near S_a, these two channels interact very weakly with the hole acceptor and play a minor role in the CT process. This explains the weak increase of the arrival rate between the A_n and GA_n series as represented in Fig. 2. As seen in Fig. 4, the substitution of the last A:T base pair by a G:C base pair has a much more important impact on the DCCs. This substitution decreases the energy of the highest DCCs by 0.5 eV. As a result, two strongly DCCs with energy of ∼1.41 eV are created. These channels interact significantly with both S_a and S_b and substantially improve CT from the hole donor to the hole acceptor. In a more general way, one can see from Fig. 4 that an A:T/G:C substitution performed near the end of the hairpin perturbs several DCCs, whereas a substitution performed at the beginning of the sequence only modifies one or two DCCs localized near S_a. Therefore, shifting the position of the G:C base pair from the beginning to the end of the hairpin gradually improves the transport properties through the base pair stack.

Fig. 4.

Spatial localization of the DCCs of hairpins A₆ and A₅G and their energies in reference to S_a energy. The four DCCs weakly modified by the A:T/G:C substitution have been shaded for clarity. S_a and S_b are not shown. The dotted lines show the hybridization of the DCC induced by the A:T/G:C substitution.

Conclusion

We report computational modeling of hole migration along short DNA hairpins performed within the SSH approach using a tight-binding Hamiltonian to describe the propagation of the hole along the base pair stack. Our results show that the position of a single G:C base pair within a poly(A)-poly(T) sequence strongly affects hole migration. Moreover, the value of the hole arrival rate at S_b depends on the location of the A:T/G:C substitution. Efficient CT was obtained for hairpins with a G:C base pair located next to the hole acceptor. By contrast, if the G:C base pair is located next to the hole donor, values of the arrival rate were found to be similar to those obtained for poly(A)-poly(T) hairpins. These theoretical results are consistent with experimental findings.

The mechanism of CT that follows from our theoretical analysis is different from the phenomenological two-step hopping mechanism recently proposed to explain the charge propagation along hairpins containing a single G:C base pair. Instead of this sequential hopping, our calculations show an intermediate situation with complete delocalization of the charge density along the entire base pair stack. The replacement of an A:T base pair by a G:C base increases the charge density temporarily localized on this site, but a strong localization of the charge density on the G base was never obtained. For relatively long hairpins, the CT mechanism is neither a superexchange nor sequential multistep hopping mechanism but rather a progressive quantum filling of the base pair molecular orbitals.

To understand the reason for the dependence of the CT efficiency on the location of the G:C pair, we have analyzed the impact of base pair substitutions on the DCCs formed by the interacting base pairs. The replacement of the first A:T base pair with a G:C pair only affects the low energy channels strongly localized near the hole donor. Consequently, such substitution only slightly improves the efficiency of hole transfer between the hole donor and acceptor. On the contrary, if the substitution is performed near the hole acceptor, several strongly delocalized high energy channels are affected. This important modification of the conduction channels leads to larger values of the arrival rate on S_b. For example, our calculations predict that the arrival rate obtained for hairpin A₅G is fivefold larger than the one obtained for hairpin A₆. Our results may also be transferable to CT in organic material, such as discotic crystals or organic semiconductors, where the charge propagation is influenced by coherent and incoherent processes.

Materials and Methods

The tight-binding Hamiltonian describing the hole motion on the base pairs has been parametrized using DFT/MD simulations (18, 46). Random fluctuations of the diagonal and off-diagonal terms in the Hamiltonian of the system were included in the model to simulate the dynamical disorder induced by the large deformations of the hairpin. These fluctuations follow a Gaussian distribution whose parameters have been extracted from the results of MD simulations. During the simulations of the hole dynamics, five quantum modes were explicitly treated in the bath Hamiltonian. These quantum modes model the intramolecular vibration modes of the molecules. The energies of these modes were randomly chosen following a Gaussian-distributed random generator with parameters providing the best fit to the super-ohmic spectral density of the bath. Quantum jumps were performed in the bath manifold with an average lifetime of the bath mode of ∼10 fs. The dynamics were solved 500 times with time steps of 1 fs to converge to the final evolution of the hole density. The details of the method used to simulate the dynamics can be found in SI Text and in our previous study (47).