SUMMARY
The NIH project ”Inflammatory and Host Response to Injury” (Glue) is being conducted to study the changes in the body over time in response to trauma and burn. Patients are monitored for changes in their clinical status, such as the onset of and recovery from organ failure. Blood samples are drawn over the first days and weeks after the injury to obtain gene expression levels over time. Our goal was to develop a method of selecting genes that differentially expressed in patients who either improved or experienced organ failure. For this, we needed a test for the association between longitudinal gene expressions and the time to the occurrence of ordered categorical outcomes indicating recovery, stable disease, and organ failure. We propose a test for which the relationship between the gene expression and the events is modeled using the cumulative proportional odds model that is a generalization of the Pooling Repeated Observation (PRO) method. Given the high-dimensionality of the microarray data, it was necessary to control for the multiplicity of the testing. To control for the false discovery rate (FDR), we applied both a permutational approach as well as Efron's empirical estimation methods. We explore our method through simulations and provide the analysis of the multi-center, longitudinal study of immune response to inflammation and trauma (http://www.gluegrant.org).
Keywords: Microarray analysis, ordinal data, score test, multiple testing, permutation test
1. Introduction
The Inflammation and Host Response to Injury (known as the Glue study) is a multi-centered project, sponsored by the National Institute of Health, to study the immunologic responses to severe injury (http://www.gluegrant.org) [1]. The primary goal of this project is to examine the complex set of events that lead to the body's immune response to injuries from trauma or severe burns. These responses lead to an inflammatory process that, while necessary for healing, can lead to a cascade of events that result in organ failure or eventual death. In the Glue study blood samples were collected at pre-determined times for micro-array analysis. Study investigators were interested in whether gene expression changes over time correlate with the observable clinical events and well-defined physiologic changes that occur in trauma patients. For this, we needed a method that would simultaneously detect genes whose differential expression is associated with either recovery or progression to organ failure.
Many methods have been proposed for relating gene microarrays to either continuous or categorical measurements. Ring and Ross [2] offer a comprehensive review of methods that use microarrays for tumor classification. Techniques have been proposed for differentiating gene expressions over time [3], [4], or for relating longitudinal expressions to a binary outcome variable [5]. Also, methods have been developed for the analysis of the impact that changes in gene expression level have on a failure time outcome [6]. However, there are no methods available for identifying genes whose changes over time are related to ordered events.
Ordinal responses recorded over time are common in a variety of applications. For example, in studies of management of pain, subjects are asked to evaluate their level of pain on several occasions, in order to assess the effectiveness and duration of anti-pain medications. Such responses are naturally recorded using an ordinal scale. Ordinal responses, however, pose additional difficulties compared to the usual, say, continuous response variable in an ordinary regression model. This is because the discreteness of the response variable implies a differing scale for a linear combination of predictors. Generalized linear models (GLMs) were developed as an extension to the ordinary regression models in order to accommodate non-continuous types of response variables.
For the Glue study, investigators believed that the gene expression over time is different in patients who will recover compared to those who will not recover or from those who will develop life-threatening complications such as a multiple organ dysfunction syndrome (MODS). For example, if for a gene effects inflammation, an increase in the expression of the gene could be associated with organ failure, while a decrease could be associated with recovery. Instead of recording only whether a recovery event occurred or not, as we would do in a failure time analysis, we observe the occurrence of one of three possible outcomes over time and a gene microarray collected at several scheduled times in the study. Thus, we consider a longitudinally collected measurement and an ordered categorical response [7]. Our goal is to devise a one-degree of freedom hypothesis test for genes that have an opposing effect between the two extreme (absorbing) outcome categories. This single test could provide a powerful test of the impact of the gene on both recovery and failure.
A significant problem posed by the high-dimensionality of the microarray data is the number of tests that must be performed, both in computational intensity and multiplicity of hypothesis testing that requires a careful consideration of error control. With regard to computational intensity, we seek a test statistic that can be rapidly calculated. With regard to multiplicity of testing, a common approach is to apply the concept of the “False Discovery Rate” (FDR) popularized by various authors [8], [9], [10]. The FDR is the proportion of falsely discovered genes among those ’discovered’ (i.e. the corresponding test statistics declared significant). However, the number of falsely discovered can not be directly observed, hence an issue arises in how to estimate this quantity. In addition, thousands of gene expression measurements in a microarray are not believed to be mutually independent, but measuring the underlying correlation is impossible given the extreme high-dimensionality of the data. Thus, the statistical methods need to somehow correct for this possible correlation without explicitly measuring it.
In this paper, we will propose a test for the effect of longitudinal changes in a gene array on the occurrence of ordered categorical outcomes. We apply this test for analysis of the Glue data. A computer program that implements our proposed methods was written in R (www.r-project.org) and made available at www.hedwig.mgh.harvard.edu/biostatistics/software.php. Details on the parallel computing interface, which we implemented by employing a 30-node computer cluster, has also been made available [11].
2. Model
Consider n subjects followed over time during which we record the occurrence and timing of one of 3 possible ordered outcomes of interest. Let Δ denote the categorical outcome variable, so that Δit = j indicates that subject i experienced a category j event at time t, where i = 1, . . . , n, j = 1, 2, 3, and t ∈ τ, a set of exact event times. The ordering among the outcome categories reflects the natural ordering among clinical events. For the Glue data, the ordered categories of events were recovery, unchanged status, or organ failure. An important distinction is that the two outer, extreme categories represents an ’absorbing’ state, which implies that if and when a patient experiences these categories of response, that patient is considered to have reached the end of the study follow-up. The middle category, j = 2, indicates the patient is still at risk for the development of any of the two extreme categories of response. The exact event times are recorded when the event happens, but gene arrays levels are only available at pre-determined fixed points in time. The indicator δijt = I(Δit = j) records whether subject i moves to category j at time t.
Let Xit denote a gene expression level (for a particular gene) for subject i at time t. We suppress the index indicating the particular gene in the notation below, but note that each test is performed for each gene separately. We are interested in making inferences about πijt = p(Δit ≤ j|Xit), which is a probability of a subject i having an event in category j or lower at time t, given the covariate value Xit at time t. We want to construct a test of hypothesis to assess whether the probability of any event is independent of the gene expression level, H0 : πijt = p(Δit ≤ j|Xit) = p(Δit ≤ j). The relationship between the longitudinal gene array (covariate) and response categories (recovery or MODS) can be modeled via the cumulative proportional odds model. A gene expression on a single gene is viewed as a continuous variable whose level varies over an interval. Under the assumption of the proportional odds, the effect of a covariate is proportional across categories of events represented by cumulative odds model:
| (1) |
Thus, the cumulative proportional odds model conveniently describes the relationship we are interested in: the covariate effects are assumed to be homogeneous on a log-odds scale. The odds ratio of categories 1 and 2 vs. category 3 is the same as the odds ratio of category 1 vs category 2 and 3. This allows for the development of a one-degree test of hypothesis for a single parameter of interest. The association between X and Δ is reflected by β ≠ 0. The parameters μjt describe the cumulative odds of the jth category when β = 0. A necessary assumption of this model is that μ1t ≤ μ2t. Although the parameter β could be different for each category of event, βj, j = 1, 2, our goal is to devise a one-degree of freedom hypothesis test for genes that have an opposing effect between the two extreme outcome categories. We can write the likelihood for this model,
| (2) |
so that the log-likelihood is
| (3) |
The derivation makes use of the fact that , i.e., any single subject i can be in only one event category at any single time t.
Under the null hypothesis of no gene effect the model that we propose is very similar to a negative binomial model. The waiting time, considered as an integer, for the event to occur is where p0 is the probability of staying sick and p1, and p2 are the probability of death or recovery. Although this model is derived using an independence argument, it is a reasonable model for time to an event without concern for independence. Under the alternative hypothesis, this model is augmented by the effect of the gene using a proportional odds assumption. We do not feel that we are making a strong use of independence but rather positing a reasonable model for the probability of an event in this setting.
Let indicate the total number of patients with each category of events at each time, and is the total number at risk just before time t. Note that the parameters μ1t and μ2t, which capture the cumulative probability of each category under independence, can be treated as nuisance parameters, so that their maximum likelihood estimates, , , are solutions to partial derivatives of (3), set to equal to 0 and evaluated at β = 0:
| (4) |
| (5) |
From the second partial derivative equation:
| (6) |
which, when substituted into the first equation, produces:
| (7) |
Finally, we substitute (7) into (6) to obtain the following two identities:
| (8) |
2.1. Test Statistic
The score test statistic, derived from (3) and (8), is then:
| (9) |
This statistic can be used to test the null hypothesis, H0 : β = 0, about the relationship between a genomic covariate and the occurrence of the events of interest. If j = 1 and j = 3 denote the event of organ failure and respiratory recovery, respectively, then the test statistic in (9) captures the relationship between the covariate value and the ordinal nature of the events of failure and recovery. Furthermore, the test is two-sided, where positive values indicate a positive relationship of gene expression to the probability of a respiratory recovery and a negative relationship to the probability of organ failure. Likewise, negative values of the test statistic point to the negative association of the genomic covariate to the respiratory recovery and a positive relationship to organ failure. Positive relationship between a gene and the event means that the elevation in expression is related to a shorter time to the event.
This approach is also closely related to the analysis called the pooling repeated observation (PRO) method [12]. Namely, the PRO method treats each time interval between two examinations as a mini follow-up study and pools observations over all intervals to examine the relationship between a time-varying covariate and a disease endpoint using a logistic regression model. In our development, we extend this to a multi-category endpoint variable and utilize a form of polytomous logistic regression model.
The motivation for the ordinal model we use is provided by the ”threshold concept” [13], which is that there exists a continuous, latent variable that has been discretized by the ordered categories of the observed events. For an ordinal variable with J categories, this means there are J – 1 thresholds that separate the underlying unobserved continuous variable into the observed ordinal event categories. While the ”threshold concept” provides a convenient framework for the motivation of ordinal models, the assumption itself is not essential for the development of these models.
2.2. Variance Estimator
Because the gene expression data was only collected at fixed time points, the value of the gene expression level may be unknown at the time of the observed event. To handle this problem, we propose to predict the unknown value Xit of the gene expression at the time of the observed event by fitting subject-specific linear regressions, using the data up to and including the time of the event, Xit = α0i + α1i t + eit, t = 1, . . . , mi where mi is the total number of available observations up to time t, for subject i. Here, ei reflect the variability in estimating Xit with . Conditional on the random effects αi = (α0i, α1i), and on a subject's at-risk status, ei are assumed to be multivariate normal distributed with zero mean and independent variance σ2. Then, the predicted value X̂it has the expected value Xit and variance:
where SSit is the corresponding sum of squared differences from the mean, using values up to an including time t.
We can now proceed to find an estimator for variance of the statistic in (9). As before, we denote by nt the total number of subjects at risk at time t. If we define the vectors , and Yit = [1 – δi1t 1 – δi3t]T, then the contribution of individual i to the score test statistic in (9) can be re-expressed as
Let , the observed proportion of subjects with an event type j at time t. Since , it follows by the Slutsky theorem that
| (10) |
Thus, we can write,
| (11) |
and
We can now proceed as follows:
| (12) |
where,
| (13) |
and since , the individual contribution to the variance at each time t, for subject i is:
In practice, these quantities are estimated by replacing with and pit with p̂it. The in can be estimated by the pooled estimate of the residual sums of squares over all subjects. The theoretic details supporting the derivation can be found in [14], (Sections II.1 and V.6).
Finally, it follows that
which can be used in order to construct a variance-stabilized version of (9).
3. Multiple Hypothesis Testing
The derivation of the test statistic in (9) and its estimate of variance concentrated on an evaluation of a single gene at a time. Once we obtain a set of gene-specific test statistics calculated from the observed data, we want to assign significance to each, preferably taking into account the entire set of q statistics, where q is the number of genes collected at each time point. Note that since the gene array data is high-dimensional, q may be a very large number. Thus, the question of which longitudinal gene expressions are associated with the ordinal categories of events can be reexpressed as a multiple hypothesis testing problem where H0 : βk = 0, k = 1, . . . , q.
In order to address the multiplicity of testing, we consider a testing procedure which controls for the number of false positive findings, a standard approach to data from genome-wide studies. For each value of the gene-specific test statistic Tk, we consider the number of falsely positive findings (FP) among the total number called significant (TP) when Tk is used as a cutoff value,
The expected value of this ratio is referred to as the False Discovery Rate (FDR) for statistic Tk [15],
| (14) |
An estimate of FDR(Tk) is possible by directly estimating the numerator and the denominator. We call this estimator the False Positive Ratio (FPR) in order to emphasize it's derivation.
We consider two approaches which differ in how they estimate both the numerator and the denominator of this quantity. One is to perform permutations in order to simulate the null joint distribution of the test statistics and use it to estimate the number of falsely rejected null hypotheses. Permutation-based multiple testing techniques are commonly suggested as a way to account for the dependencies [16]. Hypothesis testing is performed by simulating the joint null distribution of the test statistics using permutations to determine the statistical significance of each statistic. The second testing approach we examine is known as local false discovery rate, proposed by Efron [9]. This approach includes a Bayes-based plan for empirical estimation of the empirical null distribution of the test statistics which is then used for determining significance of the test statistics.
3.1. Permutation-based multiple testing
One way to estimate the numerator of the expression in (14) is to simulate the joint null distribution of the test statistics using permutations which removes the need for explicitly specifying the joint distribution of thousands of genes [10]. The problem with using permutations of longitudinally collected covariates is that no samples were collected after the absorbing event for each patient, and even if they were, the gene expression values after the event may have been affected by the event which would preclude their use. As an alternative, we permute the event categories δ among subjects in a risk set at each event time, leaving the size of each risk set fixed. In other words, the number of subjects with events is kept fixed at each event time, but their event categories are randomly exchanged among those currently at risk.
We denote the q test statistics calculated on the observed data as T = [T1 . . . Tq], and permutation-based simulated statistics as . Namely, for each observed test statistic Tk, we use the permutation-based simulated null distribution to estimate the numerator in (14).
At each observed event time, we permute the event indicators among subjects at risk at that time. In other words, the number of subjects with events is kept fixed at each event time, with their event indicators randomly exchanged among those currently at risk. In what follows, we outline the algorithm as if all tests statistics, both those calculated on the original data and those calculated on the perturbed data, are positive. We do this for the ease of presentation, otherwise only the notation would become more involved. Let T = [T1, . . . , Tq] be test statistics calculated on each of the q-genes in the original data. Here, I(·) is the usual indicator function, where I(a) = 1, if a true.
The permutation-based testing algorithm proceeds as follows:
At each observed event time t, permute event categories among subjects still at risk at that time; This is equivalent to choosing njt, j = 1, 2, 3 elements out of nt, at time t;
Using such perturbed data, calculate a set of q test statistics, ;
- Compare each original Tk with all permutation-based T* and call the number of false positives the number among T* that are greater than Tk,
Repeat steps 1-3 many times. For each gene k, k ∈ {1, . . . q}, this produces a sequence of numbers, one per each permutation. Denote by the average value of such sequence for test statistic Tk;
- For each gene, the estimated proportion of false positives is the ratio of over the total number of statistics called significant when Tk is used as a cut-off value, i.e., . Thus, the estimate of the false positive ratio (FPR) for Tk is:
If a test statistic has an estimated proportion of false positives below a desired, prespecified level, say 10%, then the hypothesis is rejected and the observed test statistic is declared statistically significant. Our testing procedure is similar to the approach proposed by [15], when the estimated proportion of null hypotheses is set to 1, and the results are described in terms of the test statistic (rather than the appropriately defined p-value).
3.2. Local false discovery rate
The second approach to multiple testing we consider does not employ permutations in order to simulate a null distribution of the test statistics. Efron [9] suggests that the simultaneous testing problems which involve a large number of null hypotheses, lend themselves to the empirical estimation of the null hypothesis distribution under the assumption that the observed distribution is a mixture of two normal distributions representing null and non-null genes. He allows the possibility that even the null genes may show a small experimental effect that he attributes to possible unobserved covariates. He suggests using the terms interesting and uninteresting rather than null and non-null. This Bayesian-based version of the FDR concept is known as the local false discovery rate. The empirical estimate of the null distribution is based on a density-fitting method, the details of which can be found in [9]. In short, the algorithm proceeds as follows:
Using the observed data, obtain an empirical estimate of the null hypothesis distribution, f̂0(·); This involves estimating the proportion of truly null statistics;
Approximate the density of the observed test statistics, f̂(·), using any density-fitting method;
Calculate the ratio f̂0(·)/f̂(·), and call all statistics with this ratio less than pre-specified level (e.g., 10%) as significant.
Empirical estimation of the null distribution has an advantage over the permutation-based method, since it does not require computationally lengthy permutations of the original data. Furthermore, more complex data structures, such as longitudinal gene expressions and time to event data, require careful consideration of the most appropriate permutation algorithm, as it may not always be clearly how to perform the permutation. Furthermore, using “local FDR” allows for the possibility that “null” genes may still show a minor experimental effect which is something we have often observed in our data. For instance, we have noted small but statistically significant changes in the putative expression of genes on the Y chromosome (male chromosome) in women where no changes should have occurred.
4. Simulations
In order to perform simulations to assess validity and performance of our proposed score test statistic (9) it was necessary to develop a method to generate longitudinal gene expressions with associated ordered categorical events. Note that we needed to generate a subset of genes that are to be significantly related to the probability of an event, while the remaining genes were not associated with events. In our simulations, 50 of the 500 simulated genes (i.e., 10%) are generated using the algorithm below.
Generate a random intercept and slope (α0i and α1i) for each subject by sampling from a bivariate normal distribution with zero mean and non-identity variance-covariance matrix, Σ, estimated from the observed data; For k = 1, . . . , s ”significant” genes, longitudinal trajectories are then is a zero-mean, normally distributed measurement error, with variance , generated independently for each gene;
- Choose a value of the association parameter b and generate subject- and time- specific event probabilities pi1t, pi2t, pi3t using the identities derived from the proportional odds model in the following way. If we define
then it follows from the proportional odds model: pi1t = ε(μ1), pi2t = ε(μ2) – ε(μ1), and pi3t = 1 – ε(μ2). Use these probabilities to sample from a multinomial distribution with three categories to determine the status of the event category (0 or 1) at each time for each subject in the risk set at that time.
The algorithm stops when the pre-determined total length of followup is reached. The produced timing of the ordinal events is ’linked’ to the longitudinal trajectories through the random effects α1, α2. Namely, since the same random effects generated in Steps 1-2 are used in Step 3 to generate subject- and time-specific event probabilities (for all s genes set to be associated with the time to an event), subjects with comparable random effects get assigned similar event times. The longitudinal gene expressions for the remaining 450 genes are generated similarly, but using different random effects for each gene separately.
We were concerned with selecting genes one at a time that had an effect on recovery or death and we wanted to allow the possibility that several of them were important. The problem is that if we use some linear combination of the genes to influence the probability of an event in the simulation then the effect of each individual gene would be too small to pick up. Furthermore data generated from the combination would not fit our model for each individual gene. We therefore decided to simulate the data assuming there was some common trajectory that affected the transition probabilities and all the gene expression values shared this underlying trajectory. This would simulate the real life situation that many gene expression values are highly correlated because they are the reflection of the activation of the same network.
We generated 500 samples of data. Each sample consists of 100 subjects with 500 longitudinal gene expressions over 7 time-points. Using the above algorithm, 50 out of 500 genes were set to be significantly associated with the probability an event. Testing was done for five choices of the association parameter b, as well as two values for the measurement error, . The bs were chosen to give a reasonable range of effects, corresponding to odds ratios from 1 to 20. Within each sample, 500 permutations were performed in order to obtain a permutation-based estimate of false positive ratio. The two testing approaches are presented in the two parts in Table I. For example, in the top part of the table which presents simulation results for local FDR testing method, when the association parameter b is set to 2.5 and the measurement error of individual genes is , the median number of genes found significant over 500 samples is 43 genes, with an interquartile range of (35, 50). The median false positive proportion over 500 simulations is 0.02, with an interquartile range of (0, 0.05). For the same parameters in the bottom part of the table, the median number of false positives is 52 (46,55). The median false positive proportion over 500 simulations is 0.10, with an interquartile range of (0.07, 0.13). The last column, where b = 0, is included as a comparison and to check whether the test exhibits reasonable Type I error rates. Namely, if the association parameter is set to zero, b = 0, any significant genes should be found purely by chance, and we would expect the total number of significant genes to be zero.
Table I.
Simulation results n = 100 subjects; p = 500 genes (10% significant); significance cut-off = 0.10 500 replications; 500 permutations within each replication; medians (IQR*) presented
| Local FDR test |
|||||
|---|---|---|---|---|---|
| median (IQR) | b = 3 | b = 2.5 | b = 1.5 | b = 1.0 | b = 0 |
| # positive | 50 (47, 50) | 48 (39, 50) | 45 (37, 49) | 43 (36, 49) | 0 (0, 44) |
| prop. false + | 0.00 (0.00, 0.01) | 0.00 (0.00, 0.01) | 0.03 (0.00, 0.07) | 0.10 (0.00, 0.14) | – |
| # positive | 48 (39, 50) | 43 (35, 50) | 41 (27, 47) | 40 (23, 45) | 0 (0, 25) |
| prop. false + | 0.00 (0, 0.04) | 0.02 (0, 0.05) | 0.03 (0, 0.10) | 0.08 (0.02, 0.16) | – |
| Permutation-based test |
|||||
|---|---|---|---|---|---|
| median (IQR) | b = 3 | b = 2.5 | b = 1.5 | b = 1.0 | b = 0 |
| # positive | 56 (54, 58) | 54 (52, 56) | 47 (35, 52) | 41 (28, 52) | 0 (0, 1) |
| prop. false + | 0.10 (0.07, 0.15) | 0.09 (0.07, 0.12) | 0.10 (0.07, 0.12) | 0.09 (0.07, 0.13) | – |
| # positive | 55 (53, 58) | 52 (46, 55) | 47 (35, 52) | 40 (25, 51) | 0 (0, 1) |
| prop. false + | 0.10 (0.07, 0.15) | 0.10 (0.07, 0.13) | 0.10 (0.07, 0.12) | 0.08 (0.07, 0.13) | – |
IQR: Inter-Quartile Range
Inspection of the simulation results reveals an interesting difference between the two testing approaches. While the permutation-based test (lower table) performs well when the association parameter b is set to 3, 2.5, or 1.5, the local FDR approach (top table) has a lower than 10% proportion of false positive for those same values of b. Furthermore, while for both approaches the median number of found positive decreases as b decreases, the proportion of false positives decreases for the permutation-based method, but increases for the local FDR method. As b decreases from 3 to 1.0, the proportion of false positives in the top part of the table increases from 0 to 0.08 (10% being the ‘set’ false positive rate), while it remains stable for values 3, 2.5, or 1.5 in the bottom part of the table that corresponds to the permutation-based simulation.
The explanation for these differences can be found upon closer examination of the two algorithms. Namely, the local FDR algorithm constructs an estimate of the null distribution density curve by examining the distribution's mode and the variability around it in the observed distribution. If there is a group of test statistics away from the central, presumably null, bulk of the test statistics, the local FDR method will be sensitive to detecting the extreme values and would have a small number of false positive statistics. The permutation-based null distribution, on the other hand is centered around zero which results in higher number of test statistics found significant as well as a higher, yet more stable, number of false positive statistics.
5. Analysis of Trauma Data
The Glue study is generating an enormous and complex dataset as patients are closely followed and genomic data are collected on seven days during one month of followup. In addition, a large set of clinical and laboratory information used to assess recovery and organ failure are collected. An important observable clinical event in trauma patients is the time to a respiratory recovery, defined as the number of days from injury until a patient no longer needs a mechanical respirator. Such an event represents a positive clinical outcome and can be viewed as a marker of improving overall health. Another critical, observable event occurring in these patients is the multiple organ dysfunction syndrome (MODS) which reflects a complex disruption of the immune system. The Glue investigators want to identify families of genes for which temporal changes in expression prior to an occurrence of an important clinical event can help predict the course of recovery.
Data on 107 subjects with complete entries at the time of our analysis are presented. For the purpose of our analysis, the ordinal outcome variable is defined to have three categories: MODS, no change, and respiratory recovery. The ’no change’ category includes patients who neither developed a multiple organ failure nor recovered (and thus remained on the ventilator). In order to apply the described model, we assume constant covariate effect for both the log odds ratio of no MODS (j = 2 or 3) versus MODS (j = 1) and for the log odds ratio of no recovery (j = 1 or 2) vs. respiratory recovery (j = 3).
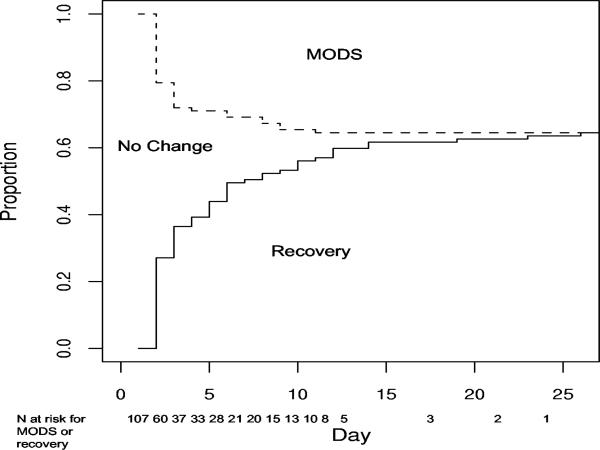
Figure 1 shows the distribution of types of events over all observed event times in this study. For each subject experiencing an event, only the time to the first event of either type is reported. There were 38 type 1 event (MODS) and 69 type 3 events (respiratory recovery). The study times ranged from 2 to 26 days, and the majority of both types of events occurred early in the study.
Figure 1.
Observed events over time
Genomic data collected on days 0, 1, 4, 7, 14, 21, and 28 were generated using commercially available oligonucleotide array technology (Affymetrix). Prior to any statistical analysis, data were normalized across arrays to achieve comparable levels, using the ’Invariant Set’ method as developed in the dChip software. Also, gene expressions were extracted from oligonucleotide probesets by employing a PM-only analysis of Li and Wong [17]. The gene expression values were log-transformed prior to any calculations.
To reduce the overwhelming dimensionality of a microarray, we first excluded those genes labeled ’Absent’ over all arrays by the Affymetrix software (Santa Clara, CA). In this context, absent means that the expression level is below the threshold of detection and the expression level is most likely not different from zero. We then performed a simple filtering of genes and include only those genes whose estimated coefficient of variation (CV) exceeded a threshold. The test statistic (9) that measures the association between gene expression and the category of events is calculated for each gene separately. We performed the two testing procedures described in above in order to determine the significance of each gene-specific test statistic. The results illustrate a differences between the testing methods. Firstly, the total number that would be considered significant if no adjustment for multiplicity of testing were done, (i.e., test statistics were compared with the 10th percentile of the standard normal distribution, z.10 = 1.645) is 231 genes among the total number of 3, 380 investigated. When we applied the permutation-based testing procedure, 65 genes were identified to be statistically significant at the 10% FDR level. At the same level, the local FDR approach identified 33 genes as significant, with a total of 21 genes appearing in both sets. Depending on the wealth of the prior knowledge regarding the selected genes, one would proceed with investigating further either the union or the intersection of these two set. A listing of a subset of selected genes is presented in the Web Tables.
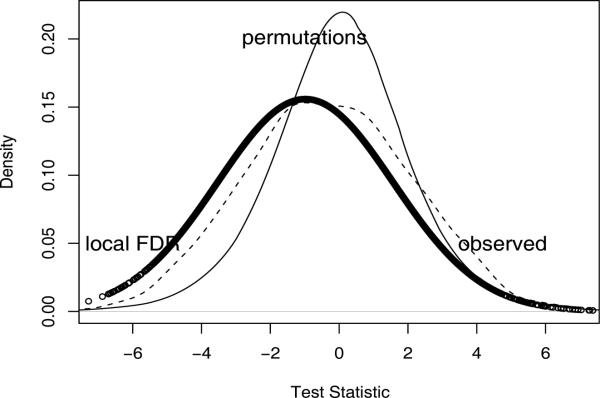
Figure 2 provides an insight about the nature and source of the differences in the number of genes found significant between these two testing procedures. The empirical estimate of the null hypothesis distribution (solid thick line) used in Efron's local FDR is centered around the observed mode of the distribution of test statistics. The fact that this mode is less than zero implies that in general higher gene expression levels are associated with a decreased chance of recovery. Also the standard deviation of the distribution is greater because there was variation in this effect. Both effects may be biological or artifactual. The advantage of the local FDR is that it doesn't matter because the genes that are ”different” than the norm are selected. Details on the estimation of the empirical mode and the width of the central peak of the observed distribution of the test statistics can be found in [9]. The permutation-based null hypothesis (thin solid line), on the other hand, is centered around zero. Figure 2 also includes an approximate distribution of the observed test statistics, obtained by kernel density estimation (e.g., density() function in the R package, dash line). Since the sign of the significant test statistic points to the direction of the association between the corresponding gene expressions and the event variable (MODS, no change, respiratory recovery), the choice of the multiple testing algorithm can lead to different gene selection results.
Figure 2.
Null hypothesis distribution for different multiple testing procedures
6. Discussion
We provide a method for the identifying longitudinal gene expressions associated with ordered categorical events. The categorical outcome variable consists of three ordered categories of events where the two outer categories are of the absorbing state. Our model is designed to identify genes whose expression changes over time have opposing relationship with the two extreme categories of events. Our approach addresses several issues posed by the analysis of such data. We address the issues of intermittently collected covariate data, unknown longitudinal behavior of a single gene expression, as well as the multiplicity of hypothesis testing when simultaneously considering many genes.
It should be noted that our permutation-based testing procedure involves the permutation of event categories among subjects at-risk at a given time. If we were to instead permute subjects and their corresponding longitudinal microarray histories, we would encounter an additional problem of missing covariate values as we permute subjects’ covariate histories of different lengths. It is possible to fill-in such data using values of subjects with complete data whose data are close on the known variables. This would require a definition of a distance metric in order to select subjects that are ’close’ or ‘similar’ to the subject with the missing observation.
We utilized a random effects model for the relationship of the covariate with time; however, more complex longitudinal models can easily be incorporated into our approach. A minimum set of assumptions regarding the functional relationship between longitudinal gene expression and timing of the events will depend on an individual biological problem at hand. For example, a natural extension would be to implement the approach of Song et al. [18], which requires only the assumption that the random effects have a smooth density. Another modification, which may be relevant in some applications, is to devise a multiple imputation procedure for the unknown covariate values. Although this will certainly add to the overall computational complexity, it would be interesting to explore whether it can be incorporated so as to take advantage of the computations already in place and the high-dimensionality of the data. Finally, in order to make the proposed test statistics more robust to potential outliers, the actual values of gene expressions may have to be replaced by ranks or some function of the ranks. The random effects model allowed us to handle the fact that the value of the gene expression was not available at the time of each event. One could consider simpler approaches to this such as carrying the last observation forward (LOCF method) to assign a value to the gene expression at each event. This is a reasonable alternative if the event times are close together and would avoid the use of the random effects model. However if the events are far apart and there is a monotonic effect of time on the gene expression level, then the LOCF method can create a bias.
We were interested in identifying a set of genes that could be investigated further for their utility in describing the population of trauma patients. Since this particular population has not been extensively studied in the past, our approach is exploratory in nature and represents a ’first step’ in a series of analysis that could possibly involve employing the found genes to predict future events in a single patient. Motivated by the need to find potential genes where expression changes indicate transition from ’no-change’ to either improvement or worsening of symptoms, our method utilizes a strong assumption of homogeneity of the odds ratios among the three categories of response. The assumption of the ’opposing effect’ also allows for a construction of a relatively simple 1-degree score test, which in turn enables us to construct a well-controlled multiple testing procedure. It may be possible to develop more complicated models where there are more than three states and more than one non-absorbing state. However, our goal was to test the effect of individual genes in as powerful a way as possible using information on both the recovery and the onset of organ failure. This suggests a test based on one parameter which measures the effect of each gene on both events. This model is the same whether you are modeling the transitions or the states because patients are always in the same state to begin with. With more states, it becomes impossible to have a single parameter capturing the effect on all events. For instance, if we had two non-absorbing states, a patient could move back and forth between them and it would be difficult to order these transitions so that we could develop a one-parameter model to measure the gene effect. It would be possible to develop more complex models or to have different parameters for different transitions, but one would lose the simple test for gene effect in order to gain this flexibility. Furthermore, although we know the genes are related, we used marginal methods to study gene at a time, which is a standard in this field. In general, if one is interested in estimation, more complex models could be advantageous. However, with high dimensional data testing, not estimation, is usually the analysis of interest because the primary purpose of genomic analysis is the discovery of genes that deserve a deeper study. Once a list of interesting genes is established, we can use bioinformatics tools to analyze them simultaneously to determine biologic pathways represented by the groups of these genes that are associated with recovery and failure. Interpretation of this analysis would require the collaboration of basic scientists in the Glue project, which is now underway.
Acknowledgments
The work presented in this manuscript is a part of the doctoral thesis of Natasa Rajicic in the Department of Biostatistics, Harvard School of Public Health, Boston, Massachusetts.
The financial support was provided by the following three awards: NIH Grants CA74302 and HD055201, Dr. Finkelstein, primary investigator, and Large-Scale Collaborative Project Award (U54-GM62119) from The National Institute of General Medical Sciences, NIH.
We extend our thanks to Drs. Cheng Li, John Storey, John Quackenbush and Robert Tibshirani for their helpful suggestions and review. The application specialist, Peter Lazar, engineered and maintained the computing parallel system used in our analysis.
The following is a list of participating investigators of the Inflammation and the Host Response to Injury research project: Henry V. Baker, Ph.D., Ulysses Balis, M.D., Paul Bankey, M.D., Timothy R. Billiar, M.D., Bernard H. Brownstein, Ph.D., Steven E. Calvano, Ph.D., David G. Camp II, Ph.D., George Casella, Ph.D., Irshad H. Chaudry, Ph.D., J. Perren Cobb, M.D., Joseph Cuschieri, M.D., Ronald W. Davis, Ph.D., Asit K. De, Ph.D., Celeste C. Finnerty, Ph.D., Bradley Freeman, M.D., Richard L. Gamelli, M.D., Nicole S. Gibran, M.D., Brian G. Harbrecht, M.D., Douglas L. Hayden, M.A., Laura Hennessy, R.N,. David N. Herndon, M.D., Jureta W. Horton, Ph.D., Marc G. Jeschke, M.D., Ph.D., Jeffrey Johnson, M.D., Matthew B. Klein, M.D., James A. Lederer, Ph.D., Stephen F. Lowry, M.D., Ronald V. Maier, M.D., John A. Mannick, M.D., Philip H. Mason, Ph.D., Grace P. McDonald-Smith, M.Ed., Carol L. Miller-Graziano, Ph.D., Michael N. Mindrinos, Ph.D., Joseph P. Minei, M.D., Lyle L. Moldawer, Ph.D., Ernest E. Moore, M.D., Avery B. Nathens, M.D., Ph.D., M.P.H., Grant E. O'Keefe, M.D., M.P.H., Laurence G. Rahme, Ph.D., Daniel G. Remick, Jr. M.D., Michael B. Shapiro, M.D., Geoffrey M. Silver, M.D., Richard D. Smith, Ph.D., John Storey, Ph.D., Robert Tibshirani, Ph.D., Ronald G. Tompkins, M.D., Sc.D., Mehmet Toner, Ph.D., H. Shaw Warren, M.D., Michael A. West, M.D., Wenzhong Xiao, Ph.D.
REFERENCES
- 1.National Institute of General Medical Sciences (NIGMS) [02 February 2008];Inflammation and Host Response to Injury: a multi-disciplinary research project. http://www.gluegrant.org.
- 2.Ring BZ, Ross DT. Microarrays and molecular markers for tumor classification. Genome Biology. 2005;3:2005.1–6. doi: 10.1186/gb-2002-3-5-comment2005. PMID: 12049658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Luan Y, Li H. Clustering of time-course gene expression data using a mixed-effects model with B-splines. Bioinformatics. 2005;19(4):474–482. doi: 10.1093/bioinformatics/btg014. [DOI] [PubMed] [Google Scholar]
- 4.Yeung KY, Medvedovic M, Bumgarner RE. Clustering gene-expression data with repeated measurements. Genomic Biology. 2003;4(5):R34. doi: 10.1186/gb-2003-4-5-r34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Storey JD, Xiao W, Leek JT, Tompkins RG, Davis RW. Significance analysis of time course microarray experiments. Proceedings of the National Academy of Science. 2005;102(36):12837–12842. doi: 10.1073/pnas.0504609102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rajicic N, Finkelstein DM, Schoenfeld DA. Survival analysis of longitudinal microarrays. Bioinformatics. 2006;22:2643–2649. doi: 10.1093/bioinformatics/btl450. [DOI] [PubMed] [Google Scholar]
- 7.McCullagh P, Nelder JA. Generalized Linear Models. 2nd ed. Chapman & Hall; London, UK: 1989. [Google Scholar]
- 8.Tusher V, Tibshirani R, Chow G. Significance analysis of microarrays applied to the ionizing radiation response. Proceedings of the National Academy of Science. 2001;98:5116–5121. doi: 10.1073/pnas.091062498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Efron B. Large-scale simultaneous hypothesis testing: the choice of null hypothesis. Journal of the American Statistical Association. 2004;99(465):96–104. [Google Scholar]
- 10.Storey JD, Tibshirani R. Estimating false discovery rates under dependence, with application to DNA microarrays. Department of Statistics, Stanford University. 2001:2001–28. [Google Scholar]
- 11.Lazar P, Schoenfeld D. Self-contained parallel system for R. MGH Biostatistics; Boston, MA: 2004. http://cran.r-project.org/src/contrib/Descriptions/biopara.html. [Google Scholar]
- 12.D'Agostino RB, Lee ML, Belanget AJ, Cupples LA, Anderson K, Kannel WB. Relation of pooled logistic regression to time dependent Cox regression analysis: the Framingham Heart Study. Statistics in Medicine. 1990;9:1501–1515. doi: 10.1002/sim.4780091214. [DOI] [PubMed] [Google Scholar]
- 13.Hedeker D, Mermelstein RJ. Analysis of longitudinal substance use outcomes using ordinal random-effects threshold regression models. Addiction. 2000;95:S381–S394. doi: 10.1080/09652140020004296. [DOI] [PubMed] [Google Scholar]
- 14.Gut A. An Intermediate Course in Probability. Springer-Verlag; New York, Inc: 1995. p. 35. [Google Scholar]
- 15.Storey JD, Tibshirani R. Statistical significance for genomewide studies. Proceedings of the National Academy of Science. 2003;100(16):9440–45. doi: 10.1073/pnas.1530509100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Westfall P, Young S. p-Value adjustments for multiple tests in multivariate binomial models. Journal of the American Statistical Association. 1989;84(407):780–786. [Google Scholar]
- 17.Li C, Wong WH. Model-based analysis of oligonucleotide arrays: Expression index computation and outlier detection. Proceedings of the National Academy of Science. 2001;98(1):31–36. doi: 10.1073/pnas.011404098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Song X, Tsiatis AA, Davidian M. A Semiparametric likelihood approach to joint modeling of longitudinal and time-to-event data. Biometrics. 2002;58:742–53. doi: 10.1111/j.0006-341x.2002.00742.x. [DOI] [PubMed] [Google Scholar]