Computational approaches to understand cardiac electrophysiology and arrhythmias

Abstract

Cardiac rhythms arise from electrical activity generated by precisely timed opening and closing of ion channels in individual cardiac myocytes. These impulses spread throughout the cardiac muscle to manifest as electrical waves in the whole heart. Regularity of electrical waves is critically important since they signal the heart muscle to contract, driving the primary function of the heart to act as a pump and deliver blood to the brain and vital organs. When electrical activity goes awry during a cardiac arrhythmia, the pump does not function, the brain does not receive oxygenated blood, and death ensues. For more than 50 years, mathematically based models of cardiac electrical activity have been used to improve understanding of basic mechanisms of normal and abnormal cardiac electrical function. Computer-based modeling approaches to understand cardiac activity are uniquely helpful because they allow for distillation of complex emergent behaviors into the key contributing components underlying them. Here we review the latest advances and novel concepts in the field as they relate to understanding the complex interplay between electrical, mechanical, structural, and genetic mechanisms during arrhythmia development at the level of ion channels, cells, and tissues. We also discuss the latest computational approaches to guiding arrhythmia therapy.

this article is part of a collection on Systems and Computational Approaches to Cardiovascular Physiology. Other articles appearing in this collection, as well as a full archive of all collections, can be found online at http://ajpheart.physiology.org/.

Introduction

For over half a century, mathematical models of cardiac physiology have been used to complement experimental findings and clinical observations to improve understanding of cardiac electrical function in health and disease. The earliest models of cardiac cellular electrophysiology described the flow of currents across the cell membrane with just a few parameterized processes dependent on voltage and time (16, 79, 137, 155). In the last twenty years an explosion in development of sophisticated models has occurred, concomitant with improved computational speed, accuracy, and cost. More recently, advances have been made in numerical techniques and distributed computing (2, 168), the implementation of customizable modeling platforms such as Continuity (http://www.continuity.ucsd.edu/Continuity), CHASTE and OpenCMISS (19, 34), and infrastructures aimed at facilitating exchange of models such as CellML and FieldML (19, 34, 53, 177a, 243). Sophisticated cellular models take into account various properties and modulators of cell function including ionic homeostasis, metabolism, cell signaling, hormonal regulation, and genetic defects that alter the behavior of electrical components and cellular action potentials (APs). Individual cardiac model “cells” are now routinely replicated and coupled, creating mathematical representations of cardiac tissue in one, two, or three dimensions with incorporation of complex anatomical heterogeneities including anisotropy, structural features, and distinct cells with specifically associated electrophysiological characteristics (11–14, 15a, 23–26, 28, 30, 58, 88, 98, 108, 110, 114, 118–120, 129, 147, 149, 153, 154, 162, 188, 189, 191, 209, 228, 233, 245).

In order for the heart to function as a mechanical pump, a regular and orderly electrical activation sequence must occur with each heartbeat. Cardiac arrhythmias, the disruption of proper electrical activation, can impair pump function and result in death. The mechanisms by which arrhythmias arise are multiple and complex. Here we review examples of the latest modeling efforts undertaken with the common goal to predict emergent cardiac electrophysiology and arrhythmogenesis. We also discuss how in silico approaches are beginning to aid therapeutic efforts.

Models to Address Ion Channel-Based Mechanisms of Cardiac Arrhythmia

We begin our review with a discussion of ion channels, as alterations in their behavior at the cellular level can lead to changes in AP morphology and the development of arrhythmia triggers at the tissue level, increasing susceptibility to arrhythmias. For heritable arrhythmia syndromes, the most fundamental derangement is by mutation in genes encoding cardiac ion channels that results in congenital arrhythmia syndromes linked to clinical phenomena such as long-QT (LQT) syndrome (LQTS), Brugada syndrome (BrS), and isolated cardiac conduction disorder (ICCD) (56, 221, 247a, 253, 256). Occasionally, the genetic lesion leads to the disease state in an obvious way. An example is the LQT type 3-linked ΔKPQ mutation in SCN5A, the gene encoding the α-subunit of the cardiac Na⁺ channel, which alters the inactivation peptide in the III to IV linker of the voltage-gated Na⁺ channel (Na_V1.5) protein. The mutation logically leads to disruption of channel inactivation and a pathological abundance of late Na⁺ current. The result is a prolongation of the AP duration (APD) and consequent QT interval prolongation. A computational analysis was used to confirm the link between genotype and phenotype and to reveal the mechanism of bradycardia-provoked arrhythmia proclivity (57, 59).

More often, however, the relationship between genetic lesion and phenotype is complex: mutations at multiple loci can produce the same phenotype (56, 186), or a single mutation at a particular locus can surprisingly result in different phenotypes (56, 58, 94). Both gain and loss of function in sodium channels can arise from mutations and lead to varied disease states (7, 15a, 38, 42, 56, 57, 59, 62, 94, 96, 183, 186, 221, 236, 241, 253). Computational modeling has been widely used to provide insight into the seemingly confounding relationships between genetic alterations and proarrhythmic phenotypes (3, 4, 7, 15a, 17, 18, 38, 57–60, 62, 120, 123, 156, 183, 198, 201, 253, 256).

LQTS is frequently associated with gain-of-function sodium channel mutations, whereas BrS and ICCD are commonly associated with reduced sodium current (I_Na) resulting from loss-of-function sodium channel mutations. Interestingly, mutations have been identified in patients that are linked to both BrS and LQTS (56, 94). Computational modeling has suggested transmural electrophysiological heterogeneities as one plausible mechanism to explain apparently paradoxical phenotypic disease manifestations. LQTS was predicted to result from longer APD (manifesting as a prolonged QT interval on the ECG) in the midmyocardial layer because of a mutation-induced increase in the noninactivating component of I_Na, combined with relatively less repolarizing current, which may even allow arrhythmogenic early afterdepolarizations (EADs) to develop (58).

The mechanism underlying the BrS phenotype is, however, an active area of debate (241, 247a). Computational modeling has lent support to the “repolarization hypothesis” where reduced I_Na results in more profound APD shortening in the epicardial cell layers, where there is a higher density of transient outward potassium current (I_to) and slowly activating delayed rectifier potassium current (I_Ks). The more dramatic loss of AP plateau in epicardial cells, compared with other layers, may result in a gradient of plateau potential across the ventricular wall that could increase the likelihood of a reentrant arrhythmia (58). On the ECG, this gradient manifests as ST elevation in the right precordial leads, a diagnostic hallmark of BrS (231).

As opposed to the repolarization hypothesis, the “depolarization hypothesis” postulates that BrS can result from reduced I_Na that is a result of a depolarizing shift in the channel activation curve (15a, 62, 241, 253). According to this hypothesis, reduced I_Na produces right ventricular conduction delay and a transmural activation gradient. Computational modeling (15a, 62, 253) has demonstrated that this is a plausible mechanism for producing the ST-segment elevation observed in BrS patients. This mechanism is also consistent with that suggested by a modeling study investigating the G514C mutation linked to ICCD (253). Regarding ICCD, simulations demonstrated that a depolarizing shift in the activation curve resulted in a reduced conduction velocity (CV) and an increase in the amount of stimulus current required to excite coupled tissue (221).

There is no reason to believe that the depolarization and repolarization hypotheses are mutually exclusive, since modeling studies have helped establish the plausibility of both mechanisms. In this vein, computational approaches could also be used to guide treatment. Experimentally determined effects of mutations on ion channel kinetics can be modeled, and simulation carried out in realistic, or even patient-derived tissue models (5, 11, 48, 55, 98, 99). From here, it may be possible to determine patient-specific Brugada mechanisms-defective depolarization or defective repolarization, which would inform appropriate therapy. As discussed later in this review, efforts are underway to arrive at a framework for better predicting responses to drug therapy in patients.

Computational modeling has also been used to yield insight into phenotypes associated with potassium current defects. A simulation study predicted the relationship between human ether-a-go-go-related gene (hERG)-1a/1b channels [underlying cardiac rapid component of the delayed inwardly rectifying potassium current (I_Kr) repolarizing current], drug sensitivity, and arrhythmia proclivity (198). These simulations showed that altered channel kinetics can explain reduced rectification and an increase in current during repolarization. The model also predicted that because the homomeric form of hERG possesses additional blocked states that the heteromeric form does not, E-4031 drug sensitivity is reduced for the heteromeric form. Finally, this study demonstrated that APD measured at 90% repolarization becomes longer with increasing doses of E-4031. Given that APD prolongation can be proarrhythmic, these simulations suggest that drugs that block hERG are more arrhythmogenic for the 1a homomer than the 1a/1b heteromer.

Another area where computational model has recently proved useful is in teasing out the effects of sex steroid hormones, which modify ion channel gating and play a role in cardiovascular event risk. Experimental and clinical studies in conjunction with computer-based simulation have helped to explain in part why women have been reported to suffer a higher risk of a first cardiac event between the ages of 15 and 40 (135) and are at a higher risk than men of inherited and acquired LQTS and associated Torsades de Pointes, a particularly lethal ventricular tachycardia (1, 81, 112, 165, 181, 217). They also have suggested mechanisms for why females have been reported to be at higher risk of proarrhythmic consequences of Class III antiarrhythmics and other drugs that block hERG (69, 127, 133, 139, 166, 167, 194, 214).

The sex steroid hormone estrogen has been shown to interact with and reduce I_Kr (100, 122), and susceptibility to drug-induced arrhythmias has been reported to be higher during the late follicular phase, when estrogen levels are highest (150). On the other hand, progesterone appears to shorten the QT interval and reduce arrhythmia incidence associated with LQTS (150, 151). Recent modeling studies have been undertaken in which effects of sex hormones on L-type calcium and repolarizing ionic currents have been incorporated (89, 151, 232, 249). These model predictions have resulted in a better understanding of the mechanisms by which estrogen mediates increased susceptibility to drug-induced arrhythmias (249) and by which progesterone and testosterone yield protective effects (89, 151, 249) (Fig. 1). However, these studies have not yet taken into account changes in L-type calcium channel expression and structural remodeling that has been reported in experiments following chronic hormone exposure (163, 164). Incorporating such changes may shed light on whether altered channel kinetics or changes in transmural propagation play a more significant role in sex-related arrhythmia risk disparity.

Fig. 1.

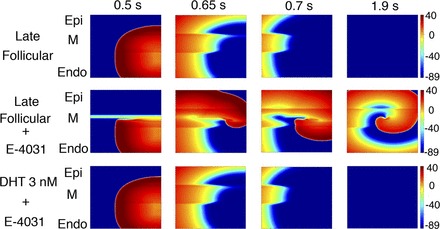
Human ether-a-go-go-related gene (hERG)-blocking drugs in the presence of high estrogen concentrations enhance arrhythmogenicity. Top: using the model described in Yang et al. (249), the authors simulated the late follicular phase of the reproductive cycle when estrogen levels are highest. An ectopic stimulus that was delivered (left) failed to initiate reentry. However, when the late follicular phase was simulated in the presence of the hERG-blocking drug E-4031 (middle), the premature stimulus led to the initiation of reentry. Reentry was not initiated when E-4031 administration was simulated in the presence of high testosterone levels (bottom). Epi, epicardial; M, M cell; Endo, endocardial; DHT, dihydrotestosterone. Figure is from Yang et al. (249), used with permission.

Models of Normal and Pathological Cardiac Regulation by Subcellular Signaling

Obviously, ion channels do not function in isolation. Rather, ion channels and pumps are modulated by elaborate signaling networks. Cell signaling networks regulate multiple aspects of cardiac tissue function, including AP morphology, calcium handling, contraction, metabolism, and gene regulation (140, 174, 195). A quantitative understanding of regulation by signaling networks is crucial for appreciating how many cell components interact to produce arrhythmias in both healthy and diseased states but is still a challenge owing to overlapping layers of interdependencies between networks, as well as multiple feedback loops within networks (202).

A crucial and well-studied player in cell signaling is Ca²⁺/calmodulin-dependent protein kinase II (CaMKII), a multifunctional enzyme that both directly and indirectly modulates the function of several critical cell components, including depolarizing voltage-gated sodium and L-type calcium channels, repolarizing currents I_to, and inwardly rectifying potassium current (I_K1), Sarcoplasmic reticulum (SR) calcium handling components ryanodine receptor (RyR) and sarco(endo)plasmic reticulum Ca²⁺-ATPase (SERCA), and gene transcription within the nucleus (see Fig. 2) (146). Recent simulation studies using models that include CaMKII signaling have complemented experiments and yielded mechanistic insights into relationships between CaMKII and increased arrhythmia susceptibility caused by altered ion channel dynamics, reduced CV leading to conduction block, and impaired calcium cycling in the ischemic border zone (52, 93, 107, 134). Hashambhoy and others (101–103) have also recently developed models of I_Na, L-type Ca²⁺ current (I_Ca,L), and RyR leak modulation by CaMKII, investigating links to arrhythmogenesis.

Fig. 2.

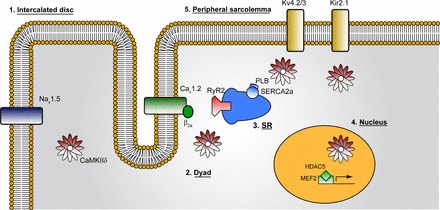
Ca²⁺/calmodulin-dependent protein kinase II (CaMKII) targets diverse intracellular substrates to regulate heart function. CaMKII targets critical sarcolemmal ion channels important for cell excitability, including voltage-gated Na⁺ channels (Na_v1.5), L-type Ca²⁺ channels (Ca_v1.2, α- and β-subunits), as well as repolarizing currents Kv4.3 (transient outward K⁺ current, I_to) and Kir2.1 (inwardly rectifying K⁺ current, I_K1). CaMKII also regulates sarcoplasmic reticulum (SR) Ca²⁺ release and reuptake via direct phosphorylation of ryanodine recptor 2 (RyR2) SR Ca²⁺ release channels and phospholamban (PLB). In the nucleus, CaMKII phosphorylates histone deacetylase 5 (HDAC5), a repressor of myocyte enhancer factor-2 (MEF2), to regulate transcription of hypertrophic gene program. SERCA2a, sarco(endo)plasmic reticulum Ca²⁺-ATPase 2a. Figure and legend are from Mohler and Hund (146), used with permission.

The β-adrenergic signaling cascade, which modulates some of the same targets as CaMKII, plays critical roles in the regulation of contractility, metabolism, and gene regulation (20, 195, 200). β-Receptor activation leads to increased levels of cAMP within the cell, which then promotes dissociation of PKA, enabling it to phosphorylate and modulate multiple targets and processes including I_Na, I_Ks, RyRs, SERCA, the Na-K pump, troponin I, glycolytic metabolism, and cross-bridge formation (21, 140, 195, 207).

β-Adrenergic signaling has been implicated in multiple arrhythmia diseases including catecholaminergic polymorphic ventricular tachycardia [resulting from abnormal calcium cycling because of increased β-adrenergic tone (21, 80, 123, 140, 195, 207)] and LQT1 [caused by modulation of I_Ks, disrupting repolarization with proarrhythmic consequences (257)]. β-Blockade is commonly prescribed to reduce the likelihood of arrhythmia in patients with LQT, but a recent modeling study (7) calls into question the validity of this treatment strategy for a subset of patients with LQT and suggests that β-blockers may actually be proarrhythmic in patients with LQT3.

Several groups have used computational modeling to explore the links between β-adrenergic signaling, excitation-contraction (EC) coupling, genetic mutations, and arrhythmogenesis (104, 200–202, 213). In one study (201), it was found that a known gene mutation implicated in LQTS was not sufficient to cause QT prolongation on its own but required β-adrenergic stimulation. When this model was implemented in a three-dimensional (3-D) rabbit ventricular wedge framework, there was increased transmural dispersion of repolarization and T-wave abnormalities on simulated ECGs.

More recently, computational models have incorporated signaling by both PKA, which participates in a feedback loop with β-adrenergic receptors via cAMP, and CaMKII. These two pathways engage in significant cross talk, though there are still open questions related to specific interactions (213). One model that incorporated PKA and CaMKII-dependent modulation of multiple calcium handling processes is shown in Fig. 3. This model represents dual phosphorylation of I_Ca,L, RyR, and phospholamban by PKA and CaMKII, as well as additional phosphorylation of additional targets by either kinase. Using this model, the authors (213) found that β-adrenergic enhancement of calcium transients was assisted by a synergistic relationship between PKA and CaMKII-dependent phosphorylation of multiple targets. A separate model incorporating both PKA and CaMKII signaling, developed by Heijman et al. (104), introduced two distinct β-adrenergic receptor isoforms. In this study, the authors used their model to shed insight on control of local cAMP levels and receptor-specific modulation of AP and calcium transient properties. The model also predicted that isoform-specific reduction of β-adrenergic receptor activation, reduced compartmentation of cAMP, and CaMKII inhibition will reduce the occurrence of afterdepolarizations during β-adrenergic stimulation.

Fig. 3.

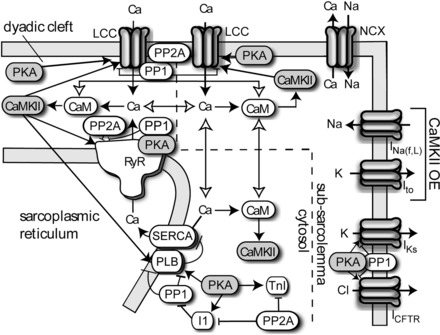
Schematic from the Soltis-Saucerman model. CaMKII is activated by Ca²⁺/CaM binding in the dyadic cleft, subsarcolemma, and cytosolic compartments. Active CaMKII phosphorylates L-type calcium channel (LCCs), RyRs, and PLB. During overexpression (OE) simulations, CaMKII-dependent alterations to fast and late sodium currents (I_Na,f,L) and I_to were included. PKA phosphorylates LCCs, RyRs, PLB, inhibitor-1, troponin I (TnI), slow component of the delayed inwardly rectifying potassium current (I_Ks), and cystic fibrosis transmembrane conductance regulator (CFTR) and phosphatases 1 (PP1) and 2A (PP2A) oppose phosphorylation by either kinase. NCX, Na⁺-Ca²⁺ exchanger. Figure and legend are from Soltis and Saucerman (213), used with permission.

As stated above, the mechanisms by which the PKA and CaMKII pathways communicate with one another are still unresolved. However, computational models are particularly well suited for tackling this type of problem, as links between any two components in the system can be selectively ablated or augmented. For example, how critical is phospholamban to this cross talk? One could selectively ablate phosphorylation of phospholamban by either PKA or CaMKII in the Soltis-Saucerman model (213) and assess whether the synergistic inotropic responses are still intact. Or perhaps the amount of cross talk depends on the amount of available calcium? Calcium availability can be easily reduced in a computational model and can be implemented experimentally with calcium buffers.

Models of EC Coupling

The cell signaling networks discussed in the previous section play many important roles, not the least of which is modulation of EC coupling, the many processes within the myocyte that participate in calcium handling and translate the influx of calcium from the extracellular space to contraction. A major challenge to the cardiac modeling field has been to develop complete descriptions of subcellular calcium handling. Accurate representation of myocardial calcium dynamics is crucial, as many congenital and acquired arrhythmia syndromes result from direct or indirect dysfunctions of calcium handling. Arrhythmogenic phenomena including delayed afterdepolarizations (DADs) and EADs, premature ectopic beats, alternans, and initiation of ventricular tachycardias and fibrillation are all linked to aberrant calcium dynamics (205). However, accurate representation of calcium dynamics and EC coupling is among the most complicated aspects of cardiac electrophysiology modeling. Entry of calcium into the cell via L-type calcium channels triggers additional influx of calcium into the myoplasm as calcium is released from the SR through RyR units. Even among these components complex dynamics can arise, since there is negative feedback between myoplasmic calcium and L-type calcium channel activity due to calcium-dependent inactivation of the channel and positive feedback as local calcium release from RyR units causes neighboring units to open and release additional calcium from the SR. Additionally, there is a positive relationship between the amount of calcium released from the SR and SR load, the nonlinear nature of which contributes to other important properties fundamental to calcium handling such as SR leak and EC coupling gain. These relationships have been captured mathematically (207).

As our understanding of EC coupling has advanced, models have been developed to explore subcellular processes by representing discrete compartments within the cardiac diad where L-type calcium channels and RyRs are found in close proximity and even within the SR (39, 47, 85, 179, 180, 207, 242). Simulations using models with realistic architecture have investigated the effects of surface charge on local calcium concentration within the diad (39); spontaneous calcium release from the SR (47) [including “rogue” RyRs (136)]; the relationship between SR load, calcium spark amplitude, and RyR sensitivity (180); and the relationship between diadic volume, number of L-type calcium channels, and EC coupling (85). Experiments by Gaeta and others (82) who used dynamic pacing to abolish alternans showed that subcellular calcium alternans developed as electrical and whole cell calcium alternans was attenuated. Simulations in a model that included a spatially extended representation of the SR provided insight into the mechanism by which subcellular alternans developed (82). In particular, the simulations showed that subcellular alternans can arise from a dynamical mechanism known as a Turing instability and does not require the presence of subcellular heterogeneity.

Models of calcium handling components are becoming more sophisticated, one example of which being a recent model of SERCA that includes dependence on myoplasmic and SR calcium concentrations and allows for variable calcium-proton transport ratios (226). Just as models of SERCA have become more sophisticated, so have models of Na⁺-Ca²⁺ exchanger (NCX). Current model representations of NCX have incorporated sodium and calcium concentration dependence (73, 207) and have been used in studies exploring the relationship between stimulus frequency, intracellular sodium concentration, and AP morphology (73). More recently, Sher and colleagues (210) developed a model that introduced NCX current in the T tubules. Using this model, they were able to provide an explanation for an apparent experimental inconsistency regarding when calcium entry via NCX occurs during an AP and when NCX current is believed to become inward. Other computational studies have suggested that inhibiting NCX can prevent EAD-triggered Torsades de Pointes in LQTS (143) and investigated the effects of knocking out NCX function in a number of different cardiac cell models (156).

Under pathological conditions leading to acidosis and reduced ATP availability, several components responsible for calcium handling become profoundly inhibited. To investigate these effects, models have been developed that incorporate SERCA ATP dependence (226) as well as pH inhibition of SERCA (226) and NCX (63). Realistic calcium buffering by calsequestrin and calmodulin have been present in models since the late 1990s (85, 207, 208).

To generate muscle contraction, calcium released from the SR must bind to troponin, the affinity of which is also pH dependent. Crampin and Smith (63) modified a preexisting model to incorporate this pH dependence in simulations examining the effects of respiratory acidosis on calcium concentrations and tension development.

Afterdepolarizations are a manifestation of aberrant calcium handling and play a role in arrhythmogenesis. While we discuss afterdepolarizations later in the context of source-sink relationships, there are several interesting computational studies that have explored the mechanisms by which afterdepolarizations arise and the roles that afterdepolarizations play in subsequent arrhythmia triggering. In one study that examined the emergence of EADs from a dynamical systems perspective, EADs were reported to be caused by Hopf and homoclinc bifurcations (225). This study also provided an explanation for the irregular patterns of EADs that are often observed. A study by Huffaker et al. (106) sought to explain how EADs might occur at fast heart rates, despite being classically believed to occur at slow rates (106). The authors arrived at two possible mechanisms, one similar to that which produces DADs and another that is similar to the mechanism that produces EADs at slow heart rates. In a comprehensive study using 37 different cardiac models representing a variety of species of cell types (78), the authors examined the mechanism underlying calcium-induced DADs. They concluded that elevated SR calcium load is not required for the generation of DADs, although it can serve as a modulator. Rather, DADs require elevated calcium concentrations in the dyadic subspace and the cytosol, increasing the open probability of RyR. In a study that examined the consequences of EADs (44), the authors tested whether both I_Na- and I_Ca,L-mediated conduction can coexist in homogenous tissue. The simulations suggested that this is indeed possible in tissue that is prone to EADs and that the interaction between the two different types of wavefronts can give rise to polymorphic ventricular tachycardia.

Unresolved questions remain with regard to the mechanisms of SR calcium release and the propagation of calcium waves, and much work has been dedicated to this question [for examples, see the following studies (47, 180, 193, 242)]. For example, an interesting study by Ramay et al. (180) addressed two current and related controversies: the speed of calcium diffusion within the SR and how local SR calcium dynamics affect calcium wave propagation. The authors found that local increases in SR calcium concentration can enhance wave propagation, but only when SR calcium diffuses at slow rates. However, what are the larger implications for arrhythmogenesis? Given that electrical activity emerges from the complex interactions of so many cell components and that arrhythmogenesis is affected by factors such as cellular coupling and tissue heterogeneity (8, 11, 50, 65, 115, 245, 247), it is likely that merging these sophisticated calcium models with realistic tissue models (99, 227, 229) will provide the ability to answer the logical next questions. For example, are the frequency of afterdepolarizations or the initiation of reentry strongly affected by SR calcium diffusion and/or local SR calcium dynamics? Varying these parameters in a merged model would enable us to answer these questions.

Metabolic Links to Electrical Dysfunction

While much of the preceding discussion has focused on abnormal calcium handling and ion channel function, defects in cell metabolism and mitochondrial function have also been implicated in the genesis of arrhythmias, as well as cardiac glycoside toxicity (9, 35, 132). It is critically important to better understand mitochondrial function in health and disease, since it contains its own subset of metabolic pathways and channels that contribute to or underlie pathologies (9, 35, 239, 255). The mitochondria also exhibit complex behavior such as traversing waves of membrane depolarization (138). Some proposed mechanisms for mitochondrial involvement in arrhythmogenesis include reactive oxygen species (ROS)-induced ROS release, altered intracellular calcium dynamics (mediated by the mitochondrial calcium uniporter), and collapse of mitochondrial membrane potential (mediated by the inner membrane anion channel, mitochondrial permeability transition pore, and mitochondrial ATP-sensitive potassium channels), leading to loss of ATP production (9).

Mitochondria are linked to arrhythmogenesis, as the ATP they produce is necessary for the proper function of several cell components that are critical determinants of electrical activity, including SERCA, the Na-K pump, and L-type calcium channels (142, 223, 226). In addition to these, much attention has been focused on sarcolemmal ATP-inactivated potassium efflux channels, as they are believed to be responsible for increased APD heterogeneity during metabolic stress, which creates a substrate that is more arrhythmogenic (9, 35). Recent computer simulations in this area have made use of models that investigate the positive feedback loops underlying ROS-induced ROS release (254), as well as detailed models of mitochondrial metabolism (239), including integration with AP generation and EC coupling (Fig. 4) (170, 255). Simulations performed in the study of Zhou et al. (255) demonstrated links between oscillations of mitochondrial inner membrane potential induced by ROS-induced ROS release, decreased ATP-to-ADP ratio in the cytoplasm, and AP shortening cause by increased ATP-regulated potassium channel current (I_KATP) activation.

Fig. 4.

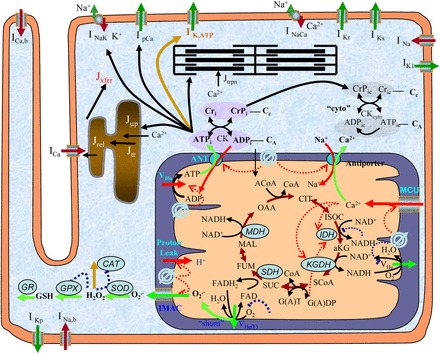
General scheme of the excitation-contraction coupling, mitochondrial energetics, and reactive oxygen species (ROS)-induced ROS release (ECME-RIRR) model. The electrophysiological module describes the major ion channels underlying the action potential (e.g., ATP-sensitive potassium channel) and the processes involved in Ca²⁺ handling (e.g., transport of Ca²⁺ across the sarcolemma, SR), and the inner mitochondrial membrane channels (e.g., Ca²⁺ uniport). The mitochondrial module accounts for the major components of mitochondrial energetics such as the TCA cycle and oxidative phosphorylation. The RIRR module describes ROS production (from the electron transport chain), transport (through IMAC), and scavenging (e.g., by the superoxide dismutase and glutathione peroxidase enzymes). The mitochondrial energetics and ROS are linked to cellular electrical activity through the ATP-sensitive K⁺ channel (K_ATP) current, which is activated when the ADP/ATP increases. Figure and legend are from Zhou et al. (255), used with permission. See Zhou et al. (255) for definitions of all abbreviations appearing in figure.

Metabolic stress that results from myocardial ischemia and reperfusion (I/R), collectively referred to as I/R injury, culminates in a wide variety of electromechanical dysfunctions, including lethal arrhythmias such as ventricular tachycardia and ventricular fibrillation (VF) (145). The impact of I/R injury is expected to increase concomitantly with an aging population and the associated increased risk of ischemic heart disease (76, 145, 170, 255), but efforts to develop a useful therapy to treat I/R injury in the clinical setting have thus far been largely unsuccessful (68, 251). As I/R injury stems from pathological changes in many components that exist as part of the highly coupled and nonlinear system of cardiomyocyte physiology (Fig. 5), it has been increasingly apparent in recent years that a detailed analysis of multiple pathways is required to sufficiently understand the problem. As such, several groups have developed and used models of cardiomyocyte ischemia and/or reperfusion. Some models have focused on specific components, such as SERCA (226), L-type calcium channels, and I_KATP (63, 77, 142), whereas others have focused on specific facets of ischemia, including studies of how respiratory acidosis affects development of contractile force (63) and which components play the biggest role in the accumulation of extracellular potassium during ischemia, a common proarrhythmic observance (223).

Fig. 5.

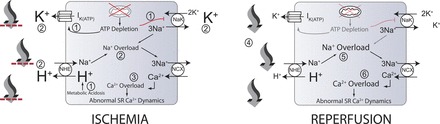
Some events that occur during myocardial ischemia and reperfusion. During ischemia, ATP depletion leads to inhibition of the sodium-potassium exchanger (NaK) and increased efflux through the ATP-regulated K⁺ channel current (I_KATP) (1). Also, increased anaerobic metabolism produces a metabolic acidosis (1). Increased I_KATP and decreased NaK flux contribute to the accumulation of extracellular potassium (2) (larger font). In addition, intracellular acidosis drives increased flux through the sodium-hydrogen exchanger (NHE), contributing to extracellular acidosis (larger font) and intracellular sodium accumulation (2), worsened by decreased NaK flux. Increased intracellular sodium results in the sodium-calcium exchanger (NCX), operating more in the reverse mode, contributing to increased myoplasmic calcium concentration (3). High intracellular calcium concentrations can lead to abnormal sarcoplasmic reticulum calcium cycling and proarrhythmic phenomena. Upon reperfusion, washout of acidotic, hyperkalemic extracellular fluid occurs (4), reducing the concentrations of extracellular potassium and protons (smaller font). The resulting proton gradient allows increased flux through the NHE, resulting in exacerbations of intracellular sodium (5) and calcium (6) overloads (larger font) and additional proarrhythmic phenomena. Note that numbers in this legend correspond to encircled numbers in figure, not references. Figure and legend are from Roberts and Christini (184), used with permission.

Still other efforts have led to the development of more integrated models of I/R pathophysiology (45, 208, 228). A recent study (184), which used the first model to fully couple intra- and extracellular pH systems, suggested that inhibition of the Na⁺-H⁺ exchanger (NHE) as a strategy to reduce sodium overload during reperfusion may, in fact, be detrimental. Simulations showed that inhibition of intracellular pH recovery resulting from NHE inhibition paradoxically fails to attenuate sodium and calcium overload (despite reduced sodium influx via the NHE), in agreement with at least some experimental observations (196), and that the failure to attenuate sodium and calcium overload is caused by inhibition of other cellular components that are sensitive to pH. The ability to monitor many system parameters throughout an entire simulated experiment allowed for insight that cannot be obtained with in vitro and in vivo approaches, where typically only one or two parameters can be observed in a given experiment.

With regard to I/R injury, there are many interesting unanswered questions. For example, with regard to calcium overload, which is more important: the amount of rise in myoplasmic calcium, the rate at which it occurs, or both? Models could be used to strictly control the degree and rate of calcium accumulation while observing the resulting effects on individual components of the calcium handling system. Another question relates to the utility of suppressing pH recovery during reperfusion, which has been proposed as a strategy to limit reperfusion injury. This has shown to have some benefit in animal experiments (109, 171), but the jury is still out on whether this is an appropriate strategy given the myriad detrimental effects induced by acidosis (160, 161). In addition, in one experiment (109), intracellular pH recovery was only stifled for a short time, presumably other components in the system compensated, allowing intracellular pH to recover. Detailed models in which individual components can “see” different pH values can answer questions such as what cell components allow intracellular pH recovery in the face of prolonged extracellular acidosis and whether prolonged acidosis is likely to benefit electrical or mechanical function.

It should be noted that there are difficulties associated with developing and using models to address these types of questions, where multiple outputs (e.g., sodium and calcium concentrations, intra- and extracellular pH, ion channel, and pump fluxes) must be observed at the same time. Models must of course be informed by experimental data, so for complex models it is necessary to cull data from a wide variety of sources. Given that data must be used from different laboratories that employ different techniques and reagents, as well as experiments performed sometimes a decade or more apart, tuning and validating models against known behavior for many different parameters is often difficult. In particular, modeling changes in ion concentrations is particularly challenging, as sodium, calcium, and potassium are all tightly linked through sodium-calcium and sodium-potassium exchange, both of which are modulated by multiple metabolic changes. There are myriad other ways in which a change in the concentration of one ionic species can indirectly affect others. As an example, elevated intracellular sodium can lead to increased calcium load via reverse sodium-calcium exchange, but elevated calcium will also decrease the inward driving force and facilitate calcium-induced inactivation of L-type calcium channels. Such a plethora of direct and indirect effects makes accurate modeling of multiple ionic species extremely challenging. Developing better models, whether of ischemia or other metabolic syndromes, would be greatly aided by greater consistency in experimental protocols such as those recently described in regard to electrophysiology (177a). Returning to I/R injury, it would be highly desirable to have a core group of experiments in which sodium, potassium, calcium, pH, phosphometabolite concentrations, membrane voltage, and force development were all measured at the same temperature, using the same buffers, and at the same pacing frequencies. This would require several different experiments of course, but if they were all performed by the same group and, ideally, within a short period of time, many confounding factors that plague model development could be mitigated.

Perturbations in Channel Function Alter Cardiac Dynamics

Our discussions thus far have focused on events at the single cell level. However, the heart is of course a 3-D structure, and there are important phenomena relating to arrhythmogenesis that only emerge at higher dimensions. Perturbations in the function of cardiac ion channels and pumps not only alter single cell properties such as APD restitution and excitability but can also lead to changes in tissue-level properties such as CV, CV restitution, dispersion of repolarization, and conduction block (1, 3, 4, 17, 18, 38, 44, 46, 49–51, 56–59, 62, 64a, 73, 74, 77, 83, 89, 92, 94, 113, 115, 120, 134, 142, 143, 147, 148, 158, 164, 182, 188, 190, 198, 199, 201, 203, 208, 209, 221, 236, 249, 252, 253, 256). The relationships between these properties and arrhythmia susceptibility are often complex, involving multiple components of a highly coupled nonlinear system over a wide range of scales in time and space (85, 105, 114, 170, 173, 227, 255). Computational approaches have been widely used to identify the fundamental dynamical determinants of arrhythmia (4, 41, 49, 50, 64a, 71, 118, 120, 203, 204, 246, 248).

An example of a dynamical process that promotes arrhythmia is the dynamical oscillation of cardiac tissue in time and/or space known as APD alternans that can precede a series of degenerating events leading to VF (86, 176, 222). The proclivity of a tissue to develop temporal alternans is related to the steepness of the APD restitution curve (the relationship between APD and preceding diastolic interval). Modeling studies have suggested that a steep APD restitution curve is necessary for the development of temporal alternans (97, 157), and pharmacological flattening of the curve has been shown to reduce the incidence of VF in both modeling and experimental studies (83, 182). However, the requirement of a steep restitution curve (slope > 1) may be too simplistic. Other modeling studies suggest that additional factors such as CV restitution, short-term cardiac memory, electrotonic effects, and the range of diastolic intervals over which the slope is >1 are important factors in determining whether alternans and spiral wave breakups occur (50, 51, 70, 224). Modeling studies have also suggested that alternans can result from stochastic fluctuations in I_Ks gating (173) and might be predicted by analyzing responses to stochastic pacing (128).

It is also widely accepted that AP alternans can arise as a consequence of calcium transient alternans (54, 177). As such, a great deal of effort has been invested to understand both the mechanisms by which calcium transient alternans arises and how calcium-driven AP alternans contributes to arrhythmogenicity (8, 28, 82, 105, 113, 130, 193, 240). These studies have identified multiple mechanisms by which calcium alternans can arise, as well as the contributions of AP alternans to arrhythmia initiation. For example, cellular uncoupling (113) can lead to development of calcium transient and subsequent APD alternans, as can SERCA failure (15).

Source-Sink Relationships and Propagation of Arrhythmia Triggers

Continuing with our discussion of how single cell events can translate to arrhythmias at the tissue level, a fundamental question concerns how afterdepolarizations, which presumably arise in a limited number of cells, propagate and lead to premature ventricular complexes (PVCs), which serve as arrhythmia triggers. When cardiac tissue is depolarized, the leading edge of the activation wave acts as a source of depolarizing current, and neighboring tissue acts as a current sink. If the source-sink mismatch is too great, propagation will fail and afterdepolarizations will not be able to manifest as potentially dangerous PVCs. Simulations (191, 209) and experiments have explored the question of source-sink effects on wave propagation in healthy and diseased tissue since the late 1990s. Shaw and Rudy (209) found that reduced cell excitability decreased the “safety factor” (a metric of how likely wave propagation would occur), owing to reduced CV, although paradoxically the study found that decreased cellular coupling helped to preserve the safety factor in the face of decreased CV. This study also suggested using drugs that inhibit L-type calcium current as a therapeutic approach to suppress ectopic stimulus triggering. In a separate study investigating the dispersion of repolarization and sink-source mismatch during ischemia (191), the authors found that the dispersion of repolarization increased with the severity of ischemia. However, the authors also identified a strong relationship between activation patterns following premature stimulation and source-sink mismatch (as represented by a safety factor), leading to the conclusion that refractoriness is not the sole contributor to unidirectional block and subsequent reentry. Using a detailed model of the canine Purkinje ventricular junction and varying the amount of heterogeneity, Aslanidi et al. (13) demonstrated that there is an optimal CV at which conduction through the junction is characterized by the maximum safety factor. The safety factor, which itself has been calculated in different ways, has often been useful in only one dimension, prompting a new formulation (33) to be developed that is appropriate for one- and two-dimensional simulations.

A recent modeling study (247) focused on quantifying the number of contiguous cells susceptible to forming EADs and DADs and the number of surrounding nonsusceptible cells necessary for afterdepolarizations to propagate and excite surrounding tissue in one, two, and three dimensions. These simulations found that normal healthy, well-coupled tissue protects against afterdepolarizations turning into PVCs, but a variety of electrical and tissue remodeling processes that are commonly observed in diseased hearts markedly erode this protection.

There is also interest in understanding that the effects of fibroblasts in cardiac tissue, which increase with age and many disease processes (36, 37, 244), are associated with an increased arrhythmia risk and can form electrical connections with myocytes (84, 90). A number of modeling studies incorporating representations of fibroblasts have been undertaken to gain further understanding of how fibroblasts affect normal excitability and promote arrhythmia formation (110, 111, 197, 220, 244, 245). These studies have found that fibroblasts can promote arrhythmia formation in several ways, including prolonging the refractory period, acting as obstacles to wave propagation, and electrotonic effects that depolarize myocyte resting membrane potential.

Tissue Structure and the Role of Geometry

The heart is a profoundly heterogeneous tissue. Within and between chambers, there are variations in muscle thickness, fiber orientation, and ion channel densities that affect propagation of electrical waves and development of contractile force. These heterogeneities are believed to play a role in the breakup of “rotors” during fibrillation (117). In addition, there are structures that can act as barriers to electrical activation and serve as anchors for spiral waves during reentrant arrhythmias. As such, there is interest in developing more realistic 3-D representations of heart tissue, which is increasingly feasible as computational power continues to rise in terms of speed and fall in price.

To obtain data about 3-D structure, magnetic resonance imaging and histology data have been employed. These data, including fiber orientation and sheet geometry, have been implemented in ventricular models (25, 99, 169, 229) (see Fig. 6). Other models have incorporated closed-loop representations of systemic and pulmonary circulation to simulate changes in pressure over time (119, 206). These and other realistic 3-D models have been used to study changes in length-dependent force in the setting of heart failure (154), structural changes following myocardial infarction (230), the effects of antiarrhythmic drugs on arrhythmia propensity (147), tissue vulnerability to electric shock (24, 26, 187), and bath-loading effects (23) and have complemented efforts to noninvasively map electromechanical activation sequences (172).

Fig. 6.

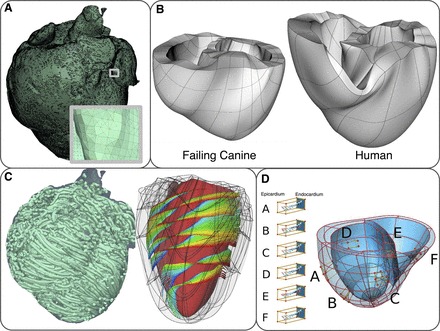
Computational meshes and fiber and sheet structure. A: computational mesh of infarcted canine ventricles for the electrical component of an electromechanics model. A, inset: zoomed-in image of the mesh, showing the mesh details. B: computational meshes for the mechanics component. C: fiber and sheet orientations obtained from diffusion tensor magnetic resonance images. Fiber orientation is for the infarcted canine heart. Sheet orientation is shown on the endocardium in diastole. D: human ventricles with rule-based fiber orientation. D, A–F: transmural changes in fiber angle for different regions in the ventricle. Figure and legend are modified from Trayanova et al. (227), used with permission.

In recent years, the specialized network of cells that make up the Purkinje system (PS) and are crucial for proper electrical conduction has been incorporated into some ventricular models (14, 29, 30, 32, 66, 67, 172, 189, 216). These studies have been used to gain insight into how ectopic stimuli arise from the PS, responses to defibrillatory shocks (the effects of which are modified by the PS), and cardiac resynchronization therapy for patients with heart failure. The structures of the PSs in these models were deduced from MRI data, which will hopefully allow for patient-specific models of ventricular conduction in the future.

Future Directions

While it is clear that computational modeling has helped further our understanding of the mechanisms of cardiac arrhythmogenesis in many ways, there are several new areas where modeling is being used and is particularly exciting, including the development of models for drug efficacy screening, patient specific therapy, and computer-guided nonpharmacological therapy.

Models to Predict Drug Therapy Effects

The first such area concerns predicting the effects of drug therapy. Given that a large number of drugs fail to succeed in the clinical setting owing to proarrhythmic adverse effects and that many antiarrhythmic drugs actually do more harm than good (72, 235), there have been a number of recent modeling studies that aim to predict how antiarrhythmic drugs alter ion channel activity and propensity for arrhythmia (6, 7, 64, 144, 147, 153, 212). As more data become available, increasingly sophisticated models are made possible, incorporating information on relative fractions of charged and uncharged forms of drug, metabolites, and affinities for different ion channel states, which underlies the use-dependent blocking behavior that many antiarrhythmics exhibit (40, 95, 147, 215). Importantly, as more electrophysiology data become available from healthy human tissue, modeling efforts can increasingly reflect human physiology rather than that of other species (75, 159). However, there are still significant challenges to computer-based screens for drug efficacy.

In a recent proof-of-concept study of computer-based drug screening (147), the authors compared the effects of the common antiarrhythmic drugs flecainide and lidocaine in silico. The model predicted mild depression of single cell cellular excitability by flecainide, suggesting its therapeutic potential to suppress ectopic arrhythmia triggers. No overt proarrhythmic potential was ever observed in cells. However, in tissue-level simulations, the outcome was dramatically different. Substantial use-dependent block with flecainide resulted in insufficient Na⁺ channel availability for successful conduction, a higher dimensional phenomenon that emerged as a result of increased electrotonic load in coupled tissue. Proarrhythmic conduction block sometimes led to development of tachycardia indicated by spiral wave reentry. The poor outcomes predicted by the model for flecainide were not observed for lidocaine, consistent with the strong clinical safety profile for lidocaine. The model predictions were verified both experimentally in the rabbit heart and in MRI-based human 3-D ventricle models.

Two other recent modeling studies have aimed to fill the need for effective screening of antiarrhythmic compounds (64, 144). These studies adopted a different approach, using experimentally measured dose-effect data to scale ion channel conductances [but not explicitly taking into account drug effects on gating, as in Moreno et al. (147)]. However, both efforts incorporated drug effects on multiple ion channels at once and were able to screen a relatively large number of compounds. In the study of Davies et al. (64), the authors developed an in silico canine ventricular cell model that incorporated concentration-effect data of 53 test compounds on five different ion channels. They found their system to be 82% sensitive, 79% specific, and 81% predictive, using APD measured at 90% repolarization changes > 10% as a threshold. In a predecessor study (144), the authors collected data on the effects of 31 different drugs on hERG, I_Na, and I_Ca,L currents. The authors concluded that using multiple ion channels improved the reliability of safety screens over using hERG block alone.

Other approaches to predicting drug effects have included atrial-specific sodium channel modeling (6, 153) and focusing on specific drugs such as lidocaine (147), flecainide (147), ranolazine (148, 153), and bupivacaine (212) in detailed models. In the study of Aguilar-Shardonofsky et al. (6), the authors implemented a model of state-dependent sodium channel block in both atrial and ventricular myocyte models with the aim of identifying pharmacodynamic parameters that will allow for the design of drugs that are selective for atrial tissue and effectively terminate atrial fibrillation (AF) with minimal ventricular proarrhythmic potential. The authors found that the most AF-selective drugs (those that block sodium channels at rates common during AF but not at ventricular resting rates) could terminate AF 33% of the time, whereas a number of other drugs could terminate AF 100% of the time but with slightly higher ventricular proarrhythmic potential.

With a similar goal of designing safer antiarrhythmics, the authors in (212) used molecular dynamics and docking simulations to better understand the stereoselective block of hERG by bupivicaine. With regard to ranolazine, two-dimensional computer simulations (148) were used to provide an explanation for why the drug was able to reduce the incidence and sustainability of VF in rat hearts. The simulations suggested that the beneficial effect was mediated by late sodium current blockade, reducing the number of foci serving as triggers. In a separate study (153), the authors employed a Markovian sodium channel gating model that incorporated experimentally observed differences in gating between atrial and ventricular channels. The simulations suggested that ranolazine's significant atrial selectivity results from the difference in AP shape between atrial and ventricular cells, as well as a steeper voltage dependence for the drug unbinding time constant.

It is worthwhile to point out potential advantages inherent to computational approaches to studying arrhythmia mechanisms and tailoring pharmacological therapy. First, models can be used to quickly survey a large range of drug compounds and concentrations under different conditions of pacing protocol, heart rate, and additional conditions that may influence arrhythmia susceptibility (e.g., ischemia, chronic heart failure). Because of expense, time, and technical limitations, in vitro and in vivo experiments are confined to relatively narrow ranges of drug concentrations, pacing protocols, etc.

An additional advantage of computational models is that many parameters can be monitored throughout a simulation. In addition, very specific perturbations can be made to the system under study, without confounding off-target effects, if desired. These benefits make it possible to disentangle contributions by specific components to complex phenotypes. For example, one reason that predicting drug effects has been so difficult is that there is bidirectional feedback between drugs and their targets. Drugs affect AP morphology, and in turn AP properties, affect drug binding to ion channels. Additional reasons include the fact that many drugs are promiscuous and interact with proteins other than the intended targets and that biological systems exhibit many nonlinear dependencies across multiple scales of time and space, meaning that they often exhibit nonintuitive behavior (195).

Furthermore, computational approaches potentially allow certain problems associated with animal studies to be circumvented. A fundamental limitation of animal-based studies is that there are species-dependent differences with regard to parameters that affect cell electrical properties and response to pharmacological intervention (10, 27, 158, 237, 257). In addition, animal studies are conducted either in healthy hearts or hearts in which a disease has been induced artificially. While computer models are of course not human, they can be informed by data from healthy and diseased human heart tissue, which continues to be acquired (41, 74, 87, 91, 92, 121, 190, 218). That being said, there are significant barriers to obtaining this data. Human heart tissue, especially reasonably healthy tissue, is in short supply (159), not to mention logistically difficult to transition from procurement to experiment in a timely manner. In addition, there is significant variation among the patients who serve as donors for human tissue, both in terms of genetic diversity and the prevalence of possible subclinical disease. This means that a large number of hearts will be necessary for the derivation of trustworthy model parameters when developing generic human models.

Computational Models to Guide Ablation Procedures and Biological Pacemakers

Two additional areas of arrhythmia therapy that will undoubtedly benefit from in silico approaches are ablation therapy and the development of biological pacemakers. Patients with recurrent arrhythmias that cannot be controlled pharmacologically typically undergo cardiac ablation therapy to disrupt arrhythmia pathways or triggers. Currently, ablations are guided by graphic representations of a patient's heart that are overlaid with information detailing electrical activity measured at different points inside the heart. However, the currently used representations are wanting for detailed resolution and realistic geometry. Detailed in silico reconstructions of hearts currently under development (5, 24, 55, 88, 99, 124, 172, 185, 230) may provide an alternative approach and allow for patient-specific high-resolution models containing accurate representations of electrical and mechanical activation. These reconstructions could be used to simulate clinically observed arrhythmias and guide ablation procedures based on patient-specific structure and functional abnormalities. On a related note, modeling has been used to address the problem of optimal implantable device location in the context of magnetic resonance imaging safety (141).

Patients with bradycardia-linked arrhythmia stemming from disorders of sinoatrial (SA) and atrioventricular (AV) nodes or from heart block are generally treated with implantable artificial pacemakers. Whereas these devices are exceptionally effective and have continuously improved over the past decades, they are still limited by finite battery life and malfunctions such as lead fracture. As such, there is a desire to develop biological pacemakers (192), although there is no doubt that engineering these pacemakers will be extremely challenging. For example, the SA node is a complex structure possessing heterogeneities of cell type and size, intercellular coupling, calcium handling, and ion channel densities generating different AP shapes (31). Design of a successful biological pacemaker will require engineering of ion channels with specifically tuned kinetics, and the problem of seamless coupling of the pacemaker to existing tissue that is required to maintain rapid conduction and coordinated contraction will need to be solved.

In recent years, several mathematical models of the SA and AV nodes have been developed (38, 43, 108, 129, 149, 162, 252). These models have been used to reveal the roles of SCN5A mutations in sick sinus syndrome, L-type calcium current in AV nodal reentry, the roles of I_Na and hyperpolarizing activated current in proper SA node function, and autonomic modulation of the SA node and how fibroblast density and coupling strength may affect conduction in the SA node. Extensions of models such as these, combined with sophisticated electromechanical models and ion channel kinetics described elsewhere in this review, will be important tools in the development of safe and effective pacemakers as advances in tissue engineering technology are made.

Patient-Specific Modeling

Given the large amount of variability between patients in underlying pathology, there is great interest in tuning therapies to individual patients to maximize response. Phrases like “personalized medicine” often evoke thoughts of analyzing a patient's genome and/or proteome to determine the most effective therapy and even predict disease progression. However, within the realm of cardiology, there are more pragmatic approaches that are likely to yield benefit in the near future and can be aided by computational modeling. One such approach is to arrive at an accurate representation of a patient's myocardial structure, including geometry and heterogeneity. Some recent efforts in this area and their uses have been discussed above, although one additional example is a patient-specific model of dyssynchronous heart failure (5). In this proof-of-concept study, data from electrocardiography, Doppler echocardiography, intracardiac pressure measurements, and electrical activation mapping of a patient with left bundle branch block and previous myocardial infarction were combined to obtain a model that captured anatomical detail, electrical activity, biomechanics, and hemodynamics before and after the placement of a device for cardiac resynchronization therapy.

A different type of patient-specific therapy will use genetic information in patients with inherited channelopathies to dictate pharmacological treatment. Several groups have employed models to investigate how mutations in sodium and hERG channels could produce either shortening or lengthening of APD (4, 7, 17, 18, 60). In one of the first studies of this nature (60), it was suggested that in patients afflicted with LQTS stemming from a sodium channel ΔKPQ mutation, low-dose mexiletine can restore normal repolarization, whereas lidocaine would be less effective. In addition, a more recent modeling study (7) suggested that in patients with the ΔKPQ mutation, β-blocker therapy may not be appropriate, in contrast with other LQTS subtypes, one of which has been linked to a hERG mutation (17, 18). In addition to the aforementioned studies that replicated the effects of specific mutations, a novel approach has been used to quantify repolarization reserve in the context of I_Kr blockade (199). This study found that the response to pharmacological blockade in simulated human myocytes depended on the current density and gating kinetics of several different ion channels, all of which can vary from patient to patient depending on genetics and disease processes. These examples highlight that determining the optimal therapy for a patient will not only require determining which mutation(s) are responsible, or are likely to result in abnormal electrophysiology, but also gaining an understanding of how these changes that occur at the cellular level emerge as whole organ phenomena.

Challenges

While computational methods hold great promise for advancing our understanding of disease mechanisms and developing new therapies, such methods must gain acceptance by experimentalists and clinicians alike before this promise can be fulfilled. To this end, there are two prominent obstacles that must be overcome: proof of utility and clinical relevance.

Validation of Model Predictions Is Necessary

The usefulness of mathematical models largely lies in the fact that they enable us to examine systems in ways that are not available via “wet lab” methods. However, model predictions are only valuable if they facilitate progress in elucidating the underlying biology of interest. In other words, it is not sufficient for models to merely reproduce previously observed physiological behavior; they must also yield predictions that are correct and can guide further experimental work. Recent work by our group investigating the anti- or proarrhythmic effects of lidocaine and flecainide provides one example of this synergy (147), but there are others. Pertaining to the earlier discussion of the relationship between APD restitution and VF, a concept that was borne out of modeling studies (97, 157), subsequent experiments were able to confirm this hypothesis (83, 182). Also, relating to work cited in earlier discussion, modeling studies suggesting that it is possible to generate calcium transient alternans by a dynamical mechanism were subsequently verified by in vitro studies (82). In more recent work exploring aberrant calcium dynamics and arrhythmogenesis (116), theoretical work suggesting that mechanical forces affect calcium overload and facilitate arrhythmogenesis was subsequently verified by experimental findings. In a study of cell volume homeostasis (219), the authors sought an explanation for how cell volume remained constant even when NaK (which normally plays a significant role in volume regulation) was inhibited. Computer simulations suggested that NCX, the plasma membrane Ca²⁺-ATPase, and low membrane permeabilities to sodium and chloride could account for volume homeostasis in the face of NaK inhibition. Subsequent experiments were able to confirm the model predictions. Switching to mechanisms of mitochondrial failure, in their study Zhou et al. (254) sought an explanation for how oscillations or the collapse of mitochondrial energy states are synchronized across the mitochondrial networks in cardiac cells. One- and two-dimensional mathematical models of mitochondrial networks were constructed, with the interactions between nodes being characterized by reaction-diffusion equations representing ROS-induced ROS release. Subsequent experiments validated model behavior and provided new evidence that depolarization of mitochondrial inner membrane potentials is superoxide mediated.

Utility of Computational Modeling Studies in the Clinical Setting

The second obstacle is that modeling approaches must demonstrate clinical utility. While understanding processes occurring at the subcellular and cellular levels are undeniably important for elucidating fundamental arrhythmia mechanisms and designing new therapies, it is ultimately emergent phenomena in the organ that kill patients. Models that translate cellular events into clinically relevant phenomena such as ectopic stimulation and reentrant arrhythmias and that employ realistic tissue structure and heterogeneity will hopefully convince more clinicians that computational approaches are an important way to complement more traditional experimental approaches. Fortunately, increases in processor power, parallelization, and increased use of general-purpose graphical processing units (238) have enabled true multiscale simulations. Modern cardiac models have incorporated cellular processes regulating membrane voltage and calcium handling, actin-myosin cross bridging, valve structures, realistic tissue geometry, and blood flow, including loading of the pulmonic and systemic circuits (98, 99, 114, 229, 233). Such models have been used to investigate arrhythmias arising from the PS (66) and regionally ischemic tissue (114, 115), electromechanical delay (98), and the effects of bundle branch block on cardiac output (233) and have been used to compare different types of left ventricular assist devices on left ventricular peak pressure and ATP consumption (131). Pertaining to the study of AF, structurally realistic models have been used to investigate how ectopic stimuli initiate atrial flutter/fibrillation (88), the role of fibroblasts in complex fractionated atrial electrograms (11) and the estimation of APD from electrograms (234).

In addition, computational methods have been making direct use of patient data and guiding procedures. In one study (152), monophasic APs were recorded in patients and correlated with T-wave alternans and the risk for developing lethal ventricular arrhythmias. Computer modeling was used in this study to provide a mechanistic explanation for the observed AP amplitude alternans. In another study (48), ECG recordings from patients were complemented with pseudo-ECGs calculated from an MRI-based human ventricular model to examine the relationships between premature activation, QT interval dynamics, and the onset of ventricular tachycardia in the setting of myocardial infarction. Computational modeling has also been used to complement recordings of epicardial activation in patients who experienced VF and global ischemia during cardiac surgery (61). Making use of computational tools in a different way, a technique called noninvasive electrocardiographic imaging (ECGI), reconstructs an electrical activation map by merging ECGI data with a reconstruction of a patient's heart from CT scan images (178). ECGI has been used to guide epicardial ablation in a patient with recurrent ventricular tachycardia (126) and has been used to evaluate electrical dyssynchrony in pediatric patients either being considered for or undergoing resynchronization therapy (211).

Conclusions

Elucidating the basic mechanisms of cardiac electrophysiology, arrhythmia mechanisms, and devising effective and safe treatments for arrhythmias may best be served by a combination of in vitro, in vivo, and in silico approaches. Here we have reviewed a subset of the current in silico approaches that are being used for state-of-the-art simulation of cardiac electrical activity. As data from experimental studies continue to emerge, computing power continues to increase, and modeling techniques become more sophisticated, in silico approaches will serve as increasingly powerful tools with which progress in arrhythmia therapy will be made.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

B.N.R. prepared figures; B.N.R., P.-C.Y., S.B.B., J.D.M., and C.E.C. drafted manuscript; J.D.M. and C.E.C. edited and revised manuscript; C.E.C. approved final version of manuscript.