Thermophilic proteins: insight and perspective from in silico experiments^†

Abstract

Proteins from thermophilic and hyperthermophilic organisms are stable and function at high temperature (50-100 °C). The importance of understanding the microscopic mechanisms underlying this thermal resistance is twofold: it is key for acquiring general clues on how proteins maintain their fold stable and for targeting those medical and industrial applications that aim at designing enzymes that can work in harsh conditions. In this tutorial review we first provide the general background of protein thermostability by specifically focusing on the structural and thermodynamic peculiarities; next, we discuss how computational studies based on Molecular Dynamics simulations can broaden and refine our knowledge on such special class of proteins.

1 Introduction

In nature, some organisms are found to thrive in extreme environments and thermodynamic conditions, for example thermophiles and hyperthermophiles where biological growth is optimal between 50 and 100 °C¹. In these cases the molecular machinery of the host organism is suited to resist and function at elevate temperatures.

Proteins from these organisms, that we refer to as thermophiles in the following^*, are extremely appealing since they manifest an enhanced stability that help to retain (or activate) their function at high temperature, i.e. making them good candidates to perform catalytic activities in harsh conditions. Thermophilic enzymes already find a strategic place in the biotechnology and chemical processing³. Therefore, understanding the molecular basis of protein thermostability is key for the design of proteins to target specific industrial and medical applications demanding special stability.

In the past years, the focus of the scientific community was directed to sort out the structural peculiarities of thermophiles¹. Despite the fact that not a unique and ultimate cause for stability was identified, a collection of important ingredients have been singled out, providing general clues on how proteins stabilize their fold. For example, it was appreciated that thermophiles are characterized by shorter loops and by anchored C-,N-terminals, factors believed to protect the protein matrix from water penetration and prevent unfolding. The statistical analysis of the amino-acids composition of proteins from thermophiles provided other interesting evidences, e.g. the overall enrichment in charged amino-acids found in thermophiles points towards the crucial stabilizing role of electrostatic interactions^2,4.

Insights on the protein structure and composition complement the thermodynamic perspective of protein stabilization. Indeed, from the thermodynamic point of view several mechanisms are plausible⁵. With respect to their mesophilic homologues, thermophiles could be stabilized by few specific extra-interactions contributing to lower the enthalpy of the folded state. For example, the observed surplus of charged aminoacids favors the creation of ion-pair and h-bond networks across the protein matrix. At the same time thermophiles could be more stable resulting from a reduced entropy difference between the folded and the unfolded state. For the latter possibility, two scenarios are possible. In the first one, the energy landscape of the folded state is broad and the conformational entropy gets close to that of the unfolded random-coil. In the second case, the unfolded state is characterized by a relative lower entropy possibly caused by residual native interactions that reduce the available protein conformations.

How enthalpic vs entropic forces finely tune this special class of protein is a fundamental and yet open question. Finally, the stability could be intended in a kinetic sense, in other words the free energy barrier separating the folded and unfolded state is higher in thermophiles trapping the protein in the native configuration even at high temperature. It is appreciated that localized salt-bridges contribute to this kinetic trapping⁶.

A complementary intriguing aspect concerns the correlation between protein stability and function^1,5. Enzymes typically show a maximum in activity at an optimal temperature, due to the raise of the catalytic constant k_c for an unperturbed enzymatic site, followed by a decrease at higher temperature due to the structural alteration in the protein structure, as sketched in Fig. 1. Mesophilic and thermophilic proteins exhibit the same behavior, with the maximum of activity shifted at a temperature that mostly corresponds to the maximum in stability. In addition, thermal resistance can bring the maximum in activity of thermophiles even beyond the boiling point of water.

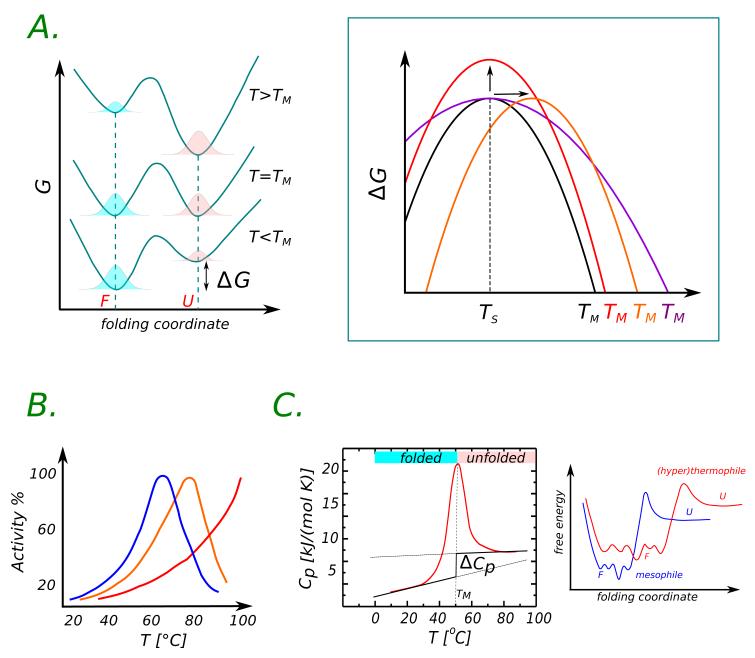
Fig. 1.

Panel A. Free energy profile for a two-state model of protein folding/unfolding. The free energy landscape changes by varying temperature making one state more favorable than the other. At the melting temperature T_M the probabilities for the protein to be in the folded or unfolded state are equal. The change in the free energy difference between the unfolded and folded state as a function of temperature produces the so-called stability curve (black curve in the right panel). Three distinct mechanisms that shift the melting temperature toward higher values are represented: the up-shift (red), the right-shift (orange), the broadening (indigo). Panel B. Activity curve for mesophilic, thermophilic and hyperthermophilic species. Increasing temperature the activity increases since it is more favorable for the system to cross the barrier related to the catalytic reaction, beyond an optimal temperature the degradation of the active site is due to the onset of unfolding causing the reduction in activity. Panel C. Typical thermogram from DSC experiments. The heat capacity of unfolding is given by the difference between the two baselines corresponding to the folded and unfolded states. At the melting temperature T_M, C_p shows a peak due to the enhanced transitions between folded and unfolded states.

Since thermophiles generally lack activity at ambient condition, it was proposed a strict link between protein motion, function and stability: assuming that activity depends on protein flexibility, the poor catalytic power monitored at ambient condition features a reduced motion of the protein, hence an increased rigidity characterizes the protein matrix and this is thought to confer thermal resistance. Activity is recovered only at higher temperature when the flexibility of the protein is reactivated. This link is often referred to as the Somero’s corresponding state concept: mesophiles and thermophiles show similar flexibility and activity at their respective optimal growth temperatures⁷. However, it must be anticipated that the link between protein activity and motion needs to be clarified; indeed concerning the catalytic step of the enzyme the different behavior between mesophiles and thermophiles could be understood in term of the transition state theory (TST). According to TST the catalytic kinetic constant shows an exponential dependence on the free energy barrier for the reaction (ΔG^‡) and a monotonic dependence on temperature: k_c ∝ k_bTexp(−ΔG^‡/k_bT). The lack of activity at ambient condition can be seen as caused solely by a higher ΔG^{‡ 8}. Needless to say, the investigation of how temperature affects protein function and how this correlates to protein motion and stability is a challenging line of research for the years to come.

The study of protein thermostability has greatly benefitted from the application of computational methods as for example the comparative study of protein sequence and structures⁹ and the calculation of the electrostatic contribution to stability¹⁰. Given the ever growing computational power available to scientists, more is expected for the future. In the body of this review, we will first present the main results gathered from past investigations and later we will discuss the computational strategies that could be adopted to tackle the open problems presented above. From this perspective, we will focus in particular on the Molecular Dynamics (MD) technique, since it is nowadays occupying a privileged place in the in silico study of biomolecules.

In MD the motion of individual atoms is determined by solving the classical Newton’s equation of motion once the elementary interatomic forces are provided. For the simulations of biomolecules accurate force fields have been developed in recent years¹¹. The MD technique allows to follow at the microscopic level of detail the time evolution of biomolecules, hence computing the ensemble average and fluctuation of quantities of special relevance for protein conformation and solvation. This bottom-up perspective is unique for acquiring knowledge on the microscopic details of protein thermostability and relating it to a rigorous thermodynamic/statistical mechanics framework. Unfortunately, the current limitation in the timescales accessible by simulation precludes the direct observation of protein large-scale rearrangements, such as unfolding or refolding processes that lay at the basis of a thermodynamic treatment of protein stability. As a workaround, simplified models based on a coarse-graining of the atomic level, are being developed and applied to explore processes occurring for times longer than the microsecond scale, including protein folding, aggregation and large-scale fluctuation, membrane fusion and dynamics, and so on. Another strategy for shortening the time gap is to use an implicit representation of the solvent, such as water or a membrane, or the saline environment.

Besides the brute force application of MD, simulation allows to perform ad hoc visionary experiments, based on virtual alchemical, thermodynamic or kinetic transformations, to provide a wealth of precious informations to experimentalists and theoreticians. On this regards, a large theoretical effort is devoted to the development of methods that enable to determine the free energy curves encoding protein stability and the strength of the forces that keep together the folded conformation, ranging from the flexibility/plasticity of portions of a protein in relation to the enzymatic function to the observation of the folding/unfolding transition. Breathing motions and folding/unfolding transitions frequently occur over times exceeding the microsecond scale.

Finally, it is worth mentioning that multi-scaling approaches are also emerging as a powerful strategy for coping with the intrinsic variety of timescales pertinent to biological systems. Mixed quamtum/classical methods are now an essential tool for investigating enzymatic activity and this could be coupled to simplified models used to sample the protein conformational landscape and get insight on the relationship between protein conformation and function.

As a matter of fact, MD provides a unique companion to wet lab experiments: as the information accessed by instruments cannot deliver a complete picture of the complexity of proteins, in simulation the trade-off between physical realism and computational feasibility allows to gather those information from a model oriented viewpoint. The synergy between experiments and simulation finds it full expression in complementing and cross-fertilizing each other.

2 Thermal Stability

In this section we introduce the problem of protein thermal stability. First, we overview the basic thermodynamics background and we highlight the specific aspects that differentiate thermophilic from mesophilic proteins. Later on, we focus on the mechanism and the microscopic features that correlate to protein stability and function at high temperature.

2.1 Lessons from thermodynamics

In most cases, soluble proteins function in their folded state, a 3D organization of the polypetdic chain that reduces the exposure to water of hydrophobic groups and is stabilized by intramolecular interactions, such as van der Waals and electrostatic non-bonded contributions, local covalent bridges (disulfide) as well as solvation. The biologically active conformation of a protein can be viewed as a consequence of the main thermodynamic force acting on its aminoacidic elements, the hydrophobic effect. As for the water-oil paradigm, non-polar groups do not like to be hydrated in water and aggregate to form the protein core, contrasting effectively the entropic cost of disrupting the water hydrogen-bond network. Enthalpic, atom-based, interactions may ease this hydrophobic collapse and make their way in modeling the final protein shape.

Protein stability relates to the energetics of the unfolding transition from the native F to the unfolded state U. The transition takes place for example by raising/lowering temperature or by using chemical denaturants and it can be reversible (F ↔ U) or irreversible (F → U). Changes in pH and pressure cause unfolding as well. Irreversibility usually occurs by aggregation or chemical modification. Irreversible unfolding can be ascribed to a first-order kinetic reaction, with a rate constant that depends on temperature and environmental factors.

Experimentally, protein stability is measured by the difference in free energy between folded and unfolded conformations in equilibrium conditions. In cases of reversible transition, thermodynamics is the conceptual framework to interpret data, such as the balance between folded/unfolded conformers, whereas, if a protein unfolds irreversibly or follows a complex unfolding pathway, a quantitative thermodynamic analysis is inappropriate.

The Gibbs free energy difference of unfolding is given by ΔG = G(U) − G(F) = −k_bT log(〈U〉/〈F〉), where 〈U〉 and 〈F〉 are populations of the respective F and U states. When looking at stability as a function of a state variable, such as temperature, the free energy profile is globally modified in a way to alter the content of folded or unfolded structures in a statistical sense. The variation of the free energy curve with temperature provides the so-called stability curve, ΔG(T), drawn in Fig. 1, Panel A. The curve looks as a skewed inverted parabola, with a maximum at the temperature of maximum stability, T_s. Its shape is the result of cancellations of large contributions stemming from enthalpic and entropic terms. The maximum in stability relates to enthalpic contributions, as the entropic one cancels out at this temperature⁵. Focusing on the high temperature regime, the melting temperatures, T_m, individuates the zero of the parabola above the T_s, in other words the temperature at which the population of F and U states are equal. For T > T_m the protein is in the unfolded state.

Thermophilic and hyperthermophilic species are more stable than the mesophilic ones because T_m can reach the boiling temperature of water and above. In principle, the higher melting temperature observed for thermophiles could result from the up-shift, the right-shift or the broadening of the stability curves¹², see Fig. 1, Panel A; each of these caused by the different protein characteristics. A recent comparative study¹³ reported that the majority of thermophiles presents an up-shift of the stability curve (77%) while for a few others (31%) the stability curve is right-shifted by rigidly moving T_s to higher values. In addition the heat capacity of unfolding is often smaller for thermophiles (70%), and therefore, as discussed in detail later on, the higher melting temperature could result from a broadened free energy profile. In general, thermophilic proteins seem to choose any of these strategies or a combination thereof, and it is now accepted that no single molecular mechanism but rather a combination of stabilizing causes lay at the basis of thermal resistance.

While for the up-shift and right-shift scenario it is possible to ascribe the change of the stability curve to single optimized intra-protein interactions that confer structural robustness to the protein, the broadening of the stability curve suggests that more complex molecular mechanism stay at the origin of thermostability. Moreover, it is worth keeping in mind that the overall free energy difference between unfolded and folded states is as small as 0.1 kcal/mol per residue, and the overall stability of the folded state corresponds to a few extra hydrogen bonds. Consequently, several mechanisms could act together to shift the melting temperature by a few tens of degrees and these can arise from both intra-protein contacts or from solvation. It is estimated that increasing the denaturation temperature by 50K involves a change in free energy of unfolding by only a few kcal/mol¹⁴.

Differential scanning calorimetry is the experimental technique that probes the free energy landscape by measuring the heat capacity with respect to a reference state, ΔC_p, as a function of temperature. According to the thermodynamic definition, C_p = −Td²G/dT², the heat capacity is proportional to the curvature of the stability curve versus temperature, and its positive (negative) variation corresponds to a more curved (flat) profile.

The heat capacity upon protein unfolding is usually positive¹⁵, and specifically the variation measured for thermophiles is smaller than that of mesophiles. This smaller variation can be rationalized considering the protein composition and structure. In fact, the solvation of hydrophobic and polar groups gives an opposite contribution to ΔC_p: a positive ΔC_p is associated to dominant hydrophobic interactions while solvation of polar group has a negative sign. However, which components dominates the measured heat capacity upon unfolding is still debated¹⁶, hydration surely gives an important contribution but the fluctuation and extension of the intra-protein non-bonded interactions have to be considered too.

A simplified, two-energy model allows us to interpret the heat capacity by discriminating the role of enthalpic fluctuations from enthalpy itself, suggesting for the former a relevant role in thermostability¹⁶. Since ΔC_p relates to enthalpy fluctuation, C_p =< δH² > /k_bT², the small heat capacity of unfolding in thermophiles suggests that enthalpic fluctuations in the folded and unfolded states are closer than in mesophiles. This could imply that the conformational landscape associated to the folded state of thermophiles is wider and smoother with respect to that of mesophiles, allowing the protein to visit more conformational basins, as pictorially represented in the sketch of Fig. 1, Panel C. Unfortunately, a direct connection between the enhanced enthalpy fluctuations in the folded state with specific molecular interactions or structural motifs still lacks: since ΔC_p entails both entropic and enthalpic contributions, assessing the prevailing one is a very difficult task. As discussed in the next paragraph, the results from recent theoretical calculations¹⁷ of the low-frequency vibrational density of states of thermostable proteins support the suggestive picture of a flatter conformational landscape of thermophiles.

At variance with the picture described above, the measured small heat capacity of unfolding could be traced back to a different behavior in the unfolded state of thermophiles. Namely, studies on Ribonucleases H from Thermus thermophilus and Escherichia coli¹⁸, two proteins owning an high degree of homology but a marked difference in the heat capacity upon unfolding, suggest that the unfolded state of the thermophilic variant is characterized by residual native hydrophobic clusters and does not appear as a fully solvated random-coil. Hence, upon unfolding not all hydrophobic groups are exposed to water, reducing the contribution to ΔC_p. The finding was supported by site directed mutagenesis. The idea that native residual interactions in the unfolded state could be at the origin of thermostability is also proposed by recent analysis of thermodynamic data on a large set of homologue proteins¹⁹.

So far, we have discussed thermal resistance considering its thermodynamics origin but it is plausible to think thermostability in a kinetic sense. Kinetic stability depends on the rate of unfolding, which in turn depends on the barrier separating folded and unfolded states. The rate of reversible unfolding correlates with thermodynamic stability because a more stable protein is likely to present a higher barrier for unfolding.

Kinetic stability is the phenomenon mirroring irreversible unfolding: once unfolding occurs, bearing a large dissipation of the free energy available at equilibrium, the probability for a protein to recover the native state is negligible. Analogously, kinetic stability refers to the tendency to hold such amount of structural order and related free energy content for a time sufficient to carry out the biological course, before unfolding definitively occurs.

Arguably, kinetic trapping is a candidate for protein stability, as the unfolding barrier is typically larger than thermal energy to keep a protein in a defined conformation. Early calorimetric studies have suggested that thermostability in proteins like Rubredoxin is induced by kinetic trapping rather than thermodynamic stabilization⁶.

2.2 In search of microscopic details

Thermal stability is related to the fine details of the protein primary sequence and structure. In discerning the molecular basis of stability, the main forces acting on the protein matrix need to be considered. Indeed, the fold of a protein is the result of a delicate balance between attractive/repulsive interactions, excluded volume effects and topological contraints.

From the structural point of view, the thermal resistance of thermophiles could be either the result of local stabilization, i.e. a few key interactions that protect the protein matrix from thermal excitation, or global properties¹. From the point of view of thermodynamics, stabilization could mainly arise from enthalpic contributions or could have an entropic origin²⁰. By systematic comparison of the structure and composition of mesophilic, thermophilic and hyperthermophilic homologues, several aspects have been identified that could be relevant to thermal resistance.

At first, from the structural perspective, optimized packing of residues throughout the macromolecule is often advocated as the molecular mechanism strengthening the protein structure and conferring special rigidity based on enthalpic forces. On this regards, hydrophobic interactions in the core, as well as the links between secondary structure elements and domains via h-bonds and salt-bridges, all concur in enhancing the cohesion of the fold.

The role of conformational fluctuations is another issue that attracts attention, as it modulates the temperature response of protein and supports a correlation between thermodynamic stability and enzymatic function. Let us recall that thermophiles generally lack activity at ambient condition, recovering function only at the optimal growth temperature. This is thought to be caused by suppressed motions and reduced flexibility.

Given the Arrhenius-like dependence of fluctuations in a simple model of a flexible macromolecule, one may expect that protein flexibility follows temperature similarly to the enzymatic activity. This would reflect the strong ties between accessibility of the active site by solvent and substrates, and the catalytic rate constant.

If fluctuation amplitudes of different species are similar in their host microorganisms at their physiological temperature, they would conform to Somero’s corresponding states concept⁷, stating that homologue proteins have comparable flexibilities at the respective working temperatures. This paradigm has met a vast consensus in the biochemical community over the years^21-23

It should be borne in mind, however, that a precise definition of flexibility is unspecified in the corresponding states concept. In reality, fluctuations can affect locally the atomic motion, the long wavelength motion of protein subunits, or specific regions of the protein matrix that are relevant to accessing the active site. Moreover, in view of the structural and dynamical heterogeneity of proteins, a clear-cut relationship between protein motion, fluctuations and activity escapes any explanation provided so far (we point the reader to the very interesting discussion proposed recently by Kamerlin and Warshel²⁴).

In analogy with the resistance of civil buildings against external agents, some researchers view thermal resistance as resulting from the entropic reservoir arising from internal modes, as signaled by the enhancement of fluctuations with the degree of thermophilicity. Fluctuations are regarded as forming an entropic reservoir that softens the internal motion in certain macromolecules, protecting them against thermal stress. Experimental evidences proved that thermophiles show the same (or even higher) degree of flexibility of mesophiles at the same temperature^25-27.

Finally, recent research focuses on the role of hydration^28,29 and the organization of the surrounding water in enhancing protein robustness^30,31. The formation of a collective network, that is, a web of hydrogen bonds surrounding the maromolecule, could create a sufficient protecting envelope that sustains the protein scaffolding. The study of the morphological details³² of the protein-water interface points in this direction as much as the observation that melting of the protein-water hydrogen network acts as a precursor to protein unfolding³⁰.

The explanations summarized above have a common denominator: they may all shift the melting curve and contribute by few kcal/mol in energy to stabilization. Moreover, they typically involve the global spatial arrangement of the protein by impacting the low-frequency region of the protein spectrum and slowing down the unfolding kinetics.

In the remainder of this review, we address the issue of how computational studies may complement experimental investigations to shed light on this challenging and fascinating field.

3 Thermostability in silico

3.1 In silico experiments: What we discovered so far

In this section, we focus on those computational studies that have tackled protein thermostability and addressed the open problems listed in the preceeding section. It is convenient to group these studies in three categories: 1) comparative studies of homologue structures and sequences, 2) electrostatic calculations, 3) molecular dynamics simulations of proteins in solution. This classification is somehow rough since the methodologies are often cross-linked or applied in parallel. As a general consideration, the methodology in use drives the type of questions that can be addressed with some success. For instance, electrostatic calculations permit to evaluate the contribution of salt-bridge and h-bond networks to protein thermostability, while MD simulations are naturally exploited to inquire the flexibility/rigidity duality and get insight into kinetic stability.

3.1.1 Comparing structures

The ever growing number of protein structures available to scientists has boosted the comparative study of homologue proteins. The goal of these studies is to single out the specific elements that correlate to thermostability from both the structural and compositional points of view. In several studies, it became clear that not a unique structural patterns could be identified but a variety of them. For example, thermophiles are characterized by shorter loops that are thought to compact the fold; they also present longer α-helices which larger dipoles that contribute to the cohesion of the protein matrix via dipolar interactions¹. On the other hand, the common belief that thermostability relates to better internal packing of the amino acids is not fully supported by recent investigations³³. In term of composition, a marginal surplus of prolines have been counted in the majority of thermophiles, as the proline amino acid can adopt only a few configurations, its presence in a protein decreases the entropy of the unfolded state hence giving a favorable contribution to stability¹. However, the most important finding is probably the surplus of charged amino-acids and salt-bridges detected in thermophiles, on average 8/9 salt-bridges per 100 amino acids, a percentage about twice larger than in mesophilic proteins⁴. Among the positively charged amino-acids, lysine gives the most important contribution to the charge excess. It was calculated that lysine has high configurational entropy in both the folded and unfolded states of a protein³⁴, and its presence reduces the unfolding entropy difference and has a stabilizing effect. This entropic factor must considered on top of electrostatic stabilization.

3.1.2 Charges and stability

Electrostatic calculations have been performed on several pairs of protein homologues from mesophilic and thermophilic organisms, with the aim of evaluating the role of electrostatic interactions to stability. In their seminal work, Xiao and Honig¹⁰ have reported that for thermophilic proteins this stabilizing contribution is as large as 3 ÷ 20 kcal/mol with respect to their mesophilic homologues. This electrostatic stabilization is not achieved in a unique way but varies with the protein families. In some cases, stability derives from long range interactions between charged aminoacids. This stabilization generally results from a spatial distribution of amino-acids that minimizes the repulsive forces between like charges. Alternatively, as in the case of localized salt-bridge and h-bond networks, short-range interactions play the major role.

Salt-bridges represent structural clamps, they are generally located at the surface of the protein and are thought to confer both thermodynamics and kinetic stability⁶. Networks of ion-pairs are also detected in the interior of proteins. Their contribution to stability depends on the magnitude of the associated desolvation penalty and the interactions with the local environment. When a charged amino-acids is buried in the interior of the protein, the associated energetic cost depends on the dielectric constant of the aqueous environment (ε_s) and protein core (ε_p). For a simple spherical charge q of radius R, this penalty being $\Delta W=\frac{q^2}{2R}\left(\frac{1}{{\epsilon }_p}-\frac{1}{{\epsilon }_s}\right)$. This contribution clearly depends on the degree of exposure of the charged amino acids, as discussed by Xiao and Honig¹⁰ for the ferrodoxin and the CheY families. The desolvation penalty can be compensated by favorable local interactions, for this reason buried charges are often involved in a network of salt-bridges or h-bonds. According to a recently proposed model³⁵, networks of salt-bridges and h-bonds also explain the lower specific heat of unfolding measured experimentally in thermophilic proteins as compared to mesophilic ones. Since the water dielectric constant decreases with increasing temperature, while the dielectric constant of a protein is supposed to be rather insensitive to temperature, the desolvation penalty becomes less critical, thus enhancing the stabilizing effect of ion-pairing.

Strategic salt-bridges located in proximity of the active-site contribute to the stability of this key region of the protein. This fact was pointed out by Nussinov and coworkers in their study of glutamate dehydrogenase monomer homologues³⁶, see Fig. 2, Panel A. Their finding suggests that the response of the protein matrix to raising temperature is nonuniform. It was concluded that the special resistance of the active site is a necessary condition for thermophiles to recover their activity at high temperature. However, the explicit link between stabilizing salt-bridges and protein activity has not yet been clearly assessed. For instance, it was recently reported that at ambient temperature the difference between the redox potentials of the Rubredoxin from the mesophile Clostridium pasterium and from the thermophile Pirococcus furiousus cannot be explained by simply counting the charged amino acids and their salt-bridging in proximity of the redox site (FeS complex)³⁷. In fact, the main effect (twice larger) is caused by the charge distribution on the atoms of backbone surrounding the site.

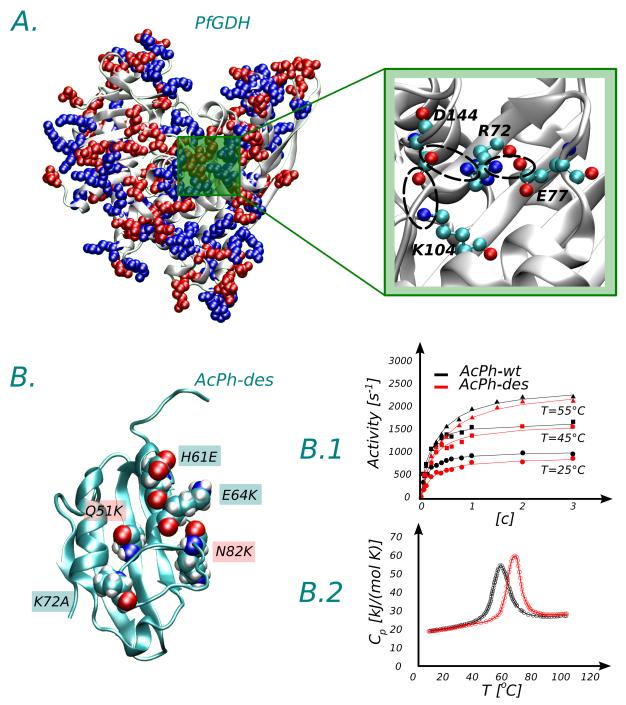
Fig. 2.

Panel A. Distribution of charged amino acids in the monomer glutamate dehydrogenase from Piroccocus furiosus (Pf) [PDB code 1GTM, chain B], PfGDH. Negatively charged amino acids (Asp,Glu) are colored in red while positively charged amino acids (Lys,Arg,His) are colored in blue. In the monomer of the hyperthermophilic variant PfGHD, 40 salt-bridges are detected, while only 20 are present in the mesophilic variant from Clostridium symbiosum. The inset illustrates the distribution of charged amino acids in the active site. A network of three ion pairs is detected involving lysine 104, which is implicated in the activity of the protein (see Ref.³⁶ for details). Panel B. Designed mutant of the human protein acylphosphatase (AcPh-des). The mutations have been generated via charge optimization⁴¹. Amino acid numbering is in accord with the [PDB code 2K7J]. The mutant is obtained by the introduction of 5 punctual mutations. Three mutations (H61E, E64K, K73E) reverse the wild-type amino acid charge, while other two introduce extra charge (Q51K, N82K). The designed mutant maintains the activity of the wild-type (B.1, activity vs substrate concentration) but is more stable (B.2, heat capacity vs temperature. The peak indicates the melting temperature of the system.). Data in B.1 and B.2 have been extracted from the original work⁴¹ using the software PlotDigitizer.

The optimization of charge-charge interactions, as studied via computational modeling, was shown to be a successful strategy to increase protein thermostability^38,39. Makhadtadze and coworkers have designed a protocol for generating and accumulating single point mutations on a protein surface in order to maximize the electrostatic contribution to stability⁴⁰. Mutants were generated via a genetic algorithm, while their relative stability was quantified via the Tanford-Kirkwood electrostatic model. The electrostatic optimization results from either charge addition/removal or charge reversion. The method was successfully tested experimentally⁴¹. A set of mutants of two human enzymes (the acylphospatase and the Cdc42 GT-Pase) were selected in silico using the computational approach and then expressed in vitro. Experimentally, the mutants were found to be more stable with respect to the WT, to remain soluble in solution without aggregating and to retain their activity, as illustrated in Fig. 2, Panel B.

3.1.3 And yet it moves

Molecular dynamics simulations have been carried out on several pairs of homologues and on laboratory made mutants that own increased thermostability with respect to the WT. In their seminal work, Lazaridis, Lee and Karplus⁴² have compared the dynamics of the Rubredoxin protein from two hyperthermophilic and mesophilic organisms on the timescale of hundreds of picoseconds and at different temperatures. Since then, the size and number of the studied proteins and the timescale sampled by the simulations have been steadily increasing. To date, comparative simulations extending to tenths of nanoseconds and longer are commonly found in the literature⁴³.

MD simulations have been used to assess the relative stability of homologue proteins. This is achieved by comparing the protein behavior at high temperatures. A critical validation of simulations relies on the observation that thermophiles resist more to high temperatures than the mesophilic homologues. Simulation results respect this basic fact, implying that the classical force fields routinely used in MD simulations contain all the necessary ingredients for discriminating thermostability. This resistance is mirrored by the observation of preserved 3D structures over the simulation time, the stability of the secondary structure elements and the evolution of native contacts, see the graph in Fig. 3, Panel A.

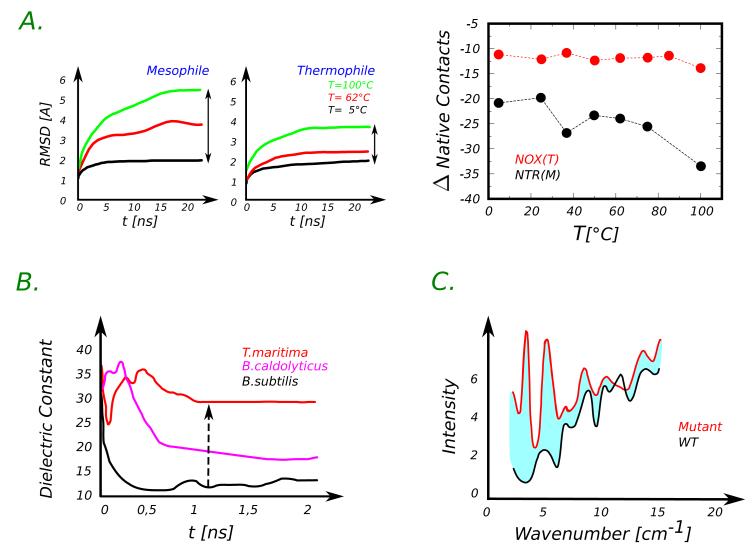
Fig. 3.

Panel A. Thermophilic (NOX) and mesophilic (NTR) homologues of the nitroreductase fold, as studied by MD⁴³. The time evolution of the root mean square displacement (RMSD) with respect to the crystallographic configuration is reported in the left panels for the two proteins. The structure of the thermophilic protein remains close to the native structure even at high temperature (100°C) while the mesophilic counterpart initiates unfolding. The thermophile maintains its native contacts along the scanned temperatures while the mesophile starts losing its native contacts around 40°C. Data are extracted from figures 1 and 7 of Ref.⁴³. Panel B. Dielectric constant (ε_p) of three homologue proteins estimated using the Fröhlich-Kirkwood equation⁴⁶, $\frac{2{\epsilon }_s({\epsilon }_p-1)}{(2{\epsilon }_w+{\epsilon }_p)}=\frac{<\Delta M_p^2>}{k_{b}T{r}_p^3}$, with ε_s being the solvent dielectric constant, $\Delta M_p^2$ the fluctuation of the protein dipole moment and r_p the effective radius of the protein modeled as a spherical globule. Results show that for thermophiles the dielectric constant ε_p is larger than for mesophiles (see Fig. 3 in Ref.⁴⁶). Panel C. Low-frequency density of states, as computed in Ref.¹⁷ for a WT (black) and thermostable mutant (red). All data have been digitalized using the software PlotDigitizer and smoothed for the sake of clarity.

Accessing protein dynamics allows to inquire whether thermostability correlates with protein rigidity. In this regard, it is important to first pose a preliminary question. Flexibility can be defined in many different ways depending on the spatial and temporal scales. Microscopically, the common indicators used in the analysis of MD trajectories are the atomic fluctuations around their average position or the displacement with respect to a reference configuration (i.e. crystal structure) principal component analysis. The latter allows to extract the effective directions along which the fluctuations of the protein are larger. Lazaridis, Lee and Karplus⁴² reported that, at ambient condition and on the short time scale of hundred of picoseconds, the hyperthermophilic Rubredoxin is slightly more rigid than the mesophilic variant, but subsequent simulations extending over few nanoseconds showed an opposite behavior⁴⁴. Very recently, Merkley et al.⁴³ have shown that, on the timescale of tenths of nanoseconds and considering different metrics for flexibility, the thermophilic and mesophilic homologues of the nitroreductase fold manifest the same degree of flexibility. Wintrode and coworkers¹⁷ focused on a family of laboratory evolved enzymes and found that the thermostable mutants are more flexible. They also observed that the mutants are characterized by an increased population of the low frequency vibrational modes with respect to the WT, see Fig. 3, Panel C .

Since flexibility varies along the protein chain, the comparison of the dynamics of homologues helps identifying the special spots in the protein matrix that either manifest a strong resistance to thermal stress or favor the unfolding process. Lazaridis, Lee and Karplus⁴² pointed out that the unfolding pathway at very high temperatures (400/500 K) is basically the same for the meso- and hyperthermophilic Rubredoxin: unfolding is initiated by large loop motions that expose the core of the protein to water penetration. Comparison of thermostable mutants with respect to the WT also singled out the loop regions as critical elements of thermostability^17,45. Hence, mutations that alter the conformational landscape of loops by favoring the screening to solvent were suggested as a viable strategy to protein stabilization.

Extended salt-bridges and h-bonds networks that cross-anchor secondary structure fragments provide a possible molecular mechanisms to confer such shielding to water penetration^30,43. It is worth recalling that structural investigations have appreciated that the folds of thermophiles are commonly characterized by short loops¹. Although high flexibility may be considered as a source of entropic stabilization, large amplitude motions could also favor the disruption of the protein matrix by easing unfolding via water breaching. However, large amplitude motions can be accommodated in different ways to prevent protein denaturation. For instance, relative low frequency motion of intact secondary structures could help dissipating thermal stress without compromising the protein integrity^17,30. The resistance to thermal perturbation of the active site and its local environment is essential as well. The surplus of kinetically stable links (h-bonds and ion-pairs) has been observed to characterize thermophiles in the active site region⁴³. This feature is also observed in simulations of laboratory created mutants¹⁷.

Flexibility contributes to protein stability as mediated by electrostatics. This aspect was pointed out in an important work by Dominy, Minoux and Brook III⁴⁶. These authors studied a set of proteins from the Csp and the CheY families by using MD simulations with an implicit solvent. They used the formalism of the Fröhlich-Kirkwood theory to relate the dielectric constant of the protein to the square fluctuation of the protein dipole moment. According to those calculations, the thermophilic variants all have higher dielectric constant with respect to the mesophiles, see Fig. 3, Panel B. This is caused by the charge enriched surfaces and not by the difference in flexibility. According to this study, higher protein dielectric constant reduces the desolvation penalty and therefore favors protein stability.

While MD simulations indicate similar flexibility for thermophilic and mesophilic proteins, other studies based on the constraint network analysis (CNS) are supportive of a correlation between thermostability and protein rigidity⁴⁷. This correlation was recently tested against a large set of pairs from meso-, thermo- and hyperthemophilic organisms⁴⁸. The thermophiles share the same structural rigidity patterns with their mesophilic homologues but the internal connectivity, represented by a percolating network of contacts, is more resilient to temperature. For the majority of studied proteins, the calculated melting temperature is higher for the thermophiles, as expected. The connectivity of the active site with the rest of the protein was shown to be a key element for relating the partition of rigidity/flexibility with protein activity.

Unfortunately, up to now a comprehensive understanding of the correlation between protein activity and thermal resistance is still lacking. Only few computational/theoretical works tackled this issue directly. We mention the computational efforts aimed at explaining the variability of the redox potential measured in Rubredoxin homologues (see Ref.³⁷ and references therein).

Concerning enzymatic activity, to the best of our knowledge only Warshel and coworkers⁸ challenged the problem of studying the catalytic step of the enzyme dihydrofolate reductase. In this work, the mesophilic and thermophilic variants of the enzyme were studied by a multiscale strategy. While coarse-grained and atomistic simulations were used to sample the folding free energy landscape of the proteins, the Empirical Valence Bond method was adopted to gain insight into the chemical reaction, by providing quantities such as the activation barrier and the reorganization free energy. The main finding of this work was that the catalytic step and the protein flexibility are uncorrelated. While the thermophilic protein reveals a reduced flexibility in the folding free energy landscape, this fact does not impact the chemical reactivity, since the reaction coordinate is orthogonal to the conformational coordinate. The frequencies characterizing the motion along the reaction coordinate were found to be identical in both enzymes, the thermophile showing however larger displacements and hence a larger reorganization energy. According to Warshel et al.⁸, the reduced catalytic activity of thermophiles at ambient condition may depend solely on their higher activation energy with respect to mesophiles. The recovery of catalytic power at higher temperature should be traced back to the temperature dependence of the reaction constant.

We conclude this section with a discussion on the effect of coupling between thermostable proteins and the solvent. The response of the solvent to temperature has been appreciated as a possible source of thermostability since a lower dielectric constant ε_s reduces the desolvation penalty. It is also worth stressing that salt-bridges, a source of thermodynamic and kinetic stability, are strongly influenced by their local solvation, i.e. at high temperature the potential of mean force between two charged side chains shows two distinct minima, one of which corresponds to water separated contacts⁴⁹.

Water acts on protein stability and to the kinetics of unfolding. Structural water and cavity filling are supposed to confer local extra-stability to the protein matrix and to induce global extra-flexibility for compensating the water confinement in cavities. Yin, Hummer and Rasaiah²⁸ have provided evidence that, for the thermophilic tetrabranchion stalk segment, the complex is stabilized by the filling of internal cavities and denaturation is anticipated by cavity drying. On the other side, it is also well established that unfolding proceeds via the disruption of the protein connectivity partially triggered by water penetration. Recent MD simulations of meso, thermo and hyperthermophilic variants of the EF-Tu G-domain have suggested that the strong coupling between the surface of the thermophiles, enriched in charged groups, and water could prevent water penetration at high temperatures^30-32.

3.2 In silico experiments: a road map for the coming days

The studies mentioned so far have tackled the problem of protein stability and its relationship to enzymatic dynamics and function. For instance, electrostatic calculations have estimated the contribution of global and local electrostatic interactions to thermostability. However, in this kind of calculations other key contributions are omitted or approximated, like hydrophobic interactions, the coupling between the protein and the hydration shell, the conformational entropy of the protein. On the other hand, MD simulations have explored the differences in flexibility/rigidity between pairs of homologues, but the observations are not easily translated in term of free energy differences. The work of Dominy and coworkers⁴⁶ moved in this direction by relating protein flexibility to electrostatic stabilization and by computing the internal dielectric constant of meso and thermophilic proteins. A complementary approach is represented by the study performed by Wintrode and coworkers¹⁷ in which the vibrational density of state at low frequency is used to derive the increased conformational entropy of the folded state and the increased heat capacity of the thermostable mutants. An explicit calculation of the entropic contribution to protein stability associated to salt-bridges was presented in Ref.⁵⁰, where the thermostability of a α-helix coiled coil peptide trimer was investigated.

Nowadays, computer facilities as much as the development of new sophisticated methodologies pave the way for new studies on protein thermostability. In the following, we will draw an hypothetical roadmap for this challenging research.

3.2.1 Exploring the landscape

Let us start from the problem of protein stability from both the kinetic and thermodynamic perspective. Several computational strategies may be foreseen to shed new light on the microscopic origin of the thermal resistance.

The development of new algorithmic paradigms and the progress in hardware technology are boosting the capabilities of computer simulations. The brute force application of Molecular Dynamics allows to study thermal resistance and protein unfolding without resorting to unphysical accelerations to induce the process. In a recent comparative investigation, the simulations of a pair of meso/thermophilic proteins have been extended to tenths of nanoseconds for each targeted temperature⁴³. In the present scenario, it is reasonable to plan a comparative study in the hundred of nanoseconds timescale and even longer.

The access to special high-performance hardware and software largely stretches the accessible timescale. For instance, in a recent work the DE Shaw research team⁵¹ reported on MD simulations of the small BPTI protein in the millisecond range. The brute force approach can be used to acquire important knowledge on the relative kinetic stability of homologue proteins and to focus on the early steps on the unfolding process. This allows to locate the weak spots of the protein matrix and hence to design ad hoc stabilizing mutations. In addition, the larger sampling of the conformational landscape allows to assess the balance between flexibility and rigidity in the protein matrix, with special focus on enzymatic function, as discussed later on. The growing computer power is also essential to extend the comparative investigation to larger systems, i.e. multi-domain proteins like the three domain EF-Tu, or assembled complexes.

Since conformational transition must be weighted statistically, the accurate sampling of the free energy landscape is the nodal problem to be addressed. One possible strategy is to enlarge the ensemble of simulated trajectories, as routinely done in the folding@home project⁵². Several independent trajectories are evolved in parallel, thus allowing the system to sample the phase space starting from very different initial conditions. In the context of thermophilic proteins, extensive sampling in the trajectory space should be used to extract the kinetics of the transitions between conformational basins and therefore provide a description of the different landscape underlying meso and thermophilic homologues. This extensive campaign would allow to single out possible differences in free energy and multi-minima distributions as well as their temperature dependence.

The simulation of many independent trajectories is costly and several techniques exist for easing the task of sampling. For example, the Replica Exchange Molecular Dynamics (REMD) technique⁵³ is similar in spirit to what described above since it allows to evolve independent copies of a system, with each copy evolved at a different physical temperature. The method is useful for exploring the conformational landscape of proteins since the runtime exchange between the copies favor the crossing of high energy barriers otherwise trapped in local minima. Temperature dependent properties can be readily extracted. For instance, the heat capacity curve as a function of temperature and the melting temperature of homologue pairs can be compared. On the other hand, the properties of the unfolded ensemble above the melting temperature provide a clue to assessing the contribution from individual amino-acids or protein fragments to the unfolding heat capacity. This knowledge can support the interpretation of experimental data from differential scanning calorimetry¹⁶. Finally, the reconstructed free energy landscape allows to gain insight into the unfolding/folding pathway.

Unfortunately, the application of the method has some practical limitations since it is known to perform unsatisfactorily when increasing the system size. As a reference to the state of the art of the technique, we cite the work of Day and coworkers⁵⁴ on the temperature and pressure folding/unfolding of the Trp-cage protein in explicit solvent.

While REMD uses temperature as a tuning parameter for exploring the conformational landscape, other methods rely on the definition of mechanical Collective Variables (CVs) or, in some cases, by simply locating stable conformational basins. These methods are appealing for the purpose of monitoring protein transitions that can be connected to some internal degrees of freedom, such as domain relative distances, amino-acid or secondary structure orientation and position and solvent⁵⁵. As an example of recent applications, we cite the study of protein conformational transitions in GroEL and HIV-1 gp120 via Temperature Accelerated Molecular Dynamics⁵⁶, the calculations based on the String Method of the free energy along the transition path connecting two conformers of the Miosin VI protein⁵⁷, the investigation of protein transition in Kinase biased by Metadynamics⁵⁸.

The definition of specific mechanical CVs is of interest for the study of thermophilic proteins since it allows to quantify the contribution of specific interactions (i.e. salt-bridge networks, localized hydrophobic contacts) to protein stability. The application of mechanical stress in out-of-equilibrium simulations is another viable route for assessing the relationship between mechanical and thermodynamic stability. Steered MD simulations can be used in conjunction with atomic force microscopy pulling experiments. This technique allows to compare the different response of homologue pairs to external forces. Finally, with respect to the problem of kinetic stability, one can focus on those computational methods that enhance the sampling of the reaction path connecting the folded and unfolded (partially unfolded) states. As a reference, we mention the recently application of Milestoning to peptide unfolding kinetics⁵⁹.

3.2.2 Looking into the active site

The stability of proteins at high temperature is one aspect of thermal adaptation; when dealing with thermophiles one wants also to understand why activity is almost maximal at the growth temperature and is strongly reduced at ambient condition. In the context of enzymatic activity, it is worth facing the problem by considering separately the chemical step of the catalytic reaction and the binding/unbinding process of the substrate with the enzyme.

The computational study of a chemical reaction occurring in the active site is necessarily based on the treatment of some degrees of freedom at the quantum level. In a chemical reaction bond breaking and forming must be accounted for and a simple classical model for the substrate and enzyme is inadequate. For computational reasons, it is however unfeasible to treat the whole system at quantum level and a mixed approach is the only possibility: the electronic structure of a specific region of the system is described explicitely (i.e. the substrate and the active site) while the remainder is modeled classically. This mixed approach is referred to as Quantum Mechanics/Molecular Mechanics (QM/MM). As pointed out in Ref.⁶⁰, when studying enzymatic activity, nuclear quantum mechanical effects may also be important since they impact the rate constant of the reaction.

The available computer power allows to use QM/MM routinely for generating dynamics of protein/substrate complexes. However, a great computational effort is required for computing the activation free energy of the reaction under study and estimate the corrections due to recrossing and/or nuclear effects. The advanced sampling techniques described above can be adapted to study reactivity via mixed quantum classical simulations, i.e. by introducing ad hoc CVs acting on the nuclei or the valence electrons. The precise quantification of the factors influencing the constant rate of catalytic reactions is of vital importance for understanding the activity regime that differentiates mesophilic from thermophilic enzymes⁸. At first, it is of interest to evaluate the activation energy for a reaction occurring in pairs of homologue enzymes. The lack of activity at ambient conditions of the thermophiles is expected to correlate with an higher activation barrier. Direct investigation allows to single out the specific interactions. The recovery of activity at higher temperature could be a simple consequence of the exponential dependence of the rate constant with the inverse of the temperature without resorting to any change in the activation free energy. Sampling the conformation of the protein at high temperature and evaluating the activation free energy at high temperature would indicate if thermal excitations also drive a rearrangement of the active site and lowers the barrier. For mesophiles, sampling at high temperature would clarify how thermal excitation locally destroys the catalytic propensity of the active site via partial unfolding.

A problem related to conformational sampling must be put forward. At first, protein (or protein /substrate) dynamics generally spans a very broad temporal range while proteins visit a large set of conformational states. QM/MM based free energy calculations would hardly account for this multi-minima conformational landscape in full. Therefore, the computed activation barrier correlates the reaction occurring in a specific active site/protein state, a local minimum in the conformational space. If the timescale of the reaction is shorter than the characteristic transition between conformational states, a multi-scale approach is appropriate. Simulations at low resolution performed by using fully classical atomistic or coarse-grain models can be used for selecting an ensemble of representative configurations. Each of these configurations is an independent seed for estimating via QM/MM method the activation free energies. For an interesting discussion on the issue we refer to⁶¹ and references therein. Similarly, the high temperature sampling needs to be long enough to allow for local unfolding to occur, being specially important for inquiring the degradation of activity in mesophiles.

The formation/dissociation of protein/substrate complex represents the second problem to consider. Indeed, it is plausible that thermophiles have a low affinity with their substrates at ambient conditions while upon temperature increase, conformational changes and fluctuations facilitate the binding process. The other way around in mesophiles is that peculiar activated motions cause the occlusion of active site at high temperature and hence make the binding unfavorable. The binding free energy can be calculated in different ways, either by using simplified scoring functions as in docking experiments or via extended free energy calculations based on atomistic simulation⁶².

The details of the binding path are of extreme importance as well. The effect of temperature on the coupling between the substrate/protein along this path is a strategic aspect to be elicited in the future. The (in)activation of the binding in (meso)thermophiles as temperature increases could be traced back to a particular region of the protein surface. A plethora of methods stand on the shelf for this purpose. Here we just cite a very interesting work in which a large set of independent MD simulations performed on GPUs (graphics processing unit) are used to explore the binding process of an inhibitor to the trypsin protein⁶³. Moreover, it is widely recognized that the desolvation of the active site is an important factor for the process, and different computational strategies have been proposed to account for it explicitly (see for instance Ref.⁶⁴). In the future, it would be very appealing to perform comparative studies to characterize the role of water along the binding process in thermophiles as a function of temperature.

4 Conclusions

This tutorial review focused on thermophilic proteins and on how computational methods can be used to investigate the microscopic origin of protein thermostability. The Molecular Dynamics technique and advanced methodology for free-energy calculations, conformational landscape sampling, mixed quantum/classical simulations represent a complete toolbox for gaining insight on strategic issues underlying protein thermal resistance, i.e. the rigidity/flexibility trade-off, the role of solvent, the effect of temperature on the enzymatic activity and its correlation to protein motion and conformation. The study of thermostable proteins is of broad interest since it has the potential to deliver unique knowledge on the forces that stabilize a protein fold and ease the functionality. This is key for engineering enzymes capable to work in harsh conditions. Moreover, this knowledge can be exported to study the behavior of proteins interacting with nanomaterials, solubilized in exotic environments (i.e. organic solvent), or placed in special crowded spaces.