Molecular dynamics simulations of G-DNA and perspectives on the simulation of nucleic acid structures

Abstract

The article reviews the application of biomolecular simulation methods to understand the structure, dynamics and interactions of nucleic acids with a focus on explicit solvent molecular dynamics simulations of guanine quadruplex (G-DNA and G-RNA) molecules. While primarily dealing with these exciting and highly relevant four-stranded systems, where recent and past simulations have provided several interesting results and novel insight into G-DNA structure, the review provides some general perspectives on the applicability of the simulation techniques to nucleic acids.

1. Introduction

Guanine quadruplex molecules (G-DNA) are arguably the most important non-canonical DNA structures [1–7]. The basic structural unit of G-DNA is a planar quartet of cyclically bound guanines stabilized by monovalent ions. Several consecutive quartets stack together to form the G-DNA stem with the monovalent ions lining up in its channel. Fig. 1 shows a simple stem model with 2 quartets stabilized by one channel K⁺. The G-DNA molecule can consist of four, two or one separate sequences that come together with the strands that make up the G-DNA stem in various combinations of parallel and anti-parallel strand orientations. The biochemically most relevant variants are the single-stranded (monomer) topologies. Monomeric and dimeric quadruplexes, made up of one or two sequences of DNA, need single stranded loops to connect their strands. The loop structures are highly relevant and critical elements of the biological role of G-DNA. Although the G-DNA stem architecture looks at first sight simple, in reality it shows enormous richness of topological variants which often are extremely sensitive to the base sequence and the surroundings [1,8–12]. Even a change of a terminal base in the DNA chain can sometimes influence the overall quadruplex topology [13].

Fig. 1.

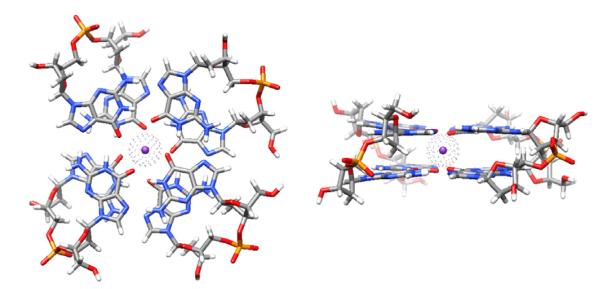
Left – 2-quartet G-DNA stem with anti-parallel down-down-up-up (from bottom left counterclockwise) 5′-GpG-3′ strand orientation and with anti-syn bases in 5′-3′ direction in all strands. The structure is colored by atom types with the integral bound K⁺ ion shown with a van der Waals sphere. Right – side view.

Potential quadruplex forming sequences are abundant in the genome, for example, at the telomeric regions and in promoters of many oncogenes [14–17]. Quadruplex structures may be formed in untranslated regions of messenger RNAs and contribute to translation regulation [18–22] and even splicing [23]. Thus, G-DNA and G-RNA may have numerous biological roles, and may even be a potential target in anticancer therapy [24]. The basic G-DNA architecture may serve as a scaffold for aptamers [25]. The fascinating motif characterized by cation stabilized quartet stems may be also utilized in supramolecular assemblies [26–28].

From the physical-chemistry point of view, G-DNA structures exhibit a very subtle and intricate balance between the molecular forces and energy terms that stabilize the molecule. The stems show the striking combination of quartet base pairing with extensive stacking complemented by the stabilizing role of the monovalent ions. The otherwise very stiff G-DNA stem becomes highly dynamic without the ions [29–31]. This ion-free configuration is thermodynamically very unstable, and kinetically tends to disintegrate, unless some ions are captured quickly enough [30,32]. The ions are thus integral components of quadruplex molecules. The single-stranded loops have varied topologies/conformations stemming from the overall G-DNA stem fold combined with a complex balance between stacking, solvation, non-canonical backbone conformations and other energy contributions [33,34].

Due to their biological roles and uniqueness of molecular architectures, G-DNA molecules represent an attractive target for computational chemistry, and particularly for classical molecular dynamics (MD) simulations with explicit inclusion of solvent and counterions [35,36]. Before the advances in simulations protocols including the appropriate treatment of long range electrostatics in the early 1990s [37], stable simulations of nucleic acids were not possible, as highlighted by profound instabilities of ions in early explicit solvent G-DNA MD studies [38], nicely illustrating swift accumulation of errors in simulations not using Ewald (and most commonly the fast particle mesh Ewald (PME)) treatment of electrostatics.

The first G-DNA simulations using appropriate force fields and simulation protocols were published starting in 1998 [39], around the same time as the simulation study of i-tetraplex was reported [40]. These G-DNA studies were executed with the AMBER suite of programs [41,42] and the first (original) generation of the Cornell et al. all atom pair-additive nucleic acids force field (ff94) [43]. Our first study was based on at that time an impressive 20 ns of simulation trajectories [29]. The study provided several results that remain entirely valid until now, which is not always the case in MD simulation literature. For example, it captured the unique stiffness of the native cation-occupied quadruplex stem, demonstrated that the stem is visibly destabilized in absence of the ions suggesting that G-DNA stem is never left completely without ions, revealed hydration of the stem cavities without ions, highlighted that the stem can survive quite well with incomplete number of ions and predicted existence of parallel stranded G-DNA stems with strand-slippage and incomplete number of quartets. The study revealed profound structural conflicts in X-ray structure of (G₄T₄G₄)₂ G-DNA with edge loops while supporting the alternative diagonal loop fold predicted by NMR (and later finally confirmed by X-ray crystallography) [44–46]. The simulations demonstrated imperfect local description of the ions inside the stem, such as bifurcated H-bonding of the quartets. The initial investigation indicated that carefully executed and analyzed simulations have potential to provide interesting information about G-DNA. Since then, many more simulation studies of G-DNA were published, essentially all with the same basic force field and methodology [30–32,34–36,47–75]. In 2010, the state of the art reached a combined total of 12 μs of simulation data in a single simulation study, surpassing the 1999 study by almost three orders of magnitude [69].

2. What can simulations tell about G-DNA and other nucleic acids?

When assessing the outcome of simulations, it is important to understand what exactly the technique does and what are its basic limitations and approximations. Explicit solvent MD is an atomistic single-molecule technique dealing with a solute molecule or molecular complex in aqueous solution. The studied system starts with a precise starting geometry (set of atomic coordinates) usually derived from high resolution experimental structures, most often from X-ray crystallography and increasingly NMR. The quality of starting geometry critically affects the subsequent simulation for two reasons. First, the simulation time scale may be insufficient to overcome thermal barriers to conformational change that remove deficiencies of the starting structures. Second, the quality of the theoretical model of the biopolymer (the force field, see below) may be not robust enough to find the correct structure. Yet, at the same time, simulations may be useful to detect inaccuracies in experimental structures as evidenced by rapid structural change in molecular dynamics when the system is evidently high in energy at the start (provided it is not locked in this geometry by many other contacts).

A conservative task for simulations is to investigate the known experimental structures and their straightforward modifications (such as base substitutions, different protonation states, etc.)[48,53,76–80]. More ambitious is to try to use simulations for some predictions of new structures, and in extreme cases, to simulate the folding pathways of the molecule. Although we do not want to rule out such computational efforts entirely, they are in general more risky and require a deep understanding of the approximations. There are many studies in the contemporary literature that do not sufficiently respect the limitations of the simulation techniques, even if and often published in high-quality journals, since the results look at first more attractive compared to studies that are executed in a more conservative manner.

Having the starting structure, the biomolecular system surrounded by an environment of water and ions undergoes 1–1000 + ns of dynamics starting from the initial geometry. The method mimics the genuine thermal fluctuations of the initial structure. Next, we attempt to deduce from these simulation runs (which are still very short compared with most real dynamics) useful information about the studied molecule. With the advance of new powerful hardware such as graphics processing units (GPUs) or even specialized hardware, the simulation time scale will be gradually shifting to multiple microseconds or even millisecond time scales [81–83].

3. How to compare simulation with experiment?

It is often assumed that solution simulation is attempting to mimic solution experiment. However, the simulation conditions are specific and do match any experiment (and vice versa). The typical molecular dynamics simulation takes a single biomolecule, for example a G-DNA stem, and surrounds this by a finite amount of solvent and ions while imposing periodic boundary conditions. The size of solvent box is chosen to be small enough to allow fast enough simulations while also trying to mimic conditions that are reasonably close to the properties of infinite solvent away from the solute. Although at a relatively very high G-DNA (solute) concentration ( ~5–50 mM) due to the finite solvation (i.e., the number of water molecules per solute molecule), this does not mimic a true solution. The periodically placed G-DNA molecules obviously cannot interact except periodically. For example, despite being at high concentration, the G-DNA molecules cannot aggregate (unless of course multiple G-DNA molecules are present in the same unit cell), and there are potential, albeit generally small in high dielectric solvents, artifacts due to periodicity [84,85]. Beyond the issues of finite size, high solute concentration and periodicity, there are also potential issues with the salt (see below). The point of discussion here is to highlight that simulations should primarily serve as an autonomous complement to experiments. For example, RNA kink-turns [86–88] or 5′-UAA/5′-GAN RNA internal loops [89,90] are important RNA building blocks, recurrent in ribosomes, that require stabilization by additional interactions or even remodeling by surrounding proteins or RNA. Thus, their equilibrium solution structures in isolation (e.g. by NMR) show their equilibrium solution geometries different from those found in the ribosome, and therefore these have limited biochemical relevancy. At the same time and in contrast to solution experiments, simulations can neatly investigate properties of these RNAs in their biochemically relevant topologies, by subtracting them from the ribosomal X-ray structures and then simulating in isolation. If the unfolding is prevented on the simulation time scale by sufficiently large energy barrier, the simulation is unaffected by the existence of another more stable structure that is not sampled. Thus, the simulations gather useful data about the relevant structures. In this particular case drawing strict analogy between solution simulation and solution experiment is misleading. The simulations need to be linked to the starting ribosomal structure. Similarly, in the quadruplex area, it is legitimate to use simulations for substates of G-DNA stems that are not known from experimental studies but may participate in the formation/folding path of the quadruplexes [30]. It is also possible to investigate a G-DNA topology which, for a given sequence, is known to not be populated under typical experimental conditions. The aim for example can be to understand the reasons why the molecule is not preferred and how it may differ from the experimentally observed topologies (structurally and energetically). On the other hand, when assessing the applicability of the simulations, it is also fair to admit that experimental results may be affected by limitations. X-ray structures may to certain extent be affected by crystal packing effects [91–93]. NMR studies sometimes require sequence modifications or other engineering tricks to resolve the structures [94,95]. Although rarely discussed, thermodynamics and kinetics of small DNA systems are likely markedly influenced for example by the chromophores attached in the FRET experiments, considering the sensitivity of the DNA structural dynamics to even the most subtle sequence changes [96]. Actually, simulations may be used to probe the impact of attaching the chromophores [96].

The typical simulation can be summarized in the following way. We set up the starting structure (usually taken from experiment, sometimes with modifications), we immerse it into water box under periodic boundary conditions, set up the simulation temperature (using thermal bath, thermostat) and then we allow the system to experience thermal fluctuations while analyzing its behavior. Thus, simulations can be viewed as an alternative tool in the portfolio of available methods to complement experimental techniques and to ask specific questions about the molecules. The right approach is to assess what a hypothetical single molecule experiment matching the simulation protocol and conditions could tell about the investigated molecule, and to design the simulations accordingly. As noted above, one has to be very conservative and careful when attempting any model building not directly based on atomistic experiment, even for parts of the molecule. Good computational study should always present a paragraph assessing its limits, brief overview of the relevant computational literature and the numbers/structures should not be presented in an experiment-like manner.

4. Force field limitations and development

The greatest advantage of the simulation technique is the unsurpassed level of detail of all aspects of the time evolution (with sub-ps time resolution) of the three-dimensional structure and (to certain extent) energetics, including the positions of all water molecules (including their hydrogens) and ions. This is information that is impossible at present to obtain in such fine detail from experiment. However, MD simulations are faced with two well-known and significant limitations. First, the simulations are very short compared to the major part of biochemically relevant biomolecular dynamics, for example, base pair opening (or breathing) which occurs on micro- to milli-second timescales [97–99] or biomolecular folding which occurs on time scales from microseconds to days [100]. The short timescales imply that only limited sampling around the starting geometry is possible. If the starting structures are not representative, such sampling may lead to inaccurate interpretations. This was highlighted earlier as a risky use of simulation, i.e., to characterize putative hypothetical model structures through simulation since stable simulation around the initial geometry may only demonstrate metastability of the structure. Second, a fundamental limitation not only not waning but actually becoming more acute with faster computers is the approximate nature of the present biomolecular force fields, which are simple, atomistic analytical functions relating structure with potential energy. If these lack accuracy, given sufficient computer power simulations will move to non-representative or incorrect geometries (Fig. 2). With history as a guide, this has been the primary means by which deficiencies in the underlying potential were found. When simulation timescales were only possible on the timescale of picoseconds, DNA simulations even with inaccurate treatments of the electrostatics and primitive force fields were “stable”[101,102]. As parallel implementations of the molecular dynamics codes became more readily available it became clear that not only better force fields, but better treatments of the long range electrostatics were necessary [103,104] as was previously mentioned. Upcoming, after the basics of the force field are introduced, we will discuss significant findings that led to or necessitated force field improvements while presenting the current status of nucleic acid force fields.

Fig. 2.

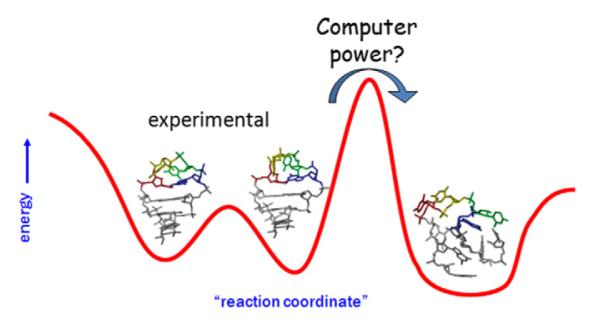
Cartoon (model case) of a reaction coordinate highlighting potential issues with conformational sampling and accuracy of the applied force field. In short simulations, sampling will be restricted to near the initial structure. If this is an experimental structure, sampling may provide an accurate representation of the equilibrium fluctuations, for example between two populated UUCG tetraloop geometries as depicted. If the structure is not representative of the true structure, sampling may be trapped in metastable states. Given longer simulation times and/or application of enhanced sampling methods it may be possible to overcome energetic barriers to either non-representative structures or more representative structures. However, if the non-representative structures are in fact lower in free energy due to force field inaccuracies returning to the representative experimental structure will not be possible. In our particular case we show a case of a stem-loop RNA structure, where not only the tetraloop structure is lost but also the stem collapses.

The gradient of the molecular mechanics potential energy representations effectively defines a force for each single Cartesian XYZ coordinate of the system. The molecular mechanical force field representation is actually rather simple and consists, at the first level of description, of a set of harmonic springs for bond lengths and valence angles, supplemented by dihedral profiles to represent the covalent connectivity [43]. Although it is possible to add in higher order descriptions to better represent coupled dynamics such as bend-stretch coupling and non-harmonic terms, the simple approximation does surprisingly well for biological molecules like proteins and nucleic acids that do not often contain highly strained rings or unusual covalent connectivities. A consequence of the harmonic covalent bond description is that covalent bond breaking and making, i.e., chemical reactions, are not possible. Inter-atomic interactions are approximated by (i) Lennard–Jones spheres to represent atomic repulsions and dispersion attraction and (ii) point charges, specific for each atom depending on its context. The charges are localized at the atomic centers and are most commonly fixed, i.e., they do not change upon solute conformational changes and do not respond to its exposure to external electric fields. The force field description of non-covalent interactions is obviously nonphysical with many effects (such as polarization and charge transfer effects) neglected by definition. Since force fields neglect non-additive contributions, they are called “effective pairwise additive force fields”. The neglected contributions are somehow effectively but “un-physically” accounted for by parameters of the explicit force field terms during the fitting procedure. Most of this “slop” or error falls into the dihedral force field terms.

Bond and angle parameters can be derived from X-ray structural data (to get equilibrium distances and angles), and IR and microwave spectroscopy (for the stretching and bending force constants), and/or high level quantum mechanics (QM) computations. Van der Waals radii and well-depths can be derived by matching experimental densities and heats of vaporization as validated by the original OPLS approach [105], high level QM, and/or through ad hoc assumptions. As electrostatic interactions are critical, not only to represent the nucleic acid poly-anion but also to provide a balance between hydrogen bonding in base pairs and stacking, care needs to be levied on the means to parameterize the atomic charges. There are two commonly applied approaches: (i) parameterizing the atomic charges through fits to QM-derived electrostatic potentials (see below) or (ii) by fitting the force field to reproduce QM computations of interaction energies of small model systems interacting with ligands like water. The former approach is common of the AMBER force fields and has evolved from electrostatic potential fits [106] to restrained electrostatic potential fits to prevent artificial growth in the charges of buried atoms [107], to more systematic restrained electrostatic potential fits that remove artifacts from orientation and use multiple conformations for fitting [108]. The approach (ii) is characteristic of CHARMM force field (see below), although recently also the CHARMM community appears to consider the RESP philosophy [109].

The most difficult and arbitrary task in force field parameterization is the fitting of the dihedral potentials. Their actual physical meaning is not clearly defined. Rather than solely being related to real electronic structure contributions, they represent ad hoc functions used for the final tuning of the force field. Dihedral parameterization makes up for the absences in the simple potentials and has very large impacts on the simulation. As a result, essentially all recent refinements of established force fields for nucleic acids and proteins have been based on modifications of the dihedral profiles. For further insight into the force field representation, issues with electrostatics and solvation, and setup and analysis of simulations, please refer to more detailed protocols previously published [110–114].

Although a variety of nucleic acid force fields are available, the two most widely used additive pairwise approaches are the AMBER, based on the Cornell et al. second generation force field (ff94) [43] and the CHARMM force fields starting with the CHARMM all27 parameterization [115,116]. They have similar functional forms but differ in parameterization.

The original “AMBER” nucleic acid force field, previously referred to as parm94 based on the name of the parameter file (parm94.dat), was renamed to ff94 to provide a more consistent naming scheme for the all atom force fields in AMBER. There are many available variants of the Cornell et al. (AMBER) force field that involve slight or large changes to the dihedral terms. Older variants include ff94, ff98 (tuned via simulation with tweaks to the glycosidic χ and anomeric O–C–C–O torsions in an attempt to improve systematically too low helical twist of B-DNA with ff94) [117] and ff99 (further slight adjustments in same torsions)[118]. A further revision is ff99 plus parmbsc0, which fixes a major problem with γ backbone torsion tending to trans [119]. Most recently, the parmχOL₃ [120,121] χ-modification has been released which is specifically designed for RNA simulations in combination with ff99 + parmbsc0. There have been two additional attempts to modify the χ-profile, with rather limited testing [122,123].

The CHARMM all27 force field describes B-DNA well, but has not yet been systematically or extensively tested for either folded RNAs or non-canonical DNAs [124]. We have recently reported not fully satisfactory behavior of G-DNA stems with CHARMM with a loss of the ion from the stem [72]. However, our testing has been far from exhaustive and should in no case be taken as a final suggestion regarding applicability of CHARMM to G-DNA. The CHARMM RNA force field has been substantially revised in 2011 by complete reparameterization of the dihedral parameters of the 2′-hydroxyl proton of the ribose to suppress large instabilities in A-RNA simulations [125]. In addition, tuning of the ε/ζ dihedrals of CHARMM specifically for B-DNA has been recently reported, in order to balance the BI/BII substates [126]. Both reparameterizations still await more extensive testing for noncanonical systems. The CHARMM developers also work on parameterization of a polarizable force field for nucleic acids [109], albeit it is difficult to predict when will such force field be fully available and what will be its performance. Both AMBER and CHARMM offer high-quality protein force fields for a consistent description of NA-protein complexes [124].

Regarding the GROMOS nucleic acids force field [127], there are basically no successful independent tests by groups not linked to the developers of the force field. The 2005 force field demonstrated a tendency towards A-DNA structure in simulation of DNA duplexes [127]. Recent studies reported major instabilities in GROMOS B-DNA simulations [128] and complete loss of G-DNA structure within 10 ns [70], in line with our unpublished independent tests.

Since G-DNA simulations were almost exclusively carried out with variants of the Cornell et al. nucleic acid force fields, let us comment a bit further on their performance and recent tuning efforts. The original (1994) ff94 version was for a long time assumed to give sufficiently good description of B-DNA [103,129–137] although helical twist was known to be underestimated compared to X-ray and high-quality NMR data. Nevertheless, the issue of B-DNA helical twist is complex. Helical twist of 36° is often cited as canonical. However, this may be influenced by crystal packingwith 10-mer DNA duplexes that pack in the crystal to form a full helical turn/repeat. Other data suggest that helical twist in solution should be ~34° [138–140]. Nevertheless, the high resolution and accurate NMR structure of the d(CGCGAATTCGCG)₂ dodecamer refined with residual dipolar coupling restraints is in very close agreement with the corresponding X-ray structure [141], questioning suggestions that there is a systematic difference between X-ray and solution structures. Since the ff94 force field underestimates even the 34° helical twist, ff98 and ff99 (see above) refinements of the force field were proposed [117]. Both ff98 and ff99 perform rather similarly to ff94 with the exception of a slightly higher average twist and slower sugar repuckering rates. These force fields were applied to many other DNA and RNA systems, and the vast majority of the G-DNA simulations reported to date were done with the ff94-99 variants.

One of the main reasons for success of the Cornell et al. force field [43] is its elegant and simple electrostatic model. The partial atomic charges, which per se do not have any physical meaning [142], are fit to reproduce an observable calculated from Quantum mechanics known as electrostatic potential (ESP) around small nucleic acids fragments (essentially nucleotides). As the ESP is a very important determinant of the electrostatic part of the molecular interactions, the ESP-fitted point charge model is optimal (within this force field approximation) to describe base stacking, base pairing and other interactions involving nucleic acids bases. (Note, however, that there are important short-range coulombic effects not included in this approximation [143]) Of course, for the flexible and anionic sugar-phosphate backbone this approach is less justified. However, without fundamentally changing the force field function, our options for accurate treatment of backbone are more limited [144]. Use of a constant (conformation-independent) set of charges does not allow full description of the backbone potential energy surface.

As computer power increased and more and more groups were assessing and validating the methodology in longer simulations, hints of problems in the backbone conformations emerged in the 2000–2004 time frame. At first it was thought that these substates were minor populations and reversible [145,146], however, it gradually became clear that the flips to non-canonical geometries were irreversible since they were effectively lower in free energy. An example is the extension of our DAPI-bound DNA simulations[147] which were run continuously on idle cluster computer cycles starting in ~2002 for multiple years demonstrating progressively further degradation (and no reparation) of the nucleic acid helix. Similarly, in simulation of d(GCGC)₂ we showed conversion to an unknown and anomalous geometry that was convincingly found in simulation to be more stable than the canonical B-DNA structure. These simulations helped to identify the problem and facilitated work on an appropriate force field tuning. We show the disrupted DNA duplex structure of DAPI bound DNA and also the anomalous d(GCGC)₂ structure in Fig. S1 of Supporting information (Cheatham, unpublished data). Onset of these problems was detected in B-DNA simulations once slightly longer (15–50 + ns) MD simulations of B-DNA became available. The accumulation of irreversible, experimentally unobserved backbone sub-states, led to progressive degradation of the entire B-DNA structure [119]. This degradation was not clearly articulated in the first studies, so readers were left in the dark regarding the full impact of the backbone flips. The main feature of these sub-states was a γ-trans geometry of the backbone which coupled to tilting of the furanose rings into the plane of the base [119]. γ-trans can perhaps occur in DNA–protein complexes but should not occur at high occupancy in naked B-DNA [145]. All these findings finally prompted reparameterization of the α and mainly γ backbone dihedrals, leading to parmbsc0 (“Barcelona”) force field [119]. Parmbsc0 allows stable microsecond-timescale simulations of B-DNA [148] and even repairs partially degraded B-DNA structures [119].

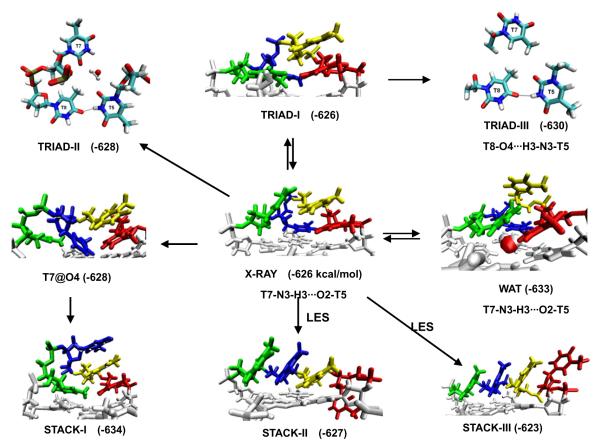
As early as in 2004, we also reported unstable structures of the diagonal loops of the (G₄T₄G₄)₂ G-DNA [52]. While the stem part of the molecule was stable, we have been loosing the experimentally observed (NMR and several independent X-ray studies) four-thymine loop geometry. Ion-binding at the stem-loop junction was not reproduced. The parmbsc0 still does not correctly describe the d(G₄T₄G₄)₂ loops, as well the propeller loops of the parallel form of the human telomeric G-DNA, although it appears to provide at least partial improvement in the later case [72]. Fig. 3 presents major extension of our previously published simulations of the d(G₄T₄G₄)₂ system. The simulations sample a wide range of the four-thymidine loop topologies and do not reproduce the native structure.

Fig. 3.

Diverse geometries of diagonal dT₄ loop of the Oxytricha nova telomere G-DNA (G₄T₄G₄)₂ in MD simulations. The first to the last loop residues are shown in red, yellow, blue and green respectively. Free energy (in kcal/mol, MM-PBSA method) and hydrogen bonds within the loop are shown. The loop free energy was calculated as earlier [52]. The arrows show the directions of structural transitions observed during the MD simulations. LES denotes the simulations with the locally enhanced sampling method applied. The stable water molecules observed in the TRIAD-II and WAT geometries are also shown. In TRIAD-I, the last loop residue moved down to form stacking with terminal quartet, and the interactions between other loop residues are similar to the experimental geometry. In TRIAD-II and TRIAD-III, new h-bond formed between T5 and T8, and the original h-bond between T5 and T7 is broken. The conformation of T6 of triad-II and traid-III is similar to that of triad-I and is not shown for clarity. The experimental structure is definitely not reproduced and is often replaced by structures with enhanced base stacking, either between the thymines or with the terminal quartet.

As most G-DNA simulations were reported before the advance of the parmbsc0 correction, a legitimate question is, have these simulations been affected by the imbalanced description of the α/γ backbone space? We suggest that the G-DNA simulation studies were not substantially affected. The simulation timescale was short and there has been no observation of any degradation of the G-DNA stems. Nevertheless, our recent reference calculations on G-DNA stems (Sponer, Jurecka et al., ms in preparation) indeed show that without the parmbsc0 correction there is gradual accumulation of wrong γ-trans backbone states (when not seen in experiment) in G-DNA stems. (Such γ-trans states are only reversibly sampled with parmbsc0.) This leads to similar structural effects as in B-DNA simulations (reduction of twist), however, the overall rigidity of the G-DNA stems appears to protect the stem from a detrimental degradation. Thus, based on our simulations and MM-PBSA free energy computations we suggest that native cation-stabilized G-DNA stems are reasonably (albeit not perfectly) described as correct global minima with any variant of the force field [30]. There is no contradiction between this statement and the loop (and B-DNA) problems described above. Different nucleic acid topologies may be described with different success by the force field, depending on specific balance of the key energy contributions and compensation of errors with a given force field. Thus, different performance of the force fields for G-DNA stems, G-DNA loops and B-DNA is not so surprising. The G-stems are in general described more reliably than the loops. Different parts of the molecule may be described with different accuracy in a given simulation. Simulated G-stems highly profit from their stabilization via cation-stabilized quartets and quartet-stacks. Both contributions are quite well described by the force field. The hairpin loops continue to represent a real challenge for the force field description[124].

The γ-trans degradation has never substantially affected RNA canonical A-duplex simulations, as the γ-trans sub-states in A-RNA helices are reversible and correspond to minor sub-states observed in experimental RNA structures [149]. Initially, it was not clear if parmbsc0 brings any really substantial changes for RNAs while all AMBER force field variants were assumed to be more or less good for A-RNA [150]. Ultimately, however, a major degradation was discovered also for RNA structures, occurring with all these force field variants. On sufficiently long timescales (which vary dramatically with the studied system) RNA helices undergo irreversible transitions to meaningless ladder-like structures characterized by shifting the glycosidic torsion angle χ from the anti to the high-anti region[151] (Fig. 4). Most likely, in sufficiently long simulations any or almost any RNA would ultimately degrade to the high-anti χ structure. This has prompted one-dimensional (1D) reparameterization of the χ torsion angle using highest-quality QM calculations and considering the influence of solvent on both the QM and MM components of the procedure [120,121]. The parmχOL₃ (“Olomouc”) variant, besides eliminating the ladder-like degradation, improves the shape and position of the syn region and the syn–anti balance (Fig. 5). For RNA, the best performance is achieved when combining parmχOL₃ with parmbsc0. However, the parmχOL₃ should not be applied to DNA as it was not possible to simultaneously fix the χ profile for DNA and RNA by a 1D reparameterization, i.e., without accordingly modifying some other force field terms. Thus, presently the best option is to use parmbsc0 for DNA and parmbsc0 + parmχOL₃ for RNA. These are the only force fields preventing massive degradation on longer time scales. This recommendation holds also for G-RNA, as high-anti χ may accumulate in their stems (unpublished results).

Fig. 4.

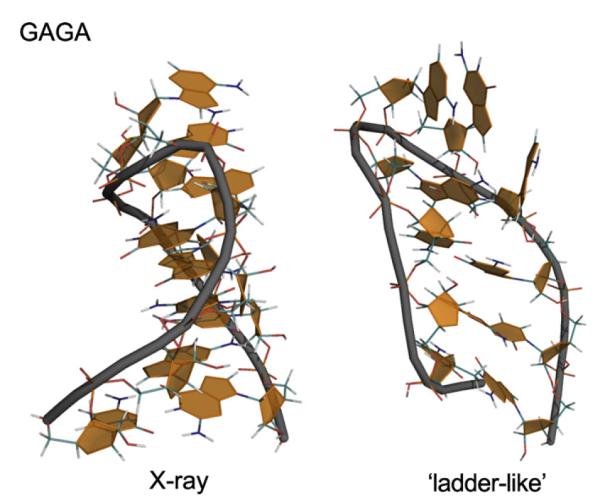
When the force field does not provide stable global minimum, the simulated molecule sooner or later degrades when starting from the correct structure and obviously can never fold properly when folding is attempted (cf. Fig. 2). GAGA RNA stem-tetraloop segment of Sarcin Ricin loop of large ribosomal subunit; PDB ID 1Q9A; residues 2658–2663 capped by two additional C/G base pairs (left) and its complete degradation (right) to ladder-like structure when the parmχOL₃ correction is not used. According to [120]. Similar problems are likely to occur in long enough simulations of G-RNA.

Fig. 5.

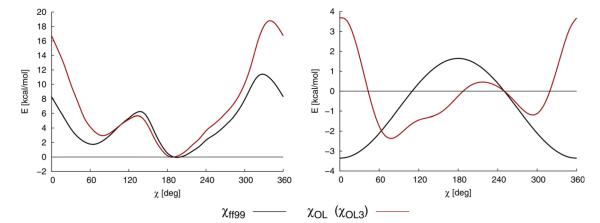
Example of dihedral profiles in MM. Complete MM torsion profile (i.e., all the force field terms) for the χ angle (on the left) calculated in vacuum and the net χ dihedral term (on the right) of ff99 or parmbsc0 (black) and parmχ_OL3 (red). Data for model of RNA cytidine are shown [121]. Note that the “Olomouc” force field is a major reparameterization. The modest difference in the slope in the anti to high anti region ( ~190°–280°) is critical to prevent degradation of RNA simulations to structures with DNA-like high-anti χ. (Parmχ_OL3 and parmχ_OL are abbreviations of the same force field, the dual name is due to historical reasons) [120,121]. Although the “toxicity” of the high-anti bias of the original force field versions for G-RNA has not been tested, we advise to use the parmbsc0 + parmχ_OL3 force field combination for longer G-RNA simulations. The G-RNA loop regions are definitely going to profit from applying the parmχ_OL3.

The ff99 + parmbsc0 for DNA and ff99 + parmbsc0 + parmχOL₃ for RNA have been denoted as the ff10 force field in AMBER. Note that ff10 is an internal abbreviation of a set of force fields in the AMBER suite of programs while the force fields should always be cited by their specific names and original citations [43,117–121]. The ff03 abbreviation caused in the past confusions since multiple NA simulation studies senselessly cited as ff03 another AMBER nucleic acid force field when if fact it is only a protein force field that has entirely no nucleic acids parameters. (Note also that in some papers the Olomouc RNA force field is cited as parmχOL, but this is exactly the same version as parmχOL₃.) Another force field χ variant also eliminates RNA ladders [122], however, as it overcorrects the high-anti problem it leads to reduction of A-RNA compactness [120,121].

Specific feature of G-DNA molecules is alternation of syn and anti nucleotides for anti-parallel stems. The currently available parmbsc0 force field is definitely imperfect in the syn region, with minimum incorrectly placed (for nucleoside) around 50° instead of 70°. This may somewhat affect the G-DNA stem structures as well as free energy computations of alternative stem arrangements. Work is in progress to prepare a version that would improve the syn DNA region and properly balance it with anti. A promising variant provisionally designated as parmχOL₄ has been created, which appears to somewhat (at least structurally) improve the simulations of antiparallel G-DNA stems (Sponer, Jurecka et al., manuscript in preparation). Full testing of this variant is not completed yet. Nevertheless, parmbsc0 can be quite safely used for G-DNA stem simulations for the moment being.

5. Inclusion of ions

Nucleic acids structures in nature are known to be sensitive to ionic conditions and should show influences due to concentration and ion type in simulation. However, comparing ion conditions in experiments and in simulations is not straightforward. There are substantial differences in the manner how ions are treated in simulations and in solution experiments. Simple comparison of experimental and simulation ion conditions without considering the other aspects and approximations may be misleading.

First, the force field ions approximated by van der Waals spheres with constant point charges differ from the real ions. Second, the present simulations are done with small solvent boxes, using periodic boundary condition and the particle Mesh Ewald (PME) formalism. Large boxes are not presently used since they would slow down the simulations. With small box the ion distribution at the box border does not reach bulk properties [152]. The ion binding sites around the solute are probably well captured (within the force field approximation) but the exchange between different binding sites may be affected by the small box size to certain extent. These effects have, however, not been quantified until now. The same is true also for possible artifacts due to the PME method. Since DNA has –1 charge per each phosphate, net-neutralization (one ion per one phosphate) with present solvent boxes leads to cation concentrations of ~0.2–0.3 M (it is not valid for protein nucleic acids complexes). This can be calculated by comparing the number of ions with the number of waters or with the box size. Adding excess salt further increases the cation concentration. The formal solute concentration is large ( ~0.01 M) but solute – solute contacts are prevented by the periodicity. The simulations are short and mostly stay within one conformational substate, so they are likely less sensitive to ion treatment than nucleic acids folding experiments.

Most nucleic acid simulations published so far have been done with either net-neutralizing sets of monovalent cations, usually Na⁺ or K⁺, or net-neutralizing along with ~100–200 mM added monovalent salt (excess-salt simulations). We are not aware of any report proving markedly different nucleic acid structural dynamics with net-neutral and excess salt conditions, however there are issues with specific ion parameters and lack of their mutual balance [153]. We have explicitly compared simulations with different ion conditions for several classes of nucleic acids and the results are so far similar [154,155]. Experimentally detected ion binding sites are usually well reproduced; cf., e.g. the theoretically predicted and subsequently experimentally confirmed monovalent ion binding site in catalytic pocket of a ribozyme [156,157]. As long as at least net-neutralizing salt it present, it seems the results are not dramatically affected by details of ion treatment. In fact, duplex DNA seems not sufficiently sensitive to salt as structures are not altered at high salt concentrations ( ~5 M, Cheatham, unpublished data) or even in runs with modeled condition having no mobile counterions, where the neutralization of the box is formally achieved by distributing the compensatory charge over all the water molecules or through application of tin-foil boundary Ewald methods [158]. The latter is somewhat surprising in that d(CGCGAATTCGCG)₂ DNA duplex structure is maintained at least to 750 ns of simulation yet it is expected to denature under such unnatural low salt conditions. Fortunately, and more accurately, RNA structures without net-neutralizing cations immediately disrupt and denature as expected (Cheatham, unpublished data). The jury is still out on how well the simple point charge models of ions can reproduce salt effects on nucleic acid structure and dynamics and suggests that salt inclusion in contemporary simulations is not yet perfect.

Obviously, G-DNA is a specific system where ion interactions are critical as the structure contains integral ions in the stem. There are several known problems in studies of G-DNA molecules that appear to be related to the ion approximations. In the first study, we reported some deformation (bifurcated base pairing) of inner quartets of G-DNA stem [29]. The simulation behavior (as well as reference QM computations) gives an impression that the radius of the ions is too large to optimally describe the ion interactions inside the stems [29,35,72]. This reduces the capability of Na⁺ to visit the quartet planes and may lead to occasional expulsion of K⁺ from the stem. We suggested that ad hoc reduction of the radius of K⁺ inside the stem may be considered in simulations. It is likely that the ion binding strength is somewhat underestimated. All these issues may be well visualized and explained by comparing force field calculations on ion-guanine interactions with reference QM data [35]. A clear issue (so far with all of the various ion force field variants and with net-neutral as well as excess salt conditions) is loss of the experimentally determined ion binding site at the stem-loop junction of the (G₄T₄G₄)₂ G-DNA [72]. On the other hand, this is probably the only documented case where established monovalent ion binding sites are not well reproduced by simulations. Many RNA binding sites have been correctly reproduced or even predicted by simulations while we assume that the overall description of ions insides the G-DNA stems is reasonable. Although there are diverse pair-additive parameter sets for monovalent ions available in the literature, the actual differences among them are relatively subtle, as changes in well depth and radius compensate for each other. A notable artifact treated recently was clustering (salt crystallization) of cations and anions in excess salt simulations with certain inappropriate combinations of cation and anion parameters. This is avoided when latest parameterizations are used [159]. This problem never affected simulations under net-neutralization conditions and for such simulations the traditional Aqvist parameters [160] can still be safely used.

Recent RNA simulations revealed that the simulation results are affected by the water model to a certain extent and there is a coupling between the solute force field and water model properties [154]. We presently test if the water model might have some effect on G-DNA simulations.

6. MM-PBSA and two recent examples of its application on G-DNA research

The basic unrestrained simulations can be complemented or supplemented by additional techniques. One popular method is the MM-PBSA technique that aims to estimate relative free energies of the simulated system based on combining the explicit solvent simulation trajectories with postprocessing using continuum solvent approximation [161,162]. MM-PBSA free energy analysis extracted from the relevant MD trajectories is a useful way to compare stabilities of different conformations of a solute. This method has been successfully applied in previous G-DNA research in analysis of possible kinetic intermediates participating in formation of parallel-stranded G-DNA stem [30] and in qualitative ranking of different loop topologies [54]. In contrast to common applications of MM-PBSA, G-DNA free energy computations require inclusion of the channel-bound ions [30]. Recently, we attempted to use the method for a qualitative analysis of folding rules of G-DNA molecules using the parmbsc0 force field. We first analyzed a set of model 2-quartet stems with various glycosidic steps and strand orientations (Fig. 6) [71]. Through comparing the total free energy estimates of these models, we derived relative stabilities of the four possible 5′-GpG-3′ glycosidic steps along G-DNA strand, with a predicted stability ranking order of syn–anti > anti–anti > anti–syn > syn–syn. Then folding rules were proposed for the stems: anti-parallel G-DNA stems are prone to form more syn–anti steps and avoid unfavorable anti–syn and syn–syn steps. These rules could give reasonable explanations for glycosidic conformational patterns of most anti-parallel G-DNA structures reported to date. Then, we analyzed different loop topologies, lengths and sequences. Simulations were run on a variety of single-loop G-DNA models followed by MM-PBSA calculations [34]. We have: (i) demonstrated instability of the left-heading (i.e., the loop formed when the G-tract with its 5′ → 3′ direction pointing upward for the viewer turns left to connect to the next G-tract) propeller loop; (ii) explained preference of human telomere sequences to predominantly adopt hybrid type structures and (iii) hypothesized about involvement of higher-order multimers in parallel/anti-parallel equilibrium (Fig. 7). These applications exemplify that when appropriately applied, MD simulation followed by MM-PBSA analysis could provide us with valuable information. However, the computational results are still facing challenges: even though the calculated relative stability of the four glycosidic steps could reasonably explain the glycosidic conformation for anti-parallel G-DNAs, it cannot explain why tetrameric G-DNAs always form parallel structures with all-anti conformation. The calculated results showing that anti-parallel G-DNA stem is more stable than its parallel counterpart is contrary to usual expectations. One of the explanations could involve multimerization of the parallel stems in the experiments, which might shift the equilibrium in favor of parallel stranded structures (Fig. 7). However, this is hypothetical and controversial, albeit supported by some recent experimental work [163]. Therefore, rather than trying to unveil the truth solely by computational techniques, we are more wiling to work for the experimental scientists, providing them with more adjunct information and alternative perspectives. Careful comparison with experiments gives us clues for further method refinement. When applying the MM-PBSA method, users need to keep in mind that it is a method based on several approximations such as continuum solvent assumptions (neglect of specific “atomistic” hydration) and a simplified entropy term [161]. In addition, the method neglects the important energy terms associated with polarization of the solute by solvent and obviously suffers from all the other force field limitations. Even when predicting correct trends, empirical experience tells that MM-PBSA often exaggerates the free energy differences. Work is in progress to address the issue of stability of parallel and antiparallel G-stems by advanced electronic structure (QM) computations. Thus, accuracy of the MM-PBSA approach should not be overrated and some bias in predicting the parallel vs. antiparallel stem stability cannot be ruled out. Comparing different antiparallel stem arrangements may be easier. To make the whole story more complex, very recent high resolution X-ray structure of parallel stranded tetrameric (GGGG)₄ quadruplex clearly shows the first (5′-) quartet being all-syn while the remaining quartets are all-anti [164]. Although not mentioned by the authors, it would be fully in line with our theoretical prediction [71]. We, however, suggest that in this particular case an important factor is absence of any additional nucleotide at the 5′-end of the strands (which contrasts the preceding experiments). It allows formation of syn specific stabilizing terminal intranucleotide 5′OH…(G)N3 H-bonds. This indicates that presence or absence of upstream non-G nucleotides may substantially affect the arrangement of the terminal quartets, again basically in line with the computations that predict strong stabilizing role of these terminal H-bonds [71].

Fig. 6.

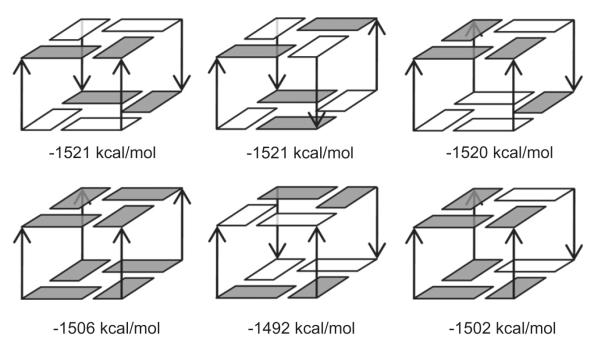
Total free energies of the six 2-quartet stem models were estimated with the MM-PBSA method. All models in the first row are composed of four syn-anti 5′-3′ steps, with difference in strand orientations. The three models in the second row are composed of four anti–anti steps, four anti–syn steps and three anti–anti + one syn–syn steps, respectively. The total free energy estimates shown below each model are adapted from our previous work, without the spurious 5′-end H-bonds energies [71]. Through comparing the total free energy estimates of these simplified models, relative stabilities of the four glycosidic steps and basic rules for strand orientation in G-stems were obtained [71]. White box is for syn and solid box is for anti glycosidic bond orientations. The channel cation (K⁺) in each model is not shown. The Figure is adapted from Ref. [71].

Fig. 7.

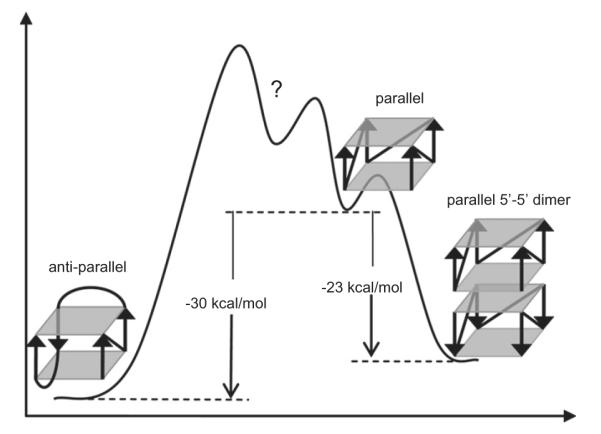
Hypothetical free energy curve of various structural forms of human telomeric G-DNA (adapted from Ref. [34]) suggested based on MM–PBSA calculations. Anti-parallel human telomeric G-DNA is more stable than the parallel counterpart. Dimerization of the parallel G-DNA structures is predicted to lead to stabilization, though, in this particular case, it is still not sufficient to make the allparallel quadruplex more stable (trimers or other types of dimers were not tested and therefore are not included). Note, however, that such challenging computations can already be significantly affected by the force field and MM–PBSA approximations (see the text).

There are numerous and diverse other methods that can be used as complements of standard simulations. Their full description is beyond the size limits of our paper. When applying these methods, it is always crucial to understand and respect their limits. Let us give at least one additional example. Popular and easily applicable tool to analyze trajectories is essential dynamics analysis (EDA). EDA aims to subtract “essential modes of motion” from the MD trajectories by filtering out the noise. However, EDA is based on substantial approximations and is prone to over-interpretation, i.e., identifying (false positive) essential modes which in fact cannot be confirmed in real trajectories [165]. The analysis should be done by grouping the leading (presumably noise-free) components together to visualize the noise-free dynamics. It is risky (albeit often seen in the literature) to try to interpret the individual modes separately. EDA is based on linear principle component analysis (PCA), i.e., it assumes linearity. However, the real motions can show substantial non-linear correlations that bias the linear PCA. Additional mathematical assumptions are that the principal components are orthogonal and that the mean and the variance fully describe the data distributions. The later requires Gaussian or another exponential type of distribution. If these conditions are not fulfilled, the analysis can be biased. Finally, EDA requires high ‘signal-to-noise’ ratio. Therefore, EDA appears more suitable to analyze structural transitions but is less useful to highlight mere stochastic thermal fluctuations of flexible molecules.

7. Studies of G-DNA complexed with ligands

Small molecule ligands can stabilize or alter quadruplex structure to modify function; therefore quadruplex binders have been actively explored as anti-cancer agents and a number of recent reviews highlight the role of G-DNA as a therapeutic target [4,166]. The explosion in study of quadruplex–ligand interactions has led to special journal issues devoted to the topic, for example a recent issue of Current Pharmaceutical Design related to G-quadruplex ligands [167]. Computer-aided and/or structure-based drug design methodologies are often applied to find and optimize ligands interacting with specific quadruplex targets. This includes straightforward modeling and structural analysis [168,169], and more detailed molecular docking [170–173], molecular dynamics and free energy simulation approaches [36,51,61–65,67,68,70,73,174–179]. Recent reviews provide more in-depth discussion of the use of modeling methods to target not only G-DNA [180] but also G-RNA [181]. Such modeling methods can often improve our understanding of quadruplex–ligand interactions. For example, many G-DNA ligands take advantage of π-stacking to facilitate interaction with the quartets, however, they lack specificity. Modeling approaches can aid in design by probing sequence and structure dependent differences in the groove structures [182] and also the influences of ions [65]. A common theme across most of the more detailed simulation approaches is the application of the well-validated AMBER force fields, including the general AMBER force field (GAFF) for treatment of the ligands (see below). MM-PBSA technologies have also often been applied as post-processing methods, despite limitations in accurate estimates of solute entropies, and the critical dependence of the results on the applied approximations (see above and below).

When assessing reliability of G-DNA ligand binding computations, we always need to consider several issues: (i) quality of the starting structure, i.e., the computations are straightforward when reliable X-ray structure is available but may be unrealistic if docking needs to be performed; (ii) quality of the ligand force field (see below) and (iii) the expected goals. While qualitative insights are achievable, quantitative modeling or calculations of binding free energies are difficult and the expectations should not be exorbitant.

Above we explained the necessity of substantial tuning of the NA force field to prevent entire degradation of both DNA and RNA, despite its very careful original parametrization. Parameterization of a reliable ligand force field could be equally complex issue. An advantage is that we deal with monomeric molecule, so that small errors in parametrization do not accumulate as in case of biopolymer force field. Relatively safe could be computations with largely planar stacked systems (which would often be relevant to G-DNA). On the other hand, parameterization of a reliable force field for complex ligands such as aminoglycosides with multiple flexible rings would be difficult, if possible at all. The force field performance will also be limited by missing energy contributions. Polarization terms are important for highly charged ligands, halogen H-bonding cannot be accurately described by atom-centered point charge model due to profoundly anisotropic charge density on the halogen atom [183,184], metal centers are difficult to describe, to mention just some issue in ligand force field parametrization. In general, van der Waals terms can be adapted from the biomolecular force fields. Parameters describing bond lengths and angles are only weakly coupled to the other force field terms and can be derived from experimental data and high-quality QM computations. Charges can be derived consistently with the force field using, in case of AMBER, the antechamber program to generate approximate AM1/BCC charges consistent with the AMBER force field. Better agreement comes from the application of the restrained electrostatic potential fits (RESP) of optimized geometries at the H/6-31G* QM level of theory [107,118,185]. To avoid fit dependencies on the orientation of the molecules and to facilitate multiconformation fitting, the RED Perl scripts can be applied[108,186]. Derivation of charges, however, may be tricky for complex molecules. Care should be taken regarding the genuine conformational dependence of the electrostatic potential (which affects the subsequently derived fixed charges), poorly represented buried atoms, and equivalency of chemically equivalent atoms (i.e., methyl hydrogen’s, etc.). However, then again we finally face the daunting task of having correct (or appropriate) dihedral parametrizations (as explained above, the essentially unphysical dihedral terms are coupled with the other force field terms). The only rigorous way is to make reference high-quality QM computations torsion after torsion, and to fit the dihedral terms.

For simulations done with the AMBER force fields, the common methodology to specify the ligand force field is the general amber force field (GAFF) for organic molecules [187]. GAFF is an extension of the AMBER force fields parametrized for wide range of organic molecules, mainly the drug-like molecules. Its original version uses 33 basic and 22 special atom types to include major part of the chemical space composed of H, C, N, O, S, P, F, Cl, Br and I atoms. An automated, table-driven procedure (antechamber and Leap) assigns atom types, charges and force field parameters to a wide range of organic compounds [188]. This very useful procedure can in no case replace specific and detailed hand parametrization of a given compound and the results, although often promising, are not necessarily guaranteed. For more accurate modeling, one could use such parameters as the starting point, verify them carefully via reference QM computations, and then eventually refine. The organic molecules are so complex and the force fields so empirical in nature that it is unthinkable to create a really automated procedure of deriving a force field, resembling the way how good quality QM methods can derive properties of molecules just by specifying geometry, total charge and multiplicity [124,142]. It is also to be noted that the reference QM calculations used to derive GAFF data in 2004 would not be considered as being of benchmark quality by today standards.

The force field issue is also limiting simulations of nucleic acids with modified or alternative backbone. Their advanced parametrization would require the same effort as parametrization of the original force field, including extensive testing in simulations. Testing options are, however, limited by the lack of the reference data.

Many studies attempt to calculate free energies of ligand binding, mostly using the popular MM-PBSA method. As stressed above, the technique is approximate, and it is not likely that a major improvement will be achieved in a foreseeable future. One of the principle limitations of all (MM as well as QM) continuum solvent approaches in evaluations of binding energies is sensitivity of calculated solvation free energies to the atomic radii. Atomic radii are empirical parameters of the method, they do not correspond to “real” physical properties (atoms are not van der Waals spheres and are in general not spherical). The uncertainty of solvation energies obviously transfers to calculations of binding free energies. The best performance of continuum solvent methods is achieved when they are specifically adjusted for a specific class of molecules and molecular complexes, provided there are reference data for such parameterization. As example of recent free energy studies, Li et al. reported calculated MM-PBSA binding free energy between G-DNA and perylene diimide Tel01 derivative of ~–35 kcal/mol [62]. This is rather far away from the usual experimental range of DNA – ligand binding of ~–10 kcal/mol. It confirms that MM-PBSA, while often giving correct trends does not give correct absolute values and often exaggerates the free energy differences (the particular study is executed correctly and also provides fairly good discussion of the limitations). In another study, Agrawal et al. evaluated eight different 1:1 telomestatin – G-DNA complexes and obtained estimated free energies ranging from −1 to −16 kcal/mol [73].

8. More examples of applications

There are numerous applications of computational studies to G-DNA available in the literature, some of them already mentioned above. Several older studies were reviewed in our preceding review [35]. For example, Stefl et al. simulated (using ff99) possible intermediates (including two-, three-, and four-stranded assemblies with out-of-register basepairing between guanines) in the formation pathway of four-quartet parallel G-stem [30]. “Cross-like”’ strand dimers may be the first complexes involved in the process. The process may proceed with association of additional strands, creating pockets for initial ion binding, and forming the first quartet. Once a single quartet forms, it is stabilized by ions. The last stages of the formation process likely involve four-stranded stems with slipped stems. The basic results are supported by several experimental findings [189–191]. Simulations were also used to analyze guanine to inosine or 6-thioguanine substitutions in G-DNA stems [48,53]. In the absence of ion stabilizing the quartet, inosine becomes destabilizing due to lack of the H-bonds involving the N2 amino group. Inosines thus could affect the folding path of G-DNA. 6-thioguanine destabilizes four-stranded G-DNA structures due to steric reasons. Spackova et al. carried out simulations of G-DNA stems with mixed GCGC quartets and demonstrated that interaction of cations with the all-guanine quartets is the leading contribution for the stability of the four-stranded assemblies, while the mixed quartets are rather tolerated within the structure and do not prefer to interact with ions [31]. Chowdhury and Bansal studied dynamics of ions in a parallel 7-quartet G-stem channel with a time scale 6 ns. They have visualized relocations of the ions in the channel, hydration, as well as ion binding in the grooves [47,49]. Stability and migration of ions and water in parallel stranded G-DNA “G4-wires” by molecular dynamics simulations were later investigated by Cavallari et al., with systems ranging from 4 to 20 consecutive quartets, with simulation time-scale up to 20 ns and different ion types [57]. Details of the ion dynamics and distribution are given. Collie et al. reported ~20 ns scale simulations on their X-ray structures of RNA and DNA bimolecular human telomeric quadruplex, including simulations with bound napthalene diimide ligands [64]. These simulations also clearly demonstrate the role of RNA 2′ OH groups and appear to rationalize ligand binding selectivity of the RNA quadruplex in comparison to the DNA quadruplex. Pagano et al. compared structural dynamics of an end to end stacked dimer of unusual parallel-stranded RNA r(GGAGGUUUUGGAGG) quadruplexes with nucleobase hexads (facilitating the dimerizations) and antiparallel dimeric diagonal-loop DNA quadruplex of the same sequence [74]. They also investigated hypothetical hybrid RNA–DNA structure adopting the fold based on the RNA quadruplex. Each system was simulated for 40 ns with ff98 force field. Irreversible γ-trans flips were reported, but no structure degradation (see above). The simulations were initiated without bound structural ions, however, the simulation time scale was sufficient to spontaneously re-distribute the ions in the quadruplexes. The MD simulations did not support Brownian dynamics prediction of ion binding in the hexad regions. The role of the 2′-OH group of ribose in stabilizing G-RNA folds by noncanonical H-bonds has been highlighted. Fadrna et al. demonstrated, that accurate loop description is not achieved with contemporary force field, at least for some loops (see also above) [52,72]. Formation of artificial “overstacked” topologies with the loop bases stacked on the outer quartet was detected (cf. also Fig. 3). Still, Hazel et al. [54] and Cang et al. [34] (see above) rather successfully utilized simulations followed by MM-PBSA computations to qualitatively analyze various G-DNA loop sequences and arrangements. The results appear to agree with several experimental findings, for example, an explanation was found for the distinct patterns of observed dimer topology for sequences with T₃ and T₂ loops, which depend on the loop lengths, rather than only on G-quartet stability [54]. Neidle’s laboratory demonstrated in a number of studies that molecular simulations can be used as a qualitative complement to experimental structural studies, for example in case of RNA telomeric quadruplex, quadruplex – drug systems, quadruplex loops, etc. [54,55,58,64,70,179].

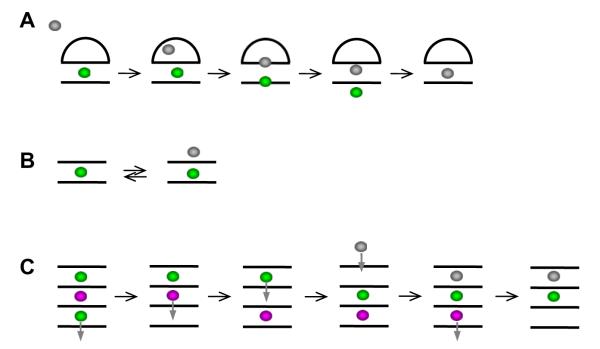
Extensive simulations (16 μs in total, parmbsc0) on 2-quartet 15-mer thrombin binding G-DNA aptamer were reported recently by Golovin et al. [32,69]. They specifically investigated capture of ions by initially vacant stems and demonstrated that binding of ions to G-DNA is complex multiple-pathway process, which is strongly affected by the type of the cation [32]. The individual ion binding events are substantially modulated by the connecting loops of the aptamer, which play several roles. They stabilize the molecule during time periods when the bound ions are not present, they modulate the route of the ion into the stem and they also stabilize the internal ions by closing the gates through which the ions enter the quadruplex. They also reported the first full spontaneous exchange of internal cation between quadruplex molecule and bulk solvent at atomistic resolution [32] (Fig. 8). The expulsion of the internally bound ion is correlated with initial binding of the incoming ion. The incoming ion then readily replaces the bound ion while minimizing destabilization of the G-stem during the exchange. Very recently, free energy landscape of different ions moving through four-quartet parallel stem has been evaluated by Akhshi et al., using explicit solvent simulations with the CHARMM27 force field while artificially enforcing the ion movement using biasing force [192]. Although not fully clear from the description, the free energy seems to be assessed with single ion present in the stem, which would neglect the correlation and mutual energy influence among the ions in fully occupied stem. The authors also demonstrate that passing the ion perpendicularly, i.e., between the quartets, would be very costly. Nevertheless, the above work by Golovin et al. [32] indicates that such events occasionally can occur, especially for ion entry into the stem lacking ions. Such movement, however, requires large spontaneous G-stem fluctuation to occur first which is probably not within the reach of the biased simulations. These two studies nicely complement each other and illustrate what kind of different results can be obtained from the basic simulations and from biased simulations.

Fig. 8.

A) The first spontaneous exchange of internal ion seen in a G-DNA simulation, in this particular case 2-quartet G-DNA thrombin binding aptamer construct without its bottom loops. The expulsion of an internally bound ion is correlated with capture of incoming ion, which prevents any destabilization of the quadruplex during the exchange. (B) Typical ion dynamics of two quartet stem repeatedly seen during simulations [32]. The simulations illustrate that G-DNA stems can fully exchange ions with bulk without being actually destabilized by temporary reduction of the number of the ions in the channel. The approach of the bulk ion affects the free energy of the bound ion and increases the likelihood of its expulsion. (C) Hypothetical model how four – quartet stem can smoothly exchange the internal ion (magenta) with bulk using series of microstates with 3 and 2 channel bound ions, even without cooperating with the incoming ion.

Molecular simulations were also used to investigate gas phase dynamics of G-DNA, in an attempt to complement the mass field spectrometry experiments [56,193]. In presence of ions, the molecules remain stable and display structures that closely resemble those found in solution simulations. In the absence of the crucial cations, the trajectories become unstable and in general the quadruplex structure is lost [56].

Li et al. used steered dynamics (one of the techniques to enhance sampling which is pulling the molecule by a force) to force unfolding of parallel stranded fold of human telomeric DNA quadruplex [60]. Although such methods obviously have limitations, they may be useful in qualitative studies of unfolding of various G-DNAs. The simulation pulling rates are inevitably orders of magnitude larger than achieved in common experiments. More recently, free energy of forced thrombin binding aptamer G-DNA unfolding via separating the ends using biasing force has been reported[194]. In recent years, additional successful applications of MD simulations have appeared that serve as an important adjunct method to functional studies or experimental techniques [195–199]. For example, Andrushchenko et al. clearly demonstrated that MD simulations were essential to subsequently theoretically derive realistic IR and vibrational circular dichroism spectra of parallel stranded G-DNA [196].

9. Perspectives on the simulation of nucleic acids

How long do simulations of nucleic acids need to be? In the first studies, we were excited by timescales of 0.5–5 ns per simulation. Even such short simulations can sometimes provide useful data. However, with better computers and experience, we would suggest that the minimal length of the individual simulations should be ~25–50 ns, as when the initial structure is already reasonably relaxed, in many cases, the simulations can correctly reflect many aspects of the simulated molecules. To see more dynamics and substates that are separated by modest barriers from the start, simulations on the timescale of 100–1000 ns each are likely required. 1 ns simulation can overcome activation barriers of ~5 kcal/mol while 100 ns simulation of ~8 kcal/mol. As different systems have very diverse richness of their conformational space from both thermodynamics and kinetics point of view, it is not possible to suggest any “black-box” recipe about the simulation length. This must be judged case by case. For certain goals multiple 25 ns simulations are reasonable, for others ms time scale would be insufficient. We always need to carefully contemplate what a real single molecule could do on a given timescale assuming a given starting structure and the simulation conditions, as explained above. Good advice is to try to work at the limits of the existing computers. The longer the simulations are, the bigger the chance that some interesting developments are not missed. Of course, the longer the simulations are the more likely we are going to face limitations of the force field.

It is better to have a set of multiple (say 5–10) trajectories (however, each sufficiently long) than to rely on just single very long trajectory with the same aggregate length. Although the MD simulations are based on deterministic description, they in reality are stochastic in nature. Empirical experience suggests that with prolongation of the simulations, at least on the presently common time scale, the probability of capturing a structural change may be fading away. A single trajectory may also be spoiled by a rare irreversible event in early stages leading to potentially incorrect interpretations. On the other hand, we do not suggest to always over and over again repeat the same simulation, in analogy to repeating an experimental measurement multiple times. For example, when investigating a role of base substitution and modification of a given local region, we may be getting valid multiple simulation statistics for regions that are sufficiently separated from the modified area and about the overall dynamics. Such simulations, albeit simulating different systems, can very well serve as multiple simulations for evaluation of many features of the studied systems.

Evidently, even after the most recent adjustments, the force fields remain far from perfect. It is likely that an increased sampling, expected from an improvement in computational hardware and algorithms, may in the future uncover additional force field artifacts that are currently hidden at (sub)microsecond simulation timescales due to a high free energy barrier separating the starting native state and the potential artificial state. One has to be especially careful with simulation methods attempting to enhance sampling, such as replica-exchange molecular dynamics, locally enhanced sampling and targeted MD. Such methods, on the one hand, are obviously highly desirable. On the other hand, their application is not straightforward. First, these methods are always based on (significant) approximations additional to those used in standard unrestrained simulations. Forcing a conformational change through a drastic time-dependent root-mean-square distance (RMSD) penalty function in targeted MD is not the same as to observe the change spontaneously during unrestrained simulations. Targeted MD is applicable to simple pathways such as the A-to-B-DNA transition, but more complex changes may easily go beyond the applicability of the method [200]. The approximations underlying “sampling-enhancing” methods are not always fully acknowledged and respected in the literature. It is challenging for the non-expert to fully understand the significance of the computations unless clearly articulated by the authors [201]. There is always some penalty for improving the sampling problem. These otherwise highly valuable methods in no case can completely replace conventional, unrestrained simulations that remain the gold standard.

Despite the remaining limitations, the performance of well-calibrated force fields for nucleic acids is remarkable considering their striking simplicity. Given the difficulties in the development of polarization force fields and the expensive nature of sufficiently accurate QM descriptions, it is likely that refined pair-additive force fields will dominate NA simulation studies over the next decade. There is still a space for further tuning of the current force field though it is fair to acknowledge that limited flexibility and unphysical nature of such a simple functional form definitely does not allow parameterization of a perfect force field. Thus sooner or later the capability for tuning the force field via dihedral terms will be exhausted.

Despite being outside the scope of this review, electronic structure (QM) computations may in future complement atomistic simulations, although the QM computations will always lag behind the simulations regarding the completeness of the system and sampling. For example, rather straightforward and common are gas phase QM computations of structures and energies of nucleobase quartets and their interaction of ions [202–206]. While such computations per se should be (considerably) more accurate than equivalent force field evaluations, it is difficult to extrapolate the model-system results to complete and solvated nucleic acid systems. So, we need QM methods that include the whole molecule and also its environment.

Challenging are studies that attempt to go beyond what classical MD can capture, such as studies investigating electronic and conduction properties of G-DNA and G-quartet systems in general (G4-wires) [207–209]. These studies often use classical simulations to generate pool of structures for the electronic structure computations. It is hoped, that classical simulation studies will be in future directly complemented by structure-energy analyses using modern QM and hybrid QM/MM-MD approaches, as attempted by Golovin et al. for ion binding to G-DNA [32]. Although these methods presently face major sampling limitations (and may in some cases still be not accurate enough) they should in the near future allow at least side by side comparisons of force field and electronic structure descriptions on real (full) G-DNA structures. This should provide much better assessment of the accuracy limits of the force fields and clarify interpretation of the simulation results.