Abstract
We have analyzed the thermodynamic properties of the von Willebrand factor (VWF) A3 domain using urea-induced unfolding at variable temperature and thermal unfolding at variable urea concentrations to generate a phase diagram that quantitatively describes the equilibrium between native and denatured states. From this analysis, we were able to determine consistent thermodynamic parameters with various spectroscopic and calorimetric methods that define the urea–temperature parameter plane from cold denaturation to heat denaturation. Urea and thermal denaturation are experimentally reversible and independent of the thermal scan rate indicating that all transitions are at equilibrium and the van't Hoff and calorimetric enthalpies obtained from analysis of individual thermal transitions are equivalent demonstrating two-state character. Global analysis of the urea–temperature phase diagram results in a significantly higher enthalpy of unfolding than obtained from analysis of individual thermal transitions and significant cross correlations describing the urea dependence of 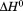 and
and 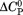 that define a complex temperature dependence of the m-value. Circular dichroism (CD) spectroscopy illustrates a large increase in secondary structure content of the urea-denatured state as temperature increases and a loss of secondary structure in the thermally denatured state upon addition of urea. These structural changes in the denatured ensemble make up ∼40% of the total ellipticity change indicating a highly compact thermally denatured state. The difference between the thermodynamic parameters obtained from phase diagram analysis and those obtained from analysis of individual thermal transitions illustrates that phase diagrams capture both contributions to unfolding and denatured state expansion and by comparison are able to decipher these contributions.
that define a complex temperature dependence of the m-value. Circular dichroism (CD) spectroscopy illustrates a large increase in secondary structure content of the urea-denatured state as temperature increases and a loss of secondary structure in the thermally denatured state upon addition of urea. These structural changes in the denatured ensemble make up ∼40% of the total ellipticity change indicating a highly compact thermally denatured state. The difference between the thermodynamic parameters obtained from phase diagram analysis and those obtained from analysis of individual thermal transitions illustrates that phase diagrams capture both contributions to unfolding and denatured state expansion and by comparison are able to decipher these contributions.
Keywords: denatured state expansion, Urea–temperature phase diagram, circular dichroism, fluorescence, differential scanning calorimetry, Von Willebrand factor
Introduction
More than two decades ago, a new method was developed in the Pace lab for determining the heat capacity change for two-state reversible protein unfolding (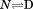 ) that did not require a calorimeter.1 This method utilized spectroscopy to monitor the denaturation of proteins by urea at variable temperature combined with thermal denaturation in the absence of urea. Urea- and temperature-induced unfolding transitions were analyzed by the linear extrapolation method2 and van't Hoff analysis. The free energies obtained by linear extrapolation to zero urea,
) that did not require a calorimeter.1 This method utilized spectroscopy to monitor the denaturation of proteins by urea at variable temperature combined with thermal denaturation in the absence of urea. Urea- and temperature-induced unfolding transitions were analyzed by the linear extrapolation method2 and van't Hoff analysis. The free energies obtained by linear extrapolation to zero urea,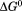 , and by the van't Hoff equation knowing the enthalpy,
, and by the van't Hoff equation knowing the enthalpy,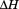 , at the melting temperature, Tm, within the thermal transition were fit using the Gibbs–Helmholtz equation3 to obtain the heat capacity,
, at the melting temperature, Tm, within the thermal transition were fit using the Gibbs–Helmholtz equation3 to obtain the heat capacity,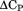 .
.
At the time, the linear extrapolation method was gaining wide acceptance because the stability of many, although not all, proteins obtained from linear extrapolation was comparatively independent of the chemical denaturant used.4,5 Moreover, it had been recently demonstrated that the 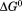 obtained from extrapolation complied with the properties of path independence required for all thermodynamic functions of state.6 The advantage of this approach was that it provided a means to quantify the thermodynamic stability of proteins over the full range of temperature enabling a robust determination of the heat capacity term in the Gibbs–Helmholtz equation. It also obviated problems of protein solubility at concentrations required for calorimetry.
obtained from extrapolation complied with the properties of path independence required for all thermodynamic functions of state.6 The advantage of this approach was that it provided a means to quantify the thermodynamic stability of proteins over the full range of temperature enabling a robust determination of the heat capacity term in the Gibbs–Helmholtz equation. It also obviated problems of protein solubility at concentrations required for calorimetry.
The first graphical urea–temperature phase diagram to appear in the literature was published by the Scholtz lab using the Escherichia coli (E. coli) histidine-containing phosphocarrier protein of the phosphoenolpyruvate-dependent carbohydrate transport system.7 The purpose was to provide a complete two-dimensional characterization of the unfolding to determine the urea dependence of the enthalpy and heat capacity and the temperature dependence of the m-value, the slope 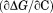 that quantifies the cooperativity of urea denaturation. The m-value was independent of temperature over a 45ºC range, mapping the
that quantifies the cooperativity of urea denaturation. The m-value was independent of temperature over a 45ºC range, mapping the 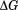 obtained from both urea and thermal denaturations onto the Gibbs–Helmholtz equation, which resulted in continuous functions and identical measures of the calorimetric and van't Hoff enthalpies verified two-state character. More recently, the DNA-binding domain of Lac repressor was rigorously subjected to urea–temperature phase diagram analysis by the Record lab who observed circular dichroic equivalence of the thermally and urea-denatured states and a miniscule temperature dependence of the m-value.8 Urea denaturation of RNase T1 and A also show a temperature insensitive m-values.1,9 Guanidine hydrochloride-temperature phase diagrams have also demonstrated that the m-values for lysozyme, Barstar, and the thermophilic variant of RNase H are constant with temperature.10–12 These early studies provided experimental validation of the use of the linear extrapolation model to determine the thermodynamic stability of proteins by denaturants at various temperatures, but they also illustrated that when proteins are two-state and reversible, the cooperativity of denaturant-induced protein unfolding was invariant with temperature, at least within experimental error.
obtained from both urea and thermal denaturations onto the Gibbs–Helmholtz equation, which resulted in continuous functions and identical measures of the calorimetric and van't Hoff enthalpies verified two-state character. More recently, the DNA-binding domain of Lac repressor was rigorously subjected to urea–temperature phase diagram analysis by the Record lab who observed circular dichroic equivalence of the thermally and urea-denatured states and a miniscule temperature dependence of the m-value.8 Urea denaturation of RNase T1 and A also show a temperature insensitive m-values.1,9 Guanidine hydrochloride-temperature phase diagrams have also demonstrated that the m-values for lysozyme, Barstar, and the thermophilic variant of RNase H are constant with temperature.10–12 These early studies provided experimental validation of the use of the linear extrapolation model to determine the thermodynamic stability of proteins by denaturants at various temperatures, but they also illustrated that when proteins are two-state and reversible, the cooperativity of denaturant-induced protein unfolding was invariant with temperature, at least within experimental error.
The temperature dependence of the m-value is directly related to the urea dependence of 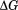 and
and 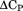 through the urea and temperature mixed derivative of the natural logarithm of the equilibrium constant between,
through the urea and temperature mixed derivative of the natural logarithm of the equilibrium constant between,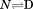 .13 In principle, the m-value can have a temperature dependence because it represents the sum of the thermodynamics of transfer from water to aqueous urea of all protein groups that become newly exposed on protein unfolding. We have shown that m-values can be quantitatively predicted over a wide range of stability for a variety of proteins using the Transfer Model and protein group transfer free energies from water to urea determined at 25ºC.14,15 Transfer free energies are based on the differential solubility of protein groups (amino acid side chains and the peptide backbone unit) in water and aqueous urea and should also depend on temperature because solubility varies with temperature depending on the heat of dissolution.16 However, it is likely that the temperature dependence of group transfer free energies is small because their absolute magnitudes are also small. Therefore, any significant changes in these thermodynamic parameters with respect to temperature and urea are more likely to reflect folding properties of proteins such as the population of intermediates in the unfolding pathway, as with the VWF A1 domain and the drosophila notch ankyrin repeat domain,17,18 or changes in the physical and structural character of the native and/or denatured states.
.13 In principle, the m-value can have a temperature dependence because it represents the sum of the thermodynamics of transfer from water to aqueous urea of all protein groups that become newly exposed on protein unfolding. We have shown that m-values can be quantitatively predicted over a wide range of stability for a variety of proteins using the Transfer Model and protein group transfer free energies from water to urea determined at 25ºC.14,15 Transfer free energies are based on the differential solubility of protein groups (amino acid side chains and the peptide backbone unit) in water and aqueous urea and should also depend on temperature because solubility varies with temperature depending on the heat of dissolution.16 However, it is likely that the temperature dependence of group transfer free energies is small because their absolute magnitudes are also small. Therefore, any significant changes in these thermodynamic parameters with respect to temperature and urea are more likely to reflect folding properties of proteins such as the population of intermediates in the unfolding pathway, as with the VWF A1 domain and the drosophila notch ankyrin repeat domain,17,18 or changes in the physical and structural character of the native and/or denatured states.
Using the thermodynamic property of proton inventory which measures the change in protonation of ionizable sidechains upon denaturant-induced unfolding, the Bolen lab illustrated cases in which proteins that appeared two-state by spectroscopic means could have substantial thermodynamic variability in either the native, denatured or both ensembles.5,19 This variability was also manifested in the physical dimensions of thermodynamic ensembles, particularly denatured state ensembles.20–22 Pace illustrated that a greater hydrophobicity results in more compact denatured states with extensive secondary structure and smaller m-values.23 Given that the hydrophobic effect strengthens with increasing temperature, protein denatured states should contract depending on their hydrophobicity as the temperature rises.24 Yet expansion of the thermally denatured state of a simple two-state folder by urea and contraction by osmolytes has also been attributed to hydrogen bonding on the correlative basis of group transfer free energies.25
Here, we show using the phase diagram method,13 that the thermodynamics associated with the expansion of the denatured state ensemble by urea can be quantified. The protein is the von Willebrand factor (VWF) A3 domain (23 kDa) which adopts a α/β-Rossmann type fold that is cross-linked by a single disulfide bond at the N and C termini. This protein reversibly unfolds in urea26 and it is demonstrated that thermal unfolding is also both experimentally reversible and independent of thermal scan rate with no evidence of intermediates and therefore consistent with a classical two-state folder. Despite a tendency to aggregate at high protein concentrations and temperatures, the thermally denatured state expands upon addition of urea and the urea-denatured state contracts with increasing temperature as indicated by far UV circular dichroism (CD). Comparison of the thermodynamic enthalpy derived from van't Hoff and calorimetric analysis of individual thermal transitions with the phase diagram analysis demonstrates that although  , urea more completely denatures A3 resulting in a significantly higher enthalpy obtained from the phase diagram method. The expansion/contraction of the denatured state ensemble is also manifested in the urea concentration dependence of the higher order thermodynamic parameters,
, urea more completely denatures A3 resulting in a significantly higher enthalpy obtained from the phase diagram method. The expansion/contraction of the denatured state ensemble is also manifested in the urea concentration dependence of the higher order thermodynamic parameters,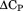 and its temperature dependence, that results in a complex temperature dependence of the m-value. Finally, the difference in the stability curves obtained by the phase diagram method and from thermal denaturation in the absence of urea is discussed in terms of the free energy associated with denatured state expansion.
and its temperature dependence, that results in a complex temperature dependence of the m-value. Finally, the difference in the stability curves obtained by the phase diagram method and from thermal denaturation in the absence of urea is discussed in terms of the free energy associated with denatured state expansion.
Results
Spectra of native and urea-denatured states
As the scope of this study is to give a detailed description of the urea–temperature phase diagram between the native and the unfolded states of the A3 domain, we began our experiments by characterizing the CD and fluorescence (FL) spectral properties of this domain. Figure 1(A) shows an alpha helical dominated spectrum of native A3 with two characteristic minima at 222 and 208 nm and a maximum at ∼195 nm. In the presence of 9 M urea, A3 is fully denatured and exhibits a mostly random coil-like spectrum. The intrinsic fluorescence spectrum of native A3-domain [Fig. 1(B)] has a wavelength of maximum intensity,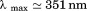 , upon excitation at 280 and 295 nm. In the crystal structure, three of the four tyrosines are mostly solvent-exposed on the protein surface, whereas the tryptophan is well buried in the interior of the protein molecule. Upon unfolding in 9 M urea, all fluorophores become fully solvent exposed, the FL intensity decreases and
, upon excitation at 280 and 295 nm. In the crystal structure, three of the four tyrosines are mostly solvent-exposed on the protein surface, whereas the tryptophan is well buried in the interior of the protein molecule. Upon unfolding in 9 M urea, all fluorophores become fully solvent exposed, the FL intensity decreases and 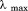 is red-shifted to ≃ 361nm.
is red-shifted to ≃ 361nm.
Figure 1.
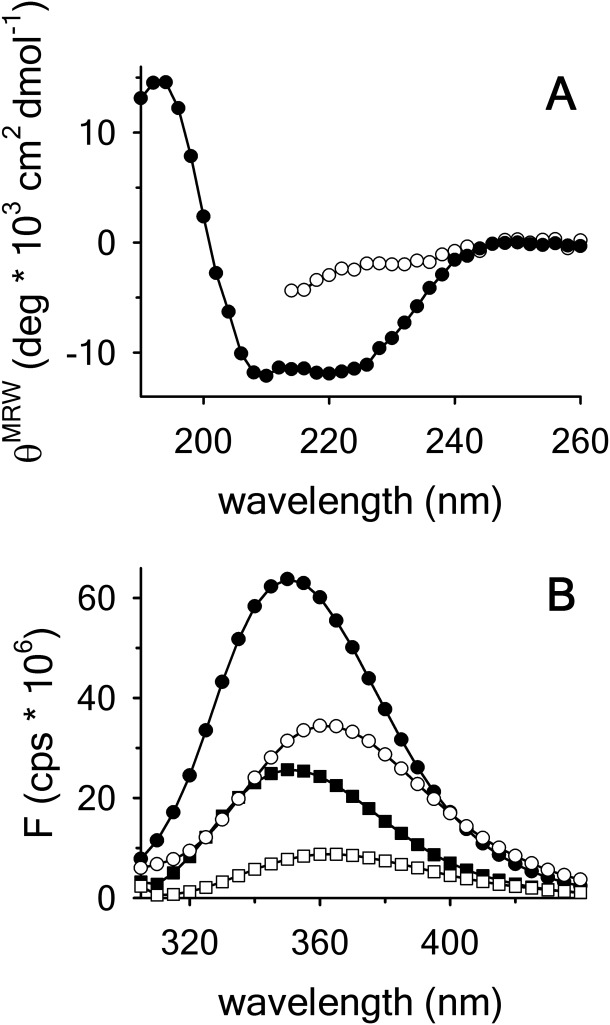
(A) Far UV CD spectra of A3 in buffer (•) and 9 M urea (○). (B) FL emission spectra of A3 in buffer with excitation at (280 • and 295 nm ▪) and 9 M urea (280 ○ and 295 nm □).
Thermal denaturation in the absence of urea
Thermal unfolding of the A3 domain was performed as a function of protein concentration and temperature scan rate using both FL and CD. Figure 2(A) shows the change in the intrinsic fluorescence intensity as a function of temperature at defined protein concentrations ranging from 0.1 to 2 μM at a scan rate of 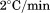 . This FL experiment was also done at
. This FL experiment was also done at 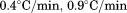 , and
, and 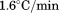 . The midpoint of thermal unfolding is
. The midpoint of thermal unfolding is 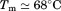 . The FL intensity was found to be linear with respect to protein concentration at all temperatures [inset of Figure 2(A)]. The slope of this linear dependence,
. The FL intensity was found to be linear with respect to protein concentration at all temperatures [inset of Figure 2(A)]. The slope of this linear dependence,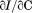 plotted at the various scan rates in Figure 2(B), demonstrates that the Tm is independent of the scan rate within experimental error. Monitoring CD at 222 nm with 1 μM protein concentration also shows that within experimental error, the change in secondary structure content has the same scan rate independent Tm, Figure 2(C).
plotted at the various scan rates in Figure 2(B), demonstrates that the Tm is independent of the scan rate within experimental error. Monitoring CD at 222 nm with 1 μM protein concentration also shows that within experimental error, the change in secondary structure content has the same scan rate independent Tm, Figure 2(C).
Figure 2.
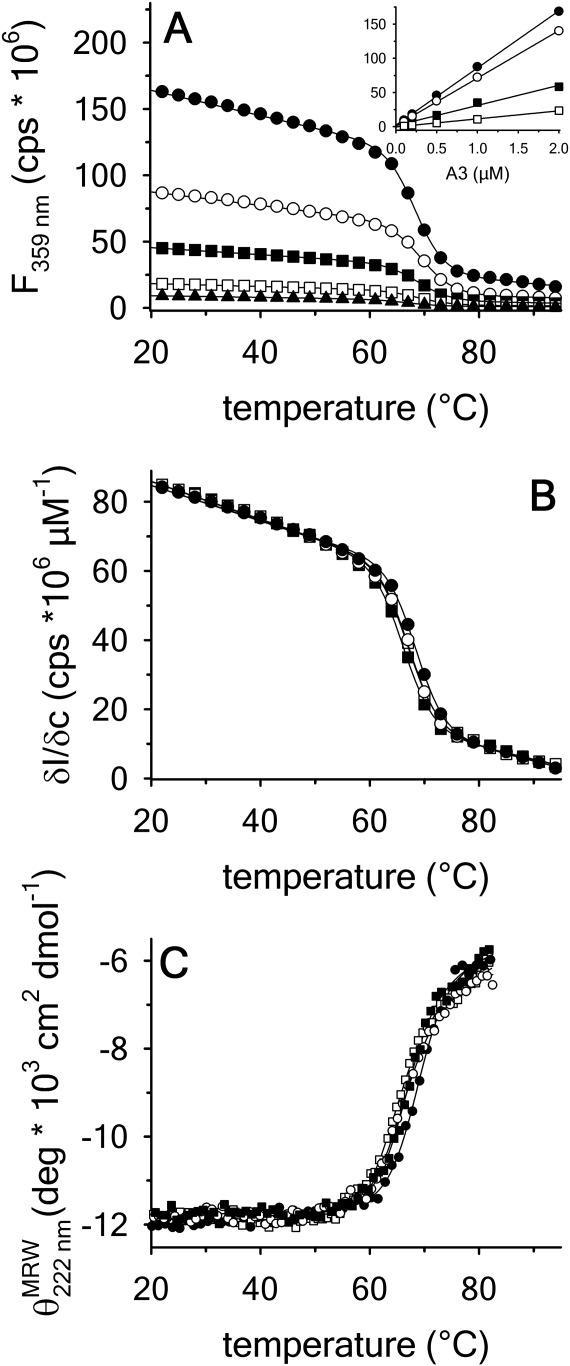
Thermal denaturation of A3 monitored by (A) FL emission at 359 nm with excitation at 280 nm as a function of A3 concentration at a scan rate  . 2 µM (•), 1 µM (○), 0.5 µM (▪), 0.2 µM (▪), 0.1 µM (▲). Inset of (A)—Linear dependence of FL intensity as a function of protein concentration at 20°C, 50°C, 65°C and 80°C from top to bottom. (B) Slope of FL intensity with respect to protein concentration
. 2 µM (•), 1 µM (○), 0.5 µM (▪), 0.2 µM (▪), 0.1 µM (▲). Inset of (A)—Linear dependence of FL intensity as a function of protein concentration at 20°C, 50°C, 65°C and 80°C from top to bottom. (B) Slope of FL intensity with respect to protein concentration 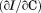 at 0.4°C/min (▪), 0.9°C/min (▪), 1.6°C/min (○), and 2.0°C/min (•). (C) Far UV CD at 222 nm at 0.5°C/min (▪), 1.0°C/min (▪), 1.5°C/min (○), and 2.0°C/min (•).
at 0.4°C/min (▪), 0.9°C/min (▪), 1.6°C/min (○), and 2.0°C/min (•). (C) Far UV CD at 222 nm at 0.5°C/min (▪), 1.0°C/min (▪), 1.5°C/min (○), and 2.0°C/min (•).
Using differential scanning calorimetry (DSC), we scanned from 10ºC to 95ºC. The heat capacity of unfolding yields a symmetrical peak centered on 67 ± 1.2°C, Figure 3(A). The inset demonstrates that the following scan is calorimetrically irreversible. Visual inspection of the protein sample after the experiment indicated aggregation of the thermally denatured state. DSC was also performed as a function of protein concentration between 10 and 70 μM as shown by the excess heat capacity in Figure 3(B). Analysis of the data gave a constant Tm and enthalpy 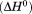 with respect to protein concentration within experimental error. The van't Hoff and calorimetric enthalpies were
with respect to protein concentration within experimental error. The van't Hoff and calorimetric enthalpies were 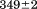 and
and 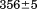 kJ/mol, respectively. Thermal aggregation of the denatured state prevented accurate determination of the calorimetric partial molar heat capacity change
kJ/mol, respectively. Thermal aggregation of the denatured state prevented accurate determination of the calorimetric partial molar heat capacity change 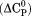 of the transition because of post-denaturation baseline noise evident in Figure 3(A).
of the transition because of post-denaturation baseline noise evident in Figure 3(A).
Figure 3.
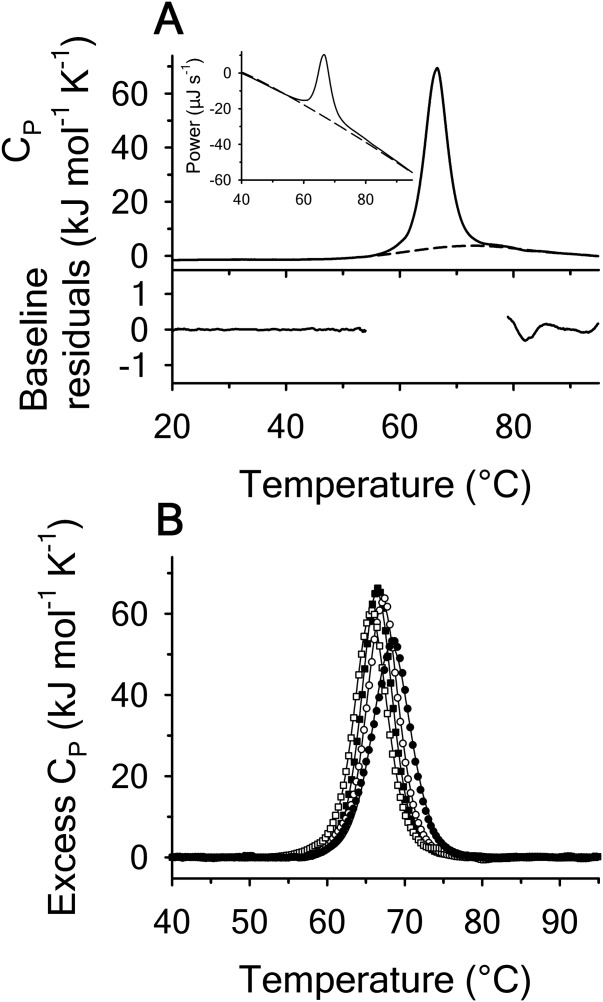
Thermal denaturation of A3 monitored by DSC at a scan rate = 2°C/min. (A) Heat capacity trace of 50 µM A3 relative to the second irreversible scan with polynomial baseline indicated as dashed line. Residuals of the baseline fit to pre- and post-denaturation. Inset of (A) example instrument data for protein scan (solid line) followed by second irreversible scan (dashed line). (B) Protein concentration dependence of the excess heat capacity at 10 µM (•), 30 µM (○), 50 µM (▪), and 70 µM (▪) after subtraction of the polynomial baseline.
For all of the methods employed in thermal denaturation, Figure 4 plots the Tm and 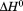 as a function of thermal scan rate at all protein concentrations examined within the first and second standard deviations from the average. Figure 4 demonstrates that all parameters derived from the unfolding transitions are independent of the thermal scan rate within experimental error. In addition, Figures 4 also demonstrate that the thermodynamic stability of A3 is not dependent on protein concentration within the ∼3 orders of magnitude range investigated, (0.1–70 μM).
as a function of thermal scan rate at all protein concentrations examined within the first and second standard deviations from the average. Figure 4 demonstrates that all parameters derived from the unfolding transitions are independent of the thermal scan rate within experimental error. In addition, Figures 4 also demonstrate that the thermodynamic stability of A3 is not dependent on protein concentration within the ∼3 orders of magnitude range investigated, (0.1–70 μM).
Figure 4.
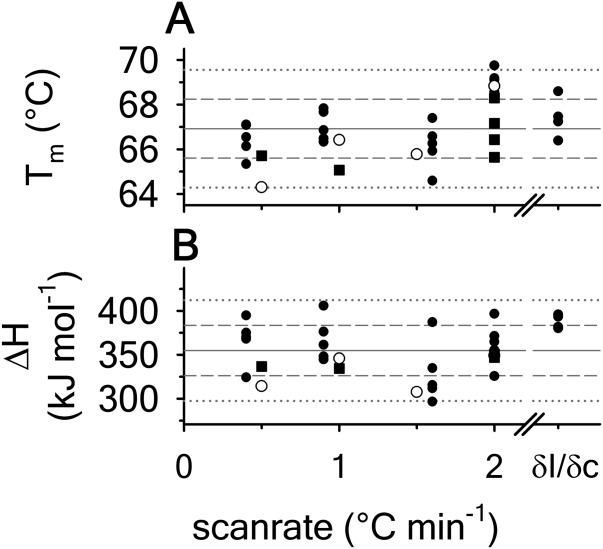
Thermal denaturation parameters, Tm and 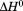 as a function of scan rate obtained from independent analysis of all protein concentrations. FL (•); CD (○); DSC (▪). Horizontal gray lines represent the average (solid), one standard deviation (dashed) and two standard deviations (dotted) of data from all methods.
as a function of scan rate obtained from independent analysis of all protein concentrations. FL (•); CD (○); DSC (▪). Horizontal gray lines represent the average (solid), one standard deviation (dashed) and two standard deviations (dotted) of data from all methods.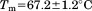 and
and 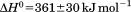 . Analysis of the slope of the FL intensity (right) with respect to protein concentration yields
. Analysis of the slope of the FL intensity (right) with respect to protein concentration yields 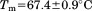 and
and 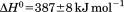 .
.
Extent of thermal reversibility
FL was used at 0.1 μM protein concentration and a faster thermal scan rate of  to minimize aggregation and determine the extent of thermal reversibility. Figure 5(A) shows 18 repeat scans to progressively higher temperatures followed by cool-downs and 30 min equilibrations at 10ºC on the same protein sample. The inset of Figure 5(A) is a measure of the extent of thermal reversibility as a plot of the percent recovery of the FL intensity after the cool-downs and equilibrations. Although this experiment retains the history of the previous scans, the inset demonstrates that up to 60°C, A3 is still 100% reversible. Upon scanning through the transition to 72°C, A3 is still ≥90% reversible and up to 95°C, A3 is ≥ 60% reversible. The same experiment was also performed using DSC with 70 μM protein sample. Whereas a complete scan from 10°C to 95°C completely aggregates the protein, step-wise repeat scans to incrementally higher temperatures did yield partial reversibility when compared to the single scan over the full temperature range, Figure 5(B). The extent of visible aggregation shown in Figure 5(C) was determined from light scattering during the thermal scan as a function of protein concentration ranging from 20 μM down to 0.5 μM. At concentrations ≤10 μM, there is no visible aggregation at temperatures ≤60°C and at 0.5 μM no visible aggregates are observed by light scattering at any temperature.
to minimize aggregation and determine the extent of thermal reversibility. Figure 5(A) shows 18 repeat scans to progressively higher temperatures followed by cool-downs and 30 min equilibrations at 10ºC on the same protein sample. The inset of Figure 5(A) is a measure of the extent of thermal reversibility as a plot of the percent recovery of the FL intensity after the cool-downs and equilibrations. Although this experiment retains the history of the previous scans, the inset demonstrates that up to 60°C, A3 is still 100% reversible. Upon scanning through the transition to 72°C, A3 is still ≥90% reversible and up to 95°C, A3 is ≥ 60% reversible. The same experiment was also performed using DSC with 70 μM protein sample. Whereas a complete scan from 10°C to 95°C completely aggregates the protein, step-wise repeat scans to incrementally higher temperatures did yield partial reversibility when compared to the single scan over the full temperature range, Figure 5(B). The extent of visible aggregation shown in Figure 5(C) was determined from light scattering during the thermal scan as a function of protein concentration ranging from 20 μM down to 0.5 μM. At concentrations ≤10 μM, there is no visible aggregation at temperatures ≤60°C and at 0.5 μM no visible aggregates are observed by light scattering at any temperature.
Figure 5.
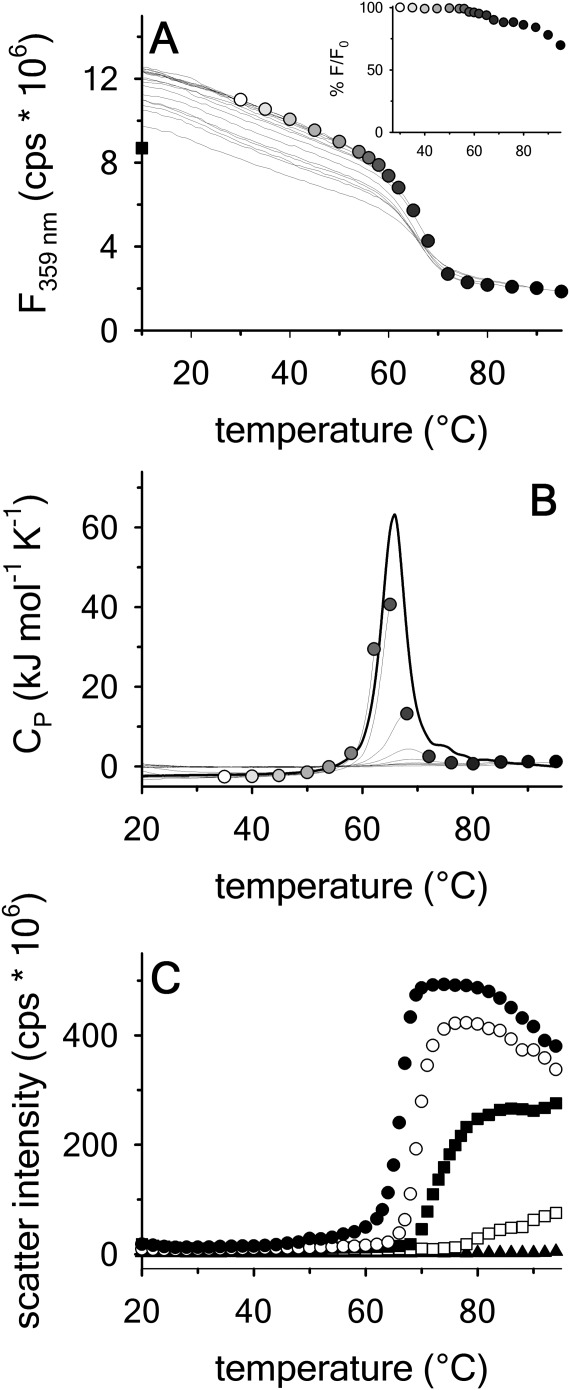
Test for thermal reversibility at scan rate = 2°C/min. Repeated scans on the same protein sample from 10°C to the indicated temperature followed by a drop back down to 10ºC and equilibration for 30 min. Inset of (A) Percent reversibility at 10°C after scanning to the indicated temperature. (A) 0.1 µM A3 by FL emission at 359 nm excitation at 280 nm. Square at 10°C represents the FL intensity after the last scan to 95°C. (B) 70 µM A3 by DSC. (C) Thermal aggregation of the denatured state of A3 monitored by light scattering at an excitation and emission wavelength of 600 nm as a function of A3 concentration at a scan rate 1.6°C/min. 20 µM (•);10 µM (○); 5 µM (▪); 2 µM (▪); 0.5 µM (▲).
Isothermal urea denaturation and iso-urea thermal denaturation
To ascertain a complete stability profile as a function of temperature, urea denaturations at defined temperatures and thermal denaturations at defined urea concentrations were performed. Figure 6 shows the urea unfolding of A3 between –5ºC and 45ºC by CD (panel A) and between 10ºC and 30ºC by FL (panel B). Like the thermal denaturations, increasing urea causes a loss of secondary structure and exposure of the tryptophan and tyrosines decreases the FL intensity. The inset of panel B shows that  becomes red-shifted from 352 to >360 nm upon unfolding. Figure 6(C) shows that the thermal denaturation monitored by CD as a function of increasing urea concentration simultaneously decreases the Tm and increases the extent of unfolding at higher temperatures as seen by the denatured state baseline shift to lower magnitudes of ellipticity. At high urea concentrations, the urea-denatured state gains secondary structure as the temperature increases. While FL is not sensitive to the extent of unfolding in the denatured state, it does show a decreasing Tm with increasing urea, Figure 6(D).
becomes red-shifted from 352 to >360 nm upon unfolding. Figure 6(C) shows that the thermal denaturation monitored by CD as a function of increasing urea concentration simultaneously decreases the Tm and increases the extent of unfolding at higher temperatures as seen by the denatured state baseline shift to lower magnitudes of ellipticity. At high urea concentrations, the urea-denatured state gains secondary structure as the temperature increases. While FL is not sensitive to the extent of unfolding in the denatured state, it does show a decreasing Tm with increasing urea, Figure 6(D).
Figure 6.
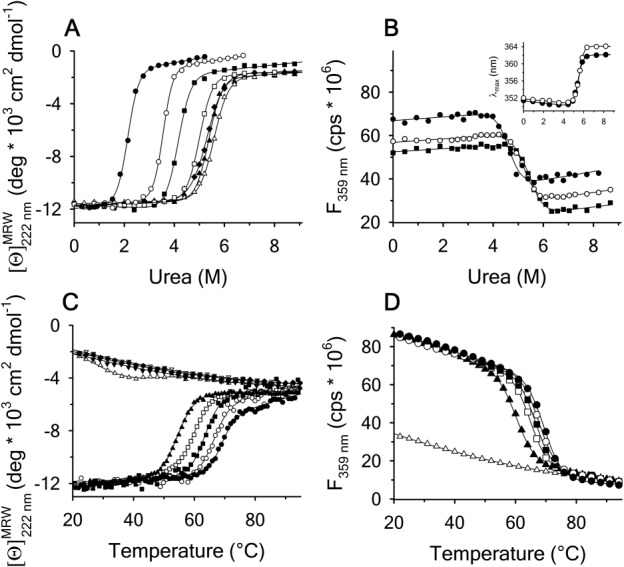
Urea denaturation of A3 at variable temperature monitored by (A) CD at 222 nm at −5°C(•), 0°C(○), 15°C(▪), 25°C(▪), 35°C(▲), and 45°C (filled diamonds). (B) FL emission at 359 nm with excitation at 280 nm at 10°C (•), 20°C(○), and 30°C(▪). The same unfolding trend was also observed with excitation at 295 nm. Inset of (B)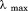 at 20°C; 280 (•) and 295 nm (○). Thermal denaturation of A3 at variable urea concentration monitored by (C) CD at 0 M (•), 1 M (○), 2 M (▪), 3 M (▪), 4 M (▲), 6 M (▵), 7 M (▼) 8 M (▿), and 9 M (filled diamonds) urea, and (D) FL at 0M (•), 0.5M (○), 1.5M(▪), 2.5M(▪), 3.5M(▲), and 9 M(▵) urea.
at 20°C; 280 (•) and 295 nm (○). Thermal denaturation of A3 at variable urea concentration monitored by (C) CD at 0 M (•), 1 M (○), 2 M (▪), 3 M (▪), 4 M (▲), 6 M (▵), 7 M (▼) 8 M (▿), and 9 M (filled diamonds) urea, and (D) FL at 0M (•), 0.5M (○), 1.5M(▪), 2.5M(▪), 3.5M(▲), and 9 M(▵) urea.
Figure 7 shows the temperature dependence of the unfolding free energy (panel A) and urea-dependent cooperativity of unfolding (panel B) derived from the analysis of individual isothermal urea-denaturation transitions shown in Figure 6(A,B). Both CD and FL yield consistent values of the stability,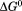 , and the m-value as a function of temperature. In panel A,
, and the m-value as a function of temperature. In panel A,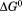 was fit using Eq. (5). Extrapolation of
was fit using Eq. (5). Extrapolation of 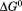 to high and low temperature results in a melting temperature,
to high and low temperature results in a melting temperature,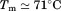 , and a cold denaturation temperature,
, and a cold denaturation temperature,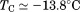 . In panel B, m/RT was fit using Eq. (10). This urea-dependent cooperativity of unfolding progressively decreases in magnitude as the temperature increases. The parameters for isothermal analysis are given in panel A of Table I. Figure 7(c) shows the urea and temperature dependence of the enthalpy derived from the analysis of individual iso-urea thermal denaturation transitions shown in Figure 6(C,D). Both CD and FL yield consistent values of the enthalpy of thermal unfolding as a function of urea and temperature. In panel C,
. In panel B, m/RT was fit using Eq. (10). This urea-dependent cooperativity of unfolding progressively decreases in magnitude as the temperature increases. The parameters for isothermal analysis are given in panel A of Table I. Figure 7(c) shows the urea and temperature dependence of the enthalpy derived from the analysis of individual iso-urea thermal denaturation transitions shown in Figure 6(C,D). Both CD and FL yield consistent values of the enthalpy of thermal unfolding as a function of urea and temperature. In panel C, 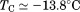 was fit using Eq. (15). At the
was fit using Eq. (15). At the 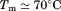 , the enthalpy of thermal denaturation decreases linearly with respect to both urea concentration (
, the enthalpy of thermal denaturation decreases linearly with respect to both urea concentration (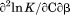 ) and temperature (∂2ln K/∂β2). The parameters for iso-urea analysis are given in panel B of Table I.
) and temperature (∂2ln K/∂β2). The parameters for iso-urea analysis are given in panel B of Table I.
Figure 7.
(Panel A) obtained from isothermal urea denaturation as a function of temperature. (Panel B) Cooperativity of isothermal urea denaturation
obtained from isothermal urea denaturation as a function of temperature. (Panel B) Cooperativity of isothermal urea denaturation  as a function of temperature. (Panel C) Temperature and urea dependence of the enthalpy obtained from iso-urea thermal denaturation. CD (▪); FL (•).
as a function of temperature. (Panel C) Temperature and urea dependence of the enthalpy obtained from iso-urea thermal denaturation. CD (▪); FL (•).
Table I.
Thermodynamic Parameters Defining the VWF A3 Domain Urea–Temperature Phase Diagram
| Taylor expansion thermodynamic parameters | Classical thermodynamic parameters | ||||
|---|---|---|---|---|---|
| (A) Isothermal urea denaturation branch | |||||
| Tc | 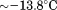 |
||||
| Tm | 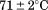 |
||||
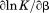 |
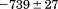 kJ/mol kJ/mol |
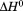 |
739 ± 27 kJ/mol | ||
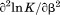 |
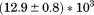 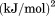
|
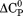 |
 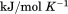
|
||
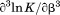 |
Not Included | 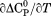 |
Not included | ||
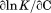 |
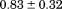 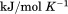
|
m |
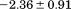 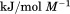
|
||
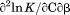 |
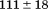 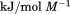
|
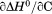 |
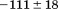 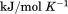
|
||
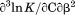 |
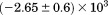 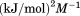
|
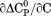 |
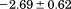 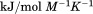
|
||
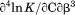 |
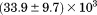 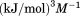
|
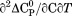 |
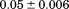 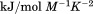
|
||
| (B) Iso-urea thermal denaturation branch | |||
| Tc | 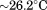 |
||
| Tm | 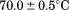 |
||
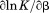 |
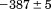 kJ/mol kJ/mol |
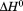 |
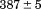 kJ/mol kJ/mol |
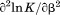 |
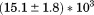 
|
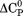 |
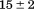 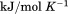
|
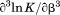 |
Not included | 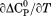 |
Not included |
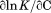 |
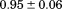 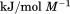
|
m |
 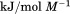
|
| ∂2ln K/∂C∂β |
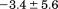 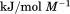
|
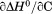 |
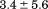 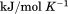
|
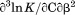 |
Not included | 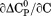 |
Not included |
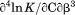 |
Not included | 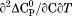 |
Not included |
| (C) Global analysis of the phase diagram | |||
| Tc | 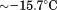 |
||
| Tm | 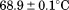 |
||
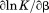 |
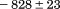 kJ/mol kJ/mol |
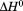 |
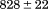 kJ/mol kJ/mol |
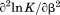 |
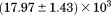 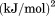
|
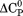 |
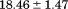 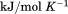
|
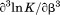 |
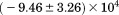 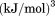
|
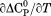 |
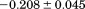 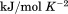
|
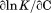 |
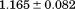 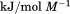
|
m |
 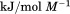
|
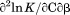 |
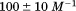 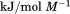
|
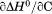 |
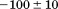 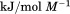
|
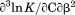 |
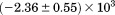 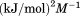
|
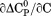 |
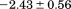 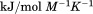
|
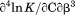 |
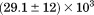 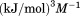
|
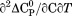 |
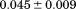 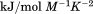
|
All parameters are referenced to the indicated Tm in the absence of urea.
Urea–temperature phase diagram
The unfolding midpoints derived from the isothermal and iso-urea studies determine the shape of the urea–temperature phase diagram where the protein exists as a mixture of 50% populations of native and denatured states. Figure 8 illustrates this phase diagram as a plot of urea concentration versus temperature derived from the unfolding transitions in Figure 6. This phase diagram is composed of urea-transition midpoints (cm) from isothermal urea denaturations in the low-temperature regime and melting temperatures (Tm) from thermal denaturations at defined urea concentrations in the high-temperature regime. The A3 domain is in the native state at concentrations and temperatures under the curve and in the denatured state above the curve. The dashed line on the isothermal urea denaturation branch of the phase diagram is a result of Eq. (16), a ratio of Eqs. (5) and (10) used to fit the temperature dependence of 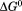 and m/RT in Figure 6(A,B). The dashed line on the iso-urea thermal denaturation branch of the phase diagram is a fit to Eq. (16) for
and m/RT in Figure 6(A,B). The dashed line on the iso-urea thermal denaturation branch of the phase diagram is a fit to Eq. (16) for 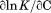 while holding constant the parameters obtained from the fitting of the urea and temperature dependence of the enthalpy in Figure 6(C). The solid line represents a refined global fit of both isothermal and iso-urea data to Eq. (16) using the fitting results of isothermal urea denaturation as starting parameters for the global fit. The parameters for global analysis are given in panel C of Table I. The overall variance of the residuals in the global analysis reduced to 0.031 demonstrating a robust description of the data over the full temperature range of stability.
while holding constant the parameters obtained from the fitting of the urea and temperature dependence of the enthalpy in Figure 6(C). The solid line represents a refined global fit of both isothermal and iso-urea data to Eq. (16) using the fitting results of isothermal urea denaturation as starting parameters for the global fit. The parameters for global analysis are given in panel C of Table I. The overall variance of the residuals in the global analysis reduced to 0.031 demonstrating a robust description of the data over the full temperature range of stability.
Figure 8.
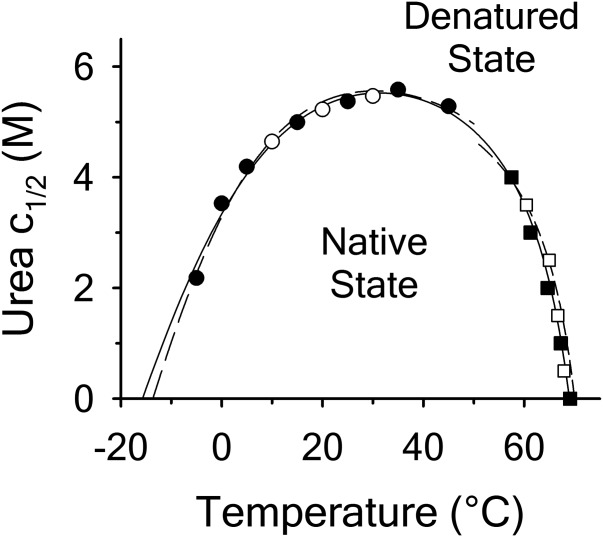
Urea–temperature phase diagram (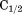 vs. T) defines the 50% folded/unfolded boundary for the two-state unfolding of A3. Isothermal urea denaturation by FL (○) and CD (•). Iso-urea thermal denaturation by FL (▪) and CD (▪). Dashed lines represent separate fitting of the isothermal urea denaturation and iso-urea thermal denaturation branches of the phase diagram. Solid line represents the global fit of the phase diagram over the full temperature range for all methods employed.
vs. T) defines the 50% folded/unfolded boundary for the two-state unfolding of A3. Isothermal urea denaturation by FL (○) and CD (•). Iso-urea thermal denaturation by FL (▪) and CD (▪). Dashed lines represent separate fitting of the isothermal urea denaturation and iso-urea thermal denaturation branches of the phase diagram. Solid line represents the global fit of the phase diagram over the full temperature range for all methods employed.
Comparison of the fitting results in Table I demonstrates that the isothermal urea analysis agrees better with the global analysis than does the iso-urea thermal analysis. Isothermal urea analysis results in a cold-denaturation temperature,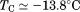 ; close to that obtained from the global analysis,
; close to that obtained from the global analysis,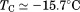 . Fitting the iso-urea thermal denaturation branch of the phase diagram results in a much higher cold-denaturation temperature,
. Fitting the iso-urea thermal denaturation branch of the phase diagram results in a much higher cold-denaturation temperature,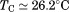 , where the protein is known to be folded. Although the isothermal urea and iso-urea thermal analysis compared well with the global analysis within the temperature range of the data, the extrapolation of the iso-urea thermal analysis to lower temperatures is limited by the small range of the thermal unfolding data,
, where the protein is known to be folded. Although the isothermal urea and iso-urea thermal analysis compared well with the global analysis within the temperature range of the data, the extrapolation of the iso-urea thermal analysis to lower temperatures is limited by the small range of the thermal unfolding data,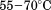 . Isothermal urea denaturations were done over a larger temperature range between –5°C and 45ºC. We performed a statistical comparison of the resulting parameters from each analysis by calculating the standard error on the difference [(global – isothermal urea) – (global – iso-urea thermal)] to identify which parameters are statistically different in each type of analysis. A paired t-test was also performed. These comparisons demonstrated that the only parameters statistically different among the three analyses were the enthalpy (
. Isothermal urea denaturations were done over a larger temperature range between –5°C and 45ºC. We performed a statistical comparison of the resulting parameters from each analysis by calculating the standard error on the difference [(global – isothermal urea) – (global – iso-urea thermal)] to identify which parameters are statistically different in each type of analysis. A paired t-test was also performed. These comparisons demonstrated that the only parameters statistically different among the three analyses were the enthalpy (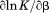 ), its urea concentration dependence (
), its urea concentration dependence (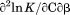 ), and the m-value (
), and the m-value (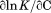 ). The heat capacity (
). The heat capacity (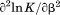 ) and its urea concentration and temperature dependencies were not statistically different from each type of analysis. The iso-urea thermal analysis resulted in a significantly lower enthalpy (387 ± 5 kJ/mol) than the global analysis. Figure 9 demonstrates that all van't Hoff, calorimetric, and iso-urea thermal phase diagram analyses of the data result in a statistically equivalent measure of the enthalpy of thermal denaturation, whereas analysis of the isothermal urea-denaturation branch and global analyses of the phase diagram resulted in enthalpies that were 2–2.3 fold greater in magnitude.
) and its urea concentration and temperature dependencies were not statistically different from each type of analysis. The iso-urea thermal analysis resulted in a significantly lower enthalpy (387 ± 5 kJ/mol) than the global analysis. Figure 9 demonstrates that all van't Hoff, calorimetric, and iso-urea thermal phase diagram analyses of the data result in a statistically equivalent measure of the enthalpy of thermal denaturation, whereas analysis of the isothermal urea-denaturation branch and global analyses of the phase diagram resulted in enthalpies that were 2–2.3 fold greater in magnitude.
Figure 9.
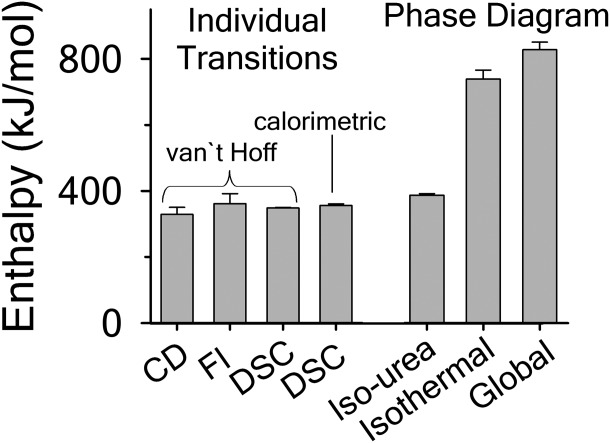
Comparison of the enthalpy 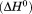 obtained from thermal denaturation using the various experimental methods and the enthalpy obtained from fitting the iso-urea thermal denaturation and isothermal urea denaturation branches of the phase diagram and the global fitting of the phase diagram.
obtained from thermal denaturation using the various experimental methods and the enthalpy obtained from fitting the iso-urea thermal denaturation and isothermal urea denaturation branches of the phase diagram and the global fitting of the phase diagram.
Discussion
The data presented demonstrate that the isolated A3 domain fragment of VWF behaves thermodynamically as a monomeric protein that reversibly unfolds in a two-state manner between the native and denatured conformations.
Although the unit cell of the crystal structure contains two A3 domain macromolecules,27 in solution the domain behaves as monomer because the transition midpoints do not depend on the protein concentration over an experimental range of three orders of magnitude. For proteins that noncovalently dimerize or oligomerize, the apparent urea and thermal unfolding midpoints will depend on protein concentration.13,28
Reversibility of isothermal urea denaturation has been previously demonstrated by equilibrating a sample containing A3 in 8 M urea at 25ºC for 1 h, diluting it to urea concentrations within the transition and equilibrating for an additional 1 h prior to taking a spectral measurement.26 Thermal reversibility was demonstrated here by repeated scans interspersed with low-temperature equilibrations [Figure 5(A)]. In addition to experimental verification of thermal reversibility, empirical evidence demonstrated that the thermal unfolding transition was not kinetically controlled because the Tm and 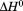 are, within experimental error, independent of the thermal scan rate (Figure 4). Further evidence of the lack of kinetic effects was demonstrated calorimetrically by the symmetric excess heat capacity curves centered on the Tm [Figure 3(B)]. The presence of kinetic irreversibility is known to produce a thermal scan rate dependence and also to skew the excess heat capacity curves to lower temperatures.29 Even though the unfolding of A3 is at a thermodynamic equilibrium throughout the transition, irreversibility eventually arises because of denatured state aggregation [Figure 5(C)]. Because we observe a symmetrical transition that is scan rate independent and experimentally reversible, the aggregation of the thermally denatured state must be kinetically slow at temperatures below and within the thermal transition.
are, within experimental error, independent of the thermal scan rate (Figure 4). Further evidence of the lack of kinetic effects was demonstrated calorimetrically by the symmetric excess heat capacity curves centered on the Tm [Figure 3(B)]. The presence of kinetic irreversibility is known to produce a thermal scan rate dependence and also to skew the excess heat capacity curves to lower temperatures.29 Even though the unfolding of A3 is at a thermodynamic equilibrium throughout the transition, irreversibility eventually arises because of denatured state aggregation [Figure 5(C)]. Because we observe a symmetrical transition that is scan rate independent and experimentally reversible, the aggregation of the thermally denatured state must be kinetically slow at temperatures below and within the thermal transition.
All spectroscopic and calorimetric experiments indicate that the unfolding of A3 is two-state with no evidence of intermediates. If intermediates were significantly populated, CD and FL would show multiple or asymmetric transitions and DSC would present two or more peaks that may or may not overlap. Additional thermodynamic evidence of two-state character is inferred by the agreement between the thermodynamic parameters obtained from CD and FL because each reports on a different structural property, backbone secondary structure, and global tertiary structure through exposure of tryptophan and tyrosine (Figure 7). Furthermore, the van't Hoff enthalpy derived from fitting the spectroscopic thermal unfolding transitions in the absence of urea is equal to the calorimetric enthalpy within experimental error [Figure 4(B)]. Agreement between van't Hoff and calorimetric enthalpies has historically been a stringent test for defining two-state character.30
Comparison of the thermodynamic parameters obtained from global analysis of the phase diagram to those obtained from iso-urea thermal analysis and analysis of individual thermal unfolding transitions in the absence of urea reveals a primary discrepancy in the enthalpy of unfolding. While both calorimetric and van't Hoff two-state analyses are in agreement with 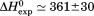 kJ/mol, global analysis of the phase diagram results in
kJ/mol, global analysis of the phase diagram results in 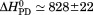 kJ/mol. The experimentally observed enthalpy change is only 44±4% of that obtained from the phase diagram analysis and this results in a profound difference between the free energies of unfolding as illustrated in Figure 10. At first glance, these discrepancies seem untenable for a simple two-state thermodynamic equilibrium between native and denatured states, yet there is no evidence for the significant population of intermediates by any of the methods used to interrogate the unfolding. One reason for these discrepancies might be that aggregation of the thermally denatured state lowers the detectable enthalpy change of unfolding because of an exothermic heat of protein association into aggregates. However, this argument breaks down when one considers that the same thermodynamics are obtained at 0.1 μM protein concentrations which is much less than protein concentrations used for DSC and where aggregation is detectable by light scattering (Figure 5). If unfolding is reversible two-state and aggregation effects on the observable thermodynamics is negligible, then what is the cause of these discrepancies?
kJ/mol. The experimentally observed enthalpy change is only 44±4% of that obtained from the phase diagram analysis and this results in a profound difference between the free energies of unfolding as illustrated in Figure 10. At first glance, these discrepancies seem untenable for a simple two-state thermodynamic equilibrium between native and denatured states, yet there is no evidence for the significant population of intermediates by any of the methods used to interrogate the unfolding. One reason for these discrepancies might be that aggregation of the thermally denatured state lowers the detectable enthalpy change of unfolding because of an exothermic heat of protein association into aggregates. However, this argument breaks down when one considers that the same thermodynamics are obtained at 0.1 μM protein concentrations which is much less than protein concentrations used for DSC and where aggregation is detectable by light scattering (Figure 5). If unfolding is reversible two-state and aggregation effects on the observable thermodynamics is negligible, then what is the cause of these discrepancies?
Figure 10.
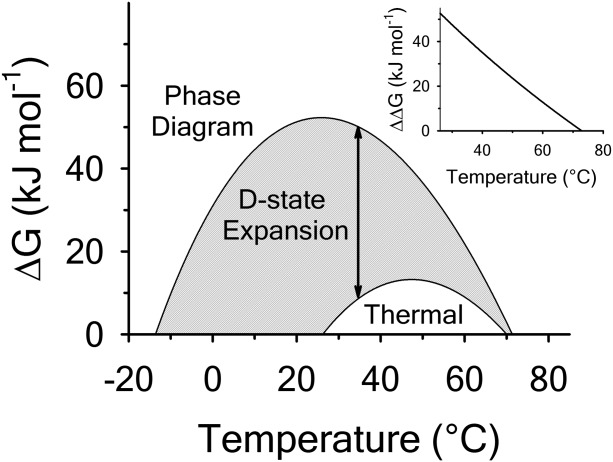
Comparison of the free energy 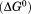 of unfolding derived from global analysis of the urea–temperature phase diagram with the free energy of thermal denaturation in the absence of urea. The gray area highlights the difference plotted in the inset as
of unfolding derived from global analysis of the urea–temperature phase diagram with the free energy of thermal denaturation in the absence of urea. The gray area highlights the difference plotted in the inset as 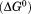 corresponding to the free energy of denatured state expansion.
corresponding to the free energy of denatured state expansion.
Upon closer inspection of Figure 6(A,C), CD reveals additional information about the thermodynamic states that FL and calorimetry do not capture. The native state of A3 has an ellipticity 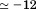 and up to 4M urea and 40°C, this secondary structure is constant. In the presence of 7–9 M urea, the urea denatured state gains secondary structure content as the temperature is raised ranging from
and up to 4M urea and 40°C, this secondary structure is constant. In the presence of 7–9 M urea, the urea denatured state gains secondary structure content as the temperature is raised ranging from  ellipticity units at 0ºC to
ellipticity units at 0ºC to 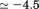 ellipticity units at. By contrast, the thermally denatured state in the absence of urea at 80°C has an ellipticity of = −6 and the secondary structure content of this state progressively decreases upon addition of urea. Relative to the native state and the urea-denatured state, the thermally denatured state at 80°C has an ellipticity ranging between =−60% and 80% of the total ellipticity change over the full range of temperature. The remainder of the total change is because of the loss of secondary structure content of the thermally denatured state as a function of increasing urea at high temperature and the loss of secondary structure in the urea-denatured state at low temperature.
ellipticity units at. By contrast, the thermally denatured state in the absence of urea at 80°C has an ellipticity of = −6 and the secondary structure content of this state progressively decreases upon addition of urea. Relative to the native state and the urea-denatured state, the thermally denatured state at 80°C has an ellipticity ranging between =−60% and 80% of the total ellipticity change over the full range of temperature. The remainder of the total change is because of the loss of secondary structure content of the thermally denatured state as a function of increasing urea at high temperature and the loss of secondary structure in the urea-denatured state at low temperature.
Recent literature has correlated the amount of ordered secondary structure content of proteins relative to their denatured state to the degree of compactness as given by the ratio of the denatured and native state hydrodynamic volumes. Using the relationship of Uversky and Fink,31 the ellipticities we observe indicate that the thermally denatured state has a hydrodynamic volume that is 1.8 times greater than the native state and the 9 M urea denatured state can range between ∼2.5 and 6 times larger than the native state over the full range of temperature. The moderate increase in hydrodynamic volume of the thermally denatured state over that of the native state illustrates that the thermally denatured state is highly compact relative to the urea-denatured state. These relationships indicate that physical character of the native state is fixed as a function of both urea and temperature, but that the denatured state has a variable physical character that expands with increasing urea and decreasing temperature.
The resulting discrepancy between the enthalpy derived from individual unfolding transitions and what is obtained from the phase diagram method indicates that the thermodynamic character of the unfolding is linked to the physical character of the states involved. Enthalpy is known to scale with the amount of solvent accessible surface area changes on unfolding.32 Because 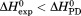 and the physical character of the native state is fixed, the thermally denatured state exposes less surface area than the urea-denatured state. This linkage between the thermodynamic character and the macromolecular dimensions of the denatured state is also evident by the temperature dependence of the
and the physical character of the native state is fixed, the thermally denatured state exposes less surface area than the urea-denatured state. This linkage between the thermodynamic character and the macromolecular dimensions of the denatured state is also evident by the temperature dependence of the 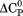 and the m-value.
and the m-value.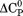 also scales with the change in solvent accessible surface area on unfolding.33 Given a fixed native state character, a negative
also scales with the change in solvent accessible surface area on unfolding.33 Given a fixed native state character, a negative 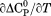 indicates that the surface area of the thermally denatured state decreases with increasing temperature. Furthermore, the m-value in Figure 7(B) also decreases in magnitude as a function of temperature. Because the m-value is proportional to the thermodynamic contributions of protein groups that become solvent exposed on unfolding,14 it represents the energetic equivalent of the size of the cooperative unfolding structural unit. This cooperative unit becomes smaller as temperature increases. With a fixed physical thermodynamic character of the native state, the only way the size of the cooperative unit can become smaller with increasing temperature is if the denatured state becomes more compact and structurally ordered. Thus, the negative temperature derivative of the
indicates that the surface area of the thermally denatured state decreases with increasing temperature. Furthermore, the m-value in Figure 7(B) also decreases in magnitude as a function of temperature. Because the m-value is proportional to the thermodynamic contributions of protein groups that become solvent exposed on unfolding,14 it represents the energetic equivalent of the size of the cooperative unfolding structural unit. This cooperative unit becomes smaller as temperature increases. With a fixed physical thermodynamic character of the native state, the only way the size of the cooperative unit can become smaller with increasing temperature is if the denatured state becomes more compact and structurally ordered. Thus, the negative temperature derivative of the 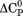 obtained from the phase diagram analysis and the decreasing magnitude of the m-value with respect to temperature are thermodynamic manifestations of the physical dimensions of the denatured state ensemble.
obtained from the phase diagram analysis and the decreasing magnitude of the m-value with respect to temperature are thermodynamic manifestations of the physical dimensions of the denatured state ensemble.
The thermodynamics of denatured state expansion are profound when viewed from the perspective of free energy. Figure 10 compares the thermodynamic stability curves of A3 obtained from analysis by the phase diagram method with that of thermal unfolding in the absence of urea. The difference in these stability curves (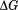 ) illustrates the many kilojoules of free energy resulting from the urea-induced expansion of the denatured state ensemble. Phenomenologically, it represents the excess free energy required to denature residual structure in the denatured state ensemble. This difference is approximately linear (inset) with respect to temperature because the primary difference is the enthalpy. There is no indication that this expansion is cooperative because the magnitude of the ellipticity of the thermally denatured state decreases linearly with respect to urea concentration at 85ºC and as the temperature is lowered, the ellipticity of the urea-denatured state also decreases in a curvilinear manner. Perhaps the reason for the large free energy of denatured state expansion is because of the single disulfide bond that crosslinks the N and C termini. This disulfide restricts the conformational entropy of the protein chain which constrains both the thermally and urea-denatured states. As a result, the thermally denatured state is so compact that it is on the verge of collapse to the folded state, but because of reduced solubility it is also poised to aggregate at higher concentrations.
) illustrates the many kilojoules of free energy resulting from the urea-induced expansion of the denatured state ensemble. Phenomenologically, it represents the excess free energy required to denature residual structure in the denatured state ensemble. This difference is approximately linear (inset) with respect to temperature because the primary difference is the enthalpy. There is no indication that this expansion is cooperative because the magnitude of the ellipticity of the thermally denatured state decreases linearly with respect to urea concentration at 85ºC and as the temperature is lowered, the ellipticity of the urea-denatured state also decreases in a curvilinear manner. Perhaps the reason for the large free energy of denatured state expansion is because of the single disulfide bond that crosslinks the N and C termini. This disulfide restricts the conformational entropy of the protein chain which constrains both the thermally and urea-denatured states. As a result, the thermally denatured state is so compact that it is on the verge of collapse to the folded state, but because of reduced solubility it is also poised to aggregate at higher concentrations.
In conclusion, our results demonstrate that when thermally denatured states are highly compact, comparative analysis of individual thermal transitions by either van't Hoff or calorimetric methods combined with phase diagram methods using urea at variable temperature can result in energetics associated with denatured state expansion. For the A3 domain, this is primarily evident in the excess enthalpy of urea denaturation relative to thermal denaturation in the absence of urea, but it is also manifested in urea dependence of the higher order terms that define the stability curve and in the temperature dependence of the m-value. The combined analysis presented here offers a distinct advantage over traditional methods because of its ability to decipher the energetics of unfolding from the energetics of unfolding residual structure in the denatured state ensemble.
Materials and Methods
Protein expression and purification
cDNA of recombinant VWF-A3 (amino acids S1671–G1874) domain was expressed in E. coli M-15 cells as a fusion protein containing an N-terminal 6×His tag using BamHI and HindIII restriction sites in the Qiagen pQE-9 plasmid vector and purified from inclusion bodies by  affinity chromatography.26 The purity was verified by coomassie stained SDS-PAGE and also by size exclusion chromatography using a Phenomenex SEC S3000 column on a BioCAD Sprint perfusion chromatography system. A3 was stored in TBS-T (25 mM Tris-Cl,
affinity chromatography.26 The purity was verified by coomassie stained SDS-PAGE and also by size exclusion chromatography using a Phenomenex SEC S3000 column on a BioCAD Sprint perfusion chromatography system. A3 was stored in TBS-T (25 mM Tris-Cl,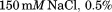 Tween-20, pH 7.4) on ice until experimentation when it was dialyzed against a temperature stable buffer mixture containing 10 mM NaAcetate, 10 mM NaPhosphate, 10 mM Glycine, 150mMNaCl, 1mM EDTA, and pH = 8.
Tween-20, pH 7.4) on ice until experimentation when it was dialyzed against a temperature stable buffer mixture containing 10 mM NaAcetate, 10 mM NaPhosphate, 10 mM Glycine, 150mMNaCl, 1mM EDTA, and pH = 8.
Spectroscopy
Protein concentration was quantified using UV absorption at 280 and 333 nm (to correct for light scattering) on a Shimadzu UV2101PC spectrophotometer using an extinction coefficient of 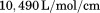 in water calculated from 4 tyrosines and 1 tryptophan.34,35 All experiments using spectroscopic observables were performed on an Aviv Biomedical Model 420C CD spectrometer and a Horiba Jobin-Yvon Fluorolog 3 spectrofluorimeter equipped with a Wavelength Electronics Model LF1-3751 temperature controller.
in water calculated from 4 tyrosines and 1 tryptophan.34,35 All experiments using spectroscopic observables were performed on an Aviv Biomedical Model 420C CD spectrometer and a Horiba Jobin-Yvon Fluorolog 3 spectrofluorimeter equipped with a Wavelength Electronics Model LF1-3751 temperature controller.
Far UV CD spectra between 190 and 260 nm were recorded at 1 nm wavelength increments with 20 s integration time at 1 nm bandwidth using a 0.1 mm quartz cell. Ellipticity values with a photomultiplier amplifier voltage above 600 V were not evaluated. Circular dichroic ellipticity 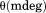 was converted to mean residue molar ellipticity
was converted to mean residue molar ellipticity 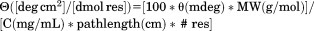 .
.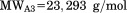 and the number of residues
and the number of residues 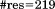 includes residues derived from the plasmid construct.
includes residues derived from the plasmid construct.
FL emission spectra (excitation wavelengths of 280 and 295 nm) between 305 and 440 nm were recorded at 0.5 nm wavelength increments with 1 s integration time using a micro quartz cell. Relative FL intensity is reported as signal intensity divided by the intensity of the reference. All measured spectra were corrected for the background ellipticity and FL of the buffer.
Calorimetry
DSC was performed on a TA Instruments NanoDSC equipped with a fixed capillary cell design at 3 atm pressure. The calorimeter was calibrated at each scan rate by performing a cell balance scan and residual scans as described in the manual. All buffers and protein samples were degassed with moderate stirring for 10 min prior to use in a standard glass vacuum desiccation chamber. The calorimeter was equilibrated overnight on buffer present in both the reference and sample cells with repeat thermal scans until a stable baseline was obtained after which the buffer in the sample cell was replaced with protein solution during the equilibration step between scans. One measurement per second was recorded over a range of 20ºC – 95ºC. DSC traces were corrected for a subsequent irreversible scan that was used as the baseline. Calorimetric power compensation 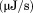 was converted to molar heat capacity
was converted to molar heat capacity 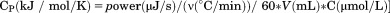 . Excess molar heat capacity
. Excess molar heat capacity 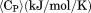 , was obtained by subtracting polynomial baseline to the pre- and post-transition regions of the heat capacity traces using a Mathematica (Wolfram, Inc., Champaign, IL) script developed in our laboratory.
, was obtained by subtracting polynomial baseline to the pre- and post-transition regions of the heat capacity traces using a Mathematica (Wolfram, Inc., Champaign, IL) script developed in our laboratory.
Thermal denaturation and reversibility
Thermal denaturation was also performed using FL and far UV CD. Thermal scans were recorded using 1 cm teflon-capped quartz cells under moderate stirring with 15 min prior equilibration at 10ºC. Using FL, the scan rate and protein concentration dependency was determined at 2.0, 1.6, 0.9, and 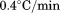 for each concentration of 2.0, 1.0, 0.5, 0.2, and 0.1 μM. Relative FL emission intensity at 359 nm with 280 nm excitation was collected for 4 s and averaged at each temperature point between 10°C and 60°C. Using CD at 222 nm, the scan rate dependence for 1 μM protein was determined at 0.5, 1.0, 1.5, and
for each concentration of 2.0, 1.0, 0.5, 0.2, and 0.1 μM. Relative FL emission intensity at 359 nm with 280 nm excitation was collected for 4 s and averaged at each temperature point between 10°C and 60°C. Using CD at 222 nm, the scan rate dependence for 1 μM protein was determined at 0.5, 1.0, 1.5, and 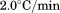 with a 20 s integration time and 1 nm bandwidth. Thermal denaturation of 1 μM A3 in the presence of various urea concentrations was determined by both CD and FL at
with a 20 s integration time and 1 nm bandwidth. Thermal denaturation of 1 μM A3 in the presence of various urea concentrations was determined by both CD and FL at 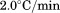 .
.
Right angle light scattering at 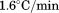 as a function of the temperature was measured to determine the extent of aggregation using excitation and emission wavelengths
as a function of the temperature was measured to determine the extent of aggregation using excitation and emission wavelengths 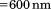 . Light scattering was averaged for 30 s at each temperature.
. Light scattering was averaged for 30 s at each temperature.
To ascertain the extent of thermal reversibility in the absence of urea, both FL and DSC were used to acquire repeat thermal scans at 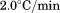 on a single protein sample from 10°C to incremental temperatures throughout the range of the thermal transition up to 95°C, interspersed with cool downs and 30 min equilibrations at 10°C. A protein concentration of 0.1 μM in a 1 cm teflon-capped quartz cell with moderate stirring was used for FL and 70 μM was used for DSC.
on a single protein sample from 10°C to incremental temperatures throughout the range of the thermal transition up to 95°C, interspersed with cool downs and 30 min equilibrations at 10°C. A protein concentration of 0.1 μM in a 1 cm teflon-capped quartz cell with moderate stirring was used for FL and 70 μM was used for DSC.
Isothermal urea denaturation
Urea denaturation was performed at defined temperatures by incubating separate protein samples at various concentrations of urea in a water bath overnight. Far UV CD at 222 nm and FL emission at 359 nm with either 280 or 295 nm excitation was used to monitor the unfolding transition. 10 μM protein in a 1 mm quartz cell was used for CD and 2 μM in a microquartz cell was used for fluoresence. The FL emission red shift on unfolding by urea at 20°C was monitored by collecting spectra between 330 and 370 nmat 2 nm intervals with 0.5 s integration time. The maximum wavelength of emission intensity 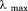 was determined by fitting the spectra with the Gaussian function
was determined by fitting the spectra with the Gaussian function 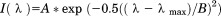 .
.
Analysis of individual unfolding transitions
All nonlinear least squares fitting routines were performed with gnuplot version 4.4.2. Unfolding transitions monitored by CD and FL spectroscopy were analyzed using Eq. (1) where S is the spectroscopic observable, SN and SD are linear baselines for the native and denatured state spectroscopic observables and K is the unfolding equilibrium constant.
| (1) |
Unfolding transitions monitored by DSC were analyzed by two methods to obtain both calorimetric and van/t Hoff enthalpies. The calorimetric enthalpy 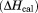 of the transition was determined from the area under the excess molar heat capacity curve and the van/t Hoff enthalpy
of the transition was determined from the area under the excess molar heat capacity curve and the van/t Hoff enthalpy 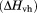 was obtained from fitting the excess molar heat capacity curve to Eq. (2), where the excess molar enthalpy of the transition,
was obtained from fitting the excess molar heat capacity curve to Eq. (2), where the excess molar enthalpy of the transition,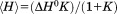 and
and 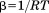 .
.
| (2) |
For the analysis of individual unfolding transitions, the urea concentration and temperature dependence of the equilibrium constant were expressed as linear functions of the natural logarithm of K with respect to 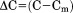 and
and 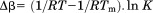 is equal to 0 at the midpoints of the isothermal urea and iso-urea thermal transitions (cm and Tm).
is equal to 0 at the midpoints of the isothermal urea and iso-urea thermal transitions (cm and Tm).
| (3) |
| (4) |
Phase diagram analysis
Analysis of individual transitions at various temperatures and urea concentrations provides the zero order (cm and Tm) and first order parameters (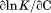 and
and 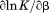 ). The zero order parameters define where the native and denatured states are equally populated and the first order parameters define the cooperativity of the unfolding transition either by urea or temperature. To ascertain higher order parameters that further define the urea and temperature dependence of the unfolding, a standard Taylor expansion of the equilibrium constant (
). The zero order parameters define where the native and denatured states are equally populated and the first order parameters define the cooperativity of the unfolding transition either by urea or temperature. To ascertain higher order parameters that further define the urea and temperature dependence of the unfolding, a standard Taylor expansion of the equilibrium constant (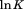 ) and the first order parameters as a function of
) and the first order parameters as a function of 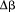 and urea concentration is used as we previously described.13 All parameters are defined with reference to the Tm of thermal denaturation in the absence of urea. For the sake of completion, Eq. (5) expands
and urea concentration is used as we previously described.13 All parameters are defined with reference to the Tm of thermal denaturation in the absence of urea. For the sake of completion, Eq. (5) expands 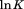 as far as the third derivative with respect to β,
as far as the third derivative with respect to β,
| (5) |
in which these parameters are related to the classical thermodynamic parameters,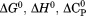 , and the temperature dependence of
, and the temperature dependence of 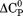 via the following relationships.
via the following relationships.
| (6) |
| (7) |
| (8) |
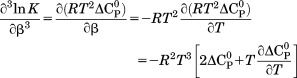 |
(9) |
Likewise, the urea-dependent cooperativity of the unfolding transition,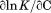 , is expanded to the third derivative with respect to β,
, is expanded to the third derivative with respect to β,
| (10) |
accounting for the urea concentration dependence of the classical thermodynamic parameters,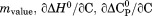 , and
, and 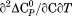 via the following relationships.
via the following relationships.
| (11) |
| (12) |
| (13) |
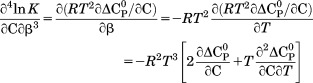 |
(14) |
The thermal cooperativity of the unfolding transition,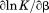 , is a two-dimensional function of temperature and urea concentration that describes the enthalpy of unfolding in terms of the parameters listed above.
, is a two-dimensional function of temperature and urea concentration that describes the enthalpy of unfolding in terms of the parameters listed above.
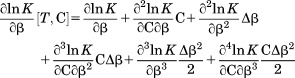 |
(15) |
Taking the ratio of Eqs. (5) and (10) yields the phase diagram in terms of the temperature dependence of the urea concentrations at which native and denatured states are 50% populated.
| (16) |
The criteria used to determine the number of parameters to include in the fitting was based upon the minimal number required to sufficiently describe the data within the data range, a minimal root mean square deviation of the residuals and asymptotic standard errors typically less than 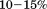 but no greater than 40%.
but no greater than 40%.
Acknowledgments
Early in the work, Miguel A. Cruz was helpful in discussions and providing the expression system for the VWF A3 domain, which we gratefully acknowledge. We also would like to thank Drs. Jörg Rösgen, Steve Whitten, and Luis Holthauzen for helpful discussions and comments throughout the work. This work was supported by National Heart Lung and Blood Institute of the National Institutes of Health HL109109.
Glossary
- CD
circular dichroism
- DSC
differential scanning calorimetry
- FL
fluorescence
- VWF
von Willebrand factor.
References
- 1.Pace CN, Laurents DV. A new method for determining the heat capacity change for protein folding. Biochemistry. 1989;28:2520–2525. doi: 10.1021/bi00432a026. [DOI] [PubMed] [Google Scholar]
- 2.Pace CN. The stability of globular proteins. CRC Crit Rev Biochem. 1975;3:1–43. doi: 10.3109/10409237509102551. [DOI] [PubMed] [Google Scholar]
- 3.Becktel WJ, Schellman JA. Protein stability curves. Biopolymers. 1987;26:1859–1877. doi: 10.1002/bip.360261104. [DOI] [PubMed] [Google Scholar]
- 4.Santoro MM, Bolen DW. Unfolding free energy changes determined by the linear extrapolation method. 1. Unfolding of phenylmethanesulfonyl alpha-chymotrypsin using different denaturants. Biochemistry. 1988;27:8063–8068. doi: 10.1021/bi00421a014. [DOI] [PubMed] [Google Scholar]
- 5.Bolen DW, Yang M. Effects of guanidine hydrochloride on the proton inventory of proteins: implications on interpretations of protein stability. Biochemistry. 2000;39:15208–15216. doi: 10.1021/bi001071d. [DOI] [PubMed] [Google Scholar]
- 6.Bolen DW, Santoro MM. Unfolding free energy changes determined by the linear extrapolation method. 2. Incorporation of delta G degrees N-U values in a thermodynamic cycle. Biochemistry. 1988;27:8069–8074. doi: 10.1021/bi00421a015. [DOI] [PubMed] [Google Scholar]
- 7.Nicholson EM, Scholtz JM. Conformational stability of the Escherichia coli HPr protein: test of the linear extrapolation method and a thermodynamic characterization of cold denaturation. Biochemistry. 1996;35:11369–11378. doi: 10.1021/bi960863y. [DOI] [PubMed] [Google Scholar]
- 8.Felitsky DJ, Record MTJ. Thermal and urea-induced unfolding of the marginally stable lac repressor DNA-binding domain: a model system for analysis of solute effects on protein processes. Biochemistry. 2003;42:2202–2217. doi: 10.1021/bi0270992. [DOI] [PubMed] [Google Scholar]
- 9.Baskakov IV, Bolen DW. The paradox between m values and deltaCp's for denaturation of ribonuclease T1 with disulfide bonds intact and broken. Protein Sci. 1999;8:1314–1319. doi: 10.1110/ps.8.6.1314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chen BL, Schellman JA. Low-temperature unfolding of a mutant of phage T4 lysozyme. 1. Equilibrium studies. Biochemistry. 1989;28:685–691. doi: 10.1021/bi00428a041. [DOI] [PubMed] [Google Scholar]
- 11.Hollien J, Marqusee S. A thermodynamic comparison of mesophilic and thermophilic ribonucleases H. Biochemistry. 1999;38:3831–3836. doi: 10.1021/bi982684h. [DOI] [PubMed] [Google Scholar]
- 12.Agashe VR, Udgaonkar JB. Thermodynamics of denaturation of barstar: evidence for cold denaturation and evaluation of the interaction with guanidine hydrochloride. Biochemistry. 1995;34:3286–3299. doi: 10.1021/bi00010a019. [DOI] [PubMed] [Google Scholar]
- 13.Holthauzen LM, Auton M, Sinev M, Rosgen J. Protein stability in the presence of cosolutes. Methods Enzymol. 2011;492:61–125. doi: 10.1016/B978-0-12-381268-1.00015-X. [DOI] [PubMed] [Google Scholar]
- 14.Auton M, Holthauzen LM, Bolen DW. Anatomy of energetic changes accompanying urea-induced protein denaturation. Proc Natl Acad Sci USA. 2007;104:15317–15322. doi: 10.1073/pnas.0706251104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Auton M, Rosgen J, Sinev M, Holthauzen LM, Bolen DW. Osmolyte effects on protein stability and solubility: a balancing act between backbone and side-chains. Biophys Chem. 2011;159:90–99. doi: 10.1016/j.bpc.2011.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Murphy KP, Gill SJ. Calorimetric measurement of the enthalpy of dissolution of diketopiperazine in water as a function of temperature. Thermochim Acta. 1989;139:279–290. [Google Scholar]
- 17.Auton M, Sedlak E, Wu T, Zhu C, Cruz MA. Changes in thermodynamic stability of von willebrand factor differentially affect the force-dependent binding to platelet GPIbalpha. Biophys J. 2009;97:618–627. doi: 10.1016/j.bpj.2009.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zweifel ME, Barrick D. Relationships between the temperature dependence of solvent denaturation and the denaturant dependence of protein stability curves. Biophys Chem 101–102. 2002:221–237. doi: 10.1016/s0301-4622(02)00181-3. [DOI] [PubMed] [Google Scholar]
- 19.Ferreon AC, Bolen DW. Thermodynamics of denaturant-induced unfolding of a protein that exhibits variable two-state denaturation. Biochemistry. 2004;43:13357–13369. doi: 10.1021/bi048666j. [DOI] [PubMed] [Google Scholar]
- 20.Yang M, Ferreon AC, Bolen DW. Structural thermodynamics of a random coil protein in guanidine hydrochloride. Proteins Suppl. 2000;4:44–49. doi: 10.1002/1097-0134(2000)41:4+<44::aid-prot40>3.3.co;2-z. [DOI] [PubMed] [Google Scholar]
- 21.Baskakov IV, Bolen DW. Monitoring the sizes of denatured ensembles of staphylococcal nuclease proteins: implications regarding m values, intermediates, and thermodynamics. Biochemistry. 1998;37:18010–18017. doi: 10.1021/bi981849j. [DOI] [PubMed] [Google Scholar]
- 22.Qu Y, Bolen CL, Bolen DW. Osmolyte-driven contraction of a random coil protein. Proc Natl Acad Sci USA. 1998;95:9268–9273. doi: 10.1073/pnas.95.16.9268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Pace CN, Huyghues-Despointes BMP, Fu H, Takano K, Scholtz JM, Grimsley GR. Urea denatured state ensembles contain extensive secondary structure that is increased in hydrophobic proteins. Protein Sci. 2010;19:929–943. doi: 10.1002/pro.370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tanford C. Chapter Four - The Effect of Temperature. Anomalous Entropy and Heat Capacity. The hydrophobic effect—formation of micelles and biological membranes. New York: John Wiley & Sons,; 1973. pp. 16–23. [Google Scholar]
- 25.Holthauzen LM, Rosgen J, Bolen DW. Hydrogen bonding progressively strengthens upon transfer of the protein urea-denatured state to water and protecting osmolytes. Biochemistry. 2010;49:1310–1318. doi: 10.1021/bi9015499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Auton M, Cruz MA, Moake J. Conformational stability and domain unfolding of the von Willebrand factor A domains. J Mol Biol. 2007;366:986–1000. doi: 10.1016/j.jmb.2006.10.067. [DOI] [PubMed] [Google Scholar]
- 27.Bienkowska J, Cruz M, Atiemo A, Handin R, Liddington R. The von willebrand factor A3 domain does not contain a metal ion-dependent adhesion site motif. J Biol Chem. 1997;272:25162–25167. doi: 10.1074/jbc.272.40.25162. [DOI] [PubMed] [Google Scholar]
- 28.Robinson CR, Rentzeperis D, Silva JL, Sauer RT. Formation of a denatured dimer limits the thermal stability of Arc repressor. J Mol Biol. 1997;273:692–700. doi: 10.1006/jmbi.1997.1342. [DOI] [PubMed] [Google Scholar]
- 29.Kurganov BI, Lyubarev AE, Sanchez-Ruiz JM, Shnyrov VL. Analysis of differential scanning calorimetry data for proteins. Criteria of validity of one-step mechanism of irreversible protein denaturation. Biophys Chem. 1997;69:125–135. doi: 10.1016/s0301-4622(97)80552-2. [DOI] [PubMed] [Google Scholar]
- 30.Sturtevant JM. Biochemical applications of differential scanning calorimetry. Annu Rev Phys Chem. 1987;38:463–488. [Google Scholar]
- 31.Uversky VN, Fink AL. The chicken-egg scenario of protein folding revisited. FEBS Lett. 2002;515:79–83. doi: 10.1016/s0014-5793(02)02441-9. [DOI] [PubMed] [Google Scholar]
- 32.Hilser VJ, Gomez J, Freire E. The enthalpy change in protein folding and binding: refinement of parameters for structure-based calculations. Proteins. 1996;26:123–133. doi: 10.1002/(SICI)1097-0134(199610)26:2<123::AID-PROT2>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- 33.Myers JK, Pace CN, Scholtz JM. Denaturant m values and heat capacity changes: relation to changes in accessible surface areas of protein unfolding. Protein Sci. 1995;4:2138–2148. doi: 10.1002/pro.5560041020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Pace CN, Vajdos F, Fee L, Grimsley G, Gray T. How to measure and predict the molar absorption coefficient of a protein. Protein Sci. 1995;4:2411–2423. doi: 10.1002/pro.5560041120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Edelhoch H. Spectroscopic determination of tryptophan and tyrosine in proteins. Biochemistry. 1967;6:1948–1954. doi: 10.1021/bi00859a010. [DOI] [PubMed] [Google Scholar]


