On the nature of the light produced within PMMA optical light guides in scintillation fiber-optic dosimetry

Abstract

The goal of this study was to evaluate the nature of the stem effect light produced within an optical fiber, to quantify its composition, and to evaluate the efficiency of the chromatic technique to remove the stem effect. Spectrometry studies were performed during irradiations of a bare PMMA optical fiber with kilovoltage x-rays from a superficial therapy unit, an Ir-192 high-dose-rate brachytherapy source, a Co-60 external-therapy unit, and megavoltage electrons and x-rays from a linear accelerator. Stem effect spectra can be accurately modeled by a linear combination of the Cerenkov light and fluorescence emitted spectra. Fluorescence light contributes more for lower-energy modalities. Cerenkov light contributes more as the energy increases above the threshold for its production. The chromatic stem effect removal technique is accurate in most of the situations. However, noticeable differences were obtained between very specific high-energy irradiation conditions. It would be advantageous to implement an additional channel in the chromatic stem effect removal chain or implement a spectral approach to independently remove the Cerenkov and the fluorescence components from the signal of interest. This would increase the accuracy and versatility of the actual chromatic stem effect removal technique.

1. Introduction

It has been well established that accuracy in scintillation fiber-optic dosimetry depends on removal of spurious light components from the signal of interest (Archambault et al., 2006; Beddar et al., 1989; Beddar et al., 1992a, 1992b, 1992c; Clift et al., 2002; De Boer et al., 1993; Fluhs et al., 1996; Fontbonne et al., 2002; Létourneau et al., 1999; Marckmann et al., 2006; Therriault-Proulx et al., 2011a). Beddar et al. (1989) first showed that light generated in a transparent medium by high-energy photon and electron beams during radiotherapy is mainly due to the Cerenkov effect. Cerenkov light is produced only when electrons have energy greater than the threshold energy of the transparent medium they pass in. In scintillation fiber-optic detectors, the most important transparent medium is the optical fiber guide, which transmits light from the scintillation component to the photodetector. For most types of optical fibers used in scintillation detectors, the threshold energy is between 100 keV and 200 keV (Beddar et al., 1992a). In the case of polymethyl-methacrylate (PMMA) fiber, an optical fiber widely used in scintillation dosimetry, the threshold energy is ~178 keV.

The term “stem effect” was introduced by Beddar et al. (1992a) to refer to Cerenkov light as well as any other spurious light produced in the optical fiber of a scintillation fiber-optic detector. De Boer et al. (1993) showed that, under certain irradiation conditions, the stem effect generated in a silica fiber was composed of Cerenkov light and another component called fluorescence. Fluorescence was shown to be produced at any (non–threshold specific) energy. Since the Cerenkov component was shown to be dominant during high-energy irradiation, most studies related to the stem effect have focused on the characteristics of Cerenkov light and on its removal during plastic scintillation dosimetry (Archambault et al., 2006; Beddar et al., 1989; Beddar et al., 1992; De Boer et al., 1993; Clift et al., 2002; Fontbonne et al., 2002; Lambert et al., 2008). Nowotny (2007) examined the characteristics of the fluorescence component for development of a scintillation fiber-optic detector for lower-energy applications and found that PMMA fibers had the lowest fluorescence yield of the tested commercial optical fibers.

Various techniques have been proposed for removing all of the stem effect or its dominant component from the signal of interest (Archambault et al., 2006; Beddar et al., 1992a, 1992b; Clift et al., 2002; Lambert et al., 2008). Beddar et al. (1992a) proposed using two optical fibers: one that is not attached to the scintillator, which carries only the background noise, and another that is coupled to the scintillator, which carries the total signal. This method was shown to be accurate when the detector was not placed in high-dose-gradient regions. De Boer et al. (1993) proposed using a single fiber and measuring the light in a specific wavelength window to minimize the stem effect-to-scintillation light ratio. However, as measurable levels of Cerenkov light are emitted over the whole visible light spectrum, this technique only partially removed the stem effect. Clift et al. (2002) proposed using a scintillation component with a slower response than the response produced by the Cerenkov component to temporally discriminate between the two components. This technique required a very fast and accurate photodetector and was limited by the fact that the temporal response of irradiation modalities is not a step function. Fontbonne et al. (2002) introduced the idea of using a chromatic removal technique, which has been shown to be the most convenient and accurate technique for removing the Cerenkov light from the dose signal (Archambault et al., 2006). The technique takes advantage of the fact that scintillation and Cerenkov light have different spectra of emission. The dose can be assessed by measuring the light in two different wavelength regions of the optical spectrum, as follows:

$$d=A\ast M_{\mathit{Green}}+B\ast M_{\mathit{Blue}}$$ (1)

where d is the dose, A and B are calibration factors, and M_Green and M_Blue represent the amount of light in, respectively, the green and blue regions of the optical spectrum. This technique has been shown to be accurate for high-energy electrons and photons, as well as for Ir-192 high-dose-rate (HDR) brachytherapy energies (Archambault et al., 2006; Frelin et al., 2005; Guillot et al., 2011; Therriault-Proulx et al., 2011a). Guillot et al. (2011) reformulated Eq. (1) in such a way that one of the two calibration factors is the ratio of the stem effect in each wavelength window, allowing each factor to be determined independently (see Eqs. (2) and (3)).

$$d=a\ast (M_{\mathit{Green}}-b\ast M_{\mathit{Blue}})$$ (2)

where

$$b=\frac{M_{\mathit{Green},\mathit{stem}}}{M_{\mathit{Blue},\mathit{stem}}}$$ (3)

In theory, the chromatic removal technique performed using either Eq. (1) or Eq. (2) should be effective as long as the relative spectral composition of the stem effect light produced under measurement conditions is similar to the stem effect light produced when the detector was calibrated. Recently, Archambault et al. (2012) proposed a generalized mathematical formalism that allows accounting for more than 2 light-emitting components, which was verified experimentally by Therriault-Proulx et al. (2012) using multi-point plastic scintillation detectors that use a single-fiber collection optical guide. One possibility to account for additional light-emitting components is to go from a bichromatic to a polychromatic approach by adding terms to Eq. (1):

$$d=A\ast M_{\mathit{Green}}+B\ast M_{\mathit{Blue}}+C\ast M_{\mathit{other}}+\dots$$ (4)

Another approach – the spectral approach – is to access and use the output spectrum r from every individual light-emitting element and assume the total light spectrum m to be a linear superposition of these (Archambault et al., 2012; Therriault-Proulx et al., 2012). Therefore, the output spectrum acquired by a suited apparatus (e.g., a spectrometer) is given by:

$$\mathbf{m}={\mathbf{r}}_1{\text{x}}_1+{\mathbf{r}}_2{\text{x}}_2+{\mathbf{r}}_3{\text{x}}_3+\dots$$ (5)

where x_i is the proportionality factor for light-emitting component i, whether it is coming from scintillation or contamination. Dose can be calculated from the value of x_i following a known-dose calibration (d_i,calib.) for which the value of x_i,calib. was also calculated (see Eq. 6), as follows:

$${\text{d}}_{\text{i}}={\text{d}}_{\text{i},\text{calib}.}({\text{x}}_{\text{i}}/{\text{x}}_{\text{i},\text{calib}.})$$ (6)

Since it is known that contamination light has multiple sources, there may be situations where the formalism from Fontbonne et al. (2002) and Guillot et al. (2011) leads to inaccurate dosimetry, particularly when the fluorescence component becomes significant. Thus, a better understanding of the nature of the stem effect produced in optical fibers is needed.

The primary goal of this work was to quantify the composition of the stem effect light produced within an optical fiber for various radiotherapy modalities over a wide range of clinically relevant energies. The hypothesis was that the stem effect could be a linear combination of its components. To discriminate the fluorescence from the Cerenkov light, a spectrometry study was performed. The efficiency of the bichromatic stem effect removal technique was also evaluated.

2. Materials and methods

The light emission response of a PMMA optical fiber (Eska Premier GH-4001, Mitsubishi Rayon Co. Ltd, Tokyo, Japan) was studied under exposure to photon and electron beams of different energies. As already mentioned, the PMMA fiber has been used in various scintillation fiber-optic dosimetry studies (Andersen et al., 2009a, 2009b; Archambault et al., 2010; Beddar et al., 1992a; Fontbonne et al., 2002; Guillot et al., 2011; Marckmann et al., 2006; Nowotny, 2007; Therriault-Proulx et al., 2011a). This fiber is composed of a 0.98-mm-diameter PMMA core with a 0.01-mm polymer cladding surrounded by a 0.6-mm-thick black polyethylene jacket. The fiber used in these experiments was 15 m in length. One end of the fiber was coupled to a SubMiniature version A 905 connector to ensure a precise connection to a spectrograph (Shamrock 163, Andor Technology, Belfast, N. Ireland). Light was diffracted in the spectrograph up to a charge-coupled device camera (CCD iDus, Andor Technology). The imaging area was 26.6 × 6.6 mm², allowing for spectrometry covering a 400-nm wavelength window. Light spectra for a wavelength range of 300–700 nm were obtained, with a spectral resolution of 0.5 nm. The spectrometry setup response was calibrated using a light source with a known spectrum (LS-1 Light Source, Ocean Optics, Inc., Dunedin, FL) illuminating the end of the optical fiber. Gain on each pixel was calculated and adjusted to obtain the actual light spectrum for each spectral measurement.

Table 1 presents the various conditions under which the fiber was irradiated. For each irradiation condition, at least 5 light spectra were acquired as well as 5 background spectra (without irradiation). Median filtering was applied to each set of spectra to remove unwanted noise in the spectra obtained under irradiation. The median of the values obtained from similar spectral acquisitions composed the resulting spectrum. The resulting background spectrum was then subtracted from the resulting signal spectrum. Another median – a sliding one – was also applied to smooth out the obtained spectra.

Table 1.

Radiotherapy modalities and conditions used to irradiate the PMMA fiber

Radiotherapy modality	Model	Energy level	Conditions
Superficial therapy unit	Phillips RT-250	75 kVp 125 kVp 250 kVp	SAD = 36 cm d = 0 cm 15 × 15-cm2 field
Ir-192 HDR brachytherapy source	Nucletron microSelectron V2	Ir-192 spectrum (from 0.136 to 1.06 MeV)	Source-to-fiber distance of 0.5 cm to 5 cm
Co-60 external-beam unit	Theratron TH-780	Co-60 spectrum	SAD = 80 cm d = 0, 1, 2, and 3 cm 10 × 10-cm2 field
Linear accelerator	Siemens PRIMUS	Photons: 6 MV and 15 MV Electrons: 5, 7, 8, 10, 12, and 15 MeV	SAD = 100 cm d = 0, 1, 2, and 3 cm 10 × 10-cm2 field

SAD = source-to-axis distance; d = depth

Based on the spectral approach described previously (see Eq. 5), the assumption was made that the stem effect spectrum (m_Stem) can be expressed as a linear superposition of the Cerenkov and fluorescence spectra (r_Cerenkov and r_Fluo, respectively), as follows:

$${\mathbf{m}}_{\mathbf{Stem}}={\text{x}}_{\text{Cerenkov}}\ast {\mathbf{r}}_{\mathbf{Cerenkov}}+{\text{x}}_{\text{Fluo}}\ast {\mathbf{r}}_{\mathbf{Fluo}}$$ (7)

where x_Cerenkov and x_Fluo are the proportionality factors describing the contribution from each component.

The fluorescence spectrum was defined as the spectrum obtained under irradiation at 75 kVp (an energy where production of the Cerenkov effect is impossible). The spectrum obtained by irradiation with a 15-MeV beam at 45-degree incidence was designated as the “pure” Cerenkov spectrum (Beddar et al., 1992a). Even though it is impossible to prevent production of other sources of spurious light, this experimental setup maximized the Cerenkov production. All the recorded spectra in this study were normalized to the area under the curve to compare their shape and calculate their composition in fluorescence and Cerenkov. The assumption that a stem effect spectrum can be modeled accurately as a linear superposition of the fluorescence and Cerenkov was verified. The coefficient of variation (CV) of the root-mean-square-deviation (RMSD) was used as an indicator of the goodness of fit and is calculated as follows:

$$\mathit{RMSD}=\sqrt{\frac{{\sum }_{i=1}^n{(m_{\mathit{superposition},i}-m_{\mathit{meas},i})}^2}{n}}$$ (8)

$$CV=\frac{\mathit{RMSD}}{\overline{m_{\mathit{meas}}}}$$ (9)

where n is the number of considered wavelengths of the spectrum, and m_{superposition,i} and m_meas,i are values for a specific wavelength of the normalized spectra obtained from the linear superposition and measurement, respectively. $\overline{m_{\mathit{meas}}}$ is the average value of the measured spectrum. In this study, the wavelengths between 400 nm and 700 nm were considered in the calculation and CV was calculated for all the irradiation conditions.

In the present study, the effect on the widely used chromatic removal approach (Eq. 1–3) of a change on the stem effect spectrum was investigated. The impact on calibration coefficient b (see Eq. 3) with increasing contribution of a fluorescence component was calculated. M_Blue,stem and M_Green,stem were calculated as the integration of the spectrum from 400 nm to 500 nm and from 500 nm to 600 nm, respectively. For most irradiations, the incident beam was perpendicular to the optical fiber. However, irradiations with the incident beam at a 45° angle to the optical fiber were also performed to evaluate the fiber’s response in a Cerenkov-dominated situation (Beddar et al., 1992a; Law et al., 2006).

Spectra normalized to dose and fiber length were also obtained for a comparison based on absolute intensity. Dose to the fiber was calculated on the basis of the geometry of the experimental setup, irradiation conditions, and duration of spectral acquisition. For the superficial therapy unit, dose was calculated using previous measurements at a source-to-axis distance of 36 cm and associated backscatter factor for a 15 × 15-cm² field at the 3 energies. For the Ir-192 HDR brachytherapy source, the fiber was placed parallel to the longitudinal axis of the source at a distance of 3 cm. The position of the source was determined by using a X-ray film. The integrated dose to the fiber was obtained from the activity of the source (2.588 × 10¹¹ Bq) and the theoretical data published by Daskalov et al. (1998) using that specific source type. Dose to the fiber from the Co-60 external-beam unit was calculated using the Co-60 source characteristics and assuming a constant off-axis dose deposition. Dose to the fiber from the linear accelerator was calculated using the measured outputs and characteristics of the linear accelerator. A Profiler 2 (Sun Nuclear Corporation, Melbourne, FL) was used to determine the off-axis ratio along the fiber’s position.

The differences between the spectra normalized to dose and fiber length obtained with the linear accelerator were investigated with the help of a simple Monte Carlo study, using BEAMnrc software (Rogers et al., 2009), on the basis of the angular distribution of electrons with depth in water.

3. Results

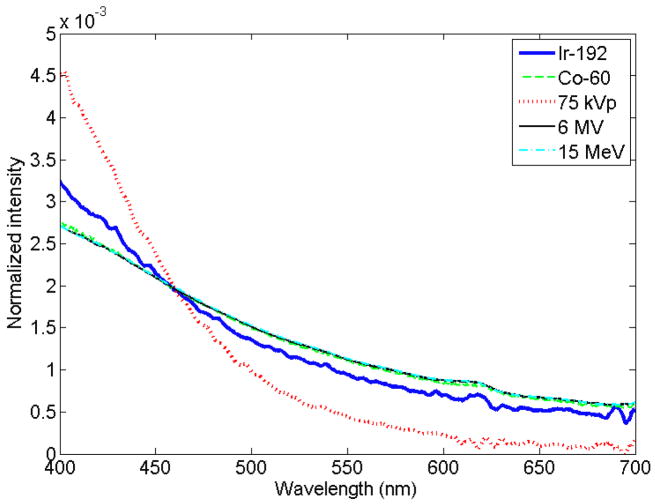
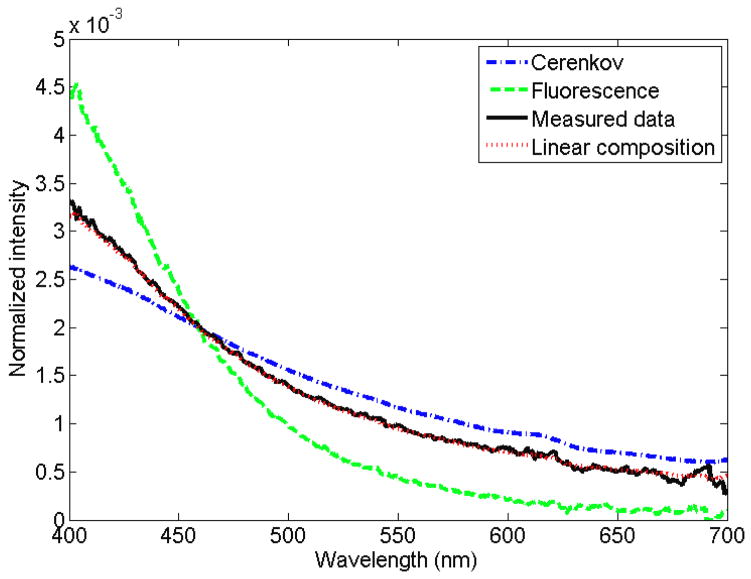
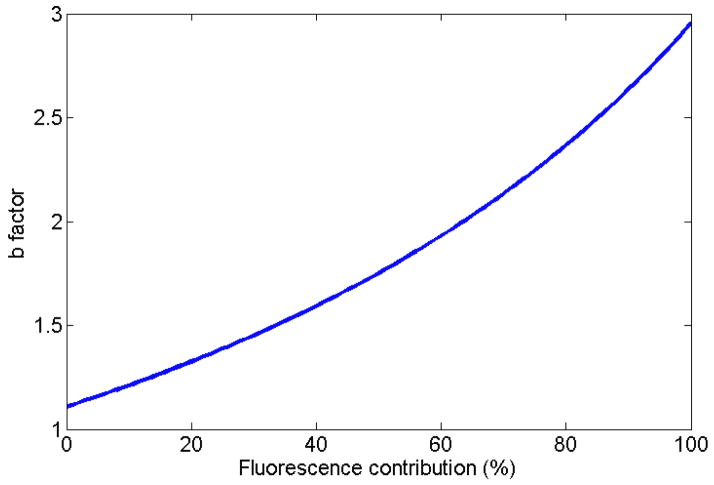
A normalized measured spectrum for each of the irradiation modalities (superficial therapy, Ir-192, Cobalt-60, linear accelerator [Linac]–photon, Linac–electron) is presented in figure 1. An example of the expression of a measured spectrum as a linear superposition of fluorescence and Cerenkov spectra is presented in figure 2, for the specific case of Ir-192 HDR brachytherapy irradiation. It was verified that all of the measured spectra can be accurately represented by a linear superposition of Cerenkov and fluorescence. The average coefficient of variation of the root-mean-square deviation was of (0.8 ± 0.7)% with a maximum of 3.1%. This supports the assumption that a linear superposition can model the stem effect accurately. For a better view of the differences in stem effect composition within and between each modality, a complete compilation is provided in table 2, which gives the contribution of fluorescence for every irradiation performed. The high-energy modalities’ acquired stem effect spectra were mostly composed of light from the Cerenkov effect (94% to 100% contribution), while the fluorescence was more important for Ir-192 HDR brachytherapy (25 ± 2)% and superficial therapy unit irradiations (99 ± 1)%. In order to better understand the impact of a change in the composition of the stem effect on the chromatic removal technique, the variation of the b factor in eqs. (2) and (3) as a function of the fluorescence contribution was studied (see figure 3).

Figure 1.

Relative spectra of light emission from irradiation of a bare fiber with various modalities. Data were normalized to the area under the curve. The Co-60, 6 MV and 15 MeV lines may be hard to distinguish since they lay on top of each other.

Figure 2.

Expression of the Ir-192 light spectrum through a linear superposition of the Cerenkov (15 MeV, at 45°) and fluorescence (75 kVp) normalized spectra.

Table 2.

Relative contribution of fluorescence to the stem effect light for different irradiation modalities, energies, and depths in the phantom.

Linear accelerator
	0cm	1cm	2cm	3cm	0cm, 45deg
6 MV	(4.03 ± 0.14)%	(3.51 ± 0.07)%	(3.45 ± 0.02)%	(3.51 ± 0.08)%	(1.37 ± 1.24)%
15 MV	(3.22 ± 0.11)%	(3.10 ± 0.06)%	(3.01 ± 0.05)%	(3.00 ± 0.04)%	(1.10 ± 1.14)%
5 MeV	(6.42 ± 0.55)%	(2.43 ± 0.03)%	(2.70 ± 0.06)%	(2.61 ± 0.17)%	(0.14 ± 0.02)%
7 MeV	(6.42 ± 0.14)%	(3.21 ± 0.04)%	(2.33 ± 0.02)%	(2.79 ± 0.08)%	(0.04 ± 0.01)%
8 MeV	(6.23 ± 0.12)%	(3.86 ± 0.20)%	(2.54 ± 0.03)%	(2.37 ± 0.08)%	(0.04 ± 0.01)%
10 MeV	(6.43 ± 0.14)%	(4.39 ± 0.13)%	(2.84 ± 0.04)%	(2.32 ± 0.06)%	(0.04 ± 0.01)%
12 MeV	(5.74 ± 0.07)%	(4.66 ± 0.14)%	(3.54 ± 0.04)%	(2.58 ± 0.04)%	(0.00 ± 0.01)%
15 MeV	(5.09 ± 0.02)%	(4.52 ± 0.17)%	(3.86 ± 0.02)%	(3.05 ± 0.06)%	(0.00 ± 0.00)%

Cobalt-60		Superficial therapy		Ir-192
0 cm	(5.65 ± 0.73)%	75 kVp	(100.00 ± 2.09)%	1 cm	(24.60 ± 2.37)%
1 cm	(5.88 ± 0.22)%	125 kVp	(98.99 ± 2.28)%	2 cm	(22.74 ± 1.66)%
2 cm	(5.80 ± 0.10)%	250 kVp	(98.28 ± 0.42)%	3 cm	(24.88 ± 3.05)%
0 cm, 45°	(2.67 ± 0.04)%	250 kVp, 45°	(97.69 ± 0.50)%	5 cm	(28.71 ± 4.96)%
2 cm, 45°	(2.93 ± 0.12)%			3 cm, 90°	(23.95 ± 3.98)%

Figure 3.

Effect on the b factor (see Eq. 3) of a change in the composition in fluorescence of a stem effect spectrum.

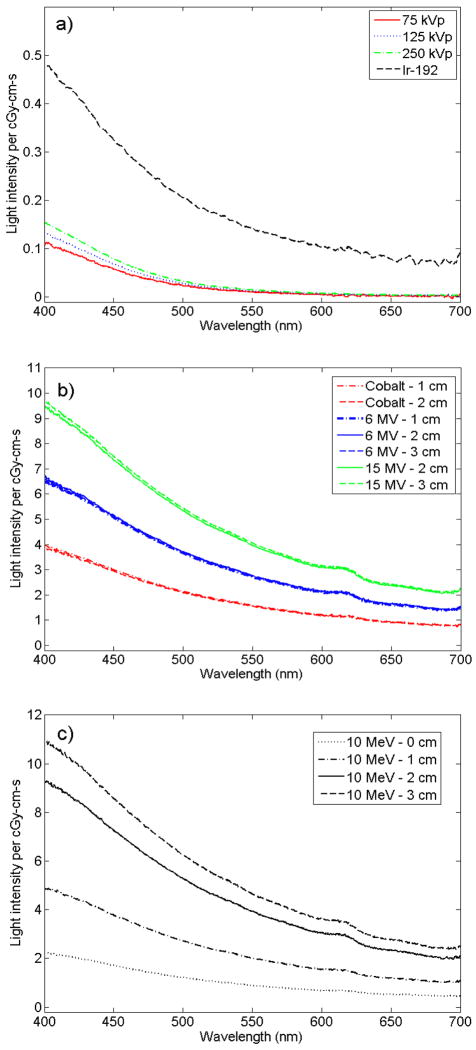
The dose and fiber length–normalized spectra revealed additional physical information about the stem effect light produced. The spectra measured using 75-kVp, 125-kVp, and 250-kVp beams as well as with the Ir-192 HDR source showed different intensities, with a higher response at higher energies (figure 4a). Also, the spectra obtained from irradiation with Co-60, 6-MV, and 15-MV beams differed from each other (figure 4b). However, the spectra obtained at each of these energies did not change much with depth. In contrast to this, the electron beams showed important differences in light measured for different depths (figure 4c). These results are discussed on the basis of difference in electron angular distributions with depth in water for different high-energy beams. These were obtained from Monte Carlo simulations and are presented in figure 5. The main result from the simulation is that electrons were scattered more widely as the depth increased for the electron beam, but the increase in scattering was not as notable for the photon beam.

Figure 4.

Dose- and fiber length–normalized spectra of light emission per cGy-cm-s from irradiation of a bare fiber with a) the Ir-192 HDR source and superficial therapy unit, b) the linear accelerator photon as well as the Co-60 beam, or c) the linear accelerator electron beam.

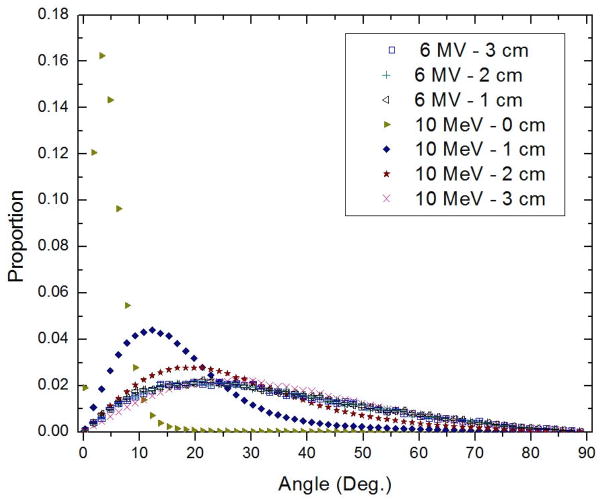
Figure 5.

Angular distribution of electrons crossing a plane at different depths for a 6-MV photon beam and a 10-MeV electron beam, with a source-to-axis distance of 100 cm. Data were obtained from a Monte Carlo simulation using the BEAMnrc code.

4. Discussion

The findings of this study show that the stem effect light can be expressed as a linear combination of Cerenkov light and fluorescence. The fluorescence component produced in optical light guides was shown to be present over the entire range of clinically relevant irradiation energies, including megavoltage energies. Irradiations with 12-MeV and 15-MeV electron beams at a 45-degree angle to the fiber showed the smallest fluorescence contributions. This was expected since they correspond to enhanced Cerenkov production conditions, where a large proportion of the Cerenkov light is coupled and transmitted along the optical fiber (Beddar et al., 1992a; Law et al., 2006). Differences between irradiations at high energy with the optical fiber at the surface and with the optical fiber at a deeper position can be explained by a difference in the contribution of scattered particles, leading to differences in the amount of Cerenkov light that will be successfully transmitted along the optical fiber. At the surface, most of the electrons depositing dose will be created following the beam line and are unlikely to be coupled in the optical fiber, thereby decreasing the Cerenkov contribution. This explanation is supported by the Monte Carlo results shown in figure 5. The widening of the distribution of electron angles and movement of the peak of the distribution toward a higher angle for the electron beam resulted in an increase of Cerenkov light transmitted to the fiber with depth, as previously explained by Beddar et al. (1992a).

The 250-kVp beam was the only one of the 3 beam outputs from the superficial therapy unit that produced a small amount of Cerenkov. This makes sense considering that this was the only beam with a part of its energy spectrum over the threshold for Cerenkov production in PMMA (~178 keV). However, as shown in figure 4a, removing the stem effect is not the only challenge for low-energy dosimetry. The difference in light emission spectra per dose and fiber length for different energy spectra indicates that the energy mass attenuation coefficient cannot be considered constant for the kV energies investigated (Lessard et al., 2012).

The spectral composition obtained by irradiation with an Ir-192 HDR source did not differ much with different source-to-fiber radial distances. This is a modality for which contributions from both fluorescence and Cerenkov are far from negligible. However, the intensity of the spectral light emitted per cGy-cm-s is low, and the ratio of fluorescence and Cerenkov are relatively constant over various conditions when taking into account the uncertainties. The latter actually explain why accurate measurements were obtained in a previous phantom dosimetry study during Ir-192 HDR brachytherapy using a plastic scintillation detector (Therriault-Proulx et al., 2011b).

The presence of more than one stem effect component does not necessarily invalidate the current chromatic technique (Eqs. 1 and 2) used for stem effect removal. Indeed, it is the variation in the stem effect spectrum between the calibration conditions and the measurement conditions that defines the accuracy of the chromatic technique for stem effect removal. The effect of a change in the stem effect composition on factor b was illustrated in the Results section (see figure 3). In this study, the b factor was shown to vary proportionally with the fluorescence contribution at a rate of about 1% per percent for contributions ranging from 0% to 40%.

For the case of a 7-MeV beam, if the b factor calibration was performed at 0-cm depth and 45-degree irradiation angle, and the detector happened to be used at 0-degree angle for the same 0-cm depth, there would then be an overcompensation for the stem effect, resulting in 6% more signal removed by the second term of Eq. (2). Therefore, it is very important to carefully choose the calibration conditions and the modality to use for calibration.

These results show that, for Ir-192 HDR brachytherapy, it is very important to calibrate the fiber detector using the same irradiation modality since using another modality would lead to discrepancies in the b factor determination of at least 20%. Similarly, for measurements using the superficial therapy unit, it is recommended that the calibration be performed using the same modality.

However, this is not as straightforward for high-energy modalities (Co-60, Linac-photons, Linac-electrons). It may sometime be more convenient or more precise to calibrate the detector using one modality and then use the detector for another modality. If a Linac 6-MV beam was used for calibration (at a depth of 1 cm, 2 cm, or 3 cm), the measurement under perpendicular irradiation at any other energy or beam type (photon or electron) using a Linac would suffer only a 1.1% maximum difference. However, there could be situations (fiber at the surface, or irradiation at a different angle) where that difference would be higher. According to the present measurements, a calibration at 2-cm depth under Co-60 irradiation (fluorescence contribution = (5.80 ± 0.10)%) would lead to a difference in the b factor calculation of about 2.3% for its use at 6 MV in electronic equilibrium conditions (fluorescence contribution = (3.49 ± 0.03)%). It would definitely be better to perform the determination of the b factor using the same modality, but it is important to keep in mind that a 2% error on the b factor calculation does not necessarily imply a 2% error on each dose measurement. The relative error on dose measurement can be deduced from (2) and is given by:

$$\text{Rel}.\text{dose}\text{error}=[{\text{E}}_{\text{b}}\ast {\text{b}}_{\text{theo}}\ast {\text{M}}_{\text{Blue}}]/[{\text{M}}_{\text{Green}}-{\text{b}}_{\text{theo}}\ast {\text{M}}_{\text{Blue}}]$$ (10)

where E_b is the relative error on b and b_theo is the theoretical value for b. The impact on the dose measurement accuracy then also depends on the irradiation conditions as well as on the spectrum of the scintillating element used.

Archambault et al. (2006) showed that the chromatic technique was one of the most robust techniques for removing the stem effect. Implementing additional precautions over the choice of calibration conditions would improve the accuracy of this technique. However, to ensure even better versatility and accuracy, an additional term could be added, as proposed previously (see Eq. 4) (Archambault et al., 2012). This expanded chromatic technique would alleviate the need for consistency of the proportion of fluorescence and Cerenkov in the stem effect spectrum between the calibration and measurement conditions. Once calibrated, the detector could be used for a wide variety of irradiation conditions, energies, and modalities. Implementing a spectral approach would also be valid. A simpler version of this technique was actually used in this study to characterize the relative amount of Cerenkov and fluorescence in the stem effect (see Eq. 7). One advantage of this technique is that each term in the equation accounts for the different light-emitting components individually.

5. Conclusion

Removing the stem effect light from the signal of interest is one of the main challenges in scintillation fiber-optic dosimetry. In this study, it was shown that the stem effect light generated in a PMMA fiber can realistically be modeled as a linear superposition of Cerenkov and fluorescence light. The proportion of fluorescence and Cerenkov light induced in the fiber decreases as the irradiation energy increases. We showed that the fluorescence component, even if smaller than the Cerenkov component, is non-negligible at higher energies. The consistency between Cerenkov and fluorescence light during calibration and dosimetry conditions affects the accuracy of the chromatic removal technique. The addition of a third term to the actual dose determination equation from the chromatic technique or the implementation of a spectral approach would remove the requirement for such consistency. This would, in turn, increase the versatility and robustness of an already accurate stem effect removal.