THE SCREENING AND RANKING ALGORITHM TO DETECT DNA COPY NUMBER VARIATIONS

Abstract

DNA Copy number variation (CNV) has recently gained considerable interest as a source of genetic variation that likely influences phenotypic differences. Many statistical and computational methods have been proposed and applied to detect CNVs based on data that generated by genome analysis platforms. However, most algorithms are computationally intensive with complexity at least O(n²), where n is the number of probes in the experiments. Moreover, the theoretical properties of those existing methods are not well understood. A faster and better characterized algorithm is desirable for the ultra high throughput data. In this study, we propose the Screening and Ranking algorithm (SaRa) which can detect CNVs fast and accurately with complexity down to O(n). In addition, we characterize theoretical properties and present numerical analysis for our algorithm.

1. Introduction

The problem of change-points detection has been studied by researchers in various fields including statisticians, engineers, economists, climatologists and biostatisticians since 1950s. We refer to Bhattacharya (1994) for an overview of this subject. In this paper, we focus on a high dimensional sparse normal mean model

$$Y_i={\mu }_i+{\epsilon }_i,1\le i\le n,$$ (1.1)

where Y = (Y₁, …, Y_n)^T is a sequence of random variables, its mean μ = (μ₁, …, μ_n)^T is a piecewise constant vector and the errors ε_i are i.i.d. ~ N(0,σ²). A change-point in this model is a position τ such that μ_τ ≠ μ_τ+1. Assume that there are J change-points 0 < τ₁ < … < τ_J < n. We are interested in the case when n is large, and J is small. The goal is to estimate the number of change-points, J, and the location vector τ = (τ₁, …, τ_J)^T. Note that all positions are potential candidates for a change-point, which makes the problem high dimensional and hard to solve. However, the small J implies the sparse structure of the model, which we can utilize to develop fast and efficient algorithms.

1.1. Background

The main motivation of this project is to develop efficient statistical techniques for DNA copy number variation (CNV) detection, for which model (1.1) plays an important role, for example, Olshen et al. (2004), Huang et al. (2005), Zhang and Siegmund (2007), Tibshirani and Wang (2008), among others. The DNA copy number of a region is the number of copies of the genomic DNA. CNV usually refers to deletion or duplication of a region of DNA sequences compared to a reference genome assembly. Recent studies in genetics have shown that CNVs account for a substantial amount of genetic variation and provide new insights in disease association studies [Freeman et al. (2006), McCarroll and Altshuler (2007)]. Identification of CNVs is essential in the systematic studies of understanding the role of CNV in human diseases. Over the last decade, efforts have been made to detect DNA copy number variation with the help of significant advances in DNA array technology, including array comparative genomic hybridization (aCGH), single nucleotide polymorphism (SNP) genotyping platforms, and next-generation sequencing. We refer to Zhang et al. (2009) for a nice review of these technologies. These various platforms and techniques have provided a large amount of data that are rich in structure, motivating new statistical methods for their analysis.

1.2. Current segmentation methods

Historically, the case that there is at most one change-point in model (1.1) has been intensively studied. See Sen and Srivastava (1975), James, James and Siegmund (1987), among others. The problem of single change-point detection is equivalent to the following hypothesis testing problem:

$$\begin{array}{cc}\hfill H_0:{\mu }_1& =\cdots ={\mu }_n,\text{against},\hfill \\ \hfill H_1:{\mu }_1& =\cdots ={\mu }_j\ne {\mu }_{j+1}=\cdots ={\mu }_n\text{for some}j.\hfill \end{array}$$ (1.2)

Let S_k be the partial sum of observations ${\sum }_{i=1}^k{Y}_i$. WhenVar(Y_i) is known, a commonly used test statistic is the log likelihood ratio statistic

$$T_n=\underset{1\le j\le n-1}{\text{max}}\left\{{(j{S}_n∕n-S_j)}^2\left[j(1-j∕n)\right]\right\}.$$ (1.3)

The log likelihood ratio test is usually satisfactory although the distribution of T_n is quite complicated. We refer to CsörgŐ and Horváth (1997) for the theoretical analysis of the log likelihood ratio test.

When there are multiple change-points, the problem is much more complicated. Here we briefly review several popular approaches, including an exhaustive search with the Schwarz criterion [Yao (1988), Yao and Au (1989)], the circular binary segmentation method [Olshen et al. (2004), Venkatraman and Olshen (2007)] and the ℓ₁ penalization method [Huang et al. (2005), Tibshirani et al. (2005), Tibshirani and Wang (2008)].

To estimate J and τ, an exhaustive search among all possibilities $0\le \tilde{J}\le n-1$ and $0<{\tilde{\tau }}_1<\cdots <{\tilde{\tau }}_{\tilde{J}}<n$ can be applied, theoretically. Let $\tilde{\tau }={({\tilde{\tau }}_1,\dots ,{\tilde{\tau }}_{\tilde{J}})}^T$. For each candidate $(\tilde{J},\tilde{\tau })$, the MLE for the variance, ${{\widehat{\sigma }}^2}_{(\tilde{J},\tilde{\tau })}$, can be calculated by the least squares method. Yao (1988), Yao and Au (1989) applied the Schwarz criterion, or the Bayesian Information Criterion (BIC), to estimate the number and locations of change-points and showed the consistency of the estimate. In particular, the number of change-points is estimated as

$$\widehat{J}=\underset{\tilde{J}}{\text{argmin}}\frac{n}{2}\text{log}{\widehat{\sigma }}_{\tilde{J}}^2+\tilde{J}\text{log}n\text{where}{\widehat{\sigma }}_{\tilde{J}}^2=\underset{\tilde{\tau }}{\text{min}}{\widehat{\sigma }}_{(\tilde{J},\tilde{\tau })}^2.$$ (1.4)

Once $\widehat{J}$ is determined, the location estimator is defined as

$$\widehat{\tau }=\underset{\tilde{\tau }}{\text{argmin}}{\widehat{\sigma }}_{(\widehat{J},\tilde{\tau })}^2.$$

Unfortunately, when n is large, these estimators are not attainable due to the computational complexity. Braun, Braun and Müller (2000) employed a dynamic programming algorithm to reduce the computational burden to the order of O(n²). But it is still computationally expensive for large n.

An alternative approach is through the binary segmentation method, which applies the single change-point test recursively to determine all the change-points. As pointed out in Olshen et al. (2004), one of the drawbacks is that the binary segmentation can hardly detect small segments buried in larger ones. To overcome this problem, Olshen et al. (2004) introduced a Circular Binary Segmentation (CBS) method and applied it for CNV detection. Lai et al. (2005) compared 11 algorithms on the segmentation in array CGH data and reported that CBS is one of the best. However, they found that CBS was also one of the slowest algorithms. The computational complexity of these recursive algorithms are at least O(n²). Venkatraman and Olshen (2007) proposed a faster CBS algorithm by setting an early stopping rule. The improved algorithm works much faster in practice without loss of much accuracy.

Another alternative to exhaustive searching is the ℓ₁ penalization approach. Huang et al. (2005) studied the change-points detection problem via the following optimization problem:

$$\text{minimize}\parallel \mathbf{Y}-\mu {\parallel }^2\text{subject to}\sum _j\mid {\mu }_j-{\mu }_{j+1}\mid \le s.$$ (1.5)

Tibshirani and Wang (2008) applied the fused lasso [Tibshirani et al. (2005)] for change-points detection, which

$$\text{minimizes}\parallel \mathbf{Y}-\mu {\parallel }^2\text{subject to}\sum _j\mid {\mu }_j\mid \le s_1,\sum _j\mid {\mu }_j-{\mu }_{j+1}\mid \le s_2.$$

They added one more constraint since they assume that μ itself is a sparse vector.

In fact, the simpler one of the above two, that is, (1.5), is equivalent to the lasso after a reparametrization ξ_j = μ_j+1 − μ_j, j = 1, …, n − 1. The complexity of the fastest algorithm to solve the lasso is at least O(n²) [Friedman et al. (2007)]. See also recent developments on the fused lasso [Rinaldo (2009), Hoefling (2010), Zhang et al. (2010), Tibshirani and Taylor (2011)].

We consider all aforementioned methods as global methods, in the sense that they use all data points repeatedly in the process of determining change-points. Consequently, the algorithms are usually computationally expensive. To the best of our knowledge, the algorithms for the change-point detection that possess consistency properties have the computational complexities in the order of O(n²) or higher, although there are other algorithms that are shown to be fast numerically but whose theoretical properties in consistency and computational complexities are not well understood. As pointed out in Braun, Braun and Müller (2000), the construction of efficient O(n) algorithms which scale up to large sequences remains to be an important research topic.

Last but not least, it is worth mentioning that the PennCNV [Wang et al. (2007)] is a fast and efficient algorithm to detect CNVs, although it is based on a different model from (1.1).

1.3. An approach via local information

To detect the change-points, we need to examine the sequence both globally and locally. Heuristically, there should exist a neighborhood around a change-point that contains sufficient information to detect the change-point. For instance, it is unlikely for the value of Y_10,000 to contribute much information for detecting a change-point around the position 100. Therefore, global methods mentioned in the last subsection may not be efficient. By focusing on a local region, we can reduce the computational burden, especially when the data set is huge. Based on this philosophy, we propose the Screening and Ranking algorithm (SaRa), which is a powerful change-point detection tool with computational complexity down to O(n).

Roughly speaking, the idea is to find a locally defined diagnostic measure D to reflect the probability of a position being a change-point. By calculating the measure D for all positions, which we call the screening step, and then ranking, we can quickly find a list of candidates that are most likely to be the change-points. In fact, such diagnostic measures have been proposed and used in related literature, for example, Yin (1988), Gijbels, Hall and Kneip (1999). For example, at a point of interest x, a simple diagnostic function is the difference of the average among observations on the left-hand side and the right-hand side, that is, $D\left(x\right)={\sum }_{t=1}^h{Y}_{j+1-t}∕h-{\sum }_{t=1}^h{Y}_{j+t}∕h$. The larger |D(x)| is, the more likely that x is a change-point. Note that, to calculate D(x), we need only the data points near the position x. Therefore, the strategy through a local statistic can save a lot of time, compared to global methods. Moreover, we will show that this fast algorithm is also accurate by theoretical and numerical studies. In particular, the SaRa satisfies the sure coverage property, which is slightly stronger than model consistency.

To summarize, the local methods are usually more efficient than global ones to solve the change-points problem for high-throughput sequencing data, and it is feasible to evaluate their computational and asymptotic properties. With these merits, we believe the local methods have been under utilized and deserve more attention and development in solving change-points problems.

This paper is organized as follows. In Section 2 we introduce the screening and ranking algorithm to solve the change-points problem (1.1). In Section 3 we study the theoretical properties of the SaRa and show that it satisfies the sure coverage property. Numerical studies are illustrated in Section 4. Proofs of theorems and lemmas are presented in the supplementary material [Niu and Zhang (2012)].

2. The screening and ranking algorithm

2.1. model (1.1) revisited

In model (1.1), assume the mean of each variable in the j th segment is β_j, that is, μ_i = β_j, for all integers i ∈ (τ_j, τ_j+1. For clarity, the errors ε_i are assumed to be i.i.d. N(0,σ²) as before, although the normality may be relaxed. Note that in some of the existing work, the step function μ is defined as a left-continuous function on unit interval [0, 1], and change-points 0 < t₁ < … < t_J < 1 are discontinuities of μ(x). Two notations are consistent with convention $\mu \left(\frac{i}{n}\right)={\mu }_i$ and t_j = τ_j/n.

For 0 ≤ J < ∞, we refer to the Gaussian model (1.1) with J change-points as ${\mathcal{M}}_J$. After a reparameterization of ${\beta }_j={\beta }_0+{\sum }_{l=1}^j{\delta }_l$, that is, δ_j = β_j − β_j−1, J = 1, …, J, model ${\mathcal{M}}_J$ has parameters

$$\theta =({\beta }_0,{\delta }_1,\dots ,{\delta }_J,{\tau }_1,\dots ,{\tau }_J,{\sigma }^2)$$

to be determined. Let τ = (τ₁,…, τ_n) and = δ = (δ₁,…, δ_n) be the change-points location vector jump-size vector, respectively. The purpose is to estimate J as well as the model parameter vector θ. Since n is large and J ≪ n, the variance σ², or an upper bound of σ², can be easily estimated. Once J and τ are well estimated, β₀ and δ can be estimated by the least squares method. In short, the main task is to estimate the number of change-points J and the location vector τ.

Roughly speaking, to detect the change-points in model (1.1), the SaRa proceeds as follows. In the screening step, we calculate at each point x a local diagnostic function D(x) which depends only on the observations in a small neighborhood [x − h, x + h]. In the ranking step, we rank the local maximum of the function |D(x)| and the top $\widehat{J}$ points ${\widehat{\tau }}_1,\dots ,{\widehat{\tau }}_{\widehat{J}}$ will be the estimated change-points, where $\widehat{J}$ can be determined by a thresholding rule or Bayesian information criterion.

In the following subsections, we describe the SaRa in detail.

2.2. Local diagnostic functions

We begin with the local diagnostic function which is crucial in the SaRa. Roughly speaking, an ideal local diagnostic statistic at a position, say, x, is a statistic whose value directly related to the possibility that x is a change-point. For model (1.1), we first introduce two simple examples of a local diagnostic statistic.

An obvious choice is $D\left(x\right)={\sum }_{k=1}^h{Y}_{x+1-k}∕h-{\sum }_{k=1}^h{Y}_{x+k}∕h$, for a fixed integer h [Yin (1988)]. It is simply the difference between averages of h data points on the left side and right side of x. Heuristically, consider the noiseless case in which Y = μ is a piecewise constant vector. D(x) is simply a piecewise linear function, whose local optimizers correspond to the true change-points. Obviously, the quantity of D(x) reflects the probability that x is, or is near to, a change-point.

An alternative choice is the “local linear estimator of the first derivative,” studied in Gijbels, Hall and Kneip (1999). Intuitively, if we use a smooth curve to approximate the true step function μ, the first derivative or slope of the approximation curve should be large around a change-point and near zero elsewhere. The approximation curve as well as its first derivative can be calculated easily by local polynomial techniques. Therefore, a local linear estimator of the first derivative is a reasonable choice for the local diagnostic statistic.

In both examples above, the local diagnostic statistics are calculated as linear transformations of data points around the position of interest. We may consider a more general form of local diagnostic functions, which is the weighted average of Y_i's near the point of interest x,

$$D(x,h)=\sum _{i=1}^n{w}_i\left(x\right)Y_i,$$

where the weight function w_i(x) = 0 when |i − x| > h.

In the first example, we have

$$w_i\left(x\right)=\{\begin{array}{cc}1∕h,\hfill & 1-h\le i-x\le 0,\hfill \\ -1∕h,\hfill & 1\le i-x\le h,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$ (2.1)

To present the weight vector in a kernel, K(u), the weight can be chosen as $w_i\left(x\right)=\mathrm{sgn}(x+\frac{1}{2}-i)\cdot K_h(i-x)$, where K_h(u) = h⁻¹ K(u/h). The equal-weight case (2.1) is a special case corresponding to the uniform kernel $K\left(u\right)=\frac{1}{2}\cdot 1_{\{\mid u\mid \le 1\}}$.

For the second example, at the point of interest x, the local linear estimator of the first derivative is

$$D(x,h)=\sum _{i=1}^n{w}_i{Y}_i,$$

, where $w_i=\frac{1}{S_{n,0}{S}_{n,2}-S_{n,1}^2}{K}_h(i-x)[S_{n,0}(i-x)-S_{n,1}]$, and $S_{n,l}={\sum }_{i=1}^n{K}_h(i-x){(i-x)}^l,l=0,1,2$. Note that this is simply the local linear estimator for the first derivative with kernel K(u) and bandwidth h. See Fan and Gijbels (1996) or Gijbels, Hall and Kneip (1999). In the supplementary material [Niu and Zhang (2012)], a class of more general local diagnostic statistics is introduced.

In all numerical studies within this paper, we use only the equal-weight diagnostic function (2.1) for properly chosen h, because of the piecewise constant structure of the mean μ. In Section 2.5 we discuss the choices of weight and bandwidth in detail. From now on, we denote the diagnostic function by D(x, h) when h is specified. When the context is clear, we may simply use D(x).

2.3. The screening and ranking algorithm

Given an integer h, the local diagnostic function D(x, h) can be calculated easily. Obviously, a large value of |D(x, h)| implies a high probability of x being or neighboring a change-point. Therefore, it is reasonable to find and rank the local maximizers of |D(x, h)|. To be precise, we first define the h-local maximizer of a function as follows.

Definition. For any number x, the interval (x − h, x + h) is called the h-neighborhood of x. And, x is an h-local maximizer of function f(·) if f reaches the maximum at x within the h-neighborhood of x. In other words,

$$f\left(x\right)\ge f(x\prime )\text{for all}x\prime \in (x-h,x+h).$$

.

Since we always consider the h-local maximizer of |D(x, h)|, we may omit h when the context is clear. Let $\mathcal{LM}$ be the set of all local maximizers of the function |D(x, h)|. We select a subset $\widehat{\mathcal{J}}=\{{\widehat{\tau }}_1<{\widehat{\tau }}_2<\cdots <{\widehat{\tau }}_{\widehat{J}}\}\subset \mathcal{LM}$ by a thresholding rule

$$\mid D(\widehat{\tau },h)\mid >\lambda .$$ (2.2)

.

The index set, $\widehat{\mathcal{J}}$, and $\widehat{J}$ are the SaRa estimators for the locations and the number of change-points, respectively. A choice of the threshold λ by asymptotic analysis is given in Section 3. An alternative way to determine $\widehat{J}$ is by a Bayesian-type information criterion [Yao (1988), Zhang and Siegmund (2007)]. By ranking local maximizers of |D(x)|, we get a sequence x₁, x₂,… with |D(x₁)| > |D(x₂)| > … Plugging the first $\tilde{J}$ x_i's into

$$\text{BIC}\left(\tilde{J}\right)=\frac{n}{2}\text{log}{\widehat{\sigma }}_{\tilde{J}}^2+\tilde{J}\text{log}n,$$

, where ${\widehat{\sigma }}_{\tilde{J}}^2$ is the MLE of the variance assuming $x_1,\dots ,x_{\tilde{J}}$ are change-points. Then $\widehat{J}=\mathrm{argmin}\mathrm{BIC}\left(\tilde{J}\right)$ is the estimate for the number of change-points and $({\widehat{\tau }}_1,\dots ,{\widehat{\tau }}_{\widehat{J}})=(x_{\left(1\right)},\dots ,x_{\left(\widehat{J}\right)})$ is the estimate for the location vector, where x(·) are the order statistics of $x_1,\dots ,x_{\widehat{J}}$. The procedure for the modified BIC, proposed in Zhang and Siegmund (2007), is the same as the BIC except using

$$m\text{BIC}\left(\tilde{J}\right)=\frac{n}{2}\text{log}{\widehat{\sigma }}_{\tilde{J}}^2+\frac{3}{2}\tilde{J}\text{log}n+\frac{1}{2}\sum _{i=1}^{\tilde{J}+1}\text{log}(x_{\left(i\right)}∕n-x_{(i-1)}∕n),$$

, where $x_{\left(0\right)}=0\text{and}{x}_{(\tilde{J}+1)}=n$.

2.4. Computational complexity

One of the advantages of the SaRa is its computational efficiency. To calculate the SaRa estimator, there are three steps: calculate local diagnostic function D, find its local maximizers, and rank the local maximizers. For the equal-weight case, it takes O(n) operations to calculate D, thanks to the recursive formula

$$D_h(x+1)=D_h\left(x\right)+(2Y_{x+1}-Y_{x-h+1}-Y_{x+h+1})∕h.$$

. Moreover, 2n comparisons are sufficient to find local maximizers of D. Note that there are at most n/h of h-local maximizers by definition, which implies that only $O\left(\frac{n}{h}\text{log}\frac{n}{h}\right)$ operations are needed to rank these local maximizers. As h is suggested to be O(log n) by asymptotic analysis, $O\left(\frac{n}{h}\text{log}\frac{n}{h}\right)=O\left(n\right)$. In fact, by the thresholding rule, we may not have to rank all the local maximizers, which can save more time. Altogether, it takes O(n) operations to calculate the SaRa estimator.

For the general case, the computational complexity is O(nh) = O(n log n). Therefore, the SaRa is more efficient than the O(n²) algorithms.

2.5. The multi-bandwidth SaRa

In the SaRa procedure, involved are several parameters such as bandwidth h, weight w and threshold λ. Although we give an asymptotic order of these quantities in Section 3, it is desirable to develop a data adaptive technique to determine their values.

Similar to other kernel-based methodologies, the choice of the kernel function, or the weight, is not as crucial as the bandwidth. In this paper, since we consider model (1.1) with piecewise constant mean μ, the equal-weight (2.1) performs well. In some potential applications, when the mean μ is piecewise smooth, the local linear estimator of the first derivative is more appropriate.

Choosing the optimal bandwidth is usually tricky for algorithms involving bandwidths. To better understand the bandwidth selection problem, let us look at the local diagnostic statistic D(x) more carefully. In fact, D(x) is just a statistic used to test the hypothesis

H₀ : there is no change at x vs H₁ : there is a change at x. Consider the simplest case when there is no other change-point nearby. We have

$$D(x,h)~N\left(\delta ,\frac{2}{h}\right),$$ (2.3)

, where δ is the difference between the means on the left and right of x. Obviously, the larger the h is, the more powerful the test is. Therefore, when applying the SaRa to detect change-points, we prefer to use long bandwidth for a change-point at which the mean function jumps only slightly. However, when using a large bandwidth, there might be other change-points in the interval (x − h, x + h). Then (2.3) does not hold anymore. To lower this risk, we prefer small bandwidth, especially at a point where the jump size is large. In summary, the bandwidth is of less concern when the change-points are far away from each other and the mean shifts greatly at each change-point. Otherwise, we need to choose the bandwidth carefully. Moreover, the optimal bandwidths for various positions may be different. It is not an easy task to determine the optimal bandwidth for each position when we do not have any prior knowledge of change-points.

The choice of the threshold λ is easy if we know in advance that the jump sizes are more than a constant c for all change-points or we target on only the change-points where the mean shifts tremendously. Otherwise, the choice can be tricky. If we do not use a uniform bandwidth for all points, we may have to use different thresholding rules for different positions.

From the discussion above, we see that it is necessary to develop a data-adaptive method for parameter selection to enhance the power of the SaRa. Here we propose the multi-bandwidth SaRa, which can choose the bandwidth and threshold implicitly and data-adaptively for each change-point. The procedure of multi-bandwidth SaRa is as follows. In Step 1, we select several bandwidths, say, h₁, …, h_K, and run the SaRa for each of these bandwidths. We can use a conservative threshold, say, ${\lambda }_k=C\sqrt{2∕h_k}\widehat{\sigma }$ with C = 2 or 3. Note that |D(x, h_k)|, k = 1, …, K, typically have different local maximizers, especially when the signal-to-noise ratio is small. We collect these SaRa estimators which constitute a candidate pool with a moderate size. In Step 2, we may apply the best subset selection with a BIC-type criterion [Yao (1988), Zhang and Siegmund (2007)] to the candidate pool. For example, (1.4) can be used to estimate the number and locations of change-points. That is, the candidate pool has a much smaller size than n and can cover the true change-points in the sense of Theorem 1 in Section 3. In practice, we recommend a forward stepwise selection or backward stepwise deletion instead of the best subset selection when the candidate pool is still big. For instance, to employ the backward stepwise deletion method, we delete the elements one by one from the candidate pool. At each step, we delete the one which leads to the least increase for ${\widehat{\sigma }}^2$ in (1.4). The procedure stops if $\frac{n}{2}\text{log}{\widehat{\sigma }}_J^2+J$ log n stops decreasing, where J is the of the remaining candidate pool.

We may consider that the multi-bandwidth SaRa is a combination of local and global methods. In the first step, the fast local method is employed to reduce the dimensionality. In the second step, the global method is applied for accurate model selection. Moreover, the second step also serves as a parameter selection tool for the SaRa. For example, imagine the case that j = 100 is a change-point, and the SaRa with bandwidths h = 10, 15 and 20 suggests 97, 99 and 105 as the estimates of the change-point, respectively. The second step of the multi-bandwidth SaRa, that is, the subset selection procedure with the BIC-type criterion, might suggest 99 as the change-point. In this case, the bandwidth is selected implicitly as 15. As a result, the multi-bandwidth SaRa behaves like the SaRa with the optimal bandwidth at each change-point, which is also verified by the numerical studies. Note that we can use the strategy of the multi-bandwidth SaRa for a single bandwidth h, which usually improves the performance. The reason is that the SaRa arranges the location estimators in the order of magnitudes of the local diagnostic functions, while the multi-bandwidth SaRa can rearrange the order using the best subset selection by making use of global information, and, hence, the multi-bandwidth SaRa is more reasonable in most cases. In this procedure, the threshold parameter is selected implicitly for each position by the subset selection procedure.

The computation cost of Step 2 in the multi-bandwidth SaRa depends on the size of the candidate pool, which is highly related to the true number of change-points J. With J ≪ n, the size of the candidate pool can be well controlled by setting appropriate threshold λ_k. Thanks to the sequential structure of observations, the backward stepwise selection can be employed for subset selection efficiently. In applications when n is large, Step 2 will not increase the computation time significantly.

In practice, we still have to choose bandwidths h₁, …, h_K for the multi-bandwidth SaRa, although their values are not as crucial as the one in the original SaRa. The choice of these bandwidths should depend on the applications, in which certain information may be available. If not, a default setting of K = 3, h₁ = logn, h₂ = 2 logn andh₃ = 3 log n is recommended.

3. Sure coverage property

The main purpose of this section is to show that the SaRa satisfies the sure coverage property. In other words, the union of intervals $\widehat{\mathcal{J}}\pm h$ selected by the SaRa includes all change-points with probability tending to one as n goes to infinity. The nonasymptotic probability bound is shown as well. It will also be clear that the sure coverage property implies model consistency of the SaRa.

Let J = J(n) be the number of change-points in model (1.1). We denote the set of all change-points by $\mathcal{J}=\{{\tau }_1<{\tau }_2<\cdots <{\tau }_J\}$. We assume τ₀ = 0 and τ_J+1 = n for notational convenience. For simplicity, we assume that the noises are i.i.d. Gaussian with variance σ². We will use the equally weighted diagnostic function (2.1) with bandwidth h in this section, but all theorems can be easily extended for all weights in the family $\mathcal{W}$, defined in the supplementary material [Niu and Zhang (2012)]. We write $\widehat{\mathcal{J}}={\widehat{\mathcal{J}}}_{h,\lambda }$, defined by the thresholding rule (2.2), which depends on the choices of the bandwidth h and the threshold λ.

Define δ = min_1≤j≤J |δ_j|, L = min_1≤j≤J+1(τ_j − τ_j−1. Intuitively, when δ and L too small, no methods can detect all change-points. A key quantity for detecting change-points is S² = δ²L/σ². We assume

$$S^2={\delta }^{2}L∕{\sigma }^2>32\text{log}n.$$ (3.1)

Theorem 1. Under Assumption (3.1), there exist h = h(n) and λ = λ(n) such that $\widehat{\mathcal{J}}={\widehat{\mathcal{J}}}_{h,\lambda }=\{{\widehat{\tau }}_1,\dots ,{\widehat{\tau }}_{\widehat{J}}\}$ satisfies

$$\underset{n\to \infty }{\text{lim}}\mathbf{P}(\{\widehat{J}=J\}\cap \{\mathcal{J}\subset :\widehat{\mathcal{J}}\pm h\})=1,$$ (3.2)

where by $\mathcal{J}\subset :\widehat{\mathcal{J}}\pm h$ we mean ${\tau }_j\in ({\widehat{\tau }}_j-h,{\widehat{\tau }}_j+h)$ for all j ∈ {1, …, J}. In particular, taking h = L/2 and λ = δ/2, we have

$$\mathbf{P}(\{\widehat{J}=J\}\cap \{\mathcal{J}\subset :\widehat{\mathcal{J}}\pm h\})>1-8S^{-1}\text{exp}\{\text{log}n-S^2∕32\}.$$ (3.3)

Remark 1. We believe Theorem 1 can be generalized to the non-Gaussian case, although we may need a stronger condition than (3.1) in order to bound the tail probability by Bernstein's inequality. However, the theoretical results are likely to be more complicated.

Remark 2. We take h = L/2, λ = δ/2 and constant 32 in Assumption (3.1) for clearer demonstration of our proof. Obviously the optimal constant in Assumption (3.1) to make (3.2) hold depends on the choice bandwidth h, threshold λ as well as the usually unknown true data generating process.

Remark 3. If L = o(n) [e.g., in Assumption (3.1), δ and σ are constants, L is of order log n], by Theorem 1, with probability tending to 1, we have $\widehat{J}=J$ and $\mid {\widehat{\tau }}_i-{\tau }_i\mid <h$. In particular, $\mid {\widehat{\tau }}_i∕n-{\tau }_i∕n\mid \to 0$, which implies consistency [in the sense of Yin (1988), Yao and Au (1989)] of the SaRa. In fact, the conclusion of Theorem 1 is slightly stronger than model consistency since it shows $\mid {\widehat{\tau }}_i∕n-{\tau }_i∕n\mid \to 0$ uniformly with an explicit rate. Moreover, in the conventional asymptotic analysis, it is usually assumed that J is fixed and τ_i/n → t_i is constant for each i, as n goes to infinity, which implies L/n → constant. Our asymptotic setting (3.1) is more challenging but it incorporates L, δ and n better.

4. Numerical results

4.1. Simulation I: Detecting for a single change-point

Although the SaRa, as a change-point detecting tool, is designed for large data sets with multiple change-points, we may also compare its power with classical methods in the conventional setting. In this subsection, we consider the hypothesis testing problem (1.2) (with a known variance) and compare the SaRa with the likelihood ratio test (1.3).

We assume Y_i ~ N(μ_i, σ²) with known σ² in hypothesis testing problem (1.2). Let n = 100. The maximum of the diagnostic function max_1≤x≤99 |D(x, h)| can serve as a test statistic and can be viewed as the simplest version of SaRa. We consider only the equal weight case (2.1) for simplicity. We compare three test statistics, the log likelihood ratio test statistic (1.3) and the SaRa with bandwidths h = 10 and h = 15. We run 10,000 replications to get distributions of the three test statistics under the null hypothesis. We control the type I error to the levels α = 0.05 and 0.01, respectively, and examine the powers of the three tests when the change-point locations are 10, 30, 50 and uniformly distributed, respectively.

In Figure 1, we see that the power increases as the Jump size to Standard deviation Ratio (JSR) increases. The likelihood ratio test is more powerful when the change-point location is near the middle and less powerful otherwise. The tests using the SaRa are robust with respect to the location since the diagnostic function is locally defined. It is not surprising that the likelihood ratio test performs better overall since the SaRa-based tests use information only within a small neighborhood. However, we see that the SaRa-based tests perform well when the JSR is greater than 1.5, and the SaRa with h = 15 outplays the likelihood ratio test when the locations are far from the middle or random.

Fig. 1.

Power comparison of the three tests under different Jump size to Standard deviation Ratios (JSR), change-point locations (Lo) and type I errors (α). Black solid, red dashed and blue dotted lines correspond to the likelihood ratio test, and SaRa with bandwidths 10 and 15, respectively. The results are based on 10,000 replications.

4.2. Simulation II: Sure coverage property

In this subsection we test the SaRa on a simple but challenging example. Consider the situation when there is a small CNV with length L buried in a very large segment with length n, where L = O(log n). Explicitly, we assume the true mean vector μ = E(Y) satisfying μ_i = 0 + δ · I_{{n/2<i≤n/2+L}}. In other words, among all n positions, there are two change-points located on the position n/2 and n/2 + L with jump sized δ and −δ. The locations and the number of aberrations do not influence our method. We set (n, L) = (400, 12), (3000, 16), (20,000, 20) and (160,000, 24), which satisfy approximately L ≈ 2 log n. We fix the jump size δ = 1 and assume that the noises are i.i.d. $\mathcal{N}(0,{\sigma }^2)$ with σ = 0.5 and 0.25, so S² ≈ 8 log n and 32 log n respectively. We run the SaRa with the thresholding rule (2.2), taking $h=\frac{3}{4}L$ and $\lambda =\frac{3}{4}\delta$. We list the simulation results in Table 1, based on the 1000 replications. We see that the SaRa can estimate the number of change-points as well as their locations accurately in the less noisy case. The two change-points can be detected with very high probabilities and the estimated errors are very small with the average below one and median at zero. Even in the noisy case, the two points can be detected with very high probabilities, and the number of the false discovered change-points is very small, at most 1 in most cases. The simulation results match our theory perfectly.

Table 1.

The estimated model sizes $\widehat{J}$ and Sure Coverage Probabilities (SCP) of SaRa by the thresholding rule under different settings (n, L) and noise levels σ. Column 3 lists the distribution and mean value of the estimated number of change-points. Columns 4 and 5 list SCPs of two change-points as well as mean distance between estimated change-point locations and true locations. The results are based on 1000 replications

		Number of change-points				Change-point 1 SCP (Mean)	Change-point 2 SCP (Mean)
(n,L)	σ	$\widehat{J}=2$	<2	>2	Mean
(400, 12)	0.5	63.5%	11.7%	24.8%	2.175	91.3% (0.756)	91.3% (0.716)
	0.25	98.2%	1.8%	0.0%	1.980	98.9% (0.129)	99.1% (0.119)
(3000, 16)	0.5	60.3%	8.3%	31.4%	2.306	92.8% (0.814)	93.4% (0.776)
	0.25	98.1%	1.9%	0.0%	1.980	99.3% (0.118)	98.7% (0.129)
(20,000, 20)	0.5	60.2%	6.3%	33.5%	2.343	94.3% (0.862)	94.8% (0.841)
	0.25	99.3%	0.7%	0.0%	1.993	99.5% (0.139)	99.8% (0.108)
(160,000, 24)	0.5	49.5%	5.0%	45.5%	2.599	95.8% (0.877)	95.0% (1.013)
	0.25	99.5%	0.5%	0.0%	1.995	99.8% (0.096)	99.7% (0.148)

4.3. Simulation III: An example in Olshen et al. (2004)

This simulation example, adapted from [Olshen et al. (2004)], is more complex and realistic. The true data generating process is as follows:

$$Y_i={\mu }_i+0.25\sigma \text{sin}\left(a\pi i\right)+{\epsilon }_i,i=1,\dots ,n,$$ (4.1)

where the error term ε follows Gaussian distribution N(0,σ²). The total number of markers n equals 497. There are six change-points along μ with position τ = (137,224,241,298,307,331), μ₀ =−0.18, and δ = (0.26,0.99,−1.6,0.69,−0.85,0.53). A sinusoidal trend was added to mimic the periodic trend found in the a-CGH data. The noise parameter σ was set to be one of 0.1 or 0.2, and the trend parameter a ε{0,0.01,0.025} corresponds to none, long and short trends, respectively. A simulated data set with σ = 0.2 and a = 0 is illustrated in Figure 2. Among the six change-points, the ones at 137, 298 and 307 are more difficult to detect, since the jump size at 137 is small, and the length of CNV between 298 and 307 is quite short.

Fig. 2.

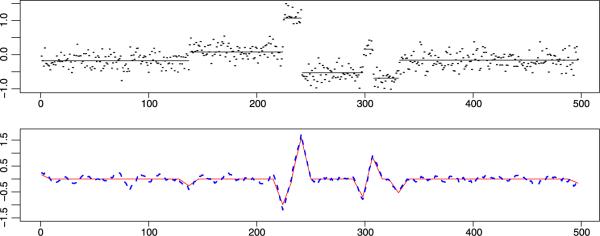
Above: example of one Monte Carlo sample of simulation model (4.1) with σ = 0.2, a = 0; bottom: the local diagnostic functions with bandwidth h = 9, with noise (blue dashed line) and without noise (red solid line).

We applied a few methods to the 1000 simulated data sets of 497 points. The first method is the fast CBS algorithm by package DNAcopy [Venkatraman and Olshen (2007)]. Since CBS is quite sensitive and may lead to many false positives, we also tried the two-stage procedure CBS-SS, which employs subset selection (SS) with modified BIC [Zhang and Siegmund (2007)] to delete false positives. The second method is the SaRa. We tried a few different bandwidths (h = 9, 15 and 21) to test its performance. The model size was determined by the modified BIC, described at the end of Section 2.3. We also applied the multi-bandwidth SaRa (m-SaRa). For the m-Sara,we first used three bandwidths h = 9, 15 and 21 and chose the threshold $\lambda =2\sqrt{2∕h}\cdot \widehat{\sigma }$for each h to select candidates.Then we applied the backward stepwise deletion to get our final estimate from the set of candidates. (Applying the best subset selection would be better but a little slower. There are about 20 candidates.) The results for the noisy case (σ = 0.2) are illustrated in Table 2, which lists the number of change-points detected by these methods under different trends. We did not assume the noise variance is known, so all the variances in different scenarios were estimated. To estimate the variance, we first estimated the mean μ_i for each point using a local constant regression. Then the variance can be estimated by the residual sum of squares divided by n. We omitted the less noisy case σ = 0.1 since all methods performed well except the fast CBS, which produced a few false positives. For σ = 0.2, the SaRa may underestimate the number of change-points when the bandwidth is too large or too small. The SaRa with bandwidth h = 15 is better than CBS. h = 9 or h = 21 is not optimal since it is hard to detect the first change-point with small bandwidth and it is difficult to detect the CNV between 298 and 307 with too large bandwidth. However, large bandwidth helps a lot for the first change-point and small bandwidth gives a more accurate estimate for the fourth and fifth change-points. It is not surprising that the multi-bandwidth SaRa, which combines the power of all bandwidths, performs best in this complex and noisy example. We also observed that the two-stage procedure CBS-SS can improve the CBS by deleting false positives. The performances of CBS-SS and m-SaRa are comparable.

Table 2.

Number of change-points detected by the CBS algorithm and SaRa

			Number of change-points
σ	Trend	Method	≤5	6	7	8	>8
0.2	None	fast CBS	0	872	88	39	1
0.2	None	CBS-SS	2	998	0	0	0
0.2	None	SaRa (h = 9)	166	639	150	36	9
0.2	None	SaRa (h = 15)	42	901	51	6	0
0.2	None	SaRa (h = 21)	157	833	10	0	0
0.2	None	m-SaRa	0	998	2	0	0
0.2	Short	fast CBS	0	678	194	101	27
0.2	Short	CBS-SS	9	991	0	0	0
0.2	Short	SaRa (h = 9)	220	584	156	37	3
0.2	Short	SaRa (h = 15)	100	780	107	10	3
0.2	Short	SaRa (h = 21)	350	586	60	4	0
0.2	Short	m-SaRa	0	992	8	0	0
0.2	Long	fast CBS	1	695	148	135	21
0.2	Long	CBS-SS	6	991	3	0	0
0.2	Long	SaRa (h = 9)	263	597	121	15	4
0.2	Long	SaRa (h = 15)	101	840	53	6	0
0.2	Long	SaRa (h = 21)	317	669	14	0	0
0.2	Long	m-SaRa	0	960	40	0	0

In Table 3 we report the detection rate and average falsely discovered count for the CBS-SS and m-SaRa. We use an aggressive criterion which considers the change-point undetected if the estimation error is above 5. A location estimator is falsely discovered if there is no true change-point within distance of 5. The detection rates of two methods are similar. In the cases with trends, the multi-bandwidth SaRa is slightly better.

Table 3.

Detection rates for each change-point and Average Falsely Discovered (AFD) Count

Trend	Method	CP1	CP2	CP3	CP4	CP5	CP6	AFD
None	CBS-SS	92.8%	100%	100%	99.8%	99.8%	99.6%	0.076
None	m-SaRa	90.6%	100%	100%	99.9%	100%	100%	0.097
Short	CBS-SS	80.9%	100%	100%	99.1%	99.1 %	100%	0.191
Short	m-SaRa	83.0%	100%	100%	99.9%	100%	100%	0.179
Long	CBS-SS	81.2%	100%	100%	99.7%	99.8%	97.1%	0.217
Long	m-SaRa	87.1%	100%	100%	99.9%	100%	99.8%	0.172

4.4. Application to Coriel data

To test the performance of our algorithm, we apply it to the Coriel data set which was originally studied by Snijders et al. (2001).This is a typical aCGH data set, which consists of the log-ratios of normalized intensities from the disease vs control samples, indexed by the physical location of the probes on the genome. The goal is to identify segments of concentrated high or low log-ratios. This well-known data set has been widely used to evaluate CNV detection algorithms; see Olshen et al. (2004), Fridlyand et al. (2004), Huang et al. (2005), Yin and Li (2010), among others. The Coriel data set consists of 15 fibroblast cell lines. Each array contains measurements for 2275 BACs spotted in triplicates. There are 8 whole chromosomal alterations and 15 chromosomes with partial alterations. All of these aberrations but one (Chromosome 15 on GM07801) were confirmed by spectral karyotyping.

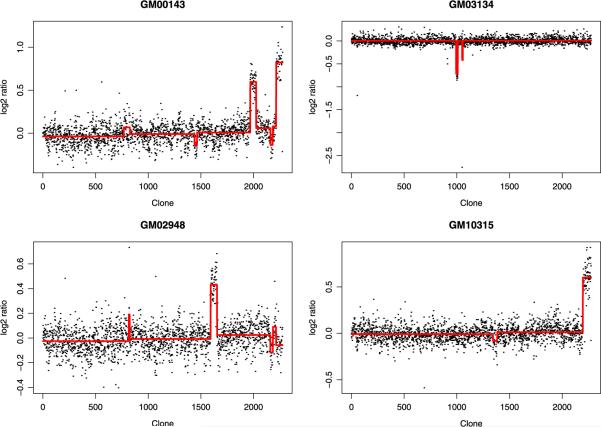
The outcome variable used for the SaRa algorithm was the normalized average of the log₂ ratio of test over reference. Note that in this data set there are only three possible mean values corresponding to loss (monosomy), neutral and gain (trisomy). However, we did not assume we know this fact in advance. We applied the multi-bandwidth SaRa with h = 9, 15 and 21 directly to the data set, and used the backward stepwise deletion with modified BIC to select change-points from all candidates suggested by the SaRa. As a result, the multi-bandwidth SaRa identified all but two alterations (Chromosome 12 on GM01535 and Chromosome 15 on GM07081). For Chromosome 12 on GM01535, the region of alteration is represented by only one point and was hence difficult to detect. For Chromosome 15 on GM07081, our result agrees with Snijders et al. (2001) that there is no evidence of an alteration from the data set. Our method also found a few alterations that were not detected by spectral karyotyping. The multi-bandwidth SaRa suggests that there might be CNVs on chromosomes 7, 11, 21 for GM00143, chromosome 8 for GM03134, chromosomes 7, 21 for GM02948, and chromosome 11 for GM10315 (see Figure 3). And most of these additional CNVs are short aberrations. They may be false positives or true ones that cannot be confirmed by spectral karyotyping due to its low resolution. We also tried fast CBS to analyze this data set and found that CBS selected more than 100 change-points. The result has been listed in Yin and Li (2010), so we omit it here.

Fig. 3.

Estimated mean functions by the multi-bandwidth SaRa on four cell lines.

4.5. Application to SNP genotyping data

Due to the low resolution, aCGH techniques are effective to detect only long CNVs of tens or hundreds of kilobases. By recent studies [Conrad et al. (2006), McCarroll et al. (2006)], it has been shown that short CNVs are common in the human genome. The genome-wide SNP genotyping arrays, which are able to assay half a million SNPs, improve the resolution greatly and offer a more sensitive approach to CNV detection.

We illustrate the SaRa using SNP genotying data for a father–mother-offspring trio produced by the Illumina 550K platform. The data set can be downloaded along with the PennCNV package. The data consist of the measurements of a normalized total signal intensity ratio called the Log R ratio, that is, calculated by log₂(R_obs/R_exp), where R_obs is the observed total intensity of the two alleles for a given SNP, and R_exp is the expected intensity computed from linear interpolation of the observed allelic ratio with respect to the canonical genotype clusters [Peiffer et al. (2006)]. For each subject, the Log R ratios along Chromosomes 3, 11 and 20 are included in the data set. There are 37,768, 27,272 and 14,296 SNPs in Chromosomes 3, 11 and 20, respectively. Similar to the aCGH data, the segments with concentrated high or low Log R ratios correspond to gains or losses of copy numbers.

We employed the SaRa, multi-bandwidth SaRa, CBS, the fused lasso (FL) and PennCNV to detect CNVs in this data set. We used R packages DNAcopy (version 1.14.0), cghFLasso (version 0.2–1) and free software PennCNV for the last three algorithms. The SaRa and m-SaRa were implemented by the R program. For the SaRa, we took h = 10 and $\lambda =2\sqrt{\text{log}n}\cdot \sqrt{2∕h}\cdot \widehat{\sigma }$. For the m-SaRa, we used three bandwidths h = 10, 20 and 30 and the threshold $\lambda =3\sqrt{2∕h}\cdot \widehat{\sigma }$ in the first step. The backward stepwise selection with modified BIC was employed in the second step.

The result for the offspring is listed in Table 4. The fused lasso and CBS detected too many change-points, most of which are most likely to be false positives. The performance of the SaRa and PennCNV are similar. In particular, the SaRa can identify all 4 CNVs found by PennCNV as well as an additional one on Chromosome 20 from position 5,851,323 to 5,863,922 kilobase. It seems that the m-SaRa did not perform as well as the SaRa in this example. The reason is two-fold. First of all, the signal to noise ratio (i.e., jump size to standard deviation ratio) is large for this data set. Therefore, the simple SaRa works very well. Second, in the second step of the m-SaRa, the modified BIC was employed for model selection. The modified BIC assumes a uniform prior over the parameter space [Zhang and Siegmund (2007)], which may not be satisfied since the CNVs are very short in this example.

Table 4.

Number of change-points detected for the offspring by different methods

	SaRa	m-SaRa	CBS	FL	PennCNV
Chromosome 3	2	19	46	511	2
Chromosome 11	4	2	29	345	4
Chromosome 20	4	7	16	143	2

All computations were done on a 3.33 GHz Intel(R) Core(TM)2 Duo PC running the Windows XP operating system. It took about 16 s for the PennCNV to show the result for all 3 subjects. So the computation time for each subject is about 5 s. All other algorithms were operated in R software. The computation time for each algorithm is listed in Table 5. All algorithms are fast and practical. In particular, the SaRa is one of the fastest. Moreover, we observed that the computation time for the SaRa increases linearly with the sample size.

Table 5.

Computation time (in seconds) for different methods

	Number of SNPs	SaRa	m-SaRa	CBS	FL
Chromosome 3	37,768	1.63	8.93	63.28	3.10
Chromosome 11	27,272	1.16	2.64	34.05	1.79
Chromosome 20	14,296	0.61	1.67	17.37	0.66

Overall, the SaRa and PennCNV are the best among all algorithms. The fused lasso and CBS mainly target on the aCGH data and may not be suitable for the SNP genotyping data. The m-SaRa equipped with a proper Bayesian-type information criterion is potentially useful. In the SaRa, we used h = 10 since it is known that the CNVs are quite short. The thresholds were chosen by asymptotic analysis of the extremal values of D(x). In fact, it was quite obvious when the local maximizers were ranked. For the offspring, there were only 10 local maximizers at which the values of |D(x)| were larger than 0.57. The values of |D(x)| at other local maximizers were less than 0.26.

It is surprising that the SaRa and PennCNV can give similar results since they are based on different models. The advantage of PennCNV is that it can utilize more information, that is, the finite states of copy numbers and the B Allele Frequency (BAF) besides the Log R ratio. The value of the SaRa is its simplicity and generality. The SaRa can be implemented easily and is potentially useful in other multiple change-points problems.

5. Discussion

Motivated by copy number variation detection, many multiple change-point detection tools have been invented and developed recently. However, faster and more efficient tools are needed to deal with the high dimensionality of modern data sets. Different from other approaches, we propose a screening and ranking algorithm, which focuses on the local information. It is an extremely efficient method with computational complexity down to O(n) and suitable for huge data sets. Moreover, it is very accurate and satisfies the sure coverage property. Note that, as far as we know, very few theoretical results have been developed for multiple change-points detection tools. Besides the efficiency and accuracy, the SaRa is easily implementable and extendable. For example, since only local information is involved in the computation, it is easy to extend it to an on-line version, which may be useful for financial data. In addition, we may use the SaRa for the heteroscedastic Gaussian model when the variance is not constant. We can estimate the variance using local information and take it into account when calculating local statistics D(x, h). We should note, however, that both the implementation and theory for the heteroscedastic variances will be more complicated and will require further extensive effort. In the SaRa procedure, the choices of bandwidth h and threshold λ are important. In applications, optimal choices of these parameters may depend on the positions and jump-sizes of change-points. In this case, the multi-bandwidth SaRa, which selects parameter implicitly and data-adaptively, is practically useful. Knowledge about the data can be particularly useful in determining reasonable or meaningful gaps between change-points and and jump-sizes at change points, which can prevent us from using poor choices of bandwidth h and threshold λ.

The SaRa is a useful method for solving change-points problems for a high dimensional sparse model such as (1.1) and can be generalized to solve more general change-point problems. However, we should point out that the SaRa can be improved for CNV detection since model (1.1) may not capture all the characteristics of the CNV problem. For example, CNVs can be short. Then, it is better to modify the SaRa accordingly to improve its power.