Molecular dynamics simulations of the intramolecular proton transfer and carbanion stabilization in the pyridoxal 5′-phosphate dependent enzymes l-dopa decarboxylase and alanine racemase

Abstract

Molecular dynamics simulations using a combined quantum mechanical and molecular mechanical (QM/MM) potential have been carried out to investigate the internal proton transfer equilibrium of the external aldimine species in l-dopa decarboxylase, and carbanion stabilization by the enzyme cofactor in the active site of alanine racemase. Solvent effects lower the free energy of the O-protonated PLP tautomer both in aqueous solution and in the active site, resulting a free energy difference of about – 1 kcal/mol relative to the N-protonated Schiff base in the enzyme. The external aldimine provides the dominant contribution to lowering the free energy barrier for the spontaneous decarboxylation of l-dopa in water, by a remarkable 16 kcal/mol, while the enzyme l-dopa decarboxylase further lowers the barrier by 8 kcal/mol. Kinetic isotope effects were also determined using a path integral free energy perturbation theory on the primary ¹³C and the secondary ²H substitutions. In the case of alanine racemase, if the pyridine ring is unprotonated as that in the active site, there is destabilizing contribution to the formation of the α-carbanion in the gas phase, although when the pyridine ring is protonated the contribution is stabilizing. In aqueous solution and in alanine racemase, the α-carbanion is stabilized both when the pyridine ring is protonated and unprotonated. The computational studies illustrated in this article show that combined QM/MM simulations can help provide a deeper understanding of the mechanisms of PLP-dependent enzymes. This article is part of a Special Issue entitled: Pyridoxal Phosphate Enzymology.

1. Introduction

Pyridoxal 5′-phosphate (PLP) is an ubiquitous coenzyme derived from vitamin B₆, which plays a crucial role in a variety of chemical transformations [1,2]. With the aid of PLP, enzymes perform a wide range of amino acid related chemistry, including decarboxylation, racemization, transamination, aldol condensation, α,β-elimination, and β,γ-elimination. One of the major tasks of PLP is the stabilization of the reactive Cα carbanion intermediate to increase the carbon acidity of amino acids [1]. For instance, the pKa of zwitterionic glycine is 28.9, [3] making the removal of the Cα-proton extremely difficult. Employing combined quantum mechanical and molecular mechanical (QM/MM) methods, we have investigated some of the roles that the PLP cofactor plays in enzymatic catalysis, including the stabilization of the α-carbanion of the external aldimine adduct in the amino acid racemization reaction catalyzed by alanine racemase, [4,5] and the effect of the internal tautomerization between the N-protonated Schiff base and O-protonated pyridine substituent on the decarboxylation by l-dopa decarboxylase [6]. These studies provided additional insights into the understanding of PLP chemistry.

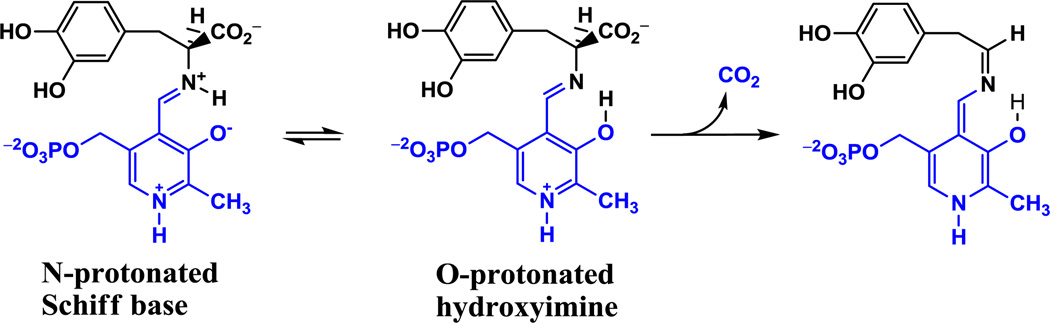
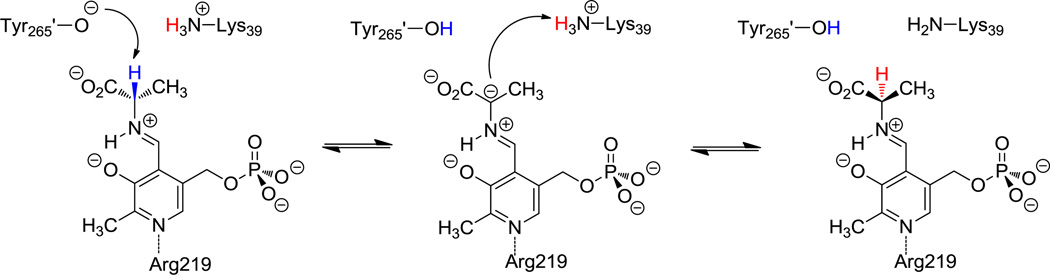
The proton that forms an internal hydrogen bond between the imine nitrogen and the 3-oxo anion of the external aldimine between PLP and an amino acid substrate can undergo an intramolecular proton transfer from the N-protonated Schiff base to the O-protonated hydroxyimine, formally corresponding to a tautomerization equilibrium (Scheme 1) [6]. This equilibrium plays a role that affects the reactivity of the PLP Schiff base in the active site. Richard and coworkers suggested that PLP-dependent enzymes select the zwitterionic external aldimine complex, in which pronation at the imine nitrogen is preferred [1,7]. Consequently, the α-carbon acidity is relatively high for a carbon acid with pKa of about 17 as a result of carbanion stabilization [4,5,8]. Toney and Limbach and their coworkers demonstrated that the intramolecular proton transfer is coupled to the protonation state of the pyridine ring, which favors the N-protonated Schiff base (PSB) in solid state and in polar aprotic solvent when the pyridine ring is protonated [9,10]. However, there is no coupling in aqueous solution due to competition between intramolecular and intermolecular hydrogen bonds [11,12].

Scheme 1.

Illustration of the internal proton transfer of the external aldimine between PLP cofactor and l-dopa, and the decarboxylation reaction catalyzed by l-dopa decarboxylase.

The external aldimine between PLP and an amino acid substrate consists of three titratable sites in addition to the phosphate group, [10,13] including the pyridine nitrogen, the 3-oxo oxygen and the imine nitrogen of the Schiff base linkage; the specific protonation state and site are critical to catalysis [12]. Under physiological conditions, the external aldimine would retain only one proton, whereas the protonation of the pyridine nitrogen site is strongly dependent on the amino acid with which it forms a specific hydrogen bond in the active site. Typically, the pyridine nitrogen of PLP is protonated, making hydrogen-bonding interactions either with an anionic residue, such as Asp or Glu found in aminotransferases, or with a polar residue, Ser or Thr, in enzymes of the tryptophan synthase family [2,14]. The pyridinium ion of PLP acts as an effective electron sink, stabilizing the carbanion intermediate by forming a quinonoid species. In the enzyme l-dopa decarboxylase, [15] which catalyzes the conversion of l-dopa into dopamine in the treatment of Parkinson's disease; [16,17] the carboxylate side chain of Asp271 accepts a hydrogen bond from the protonated pyridinium ion of PLP [15]. On the other hand, Alanine racemase, [2,14] which catalyzes the interconversion of L- and d-alanine in the process of forming the peptidoglycan layer of bacterial cell walls, [18] is rather unique in that the PLP pyridine is unprotonated as revealed in the X-ray structure, in which Arg219 donates a hydrogen bond to the pyridine nitrogen, preventing the formation of a cationic pyridinium ion [19,20]. This is further supported since the quinonoid intermediate was not observed in wild-type Ala [21]. Despite the fact that the pyridine is unprotonated in alanine racemase (AlaR), the apparent pKa of the Cα proton in the Ala-PLP adduct is similar to those in other PLP-dependent enzymes [21].

In the following, we describe our computational investigations on two PLP-dependent enzymes. In particular, we focus on the carbanion stabilization and amino acid racemization by alanine racemase (AlaR, EC 5.1.1.1) and on the internal conformation of the PLP cofactor itself and its effects on the decarboxylation reaction of l-dopa by Dopa decarboxylase (DDC, EC 4.1.1.28). We first provide a summary of the computational methods used in our studies, which is followed by discussion of the key findings on these two enzymatic systems.

1.1. Computational methods

Computational studies of enzymatic processes require three key ingredients in order to provide an understanding of the mechanism and the origin of catalysis [22]. First, one needs to employ a potential energy function that is capable of quantitatively describing the bondforming and bond-breaking process in a catalyzed reaction. This includes the description of the multidimensional potential energy surface and the structural change of the substrate and key amino acids involved in the chemical process along the entire reaction coordinate [23]. In our work, we have developed a combined quantum mechanical and molecular mechanical (QM/MM) approach, [22,24] in which the substrate and the residues directly participating in the chemical process are treated explicitly by a wave function method or density functional theory. The remainder of the enzyme and solvent molecules, which are essential in providing the electrostatic polarization of the active site and modulating the dynamics and reactivity of the system, is approximated by an empirical force field, or molecular mechanics. The instantaneous electrostatic potential is incorporated into the electronic structure calculations on-the-fly during the dynamics simulations [23]. This requires careful validation of the potential energy function and the transition structure for a chemical reaction in the gas phase against ab initio and density functional theory results. Some authors argue that it is sufficient to calibrate the force field, by fitting the barrier and reaction free energy to two adjustable parameters in water and in the enzyme, but it is critical to be able to determine solvent effects as well as the stabilization of the transition state by an enzyme using the same inherent gas-phase potential energy function directly.

Second, we carry out molecular dynamics simulations to sample the protein dynamic fluctuations and to determine the potential of mean force, or the free energy reaction profile, along a well-defined reaction coordinate for a given enzymatic process [22]. This is important because reaction profiles generated from an energy minimization techniques can be trapped into local minima such that a small change in atomic coordinates by a few tens of an angstrom from key amino acid residues can lead to large energy changes.

Finally, for reactions involving hydrogen (proton, hydride, or radical) transfers or even heavy atom transfer, it is often necessary to explicitly consider nuclear quantum effects (NQE), [25] which include zero-point energy contributions and quantum mechanical tunneling, to quantitatively estimate the rate constant of enzymatic reactions [26]. Furthermore, one of the most direct probes of the transition structure of enzymes is experimental measurement of kinetic isotope effects. Computational studies that incorporate NQE in dynamics simulations can help interpret experimental results, and provide a deeper understanding of and a predicting tool for enzymatic processes. We have developed an integrated Feynman path integral and free energy perturbation approach in umbrella sampling simulations, called the PI-FEP/UM method, [27,28] to generate the quantum mechanical potential of mean force along a centroid reaction coordinate. More importantly, the PI-FEP/UM method allows both primary and secondary KIE for enzymatic reactions to be accurately determined in statistical mechanical simulations.

1.2. Combined QM/MM potentials

In all simulations, the potential energy surface of the systems was treated with a combined quantum mechanics–molecular mechanics (QM/MM) approach, in which the active site of the enzymes is modeled by an electronic structure method [22,24,29]. In both enzyme systems, dopa decarboxylase and alanine racemase, discussed in this article, we employed the semiempirical Austin Model 1 (AM1) formalism; [30] however, we used different strategies in the specific applications to achieve the desired accuracy. For the decarboxylation reaction of the external aldimine substrate PLP(H⁺)-l-dopa (protonated pyridine PLP), which consists of a total of 39 atoms, [6] the original AM1 model [30] was used directly without further modification. Previous studies of several decarboxylation reactions, including the decarboxylation of 3-Carboxybenzisoxazole in Water, [31] orotidine 5′-monopho-sphate (OMP) in water and in OMP decarboxylase, [32,33] biotin carboxylation by acetyl-CoA carboxylase, [34] N-methyl picolinate decarboxylation in water, [35] and the closely related l-ornithine by ornithine decarboxylase [36] have shown that the AM1 model can yield good geometrical and energetic results for the decarboxylation reaction. On the other hand, for the proton abstraction and addition of the external aldimine of the PLP-alanine complex, the performance of the original AM1 model is not quantitatively accurate. In this case, we developed a specifically parameterized version of the semiempirical Hamiltonian, called AM1-SRP by reoptimizing the AM1 parameters to reproduce a large set of high-level QM data at the DFT (mPW1PW91/6–311++G(3df,2p)//mPW1PW91/6–31 +G(d)) level of theory [4,5]. Consequently, the reaction specific AM1-SRP model can yield results as accurately as DFT calculations for the AlaR reaction, but with a fraction of the computational costs as the ab initio approach. This allows us to carry out extensive configurational sampling of the protein system in molecular dynamics simulations.

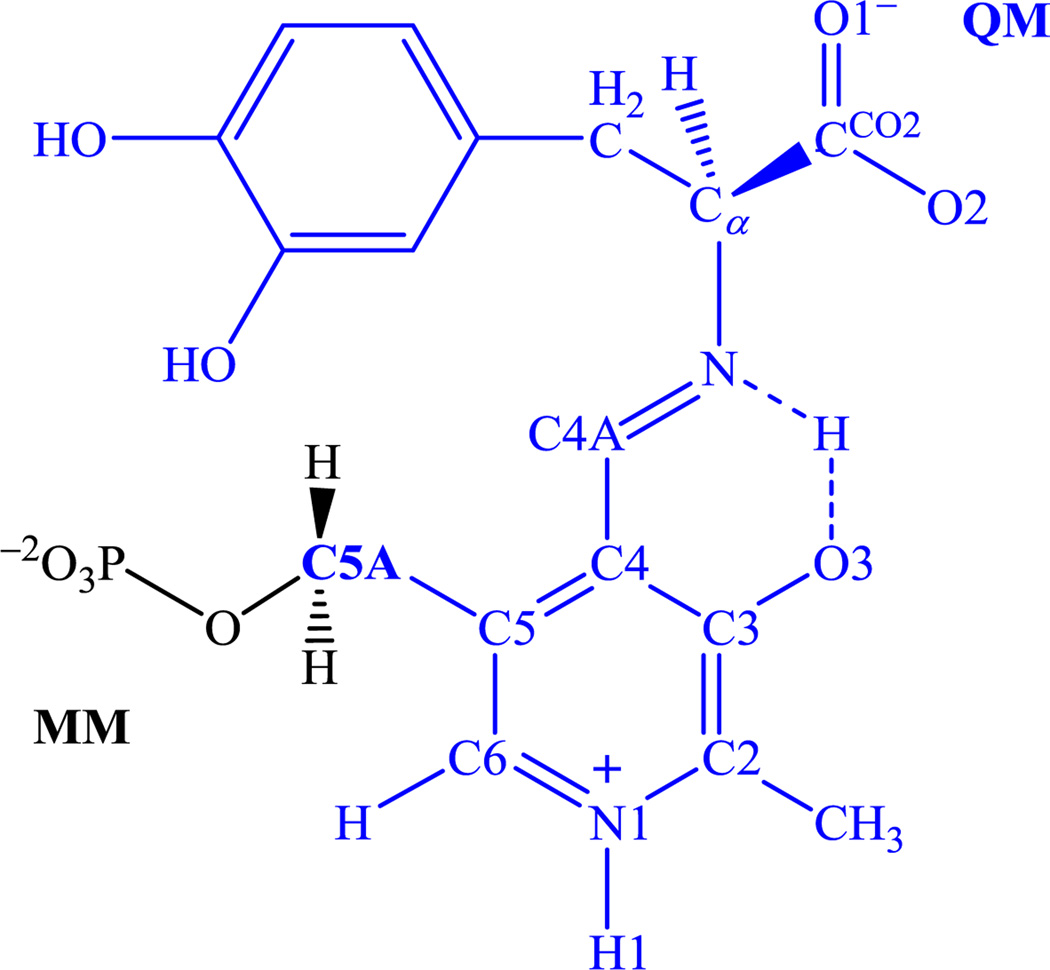
In both cases, the boundary between QM and MM regions is located at the C5A position (Scheme 2), which is described by the generalized hybrid orbital (GHO) method [37,38]. For the MM region, the CHARMM22 all-atom force field [39] was used to represent the protein and the phosphate group of the PLP, whereas the three point charge TIP3P model [40] was used to describe water.

Scheme 2.

The l-dopa-PLP external aldimine depicting the division of atoms treated quantum mechanical and classically as separated by the boundary atom at the C5A position.

1.3. Molecular dynamics simulations

Typically, in our treatment of enzymatic reactions, [22] we perform molecular dynamics simulations to obtain the free energy profile along a predefined reaction coordinate under periodic boundary conditions in the isothermal-isobaric (NPT) ensemble at 298.15 K and 1 atm. Long-range electrostatic interactions are modeled by using a QM/MM particle-mesh Ewald method, [41] whereas van der Waals interactions were feathered to zero between 12 Å and 13 Å with a shift function. The integration step in dynamics simulations is 1 fs.

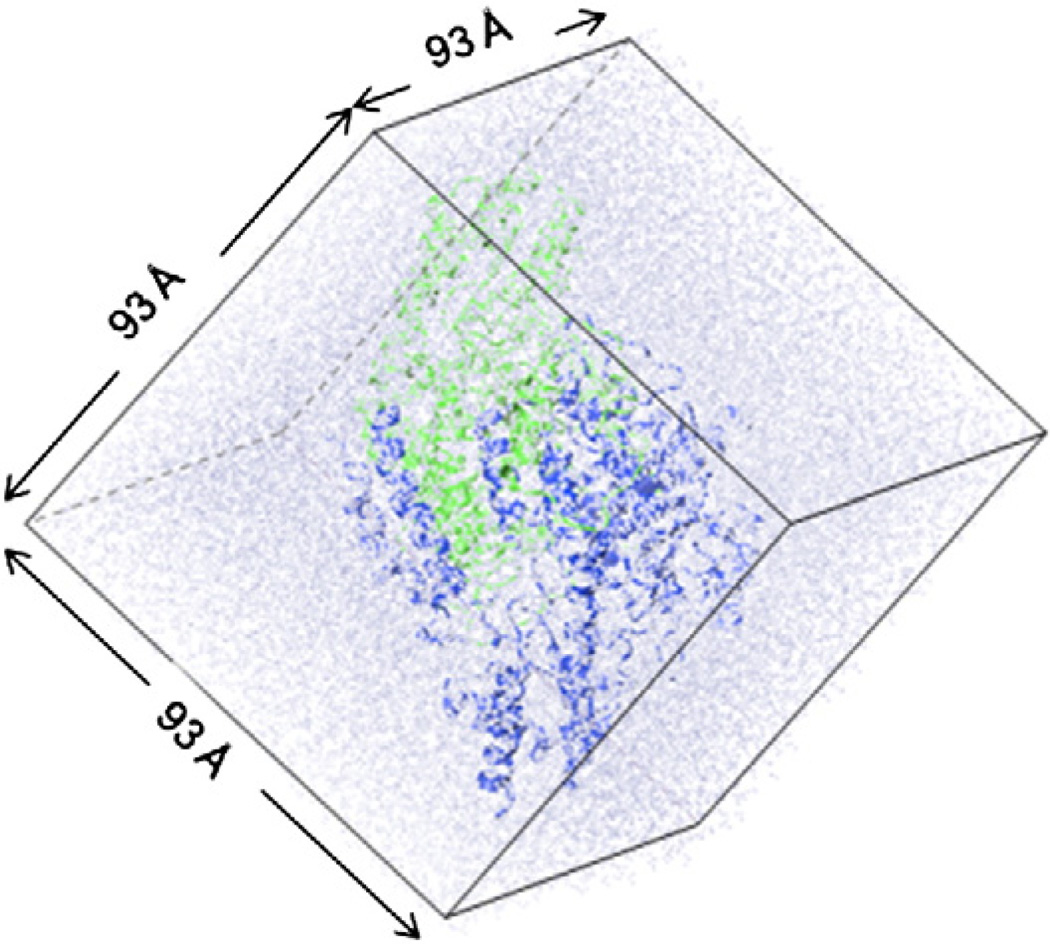
As an illustrative example, the enzyme DDC was embedded in a cubic box of water molecules about a size of 93 × 93 × 93 ų [6,42]. The final computational model consisted of 75,514 atoms, including 20,203 water molecules (Fig. 1). For comparison with the uncatalyzed reaction in water, we placed the external aldimine in a box of water with a box length of 45 Å. We then include sodium and chloride ions to neutralize the systems or to yield the desired ionic concentration.

Fig. 1.

Simulation model of the fully solvated DDC dimeric protein in a box of water under periodic boundary conditions

The potential of mean force was obtained from a series of umbrella sampling simulations, one for each reaction path (mechanism). In the case of AlaR, we also considered amino acid mutations. For the DDC decarboxylation reaction, the reaction coordinate, as depicted in Scheme 2, is defined as the distance between the carboxyl carbon (C) and the α-carbon (C_α) of the amino acid l-dopa:

$$RC\equiv R(C_{\alpha }-C^{C{O}_2^{-}})$$

For the AlaR proton transfer reaction, the antisymmetric stretch was employed as the reaction coordinate. We used a total of 13 windows for the enzymatic reactions and 12 windows for the model reactions. For the enzymatic simulations, each window consisted of 30-ps equilibration, followed by additional 30 to 100 ps for averaging and trajectory collection. The weighted histogram analysis method [43] was used to analyze the probability density and to obtain the free energy profiles for the unbiased systems along the proton transfer reaction coordinate.

1.4. Computation of kinetic isotope effects

The potential of mean force obtained from classical molecular dynamics simulations above, employing a combined QM/MM potential, does not include nuclear quantum effects (NQEs), which are required to compute kinetic isotope effects (KIEs). We have developed a coupled free energy perturbation and umbrella sampling simulation technique in Feynman centroid path integral calculations (PI-FEP/ UM) [27,28] to incorporate the NQE. It is important to note that the ratio of the quantum partition function for different isotopes, which yields the corresponding KIE, is determined directly by free energy perturbation from a light isotope mass into a heavier one within the same centroid path integral simulation. Consequently, the PI-FEP/UM method can yield highly accurate results on computed KIEs [27,44].

In the centroid path integral simulation, we represent each quantized atom by a ring of particles or beads, whose geometrical center (centroid) is constrained to its classical position [45,46]. Thus, for each classical configuration sampled in molecular dynamics umbrella sampling simulations, we perform PI sampling to obtain the NQEs for nuclear motions [27,47,48]. When the PI calculations are performed along the reaction coordinate, we obtain a quantum mechanical correction at each point of the reaction coordinate, resulting in a QM-PMF as a function of the centroid reaction coordinate. We found that the use of 32 beads for each quantized particle is sufficient to yield converged results [4,27,28,35,44,49]. About 150,000 path integral configurations were sampled, as in the case of l-dopa decarboxylase, which was further divided into ten separate averaging blocks to determine statistical deviation in the computed ensemble averages.

2. Results and discussion

2.1. The internal proton transfer equilibrium of PLP

The importance of the internal proton transfer between the N-protonated Schiff base and the O-protonated hydroxyimine tautomers of pyridoxal 5′-phosphate has long been recognized [1]. Recently, we carried out a systematic investigation of the effects of substituent, solvation, and enzyme active site [6]. To achieve this goal, we first examined the intrinsic effect of protonation at the pyridine ring in the external Schiff base, and functional group substitution on the imino nitrogen in the gas phase using a hybrid density functional theory with B3LYP/6–311+G(d,p). Then, solvation effects were evaluated using a dual-level QM/MM simulation approach [50,51]. This is followed by computation of the PMF for the intramolecular proton transfer reaction of the PLP(H+) -l-dopa substrate in dopa decarboxylase. Finally, we examined the effects on enzyme catalysis, making use of the decarboxylation of l-dopa as a specific application [42].

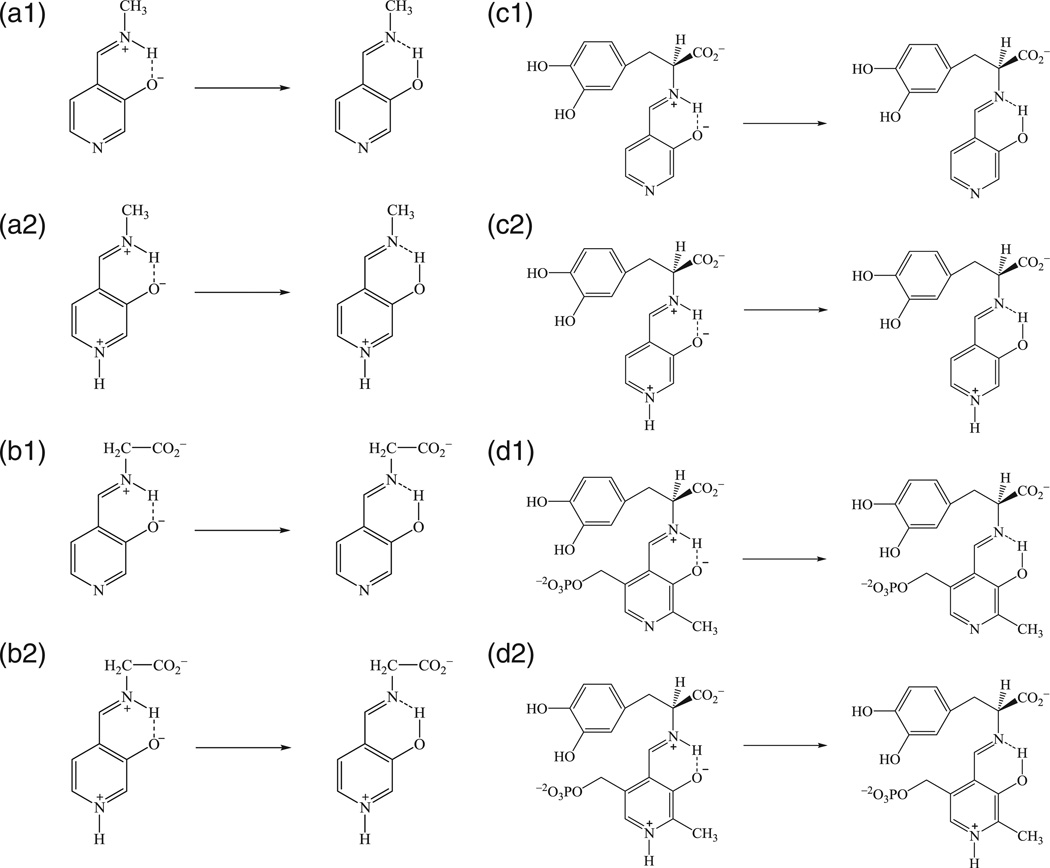
Two main factors influence the tautomeric equilibrium of the PLP -Schiff base: (a) the protonation state of the pyridine ring, and (b) the substituent on the imino nitrogen of the Schiff base. The pyridine nitrogen of the external aldimine substrate has a pKa of about 5.8 in aqueous solution [1,12]. However, in the active sites of most PLP-dependent enzymes, the pyridine nitrogen is assumed to be protonated due to stabilization through ion-pair interactions with a basic residue such as Glu and Asp or hydrogen bonding to polar residues such as Ser and Thr. In exceptional situations, such as in the active site of AlaR, the pyridine nitrogen is unprotonated and accepts a hydrogen bond from an arginine residue. We designed eight model reactions, a1/a2, b1/b2, c1/c2, and d1/d2 (Scheme 3), corresponding to the unprotonated (1) and protonated (2) pyridine ring, and different substitutions on the imino group (a–d) [6].

Scheme 3.

Model reactions for intramolecular proton transfer reaction in aqueous solution.

Overall, we found that the presence of a carboxylate anion on the α-carbon of the imino group helps to stabilize the N-protonated Schiff base (PSB) configuration, and shifts the equilibrium from the O-protonated tautomer to the PSB configuration. Furthermore, protonation of the PLP pyridine nitrogen drives the equilibrium toward the PSB direction. Solvent effects can favor either tautomeric configurations, depending on the electrostatic properties of the substituent on the imino nitrogen. With a carboxylate group on the α-carbon, solvent effects shift the equilibrium in the direction of the O-protonated tautomer. Reaction d2 is the full external aldimine model for the DDC-catalyzed reaction. In the gas phase, the PSB is predicted to be the most stable configuration, which is the form expected in enzyme active sites and has been proposed to provide stabilization of the amino acid carbanion substrate. However, the equilibrium is shifted to the O-protonated hydroxyimine side with a lower free energy of −2.0 kcal/mol as a result of a net solvation effect of −9.1 (−2.0–7.1) kcal/mol. Apparently, the O-protonated form of the tautomer in reactions b–d can gain greater solvation stabilization of the carboxylate and pyridinium groups without the interference of an internal zwitterion.

Examination of the results in Table 1 reveals that in the gas phase, protonation at the pyridine nitrogen (reactions 1) shifts the intramolecular proton transfer toward the N-protonated Schiff base by ca. 5 kcal/mol relative to those of reactions 2. This may be attributed to the stabilization the oxy-anion configuration through induction effects, and the protonated pyridine ring favors electrostatic stabilization of the zwitterionic configuration more than that of the covalent neutral tautomer. On the other hand, substitution of the α-carboxylate group in reaction b stabilizes the PSB isomer by about 7 kcal/mol relative to parent compounds in reaction a, while inclusion of the l-dopa group in reaction c results in similar effects (Table 1). The carboxylate effects can be attributed to ion-pair interactions between the carboxylate ion and the zwitterionic Schiff base (b–d).

Table 1.

Computed free energies of tautomerization reaction (N-protonated Schiff base→O-protonated Hydroxyimine) for the model reactions located in the gas phase and in aqueous solution, and for the reaction in dopa decarboxylase at 298.15 K^a.

Reaction	ΔGgas	ΔGPMF'b
a1	−4.4c	1.4
a2	0.4c	2.9
b1	2.3c	−0.1
b2	7.4d	−2.4
c1	0.9c	−0.7
c2	7.0d	−1.3
d1	5.0e	−0.9
d2	7.1d	−2.0
d2 in DDC	−	−1.3

^aAll energies are given in kcal/mol.

^bCorrection of B3LYP/6–311+G(d,p) gas-phase energy has been made to the lower-level (AM1) energy, i.e., $\Delta G_{PMF}=\Delta G_{PMF}^{AM1}-\Delta G_{gas}^{AM1}+\Delta G_{gas}^{B3LYP/6-311+G(d,p)//AM1}$.

^cB3LYP/6–311+G(d,p)//B3LYP/6–311+G(d,p).

^dB3LYP/6–311+G(d,p)//HF/6–311+G(d,p).

^eB3LYP/6–311+G(d,p)//HF/6–31+G(d).

Solvent effects were evaluated by the use of dual-level combined QM/MM simulations of the potential of mean force for the intramolecular proton transfer (Table 1), in which solvation effects from molecular dynamics simulations were carried out at the lower level of theory of AM1 model, but the intrinsic free energy difference in the gas phase was determined using the B3LYP/6–311+G(d,p) results as the higher level of theory. We found that solvation stabilizes the zwitterion of the PLP Schiff base by 5.8 and 2.5 kcal/mol for reactions a1 and a2, respectively, relative to the gas phase equilibrium. In the unprotonated-pyridine system (a1), the protonated Schiff base has a greater dipole than the O-protonated hydroxyimine configuration, resulting in greater solvation effects in water. For reactions b1 and c1, aqueous solvation stabilizes the O-protonated hydroxyimine by 2.4 and 1.6 kcal/mol, respectively, when the pyridine ring is unprotonated, and the effects are increased to 8– 10 kcal/mol if pyridine is protonated (b2 and c2) [6].

Experimentally, Sharif et al. [9,10] found that the intramolecular proton transfer is coupled with hydrogen bonding interactions at the pyridine ring. A protonated pyridine strongly favors the N-protonated Schiff base in the solid state and in polar aprotic solvents. However, the intramolecular hydrogen bond is not coupled to the protonation state of the pyridine ring in aqueous solution [12]. This has been attributed to competing hydrogen bonding interactions with water, causing the imino group to rotate out of the aromatic plane. This observation is in accord with the results of reaction a1 (Scheme 2) in Table 1.

The dual-level QM/MM simulations showed that the O-protonated PLP(H⁺)- l-dopa cofactor is preferred by −1.3 kcal/mol over the zwitterionic PSB isomer in the active site of DDC [6]. The computed free energy barrier is about 5 kcal/mol from B3LYP:AM1/QM/MM simulations, suggesting that both tautomeric structures can be rapidly inter-converted in the enzyme. Specific hydrogen bonding and electrostatic interactions between the aldimine Schiff base and active site residues are important in controlling the formally keto-enol equilibrium of the PLP cofactor in PLP-dependent enzymes. In DDC, Asp271 forms an ionpair with the protonated pyridine nitrogen, while Lys303 helps to stabilize the Schiff base nitrogen in the O-protonated tautomer. Importantly, Thr246 plays a double role of hydrogen bond donor to stabilize the phenolate ion in the N-protonated Schiff base configuration, and a hydrogen bond acceptor to favor the phenolic moiety of the O-protonated tautomer.

2.2. Decarboxylation and kinetic isotope effects in dopa decarboxylase

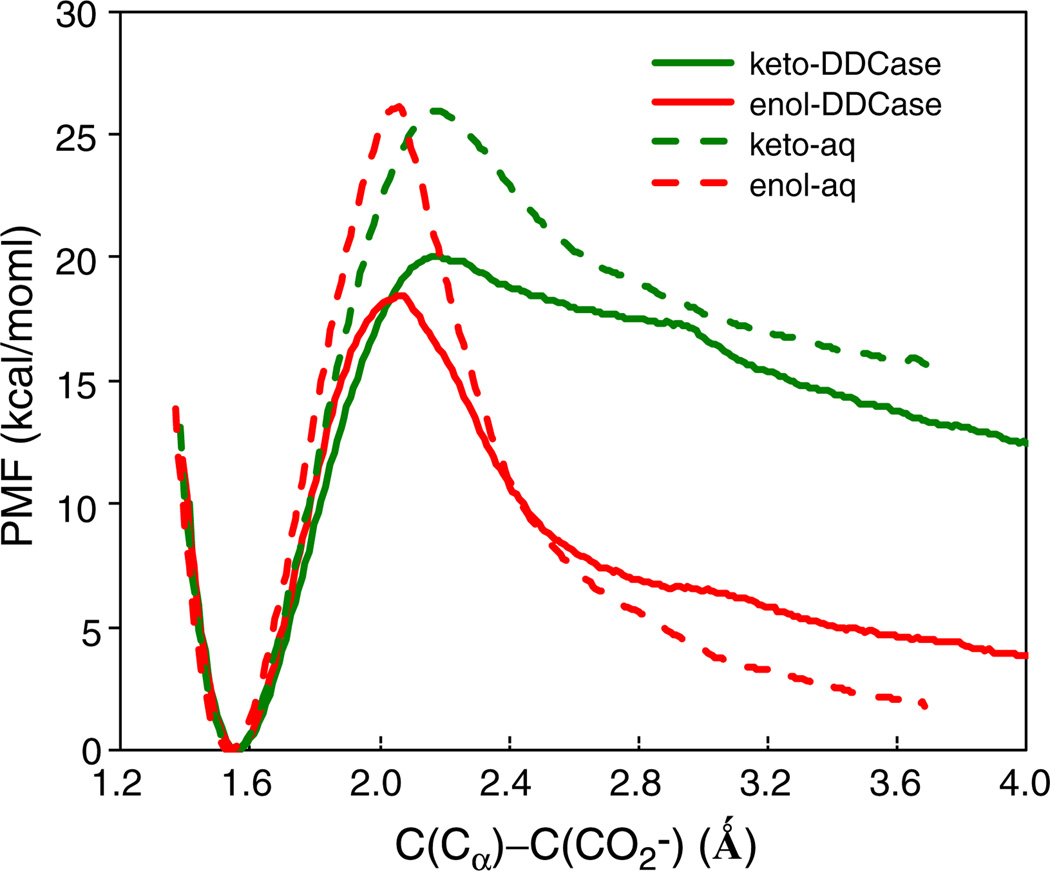
Fig. 2 shows the computed potentials of mean force, including NQE, for the DDC-catalyzed and the corresponding uncatalyzed PLP-dopa external aldimine in water [42]. In aqueous solution, the free energy barriers for the decarboxylation reaction of the PLP-dopa external aldimine complex are essentially the same both for the zwitterionic PSB and the neutral O-protonated hydroxyimine tautomers, suggesting that there is no particular preference for the α-carbanion stabilization by a neighboring (N-protonated) iminium ion in the dopa decarboxylation reaction. The enzyme lowers the free energy barrier by about 6 kcal/mol with the PLP cofactor in the N-protonated PSB and by 8 kcal/mol in O-protonated PLP configuration. The computed barrier height is 17.3 kcal/mol including NQEs, which is in reasonable accord with the experimental value of 16.0 kcal/mol [17]. The uncatalyzed decarboxylation of the external aldimine has a barrier of 42 kcal/mol in water, consistent with Wolfenden's experimental data on similar systems (41 kcal/mol) [52]. Thus, the PLP cofactor itself provides a dominant contribution to the overall catalytic effects, [1] lowing the decarboxylation barrier by about 16 kcal/mol. The enzyme further lowers the barrier by another 8 kcal/mol.

Fig. 2.

Computed potentials of mean force for the enzyme-catalyzed (solid) and uncatalyzed (dashed) decarboxylation of the PLP-dopa external aldimine in the N-protonated (keto) configuration in green and O-protonated (enol) tautomer in red

Fig. 2 shows that the product region is more strongly stabilized for the reaction in the O-protonated PLP configuration. This may be somewhat surprising since the N-protonated Schiff base linkage has been proposed to provide key stabilization of the α-carbanion; [1] however, the zwitterions of the PLP cofactor interferes with hydrogen bonding interactions with the solvent, and the neutral O-protonated PLP configuration favors stabilization of the carbanion from the decarboxylation reaction.

Listed in Table 2 are the computed 1° and 2° KIEs from PI-FEP/UM simulations along with key geometrical results at the transition state. In DDC, we obtained values of 1.053 and 1.047, respectively, for the reaction of the O-protonated and the N-protonated isomer of the external aldimine [42]. The experimental KIEs for the present DDC decarboxylation have not been measured, but the range of the computed KIEs is in good accord with experiments on PLP-dependent enzymes, which provides a validation of the present PI-FEP/UM method [53,54]. The calculated carboxyl ¹³C-KIEs in Table 2 are closely related to the variations in the O – C – O bond angle of the carboxylate group. The transition state of the O-protonated tautomer in the active site has the smallest O – C – O bond angle of the four decarboxylation reactions, indicating an early transition state with the least gain in bond order on the CO₂ group. On the other hand, the N-protonated isomer has the largest O – C – O angle, indicative of enhanced force constant in the CO₂ stretch and a late transition state (mirrored by a larger value in the reaction coordinate). Thus, for the N-protonated configuration of the PLP cofactor in the enzymatic reaction, the reduction in the difference of zero-point energy (ZPE) (between ¹²C and ¹³C) associated with the C_α – C stretch is accompanied by an increase in the O – C – O stretching frequency, orthogonal to the reaction coordinate, in going from the reactant to the transition state. The two compensating factors yield a smaller computed carboxyl KIE in the N-protonated PLP aldimine substrate. The change in O – C – O angle is less for the O-protonated configuration, resulting in a greater KIE at the carboxyl site of the substrate.

Table 2.

Computed kinetic isotope effects and selected geometrical parameters at the transition state. Bond distances are given in angstroms, and angles are in degrees. Standard errors (±1σ) in computed kinetic isotope effects are determined over ten separated block averages. Each KIE is obtained by using all data sampled in the PI-FEP/UM simulations.

	Dopa decarboxylase		Aqueous solution
	O-protonated	N-protonated	O-protonated	N-protonated
12k/13k(C)	1.053 ± 0.002	1.047 ±0.003	1.053 ±0.003	1.049 ±0.002
12k/13k(Cα)	1.037 ±0.006	1.026 ±0.005	1.030 ±0.003	1.034±0.003
1k/2k(Hα)	1.053 ±0.032	1.144±0.066	0.975 ± 0.051	1.137±0.051
Rc(Cα-C)	2.07	2.17	2.06	2.17
R(Cα=N)	1.36 ±0.02	1.39 ±0.03	1.34 ±0.02	1.38 ±0.02
θ(O=C=O)	148.6 ± 4.4	153.8 ±4.2	150.5 ±5.4	153.2 ±4.5

The rehybridization at the C_α position from sp³ to sp² along the decarboxylation path is best reflected by the 2° ¹k/²k(H_α) KIEs (Table 2). The development of the C_α=N double bond character is indicated by the distance R(C_α=N) in Table 2. In the N-protonated configuration (a longer C_α=N bond distance at the transition state), the dominant factor is the change in the C – H deformation mode, giving rise to greater decrease in ZPE, thereby, relatively large secondary KIEs. For the O-protonated isomer of the cofactor, a greater C_α=N double bond character is developed, resulting in an increase in the C\H stretch at the transition state. Thus, the 2° ¹k/²k(H_α) KIEs are relatively small and even inverse for the reaction in water (Table 2). It would be interesting to use the predicted trends in the primary and secondary KIEs on carbon and hydrogen to experimentally distinguish between the N-protonated and O-protonated tautomers of the PLP-dopa external aldimine in the DDC-catalyzed decarboxylation.

2.2.1. Enhancement of α-carbon acidity by PLP and alanine racemase

AlaR catalyzes the interconversion between l-Ala and d-Ala (Scheme 4), [55,56] which is involved in the formation of glycan in bacterial cell walls, making it an interesting target for drug design [57]. The mechanism of the racemization reaction has been studied extensively both experimentally [21,56,58–62] and theoretically [4,5]. The enzymatic process is accomplished by the acid–base pair residue Tyr265′ (prime indicates residues from the second subunit) and Lys39, [21,58,59] which are located on opposite sides of the PLP conjugated plane, ideally position for a two-step proton transfer. The proton abstraction by Tyr265′ is the rate-limiting step based on mutation and kinetic isotope effect measurements [21,58–61]. Toney and co-workers have presented a comprehensive free-energy profile for this reaction [61,62].

Scheme 4.

Reaction steps for the alanine racemase catalyzed reaction.

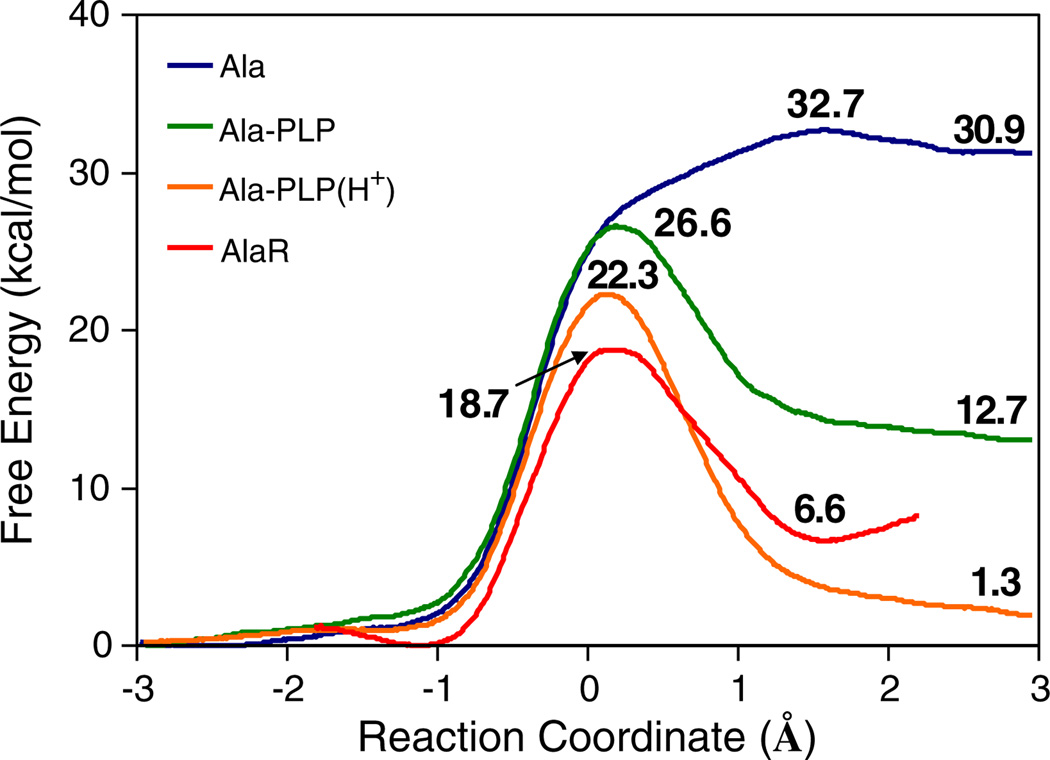
To understand the catalytic role of PLP, we analyzed a series of model reactions in the gas-phase, in aqueous solution phase, and in the enzyme. Phenolate anion was used to model Tyr265′ in AlaR, and the free energy changes of the Cα hydrogen abstraction of zwitterionic Ala, in Ala-PLP, and in Ala-PLP(H⁺) by a phenolate ion were determined in the gas-phase and in water. We found that when Ala is fused to pyridoxal through a protonated Schiff base, where the Ala-PLP protonation state of the pyridine ring is taken to be the same as in the enzyme, there is an inherent anti-catalytic effect due to the PLP cofactor. This may be ascribed to the formation of a doubly negative charge, which is highly unfavorable in the gas-phase. However, when the pyridine nitrogen is protonated as in Ala-PLP (H⁺) there is an appreciative catalytic effect, even in the gas-phase. Interestingly, when these model reactions were immersed in an aqueous solution, a noticeable catalytic effect (i.e. barrier reduction) is observed both using Ala-PLP and using Ala-PLP(H⁺) as the substrate (Fig. 3) [4,5]. Additionally, the stability of the intermediate Cα-carbanion is greatly enhanced when Ala is fused to the PLP cofactor. Interestingly, this effect is greater in the N-protonated cofactor form, thus the Ala-PLP(H⁺) has a greater ability to stabilize the Cα carbanion than the unprotonated-pyridine form.

Fig. 3.

Computed classical potentials of mean force for proton abstraction reactions of alanine and a phenoxide ion in various forms: blue, alanine zwitterion; green, Ala-PLP; and orange, Ala-PLP(H+) all in water; and red, Ala-PLP in alanine racemase.

Based on these simulations we estimated the pKa values of the external aldimine and related species. The computed pKa for Ala based on the PMF and the experimental value for phenol (10.0), is 32.7, comparable to a value of 28.9 for Gly [63]. The pyridine-protonated PLP cofactor reduces the Ala Cα pKa value by nearly 22 units, whereas the pKa is reduced by 13.4 units in the unprotonated form. For comparison, Dixon and Bruice reported a pKa of 12 for Ala-PLP(H⁺) and 14 for Ala-PLP [64]. Richard et al. found recently that the PLP(H⁺) co-factor increases the Cα-acidity of Gly by ca. 12 pKa units, i.e. from 29 to 17 [1,8]. Moreover, the pyridine-unprotonated Gly-PLP external aldimine is estimated to have an intermediate value between the two.

The Ala-PLP carbanion intermediate is further stabilized by the enzyme environment in the AlaR catalyzed reaction (Fig. 3). Indeed, it was found that the pKa shift due to the cofactor is 13.4, while the enzyme further reduces this value by 7.1. The reaction barrier is similarly reduced compared to the Ala-PLP reaction in aqueous solution. Interestingly, the PLP-independent enzyme proline racemase achieves a similar catalytic effect in the absence of a cofactor [65]. The role of nuclear quantum effects were also investigated for the AlaR reaction and it was found that zero-point energy effects were similar to that expected for C-H activation reactions, while tunneling effects were found to be negligible [4].

2.3. Mutant alanine racemase

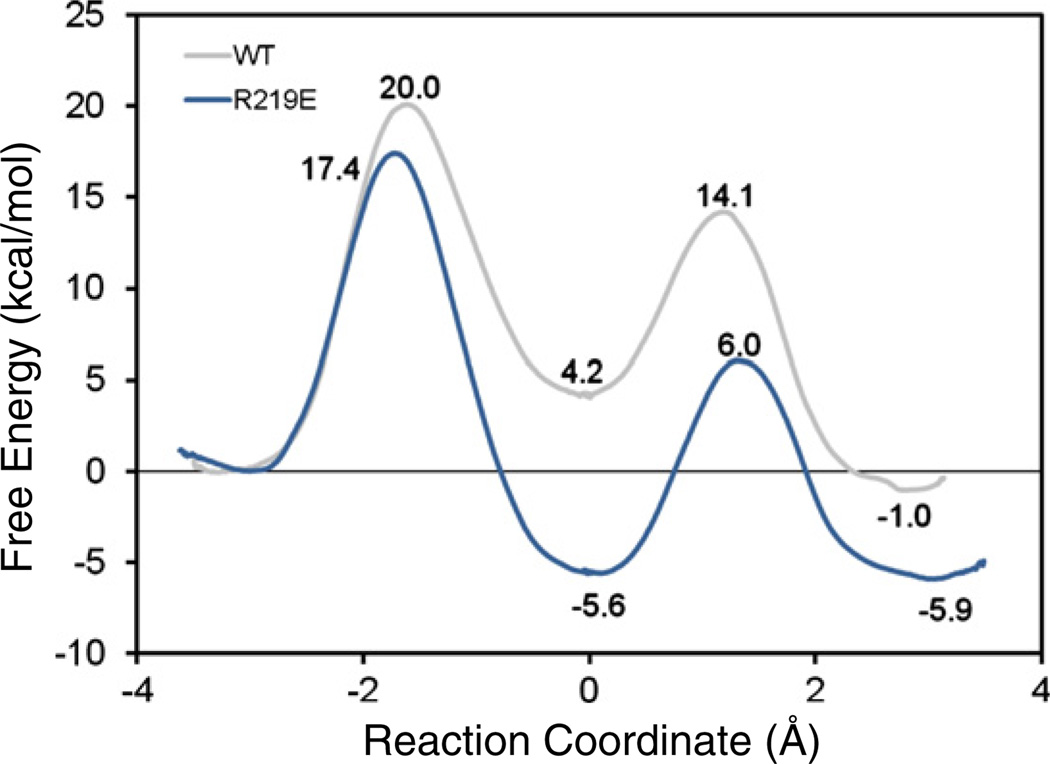
In an effort to understand the role of protonation of the pyridine nitrogen in PLP, we also studied the Arg219Glu mutant [66]. In this mutant, the pyridine nitrogen interacts with the Glu residue, necessitating a protonated state. We found that the enzyme is able to somewhat enhance the catalytic effect or the Cα-acidity beyond the effect in water. In the Arg219Glu mutant the stability of the Ala-PLP (H⁺) cofactor is greatly enhanced compared to Ala-PLP in the wildtype enzyme (Fig. 4), although this is likely not due to the protein environment. Indeed, the catalytic effect of the Arg219Glu mutant of AlaR may be ascribed to the inherent ability of the fused substrate-cofactor moiety, Ala-PLP(H⁺), to stabilize the carbanion intermediate (Fig. 3). Note that the free energies in Fig. 4 were determined starting from a completely separate setup and initial equilibrations; the slight free energy difference on the wild-type enzyme indicates the range of uncertainties of such free energy simulations on enzymatic reactions. The enhanced stability of the intermediate in the Arg219Glu mutant increases its life-time and likelihood of side reactions. Analysis of the electronic distribution in the intermediate suggests that this is not primarily due to charge delocalization into the pyridine moiety, but into the Schiff base moiety and carboxylate unit, in accordance with the work of Richard and co-workers [1]. Indeed, the principle effect of the protonated cofactor is to reduce the total charge of the substrate-cofactor adduct, which enhances the intrinsic Cα-acidity.

Fig. 4.

Computed potentials of mean force for the alanine racemization reaction catalyzed by the wild-type and Arg219Glu mutant enzymes

The increased intermediate life-time opens the way for potential side-reactions, which would reduce the activity and specificity for racemization for this mutant. Specifically, it has been suggested that transamination of PLP to Pyridoxamine-5′-Phosphate (PMP), initiated by a 1,3 proton transfer from the Ala's Cα to the C4′ of the cofactor by the Lys39 amine/ammonium group, might occur [67–69]. Hence we decided to investigate the possibility of a 1,3-proton transfer in the quinonoid intermediate. We found that a 1,3-proton transfer is indeed likely to occur in the mutant form of the enzyme, thus providing a rationale for the observed transamination ability in Arg219Glu. These results suggest that the Arg219Glu mutant can catalyze other reactions in addition to the natural racemization of L/d-Ala, in contrast to the case of the WT AlaR. This is in accordance with the experimental study by Yow et al. which showed the appearance of the characteristic absorbance peak at 300–360 nm of PMP in the Arg219Glu mutant providing evidence for the transamination products [67]. Additionally, the work of Fenn et al. indicated transamination in mutant systems [68,69]. Interestingly, AlaR may be engineered to provide additional functionalities, namely Tyr265′ Ala, which exhibits aldolase activity [70,71].

Analogously, we may compare with d-amino acid transaminase which employs PLP as a cofactor in the conversion of d-amino acids into their corresponding α-keto acids. In this enzyme, Glu177 interacts with the pyridine nitrogen. However, it has been observed that the Glu177Lys mutant enzyme increases its racemase activity 10- fold, while decreases its specific transaminase activity by more than 1000-fold [72]. Interestingly, the crystal structure of this mutant shows that the Lys177 residue points away from the cofactor nitrogen, possibly due to electrostatic repulsion, or steric congestion due to the bulkier nature of Lys compared to Glu. This further underscores the role of this active pocket position in controlling reaction specificity.

3. Conclusions

Molecular dynamics simulations have been carried out on two pyridoxal 5′-phosphate-dependent enzymes to investigate the internal proton transfer equilibrium of the external aldimine species in l-dopa decarboxylase, and carbanion stabilization by the enzyme cofactor in the active site of alanine racemase. In both studies, we employed a combined quantum mechanical and molecular mechanical (QM/MM) approach to model the proton transfer processes and the chemical reactions catalyzed by the enzymes. In the case of DDC, we found that although the N-protonated Schiff base of the external aldimine between an amino acid substrate and PLP is the preferred configuration in the gas phase, solvent effects stabilize the O-protonated hydroxyimine tautomer both in aqueous solution and in the active site. The free energy difference is about −1 kcal/mol in favor of the O-protonated isomer in the enzyme. Since the computed free energy barrier for the internal proton transfer process is only 5 kcal/mol, it suggests that there is rapid equilibrium between the two conformers, both of which are accessible during an enzymatic reaction. In the case of l-dopa decarboxylase, the formation of the external aldimine provides the dominant contribution to lowering the free energy barrier for the spontaneous decarboxylation of an amino acid in water, by about a remarkable 16 kcal/mol. The enzyme l-dopa decarboxylase provides a further stabilization of the transition state by 8 kcal/mol, resulting in a net computed barrier of about 17 kcal/mol in the enzymatic process. Kinetic isotope effects were also determined using an integrated path integral free energy perturbation theory and umbrella sampling simulation (PI-FEP/UM) on the primary ¹³C and the secondary ²H substitutions. It appears that there is sufficient difference in the computed KIEs between the N-protonated and O-protonated PLP configurations to allow these two isomers to be distinguished experimentally. We predicted that in the enzyme active site, the O-protonated tautomer of the PLP-dopa external aldimine exhibits a 2° deuteron KIE below 1.10 and a primary ¹³C KIE of greater 1.05, whereas the N-protonated isomer shows a 2° ¹k/²k(H_α) KIE above 1.10.

In the case of alanine racemase, we found that there are significant solvent effects on the stabilization of the α-carbanion of the external aldimine. In the configuration in which the Schiff base is protonated, but the pyridine ring is unprotonated as that in the active site of AlaR, there is destabilizing contribution to the formation of the α-carbanion in the gas phase, although when the pyridine ring is protonated the contribution is stabilizing. In aqueous solution, the α-carbanion is stabilized both when the pyridine ring is protonated and unprotonated, while AlaR provides strong stabilization of the α-carbanion in the active site. Computational studies of the mutation by replacing Arg219, which donates a hydrogen bond to the pyridine nitrogen in the active site of AlaR, with a Glu residue, showed some stabilization of the Cα carbanion over that in aqueous solution. In the mutant, the pyridine ring of the PLP cofactor is protonated, donating a hydrogen bond to the mutated residue Glu219. The computational studies illustrated in this article show that combined QM/MM simulations can help provide a deeper understanding of the mechanisms of PLP-dependent enzymes.

Glossary

Abbreviations

AM1

Austin Model 1

AlaR

Alanine racemase

DDC

l-dopa decarboxylase

KIE

Kinetic isotope effects

NQE

Nuclear quantum effects

PI-FEP/UM

Path integral-free energy perturbation and umbrella sampling

PLP

Pyridoxal 5'-Phosphate

PSB

Protonated Schiff base

QM/MM

quantum mechanical and molecular mechanical