Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2013 Sep 3;110(38):15354–15359. doi: 10.1073/pnas.1305529110

Macroevolutionary speciation rates are decoupled from the evolution of intrinsic reproductive isolation in Drosophila and birds

Daniel L Rabosky a,1, Daniel R Matute b
PMCID: PMC3780891  PMID: 24003144

Significance

Rates of species diversification vary widely in the natural world, leading to profound differences in species richness among different kinds of organisms. Variation in the rate at which new species arise is frequently assumed to result from factors that influence the rate at which populations become reproductively isolated from each other. We tested this assumption in Drosophila flies and birds. Surprisingly, we find no evidence that the propensity of organisms to evolve reproductive isolation predicts the rate at which they form new species over geological timescales. These results suggest that factors that cause intrinsic reproductive isolation may play less of a role in explaining biological diversity than generally assumed.

Keywords: mechanism of speciation, hybrid incompatibility, speciation gene, species concept

Abstract

The rate at which speciation occurs varies greatly among different kinds of organisms and is frequently assumed to result from species- or clade-specific factors that influence the rate at which populations acquire reproductive isolation. This premise leads to a fundamental prediction that has never been tested: Organisms that quickly evolve prezygotic or postzygotic reproductive isolation should have faster rates of speciation than organisms that slowly acquire reproductive isolation. We combined phylogenetic estimates of speciation rates from Drosophila and birds with a method for analyzing interspecific hybridization data to test whether the rate at which individual lineages evolve reproductive isolation predicts their macroevolutionary rate of species formation. We find that some lineages evolve reproductive isolation much more quickly than others, but this variation is decoupled from rates of speciation as measured on phylogenetic trees. For the clades examined here, reproductive isolation—especially intrinsic, postzygotic isolation—does not seem to be the rate-limiting control on macroevolutionary diversification dynamics. These results suggest that factors associated with intrinsic reproductive isolation may have less to do with the tremendous variation in species diversity across the evolutionary tree of life than is generally assumed.

A central challenge at the interface between macroevolution and microevolution is to explain the population-level processes that contribute to biological variation in diversification rates and species richness (1). Phylogenetic evidence for biological variation in the rate of species diversification is widespread (2, 3), and numerous studies have now linked specific traits to the dynamics of speciation and extinction as realized over macroevolutionary timescales (2, 4). At the population level, a microevolutionary research program on the biology of speciation has focused on the factors that lead to various forms of reproductive isolation (RI) between populations (5, 6). Explaining how and why RI evolves is generally considered to be the central and defining challenge in the study of speciation (2, 7–9), and recent studies have made great progress toward explaining the genetic and ecological basis for various forms of RI (7, 8, 10).

Most microevolutionary research on speciation implicitly assumes that RI is the defining and rate-limiting step in the speciation process (7, 8, 11), but the evolution of RI need not bear any predictive relationship to rates of species diversification as realized over macroevolutionary timescales (12). This has long been recognized by the paleontological community, where “successful” speciation is believed to entail not only the evolution of reproductive isolation but also the persistence of incipient species (13–15). For example, speciation might be limited primarily by the rate at which lineages form allopatric isolates (6, 16) or by the capacity for geographic range expansion (17, 18). Likewise, speciation might be limited more by factors that influence the temporal persistence of reproductively isolated populations (15, 19) than by the rate at which RI itself evolves. Finally, macroevolutionary diversity dynamics might be regulated primarily by factors that influence extinction rates (4). These factors need not be independent of reproductive isolation. For example, reproductive barriers can reduce the probability of population fusion following secondary contact between nascent species, thus exerting a direct effect on population persistence (2). Likewise, RI can influence the dynamics of geographic range evolution, which may in turn have secondary consequences for rates of demographic extinction and allospecies formation (17, 18).

Here, we provide a direct test of the relationship between reproductive isolation and macroevolutionary diversification. If the widespread variation observed in macroevolutionary diversification rates (20, 21) is attributable to factors that cause RI (2, 22, 23), then it must also be true that lineage-specific differences in the rate at which RI evolves will influence large-scale patterns of species diversification. In this context, a species with a “fast” rate of RI evolution will, all else being equal, form more reproductively isolated lineages than a species with a “slow” rate of RI evolution.

We use data from the two groups of animals for which the most extensive multispecies RI data have been compiled and for which we could derive phylogeny-based estimates of species diversification rates. The first dataset is an update of Coyne and Orr’s (2) seminal work on the relationship between genetic distance, geographic status, and reproductive isolation in Drosophila (24) and contains estimates of both premating and intrinsic postzygotic RI. The second dataset includes measurements of intrinsic postyzygotic isolation from interspecies hybridizations in birds (25, 26). We developed a modeling framework for estimating species- and clade-specific differences in the rate of evolution of RI and applied it to both birds and flies to test whether lineages that quickly evolve RI are characterized by fast rates of macroevolutionary diversification. This framework can be used to assess whether any components of reproductive isolation are associated with speciation rates as measured at macroevolutionary scales. We find significant heterogeneity within both flies and birds in the rate at which lineages evolve intrinsic postzygotic isolation. However, this variation is uncorrelated with macroevolutionary rates of species diversification. These results suggest that patterns of biological diversity may have less to do with reproductive isolation than generally assumed.

Results

We studied the evolution of reproductive isolation and its relationship to macroevolutionary diversification in Drosophila and birds. For Drosophila, premating isolation was simply the percentage of unsuccessful copulations from interspecific pairings normalized by the expected percentage from the corresponding homospecific pairing (24). For intrinsic postzygotic isolation, RI was computed from observed levels of F1 hybrid sterility and inviability (Materials and Methods and SI Materials and Methods). We developed a modeling framework that enabled us to estimate species-specific and clade-specific differences in the rate at which RI evolves, despite the fact that RI is measured as a property of pairwise crosses between species (Materials and Methods). Our models assume that each species is characterized by a specific velocity of RI evolution, ψ, which interacts additively with ψ values from any other species to generate a particular level of RI. A species with ψ > 0 will tend to accumulate reproductive isolation at a faster-than-average rate, after controlling for genetic distance and geographic status (allopatry: species do not overlap in their geographic ranges; sympatry: species overlap). Likewise, a species with ψ < 0 will tend to accumulate RI more slowly relative to the average rate across a set of taxa.

We analyzed three general models for the accumulation of RI as a function of genetic distance. The simplest model assumes that RI between any two species accumulates linearly through time. In this case, the level of RI between two species (Yij) as a function of genetic distance between them (Xij) is given by Yij = β0 + (β1 + ψi + ψj)Xij + ε, where β0 and β1 are the intercept and slope terms, and ε is an error term (Materials and Methods). We also considered a quadratic model, which allows for increasing rates of RI accumulation through time consistent with “snowball” models for the evolution of genetic incompatibilities (10, 27, 28). Finally, we considered an asymptotic model, where the rate of RI accumulation between taxa decreases through time as it asymptotically approaches an upper bound at Y = 1.0. Because observable RI values are bounded by 0 and 1, we assumed that all observations were censored beyond this range (SI Materials and Methods). For Drosophila, our models also incorporated the geographic status of species pairs (sympatric versus allopatric), because geographic status is known to influence the relationship between reproductive isolation and genetic distance (29).

We considered two additional parameterizations of each functional model (linear, quadratic, and asymptotic): a model with no species-specific differences in the rate of evolution of RI (ψ = 0 for all species), and a model with clade-specific but not species-specific differences (ψ values identical for all species within each of nine major Drosophila species groups or within 30 avian families; SI Materials and Methods). We implemented all models in a Bayesian framework, estimating species-specific or clade-specific ψ values separately for both premating and postzygotic isolation in Drosophila and for postzygotic isolation in birds (Fig. 1). We compared all fitted models using AICM (30), an information theoretic criterion similar to the widely used Akaike information criterion (AIC) that can be estimated from the posterior distribution of log-likelihoods simulated using Markov chain Monte-Carlo (MCMC) methods (Materials and Methods).

Fig. 1.

Fig. 1.

Open in a new tab

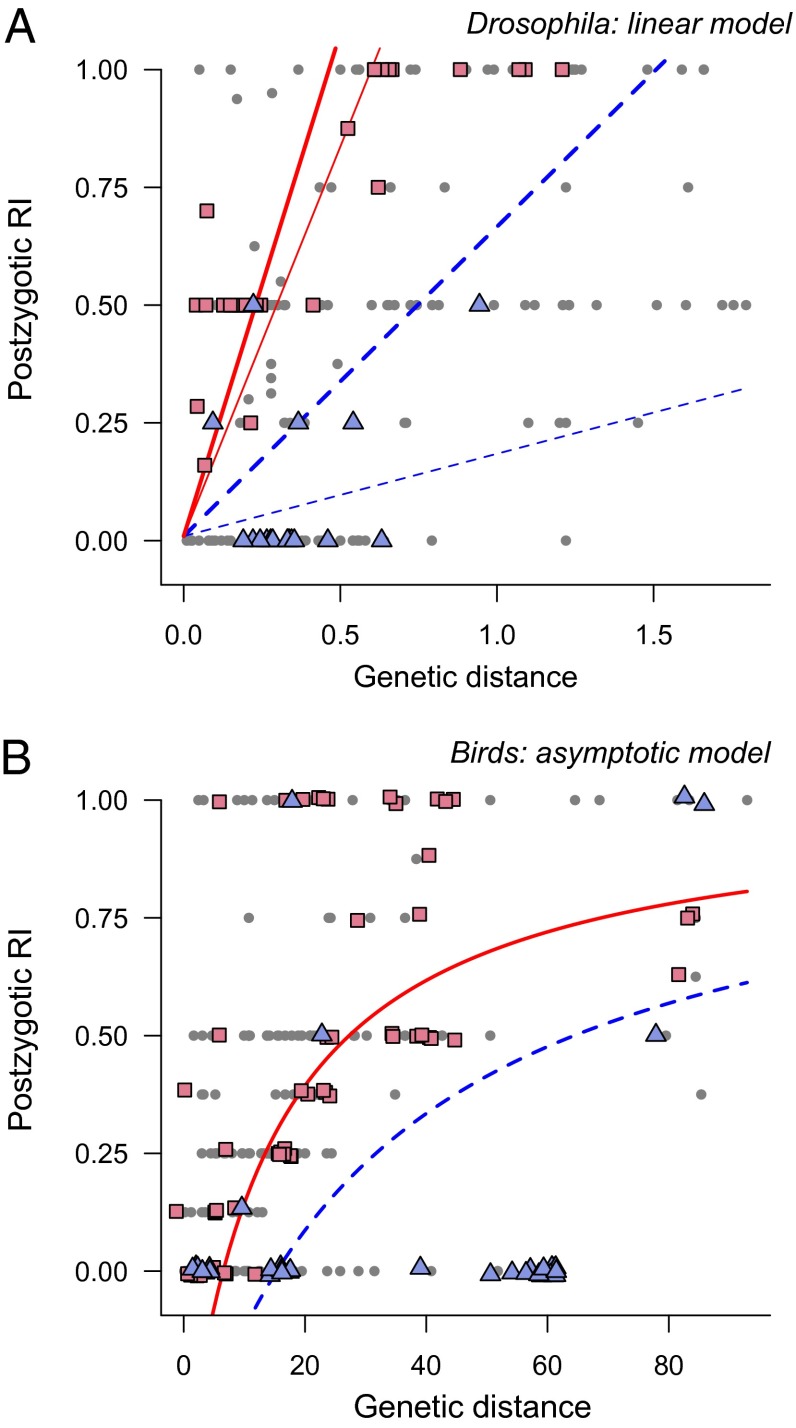
Pairwise postzygotic reproductive isolation in flies and birds. (A) Genetic distance and intrinsic postzygotic RI in 173 pairwise Drosophila crosses. Red squares denote species crosses within a representative subclade with “fast” species-specific velocities of RI evolution (D. willistoni species group); blue triangles denote species with a “slow” velocity of RI evolution (D. virilis species group). Red (solid) and blue (dashed) lines indicate corresponding clade-specific trajectories from fitted linear model; thick and thin lines denote fits for sympatric and allopatric species pairs, respectively. Postzygotic RI ranges from 0 (hybrid offspring both fertile and viable) to 1 (all hybrids are sterile or inviable). (B) Genetic distance and postzygotic RI from 287 pairwise bird crosses. Red denotes pheasants and allies (Phasianidae), a representative clade with fast species-specific velocities of RI evolution; blue denotes parrots (Psittacidae), a family with slow velocities of RI evolution. Red (solid) and blue (dashed) lines denote model-predicted relationships for these clades under the asymptotic model for the accumulation of RI through time. Points in both A and B were jittered slightly in the x-plane to reduce overplotting.

For postzygotic isolation, models with clade-specific variation in ψ generally provided a much better fit to the data than models with ψ = 0 (Drosophila: ΔAICM = 87.2; birds: ΔAICM = 61.9; Figs. S1 and S2 and Table S1). Models with clade-specific ψ values also fit better than more parameter-rich models with species-specific ψ parameters (Fig. S1 and Table S1). A linear model provides the best overall fit to the Drosophila postzygotic data (ΔAICM = 25.0 versus the next-best functional model), but linear and asymptotic models provided similar fits to the avian data (Fig. S1 and Table S1). In contrast, we found little evidence that the rate at which premating isolation evolves differs among Drosophila clades (ΔAICM = 1.0 for models with clade-specific ψ versus ψ = 0). ANOVA analyses of species-specific ψ values provide strong support for among-clade variation in the rate at which postzygotic RI evolves in both Drosophila and birds (Table S2; P < 0.001 for all models), but only a marginal effect for premating isolation was observed (P = 0.07). Under all functional models, ∼30% of the variance in species-specific ψ values was explained at the clade level for both postzygotic datasets, but only 4–11% was explained by clade for premating isolation in Drosophila (Table S2). These results indicate the presence of substantial variation in clade-specific rates of postzygotic RI evolution in Drosophila and birds (Fig. 2).

Fig. 2.

Fig. 2.

Open in a new tab

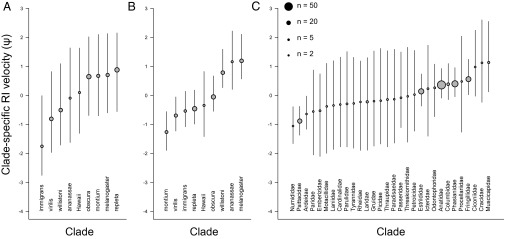
Estimates of clade-specific velocities of RI evolution (ψ). (A) Premating ψ for nine Drosophila subclades where sampling was adequate to estimate clade-specific speciation rates. (B) Postzygotic ψ for Drosophila. (C) Postzygotic ψ across 30 families of birds. Confidence intervals denote 90% Bayesian credible interval about the mean. Point size reflects the number of species from each clade for which RI data were available.

Speciation rates for nine major Drosophila subclades were computed by pairing literature estimates of species richness with phylogenetic estimates of clade age (Materials and Methods and SI Materials and Methods; Fig. S3). This approach assumes that taxonomic species are not delimited strictly on the basis of reproductive isolation; otherwise, it would be trivially true that rates of RI evolution would predict speciation rates at macroevolutionary scales. In general, this assumption is justified, because the vast majority of taxonomic species are delimited phenotypically and not in reference to an explicit criterion of reproductive isolation (31). For birds, we estimated rates of speciation on a recent time-calibrated phylogenetic tree that contained 67% of known species (20), using an automatic Bayesian model selection framework (21) that enabled us to estimate rates of speciation on every branch of the avian phylogeny (Figs. S4 and S5). Using these branch-specific speciation estimates, we computed mean speciation rates for each family of birds (n = 30) for which we had estimates of the family-specific velocity of RI evolution (Fig. 2C). We then tested whether clade-specific ψ parameters predicted variation in speciation rates among clades in both flies and birds. For birds, we also tested the relationship between ψ and estimated maximum rates of speciation within each clade. If macroevolutionary diversification rates are regulated by diversity-dependent factors (32, 33), we predict that the rate at which RI evolves is most likely to influence maximum rates of diversity accumulation and not mean rates across entire clades, which are more likely to be dampened by ecological interactions between species (34).

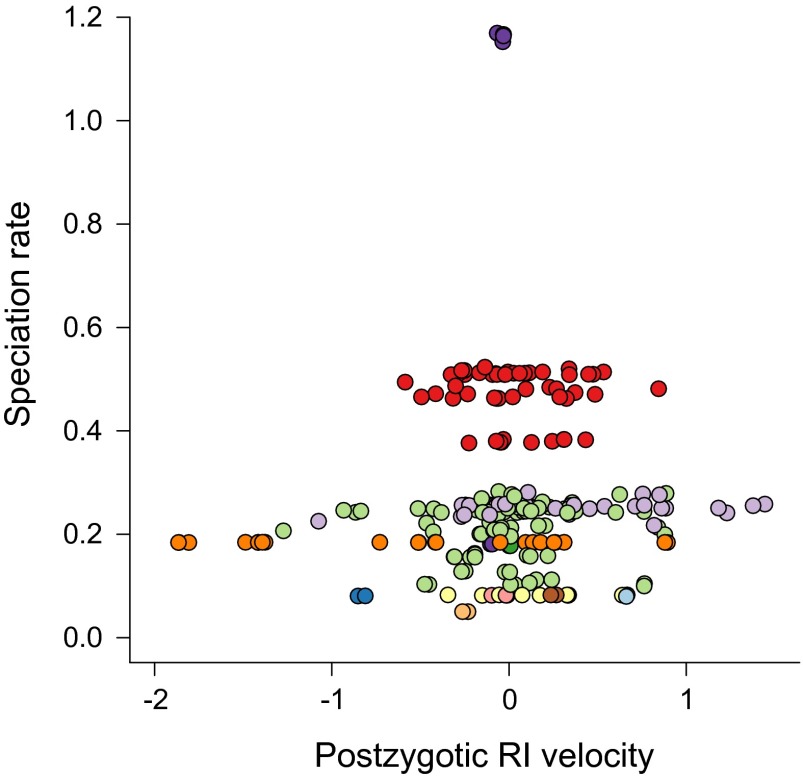
No significant positive correlations were found between any metric of macroevolutionary dynamics and clade-specific velocities of RI evolution (Fig. 3 and Table 1 and Table S3). In Drosophila, postzygotic ψ values estimated under each of three functional models showed no significant association with estimated speciation rates under either high or low extinction rates (all Pearson and Spearman P values >0.39; df = 7), and all estimated correlation coefficients were negative (Table 1 and Table S3). For postzygotic isolation in birds, no significant Pearson or Spearman correlations were observed (all P values >0.23; df = 28) across 18 combinations of functional RI model and speciation metric (Table 1, Table S3, and Fig. 3). Similar results were observed for premating isolation in Drosophila (Table 1 and Table S3), although this is unsurprising given that little variation in premating ψ was apparent among major clades.

Fig. 3.

Fig. 3.

Open in a new tab

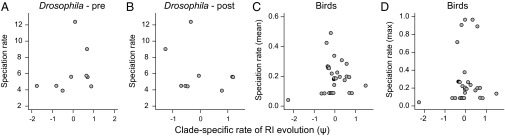
Rates of speciation are uncorrelated with clade-specific variation in the rate at which species accumulate RI (Table 1; Table S3). (A) Premating ψ and relative speciation rate across nine Drosophila clades assuming low relative extinction rates (ψ model: asymptotic). (B) Postzygotic ψ for Drosophila (linear model) and relative speciation rates. (C) Postzygotic ψ estimates and mean speciation rate across 30 avian families (ψ model: asymptotic). (D) Postzygotic ψ estimates and the maximum speciation rate for bird clades.

Table 1.

Relationship between macroevolutionary diversification rate (λ) and the rate of prezygotic and postzygotic evolution (ψ) for major clades of flies and birds

Group Model Metric Pearson correlation (P value) Spearman correlation (P value) PGLS slope PGLS P value df
Drosophila (pre) Asymptotic λ0 0.3 (0.43) 0.23 (0.55) 1.03 0.45 9(7)
Drosophila (pre) Asymptotic λ95 0.24 (0.53) 0.58 (0.11) 0.86 0.38 9(7)
Drosophila (post) Linear λ0 −0.31 (0.42) −0.08 (0.84) −1.22 0.21 9(7)
Drosophila (post) Linear λ95 −0.31 (0.41) −0.10 (0.81) −0.71 0.33 9(7)
Birds Linear λ −0.01 (0.95) 0.0 (0.98) −0.01 0.81 30(28)
Birds Linear λMAX −0.03 (0.8) 0.05 (0.77) −0.03 0.81 30(28)
Birds Linear λq80 −0.03 (0.87) 0.04 (0.82) −0.01 0.77 30(28)
Birds Asymptotic λ 0.04 (0.83) 0.05 (0.79) −0.01 0.67 30(28)
Birds Asymptotic λMAX −0.01 (0.96) 0.12 (0.54) −0.04 0.7 30(28)
Birds Asymptotic λq80 −0.01 (0.98) 0.08 (0.66) −0.01 0.73 30(28)
Open in a new tab

Results are shown only for the best-fit functional models for the accumulation of RI with genetic distance (Table S1 and Fig. S1). Linear and asymptotic models were approximately equivalent for birds and results for both models are shown. For Drosophila, λ0 and λ95 are constant-rate estimators of the speciation rate assuming no extinction (λ0) or high extinction (λ95). For birds, λ is the mean speciation rate within each family, λMAX is the maximum observed rate within each family, and λq80 is the estimated 0.80 quantile of the distribution of rates for each family. Avian results are shown only for the Hackett backbone topology; results for Ericson topology and for all other models are given in Table S3. The BAMM model used for the avian dataset estimates speciation rates separately from extinction rates.

We also performed phylogenetic generalized least-squares (PGLS) regressions to account for phylogenetic autocorrelation of diversification rates and ψ (35). In general, these results trended toward negative relationships between macroevolutionary dynamics and ψ (Table 1 and Table S3), but no significant relationships were observed (all P values >0.21). We then estimated the instantaneous rate of species formation for each of the 244 species of birds in the reproductive isolation dataset (Fig. S5). We tested whether species-specific ψ values could account for any variation in lineage-level speciation rates across the radiation of extant birds. We found no relationship between the rate at which individual lineages acquire intrinsic postzygotic RI and their instantaneous rate of speciation (Fig. 4; linear model: slope = 0.0093, t = 0.036, PGLS P = 0.97, df = 244; asymptotic model: slope = 0.074, t = 0.19, PGLS P = 0.85).

Fig. 4.

Fig. 4.

Open in a new tab

Relationship between rates of speciation and species-specific velocities of postzygotic RI evolution across 244 species of birds. Instantaneous rates of speciation were estimated for each lineage under a statistical model that allowed each species to have a potentially unique rate of speciation (Fig. S5). Identically colored points denote species from the same order. Species that quickly evolve intrinsic reproductive isolation from other species do not speciate at faster rates than other species.

We then performed a series of power simulations to assess whether our analyses would have had sufficient power to detect a relationship between ψ and speciation rates if such a relationship existed. We simulated pairwise reproductive isolation datasets that were structurally identical to the Drosophila and avian datasets considered here (Materials and Methods), but with known correlations between ψ and the rate of speciation and an error variance estimated from the observed data. Given the data and analysis protocol considered here, we have moderate power to infer a true correlation between ψ and diversification rate in both the Drosophila and avian postzygotic RI datasets (Fig. S6).

Discussion

Macroevolutionary analyses have discovered compelling evidence for biological variation in diversification rates in a wide range of taxa. However, it has been difficult to link the patterns of species origination and extinction as realized over geological time to specific mechanisms that occur within and between populations at ecological timescales. Previous studies have speculated that some biological traits might influence macroevolutionary dynamics via their effects on the rates at which populations evolve reproductive isolation (2, 22, 23, 36). By quantifying lineage-specific variation in the rate at which species accumulate RI, our study provides a direct test of the relationship between RI and macroevolutionary diversification. If the causes of speciation at macroevolutionary scales are merely the long-term manifestation of processes we typically study at microevolutionary scales, we should observe a coupling between rates of evolution of RI and macroevolutionary diversification. We found that clades of both flies and birds differ significantly in the rate at which they evolved intrinsic postzygotic isolation, but this variation is decoupled from macroevolutionary diversification dynamics. For Drosophila, we also found a lack of relationship between premating sexual isolation and macroevolutionary diversification, although the differences in rates of premating RI evolution across Drosophila clades are not significant.

Our results bear most directly on the relationship between intrinsic genetic incompatibilities and speciation. The genetic factors that contribute to hybrid inviability and sterility have been widely studied, owing in large part to the relative ease with which controlled laboratory crosses can be performed between different species (2, 37, 38). Most researchers recognize that RI can take many forms, but genetic incompatibilities are nonetheless assumed to play an important role in speciation (2, 39, 40). Genetic incompatibilities have even been proposed to play a role in bird speciation (37, 41), where sexual and ecological isolation is common between closely related species pairs (37). Interestingly, the idea that postzygotic isolation contributes little to the onset of bird speciation was suggested previously (42) but had not been tested. Our results constitute a formal test of this idea and suggest that hybrid incompatibilities in birds may have little to do with the macroevolutionary realization of the speciation process.

Given the observed levels of variation in macroevolutionary diversification rates and rates of postzygotic RI evolution across clades, we find it surprising that we see no hint of a relationship between these quantities (Table 1 and Fig. 3 and Table S3). Reproductive isolation data are notoriously noisy (e.g., Fig. 1), but our power simulations (Fig. S6) indicate that moderate correlations between postzygotic ψ and the rate of speciation could have been inferred under our analytical protocol. It is true that weaker correlations between RI and speciation would have been more difficult to detect in these datasets, and future work may yet find that the rate of evolution of RI plays at least a minor role in shaping variation in speciation rates in these clades. We found little evidence for clade-specific variation in premating ψ for Drosophila, suggesting that the causes of variation in macroevolutionary diversification among Drosophila clades is unlikely to be explained by differences in the rate at which clades evolve premating isolation. The overall structure of premating and postzygotic datasets for Drosophila is similar, and the number of crosses in the premating dataset exceeds that of the postzygotic dataset; we thus attribute our failure to find clade-specific differences in premating ψ to a lack of biologically meaningful variation in this parameter rather than lack of statistical power.

Under a strict biological species concept, speciation is defined as the evolution of reproductive isolation, but a more inclusive view of the speciation process allows for the possibility that other factors limit the rate at which speciation occurs. Many researchers have suggested that speciation might be limited primarily by factors associated with the persistence of incipient species (13–15). Models of ephemeral speciation propose that it is relatively easy for lineages to form incipient species, but the vast majority of new species do not persist over macroevolutionary timescales (15, 19). This view is closely related to Darwin’s perspective on speciation, whereby ecological character divergence plays a critical role in mediating the temporal persistence of new species (43–45). Anecdotally, at least, it seems clear that many examples of rapid speciation in nature are limited by population persistence. Stickleback fishes, for example, can evolve reproductive isolation very quickly in postglacial lakes, but nascent species pairs typically fail to persist over geological timescales (46). We speculate that primary controls on species persistence may involve factors associated with geographic range expansions (17), including ecological divergence between incipient species (47) and antagonistic interactions with pathogens (48). Addressing these issues will require careful consideration of the nature of species themselves (16), and it is possible that the manner in which species are defined could influence the results of analyses such as those presented here (49).

For many decades, researchers have sought to explain the mechanisms that lead to reproductive isolation between incipient species (5, 6). Reproductive isolation clearly plays an important role in maintaining species boundaries, but there is yet no evidence that any forms of reproductive isolation influence speciation rates as realized over macroevolutionary timescales. We have described a general framework that can be used to test whether any components of reproductive isolation are associated with speciation as measured at macroevolutionary scales, provided that broadly comparative data on pairwise RI can be obtained.

Our results are based on two of the most exhaustive compilations of RI ever assembled for any group of organisms (24–26, 50) and include many decades of work by dozens of researchers. The results reported here pertain strictly to Drosophila and birds and suggest an acute need for empirical studies on the evolution of reproductive isolation from groups of organisms that vary widely in their rate of macroevolutionary diversification. Numerous studies have assessed components of RI at relatively fine taxonomic scales (51, 52), but we suggest that future research should explicitly target groups that are known to differ in diversification rate. At present, we do not understand the evolutionary and ecological mechanisms that underlie differential rates of species diversification in Drosophila, birds, and other taxa. However, a complete explanation for speciation in nature may require that we broaden our explanatory paradigm beyond the mechanisms that underlie reproductive isolation.

Materials and Methods

RI Data.

We compiled literature data on RI for birds (26) and Drosophila (24, 50). Prezygotic (premating) RI in the dataset was based on laboratory copulation experiments (24), and the overall level of premating RI was computed as 1 − (frequency of heterospecific matings)/(frequency of homospecific matings). We used Yukilevich’s (24) estimates for postzygotic RI in our analyses, which assign each species cross a value between 0 and 1, based on the percentage of sterile or inviable F1 offspring for each interspecific cross. The full avian dataset consisted of postzygotic RI estimates from 407 hybridizations (26). The data were scored on a scale of 1–5, with 1 indicating fertility of the crossed pair, 3 indicating that F1s in both directions were viable but infertile, and 5 indicating that no F1s were viable. We converted these to a [0, 1] scale for comparison with Drosophila. Excluding intraspecific crosses and crosses involving species that were not present in the Jetz et al. (20) phylogeny left a total of 244 species and 287 crosses.

Phylogenies.

We inferred a phylogeny for major Drosophila lineages using DNA sequence alignments from a recent phylogenetic study of the genus (53). We trimmed the taxon set to include 94 species that we believed to be important for estimating the relative crown-clade age for each of nine major subclades for which we could obtain estimates of species richness (SI Materials and Methods). We analyzed the resulting dataset of 94 taxa using an uncorrelated lognormal relaxed-clock model of sequence evolution in the program BEAST. We used two phylogenies as a framework for estimating speciation rates in birds (Fig. S5) and for avian PGLS analyses (Fig. S4). Both are derived from the Jetz et al. (20) time-calibrated phylogeny for all birds. We analyzed maximum clade credibility (MCC) trees for both backbone trees used by Jetz et al. (20). These trees contained only the 6,670 species for which genetic data were available; we did not include those species whose phylogenetic positions were estimated from taxonomic information alone (20).

Rate of RI Evolution.

We assumed that each species was characterized by a specific tempo of RI evolution, which we denote by ψ. Individual ψ values interact additively, such that the expected rate of evolution of reproductive isolation from a given cross between the i’th and j’th species is proportional to ψi + ψj. In addition to the linear model described in the main text, we considered an asymptotic model, such that Yij = ε + (β0 + δXij)/(1 + δXij), where δ = (β1 + ψi + ψj) and ε is sampled from the error distribution for pairwise RI observations. We also considered a quadratic model, where reproductive isolation was modeled as 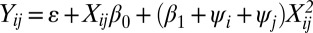Inline graphic. For Drosophila, our model also incorporated the geographic status of species pairs (sympatric versus allopatric), because geographic status is known to influence the relationship between reproductive isolation and genetic distance (50, 54). Models to account for sympatric and allopatric taxa were identical to those described above but contained separate β0 and β1 parameters for sympatric and allopatric species pairs (SI Materials and Methods). Thus, the full linear model for the Drosophila datasets is given by

graphic file with name pnas.1305529110uneq1.jpg

where β0,A and β0,S denote parameters for allopatric and sympatric species pairs and c is an indicator variable that takes a value of 1 if the species pair is sympatric and 0 if allopatric. We implemented all models in a Bayesian framework to estimate marginal posterior distributions and maximum a posteriori (MAP) estimates for ψ and all other parameters. We compared models using a posterior-simulation based version of the AIC criterion, known as AICM. AICM can be computed directly from MCMC simulation output as AICM = 2L − 2S, where L and S denote the mean and variance of the posterior log-likelihoods (30). Full details of the modeling approach are given in SI Materials and Methods.

Diversification Rates.

Using BEAST-derived estimates of crown-clade age for Drosophila clades, we computed estimators of net speciation rates (55) under relative extinction rates of 0 and 0.95. For PGLS analyses involving Drosophila, we pruned the MCC tree to include only representatives from each of the nine major clades outlined in SI Materials and Methods. For birds, we estimated branch-specific rates of speciation using a new Bayesian method (BAMM) for the analysis of speciation and extinction rates on molecular phylogenies (21). BAMM enables reconstruction of marginal posterior distributions of speciation and extinction rates on each branch of a reconstructed phylogenetic tree (21). The avian trees contained only 67% of avian species, and we analytically accounted for incomplete taxon sampling directly in the BAMM model itself (21). We modified BAMM to allow rates of speciation to change exponentially through time within particular shift regimes, thus allowing the model to explicitly account for diversification rate variation through time and among lineages (SI Materials and Methods). We performed BAMM analyses on both Hackett and Ericson backbone topologies and report all rates and correlations in Table S3.

Power Analyses.

For each RI dataset, we simulated pseudodatasets with a known correlation between RI and macroevolutionary diversification. We first sampled ψ values for each clade from a distribution with variance identical to the observed (estimated) distribution. We then generated RI observations using the MAP parameter estimates for each dataset, including random noise sampled from the fitted error distribution. All datasets simulated in this fashion contain the same number of pairwise crosses per clade as the observed data. We then sampled diversification rates from a lognormal distribution parameterized to have the same mean and variance as the observed distribution such that the Pearson correlation between clade-specific ψ values and diversification was between 0.25 and 1.0. We estimated MAP parameter values for each simulated dataset and evaluated the correlation between the estimated ψ values and speciation rates. A total of 2,000 simulations were performed for each dataset (SI Materials and Methods and Fig. S6).

Supplementary Material

Supporting Information
supp_110_38_15354__index.html (7.5KB, html)

Acknowledgments

Comments from anonymous reviewers greatly improved the quality of this work. This work was supported by the Miller Institute for Basic Research in Science at the University of California, Berkeley; by the US National Science Foundation (DEB-1256330); and by the Chicago Fellows Program at the University of Chicago.

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1305529110/-/DCSupplemental.

References

  • 1.Kisel Y, et al. Testing the link between population genetic differentiation and clade diversification in Costa Rican orchids. Evolution. 2012;66(10):3035–3052. doi: 10.1111/j.1558-5646.2012.01663.x. [DOI] [PubMed] [Google Scholar]
  • 2. Coyne JA, Orr HA (2004) Speciation (Sinauer, Sunderland, MA)
  • 3.Rabosky DL, McCune AR. Reinventing species selection with molecular phylogenies. Trends Ecol Evol. 2010;25(2):68–74. doi: 10.1016/j.tree.2009.07.002. [DOI] [PubMed] [Google Scholar]
  • 4.Jablonski D. Species selection: Theory and data. Annu Rev Ecol Evol Syst. 2008;39:501–524. [Google Scholar]
  • 5.Dobzhansky TH. Genetics and the Origin of Species. New York: Columbia Univ Press; 1937. [Google Scholar]
  • 6.Mayr E. Animal Species and Evolution. Boston: Belknap Press Harvard Univ Press; 1963. [Google Scholar]
  • 7.Nosil P, Schluter D. The genes underlying the process of speciation. Trends Ecol Evol. 2011;26(4):160–167. doi: 10.1016/j.tree.2011.01.001. [DOI] [PubMed] [Google Scholar]
  • 8.Sobel JM, Chen GF, Watt LR, Schemske DW. The biology of speciation. Evolution. 2010;64(2):295–315. doi: 10.1111/j.1558-5646.2009.00877.x. [DOI] [PubMed] [Google Scholar]
  • 9.Turelli M, Barton NH, Coyne JA. Theory and speciation. Trends Ecol Evol. 2001;16(7):330–343. doi: 10.1016/s0169-5347(01)02177-2. [DOI] [PubMed] [Google Scholar]
  • 10.Matute DR, Butler IA, Turissini DA, Coyne JA. A test of the snowball theory for the rate of evolution of hybrid incompatibilities. Science. 2010;329(5998):1518–1521. doi: 10.1126/science.1193440. [DOI] [PubMed] [Google Scholar]
  • 11.Maheshwari S, Barbash DA. The genetics of hybrid incompatibilities. Annu Rev Genet. 2011;45:331–355. doi: 10.1146/annurev-genet-110410-132514. [DOI] [PubMed] [Google Scholar]
  • 12.Wiens JJ, Engstrom TN, Chippindale PT. Rapid diversification, incomplete isolation, and the “speciation clock” in North American salamanders (Genus Plethodon): Testing the hybrid swarm hypothesis of rapid radiation. Evolution. 2006;60(12):2585–2603. [PubMed] [Google Scholar]
  • 13.Allmon WD. A causal analysis of the stages in allopatric speciation. In: Futuyma DJ, Antonovics J, editors. Oxford Surveys in Evolutionary Biology. Oxford: Oxford Univ Press; 1992. pp. 219–257. [Google Scholar]
  • 14.Ricklefs RE, Bermingham E. The causes of evolutionary radiations in archipelagoes: Passerine birds in the lesser antilles. Am Nat. 2007;169(3):285–297. doi: 10.1086/510730. [DOI] [PubMed] [Google Scholar]
  • 15.Stanley SM. Macroevolution: Pattern and Process. San Francisco: Freeman; 1979. [Google Scholar]
  • 16.Wiens JJ. What is speciation and how should we study it? Am Nat. 2004;163(6):914–923. doi: 10.1086/386552. [DOI] [PubMed] [Google Scholar]
  • 17.Price TD. The roles of time and ecology in the continental radiation of the Old World leaf warblers (Phylloscopus and Seicercus) Philos Trans R Soc Lond B Biol Sci. 2010;365(1547):1749–1762. doi: 10.1098/rstb.2009.0269. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Weir JT, Price TD. Limits to speciation inferred from times to secondary sympatry and ages of hybridizing species along a latitudinal gradient. Am Nat. 2011;177(4):462–469. doi: 10.1086/658910. [DOI] [PubMed] [Google Scholar]
  • 19.Rosenblum EB, et al. Goldilocks meets Santa Rosalia: An ephemeral speciation model explains patterns of diversification across time scales. Evol Biol. 2012;39(2):255–261. doi: 10.1007/s11692-012-9171-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Jetz W, Thomas GH, Joy JB, Hartmann K, Mooers AO. The global diversity of birds in space and time. Nature. 2012;491(7424):444–448. doi: 10.1038/nature11631. [DOI] [PubMed] [Google Scholar]
  • 21.Rabosky DL, et al. Rates of speciation and morphological evolution are correlated across the largest vertebrate radiation. Nat Commun. 2013;4:1958. doi: 10.1038/ncomms2958. [DOI] [PubMed] [Google Scholar]
  • 22.Hodges SA. Floral nectar spurs and diversification. Int J Plant Sci. 1997;158:S81–S88. [Google Scholar]
  • 23.Panhuis TM, Butlin R, Zuk M, Tregenza T. Sexual selection and speciation. Trends Ecol Evol. 2001;16(7):364–371. doi: 10.1016/s0169-5347(01)02160-7. [DOI] [PubMed] [Google Scholar]
  • 24.Yukilevich R. Asymmetrical patterns of speciation uniquely support reinforcement in Drosophila. Evolution. 2012;66(5):1430–1446. doi: 10.1111/j.1558-5646.2011.01534.x. [DOI] [PubMed] [Google Scholar]
  • 25.Gray AP. Bird Hybrids, A Check-List with Bibliography. Farnham, UK: Commonwealth Agricultural Bureaux; 1958. [Google Scholar]
  • 26.Price TD, Bouvier MM. The evolution of F1 postzygotic incompatibilities in birds. Evolution. 2002;56(10):2083–2089. [PubMed] [Google Scholar]
  • 27.Moyle LC, Nakazato T. Hybrid incompatibility “snowballs” between Solanum species. Science. 2010;329(5998):1521–1523. doi: 10.1126/science.1193063. [DOI] [PubMed] [Google Scholar]
  • 28.Wang RJ, Ane C, Payseur BA. The evolution of hybrid incompatibilities along a phylogeny. Evolution. 2013 doi: 10.1111/evo.12173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Servedio MR, Noor MAF. The role of reinforcement in speciation: theory and data. Annu Rev Ecol Evol Syst. 2003;34:339–364. [Google Scholar]
  • 30.Raftery AE, Newton MA, Satagopan JM, Krivitsky PN. Estimating the integrated likelihood via posterior simulation using the harmonic mean identity. In: Bernardo JM, Bayarri MJ, Berger JO, Dawid AP, editors. Bayesian Statistics. Oxford: Oxford Univ Press; 2007. pp. 1–45. [Google Scholar]
  • 31. Mallet J (2007) Species, concepts of. Encyclopedia of Biodiversity, ed Levin SA (Elsevier, Amsterdam)
  • 32.Rabosky DL, Lovette IJ. Density-dependent diversification in North American wood warblers. Proc Biol Sci. 2008;275(1649):2363–2371. doi: 10.1098/rspb.2008.0630. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Sepkoski JJ. A kinetic model of Phanerozoic taxonomic diversity I. Analysis of marine orders. Paleobiology. 1978;4:223–251. [Google Scholar]
  • 34.Rabosky DL. Primary controls on species richness in higher taxa. Syst Biol. 2010;59(6):634–645. doi: 10.1093/sysbio/syq060. [DOI] [PubMed] [Google Scholar]
  • 35.Grafen A. The phylogenetic regression. Philos Trans R Soc Lond B Biol Sci. 1989;326(1233):119–157. doi: 10.1098/rstb.1989.0106. [DOI] [PubMed] [Google Scholar]
  • 36.Lanfear R, Ho SYW, Love D, Bromham L. Mutation rate is linked to diversification in birds. Proc Natl Acad Sci USA. 2010;107(47):20423–20428. doi: 10.1073/pnas.1007888107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Price T. Speciation in Birds. Greenwood Village, CO: Roberts and Company; 2008. [Google Scholar]
  • 38.Matute DR, Coyne JA. Intrinsic reproductive isolation between two sister species of Drosophila. Evolution. 2010;64(4):903–920. doi: 10.1111/j.1558-5646.2009.00879.x. [DOI] [PubMed] [Google Scholar]
  • 39.Gavrilets S. Fitness Landscapes and the Origin of Species. Princeton: Princeton Univ Press; 2004. [Google Scholar]
  • 40.Wu C-I, Ting C-T. Genes and speciation. Nat Rev Genet. 2004;5(2):114–122. doi: 10.1038/nrg1269. [DOI] [PubMed] [Google Scholar]
  • 41.Qvarnström A, Rice AM, Ellegren H. Speciation in Ficedula flycatchers. Philos Trans R Soc Lond B Biol Sci. 2010;365(1547):1841–1852. doi: 10.1098/rstb.2009.0306. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Grant PR, Grant BR. Genetics and the origin of bird species. Proc Natl Acad Sci USA. 1997;94(15):7768–7775. doi: 10.1073/pnas.94.15.7768. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Darwin C. On the Origin of Species by Means of Natural Selection. London: John Murray; 1859. [Google Scholar]
  • 44.Pfennig DW, Pfennig KS. Evolution’s Wedge: Competition and the Origins of Diversity. Berkeley: Univ California Press; 2013. [Google Scholar]
  • 45.Reznick DN, Ricklefs RE. Darwin’s bridge between microevolution and macroevolution. Nature. 2009;457(7231):837–842. doi: 10.1038/nature07894. [DOI] [PubMed] [Google Scholar]
  • 46.McKinnon JS, Rundle HD. Speciation in nature: the threespine stickleback model systems. Trends Ecol Evol. 2002;17:480–488. [Google Scholar]
  • 47.Pigot AL, Tobias JA. Species interactions constrain geographic range expansion over evolutionary time. Ecol Lett. 2013;16(3):330–338. doi: 10.1111/ele.12043. [DOI] [PubMed] [Google Scholar]
  • 48.Ricklefs RE. Host-pathogen coevolution, secondary sympatry and species diversification. Philos Trans R Soc Lond B Biol Sci. 2010;365(1543):1139–1147. doi: 10.1098/rstb.2009.0279. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 49.Ezard THG, Pearson PN, Aze T, Purvis A. The meaning of birth and death (in macroevolutionary birth-death models) Biol Lett. 2012;8(1):139–142. doi: 10.1098/rsbl.2011.0699. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Coyne JA, Orr HA. Patterns of speciation in Drosophila. Evolution. 1989;43:362–381. doi: 10.1111/j.1558-5646.1989.tb04233.x. [DOI] [PubMed] [Google Scholar]
  • 51.Mendelson TC. Sexual isolation evolves faster than hybrid inviability in a diverse and sexually dimorphic genus of fish (Percidae: Etheostoma) Evolution. 2003;57(2):317–327. doi: 10.1111/j.0014-3820.2003.tb00266.x. [DOI] [PubMed] [Google Scholar]
  • 52.Stelkens RB, Young KA, Seehausen O. The accumulation of reproductive incompatibilities in African cichlid fish. Evolution. 2010;64(3):617–633. doi: 10.1111/j.1558-5646.2009.00849.x. [DOI] [PubMed] [Google Scholar]
  • 53.van der Linde K, Houle D, Spicer GS, Steppan SJ. A supermatrix-based molecular phylogeny of the family Drosophilidae. Genet Res. 2010;92(1):25–38. doi: 10.1017/S001667231000008X. [DOI] [PubMed] [Google Scholar]
  • 54.Nosil P. Degree of sympatry affects reinforcement in Drosophila. Evolution. 2013;67(3):868–872. doi: 10.1111/j.1558-5646.2012.01817.x. [DOI] [PubMed] [Google Scholar]
  • 55.Magallón S, Sanderson MJ. Absolute diversification rates in angiosperm clades. Evolution. 2001;55(9):1762–1780. doi: 10.1111/j.0014-3820.2001.tb00826.x. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_110_38_15354__index.html (7.5KB, html)
1305529110_pnas.201305529SI.pdf (1.1MB, pdf)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES