Predicting Functionally Informative Mutations in Escherichia coli BamA Using Evolutionary Covariance Analysis

Abstract

The essential outer membrane β-barrel protein BamA forms a complex with four lipoprotein partners BamBCDE that assembles β-barrel proteins into the outer membrane of Escherichia coli. Detailed genetic studies have shown that BamA cycles through multiple conformations during substrate assembly, suggesting that a complex network of residues may be involved in coordinating conformational changes and lipoprotein partner function. While genetic analysis of BamA has been informative, it has also been slow in the absence of a straightforward selection for mutants. Here we take a bioinformatic approach to identify candidate residues for mutagenesis using direct coupling analysis. Starting with the BamA paralog FhaC, we show that direct coupling analysis works well for large β-barrel proteins, identifying pairs of residues in close proximity in tertiary structure with a true positive rate of 0.64 over the top 50 predictions. To reduce the effects of noise, we designed and incorporated a novel structured prior into the empirical correlation matrix, dramatically increasing the FhaC true positive rate from 0.64 to 0.88 over the top 50 predictions. Our direct coupling analysis of BamA implicates residues R661 and D740 in a functional interaction. We find that the substitutions R661G and D740G each confer OM permeability defects and destabilize the BamA β-barrel. We also identify synthetic phenotypes and cross-suppressors that suggest R661 and D740 function in a similar process and may interact directly. We expect that the direct coupling analysis approach to informed mutagenesis will be particularly useful in systems lacking adequate selections and for dynamic proteins with multiple conformations.

AS a Gram-negative bacterium, Escherichia coli is enveloped by two membranes, a cytoplasmic or inner membrane comprising a phospholipid bilayer and an outer membrane (OM) comprising an asymmetric bilayer with a phospholipid inner leaflet and a lipopolysaccharide outer leaflet (Kamio and Nikaido 1976; Silhavy et al. 2010; Ricci and Silhavy 2012). An aqueous compartment called the periplasm separates the two membranes. Diffusion from the extracellular milieu into the periplasm is facilitated by β-barrel proteins embedded in the OM (OMPs) (Nikaido 2003). OMPs have additional structural and enzymatic functions (Tamm et al. 2004); however, all essential OMPs function in OM biogenesis.

The folding and assembly of nascent OMPs is catalyzed by the β-barrel assembly machine (Bam) complex at the OM. The Bam complex is composed of BamA, itself an OMP, and four associated lipoproteins, BamBCDE (Wu et al. 2005; Sklar et al. 2007a). BamA is thought to be the central complex member. It contains five periplasmic polypeptide transport associated (POTRA) domains, which scaffold the lipoproteins and likely interact with substrate (Kim et al. 2007). Its β-barrel domain contains an extended extracellular loop, loop 6 (L6), which can adopt protease-sensitive and -resistant conformations, indicating that BamA undergoes conformational changes during OMP assembly (Rigel et al. 2012, 2013). L6 also contains an RGF/Y motif conserved among Omp85/TpsB family members, including the BamA paralog FhaC (Moslavac et al. 2005; Jacob-Dubuisson et al. 2009). Mutations in this conserved motif have been shown to affect function in both BamA and FhaC (Delattre et al. 2010; Leonard-Rivera and Misra 2012). But despite considerable work, little is known at a mechanistic level about how the Bam complex functions. It is unclear how nascent OMPs are recognized by the complex, how folding and insertion are coordinated and catalyzed by the complex, or what roles different complex members play in these processes.

Genetics offers a natural approach to answer these questions; however, informative bam mutations have been difficult to find. Since overall complex membership and function have already been determined, genetics turns to a search for mutations that will provide insight into the details of function. This means identifying point mutations or small deletions that have subtle effects on complex function. Subtlety is particularly important in the case of bamAD, since these genes are essential (Gerdes et al. 2003; Onufryk et al. 2005; Wu et al. 2005). But the search for functionally informative mutations is hampered by the fact that a direct selection for bam mutations does not exist.

To date, the genetic approach to uncovering Bam complex function is based on random mutagenesis of complex members followed by screens for membrane-permeability defects, which manifest in the absence of proper Bam function (Ruiz et al. 2005, 2006; Malinverni et al. 2006; Sklar et al. 2007a; Vuong et al. 2008; Rigel et al. 2012). This is an inefficient process. Screens for OMP assembly defects are mostly low throughput. Moreover, Bam complex members, particularly BamA, are robust to point mutation. This is not surprising given that β-barrel OMPs are extremely stable: the first temperature-sensitive (Ts) bamA allele reported contained nine amino acid substitutions (Doerrler and Raetz 2005). In some cases bam mutations have been found by selecting for suppressors of generalized membrane-permeability defects, but this too is inefficient, as there are myriad ways to reduce membrane permeability without affecting Bam function.

As the identification of informative mutations has been the rate-limiting step in our analysis of the Bam complex, we have sought means to target promising mutations using bioinformatics, specifically by using covariance analysis. Because protein sequence is constrained by selection, a protein’s evolutionary record contains information about the functional importance of its residues. This is the basis of conservation analysis, which identifies positions where selection favors one or a small number of specific residues. Along similar lines, covariance analysis uses the evolutionary record to identify pairs of positions where selection favors coordinated changes to residue identity. Covariance implies a functional interaction between positions—for functional reasons, the positions coevolve. Generally these functional reasons can be divided into three classes: (i) direct physical interactions such as a salt bridge or a hydrogen bond, (ii) indirect physical interactions in which positions participate in a network of energetically connected residues that promote conformational changes as in the case of allostery, and (iii) mechanistic interactions, e.g., in the active sites of proteins (Lockless 1999; Smock et al. 2010; Reynolds et al. 2011). It follows that covariance analysis could be a useful way to identify candidate mutations: it can identify a class of positions that are functionally important but not perfectly conserved, and, by reporting pairs of interacting positions, it provides insight into related residues.

Recent advances in the number of available sequences and the quality of algorithms have made covariance analysis widely feasible (Halabi et al. 2009; Cocco et al. 2012; Marks et al. 2012). To identify mutational targets in the Bam complex we employed the method of mean-field, direct coupling analysis (mfDCA or DCA) (Marks et al. 2011; Morcos et al. 2011; Hopf et al. 2012). The power of DCA lies in its ability to overcome the statistical noise created by chains of interacting residues that lead to indirect couplings between distant residues. For example, if positions i and j co-vary and positions j and k co-vary, then positions i and k will likely co-vary even if there is no functional basis for this covariance (Weigt et al. 2009; Burger and Van Nimwegen 2010; Marks et al. 2011; Morcos et al. 2011; Hopf et al. 2012). These transitive correlations can extend beyond three positions, creating large, nonspecific networks of correlated residues (Lapedes et al. 1999). DCA uses a global statistical model to exclude transitive correlations by reducing the observed correlations to a small subset of causative couplings that best explain the evolutionary sequence data. Whereas pre-DCA algorithms yield a true positive (TP) rate of 20–30% for the top 20 predicted pairs (as determined by proximity in known structures), DCA yields TP rates of 60–80% or better (Marks et al. 2011). DCA has been used successfully as a means of predicting protein structure, and it was recently used to identify interdomain contacts in the Bacillus subtilis sensor histidine kinase KinA for targeted mutagenesis (Dago et al. 2012; Szurmant and Hoch 2013).

Here we apply covariance analysis based on the DCA algorithm to predict functionally informative mutations in the central Bam complex member BamA. We identify BamA R661 and D740 as candidates for site directed mutagenesis and show by genetic means that these positions are functionally related. We also seek to optimize the DCA method and find that our modifications greatly increase TP rates for the BamA paralog FhaC.

Methods

MSA construction

BamA and FhaC multiple sequence alignments (MSAs) were generated using HHblits and the UniProt20 database (Remmert et al. 2012). E. coli K-12 BamA and Bordetella pertussis Tohama I FhaC sequences were used to query the database. Two search iterations were performed (-n 2), and the maximum number of sequences allowed to pass the second prefilter was set high enough to prevent sequence loss (-maxfilt 40000). No sequences were filtered out while generating MSA output (-all). In accordance with Hopf et al. (2012), multiple MSAs were generated for each protein using different E-value cutoffs, and an MSA for each protein was chosen to optimize the tradeoff between sequence number and sequence quality. In each case the MSA with the largest number of sequences was chosen such that at least 70% of the positions to be analyzed contained no more than 30% gaps. Because sequence fragments exist in the database and partial sequences were also subject to covariance analysis, any sequence fragment that did not contain a residue within our region of interest was removed from the MSA. MSA columns corresponding to gapped positions in the query sequence were also removed along with any column containing >40% gaps. The result was an MSA comprising M sequences of length L.

Covariance analysis

Covariance analysis was performed using DCA within a mean-field approximation. The DCA approach is well reported (Weigt et al. 2009; Marks et al. 2011; Morcos et al. 2011; Cocco et al. 2012; Hopf et al. 2012) and a summary of the DCA method employed here can be found in Supporting Information, File S1. Briefly, we note that DCA involves the construction of a connected correlation matrix from reweighted frequency counts determined from the MSA according to the relationships

$$C_{ij}{\left(A,B\right)}_{i\ne j}=f_{ij}\left(A,B\right)-f_i\left(A\right)f_j\left(B\right)$$ (1)

$$C_{ij}{\left(A,B\right)}_{i=j,A\mathrm{=}B}=f_i\left(A\right)\left(1-f_i\left(A\right)\right),$$ (2)

where f_i(A) is the frequency of amino acid A in MSA column i, f_j(B) is the frequency of amino acid B in MSA column j, and f_ij(A,B) is the frequency of amino acid pair (A, B) in columns i and j. Equation 1 is a local measure of intercolumn sequence correlation that measures whether amino acid pair (A, B) is seen more frequently than expected by chance given the single amino acid frequencies in columns i and j. The major diagonal of the empirical correlation matrix corresponds to the case where i = j, and a single MSA column is being compared to itself (Equation 2); it provides a measure of sequence variance or amino acid conservation. The DCA global statistical model derives from inversion of the empirical correlation matrix C during which all matrix entries interact. Note that direct information DI_ij scores were filtered to remove pairs of positions separated by less than five amino acids in primary sequence. Also, in our analysis of FhaC, pairs comprising residues that are not resolved in crystal structure 2QDZ were not considered (Clantin et al. 2007).

Matrix shrinkage

To reduce the effects of noise caused by the limited number of available sequences, we used matrix shrinkage to impose structure on the empirical correlation matrix C. The resulting composite matrix C* is a weighted sum of model M and sample C matrices,

$${\mathbf{\text{C}}}^{*}=\alpha \mathbf{\text{M}}+\left(1-\alpha \right)\mathbf{\text{C}},$$ (3)

where the shrinkage intensity parameter α controls the relative weighting of model and sample matrices, and M = diag(C) as described in Results. After shrinkage the composite matrix C* is inverted to determine the coupling energies e_ij(A, B).

Sequence entropy

The sequence conservation at a given position i is quantified using the informational entropy or Shannon entropy as in Fodor and Aldrich (2004):

$$S_i={\displaystyle \sum _{A=1}^q{f}_i\left(A\right)\ln \left(f_i\left(A\right)\right)}.$$ (4)

For a q = 21 state system, S_i can range from 0.00 to 3.04 nats; however, in practice pseudocounts limit the value of S_i to between 2.12 and 3.04 nats. Pairs were classified by their minimum positional entropy, $S_{\min \left(i,j\right)}\equiv \min \left\{S_i,S_j\right\}$, since this value seems to limit DI_ij score, the measure of pair covariance returned by DCA. Pairs containing even one conserved position tend to have low DI_ij scores, while high-scoring pairs generally contain two nonconserved positions (Figure S1).

DIZ_ij scoring

DI_ij scores were grouped into 20 bins according to minimum positional entropy S_min(i,j). The average and standard deviation were calculated for each bin containing DI_ij scores and used to calculate DIZ_ij scores according to the relationship

$$DI{Z}_{ij}=\frac{D{I}_{ij}-{\overline{DI}}_{\text{Bin}}}{S_{D{I}_{\text{Bin}}}},$$ (5)

where ${\overline{DI}}_{\text{Bin}}$ is the average DI_ij score for a given bin, and $S_{D{I}_{\text{Bin}}}$ is the standard deviation for that bin. DIZ_ij scores are then compared across all bins to generate a ranked list of all pairs ordered by DIZ_ij score.

Mutual information (MI)

MI_ij scores were calculated as

$${\text{MI}}_{ij}={\displaystyle \sum _{A,B=1}^q{f}_{ij}\left(A,B\right)\hspace{0.17em}\ln \left(\frac{f_{ij}\left(A,B\right)}{f_i\left(A\right)f_j\left(B\right)}\right)},$$ (6)

where single and pair amino acid frequencies are calculated with sequence down-weighting but do not incorporate pseudocounts (Atchley et al. 2000). Note that informational entropy S_min(i,j) calculations are still performed using pseudocount-based frequencies in order to maintain a similar entropy range to that obtained for DCA predictions.

Computation and graphics

All computations were performed using Python 2.7.3 (http://www.python.org) supplemented with various modules including NumPy 1.6.2 and SciPy 0.11.0 (Jones et al. 2001). Figure 1, Figure 5, Figure S1, Figure S3, and Figure S4 were produced using the matplotlib 1.0.1 package (Hunter 2007). Figure 2 was generated using the PyMOL Molecular Graphics System, v. 1.5.0.4 (Schrödinger, LLC).

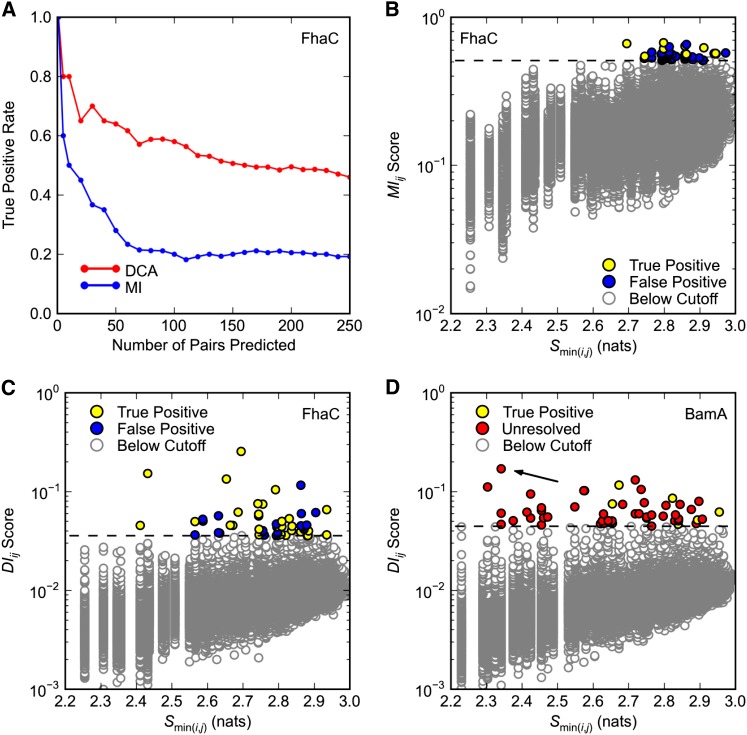
Figure 1.

Covariance analysis of FhaC and BamA. Predicted pairs with a minimum interatomic distance ≤8 Å in (A–C) FhaC structure 2QDZ or (D) BamA structure 3OG5 are considered true positives. Only pairs separated by at least five positions in primary sequence are considered. (A and C) Direct Coupling Analysis (DCA) was applied to FhaC positions 33–584 (see Methods). (A) Comparison of DCA and mutual information (MI) methods. True positive rates are plotted over the top 250 pairs predicted by DCA and MI. (B) Dependence of MI_ij scores on minimum pair entropy S_min(i,j). MI was applied to FhaC positions 33–584. Dashed black line is the cutoff for pairs with the 50 highest MI_ij scores. (C and D) Dependence of DI_ij scores on minimum pair entropy S_min(i,j) for (C) FhaC and (D) BamA. Dashed black line is the cutoff for pairs with the 50 highest DI_ij scores. (D) DCA was applied to BamA positions 347–810. Since BamA structure 3OG5 comprises only positions 262–421, most pairs are unresolved. There are no false positives in the top 50 predictions. Arrow indicates pair R661–D740.

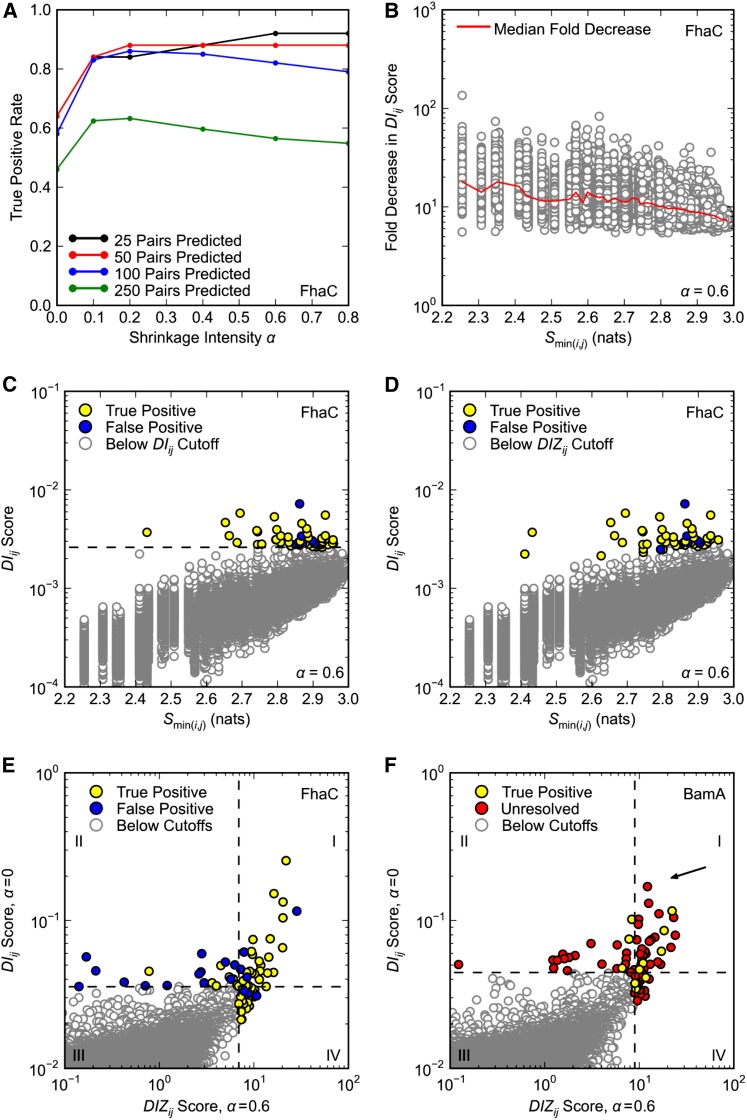
Figure 5.

Optimization of DCA. Only pairs separated by at least five positions in primary sequence are considered. (A–E) DCA was applied to FhaC as in Figure 1, A and B, with the same definition of true positives. (A) Effect of shrinkage intensity α on DCA true positive rates. (B) Effect of shrinkage intensity α = 0.6 on DI_ij scores. Fold reduction in DI_ij score is plotted against the minimum pair entropy S_min(i,j) for each pair; the red curve shows the median fold reduction in DI_ij score over 50 bins of S_min(i,j). (C and D) DI_ij scores for shrinkage intensity α = 0.6 plotted against minimum pair entropy S_min(i,j). The top 50 pairs according to (C) DI_ij and (D) DIZ_ij scoring (α = 0.6) are highlighted. In C the dashed black line is the cutoff for pairs with the 50 highest DI_ij scores. (E and F) Overlap of the top 50 (E) FhaC and (F) BamA pairs according to DI_ij scoring (α = 0) and DIZ_ij scoring (α = 0.6). Horizontal and vertical dashed lines correspond to the cutoffs for pairs with the 50 highest DI_ij and DIZ_ij scores, respectively. (F) DCA was applied to BamA as in Figure 1D, with the same definition of true positives. There are no false positives. Arrow indicates pair R661–D740.

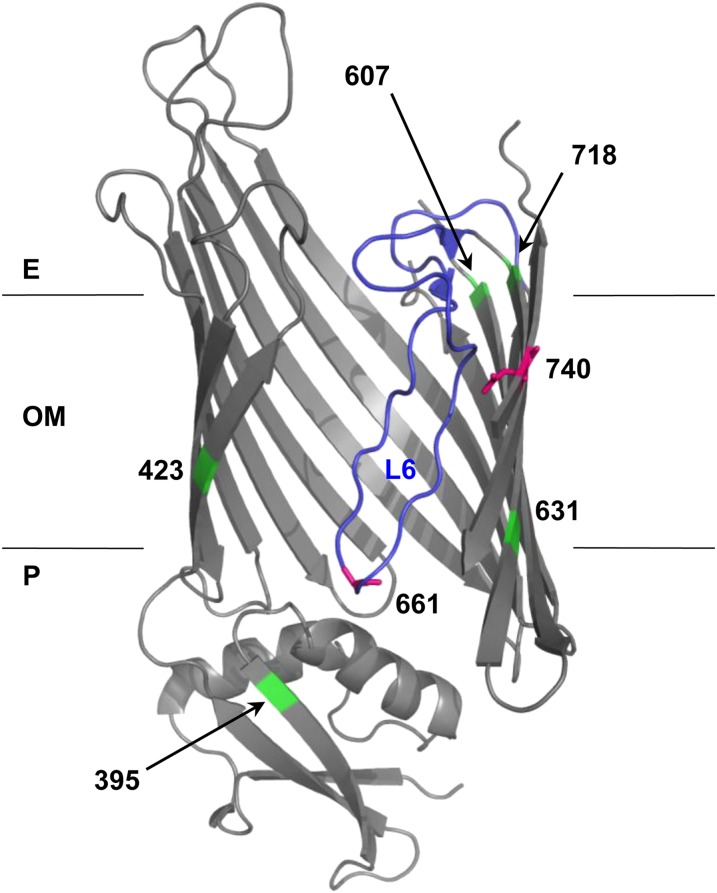
Figure 2.

Structural model of BamA mutations. BamA mutation positions (661 and 740; magenta) and suppressor positions (395, 423, 607, 631, and 718; green) were mapped onto FhaC structure 2QDZ based on the alignment of BamA and FhaC query sequences. Alignment of E. coli BamA POTRA5 (residues 347–421) and B. pertussis FhaC POTRA2 (residues 165–238) was performed using the NCBI online alignment tool COBALT (Figure S2) (Papadopoulos and Agarwala 2007). The BamA–FhaC alignment in Jacob-Dubuisson et al. (2009) was used to model β-barrel residues. Loop 6 (L6) is colored blue. Note that the loop is not well resolved in the FhaC structure, so Clantin et al. (2007) modeled it as a polyalanine chain. The outer membrane (OM), periplasm (P), and extracellular milieu (E) are indicated.

Bacterial Strains and Growth Conditions

All strains used in this study are listed in Table S1 and were constructed using standard microbiological techniques. Strains were grown in LB and supplemented with 25 μg/ml kanamycin when appropriate. All bacterial cultures were grown under aerobic conditions at 37° unless otherwise noted. For efficiency of plating (EOP) assays, serial dilutions of stationary-phase cultures of indicated strains were spotted onto LB agar containing 50 μg/ml erythromycin, 625 μg/ml bacitracin, 50 μg/ml novobiocin, 10 μg/ml rifampin, or 0.5% SDS + 1.0 mM EDTA.

Site-directed mutagenesis

bamA missense mutants were generated in pZS21::bamA (pDPR1) using the Stratagene QuikChange site-directed mutagenesis kit per the manufacturer’s instructions. Primers used to introduce the mutations are listed in Table S2. All mutations were confirmed by sequencing.

Western blot analysis

Cultures were grown overnight and then back-diluted 1:500 into fresh LB containing 25 μg/ml kanamycin. One-milliliter samples were then collected from cultures grown under each condition at OD₆₀₀ = ∼1. Harvested samples from both conditions were normalized by optical density, pelleted (5000 × g, 10 min), and resuspended in SDS–PAGE sample buffer. Samples were then boiled for 10 min and subjected to electrophoresis through 10% SDS–PAGE. Previously described rabbit polyclonal antibodies against BamA (1:30,000 dilution) (Wu et al. 2005), BamC (1:30,000 dilution) (Sklar et al. 2007b), and LamB/OmpA (1:30,000 dilution) (Walsh et al. 2003) and donkey ECL horseradish-peroxidase-conjugated anti-rabbit IgG (GE Life Sciences) (1:8,000 dilution) were used for immunoblots. Protein bands were visualized using the ECL antibody detection kit (GE Healthcare) and Hyblot CL film (Denville Scientific).

Electrophoretic mobility assay

One-milliliter samples of the indicated strains were obtained at OD₆₀₀ = ∼1. Cells were lysed gently to prevent OMP denaturation using a previously described technique (Misra et al. 1991). Briefly, samples were resuspended in a 20 mM Tris–HCl (pH 7.5) 1 mM EDTA solution containing 5 mg/ml lysozyme and subjected to repeated freeze-thawing. DNase I was added to a final concentration of 0.1 mg/ml and proteins were solubilized by addition of 2× SDS solution (4% SDS, 40 mM Tris–HCl (ph 7.5), 20 mM EDTA). SDS–PAGE sample buffer was then added and samples were incubated at either 100° or 24° for 10 min prior to SDS–PAGE, which was conducted at 4° to prevent denaturation during electrophoresis. BamA was detected immunologically as described above.

Genetic selection

Spontaneous SDS-resistant suppressors of bamAD740G were isolated by plating overnight cultures of a strain carrying this allele at 37° on LB agar containing 0.5% SDS and 1.0 mM EDTA. Intragenic suppressor (plasmid-linked) mutations were mapped by purification and retransformation of the pBamA^D740G plasmid into JCM320, and the causative mutations were identified by DNA sequencing.

Results

DCA of FhaC identifies pairs of interacting residues

Before analyzing covariance within BamA, we tested the ability of DCA to identify pairs of interacting positions in FhaC, a BamA paralog with a known crystal structure. Cross-referencing high-scoring pairs with their proximity in known structures offers a simple test of DCA accuracy. Throughout our analysis, we consider all high-scoring residue pairs with a minimum interatomic distance ≤8 Å in the corresponding crystal structure to be true positives (TPs). The 8-Å cutoff was chosen in accordance with Morcos et al. (2011).

A MSA of 6410 FhaC sequences was generated using an FhaC query from B. pertussis. DCA was applied to FhaC residues 32–584, which excludes the signal sequence. The result is a list of all position pairs (i, j), where i > j, ordered by direct information score DI_ij. DI_ij score is a scalar measure of the extent to which sequence information at one position can predict sequence information at another, and it is used as a proxy for functional interaction in DCA. Pairs of positions separated by less than five amino acids are filtered out of the ranked DI_ij score list in order to avoid the trivial finding that neighboring residues interact.

We found that FhaC is amenable to DCA. As expected, DCA yields higher TP rates than earlier methods like MI, which are based on local statistical models (Figure 1A). We take the TP rate for the top 50 predictions (TP₅₀) as a measure of algorithm performance, since 50 pairs of residues is a reasonable set to test experimentally. DCA yields a TP₅₀ rate of 0.64 compared to 0.28 for MI (Figure 1, A and B compared to 1C). Even over 250 predictions the DCA TP rate is 0.46, meaning that roughly one in two predictions represent plausible physical interactions according to the FhaC crystal structure. This is 14 times the TP rate expected for randomly selected pairs.

DCA also has the advantage of identifying covariance between conserved positions. Taking the lower of the two sequence informational entropies for each pair S_{min(i, j)} as a measure of pair conservation, we found that the top 50 DCA predictions have a wider distribution of conservation scores than the top 50 MI predictions (compare Figure 1, B and C). The lack of conserved pairs in the MI top 50 is not surprising: it has been established that covariance algorithms based on local statistical models act partly as conservation filters, identifying covariance in a particular range of the entropy spectrum, which varies with the algorithm (Fodor and Aldrich 2004). The fact that DCA identifies covariance between conserved positions is particularly important for genetics applications, since we expect functionally important residues to be relatively well conserved.

DCA of BamA implicates R661 and D740 in a functional interaction

Encouraged by the promising results obtained for FhaC, we applied DCA to BamA. A BamA query sequence from E. coli K–12 was used to construct an MSA comprising 3073 BamA homologs. DCA was applied to residues 347–810, corresponding to the BamA POTRA5 and β-barrel domains. POTRA5 was included as a positive control, as a crystal structure for this domain is available. Of the top 50 BamA pairs, 8 fall entirely within POTRA5, allowing their proximity to be determined. All 8 pairs have minimum interatomic distances below the 8Å cutoff, suggesting that BamA, like FhaC, is amenable to DCA (Figure 1D, yellow points). Again, low-entropy pairs are well represented among the top 50 predictions (Figure 1D).

The top ranked BamA pair, R661–D740, has a number of interesting features. Alignment of BamA and FhaC suggests that R661 is part of a conserved RGF/Y motif in extracellular L6 of BamA, which is thought to undergo conformational changes during OMP assembly and may fold into the lumen of the β-barrel (See Discussion). As a charged β-barrel residue, D740 is almost certainly facing the hydrophilic environment of the β-barrel lumen, making a direct R661–D740 interaction plausible (Figure 2, magenta). This is exactly the kind of long-distance, dynamic interaction that might provide insight into BamA function. Given its prediction rank, conservation, and the structural logic described, we chose to further characterize the R661–D740 pair by genetic analysis.

BamA R661 and D740 substitutions increase OM permeability

To determine whether the covariance observed for R661 and D740 reflects a functional relationship, we introduced glycine substitutions at each of these positions and determined the effects of these mutations on the folding and function of BamA. bamAR661G and bamAD740G mutations were generated on a low-copy vector (pZS21) containing the bamA ORF. Each resulting allele was introduced into JCM320, a strain in which expression of an ectopic, chromosomal wild-type allele of bamA is induced by addition of arabinose. When arabinose is excluded from the growth medium, only the plasmid-borne mutant allele of bamA is expressed.

Because Bam is involved directly in OM biogenesis, mutations that compromise Bam function generally cause increased sensitivity to a variety of antibiotics and small molecules (Ruiz et al. 2005, 2006; Malinverni et al. 2006; Sklar et al. 2007a; Vuong et al. 2008; Rigel et al. 2012). To determine whether the bamAR661G and bamAD740G mutations influence OM permeability, we assessed the growth of JCM320 containing pBamA^R661G, pBamA^D740G, or pBamA^R661G+D740G on LB plates supplemented with various antimicrobial or detergent compounds in the absence of arabinose. We found that strains expressing bamAR661G or bamAD740G are comparable to strains expressing the wild-type allele with respect to erythromycin and rifampin resistance, but unlike the wild type they do not grow in the presence of the anionic detergent SDS (Figure 3A).

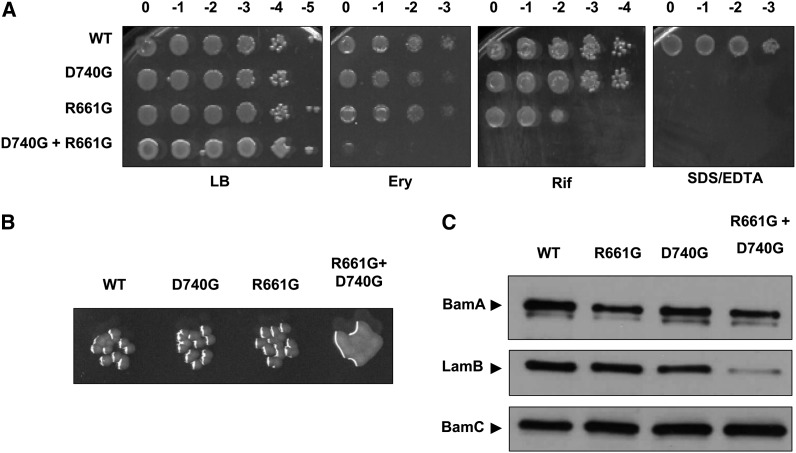
Figure 3.

Phenotypic characterization of BamA barrel mutants. (A) Tenfold dilutions of stationary-phase cultures of the indicated mutants were spotted onto LB with or without 50 μg/ml erythromycin (Ery), 10 μg/ml rifampin (Rif), or 0.5% SDS + 1.0 mM EDTA and incubated at 37°. Column headings represent log concentrations relative to undiluted cultures. (B) Close-up of colonies from Figure 3A. Colonies formed by the indicated strains are shown following overnight growth on LB at 37°. The bamAR661G+D740G double mutant exhibits mucoidy under these conditions. (C) Levels of BamA and the major OMP LamB in exponential phase whole-cell extracts of the indicated strains were determined by SDS–PAGE and immunoblotting. The OM lipoprotein BamC, levels of which are not affected by OMP biogenesis defects, is shown as a control.

Although neither individual mutation increases sensitivity to most antibiotics in the panel described above, combining the bamAR661G and bamAD740G mutations influences OM permeability dramatically: a strain expressing the double mutant (bamAR661G+D740G) is highly sensitive to all compounds tested (Figure 3A). In addition, the double-mutant strain exhibits mucoidy and forms unusually small colonies at 42° (Figure 3B).

bamAR661G and bamAD740G mutations compromise BamA stability

The notion that R661 and D740 are functionally linked is thus far corroborated by the phenotypic similarity between strains expressing bamAR661G and bamAD740G single mutations as well as the apparent synergism observed in the bamAR661G+D740G double-mutant strain. To test more directly the effect that these mutations have on the structure and function of BamA, we determined the steady-state levels of a model BamA substrate, the maltose channel LamB, and of BamA itself in each mutant background. We observed comparable whole-cell levels of LamB in the single mutants in comparison to the wild type, suggesting that these mutations do not compromise OMP assembly in any appreciable way (Figure 3C). However, we observed a modest reduction in the steady-state levels of BamA in the context of either the R661G or D740G substitution, suggesting that these mutations in some way perturb the biogenesis of BamA itself (Figure 3C). In the bamAR661G+D740G double mutant, a LamB assembly defect was also evident even though BamA levels were unchanged from those in the single mutants (Figure 3C). This finding further implies a synergistic effect upon combination of these mutations.

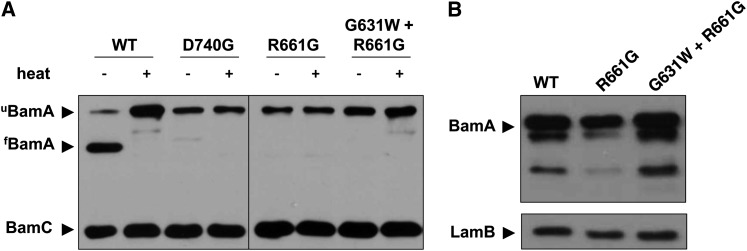
To further characterize the impact of the bamAR661G and bamAD740G mutations on BamA folding, we exploited a well-described property common to OM β-barrel proteins known as heat modifiability. The BamA β-barrel is generally resistant to SDS denaturation but sensitive to heat denaturation. When cell extracts are subjected to SDS–PAGE following lysis at room temperature, BamA remains fully folded and, consequently, migrates at a lower apparent molecular weight than heat-denatured BamA (see Figure 4A). However, mutations that affect folding or stability of the BamA β-barrel domain result in unfolding of the β-barrel even at low temperature, thus altering electrophoretic mobility (Tellez and Misra 2012). We observe that both the bamAR661G and bamAD740G mutations abrogate heat modifiability of BamA, sensitizing the β-barrel to SDS denaturation even at room temperature (Figure 4A).

Figure 4.

BamA folding and stability in the presence of barrel mutations and suppressors. (A) Samples of the indicated strains were lysed gently and incubated at either 100° (+) or 24° (−) for 10 min prior to SDS–PAGE. Stably folded BamA (^fBamA) migrates at a lower apparent molecular weight than the denatured protein (^uBamA). (B) Whole-cell extracts were prepared using stationary-phase (overnight) cultures of the indicated strains. Samples were subjected to SDS–PAGE and immunoblotting for BamA and LamB.

Mutual intragenic suppressors relieve defects related to R661 and D740 substitutions

Spontaneous intragenic suppressors of the bamAD740G mutation were isolated by incubating the strain expressing this variant at 37° on LB plates containing 0.5% SDS/1 mM EDTA. Those colonies that arose were purified, and the pBamA^D740G plasmid was purified from each suppressor for linkage analysis. Intragenic suppressor mutations were mapped by transforming the parental bamA depletion strain (JCM320) with plasmid purified from each suppressor strain. The plasmid-borne bamA ORF was then sequenced in those transformants that exhibited the suppressor phenotype (SDS/EDTA^R).

In addition to revertants, six independent intragenic suppressor mutations that restore the permeability barrier in the bamAD740G mutant were identified (Table 1). Second-site substitutions in BamA that confer detergent resistance map to several locations based on sequence alignment with FhaC: β11/β12, the neighboring β-strands that are separated by Loop 6 (G631V, G631W, F718L); the extracellular end of β10 (E607A); β1 (T423I), and the C-terminal POTRA domain (P5) within the periplasmic extension (F395V) (Figure 2, green; see Figure S2 for POTRA alignment) (Papadopoulos and Agarwala 2007; Jacob-Dubuisson et al. 2009).

Table 1. Effect of bamAD740G suppressor mutations on SDS-EDTA sensitivity.

Parent allele	Intragenic secondary mutations and phenotypesa
		POTRA5			β-barrel
	Noneb	395V	423I	607A	631V	631W	718L
bamAWT	R	R	R	R	R	R	R
bamAR661G	S	R	R	R	R	R	R
bamAD740G	S	R	R	R	R	R	R

^aPhenotype refers to the growth of strains with the indicated genotypes on LB containing 0.5% SDS + 1.0 mM EDTA. Strains that exhibit growth after overnight incubation at 37° are considered resistant (R), and those that do not are considered sensitive (S).

^bNo secondary mutation.

Given the postulated functional relationship between R661 and D740, we reasoned that if these residues indeed participate in a common chemical process, then suppressor mutations that restore OM permeability in one mutant (bamAD740G) might well have the same effect in the other (bamAR661G). To test this, we introduced each of the suppressor mutations listed above into pBamA^R661G by site-directed mutagenesis and determined the permeability phenotypes of the resulting strains. As shown in Table 1, each mutation isolated as a suppressor of bamAD740G also restores SDS/EDTA resistance in the bamAR661G mutant, implying that the bamAD740G and bamAR661G mutations give rise to a common defect that causes detergent sensitivity.

As each of the intragenic suppressor mutations restores detergent resistance to the bamAD740G and bamAR661G mutants, we wished to determine whether heat modifiability is also restored in the presence of these mutations. Although the G631W substitution restores BamA levels and wild-type detergent sensitivity for each point mutant (Figure 4B and Table 1), BamA^R661G migrates as an unfolded species in the absence of heat treatment even in combination with the G631W suppressor (Figure 4A). Apparently the suppressors described here need not restore function by restoring BamA β-barrel stability.

Adding a structured prior to the empirical correlation matrix increases TP₅₀ rates for FhaC

While DCA was successful in identifying the BamA R661–D740 pair, we wondered if the algorithm might be further optimized for our purposes. There are a number of reasons to expect that OMPs like BamA and FhaC might pose a problem for DCA. The β-barrel of OMPs is a unique structure, one on which DCA has not yet been tested. More generally, OMPs are large proteins, and the number of sequences required to accurately estimate covariance matrix entries scales with protein length L. In this analysis the effective number of sequences used is relatively small, on the order of 3–4L, which may lead to some spurious correlations caused by noise.

To address the noise caused by small sequence sample size, we use a statistical technique called shrinkage to regularize the empirical correlation matrix C (Ledoit and Wolf 2003, 2004; Jones et al. 2012). Although the empirical correlation matrix as a whole is highly undersampled, the single-site frequencies that determine the variances along the major diagonal are well sampled. This suggests that we can use these frequencies to impose structure on the covariance matrix. To this end we calculated an estimator C* of the true covariance matrix as a weighted average of a model matrix M and the empirical correlation matrix C,

$${\mathbf{\text{C}}}^{*}=\alpha \mathbf{\text{M}}+\left(1-\alpha \right)\mathbf{\text{C}},$$ (7)

where α ∈ (0,1) is the shrinkage intensity, which determines the amount of structure imposed on the data. (Note that for a shrinkage intensity of 0, C* equals C, and DCA is unchanged from its original form.) The model matrix M is defined as

$$\mathbf{\text{M}}=\text{diag}\left(C\right),$$ (8)

where diag(C) is a matrix with the same dimensions and major diagonal as C but with off diagonal entries equal to zero. The model implies that to first order, we expect residues at different sites to mutate independently of one another and according to the frequencies present in the data. The validity of this model is an area of ongoing investigation; in this manuscript we simply ask whether applying shrinkage in this way improves our ability to identify residue pairs that are in close proximity in the FhaC structure.

Using FhaC as a test case, we found that using a nonzero shrinkage intensity α significantly improves DCA TP rates. The TP₅₀ rate was 0.84 or above for all α tested between α = 0.1 and α = 1.0 compared to 0.64 for α = 0 (Figure 5A). The positive effect of increasing α continues through at least the top 250 predictions, where, for example, α = 0.2 improves the TP rate from 0.46 to 0.63 (Figure 5A). Throughout the rest of our analysis we employ α = 0.6 as it seems to have a slight advantage over other α when making 50 or fewer predictions. Optimization of α is the subject of ongoing investigation.

Interestingly, we found that increasing α has a disproportionate effect on pairs containing conserved position(s). While setting α = 0.6 causes at least a fivefold decrease in the DI_ij scores for all pairs, the effect is greater for more conserved pairs as shown by the median fold decrease plotted in Figure 5B (red curve). This causes a relative increase in the DI_ij scores of less-conserved pairs (Figure 5C). The fact that conserved pairs are less represented among top predictions when α = 0.6 is troubling from a genetics standpoint. In this context one is searching for pairs that have functional importance, i.e., pairs likely to give selectable phenotypes when mutated. To the extent that the residues in such pairs are conserved, they will be missed by a method that is overly biased toward pairs of low conservation.

To balance the bias of DI_ij scoring that comes with increasing α, we developed a new scoring protocol. While DI_ij scores for low entropy pairs may be an order of magnitude lower than those for pairs of high entropy, we recognize that there are local outliers even at the low end of the entropy spectrum. To identify these outliers, we begin by binning pairs according to sequence entropy and then use DI_ij scores to calculate Z-scores on a per-bin basis. The resulting DIZ_ij scores are then compared and ordered across bins. As expected, DIZ_ij scoring expands the distribution of entropies among the top 50 scores to include more low-entropy pairs for α = 0.6 (compare Figure 5, C and D). Importantly, the entropy range has not simply expanded to include more false positives: DIZ_ij scoring corrects the DI_ij scoring bias for α = 0.6 with only a minor reduction in TP₅₀ rate, which drops from 0.88 to 0.86 (Figure 5, C and D).

Despite significant changes to the method, there is notable overlap between ${\text{DCA}}_{D{I}_{ij}}^{\alpha =0}$ and ${\text{DCA}}_{DI{Z}_{ij}}^{\alpha =0.6}$ predictions. Of the top 50 pairs predicted by each method, 28 are shared, including 24 TPs (Figure 5E, quadrant I). Indeed, it is generally true that ${\text{DCA}}_{D{I}_{ij}}^{\alpha =0}$ and ${\text{DCA}}_{DI{Z}_{ij}}^{\alpha =0.6}$ scores are correlated (Figure S3). However, ${\text{DCA}}_{DI{Z}_{ij}}^{\alpha =0.6}$ also identifies a set of nonoverlapping pairs with a particularly high TP rate of 0.86, which is more than double the TP rate of the set of nonoverlapping ${\text{DCA}}_{D{I}_{ij}}^{\alpha =0}$ pairs (Figure 5E, quadrants II and IV).

Encouraged by the results for FhaC, we repeated our analysis of BamA using ${\text{DCA}}_{DI{Z}_{ij}}^{\alpha =0.6}$. We found that of the 8 intra-POTRA5 interactions among the DIZ_ij top 50, all are TPs, suggesting that ${\text{DCA}}_{DI{Z}_{ij}}^{\alpha =0.6}$ also performs well for BamA (Figure 5F). Again there is significant overlap between ${\text{DCA}}_{D{I}_{ij}}^{\alpha =0}$ and ${\text{DCA}}_{DI{Z}_{ij}}^{\alpha =0.6}$ predictions—28 pairs including 5 TPs (Figure 5F, quadrant I). We note that the R661–D740 pair is among these shared predictions.

Discussion

The number of available sequences poses a major problem for covariance analysis. In general for a covariance matrix to be invertible, one needs at least as many independent observations as parameters and perhaps 10 times this number for a good approximation (Ledoit and Wolf 2004). When one considers estimating the covariance matrix of large proteins or protein complexes, the lack of adequate sequence data becomes overwhelming, especially since many sequences are not truly independent due to phylogeny. Yet our successful results for FhaC (438 amino acids) and BamA (393 amino acids) agree with the findings of studies showing that DCA works relatively well even for large proteins (Hopf et al. 2012). Much of this success is likely due to the use of large numbers of pseudocounts, an approach that bears striking similarity statistical shrinkage in practice. Our results for FhaC and BamA suggest that DCA might be improved significantly by a unified approach to data regularization combining the benefits of both pseudocounts and shrinkage.

While this is not the first time shrinkage has been applied to the problem of protein covariance, it is to our knowledge the first time it has been applied to DCA. Our model matrix M also differs markedly from previous studies, which use a single variance measure or factor to weight all variables on the matrix diagonal. Jones et al. (2012) recently reported using the model ${\mathbf{\text{M}}}_{\overline{s}}=\overline{S}\mathbf{\text{I}}$ to regularize a protein covariance matrix where $\overline{S}$ is the mean of the variances occupying the diagonal of the empirical correlation matrix C and I is the identity matrix. We found that our model matrix M, which allows for positional effects on amino acid frequencies, outperforms ${\mathbf{M}}_{\overline{s}}$ when used with DCA, increasing FhaC TP₅₀ rates from 0.76 to 0.88 (Figure S4). Whether the benefit of model matrix M is unique to FhaC remains to be seen; however, our results clearly suggest that shrinkage can be used to improve DCA output.

Highly conserved residues also pose a problem for covariance analysis. Every unique sequence in a MSA represents an evolutionary experiment in which selection has tested the relationship between protein sequence and function. DCA analyzes these experiments and returns a measure of positional coupling; however, our confidence in that measure depends on the number of experiments, i.e., the extent of perturbation at each position. For FhaC our finding that finite α, which disproportionately lowers the DI_ij scores of conserved pairs, increases initial TP₅₀ rates suggests that the DI_ij scores of conserved pairs are otherwise overinflated. Indeed, some implementations of DCA filter out the most conserved residues to reduce initial false-positive (FP) rates (Marks et al. 2011; Hopf et al. 2012). The negative correlation between TP rates and pair conservation is problematic for genetics, as one expects functionally important pairs to be relatively well conserved as in the case of R661–D740 of BamA. DIZ_ij scoring solves this problem by including conserved pairs among the DCA^α=0.6 top 50 without significantly diminishing TP₅₀ rates, at least for FhaC.

While ${\text{DCA}}_{DI{Z}_{ij}}^{\alpha =0.6}$ improves TP₅₀ rates, we note that our TP designation is based exclusively on residue proximity as determined from crystal structures. Among other possible causes of covariance, TP rates do not account for possible direct physical interactions in alternative conformations, potential multimerization sites, or indirect interactions via small molecules or other factors involved in allostery or substrate binding. For instance, the highest ranked FhaC pair according to ${\text{DCA}}_{DI{Z}_{ij}}^{\alpha =0.6}$ is T88–P118, an FP based on the FhaC crystal structure; however, T88 and P118 are separated only by 12 Å, compared to a 34-Å average separation for all FhaC residues. Furthermore, T88 and P118 each lie in a disordered and partially unresolved region linking an N-terminal β-barrel plug to POTRA1. It may be that T88 and P118 actually participate in a physical interaction in vivo. It is therefore likely that some FPs may represent true biological interactions. Similarly, it is likely that many of our TPs, while colocalizing in a given structure, may not yield selectable phenotypes when mutated. Whether ${\text{DCA}}_{D{I}_{ij}}^{\alpha =0}$, ${\text{DCA}}_{DI{Z}_{ij}}^{\alpha =0.6}$, or some other DCA variant is best suited to identify functionally related residues is still an open question, and we note that both methods ranked the functionally related BamA R661–D740 pair among the top 50 predictions.

There is substantial data suggesting that BamA R661 is important for function. R661 lies in the highly conserved RGF/Y motif of L6. It has been shown that deletion or wholesale substitution of the BamA RGF/Y motif renders cells conditionally lethal when grown on rich media, confers sensitivity to membrane impermeant antibiotics, reduces levels of BamA and OMPs, and causes β-barrel instability (Leonard-Rivera and Misra 2012). A bamAR661E allele was also found to confer antibiotic sensitivity, reduce BamA levels, and destabilize the β-barrel (Leonard-Rivera and Misra 2012). The importance of R661 and the RGF/Y motif is also evident in work with the BamA paralog FhaC, a member of the two-partner secretion (TpsA/TpsB) pathway for filamentous hemagglutinin adhesin (FHA). Deletion of FhaC L6 does not prevent its own folding and assembly but does prevent FhaC from exporting its TpsA partner, FHA. Likewise, mutation of the R661 analog reduces FHA secretion by 90% (Clantin et al. 2007; Delattre et al. 2010).

While there is no prior evidence that BamA D740 is important for function, it has been established that other β-barrel residues play more than a simple structural role in BamA. β-barrel mutations have been found to suppress the severe conditional growth phenotype exhibited by bamBE double mutants (Tellez and Misra 2012). The fact that β-barrel mutations can restore function to a Bam machine lacking two lipoprotein components implies that these residues contribute to overall complex function. Interestingly, bamBE double mutants show BamA β-barrel instability, which is not always corrected by suppressors of the conditional growth defect (Tellez and Misra 2012). But without DCA analysis there was little reason to expect that D740 in particular is important for function and none to suggest that R661 and D740 engage in a functional interaction.

Three lines of genetic evidence presented here support the prediction that BamA R661 and D740 interact in vivo. First, the bamAR661G and bamAD740G single mutations confer similar phenotypes, compromising the OM permeability barrier, reducing levels of BamA, and decreasing β-barrel stability. The effect on β-barrel stability is the most compelling of these phenotypes because it is unique: we have a number of BamA missense mutations that affect OM permeability, OMP assembly, and BamA levels without affecting heat modifiability of the BamA β-barrel. Second, the bamAR661G+D740G double mutant shows synthetic phenotypes including increased permeability to small molecule antibiotics and reduced levels of the model OMP LamB. Third, we found that the bamAR661G and bamAD740G alleles share common suppressors, suggesting that each confers a similar defect. Together these data strongly support the DCA prediction that R661 of L6 and D740 of the β-barrel engage in a functional interaction, and we suggest that this interaction is direct.

There is precedent for a direct interaction between BamA L6 and the β-barrel. While no structure for the BamA β-barrel is currently available, a nearly full-length FhaC crystal structure has been solved (Clantin et al. 2007). Resolution of L6 is not sufficient to establish definitive interactions among loop and β-barrel residues; however, it is clear that L6 can fold into the lumen of the FhaC β-barrel. It has also been established that FhaC L6 has a surface-exposed conformation, which can be detected by susceptibility to exogenous protease added to whole cells (Jacob-Dubuisson et al. 1999; Guédin et al. 2000). Importantly, L6 is accessible to protease only when the FhaC substrate FHA is present, indicating that loop localization is related to substrate binding and secretion (Jacob-Dubuisson et al. 1999; Guédin et al. 2000). In similar protease experiments, E. coli BamA has also been shown to adopt multiple conformations (Rigel et al. 2012). Cysteine labeling with a high M_r polyethylene glycol derivative identifies two residues in L6, C690, and C700, as part of this conformational change, suggesting that, like FhaC, BamA L6 has luminal and extracellular conformations involved in substrate assembly (Rigel et al. 2013).

Given the potential for L6 to interact with the β-barrel and the obvious chemical logic to an arginine–aspartate interaction, we propose that R661 and D740 form a salt bridge in vivo. That substitution of either residue with glycine causes destabilization of the β-barrel suggests this putative salt bridge is important for BamA stability, although it is not essential for function as neither the bamAR661G nor the bamAD740G mutation confers a striking OMP assembly defect. This separability of β-barrel stability and function is further supported by the fact that suppressors of the bamAR661G and bamAD740G mutations restore SDS–EDTA resistance without restoring β-barrel stability. It is likely that these are bypass suppressors that restore BamA function without restoring the L6–β-barrel interaction lost with disruption of the R661–D740 salt bridge.

The synthetic phenotypes displayed by the bamAR661G+D740G double mutant are not readily explained by loss of the putative R661–D740 salt bridge alone, since either single mutation would completely disrupt the ionic interaction. To explain their synthetic phenotypes, we hypothesize that R661 and D740 have secondary functions separate from their common salt bridge, which are important for stabilization of the β-barrel. This hypothesis follows from the fact that β-barrel stability is maintained even in the absence of BamE, a condition under which L6 shows increased dissociation from the β-barrel (Tellez and Misra 2012; Rigel et al. 2012, 2013). Because the putative R661–D740 salt bridge is almost certainly disrupted when L6 adopts its loop-out conformation, these data suggest that the salt bridge alone cannot account for stability of the β-barrel. Rather, it is likely that these residues participate in other direct—possibly ionic—interactions that stabilize the β-barrel in alternative conformations of BamA. The synthetic effects observed in a bamAR661G+D740G double mutant would then be caused by the loss of these secondary interactions.

Our current model of BamA function proposes that OMP assembly is accomplished through conformational cycling of BamA and its essential lipoprotein partner BamD (Ricci et al. 2012; Rigel et al. 2013). In this cycle BamA adopts at least two distinct conformations, characterized by the luminal and extracellular conformations of L6, each of which seems to be stabilized by R661 and D740. Given the dramatic change in substrate conformation that occurs during OMP assembly, it is not surprising that the Bam machine might undergo significant conformational changes itself.

Such a model requires that BamA integrate signals of substrate binding, folding, and assembly, of lipoprotein conformations, and of its own domain conformations in order to execute OMP assembly. This process implies a complex network of residues spanning multiple proteins that serves to communicate, transduce, and execute conformational changes. For instance, BamA POTRA5 has been implicated in communicating conformational changes between BamAD (Ricci et al. 2012). Whether R661 and D740 help regulate this process is unclear, but we note that the suppressors common to the bamAR661G and bamAD740G alleles are distributed throughout POTRA5 and the BamA β-barrel.

We are just beginning the process of discovering the network of Bam residues involved in OMP assembly, but it seems that DCA will be an integral part of this work. The limiting step in our analysis so far has been the identification of informative mutations. BamA is robust to point mutation, and there is no straightforward selection for Bam mutants. DCA has the potential to circumvent these difficulties in this and in many other complicated genetic systems. DCA is likely to prove particularly useful for uncovering the kind of complex residue network that we hypothesize may play an important role in BamA function. By identifying functionally related residues, DCA of Bam components may yield network residues in pairs or even groups. Combined with suppressor analysis, this approach has the potential to greatly accelerate our line of genetic inquiry and others like it across experimental systems and organisms.