Accumulation of Spontaneous Mutations in the Ciliate Tetrahymena thermophila

Abstract

Knowledge of the rate and fitness effects of mutations is essential for understanding the process of evolution. Mutations are inherently difficult to study because they are rare and are frequently eliminated by natural selection. In the ciliate Tetrahymena thermophila, mutations can accumulate in the germline genome without being exposed to selection. We have conducted a mutation accumulation (MA) experiment in this species. Assuming that all mutations are deleterious and have the same effect, we estimate that the deleterious mutation rate per haploid germline genome per generation is U = 0.0047 (95% credible interval: 0.0015, 0.0125), and that germline mutations decrease fitness by s = 11% when expressed in a homozygous state (95% CI: 4.4%, 27%). We also estimate that deleterious mutations are partially recessive on average (h = 0.26; 95% CI: –0.022, 0.62) and that the rate of lethal mutations is <10% of the deleterious mutation rate. Comparisons between the observed evolutionary responses in the germline and somatic genomes and the results from individual-based simulations of MA suggest that the two genomes have similar mutational parameters. These are the first estimates of the deleterious mutation rate and fitness effects from the eukaryotic supergroup Chromalveolata and are within the range of those of other eukaryotes.

MUTATIONS are the ultimate source of variation responsible for evolutionary change. Thus, knowledge of the rate and fitness consequences of spontaneous mutations is essential to understanding evolution (Charlesworth 1996). These parameters have been estimated in a handful of species and have provided many important insights into the evolutionary process (reviewed in Lynch et al. 1999; Halligan and Keightley 2009; Lynch 2010). For example, the observation that the deleterious mutation rate is less than one per genome per generation in several species suggests that the mutational deterministic hypothesis is insufficient to explain the widespread maintenance of sexual reproduction (Kondrashov 1988; Halligan and Keightley 2009). However, among eukaryotes, these mutational parameters have been estimated only in Opisthokonta (animals, fungi, and relatives) and Archaeplastida (red and green algae, land plants, and relatives), leaving the majority of eukaryotic diversity unexamined.

Mutation accumulation (MA) is the best experimental tool with which to study mutation rates and fitness effects. Typically, MA experiments consist of allowing spontaneous mutations to arise and fix in parallel, replicate populations over many generations. Small populations are used to reduce the effectiveness of natural selection in determining the fate of new mutations. The quality of the estimates of mutational parameters derived from MA experiments is constrained by the biology of the organism used. Organisms with long-generation times experience a slow rate of MA [e.g., one experiment on Arabidopsis thaliana (Shaw et al. 2000), which has a generation time of ∼10 weeks, lasted only 17 generations], leading to imprecise estimates. Other organisms cannot be maintained at a constant population size and must be allowed to expand between transfers (Kibota and Lynch 1996), which allows the purging of mutations with strongly deleterious effects, leading to biased estimates.

The ciliated unicellular eukaryote Tetrahymena thermophila (Chromalveolata) is particularly suitable for MA because of its unusual nuclear architecture and short generation time. Like most ciliates, T. thermophila maintains two types of nuclear genomes: a transcriptionally active somatic genome in the macronucleus, and a sequestered, largely transcriptionally inert, germline genome in the micronucleus. While a cell reproduces asexually, germline DNA is not transcribed, and therefore mutations in that genome will have no phenotypic consequences. Indeed, cells that have lost their germline genomes are capable of normal asexual reproduction (Nanney 1974; Allen et al. 1984). Natural selection will “see” new germline mutations only after conjugation when the cell generates a new somatic genome from its germline genome.

Here, we have conducted an MA experiment to determine the rate and fitness effects of spontaneous mutations in the germline and somatic genomes of T. thermophila. MA in the germline proceeds as for any asexual, diploid eukaryote, except that all mutations are actually neutral. The expected number of new germline mutations per MA line per generation is 2UN, where U is the deleterious mutation rate per haploid germline genome per generation and N is the population size. Since the micronucleus divides mitotically and these mutations are hidden from selection, the probability of fixation of a diploid genotype containing a new mutation in a heterozygous state is 1/N. Thus, an MA line will accumulate deleterious mutations at a rate of 2U per generation. After t generations, an MA line is expected to carry k = 2Ut deleterious germline mutations (in a heterozygous or heteroallelic state).

To assay the fitness of the germline genome of an MA line we constructed a genomic exclusion (GE) line (Figure 1). If an MA line has k mutations in a heterozygous state, a GE line derived from it will have a subset of, on average, k/2 mutations in a homozygous state in both the germline and somatic genomes; different GE lines will have different combinations of the original k mutations. If we assume that the fitness of a genotype containing a deleterious mutation in the homozygous state is 1 − s and that all mutations have equal effects, then, following the approach of Bateman (1959) and Mukai (1964), the expected decline per generation in the mean fitness of MA lines after GE relative to the ancestor is given by ΔM = –Us, and the expected increase per generation in the among-line variance in fitness is given by ΔV = Us². These expressions allow us to construct Bateman–Mukai estimators for the mutational parameters in our experiments (Table 1, single GE). As expected, deleterious mutations in the germline genome caused the mean fitness of GE lines derived from MA lines to decline and the variance in fitness among these lines to increase. Analysis of multiple GE lines and backcrosses of these lines with the ancestor suggest that most accumulated germline mutations are mildly recessive when expressed in the somatic genome. We found little evidence for the accumulation of either beneficial or lethal mutations in germline genomes. Our estimates of mutational parameters for the germline genome are consistent with estimates from MA experiments in other eukaryotes.

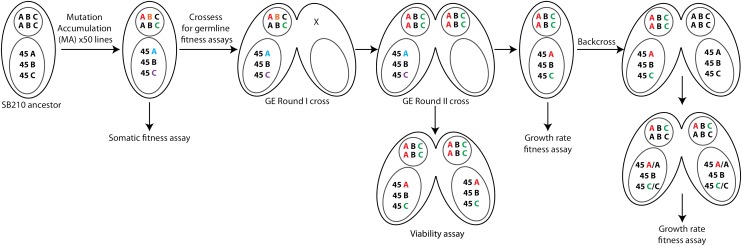
Figure 1.

Experimental design. Fifty independent MA lines were started from an SB210 ancestor. Three hypothetical loci are shown: A, B, and C. Each locus is present in two copies in the diploid germline genome and in ∼45 copies in the somatic genome. Each line was allowed to accumulate mutations independently, in both the somatic and germline genomes, shown in the lower large oval or smaller circle in each cell, respectively. Different colored letters indicate independent mutations at the three loci and two genomes. Fitness effects of mutations in the somatic genome were assayed directly on the MA lines (Somatic fitness assay). Measures of fitness effects of germline mutations required further genetic manipulations (Crosses for germline fitness assays). First, two rounds of genomic exclusion (GE) crosses were performed. In the GE round I cross, an MA line is mated with a “star” strain with a nonfunctional germline genome, indicated in the figure by an X where the germline genome should be. The resulting progeny are whole-genome homozygotes (of randomly chosen alleles) in the germline genome, but maintain the parental somatic genome. Mating in GE round II results in the formation of new somatic nuclei that are homozygous for the alleles found in the germline genome after GE round I. Mating pairs in round II GE crosses were picked and assessed for survival (Viability assay). Independently, single-cell progeny of round II GE crosses were isolated and assessed for growth rate (Growth rate fitness assay). To test for dominance effects, GE progeny were backcrossed to an ancestral cell (after GE), and heterozygous progeny were assayed for growth rate immediately after conjugation to maintain heterozygosity that would otherwise be lost to phenotypic assortment during many cell divisions.

Table 1. Expected values of experimental and mutational parameters for different types of data used in this study.

Parameter	Single GE	Multiple GE	Backcross
ΔM	–Us	–Us	–Uhs
ΔV	Us2	Us2/2
U	(ΔM)2/ΔV	(ΔM)2/(2ΔV)
s	–ΔV/ΔM	−2ΔV/ΔM
h		ΔMBX/ΔMGE

Single GE, one GE per MA line; Multiple GE, several GE per MA line; Backcross (BX), multiple GE per MA line followed by backcrossing to the ancestor. From these experiments we measured the following two quantities directly: ΔM, change in the mean fitness of the lines per generation; ΔV, change in the among-line variance per generation. (In the single GE experiments these quantities were measured across MA lines; in the multiple GE and backcross experiments they were measured among replicate GEs within a single MA line.) From these quantities we estimated the mutational parameters: U, deleterious mutation rate per haploid germline genome per generation; s, deleterious effect of a mutation when in a homozygous state; h, dominance coefficient of a mutation. (The fitness of a genotype containing a mutation in the homozygous state is 1 − s; that of a genotype containing the same mutation in the heterozygous state is 1 − hs; ΔM_BX = 1 − M_BX, ΔM_GE = 1 − M_GE.) The expressions assume that all mutations have equal effects, following the approach pioneered by Bateman (1959) and Mukai (1964).

MA in the somatic genome differs from that in the germline genome in two ways. First, mutations in the somatic genome have immediate phenotypic consequences and are exposed to selection. Second, the somatic genome is 45-ploid and the macronucleus in which it is carried divides by a mechanism (amitosis) that causes the copy number of somatic mutations to fluctuate stochastically from generation to generation. In our experiment the MA lines did not appear to accumulate any somatic mutations. However, we found no evidence that the germline and somatic genomes of T. thermophila have different mutational parameters.

Materials and Methods

Strains and media

We used the inbred T. thermophila strain SB210 as the ancestor for the MA experiment. SB210 carries resistance to 2-deoxy-d-galactose (2-dgal) in its germline genome but not in its somatic genome (Mayo and Orias 1981). Thus, only cells that have completed conjugation and development are resistant to 2-dgal, allowing us to test for successful conjugation. We used the B*VII strain, which lacks a functional micronucleus, for GE (Figure 1) (Cole and Bruns 1992). SB210 and B*VII express mating types VI and VII, respectively.

Throughout the MA experiment, we cultured cells in SSP medium: 2% proteose peptone (EMD Chemicals, Gibson, NJ), 0.2% glucose, 0.1% yeast extract (BD, Sparks, MD), and 0.003% Fe-EDTA (Acros Organics, Fair Lawn, NJ) (Gorovsky et al. 1975). Cells were incubated on a shaker at 200 rpm and 30° and starved in Tris buffer (10 mM Tris–HCl pH 7.5) in preparation for conjugation (Bruns and Brussard 1974). We used a 2% proteose peptone solution for mating pair refeeding during conjugation (Bruns and Cassidy-Hanley 1999).

Mutation accumulation experiment

We established 50 MA lines from single-cell isolates of strain SB210 (Figure 1). Each line was grown to log phase in 3 ml of fresh SSP medium. When cultures reached log phase, usually after 3–4 days, each line was passaged by single-cell transfer. Four to eight replicates were prepared for each MA line to prevent accidental extinction. The average proportion of successfully established cultures out of the first four replicates was 51% (SD = 29%) and did not change significantly over the course of MA (one-way ANOVA for t = 0, 500, and 1000 generations: F_2,144 = 0.89, P = 0.4).

Prior to each transfer, we measured the optical density at 650 nm (OD₆₅₀) of the log-phase culture on a Versamax microplate reader (Molecular Devices, Sunnyvale, CA). We used these measurements to calculate the number of cell divisions between two transfers using a standard curve for the ancestor. Cell size was monitored to assure consistency of these measurements (Supporting Information, File S1). When an MA line took >7 days to reach a detectable OD₆₅₀, we measured cell density using a C-Chip hemocytometer (Incyto, SKC, Korea). We estimate that, on average, cultures underwent 19.4 generations between transfers. Single-cell transfers were repeated until each line had undergone 51 transfers or ∼1000 generations. This took up to 256 days for the slowest-growing lines.

On the few occasions when none of the replicate single-cell transfers survived, we reinitiated the MA line using a starvation backup culture. We made backups by washing and resuspending cells from the log-phase culture in Tris buffer. To reinitiate a line, starved cells were washed four times in 100-μl drops of Tris buffer with 10 units penicillin, 10 µg streptomycin, and 0.025 µg amphotericin B (Amresco, Solon, OH). Single cells were then transferred to the growth medium in 16 replicates. As a result of these procedures we lost only one cell line (because of fungal contamination).

Cells from each MA line were cryopreserved in liquid N₂ (Bruns et al. 1999) every 200 generations. Three milliliters of early log-phase cultures were centrifuged (1100 g, 3 min), the supernatant was removed, and 100 μl of cells were transferred to 500 μl Tris buffer, with at least two replicates. After 2 days, cells were frozen to –80° in 8% DMSO (Sigma-Aldrich) and stored in liquid N₂.

Somatic fitness assays

After 1000 generations of MA, frozen lines were thawed and transferred to prewarmed SSP medium, following Bruns et al. (1999). We were unable to recover some cultures, possibly due to cells having entered the late-log phase or being at too low density when frozen. To detect changes in fitness associated with somatic mutations, we directly assayed the thawed cultures, from all time points simultaneously (Figure 1). We counted 10 cells from each culture and inoculated them into 180 μl SSP with 18 units penicillin, 18 µg streptomycin, and 0.045 µg amphotericin B on a 96-well plate. After 14 hr of pre-incubation at 30°, we loaded the cultures onto a microplate reader at 30°, which measured OD₆₅₀ every 5 min for 60 hr. The location of cultures on a plate was randomized in each of three to five of replicates in different blocks. We calculated maximum population growth rate (r_max) in a culture using the approach described in Wang et al. (2012).

We assayed “somatic fitness” in 4 lines from the initial culture, 16 lines at t = 200 generations of MA, 6 lines at t = 400, 10 lines at t = 600, 13 lines at t = 800, and 38 lines at t = 1000 generations.

Germline fitness assays

To measure the fitness effects of germline mutations, we derived a GE line from each MA line (Figure 1) (Bruns and Cassidy-Hanley 1999). This involves conjugation of an MA line with the B*VII strain (which has a dysfunctional micronucleus) and, after two rounds of crosses, results in genetically identical progeny that are homozygous in both somatic and germline genomes for approximately half of all germline mutations present before GE. Mitochondria, however, are uniparentally inherited, so half of the progeny will have mitochondria from the MA line and half from B*VII. We have not evaluated the mitochondrial genotypes of GE lines in our study.

In GE round I crosses, cells from MA lines and B*VII were cultured in 5.5 ml SSP until they reached a density of ∼2 × 10⁵/ml, at which time they were centrifuged and starved for 1–3 days in Tris buffer. One milliliter of starved MA culture was mixed with 1 ml starved B*VII and incubated on a six-well plate in a wet chamber at 30°. After 6–8 hr, mating pairs were refed to a final concentration of 1% proteose peptone. Two hours after refeeding, we isolated 16–48 mating pairs and inoculated each into 800 μl SSP on a 48-well plate.

GE round II crosses were performed by culturing and starvation of successful round I cultures. Two milliliters of starved cultures were allowed to mate and 24–96 single mating pairs were isolated as above. Round II offspring viability was defined as the fraction of mating pairs that produced live progeny after 72 hr. Progeny cells from round II were exposed to 2-dgal (Sigma-Aldrich) to assay for successful conjugation (Cole and Bruns 1992). Drug effects were checked 96 hr after 2-dgal was added to the culture. Progeny cells resistant to 2-dgal were then used in fitness assays as described in the previous section.

We assayed “germline fitness” for a single GE line per MA line (except for the ancestor; also, see Multiple GEs and backcrosses). GE crosses were repeated at least twice in cases where there was no mating or no drug-resistant progeny. GE crosses were successful for 25 independent MA lines at one or more of generations t = 200, 800, and 1000 (Figure S1).

Multiple GEs and backcrosses

To validate the germline mutational parameters, we conducted multiple independent GE crosses on four MA lines at generation t = 1000 (Figure S1, * labeled lines). We followed the GE procedures described above, isolating 48 mating pairs in each GE round. We recorded the viability of mating pairs.

We assayed the fitness of the multiple GE lines as above, except that we inoculated 1 cell/well, instead of 10. To estimate the dominance coefficient of germline mutations, we backcrossed the multiple GE lines to a GE line derived from the ancestor (4-0-AI1). Seven to 12 GE lines per MA line resulted in successful backcrosses. We measured fitness after backcross as described above, except that we inoculated single mating pairs into a 96-well plate and incubated them for <48 hr at 30° to avoid loss of heterozygosity from phenotypic assortment (Doerder et al. 1992). The fitness of 4-0-AI1 was also measured in each assay of GE lines before and after backcross.

Statistical analyses

Evolutionary responses:

To infer mutational parameters for both the germline and somatic genomes, we measured the evolutionary responses in the mean fitness of MA lines and the variance in fitness among MA lines. We measured fitness as the maximum population growth rate (r_max) divided by that of the ancestor. Values were natural-log transformed to increase normality and homogeneity of variances. We used a Bayesian approach, fitting linear mixed models separately for the germline and somatic fitness data using Markov chain Monte Carlo with the MCMCglmm 2.15 package (Hadfield 2010) in R 2.13.0 (R Development Core Team 2011). “Generation” was treated as a categorical fixed effect and “MA Line” and “Plate” were treated as categorical random effects. Separate among-MA line variance components were fit for each Generation using the “idh” variance function. We used weakly informative proper priors. For the germline fitness data, the priors for the fixed effects were normally distributed with mean 0 and variance 10¹⁰; the priors for the random effects were inverse Wishart distributed with variance at the limit V = 1 and degree of belief ν = 0.002. For the somatic fitness data, the priors were as for the germline fitness data, except that the priors for the random effects were inverse Wishart distributed with V = 0.1 and ν = 0.0002. The posterior distributions of each parameter contained 2 × 10⁵ independent iterations (see File S2 for more details on the MCMC analysis). We used the linear mixed model to estimate the mean fitness of the lines (M_t) and the among-line variance component (V_t) at each generation t.

Bateman–Mukai estimates of mutational parameters:

To estimate the change in mean fitness per generation (ΔM) and the change in the among-line variance in fitness per generation (ΔV) we used weighted least-squares regression of M_t and V_t, respectively, against t, where each value was weighted by the inverse of the variance of its posterior distribution. We used the Bateman–Mukai estimators listed under “single GE” in Table 1 to calculate the germline haploid deleterious mutation rate (U) and the deleterious effect of a mutation (s). The posterior distribution of a composite parameter (e.g., s = –ΔV/ΔM), was obtained by calculating the composite parameter for each combination of values from the joint posterior distributions of its constituent parameters. We report the posterior median and 95% credible intervals for any parameters and composite parameters obtained from the linear mixed model.

We evaluated the estimates of M_t, ΔM, and ΔV, by the extent to which their posterior distribution overlaps with zero. This approach is not appropriate for the estimates of V_t because their prior specification implies that they must be positive; instead we compare different models using the Deviance Information Criterion, DIC (Spiegelhalter et al. 2002; Barnett et al. 2010; Wilson et al. 2010).

Maximum-likelihood estimates of mutational parameters:

We analyzed the estimates of line means at t = 0 and 1000 (obtained from the linear mixed model described in the previous section) using the MLGENOMEU 2.08 software (Keightley 1994; Keightley 1998; Keightley and Ohnishi 1998). The mean fitness of a single GE line is assumed to be given by the sum of the mean fitness of the ancestral line (M₀), a normally distributed environmental effect with variance V_e, and an unknown number of mutational effects. We assume that the number of deleterious mutations k acquired by each MA line per generation is Poisson distributed with parameter 2U and that the deleterious effects of these mutations when in a homozygous state (s) come from a gamma distribution with scale and shape parameters α and β, respectively, such that the mutational effects have mean s = β/α and variance V_s = β/α². When β = 1, mutational effects are exponentially distributed; as β → 0, the distribution becomes increasingly leptokurtic (L-shaped), such that most mutations have negligible effects (s ≈ 0), but a small proportion of mutations have very large effects; as β → ∞, the distribution approaches equal effects (i.e., V_s = 0), as assumed by the Bateman–Mukai method.

We calculated the likelihood L of the data as a function of the mutational parameters (U, α, and β) by numerical integration, and the overall log-likelihood (Σ ln L) was the sum of ln L for the single GE line means. We estimated each mutational parameter by finding the maximum log-likelihood for a series of fixed values of that parameter while allowing the other parameters to vary. Approximate 95% confidence limits for each parameter were calculated by the profile likelihood method as the values of the parameter that cause a drop in log-likelihood of 1.92 (half of the 95th percentile of the χ² distribution with 1 degree of freedom) while keeping other parameters constant.

Dominance:

A linear mixed model was fit to the multiple GE and backcross experiments as for the single GE experiment. “Treatment” (GE or backcross) and “MA line” were treated as crossed fixed effects and “Replicate line” and “Plate” were treated as random effects. Separate among-replicate line variance components were fit for each Treatment using the idh variance function (see File S2 for more details on the MCMC analysis). We used the linear mixed model to estimate the mean fitness of the lines (M₁₀₀₀) and the among-line variance component (V₁₀₀₀) at generations t = 0 and 1000 in each treatment. For each treatment, we estimate the change in mean fitness and the change in the among-line variance in fitness as ΔM = (M₁₀₀₀ – M₀)/1000 and ΔV = V₁₀₀₀/1000, respectively. We used the Bateman–Mukai estimators listed under multiple GE and backcross in Table 1 to calculate the germline mutational parameters U, s, and h (dominance coefficient).

Mutations with effects on viability:

In addition to population growth rate, we considered GE round II viability as a fitness component. We estimated mutational parameters for this trait using approximate Bayesian computation (ABC) (Beaumont et al. 2002). The ABC modeling process involved simulating our viability data under a model of GE. We assumed that an MA line carries k mutations that are capable of influencing viability in a heterozygous state. GE samples each of these mutations with probability P = 0.5 and makes them homozygous. The viability of a GE genotype with k_GE mutations is w = w₀ (1–s)^k_GE, where s is the effect of a mutation and w₀ is the viability of a genotype with no mutations. We assumed that all mutations have the same effect and act multiplicatively (the latter is appropriate if s can be large). We then simulated an experiment involving n round II GE crosses as a binomial process with probability of survival (i.e., “success”) w.

For each MA line tested (t = 0 ancestor, and t = 1000 MA lines 5, 40, 44, and 50) we generated 4 × 10⁶ simulated data sets involving N independent GE crosses (e.g., n = 48 and N = 20 for MA line 40). Values for the number of mutations were drawn at random from a uniform prior of k ∼ [0, 30], and those for the mutational effect were drawn at random from a uniform prior of s ∼ [0, 1], independently from k. Values for the logit of baseline viability, ln[w₀/(1 – w₀)], were drawn from a normal distribution with mean 1.6977 (corresponding to w₀ = 0.845) and standard deviation = 0.2364. These values were estimated from the GE viability data for the ancestor using a generalized linear model with logit link and quasibinomial errors.

We compared the results from the simulated data to the empirical data using the following four summary statistics on the proportion of viable round II GE crosses: mean, standard deviation, skewness, and kurtosis. From a set of 4 × 10⁶ simulations, we retained the 10⁴ simulations (0.25% of the full set) with the lowest Euclidian distance to the summary statistics using the R package abc 1.4 (Csilléry et al. 2012). To estimate the posterior distribution of the parameters k and s from the accepted simulations, we corrected for the discrepancy between the accepted and the observed summary statistics using the local linear regression method with log-transformed parameters (Beaumont et al. 2002). Unless otherwise stated, we report the posterior median and 95% CI of k and s. We validated all our estimates using posterior predictive checks (Csilléry et al. 2012).

Evolutionary simulations

To evaluate the effect of MA on the somatic genome we conducted individual-based simulations. Evolution follows a Wright–Fisher scheme (Ewens 2004) of reproduction–mutation–selection of a population of constant size N. To advance the population one generation, individuals are sampled randomly, copied, mutated, and allowed to survive with a probability proportional to their somatic fitness until the population size N is reached.

Individuals consist of a diploid germline genome and a 45-ploid somatic genome, each with L loci, and reproduce asexually. Each allele at each locus in both genomes can irreversibly mutate to a deleterious form. Each somatic locus i contributes equally and additively to fitness, in proportion to the number k_i of mutant copies at that locus. Thus, the fitness of a genotype is given by

$$w=1-s{{\displaystyle \sum _{i=1}^L\left(\frac{k_i}{45}\right)}}^{-{\log }_2{h}_i},$$ (1)

where s is the deleterious effect of a mutation present in k = 45 copies and h_i is the dominance coefficient at locus i, defined as the expected effect of having k = 22.5 copies of a mutant allele. Additive effects correspond to h = 0.5. The germline genome does not contribute to fitness.

Asexual reproduction proceeds by generating an individual with a germline genome identical to its progenitor (mitosis) and a somatic genome obtained by duplicating and sampling without replacing each of the progenitor’s somatic loci until 45-ploidy is reached (amitosis). Mutations at intermediate copy number (0 < k < 45) in the somatic genome will increase or decrease stochastically in copy number within individuals from generation to generation, until they ultimately fix or disappear (phenotypic assortment, Doerder et al. 1992). This is not true in the germline genome, where all the descendants of an individual carrying a germline mutation will also contain that mutation. At reproduction, each allele at each locus in each genome mutates at rate µ; the germline haploid deleterious mutation rate is U = Lµ.

To measure the germline fitness of a simulated MA line, we simulated the construction of a single GE line for each MA line. We generated a homozygous version of the individual by randomly picking one of the copies at every locus and copying it to the other locus. This fully homozygous germline genome was then allowed to generate a new 45-ploid somatic genome and fitness was calculated using Equation 1.

Results

Germline genome

Evolutionary response:

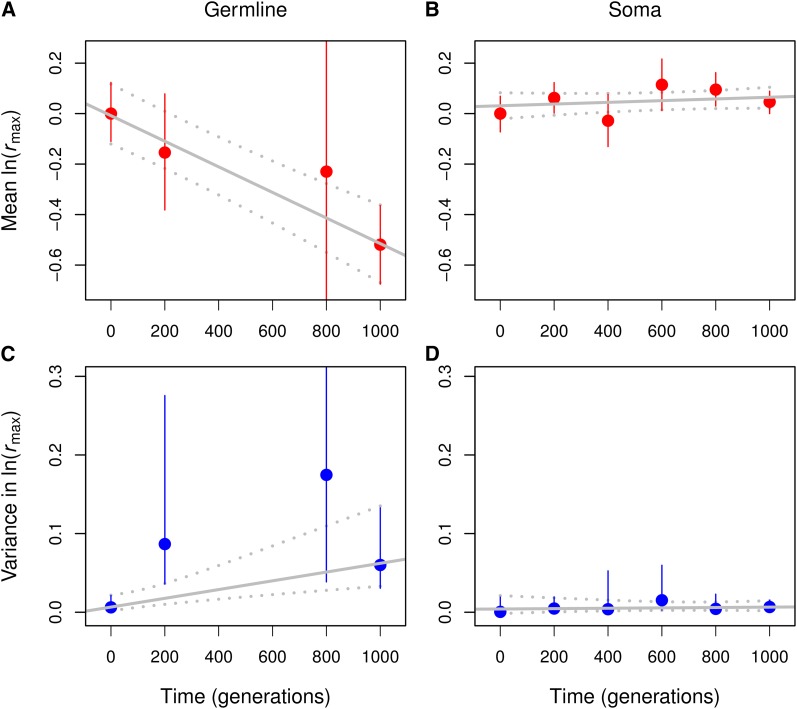
To evaluate the fitness consequences of MA in the germline genome, we measured the maximum population growth rate (r_max) of 25 MA lines after GE at different times during evolution (Figure S1). After 1000 generations of MA, the mean ln(r_max) of 19 single GE lines was 51.9% lower than that of the ancestor (95% credible interval; CI, 36.5%, 67.6%). Taking into account additional data from generations 200 and 800, we estimate that mean ln(r_max) declined by ΔM = –0.0509% per generation (Table 3, Figure 2, and Figure 3A). Concurrently, the among-line variance in fitness also changed over time (Table 2): it increased at a rate of ΔV = 0.00552% per generation (Table 3 and Figure 3C). The decline in mean fitness and the increase in variance in fitness among GE lines derived from MA lines indicate that the MA lines have accumulated deleterious germline mutations.

Table 3. Estimates of mutational parameters.

Parameter	Data	Method	Estimate (95% CI)
ΔM	SGE	LMM	−0.0509% (–0.0649%, –0.0368%)
ΔV	SGE	LMM	0.00552% (0.00227%, 0.01279%)
Ve	SGE	LMM	0.0281 (0.0237, 0.0337)
Vm/Vea	SGE	LMM	0.0981% (0.0397%, 0.231%)
U	SGE	BM/LMM	0.00470 (0.00154, 0.01249)
s	SGE	BM/LMM	0.109 (0.0437, 0.272)
U	SGE1000	ML	0.00444 (0.00231, 0.00926)
s	SGE1000	ML	0.118 (0.0578, 0.194)
β	SGE1000	ML	∞ (0.00699, ∞)
ΔM	MGE	BM/LMM	−0.0403% (–0.0543%, –0.0264%)
ΔV	MGE	BM/LMM	0.000396% (0.000088%, 0.001027%)
Ve	MGE	BM/LMM	0.0158 (0.0126, 0.0200)
U	MGE	BM/LMM	0.0205 (0.00583, 0.101)
s	MGE	BM/LMM	0.0198 (0.00423, 0.0558)
h	MGE/BX	BM/LMM	0.257 (–0.0221, 0.622)
UL	Viability		<0.000374
U	Viability	ABC	0.00337 (0.00079, 0.00596)b
s	Viability	ABC	0.325 (0.136, 0.514)b

Parameters: ΔM, change in mean fitness per generation; ΔV, change in variance in fitness per generation; V_e, environmental variance; V_m/V_e, mutational heritability, where V_m = ΔV/2; U, deleterious mutation rate per haploid genome per generation; s, homozygous effect of a deleterious mutation; β, shape parameter of the gamma distribution of mutational effects; h, dominance coefficient; U_L, lethal mutation rate per haploid genome per generation. Data: SGE, MA experiment, single GE; SGE1000, single GE excluding data from t = 200 and 800 generations; MGE, multiple GE; BX, multiple backcrosses; Viability, viability in GE round II crosses. Approaches: LMM, linear mixed model; BM, Bateman-Mukai estimators (Table 1); ML, maximum likelihood; ABC, approximate Bayesian computation.

^aMutational heritability must be interpreted with caution in this system: although mutations may arise in the germline genome each generation, these mutations are not expressed, and therefore do not contribute to the mutational variance, except after conjugation occurs, which happens at most every ∼50 generations (Lynn and Doerder 2012).

^bMean and 95% confidence interval of the estimates shown in Figure 5B.

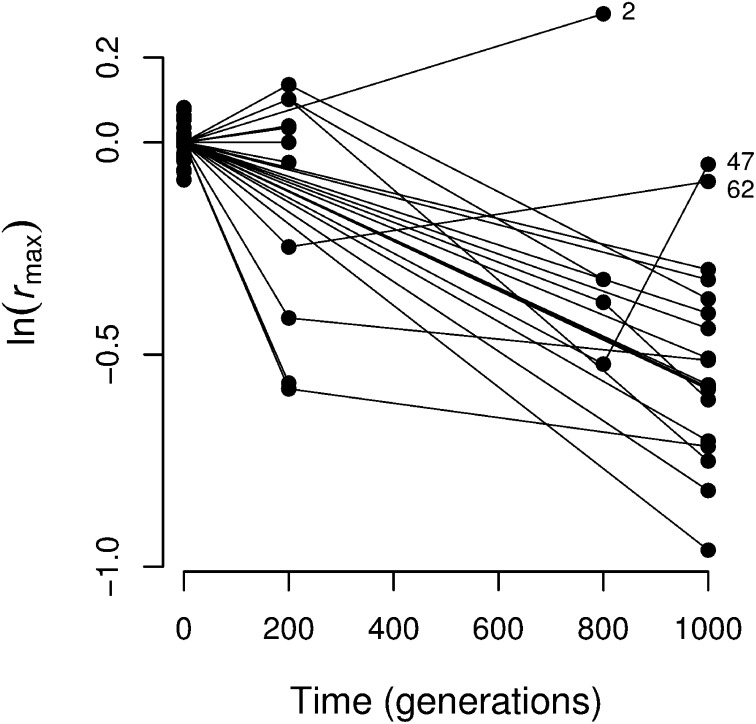
Figure 2.

Germline fitness during the course of the MA experiment. Each point shows the mean fitness of one GE line derived from an MA line (see Figure S1 for a detailed history of the MA lines). We measured fitness as maximum population growth rate (r_max) relative to the ancestor. The mean fitness of each line was estimated through a linear mixed model. Lines connect single GE lines derived from the same MA line at different times. Numbers indicate lines discussed in the Beneficial mutations section of Results.

Figure 3.

Accumulation of spontaneous mutations in the germline and somatic genomes of T. thermophila over 1000 generations. Gradual accumulation of deleterious mutations in the germline genome causes mean fitness to decrease (A) and among-line variance in fitness to increase (C). In contrast, neither the mean nor the among-line variance in somatic fitness change significantly over the course of the experiment (B and D). Means and among-line variance components were estimated through linear mixed models. Error bars are 95% credible intervals (CIs), based on the posterior distribution of the mixed model. In A and C, the CIs for t = 800 generations are truncated to improve visualization (the wide CIs are caused by the large variance among a small number of lines; Figure 2). Solid lines are weighted least-squares regression fits where the mean or among-line variance at each time was weighted by the inverse of the variance of the posterior distribution; the dotted lines show the 95% CIs on the fits calculated from the posterior distribution.

Table 2. Deviance Information Criterion (DIC) analysis of among-line variance components in the MA experiment.

Model	Germline	Soma
V0 = V200 = … = V1000 = 0	92.32	−245.21
V0 = V200 = … = V1000 > 0	−78.07	−293.58
V0 ≠ V200 ≠ … ≠ V1000 > 0	−178.45	−286.02

Three linear mixed models were fit making different assumptions on the among-line variance components at different generations: (1) equal to zero, (2) equal to each other, and (3) different from each other. Generation was treated as a fixed effect and MA line and Plate were treated as random effects. The germline and somatic fitness data were analyzed separately. Values are the DIC corresponding to each model. Lower values of DIC indicate a better fit (Spiegelhalter et al. 2002). A difference in the DIC of five is considered substantial, and a difference of 10 rules out the model with the larger DIC (Barnett et al. 2010). Values in italics indicate the simplest adequate model.

Bateman–Mukai estimates of mutational parameters:

Applying the estimators in Table 1 (single GE) to our ln(r_max) data we obtain U = 0.00470 and s = 0.109 (Table 3). These parameters suggest that each MA line (from which the assayed GE line was generated) carried ∼U × 2 × 1000 = 9.4 deleterious mutations in the diploid germline genome at the end of the experiment (95% CI, 3.1, 25.0).

Maximum-likelihood estimates of mutational parameters:

Bateman–Mukai estimates of mutational parameters have two limitations. First, the assumption of equal effects may not be met, which can cause U to be underestimated and s to be overestimated. Second, because both ΔM and ΔV feature reciprocally in the formulas for both U and s in Table 1, there is a strong negative sampling covariance between Bateman–Mukai estimates of the two mutational parameters (Lynch et al. 1999). To address these limitations, we also estimated the mutational parameters using maximum likelihood (ML). The ML approach has the advantage that it takes into account the actual distribution of line mean fitness, rather than just the mean and variance of this distribution.

We began by estimating the shape parameter of the gamma distribution β by finding the maximum log-likelihood for a series of fixed values of that parameter while allowing U and s to vary. The analysis shows that the log-likelihood is maximized for β → ∞ (equal effects), although the lower 95% confidence limit is β = 0.00699 (a strongly leptokurtic distribution). Assuming equal effects, we get the following ML estimates of germline mutational parameters: U = 0.00444 and s = 0.118 (Table 3). The ML estimates are almost identical to those obtained using the Bateman–Mukai method (Table 3).

Dominance:

GE lines allow us to only estimate the effects of mutations in a homozygous state. To evaluate the dominance coefficient of these mutations we have taken four MA lines (Figure S1) and generated multiple (16–27) GE lines from each. We then backcrossed each GE line to the ancestor and generated 7–12 backcross lines for each MA line (backcrossing was unsuccessful for some GE lines) (Figure 4). A GE line derived from an MA line with k germline mutations is expected to have k/2 mutations in a homozygous state. A backcross line derived from this GE line will have the same deleterious mutations but in a heterozygous state. By combining the data from both GE and backcross lines, we can estimate the dominance coefficient of a mutation (h), such that the fitness of a genotype containing a mutation in the heterozygous state is 1 – hs (Table 1). Furthermore, the mean and variance in fitness among the multiple GE lines generated from a given MA line can also be used to estimate mutational parameters for that line (Table 1, Multiple GE, third column).

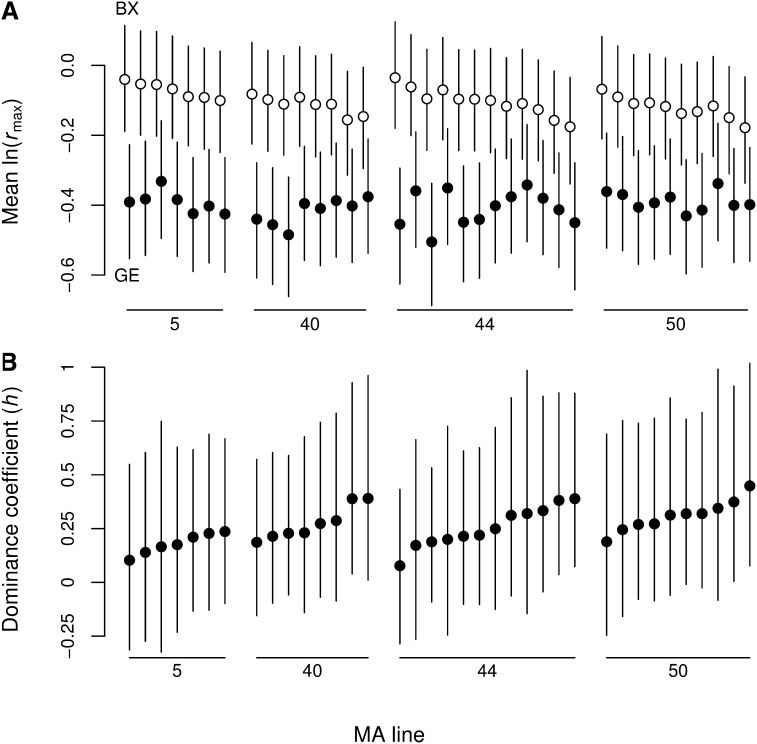
Figure 4.

Most mutations are incompletely recessive. (A) Results of multiple GE per MA line followed by backcrossing to the ancestor (BX). Line means were estimated from a linear mixed model. (B) Estimates of the dominance coefficient (h) based on the data in A (Table 1). GE and backcross lines within each mutation accumulation line and their corresponding values of h are ordered according to increasing h. Error bars, 95% CIs.

Applying these estimators to our multiple GE data we get U = 0.0205 and s = 0.0198 (Table 3). Differences among MA lines were small and therefore were ignored (Table 4). The estimate of the dominance coefficient (h = 0.257, Table 3) suggests that most of the mutations in these lines are incompletely recessive (Figure 4).

Table 4. DIC analysis of variation among MA lines in the GE and backcross experiments.

Model	DIC
Treatment	−246.97
Treatment + MA line	−248.64
Treatment + MA line + Treatment:MA line	−248.47

Three linear mixed models were fit making different assumptions about the fixed effect MA line (4, 40, 44 or 50; Figure 4). Treatment (GE or backcross) was also treated as a fixed effect and Replicate line and Plate were treated as random effects. Values are the DIC corresponding to each model. The value in italics indicates the simplest adequate model. See legend of Table 2 for more details.

Lethal mutations:

Our estimates of mutational parameters so far assume that a GE cross generates an unbiased sample of the mutations carried by an MA line. This will not be the case if some of those mutations are lethal. If an MA line contains k_L unlinked lethal mutations, then a GE line derived from it will be free of lethal mutations only with probability 1/2^k_L. To test for the presence of unlinked lethal mutations, we conducted multiple, independent GEs and estimated the viability of each resulting GE line.

During GE round I, cells pair and the MA strain transfers a haploid pronucleus to the “star” strain, but a new somatic genome does not develop. During GE round II, germline mutations become expressed in the soma (Figure 1). For each of four MA lines, we conducted a large number of independent GE round I crosses (144–288 mating pairs were isolated per MA line). We obtained 91–181 independent surviving GE round I pairs per MA line, each containing a different germline genome. For each of these progeny, we set up 48 replicate round II GE crosses. The germline genomes of each of these 48 replicates are identical, so if none of them survived, it would be strong evidence that the GE progeny had “picked up” a lethal mutation. Sixteen to 30 independent GE round I mating pair cultures from each MA line succeeded in round II GE crossing.

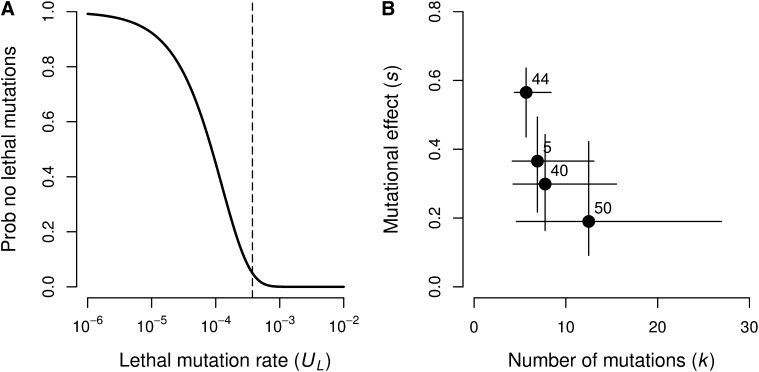
Only 3 of 84 independent GE crosses from 4 MA lines displayed 0/48 = 0% viability in GE round II, and all 3 of these were from the same MA line (44), which had 30 independent GE trials. If this MA line contained a lethal mutation that completely determined GE line viability, then the probability that only 3/30 or fewer independent GE lines show 0% viability is P = 4.2 × 10⁻⁶; the equivalent probabilities for each of the other 3 MA lines are all P ≤ 1.5 × 10⁻⁵. These results suggest that it is unlikely that the 4 MA lines carry any lethal mutations. A lethal mutation rate of U_L = 0.000374/haploid/genome/generation would imply a probability of P = 0.05 of not finding any lethal mutations in 4 MA lines after t = 1000 generations (Figure 5A). We conclude that the lethal mutation rate in our experiment was U_L < 0.000374.

Figure 5.

Mutations with effects on viability in GE round II. (A) Probability that four MA lines did not accumulate any lethal mutations after t = 1000 generations given a range of lethal mutation rates (U_L). The dashed line marks the value of U_L corresponding to a probability of 5%. (B) Number of mutations and their effect on viability in four MA lines. Values are estimates and 95% CIs from an ABC analysis of the GE round II viability data. Numbers indicate the MA line used.

Mutations with effects on viability:

Although the four MA lines described in the previous section do not appear to carry any lethal mutations, the average viability of these lines, that is, the percentage of GE round II crosses that survived, was 20.4% (95% CI, 17.4%, 23.8%), whereas that of the ancestor was 84.5% (95% CI, 77.5%, 89.7%). These results indicate that the four MA lines do carry mutations that reduce GE round II viability.

Using ABC, we estimate that the MA lines we tested contain, on average, k = 6.75 mutations with a deleterious effect on GE round II viability of s = 0.325 (Table 3). Our estimate of k indicates a deleterious mutation rate for viability of U = 0.00337 (Table 3).

Beneficial mutations:

In the analysis so far we have assumed that only deleterious mutations have accumulated in the germline genome. The accumulation of beneficial mutations during our experiment can be inferred in two ways. First, if a GE line has a higher fitness than the ancestor then it is likely to carry one or more beneficial mutations. This is the case with the GE line derived from MA line 2 (Figure 2), which after 800 generations, showed a relative fitness of 3.86 standard deviation $\left(\text{SD}=\sqrt{V_0}\right)$ higher than that of the GE lines derived from the ancestor (95% CI, 1.23 SD, 6.58 SD). The probability that, of 33 GE lines carrying no mutations (beneficial or deleterious), 1 GE line shows a mean fitness as high as that of line 2 after 800 generations is P ≈ 2 × 10⁻⁶ (assuming that measurement error and environmental variation cause normally distributed deviations consistent with the observed variance among replicates of the ancestor). This probability is an upper bound because, assuming a deleterious mutation rate of U = 0.0047, the probability that a GE line derived from an MA line that has evolved for 800 generations contains no deleterious mutations is P = 0.023. Five MA lines (4, 12, 34, 42, and 65) show higher fitness at generation 200 than that of the ancestor, but in all cases they are <1.8 SD higher, so they provide only weak evidence for beneficial mutations.

Second, if a GE line has a higher fitness than that of a GE line derived from an earlier generation of the same MA line, then it may carry beneficial mutations. Meeting this condition, however, is only weak evidence for beneficial mutations because two GE lines derived from the same MA line at different times are also likely to differ over which mutations present in the MA line at the earlier time happen to be sampled during the independent GE crosses. The strongest example of this kind is given by MA line 47: the GE line derived at generation 800 shows a lower fitness (–0.523; 95% CI, –0.746, –0.293) than that derived independently at generation 1000 (–0.052; –0.239, 0.125). MA line 62 also shows a small increase between generations 200 and 1000 but the 95% CIs overlap (not shown).

Somatic genome

To assess the fitness consequences of MA in the somatic genome, we measured the r_max of 42 MA lines (without GE) at different times during evolution. Mean ln(r_max) increased slightly by ΔM = 0.00333% per generation, and the 95% CI overlapped with zero (–0.00285%, 0.00949%; Figure 3B and Figure 6). Similarly, although the among-line variance component changed over time (Table 2), it showed only a weak trend (Figure 3D and Figure 6): ΔV = 0.00018% per generation (95% CI, –0.00156%, 0.00138%). These results indicate that the MA lines have not accumulated any somatic mutations.

Figure 6.

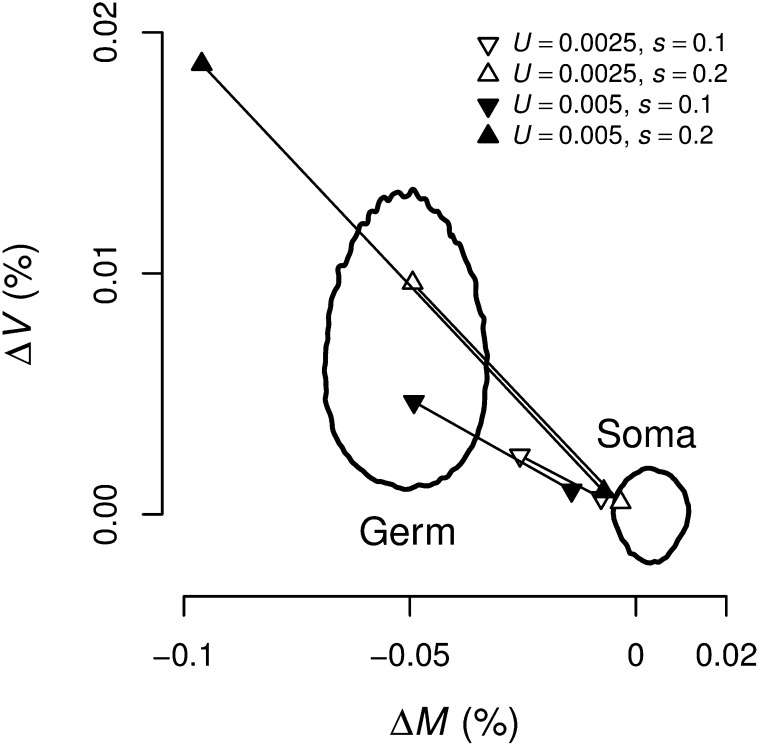
The responses in germline and soma can be explained by the mutational parameters of the germline genome. The solid black ovoid lines mark the 95% credible regions for the responses in the germline (left) and somatic (right) mean (ΔM) and variance (ΔV) in fitness estimated from the single GE experiment. The triangles show values of ΔM and ΔV for germline and soma from simulations assuming that different deleterious mutation rates and effects. In all simulations, we assumed that deleterious mutations act additively in the soma, h = 0.5. Under U = 0.0025 and s = 0.2 the simulations agree with the observed responses.

The difference in evolutionary response in the germline and somatic genomes does not imply that the two genomes have different mutational parameters. Somatic mutations, unlike germline mutations, are not all neutral during MA, and therefore selection is expected to affect the fate of mutations in the somatic genome. Thus, even if MA is driven by identical mutational parameters in the two genomes, the rate of MA in the soma is expected to be slower than that in the germline (Figure 6). Due to the complex structure and mode of inheritance of the somatic genome, the relationship between somatic mutational parameters and the resulting evolutionary responses during MA is unknown. Therefore, we used individual-based simulations to compare mutational parameters in the two genomes (Figure 7). The results of these simulations confirm that mutational parameters within the 95% CIs of the germline Bateman–Mukai estimates (U = 0.0025, s = 0.2 and h = 0.5; Table 3) lead to ΔM and ΔV trends in both the germline and soma within the 95% CI of the observed trends (Figure 6). Thus, we cannot reject the hypothesis that the two nuclear genomes in T. thermophila have the same deleterious mutational parameters.

Figure 7.

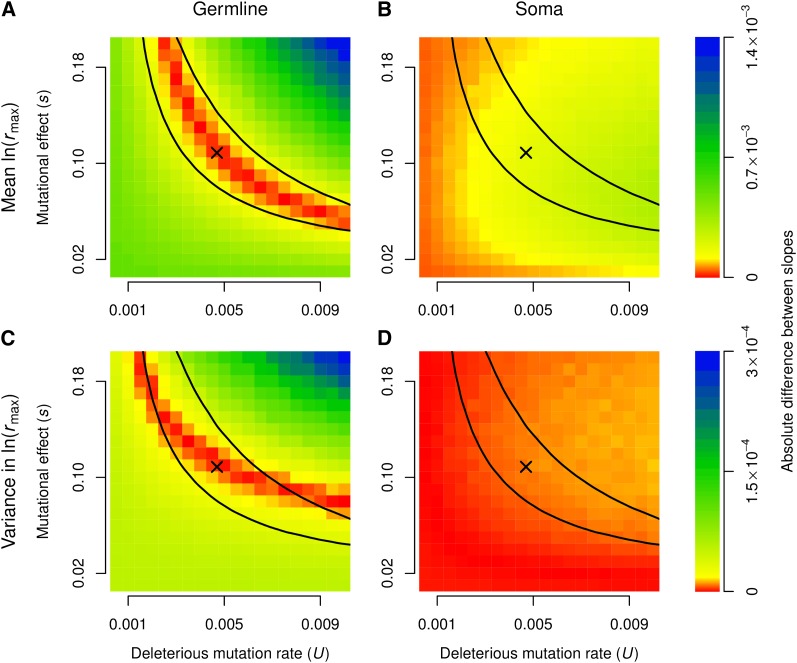
Comparison between experimental and simulated data. The slopes of the regressions shown in Figure 3 are compared to those obtained from individual-based simulations of mutation accumulation under a broad range of values of the deleterious mutation rate per haploid germline genome per generation (U) and the deleterious effect of a mutation when in a homozygous state (s). For each combination of mutational parameters, we simulated 1000 MA lines. We set the number of loci to L = 100. Each simulated MA line was allowed to evolve for 1000 generations with a constant population size of N = 10 (the estimated effective population size in our MA experiment, obtained by taking the harmonic mean of successive doublings from population size of 1 until the final population size is reached). We assumed that mutations in the somatic genome acted additively on fitness (h = 0.5). Colors indicate absolute differences between the slopes, such that low values (red) denote better fits and higher values (blue) worse fits. The X marks the Bateman–Mukai estimates of the mutational parameters (Table 2); the black line marks the 95% credible region based on the joint posterior distribution of the mutational parameters.

Discussion

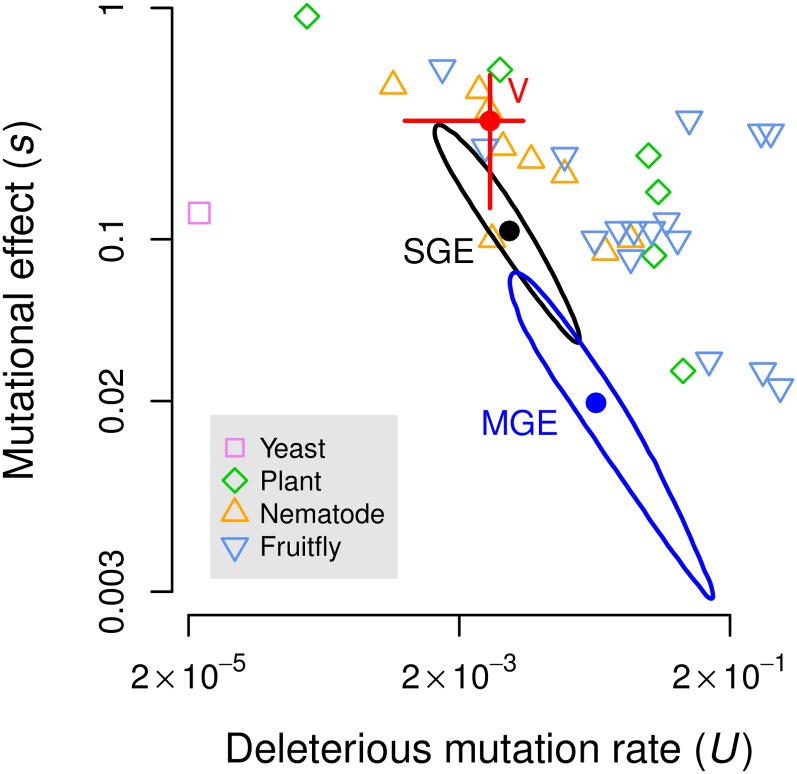
Our main estimates of the deleterious mutation rate (U = 0.0047) and average fitness effect of a deleterious mutation (s = 0.11) in T. thermophila are somewhat lower than typical estimates from other eukaryotes (Figure 8, SGE; Table 3). Sung et al. (2012) have recently used an MA experiment to estimate the base substitution mutation rate (U_BS) in another ciliate, Paramecium tetraurelia, and found this rate to be an order of magnitude lower than that of any other eukaryote in which it has been studied. P. tetraurelia has a genome architecture similar to T. thermophila, but expresses its germline genome via autogamy at least every 75 asexual divisions. Given our parameter estimates, it is unlikely that U_BS is as low in T. thermophila as it is in P. tetraurelia. We estimate that, after 1000 generations of MA, there are approximately nine deleterious mutations in T. thermophila. Using the U_BS from P. tetraurelia, we would predict only approximately four base substitutions per line, and even fewer indels. This is not enough to account for our observed results, even if all molecular mutations had resulted in deleterious fitness effects, which is highly unlikely.

Figure 8.

Mutational parameters of T. thermophila in the context of those of other eukaryotes. Solid circles and elliptical shapes indicate the estimates based on r_max and 95% credible regions, respectively, from single GE (SGE) and multiple GE (MGE) data (Table 3). The red circle and error bars indicate the mean and 95% confidence interval of the estimates based on viability (V) shown in Figure 5B. The data from other species were taken from Table 2 of Halligan and Keightley (2009). The medians of the 32 estimates of mutational parameters from other species are: U = 0.0333 and s = 0.144. Note that both axes are log-transformed.

Surprisingly, our ML analyses indicate that the distribution of mutational effects in T. thermophila is best approximated by the equal effects model (shape parameter, β → ∞). An alternative explanation is that the distribution of mutational effects is complex (e.g., a bimodal distribution including a high probability of slightly deleterious mutations and a second peak of moderately deleterious mutations) and not well approximated by any gamma distribution (Davies et al. 1999; Halligan and Keightley 2009). These hypotheses could be tested by repeating the multiple GE analysis for more MA lines, which would allow us to estimate the variance in mutational effects (V_s) directly.

In a survey of MA studies, Halligan and Keightley (2009) noted that the dominance of new mutations has been studied only in a handful of organisms and is not well understood even in those. Therefore, estimates in additional organisms are valuable. Our estimate of the average dominance coefficient of new mutations (h = 0.257) is broadly consistent with previous estimates from other species (Halligan and Keightley 2009; Agrawal and Whitlock 2011; Manna et al. 2011). Recently, Manna et al. (2011) have predicted that the average dominance coefficient of new mutations of small effect should be h ≈ 0.25 if organisms are subject to stabilizing selection on an arbitrary set of phenotypic traits.

Our observation that four MA lines failed to accumulate any germline lethal mutations indicates that lethal mutations are unlikely to bias our estimates of mutational parameters. It also suggests that the lethal mutation rate in T. thermophila is <10% of the mutation rate to deleterious mutations of smaller effect. Previous studies in yeast estimate the recessive lethal mutation rate to be ∼0.00007 (Hall and Joseph 2010) and 0.00031 (Wloch et al. 2001), which make up 12–30% of total mutations with fitness effects. There are few estimates of lethal mutation rate because in MA studies of most species, unlike T. thermophila, mutations are exposed to selection throughout the course of the experiment (but see Simmons and Crow 1977).

Although we failed to detect lethal mutations, our data allowed us to consider an additional fitness component: viability. Estimates of mutational parameters based on the viability of GE round II lines correspond reasonably well with those based on population growth rate, but with larger effects (Figure 8, V, and Table 3). The difference between the mutational parameter estimates based on these two different fitness components is likely due to different sets of genes affecting viability, i.e., successful development after conjugation vs. growth by asexual reproduction. Because we do not know how frequently conjugation occurs in natural populations relative to asexual reproduction, it is unclear what combination of these parameters is most biologically relevant (but see Doerder et al. 1995).

Our estimates of U and s based on single and multiple rounds of GE are not entirely consistent with each other, although their credible regions overlap (Figure 8, SGE and MGE; Table 3). The discrepancy is due to the fact that the variance among single GE lines each derived from a different MA line (V_SGE) is more than an order of magnitude higher than the variance among multiple GE lines within a particular MA line (V_MGE) (Table 3, ΔV), whereas we expected only a twofold difference (Table 1). In simulations, the probability of finding such a low value of V_MGE with the mutational parameters estimated in the single GE experiment (U = 0.0047, s = 0.11) is P = 0.0016 (based on 10⁶ simulated data sets, with four MA lines and nine independent GE lines per MA line, not shown). The cause of the difference between V_SGE and V_MGE is unclear. The assays in the single GE and multiple GE experiments were not conducted at the same time, so the possibility of experimental error cannot be excluded.

Many factors are expected to affect both V_SGE and V_MGE, such as variable mutational effects, epistatic interactions between mutations, and selection during the formation of GE lines. However, none of these factors is expected to change the V_SGE/V_MGE ratio dramatically. For example, positive epistasis between mutations causes both V_SGE and V_MGE to decrease, whereas negative epistasis does the opposite. It is conceivable that the four MA lines tested in the multiple GE experiment contained unusually positively epistatic mutations, but that seems unlikely. Crosses between backcross lines derived from different MA lines could be used to test for directional epistasis among mutations (deVisser et al. 1996, 1997; West et al. 1998).

One process that would be expected to affect the V_SGE/V_MGE ratio is variation in mutation rate among lines. If different MA lines have different U, then the expected value of V_SGE will increase, while the expected value of V_MGE will remain roughly constant. The germline mutation rate of an individual in an MA line is determined by its somatic genome and, therefore, might have evolved during the experiment. An alternative explanation would be epigenetic differences among MA lines. Given the role of small RNAs in macronuclear development after conjugation (Mochizuki and Gorovsky 2004), it is possible that epigenetic changes that occur during MA are inherited through GE, which would increase V_SGE relative to V_MGE. Sequencing of the germline genomes of multiple lines will allow us to discriminate between these hypotheses.

In an earlier MA study in T. thermophila, Brito et al. (2010) used the rate of clonal extinction as a measure of fitness effects of somatic mutations. They found that ∼1.25 MA lines per bottleneck went extinct and interpreted this as evidence for the rapid accumulation of deleterious mutations in the somatic genome. They speculated that their lines had experienced gains and/or losses of chromosomes during amitosis. We found no evidence that our MA lines accumulated any deleterious somatic mutations over the course of 1000 generations. However, our experimental design, involving multiple single-cell transfer cultures at each bottleneck event, did not allow us to detect the kinds of lethal somatic mutations hypothesized by Brito et al. (2010).

The comparison of mutational parameters from somatic and germline genomes does not allow us to reject the hypothesis that these genomes experience the same rates and average fitness effects of mutations. Despite our inability to detect a difference, it remains possible that the germline and somatic genomes in T. thermophila do experience different mutational processes due to different DNA polymerase or repair machinery operating in the different genomes. Further study of mutation in this species, including resolving the molecular basis of mutation in the two genomes, will help further address this question.

In any MA study, the choice of a starting individual or lineage may affect the final parameter estimates as there are likely to be differences in mutational processes between individuals. Here, we used the SB210 strain because it is well characterized genetically (Eisen et al. 2006) and allowed us to test for successful completion of conjugation. However, this strain may have gained widespread use in part because of its ability to be cultured asexually for many generations without losing the ability to successfully undergo conjugation. This does not seem to be the case for all T. thermophila strains (Shabatura and Doerder 1981). Thus, it is possible that SB210 has a lower mutation rate than other strains of the same species. The choice of starting strain may also help explain the difference in transfer failure between our study and that of Brito et al. (2010). Studies of mutational parameters in other isolates could reveal the degree of variation in these traits among individuals within a species.