Abstract
The dengue viruses exist as four antigenically distinct serotypes. These four serotypes co-circulate and interact with each other through multiple immune-mediated mechanisms. Though the majority of previous efforts to understand the transmission dynamics of dengue have assumed identical characteristics for these four serotypes, empirical data suggests that they differ from one another in important ways. Here, we examine dynamics and persistence in models that do not assume symmetry between the dengue viruses. We find that for serotype transmission rates that are only slightly asymmetric, increased transmissibility of secondary infections through immune enhancement increases the persistence of all dengue viruses in opposition to findings in symmetric models. We identify an optimal magnitude of immune enhancement that maximizes the probability of persistence of all four serotypes. In contrast to other pathogen systems where heterogeneity between serotypes in transmissibility facilitates competitive exclusion (Bremmermann and Thieme, 1989), here we find that in the presence of Antibody Dependent Enhancement (ADE) heterogeneity can increase the persistence of multiple serotypes of dengue.
Keywords: Dengue, Antibody dependent enhancement, Serotypical asymmetry, Dengue vaccine
1. Introduction
The dengue viruses cause the highest rates of morbidity of any mosquito-borne virus, infecting an estimated 50–100 million individuals each year (World Health Organization, 2009). These viruses interact with each other in various ways through multiple types of immunity induced in human hosts. They exist as four antigenically distinct serotypes. The term serotype is used to describe viruses that induce an overlapping immune response to each other. Infection with any dengue virus provides long-term protection against infection with another virus of the same serotype, but only short-lasting immunity to the other serotypes (Sabin, 1952; Burke et al., 1988). As a consequence, secondary infections after cross-immunity has waned are frequent; tertiary and quaternary infections, although possible, are very rare (Gibbons et al., 2007).
In addition, there is evidence that secondary infections are enhanced via immune interactions (Sabin, 1952; Burke et al., 1988). Immune enhancement of infection has been the subject of intense interest in dynamic transmission models (Ferguson et al., 1999a;Cummings et al., 2005; Schwartz et al., 2005; Wearing and Rohani, 2006; Adams et al., 2006; Nagao and Koelle, 2008; Recker et al., 2009;Wikramaratna et al., 2010, Lourenco and Recker, 2010). Theoretical models have implemented the impact of immune enhancement in multiple ways: assuming that primary recovereds have a higher susceptibility, that secondary infections are either more infectious or more severe, or some combination of these factors. Much of this work has suggested that the dynamics resulting from incorporating enhancement are inconsistent with observed patterns of incidence, with oscillation amplitudes in incidence that are much too large and periods that are much too long (Cummings et al., 2005; Adams et al., 2006; Wearing and Rohani, 2006; Nagao and Koelle, 2008). In almost all cases, all of these models have assumed perfect symmetry between the dengue serotypes in transmissibility, immune enhancement and other characteristics affecting their transmission. Here, we demonstrate that the results of symmetric models are very different from asymmetric models, and thus the work that has been done so far is a limited case of the full dynamics of the dengue system. Critically, inclusion of small amounts of heterogeneity that simply break unrealistic assumptions of perfect symmetry leads to a reversal of earlier findings that immune enhancement leads to increased extinction of dengue strains (Cummings et al., 2005).
There is ample biological and epidemiological evidence that the serotypes (and genotypes within serotypes) differ in important aspects of their natural history and transmissibility. Researchers have found significant differences in infection kinetics between dengue serotypes (Tricou et al., 2011). Heterogeneity has also been found in the duration of fever between dengue viruses (Nishiura and Halstead, 2007). Evidence exists that the severity of disease varies by serotype (Vaughn et al., 2000; Watts et al., 1999;Balmaseda et al., 2006; Fried et al., 2010) and by differences in vector efficiency (Armstrong and Rico-Hesse, 2003; Pepin et al., 2008). Serological evidence also shows large differences between serotype-specific seroprevalence (Sangkawibha et al., 1984;Graham et al., 1999). Serological data has been used to estimate forces of infection and basic reproductive numbers for each serotype (Ferguson et al., 1999b). These estimates show substantial differences between serotypes. In each of these settings, only particular genotypes were circulating and potentially accessed, so it is difficult to draw clear distinctions about the characteristics of serotypes in aggregate. However, the evidence suggests that serotypes (and genotypes within serotypes) can not be assumed to be identical in many epidemiologically important characteristics.
In theoretical models of dengue transmission, assumptions of symmetry across the dengue serotypes are the norm. The majority of known papers that have been published on dengue transmission have assumed symmetry between the dengue serotypes in all modeled characteristics. In rare cases where heterogeneity is included, it has been included for mortality (Wearing and Rohani, 2006), or the transmissibility of only single serotypes or genotypes, assuming all others to be some base value (Cummings et al., 2005, Lourenco and Recker, 2010). In one other case, competition and exclusion due to differences in transmissibility were specifically examined. However this work analyzed steady state behavior and only included two serotypes (Feng and Velasco-Hernandez, 1997). Another study focused on investigating the relationship between immunological distance and cross enhancement with two co-circulating serotypes. The authors of this work considered slight differences in the transmission rates or the disease-induced mortality rates but did not carry out a systematic study of such serotype asymmetries (Adams and Boots, 2006).
Heterogeneity between dengue serotypes has important implications for transmission dynamics, competition between dengue viruses (Holmes and Twiddy, 2003; Zhang et al., 2005) and vaccines (Billings et al., 2008). Here, we assess the impact of transmission rate asymmetries (and by extension the basic reproductive number from host to host) in conjunction with the value of the antibody-dependent enhancement factor.
2. Background
2.1. Mathematical model
To investigate extinction, we use a stochastic, discrete individual modeling approach that we simulate using realizations approximating a probabilistic master equation (Gillespie, 1977). The compartmental structure of the model is based on the standard Susceptible, Exposed, Infected and Recovered (SEIR) epidemiological model. The equations governing the mean field dynamics are given by
| (1a) |
| (1b) |
| (1c) |
| (1d) |
| (1e) |
| (1f) |
| (1g) |
where the serotype index i and all the sums above run from one to four. We use S for the number of susceptible individuals to the four dengue serotypes in the population; Ei, Ii and Ri represent the number of people exposed, infected and recovered from a primary infection of serotype i, respectively. The quantities Eij, Iij and Rij represent the number of people exposed, infected and recovered from a secondary infection of serotype j after having a primary infection of serotype i, respectively. Since we assume that a primary infection with serotype i confers lifelong immunity to that serotype, in the classes Eij and Iij we restrict the model by taking i≠j. Finally, R** represents the number of people that have recovered from all secondary dengue infections and are considered to be immune to any further infections. The birth and death rates are chosen to be the same and equal to μ, making the total population N constant in time. There is no increase in the death rate due to infection since the case fatality rate is low (Shepard et al., 2014).
In the past, some mathematical models of dengue epidemics have explicitly included vector dynamics (Wearing and Rohani, 2006). However, we do not account for the mosquitoes explicitly in our model. Assuming that the mosquito population is effectively at steady state, the effect of vectors on dynamics can be absorbed into the four transmission rates βi (Wearing and Rohani, 2006). The latent and recovery periods 1/γ and 1/σ, respectively, are assumed to be the same across all serotypes. We do not account for periods of cross-protection after the first infection as other authors have done (Adams et al., 2006; Wearing and Rohani, 2006;Nagao and Koelle, 2008). We consider that secondary infections contribute more strongly to the force of infection compared to primary infections due to the phenomenon of Antibody Dependent Enhancement (ADE). This effect is captured in the four ADE φi≥1 parameters in the equations and quantify the increased transmissibility of serotype i from its secondary infecteds, regardless of their primary-infecting serotype. The model accounts for secondary heterogenous infections; however, tertiary and quaternary infections are not considered since the epidemiological data shows them to be quite rare (Gibbons et al., 2007). In all our numerical simulations, the values of μ, γ and σ are equal to the values given in Table A1.
2.2. Summary results of the symmetric model
Previous work has demonstrated that deterministic serotypesymmetric models of dengue epidemics can display very complex temporal dynamics and various bifurcations (Cummings et al., 2005; Schwartz et al., 2005, Bianco et al., 2009). With symmetric base transmission rates equal to βi = 500, Eq. (1) converge to a serotype symmetric stationary state for all ADE factor values between φ = 1.0 and approximately 1.85. At that value, the model of Eqs. (1) undergoes a Hopf bifurcation. For values of ADE just above this threshold, the system displays periodic oscillations in the long time limit. A second bifurcation at φ≃1.93 renders the periodic oscillatory dynamics unstable and the system begins to display chaotic dynamics. At even higher values of the ADE factor, there are narrow windows where the chaotic motion ceases and stable periodic oscillations ensue (see Fig. S1 in the electronic supplementary material). Bianco et al. (2009) found that the inclusion of weak cross-immunity between serotypes reduced the parameter range for which chaotic dynamics are observed.Recker et al. (2009) also found that including both enhanced transmissibility and susceptibility in those with immunity to just one serotype reduced the parameter space for which chaotic dynamics are observed.
2.3. Asymmetry studies
We considered asymmetry in the base transmission rates βi and the ADE factors φi, for i = 1, 2, 3, 4. We kept all other parameters the same across serotypes, including the incubation period as well as the rates of recovery and mortality. The values of all other parameters are given in Table A1.
For our investigation of asymmetric transmission rates, we first assigned 400 different sets of normally distributed transmission rates for each of the four serotypes as . Here, is a Gaussian random variable with a mean of zero and variance equal to one. For each set of transmission rates, we generated a realization of 100 years of the master equation that gives rise to Eqs. (1) at 150 different values of the symmetric (i.e., identical for all possible secondary infections) ADE factor φ, uniformly distributed on the interval 1.0≤φ≤3.0. We used the τ–leap stochastic simulation algorithm (SSA) (Gillespie, 1977, Cao et al.) for our simulations. At each value of φ, the initial conditions for the stochastic runs are extracted from simulations of the deterministic system (1) long enough so that transients have decayed. We determined whether serotype extinctions occur over a timespan of 100 years, at the 150 different values of the parameter φ, in a population of 10 million people.
We investigated the case of asymmetric ADE factors in an analogous fashion, assigning normally distributed ADE factors and took all the transmission rates equal across serotypes and varied them over the interval 300≤β ≤700 (or 3≤ R0 ≤5, obtained from the approximate expression R0i = (βi/(μ + σ))γ= (μ + γ), i = 1, 2,…4, see Anderson and May (1992)).
3. Results
3.1. Stochastic serotype extinctions
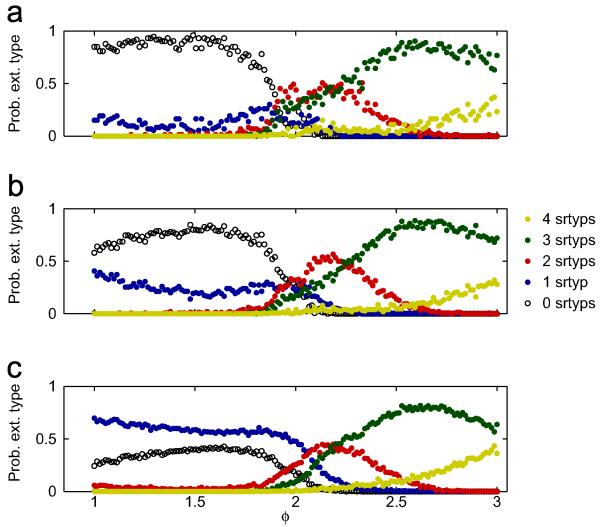
Fig. 1 shows the probability of observing 0–4 serotypes going extinct in a span of 100 years, at different values of φ, for the 400 sets of transmission rates βi. We show the probabilities of observing each type of extinction for low CV (<0.07), medium CV (<0.1) and all 400 sets of β’s in Fig. 1a-c, respectively. Interestingly, Fig. 1a-c shows that the probability of observing zero extinctions is non-monotonic as a function of φ and that an ADE factor φ≈1.5–1.6 appears to be optimal for the persistence of all four serotypes, i.e., no serotype goes extinct in the 100 year interval. Comparing Fig. 1a-c shows that all-around persistence is higher for the runs with lower CV (β). It is quite remarkable that the probability of any particular type of extinction is a continuous function of φ and that there exist intervals in φ where a given type of extinction is relatively dominant. In the supplement, we include a color coded map with the full information on how many serotypes went extinct at each value of φ, for each of the 400 runs (Fig. S2). In that figure, the 400 sets are ordered by coefficient of variation of the four transmission rates CV(βi).
Fig. 1.
Probability of observing a 0–4 serotypes going extinct in 400 stochastic simulations with asymmetric transmission rates, spanning 100 years, as a function of the ADE factor φ. For each run, the transmission rates are distributed as with β0 = 500 and σβ = 75. Panel (a): probability of observing extinctions of 0–4 serotypes for the 73 runs with CV <0.07, over the said time period, as a function of φ. Panel (b): same as in (a), except that we keep the 150 runs with CV (β)<0.1. Panel (c): same as in (a) and (b), except that the full set of 400 runs is considered. Other parameter values are as in Table A1.
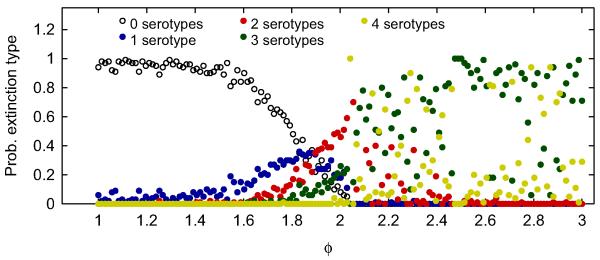
These results stand in stark contrast to the symmetric case. Fig. 2 classifies the probability of each type of extinction observed at different values of φ for symmetric transmission rates. The probability of observing zero extinctions is a monotonically decreasing function of φ (Fig. 2b). In the symmetric case, unlike the asymmetric one, greater enhancement provides no persistence benefit. It is particularly striking that the probabilities of observing zero through four serotypes going extinct are relatively continuous functions for φ≤2, but not so for larger values. When comparing Figs. 1 and 2, asymmetric transmission rates seem to introduce a hierarchy among the serotypes that ‘organizes’ the types of extinctions observed. As for the asymmetric case, the supplement contains a color coded map with the full information on how many serotypes went extinct at each value of φ, for all 100 runs (Fig. S3).
Fig. 2.
Probability of observing 0–4 serotypes going extinct in 100 stochastic simulations with symmetric transmission rates, spanning 100 years, as a function of the ADE factor φ. Here, βi = 500 and other parameter values are as in Table A1.
3.2. The relationship between extinctions and chaotic dynamics: average expansion exponents
The extinctions of three or four serotypes that are common at high values of φ are caused by the chaotic dynamics with large swings that occur at such values of the ADE factor. Since one cannot quantify the strength of chaotic dynamics in the stochastic version of our model, we carried out extensive deterministic simulations of Eqs. (1) to identify how the occurrence and strength of the chaotic dynamics at high values of φ are correlated with serotype extinctions.
Using the same sets of 400 transmission rates as in the stochastic study above, we simulated the system numerically at 100 different values of the symmetric ADE factor φ, uniformly spaced over the interval 1.7 ≤φ≤3.0. The lower bound of 1.7 is chosen to be slightly below the onset of chaotic dynamics, for all of our 400 sets of transmission rates. The initial condition at the first value of φ = 1.7 is the same for all 400 sets and is close to the endemic state of the symmetric case when all transmission rates are equal. At succeeding values of φ, we use the final state of the system at the previous value of φ as our new initial condition. Once transients have decayed, we consider that serotype i goes extinct if the sum of all classes currently infected with serotype i go below the threshold value of 10−7, in view of the population of 10 million considered here. We also quantified how prevalent and intense the chaotic dynamics of the system are, by calculating an Average Expansion Exponent (AEE); a positive AEE strongly suggests chaotic dynamics. We track extinctions and AEEs at each of the 100 values of φ between 1.7 and 3.0 and for the 400 different sets of transmission rates. See the electronic supplementary material Text S2 for more details on how we calculate the AEEs.
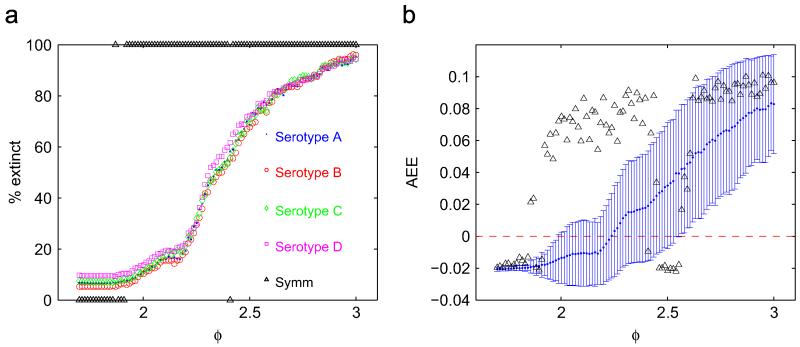
We show the fraction of runs that display serotype-specific extinctions as a function of the ADE factor for β0 = 500 (Fig. 3a). The probability of observing infecteds below threshold increases quickly for ADE factors greater than 2.2, approximately. These low minima are the consequence of large amplitude swings arising from the chaotic nature of the dynamics that is prevalent at these values of the ADE factor. This is evident from the strong correlation between the likelihood of serotype extinctions and the magnitude of the AEE (Fig. 3b). The onset of chaotic dynamics is slightly shifted to higher ADE values in the case of asymmetric transmission rates (note the interval 1.9≤φ≤2.3 in Fig. 3b). This is reflected in the difference in the likelihood of extinctions when comparing asymmetric and symmetric cases over the same range of ADE factors. Analogous results for the case β0 = 300 are shown in Fig. S4b and S4d in the electronic supplementary material.
Fig. 3.
Plot of the ADE factor vs. proportion of runs that have minima of the infected classes below a threshold of 10−7 (a). Plot of the AEE (see text) at each value of the ADE factor; the errorbars indicate one standard deviation over the 400 runs (b). The black markers indicate the strictly serotype-symmetric situation. The asymmetric transmission rates are exactly the ones used in Fig. 1 while the symmetric ones are βi = 500, as in Fig. 2; other parameter values are as in Table A1. The values of the birth/death rates, duration of the incubation period and recovery rate are as in Table A1.
3.3. Comparison of model behavior to incidence data from Thailand
To judge the validity of our models and to investigate the impact of heterogeneity on the comparison of simulated time series to observed time series of dengue incidence, we compared our model output to data from Thailand. Serotype-specific incidence from Bangkok, Thailand from 1973 to 2010 shows large-amplitude oscillations with the different serotypes out of synchrony. The data show peaks in Fourier spectra at 1 year and 5–10 years (Fig. S5 in the electronic supplementary material). We compare this with Fourier spectra of our model at different parameterizations and with the inclusion of a seasonal driver (Figs. S6 and S7 in the electronic supplementary material). Our simulations show significant Fourier power at annual periods as well as dominant components are between 4 and 8 years, roughly consistent with data. Hence, the period of oscillation does not seem to be greatly dependent on the degree of asymmetry of the transmission rates. Appendix A shows a complete analysis of these data and simulations.
3.4. The effect of asymmetries on vaccination
A natural extension of our work is to consider the effect of heterogeneity in transmission on the performance of dengue vaccines and the adverse effects that may arise after massive vaccination is applied to human populations. A dengue vaccine candidate is now in advanced stages of development (Guy et al., 2010, 2011). The preliminary results show that vaccinees obtain immune protection against all serotypes, though recent results suggest efficacy to only a subset (Hirschler and Regan, 2012; Guy et al., 2010, 2011). A consequence of heterogeneity in transmissibility is that certain serotypes may be controlled more easily than others by vaccination, though it is difficult to anticipate the effects.
We considered the effect of vaccines in our stochastic framework. Since the full effects of the upcoming vaccine on human subjects are not entirely known, we made a number of assumptions regarding how the vaccine protects vaccinees. At birth, each individual is vaccinated with a probability equal to vprob. The vaccinee becomes immune to serotype i with probability equal to the ith vaccine efficacy veff, i; these probabilities are considered to be independent for different serotypes. Vaccinated individuals immune to a single serotype i are put in the Ri compartment, exactly as if they had suffered an infection from serotype i and may become infected with a second serotype different to i. On the other hand, vaccinees immune to two or more serotypes are put in the permanently recovered class R** and may not suffer future infections.
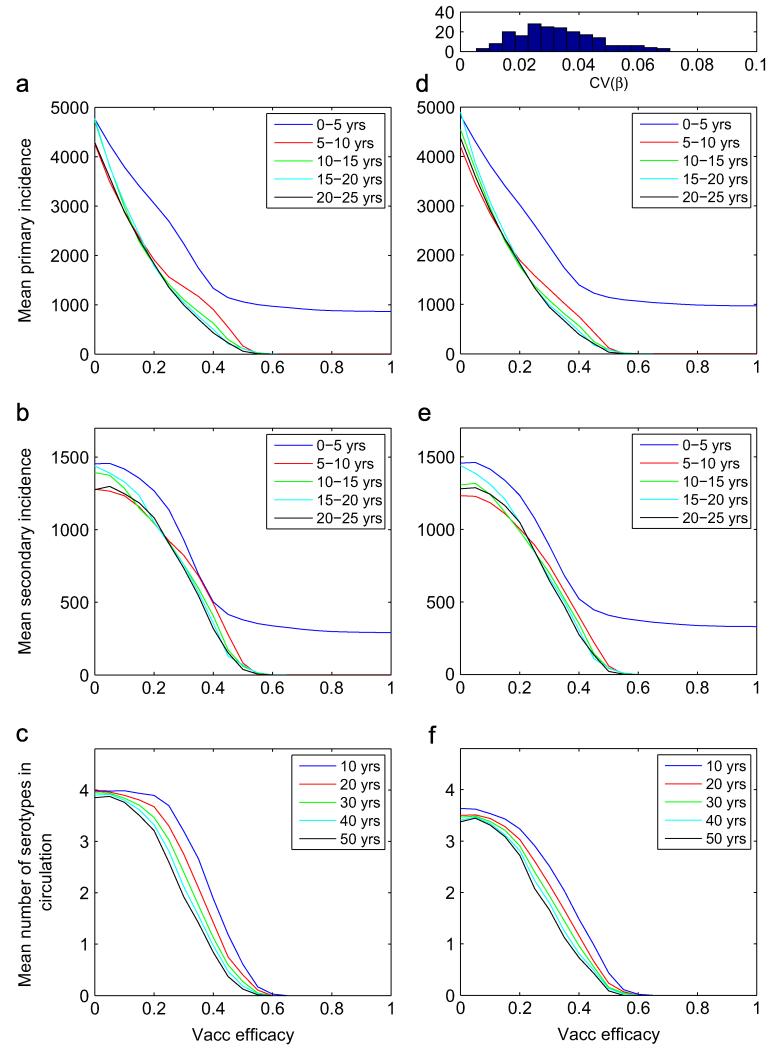
Fig. 4 shows how the temporal averages of the primary and secondary incidences, as well as the number of co-circulating serotypes at different times are affected by different vaccine efficacies, for φ = 1.7, respectively. For the asymmetric runs (right column), 200 normally distributed sets of transmission rates were generated as , for the four serotypes; here β0 = 500 and σβ = 20. The 200 coefficients of variation of the four transmission rates are distributed according to the histogram on top of panel (d) of the figure. For this study, the vaccine efficacy is identical for all serotypes, veff, i = veff, and all new births undergo vaccination, vprob = 1. At each value of the vaccine efficacy, the initial condition is the endemic state in the absence of vaccine. With a vaccine efficacy that is serotype-independent, a vaccinee becomes immune to 4veff serotypes, on average.
Fig. 4.
Time average of the primary (a and d) and secondary (b and e) incidences over the time periods indicated in each panel; and mean number of serotypes co-circulating after the time period indicated (c and f), for different values of the serotype-independent vaccine efficacy. The left column corresponds to symmetric transmission rates, while the column on the right corresponds to asymmetric ones. The results in each column were obtained with 200 stochastic simulations at each value of the vaccine efficacy. The histogram above panel (d) shows the distribution of the coefficient of variation of the four transmission rates over the 200 runs. Here, φ = 1.7. Table A1
The results show that the primary and secondary incidences during 25 years of simulation, averaged over five year intervals, are monotonically decreasing as the vaccine efficacy increases. The qualitative shape of these graphs remains unchanged between the symmetric/asymmetric cases. However, we note that the secondary incidence decreases much more slowly than the primary one, especially at very low values of the vaccine efficacy. At such low efficacies, many vaccinees become immune to a single serotype and later on become secondary cases in the future. On average, vaccinees become immune to one serotype at veff 0.25; at this value, the averaged secondary incidence as a function of the efficacy begins to drop faster. Vaccinees become immune to two serotypes, on average, when veff = 0.5; this forces the extinction of all serotypes beyond this efficacy.
The results for serotype persistence differ between the symmetric and asymmetric cases (Fig. 4c and f). At low vaccine efficacies, serotypes with symmetric transmission rates have a notably greater probability of surviving for extended periods of time, when compared with serotypes with asymmetric transmission rates, both at φ = 1.7. However, since the difference in persistence between symmetric and asymmetric transmission rates under mass vaccination occurs at very low values of the vaccine efficacy, the difference is unlikely to play a role in realistic situations.
Fig. S9 in the electronic supplementary material shows similar time-averaged incidence results for φ = 1.0. The differences in serotype persistence results between φ = 1.0 and 1.7 are discussed in the electronic supplementary material Text S3.
3.5. Asymmetry in the ADE factors
Our investigations show that asymmetry in the ADE factors has a very different impact on the dynamics of the system compared to asymmetry in the transmission rates. We found no clear trend between the standard deviation of the four ADE factors and the likelihood of observing either serotype extinctions or chaotic dynamics over the whole interval 300≤β≤700. These results suggest that asymmetric ADE factors across serotypes have little to no effect in suppressing the tendency of the system to behave chaotically and thus limit extinction events. However, we found that the percent of time series that go extinct as a function of the base transmission rate decreases at the higher end of the interval 300≤β≤700 (Fig. S8 in the electronic supplementary material). A factor that plays a role in this effect is that higher values of the base transmission rate common to the four serotypes produce a shift in the endemic state and the whole dynamics to higher numbers in the infected class.
4. Discussion
We have studied the dynamic consequences of combining asymmetry in the transmission rates and ADE factors greater than one for the four serotypes in a dengue fever model. Our investigations demonstrate that when the transmission rates are slightly different, there exists an optimal ADE factor value that maximizes the likelihood of serotype persistence. At values of the ADE factor just higher than the optimal one, chaotic dynamics with largeamplitude oscillations become prevalent. In contrast, asymmetries in the ADE factors across serotypes do not seem to have the same persistence-enhancing property nor sensitivity.
It is notable that asymmetry in this system in conjunction with an ADE factor higher than one promotes coexistence of multiple serotypes, while in other systems, asymmetry leads to the competitive displacement of those serotypes or strains with a reduced transmissibility (Lipsitch et al., 2009). Dynamically, this may be due to ADE having an effect on transmissibility that depends on the prevalence of heterotypic immunity. ADE increases the transmissibility of pathogens when immunity to other serotypes is highly prevalent. However, as a serotype begins to displace others, this transmissibility advantage declines, and reduces the probability that one serotype will completely displace others. ADE may be particularly advantageous to a virus, as it increases transmissibility only during times when competition for susceptible individuals is high. In contrast, the increase in transmission conferred by enhancement decreases when the prevalence of other serotypes is low, reducing the probability that other serotypes will be driven to extinction.
In the past, high values of the ADE factor have been called into question in the modeling of dengue because of the inconsistency between chaotic dynamics and field data. This is due to the fact that when observing chaotic oscillations in the model, extinction events have a high probability of occurring, even though the disease is prevalent in the data. Thus, there appears to be a ‘barrier’ on the ADE factor scale, beyond which the persistence of multiple serotypes becomes very unlikely. It is noteworthy that in the model with asymmetric transmission rate, the ADE threshold value at which chaos sets in is higher, on average, when compared to the symmetric model (φ≈1.8 for the symmetric model and φ≈2.3, on average, for the asymmetric models; see Fig. 3).
We have not included several elements that have been previously included in dengue transmission models: namely (i) dynamics of the vector; and (ii) periods of cross-protection after the first infection. We note that the objective of this work is not to describe the temporal dynamics of dengue epidemics with quantitative precision; rather, it is to investigate the dynamical consequences of serotype asymmetry that has not been systematically studied in the past. We note that inclusion of heterogeneity in transmissibility does not add model complexity but instead generalizes an overly restrictive assumption of perfect symmetry between dengue serotypes.
We emphasize that the breadth of behavior observed in models that include antibody dependent enhancement, short-term cross protection and/or seasonality is large when secondary (or tertiary or quaternary) infections are considered. Our results do not conclusively support a role for antibody dependent enhancement in explaining observed patterns. Rather, our results suggest that dismissal of ADE as a feature of dengue dynamics by previous modeling work (including our own) were premature in being based on a narrow range of models. For instance, ADE could result in enhanced viremia and transmissibility in only a small proportion of those infected for a second time by dengue. Models constructed thus far have assumed a mean increase in transmissibility rather than some heterogeneity. As always, more empirical observation at both the population and individual level would be useful in choosing between these models. Additionally, more rigorous statistical inference techniques may help to distinguish between these phenomena (Shrestha et al., 2011).
Since empirical data shows asymmetries in transmissibility of dengue serotypes, ADE is evolutionarily advantageous in areas where all four serotypes co-circulate. Because ADE is advantageous to all serotypes, we might expect to see increasing severity of secondary cases over time and with the accumulation of high amounts of immunity, as has been seen in both Asia and the America (Nisalak et al., 2003; OhAinle et al., 2011).
Supplementary Material
HIGHLIGHTS.
The consequences of dengue serotype heterogeneity remains an important and open question.
The majority of models assume dengue serotypes with identical characteristics.
Differences in the transmission of dengue serotypes are here considered systematically.
Serotype persistence is enhanced by asymmetries combined with immune enhancement.
Serotype asymmetries may complicate the control of dengue through vaccination.
Acknowledgments
The authors gratefully acknowledge the Office of Naval Research for their support. The authors are supported by Award Number R01GM090204 from the National Institute of General Medical Sciences. DATC was also supported by the National Institute of General Medical Sciences Models of Infectious Disease Agent Study (MIDAS) grant 1U54GM088491-0109. DATC holds a Career Award at the Scientific Interface. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of General Medical Sciences or the National Institutes of Health.
Appendix A. Comparison of spectral analysis of Thailand data
The spectral composition of the data in Fig. S5 in the electronic supplementary material was obtained with the discrete Fourier transform (DFT). The growing mean value of cases in Fig. S5a is mainly due to under-reporting in the early years. The large magnitude of the ≈19 year component in Fig. S5b is most likely an artifact of the DFT algorithm, arising from the growing mean in the disease incidence in the data.
For a better comparison with field data, we included seasonality in our model by changing all base transmission rates according to βi→βi(1 + 0.05 cos (2πt)) and used the DFT to study their spectral compositions. Fig. S6a in the electronic supplementary material shows a contour plot of the squared magnitude of the different frequency components as a function of the ADE factor, averaged over 400 runs and over the 4 serotypes; here β0 = 500. We exclude the time series of serotypes that are competitively excluded over the whole range 1.7≤φ≤3. Panel (a) clearly shows the yearly component due to the seasonal drive throughout the φ interval, as well as strong subharmonic responses with periods of 2 and 4 years in certain ranges of φ. Beyond the averaged onset of oscillations (φ≈2.1), a wider range of periods have significant contributions; the dominant components are between 4 and 8 years. Fig. S6b shows a color-coded histogram of the single dominant frequency of the data in Fig. S6a (ignoring the zero-frequency component). Panel (b) shows that the dominant component is the yearly one up to φ≈2.1 and it becomes more dispersed for higher φ values; the range between 4 and 6 year is particularly populated. We find no instances of dominant periods beyond 10 years. The case with β0 = 300 shows similar behavior but has Fourier components at slightly higher periods than before. Here the dominant periods extend up to 15 years (Fig. S7 in the electronic supplementary material).
Our results are consistent with previous modeling studies that have found strong spectral components for periods of oscillation of 1 year and for periods between approximately 3 and 10 years (Wearing and Rohani, 2006; Nagao and Koelle, 2008; Adams et al., 2006).
Table A1.
Typical values/ranges of the model parameters
| Parameter | Typical value | Reference |
|---|---|---|
| βi (transmission rate for serotype i) | 400–600 yr−1 | Ferguson et al. (1999b) |
| R0 (basic reproductive number) | 4–6 | – |
| μ (birth/death rate) | 0.02 yr−1 | Ferguson et al. (1999a) |
| γ (1/latent period) | 70 yr−1 | Nishiura and Halstead (2007) |
| σ (1/recovery period) | 100 yr−1 | Ferguson et al. (1999a) |
| φi (ADE factor for serotype i) | 1.7–3.0 | – |
| σβ (degree of asymmetry in transmission rates) | 75 | – |
| σφ (degree of asymmetry in ADE factors) | 0.4 | – |
Footnotes
Appendix B. Supplementary data
Supplementary data associated with this article can be found in the online version at http://dx.doi.org.10.1016/j.jtbi.2013.04.036.
References
- Adams B, Boots M. Modelling the relationship between antibodydependent enhancement and immunological distance with application to dengue. J. Theor. Biol. 2006;242:337–346. doi: 10.1016/j.jtbi.2006.03.002. [DOI] [PubMed] [Google Scholar]
- Adams B, Holmes E, Zhang C, Mammen JMP, Nimmannitya S, Kalayanarooj S, Boots M. Cross-protective immunity can account for the alternating epidemic pattern of dengue virus serotypes circulating in Bangkok. Proc. Natl. Acad. Sci. USA. 2006;103:14234–14239. doi: 10.1073/pnas.0602768103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson R, May R. first ed Oxford University Press; Oxford: 1992. Infectious Diseases of Humans: Dynamics and Control. [Google Scholar]
- Armstrong P, Rico-Hesse R. Efficiency of dengue serotype 2 virus strains to infect and disseminate in Aedes Aegypti. Am. J. Trop. Med. Hyg. 2003;68(5):539–544. doi: 10.4269/ajtmh.2003.68.539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balmaseda A, Hammond S, Perez L, Tellez Y, Saborio S, Mercado J, Cuadra R, Rocha J, Perez M, Silva SEA. Serotype-specific differences in clinical manifestations of dengue. Am. J. Trop. Med. Hyg. 2006;74:449–456. [PubMed] [Google Scholar]
- Bianco S, Shaw L, Schwartz I. Epidemics with multistrain interactions: the interplay between cross immunity and antibody-dependent enhancement. Chaos. 2009;19:043123. doi: 10.1063/1.3270261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Billings L, Fiorillo A, Schwartz I. Vaccinations in disease models with antibody-dependent enhancement. Math. Biosci. 2008;211(2):265–281. doi: 10.1016/j.mbs.2007.08.004. [DOI] [PubMed] [Google Scholar]
- Burke D, Nisalak A, Johnson D, Scott R, et al. A prospective study of dengue infections in Bangkok. Am. J. Trop. Med. Hyg. 1988;38(1):172. doi: 10.4269/ajtmh.1988.38.172. [DOI] [PubMed] [Google Scholar]
- Cao Y, Gillespie D, Petzold L. Efficient step size selection for the tau-leaping simulation method. J. Chem. Phys. 124:044109. doi: 10.1063/1.2159468. [DOI] [PubMed] [Google Scholar]
- Cummings D, Schwartz I, Billings L, Shaw L, Burke D. Dynamic effects of antibody-dependent enhancement on the fitness of viruses. Proc. Natl. Acad. Sci. USA. 2005;42:15259–15264. doi: 10.1073/pnas.0507320102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng Z, Velasco-Hernandez J. Competitive exclusion in a vector-host model for the dengue fever. J. Math. Biol. 1997;35(5):523–544. doi: 10.1007/s002850050064. [DOI] [PubMed] [Google Scholar]
- Ferguson N, Anderson R, Gupta S. The effect of antibody-dependent enhancement on the transmission dynamics and persistence of multiple-strain pathogens. Proc. Natl. Acad. Sci. USA. 1999a;96(2):790–794. doi: 10.1073/pnas.96.2.790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson NM, Donnelly C.a., Anderson RM. Transmission dynamics and epidemiology of dengue: insights from age-stratified sero-prevalence surveys. Philos. Trans. R. Soc. London B, Biol. Sci. 1999b;354(1384):757–768. doi: 10.1098/rstb.1999.0428. http://dx.doi.org/10.1098/rstb.1999.0428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fried J, Gibbons R, Kalayanarooj S, Thomas S, Srikiatkhachorn A, Yoon I, Jarman R, Green S, Rothman A, Cummings D. Serotype-specific differences in the risk of dengue hemorrhagic fever: an analysis of data collected in Bangkok, Thailand from 1994 to 2006. PLoS Neglect. Trop. D. 2010;4:e617. doi: 10.1371/journal.pntd.0000617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibbons R, Kalanarooj S, Jarman R, Nisalak A, Vaughn D, Endy T, Mammen M, Srikiatkhachorn A. Analysis of repeat hospital admissions for dengue to estimate the frequency of third or fourth dengue infections resulting in admissions and dengue hemorrhagic fever, and serotype sequences. Am. J. Trop. Med. Hyg. 2007;77(5):910–913. [PubMed] [Google Scholar]
- Gillespie D. Exact stochastic simulation of coupled chemical-reactions. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
- Graham R, Juffrie M, Tan R, Hayes C, Laksono I, Ma’roef C, Porter K, Halstead S.e.a. A prospective seroepidemiologic study on dengue in children four to nine years of age in Yogyakarta, Indonesia I. Studies in 1995-1996. Am. J. Trop. Med. Hyg. 1999;61:412–419. doi: 10.4269/ajtmh.1999.61.412. [DOI] [PubMed] [Google Scholar]
- Guy B, Saville M, Lang J. Development of Sanofi Pasteur tetravalent dengue vaccine. Hum. Vaccin. 2010;6:696–705. doi: 10.4161/hv.6.9.12739. [DOI] [PubMed] [Google Scholar]
- Guy B, Almond J, Lang J. Dengue vaccine prospects: a step forward. Lancet. 2011;377:381–382. doi: 10.1016/S0140-6736(11)60128-1. [DOI] [PubMed] [Google Scholar]
- Hirschler B, Regan J. World’s first dengue vaccine beats three virus strains, reuters. 2012 Jul; 〈 http://www.reuters.com/article/2012/07/25/us-sanofidengue-idUSBRE86O07E20120725 〉 . [Google Scholar]
- Holmes E, Twiddy S. The origin, emergence and evolutionary genetics of dengue virus. Infect. Genet. Evol. 2003;3(1):19–28. doi: 10.1016/s1567-1348(03)00004-2. [DOI] [PubMed] [Google Scholar]
- Lipsitch M, Colijn C, Cohen T, Hanage W, Fraser C. No coexistence for free: neutral null models for multistrain pathogens. Epidemics. 2009;1:2–13. doi: 10.1016/j.epidem.2008.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lourenço J, Recker M. Viral and epidemiological determinants of the invasion dynamics of novel dengue genotypes. PLoS Negl. Trop. Dis. 2010;4(11):e894. doi: 10.1371/journal.pntd.0000894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagao Y, Koelle K. Decreases in dengue transmission may act to increase the incidence of dengue hemorrhagic fever. Proc. Natl. Acad. Sci. USA. 2008;105:2238–2243. doi: 10.1073/pnas.0709029105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nisalak A, Endy T, Nimmannitya S, Kalayanarooj S, Thisayakorn U, Scott R, Burke D, Hoke C, Innis B, Vaughn D. Serotype-specific dengue virus circulation and dengue disease in Bangkok, Thailand from 1973 to 1999. Am. J. Trop. Med. Hyg. 2003;68:191–202. [PubMed] [Google Scholar]
- Nishiura H, Halstead S. Natural history of dengue virus DENV1 and DENV4 infections: reanalysis of classic studies. J. Infect. Dis. 2007;195(7):1007. doi: 10.1086/511825. [DOI] [PubMed] [Google Scholar]
- OhAinle M, Balmaseda A, Macalalad A, Tellez Y, Zody M, Saborío S, Nuñez A, Lennon N, Birren B, Gordon A, et al. Dynamics of dengue disease severity determined by the interplay between viral genetics and serotypespecific immunity. Sci. Transl. Med. 2011;3(114):114ra128. doi: 10.1126/scitranslmed.3003084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepin K, Lambeth K, Hanley K. Asymmetric competitive suppression between strains of dengue virus. BMC Microbiol. 2008;8(1):28. doi: 10.1186/1471-2180-8-28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Recker M, Blyuss K, Simmons C, Hien T, Wills B, Farrar J, Gupta S. Immunological serotype interactions and their effect on the epidemiological pattern of dengue. Proc. R. Soc. London, Ser. B Biological Sciences. 2009;276(1667):2541. doi: 10.1098/rspb.2009.0331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabin A. Research on dengue during world war II. Am. J. Trop. Med. Hyg. 1952;1(1):30–50. doi: 10.4269/ajtmh.1952.1.30. [DOI] [PubMed] [Google Scholar]
- Sangkawibha N, Rojanasuphot S, Ahandrik S, Viriyapongse S, Jatanasen S, Salitul V, Phanthumachinda B, Halstead S. Risk factors in dengue shock syndrome: a prospective epidemiologic study in Rayong, Thailand. Am. J. Epidemiol. 1984;120(5):653. doi: 10.1093/oxfordjournals.aje.a113932. [DOI] [PubMed] [Google Scholar]
- Schwartz I, Shaw L, Cummings D, Billings L, McCrary M, Burke D. Chaotic desynchronization of multi-strain diseases. Phys. Rev. E. 2005;72:066201. doi: 10.1103/PhysRevE.72.066201. [DOI] [PubMed] [Google Scholar]
- Shepard DS, Suaya JA, Halstead SB, Nathan MB, Gubler DJ, Mahoney RT, Wang D, Meltzer MI. Cost-effectiveness of a pediatric dengue vaccine. Vaccine. 2014;22:1275–1280. doi: 10.1016/j.vaccine.2003.09.019. [DOI] [PubMed] [Google Scholar]
- Shrestha S, King A, Rohani P. Statistical inference for multi-pathogen systems. PLoS Comput. Biol. 2011;7(8):e1002135. doi: 10.1371/journal.pcbi.1002135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tricou V, Minh N, Farrar J, Tran H, Simmons C. Kinetics of viremia and ns1 antigenemia are shaped by immune status and virus serotype in adults with dengue. PLoS Negl. Trop. Dis. 2011;5(9 doi: 10.1371/journal.pntd.0001309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaughn D, Green S, Kalayanarooj S, Innis B, Nimmannitya S, Suntayakorn S, Endy T, Raengsakulrach B, Rothman A, Ennis F, et al. Dengue viremia titer, antibody response pattern, and virus serotype correlate with disease severity. J. Infect. Dis. 2000;181(1):2. doi: 10.1086/315215. [DOI] [PubMed] [Google Scholar]
- Watts D, Porter K, Putvatana P, Vasquez B, Calampa C, Hayes C, Halstead S. Failure of secondary infection with american genotype dengue 2 to cause dengue haemorrhagic fever. Lancet. 1999;354(9188):1431–1434. doi: 10.1016/S0140-6736(99)04015-5. [DOI] [PubMed] [Google Scholar]
- Wearing H, Rohani P. Ecological and immunological determinants of dengue epidemics. Proc. Natl. Acad. Sci. USA. 2006;103:11802–11807. doi: 10.1073/pnas.0602960103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wikramaratna P, Simmons C, Gupta S, Recker M. The effects of tertiary and quaternary infections on the epidemiology of dengue. PLoS One. 2010;5(8):e12347. doi: 10.1371/journal.pone.0012347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- World Health Organization . Dengue: Guidelines for Diagnosis, Treatment, Prevention and Control. World Health Organization; 2009. [PubMed] [Google Scholar]
- Zhang C, Mammen M, Jr., Chinnawirotpisan P, Klungthong C, Rodpradit P, Monkongdee P, Nimmannitya S, Kalayanarooj S, Holmes E. Clade replacements in dengue virus serotypes 1 and 3 are associated with changing serotype prevalence. J. Virol. 2005;79(24):15123. doi: 10.1128/JVI.79.24.15123-15130.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.