Computerized Determination Scheme for Histological Classification of Breast Mass Using Objective Features Corresponding to Clinicians’ Subjective Impressions on Ultrasonographic Images

Abstract

It is often difficult for clinicians to decide correctly on either biopsy or follow-up for breast lesions with masses on ultrasonographic images. The purpose of this study was to develop a computerized determination scheme for histological classification of breast mass by using objective features corresponding to clinicians’ subjective impressions for image features on ultrasonographic images. Our database consisted of 363 breast ultrasonographic images obtained from 363 patients. It included 150 malignant (103 invasive and 47 noninvasive carcinomas) and 213 benign masses (87 cysts and 126 fibroadenomas). We divided our database into 65 images (28 malignant and 37 benign masses) for training set and 298 images (122 malignant and 176 benign masses) for test set. An observer study was first conducted to obtain clinicians’ subjective impression for nine image features on mass. In the proposed method, location and area of the mass were determined by an experienced clinician. We defined some feature extraction methods for each of nine image features. For each image feature, we selected the feature extraction method with the highest correlation coefficient between the objective features and the average clinicians’ subjective impressions. We employed multiple discriminant analysis with the nine objective features for determining histological classification of mass. The classification accuracies of the proposed method were 88.4 % (76/86) for invasive carcinomas, 80.6 % (29/36) for noninvasive carcinomas, 86.0 % (92/107) for fibroadenomas, and 84.1 % (58/69) for cysts, respectively. The proposed method would be useful in the differential diagnosis of breast masses on ultrasonographic images as diagnosis aid.

Introduction

Mass is one of the important indications related to breast cancer on ultrasonographic images. However, it can be difficult for clinicians to determine whether a lesion with mass is malignant or benign. The positive predictive value of ultrasonography, i.e., the ratio of the number of breast cancers found to the number of biopsies, is rather low [1–4]. Unnecessary biopsies cause both physical and costly problems to the patients. To improve the positive predictive value, in the previous studies, many investigators have attempted to develop a computer-aided diagnosis (CAD) scheme [5] for distinguishing between benign and malignant masses on ultrasonographic images. Chen et al. [6, 7] utilized the textural features in breast ultrasonographic images to distinguish between benign and malignant masses by using an artificial neural network (ANN). Joo et al. [8] also employed an ANN with morphologic features. Shi et al. [9] developed a CAD scheme based on a fuzzy support vector machine to detect and classify mass from ultrasonographic images. Horsch et al. [10] extracted lesion shape, margin definition, echogenic texture, and posterior acoustic enhancement or shadowing of masses from ultrasonographic images, and they estimated the likelihood of malignancy by using linear discriminant analysis with these features. The results of these CAD schemes indicated high performance in distinguishing between benign and malignant masses. However, experienced clinicians evaluate not only the likelihood of malignancy but also the likelihood of histological classification in determining patient managements. Therefore, the computerized analysis for evaluating not only the likelihood of malignancy but also the likelihood of histological classifications for masses would be helpful to clinicians for their decisions on patient management [11–14].

On the other hand, most CAD schemes need to extract image features of masses to evaluate the likelihood of malignancy. However, clinicians’ subjective impression of these image features was sometimes different from the objective features extracted by these CAD schemes. There would be a possibility that classification accuracy is improved by use of objective features reflecting to clinicians’ subjective impression based on clinical experience. The purpose of this study was to select adequate feature extraction methods for the objective features corresponding to clinicians’ subjective impression and to develop a computerized determination scheme for histological classification of mass using the extracted objective features to assist clinicians’ interpretation. In this study, an observer study was first conducted to obtain clinicians’ subjective impression of nine image features from masses in ultrasonographic images. We defined some feature extraction methods for each of the nine image features and selected an adequate extraction method with the highest correlation coefficient between the objective features and the average clinicians’ subjective impressions. We employed multiple discriminant analysis using the extracted objective features for determining histological classification of mass. The classification accuracies were evaluated by applying the proposed method to a test set of 298 masses.

Materials and Methods

The use of this database and the participation of clinicians in the observer study were approved by our institutional review board. Informed consent was obtained from all observers.

Materials

Our database consisted of 363 breast ultrasonographic images obtained from 363 patients at Mie University Hospital, Tsu, Japan. It included 150 malignant (103 invasive and 47 noninvasive carcinomas) and 213 benign masses (87 cysts and 126 fibroadenomas). The histological classifications of these masses were proved by pathologic diagnosis. The ultrasonographic images were acquired with an Aplio (Toshiba Medical Systems Corporation) system. These ultrasonographic images were size of 716 pixels by 537 pixels with 8-bit gray scale. Figure 1 shows an example of masses with four different types of histological classifications. We divided our database into two set; 65 images (28 malignant and 37 benign masses) as a training set for the extraction method and 298 images (122 malignant and 176 benign masses) for the test set.

Fig. 1.

Four masses with different types of histological classifications. a Invasive carcinoma, b noninvasive carcinoma, c fibroadenoma, and d cyst

Observer Study for Subjective Impression

An observer study was conducted to obtain clinicians’ subjective impression of nine image features of breast masses on ultrasonographic images. The nine image features were selected by taking into account the image features that clinicians’ commonly used for describing masses on ultrasonographic images. These image features were (1) depth–width ratio, (2) degree of indistinctness in margin, (3) homogeneity in internal echoes, (4) echo level in internal echoes, (5) echo level in posterior echoes, (6) degree of round, (7) degree of polygonal, (8) degree of lobulated, and (9) degree of irregular. Three clinicians (3–7 years of experience) participated in this observer study.

The instructions to observers included: (1) the purpose of this study is to obtain basic data for clinicians’ subjective rating in a CAD scheme to assist clinicians’ interpretation of breast ultrasonographic images. (2) A test session includes 65 breast masses (28 malignant and 37 benign masses). (3) A subjective rating should be marked based on diagnosis of breast ultrasonographic on a continuous rating scale between 0.0 and 1.0 with a line-checking method. (4) A training session including three masses is provided at the beginning of this study. (5) There is no time limit.

Computerized Determination Scheme

Segmentation of Mass

For accurate quantification of the image features, the location and shape of all masses were determined by an experienced clinician.

Extraction of Nine Objective Features

In the feature extraction method, we first defined some extraction methods for each image feature. For each image feature, we selected an adequate feature extraction method with the highest correlation coefficient between the objective features and the average clinicians’ subjective impressions.

Depth–Width Ratio

We defined three extraction methods for quantifying the depth–width ratio.

1. D/W1—ratio of the long axis and the short axis in the segmented mass

2. D/W2—ratio of the height and the width for the circumscribed rectangle of the segmented mass

3. D/W3—ratio of the maximum chords in the vertical and horizontal directions

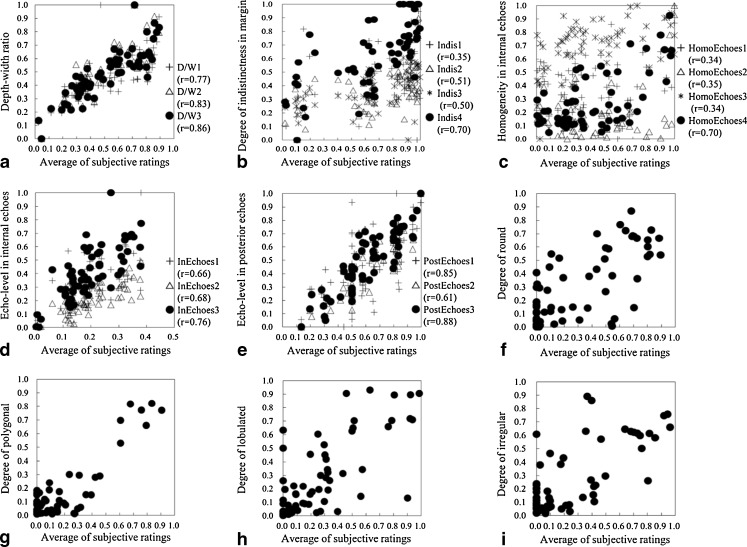
D/W1 and D/W2 were sometimes used as aspect ratio in the CAD scheme [15–17]. D/W3 was newly defined in this study because clinicians usually take into account the ratio of the maximum depth and the maximum width of a mass. Figure 2a shows the relationship between the average of the clinicians’ subjective ratings and the above three extraction methods for the depth–width ratio. D/W3 was the highest correlation coefficient (r = 0.86) among the three extraction methods. Therefore, we selected D/W3 for the depth–width ratio. A malignant mass tends to have a high depth–width ratio.

Fig. 2.

Relationship between the average of clinicians’ subjective ratings and the objective features obtained by the selected extraction method. a Relationship between the average of clinicians’ subjective ratings and the depth–width ratio, b relationship between the average of clinicians’ subjective ratings and the degree of indistinctness in margin, c relationship between the average of clinicians’ subjective ratings and the homogeneity in internal echoes, d relationship between the average of clinicians’ subjective ratings and the echo level in internal echoes, e relationship between the average of clinicians’ subjective ratings and the echo level in posterior echoes, f relationship between the average of clinicians’ subjective ratings and the output of the ANN with nine objective features, g relationship between the average of clinicians’ subjective ratings and the output of the ANN with 12 objective features, h relationship between the average of clinicians’ subjective ratings and the output of the ANN with 10 objective features, and i relationship between the average of clinicians’ subjective ratings and the output of the ANN with 11 objective features

Degree of Indistinctness in Margin

In quantifying the degree of indistinctness in margin, we defined four extraction methods.

1. Indis1—mean pixel value of gradient (Sobel) on the outline of the mass

2. Indis2—difference of the mean pixel values in the outside band and the inside band

3. Indis3—normalized radial gradient along the margin in the mass

4. Indis4—highest mean pixel value of gradient (Sobel) on four divided outlines of mass

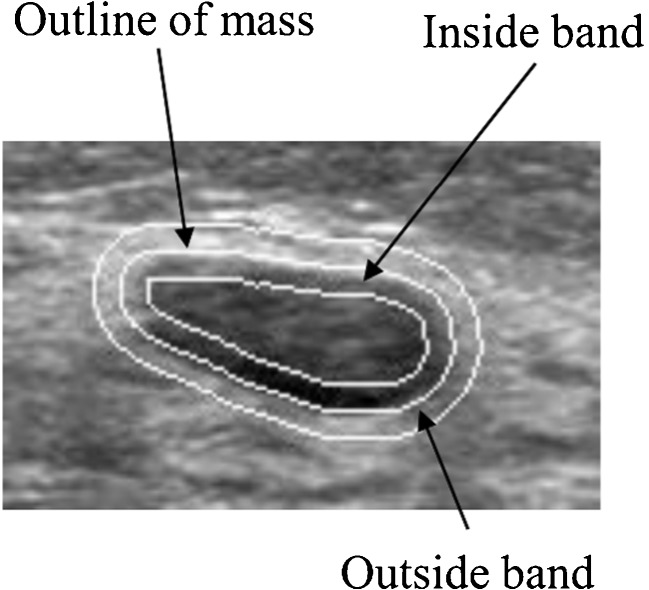
Indis1, Indis2, and Indis3 were often used for quantifying the degree of indistinctness in margins [10, 16–20]. Figure 3 shows an example of an inside and an outside band for margin of mass. Here, the outside band was given by the outside region with a width of 5 pixels around the outline of the mass region, and the inside band was given by the inside region with a width of 5 pixels around the outline of the mass region. Indis4 was newly defined because clinicians tend to evaluate an indistinct part only in margin. In Indis4, we divided the outline of a mass into four parts and determined the highest mean pixel value of gradient in these four parts. Figure 2b shows the relationship between the average of clinicians’ subjective ratings and the above four extraction methods for the degree of indistinctness in margin. Indis4 was the highest correlation coefficient (r = 0.70) among the four extraction methods. Therefore, we selected Indis4 for determining the degree of indistinctness in margin. Margin for malignant cases tends to be more indistinct than that for benign cases.

Fig. 3.

Example of an inside and an outside band for margin of mass

Homogeneity in Internal Echoes

We defined the following extraction methods.

1. HomoEchoes1—standard deviation of the intensity in a mass

2. HomoEchoes2—relative standard deviation of the intensity in a mass

3. HomoEchoes3—autocorrelation in depth of the region of interest (ROI)

4. HomoEchoes4—angular second moment

HomoEchoes1, HomoEchoes2, and HomoEchoes3 were known as the feature extraction methods for quantifying homogeneity in internal echoes [10, 14, 16, 17, 19]. However, HomoEchoes1 and HomoEchoes2 cannot properly evaluate texture because these methods do not consider pixel location information. In HomoEchoes3, autocorrelation in depth of ROI was computed from the minimal rectangular ROI containing the lesion. Autocorrelation was defined as

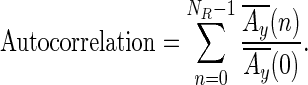1

where

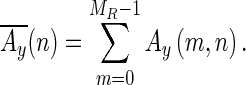2

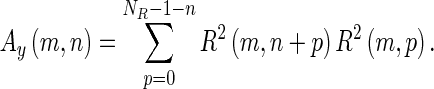3

R was the gray level value of the ROI. M_R was the number of pixels in the lateral direction of the ROI, and N_R was the number of pixels in the depth direction of the ROI. However, it would sometimes be difficult for the autocorrelation to quantify the homogeneity in internal echoes because ultrasonographic images included speckle noise. To overcome the problems, HomoEchoes4 using angular second moment (ASM) in the texture feature was defined in this study. Clinicians’ generically evaluate the homogeneity of internal echoes from inside of the mass. Therefore, we computed the ASM from inside of the mass. The ASM was defined as

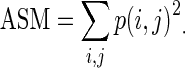4

The gray scale level on ultrasonographic images was decreased from 256 to 32 levels. Four matrices in different directions (0°, 45°, 90°, and 135°) were averaged. The distance between two points of interest was changed from 1 to 25 pixels. Here, p(i,j) was defined as the joint probability of the gray levels i and j. Figure 2c shows the relationship between the average of clinicians’ subjective ratings and the above four extraction methods for homogeneity in internal echoes. HomoEchoes4 was the highest correlation coefficient (r = 0.70) among the four extraction methods. Therefore, we selected HomoEchoes4 for homogeneity in internal echoes. A larger ASM value means more homogeneous.

Echo Level in Internal Echoes

We defined three extraction methods for the echo level in internal echoes.

1. InEchoes1—mean value of the pixels within the mass

2. InEchoes2—

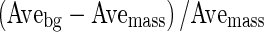
3. InEchoes3—

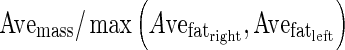
InEchoes1 and InEchoes2 were sometimes used for evaluation of the echo level in internal echoes [16, 17, 19, 21]. In InEchoes2, 5 % brighter mass pixels were first determined by a dynamic threshold to form a brighter group with the histogram technique. The average pixel value for the brighter group was defined as

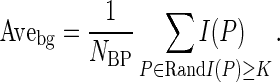5

Here, I(P) was the gray level value of mass pixel P, N_BP was the number of brighter pixels, and k was also the dynamic threshold. InEchoes2 was defined as

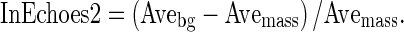6

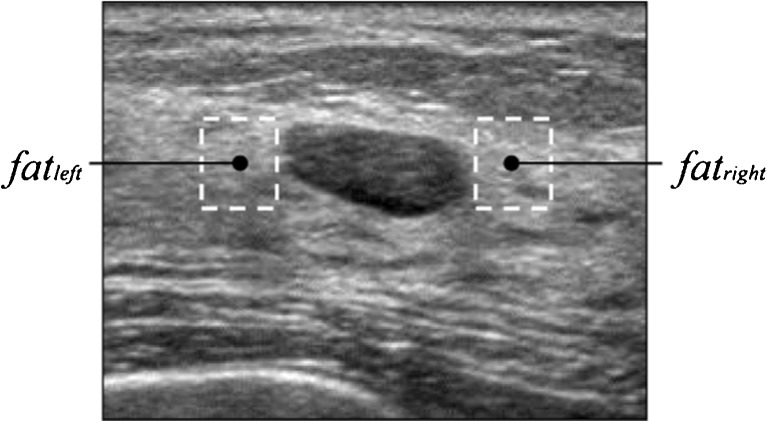
Here, Ave_mass was the mean value of the pixel value within the mass region. In clinical practice, clinicians compare echo level for the right and left fat regions with that in internal echoes within the mass. In InEchoes3, the 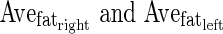was defined by the mean pixel value in the right and left fat regions, respectively. Figure 4 shows an example of the fat regions on the right and left sides. Here, the size of the fat region was (the maximum chord at vertical direction in the segmented mass) × (the maximum chord at horizontal direction in the segmented mass × 1/3). Figure 2d shows the relationship between the average of the clinicians’ subjective ratings and the above three extraction methods for the echo level in internal echoes. InEchoes3 was the highest correlation coefficient (r = 0.76) among the three extraction methods. Therefore, we selected InEchoes3 for the echo level for the internal echoes. When the echo level in internal echoes is low, there is a possibility that the mass is benign.

Fig. 4.

Example of the fat region on right and left sides

Echo Level in Posterior Echoes

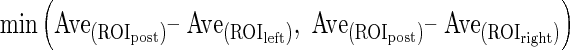
1. PostEchoes1:

2. PostEchoes2:

3. PostEchoes3:

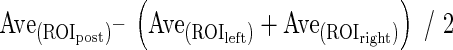
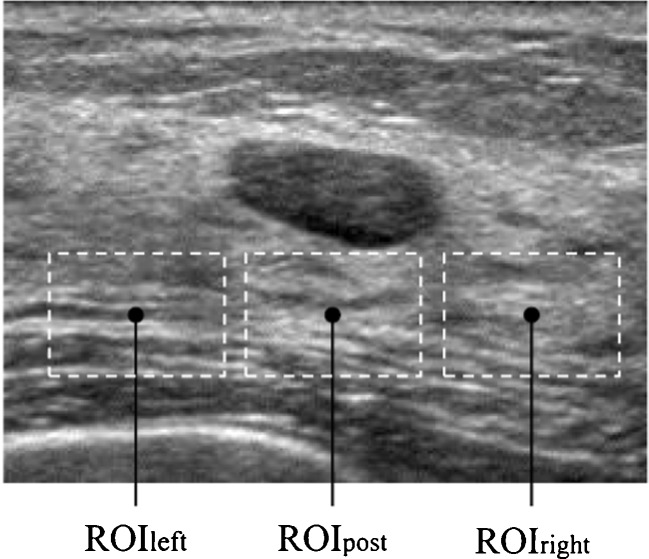
PostEchoes1 and PostEchoes2 were used for the echo level in posterior echoes in previous studies [10, 19, 21]. 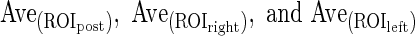were the average pixel values in each region. To avoid influence of lateral shadows, ROI_left and ROI_right were located on both sides of the posterior region of the mass. The size of the ROI was (the maximum chord at vertical direction in the segmented mass) × (the maximum chord at horizontal direction in the segmented mass × 4/5). Figure 5 shows an example of the echo level in posterior echoes. PostEchoes3 was newly defined because clinicians tend to compare the pixel values in the posterior region with those in normal tissue at the same depth. Figure 2e shows the relationship between the average of clinicians’ subjective ratings and above three extraction methods in echo level in posterior echoes. The PostEchoes3 was the highest correlation coefficient (r = 0.88) among the three extraction methods. Therefore, we selected the PostEchoes3 for the echo level in posterior echoes. The echo levels in the posterior region for a benign case tend to be higher than those for malignant cases.

Fig. 5.

Example of the ROI_left, ROI_post, and ROI_right

Degrees of Four Shapes in Mass

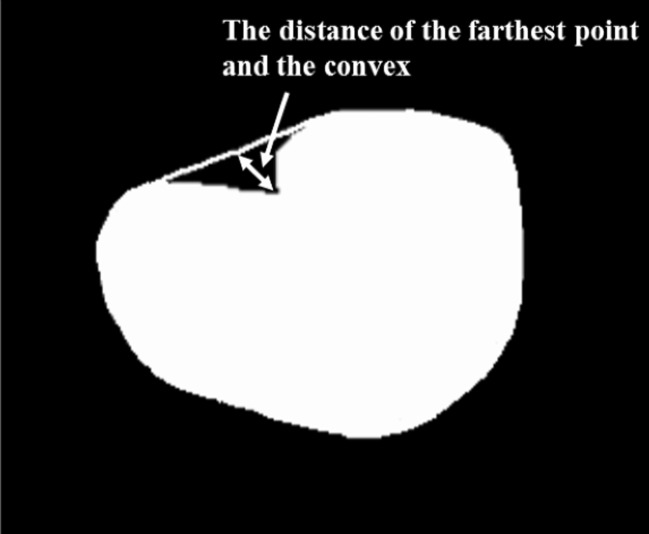
Clinicians’ evaluate the shape of mass by taking into account not only simple shape but also the other image features (e.g., the degree of indistinctness in margin). To determine the degrees of four shapes in mass, we extracted the following 15 image features from the segmented mass: (F1) the area of the mass; (F2) the filling rate of the circumscribed quadrangle; (F3) the number of lines in the segmented mass obtained by the Hough transform [22]; (F4) the number of concaves; (F5) the area of concaves; (F6) the distance of the farthest point and the convex, as shown in Fig. 6; (F7) the degree of circularity; (F8) the degree of irregularity; (F9) the number of protuberances; (F10) the ratio of the height and width for the circumscribed rectangle of the segmented mass; (F11) the ratio of the minimum distance and maximum distance between the center and the edges of the segmented mass; (F12) the ratio of the perimeter and area of the segmented mass; (F13) the ratio of the perimeter of the segmented mass and the perimeter of the corresponding best-fit ellipse of the segmented mass; (F14) the ratio of the area of the segmented mass and the area of the corresponding best-fit ellipse of the segmented mass; and (F15) the degree of the indistinctness in margin as mentioned in section B.2. (F2), (F7), (F8), (F10), (F11), and (F12) were determined as follows.

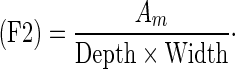7

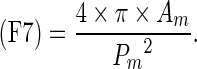8

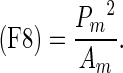9

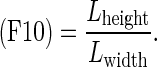10

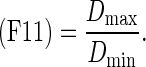11

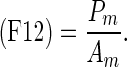12

Fig. 6.

Example of the concave region and the distance of the farthest point and the convex

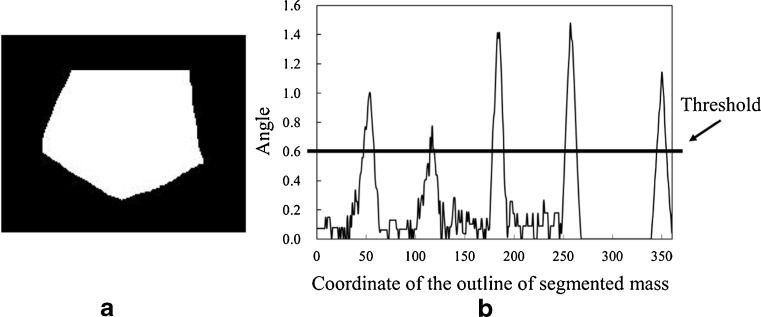
Here, A_m was the number of pixels in the segmented mass region. Width was the maximum chord in the horizontal direction in the segmented mass region and Depth was the maximum chord in the vertical direction in the segmented mass region. P_m was the perimeter of the mass. Figure 7 shows an example of L_long, L_short, D_min, and D_max. To calculate F4, we first delineated a convex hull from the segmented mass by using Sklansky’s algorithm [23]. The concaves were then identified by subtracting the segmented mass from the convex hull. Figure 8 shows the concave shape identification process. F4 was defined as the number of the identified concaves. F5 was defined as the number of pixels in the identified concaves. For calculating F9, the curvature was first calculated from the coordinate at the outline of the segmented mass. Figure 9 shows an example of a curvature calculated from the outline of the segmented mass. We defined the local maximum value by identifying each center point of the curvature that was larger than the threshold. The threshold was determined experimentally as 0.6. F9 was defined as the number of the local maxima.

Fig. 7.

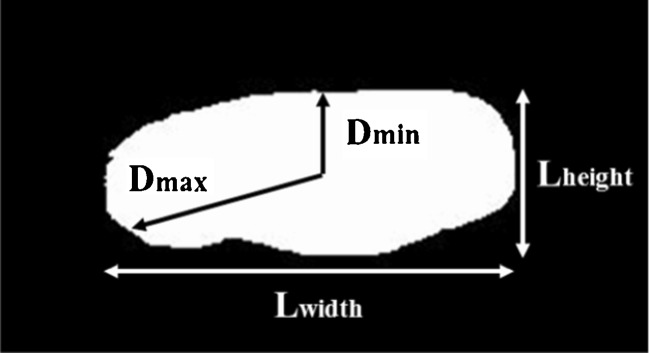
Example of the L_long, L_short, D_min, and D_max, respectively

Fig. 8.

Concave shape identification process. a Segmented mass, b convex hull, and c detected concave

Fig. 9.

Example of the calculated curvature from the outline of segmented mass. a Segmented mass and b curvature of the a segmented mass

It is difficult to compute the degrees of round, polygonal, lobulated, and irregular mass shape from these image features in a manner similar to clinicians. Since clinicians determine these degrees by their subjective impression, the degrees would be expressed by nonlinear function of the image features. An ANNs are often used to identify such function [24, 25]. Therefore, we computed the degrees of shape from these image features using an ANN that was trained to learn the relationship between the image features and the average subjective clinicians’ ratings. The ANN was a three-layered, feed forward network using a backpropagation algorithm [26]. The most appropriate combination of image features in the degree of each shape was determined by use of a leave-one-out test method [27]. The selected image features were used for the input data of the ANN whereas the average subjective ratings were used for the teacher data of the ANN. Table 1 shows the shape evaluation parameters for each ANN. These parameters were selected such that the output of the ANN provides the highest correlation coefficient to the average clinicians’ subjective ratings using the leave-one-out test method for training data.

Table 1.

Shape evaluation parameters for each ANN

Shape	Coefficient of the momentum term	Learning rate	Slant of the sigmoid function	Hidden layer neurons	Training iterations
Round	0.01	0.1	1.0	10	450
Polygonal	0.01	0.01	3	4	100
Lobular	0.1	0.1	1.5	11	1,300
Irregular	0.01	0.01	1	9	3,350

Determination of Histological Classification

Multiple discriminant analysis [26] was employed to distinguish among four different types of histological classifications. For the input of the multiple discriminant method, we used the nine objective features. Here, nine objective features were normalized. The output of the multiple discriminant analysis provided four values indicating the likelihood of each histological classification. A leave-one-out test method was used for the training and testing of the multiple discriminant analysis.

The classification accuracy for each histological classification was defined as

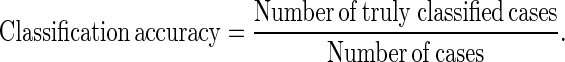13

The sensitivity [28], specificity [28], positive predictive value (PPV) [28], and negative predictive value (NPV) [28] were defined as

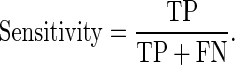14

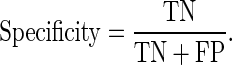15

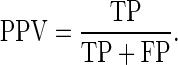16

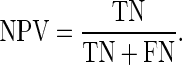17

where true positive (TP) was the number of malignant masses correctly identified as positive; true negative (TN) was the number of benign masses correctly identified as negative; false positive (FP) was the number of benign masses incorrectly identified as positive; false negative (FN) was the number of malignant masses incorrectly identified as negative.

Results

Table 2 shows the selected feature extraction method. The correlation coefficients between the averages of clinicians’ subjective ratings and the objective features obtained by the selected extraction method were 0.86 for the depth–width ratio, 0.70 for the degree of indistinctness in margin, 0.70 for the homogeneity in internal echoes, 0.76 for the echo level in internal echoes, 0.88 for the echo level in posterior echoes, 0.72 for the degree of round, 0.88 for the degree of polygonal, 0.74 for the degree of lobulated, and 0.73 for the degree of irregular, respectively.

Table 2.

Selected feature extraction method

Objective features	Selected the feature extraction method	Correlation coefficient
Depth–width ratio	Ratio of the maximum chords in the vertical and horizontal directions	0.86
Degree of indistinctness in margin	Highest mean pixel value of gradient (Sobel) on four divided outlines of the mass	0.70
Homogeneity in internal echoes	Angular second moment	0.70
Echo level in internal echoes		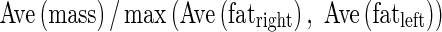0.76
Echo level in posterior echoes		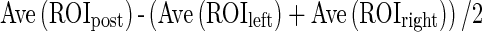0.88
Degree of round	Output value of the ANN by use of (F1), (F5), (F6), (F8), (F9), (F11), (F12), (F13), and (F15)	0.72
Degree of polygonal	Output value of the ANN by use of (F1), (F3), (F4), (F6), (F7), (F8), (F9), (F11), (F12), (F13), (F14), and (F15)	0.88
Degree of lobulated	Output value of the ANN by use of (F3), (F4), (F5), (F6), (F7), (F8), (F11), (F13), (F14), and (F15)	0.74
Degree of irregular	Output value of the ANN by use of (F1), (F3), (F5), (F7), (F8), (F9), (F10), (F11), (F13), (F14), and (F15)	0.73

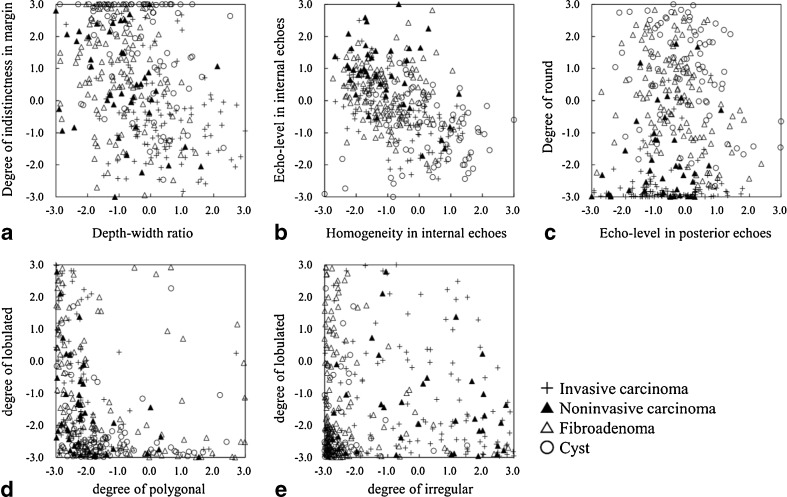
Figure 10 shows the distributions of the nine objective features obtained from all masses in our database. Mean values and standard deviations of each objective feature for the four different types of histological classifications are listed in Table 3. Here, these objective features were normalized by use of all cases in our database. The degree of indistinctness in margin, the homogeneity in internal echoes, the echo level in posterior echoes, and the degree of round shape for cysts tended to be larger than those for other histological classifications. Fibroadenoma tended to have larger values in the degree of round shape, the echo level in internal echoes, and have smaller values for the degree of irregular shape. Noninvasive carcinoma tended to have larger values for the echo level in internal echoes and the degree of irregular shape. Invasive carcinoma tended to have smaller values for the indistinctness in margin, the degree of round shape, and have larger values for the depth–width ratio, the degree of irregular shape. These objective features for each histological classification appeared the tendency similar to clinical characteristics.

Fig. 10.

Distributions of the nine objective features between a depth–width ratio and degree of indistinctness in margin, b homogeneity in internal echoes and echo level in internal echoes, c echo level in posterior echoes and degree of round, d degree of polygonal and degree of lobulated, and e degree of irregular and degree of lobulated

Table 3.

Mean values and standard deviations of each objective feature for the four different types of histological classifications

Objective feature	Histological classification
	Invasive carcinoma	Noninvasive carcinoma	Fibroadenoma	Cyst
Depth–width ratio	0.71 ± 0.94	−0.48 ± 0.99	−0.50 ± 0.68	0.14 ± 0.91
Degree of indistinctness in margin	−0.75 ± 0.73	−0.17 ± 0.93	0.19 ± 0.89	0.72 ± 0.84
Homogeneity in internal echoes	0.16 ± 0.98	−0.58 ± 0.81	−0.38 ± 0.71	0.70 ± 1.05
Echo level in internal echoes	−0.47 ± 0.71	1.05 ± 0.96	0.38 ± 0.77	−0.56 ± 0.97
Echo level in posterior echoes	−0.18 ± 0.98	−0.54 ± 0.89	0.04 ± 0.89	0.44 ± 1.06
Degree of round	−0.98 ± 0.41	−0.70 ± 0.57	0.48 ± 0.72	0.85 ± 0.77
Degree of polygonal	−0.25 ± 0.76	−0.24 ± 0.76	0.08 ± 1.17	0.31 ± 1.00
Degree of lobulated	0.25 ± 1.07	−0.13 ± 0.81	0.18 ± 1.07	−0.52 ± 0.62
Degree of irregular	0.89 ± 0.96	0.85 ± 1.06	−0.57 ± 0.38	−0.67 ± 0.20

Table 4 shows the result of test for univariate equality of group means. This test was evaluated by using the objective features in Fig. 10. The Wilk’s lambdas [29] for the degree of round shape were smaller than those for the other objective features. The F value [29] for the degree of round shape was also larger than those for any other features. This result would indicate that the degree of round shape made a larger contribution to determine four histological classifications of breast masses. On the other hand, the degree of polygonal shape had the largest Wilk’s lambda and the smallest F value. However, the p value for the degree of polygonal shape reached the level of statistical significance (p < 0.05). Thus, these nine objective features were statistically useful for determining four histological classifications of breast masses.

Table 4.

Tests for univariate equality of group means

	Wilk’s lambda	F value	p value
Depth–width ratio	0.777	34.4	<0.05
Degree of indistinctness in margin	0.779	34.0	<0.05
Homogeneity in internal echoes	0.837	23.4	<0.05
Echo level in internal echoes	0.774	34.8	<0.05
Echo level in posterior echoes	0.941	7.5	<0.05
Degree of round	0.467	136.4	<0.05
Degree of polygonal	0.956	5.5	<0.05
Degree of lobulated	0.931	8.9	<0.05
Degree of irregular	0.566	91.7	<0.05

Table 5 shows the determination results of four histological classifications by use of the multiple discriminant analysis. The classification accuracies of the proposed method were 88.4 % (76/86) for invasive carcinomas, 80.6 % (29/36) for noninvasive carcinomas, 86.0 % (92/107) for fibroadenomas, and 84.1 % (58/69) for cysts, respectively. The sensitivity, specificity, PPV, and NPV based on the classification results of histological classifications were 89.3 (109/122), 96.0 (169/176), 94.0 (109/116), and 92.9 % (169/182), respectively.

Table 5.

Determination results of four histological classifications by use of the multiple discriminant analysis

Pathological diagnosis	Classification accuracy
	Invasive carcinoma (%)	Noninvasive carcinoma (%)	Fibroadenoma (%)	Cyst (%)
Invasive carcinoma (86)	76 (88.4 %)	2 (2.3 %)	8 (9.3 %)	0 (0.0 %)
Noninvasive carcinoma (36)	2 (5.6 %)	29 (80.6 %)	5 (13.9 %)	0 (0.0 %)
Fibroadenoma (107)	4 (3.7 %)	2 (1.9 %)	92 (86.0 %)	9 (8.4 %)
Cyst (69)	1 (1.4 %)	0 (0.0 %)	10 (14.5 %)	58 (84.1 %)

Discussion

To investigate the usefulness of the nine objective features in terms of classification accuracies, we compared the proposed method with a previous method for determining histological classifications of masses [30, 31]. In this previous method, nine objective features were extracted: (1) degree of circularity; (2) degree of shape irregularity; (3) depth–width ratio; (4) degree of indistinctness in margin; (5) degree of irregularity in margin; (6) homogeneity in internal echoes; (7) echo level in internal echoes; (8) echo level in posterior echoes; and (9) degree of lateral shadows. The p value for the nine objective features in the previous method reached the level of statistical significance (p < 0.05). We employed the multiple discriminant analysis using the nine objective features for determining histological classifications of masses. The classification accuracies of the previous method were 80.2 % (69/86) for invasive carcinomas, 63.9 % (23/36) for noninvasive carcinomas, 77.6 % (83/107) for fibroadenomas, and 81.2 % (56/69) for cysts, respectively. The sensitivity, specificity, PPV, and NPV of the previous method were 85.2 (104/122), 95.5 (168/176), 92.9 (104/112), and 90.3 % (168/186), respectively. Thus, the proposed method was higher classification accuracies than the previous method. Echo level in internal echoes for noninvasive carcinoma included in our database tended to be higher than for other histological classifications. The echo level in posterior echoes for noninvasive carcinoma included in our database also tended to be lower than for other histological classifications. The previous method was not adequate to evaluate the echo level in internal echoes and the echo level in posterior echoes for the masses. Therefore, the classification accuracy of the previous method for noninvasive carcinoma was lower than that of other histological classifications.

We considered that the likelihood of malignancy for mass may be helpful to clinicians for their decisions on clinical practice. Thus, we applied the results of the histological classifications in the proposed method to distinguish between malignant and benign masses. Here, a malignant mass was defined as a mass that our histological method classified as any malignant mass, whereas a benign mass corresponded to a mass our histological method classified as any benign mass. The classification accuracies of this computerized method based on histological classifications were 89.3 % (109/122) for malignant masses and 96.0 % (169/176) for benign masses. We also investigated the performance of distinguishing between malignant and benign masses using multiple discriminant analysis with nine objective features. The classification accuracies were 87.7 % (107/122) for malignant masses and 94.9 % (167/176) for benign masses. The classification accuracies of the computerized method based on histological classifications were higher than those of the computerized method for distinction between benign and malignant masses. We also compared the computerized method based on histological classifications with two previous methods, here denoted as method1 [10] and method2 [7], used to distinguish between benign and malignant masses on ultrasonographic images. In the previous method1, we extracted four objective features of masses on ultrasonographic images. These four objective features were lesion shape, margin definition, echogenic texture, and posterior acoustic enhancement or shadowing. The p value for the four objective features in the previous method1 reached the level of statistical significance (p < 0.05). We employed the multiple discriminant analysis using the four objective features to distinguish between malignant and benign masses on ultrasonographic images. In the previous method2, we extracted 15 objective features which were block difference of inverse probabilities, block variation of local correlation coefficients, 2D normalized auto-covariance coefficients, five objective features based on a spatial gray-level dependence matrices, five objective features based on a gray-level difference matrix, and two objective features based on a neighborhood gray-tone difference matrix. The p value for the 15 objective features in the previous method2 reached the level of statistical significance (p < 0.05). We employed the multiple discriminant analysis using the 15 objective features for distinguishing between malignant and benign masses on ultrasonographic images. Table 6 shows the results of classification accuracies for the computerized method based on histological classifications and the two previous methods. The computerized method based on histological classifications was slightly lower classification accuracy for malignant masses than that of the previous method1. However, it was higher classification accuracy for benign masses than the previous method1 and the previous method2. Therefore, we believe that classifier based on the histological classifications would be useful for distinguishing between malignant and benign masses.

Table 6.

Result of classification accuracies for proposed method and two previous methods

	Classification Accuracy
	Previous method 1	Previous method 2	Proposed method
Malignant (122; invasive carcinoma and noninvasive carcinoma)	111 (91.0 %)	108 (88.5 %)	109 (89.3 %)
Bening (176; fibroadenoma and cyst)	147 (83.5 %)	144 (81.8 %)	169 (96.0 %)

In order to evaluate the usefulness of evaluating each shape, the proposed method using the degrees of four different types of the shape (total, nine features) was compared with a computerized method using directly 15 objective features to evaluate the degrees of four shapes (total, 19 features). The p values for the 19 objective features reached the level of statistical significance (p < 0.05). A multiple discriminant analysis with the 19 objective features was employed to distinguish among four different types of histological classifications of masses. The classification accuracies of this computerized method were 80.2 % (69/86) for invasive carcinomas, 69.4 % (25/36) for noninvasive carcinomas, 88.8 % (95/107) for fibroadenomas, and 85.5 % (59/69) for cysts, respectively. The sensitivity, specificity, PPV, and NPV were 87.7 (107/122), 98.9 (174/176), 98.2 (107/109), and 92.1 % (174/189), respectively. Thus, the classification accuracies by the proposed method were higher than those by the computerized method using 19 objective features.

In order to discuss the necessity of the nine objective features, we calculated classification accuracies using various combinations of these objective features. Table 7 summarizes our results. The first column displays the subsets of features selected using the stepwise method. Each row shows the classification accuracies achieved by multiple discriminant analysis with the selected features. The classification accuracies of the multiple discriminant analysis with the nine objective features were the highest. Therefore, the nine objective features would be useful for determining the histological classification of masses.

Table 7.

Classification accuracies of the multiple discriminant analysis with various combinations of objective features

Selected features	Classification accuracies
	Invasive carcinoma	Noninvasive carcinoma	Fibroadenoma	Cyst
SF6 and SF4	80.2 % (69/86)	72.2 % (26/36)	54.2 % (58/107)	72.5 % (50/69)
SF6, SF4, and SF9	75.6 % (65/86)	72.2 % (26/36)	65.4 % (70/107)	78.3 % (54/69)
SF6, SF4, SF9, and SF5	82.6 % (71/86)	75.0 % (27/36)	73.8 % (79/107)	76.8 % (53/69)
SF6, SF4, SF9, SF5, and SF3	76.7 % (66/86)	75.0 % (27/36)	79.4 % (85/107)	78.3 % (54/69)
SF6, SF4, SF9, SF5, SF3, and SF1	83.7 % (72/86)	75.0 % (27/36)	81.3 % (87/107)	76.8 % (53/69)
SF6, SF4, SF9, SF5, SF3, SF1, and SF8	84.9 % (73/86)	75.0 % (27/36)	81.3 % (87/107)	81.2 % (56/69)
SF6, SF4, SF9, SF5, SF3, SF1, SF8, and SF2	88.4 % (76/86)	80.6 % (29/36)	82.2 % (88/107)	84.1 % (58/69)
SF6, SF4, SF9, SF5, SF3, SF1, SF8, SF2, and SF7	88.4 % (76/86)	80.6 % (29/36)	86.0 % (92/107)	84.1 % (58/69)

SF1 depth–width ratio, SF2 degree of indistincness in the margin, SF3 homogeneity in internal echoes, SF4 echo level in internal echoes, SF5 echo level in posterior echoes, SF6 degree of round, SF7 degree of polygonal, SF8 degree of lobulated, SF9 degree of irregular

Many investigators have been conducted observer studies to evaluate the usefulness of a computerized scheme for distinguishing between benign and malignant lesions on clinicians’ performance. Those studied showed that the likelihood of malignancy evaluated by a computerized scheme improved clinicians’ performance in differential diagnosis. However, clinicians’ performances with a computerized scheme were lower than the accuracy of the computerized scheme [32, 33]. This would because clinicians were not able to trust a computerized scheme enough because clinicians’ subjective impression was sometimes different from objective features extracted in the computerized scheme. Therefore, we believed that it was important to extract objective features reflecting to clinicians’ subjective impression based on clinical experience. We would investigate the influence on clinicians of using the objective features reflecting to clinicians’ subjective impression in the further study.

There were several limitations in this study. One limitation was that masses were manually traced. It would be boring for clinicians to manually trace masses in clinical practice. Therefore, we have to develop a segmentation method for mass. On the other hand, we classified only four different types of histological classifications in this study. In the further study, we need to deal with more kinds of histological classifications.

Conclusions

In this study, we developed a computerized determination scheme for histological classification of mass by objective features based on clinicians’ subjective impressions on ultrasonographic images. Our computerized scheme was shown to have high classification accuracies for histological classification, would be useful in the differential diagnosis of breast masses on ultrasonographic images as diagnosis aid.