Assessing the utility of coevolution-based residue–residue contact predictions in a sequence- and structure-rich era

Significance

We develop an improved method for predicting residue–residue contacts in protein structures that achieves higher accuracy than previous methods by integrating structural context and sequence coevolution information. We then determine the conditions under which these predicted contacts are likely to be useful for structure modeling and identify more than 400 protein families where these conditions are currently met.

Abstract

Recently developed methods have shown considerable promise in predicting residue–residue contacts in protein 3D structures using evolutionary covariance information. However, these methods require large numbers of evolutionarily related sequences to robustly assess the extent of residue covariation, and the larger the protein family, the more likely that contact information is unnecessary because a reasonable model can be built based on the structure of a homolog. Here we describe a method that integrates sequence coevolution and structural context information using a pseudolikelihood approach, allowing more accurate contact predictions from fewer homologous sequences. We rigorously assess the utility of predicted contacts for protein structure prediction using large and representative sequence and structure databases from recent structure prediction experiments. We find that contact predictions are likely to be accurate when the number of aligned sequences (with sequence redundancy reduced to 90%) is greater than five times the length of the protein, and that accurate predictions are likely to be useful for structure modeling if the aligned sequences are more similar to the protein of interest than to the closest homolog of known structure. These conditions are currently met by 422 of the protein families collected in the Pfam database.

There has been long-standing interest in the prediction of residue–residue contacts based on the covariance of residue-substitution patterns in multiple aligned sequences (1). For many years, these methods met with relatively little success, but with the increase in the number of known protein sequences and improvements in methods such approaches have recently demonstrated considerable promise. The methodological improvements distinguish between direct couplings and indirect correlations that arise from chains of the direct couplings (i.e., if A is coupled to B, and B to C, one might erroneously conclude A is coupled to C). Two recent methods, Direct Coupling Analysis (DCA) and Protein Sparse InverseCOVariance (PSICOV) (2, 3), achieve this separation by inverting a residue–residue covariance matrix.

In parallel with the growth of the sequence databases, there has been a considerable increase in the number of known structures over the past decade. Comparative modeling methods, which predict protein structure based on homologs of known structures, have become increasingly powerful, and can generate models more accurate than those produced by de novo modeling in most cases. Thus, the growth in the databases over the last decade represents something of a catch-22 for contact prediction: there are many more sequences, so such predictions can be made much more accurately, but there are few protein families with the many sequences required for accurate contact prediction whose structures cannot be modeled relatively accurately using comparative modeling methods.

In this paper we begin by examining the approximations involved in the residue–residue covariation matrix inversion used by PSICOV and DCA, and show that more accurate contact predictions can be obtained using fewer sequences by going beyond the second-order approximation to the underlying distribution implicit in both methods. We then rigorously assess the utility and limits of contact prediction for protein tertiary structure modeling by evaluating the extent to which predicted contacts can contribute to modeling in the presence of the homologous structure information likely to be available.

Results and Discussion

Previous work (2–4) has demonstrated that contacts between residues in the 3D structure of a protein can be predicted with considerable accuracy for large protein families based on the evolutionary covariance observed in multiple sequence alignments. We briefly review the basis for these approaches to motivate the method described in this paper.

Given a set of data drawn from an (unknown) multivariate probability distribution , the marginal frequencies 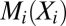, and the pair correlations 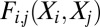can be readily computed. If the underlying distribution is Gaussian:

The parameters of the distribution can be readily obtained from the frequencies and pair correlations: 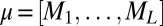and 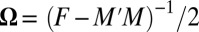. Although the observed 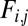are subject to chaining effects (if A is correlated with B, and B with C, then A will appear correlated with C), the 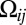are the direct couplings between variables with chaining effects eliminated.

Although they differ significantly in derivation and their estimation procedures, both DCA and PSICOV use the recipe of approximating the direct couplings with an estimate of the inverse covariance matrix, as is appropriate for a Gaussian. Our approach, called GREMLIN, avoids this approximation and instead obtains model parameters from the conditional correlations 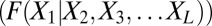using our pseudolikelihood framework (5), optimizing the learning procedure for contact prediction. A recently published method, PseudoLikelihood Maximization Direct Coupling Analysis (PLMDCA) (6), also uses a pseudolikelihood approach. Here, we go beyond PLMDCA improving the robustness of predictions with fewer sequences by incorporating prior information on pairs likely to be in contact.

Accuracy of Contact Prediction.

It was recently shown that pseudolikelihood-based contact prediction is more accurate than DCA on a set of Pfam domains with deep alignments (6). Here, we first carry out a more comprehensive comparison of contact prediction methods (GREMLIN, PSICOV, DCA, MIc, and PLMDCA) on a larger set of families with varying alignment depths. Second, we explore the utility of alternate sources of prior information in improving the accuracy of pseudolikelihood-based contact prediction.

We constructed a dataset of 329 protein targets selected from the Continuous, Automated Model Evaluation (CAMEO) server (7) (Dataset S1, details in Materials). These targets represent a snapshot of recently deposited protein structures into the Protein Data Bank and encompass a wide range of protein sizes, folds, and evolutionary histories. For each protein in the list, we constructed alignments of evolutionarily related proteins and used each method to predict contacts. We computed the accuracy of contact predictions for each method by computing the fraction of predicted contacts that had a Cβ−Cβ (Cα in the case of Glycine) distance less than 8 Å. To discount the effects of local secondary structure on accuracy, we restricted ourselves to positions at least 12 residues apart in the target sequence (results when restricted to positions at least 24 residues apart are similar; SI Appendix, Fig. S1). The methods assign a score to each contact prediction, and the predictions were ranked for each protein target based on these values.

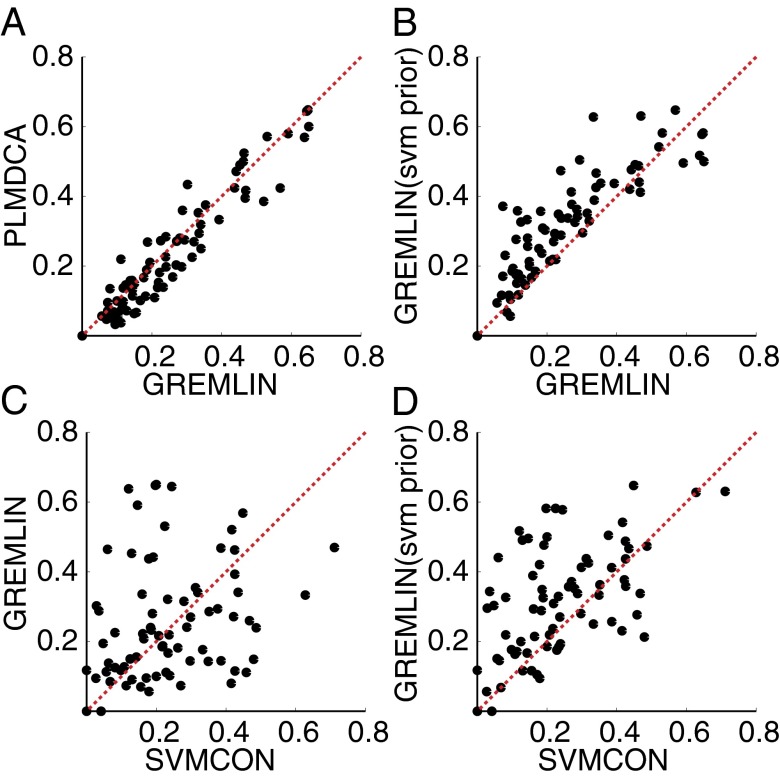
Over the CAMEO protein test set, GREMLIN’s pseudolikelihood method is more accurate than DCA, PSICOV, and MIc when no prior information was used (Fig. 1 A–C). A simple prior based on sequence separation and predicted secondary structure improves GREMLIN’s accuracy further (Fig. 1D). For the top ranked L/2 predictions (where L is the length of the target protein), the accuracy of GREMLIN with this simple prior is higher than that of the next most accurate method for a majority of targets (Fig. 1E). PSICOV accuracy is higher on average than DCA [with average product correction (APC); ref. 8] for the first L/2 predictions but falls below DCA at larger numbers of predictions. PLMDCA was much slower than other methods compared here; we therefore compared it to GREMLIN on smaller datasets in Fig. 2 and SI Appendix, Fig. S7.

Fig. 1.

Accuracy of contact prediction. Comparison of GREMLIN with DCA (A), PSICOV (B), MIc (C), and GREMLIN when no prior information is used (D). Each point corresponds to a protein, the axes indicate the accuracy of the top ranked L/2 Cβ−Cβ contacts predicted by the indicated methods. (E) (solid lines) Average accuracy for varying numbers of predictions; (broken lines) fraction of targets where GREMLIN was more accurate than the indicated method. Dependence of accuracy of the top L/5 (F) and L/2 (G) predictions on the alignment depth for a subset of 75 targets with deep alignments.

Fig. 2.

Improved contact prediction by integration coevolution and predicted structure-feature information. Accuracy of the top L/2 predictions between positions at least 12 residues apart, with and without priors on a dataset of 73 proteins that do not have homologs of known structure (Dataset S2; results between positions at least 24 residues apart are included in the SI Appendix, Fig. S7 A–D). (A) Using secondary structure and sequence separation priors, GREMLIN achieves higher accuracy than PLMDCA; (C) SVMCON and GREMLIN predictive accuracy are not highly correlated. (B and D) Integrating a Support Vector Machine (SVM) based prior into GREMLIN improves upon both methods alone.

Difference in Accuracy as a Function of the Number of Sequences.

For targets that had at least 20 L sequences (using the number of nonredundant sequences at 90% sequence identity as a measure of alignment depth), we generated subalignments and recomputed predictions for each of these. Fig. 1 F and G show the average accuracy of the methods across these targets varying the depth of the alignment: GREMLIN’s pseudolikelihood-based approach is more accurate than other methods across alignment depths, even when no prior information is used. Using prior information further improves the accuracy of predictions, especially when there are few sequences in the alignment.

The Effects of Prior Information.

We further investigated the utility of predicted secondary structure-based prior (using PSIPRED; ref. 9) as well as a more powerful prior using SVMCON—a contact prediction method that uses profile–profile similarity and secondary structure (10). To reduce the possible overlap with the protein structures used in the training of PSIPRED and SVMCON, we evaluated their contribution on a set of hard targets that are unlikely to have homologs with known structure (Dataset S2). When no prior information was used, GREMLIN and PLMDCA had similar accuracy (SI Appendix, Fig. S7) although GREMLIN was 5–20× faster. Using prior information based on secondary structure and sequence separation improved accuracy of predictions (Fig. 2A). Using a prior based on SVMCON improved results further with the resulting method outperforming SVMCON on most targets (Fig. 2 C and D). Integrating the information from profile similarity-based methods into sequence coevolution-based methods using GREMLIN thus performs better than either individual method.

Utility and Limits of Sequence Covariance-Based Contact Prediction.

Recent studies (4, 11, 12) have shown that for targets with deep alignments, the predicted contacts are sufficiently accurate to predict the 3D structures of proteins. However, because of the steady increase in the structures deposited in the Protein Data Bank (PDB; ref. 13), any given target protein of interest is also likely to have a related protein with known structure. How useful are covariance-based contact predictions for structure modeling given the homologous structure information likely to be available?

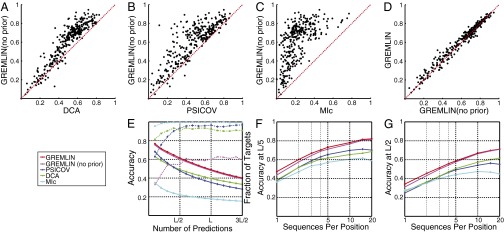
To address this question, we characterized the difference in the fit to predicted contacts of comparative models built from templates and the corresponding native structure for a large set of proteins with recently solved structures compiled from the CAMEO and Critical Assessment of Protein Structure Prediction (CASP10) experiments. If the comparative models fit the contact information as well as the native structure, this added information is likely to be not useful for model improvement. Conversely, if the contact information fits the native structure better, it should be useful for improving comparative models. For each target in the CAMEO dataset, we queried the PDB for homologs using HHsearch, and constructed homology models for the aligned residues from the hits that covered at least 75% of the protein. Because these models are generated from proteins, they are protein-like in their secondary structure composition and can be thought of as a sample of the conformational landscape of protein-like structures around the query protein. We determined the fit to predicted contacts using GREMLIN scores (Methods). The GREMLIN score (or any other measure of structure quality) is only useful for improving starting models if the native structure has a better score than these models. To assess this, we computed the difference between the scores of models and those of the corresponding native structure (GREMLINΔ) for each of the 329 proteins in the dataset. When GREMLINΔ > 0 for a model, GREMLIN scores correctly discriminate between native structure and model.

We examined the ability of GREMLINΔ to (i) rank alternate models and (ii) discriminate between models and the native structure. The distributions of GREMLINΔ for each target in the CAMEO protein dataset fall into three categories of interest based on these criteria. Category I (40% of targets, e.g., Fig. 3A, Left): GREMLINΔ does not properly discriminate between alternative models, nor between models and the native structure of the target protein—and hence the contact information is not useful for structure prediction. Category II (29% of cases; Fig. 3A, Middle): GREMLINΔ properly discriminates among models, but not between the best models and the native structure—and hence could be useful for model ranking, but not for increasing the accuracy of the best models. Category III (10% of cases; Fig. 3A, Right): GREMLINΔ properly discriminates among models and between the best models and the native structure—and hence should be useful for improving comparative model accuracy. A positive control using L perfect contacts (as ranked by GREMLIN) resulted in 97% of targets having correct ranking and discrimination (SI Appendix, Fig. S9) indicating that perfect contact information is adequate for this task for nearly all targets.

Fig. 3.

Utility of contact prediction for structure modeling. (A) Ranking of alternate models by GREMLINΔ. Three scenarios are illustrated; each represents a distinct protein target, black dots indicate alternate models, red dots indicate native structures. (Left) GREMLINΔ is not useful in selecting the closest model and does not correctly discriminate between native (target pdb:4hwnA) and homology models; (Middle) GREMLINΔ ranks homology models correctly (top five models within 0.05 of best five on average; R² between GREMLIN score and fraction of native contacts > 0.8) but adds no additional information (target pdb:4fn4D); (Right) GREMLINΔ discriminates between best model and native structure (target pdb:4hxtA). In an additional 6% of the targets, GREMLINΔ correctly discriminated the native from the homology models but there were not enough models to reliably establish accuracy of ranking. (B) predicts GREMLINΔ: GREMLINΔ versus structural similarity of homolog to native structure computed by TM-align (14) (for homologs of all targets with high-resolution crystal structures < 2.1 Å). When 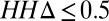(blue bars), GREMLINΔ is rarely better than random (green bars, constructed by pooling 100 permutations of predicted scores for each target). When 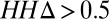(red bars), GREMLINΔ is significantly positive and contact scores successfully discriminate between native and homology model even when the homolog is likely to be from the same fold (similarity 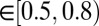). Error bars show mean and SD of distributions in all cases.

On a subset of 68 targets that had at least 50 models and 20 L sequences, increasing the alignment depth improved model ranking, as measured by multiple metrics (SI Appendix, Fig. S5), approaching its highest value for most targets with as few as 5 L sequences. This suggests that accurate global ranking is possible for the majority of targets with at least 5 L sequences. However, for most targets, HHsearch was already able to identify a homolog with similar accuracy without using this information (SI Appendix, Fig. S4); a ranking method that uses HHsearch and GREMLIN scores might improve upon both. This suggests that although infrequent, category III might represent the case of most utility for contact-based structure prediction.

Can category III be distinguished from the more frequently occurring categories I and II without knowing the native structure? We hypothesized that there might be a relationship with the closeness of the sequences in the input alignment to the native sequence compared with the templates—if the input sequences are closer to the query sequence, they could be more likely to provide information specific to its native structure. For each protein in the CAMEO dataset, we determined the difference between the HHscore of the alignment with itself and to the closest template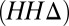. is zero when the query and template alignments are identical; it increases as the difference in the alignments increases reaching 1 when there is no homolog with known structure.

For targets with high-resolution crystal structures, there is a clear relationship between the extent the contacts are discriminative for the native structure (GREMLINΔ), and the closeness of the input sequences to the native sequence 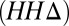. When is small (Fig. 3B, blue bars), GREMLIN discrimination is rarely better than random, but when is large (Fig. 3B, red bars), the GREMLIN score of the native structure is significantly better than that of models even in cases where the templates are likely from the same fold. can be computed for a query protein of unknown structure, which makes it a useful indicator of the utility of covariance information: in cases where the best model has a high , covariance information is likely to distinguish the native structure from the model. However, this happens relatively infrequently (4 of 329 CAMEO targets). A similar analysis on targets from the CASP10 experiment (Dataset S3) identified 6 of 67 targets with > L sequences that had ≥ 0.5 for the top-ranked model.

Frequency of Utility.

Our analysis suggests that covariance-based contact predictions are likely to rank homolog templates accurately if the alignments contain at least 5 L nonredundant sequences; if the alignment samples sequences closer to the query than the homolog, these predicted contacts should be useful for building improved structure models. We determined how frequently this scenario occurs by studying the large set of protein families in the Pfam database.

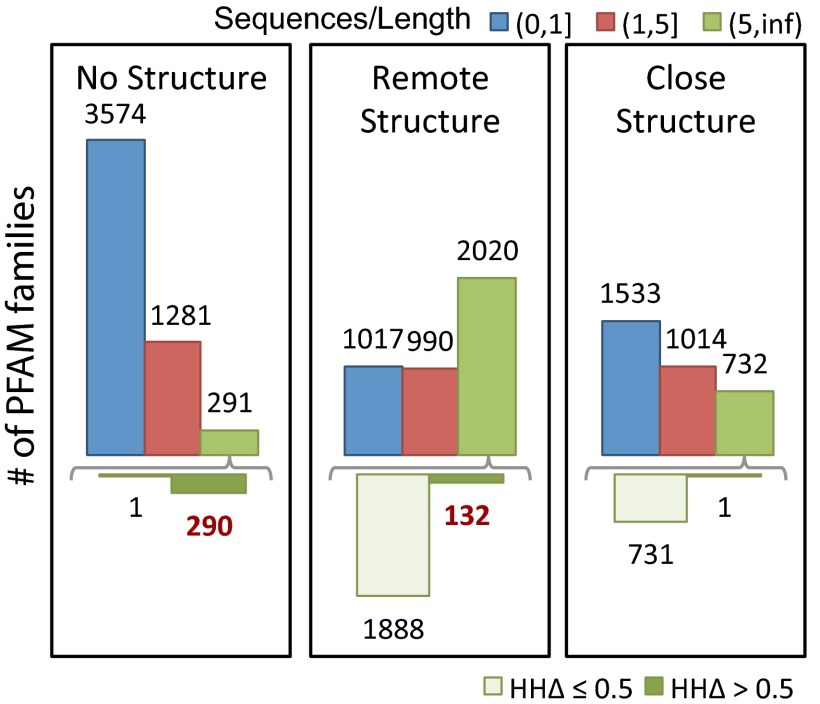
We classified families with at least 50 residues into three groups (SI Appendix, Fig. S2): insignificant homology to protein of known structure, remote homology to known structure, and close homology to known structure, based on HHsearches against the PDB (Fig. 4, Left, Center, and Right). We subdivided these groups based on the number of sequences in the family; the number with more than 5 L sequences, for which contact predictions are likely to be accurate, is indicated by the upper green bars. This subset of families was further subdivided based on (Fig. 4, Lower); as above, an 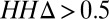(Fig. 4, lower dark green bars) indicates that an alignment constructed from the sequences in the family is significantly more similar to itself than to an alignment constructed from the closest homolog of known structure in the PDB, in which case predicted contacts are likely to be useful for structure prediction. The cases of interest, where predicted contacts are likely to be accurate and useful, are indicated in red text in the lower panel. Overall, the number of families for which predicted contacts are likely to be useful is small but not insignificant (422/12,452) and corresponds to roughly 14% of the families with adequate number of sequences [Dataset S4; this is likely a conservative estimate—the improvement in accuracy with the SVM prior could allow improved structure prediction for families with as few as 2.5 L sequences (SI Appendix, Fig. S8)]. Predicted contacts are likely most useful for membrane proteins (12, 15), protein assemblies (16), and other systems where high-resolution structural information is currently sparse.

Fig. 4.

Frequency of utility of contact prediction. The protein families in the Pfam database were divided into three groups based on the HHsearch P value of the closest protein of known structure (Left, HHsearch P value > 10^−6.5; Middle, HHsearch P value between 10⁻⁴⁰ and 10^−6.5; Right, HHsearch P value > 10⁻⁴⁰). Within each group, the number of families with sequences/length less than 1, between 1 and 5, and greater than 5 are shown in blue, red, and green, respectively (Upper bars). For families with > 5 sequences per position (Upper green bars), distribution of to the closest protein of known structure is shown in the lower panel. In cases where the difference in profiles is large (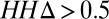: right bar in each group, Lower), these predictions are likely to improve on comparative models.

Conclusion

We have shown that integrating coevolution and predicted structure feature-based information using a pseudolikelihood approach improves accuracy of residue–residue contact prediction. Analysis of the accuracy and utility of predicted contact information suggests that a large fraction (24%) of the families in the Pfam database currently have enough sequences for contact prediction to be accurate. This fraction is likely to increase as high-throughput sequencing continues to rapidly expand the sequence databases and methods for contact prediction continue to improve. However, predicted contacts are likely to be currently useful for structure prediction only for a relatively small fraction of these proteins (14%); how this fraction evolves in the future depends on the relative rates of increase of the sequence and structure databases.

Methods

Overview of Computational Method.

GREMLIN uses a global statistical model with the following functional form:

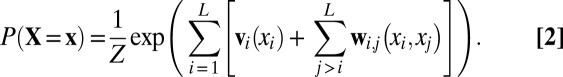When learned from a multiple sequence alignment of related proteins, as first described in ref. 17, the random variables 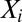represent the amino acid composition at position i, 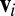is a set of parameters of the distribution that encodes the individual propensity for each amino acid at position i of the protein, and 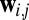is the set of parameters modeling the statistical coupling in amino acid propensities between positions i, j of the protein. Z, the partition function, is a global normalizer to ensure the probabilities sum to 1. This is a maximum-entropy model and is also referred to as a Markov Random Field (5).

Given a set of aligned protein sequences, one approach to learning v, w is by matching the moments of the distribution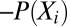, 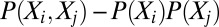etc.—to the corresponding empirical correlations 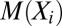, , 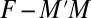etc., observed in the alignment. Solving these equations exactly results in a consistent learning procedure—in the limit of infinite data, the learnt parameters tend to the true parameters. For the model in Eq. 2, however, determining the exact solution is computationally intractable. DCA uses a Taylor series expansion of Eq. 2 (SI Appendix, Learning) and a mean-field approximation on the truncated Taylor series. The parameters under this approximation are then solved by inverting a covariance matrix (2). PSICOV uses a different sequence of approximations by first constructing a distribution with binary indicator variables and then using the approach of ref. 18 to relate the properties of this distribution to those of a related Gaussian distribution. Although PSICOV does not explicitly match moments, the resulting learning procedure also estimates Ω; DCA uses a large pseudocount to ensure that the inverted matrix is not singular (thus being similar to 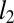regularization) and PSICOV directly estimates the inverse with a mixture of 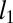and 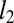regularization (3).

The GREMLIN Learning Algorithm.

GREMLIN uses a learning procedure based on optimizing the pseudolikelihood (5) of v, w, which, in log space is expressed as the sum of conditional distributions as follows:

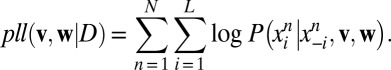Each conditional distribution models the probability of the observed amino acid at position i in the 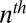sequence of the alignment, 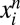, in the context of the amino acids at all other positions in that sequence, 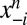and depends on the parameters v,w as:

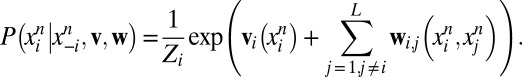The pseudolikelihood models the conditional distributions of the original joint distribution instead of the joint distribution itself. The global partition function cancels out in the conditional distribution leaving only a per-position local partition function 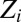that is trivial to compute making the pseudolikelihood tractable; it is also concave in v, w making it easy to maximize. Estimating the parameters by maximizing the pseudolikelihood is a consistent procedure (19).

Regularization and Priors.

The GREMLIN learning objective includes a regularization term of the form:

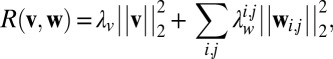where 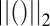refers to the 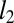vector norm of the parameter and 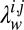defines a Gaussian prior probability with zero mean and 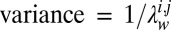on the entries in 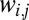. When all 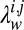have the same value as in ref. 6, the learning procedure relies completely on the data to encode any information specific to protein topologies. In data-scarce settings, the accuracy of the learning procedure can be boosted by varying 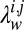to favor residue pairs that are likely to be in contact according to our prior knowledge of protein topologies. We do this using a per-residue pair 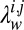that depends on 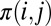, the prior probability of i, j being in contact as follows:

This framework is flexible and allows incorporation of prior information from various sources. We experimented with two priors: a simple prior based on secondary structure and sequence separation, 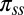(SI Appendix, Fig. S6), used by default and 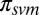, obtained by treating the probability of being in contact as estimated by SVMCON (10) as a prior. Here, 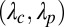were set to (0.20, 0.20) for 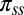and to (0.20, 1) for 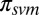based on tests with a set of targets from CASP9.

GREMLINΔ.

We define the GREMLIN score of a structure as

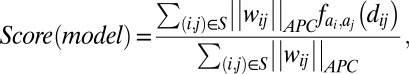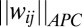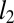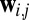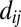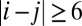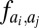
where is the APC-corrected norm (8) of as computed by GREMLIN; is the distance between the Cβ atoms of the corresponding residues in the model with amino acids a_i, a_j; and S is the set of the top L-predicted contacts with . 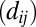is 1 if 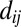is less than a cutoff which depends on the amino-acid pairs a_i,a_j, and 0 if d_ij is very large (Dataset S5). Using the top L-predicted contacts ranks structures better than using fewer contacts (SI Appendix, Fig. S3); increasing this to a larger number does not improve results significantly. We define GREMLINΔ as

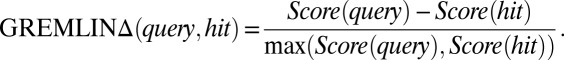The GREMLINΔ of a set of models is the lowest GREMLINΔ in the set.

HHΔ.

We used the Viterbi scores 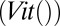as computed by HHalign (20) to determine if the alignment of sequences was closer to the query protein than a homolog.

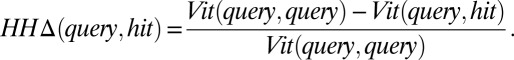Materials

CAMEO Targets.

The CAMEO webserver of the Protein Model Portal (7) evaluates the accuracy of structure prediction methods against recently released structures from the PDB on a continuous basis. The ROSETTA structure prediction software had predicted the structure of 440 targets at the time we performed this study (first date: 27 April 2012). For targets with fewer than 700 residues, we generated alignments using HHblits, discarding those that had less than L-nonredundant sequences and targets that had very similar sequences (>90% identity) to other targets in this set, resulting in 329 targets (Dataset S1). These targets had a broad diversity of folds, sizes (mean:253, min:60, max:620) and alignment depths (mean:5516, min:100, max:30107 nonredundant sequences) reflecting the diversity of the PDB.

CASP10 Targets.

We selected the 67 targets (Dataset S3) from the recently concluded CASP10 experiment with more than L nonredundant sequences.

Hard Targets.

To compare the effects of prior information on accuracy, we collected an additional set of 73 targets that do not have homolog structures in the PDB (Dataset S2).

Pfam.

For protein families in the Pfam database [ref. 21; version 26] with at least 50 positions, we constructed alignments using HHblits and queried the PDB for homologs using HHsearch starting with precomputed models (from the HHSearch database; ref. 22).

PISCES.

We accessed the PISCES database of nonredundant protein structures (23) (accession date November 3, 2012; sequence identity: 80%, minimum resolution: 2.0 Å, maximum : 0.25). We used statistics collected on this database to determine the secondary structure prior, π_ss (SI Appendix, Fig. S6) and the amino-acid specific distance function 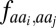(Table S5).

DCA.

We used the default settings as in (2): .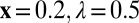

PSICOV.

We used the suggested flags that determine ρ to achieve a target density: -p, -d 0.03.

MIc.

MIc is a mutual information-based method that uses sequence profile information and sequence weighting in its computation of a score referred to as MIc. All our reported results use the default flags (24).

PLMDCA.

We used the default settings of .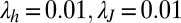

SVMCON.

We used SVMCON with the default settings.

Entropy Correction via APC.

The average product correction (8) was suggested as a way of correcting for entropic and phylogenetic biases in the sequence alignment. Although originally used for mutual information-based scores, it has also been used with norm-based scores in PSICOV (3). We applied this correction to GREMLIN and DCA as we found that it uniformly improved their accuracy; PSICOV, PLMDCA and MIc apply it by default.

Sequence Reweighting.

DCA, PSICOV and PLMDCA reweigh sequences in the input multiple sequence alignment to account for redundancy (2, 3, 6). When making predictions using GREMLIN, we reweigh sequences in a filtered alignment (filtered at 90% sequence identity) instead of using the full alignment.

HHsuite.

We used HHblits to build the alignment from the clustered uniprot database (dated Mar 2012) with the following options in addition to default settings: -nodiff, -neffmax 20, -n 4, and -maxfilt 100,000. To ensure consistency of coverage across the alignment, we removed sequences that had more than 25% gaps compared with query and sites that had more than 25% gaps. In addition, for GREMLIN, we postprocessed the alignment using HHfilter to generate a nonredundant alignment at 90% sequence identity. We queried the PDB using the global alignment mode of HHsearch and the latest PDB database (date: January 1, 2012), which preceded the participation of ROSETTA in CAMEO and CASP10. We used HHalign to compute Viterbi scores. These programs are part of HHsuite (version: 2.0.15) (20).