Model of T-Cell Nuclear Deformation by the Cortical Actin Layer

Abstract

Deformations of cell nuclei accompany a number of essential intracellular processes. Although evidence is being accumulated on the primary role actin structures play in controlling the shape of the nucleus, the mechanisms behind this phenomenon remain unknown. Here, we consider theoretically a specific paradigm of nuclear deformation, and a related actin rearrangement, in T cells stimulated by contact with a bead covered by surrogate antigens. We suggest that the nucleus is deformed by the elastic forces developed within a cylindrical layer of polymerized actin, which is generated as a result of the receptor-mediated T-cell activation. We substantiate this proposal with a theoretical analysis of mutual deformations in the actin layer and the nucleus, which recovers the experimentally observed nuclear shapes. Furthermore, we evaluate the forces developed by the actin polymerization that drives the nuclear deformation. The model predicts the mode of actin polymerization generated by the surrogate antigens covering a bead and the values of the elastic moduli of the nuclear shell. We provide a qualitative experimental support for the model assumptions by visualizing the stages of nuclear shape change and the corresponding evolution of the cortical actin.

Introduction

Emerging evidence indicates the importance of mechanical behavior of the nucleus (1,2). Such behavior includes the elastic deformation and restoration of nuclear shape in processes such as stem cell differentiation, development, homeostasis, and regulation of gene expression (3–7). Actin plays an important role in regulating nuclear shape in these different systems. Embryonic stem cells have round nuclei and lack defined actin stress fiber organization, but the induction of differentiation is accompanied by progressive formation of a perinuclear actin cap (8,9). Furthermore, the induction of pluripotency in differentiated cells is accompanied by the elimination of the actin cap (8). In developing Drosophila embryos, the nuclear shape is spherical during early blastoderm stages, but postcellularization it becomes elongated (3,4). In adherent cells, the perinuclear actin cap exerts a compressive load on the nucleus and gives it a defined shape. Disruption of these actin fibers results in a bulging of the nucleus and an increase in its height (10). In addition, depolymerization of actin or microtubules perturbs the nuclear shape as, under normal conditions, these two cytoskeletal components apply compressive and contractile forces, respectively, on the nucleus (11). Supporting this, an alteration of cytoskeletal organization in endothelial cells was observed after plating them on defined micropatterns that correlated with nuclear shape and volume (12,13). To stabilize nuclear morphology, the actin cytoskeleton is linked to the nuclear lamina and chromatin via the SUN and KASH domain proteins (14,15). Disruption of these links results in disturbed organization of the perinuclear actin and nuclear morphology, as well as impaired transmission of mechanical forces to the nucleus (14). Together, these observations highlight the importance of actin-mediated regulation of nuclear shape and its genomic functions. At the same time, the physical mechanism of this phenomenon remains unknown.

A convenient system for studying the physics of nuclear shape change, as mediated by the actin cytoskeleton, is represented by activated T cells. T cells are nonadherent and have little polymerized actin in them. Upon stimulation of their T-cell receptors by antigen-presenting cells (APCs), the T cell’s actin undergoes massive polymerization (16,17). In cells plated on surrogate antigen-coated coverslips, this leads to the generation, at the cell periphery, of submembrane actin-rich rings. These are associated with the extension of lamellipodia and cell spreading (18).

Recently, we studied the changes in nuclear shape that resulted from T-cell activation by antibody-coated paramagnetic beads, whose 4.5 μm size imitated that of the antigen-presenting cells (19). Upon binding of the beads to a T-cell surface, both the cell and its nucleus underwent substantial elongation. We presented evidence to show that polymerized actin, rather than microtubules or actomyosin contractility, were responsible for this phenomenon (19). These studies clearly indicated the importance of the actin cytoskeleton in regulating nuclear shape and size. However, the specific mechanisms of this phenomenon remained unexplored.

Here, we propose a quantitative mechanical model using antigen-coated beads to account for nuclear shape changes driven by the actin cytoskeleton during T-cell activation. We suggest that nuclear deformation is induced in this system by a submembrane cortical actin layer that undergoes remodeling into a hollow cylindrical shape after T-cell receptor activation. The hollow actin cylinder subsequently grows as a result of polymerization at the cell-bead interface and engulfs the nucleus. This leads to an elastic deformation of the latter into an elongated shape.

We substantiate this model by presenting a computational analysis of nuclear deformation induced by a cylindrical actin layer that was characterized by realistic actin density values, and elastic parameters. The model reproduces the observed shapes of deformed nuclei and makes predictions about the mode of actin polymerization, triggered by the activated T-cell receptors, and also about the values of elastic moduli of the nuclear envelope. We present partial experimental support of the model assumptions by visualizing the distribution of polymerized actin within the cell and its nucleus, when in the deformed state.

Qualitative Model

Based on the observations above, and the existing phenomenology on T-cell-activation-induced actin polymerization (16,17), we propose a model to explain nuclear deformation after T-cell stimulation by a bead coated with surrogate antigens. Activation of cell receptors results in a massive repolymerization of actin at the bead-cell interface. This is accompanied by remodeling of the submembrane actin network. The repolymerization of actin gives rise to an actin layer that has the shape of a hollow cylinder. The base of the cylinder rests on the circular cell-bead interface and the cross-section dimension is determined by the bead size (Fig. 1). Since the nuclear radius is larger than the internal radius of the growing actin cylinder, the nucleus and the actin layer mutually deform. The nucleus becomes compressed by the actin layer and elongated in the direction of the cylindrical axis. The actin layer, on the other hand, is bulged by the nucleus and its thickness changes as a result of the bulging deformation.

Figure 1.

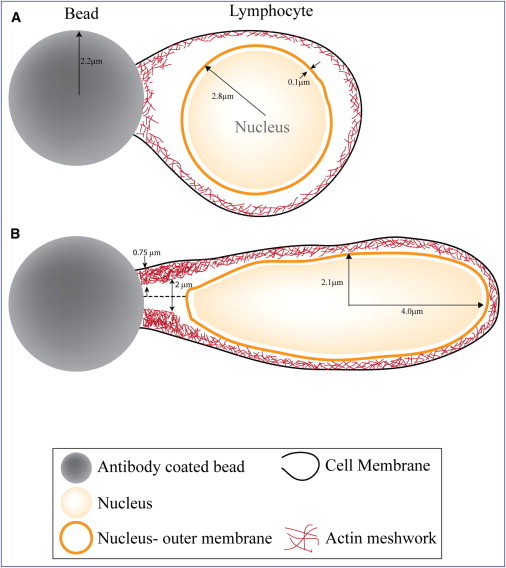
Illustration of the process of nuclear deformation in T cells. (A) Initial contact between bead and T cell. (B) Onset of actin polymerization and nuclear deformation.

We suggest the following specific scenario for the intermediate stages during the evolution of the system. After receptor activation, the actin cylinder starts growing from the cell-bead contact zone, where new actin monomers are added to the filaments constituting the layer. It subsequently elongates until its free edge reaches the nucleus. During the next stage of cylinder growth, the nucleus is pushed by elongating the actin cylinder’s free edge toward the cell pole opposite the bead until it touches the plasma membrane. The subsequent stretching of the plasma membrane prevents further movement of the nucleus. At the next stage, the continuously growing actin cylinder engulfs the nucleus, leading to deformations of both the nucleus and the actin cylinder. The forces pushing the actin cylinder, and enabling the nucleus and actin layer deformations, are produced by actin polymerization at the cell-bead interface.

Our goal is to compute the mutual elastic deformations of both the cylindrical actin layer and the nucleus. By comparing the calculated nuclear shapes with the observed ones, we will determine the elastic characteristics of the nuclear envelope and estimate the forces generated by actin polymerization at the cell-bead interface.

Physical Model and Computational Analysis Strategy

We model the preferred shape of the polymerizing actin layer as an elastic cylindrical layer with a thickness of 0.75 μm and an internal radius of 1 μm (Fig. 1). The images supporting this assumption are presented in the Experimental Support section below. The elastic moduli of the actin network constituting the layer are taken to correspond to the average values determined for actin gels: E = 10 kPa for Young's modulus (20–22) and ν = 0.4 for the Poisson ratio (23–25).

The nuclear shell is modeled to be spherical in its relaxed state with the internal and external radii equal to 2.7 μm and 2.8 μm, respectively. The elastic moduli, E_s and ν_s, of the lamin network constituting the shell have not been directly measured and therefore will be considered as free parameters whose values will be found from fitting the experimental data.

We do not assume constancy of either the outer area of the elastic shell representing the nucleus or the volume bound by this shell.

The technical complexity of the analysis is twofold. First, the diameter of the spherical shell representing the nucleus is about three times larger than the inner diameter of the actin cylinder. As a result, either the shell or the cylindrical layer, or both of them, must undergo a large deformation leading to strain, with characteristic values that can be estimated as ${\epsilon }_{\langle \theta \theta \rangle }=u_r/r\sim 50-120\%$, where r and θ denote the radial and angular coordinates in the cylindrical coordinate system related to the symmetry axis of the actin layer, and u_r is the radial component of the displacement vector (26). Hence, the deformation analysis cannot be performed in the linear elastic regime and we use a Neo-Hookean hyperelastic model (27) implemented with the finite-element method (see Supporting Material).

The second complexity is related to the fact that, according to the observations, both the shell representing the nucleus and the cylindrical actin layer are strongly deformed, meaning their effective rigidities are comparable.

The computations have been performed by using Comsol Multiphysics software as described in the Supporting Discussion.

Experimental Support

To support the model assumptions, we stimulated T cells in vitro by incubating them with surrogate antigens that activate T-cell receptors, namely, αCD3 and αCD28 antibodies (see Supporting Material, for the experimental methods used). For our experiments, we used 4.5-μm-sized superparamagnetic polymer beads that are coated with these surrogate antigens. It has previously been shown that T-cell activation resulting from such stimulation is very similar to that occurring in in vivo conditions (28). Naïve T cells were isolated from H2B-EGFP transgenic mice and activated with antibody-conjugated beads. The resulting whole-cell and nuclear shape transformations were recorded as movies (Movie S1). Time-lapse images of one such representative experiment are shown in Fig. 2. To assess the organization of actin in cells at different stages of the deformation process, rhodamine-phalloidin was used to label the polymerized actin (F-actin). The changes in shape of the polymerized actin layer, corresponding to the stages of both nuclear and cell deformation, are presented in Fig. 3. As shown in Figs. 2 and 3, the cell and the nucleus have nearly spherical shapes before stimulation (Fig. 2) while F-actin forms a thin shell between the cell surface and the nucleus (Fig. 3). After the establishment of a contact between the cell and the bead, both the nucleus and the cell become progressively more elongated (Fig. 2). Also, the polymerized actin layer undergoes a considerable rearrangement (Fig. 3), adopting an elongated shape engulfing the nucleus. In the region between the bead interface and the nuclear contact, the actin layer appears as a hollow cylinder with a cross-sectional radius increasing toward the nucleus (Figs. S1 and S2). The thickness of the actin layer is nonhomogeneous. This was established by drawing a line over the actin images and calculating the full width at half maximum from the corresponding intensity plot to a diffraction-limited resolution (Fig. S2). In the region close to the cell-bead contact, the layer is considerably thicker than in the initial state preceding cell activation and becomes thinner near, and surrounding, the nucleus (Fig. S2). The deformation and rearrangement of the whole system occurs within a few hundred seconds after the formation of a contact.

Figure 2.

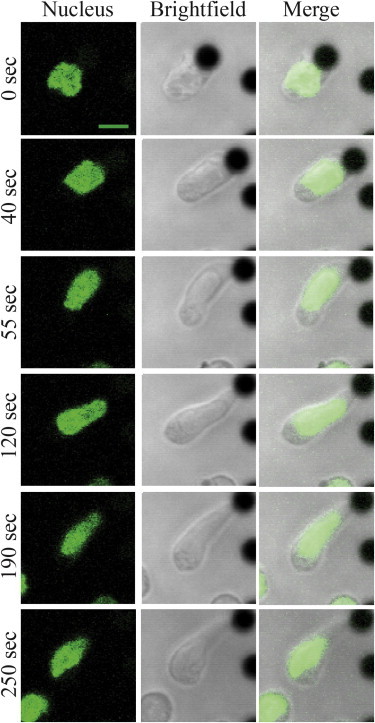
Representative time-lapse images of a naïve T cell during activation with an antigen-coated bead. Green, H2B EGFP nucleus; antigen-coated beads-black. Scale bar, 5 μm. To see this figure in color, go online.

Figure 3.

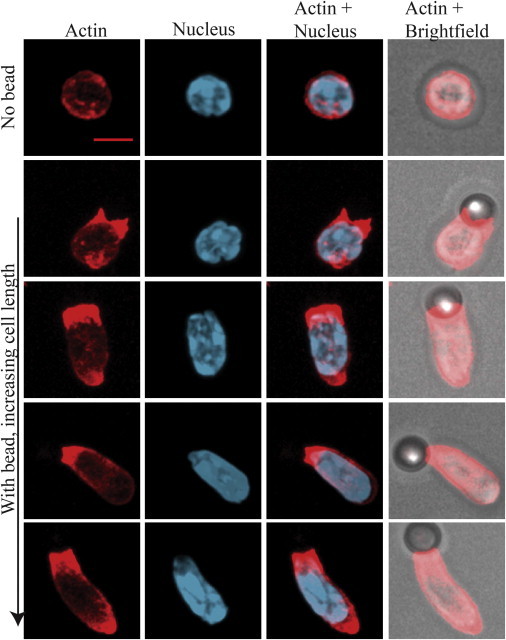
Three-dimensional projection image of actin (red), nucleus (blue), and bright field in a cell without bead (No bead) and cells activated with beads and at different extents of nuclear deformation (With bead, increasing cell length). Scale bar, 5 μm. All images were acquired 30 min after incubating cells with beads. The orientation of actin structure and nucleus should be noted with respect to bead position seen in the bright-field image. To see this figure in color, go online.

Results

Equilibrium shapes and elastic moduli

The shapes that were computed for the elastic shell representing the nucleus, and for the engulfing cylindrical elastic layer representing the hollow actin cylinder, are shown for gradually increasing values of the Young's modulus of the shell, E_s (Fig. 4). The color code corresponds to values of the elastic energy density measured in kJ/m³. Using the entire collection of computed equilibrium shapes for different values of the elastic modulus, E_s and ν_s, we generated two diagrams that describe the expected values of semiaxes of the deformed shell’s final shape (Fig. 5). The first diagram (Fig. 5 A) displays axes in absolute values, whereas the second diagram (Fig. 5 B) shows the same data as a dimensionless ratio of the polar and equatorial radii.

Figure 4.

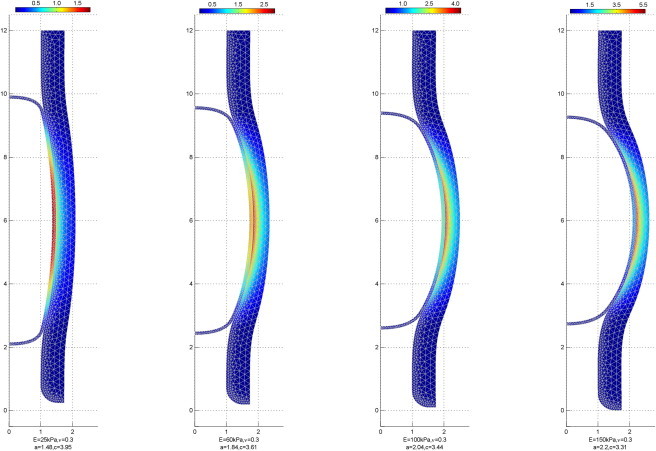
Equilibrium shapes (cross-sectional view) of the nucleus and the actin tube for increasing values of the Young's modulus of the nucleus, E_s = 25, 60, 100, and 150 kPa at ν_s = 0.3. The values of the corresponding nucleus semiaxes: equator radius, a, and polar radius, c, are represented in μm below each image. Color bars represent the volume density of the elastic energy measured in kJ/m³. To see this figure in color, go online.

Figure 5.

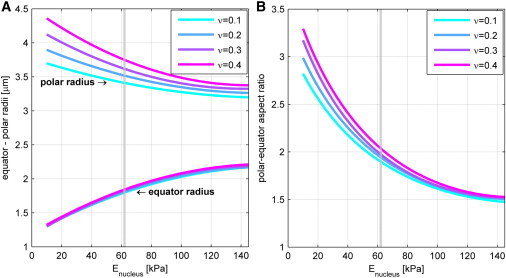
Computed dimensions of the nucleus in the semiellipsoidal approximation as a function of the elastic moduli E_s and ν_s. (A) Absolute values of the semiaxes of the final deformed nucleus. (B) Ratio of the polar radius to the equator radius. The gray dotted line represents the average observed ratio of the axes of the deformed nucleus (2:1) that corresponds to E_s ∼ 60 kPa and ν_s > 0.3.

The obtained shapes have to be compared with the typical shape of the experimentally observed deformed nuclei (see Experimental Support) (Fig. 6). The maximum aspect ratio of experimentally observed deformed nuclei is close to 2:1 (Figs. 6 B and S3). The best fitting of the computed shapes to observed shapes (Fig. 6 A) predicts the shell elastic moduli to be E_s ∼ 60 kPa and ν_s > 0. 3. The value obtained for the Young’s modulus, E_s, can be compared with the results from previously reported experiments on giant Xenopus oocytes, according to which the value of the two-dimensional Young’s modulus of the nuclear envelope is ∼25 mN/m (29). For our system, an effective two-dimensional Young’s modulus of the nuclear envelope can be obtained by integrating the determined value of E_s over the ∼100 nm thickness of the elastic shell, which gives ∼6 mN/m. Hence, the nuclear envelope of T cells appears to be somewhat softer than that of Xenopus oocytes, which may have numerous causes, including a difference in the thickness and density of the lamin layer.

Figure 6.

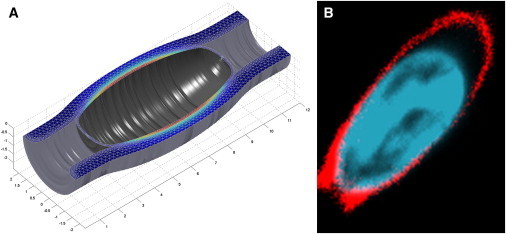
Fitting of the computed nuclear shape to the observed shape for the axis ratio 2:1. (A) Computed shape for E_s ∼ 60 kPa and ν_s > 0.3 created by rotation of the second image from the left in Fig. 4. (B) Observed shape with fluorescence imaging corresponding to the same axis ratio. Red, actin; blue, nucleus. To see this figure in color, go online.

In addition to overall deformation, our model predicts that the actin layer has to undergo a substantial reduction of thickness in the regions contacting the nucleus. According to our computations, because of the bulging deformation, the thickness of the actin layer changes from 750 nm at the cylinder base, which lies on the cell-bead interface, to values ranging from 500 nm (for a soft nucleus with E_s = 50 kPa) to 400 nm (for a stiff nucleus with E_s = 150 kPa) in the regions where the actin cylinder contacts the nucleus. These values are in agreement with the data presented in the Experimental Support section above, where the actin layer thickness changes from 750 nm at the actin cylinder base to 410 ± 92 nm at the nucleus contact point (Fig. S4). This agreement provides an additional substantiation of the values obtained for the elastic moduli of the nuclear shell.

The force provided by actin polymerization

In our model, the force, f, pushing the cylindrical actin layer toward the nucleus and driving the engulfment of the nucleus and its deformation is produced by actin polymerizing against the cell-bead interface. This occurs by a mechanism analogous to that of force generation at the leading edge of a moving cell (30,31). A qualitative consideration shows that the force needed to deform the nucleus continuously increases during the early stages of the engulfing process and reaches its maximal value, f_max, when the free edge of the actin cylinder attains the equator of the nuclear shape. The further stages of engulfing require lower values of force, and the force vanishes with completion of the nucleus coverage by the actin layer. Hence, the force requirements of nucleus engulfment and deformation are determined by the maximal force, f_max.

Calculation of the force values needed for the intermediate stages of the engulfing process turned out to be technically unfeasible (see Supporting Material). However, we were able to compute the equilibrium shapes of the nucleus and the actin layer corresponding to complete engulfment. Our analysis showed that these shapes represent a good approximation for the shapes corresponding to half engulfment and therefore can be used for calculation of the maximal force, f_max (see Supporting Material). The values of f_max computed in this approximation are presented in Fig. S8 A in dependence on the Young’s modulus of the nuclear shell, E_s. For the relevant values of E_s = 60–100 kPa, the predicted force constitutes ∼10 nN.

The obtained values of the force f_max enable an estimation of the required density of actin filaments within the cylindrical layer. We assume that each actin filament end polymerizing against the cell-bead interface develops a 1 pN force. This implies that the polymerization force is close to the stalling value of 0.8–1.5 pN (32), because of the substantial resistance to the polymerization process provided by deformation of the actin layer around the nucleus. Based on the measurements, we take the ringlike cross-section area of the cylindrical actin layer at the interface with the bead to be ∼6.5 μm². According to our computations, creation of the best-fitted nuclear shape requires the generation of 7.6 nN total force, which corresponds to E_s ∼ 60 kPa and ν_s > 0.3 for the elastic moduli of the nuclear shell. Using the numbers above, we estimate the amount of actin filament ends, ρ_a, that have to polymerize against a unit area of the actin-layer-bead interface to be ρ_a = 0.0012 nm⁻² (see Fig. S8). The value obtained is of the same order of magnitude as the surface density of actin filament ends polymerizing against the leading edge of lamellipodia in moving cells.

Discussion

The major proposal of this study is that changes observed in the shape of the nucleus in T cells activated by adhesion to antibody-coated beads are driven by a repolymerization of the cortical actin layer. This repolymerization results from the activation of T-cell receptors by the surrogate antigens coating the bead.

Specifically, we suggest that activated receptors at the cell-bead interface trigger polymerization of actin filaments, which subsequently form a cylindrical cortical layer that grows within the cell, from the bead towards the nucleus. Since the inner diameter of the actin layer is smaller than that of the nucleus, the layer first pushes the nucleus to the cell plasma membrane, which then retains the nucleus at a fixed position. Further growth of the actin cylinder drives an engulfment of the nucleus, which results in mutual deformation of both the actin cylinder and the nuclear shell and generates strains and elastic stresses within them. Furthermore, the plasma membrane also becomes stretched and stressed.

The proposal of this model was motivated by the results of previous experimental studies that demonstrated, using the drug blebbistatin to inhibit myosin II, or nocodazole to interfere with the polymerization of microtubules, that nuclear deformations are only minimally affected by the inhibition of myosin II motors (19). At the same time, polymerization of actin was essential for nuclear deformation, since treatment with cytochalasin D inhibited this process.

We substantiated this proposal with computations demonstrating that the experimentally observed nuclear shapes, as well as the shape of the surrounding layer of polymerized actin, can be explained based on a purely elastic model. These shapes result from an interplay between the elastic stresses developed within a cylindrical actin layer, which represents the repolymerized cortical actin, and an elastic shell, which represents the nucleus. According to the model, the force responsible for generation of these stresses and deformations is produced by actin polymerization at the cell-bead interface. Computation of this force (∼7.6 nN) from fitting the theoretically predicted nuclear shapes to those observed, and a related estimation of the required actin filament density within the cylindrical layer (∼0.0012 polymerizing filament ends/nm² of the cell-bead interface) indicated that the layer has to be approximately as dense as the familiar actin networks being formed, for example, in the lamellipodia of moving cells.

We provide experimental support for some of the assumptions made in the model by visualizing, in parallel with the changes in nuclear and cell shape, the structural transformations of the actin cytoskeleton. We provide evidence that, indeed, upon receptor activation, actin undergoes massive polymerization next to the cell-bead interface, and the resulting actin layer can be presented as a cylinder that is partially deformed because of nuclear engulfment and has the predicted homogeneity in thickness.

It is tempting to speculate that the stretching of the plasma membrane, which accompanies the whole process, might play a role in a periodic relaxation, and subsequent new deformation, of the nuclear shapes observed in T cells (19). Stresses generated in the plasma membrane may result in the opening of mechanosensitive calcium channels within the membrane, which would in turn trigger depolymerization of the actin cylinder, and restoration of the initial nuclear and cell shapes. The following relaxation in the stress of the membrane would result in closure of the calcium channel and renewed polymerization of the actin cylinder from the cell-bead interface and hence would initiate a new cycle of nuclear deformation.

It has to be noted that, according to our computations, the deformation of the nuclear shell was accompanied by a shrinking of its external area. This implies an emerging area mismatch between the lamin network constituting the shell and the nuclear envelope. We suggest that this mismatch results in the nuclear envelope folding between discrete spots where it is connected to the lamina. According to our estimations, the overall bending energy of the nuclear envelope membrane that results from such folding is about three orders of magnitude lower than the lamina compression energy and therefore can be neglected.

In conclusion, we emphasize that our work should not be seen as a thorough cell biological study providing full experimental proof of the mechanism, but rather as a theoretical biophysical study that suggests, to the best of our knowledge, a novel mechanism and substantiates it computationally.