Hazard Regression Models of Early Mortality in Trauma Centers

Abstract

Background

Factors affecting early hospital deaths after trauma may be different from factors affecting later hospital deaths, and the distribution of short and long prehospital times may vary among hospitals. Hazard regression (HR) models may therefore be more useful than logistic regression (LR) models for analysis of trauma mortality, especially when treatment effects at different time points are of interest.

Study Design

We obtained data for trauma center patients from the 2008–9 National Trauma Data Bank (NTDB). Cases were included if they had complete data for prehospital times, hospital times, survival outcome, age, vital signs, and severity scores. Cases were excluded if pulseless on admission, transferred in or out, or ISS<9. Using covariates proposed for the Trauma Quality Improvement Program and an indicator for each hospital, we compared LR models predicting survival at 8 hours after injury to HR models with survival censored at 8 hours. HR models were then modified to allow time-varying hospital effects.

Results

85,327 patients in 161 hospitals met inclusion criteria. Crude hazards peaked initially, then steadily declined. When hazard ratios were assumed constant in HR models, they were similar to odds ratios in LR models associating increased mortality with increased age, firearm mechanism, increased severity, more deranged physiology, and estimated hospital-specific effects. However, when hospital effects were allowed to vary by time, HR models demonstrated that hospital outliers were not the same at different times after injury.

Conclusions

HR models with time-varying hazard ratios reveal inconsistencies in treatment effects, data quality, and/or timing of early death among trauma centers. HR models are generally more flexible than LR models, can be adapted for censored data, and potentially offer a better tool for analysis of factors affecting early death after injury.

INTRODUCTION

Most of the deaths due to serious injuries occur in the first few minutes after the traumatic event.(1, 2) For patients who survive until contact with the emergency medical services (EMS) system, prehospital and hospital care may reduce mortality, and differences in the quality of that care may produce measurable differences in how much mortality is reduced. However, interventions may have complex and potentially time-variant effects on the relatively crude outcome measures commonly analyzed. For example, if arrival at a hospital is delayed, fewer patients will survive until admission, but those that do arrive will be less likely to die subsequently, so differences in the quality of hospital care may have a lesser effect on the total number of deaths. Attempts to evaluate differences in outcome among trauma centers and trauma systems, especially those restricted to hospital registry data, should properly take into account such differences in the timing of hospital intervention.

Hazard regression (HR) models are a logical way to evaluate an outcome whose occurrence at a specific time is of interest. HR models are most familiar to clinicians involved in the care of cancer or other conditions where survival is measured in months or years, but the same mathematics can be applied to conditions where survival is measured in minutes or hours. In either case, HR models can be adapted to situations where patients are observed only during a portion of the time span, or where the effects of different covariates change over time. For acute injuries, the instantaneous risk of death is most strongly affected by time from the trauma event (so it makes sense to base a HR model on this time scale) but a hospital cannot affect the risk until the patient has been received alive (so it makes sense for the HR model to incorporate hospital effects only after this point, and not necessarily assume they are constant).

Several authors have suggested that trauma deaths occurring early in the course of hospital care should be considered separately from trauma deaths occurring later,(3–5) and it is certainly possible that the quality of care at a given hospital might vary, for example, between the emergency room and the operating room. It would be possible to construct separate logistic regression (LR) models for early and late deaths, but this might be cumbersome and would still not allow for variable periods of observation, interhospital transfers, and other types of censored data. On the other hand, HR models allow the effects of covariates (including individual hospitals) to vary over time in a flexible way that can incorporate as many different time periods as might be of interest. By extension, the same principles can be applied to care in the prehospital phase, if sufficient data on prehospital care become available.

The purpose of this study was to consider the use of HR models as a method for evaluating the early care of injured patients, to confirm that results from a simple HR model are essentially equivalent to those obtained from a LR model, and to demonstrate how additional insights can be obtained from modifications of HR models that cannot be obtained from LR models.

METHODS

Data acquisition and inclusion criteria

Data on patients admitted to US trauma centers in 2008 or 2009 were obtained from the National Trauma Data Bank (NTDB) Research Data Set, in compliance with its standard Data Use Agreement. An Institutional Review Board at Maine Medical Center judged the study to be exempt from review because it used only existing anonymous data. NTDB was established by the American College of Surgeons (ACS) in 1994, and collects trauma registry data from hundreds of hospitals across the US. For the first time, the 2008 NTDB data included the number of minutes between EMS activation and hospital arrival (prehospital time, abbreviated t_p), and the number of minutes between hospital arrival and death or other disposition (hospital time, abbreviated t_h).

NTDB data files were converted for use with Stata (Version 11, StataCorp, College Station TX), and merged into a single analytic file. An outcome variable “died” was created if the patient either had an Emergency Room (ER) outcome of “Dead” or a hospital outcome of “Expired”. Injury Severity Score (ISS), maximum Abbreviated Injury Score for the head or abdominal regions (AIShead, AISabd), Glasgow Coma Scale motor score (GCSm), systolic blood pressure (BP), pulse rate (PR), age, mechanism of injury, and status as a transfer from another hospital were categorized as described for predictive modeling by the ACS Trauma Quality Improvement Program (TQIP).(6)

We excluded all data from hospitals that were not ACS-verified Level I or Level II trauma centers, hospitals where more than 1% of cases were missing vital status (dead/alive) at discharge, or hospitals with fewer than 200 cases recording an Injury Severity Score (ISS)(7) of at least 9. Individual cases were then excluded if they had an ISS that was less than 9 or invalid, if they were declared “dead on arrival” (DOA), if they had no pulse at the time of hospital admission, or if they were transferred out to another institution.

In order to enable consistent statistical analyses, remaining cases were excluded if they had been managed first in another hospital and then transferred to the trauma center, if prehospital time (t_p) could not be determined, or if the time until death (t_p +t_h) could not be determined for patients who died. If a hospital had fewer than 100 cases after this exclusion, all of its cases were excluded. Cases excluded only because of missing time data were compared to those that had not been excluded for this reason.

Brief statistical background

When an outcome of interest can be expressed as the time until an event occurs, "time-to-event" statistical methods are the standard analytic approach. Because the most common applications of these statistical methods anticipate the occurrence of an adverse event (e.g., death), this approach is often referred to as "survival analysis”. The outcome may be expressed as S(t), the probability that a subject will survive at least until time t.

A related concept is the “hazard” function h(t), which is the instantaneous probability at any given time that a subject (in our case, a patient) will experience the event in question at time t, given that they have not yet experienced the event. If we define an “integrated hazard” function

$$H(t)=\underset{0}{\overset{t}{\int }}h(u)du,$$

it can be shown that H(t) = −log(S(t)).

Hazard regression (HR) models consider h(t) to consist of some baseline hazard function, which may be expressed as h₀(t), multiplied at any time t by a factor that depends on individual characteristics (z₁, z₂, … z_n). Many applications are less concerned about the baseline hazard than the “hazard ratios” (or “incidence rate ratios”) which measure the impact of the various characteristics and whether they increase or decrease h(t).

A semiparametric (Cox) HR model makes no assumption about the form of the baseline hazard function, but assumes (subject to verification) that

$$\mathit{\text{log}}h(t)=\mathit{\text{log}}{h}_{\mathit{0}}(t)+b_1{z}_{\mathit{1}}+b_{\mathit{2}}{z}_{\mathit{2}}+\dots +b_n{z}_n.$$

Exponentiating both sides of the above equation gives

$$h(t)=(h_0(t))\left(e^{b_1{z}_1}\right)\left(e^{b_2{z}_2}\right)\dots \left(e^{b_n{z}_n}\right).$$

Thus, the factors (z₁, z₂, … z_n) have multiplicative or proportional effects upon the baseline hazard. One of the factors in a HR (or LR) model may indicate a specific hospital (1 if the patient was treated in this hospital and 0 otherwise); the coefficient associated with this indicator variable then measures the effect of that hospital, adjusted for the other patient-level variables.

When there is “left truncation” (in our case, deaths before hospital arrival), HR models can be constructed so that patients enter into the calculations only for the times during which they are actually under observation. The factors for a given patient and/or hospital (z₁, z₂, … z_n) may also be allowed to vary at different times, and their effects (b₁, b₂, … b_n) may also be modeled as constant or time-varying. The assumption of proportional hazards can be verified by obtaining a Kaplan-Meier estimate of S(t), calculating H(t) from the relationship shown above, and plotting H(t) for groups defined by the covariate of interest; under proportionality, these should be approximately parallel. If there are serious deviations from proportionality, the model can be broken up “piecewise” to reflect different effects in different time periods. These considerations allow great flexibility in the application of HR models.

Analysis for this study

An outcome of “early death” was arbitrarily defined as death occurring within a total elapsed time (t_p + t_h) no greater than 8 hours (480 minutes) after the injury event. Preliminary analyses also evaluated “early death” thresholds of 6 hours or 12 hours. Patients who died after the threshold time were considered “survivors” in the “early death” models. Since the data do not include any information about persons who were not brought to a hospital with detectable vital signs, those who are included consititute a left truncated sample of all trauma deaths, restricted to those who have survived long enough to reach a hospital. The Stata procedure “stset” allowed this structure to be incorporated in the HR models by designating the entry time as t_p and designating the exit time as the minimum of the time from injury until death or 480 minutes.

For included patients, a logistic regression (LR) model was first constructed as proposed for the ACS Trauma Quality Improvement Program (TQIP),(6) but using “early death” as an endpoint. In addition to the TQIP factors, the LR model included vital signs measured prior to hospital arrival (in addition to those measured at the time of arrival), prehospital time, and indicator variables designating each hospital. In order to maintain comparability with TQIP, we did not make any further modifications to variables or interactions. Using the same covariates included in the LR model, a HR model was constructed, censoring all observations at 8 hours.

For each hospital, LR and HR models were then constructed with an indicator variable for each index hospital. The coefficients estimated for the indicator variables in these models (relative to the other hospitals as a reference group) were interpreted as a log odds ratio and a log hazard ratio measuring the hospital effect on mortality, assuming that the effect was constant for each hospital. For each hospital, HR models were also constructed in which the hospital-specific hazards were estimated separately (piecewise) for the time periods 0–60 minutes, 61–120 minutes, and 121–480 minutes following the presumed time of injury. Each time-specific and hospital-specific hazard estimate was compared to the overall hospital-specific estimate as well as to the time-specific estimate (relative to the other hospitals as a reference group).

After completing the above analyses, the process was repeated including patients who had been transferred from another hospital. A variable indicating the transfer status of the patient (1 if the patient had been transferred and 0 otherwise) was added to the models as a covariate. For the transferred cases, t_p included time spent at the referring hospital, and entry time was specified as t_p in these models as it had been for the models that excluded transferred patients. In order to distinguish the effects of prehospital time with or without the involvement of a previous hospital, the interactions of categorized prehospital time and transfer status were also added as indicator variables in the models that included transferred patients. Results were then compared to the analyses that had excluded interhospital transfers.

RESULTS

The NTDB contained 226,734 records of patients admitted during 2008–2009 to an ACS-verified Level I-II trauma center, excluding institutions that had fewer than 200 patients with ISS of at least 9, or more than 20% with missing data. Of these 226,734 cases, only 85,327 (37.6%) were direct admissions that also had valid data for prehospital time, as well as time of death for patients who died.

Characteristics of the patients included in the principal analysis are summarized in Table 1. Among the excluded cases were 65,741 (30%) who had been transferred in from another hospital. Of the remaining 75,666 cases excluded for missing time data, there were 9,515 deaths (12.6%) compared to 3,019 deaths (3.5%) in the cases where time data were recorded. Patients excluded for missing time data were somewhat more likely to be older than 65 years (25.5% vs. 20.6%), less likely to be injured by firearm (7.6% vs. 8.0%), more likely to have a GCSm of 1 on admission (11.5% vs. 8.4%), but less likely to have a GCSm of 2–5 on admission (5.7% vs. 7.0%).

Table 1.

Patient Characteristics for the Analysis Sample, NTDB 2008–2009

	Died within 8 h (n=1,943)	Survived 8 h (n=83,384)	Total (n=85,327)
Died in hospital	1,943	1,076 (1.3%)	3,019 (3.5%)
Died within 8 h	1,943	0	1,943 (2.3%)
Age >=65 y	400 (20.6%)	17,215 (20.6%)	17,615 (20.6%)
Firearm injury	622 (32.0%)	6,238 (7.5%)	6,860 (8.0%)
ISS 25–75	1,214 (62.5%)	10,516 (12.6%)	11,730 (13.7%)
Head AIScat
AIS 1–2	129 (6.6%)	12,589 (15.1%)	12,718 (14.9%)
AIS 3–4	436 (22.4%)	26,221 (31.4%)	26,657 (31.2%)
AIS 5–6	643 (33.1%)	2,253 (2.7%)	2,896 (3.4%)
Abdomen AIScat
AIS 1–2	372 (19.1%)	16,066 (19.3%)	16,438 (19.3%)
AIS 3–4	550 (28.3%)	6,469 (7.8%)	7,019 (8.2%)
AIS 5–6	72 (3.7%)	553 (0.7%)	625 (0.7%)
Prehospital times
0–30 min	757 (39.0%)	17,669 (21.2%)	18,426 (21.6%)
31–45 min	626 (32.2%)	28,829 (34.6%)	29,455 (34.5%)
46–60 min	275 (14.2%)	19,366 (23.2%)	19,641 (23.0%)
61–90 min	227 (11.7%)	13,621 (16.3%)	13,848 (16.2%)
>90 min	58 (3.0%)	3,899 (4.7%)	3,957 (4.6%)
Prehospital physiology
Pulse <=40	153 (7.9%)	359 (0.4%)	512 (0.6%)
BP 0	247 (12.7%)	281 (0.3%)	528 (0.6%)
BP 1–89 mmHg	337 (17.3%)	3,446 (4.1%)	3,783 (4.4%)
GCSm 1	1,041 (53.6%)	3,805 (4.6%)	4,846 (5.7%)
GCSm 2–5	357 (18.4%)	8,218 (9.9%)	8,575 (10.0%)
Admission physiology
Pulse <=40	81 (4.2%)	228 (0.3%)	309 (0.4%)
BP 0	203 (10.4%)	95 (0.1%)	298 (0.3%)
BP 1–89 mmHg	576 (29.6%)	3,086 (3.7%)	3,662 (4.3%)
GCSm 1	1,355 (69.7%)	5,813 (7.0%)	7,168 (8.4%)
GCSm 2–5	234 (12.0%)	5,742 (6.9%)	5,976 (7.0%)

ISS, Injury Severity Score (maximum 75); AIScat, Maximum Abbreviated Injury Score, categorized (maximum 6); BP, blood pressure (systolic); GCSm, Glasgow Coma Scale, motor component (minimum 1, normally 6).

Patients selected for analysis were distributed among 161 hospitals, with case volumes ranging from 111 to 1671 patients. 85 (53%) of these hospitals were trauma centers with an ACS verification as Level I, 74 (46%) had an ACS verification as Level II, and 2 changed levels from one year to the next. The percentage of patients arriving at a hospital within 60 minutes of injury was 79% and ranged from 39% to 99% for different hospitals.

Calculation of an overall crude hazard rate, estimated at 15-minute intervals and not adjusted for covariates, is shown in Table 2. The hazard rate had an initial peak and gradually decreased over the 8 hour period of observation. Slight fluctuations in the numbers of deaths for successive time periods did not appear to constitute a trimodal or other anomalous distribution. Analyses using a threshold of 6 hours or 12 hours to define “early death” were very similar to those using an 8 hour threshold.

Table 2.

Crude Hazards at 15-min Intervals after Injury, for Patients Who Have Arrived at a Hospital with Detectable Vital Signs

Time in minutes (tp + th)	Patients at risk S	Admissions a	Deaths d	Hazard d/S
0– 14	0	640	0	-
15– 29	640	15,873	11	0.0172
30– 44	16,502	29,594	77	0.0047
45– 59	46,019	20,435	74	0.0016
60– 74	66,380	10,100	87	0.0013
75– 89	76,373	4,523	98	0.0013
90–104	80,818	2,069	122	0.0015
105–119	82,765	941	97	0.0012
120–134	83,609	383	86	0.0010
135–149	83,906	273	103	0.0012
150–164	84,076	124	75	0.0009
165–179	84,125	93	88	0.0010
180–194	84,130	60	86	0.0010
195–209	84,104	37	85	0.0010
210–224	84,056	37	81	0.0010
225–239	84,102	23	77	0.0009
240–254	83,958	19	76	0.0009
255–269	83,901	12	61	0.0007
270–284	83,852	13	56	0.0007
285–299	83,809	7	57	0.0007
300–314	83,759	9	41	0.0005
315–329	83,727	13	44	0.0005
330–344	83,696	10	48	0.0006
345–359	83,658	3	49	0.0006
360–374	83,612	9	46	0.0006
375–389	83,575	5	37	0.0004
390–404	85,327	3	31	0.0004
405–419	83,515	5	17	0.0002
420–434	83,503	5	32	0.0004
435–449	83,476	5	34	0.0004
450–464	83,447	2	32	0.0004
465–479	83,417	2	33	0.0004

At the beginning or each time interval i, the number or patients at risk S_i may be calculated as S_i-1 + a_i-1 − d_i-1. The hazard is the rate of death among the patients at risk during the specified time interval. Time after injury is calculated as prehospital time (t_p) plus hospital time (t_h). HR models described elsewhere in this article calculate the hazard for each minute rather than for 15-minute intervals.

Table 3 shows the odds ratios for patient-level covariates obtained from multiple logistic regression with the outcome of death within 8 hours of injury, compared with the hazard ratios for the same covariates in a HR model censored at 8 hours after injury (assuming a constant effect of the covariates over the 8 hours).

Table 3.

Results of Multivariable Logistic Regression Model Predicting Early Death (<=8 h after Injury) and Cox Proportional Hazard Regression Model (Censored At 8 h after Injury)

	Odds ratios (with 95% CI)	Hazard ratios (with 95% CI)
Age >=65 vs <65 years	4.33 (3.71–5.06)	2.91 (2.58–3.28)
Firearm injury	4.04 (3.51–4.66)	2.99 (2.68–3.35)
ISS 25–75 vs <25	3.00 (2.60–3.48)	2.51 (2.23–2.83)
Head AIScat	0.86 (0.80–0.92)	0.89 (0.84–0.94)
Abdomen AIScat	1.70 (1.57–1.83)	1.46 (1.38–1.55)
Prehospital times
1–30 min	1.00 (referent)	1.00 (referent)
31–45 min	0.84 (0.72–0.96)	0.89 (0.79–0.99)
46–60 min	0.56 (0.47–0.68)	0.63 (0.54–0.73)
61–90 min	0.41 (0.34–0.51)	0.53 (0.45–0.63)
>90 min	0.29 (0.21–0.41)	0.41 (0.31–0.55)
Prehospital physiology
Pulse <=40 vs >40	1.66 (1.16–2.36)	1.91 (1.55–2.37)
BP 0 vs >=90 mmHg	3.19 (2.37–4.29)	1.47 (1.21–1.77)
BP 1–89 vs >=90 mmHg	1.55 (1.31–1.83)	1.41 (1.24–1.61)
GCSm 1 vs 6	2.81 (2.33–3.39)	2.18 (1.87–2.55)
GCSm 2–5 vs 6	1.48 (1.23–1.78)	1.33 (1.13–1.57)
Admission physiology
Pulse <=40 vs >40	2.84 (1.81–4.45)	2.98 (2.31–3.83)
BP 0 vs >=90 mmHg	13.84 (9.81–19.5)	7.05 (5.81–8.54)
BP 1–89 vs >=90 mmHg	3.60 (3.13–4.14)	2.76 (2.47–3.09)
GCSm 1 vs 6	16.71 (13.7–20.4)	14.52 (12.2–17.3)
GCSm 2–5 vs 6	5.00 (4.06–6.14)	5.06 (4.18–6.12)

CI, confidence interval; ISS, Injury Severity Score (maximum 75); AIScat, Maximum Abbreviated Injury Score (maximum 6), categorized as 1 for AIS 1–2, 2 for AIS 3–4, or 3 for AIS 5–6; BP, blood pressure (systolic); GCSm, Glasgow Coma Scale, motor component (minimum 1, normally 6).

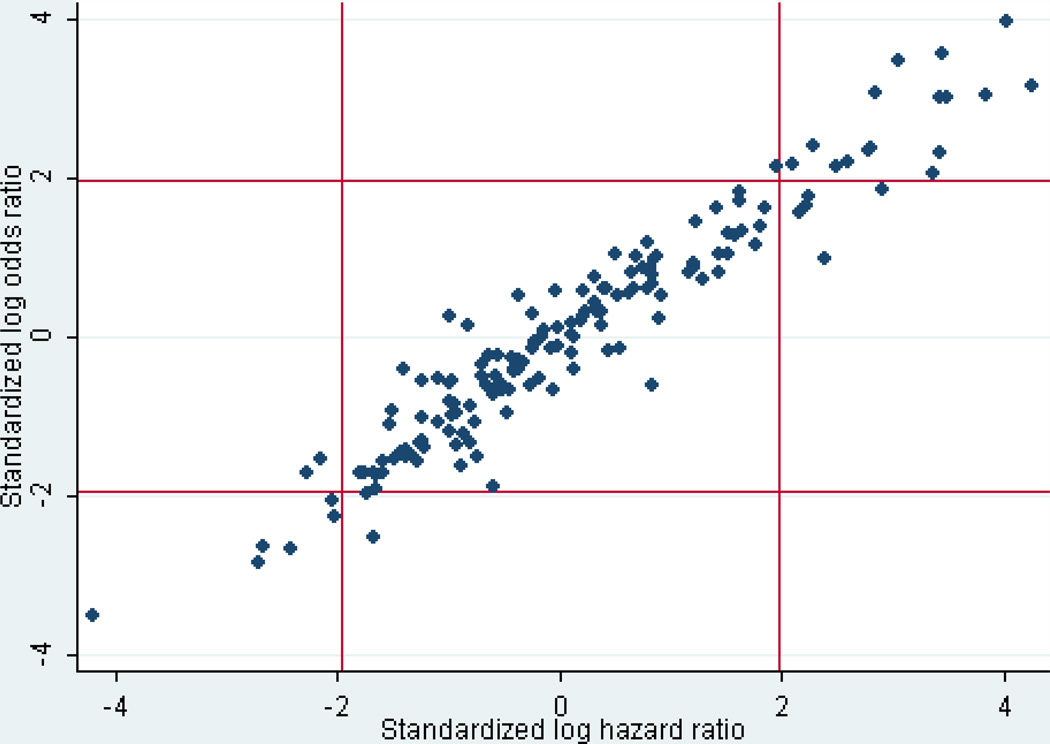
When hospital effects were considered constant, the distribution of these effects measured using hazard ratios was very similar to the distribution using odds ratios obtained from a LR model, as depicted in Figure 1 (in which the log odds ratio and the log hazard ratio are divided by their standard errors to make them comparable). However, when hospital effects were allowed to vary among the time periods 0–60 minutes, 61–120 minutes, and 121–480 minutes, there were considerable differences in the apparent effects at different times, although the absolute numbers of deaths were relatively small and the observed differences generally did not reach statistical significance.

Figure 1.

Standardized log odds ratios compared with standardized log hazard ratios for the effect on mortality attributable to the 161 sampled hospitals. The distribution of hospital effects is very similar with either model (r=0.96).

Table 4 shows odds ratios and hazard ratios where a 99% confidence interval of the hospital effect in the LR model or any of the HR models did not include the null value. There were many more high-mortality outliers than low-mortality outliers. The hazard ratio estimating the hospital effect specifically for the first hour or two was often quite different from that estimated with the assumption of a constant hazard ratio over eight hours. For example, Hospital B in Table 4 had a very high mortality for patients seen during the first hour after injury yet would not have been considered an outlier by conventional LR analysis.

Table 4.

Hospital Outliers

Hospital*	n	Died	Odds ratio	Hazard ratio (0–8 h)	Hazard ratio (0–1 h)	Hazard ratio (1–2 h)	Hazard ratio (2–8 h)
A	779	7	0.16†	0.20‡	0	0.48	0.16‡
B	1,355	42	1.21	1.46§	3.10†‖	1.69	1.15‖
C	658	18	1.86§	1.81§	0.86	3.82‡‖	1.35
D	587	22	1.91§	2.06†	3.26§	1.32	1.99†
E	1,146	38	2.05†	1.65†	1.25	1.20	1.83†
F	263	12	2.45§	2.70†	1.88	0.98	3.46‡
G	378	23	2.46†	2.25‡	0.85	1.52	2.79‡
H	428	16	2.53†	2.37†	1.21	3.64§	2.20§
I	521	20	2.64†	2.18†	1.87	3.45§	1.89§
J	607	24	2.75‡	2.29‡	3.02	0.99	2.55‡
K	323	12	2.99†	2.75†	1.34	4.93†	2.49§
L	461	10	3.08†	2.46§	0	2.34	2.69§
M	155	12	3.74†	3.44‡	4.59§	3.67§	3.13†

One low hospital outlier and 12 high hospital outliers where a 99% confidence interval or the hospital effect in the LR model or any of the HR models did not include the null value. Hazard ratios are shown first assuming that the effect of the hospital was constant over the 8 hours, and then allowing the effect of the hospital to vary for the time periods 0–1 hour, 1–2 hours, and 2–8 hours. A hazard ratio of 0 results from having no deaths in the given time interval. N=Number of patients with recorded survival times.

^*Anonymous NTDB hospitals are identified by the arbitrary letters A-M.

^†p<0.01 When comparing a hospital-specific estimate to the other hospitals as a group.

^‡p<0.00031 When comparing a hospital-specific estimate to the other hospitals as a group (0.05/161 Bonferroni correction for 161 hospital comparisons).

^§p<0.05 When comparing a hospital-specific estimate to the other hospitals as a group.

^‖p<0.05 (excluding comparisons to a hazard ratio of zero) when comparing a time-specific hazard ratio to the overall hospital hazard ratio.

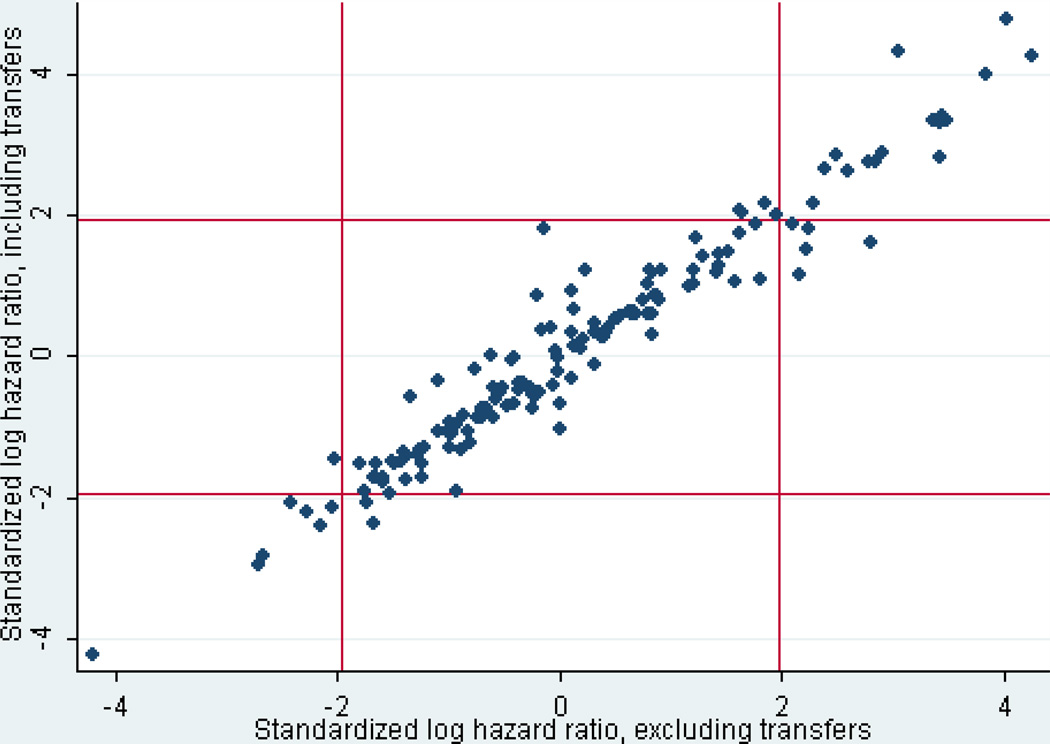
Only 122 patients had been excluded because they had been transferred out of the index hospital within the first 8 hours. However, 21,022 patients had been initially excluded because they had been transferred from another hospital to the index hospital. Analyses were repeated with the latter group included. The effects of transfer status, or the interaction of transfer status and categorized prehospital time, were not significant in the overall LR or HR models. Individual hospital effects with and without transfers were very similar (Figure 2). Of the 13 hospitals shown as outliers in Table 4 (with an arbitrary cutoff of p<.01), 12 would also appear in a similar table if transfers were included, and 2 others would be added.

Figure 2.

Standardized log hazard ratios with transferred patients included, compared with standardized log hazard ratios with transferred patients excluded. The distribution of hospital effects is very similar with either model (r=0.97).

DISCUSSION

Most studies of patients hospitalized after serious injury simply consider the outcome of survival at the time of hospital discharge, given that the patient was alive at the time of admission. Although very sophisticated and complicated mathematical models have been constructed to predict this outcome,(8–10) their validity is limited by their failure to incorporate information about the time periods before or after hospital observation.

Previous investigations have demonstrated that it may be inappropriate to consider hospital mortality, length of stay, and discharge destination independently.(5) A difference in the probability of survival at the time of hospital discharge does not necessarily imply that a similar difference will be found at the end of a specified time period.(11) Ideally, the patient’s condition at a fixed follow-up time of 30 days or more after injury would be a preferable binary outcome to measure or predict,(12) but appropriately constructed HR or other models may also be able to account for some of the differences in discharge timing and destination.(13, 14)

Arrival times may also vary from one hospital to another, especially between urban areas with rapid EMS transport times and rural areas where prolonged transportation times may result in fewer patients reaching a hospital alive. Models that do not properly allow for the “left truncated” population (that is, persons who are not transported to a hospital because they have already died) may lead to incorrect conclusions about the effect of prehospital delay.(15) HR models may also be useful in evaluating this early mortality, because they can explicitly identify the times when specific patients are actually observed in a given hospital and account for the differences in underlying risk associated with a specific time after an injury has occurred. The technique also potentially allows for a similar analysis of mortality in the prehospital phase, should such data be available, and hence provides an approach that can be extended to a more comprehensive system-based model.

Patients received in transfer from another hospital may be difficult to compare with patients received directly from the scene of an injury.(16) On the one hand, the reason for transfer is often that their injuries are more serious; on the other hand, their survival long enough to reach a second hospital implies some degree of physiologic stability. In order to focus on a uniform population, our main analysis excluded patients received in transfer. However, interhospital differences in early mortality were not much different when transfer patients were included.

Patients transferred out to another hospital also complicate any analysis of mortality. If a given hospital sends away its most serious cases, its measured effect on mortality will be falsely low. Excluding these cases from either HR or LR analysis may also introduce bias when considering hospital effects on outcome; censoring these cases in HR models is still biased because the censoring is not independent from the outcome. Few patients are transferred acutely out of a major trauma center, so these considerations do not affect the analysis in the present study. However, for a dataset containing hospitals that frequently transfer patients out in the acute phase, a possible approach would be to determine the consistency of results from analyses that exclude these cases, include them as deaths, or censor them as survivors.

If a personal identifier were available in the data that allowed tracking an individual patient from one hospital to another, it might be possible to identify transfer patients as censored from one hospital and reappearing as a readmission in another hospital. HR models could then be constructed to allow for these situations, measuring the effect of each hospital only during the time period when the given patient was actually under the care of its staff, and adding a time-dependent covariate to indicate transfer status.

Whether a LR or a HR model has been used to estimate hospital effects, the imprecision of these effect estimates also needs to be considered. Typically, confidence limits are calculated from the model, and hospitals whose confidence limits do not include a null value (e.g., an odds ratio or hazard ratio of 1) are considered “outliers”. However, testing multiple hospitals against a standard theoretically increases the frequency of Type I errors, and results may vary depending upon whether and how the confidence limits are adjusted to reduce this frequency.(17, 18) For public reporting or reimbursement decisions, some adjustment is probably warranted. The p-value threshold of 0.00031 (.05/161) in Table 4 corresponds to a Bonferroni correction of the p-value threshold of 0.05 when 161 hospital comparisons have been made.

Several authors have recently suggested that “multilevel” or “hierarchical” LR models may be preferable when comparing trauma center performance to a standard.(19–21) The potential advantages include labeling fewer hospitals as outliers, especially hospitals with smaller volumes of patients. HR models can implement a similar approach by treating the hospital effects as random rather than fixed, a modification referred to as “shared frailty”. The random effects approach may reduce concerns about multiple testing, although this opinion is not held by all statisticians.(18)

Our findings in this study confirm that the mortality hazard for injured patients admitted to a hospital has an initial peak followed by an essentially monotonic decrease. No deaths were recorded among the few patients admitted less than 15 minutes after injury (Table 2), but there is an understandable delay in the declaration of death for the most acute cases while the diagnosis is confirmed and resuscitative measures are being carried out.(2) “Interval censoring” allows HR models to accommodate these situations when the time of death cannot be exactly specified.(22, 23)

There was a general similarity of covariate effects in Table 3 between a LR model (using death within 8 hours as an outcome) and a HR model (censoring cases still alive at 8 hours). Theoretical reasons for this similarity are discussed elsewhere.(24–27) Increased age, firearm mechanism, increased severity, and more deranged physiology all were associated with increased mortality. Having controlled for ISS and GCSm, patients with serious head trauma were less likely to die within the initial 8-hour period of observation; this finding is consistent both with the physiology of death following traumatic brain injury and with the clinical practice of initial support and observation. Hospital mortality could be affected by differences in this clinical practice related to the time period of observation and local practices regarding early withdrawal of care in patients deemed to have a low probability of functional survival.

Increasing length of prehospital time was associated with lower mortality (among patients who reached the hospital alive) both in LR and HR models, a result that should be expected given that prehospital deaths have been truncated. Simply including prehospital time as a covariate in either type of model would control somewhat for patient acuity, but would require additional assumptions about independence of these times, other covariate effects, and hospital effects unless numerous interaction terms were added. HR models that include time-varying hospital effects as well as prehospital times improve model flexibility and interpretation. Furthermore, the ability to include similar time-varying prehospital effects also enhances the potential utility of HR models.

Hospital effects as shown in the first two columns of Table 4 were also relatively similar between a LR model (using only death within 8 hours as an outcome) and a HR model (censoring cases still alive at 8 hours). When hazard ratios were allowed to vary by time period, however, there were interesting differences. In particular, several of the hospitals reported no deaths within the first or even second hour. Although we had excluded patients declared dead on arrival and those with no pulse on arrival, these findings suggest that differences in measured outcomes may be due to differences in data quality as well as differences in clinical quality.

The collection of prehospital data in the NTDB is inherently challenging. There is no nationally accepted standard for EMS reporting to hospitals, EMS run sheets are not uniform, and reports are not universally available at the time of admission. Thus, the data must be gleaned from a collection of different EMS records by hospital-based personnel, and the frequency with which these data points are collected and their accuracy is a recognized weakness within the NTDB. Some of these problems have great potential to be improved with the current development of a National EMS Information System (NEMSIS).

Our study is further limited by the lack of data on prehospital time and time to death in a substantial number of NTDB records. This could be remedied to some degree by imputation methods,(28) but seems to be more frequent in fatal cases and could affect conclusions about outcomes, as could any other missing or miscoded data used for risk adjustment. However, these limitations should become less of a problem as the recording of prehospital and hospital times to the minute becomes more standard for trauma registries and data quality generally improves as a result of the TQIP program.

We believe our findings show that HR models have promise in the evaluation of hospital mortality after injury within a system of care that includes both prehospital and hospital factors, and where the period of observation and nature of interventions may vary during different phases of care. By extension, these techniques are also applicable to the analysis of care after myocardial infarction, stroke, or other acute conditions in which outcome is dependent upon a time-limited, system-based approach.