Skip to main content
NCBI home page
Plant Physiology logoLink to Plant Physiology
. 2013 Aug 7;163(2):637–647. doi: 10.1104/pp.113.224006

Multiscale Metabolic Modeling: Dynamic Flux Balance Analysis on a Whole-Plant Scale1,[W],[OPEN]

Eva Grafahrend-Belau 1,2,3,2,*, Astrid Junker 1,2,3,2, André Eschenröder 1,2,3, Johannes Müller 1,2,3, Falk Schreiber 1,2,3, Björn H Junker 1,2,3
PMCID: PMC3793045  PMID: 23926077

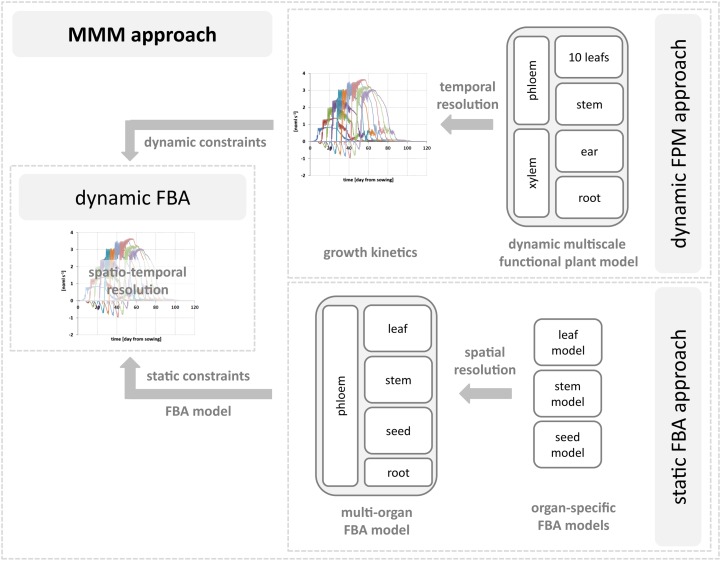
A multiscale metabolic modeling approach integrates a static multiorgan flux balance analysis model and a dynamic whole-plant multiscale functional plant model for dynamic flux balance analysis.

Abstract

Plant metabolism is characterized by a unique complexity on the cellular, tissue, and organ levels. On a whole-plant scale, changing source and sink relations accompanying plant development add another level of complexity to metabolism. With the aim of achieving a spatiotemporal resolution of source-sink interactions in crop plant metabolism, a multiscale metabolic modeling (MMM) approach was applied that integrates static organ-specific models with a whole-plant dynamic model. Allowing for a dynamic flux balance analysis on a whole-plant scale, the MMM approach was used to decipher the metabolic behavior of source and sink organs during the generative phase of the barley (Hordeum vulgare) plant. It reveals a sink-to-source shift of the barley stem caused by the senescence-related decrease in leaf source capacity, which is not sufficient to meet the nutrient requirements of sink organs such as the growing seed. The MMM platform represents a novel approach for the in silico analysis of metabolism on a whole-plant level, allowing for a systemic, spatiotemporally resolved understanding of metabolic processes involved in carbon partitioning, thus providing a novel tool for studying yield stability and crop improvement.

Plants are of vital significance as a source of food (Grusak and DellaPenna, 1999; Rogalski and Carrer, 2011), feed (Lu et al., 2011), energy (Tilman et al., 2006; Parmar et al., 2011), and feedstocks for the chemical industry (Metzger and Bornscheuer, 2006; Kinghorn et al., 2011). Given the close connection between plant metabolism and the usability of plant products, there is a growing interest in understanding and predicting the behavior and regulation of plant metabolic processes. In order to increase crop quality and yield, there is a need for methods guiding the rational redesign of the plant metabolic network (Schwender, 2009).

Mathematical modeling of plant metabolism offers new approaches to understand, predict, and modify complex plant metabolic processes. In plant research, the issue of metabolic modeling is constantly gaining attention, and different modeling approaches applied to plant metabolism exist, ranging from highly detailed quantitative to less complex qualitative approaches (for review, see Giersch, 2000; Morgan and Rhodes, 2002; Poolman et al., 2004; Rios-Estepa and Lange, 2007).

A widely used modeling approach is flux balance analysis (FBA), which allows the prediction of metabolic capabilities and steady-state fluxes under different environmental and genetic backgrounds using (non)linear optimization (Orth et al., 2010). Assuming steady-state conditions, FBA has the advantage of not requiring the knowledge of kinetic parameters and, therefore, can be applied to model detailed, large-scale systems. In recent years, the FBA approach has been applied to several different plant species, such as maize (Zea mays; Dal’Molin et al., 2010; Saha et al., 2011), barley (Hordeum vulgare; Grafahrend-Belau et al., 2009b; Melkus et al., 2011; Rolletschek et al., 2011), rice (Oryza sativa; Lakshmanan et al., 2013), Arabidopsis (Arabidopsis thaliana; Poolman et al., 2009; de Oliveira Dal’Molin et al., 2010; Radrich et al., 2010; Williams et al., 2010; Mintz-Oron et al., 2012; Cheung et al., 2013), and rapeseed (Brassica napus; Hay and Schwender, 2011a, 2011b; Pilalis et al., 2011), as well as algae (Boyle and Morgan, 2009; Cogne et al., 2011; Dal’Molin et al., 2011) and photoautotrophic bacteria (Knoop et al., 2010; Montagud et al., 2010; Boyle and Morgan, 2011). These models have been used to study different aspects of metabolism, including the prediction of optimal metabolic yields and energy efficiencies (Dal’Molin et al., 2010; Boyle and Morgan, 2011), changes in flux under different environmental and genetic backgrounds (Grafahrend-Belau et al., 2009b; Dal’Molin et al., 2010; Melkus et al., 2011), and nonintuitive metabolic pathways that merit subsequent experimental investigations (Poolman et al., 2009; Knoop et al., 2010; Rolletschek et al., 2011). Although FBA of plant metabolic models was shown to be capable of reproducing experimentally determined flux distributions (Williams et al., 2010; Hay and Schwender, 2011b) and generating new insights into metabolic behavior, capacities, and efficiencies (Sweetlove and Ratcliffe, 2011), challenges remain to advance the utility and predictive power of the models.

Given that many plant metabolic functions are based on interactions between different subcellular compartments, cell types, tissues, and organs, the reconstruction of organ-specific models and the integration of these models into interacting multiorgan and/or whole-plant models is a prerequisite to get insight into complex plant metabolic processes organized on a whole-plant scale (e.g. source-sink interactions). Almost all FBA models of plant metabolism are restricted to one cell type (Boyle and Morgan, 2009; Knoop et al., 2010; Montagud et al., 2010; Cogne et al., 2011; Dal’Molin et al., 2011), one tissue or one organ (Grafahrend-Belau et al., 2009b; Hay and Schwender, 2011a, 2011b; Pilalis et al., 2011; Mintz-Oron et al., 2012), and only one model exists taking into account the interaction between two cell types by specifying the interaction between mesophyll and bundle sheath cells in C4 photosynthesis (Dal’Molin et al., 2010). So far, no model representing metabolism at the whole-plant scale exists.

Considering whole-plant metabolism raises the problem of taking into account temporal and environmental changes in metabolism during plant development and growth. Although classical static FBA is unable to predict the dynamics of metabolic processes, as the network analysis is based on steady-state solutions, time-dependent processes can be taken into account by extending the classical static FBA to a dynamic flux balance analysis (dFBA), as proposed by Mahadevan et al. (2002). The static (SOA) and dynamic optimization approaches introduced in this work provide a framework for analyzing the transience of metabolism by integrating kinetic expressions to dynamically constrain exchange fluxes. Due to the requirement of knowing or estimating a large number of kinetic parameters, so far dFBA has only been applied to a plant metabolic model once, to study the photosynthetic metabolism in the chloroplasts of C3 plants by a simplified model of five biochemical reactions (Luo et al., 2009). Integrating a dynamic model into a static FBA model is an alternative approach to perform dFBA.

In this study, a multiscale metabolic modeling (MMM) approach was applied with the aim of achieving a spatiotemporal resolution of cereal crop plant metabolism. To provide a framework for the in silico analysis of the metabolic dynamics of barley on a whole-plant scale, the MMM approach integrates a static multiorgan FBA model and a dynamic whole-plant multiscale functional plant model (FPM) to perform dFBA. The performance of the novel whole-plant MMM approach was tested by studying source-sink interactions during the seed developmental phase of barley plants.

RESULTS

With the aim of achieving a spatiotemporal resolution of barley metabolism on a whole-plant scale, a MMM approach was developed combing static FBA and dynamic FPM (Fig. 1). Static FBA has the advantage of being applicable to large-scale systems such as highly compartmentalized plant metabolic networks (at the subcellular, tissue, and organ levels) and providing insight into metabolic steady-state flux distributions under different environmental and/or genetic backgrounds (Table I). The dynamic FPM approach permits us to analyze the transience of plant metabolism (carbon and nitrogen balance) under different environmental backgrounds on a whole-plant level by predicting the environment-dependent kinetics of carbon and nitrogen compounds and their distribution among different plant organs. The integration of the different modeling approaches allows the steady-state FBA models to be concatenated along a developmental time axis, resulting into a dFBA approach on a whole-plant scale.

Figure 1.

Figure 1.

Open in a new tab

Workflow of the MMM approach to analyze the metabolic dynamics of barley. The MMM approach integrates a static multiorgan FBA model and a dynamic FPM to perform dFBA. As a result, the spatiotemporal metabolic behavior of the multiorgan FBA model is predicted by computing a series of steady-state solutions constrained by dynamic constraints predicted by the FPM.

Table I. Comparison of the static FBA and the dynamic FPM approaches applied in the MMM approach.

Factor Static FBA Approach Dynamic FPM Approach
A priori knowledge Low High
Degree of abstraction Low High
Coverage Cell/tissue/organ Compartments/organ/whole plant
Processes Metabolic Metabolic, physiological, biophysical
Mathematical description Reaction based Process based
Time response Static Dynamic
Model size Large scale Small/medium scale
Open in a new tab

In the following, each step of the modeling approach is described, and the application of the approach is shown by a case study of source-to-sink interactions in barley metabolism.

Reconstruction of a Multiorgan FBA Model

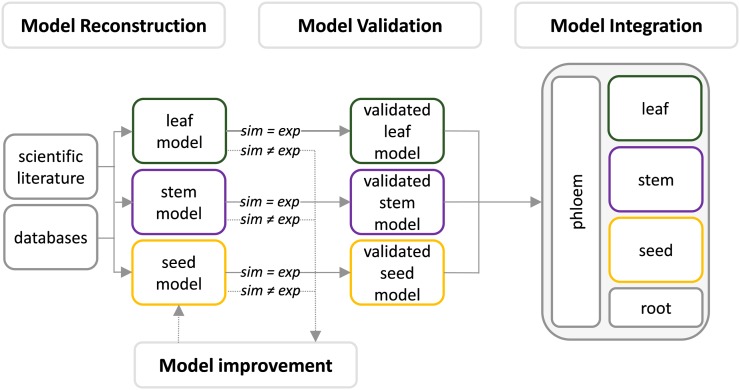
A multiorgan FBA model of barley plant metabolism was developed based on the three-step reconstruction procedure shown in Figure 2.

Figure 2.

Figure 2.

Open in a new tab

Three-step procedure to reconstruct a multiorgan FBA model. The reconstruction procedure encompasses the steps of (1) model reconstruction, resulting in organ-specific FBA models of barley leaf, stem, and seed metabolism; (2) model validation/improvement, resulting in validated organ-specific models being capable of reproducing known experimental results; and (3) model integration, resulting in a multiorgan FBA model of barley plant metabolism. exp, Experimental results; sim, simulation results.

In the first step, organ-specific FBA models of the primary metabolism of leaves, stems, and seeds were established based on biochemical, physiological, proteomic, and genomic data derived from the literature and online databases. Focusing on the generative phase of plant development, organ-specific metabolism was modeled by taking into account the primary metabolic pathways of the most prominent tissue of the respective organ. The FBA model of leaf metabolism comprises the primary metabolism of a source leaf mesophyll cell and is composed of 354 reactions and 333 metabolites. The stem model includes the primary metabolic pathways of sink and source metabolism of a storage parenchyma cell and comprises 325 reactions and 303 metabolites. The FBA model of seed metabolism represents an endosperm cell of the barley seed, as detailed by Grafahrend-Belau et al. (2009b). A detailed description of the organ-specific models comprising the set of reactions included into the models as well as experimental evidence supporting each network reaction is given in Supplemental Table S1.

In the second step, the organ-specific FBA models were validated by comparing the simulation results (e.g. predicted uptake/excretion rates, predicted pathway patterns) with experimental data taken from the literature. With respect to source leaf metabolism, the leaf model was shown to be capable of reproducing the rate of Suc synthesis in photosynthetically active barley leaves (Farrar and Farrar, 1986). The pathway pattern predicted by the stem model was found to be in broad agreement with that reported for photosynthetic tissues of monocotyledon species (see refs. in Supplemental Table S1). The validity of the seed model has already been demonstrated in previous application studies (Grafahrend-Belau et al., 2009b; Melkus et al., 2011; Rolletschek et al., 2011).

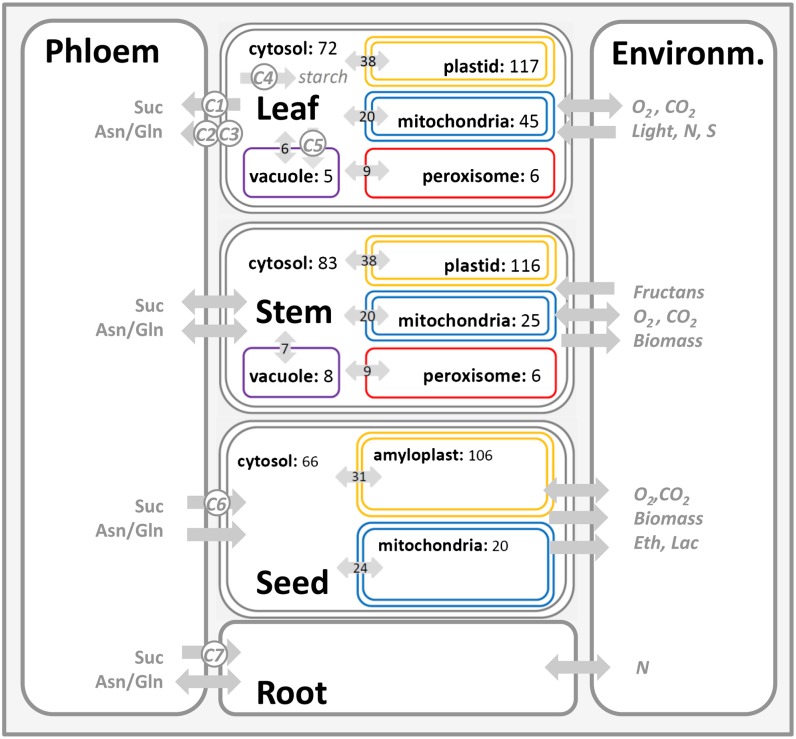
In the third step, the validated organ-specific models were combined into one multiorgan FBA model. To take into account root metabolism, a simplified root model consisting of three exchange reactions (i.e. transport of Suc, Asn, and Gln) was additionally integrated into the multiorgan model. Model coupling was done by introducing the phloem as an exchange component that mediates the transport of carbon and nitrogen components between the different plant organs, thereby connecting leaf, stem, root, and seed metabolism. The resulting multiorgan FBA model is shown in Figure 3.

Figure 3.

Figure 3.

Open in a new tab

Schematic overview of the multiorgan FBA model of barley plant metabolism. For each organ-specific model, the subcellular compartments are depicted along with the number of appendant reactions. Transport processes are represented as gray arrows, with the number of intracellular transport processes being indicated. C1 to C7 refer to the exchange fluxes predicted by the dynamic FPM and used to constrain the sequential simulation (Supplemental Table S4). Environm, Environment; Eth, ethanol; Lac, lactate; N, nitrate; S, sulfate.

The obtained large-scale metabolic network includes 890 metabolites that are synthesized, metabolized, and degraded by 702 biochemical reactions. In addition, 269 reactions describe intracellular translocation processes between different subcellular compartments (plastid, mitochondrion, peroxisome, vacuole, cytosol), transport processes between the different plant organs and the phloem, and the exchange of substances (e.g. nitrogen, sulfate, CO2, oxygen) with the environment.

Reconstruction of a Dynamic FPM

With the aim of representing the complex hierarchical organization of metabolic and physiological processes of biomass formation across different plant scales, the FPM ProNet-CN was established. ProNet-CN represents a dynamic and multiscale process network that integrates condensed submodels of biophysical, metabolic, and physiological processes related to the formation and allocation of main carbon and nitrogen components. It combines a leaf photosynthesis model describing the exchange of CO2, water vapor, and energy (LEAFC3-N; Mueller et al., 2005; Braune et al., 2009) and a multiorgan model describing the dynamics of the balance and allocation of carbon and nitrogen components between interacting cellular compartments and organs. ProNet-CN allows for analyzing the dynamics of barley plant metabolism across the entire life cycle (90 d) on an hourly basis. A simplified scheme of the model is provided in Supplemental Figure S1, and a general description is given below. For a detailed description of the model, its implementation, and validation, see Mueller et al. (2012).

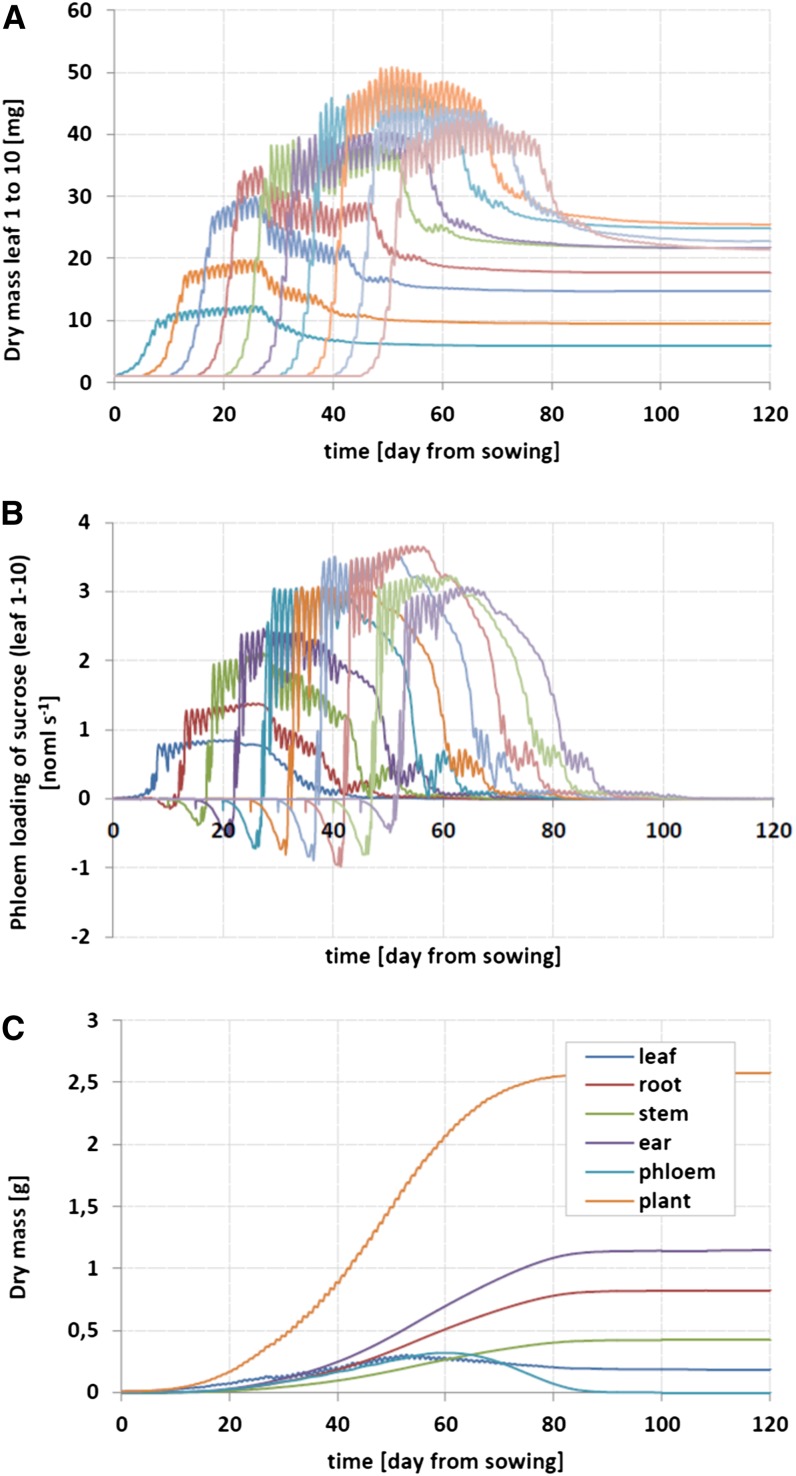
In the ProNet-CN model, plant processes are coupled across four nested scales: (1) metabolic scale, (2) reaction compartments, (3) organs, and (4) plant. To keep the complexity of the model manageable and consistent with the analytical capabilities, for the present, ProNet-CN considers a single shoot only. Water uptake and flux through the plant is assumed to be equal to the transpiration rate. Limiting soil water availability and plant water storage are not taken into account. Nitrogen uptake is described as a passive influx of nitrate via the water stream. Both individual steps and lumped sequences of biochemical reactions or transport are modeled phenomenologically in terms of Michaelis-Menten kinetics or as driven by a concentration gradient, respectively. If appropriate, extensions were introduced to account for control by concentrations of carbon or nitrogen compounds. The formation of organic nitrogen compounds is condensed to the stoichiometry of proteins and formally included into the carbon and nitrogen balance of the cytosol. The computation of respiratory carbon losses relies on the concept of growth and maintenance respiration (McCree, 1970). Leaf area growth is assumed to be proportional to the rate of synthesis of cellulose and hemicelluloses in leaves. Verification and parameterization of ProNet-CN was done based on data taken from the literature and special experiments (Mueller et al., 2012). On this basis, the model has been proven to successfully represent the diurnal and ontogenetic dynamics of the main processes of barley plant metabolism (Fig. 4). Furthermore, as reported by Mueller et al. (2012), the mass balances and growth characteristics of the individual organs as well as the whole plant generally were in good agreement with both the expected response and the experimental data.

Figure 4.

Figure 4.

Open in a new tab

Diurnal and ontogenetic time courses of dry mass of leaves (A), export or import of Suc out of/into leaves (B), and dry mass of plant organs and whole plant (C) as predicted by the dynamic FPM of barley plant metabolism. (Adapted from Mueller et al., 2012.)

Model Coupling and dFBA

The MMM approach proposed in this paper combines the multiorgan FBA model with the dynamic FPM to perform dFBA. By applying a SOA and using the multiorgan FBA model as a basis, the dFBA is implemented by dividing a selected plant growth phase into several time intervals and computing a static FBA at the beginning of each time interval. To include dynamic processes, time-dependent exchange fluxes predicted by the FPM are used to constrain the static FBA within each time interval (see “Materials and Methods”). In brief, the applied dFBA approach approximates the predicted spatiotemporal metabolic behavior of a multiorgan FBA model by a series of steady-state solutions constrained by dynamic constraints predicted by the dynamic FPM.

In the following, the application of the MMM approach is demonstrated by a case study of source-sink interactions during the generative phase of the barley plant.

Sink-Source Interactions in Barley Plant Metabolism

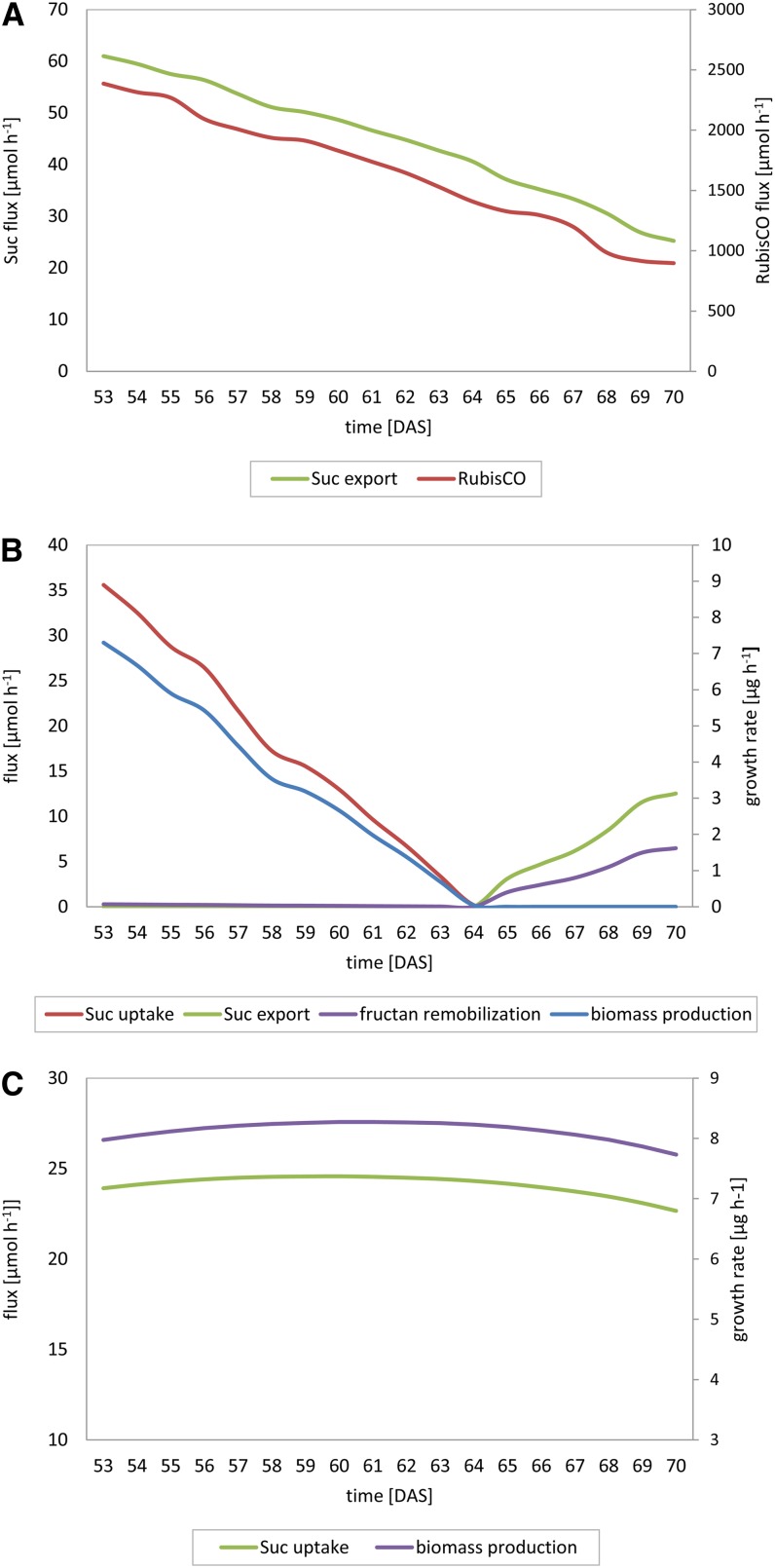
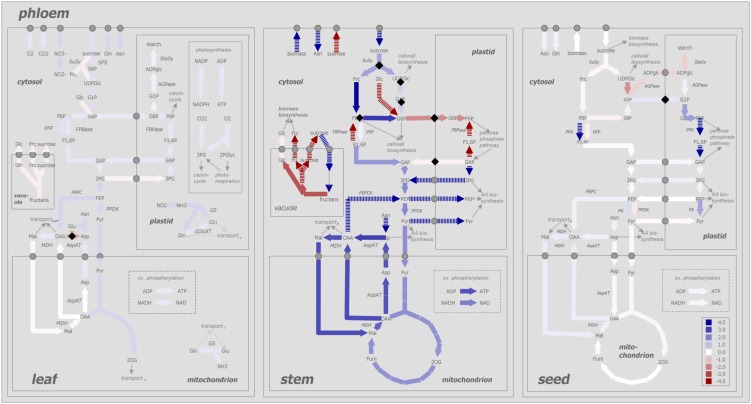
To study the effect of the senescence-related decrease in barley leaf source capacity on sink-source interactions during the generative phase of the barley plant, the proposed MMM approach was applied involving dFBA simulations from 53 to 70 d after sowing (DAS). The simulated flux values for each time step of the dFBA are listed in Supplemental Table S2. A detailed description of the applied methodology is given in “Materials and Methods.”

The dFBA predicts a sink-to-source shift of barley stem metabolism between 64 and 65 DAS (Fig. 5B). The metabolic shift is caused by a senescence-related decline in leaf source capacity, as shown by the marked decrease in photosynthetic carbon dioxide fixation and, associated therewith, a strong decline in phloem Suc loading (Fig. 5A). While leaves provide sufficient photosynthates for grain filling during early seed development, from 65 DAS on, leaf photosynthates are no longer adequate to supply the requirement of the seed for Suc (Fig. 5C), and stem reserves (fructans) are used to maintain the rate of grain filling. The sink-to-source shift of barley stem metabolism is reflected by the onset of fructan remobilization, Suc loading into the phloem, and a lack of stem biomass accumulation (Fig. 5B).

Figure 5.

Figure 5.

Open in a new tab

Simulated flux values predicted for leaf (A), stem (B), and seed (C) metabolism from 53 to 70 DAS by the dFBA approach.

Metabolic Flux Maps

To get insight into the flux distributions characterizing sink and source metabolism of the barley plant, log-ratio flux maps (for explanation, see “Materials and Methods”) depicting alterations in the organ-specific light metabolism of early (56 DAS, 2 pm) versus late (66 DAS, 2 pm) seed development were generated. The resulting organ-specific log-ratio maps are shown in Figure 6 (for a high-resolution image see Supplementary Fig. S2). The corresponding simulated flux values for 56 and 66 DAS as well as the log-ratio values are listed in Supplemental Table S3. Flux maps depicting the simulated flux values for central metabolic processes of barley seed, stem, and leaf metabolism at 56 and 66 DAS are provided in Supplemental Figures S3 and S4.

Figure 6.

Figure 6.

Open in a new tab

Organ-specific log-ratio flux maps predicted by the dFBA. The flux maps depict central metabolic processes of barley leaf, stem, and seed metabolism. Blue dashed arrows indicate metabolic routes only being active at 56 DAS. Red dashed arrows indicate metabolic routes only being active at 66 DAS. The direction of the metabolic fluxes as indicated by the arrowheads correspond to the flux directions at 56 DAS. Changes in flux direction from 56 to 66 DAS are indicated by black rhombi. Reactions are as follows: AGPase, ADP-Glc pyrophosphorylase; AspAT, Asp aminotransferase; FBPase, Fru-1,6-bisphosphatase; GOGAT, ferredoxin-dependent Glu synthase; GS, Glu ammonia ligase; MDH, malate dehydrogenase; PEPC, phosphoenolpyruvate carboxylase; PEPCK, phosphoenolpyruvate carboxykinase; PFK, 6-phosphofructokinase; PFP, diphosphate-Fru-6-P 1-phosphotransferase; PK, pyruvate kinase; PPDK, pyruvate phosphate dikinase; SPS, Suc phosphate synthase; StaSy, starch synthase; SuSy, Suc synthase. Metabolites are as follows: ADPglc, ADP-Glc; Frc, Fru; F1,6P, Fru-1,6-P; F6P, Fru-6-P; Fum, fumarate; G1P, Glc-1-P; G6P, Glc-6-P; GAP, glyceraldehyde 3-phosphate; Mal, malate; OAA, oxaloacetate; 2OG, 2-oxoglutarate; PEP, phosphoenolpyruvate; 3PG, 3-phosphoglycerate; Pyr, pyruvate; UDPglc, UDP-Glc. Other abbreviations are as follows: AA, amino acid; ox., oxidative; transportp, transportper, and transportc, transport into plastid, peroxisome, and cytosol, respectively.

In the following, the predicted organ-specific log-ratio flux maps are described, and the time-dependent changes in leaf, stem, and seed metabolism are specified.

Leaf Metabolism at 56 and 66 DAS

Light metabolism of the barley leaf at 56 and 66 DAS is characterized by source leaf metabolic processes including photosynthetic carbon dioxide fixation, Suc synthesis from Calvin cycle intermediates, photorespiration, transient starch synthesis, and phloem loading of Suc, Gln, and Asn. Ammonia resulting from nitrogen assimilation and photorespiration is assimilated into Gln via the plastidic Gln synthetase/Glu synthase cycle and the mitochondrial Gln synthetase.

The tricarboxylic acid (TCA) cycle is predicted to be noncyclic, with the reactions between 2-oxoglutarate and malate carrying no flux. The incomplete TCA cycle is involved in the provision of carbon skeletons for nitrogen assimilation and reducing power via the malate-oxaloacetate shuttle, rather than in providing ATP.

As shown by the log-ratio flux map (Fig. 6), the metabolic flux distributions in the leaf reflect the outcome of a scenescence-related decrease in leaf source capacity, as shown by the marked decrease in Suc loading, remobilization of long-term storage pools (fructans), and changes in absolute fluxes from 56 to 66 DAS. However, the ratio of internal fluxes remains almost constant, indicating that there is no major rearrangement of leaf metabolism between 56 and 66 DAS.

Stem Metabolism at 56 and 66 DAS

The log-ratio flux map of the barley stem (Fig. 6) reveals a sink-to-source shift of stem metabolism caused by the senescence-related decrease in leaf source capacity. At 56 DAS, stem metabolism is characterized by sink metabolic processes such as the synthesis of biomass components (e.g. proteins, cell wall components) and long-term storage pools (fructans), which are driven by the phloem unloading of Suc and Asn in the stem. In addition, products of Suc breakdown are fed into the cytosolic/plastidic pathway of glycolysis to fuel the TCA cycle, which acts in a cyclic mode and provides energy and reducing equivalents for (non)growth-associated processes.

Due to a decline in leaf source capacity and a concurrent increase in seed sink capacity during the major seed storage phase, stem metabolism at 66 DAS is characterized by the cessation of stem biomass accumulation and the activation of source metabolic processes. The induction of fructan remobilization in the vacuole results in the accumulation of Suc, Glc, and Fru in the cytosol, which either serves as a precursor for the resynthesis of Suc (Glc, Fru) or is directly loaded into the phloem (Suc). While the TCA cycle still acts as an important source of energy, its role in providing reducing equivalents via the malate-oxaloacetate shuttle is markedly reduced in comparison with 66 DAS.

Seed Metabolism at 56 and 66 DAS

Seed metabolism at 56 and 66 DAS is mainly characterized by processes involved in seed storage, such as the synthesis of starch and storage proteins. As shown by the log-ratio flux map (Fig. 6), differences in the primary seed metabolism at 56 and 66 DAS are related to time-dependent differences in biomass composition. At 56 DAS, seed metabolism is dominated by processes involved in cell wall synthesis (i.e. synthesis of β-glucans, arabinoxylans, cellulose) and storage protein synthesis (e.g. uptake of Asn and Gln, glycolysis-derived precursors [3-phosphoglycerate, pyruvate] for amino acid synthesis, and TCA cycle-derived carbon skeletons [2-oxoglutarate] for nitrogen assimilation), reflecting the prominent contribution of these biomass components to seed biomass at early seed development. At 66 DAS, a marked increase in starch synthesis indicates the dominant contribution of starch to seed biomass at later seed development.

DISCUSSION

MMM

In line with the declared objective of systems biology to model metabolism on an organism scale, a future goal in plant metabolic modeling is to reconstruct and analyze metabolism at the whole-plant level (Sweetlove and Ratcliffe, 2011). In this study, a first step in this direction was taken by integrating organ-specific FBA models of seed, stem, leaf, and root metabolism into one multiorgan model. Organ-specific metabolism was modeled by reconstructing the primary metabolism of the most prominent tissue of the respective organs. Although plant tissues are characterized by the existence of multiple cell types that are likely to have different metabolic capacities (Brady et al., 2007), the simplification of ignoring the presence of multiple cell types in the different organ-specific models seemed to be reasonable with respect to the biological question to be addressed here. As shown by the application example, the spatial resolution applied in the multiorgan-specific FBA model was sufficient to give insight into metabolic changes in the source/sink metabolism of the barley plant. Nevertheless, questions related to cell type-specific interactions do require a more detailed resolution by modeling cell type-specific models combined into models of multilayered plant tissues. To address these kinds of questions, our model can be extended by more detailed submodels in the future, in analogy to the few existing multicell models (Dal’Molin et al., 2010; Lewis et al., 2010).

Due to the low a priori knowledge required for the reconstruction of static FBA models, FBA has the advantage of supporting plant metabolic modeling of different degrees of abstraction, whereby the spatial resolution of the metabolic model is adaptable to the biological question to be addressed. On the other hand, dynamic processes not taken into account by the static FBA approach can be analyzed via the integration of a dynamic FPM, allowing for the performance of dFBA. Focusing on the response of the carbon and nitrogen balance of the barley plant caused by different environmental conditions or plant development, the integration of the dynamic FPM allows for taking into account temporal and environmental changes affecting whole-plant metabolism. In our application example, the dynamics of barley plant metabolism were analyzed on a daily basis. However, the dynamic FPM allows for keeping track of temporal changes with higher resolution in time (e.g. hours), such as diurnal cycles of photosynthesis.

In contrast to the existing SOA of dFBA, which are based on the integration of kinetic expressions requiring a large number of kinetic parameters (Mahadevan et al., 2002; Hjersted and Henson, 2006; Oddone et al., 2009), in this study, SOA-based dFBA was computed by integrating a dynamic FPM. A similar approach has been presented by Feng et al. (2012), who integrated FBA into a kinetic model to get insight into the dynamics of the metabolism of the unicellular Shewanella oneidensis. Another study applies dFBA by coupling a human whole-body, physiologically based, pharmacokinetic model with a hepatocyte stoichiometric model in order to investigate the effects of drug- or illness-induced changes in hepatic metabolism on a whole-body scale (Krauss et al., 2012). In general, the integration of different metabolic modeling approaches each focusing on different aspects of metabolism has the advantage of giving a systemic and more comprehensive understanding of complex metabolic processes while retaining a high level of detail at the level of intracellular flux distributions.

Sink-to-Source Transition of the Barley Stem

In this study, the multiscale modeling approach was applied to study the relations between sink and source organs of a barley plant following the transition of early seed development to seed filling. From a physiological point of view, the nutrient demand of the growing barley seed is covered by two sources: first, the current assimilation in source leaves, and second, the remobilization of reserves. During the early embryogenesis phase, the sink strength of the growing seed is covered by sufficient assimilation capacity of the leaves. With progressing maturity, the nutrient demand of the seeds increases, whereas leaf senescence leads to a decrease in the production and export of Suc. This is compensated by the remobilization of stem-derived fructan reserves. Fructans represent the largest portion of water-soluble carbohydrates in barley stems and may reach up to 45% (Blacklow et al., 1984; Schnyder, 1993). Thus, fructans are an important source of assimilates during grain filling (Gallagher et al., 1975), especially under biotic (Scott and Dennis-Jones, 1976) and abiotic (Yang et al., 2004) stresses. Fructan synthesis requires Suc as a substrate, a threshold concentration of which is required for fructan production (Pontis, 1970; Pollock and Cairns, 1991) and for the induction of gene expression and enzyme activity (Wagner et al., 1986; Pollock and Cairns, 1991). The capability of the barley stem to synthesize fructans in periods of assimilate overload and to remobilize fructans in periods of assimilate shortage allows its transition from a sink tissue to a source tissue. As the latter, the stem is able to substantially contribute to grain filling and thus to yield. With the presented MMM approach, we were able to model the sink-to-source transition of the barley stem during seed development, thereby quantifying the contribution of the stem to the deposition of starch in the seeds. The simulated contribution of the barley stem to seed filling of up to 33% at 70 DAS is in good agreement with measurements/rough estimates already given: for barley, 11% to 44% (Schnyder, 1993; Housley, 2000); for wheat, 20% to 30% (Rawson and Evans, 1971; Gebbing and Schnyder, 1999; Wardlaw and Willenbrink, 2000) or 20% to 40% (Dreccer et al., 2009).

Here, we present, to our knowledge for the first time, a systemic metabolic analysis of the interactions between vegetative (stem) and generative (seed) biomass as important processes of yield formation in plants. As reported by Daniels et al. (1982), grain yields and stem dry weight are positively correlated in barley, thus pointing to the importance of alternative carbohydrate storage pools in the analysis of source-sink interactions. The presented modeling framework forms the basis for future studies on adequate nutrient partitioning among plant organs, the optimization of which is one of the most important breeding strategies for grasses in order to increase harvest index (Reynolds et al., 2011).

CONCLUSION

Combining highly detailed, compartmentalized static metabolic models on the organ scale (barley seed, leaf, stem) and a dynamic, functional multiorgan model on the whole-plant scale, the presented novel modeling approach allows for integrating metabolic and physiological processes of carbon and nitrogen balance from subcellular metabolic processes up to growth and yield formation of the whole plant. The steady-state models are concatenated along a developmental time axis, resulting in a dFBA on a whole-plant level. Overall, the new multiscale modeling approach enables the systemic analysis of source-sink interaction during barley development resolved down to the level of single metabolic reactions. This method was applied here to simulate the source-to-sink shift of the barley stem. It provides the basis for future analyses of metabolic and physiological mechanisms controlling carbon partitioning, thereby contributing to the identification and optimization of strategies for the improvement of yield formation in an important crop plant. The underlying mathematical method is not restricted to barley but can easily be applied to other (crop) plants.

MATERIALS AND METHODS

Model Reconstruction

Multiorgan FBA Model

The organ-specific stoichiometric models of leaf, stem, and seed metabolism of the barley (Hordeum vulgare) plant were reconstructed following the reconstruction procedure described by Grafahrend-Belau et al. (2009b). A detailed description of integrating the validated organ-specific FBA models into a multiorgan model is given in “Results.”

Multiscale FPM

The multiscale FPM ProNet-CN was formulated in terms of a dynamic process network that integrates condensed submodels of the main processes of the formation and allocation of the principal carbon and nitrogen compounds and of the resulting biomass formation across different plant scales. Model formulation is outlined in “Results” and described in detail by Mueller et al. (2012).

dFBA

The primary metabolism of the barley plant was analyzed within the framework of FBA (Edwards et al., 1999). FBA is a constraint-based modeling approach developed to predict metabolic steady-state fluxes by applying mass balance constraints to a stoichiometric model. Assuming steady-state conditions, the system of mass balance equations derived from a metabolic model of n reactions and m metabolites can be represented as:

graphic file with name pp_224006_E1.jpg

with

graphic file with name pp_224006_E2.jpg

where S is the stoichiometric matrix (m × n) and v is a flux vector of n metabolic fluxes, with αi as the lower and βi as the upper bound for each vi, respectively.

FBA uses the principle of linear programming to solve the system of mass balance equations by defining an objective function and searching the solution space for an optimal flux distribution that meets a defined objective. A dynamic extension of the static FBA was described by Mahadevan et al. (2002), comprising a dynamic optimization approach and a SOA. In this paper, a derivative of the SOA was applied by dividing the selected growth phase (53–70 DAS) into 18 pseudo steady-state intervals and computing a static FBA constrained by static and dynamic constraints at each pseudo steady state. The dynamic constraints (C1–C7) were applied by taking the daily average of the exchange flux rates (hourly values) predicted by the dynamic FPM as a basis. With respect to the predicted leaf-specific rate of (1) Suc loading into the phloem (C1), (2) starch synthesis (C4), and (3) Suc transport into the vacuole (C5), the daily average was computed by summing up the hourly values of 10 leaves and taking the average. Asn (C2) and Gln (C3) exchange flux rates were computed by splitting up the nitrogen exchange flux rate predicted by the FPM according to the Asn-Gln ratio in the barley phloem sap reported by Winter et al. (1992). The computation of the dynamic constraints is described in Supplemental Table S4, a and b, and the resulting dynamic constraints are listed in Supplemental Table S4c. A description of the time-independent (static) constraints used in all simulations is given in Supplemental Table S2.

To take into account the variation of seed biomass composition during the generative phase of barley plant development, time-specific biomass expression was included for each static FBA simulation. Due to the scarcity of experimental data for the period examined, a time-specific biomass expression was generated by extrapolating seed biomass data experimentally determined for barley (genotype Golden Promise) seeds at 3 to 4 DAS, which corresponds to 53 to 55 DAS of the dynamic FPM. A detailed description of the computation of the time-specific biomass compositions is given in Supplemental Table S5.

With respect to the biomass composition of the stem required for the growth simulations of stem sink metabolism, biomass data reported for the mature stem were taken, assuming that the composition of biomass remains constant during the period examined, as expected for the end of stem extension growth. The biomass composition used to statically constrain stem growth is listed in Table II.

Table II. Biomass composition used to statically constrain stem growth.

Component Percentage of Stem Dry Weight Reference
Protein 1.529 Antongiovanni and Sargentini (1991)
Cellulose 38.939 Antongiovanni and Sargentini (1991)
HemicelluloseGlu 21.763 7.656 Antongiovanni and Sargentini (1991),Bonnett and Incoll (1993a, 1993b)
Fru 7.146 Bonnett and Incoll (1993a, 1993b)
Suc 6.125 Bonnett and Incoll (1993a, 1993b)
Fructans 16.843 Bonnett and Incoll (1993a, 1993b)
Open in a new tab

To reduce the impact of multiple optimal solutions that normally appear in FBA, at each pseudo steady state a static FBA was computed using the two-step optimization procedure shown in Table III. Assuming that barley plants make the most efficient use of the available carbon sources during the generative phase of plant development, the first step of the optimization procedure is to minimize the uptake of carbon sources (i.e. CO2 uptake into the leaf, remobilization of fructans in the stem) and the second step is to minimize the overall flux, ensuring maximal enzymatic efficiency. The computation was performed by adding the objective value of the first optimization as an additional constraint to the second optimization. All simulations were performed using the clp solver (COIN-OR Linear Program Solver; http://www.coin-or.org/Clp/index.html) within the COBRA Toolbox.

Table III. Two-step optimization procedure used in all simulations.

n, Total number of reactions in the model; vc, carbon uptake given by the uptake of CO2 into the leaf and the remobilization of fructans in the stem.

Step Optimization Objective Function Definition
1 Linear Minimize carbon uptake 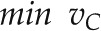Inline graphic
2 Quadratic Minimize overall flux 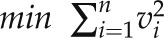Inline graphic
Open in a new tab

Generation of Metabolic Flux Maps

To get insight into the flux distributions characterizing seed, stem, and leaf metabolism during the early (50–58 DAS) and late (59–70 DAS) seed storage phases, metabolic flux maps depicting the central metabolic processes of the organ-specific light metabolism were generated for each developmental stage (early seed development, 56 DAS, 2 pm; late seed development, 66 DAS, 2 pm). Following the procedure described above, the dynamic constraints used for model simulation were computed by taking the exchange flux rates predicted by the dynamic FPM at 2 pm for 56 and 66 DAS as a basis. The computation of the dynamic constraints is described in Supplemental Table S6, a and b, and the resulting dynamic constraints are listed in Supplemental Table S6c.

The log-ratio flux map was generated by computing the log ratio for a given network reaction, ri, as follows:

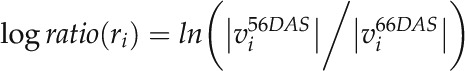graphic file with name pp_224006_E3.jpg

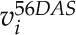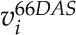where Inline graphic and Inline graphic correspond to the simulated flux values of ri at 56 (2 pm) and 66 (2 pm) DAS, respectively. Based on the resulting log-ratio values, the log-ratio flux map was created using FBA-SimVis (Grafahrend-Belau et al., 2009a).

Supplemental Data

The following materials are available in the online version of this article.

Acknowledgments

We thank Dr. Jan Hüge for providing parameters for seed biomass composition.

Glossary

FBA

flux balance analysis

dFBA

dynamic flux balance analysis

SOA

static optimization approach

MMM

multiscale metabolic modeling

FPM

functional plant model

DAS

days after sowing

TCA

tricarboxylic acid

References

  1. Antongiovanni M, Sargentini C. (1991) Variability in chemical composition of straws. Options Mediterraneennes Serie Seminaires 16: 49–53 [Google Scholar]
  2. Blacklow WM, Darbyshire B, Pheloung P. (1984) Fructans polymerized and de-polymerized in the internodes of winter wheat as grain filling progressed. Plant Sci Lett 36: 213–218 [Google Scholar]
  3. Bonnett GD, Incoll LD. (1993a) Effects on the stem of winter barley of manipulating the source and sink during grain-filling. 1. Changes in accumulation and loss of mass from internodes. J Exp Bot 44: 75–82 [Google Scholar]
  4. Bonnett GD, Incoll LD. (1993b) Effects on the stem of winter barley of manipulating the source and sink during grain-filling. 2. Changes in the composition of water-soluble carbohydrates of internodes. J Exp Bot 44: 83–91 [Google Scholar]
  5. Boyle NR, Morgan JA. (2009) Flux balance analysis of primary metabolism in Chlamydomonas reinhardtii. BMC Syst Biol 3: 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Boyle NR, Morgan JA. (2011) Computation of metabolic fluxes and efficiencies for biological carbon dioxide fixation. Metab Eng 13: 150–158 [DOI] [PubMed] [Google Scholar]
  7. Brady SM, Orlando DA, Lee JY, Wang JY, Koch J, Dinneny JR, Mace D, Ohler U, Benfey PN. (2007) A high-resolution root spatiotemporal map reveals dominant expression patterns. Science 318: 801–806 [DOI] [PubMed] [Google Scholar]
  8. Braune H, Müller J, Diepenbrock W. (2009) Integrating effects of leaf nitrogen, age, rank, and growth temperature into the photosynthesis-stomatal conductance model LEAFC3-N parameterised for barley (Hordeum vulgare L.). Ecol Modell 220: 1599–1612 [Google Scholar]
  9. Cheung CY, Williams TC, Poolman MG, Fell DA, Ratcliffe RG, Sweetlove LJ. (2013) A method for accounting for maintenance costs in flux balance analysis improves the prediction of plant cell metabolic phenotypes under stress conditions. Plant J (in press) [DOI] [PubMed] [Google Scholar]
  10. Cogne G, Rügen M, Bockmayr A, Titica M, Dussap CG, Cornet JF, Legrand J. (2011) A model-based method for investigating bioenergetic processes in autotrophically growing eukaryotic microalgae: application to the green algae Chlamydomonas reinhardtii. Biotechnol Prog 27: 631–640 [DOI] [PubMed] [Google Scholar]
  11. Dal’Molin CG, Quek LE, Palfreyman RW, Brumbley SM, Nielsen LK. (2010) C4GEM, a genome-scale metabolic model to study C4 plant metabolism. Plant Physiol 154: 1871–1885 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Dal’Molin CG, Quek LE, Palfreyman RW, Nielsen LK. (2011) AlgaGEM: a genome-scale metabolic reconstruction of algae based on the Chlamydomonas reinhardtii genome. BMC Genomics (Suppl 4) 12: S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Daniels RW, Alcock MB, Scarisbrick DH. (1982) A reappraisal of stem reserve contribution to grain yield in spring barley (Hordeum vulgare L.). J Agric Sci 98: 347–355 [Google Scholar]
  14. de Oliveira Dal’Molin CG, Quek LE, Palfreyman RW, Brumbley SM, Nielsen LK. (2010) AraGEM, a genome-scale reconstruction of the primary metabolic network in Arabidopsis. Plant Physiol 152: 579–589 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Dreccer MF, van Herwaarden AF, Chapman SC. (2009) Grain number and grain weight in wheat lines contrasting for stem water soluble carbohydrate concentration. Field Crops Res 112: 43–54 [Google Scholar]
  16. Edwards JS, Ramakrishna R, Schilling CH, Palsson BO (1999) Metabolic flux balance analysis. In SY Lee, ET Papoutsakis, eds, Metabolic Engineering. Marcel Dekker, New York, pp 13–57 [Google Scholar]
  17. Farrar SC, Farrar JF. (1986) Compartmentation and fluxes of sucrose in intact leaf blades of barley. New Phytol 103: 645–657 [Google Scholar]
  18. Feng X, Xu Y, Chen Y, Tang YJ. (2012) Integrating flux balance analysis into kinetic models to decipher the dynamic metabolism of Shewanella oneidensis MR-1. PLoS Comput Biol 8: e1002376. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gallagher JN, Biscoe PV, Scott RK. (1975) Barley and its environment. V. Stability of grain weight. J Appl Ecol 12: 319–336 [Google Scholar]
  20. Gebbing T, Schnyder H. (1999) Pre-anthesis reserve utilization for protein and carbohydrate synthesis in grains of wheat. Plant Physiol 121: 871–878 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Giersch C. (2000) Mathematical modelling of metabolism. Curr Opin Plant Biol 3: 249–253 [PubMed] [Google Scholar]
  22. Grafahrend-Belau E, Klukas C, Junker BH, Schreiber F. (2009a) FBA-SimVis: interactive visualization of constraint-based metabolic models. Bioinformatics 25: 2755–2757 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Grafahrend-Belau E, Schreiber F, Koschützki D, Junker BH. (2009b) Flux balance analysis of barley seeds: a computational approach to study systemic properties of central metabolism. Plant Physiol 149: 585–598 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Grusak MA, DellaPenna D. (1999) Improving the nutrient composition of plants to enhance human nutrition and health 1. Annu Rev Plant Physiol Plant Mol Biol 50: 133–161 [DOI] [PubMed] [Google Scholar]
  25. Hay J, Schwender J. (2011a) Computational analysis of storage synthesis in developing Brassica napus L. (oilseed rape) embryos: flux variability analysis in relation to 13C metabolic flux analysis. Plant J 67: 513–525 [DOI] [PubMed] [Google Scholar]
  26. Hay J, Schwender J. (2011b) Metabolic network reconstruction and flux variability analysis of storage synthesis in developing oilseed rape (Brassica napus L.) embryos. Plant J 67: 526–541 [DOI] [PubMed] [Google Scholar]
  27. Hjersted JL, Henson MA. (2006) Optimization of fed-batch Saccharomyces cerevisiae fermentation using dynamic flux balance models. Biotechnol Prog 22: 1239–1248 [DOI] [PubMed] [Google Scholar]
  28. Housley TL. (2000) Role of fructans redistributed from vegetative tissues in grain filling of wheat and barley. Dev Crop Sci 26: 207–221 [Google Scholar]
  29. Kinghorn AD, Pan L, Fletcher JN, Chai H. (2011) The relevance of higher plants in lead compound discovery programs. J Nat Prod 74: 1539–1555 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Knoop H, Zilliges Y, Lockau W, Steuer R. (2010) The metabolic network of Synechocystis sp. PCC 6803: systemic properties of autotrophic growth. Plant Physiol 154: 410–422 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Krauss M, Schaller S, Borchers S, Findeisen R, Lippert J, Kuepfer L. (2012) Integrating cellular metabolism into a multiscale whole-body model. PLoS Comput Biol 8: e1002750. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Lakshmanan M, Zhang Z, Mohanty B, Kwon J, Choi H, Nam H, Kim D, Lee D. (2013) Elucidating rice cell metabolism under flooding and drought stresses using flux-based modeling and analysis. Plant Physiol 162: 2140–2150 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Lewis NE, Schramm G, Bordbar A, Schellenberger J, Andersen MP, Cheng JK, Patel N, Yee A, Lewis RA, Eils R, et al. (2010) Large-scale in silico modeling of metabolic interactions between cell types in the human brain. Nat Biotechnol 28: 1279–1285 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lu C, Napier JA, Clemente TE, Cahoon EB. (2011) New frontiers in oilseed biotechnology: meeting the global demand for vegetable oils for food, feed, biofuel, and industrial applications. Curr Opin Biotechnol 22: 252–259 [DOI] [PubMed] [Google Scholar]
  35. Luo R, Wei H, Ye L, Wang K, Chen F, Luo L, Liu L, Li Y, Crabbe MJ, Jin L, et al. (2009) Photosynthetic metabolism of C3 plants shows highly cooperative regulation under changing environments: a systems biological analysis. Proc Natl Acad Sci USA 106: 847–852 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Mahadevan R, Edwards JS, Doyle FJ., III (2002) Dynamic flux balance analysis of diauxic growth in Escherichia coli. Biophys J 83: 1331–1340 [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. McCree KJ (1970) An equation for the rate of respiration of white clover plants grown under controlled conditions. In I Setlik, ed, Prediction and Measurement of Photosynthetic Productivity. Pudoc, Wageningen, The Netherlands, pp 221–229 [Google Scholar]
  38. Melkus G, Rolletschek H, Fuchs J, Radchuk V, Grafahrend-Belau E, Sreenivasulu N, Rutten T, Weier D, Heinzel N, Schreiber F, et al. (2011) Dynamic ¹³C/¹H NMR imaging uncovers sugar allocation in the living seed. Plant Biotechnol J 9: 1022–1037 [DOI] [PubMed] [Google Scholar]
  39. Metzger JO, Bornscheuer U. (2006) Lipids as renewable resources: current state of chemical and biotechnological conversion and diversification. Appl Microbiol Biotechnol 71: 13–22 [DOI] [PubMed] [Google Scholar]
  40. Mintz-Oron S, Meir S, Malitsky S, Ruppin E, Aharoni A, Shlomi T. (2012) Reconstruction of Arabidopsis metabolic network models accounting for subcellular compartmentalization and tissue-specificity. Proc Natl Acad Sci USA 109: 339–344 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Montagud A, Navarro E, Fernández de Córdoba P, Urchueguía JF, Patil KR. (2010) Reconstruction and analysis of genome-scale metabolic model of a photosynthetic bacterium. BMC Syst Biol 4: 156. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Morgan JA, Rhodes D. (2002) Mathematical modeling of plant metabolic pathways. Metab Eng 4: 80–89 [DOI] [PubMed] [Google Scholar]
  43. Mueller J, Eschenroeder A, Christen O, Junker BH, Schreiber F (2012) ProNet-CN model: a dynamic and multi-scale process network combining photosynthesis, primary carbon metabolism and effects of leaf nitrogen status. In M Kang, Y Dumont, Y Guo, eds, 4th International Symposium on Plant Growth Modeling, Simulation, Visualization and Applications, 31st. Oct.–3rd Nov. 2012, Shanghai, China. Institute of Electrical and Electronics Engineers, pp 289–296 [Google Scholar]
  44. Mueller J, Wernecke P, Diepenbrock W. (2005) LEAFC3-N: a nitrogen-sensitive extension of the CO2 and H2O gas exchange model LEAFC3 parameterised and tested for winter wheat (Triticum aestivum L.). Ecol Modell 183: 183–210 [Google Scholar]
  45. Oddone GM, Mills DA, Block DE. (2009) A dynamic, genome-scale flux model of Lactococcus lactis to increase specific recombinant protein expression. Metab Eng 11: 367–381 [DOI] [PubMed] [Google Scholar]
  46. Orth JD, Thiele I, Palsson BO. (2010) What is flux balance analysis? Nat Biotechnol 28: 245–248 [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Parmar A, Singh NK, Pandey A, Gnansounou E, Madamwar D. (2011) Cyanobacteria and microalgae: a positive prospect for biofuels. Bioresour Technol 102: 10163–10172 [DOI] [PubMed] [Google Scholar]
  48. Pilalis E, Chatziioannou A, Thomasset B, Kolisis F. (2011) An in silico compartmentalized metabolic model of Brassica napus enables the systemic study of regulatory aspects of plant central metabolism. Biotechnol Bioeng 108: 1673–1682 [DOI] [PubMed] [Google Scholar]
  49. Pollock CJ, Cairns AJ. (1991) Fructan metabolism in grasses and cereals. Annu Rev Plant Physiol Plant Mol Biol 42: 77–101 [Google Scholar]
  50. Pontis H. (1970) The role of sucrose and fructosylsucrose in fructosan metabolism. Physiol Plant 23: 1089–1100 [Google Scholar]
  51. Poolman MG, Assmus HE, Fell DA. (2004) Applications of metabolic modelling to plant metabolism. J Exp Bot 55: 1177–1186 [DOI] [PubMed] [Google Scholar]
  52. Poolman MG, Miguet L, Sweetlove LJ, Fell DA. (2009) A genome-scale metabolic model of Arabidopsis and some of its properties. Plant Physiol 151: 1570–1581 [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Radrich K, Tsuruoka Y, Dobson P, Gevorgyan A, Swainston N, Baart G, Schwartz JM. (2010) Integration of metabolic databases for the reconstruction of genome-scale metabolic networks. BMC Syst Biol 4: 114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Rawson HM, Evans LT. (1971) The contribution of stem reserves to grain development in a range of wheat cultivars of different height. Aust J Agric Res 22: 851–863 [Google Scholar]
  55. Reynolds M, Bonnett D, Chapman SC, Furbank RT, Manès Y, Mather DE, Parry MA. (2011) Raising yield potential of wheat. I. Overview of a consortium approach and breeding strategies. J Exp Bot 62: 439–452 [DOI] [PubMed] [Google Scholar]
  56. Rios-Estepa R, Lange BM. (2007) Experimental and mathematical approaches to modeling plant metabolic networks. Phytochemistry 68: 2351–2374 [DOI] [PubMed] [Google Scholar]
  57. Rogalski M, Carrer H. (2011) Engineering plastid fatty acid biosynthesis to improve food quality and biofuel production in higher plants. Plant Biotechnol J 9: 554–564 [DOI] [PubMed] [Google Scholar]
  58. Rolletschek H, Melkus G, Grafahrend-Belau E, Fuchs J, Heinzel N, Schreiber F, Jakob PM, Borisjuk L. (2011) Combined noninvasive imaging and modeling approaches reveal metabolic compartmentation in the barley endosperm. Plant Cell 23: 3041–3054 [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Saha R, Suthers PF, Maranas CD. (2011) Zea mays iRS1563: a comprehensive genome-scale metabolic reconstruction of maize metabolism. PLoS ONE 6: e21784. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Schnyder H. (1993) The role of carbohydrate storage and redistribution in the source-sink relations of wheat and barley during grain filling: a review. New Phytol 123: 233–245 [Google Scholar]
  61. Schwender J (2009) Introduction. In J Schwender, ed, Plant Metabolic Networks. Springer, New York, pp 1–7 [Google Scholar]
  62. Scott RK, Dennis-Jones R. (1976) The physiological background of barley. J Natl Inst Agric Bot 14: 182–187 [Google Scholar]
  63. Sweetlove LJ, Ratcliffe RG. (2011) Flux-balance modeling of plant metabolism. Front Plant Sci 2: 38. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Tilman D, Hill J, Lehman C. (2006) Carbon-negative biofuels from low-input high-diversity grassland biomass. Science 314: 1598–1600 [DOI] [PubMed] [Google Scholar]
  65. Wagner W, Wiemken A, Matile P. (1986) Regulation of fructan metabolism in leaves of barley (Hordeum vulgare L. cv Gerbel). Plant Physiol 81: 444–447 [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Wardlaw IF, Willenbrink J. (2000) Mobilization of fructan reserves and changes in enzyme activities in wheat stems correlate with water stress during kernel filling. New Phytol 148: 413–422 [DOI] [PubMed] [Google Scholar]
  67. Williams TC, Poolman MG, Howden AJ, Schwarzlander M, Fell DA, Ratcliffe RG, Sweetlove LJ. (2010) A genome-scale metabolic model accurately predicts fluxes in central carbon metabolism under stress conditions. Plant Physiol 154: 311–323 [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Winter H, Lohaus G, Heldt HW. (1992) Phloem transport of amino acids in relation to their cytosolic levels in barley leaves. Plant Physiol 99: 996–1004 [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Yang J, Zhang J, Wang Z, Zhu Q, Liu L. (2004) Activities of fructan- and sucrose-metabolizing enzymes in wheat stems subjected to water stress during grain filling. Planta 220: 331–343 [DOI] [PubMed] [Google Scholar]

Articles from Plant Physiology are provided here courtesy of Oxford University Press

RESOURCES