Amino acid composition of proteins reduces deleterious impact of mutations

Abstract

The evolutionary origin of amino acid occurrence frequencies in proteins (composition) is not yet fully understood. We suggest that protein composition works alongside the genetic code to minimize impact of mutations on protein structure. First, we propose a novel method for estimating thermodynamic stability of proteins whose sequence is constrained to a fixed composition. Second, we quantify the average deleterious impact of substituting one amino acid with another. Natural proteome compositions are special in at least two ways: 1) Natural compositions do not generate more stable proteins than the average random composition, however, they result in proteins that are less susceptible to damage from mutations. 2) Natural proteome compositions that result in more stable proteins (i.e. those of thermophiles) are also tuned to have a higher tolerance for mutations. This is consistent with the observation that environmental factors selecting for more stable proteins also enhance the deleterious impact of mutations.

Amino acid composition, or the occurrence frequency of amino acids in proteins, is well-conserved from species to species¹,². Fig. 1A depicts the average proteome composition of a diverse set of prokaryotes with complete proteome sets³. Fluctuations around the average, marked by the error bars, are small compared to the mean. Deviations from the average composition have been linked to cellular organization (i.e. integral membrane proteins)⁴, gene expressivity⁵, and enhancement of protein stability in response to environmental pressures, such as sulphur-starvation⁶ and high ambient temperatures⁷,⁸,⁹. Occurrence frequencies of amino acids in a protein are not set solely by functional constraints. In fact, almost all residues in a protein are “canonical,” in that they can be replaced without a change in functionality¹⁰,¹¹,¹²,¹³. Amino acid composition then is influenced by subtle selection pressures operating outside of a simple requirement for each protein's biological functionality.

Figure 1. Amino acid interaction energies and occurrence frequencies.

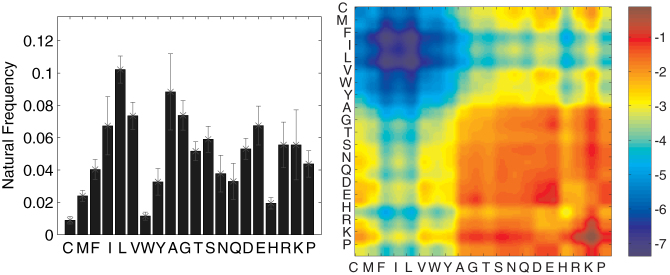
(Left A) Natural occurrence frequency of amino acids in complete proteome sets averaged over a wide variety of prokaryotes obtained from UniParc database (for a complete list see Supporting Table Information 1). Error bars denote one standard deviation fluctuations. The frequencies are well-conserved from species to species. (Right B) MJ matrix: inter-residue contact-energies between any two types of amino acids in units of k_BT, computed by Miyazawa and Jernigan³⁰.

It is also unlikely that the naturally observed amino acid composition is a historical accident. For example, in bacterial genomes the GC content's correlation with amino acid frequencies is weaker than expected¹⁴, indicative of a selective pressure maintaining protein composition close to an optimal value. The natural composition is also believed to minimize metabolic cost of amino acid biosynthesis in some organisms¹⁵. The number of codons corresponding to an amino acid is strongly correlated with its frequency¹⁶, implying that the composition might be an artifact of the genetic code. For a fixed genetic code, however, the amino acid composition can still vary with changes in the underlying genome sequence. These subtle changes in the amino acid composition of different organisms have shown to be important phenotypically, for instance distinguishing thermophiles from mesophiles⁷. If the amino acid composition is a product of evolution, what does it optimize? While it might be expected that composition is chosen to optimize thermodynamic stability of the desired native conformation (much like protein sequence), herein, we present evidence that amino acid composition minimizes the impact of residue substitutions (due to mutations, errors in transcription, and mistranslations) on protein structure.

The native folded state of a protein is sensitively dependent on its primary sequence. It has been argued, however, that the properties of the denatured states are self-averaging, so that they depend on the amino acid composition rather than the specific protein sequence¹⁷,¹⁸. For a given organism, we consider an ‘average' protein with a composition equal to the amino acid frequency in its complete proteome set. This is an approximation since the proteome composition does not necessarily reflect the composition of individual proteins. Moreover, not all proteins in the proteome have a native folded structure. These intrinsically disordered proteins¹⁹,²⁰ are not amenable to same analysis as ordered proteins. Nevertheless, we will show that our simple model of optimizing structural stability for a fixed composition is a useful metric for comparing proteome compositions of different organisms. Whenever possible, we compare the model's prediction to experimental observations to ensure validity of the assumptions.

Our physical model uses tools from statistical physics, in particular the well-studied random-energy model for proteins¹⁸,²¹,²² implemented in sequence space²²,²³. These models estimate properties of the optimal sequence by incorporating average interactions and the total number of possible sequences (design space), computed from sequence size and the number of amino acid types (20). Number of distinct amino acids types, however, is dependent on the specific form of the interactions. For example, two different residues that interact almost identically with all the other residues, are effectively one residue type. Since many amino acids are energetically similar, the effective number of amino acid types is much smaller than 20. We improve on the existing models by introducing a novel method that accurately distinguishes residues based on their interactions as opposed to labels.

First, this method is used to estimate the thermodynamic stability of the native state of folded proteins, when sequence optimization is constrained to a fixed composition. We test its validity by computing stability of proteins with amino acid composition corresponding to proteome composition of 75 prokaryotes with diverse optimal growth temperatures (OGTs)⁷ and complete proteome sets. Our estimate of stability correlates well with the OGT: higher protein stability implies a higher natural habitat temperature.

The organisms studied exhibit subtle deviations in their amino acid compositions (Fig. 1A). We asked if these distinct natural compositions were a product of selection, or alternatively random neutral drift, by comparing their attributes to a null hypothesis of random variant compositions, where each amino acid is assigned a random frequency drawn independently from a uniform distribution. Is there a property of natural proteome compositions that makes them significantly different from an average random composition? Our metrics for comparison are composition-based estimates of thermodynamic stability of proteins and their tolerance to missense mutations.

For mutation tolerance, we calculate the pair-wise similarity between residues for a given composition, by estimating stability of all subsets of amino acids. Similar amino acids reduce stability of a subset, for example a protein comprised of predominantly one hydrophobic residue type plus a negligible fraction of a hydrophilic residue type is less stable than one comprised of hydrophobic and hydrophilic residue types with equal frequencies. We verify the computed pair-wise similarity by comparing to what is expected from physical attributes of residues, such as charge and hydrophobicity. The composition-dependent pair-wise similarities computed have a striking resemblance to the observed pair-wise substitution rates between amino acids due to mutations. This is consistent with the observation that residues with similar physical properties are more likely to substitute each other. Since natural amino acid compositions seem to enhance this effect, we hypothesize that the natural compositions are tuned to mitigate the structural impact of mutations.

Natural proteome compositions can not be distinguished from an average random composition based on the estimated protein stability. However, they exhibit a tendency for minimizing impact of mutations; a significance of at best two standard deviations compared to the null hypothesis of random compositions. More importantly, thermodynamic stability of proteins with the natural compositions is positively correlated with their tolerance for mutations; a significance of six standard deviations. More stable proteins seem to have amino acid compositions that also minimize the deleterious impact of amino acid substitutions. This is consistent with the observation that the same environmental factors that select for more stable proteins, such as high temperature in the case of thermophiles, also enhance the deleterious impact of mutations²⁴. These observations suggest that the naturally-occurring amino acid compositions are under a selective pressure stemming from deleterious impact of mutations on protein structure.

The evolutionary connection between protein stability and mutation rates has been studied extensively²⁵,²⁶,²⁷,²⁸. For instance, Zeldovich et al. have placed a universal threshold on the maximum mutation rate before populations go extinct–mutational meltdown–which is lower for thermophiles compared with mesophiles²⁵. In general, evolution seems not to aspire for maximal protein stability but just enough to withstand deleterious mutations – selection-mutation balance²⁶,²⁷. As shown below, this is consistent with our observations on the role of protein composition.

Results

Estimating protein stability

It is worthwhile to define stability of a protein at the onset. Stability refers to the thermodynamic stability and is equivalent to the size of the energy gap (or the energy difference) between the native state and the first excited (misfolded) state. The energy of the native state is sensitively dependent on the sequence of the protein. For a given composition, we optimize the sequence to maximize the energy gap. The physiological stability of a protein corresponds to the probability of finding a protein in its native state at equilibrium, and depends on both the size of the energy gap and the temperature at which folding occurs. Thermophiles that have a higher energy gap, or higher thermodynamic stability, do not necessarily have a higher physiological stability since their proteins fold at a higher temperature.

Proteins are heteropolymers comprised of 20 different types of amino acids in a prescribed linear sequence. In the simplest picture, this linear sequence folds into a three-dimensional conformation that minimizes the free energy²⁹. The energy of a conformation is estimated by summing the pair-wise interaction energies of all amino acids which are in contact after folding. Closely following the pioneering approach in²¹, we consider the statistical properties of the energy of the native conformation. More precisely, instead of enumerating the energy of the native conformation for all possible sequences, we calculate the average energy (or any statistical moment of the energy) of the native state over randomly chosen sequences. We emphasize that this approach is a search in the sequence space with the protein conformation held fixed. The sequence that minimizes the energy of the fixed conformation is optimal. As we will discuss later, the energy of the optimal sequence is related to thermodynamic stability of the folded protein –a search in the conformation space.

The importance of amino acid composition enters in the statistical picture as follows: we assume that the pair-wise interaction between residue types i and j, with occurrence frequencies p_i and p_j respectively, occurs with probability p_ip_j in the folded configuration. This interaction contributes U_ijp_ip_j to the mean energy of the protein and 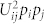to its second moment, where U_ij is the interaction energy of residue types i and j. Without loss of generality, assume that the mean interaction energy is zero.

For a protein comprised of N residues with coordination number z –typically 6 for proteins³⁰, there are Nz/2 pair-wise interactions in the folded configuration. We assume that all these interactions are independent and with statistical moments calculated above (Randomenergy assumption³¹). In the limit of large N, the energy of the native conformation E is a given by summing many independent random variables with mean zero and variance 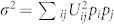. Central limit theorem implies that the distribution of E is a Gaussian with mean zero and variance N zσ²/2.

Of course, we are not interested in the energy of a random sequence, but rather that of the “optimal” sequence that minimizes E. The optimal sequence ensures that the protein folds into the desired native conformation in equilibrium. The statistical properties of the random sequences can help us estimate the energy of the optimal sequence. If we have A distinct type s of residues (alphabet size) with equal occurrence frequencies, there are A^N distinct amino acid sequences of length N. We can think of these A^N sequences as drawing A^N numbers independently from the distribution in Eq.(1). The expected minimum outcome of a number of draws from a Gaussian distribution is proportional to the square-root of the logarithm of the number of draws. The lowest expected energy of the A^N sequences is given by²³,³²,

Shakhnovich²³ introduced a method for incorporating composition into the above estimate. If the occurrence frequencies are not equal, the number of distinct sequences is given by N H({p}) in the large N limit, where H({p}) denotes the Shannon entropy³³ of the occurrence frequencies. The effective number of residue types is given by,

Plugging this into the alphabet size in Eq.(2) yields,

The estimate in Eq. (4), however, is still flawed because it neglects correlations in the interaction energies U_ij. We demonstrate this by using a simple example involving three residue types (for a full comparison of the two methods see Supporting Information).

Fig. 2 shows a three residue alphabet with equal occurrence frequencies. Eq.(3) implies an alphabet size of 3, or that number of distinct sequences is 3^N for a chain of N residues. However, the interaction matrix, U_i,j, is selected such that two of the residues are identical. We can describe the system then using two residues with modified frequencies. Eq. (3) now implies A = 1.9. Since σ is unchanged, these two equivalent descriptions of the same system give very different estimates of the lowest possible energy E_c (Eq. (2)). The discrepancy, of course, stems from the form of matrix U_ij. To correctly estimate E_c, it is imperative that interaction energies are taken into account. Namely, two residues are not different because they have different labels but because they interact with other residues differently.

Figure 2. Dependance of alphabet size on interaction energies.

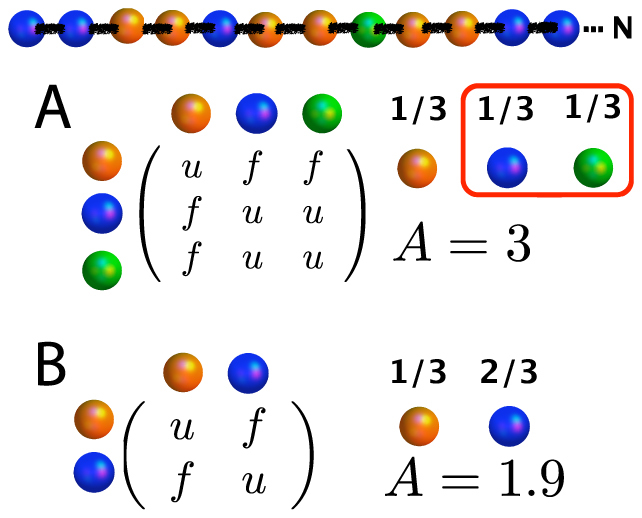
We want to determine the number of sequences of size 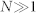comprised of three residue types (one example shown on top). (A) Three residues with equal frequencies implies A = 3 using Eq. (3), and 3^N possible sequences. The matrix shows the pairwise interaction energies between all the residue types. The blue and green residues, however, are identical energetically based on their interactions with the other residues. (B) The same system can be described using two residues, with modified frequencies. Now, A = 1.9, with only 1.9^N sequences.

Essentially, to do so, we will diagonalize the interaction matrix, and use the eigenvalues in place of energies. If two rows of U_ij are almost similar, one of the eigenvalues will be negligibly small. This will effectively remove redundancies in the alphabet. Moreover, we will introduce a set of quasi-residues with simple interactions that can be enumerated using Eq. (3). Since only energy differences are important, we set the mean to zero, by removing the (1 1 1 … 1) component of eigenvectors of matrix U and normalizing the eigenvalues accordingly. This is a more restrictive condition than simply setting the mean interaction energy to zero. We discard the component of interactions where all residues have the same mean interaction energy with a randomly chosen residue (from a uniform distribution). The remaining components highlight how different the residues are in terms of their interactions.

The second moment of the distribution of protein energies (denoted by σ before) takes the following form after diagonalization,

where index l (level) refers to the eigenvector with components 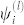, and eigenvalue λ^(l), satisfying 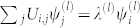. Eq. (5) is actually an approximation since we have brought to the outside the sum over eigenvectors. This decoupling is only true in the limit of uniform frequencies, since the eigenvectors are orthonormal for the real and symmetric U_ij.

Next, for each l, we introduce the quasi-residues and quasi-frequencies. The interaction strength between the quasi-residues is given by 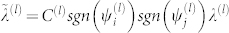, where 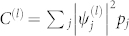is the normalization factor for quasi-frequencies defined below, and sgn denotes the sign function; sgn(x) = 1 for x ≥ 0, and sgn(x) = −1 for x < 0. The new interactions clearly only take the values ±C^(l)λ^(l). We will group all residues with positive eigencomponents 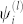into one quasi-residue type, and all the negative ones into another, defining quasi-frequencies,

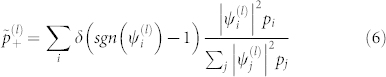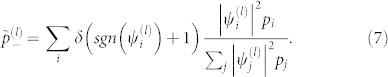The purpose of this seemingly arbitrary transformation is to achieve a simple 2-letter alphabet for each l (Fig. 3). We have absorbed all but the sign of the eigencomponents into the quasi-frequencies to create the simplest possible energetic interactions, which is easily enumerated using Eq. (3). The second moment of the energy distribution remains unchanged. However, the transformation inevitably changes the mean, which implies that σ is changed. However, this change is negligible in limit of large number of residue types with a random interaction matrix. We can easily estimate E_c for each l using Eq. (4). The overall E_c is a summation over the decoupled levels, and given by,

where 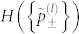is the Shannon entropy of probabilities 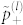and 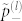. Above equation is the analogue of Eq. (2) but with the form of the interactions and the occurrence frequencies of residues taken into account. A series of assumptions were made in deriving this equation, mainly, large protein size and number of residue types, close to uniform occurrence frequencies, and an almost random interaction matrix. Whether these assumption are at all valid for proteins will be demonstrated below when we apply Eq. (8) to amino acids.

Figure 3. Estimating E_c for a general interaction matrix.

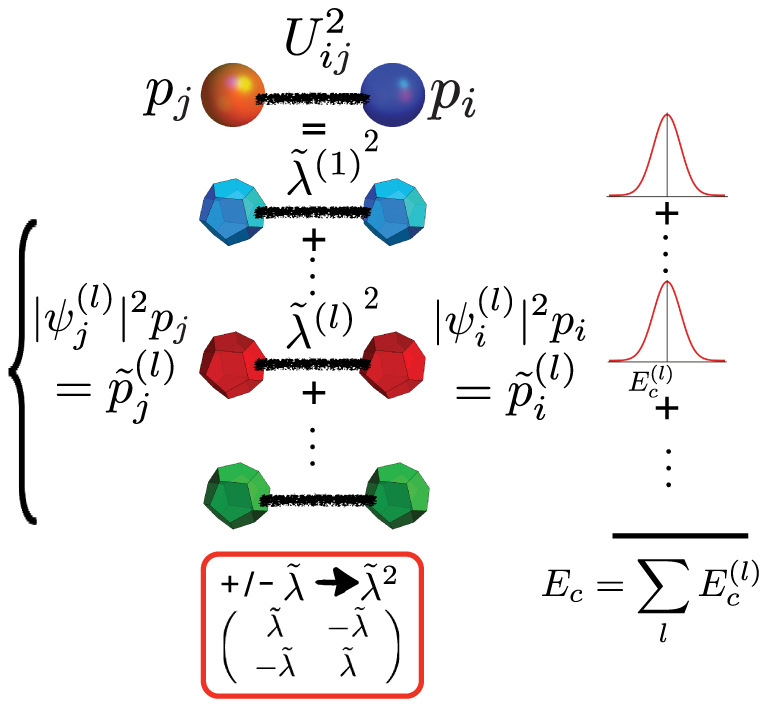
We are interested in the contribution to the second moment of the energy distribution from residue types i and j, with frequencies p_i and p_j and interaction energy U_ij. Diagonalization of interaction matrix U introduces a new set of quasi-residues (polyhedrals) with interaction energy given by 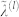and quasi-frequencies 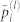. Each eigencomponent l has the simplified interaction matrix shown in the red box, for which 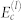can be easily estimated (Eq. (8)). The overall estimate of E_c is the summation of estimates for each l.

Although E_c is an estimate of the energy of the ground state, it is also a good metric for the size of the energy gap from the ground state to the first excited state. To accurately determine the energy gap, we need to repeat the above procedure in conformation-space as opposed to sequence-space. The energy of the first excited state can be approximated by keeping the sequence fixed and enumerating the energy of all the conformations. The conformation-space analogue of Eq.(2) –neglecting the frequencies and form of the interaction for now– is²³,

where γ is the dimensionality of the conformation-space: there are approximately γ^N distinct folded conformations for a protein of size N. The energy gap can be approximated as 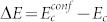²³. In this approximation, the sequence-space and conformation-space estimates of E_c are related by a constant factor, 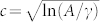, such that 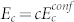. The proportionality factor c is a geometric factor that captures the difference in the dimensionality of sequence-space (alphabet size) and conformation-space. The energy gap, ΔE = (1 − c⁻¹)E_c, is proportional to E_c.

We can make a similar argument when taking into account the frequencies of the amino acids and the details of the interactions (Eq.(8)). The energy of different conformations will also exhibit correlations stemming from the detailed form of U_ij. The dimensionality of the conformation-space is effectively reduced (γ → γ_eff) by these correlations, much like the alphabet size (A → A_eff). With no prior information on the allowed conformations, we expect that the relative dimensionality of sequence and conformations spaces remains the same, namely, 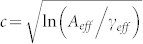. Naively, we expect the energies of the first excited state and the native ground state to scale in the same way with composition. Comparing E_c of different amino acid compositions then is equivalent to comparing their energy gaps up to a fixed scaling factor. E_c will be our metric for thermodynamic stability of an average protein constrained to a fixed composition. Of course, this is an approximation. A more accurate estimate of the energy gap requires more sophisticated methods for enumerating the allowed conformations.

Estimating stability of real proteome compositions

A low E_c (well-below the mean zero) implies a ground state which is well-isolated from the excited denatured states. This means that the protein is more thermodynamically stable because it has a larger folding gap. Biologically, more thermodynamically stable proteins are expected to occur in thermophilic organisms, which also exhibit a distinct amino acid composition (see for example7). To test the validity of the above method, we computed E_c for 75 prokaryotic organism that have optimal growth temperatures (OGTs) ranging from 8 C to 100 C (see Supporting Information Table 1 for a complete list). The composition for each organism is taken as the average amino acid occurrence frequencies in its complete proteomes set (obtained from³) and its OGT from⁷. We also assume that the average proteome composition accurately reflects the average protein composition. The contact interaction energies of amino acids are given by the Miyazawa-Jernigan (MJ) matrix (Fig. 1)³⁰. Despite its crudeness³⁴,³⁵, MJ matrix adequately captures the major attributes of amino acid interactions –i.e. hydrophobicity, polarity, etc., for this analysis.

Fig. 4A plots E_c as a function of OGT. Organisms with higher OGT have more thermodynamically stable proteins (more negative E_c). The magnitude of the correlation coefficient between E_c and OGT is 0.60 ± 0.11. The statistical error on the correlation coefficient is calculated by randomly shuffling the OGTs for fixed proteome sets. We note that higher correlations have been reported in exhaustive studies that directly compare compositions of subgroups of amino acids to the OGT (see for example7). The crudeness of OGT data, however, makes it unclear whether these enhanced correlations are physically significant or statistical artifacts. Moreover, the method proposed above has a physical motivation (estimation of folding gap using the random energy model) and requires no a priori categorization of the amino acids. The only inputs are the amino acid interaction energies and the amino acid composition.

Figure 4. Estimating E_c for real proteomes.

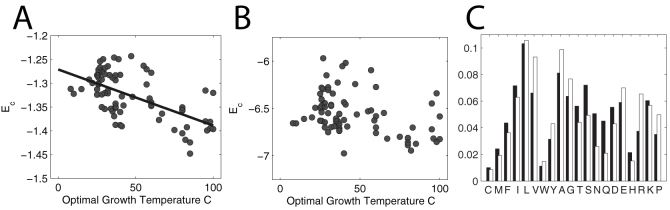
(A) Computed E_c as a function of optimal growth temperature (OGT). The correlation coefficient is 0.60 ± 0.11. More stable proteins, lower E_c, are found in thermophiles. (B) Same plot as in A but with E_c computed using Eq.4. The correlation coefficient is now significantly smaller 0.39 ± 0.10. E_c is overestimated because the alphabet size is overestimated; moreover, the E_c estimate in A discards the components of interactions that are the same for all residues. (C) Composition difference between organism with lowest OGT (black) and highest OGT (white).

To see if accounting for the interactions U_ij in the estimate of E_c is a move in the right direction, we compared the correlation between OGT and E_c estimated using Eq.(8) to that using Eq.(4). Fig. 4B shows the same plot but with E_c calculated using Eq.(4); the correlation is significantly smaller. It is reassuring that the proposed method on estimating E_c can capture the subtle composition differences between mesophiles and thermophiles (Fig. 4B).

How special are the natural amino acid compositions? It is conceivable that the natural proteome compositions are tuned to ensure a low E_c or high thermodynamical stability. We compared E_c of the natural proteome composition to that of random variant compositions. No prior was assumed on the random compositions (we will include the bias from the genetic code later); each amino acid frequency was independently drawn from a uniform distribution. These random compositions can be thought of as various plausible occurrences of historical accidents. If the natural compositions were under no selection pressure and simply a historical accident, we would expect a behavior similar to the average random composition.

In Fig. 5A, we have compared E_c of MJ matrix computed using the 75 natural proteome compositions (darker histogram) to E_c computed using random compositions (lighter histogram). The natural proteome compositions have an E_c similar (within one standard deviation) to the average E_c of the random compositions. This suggests that the natural compositions are not selected to optimize thermodynamic stability of proteins. However, it is possible that other composition-dependent metrics beside stability are under selection pressure. We consider the impact of mutations next.

Figure 5.

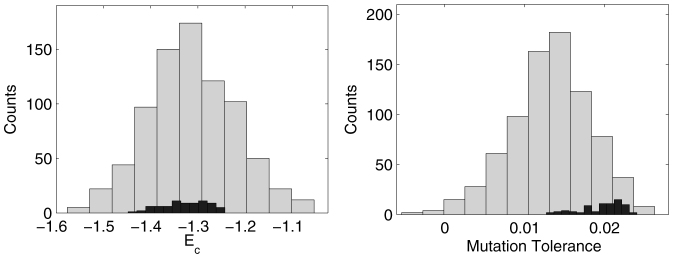
Are natural compositions special? (Left A) Histogram of E_c for the natural proteome composition (black) and random compositions from a uniform distribution (gray). The natural compositions have same average stability as an average random composition. (Right B) Histogram of 〈C〉 scores (i.e. mutation tolerance) for the same two samples. The natural compositions seem to outperform random compositions.

Quantifying interchangeability of amino acids

To achieve high thermodynamic stability, or a low E_c, we require a set of residues with the minimal redundancy. For example, one residue type A = 1 –homopolymer– will trivially have an E_c of zero (same as the energy mean) since all protein sequences would be identical. Maximum diversity A = 20 provides 20^N unique sequences for a protein of length N and the maximum number of designs for stabilizing the desired native conformation, or equivalently finding the lowest E_c (see Eq.(2)). As the diversity of interactions and residue types increases, E_c decreases.

As evident in Fig. 1B, amino acid interactions (rows of MJ matrix) are very redundant; many amino acids are energetically similar. To quantify this, we compared E_c of MJ matrix –for uniform residue frequencies– to that of random interaction matrices where each entry is drawn independently from a Gaussian distribution with the same variance as the MJ matrix. We computed the average and the standard deviation of E_c over the random interaction matrices. MJ matrix E_c is higher than the average E_c of the random matrices by roughly 8 standard deviations. Hence, the notion of alphabet size A = 20 for amino acids is not correct. For designing desired conformations, we have access to much less diversity in components types as the number of amino acids would imply.

Besides thermodynamic stability, a protein is under selection pressure to minimize structural damage caused by mutations. We hypothesize that the role of the amino acid composition is to minimize the impact of amino acid substitutions –due to mutations, errors in translations/transcriptions, on protein structure. To do so, we need to quantify how interchangeable two amino acids are.

If two amino acids are similar, their mutual presence in an alphabet reduces diversity. To quantify this, we consider all subgroups of amino acids, and count all pair-wise occurrences in subgroups that have low diversity. In particular, we calculate E_c for every 8-letter subgroup of the 20 amino acids. Note that there is nothing special about size 8. Same procedure can be conducted with different group sizes. 8-residues ensures reasonable statistics and easily tractable computations. For each of the 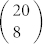subgroups, we use the original amino acid natural frequencies up to a normalization. The top 1000 subgroups with highest E_c, or equivalently lowest diversity, are selected. Pair-wise similarity is defined as the correlation coefficient of two amino acids being mutually present in the selected subgroups (see Methods). If two amino acids have a high (positive) correlation coefficient, their mutual presence effectively lowers the diversity, and they are considered similar. Conversely, amino acids that have low (negative) correlation coefficient, are energetically dissimilar, and are not found simultaneously in the set of low diversity subgroups. We stress that this correlation coefficient is not determined solely by the energetic interactions; composition is also important. For example, correlation coefficient of a pair of residues where one has negligible occurrence frequency is also negligible.

Fig. 6A shows all pair-wise correlation coefficients in a 20 × 20 matrix form (S_ij) for the average natural amino acid composition. Amino acids can be divided into similarity subgroups, where all pairs in a subgroup are highly correlated. We observe that the two dominant subgroups are comprised of either only hydrophobic residues or only hydrophilic residues. This division is the starting point of some simplified theoretical models of proteins³⁶, and is also consistent with previous studies on principal components of the MJ matrix³⁷. The correlation matrix, however, contains information beyond hydrophobicity. Amongst the hydrophilic residues, for example, aspartic acid (D) and glutamic acid (E) have a high similarity coefficient. This is expected since both residues are polar and negatively charged. More importantly, aspartic acid (D) and glutamic acid (E) are negatively correlated with lysine (K) and arginine (R), despite similar hydrophobicity measures³⁸. Physically, this stems from positive charge of lysine and arginine, and is not evident from a simple hydrophobic scale. We will use this method of quantifying residue similarity to understand the impact of missense mutations.

Figure 6. Amino acid pari-wise similarity and substitution rates.

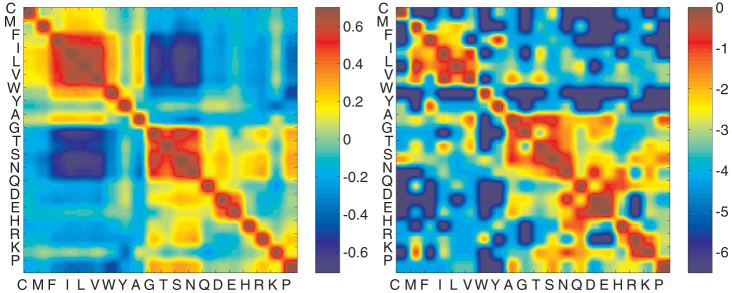
(Left A) Pair-wise similarity of amino acids, calculated from their energetic interactions (MJ matrix) and the average natural composition. There is a clear grouping of amino acids based on physical properties. Hydrophobic residues are most similar to each other, as are the hydrophilic residues. The similarity matrix, however, goes further and distinguishes residues based on charge. D and E are positively correlated because they are hydrophilic but also negatively charged. They are negatively correlated with residues K and R despite the same hydrophobicity measure, because K and R are charged positively. (Right B) PAM1 substitution matrix³⁹. Entry (i,j) is the logarithm of the probability of amino acid i substituting amino acid j after an evolutionary distance of one accepted point mutation for every 100 amino acids. This matrix has a striking resemblance to the correlation matrix.

An evolutionary justification

Fig. 6B shows PAM1 matrix –Point Accepted Mutation matrix, first composed by Dayhoff et al.³⁹. Entry (i,j) of this matrix is the probability of amino acid type i substituting an amino acid of type j, at an evolutionary distance of one accepted point mutation per 100 amino acids. Since this is very close evolutionary distance, the features of the matrix are set predominantly by mutational rates at the genome level, transcriptional/translational errors, and the genetic (codon) code, with little selection pressure⁴⁰. In fact, it is possible to compose a substitution matrix using synonymous mutation rates and the codon code –and hence no selection⁴¹, which captures the main features of PAM1 matrix (refer to Supporting Information).

There is a striking resemblance between PAM1 and the pair-wise correlation of amino acids computed in the last section (Fig. 6). This resemblance is a priori unexpected since the former is determined by mutation rates and the genetic code, and the latter computed from energetic interactions of amino acids and their frequencies. However, it implies the well-known observation that similar amino acids are more likely to substitute each other, thereby minimizing structural impact of mutations and misreadings⁴². For example, all hydrophobic residues have a common second base-pair in their codons, as do all hydrophilic residues, which minimizes phenotypic impact of single-point mutations⁴²,⁴³. This attribute of the genetic code is generally referred to as ‘error-minimizing'⁴³. A related connection between the MJ matrix and pair-wise substation rates has been reported in⁴⁴, where strongly-interacting pairs of amino acids are shown to substitute each other more frequently; this is attributed to correlated mutations that preserve the native structure of the protein.

To quantify impact of a mutation on protein structure, we weigh the similarity score with the probability of the substitution given by PAM1. This is a crude estimate but correctly reflects the biasses in the genetic code. Define the Mutation Tolerance Score 〈C〉 as,

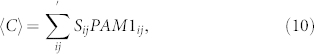where S_ij is the pair-wise similarity matrix calculated above (Fig. 6A), and PAM1_ij, entires of PAM1 matrix. The summation is over the non-diagonal elements (i ≠ j). The expected mutation tolerance 〈C〉 is higher, if more probable substitutions (high PAM1_ij) interchange amino acids with high pair-wise similarity (S_ij). The occurrence frequency of each residue is already accounted for in matrix S. A high 〈C〉 score is equivalent to a high tolerance to missense mutations.

Fig. 5B shows a histogram of 〈C〉, computed for the 75 natural proteome compositions (darker histogram) and random variant compositions (lighter histogram). As before, the random compositions assume no prior; frequency of each amino acid is drawn independently from a uniform distribution. Unlike thermodynamic stability (see Fig. 5A), tolerance to mutations seems to be enhanced in the natural compositions. We observe that at best a natural proteome composition has a tolerance that is higher than that of the average random composition by 2.2 standard deviations. This implies that the natural amino acid compositions –in conjunction with the genetic code– ensure that substitutions due to mutations or errors in transcription/translation, result in interchange of similar amino acids, thereby, minimizing impact on protein structure. Despite the intuitive nature of this result, the enhancement is not statistically significant enough to be of definite physical importance.

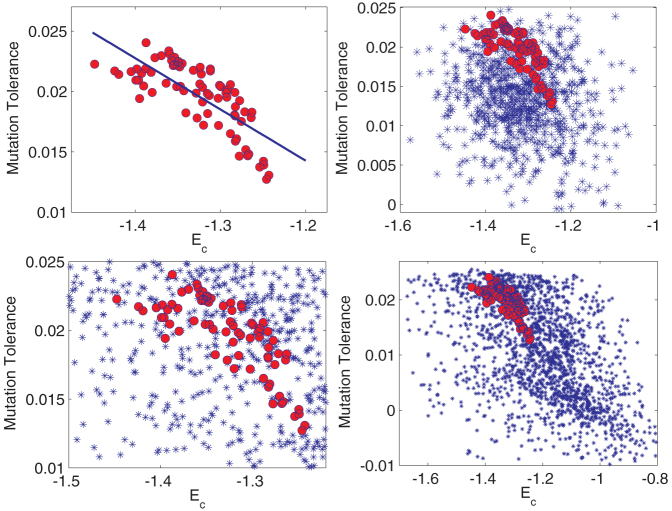
We need to explore other metrics to understand whether the amino acid composition of natural proteomes is under selection pressure. It has been observed that the same selection pressure that necessitates a higher thermodynamic stability also enhances the deleterious impact of mutations²⁴. In the case of thermophiles, mild mutations become deleterious, often lethal, with a temperature increase of 5–10°C²⁴. If the natural proteome compositions are under this selection pressure then there must exist a correlation between thermodynamic stability E_c and mutation tolerance 〈C〉. Fig. 7A shows that for the natural amino acid compositions, the two quantities are correlated with a correlation coefficient of 0.76 ± 0.12. More importantly, there is no correlation for the random compositions (see Fig. 7B), which implies a statistical significance of six standard deviations. This observation suggests that the natural amino acid compositions are highly tuned to exhibit a strong correlation between mutation tolerance and thermodynamic stability, consistent with the observation that the same evolutionary force that selects for thermodynamic stability also enhances deleterious impact of mutations.

Figure 7. Correlating thermodynamic stability and mutation tolerance.

(Top-Left, A) Thermodynamic stability (E_c) vs mutation tolerance (〈C〉 score). The correlation coefficient is 0.76 ± 0.12. (Top-Right, B) Same plot overlaid on that of random compositions (null-hypothesis) where each amino acid is assigned a random frequency independently drawn from a uniform distribution. There is no correlation for random compositions. Natural composition are tuned to increase tolerance for mutations with increasing thermodynamic stability, since both are under the same selection pressure. (Bottom, C and D) Bias of the genetic code. Same plot as (B) but the blue dots now denote stability and mutation tolerance for compositions constructed from applying the standard genetic code to random DNA sequences, where the frequency of each nucleotide type was drawn independently from a uniform distribution. The correlation between stability and mutation tolerance is negligible for random compositions even with the bias from the genetic code. (Bottom-Left, C) Same plot as D but zoomed in on the region of the natural proteome compositions.

Random compositions constructed with no prior (amino acid frequencies drawn independently from a uniform distribution) could be regarded as unphysical. For all the organisms considered, the deviations in amino acid composition come from underlying deviations in the genome sequence which is filtered in turn through the genetic code. The genetic code has not evolved over the time-scale of evolution of these organisms. It is conceivable that the bias introduced by the genetic code can potentially generate correlations between our metrics of mutation tolerance and thermodynamic stability. To test for this, we repeated the same analysis, but constructed the random compositions by applying the standard genetic code to randomly generated genomes (where the frequency of each nucleotide type was drawn independently from a uniform distribution).

As evident in Fig. 7C, the genetic code does not introduce a systematic bias. Random genomes also have negligible correlation between mutation tolerance and their estimated protein stability. Fig. 7D summarizes the unique characteristics of the natural proteome compositions. Natural proteome compositions (red circles) have similar stability E_c compared to amino acid composition of random genomes but generally higher tolerance to mutations (clustered to higher 〈C〉 Scores). More significantly, they exhibit a distinct correlation between stability and tolerance to mutations, which we attribute to a common selection pressure.

Discussion

The analysis outlined above contained one input parameter: amino acid composition. Protein stability was computed using a model that optimized the protein sequence constrained to a fixed composition. The model was a simplified lattice picture of protein folding, with the energetic interactions between amino acids given by the MJ matrix. We compared the estimated protein stability of 75 prokaryotic organisms (with a wide variety of proteome compositions) and verified the expected relationship between natural habitat temperature and stability (Fig. 4). To gauge how special the natural proteome compositions are, we compared their estimated protein stability to those from random compositions (a null hypothesis where each amino acid was assigned a frequency independently from a uniform distribution). Although a random composition is biologically meaningless, it best captures the null-hypothesis that protein composition might be a historical accident. The natural compositions result in the same thermodynamic stability as the average random composition. The variation of stability across the diverse set of organisms considered fell within one standard deviation of the variation in stability of the random compositions.

Our analysis also accounted for the impact of mutations on thermodynamic stability. A priori, the detrimental impact of an amino acid substitution is not clear, neither is its connection to thermodynamic stability. However, it is clear that composition plays a role on the severity of mutation damage. For a fixed genetic code and transcriptional/translational machinery (i.e. fixed probability of substitutions) the more frequent amino acids are more likely to be substituted. More subtly, composition also determines a given residue's neighboring amino acids in the folded state. It is unfavorable energetic interactions of a substituted residue with these neighbors that determines the energetic cost of a substitution. We proposed an estimate for mutation tolerance as a function of amino acid composition.

We compared both attributes, thermodynamic stability and mutation tolerance, of the natural amino acid compositions to those of random compositions. The purpose of this comparison was to discern how ‘special' the natural compositions are. Compared to random compositions, the natural compositions seem to be tuned to have a slightly higher tolerance for mutations (Fig. 5). The statistical significance of this effect (two sigmas) is not large enough to make it of definite physical importance. For each organism, we then compared its expected protein stability to its mutation tolerance.

Broadly, two effects might be expected from the role of composition on the relation between stability and mutation tolerance. On one hand, if an organism's composition is finely tuned to maximize stability (for example in a thermophile), the resulting energy gap might be so large that it can easily withstand the energetic cost of a deleterious amino acid substitution. This would imply that more thermodynamically stable compositions do not need to tune their mutation tolerance since the large gap makes mutations less detrimental. On the other hand, if the composition is only roughly tuned to optimize stability, and this is what the comparison to the random composition hinted at, then the energy gap is roughly constant, and the structural impact of an amino acid substitution is more detrimental in thermophiles because of the higher temperature. Consequently, it would be expected that these organism would finely tune their compositions to reduce the cost of mutations.

Recent findings support the latter picture: selective pressure does not generate the largest possible stability but enough to withstand the destabilizing impact of deleterious mutations²⁵,²⁷,²⁸. A mutation reduces the folding gap on average by roughly 1 kcal/mol (0.6 k_BT)²⁶; this is larger than the reduction in E_c (increase in the folding gap) observed above in thermophiles. Without the compensating effect of a much larger gap, mutations will be more destabilizing in thermophiles because of the elevated temperature. This is consistent with the lower mutational meltdown threshold –maximum permitted mutation rate– estimated for thermophiles compared with mesophiles²⁵,²⁶. The observation that the genome length of thermophiles is systematically shorter than that of mesophiles also validates a selective pressure that is dominated by destabilizing impact of mutations²⁵.

This is indeed what we observed from the protein compositions: a strong correlation between thermodynamic stability and mutation tolerance (Fig. 7). The statistical significance of this correlation (six standard deviations) compared to our null hypothesis, suggests that the natural proteome compositions are under a selective pressure to minimize the deleterious impact of missense mutations. For a more realistic null hypothesis, we also considered compositions constructed from applying the standard genetic code to random genomes (where each nucleotide was assigned a frequency independently drawn from a uniform distribution). The bias from the genetic code did not modify the statistical significance of the correlation observed for the natural compositions.

The intuitive explanation of the importance of composition in determining impact of substitutions on protein structure is as follows. First, the probability of a substitution of a residue is weighted by its frequency. If two residue types are rare, an occurrence of their substitution is also rare, which can enhance mutation tolerance if their substitution is especially detrimental. Moreover, to correctly estimate the structural damage of a substitution, we require knowledge of the residues adjacent to the substitution site. Composition allows us to better estimate an average ‘neighboring' residue.

It is worthwhile to restate the main assumptions going into the above analysis. First, it was assumed that protein composition was equal to the average composition of the complete proteome set of a given organism. This is clearly not true since for any given protein, the composition can fluctuate around this average depending on biological function, size, etc. We computed the distribution of E_c using the composition of individual proteins in a given organism's proteome set. The variation of E_c within an organism's proteome is at least 4 times smaller than the difference in E_c between mesophiles and thermophiles. Average proteome composition is a reasonable metric for estimating the stability of an organism's proteins.

Second, the role of disordered proteins was neglected. The optimization metric was assumed to be structural stability, which is irrelevant for proteins with disordered native states. The model used for predicting stability itself employed various approximations used in random energy model of proteins, such as a Gaussian distribution of energies and uncorrelated interactions. We also used the thermodynamic limit of number of residues in our analysis. All real proteins are finite in size; finite size corrections have been derived for the random energy model (REM)⁴⁵. Exhaustive enumeration of the folded conformations of finite-size proteins is in good agreement with REM predictions (see for instance²³ and¹⁷). Lastly, the energetic interactions between amino acids was taken from the MJ matrix, which has many limitations³⁴,³⁵. Nonetheless, a statistically significant correlation was observed when proteome composition of various organisms were compared to their optimal growth temperature (OGT), which suggested that despite the drastic approximations some information remained in the composition for determining thermodynamic stability.

The skeptical reader should treat our model as a ‘black box', which is verified by comparing its predictions to empirical observations. The predicted thermodynamic stability of natural proteomes is positively correlated with their optimal growth temperatures, despite crudeness of the temperature data. The analysis of quantifying impact of amino acid substitutions also used various approximations. If treated as a ‘black box', the confirmation for the method was displayed in Fig. 6A, where the computed pair-wise similarity of amino acids correctly captured physical attributes such as hydrophobicity and charge. In going from pair-wise similarity to the average impact of mutations, we had to use empirical values for mutation probabilities. The key biological assumption was using PAM1 matrix for determining the probability of a substitution (see the discussion above and Supporting Information). We also showed that natural amino acid compositions generating more thermodynamically stable proteins are also less susceptible to structural damage from amino acid substitutions. This is consistent with the observation that the same environmental factors that select for more stable proteins, such as high temperature in thermophiles, also enhance the deleterious impact of mutations²⁴.

For a fixed genetic code – i.e. substitution probabilities, it is possible that amino acid composition has evolved to minimize the structural impact of mutations. This is certainly true for the 75 prokaryotes considered in this analysis, which share the standard genetic code. On longer evolutionary time scales, it is also possible that the genetic code has evolved⁴⁶ to accommodate a composition constrained by other factors. The answer probably lies somewhere in between. Our results, however, imply that the natural amino acid compositions alongside the genetic code, minimize the impact of amino acid substitutions. Hence, amino acid composition can also be considered ‘error-minimizing.' This is consistent with previous observations that the genetic code is even more optimal, when impact of substitutions are weighted by their occurrence frequencies¹. It is worthwhile to repeat the above analysis for eukaryotic organisms. The connection between thermodynamic stability and mutation tolerance might disappear, since such organisms have more complex mechanisms to deal with selection pressures.

The above method for estimating heterogeneity of the amino acid alphabet (Eq.8) is completely general, and can be applied to any set of components with short-range interactions in equilibrium. This is potentially useful for understanding self-assembly in other biological systems, or designing artificial components that self-assemble into novel structures.

Methods

Matrix visualization

To visualize the 20 × 20 matrices in the paper, we replaced each entry by a 10 × 10 matrix of same value (resulting in a 200 × 200 matrix). A gaussian filter of size 8 × 8 with standard deviation of 3 was then applied, effectively creating contours between different regions of the original matrix, accentuating its features. Despite dependence of the contours on the ordering of amino acids, the size of the filter ensures that the center values remain unchanged. For amino acid correlation matrix (Fig. 6A) the diagonal entries are changed from 1 to the maximum non-diagonal value.

Pair-wise similarity

For all 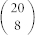residue subgroups of size 8, E_c was computed using Eq. (8) for the 8 × 8 interaction matrix of the subgroup and their normalized natural occurrence frequencies. The top 1000 subgroups with highest E_c were selected. We computed the probability of observing each residue type p_i in the selected subgroups, and the probability of mutual presence of a pair of residues p_i,j in one of the selected subgroups. The correlation coefficient is 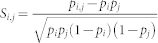. A high correlation coefficient implies high energetic similarity, resulting in a less diverse alphabet and higher E_c.

Author Contributions

S.H. is responsible for the entire content of this article.

Supplementary Material

Supplementary Information

Supplementary Information