Bioinspired tilt-angle fabricated structure gradient fibers: micro-drops fast transport in a long-distance

Abstract

Issues of surfaces, e.g., inspired from beetle's back, spider silk, cactus stem, etc., become the active area of research on designing novel materials in need of human beings to acquire fresh water resource from air. However, the design of materials on surface structure is little achieved on controlling of micro-scale drop transport in a long distance. Here, we report the ability of micro-drop transport in a long distance on a bioinspired Fibers with Gradient Spindle-knots (BFGS), which are fabricated by tilt angle dip-coating method. The micro-drop of ~0.25 μL transports in distance of ~5.00 mm, with velocity of 0.10–0.22 m s⁻¹ on BFGS. It is attributed to the multi-level cooperation of the release energy of drop coalescence along the gradient spindle-knots, in addition to capillary adhesion force and continuous difference of Laplace pressure, accordingly, water drops are driven to move fast directionally in a long distance on BFGS.

Biological models of water collection are revealed on natural surfaces with unique excellent-designed microstructures¹,²,³,⁴,⁵. For example, desert beetle's back is utilized to collect water from humid air because of alternate hydrophobic and hydrophilic micro-regions¹. A cacus O. Microdasys, which originates from the Chihuahua Desert, owning an integrated multifunctional system composed of well-distributed conical spines and trichomes on the cactus stem that facilitates efficient fog collection⁶. Besides a wonderful mechanical property⁷, the capture silk of spider has a water collecting ability resulted from a unique fiber structure that forms after the ‘wet-rebuilt’⁸ characterized by periodic ‘spindle-knots, joints’ structure made of random nanofibrils and aligned nanofibrils respectively. Inspired by the creature structure features⁹,¹⁰,¹¹,¹², biomimetic replications of water harvesting systems open the new way to design fog collection materials¹³,¹⁴,¹⁵. In previous researches, water collection materials have been designed by the cooperation of surface energy gradient¹⁶,¹⁷,¹⁸ and Laplace pressure in difference⁸. Some technologies have been utilized such as dip-coating³,⁴,⁵,⁶,⁷,⁸,⁹,¹⁰,¹¹,¹²,¹³,¹⁴, electrondynamics¹⁵, fluid-coating¹⁹, and micro-fluidic controlling techniques²⁰. These excellent materials are expected to apply in high efficiency water collection device²¹,²², humidity sensors²³,²⁴, fluid-controlling⁹, and micro-reactor devices²⁵,²⁶. However, the spindle-knot structures fabricated via previous coating method still limit to the water transport in distance, where the uniform as-distributed spindle-knots along fibers can't further drive the droplet to a long distance, e.g., the transport of micro-drop (e.g., ~0.25 μL) in long distance (e.g., ~5.00 mm) along the structure gradient fiber surface, which hasn't been reported so far. Here, to obtain a kind of material with directional water drop transport ability, a bioinspired fiber with gradient spindle-knots (BFGS) is designed carefully, and fabricated by the tilted dip-coating method based on the Rayleigh instability break-up into gradient droplets²⁷,²⁸,²⁹. It is found that the BFGS may realize the water transport in direction from smaller spindle-knots to bigger ones, which is not observed on the uniform fiber or uniform spindle-knot fiber. This finding opens a way to fabricate novel gradient functional fiber and offers the insight into the design of surface material to control the fluids movement.

Results

Fabrication and structure feature of bioinspired fibers

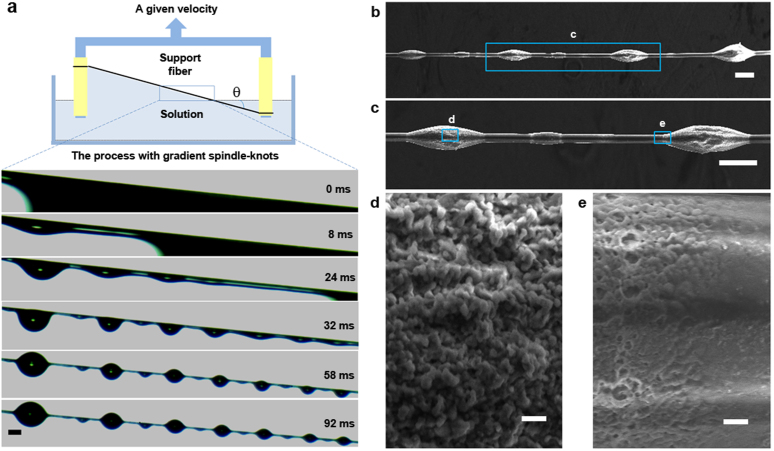
Inspired by water directional movement on wetted spider silk with spindle-knots, a new structure with gradient spindle-knots is designed to realize the fast directional movements of tiny drops in a long distance. Figure 1a shows the optical images on fabrication process of bioinspired fibers with gradient spindle-knots, via in-situ observation by using a high-speed CCD camera (Phantom v9.1, Vision Research, America). A uniform nylon fiber (~18 μm) is fixed on a support with θ angle to the horizontal line. The nylon fiber is firstly immersed into a polymer solution, Polyvinylidene Fluoride (PVDF, M_w = 530 000, Aldrich) dissolved in N,N-dimethylformamide (DMF), and then tilted-angle drawn out at a given velocity. As shown in Fig. 1a, initially, a slope PVDF film is covered on the fiber surface at the titled solid-liquid interface with gradient thickness (at 0 ms). And then it gradually spontaneously breaks into polymer droplets attributed to the Rayleigh instability¹,² beginning from up to down (at ~8–24 ms). The break-up process of the slope film is accompanied by the film sliding down (at ~8 ms). The polymer droplets automatically form symmetrical oval due to surface tension to reach the lowest energy. After stable condition of polymer droplets (in ~32–92 ms), the BFGS would be formed excellently from gradient polymer droplets (at ~92 ms). There are two reasons to explain the results of gradient spindle-knots. Firstly, the first spindle-knot forming at the earliest break place utilizes the surrounding solution to form the biggest one, which will lead to reduce the size of the second one. At the same reason, the next one is less than the previous one (Fig. 1a). Secondly, the solution covering on the fiber will gradually decrease resulting from sliding down. Some solution comes back to the solution reservoir due to the film rapidly sliding. The thickness of film is greatly related to the result of polymer droplet break up, it is estimated that the heights of polymer droplets are ranged from ~186 to ~51 μm in the time of ~92 ms, and the widths of them are ranged from ~289 to ~160 μm. When the solvent evaporate, the PVDF spindle-knots are formed along the fiber. As having been reported¹⁴, when the fiber is drawn out horizontally, the sizes of these PVDF spindle-knots are usually in the uniform distribution. Interestingly, the fiber is drawn out at a tilted angle to the horizontal line, and the polymer film can be gradient thickness. Thus result of the Rayleigh instability break-up induces the sizes of these PVDF spindle-knots to decrease gradually, accordingly, BFGS forms effectively.

Figure 1. Fabrication of BFGS and SEM images.

(a), The scheme shows the whole fabrication process. A uniform nylon fiber (~18 μm) fixed on a support is soaked into a polymer solution (PVDF/DMF) with θ angle to the horizontal line and then drawn out at a given velocity. The optical images show that a cylindrical PVDF film breaks into gradient polymer droplets beginning from up to down. The first spindle-knot is bigger than next one and so on. All the spindle-knots are sequence gradient in heights. (b), SEM images of BFGS with gradient four spindle-knots. (c), Two spindle-knots in the middle. (d), There are nano-protrusions at the maximum diameter of spindle-knot. (e), The random nano-porous structure at the minimum diameter of the spindle-knot (joint). Scale bars, 200 μm (a), 100 μm (b,c), 1 μm (d,e).

Microstructure on the surface of BFGS is observed by scanning electron microscopy (SEM, QuantaEFG250, FEI, America). Figure 1b–e show the SEM images of fiber (Fig. 1b) composed of four different sizes of spindle-knots from smaller to bigger. The height of spindle-knots are ~59 μm, ~74 μm, ~88 μm and ~118 μm, and the width of spindle-knots are ~162 μm, ~206 μm, ~235 μm and ~268 μm, respectively. The four spindle-knots open the half of apex-angles of ~25.0°, ~28.0°, ~28.5°, ~31.0° for geometry feature (smaller to bigger). Figure 1c shows the SEM images of two middle size spindle-knots as the representative. The right one is bigger than the left one. Figure 1c–d shows the gradient of roughness on the surface of spindle-knot and joint. There are nano-protrusions at the maximum diameter of the spindle-knot (Fig. 1c) and random nano-porous structure at the minimum diameter of the spindle-knot (joint, Fig. 1d), which is mimicking the random and aligned nanofibrils on the spider silk². Every spindle-knot and every joint have the similar features of roughness gradients, but gradient sizes of continuous spindle-knots along fiber form distinct feature of BFGS.

To further reveal how the fabrication conditions affect the geometric parameters (i.e., height and width) and gradient extent, a series of gradient spindle-knots is fabricated carefully under different solution concentrations and tilted angles, which are shown by the optical images and size statistical data (see Fig. S1–S2). The concentration of the polymer solution is 7%, 8%, 9%, or 10% (weight percentage of PVDF in DMF) and the title angle is 0°, 5°, 10°, or 15° with the same draw-out velocity of ~200 mm min⁻¹. The fabricated fibers can be divided into three different types according to the shape of the gradient knots on them. In the green frame images, there are no obvious gradient structures on the spindle-knots. It results from too bigger title angle and too higher concentration. Due to a bigger angle, the polymer film fractures too fast to stay enough solution on the fiber. And higher polymer solution concentration increases the result because of the larger solution film gravitation. These two reasons will lead the solution film fracture quickly when the fibers just leave the solution surface. There is little solution on the fiber to break into obvious gradient spindle-knots or make the gradient spindle-knots too short. In the images with red frame, the obvious gradient spindle-knots appear. The coating film thickness is affected by the solution concentration and title angle, and the film thickness further influence the formation of gradient spindle-knots. The effect of the concentration has been discussed by reported paper¹⁴. For coating technique to form solution film onto a fiber, the thickness of solution film is related to the concentration and viscosity of solution, draw-out velocity and surface tension, which is regulated by capillary number (Ca) with Ca = ηv/γ, where η is the solution viscosity; v is the draw-out velocity; γ is the solution surface tension. The polymer solution viscosities and surface tensions have been measured (see Supporting information, Tab. S1). The viscosities increase from ~144 to ~460 mPa·s for polymer solutions with different PVDF concentrations, while their surface tensions change from ~36.38 to ~36.82 mN m⁻¹. The angle to the horizontal line exists to make the solution film present a triangular shape when the fibers leave the solution from left to right. The gravitation of the solution film decreases from left to right on the fiber, and the length of the solid-liquid contact line is also reduced. So on the same fiber, the Ca varies with different positions, which lead to the thickness of film decreases from left to right on the fiber. The thickness determines the volume of the solution on the fiber. According to the length of two spindle-knots with L = λd, where λ is the coefficient and d is the diameter of fiber, the size of spindle-knots is determined by the volume of solution in L range on the fiber. So the height and width of spindle-knots are decreased from left to right. The lengths of pitches between two spindle-knots are also decreasing. As in our experiments, there are two effect factors for the formation of excellent gradient spindle-knots. If the angle is too bigger or the solution concentration is too higher, the solution film breaks too fast to slide down, which will lead to not enough PVDF solution on the fiber. So the gradient spindle-knots are not obvious or enough long to be used in water directional movement. Under 0° angle to the horizontal line condition, there are periodic spindle-knots as the same as reported previously¹⁴. To further reveal how the size of the gradient spindle-knots varies at optimized fabrication conditions, we select the gradient spindle-knots with solution concentrations of 7%, 8%, 9%, and 10% in 5° to the horizontal line. The statistical data about the height and width of the gradient spindle-knots and pitch between spindle-knots are shown in Figure S2a–c, respectively. The data are obtained by five repeated experiments. We define as initial position (i.e., 0 mm) of spindle-knots with ~3 mm far from the fiber support. The chart shows that height and width of gradient spindle-knots on the same fiber are declined with a linear trend, which is determined by the thickness of solution film decreasing from left to right on the fiber. At high concentration (10%), the slope rate is bigger than low concentration (7%) with height and width. At 7%, the height is from ~0.09 to ~0.05 mm, the width gradient from ~0.35 to ~0.21 mm, while the height and width ranges from ~0.17 to ~0.07 mm and ~0.50 to ~0.24 mm at 10%, respectively. The distances of two spindle-knots have no obvious difference with the concentration for the relative position of every spindle-knot. The largest pitches are close to 1.5 mm in length. The average values for largest pitch of two spindle-knots in red frame are list in Table 2. But the higher title angle (~15°) is not conducive to useful pitches in the gradient of fiber. These investigations allow us to evaluate the water directional movement ability of gradient spindle-knots fibers.

Water drop transport in one direction in a long distance

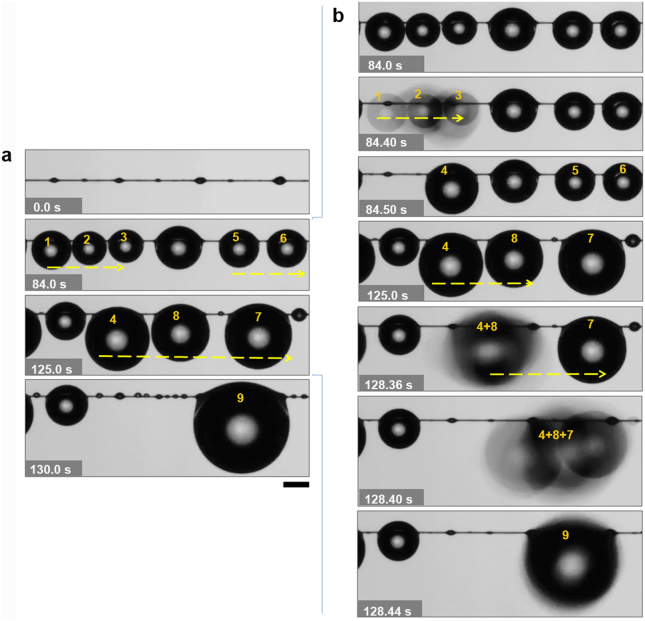
What is interesting is that BFGS we prepared display a property to transport water drops in a long distance. In our previous studies²,¹⁴,¹⁵,¹⁹,³⁰,³¹, we reproduced the structural features similar to that of wetted spider silks. Specifically, the tiny water droplets directional driving on spindle-knots and a big drop pinning between two spindle-knots (uniform spindle-knots) were investigated significantly. However, directional movements of tiny water drops are usually limited in a short distance on surfaces of most previous as-designed fibers. Here, the water directional movement of the gradient spindle-knots can be carried out under a humidity of more than 90% via fog flow at rate of ~30 cm s⁻¹, which is observed by CCD camera. As shown in Figure 2, there are four spindle-knots from smaller to bigger one on fiber (the left top), with the width ranged from ~180 to ~400 μm and height from ~75 to ~120 μm. The pitches are not more than ~1.5 mm in length. The whole process is in the time of ~130 s. In details, at ~84.0 s, water drops (1, 2, 3) are condensed on the spindle-knots. In the time of ~125.0 s, the water drops grow and meantime the drops coalesce and move towards to bigger spindle-knots direction. Subsequently, drops 1, 2 and 3 coalesce into drop 4, which are moving to the right about 2 mm at ~120 s. And drop 5 and 6 coalesce into drop 7. In the time of ~130 s, drop 4, 7 and 8 coalesce into drop 9. All whole process, the water is directionally moving across four spindle-knots in distance of ~5.0 mm. Figure 2b shows the details of water drop coalescence and movement in direction at ~84–128.44 s, where the drops (1 + 2 + 3) fast coalesce into drop 4 at ~84.40–84.50 s; drops (4 + 8) coalesce together at ~128.36 s; drops (4 + 8 + 7) coalesce directionally into drop 9 at ~128.44 s, respectively. The BFGS can be continuous to perform water drop transport and display the repeatability as shown in Fig. S3. In contrast, no obvious movements of water drops in a long distance appear on a uniform nylon fiber with PVDF coating and uniform spindle-knots fiber when they are horizontally placed under a humidity of more than 90% via fog flow at rate of ~30 cm s⁻¹, where the water drops are coalesced with surrounding drops and stay on the original position (on the uniform nylon fiber, see Fig. S4a) or stably hang on two uniform spindle-knots (on the uniform spindle-knots fiber, see Fig. S4b). In our investigation, pitch of two spindle-knots influences the distance of water transport. If the pitches of two spindle-knots are more than 1.5 mm in length, droplets doesn't usually move to far-distance another larger spindle-knot, e.g., a pitch of ~1.8 mm, which water transport is not conducive to a long distance (see Fig. S5).

Figure 2. Water drops directional movement for a long distance on BFGS.

(a), The gradient spindle-knots are from smaller to bigger. Water condensed drops (1,2,3,5,6) form on the spindle-knots (at ~84 s) and they coalesce into bigger drops (4, 8, 7), respectively, and they move fast towards the biggest spindle-knots with ~5.0 mm, to coalesce into a biggest drop 9 on the bigger spindle-knot at ~130 s. (b), The details of the water drops in directional movement. Some situations of dynamic coalescence and movement show the drops (1 + 2 + 3 → 4) at ~84.40–84.50 s; drops (4 + 8) at ~128.36 s; drops (4 + 8 + 7 → 9) at ~128.44 s, respectively. Scale bars, 500 μm.

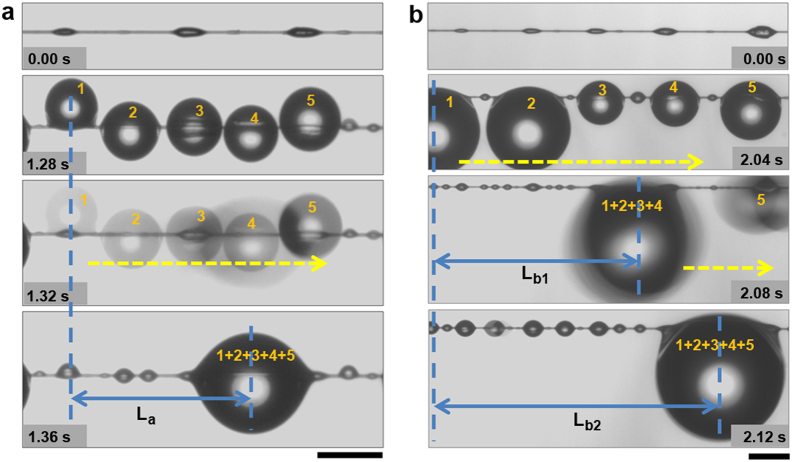
The process of water drops coalescence and transport can be different on BFGS with weak or strong gradient spindle-knots. Figure 3a shows the water drop behaviors of coalescence on weak gradient spindle-knots of BFGS. Three gradient spindle-knots (Fig. 3a, the top) in turn have ~41 μm, ~56 μm, and ~58 μm in height and ~163 μm, ~221 μm, and ~244 μm in width, respectively. The largest pitch is ~0.9 mm. The BFGS is placed horizontally, and a humidifier provides a humidity of 90%. Five drops (1,2,3,4,5) which have almost equal volumes including three ones (drops 1,3,5) covering on single spindle-knot and two ones (drops 2,4) on joints (at ~1.28 s) coalesce into one bigger drop (1 + 2 + 3 + 4 + 5) at ~1.32–1.36 s, hanging on between two bigger spindle-knots, in which process the bigger drop doesn't hang in the middle of BFGS. If the first drop (i.e., drop 1) is defined as the initial point (at ~1.28 s), the last bigger water drop (i.e., drop (1 + 2 + 3 + 4 + 5)) obtained by coalescence and movement (at ~1.36 s) is defined as the final point. The transport length L_a of drop is ~1.41 mm (see Fig. 3a, the distance between two vertical dash lines) in time of ~1.36 s. As for the strong gradient spindle-knots of fiber (Fig. 3b), where there are the five gradient spindle-knots (Fig. 3b, the top) with height of ~35 μm, ~41 μm, ~56 μm, ~58 μm, ~81 μm and width of ~139 μm, ~163 μm, ~221 μm, ~244 μm, ~302 μm, in turn, respectively. The largest pitch is ~1.1 mm. Water drops grow on the BFGS at ~2.04 s. At ~2.08 s, the first four drops (1,2,3,4) coalesce into a bigger one (1 + 2 + 3 + 4) hanging on two spindle-knots (the third and forth spindle-knots), where the transport length of drop is ~2.70 mm (L_b1) (see both vertical dash line, at ~2.04–2.08 s). This process is similar with Fig. 3a, at the time 0–1.36 s. The drop is coalesced with a small drop ((1 + 2 + 3 + 4),5) on the right (at ~2.08 s) and the last drop (1 + 2 + 3 + 4 + 5) moves to right point hanging on two biggest spindle-knots on the fiber (at ~2.12 s). The transport length (L_b2) of drop is ~3.76 mm (see Fig. 3b, the distance between both vertical dash lines, at ~2.12 s). It indicates that a longer distance (i.e., ~3.76 mm) of drop movement appears along the strong gradient spindle-knots than that (i.e., ~1.41 mm) of weak gradient spindle-knots.

Figure 3. Water drop transport on BFGS with weak/strong gradient spindle-knots.

(a), In weak gradient spindle-knots, water drops (1,2,3,4,5) hanging on single spindle-knots and joint, and form a big drop (1 + 2 + 3 + 4 + 5) via transferring from smaller spindle-knot to bigger ones at ~1.36 s. The transport length (L_a) is ~1.41 mm (see distance between both vertical dash lines) with time of ~1.36 s. (b), In strong gradient spindle-knot, water drops move directionally and hang between two spindle-knots. The length (L_b1) of movement to bigger spindle-knot is ~2.70 mm. The drop is coalesced with small drops (1,2,3,4) at ~2.08 s and the last drop (1 + 2 + 3 + 4 + 5) moves to right point location of two biggest spindle-knots (at ~2.12 s). The transport length (L_b2) is ~3.76 mm (see distance between both vertical dash lines) with time of ~2.12 s. Scale bars, 500 μm.

Furthermore, we select a gradient fiber with three different spindle-knots (i.e., height of ~43 μm, ~130 μm, ~217 μm; width of ~152 μm, ~435 μm, and ~565 μm, respectively; the largest pitch is ~1.1 mm). Water directional movement process is recorded by using CCD. In process of water drop movement as shown in Figure 4, it is found that the direction tendency of drop coalescence can also further be normal sequence and reverse sequence. In normal sequence (as shown in Fig. 4a), the observation is focused on behaviors of three water drops with volumes: Ω_D1 < Ω_D2 < Ω_D3 (~0.40 μL, ~0.63 μL, ~1.24 μL, respectively) (see Fig. 4a). The process of water drops coalescence is in manner of (D1 + D2) + D3. In details, the drop D1 coalesces with drop D2 at ~1.4 ms. Drop D(1 + 2) moves towards bigger spindle-knots and is hanging on the middle spindle-knot via the second mode (at ~9.8 ms). With the water drops growing, drop D(1 + 2) is merging with drop D3 at ~11.2 ms. Due to the biggest spindle-knot with the most capillary force, the drop D(1 + 2) + 3 is hanging stably on the biggest one at ~26.8 ms. The length of movement (L_a) is ~2.8 mm at the whole coalescence process. In reverse sequence of droplet coalescence, the observation is focused on behaviors of three water drops with volumes: Ω_D1′ ≈ Ω_D2′ ≈ Ω_D3′ (≈0.67 μL) (see Fig. 4b). The process of water drop coalescence is in manner of (D2′ + D3′) + D1′. In details, at ~2.80 ms, the drop D2′ and D3′ firstly combine together. The drop D(2′ + 3′) finally hangs stably on the biggest spindle-knots at ~8.4 ms. With the drops growing, the drop D1′ moves towards to the right due to the first way at ~960.4 ms. As the virtual frames are shown, the drop D1′ moves and hangs on the middle spindle-knot. At ~967.0 ms, the drop D1′ is merging with drop D(2′ + 3′). Drop D(2′ + 3′) + 1′ is hanging on the biggest spindle-knot at ~968.4 ms. The length of movement (L_b) is ~2.46 mm at the whole coalescence process. Even though the two processes of coalescence have the same result that three water drops coalesce into a bigger one with direction movement at the gradient spindle-knot fiber and the transport distances are no obvious disparity (~2.80 mm in normal sequence and ~2.46 mm in reverse sequence), but the reverse sequence spends more longer time (~968.4 ms) than the normal sequence (~26.8 ms). The speed of normal sequence transport (~0.105 m s⁻¹) is almost 42 times more than that of reverse sequence transport (~0.0025 m s⁻¹) on average. It illustrates that the gradient structure existence of spindle-knots on the fiber decides the action of transport and the volumes and position of water drops effect the speed of transport.

Figure 4. Water direction tendency coalescences in normal sequence and reverse sequence.

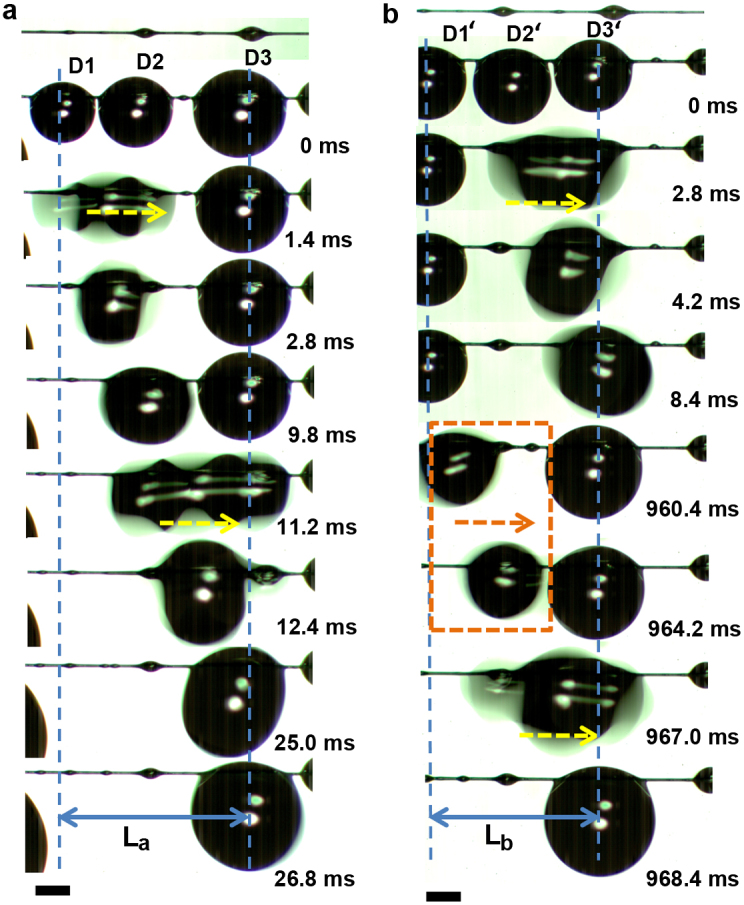
(a), In normal sequence water drops coalescence with the process of (D1 + D2) + D3. The drop D1 coalesces with drop D2 to form Drop D(1 + 2), and it moves towards bigger spindle-knots. With the water drops growing, drop D(1 + 2) is merging with drop D3 to form drop D(1 + 2) + 3. The length of movement (L_a) is ~2.80 mm with ~26.8 ms. (b), The reverse sequence of water drops coalescence. The drop D2′ and D3′ firstly combine together form the drop D(2′ + 3′). With the drops growing, the drop D1′ moves towards to the right due to the first mode (virtual frame) and coalesces with drop D(2′ + 3′) to form Drop D (2′ + 3′) + 1′. The length of movement (L_b) is ~2.46 mm with ~968.4 ms. Scale bars, 500 μm.

Velocities of micro-drop transport via coalescence

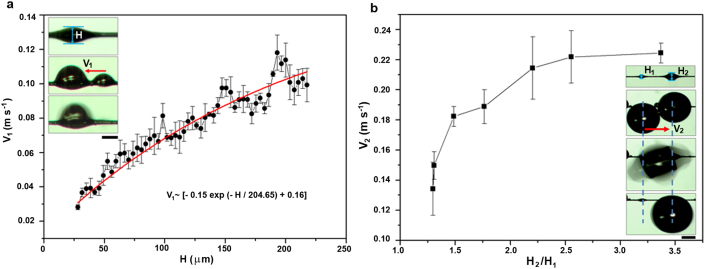
To clarify the effect of spindle-knot size on water transport ability, the gradient spindle-knot fiber is placed in mist with a fog flow at rate of ~50 cm s⁻¹, drop behaviors are recorded by a high speed CCD. Velocities (V) of water drop movement are estimated via two different statistics, i.e., one that drops coalesce on single spindle-knot, which the velocity is defined as V₁; other that drops move from small spindle-knot to big one, which the velocity is defined as V₂. We choose 55 different size spindle-knots (i.e., the height (H) of spindle-knot ranges from ~28.0 to ~217.5 μm, the half angle of that ranges from ~14.7° to ~30.8°) to test the V₁ of drops coalesce on single spindle-knot at the moment of droplet coalescence (as shown in Figure 5a). Figure 5a shows the statistical relationship between V₁ and H on single spindle-knot, there is a fitting relationship (see Supplementary information, Tab. S3): V₁ ~ [−0.15 exp (−H/204.65) + 0.16] (m s⁻¹), where the V₁ is increasing with the H, estimated V_{1, max} ~ 0.1 m s⁻¹ at H ~ 217.5 μm. A more height can offer a more difference in Laplace pressure, which would drive water drops coalescence with a high velocity. The inset (in Fig. 5a) shows the optical images of droplet movement on one spindle-knot. To reveal further the gradient effect of two spindle-knots on velocity, we select all the pitch of gradient spindle-knots are ~621 ± 48 μm, among which the small spindle-knots are chose with the same height of ~56 ± 8 μm (H₁) and the height of big ones (H₂) range from ~68 μm to ~155 μm. H₂/H₁ can be reflected the extent of gradient between adjoining spindle-knots. Figure 5b shows the relationship between V₂ and H₂/H₁. The inset in Fig. 5b shows the optical images that water drops move from the small spindle-knot to the big one via coalescence. From curve in Fig. 5b, the V₂ is rapidly increasing with H₂/H₁, and until H₂/H₁ reaches 2.25, subsequently, slows down. It is estimated V_{2, max} ~ 0.22 m s⁻¹ at H₂/H₁ ~ 2.25. This indicates that the difference of Laplace pressure plays an important role in driving water drops movement on gradient spindle-knots to extent.

Figure 5. Velocities of water drop coalescence on one spindle-knot and two adjacent spindle-knots.

(a), Relationship of velocity (V₁) and height (H) on one spindle-knot. The V₁ is increasing with H, there is a fitting relationship: V₁ ~ [−0.15 exp (−H/204.65) + 0.16] (m s⁻¹). It is estimated V_{1, max} ~ 0.1 m s⁻¹ at H ~ 217.5 μm. (b), Relationship of velocity (V₂) and height ratio (H₂/H₁) of adjacent spindle-knots. The V₂ is rapidly increasing with the H₂/H₁, until H₂/H₁ ~ 2.25, subsequently, slows down. It is estimated V_{2, max} ~ 0.22 m s⁻¹ at H₂/H₁ ~ 2.25. The insets are the optical images of drop movement process. Scale bar, a, 150 μm, b, 500 μm.

Discussion

To further reveal how the water drops move directionally on the BFGS via two modes above, we select a gradient spindle-knot fiber with two spindle-knots, which the size of two spindle-knots (Fig. 6a, the top) are respectively of height of ~178 μm (S1), ~249 μm (S2) and width of ~498 μm (S1), ~747 μm (S2). The largest pitch is ~1.1 mm. Figure 6a shows the movement processes of two water drops hanging on two spindle-knots, respectively. Two drops grow on two spindle-knots, respectively (Fig. 6a, at 0 ms), until they are big enough to coalesce into one bigger one (Fig. 6a, at ~1.4 ms). As two water drops will release energy in the coalescence process, the bigger water drop is in an unstable state which results in a large deformation to form the most stable state. It is reported a continuous diameter-gradient cone fiber makes the drop move toward direction of larger diameter³² and rough surface of fiber generates the capillary adhesion to regulate the behavior of hanging-drop³. Here, the diameter of S2 is more than S1, for S2 can provide a more capillary adhesion. The water droplet hanging on S2 is more stable than on S1 (Fig. 6a, at ~4.2–12.6 ms). At last, the water is hanging on the S2 stably (Fig. 6a, at ~23.8 ms). This process makes the water drop look for a most stable state and move from the small size spindle-knot to the bigger one (see the blue lines in Fig. 6a). The length of movement (L_a) is ~1.86 mm with time of ~23.8 ms. With the growth of these drops and others around it, it will duplicate this process to coalesce into bigger one and move toward bigger spindle-knots. In this process, the coalescence offers the energy to move, and the gradient spindle-knots further promote the movement by gradient of capillary adhesion and meantime play a role in stabilizing the water drops. The dynamic process of the coalesced drop transport can be seen in Supplementary Movie S1 (the true time of the process is ~0.048 s). Figure 6b shows optical images of the dynamic process that how a water drop hanging between two different size spindle-knots moves towards bigger spindle-knot via in-situ observation by CCD. Two spindle-knots are respectively defined S1 and S2 (Fig. 6b, the top, the same with Fig. 6a, the top). Here, α1 is the angle of liquid surface and S1. And α2 is the angle of liquid surface and S2. At 0 s, the water drop is hanging stably between two spindle-knots with different sizes. The α1 (~110°) is more than the α2 (~66°) because the size of S1 is less than that of S2 (Fig. 6b, top). Carroll³³,³⁴,³⁵and Mchale et al³⁶. describe that the gravity (G) can be balanced with capillary forces (f_c) when water droplets are hung on the fibers. On the one hand, the capillary forces are proportional to the curvature of the liquid surface. The more is curvature of the liquid surface, the more are capillary forces; or vice versa. The angle α2 (~70°) is less than α1 (~91°, Fig. 6b, at ~4.2 ms), and the curvature of liquid surface with S1 is more than that of S2. So the water drop at S1 site is moving towards to right. The angle α1 is decreasing in the process for a stable state. At S1 site, due to Laplace pressure gradient, the water drop easily moves from joint site to the hump (Fig. 6b, at ~4.2 ms). With the angle α1 decreasing, the Laplace pressure at the contact line tends to increase. It is quite difficult for the contact line to pass through location of hump. But the capillary force gradient (at S1 and S2) overcomes Laplace pressure gradient. The water drop moves from hump to the right joint site. The angle α1 (~84°) is decreasing and α2 (~69°, Fig. 6b, at ~5.6 ms) is essentially unchanged. On the other hand, a larger pearly hanging-drop is regulated by a spindle-knot due to the roughness and curvature (Fig. 1b). The roughness can enhance the pinning effect to three-phase contact line and thus cooperate with the effects of curvature and slope of hump to hang a larger volume of the extreme drop stably. However, when the liquid surface leaves S1 site (smaller spindle-knot), there is no recession barrier of contact line hanging on a uniform location. It results in an instable three-phase contact line which leads it easily sliding from spindle-knot site to the uniform location (Fig. 6b, at ~7 ms). The capillary force at this location decreases rapidly, and the capillary force at S2 site is unchanged (α1 ~ 46°, α2 ~ 63°). In this process, the water drop moves toward to bigger spindle-knot (Fig. 6b, at 0 ms, α1 ~ 38°, α2 ~ 70°). At ~21.0 ms, the water droplet is hanging on the bigger spindle-knot stably. The angle α1 and α2 are ~47° and ~55°, respectively, which is little difference. Tian et al³⁷. demonstrated that uniform spindle-knots fiber can stably pin a water drop through the combination of “slope” and “curvature” effects. The gradient spindle-knots structure successfully breaks the stability offered by two uniform spindle-knots, which leads to move. The length of movement (L_b) is ~0.873 mm with time of ~21.0 ms. Cooperation of two modes, the water drop can move on the gradient fiber from smaller spindle-knot to bigger one. There are thereby three factors to drive the water drop movement along the gradient fiber: i.e., capillary adhesion force (F_ca), difference in Laplace pressure (F_lp) along the gradient spindle-knots and also drops coalescence release energy (F_cr) as well. The capillary force that is induced by the roughness according Wenzel's law³⁸ is described as follows: 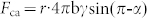, where F_ca is the capillary force of spindle-knots; r is the roughness; the b is the effective radius of silk (b_{(small knot)} < b_{(big knot)}) and α is the angle of liquid surface and spindle-knot. When α is ~90°, the 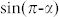reaches the max value. The α1 decreases from ~110° to ~91° (meantime move from left joint to the hump site) which leads to the capillary adhesion force increasing to prevent the drop movement from left to right. Until the liquid surface passes the hump to right joints (the b decreases sharply), the capillary adhesion force of smaller spindle-knot is less than that of bigger one. The capillary adhesion force difference drives the water drops movement towards to bigger spindle-knots. The second driving force is difference in Laplace pressure (F_lp) described as 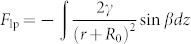, where γ is the surface tension of water; r is the local radius; R₀ is the drop radius; β is the half apex-angle of the spindle-knot (β_{(small knot)} < β_{(big knot)}); z is the integrating variable along the diameter of the spindle-knot. The Laplace pressure on the high curvature site is larger than that on the low curvature site. Firstly, the F_lp promotes tiny water drops moving from uniform fiber to the joint and then to the spindle-knot because the radius of uniform fiber (r_u) is smaller than that of joint (r_j); the r_j is less than the radius of spindle-knot (r_s). Secondly, F_lp also contributes to propelling the drop transport from small spindle-knot to big one due to F_{lp(small spindle-knot)} < F_{lp(big spindle-knot)}. The third force is drops coalescence release energy, which assists the previous forces due to the gradient structure on the fiber. Cooperation of three forces acts on these two modes to drive water drops directional movement. Figure 7 illustrates the mechanism of the water drops transport along the BFGS in a long distance. Fig. 7a-b indicates the case of the directional driving of tiny water condensed drops toward spindle-knot by the cooperation of surface energy in gradient and Laplace pressure in difference, similar to the wetted spider silk. Fig. 7c shows the first mode of water drops transport. The cooperation of difference in Laplace pressure (F_lp) along the gradient spindle-knots and drops coalescence release energy (F_cr) drives the coalescence water transporting towards big spindle-knot for a stable condition (Fig. 7c). When a bigger water drop hangs on one spindle-knot, it tends to coalesce into another water drop on the biggest spindle-knot. A coalescence water drop hanging between two spindle-knots (Fig. 7d) tends to slide from the joint of smaller spindle-knot towards the biggest one because of F_{ca(small spindle-knot)} < F_{ca(big spindle-knot)}, resulting in the angle of liquid surface and small spindle-knot α1 reducing. The second mode prompts the bigger water drop transporting towards the biggest spindle-knot and hanging on it (Fig. 7e). Cooperation of both modes drive the water drops move directionally on the BFGS in a long distance.

Figure 6. Dynamic behaviors on both modes of water drop movement in direction.

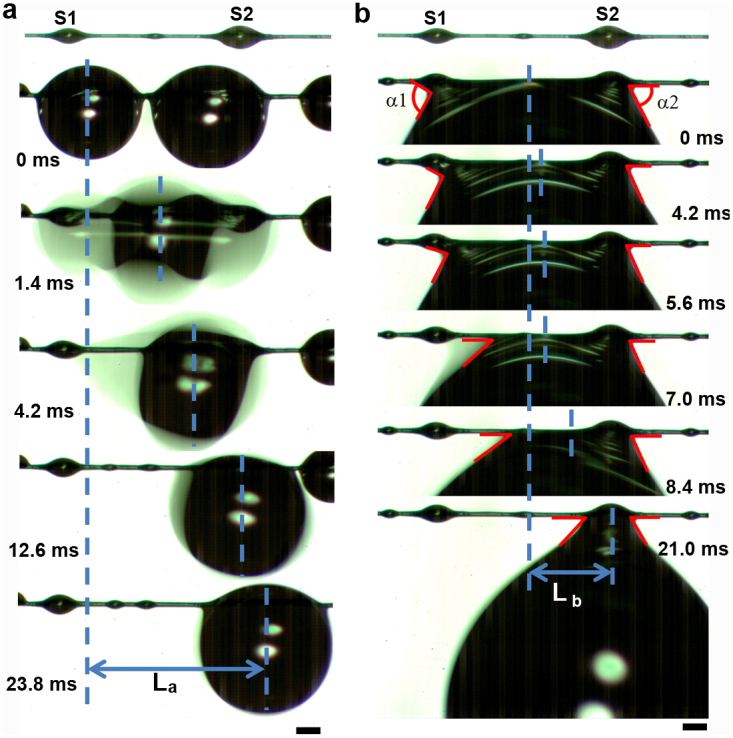
(a), The movement process of water drops hanging on a single spindle-knot. The length of movement (L_a) is ~1.86 mm with time of ~23.8 ms. (b), Water drops directional movement between two spindle-knots with different sizes. α1 and α2 are the angle of liquid surface with S1 and S2 respectively. The angle α1 is decreasing in the process for a stable state and α2 is almost unchanged. The length of movement (L_b) is ~0.873 mm with time of ~21.0 ms. Scale bars, 250 μm.

Figure 7. Illustration of water drops transport in a long distance.

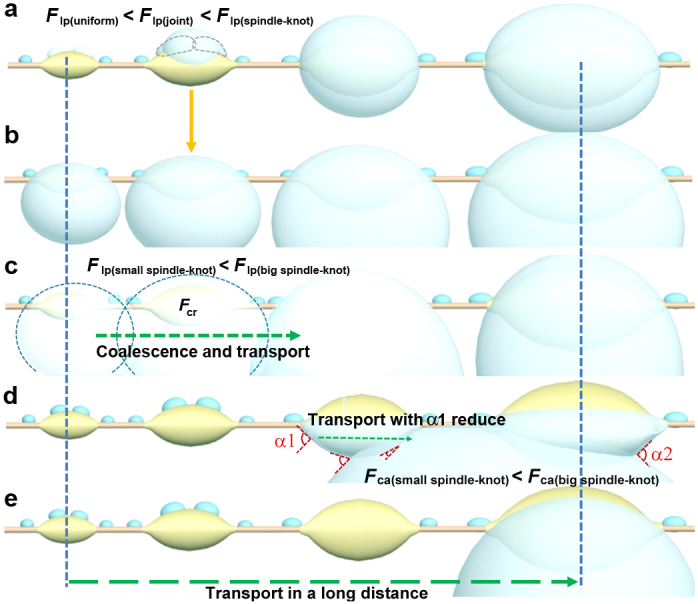
(a-b), The directional driving of tiny water condense drops toward spindle-knot by the cooperation of surface energy in gradient and Laplace pressure in difference. (c), The first mode drives the coalescence water transporting towards big spindle-knot for a stable condition via the cooperation of difference in Laplace pressure (F_lp) along the gradient spindle-knots and drops coalescence release energy (F_cr). (d), A coalescence water drop hanging between two spindle-knots tends to slide from the joint of smaller spindle-knot towards the biggest one because of F_{ca(small spindle-knot)} < F_{ca(big spindle-knot)} resulting in the angle of liquid surface and small spindle-knot α1 reducing. (e), The second mode prompts the bigger water drop transporting towards the biggest spindle-knot and hanging on it.

BFGSs display an excellent fast micro-drop transport in a long distance due to multi-level cooperation of capillary adhesion force, difference in Laplace pressure and drops coalescence release energy. The investigation of relationship between gradient structures and water transport may help us to design novel materials for a potential applications such as the fluid controlling in water-harvesting projects³⁹,⁴⁰,⁴¹ and filtering aerosols systems⁴².

Methods

The bioinspired fibers with gradient spindle-knots (BFGS) can be fabricated by the tilted dip-coating method combining Rayleigh instability technique¹,². The condition of fabricating gradient spindle-knots fibers can be optimized by tuning the concentrations of PVDF polymer solutions ranged from 7%, 8%, 9% to 10% (weight percentage) and dip-coating tilted angles ranged from 0°, 5°, 10°, to 15° to horizontal line. The whole process of fabrication is recorded by a using a high-speed CCD camera. After tilted dip-coating and dryness of fiber in ambient environment, BFGS is achieved successfully. The structures of BFGS are observed by scanning electron microscopy (SEM) at 10 kV. The tiny water drops are generated on BFGS via an ultrasonic humidifier with a fog flow. The dynamic processes of micro-drop transport are captured by a high-speed CCD camera. Statistical analysis is done by the analyst of origin8 software.

Author Contributions

Y.Z. conceived the research, Y.C. and L.W. conducted the experiments, Y.X. and L.J. analysed data. Y.Z. and Y.C. wrote the paper.

Supplementary Material

Supplementary Information

Movie S1

Supplementary Information

SI