Abstract
Prognosis plays a pivotal role in patient management and trial design. A useful prognostic model should correctly identify important risk factors and estimate their effects. In this article, we discuss several challenges in selecting prognostic factors and estimating their effects using the Cox proportional hazards model. Although a flexible semiparametric form, the Cox’s model is not entirely exempt from model misspecification. To minimize possible misspecification, instead of imposing traditional linear assumption, flexible modeling techniques have been proposed to accommodate the nonlinear effect. We first review several existing nonparametric estimation and selection procedures and then present a numerical study to compare the performance between parametric and nonparametric procedures. We demonstrate the impact of model misspecification on variable selection and model prediction using a simulation study and a example from a phase III trial in prostate cancer.
Keywords: Cox’s Model, Model Selection, LASSO, Smoothing Splines, COSSO
1. INTRODUCTION
Prognosis plays a critical role in patient treatment and decision making. What is of interest to researchers is to examine the relationship between host, tumor-related, baseline explanatory variables and clinical outcomes (Halabi and Owzar, 2010). These factors, and those which are considered to be significant, are termed prognostic. The evaluation of prognostic factors is one of the key objectives in medical research. Historically, the impetus for the identification of prognostic factors has been the need to accurately estimate the effect of treatment adjusting for these variables (Halabi and Owzar, 2010).
In using a time to event outcome, one main objective is to characterize the relationship between the event time Y and a set of baseline covariates X = (X(1), …, X(p))T. This task is often done via the proportional hazards model (Cox, 1972), which consists of a unspecified baseline hazard function and a parameterized component. In general, the Cox’s model can be written as:
| (1) |
where λ0(·) is the unspecified baseline hazard function and the log-relative risk function η(·) is commonly taken as a linear form η(X) = XTβ, where β = (β1, …, βp)T is a p-dimensional unknown regression parameters called the log-hazard ratio. The model in (1) is commonly referred to as a semiparametric model in which the primary interest is making inference on the finite number of parameters β.
Despite its widespread use, the Cox’s model relies on the linear assumption, which in many practical situations, may be rigid and unrealistic. For instance, in an example of a Veteran’s Administration lung cancer trial (Kalbfleisch and Prentice, 2002), the estimated log-relative hazard function of age has a convex shape. Such an important effect may not have been identified if the covariate effect is assumed to be linear. In a breast cancer study, Verschraegen et al. (2005) argued that the effect of tumor size on mortality is best described by a Gompertzian function. More recently, there has been a great interest in examining the nonlinear covariate’s effect when analyzing genomics data (Volpi et al., 2003).
To address nonlinear covariate effects, one common practice is to categorize a continuous variable into several discrete quantiles (Zeleniuch-Jacquotte et al., 2004). However, such discretization does not fully exploit the data and the final fitted curve is not smooth, but rather a step function. Another common practice is to transform the variable using some common mathematical functions, such as logarithm, polynomial, etc. Unfortunately, transformation methods depend heavily on researchers’ knowledge and could introduce additional modeling bias. As a result, more flexible modeling techniques are required to allow for nonlinear covariate effect.
Basis expansion and regression spline methods are popular nonparametric techniques used to characterize nonlinear effects (O’Sullivan, 1988; Gray, 1992; O’Sullivan, 1993). These methods are appealing for their low computation costs and ease of implementation. In addition, their computation difficulties are essentially the same as that of a parametric model since the nonlinear effects are described through some augmented variables. These methods, however, depend on the proper choice of basis function, degree of freedom and number of interior knots. Moreover, investigators will often face a dilemma between balancing model complexity and model goodness-of-fit. The more basis functions are used, the better one can approximate the true underlying function, but it is at the price of increasing both computation intensity and model complexity.
The smoothing splines method was first proposed in least squares regression to improve some limitations in basis expansion. It used all observed data points as interior knots and broadens the search range for a solution to an infinite dimensional space, without the extra computational intensity. This method has been further extended to survival model by Gu (1996, 1998), in which an asymptotic result was established.
Apart from handling possible model misspectification, another vital step in contemporary statistical modeling is to select a set of important covariates. Variable selection is routinely performed for several purposes, including better predicting the survival outcomes and understanding the relationship between covariates and survival outcomes. The development of novel selection procedures, such as the least absolute shrinkage and selection operator (LASSO) (Tibshirani, 1997) and the smoothly clipped absolute deviation (SCAD) (Fan and Li, 2002), center around the penalized methods. A generic penalized log-partial likelihood estimation procedure can be written as min
| (2) |
where ln(β) is the log-partial likelihood function, J(·) is a generic non-negative penalty function and λn is a regularization parameter that governs the sparsity of the parameter estimates. Fan and Lv (2010) gave a comprehensive review on the popular penalty functions.
Penalized methods have become very popular in modern statistical modeling because they simultaneously select and estimate regression parameters by shrinking some parameter estimates to exact zeros. Despite the fact that gains are expected in terms of estimation stability and prediction accuracy in a penalized framework, Tibshirani (1997) noted that penalized regression methods should be used with caution due to their linearity assumption.
Our motivating example stems from a phase III clinical trial of men with metastatic castrate-resistent prostate cancer who developed progressive disease following first-line chemotherapy. We refer to the data as the TROPIC (de Bono et al., 2010). One of the main objectives of the TROPIC trial is to identify and estimate the effects of the baseline variables on patients’ survival outcomes.
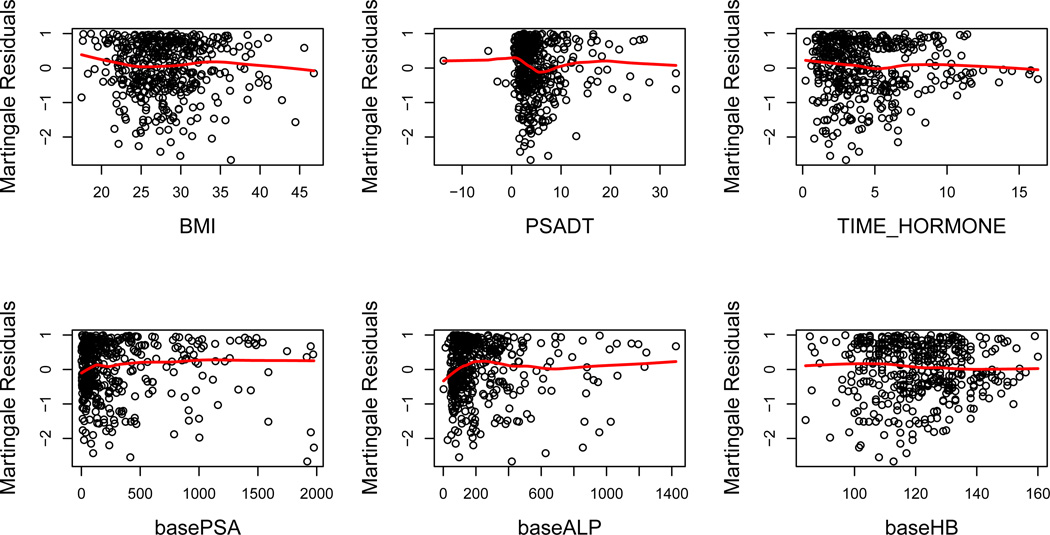
We restrict our attention to patients without missing covariates. The list of 14 baseline variables and their summary statistics are presented in Table I. Among 434 patients with complete data, 282 died before the end of the follow-up period. We fit penalized Cox’s models with LASSO and adaptive LASSO penalty to explore the sparse structure. Among 14 candidate prognostic factors, we are particularly interested in baseline PSA since it is considered an important prognostic variable in men with advanced prostate cancer (Halabi et al., 2003; Kelly et al., 2012). The size and concordance of the final LASSO model are 12 and 0.716, respectively; whereas those of the final adaptive LASSO model are 13 and 0.713. Although both penalized models select most of the 14 variables, we suspect that the survival model could be more sparse since some of the parameter estimates are very small. In addition, we are more concerned about the parameter estimate for baseline PSA, which is either very small or exactly zero. We question if the linear effect is appropriate for baseline PSA. However, the post-fitting diagnosis was however not conclusive. As the martingale residuals plots shows in Figure 1, the scatter does not reveal any specific trend and the fitted smooth curve is almost flat.
Table 1.
Variable Description and Summary Statistics.
| Variable | Description | Mean | SD |
|---|---|---|---|
| BLPAIN | Binary: 1 if the patient has baseline pain | 0.48 | - |
| BONEMET | Binary: 1 if the patient has bone metastases. | 0.88 | - |
| CAUCASIAN | Binary: 1 if the patient is Caucasian. | 0.81 | - |
| CHEMOGE3 | Binary: 1 if the patient has prior chemotherapy. | 0.29 | - |
| DPMEASBN | Binary: 1 if the patient has measurable disease. | 0.43 | - |
| TAX2PROG | Binary: 1 if the patient’s last Taxotere to progression is less than 6 months. | 0.89 | - |
| VISCMET | Binary: 1 if the patient has visceral metastases. | 0.23 | - |
| ECOG | Eastern Cooperative Oncology Group performance status of 0–2. | 0.32/0.61/0.071 | - |
| baseALP | Baseline Alkaline Phosphatase (U/L). | 221.18 | 223.96 |
| baseHB | Baseline Hemoglobin (g/DL). | 12.07 | 1.40 |
| basePSA | Baseline Prostate Specific Antigen (ng/mL). | 295.96 | 398.65 |
| BMI | Body Mass Index. | 28.01 | 4.61 |
| PSADT | Time (in days) for a patient’s PSA to double. | 5.02 | 4.90 |
| TIME_HORMONE | Time (in years) on hormone treatment. | 4.40 | 2.91 |
These three values represent the proportion of patients having performance status 0, 1 and 2.
Figure 1.
Martingale residuals plots from the fitted LASSO model. The red line is smoothed curve produced by local linear regression.
The purpose of this article is to provide a broad reviews of the existing nonparametric modeling procedures while keeping the methodological background minimal for a basic understanding. We aim at introducing the latest developments in statistical methodology to the applied side of medical research. The nonparametric procedures successfully address the impact of model misspecification on selecting important covariates and predicting time to event outcomes. Although the consequence of misspecification is comprehensible from a conceptual level, we demonstrate the superiority of modern nonparametric procedure using simulations and real trial data. Specifically, we compare the famous LASSO (Tibshirani, 1997) procedure with its nonparametric counterpart, the component selection and smoothing operator (COSSO) (Leng and Zhang, 2006), to examine the consequence of making a linear assumption on the log-relative hazard, when the covariates follow nonlinear functions. We refer to Tibshirani (1997) and Zhang and Lu (2007) for more discussions on the methodological part of LASSO, and Lin and Zhang (2006) and Leng and Zhang (2006) for COSSO. Since neither methods require any prior knowledge on the covariates, they are ideal procedures to explore the sparse structure of the survival model. To the best of our knowledge, this is the first paper that rigorously performs such comparisons. This paper also underscores the importance of examining the assumptions behind any statistical procedure and choosing the appropriate analysis tool.
The remainder of this article is organized as follows. In Section 2, we provide a general discussion of several nonparametric Cox’s models. Next, we demonstrate the usefulness of a nonparametric procedure via simulations in Section 3 and then we present the results of the simulations in Section 4. We then illustrate the concepts by using a real life example in Section 5, and in Section 6 we discuss our findings and present recommendations.
2. NONPARAMETRIC PARTIAL LIKELIHOOD ESTIMATION
Let {(yi, δi, xi) : i = 1, …, n} be the observed triplet, where yi is the observed event time, δi is the censoring status and xi is a p-dimensional covariates. Let y(1) < … < y(N) be N distinct event times, we then denote Ri = {j : yj ≥ y(i)}, i = 1, …, N, as the risk set at time y(i). Furthermore, we use the notation x(i) to represent the baseline covariates for the i-th observation whose event time is y(i).
To simplify further exposition and to alleviate the difficulty of estimating a multivariate function η(xi), we only consider the popular additive model where the function is composed of the addition of individual main effects, . Lin and Zhang (2006) discussed incorporating multi-way interactions into the estimation problem. The reader is referred to Hastie and Tibshirani (1990) for more discussions on additive models.
Early nonparametric procedures model nonlinear effects by assuming the nonlinear function can be spanned by a set of basis functions. Let ϕ1(t), …, ϕk(t) be a set of basis functions taken from a basis dictionary, for instance, the polynomial basis {ϕk(t) = tk, k ∈ ℕ}, we can model the effect of the j-th variable by letting , where βjl, l = 1, …, k, are unknown parameters (Eubank, 1999). Since the nonlinear function is known up to k parameters, the estimation problem is significantly reduced to estimate a finite number of unknown parameters. Estimating the unknown parameters is carried out by minimizing the minus log-partial likelihood plus a ridge type of penalty which is added to avoid over-smooth and produce a more stable estimator. More specifically, the minimization problem is given by:
| (3) |
where λn is a regularization parameter that governs the smoothness of the function. O’Sullivan (1988) considered a B-spline basis and proposed an estimation and tuning procedure for (3). Under suitable regularity conditions, O’Sullivan (1993) established a consistency result and proved the convergence rate matched that of the linear nonparametric regression.
The fitted curve is relatively insensitive to the choice of basis function. Common choices of basis functions include but are not limited to B-spline basis, Fourier basis, etc (Hastie et al., 2008). The success of basis expansion depends on whether the log-relative hazard function can be well-approximated by the chosen basis functions. It is impossible to verify the assumption in practice. A number of fully nonparametric methods have been proposed to improve the limitation of approximating an arbitrary function using finite basis (Wahba, 1990; Evgeniou et al., 2000). The key notion of fully nonparametric methods is making a qualitative assumption on the function, rather than deciding a predetermined form or basis. Such a qualitative assumption usually leads to infinite dimensional collections of smooth functions. Of several fully nonparametric methods, smoothing splines is the most extensively studied one which is pioneered by Wahba and her colleagues (Wahba, 1990; Gu, 2002; Wang, 2011). In a smoothing splines framework, Gu (1996, 1998) proposed to estimate the log-hazard function by solving the minimization problem:
| (4) |
where ℱ is a reproducing kernel Hilbert space (RKHS), ‖·‖2 is the squared RKHS norm, and θj, j = 1, …, p, are all smooth parameters.
The elegance of the smoothing splines method is that the minimizer of (4) has a finite representation even though we search over an infinite dimensional Hilbert space for a solution (Kimeldorf and Wahba, 1971). More specifically, the function that minimizes (4) can be written as:
| (5) |
where ci, i = 1, …, n, are unknown parameters and Kj(·, ·) is the reproducing kernel. Although the smoothing splines model was originally proposed to tackle the nonlinear effects of continuous variables, it can handle categorical variables in an unified fashion. The only difference between continuous and categorical variables is the specification of a kernel function. The reader is referred to Wahba (1990) for more discussions on reproducing kernels.
There is another class of procedures in between the parametric and nonparametric approaches called the partially linear model. A partially linear model allows the log-relative hazard function to consist of a linear component and a nonparametric component (Cai et al., 2007; Ma and Kosorok, 2005). Suppose the baseline covariates X can be separated into two non-overlapping parts: X1 and X2, where the variables in the first part have linear effects and those in the second part have nonlinear effects, then the log-hazard function in a partially linear model can be written as:
| (6) |
where γ are unknown regression parameters and η2 is an unknown function.
These two components of variables are decided a priori based on researchers’ judgement except for the categorical variables, which are commonly included in the first part of the variables. In a partially linear model, the objective is to simultaneously estimate γ and η2. Lu and Zhang (2010) proposed an estimation procedure and established an asymptotic result for partially linear model in a more general transformation model that includes the Cox’s model as a special case. Du et al. (2010) proposed a joint estimation and selection procedure in the semiparametric framework and provided a sound theoretical justification. Analogous to the linear model, the regression parameters γ in the parametric component are subjected to SCAD or adaptive LASSO penalty. The variable selection in the nonparametric component is performed in a nested fashion. A full model with interaction terms is first derived. Whenever the Kullback-Leibler distance between a full model and a reduced model is small enough, the reduced model will be selected.
Despite the various existing nonparametric estimation procedures, there are very few methods for nonparametric variable selection. This partly reflects the challenge of censored outcomes. Hastie and Tibshirani (1990) considered several nonlinear selection procedures which were essentially the same as a stepwise search, while Lin et al. (2006) proposed a hypothesis testing procedure to test covariate effects based on a smoothing splines model. More recently, regularization methods have been a great success in parametric models for their improved stability in estimation and accuracy in prediction. Leng and Zhang (2006) proposed a novel regularization method in nonparametric Cox’s model, which estimated and selected function components simultaneously by solving the optimization problem:
| (7) |
where wj, j = 1, …, p, are known weights to avoid over-penalizing prominent function components.
The novelty of (7) is the use of RKHS norms as penalty, which is referred to as the COmponent Selection and Smoothing Operator (COSSO) penalty in nonparametric literature. Leng and Zhang (2006) argued that the COSSO penalty can be viewed as a non-trivial generalization of the famous LASSO penalty in linear model. Just as the L1 penalty can perform variable selection while the L2 norm cannot in a linear model, the distinction also holds in a nonparametric model. Although a different penalty is adopted, the above optimization problem also enjoys several desirable properties such as those in a smoothing splines model given in (4). One advantage is that the minimizer of (7) also has a finite representation similar to that in (5). Later, in the numerical study, we will demonstrate the performance of COSSO and compare it with LASSO under various situations.
We conclude this section by noting some caveats in using nonparametric procedures. By design, nonparametric procedures are data-driven approaches that identify the underlying association that might be otherwise missed. It may also be equally misleading if the regularization parameter is not properly chosen. A nonlinear function can be estimated as a linear function if the regularization parameter is too large and vice versa. In addition, a nonparametric procedure is more sensitive to outliers than a parametric method due to its local fitting feature. Finally, the curse of dimensionality or data sparsity could also affect the performance of a nonparametric procedure. We will demonstrate the challenges of the nonparametric procedure when the covariates are high-dimensional later in the simulation section.
3. SIMULATION
We perform extensive simulations to demonstrate the impact of model misspecification, and use COSSO and adaptive COSSO to select and estimate function components. We also include LASSO and adaptive LASSO to compare to the nonparametric COSSO procedures. The adaptive weights for COSSO are given by the reciprocal of empirical functional L2 norm; whereas those for LASSO are given by the reciprocal of absolute regression parameter estimates from a full model as suggested by Zou (2006). The regularization parameters in COSSO are tuned by approximate cross-validation as recommended by Leng and Zhang (2006). The approximate cross-validation is a slight variation from a cross-validation score derived by Gu (2002) based on a Kullback-Leibler distance for hazard function. We employ 10-fold cross-validation to tune the regularization parameter in LASSO for a more balanced comparison between the LASSO and the COSSO procedures.
3.1 Simulation Setup
In the simulation study, we first generate independently from uniform(0,1). We define and so that , ∀j ≠ k. We use ρ = 0.6 throughout the simulation. Then we trim x(j)’s to (0,1). To examine the selection capability on categorical variables, we transform the first two variables by letting, and , where I(·) is an indicator function taking value one if the argument is true.
We generate n survival time from an exponential distribution with mean exp{−η(xi)} and consider two types of censoring time. To guarantee the independence between censoring time and survival time, the first type of censoring time is taken from an independent exponential distribution with mean V · exp{−η(xi)}, where V is a random sample drawn from uniform (a, a + 2); whereas the second type of censoring time is taken from an independent uniform (0, b). The constants a and b are chosen such that the censoring rate is controlled at pre-specified level (Halabi and Singh, 2004).
We use four criteria to assess model selection: frequency of selecting the correct model (Correct), frequency of selecting more than the important variables (Over), frequency of missing at least one important variable (Under) and the selected model size (Size). In addition, to demonstrate the model prediction, we further apply the final model on the testing data generated in the same way as the training data and compute the concordance index (Concordance) and the integrated time-dependent area under the curve (AUC) (Uno et al., 2007). The sample size in the testing data is set at 5,000.
We consider four examples in the simulation study:
Example 1:
| (8) |
In the first example, we consider two nonlinear effects in the model. Though affects the hazard function in a nonlinear fashion, the logarithm function is monotonic and only moderately deviates from a linear function in the (0, 1) interval. Hence, we question whether LASSO can identify this variable. Conversely, the quadratic effect of makes it much challenging for LASSO to detect this signal.
Example 2:
| (9) |
In the second example, although there is still one nonlinear effect in the model, its monotonicity will not be a problem for LASSO to detect the signal. The nonlinear effect is included so that we can investigate how the misspecification would affect the model performance.
Example 3:
| (10) |
In the third example, we let all the covariate effects be linear so that LASSO does not suffer from misspecification. The purpose of this example is to examine how much efficiency is lost when a complex nonparametric procedure is used when the true covariate effects are linear.
Example 4:
| (11) |
In the fourth example, we intend to examine the variable selection and prediction in a small-n-large-p situation. We generate the survival time from a Weibull distribution and use γ = 1.5 to enhance the signal strength. The covariate effects are the same as those in the first example. In this example, we first screen the number of variables down to a more manageable scale, ⌊n/log(n)⌋. More specifically, we perform the principled sure independent screening (Zhao and Li, 2012) and nonparametric independent screening method (Fan et al., 2011) before before applying LASSO and COSSO, respectively.
The number of predictors are set at 20 for the first three examples and 1,000 for the fourth example. To mimic the TROPIC data, we consider two sample sizes: n = 200, 400, and two censoring rates: 15% and 30%. Due to the computational intensity, we run each parameter combination 500 times and summarize the average performance. All computations are performed in the R environment using packages glmnet version 1.8-2 and cosso version 2.1-0. Both packages are available from the Comprehensive R Archive Network (CRAN) (R Core Team, 2012) at http://www.r-project.org.
4. SIMULATION RESULTS
Table II presents the average results of the 500 simulations for Example 1. We first focus on the scenarios when exponential failure times and exponential censoring times are assumed. When the sample size is 200 and the censoring proportion is 15%, LASSO and adaptive LASSO miss at least one important covariate 67% and 76% of the times, even though the average selected model sizes are 7.56 and 6.95, respectively. On the other hand, COSSO and adaptive COSSO select about the same model size, but their underselection rates are significantly lower, which are 9% and 16%, respectively. As for the prediction accuracy, the concordance index and the integrated time-dependent AUC for both COSSO and adaptive COSSO are about 0.65 and 0.75. On the other hand, LASSO and adaptive LASSO provide less accurate prediction as some important predictors are not selected. Their concordance index and integrated time-dependent AUC are 0.64 and 0.72, respectively.
Table 2.
Average model selection and model performance for Example 1 based on 500 Simulations. The standard errors are given in the parentheses.
| (n, Censoring Proportion) | Method | Correct | Over | Under | Size | Concordance | AUC |
|---|---|---|---|---|---|---|---|
| Exp. Survival, Exp. Censoring | |||||||
| (200,15%) | LASSO | 0.01 | 0.32 | 0.67 | 7.56 (0.12) | 0.637 (0.001) | 0.726 (0.001) |
| ALASSO | 0.00 | 0.24 | 0.76 | 6.95 (0.11) | 0.635 (0.001) | 0.723 (0.001) | |
| COSSO | 0.02 | 0.88 | 0.09 | 7.63 (0.09) | 0.653 (0.001) | 0.754 (0.001) | |
| ACOSSO | 0.07 | 0.77 | 0.16 | 6.45 (0.08) | 0.654 (0.001) | 0.755 (0.001) | |
| (200,30%) | LASSO | 0.01 | 0.33 | 0.66 | 7.37 (0.20) | 0.632 (0.001) | 0.726 (0.001) |
| ALASSO | 0.00 | 0.21 | 0.78 | 7.00 (0.18) | 0.629 (0.001) | 0.721 (0.001) | |
| COSSO | 0.02 | 0.80 | 0.18 | 7.51 (0.11) | 0.648 (0.001) | 0.756 (0.001) | |
| ACOSSO | 0.05 | 0.65 | 0.30 | 6.32 (0.10) | 0.648 (0.001) | 0.757 (0.001) | |
| (400,15%) | LASSO | 0.00 | 0.37 | 0.63 | 8.10 (0.13) | 0.645 (0.000) | 0.739 (0.001) |
| ALASSO | 0.01 | 0.25 | 0.74 | 6.72 (0.13) | 0.645 (0.000) | 0.739 (0.001) | |
| COSSO | 0.05 | 0.95 | 0.00 | 7.35 (0.08) | 0.665 (0.000) | 0.772 (0.000) | |
| ACOSSO | 0.08 | 0.91 | 0.01 | 6.34 (0.06) | 0.666 (0.000) | 0.775 (0.000) | |
| (400,30%) | LASSO | 0.01 | 0.36 | 0.63 | 8.19 (0.13) | 0.644 (0.000) | 0.744 (0.001) |
| ALASSO | 0.01 | 0.24 | 0.75 | 6.72 (0.12) | 0.643 (0.000) | 0.743 (0.001) | |
| COSSO | 0.04 | 0.93 | 0.03 | 7.51 (0.08) | 0.662 (0.000) | 0.779 (0.001) | |
| ACOSSO | 0.07 | 0.89 | 0.04 | 6.45 (0.07) | 0.664 (0.000) | 0.782 (0.001) | |
| Exp. Survival, Uniform Censoring | |||||||
| (200,15%) | LASSO | 0.01 | 0.31 | 0.68 | 7.47 (0.12) | 0.640 (0.000) | 0.720 (0.001) |
| ALASSO | 0.01 | 0.26 | 0.74 | 6.73 (0.12) | 0.638 (0.001) | 0.717 (0.001) | |
| COSSO | 0.02 | 0.84 | 0.14 | 7.73 (0.10) | 0.654 (0.001) | 0.744 (0.001) | |
| ACOSSO | 0.07 | 0.74 | 0.19 | 6.32 (0.08) | 0.655 (0.001) | 0.747 (0.001) | |
| (200,30%) | LASSO | 0.01 | 0.26 | 0.74 | 7.34 (0.12) | 0.639 (0.001) | 0.699 (0.001) |
| ALASSO | 0.00 | 0.24 | 0.75 | 7.00 (0.11) | 0.636 (0.001) | 0.696 (0.001) | |
| COSSO | 0.01 | 0.78 | 0.21 | 7.72 (0.10) | 0.650 (0.001) | 0.717 (0.001) | |
| ACOSSO | 0.07 | 0.64 | 0.29 | 6.34 (0.08) | 0.651 (0.001) | 0.720 (0.001) | |
| (400,15%) | LASSO | 0.00 | 0.32 | 0.67 | 8.03 (0.13) | 0.648 (0.000) | 0.732 (0.000) |
| ALASSO | 0.00 | 0.25 | 0.74 | 6.61 (0.12) | 0.648 (0.000) | 0.732 (0.000) | |
| COSSO | 0.03 | 0.97 | 0.00 | 7.86 (0.08) | 0.666 (0.000) | 0.762 (0.000) | |
| ACOSSO | 0.06 | 0.94 | 0.01 | 6.75 (0.07) | 0.667 (0.000) | 0.765 (0.000) | |
| (400,30%) | LASSO | 0.00 | 0.32 | 0.68 | 8.16 (0.13) | 0.648 (0.000) | 0.713 (0.001) |
| ALASSO | 0.02 | 0.25 | 0.73 | 6.72 (0.12) | 0.648 (0.000) | 0.712 (0.001) | |
| COSSO | 0.02 | 0.96 | 0.02 | 7.94 (0.08) | 0.664 (0.000) | 0.737 (0.001) | |
| ACOSSO | 0.04 | 0.92 | 0.04 | 6.87 (0.07) | 0.666 (0.000) | 0.740 (0.001) | |
Similar results are noted for the other sample sizes and censoring rates. In addition, we observe that there is only a slight difference between the two types of censoring time. Overall, the simulation results demonstrate that both LASSO and adaptive LASSO suffer from serious underselection in all circumstances despite the fact that their model sizes are relatively larger. A common feature of using cross-validation as a tuning procedure is that it is expected that all of the competing methods rarely identify the correct model and their selected model sizes are greater than four. There exists, however, some differences between the approximate cross-validation and k-fold cross-validation procedures. For instance, although the former is named approximate cross-validation, it does not involve any data partition during the computation. Furthermore, the k-fold cross-validation usually computes the partial likelihood contribution from each fold rather than the Kullback-Leibler distance.
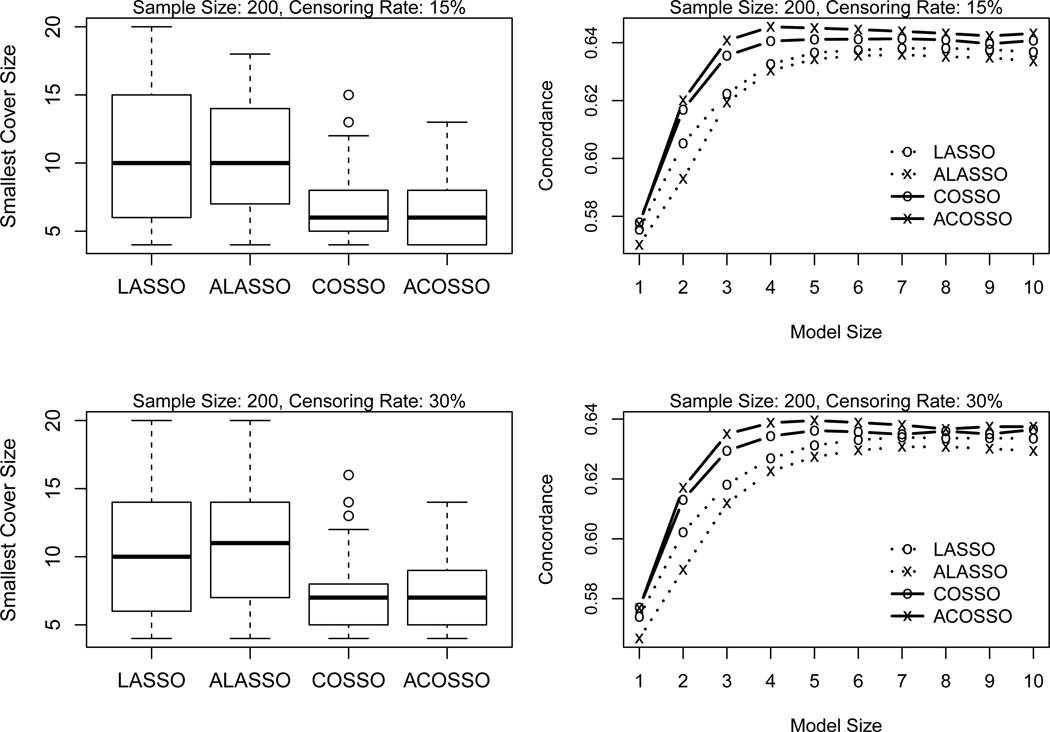
The tuning procedure provides a guidance to determine a stopping point along the solution path. Because the original notions of solution paths differ between LASSO and COSSO, we simply refer to the solution path as a sequence that indicates the order in which the variable is selected. The ideal procedure should put all of the four prominent covariates toward the beginning of the path, followed by the noise ones. Hence, a more direct approach to compare the variable selection is to use the smallest model size to cover the four important covariates. Apart from model selection, we are also interested in how the prediction accuracy varies along the solution path.
In Figure 2, we compare the smallest model that includes all important covariates on the left panel and illustrate the prediction accuracy at different model size on the right. From the boxplot on the left panel of Figure 2, we note that some signals enter the (adaptive) LASSO solution path when half of the predictors are already included. Therefore, it takes LASSO and adaptive LASSO larger model sizes (about 10 or 11) to include all the prominent covariates compared to COSSO. Since the cross-validation tuning on average selects a model of size 7, this observation also explains why LASSO procedures experience serious underselection. On the other hand, it only takes COSSO and adaptive COSSO a median model size 7 to do the same, implying the superior performance of COSSO and adaptive COSSO to their competitor. In terms of prediction accuracy, all procedures provide very similar performance at model size 1. This is because the first covariate, z(1), is most frequently chosen to enter the solution paths in the first place. As the model size increases, the separation between the two approaches becomes apparent. Since (adaptive) COSSO consistently identifies the true signals and correctly estimates their effects, it therefore produces better prediction accuracy.
Figure 2.
Smallest model size to cover all informative covariates (left panel) and prediction accuracy at different model sizes (right panel) in Example 1.
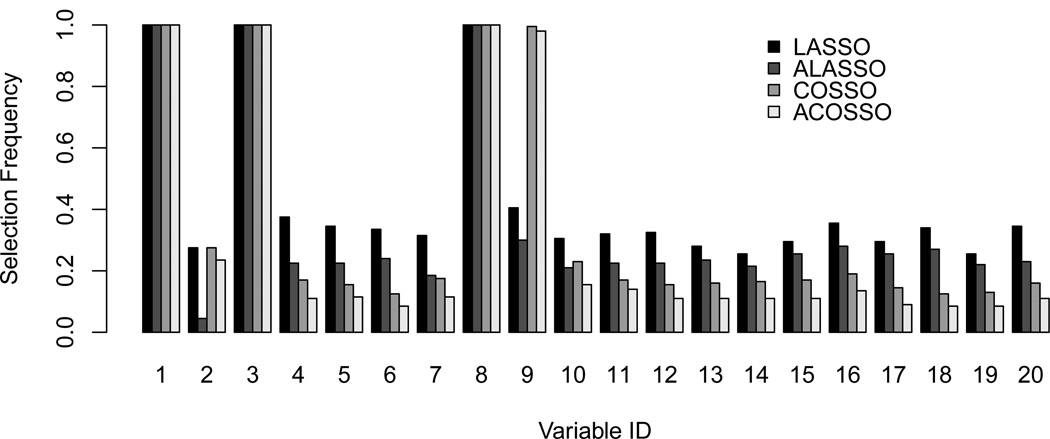
We continue the discussion based on the final models selected by cross-validation and approximate cross-validation. The LASSO procedures choose a larger model size and results in the larger standard errors for the selected model size than the COSSO procedures. To give more insights into the variable selection, we plot the frequency of selecting each of the 20 variables in Figure 3. It is clear that LASSO and adaptive LASSO have no difficulty detecting the 8th variable even though its true effect is nonlinear. However, the selection frequency for the 9th variable drops to less than 40%, making it indistinguishable from the other noise variables. Even in the cases when the 9th variable is selected, the average estimated log-hazard ratios are 0.24 and 0.10 using LASSO and adaptive LASSO, respectively. Such a positive slope estimate could lead to the misinterpretation of the effects and decrease the prognostic accuracy of the model.
Figure 3.
Appearance frequency of the variables based on 500 simulations for Example 1 using exponential censoring when the sample size is 400 and censoring rate is 15%.
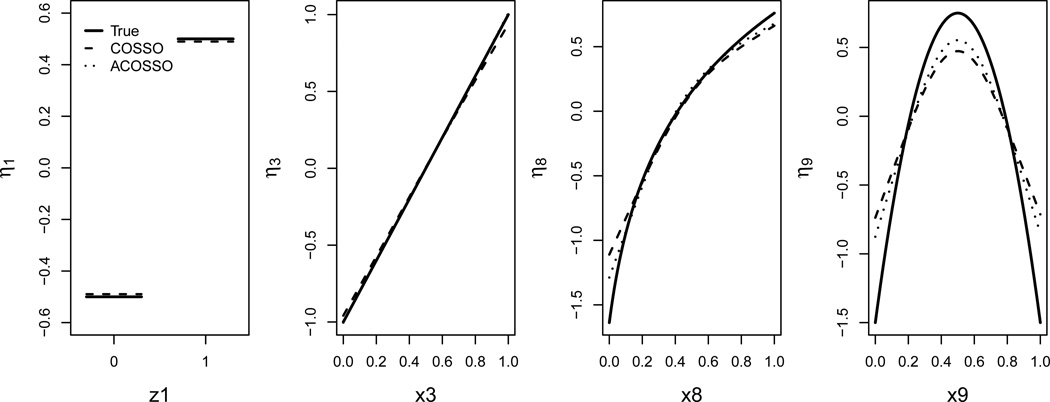
Using the first example, two facets of model misspecification are observed. First, it fails to identify all of the prominent predictors and second, it compromises the prediction performance. As a nonparametric procedure, COSSO imposes the least assumption and provides a viable alternative. Moreover, it naturally provides a graphical tool to examine the covariate effects. Figure 4 shows the average estimated function components along with the true ones. We observe that the COSSO procedures produce very good estimates for the important functional components.
Figure 4.
The average estimated function components (dashed and dotted lines) based on 500 simulations and true function component (solid line) for the four prominent components in Example 1 using exponential censoring when the sample size is 400 and censoring rate is 15%.
The simulation results for Example 2 are summarized in Table III. We demonstrate that the underselection rates for the LASSO procedures are much lower compared with those in Example 1. LASSO procedures still tend to choose a larger model size, but it also covers all of the informative predictors more often when the adaptive weights are not used. When the adaptive weights are utilized, adaptive COSSO clearly benefits more than adaptive LASSO. Moreover, adaptive COSSO not only selects the correct model more often, ranging from 14% to 30%, but also covers all important predictors using a smaller model size. In terms of model prediction, although not missing any important variables from the model, the LASSO procedures misspecify the effect of the 9th variable and therefore result in lower predictive accuracy as presented in the columns Concordance and AUC.
Table 3.
Average model selection and model performance for Example 2 based on 500 Simulations. The standard errors are given in the parentheses.
| (n, Censoring Proportion) | Method | Correct | Over | Under | Size | Concordance | AUC |
|---|---|---|---|---|---|---|---|
| Exp. Survival, Exp. Censoring | |||||||
| (200,15%) | LASSO | 0.02 | 0.95 | 0.03 | 8.79 (0.12) | 0.704 (0.000) | 0.803 (0.000) |
| ALASSO | 0.06 | 0.88 | 0.06 | 7.68 (0.11) | 0.703 (0.000) | 0.802 (0.001) | |
| COSSO | 0.08 | 0.86 | 0.06 | 6.30 (0.07) | 0.708 (0.000) | 0.808 (0.000) | |
| ACOSSO | 0.21 | 0.75 | 0.04 | 6.29 (0.08) | 0.709 (0.000) | 0.809 (0.000) | |
| (200,30%) | LASSO | 0.03 | 0.91 | 0.07 | 8.61 (0.18) | 0.701 (0.000) | 0.808 (0.001) |
| ALASSO | 0.04 | 0.85 | 0.11 | 7.80 (0.19) | 0.699 (0.001) | 0.806 (0.001) | |
| COSSO | 0.06 | 0.79 | 0.14 | 6.35 (0.11) | 0.705 (0.000) | 0.813 (0.001) | |
| ACOSSO | 0.20 | 0.70 | 0.10 | 6.11 (0.12) | 0.707 (0.000) | 0.815 (0.001) | |
| (400,15%) | LASSO | 0.02 | 0.98 | 0.00 | 9.37 (0.13) | 0.709 (0.000) | 0.810 (0.000) |
| ALASSO | 0.13 | 0.87 | 0.00 | 7.41 (0.12) | 0.709 (0.000) | 0.810 (0.000) | |
| COSSO | 0.14 | 0.85 | 0.00 | 6.07 (0.07) | 0.713 (0.000) | 0.815 (0.000) | |
| ACOSSO | 0.30 | 0.69 | 0.00 | 5.44 (0.08) | 0.715 (0.000) | 0.817 (0.000) | |
| (400,30%) | LASSO | 0.01 | 0.99 | 0.00 | 9.36 (0.13) | 0.708 (0.000) | 0.817 (0.000) |
| ALASSO | 0.09 | 0.90 | 0.01 | 7.45 (0.11) | 0.708 (0.000) | 0.817 (0.000) | |
| COSSO | 0.12 | 0.86 | 0.01 | 6.18 (0.07) | 0.712 (0.000) | 0.822 (0.000) | |
| ACOSSO | 0.14 | 0.86 | 0.00 | 6.54 (0.07) | 0.714 (0.000) | 0.825 (0.000) | |
| Exp. Survival, Uniform Censoring | |||||||
| (200,15%) | LASSO | 0.02 | 0.97 | 0.01 | 8.52 (0.11) | 0.706 (0.000) | 0.797 (0.000) |
| ALASSO | 0.06 | 0.88 | 0.06 | 7.46 (0.11) | 0.704 (0.000) | 0.795 (0.001) | |
| COSSO | 0.15 | 0.80 | 0.05 | 6.68 (0.09) | 0.709 (0.000) | 0.800 (0.000) | |
| ACOSSO | 0.21 | 0.76 | 0.03 | 6.27 (0.09) | 0.710 (0.000) | 0.803 (0.000) | |
| (200,30%) | LASSO | 0.02 | 0.95 | 0.03 | 8.48 (0.11) | 0.704 (0.000) | 0.788 (0.001) |
| ALASSO | 0.05 | 0.86 | 0.09 | 7.55 (0.11) | 0.702 (0.001) | 0.785 (0.001) | |
| COSSO | 0.12 | 0.80 | 0.08 | 6.73 (0.09) | 0.706 (0.000) | 0.790 (0.001) | |
| ACOSSO | 0.19 | 0.74 | 0.07 | 6.34 (0.09) | 0.708 (0.000) | 0.793 (0.001) | |
| (400,15%) | LASSO | 0.02 | 0.98 | 0.00 | 8.99 (0.12) | 0.710 (0.000) | 0.803 (0.000) |
| ALASSO | 0.13 | 0.87 | 0.00 | 7.12 (0.11) | 0.710 (0.000) | 0.803 (0.000) | |
| COSSO | 0.13 | 0.87 | 0.00 | 6.80 (0.09) | 0.714 (0.000) | 0.807 (0.000) | |
| ACOSSO | 0.20 | 0.80 | 0.00 | 6.56 (0.09) | 0.716 (0.000) | 0.810 (0.000) | |
| (400,30%) | LASSO | 0.02 | 0.98 | 0.00 | 9.04 (0.12) | 0.710 (0.000) | 0.795 (0.000) |
| ALASSO | 0.11 | 0.89 | 0.00 | 7.42 (0.11) | 0.710 (0.000) | 0.794 (0.000) | |
| COSSO | 0.10 | 0.90 | 0.00 | 6.88 (0.08) | 0.713 (0.000) | 0.798 (0.000) | |
| ACOSSO | 0.14 | 0.86 | 0.00 | 6.73 (0.08) | 0.715 (0.000) | 0.802 (0.000) | |
We display in Table IV the simulation results for Example 3 where all the covariate effects are linear. The results indicate that even in the home court of LASSO, COSSO still produces very competitive performance. Both LASSO and COSSO perform well in terms of model selection. Not surprisingly, LASSO consistently selects a larger model size but it also has the smaller underselection rate. As a result, LASSO produces higher prediction in all cases but the efficiency gain vanishes when the sample size gets larger. We think that the performance gap between LASSO and COSSO will eventually disappear as sample size increases.
Table 4.
Average model selection and model performance for Example 3 based on 500 Simulations. The standard errors are given in the parentheses.
| (n, Censoring Proportion) | Method | Correct | Over | Under | Size | Concordance | AUC |
|---|---|---|---|---|---|---|---|
| Exp. Survival, Exp. Censoring | |||||||
| (200,15%) | LASSO | 0.02 | 0.97 | 0.01 | 9.02 (0.12) | 0.685 (0.000) | 0.767 (0.000) |
| ALASSO | 0.05 | 0.89 | 0.06 | 7.80 (0.11) | 0.684 (0.000) | 0.765 (0.001) | |
| COSSO | 0.04 | 0.88 | 0.08 | 6.55 (0.07) | 0.683 (0.000) | 0.765 (0.001) | |
| ACOSSO | 0.10 | 0.83 | 0.07 | 6.49 (0.07) | 0.683 (0.000) | 0.763 (0.001) | |
| (200,30%) | LASSO | 0.01 | 0.94 | 0.05 | 8.88 (0.12) | 0.682 (0.000) | 0.769 (0.001) |
| ALASSO | 0.03 | 0.84 | 0.13 | 7.82 (0.10) | 0.680 (0.001) | 0.766 (0.001) | |
| COSSO | 0.04 | 0.78 | 0.18 | 6.61 (0.07) | 0.680 (0.001) | 0.766 (0.001) | |
| ACOSSO | 0.11 | 0.74 | 0.15 | 6.37 (0.08) | 0.680 (0.001) | 0.765 (0.001) | |
| (400,15%) | LASSO | 0.01 | 0.99 | 0.00 | 9.59 (0.13) | 0.692 (0.000) | 0.775 (0.000) |
| ALASSO | 0.10 | 0.90 | 0.00 | 7.33 (0.12) | 0.692 (0.000) | 0.775 (0.000) | |
| COSSO | 0.07 | 0.93 | 0.01 | 6.17 (0.06) | 0.691 (0.000) | 0.774 (0.000) | |
| ACOSSO | 0.15 | 0.85 | 0.00 | 6.54 (0.08) | 0.690 (0.000) | 0.774 (0.000) | |
| (300,30%) | LASSO | 0.01 | 0.99 | 0.00 | 9.50 (0.12) | 0.691 (0.000) | 0.780 (0.000) |
| ALASSO | 0.01 | 0.91 | 0.01 | 7.39 (0.11) | 0.691 (0.000) | 0.780 (0.000) | |
| COSSO | 0.06 | 0.93 | 0.01 | 6.16 (0.06) | 0.690 (0.000) | 0.779 (0.000) | |
| ACOSSO | 0.14 | 0.85 | 0.01 | 6.42 (0.07) | 0.690 (0.000) | 0.779 (0.000) | |
| Exp. Survival, Uniform Censoring | |||||||
| (200,15%) | LASSO | 0.02 | 0.97 | 0.01 | 8.62 (0.11) | 0.689 (0.000) | 0.764 (0.000) |
| ALASSO | 0.06 | 0.87 | 0.07 | 7.62 (0.11) | 0.687 (0.000) | 0.762 (0.001) | |
| COSSO | 0.06 | 0.86 | 0.09 | 6.36 (0.06) | 0.687 (0.000) | 0.761 (0.001) | |
| ACOSSO | 0.22 | 0.69 | 0.09 | 6.08 (0.08) | 0.686 (0.000) | 0.760 (0.001) | |
| (200,30%) | LASSO | 0.02 | 0.95 | 0.04 | 8.41 (0.11) | 0.689 (0.000) | 0.761 (0.001) |
| ALASSO | 0.06 | 0.84 | 0.10 | 7.52 (0.10) | 0.687 (0.000) | 0.759 (0.001) | |
| COSSO | 0.05 | 0.80 | 0.15 | 6.63 (0.07) | 0.686 (0.000) | 0.758 (0.001) | |
| ACOSSO | 0.20 | 0.64 | 0.16 | 6.03 (0.08) | 0.686 (0.000) | 0.757 (0.001) | |
| (400,15%) | LASSO | 0.02 | 0.98 | 0.00 | 9.04 (0.12) | 0.694 (0.000) | 0.770 (0.000) |
| ALASSO | 0.12 | 0.88 | 0.00 | 7.16 (0.11) | 0.694 (0.000) | 0.771 (0.000) | |
| COSSO | 0.12 | 0.88 | 0.00 | 6.06 (0.06) | 0.694 (0.000) | 0.770 (0.000) | |
| ACOSSO | 0.24 | 0.76 | 0.00 | 6.13 (0.08) | 0.693 (0.000) | 0.769 (0.000) | |
| (400,30%) | LASSO | 0.01 | 0.99 | 0.00 | 9.16 (0.12) | 0.695 (0.000) | 0.769 (0.000) |
| ALASSO | 0.08 | 0.92 | 0.00 | 7.40 (0.11) | 0.695 (0.000) | 0.769 (0.000) | |
| COSSO | 0.08 | 0.91 | 0.01 | 6.09 (0.06) | 0.695 (0.000) | 0.769 (0.000) | |
| ACOSSO | 0.20 | 0.80 | 0.00 | 6.23 (0.08) | 0.695 (0.000) | 0.768 (0.000) | |
In the high-dimensional example, we use the sure screening rate (SS) to show the frequency that all four prominent covariates are kept after the initial screening procedures. The simulation results are summarized in Table V. Although we conduct a variable screening before regularized methods, there are still 37 and 66 potential predictors when sample sizes are 200 and 400, respectively. As a result, we tune the regularization parameter for LASSO by BIC because cross-validation tends to select a much larger model.
Table 5.
Average model selection and model performance for Example 4 based on 500 Simulations. The standard errors are given in the parentheses.
| (n, Censoring Proportion) | Method | SS | Correct | Over | Under | Size | Concordance | AUC |
|---|---|---|---|---|---|---|---|---|
| Weibull. Survival, Exponential Censoring | ||||||||
| (200,15%) | LASSO | 0.50 | 0.00 | 0.13 | 0.87 | 13.62 (0.51) | 0.639 (0.002) | 0.688 (0.002) |
| ALASSO | 0.50 | 0.00 | 0.09 | 0.91 | 15.37 (0.22) | 0.634 (0.002) | 0.682 (0.002) | |
| COSSO | 0.60 | 0.00 | 0.36 | 0.64 | 19.55 (0.13) | 0.643 (0.002) | 0.693 (0.001) | |
| ACOSSO | 0.60 | 0.00 | 0.42 | 0.58 | 18.28 (0.13) | 0.654 (0.002) | 0.706 (0.001) | |
| (200,30%) | LASSO | 0.40 | 0.00 | 0.10 | 0.90 | 11.21 (0.52) | 0.618 (0.02) | 0.659 (0.003) |
| ALASSO | 0.40 | 0.00 | 0.05 | 0.95 | 15.87 (0.24) | 0.617 (0.02) | 0.659 (0.002) | |
| COSSO | 0.46 | 0.00 | 0.24 | 0.76 | 19.86 (0.11) | 0.628 (0.02) | 0.674 (0.002) | |
| ACOSSO | 0.46 | 0.00 | 0.26 | 0.74 | 18.60 (0.11) | 0.635 (0.02) | 0.682 (0.002) | |
| (400,15%) | LASSO | 0.95 | 0.02 | 0.12 | 0.86 | 5.00 (0.10) | 0.693 (0.01) | 0.756 (0.001) |
| ALASSO | 0.95 | 0.00 | 0.03 | 0.97 | 8.75 (0.29) | 0.689 (0.01) | 0.751 (0.001) | |
| COSSO | 0.98 | 0.00 | 0.27 | 0.73 | 24.38 (0.13) | 0.668 (0.01) | 0.725 (0.001) | |
| ACOSSO | 0.98 | 0.00 | 0.90 | 0.10 | 24.59 (0.16) | 0.695 (0.01) | 0.756 (0.001) | |
| (400,30%) | LASSO | 0.91 | 0.02 | 0.11 | 0.87 | 4.81 (0.09) | 0.688 (0.01) | 0.751 (0.001) |
| ALASSO | 0.91 | 0.00 | 0.04 | 0.96 | 9.08 (0.31) | 0.684 (0.01) | 0.745 (0.001) | |
| COSSO | 0.95 | 0.00 | 0.28 | 0.72 | 24.97 (0.13) | 0.661 (0.01) | 0.717 (0.001) | |
| ACOSSO | 0.95 | 0.00 | 0.75 | 0.25 | 25.43 (0.15) | 0.682 (0.01) | 0.741 (0.001) | |
| Weibull. Survival, Uniform Censoring | ||||||||
| (200,15%) | LASSO | 0.52 | 0.01 | 0.08 | 0.91 | 10.98 (0.52) | 0.654 (0.002) | 0.704 (0.002) |
| ALASSO | 0.52 | 0.00 | 0.06 | 0.94 | 16.06 (0.27) | 0.640 (0.002) | 0.687 (0.002) | |
| COSSO | 0.70 | 0.00 | 0.13 | 0.87 | 15.30 (0.10) | 0.664 (0.001) | 0.719 (0.001) | |
| ACOSSO | 0.70 | 0.00 | 0.02 | 0.97 | 4.59 (0.07) | 0.677 (0.001) | 0.735 (0.001) | |
| (200,30%) | LASSO | 0.41 | 0.00 | 0.06 | 0.94 | 9.39 (0.50) | 0.645 (0.002) | 0.688 (0.003) |
| ALASSO | 0.41 | 0.00 | 0.05 | 0.95 | 16.66 (0.26) | 0.632 (0.002) | 0.673 (0.002) | |
| COSSO | 0.61 | 0.00 | 0.09 | 0.91 | 15.22 (0.10) | 0.662 (0.001) | 0.711 (0.001) | |
| ACOSSO | 0.61 | 0.00 | 0.01 | 0.99 | 4.54 (0.07) | 0.676 (0.001) | 0.729 (0.001) | |
| (400,15%) | LASSO | 0.94 | 0.02 | 0.06 | 0.92 | 4.78 (0.09) | 0.697 (0.001) | 0.757 (0.001) |
| ALASSO | 0.94 | 0.00 | 0.03 | 0.97 | 8.14 (0.26) | 0.693 (0.001) | 0.753 (0.001) | |
| COSSO | 0.99 | 0.00 | 0.21 | 0.80 | 19.65 (0.15) | 0.686 (0.001) | 0.744 (0.001) | |
| ACOSSO | 0.99 | 0.00 | 0.05 | 0.95 | 6.98 (0.07) | 0.692 (0.001) | 0.753 (0.001) | |
| (400,30%) | LASSO | 0.85 | 0.01 | 0.04 | 0.95 | 4.80 (0.08) | 0.699 (0.001) | 0.756 (0.001) |
| ALASSO | 0.85 | 0.00 | 0.03 | 0.97 | 8.32 (0.28) | 0.694 (0.001) | 0.750 (0.001) | |
| COSSO | 0.98 | 0.00 | 0.15 | 0.85 | 19.39 (0.17) | 0.687 (0.001) | 0.742 (0.001) | |
| ACOSSO | 0.98 | 0.00 | 0.03 | 0.97 | 7.15 (0.10) | 0.694 (0.001) | 0.751 (0.001) | |
When the sample size is 200, the sure screening rate is only about one half and hence all the final models suffer from serious underselection. Of the four important covariates, the signal of the 9th covariate is not strong enough to survive neither the parametric nor nonparametric screening. Although the adaptive LASSO tends to select a larger size model than the LASSO, its underselection rate is even higher. We suspect the initial parameter estimate from the full model is far from the true and hence the adaptive weight does more harm than good in this case. On the contrary, the adaptive weight benefits the COSSO procedure. Even though the adaptive COSSO selects a considerably smaller model size, it helps filter out noise variables and eventually improves model prediction. When we increase the sample size to 400, the sure screening rate becomes much higher in all cases. However, the larger the sample size, the more covariates will be kept after the initial screening. It is essentially the same as the number of covariates rises as the sample size increases. As a result, COSSO suffers from enlarged feature space and performs slightly worse than LASSO.
5. APPLICATION
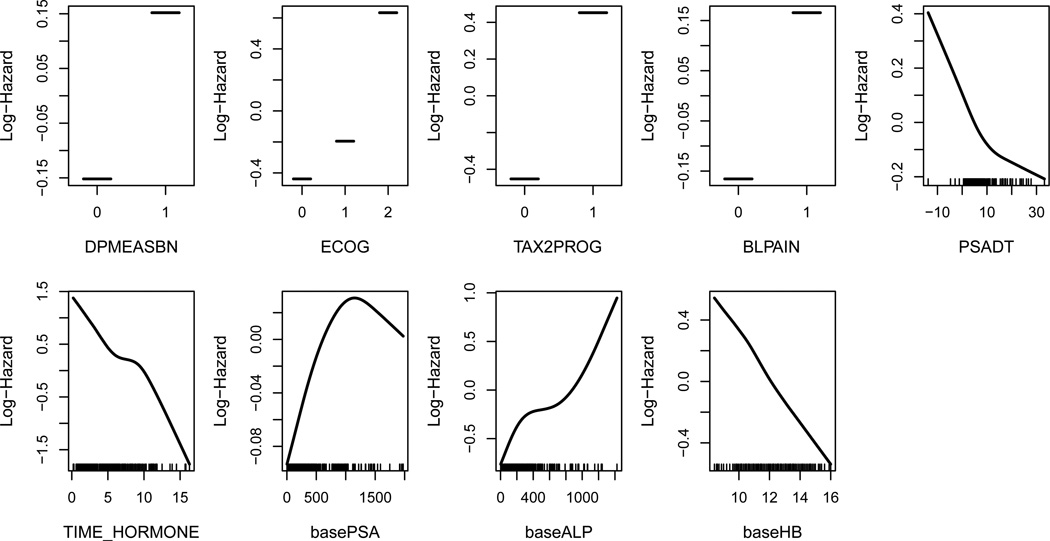
We revisit the phase III clinical trial, TROPIC, by fitting an adaptive COSSO model due to its superior performance that is observed in the simulation study. We use approximate cross-validation as the tuning procedure for COSSO. Since the primary objective of the analysis is to explore the potential nonlinear covariate effects, we use all of the patients data to estimate and select function components. The final model identifies nine variables with a concordance index of 0.723. Compared with the final LASSO and adaptive LASSO models whose concordance indices are 0.716 and 0.713, respectively, the adaptive COSSO selects a relatively parsimonious model but the concordance index is higher, suggesting possible model misspecification. The selected variables and their estimated effects are plotted in Figure 5. Among the five selected continuous variables, almost all show a near linear effect except for baseline PSA, whose estimated log-hazard function suggests a quadratic effect. Based on what we have learned from the simulation study, a covariate with non-monotone effect is not likely to be identified by the LASSO method. This finding explains why baseline PSA, which is an established prognostic factor of overall survival, has a small estimated log-hazard ratio when LASSO and adaptive LASSO are initially implemented.
Figure 5.
The estimated function components for TROPIC data. The tick mark on the x-axis represents an observed data point.
The estimated functional component also provides a useful guide to discretize continuous variables. Discretization is usually done by using sample mean or sample quantiles without using the information from log-hazard profile. For instance, instead of the mean and median of PSADT, which are 5.0 and 3.6 days, respectively, a cut-off at 10.0 days will be informative since the slope of the log-hazard function changes at this value. Similarly, for baseline PSA, we might consider two cut-offs, at, 750 and 1250, or a single cut-off at 750. Dichotomizing baseline PSA using the mean, 296, or median, 124, could mislead the association between this variable and overall survival.
6. DISCUSSION
There is a great need to correctly select and appropriately specify covariates’ effects in predicting clinical outcomes. In this article, we discuss two main aspects of contemporary statistical modeling: model specification and selection. Through extensive simulations, we demonstrate the limitations of parametric selector when the true covariate effect is misspecified. To the best of our knowledge, this is is the first study that rigorously performs such comparisons. Misspecification results in not only poor prediction but probable underselection depending on if the underlying function seriously deviates from a linear function. Correct specification of a covariate, however, is practically infeasible. The lack of a graphical exploratory tool, however, makes identifying nonlinear effects in the Cox’s model a more challenging task than the least squares regression.
Although minimizing possible misspecification, the nonparametric procedure obviously comes at a price of higher computational intensity. The COSSO optimization problem requires that we iteratively solve a smoothing splines type problem and a quadratic programming problem multiple times until the Newton-Raphson algorithm converges. For instance, in our simulation Example 3 with n = 200 and 30% censoring proportion, it takes COSSO about 0.64 second to compute the solution for a given regularization parameter. On the other hand, it only takes LASSO 0.01 second to finish the same task on a laptop computer with an Intel i5-2520M CPU and 4GB memory. The capacity of the number of covariate in nonparametric methods is usually in the order of tens. As the number of covariates or the number of events increase, the computation burden rapidly increases. As a result, when the number of covariates is greater than the sample size, existing nonparametric methods can not be directly implemented without first applying variable screening (Zhao and Li, 2012; Fan et al., 2011) or dimension reduction techniques (Li and Li, 2004; Li, 2006).
Assuming a traditional situation when the sample size is greater than the number of covariates, we make the following recommendations based on the simulation results:
If the covariate effects are all linear, LASSO and adaptive LASSO may be optimal.
If the some of the covariate effects are nonlinear, then investigators need to consider using COSSO procedure.
If the covariate effects are unclear, smoothing splines and the COSSO methods would better serve as exploratory tools to unravel the underlying covariates’ effects.
When applying both LASSO and COSSO on the same data, investigators should be cautious if their solution paths are very different. This difference suggests a possible nonlinear covariate effect, and hence COSSO should be used. Otherwise, if their solution paths are reasonably similar, linear fit should suffice and LASSO should be a better choice.
Prognostic models will continue to be used in medicine and to address important questions that are relevant to patient outcomes. They must, however, be rigorously and carefully designed to ensure reliable results. In summary, advances in computing and statistical modeling make it possible for investigators to correctly identify prognostic factors of outcomes and to increase the predictive accuracy even if the covariate effects are nonlinear. The nonparametric procedures of COSSO are easy to implement and seem to work well if the number of covariates is not too large relative to sample size. The main drawback of using this method is the computational intensity.
Footnotes
This research was supported by National Institutes of Health Grants CA 155296-1A1 and U01 CA157703.
REFERENCES
- Cai J, Fan J, Jiang J, Zhou H. Partially Linear Hazard Regression for Multivariate Survival Data. Journal of the American Statistical Association. 2007;102:538–551. [Google Scholar]
- Cox DR. Regression Models and Life Tables (with discussioon) Journal of the Royal Statistical Society, Ser. B. 1972;34:187–220. [Google Scholar]
- de Bono J, Oudard S, Ozguroglu M, Hansen S, Machiels J, Kocak I, Gravis G, Bodrogi I, Mackenzie M, Shen L, Roessner M, Gupta S, Sartor A. Prednisone Plus Cabazitaxel or Mitoxantrone for Metastatic Castration-Resistant Prostate Cancer Progressing After Docetaxel Treatment: a Randomised Open-Label Trial. Lancet. 2010;376:1147–1154. doi: 10.1016/S0140-6736(10)61389-X. [DOI] [PubMed] [Google Scholar]
- Du P, Ma S, Liang H. Penalized Variable Selection Procedure for Cox Models with Semiparametric Relative Risk. Annals of Statistics. 2010;38:2092–2117. doi: 10.1214/09-AOS780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eubank R. Nonparametric Regression and Spline Smoothing (Second Edition) New York: CRC Press; 1999. [Google Scholar]
- Evgeniou T, Pontil M, Poggio T. Regularization Networks and Support Vector Machines. Advances in Computational Mathematics. 2000;13:1–50. [Google Scholar]
- Fan J, Feng Y, Song R. Nonparametric Independence Screening in Sparse Ultra-High-Dimensional Additive Models. Journal of the American Statistical Association. 2011;106:544–557. doi: 10.1198/jasa.2011.tm09779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J, Li R. Variable Seleciton for Cox’s Proportional Hazards Model and Fraility Model. Annals of Statistics. 2002;30:74–99. [Google Scholar]
- Fan J, Lv J. A Selective Overview of Variable Seleciton in high dimensional feature space. Statistica Sinica. 2010;20:101–148. [PMC free article] [PubMed] [Google Scholar]
- Gray R. Methods for Analyzing Survival Data Using Splines, With Applications to Breast Cancer Prognosis. Journal of the American Statistical Association. 1992;87:942–951. [Google Scholar]
- Gu C. Penalized Likelihood Hazard Estimation: A General Procedure. Statistica Sinica. 1996;6:861–876. [Google Scholar]
- Gu C. Structural Multivariate Function Estimation: Some Automatic Density and Hazard Estimates. Statistica Sinica. 1998;8:317–335. [Google Scholar]
- Gu C. Smoothing Spline ANOVA Models. New York: Springer; 2002. [Google Scholar]
- Halabi S, Owzar K. The Importance of Identifying and Validating Prognostic Factors in Oncology. Seminars in Oncology. 2010;37:e9–e18. doi: 10.1053/j.seminoncol.2010.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halabi S, Singh B. Sample Size Determination for Comparing Several Survival Curves with Unequal Allocations. Statistics in Medicine. 2004;23:1793–1815. doi: 10.1002/sim.1771. [DOI] [PubMed] [Google Scholar]
- Halabi S, Small E, Kantoff P, Kaplan E, Dawson N, Levine E, Blumenstein B, Vogelzang N. Prognostic Model for Prediting Survival in Men with Hormone-Refractory Metastatic Prostate Cancer. Journal of Clinical Oncology. 2003;21:1232–1237. doi: 10.1200/JCO.2003.06.100. [DOI] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R. Generalized Additive Models. London: Chapmand and Hall; 1990. [DOI] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning (Second Edition) New York: Springer; 2008. [Google Scholar]
- Kalbfleisch J, Prentice R. The Statistical Analysis of Failure Time Data (Second Edition) Wiley: New Jersey; 2002. [Google Scholar]
- Kelly W, Halabi S, Carducci M, George D, Mahoney J, Stadler W, Morris M, Kantoff P, Monk J, Kaplan E, Vogelzang N, Small E. Randomized, Double-Blind, Placebo-Controlled Phase III Trial Comparing Docetaxel and Prednisone with or without Bevacizumab in Men with Metastatic Castration-Resistant Prostate Cancer: CALGB 90401. Journal of Clinical Oncology. 2012;30:1232–1237. doi: 10.1200/JCO.2011.39.4767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimeldorf G, Wahba G. Some Results on Techebycheffian Spline Functions. Journal of Mathematical Analysis and Applications. 1971;33:82–95. [Google Scholar]
- Leng C, Zhang HH. Model Selection in Nonparametric Hazard Regression. Journal of Nonparametric Statistics. 2006;18:417–429. [Google Scholar]
- Li L. Survival prediction of diffuse large-B-cell lymphoma based on both clinical and gene expression information. Bioinformatics. 2006;22:466–471. doi: 10.1093/bioinformatics/bti824. [DOI] [PubMed] [Google Scholar]
- Li L, Li H. Dimension reduction methods for microarrays with application to censored survival data. Bioinformatics. 2004;20:3406–3412. doi: 10.1093/bioinformatics/bth415. [DOI] [PubMed] [Google Scholar]
- Lin J, Zhang D, Davidian M. Smoothing Spline-Based Score Tests for Proportional Hazards Models. Biometrics. 2006;62:803–812. doi: 10.1111/j.1541-0420.2005.00521.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Y, Zhang HH. Component Selection and Smoothing in Multivariate Nonparametric Regression. Annals of Statistics. 2006;34:2272–2297. [Google Scholar]
- Lu W, Zhang HH. On Estimation of Partially Linear Transformation Models. Journal of the American Statistical Association. 2010;105:683–691. doi: 10.1198/jasa.2010.tm09302.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma S, Kosorok M. Penalized Log-Likelihood Estimation for Partly Linear Transformation Models With Current Status Data. Annals of Statistics. 2005;33:2256–2290. [Google Scholar]
- O’Sullivan F. Nonparametric Estimation of Relative Risk Using Splines and Cross-Validation. SIAM Journal of Scientific and Statistical Computing. 1988;9:531–542. [Google Scholar]
- O’Sullivan F. Nonparametric Estimation in the Cox Model. Annals of Statistics. 1993;21:124–145. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2012. ISBN 3-900051-07-0. URL: http://www.R-project.org/ [Google Scholar]
- Tibshirani R. The Lasso Method for Variable Selection in the Cox Model. Statistics in Medicine. 1997;16:385–395. doi: 10.1002/(sici)1097-0258(19970228)16:4<385::aid-sim380>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Uno H, Cai T, Tian L, Wei LJ. Evaluating Prediction Rules for t-Year Survivors With Censored Regression Models. Journal of the American Statistical Association. 2007;102:527–537. [Google Scholar]
- Verschraegen C, Vinh-Hung V, Cserni G, Gordon R, Royce M, Vlastos G, Tai P, Storme G. Modeling the Effect of Tumor Size in Early Breast Cancer. Annals of Surgery. 2005;241:309–318. doi: 10.1097/01.sla.0000150245.45558.a9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volpi A, Nanni O, De Paola F, Granato AM, Mangia A, Monti F, Schittulli F, De Lena M, Scarpi E, Rosetti P, Monti M, Gianni L, Amadori D, Paradiso A. HER-2 Expression and Cell Proliferation: Prognostic Markers in Patients With Node-Negative Breast Cancer. Journal of Clinical Oncology. 2003;21:2708–2712. doi: 10.1200/JCO.2003.04.008. [DOI] [PubMed] [Google Scholar]
- Wahba G. Spline Models for Observational Data. Philadelphia: SIAM; 1990. [Google Scholar]
- Wang Y. Smoothing Splines: Method and Applications. Boca Raton: CRC Press; 2011. [Google Scholar]
- Zeleniuch-Jacquotte A, Shore RE, Koenig KL, Akhmedkhanov A, Afanasyeva Y, Kato I, Kim MY, Rinaldi S, Kaaks R, Toniolo P. Postmenopausal Levels of Oestrogen, Androgen, and SHBG and Breast Cancer: Long-Term Results of a Prospective Study. British Journal of Cancer. 2004;90:153–159. doi: 10.1038/sj.bjc.6601517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang HH, Lu W. Adaptive LASSO for Cox’s Proportional Hazards Model. Biometrika. 2007;94:691–703. [Google Scholar]
- Zhao SD, Li Y. Principled sure independence screening for Cox models with ultra-high-dimensional covariates. Journal of Multivariate Analysis. 2012;105:397–411. doi: 10.1016/j.jmva.2011.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou H. The Adaptive Lasso and Its Oracle Properties. Journal of the American Statistical Association. 2006;101:1418–1429. [Google Scholar]