Abstract
Spin-triplet superconductivity in Sr2RuO4 has attracted enormous interest. Like other unconventional superconductors, superconductivity in Sr2RuO4 is in close proximity to magnetic instability. Undoped Sr2RuO4 exhibits incommensurate antiferromagnetic (AFM) fluctuations, which can evolve into static, short-range AFM order via Ti doping. Moreover, weak ferromagnetic (FM) coupling in Sr2RuO4 has also been suggested by NMR/neutron scattering experiments and studies on Ca2−xSrxRuO4 and Sr2−yLayRuO4, implying orbital dependent magnetism. We report bulk static, short-range FM order in Sr2RuO4 triggered by <2% Co doping, showing superconductivity in Sr2RuO4 is much closer to FM instability than previously reported in Ca2−xSrxRuO4. We also find Mn doping can effectively establish incommensurate AFM order, with TN ~ 50 K for 3% Mn doping. These new results place Sr2RuO4 in a unique situation where superconductivity lies directly on the borderline of two distinct magnetic states, highlighting the important role of competing magnetic fluctuations in determining superconducting properties of Sr2RuO4.
Shortly after the discovery of superconductivity at Tc ~ 1.5 K in Sr2RuO41, it was proposed that the superconductivity of this material may involve an unconventional pairing symmetry2,3,4,5. Rice and Sigrist6 proposed a phenomenological model of spin triplet p-wave superconductivity in Sr2RuO4 based on the similarities of the Fermi liquid states of Sr2RuO4 and liquid 3He as well as the ferromagnetism of relative compound SrRuO3. The notion of spin-triplet superconductivity in Sr2RuO4 has now been demonstrated by several key experiments7,8,9 and exotic properties arising from spin-triplet pairing have been observed in a growing number of experiments, such as time-reversal symmetry breaking7,10, chiral order parameter domain11 and half-quantum fluxoid states12. However, there is still no clear agreement on the exact nature of the mechanism responsible for this unconventional pairing symmetry and interest in this question has generated considerable research over the last 15 years13,14.
In many unconventional superconductors, such as high-Tc cuprates15, iron pnictides16, and heavy Fermion systems17, the superconducting state lies adjacent to static magnetic order. Such close proximity of the superconducting state to static magnetic order has naturally led to the suggestion that spin fluctuations may play a key role in the pairing mechanism of these unconventional superconductors. Given that Sr2RuO4 shows spin-triplet superconductivity, it is natural to ask whether or not its superconducting state also lies adjacent to static magnetic order. A great deal of work has been done to address this question. Early inelastic neutron scattering studies of Sr2RuO4 found evidence for incommensurate spin fluctuations at the wavevector Qic ≈ (±2π/3a, ±2π/3a, 0)18, consistent with the theoretical prediction of spin-density-wave (SDW) magnetic fluctuations driven by Fermi surface nesting between the α and β sheets derived from Ru 4dxz/yz orbitals19. Such incommensurate magnetic fluctuations can be stabilized by Ti doping20 and short-range, static incommensurate order was probed in neutron scattering measurements of the 9% Ti-doped sample21. Although these results have established that Sr2RuO4 is adjacent to incommensurate magnetic order, AFM fluctuations are expected to favor d-wave pairing over p-wave pairing19. According to the phenomenological theory by Rice and Sigrist6 and theoretical studies by several other groups22,23,24,25, ferromagnetic (FM) fluctuations are in favor of p-wave pairing. The first-principles calculations by Mazin and Singh suggest that Sr2RuO4 may possess FM fluctuations due to the fact that the Fermi-level of Ru 4dxy bands is close to a van Hove singularity (vHS)22. The evidence for FM coupling in undoped Sr2RuO4 was first observed in 17O and 101Ru NMR measurements by Imai et al.26, which showed that the spin correlations from Ru 4dxy orbitals are predominantly FM in nature. Nevertheless, later inelastic neutron scattering measurements on Sr2RuO4, while showing some evidence of magnetic excitation at zone center, suggest that FM fluctuations in Sr2RuO4 are very weak27.
Given that weak FM fluctuations coexist with incommensurate fluctuations in Sr2RuO4, one may expect a scenario where chemical doping can band selectively enhance FM fluctuations or even trigger static FM order as Ti doping selectively stabilizes the incommensurate order. Such a possibility has been examined by Kikugawa et al.28,29. They found that La3+ substitution of Sr2+ in Sr2RuO4 enhances FM fluctuations; this result has been interpreted in terms of the electron doping from La3+ bringing the Fermi level of Ru 4dxy bands close to the vHS. Also, a new phase diagram of Ca2−xSrxRuO4 recently established by μSR measurements30 reveals that a FM cluster glass discovered previously31 near x = 0.5 indeed extends to x = 1.5. Coexistence of phases with and without spin freezing is observed even in the x = 1.8 sample. These results imply that Sr2RuO4 is not far from an FM instability. Given the important role FM fluctuations are expected to play in the pairing mechanism and the observation that AFM order can be induced by a small amount of doping, it is natural to ask if FM order can also be induced in Sr2RuO4 with relatively little doping. In this Report, we show that Sr2RuO4 is indeed right on the borderline of short-range static FM order. As little as 0.8–1.5% Co doping in Sr2RuO4 can trigger static, short-range FM order. Furthermore, we find that Mn doping can enhance the incommensurate order much more significantly than Ti doping; 3% Mn doping can establish static incommensurate order with TN ~ 50 K, as opposed to TN ~ 25 K in the 9% Ti-doped sample21. These new results underline the strong competition between ferromagnetism and antiferromagnetism in Sr2RuO4 and point toward the important role of magnetic fluctuations in mediating the superconducting pairing.
Results
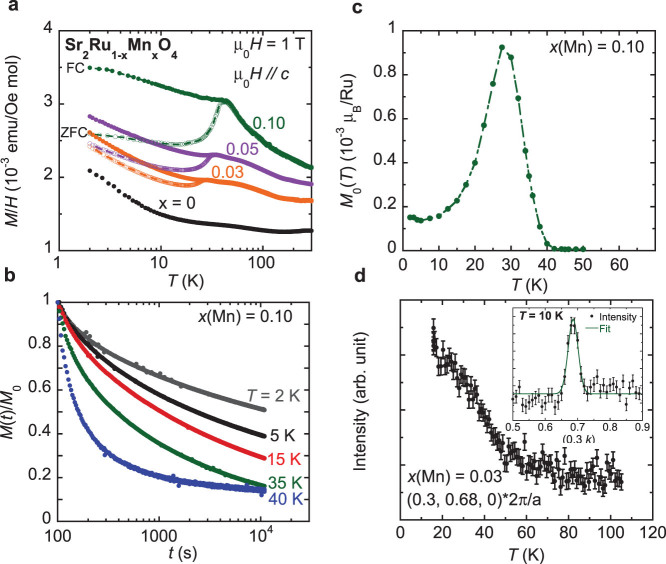
We present magnetic susceptibility data of Mn-doped samples in Fig. 1a where the data of undoped Sr2RuO4 is also given for comparison. All Mn-doped samples show irreversibility between zero-field cooled (ZFC) and field-cooled (FC) histories in susceptibility at low temperatures for field parallel c, but not for field parallel ab, indicating that Mn doping induces striking Ising anisotropy in Sr2RuO4. This observation is reminiscent of Ti-doped Sr2RuO4, which exhibits similar history dependence in magnetic susceptibility20. The susceptibility irreversibility in Ti-doped Sr2RuO4 has been shown to originate from a spin glass state at low temperatures20. To verify if the history dependence of susceptibility observed in Mn-doped Sr2RuO4 is also associated with a spin glass state, we examined the relaxation of magnetization of Mn-doped samples. In general, significant magnetic relaxation is a signature of a spin glass state. Like Ti-doped Sr2RuO4, the Mn-doped samples indeed exhibit remarkable magnetic relaxation below the temperature Tir where the irreversible behavior of susceptibility begins. Fig. 1b shows magnetic relaxation data collected on the sample with 10% Mn at various temperatures; Tir of this sample is ~40 K.
Figure 1. Magnetic properties of Sr2Ru1−xMnxO4.
(a) Magnetic susceptibility vs. temperature measured with ZFC and FC histories; (b) time dependence of remnant magnetization, measured after first zero-field-cooling the sample to a given temperature from 300 K, then applying a magnetic field of 5 T for 300 seconds and decreasing the field to zero; (c) initial remnant magnetization M0, i.e. M(t = 0), vs. temperature for 10% Mn-doped sample; (d) temperature dependence of the neutron scattering intensity of the magnetic Bragg peak at (0.3,0.68,0)*(2π/a) for 3% Mn-doped sample, inset: the magnetic Bragg peak at (0.3,0.68,0)*(2π/a).
Furthermore, we also measured the initial remnant magnetization M0 as a function of temperature for all Mn-doped samples. M0 data was collected by first zero-field-cooling the sample to a given temperature from 300 K, then applying a magnetic field of 5 T for 300 seconds and decreasing the field to zero. As seen in Fig. 1c, we observed a pronounced peak in M0(T) for the 10% Mn-doped sample at a temperature slightly below Tir, a feature similar to what was observed in Ti-doped Sr2RuO420. As mentioned in the introduction, the spin-glass state in Ti-doped Sr2RuO4 is characterized by short-range incommensurate AFM order. Given that Mn-doped samples and Ti-doped samples show strikingly similar magnetic behavior in the measurements discussed so far, it is reasonable to expect a similar spin glass state with short-range incommensurate order in Mn-doped samples. Indeed, this has been confirmed by our elastic neutron scattering measurements shown in Fig. 1d, where a magnetic Bragg peak at (0.3, 0.68, 0)*2π/a (inset) as well as the peak intensity temperature dependence are presented. These data clearly show 3% Mn-doped Sr2RuO4 forms incommensurate AFM order below TN ~ 50 K with an almost identical ordering wavevector to that found in Ti-doped Sr2RuO421. It is worth noting that Mn doping is much more effective than Ti doping at inducing incommensurate AFM order. The Néel temperature of 3% Mn-doped sample is approximately twice that of 9% Ti-doped sample (TN ~ 25 K), indicating the AFM coupling is stronger in the Mn-doped system than in the Ti-doped system.
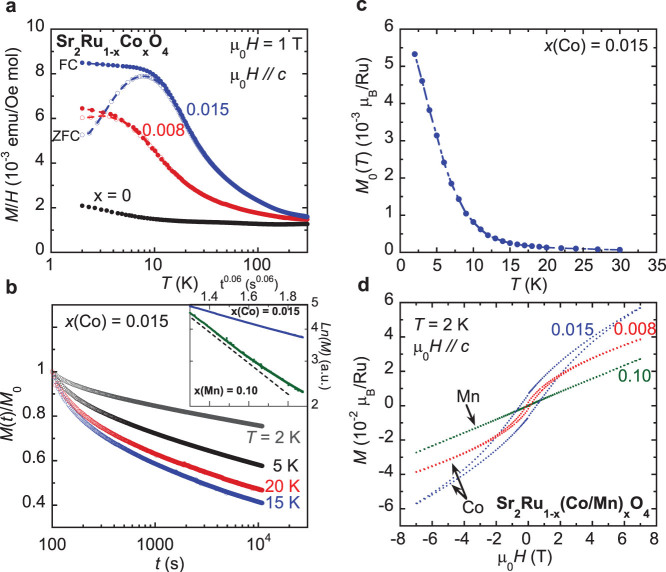
In Fig. 2a, we present magnetic susceptibility for Co-doped Sr2RuO4. Like Mn- and Ti-doped samples, Co-doped samples also show Ising anisotropy in susceptibility, with irreversibility between ZFC and FC histories apparent for field parallel c. Tir is ~4 K and 10 K, respectively, for 0.8% and 1.5% Co doping. Moreover, Co-doped Sr2RuO4 also shows relaxation of remnant magnetization below Tir, as shown in Fig. 2b. These features indicate that Co doping also leads to a low-temperature glassy state in Sr2RuO4. However, the nature of the glassy state in the Co-doped sample is distinct from that in the Mn-doped sample, as implied by comparing the initial remnant magnetization M0(T) for these two materials shown in Fig. 2c and 1c, respectively. Rather than a pronounced peak in M0(T) as seen in the Mn- and Ti-doped samples, the Co-doped sample shows a monotonic, steep increase in M0 with decreasing temperature for T < Tir (Fig. 2c). The difference in magnitude of M0 at the lowest temperatures is also remarkable: M0(T = 2 K) for the 1.5% Co-doped sample is ~35 times greater than M0(T = 2 K) for the 10% Mn-doped sample. These observations suggest that Co-doped Sr2RuO4 may form an FM cluster glass rather than a spin glass with incommensurate AFM order, as seen in the Mn-doped samples. This is indeed verified by the magnetic hysteresis as well as the exponential magnetic relaxation, as discussed below. As shown in Fig. 2d, with as little as 1.5% Co doping, the isothermal magnetization data shows significant hysteresis with a coercive force >0.50 T and remnant magnetization of ~6.5 mμB/Ru. Such hysteric behavior of magnetization develops only when the temperature is lowered below Tir (~10 K). The 0.8% Co-doped sample also shows hysteresis, although it is not as dramatic as that observed in the 1.5% Co-doped sample. In contrast, none of the Mn-doped samples studied show hysteresis in isothermal magnetization data and instead show linear field dependence, as seen in the 10% Mn-doped sample in Fig. 2d. The presence of magnetic hysteresis in the Co-doped samples clearly indicates the formation of static FM order. Such FM order should represent a short-range order, since the Arrott plot of magnetization for 1.5% Co-doped sample does not show any spontaneous magnetization for T < Tir, which is the hallmark of a long-range FM order (see Supplementary Information S1). The notion of short-range order is also consistent with the observed susceptibility data, which does not show the sharp increase usually associated with the onset of long-range FM order, but rather shows a crossover to irreversibility below Tir.
Figure 2. Magnetic properties of Sr2Ru1−xCoxO4.
(a) Magnetic susceptibility vs. temperature measured with ZFC and FC histories. (b) Time dependence of magnetization, measured after first zero-field-cooling the sample to a given temperature from 300 K, then applying a magnetic field of 5 T for 300 seconds and decreasing the field to zero. Inset: relaxation curve of M (on logarithmic scale) at 2 K for 1.5% Co- and 10% Mn-doped samples; the dashed linear line in the inset is used as a reference to show the M(t) for the 10% Mn-doped sample slightly deviates from linearity. (c) Initial remnant magnetization M0, i.e. M(t = 0), vs. temperature for 1.5% Co-doped sample. (d) Isothermal magnetization data for 0.8% Co-, 1.5% Co- and 10% Mn-doped samples.
The FM cluster glass state in the Co-doped sample is also manifested in the exponential magnetic relaxation. As shown in the inset of Fig. 2b, the time dependence of magnetization for the 1.5% Co-doped sample can be best described by M(t) ∝ exp[−(t/τ)0.06], where τ ~ 7.8 × 105 s, which resembles the exponential magnetic relaxation of the FM cluster phase observed in Ca1.5Sr0.5RuO4, where M(t) ∝ exp[−(t/τ)0.26] (τ ~ 2800 s)31. The large difference in τ and the exponent between these two systems should be attributed to the difference in FM coupling strength and the different temperature at which measurements were performed. In contrast, M(t) for the Mn-doped sample neither follows the exponential time dependence that the Co-doped sample follows (as shown in the inset of Fig. 2b), nor shows ln(t) dependence as the Ti-doped sample does (see Fig. 1b)20; this is in line with our expectation that the glassy states of Co- and Mn-doped samples are distinct.
It is important to stress that the weak ferromagnetism seen in magnetization measurements of Co-doped samples is not due to intergrowth of FM relative compound SrRuO3, as made clear by a few key observations. First, the Curie temperature Tc of SrRuO3 is 160 K for the bulk material32 and in the 110–160 K range for the phase at nanometer length scale33. Our susceptibility measurements show no features between 110 K and 160 K. Because the SQUID magnetometer is extremely sensitive to FM phases, the absence of any FM response in the 110–160 K range indicates that SrRuO3 intergrowth is negligible in our samples. Secondly, as noted above, the Arrott plot for 1.5% Co-doped Sr2RuO4 does not show spontaneous magnetization, which is inconsistent with the long-range FM order seen in SrRuO3. Finally, we have purposely measured undoped crystals with significant SrRuO3 intergrowth and found these mixed phase samples do not show magnetic relaxation behavior (see Supplementary Information S2), in contrast with the observation of magnetic relaxation in Co-doped samples. From all these observations, we conclude the FM response in our Co-doped crystals is purely an effect of doping and is not due to FM SrRuO3 intergrowth.
Co and Mn doping in Sr2RuO4 not only lead to two different spin glass states as discussed above, but also cause distinct electronic states, as evidenced by resistivity data presented in Fig. 3. For Mn-doped samples, we observe a low-temperature upturn for both in-plane (ρab) and out-of-plane (ρc) resistivity at the same temperature. Although the resistivity values of the Mn-doped samples are relatively small (e.g. ρab ~ 7.5 × 10−5 Ω cm at 2 K for 3% Mn-doping), this upturn indicates that Mn doping leads to a weakly localized state, as seen in Ti-doped samples20. To examine if such a low-temperature upturn of resistivity is associated with the Kondo effect, we have plotted the resistivity on the logarithmic scale of temperature (see Supplementary Information S3). We do not observe the expected log(T) dependence, which excludes the possibility that Mn doping results in a Kondo effect. The onset of the weakly localized state is much higher than the irreversibility temperature Tir determined from magnetization measurements, but coincides with the onset temperature of incommensurate order probed in neutron scattering, both occurring at ~50 K in the 3% Mn-doped sample. We note that the weakly localized state in Ti-doped Sr2RuO4 also begins at approximately the same temperature as incommensurate order begins to form in the system20,21. This suggests that local moments may play a role in the formation of static AFM order in both the Ti-doped system and the Mn-doped system. This will be discussed further below.
Figure 3. Electronic transport properties of Sr2Ru1−x(Co/Mn)xO4.
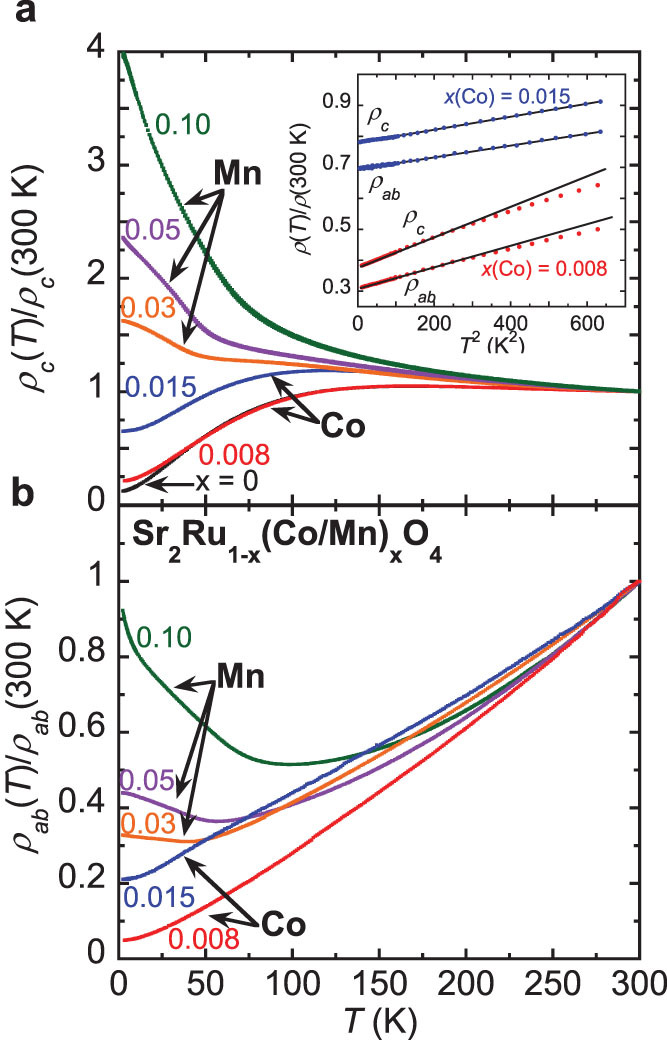
Out-of-plane (a) and in-plane (b) resistivity, normalized to room temperature resistivity. The low-temperature weakly localized state of the Mn-doped samples is apparent for both current orientations. The inset in (a) shows in-plane and out-of-plane resistivity vs. T2 for 0.8% and 1.5% Co-doped Sr2RuO4.
In contrast to Mn and Ti impurities, we see from the resistivity data in Fig. 3 that Co impurities are apparently not strong scattering centers in Sr2RuO4: ρab remains metallic all the way down to 2 K and ρc is also metallic below ~120 K in both Co-doped samples. Both ρab and ρc exhibit quadratic temperature dependences at low temperatures as shown in the inset of Fig. 3a, indicating that a Fermi liquid ground state, which is seen in undoped Sr2RuO4, survives in Co-doped samples. This is in sharp contrast to the weakly localized state seen at low temperatures for both Ti- and Mn-doped Sr2RuO4. Given that the presence of static incommensurate order is always accompanied with a weakly localized electronic state in Mn- and Ti-doped samples, the observation of Fermi liquid behavior of resistivity in Co-doped samples implies that Co doping does not induce static incommensurate order except for the short-range FM order. From our preliminary neutron scattering measurements on the 3% Co-doped sample, we indeed did not observe any signature of static incommensurate order.
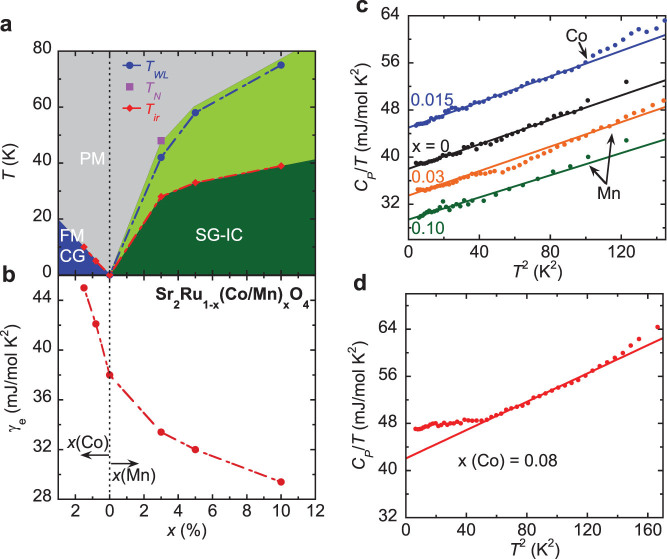
In Figure 4a we present a magnetic phase diagram for Mn- and Co-doped Sr2RuO4, which is established by the magnetization, resistivity and neutron scattering measurements described above. Symbols “ ” and “
” and “ ” represent characteristic temperatures defined from susceptibility irreversibility (Tir) and resistivity upturn (TWL), respectively. The incommensurate ordering temperature TN probed by neutron scattering in the 3% Mn-doped sample is also added to the diagram. It can be clearly seen that TN is approximately equal to TWL, but much higher than Tir for this sample. Such a large discrepancy between TN and Tir is also observed in the spin glass state of Ti-doped Sr2RuO4 and is explained in terms of a crossover transition from damped inelastic magnetic fluctuations to elastic magnetic order21. This interpretation should also be applicable to Mn-doped samples. That is, TN probed in neutron scattering should represent the onset of damped incommensurate fluctuations, while Tir corresponds to the onset of static order. Given that TWL ≈ TN for the 3% Mn-doped sample and Ti doped samples20,21, we can reasonably use TWL to track the incommensurate ordering in other Mn-doped samples. Following this definition, TN for the 10% Mn-doped sample is estimated to be ~75 K. For Co doped samples, Tir should correspond to the onset of FM cluster glass as indicated above.
” represent characteristic temperatures defined from susceptibility irreversibility (Tir) and resistivity upturn (TWL), respectively. The incommensurate ordering temperature TN probed by neutron scattering in the 3% Mn-doped sample is also added to the diagram. It can be clearly seen that TN is approximately equal to TWL, but much higher than Tir for this sample. Such a large discrepancy between TN and Tir is also observed in the spin glass state of Ti-doped Sr2RuO4 and is explained in terms of a crossover transition from damped inelastic magnetic fluctuations to elastic magnetic order21. This interpretation should also be applicable to Mn-doped samples. That is, TN probed in neutron scattering should represent the onset of damped incommensurate fluctuations, while Tir corresponds to the onset of static order. Given that TWL ≈ TN for the 3% Mn-doped sample and Ti doped samples20,21, we can reasonably use TWL to track the incommensurate ordering in other Mn-doped samples. Following this definition, TN for the 10% Mn-doped sample is estimated to be ~75 K. For Co doped samples, Tir should correspond to the onset of FM cluster glass as indicated above.
Figure 4. Magnetic phase diagram and specific heat data of Sr2Ru1−x(Co/Mn)xO4.
(a) Magnetic phase diagram; PM: paramagnetic, FM CG: ferromagnetic cluster glass, SG-IC: spin glass state with short-range incommensurate antiferromagnetic order. (b) Doping dependence of Sommerfeld coefficient γe. (c) Specific heat C divided by temperature vs. T2 for undoped, 1.5% Co-, 3% Mn- and 10% Mn-doped samples. The solid lines represent linear fits. (d) Specific heat C divided by temperature vs. T2 for the 0.8% Co-doped sample; the best linear fit (i.e. the solid line) is obtained in the 7–12 K temperature range.
Discussion
The phase diagram in Fig. 4a shows the surprising result that superconductivity in Sr2RuO4 is directly adjacent to both static incommensurate AFM order and static FM order. Notably, this phase diagram shows that superconductivity in Sr2RuO4 is much closer to the FM instability, as compared to the Ca2−xSrxRuO4 phase diagram where bulk FM cluster glass phase does not appear until x = 1.530. The fact that bulk static, short-range FM and AFM orders can be induced by <2% Co doping and 3% Mn doping, respectively, in Sr2RuO4 unambiguously demonstrates that Sr2RuO4 is in close proximity to distinct magnetically ordered states. This is in stark contrast with other unconventional superconductors, which are normally adjacent to only one ordered state, as mentioned above. The close proximity to two competing magnetic states places Sr2RuO4 in a very unique situation where superconductivity may depend on competing AFM and FM fluctuations as discussed by Singh and Mazin previously19. Since such competing magnetic fluctuations most likely come from a multiple band effect19, they may account for unusual superconducting properties in Sr2RuO4, such as orbital-dependent superconductivity3,34,35. The fact that such a small amount of doping can trigger bulk, static magnetic order in our materials also highlights the strong electron correlation effect present in Sr2RuO4.
Why do Co and Mn doping induce two distinct magnetic states in Sr2RuO4? Why can static magnetic order be established at such a low doping concentration in both scenarios? The answers to these questions are apparently instrumental to understanding of spin-triplet superconductivity in Sr2RuO4. Before we address these questions, let's first briefly summarize the current understanding of the spin-glass states induced by Ti doping20 and Ca substitution for Sr30,31, as well as enhanced FM fluctuations caused by La substitution for Sr28,29. As indicated above, the spin glass state in Ca2−xSrxRuO4 is characterized by short-range FM order. It stems from structural distortion caused by Ca substitution for Sr. Since Ca2+ has a smaller ionic radius than Sr2+, Ca2+ substitution for Sr2+ leads to RuO6 octahedral rotation for 0.5 ≤ x < 1.5, and simultaneous rotation and tilting for 0 ≤ x < 0.536. First principle calculations revealed that the RuO6 octahedral rotation leads to band narrowing and an increase in the density of states (DOS) at the Fermi level, N(EF)24, which enhances FM correlation according to Stoner criterion. For La-substituted Sr2RuO4, enhanced FM fluctuations can be attributed to the increase of N(EF) arising from electron doping as noted above28,29. As for the spin glass state with short-range AFM order stabilized by Ti doping, there are two possible mechanisms: a) since incommensurate magnetic fluctuations in Sr2RuO4 are thought to be driven by FS nesting19, the static incommensurate order caused by Ti doping may be attributed to the improved FS nesting, or b) the incommensurate order may be associated with local moment magnetism, as pointed out in Ref. 37.
Next, let's examine if the Co and Mn doping effects can be understood in term of the existing knowledge stated above. First, given the FM cluster glass forms at <2% Co doping, the structural change caused by doping is nearly negligible, as seen in our x-ray diffraction analyses. Hence the enhancement of FM correlation in Co-doped samples should not be attributed to the structural distortion as in Ca2−xSrxRuO4. However, Co doping should lead to electron doping, since Co and Ru have different chemical valence and the 3d orbital of Co2+ (3d7) or Co3+ (3d6) has more electrons than the 4d orbital of Ru4+ (4d4). If the enhanced FM correlation in Co-doped Sr2RuO4 turns out to be from the band filling as in La-substituted Sr2RuO4, we would naturally expect a remarkable change in Fermi surface properties. To verify this scenario, we performed specific heat measurements for both Co-doped and Mn-doped samples. The data are presented in Fig. 4c and 4d. All of the data below 10 K can be fitted to C = γeT + βT3 except for the 0.8% Co-doped sample, where γeT and βT3 represent electronic and phonon specific heat, respectively. The Sommerfeld coefficient γe obtained from these fittings is summarized in Fig. 4b, which shows that γe increases strikingly with Co doping, up to ~45 mJ/(mol K2) for the 1.5% Co-doped sample, but decreases with Mn-doping, down to ~29 mJ/(mol K2) for 10% Mn-doped sample. The enhancement of γe observed in Co-doped Sr2RuO4 is likely due to an increase of N(EF), suggesting that the short-range FM order in Co-doped Sr2RuO4 is the result of a Stoner instability induced by electron doping, similar to what happens in the La-doped system28,29. That is, electron doping from Co pushes the Fermi level of the Ru 4dxy band closer to the vHS.
However, if the mechanism responsible for enhanced FM correlation in both the La-doped system and the Co-doped system is the same, one obvious question remains: why is Co doping of Sr2RuO4 so much more effective than La doping at inducing static FM order? One possibility is that the Co 3d orbitals contribute to the Fermi level. Thus Co impurities, whether in the 2+ or 3+ valence state, dope more electrons than La impurities, leading to a faster increase of N(EF) with Co doping than with La doping. The faster increase of N(EF) with Co doping can be verified by comparing how γe evolves with La doping to how it evolves with Co doping. From data presented in29, we estimate γe of 5% La-doped Sr2RuO4 is approximately equal to γe of our 1.5% Co-doped sample, indicating that 1.5% Co doping leads to approximately the same increase of N(EF) as 5% La doping. Noting that the susceptibility of the 1.5% Co-doped sample is ~4–5 times larger than that seen in 5% La-doped Sr2RuO4, we find that the Wilson ratio in the Co-doped system is ~4–5 times larger than that in the La-doped system. The stronger FM interactions in Co-doped Sr2RuO4, as evidenced by the larger Wilson ratio, could lead to a longer magnetic correlation length in the Co-doped system than in the La-doped system, thus leading to static FM order that is observable by bulk magnetization measurements rather than to enhanced FM fluctuations, which are observed in the La-doped samples.
The observation that Mn doping of Sr2RuO4 is more effective than Ti doping at inducing static incommensurate AFM order could help us determine the mechanism responsible for incommensurate AFM order in these two doped systems. If the incommensurate order in Ti-doped samples is the result of an SDW instability as has been suggested21, then apparently Mn is more effective than Ti at enhancing Fermi surface nesting between the α and β sheets. One possible explanation for this is that Mn increases the size of the α sheet through hole doping, thus improving the nesting between the α and β sheets. Another intriguing possibility is that Ti- and Mn-doped samples involve local moment magnetism. As has been pointed out in Ref. 37, the Curie-Weiss-like behavior of susceptibility and the low-temperature weakly localized state of Ti-doped Sr2RuO4 may suggest local moment magnetism in the system. Mn-doped samples also show Curie-Weiss-like behavior above ~200 K and form a low-temperature weakly localized state, the onset of which is coincident with the onset of incommensurate order. Furthermore, the systematic reduction in γe with Mn doping (Fig. 4b) suggests that Mn pushes the system towards an insulating ground state. Such a reduction of γe has been observed in Sr2Ru1−xTixO4 above x = 0.02538,39 and in SrRu1−xMnxO3 above x = 0.240. In both materials, the reduction of γe corresponds to a low-temperature weakly localized or insulating state as well as antiferromagnetism. From our results, this is obviously also true for Mn-doped Sr2RuO4: the low-temperature weakly localized state and incommensurate AFM order are coupled, which could further suggest local moment magnetism in the system. Further study of this issue is necessary to help us better understand the mechanism responsible for the incommensurate order in Ti- and Mn-doped Sr2RuO4.
Finally, let us comment on the unusual behavior observed in the specific heat of 0.8% Co-doped Sr2RuO4. As show in Fig. 4d, C/T in this sample exhibits a remarkable upturn at low temperature. This feature was reproduced in two other measured samples with 0.8% Co. Such an upturn is not due to impurities since it disappears for 1.5% doping, but indicative of non-Fermi liquid behavior. This appears to be consistent with the behavior of the low-temperature resistivity of the 0.8% Co-doped sample, as seen from the inset in Fig. 3a. In both the 1.5% Co-doped sample and the undoped sample41, the T2 temperature dependence of resistivity associated with Fermi liquid behavior holds for T < 25 K. However, the resistivity of the 0.8% Co-doped sample ∝ T2 only for T < 16 K, indicating that the Fermi liquid temperature in the 0.8% Co-doped sample is lower than that in the 1.5% Co-doped and undoped samples. The lower Fermi liquid temperature in 0.8% Co-doped Sr2RuO4 can reasonably be attributed to the combined effects of chemical inhomogeneity and enhanced FM fluctuations from Co doping. Because the doping level is very low, there is undoubtedly inhomogeneity in the distribution of Co in the lattice. Hence, some areas of the crystal will have excess Co, leading to the formation of magnetic droplets with static FM order in these areas. The observation of slight hysteresis in the 0.8% Co-doped isothermal magnetization data shown in Fig. 2d is consistent with the formation of such FM clusters. Other areas of the crystal will have a deficit of Co and will not form these magnetic droplets. Rather, these areas will exhibit enhanced FM fluctuations associated with quantum criticality. The net effect is the observation of a lower Fermi liquid temperature as measured from resistivity and a low-temperature upturn in the specific heat of the 0.8% Co-doped sample. The low-temperature upturn in C/T does not show up in the 1.5% Co-doped sample. This can be attributed to the fact that the 0.8% Co-doped sample is closer to the quantum critical point than the 1.5% Co-doped sample. The higher Fermi liquid temperature observed in 1.5% Co sample is also consistent with this interpretation. We note that a similar behavior is also observed in the La-doped Sr2RuO4 system where the non-Fermi liquid behavior in specific heat is observed in the 10% La-doped sample, but not in 13% La-doped sample29.
In summary, through our studies of Mn- and Co-doped Sr2RuO4, we have demonstrated that the superconducting state in Sr2RuO4 is much closer than previously believed to static FM order and static incommensurate AFM order. FM cluster glass phase can be triggered in the system with as little as 0.8–1.5% Co doping; this is to be contrasted with the Ca2−xSrxRuO4 system, which shows an FM cluster glass phase as x is decreased to 1.5. On the other hand, we find that Mn doping induces short-range, static incommensurate AFM order, similar to the Ti doping effect previously reported. The ordering temperature TN in Mn-doped samples is much higher than that in Ti-doped samples, indicating that Mn impurities can induce stronger AFM coupling than Ti impurities. Our findings in these two doped systems not only highlight an important role of competing FM and AFM fluctuations in determining superconducting properties of Sr2RuO4, but also provide a unique playground for studying the novel physics of orbital-dependent magnetism in strongly correlated materials.
Methods
Single crystal growth and characterization
We have grown single crystals of Mn- and Co-doped Sr2RuO4 by the floating-zone method42. All single crystals selected for measurement were first screened by x-ray diffraction to ensure phase purity. The successful doping of Mn/Co into the crystals was confirmed by energy-dispersive x-ray spectroscopy (EDXS). For the Mn-doped samples, the nominal concentration of Mn and the measured concentration were comparable, similar to what was found in Ti-doped samples20. However, for the Co-doped samples, EDXS analysis showed a significant discrepancy between the nominal Co concentration and the measured Co concentration in the crystals. On average, the nominally 3% Co-doped crystals were found to have a Co concentration of ~1.5% and the nominally 1% Co-doped crystals were found to have a Co concentration of ~0.8%. Although we grew a nominally 10% Co-doped crystal successfully, EDXS analysis showed the Co concentration in the nominally 10% Co-doped samples was comparable to that in the nominally 3% Co-doped samples, indicating Co has a much lower soluble limit than Mn or Ti in Sr2RuO4. We used measured doping concentrations in the discussions given above. All magnetization data was collected by a SQUID magnetometer (Quantum Design, model VSM), all resistivity data was taken using the standard four-probe method in a physical property measurement system (PPMS, Quantum Design), and all specific heat data was measured using an adiabatic relaxation method in the PPMS.
Neutron scattering
Neutron diffraction experiments on the 3% Mn doped sample were carried out on HB1 triple-axis spectroscopy stationed in High Flux Isotope Reactor at Oak Ridge National Laboratory.
Author Contributions
J.E.O. conducted single crystal growth, structural characterization and magnetization and specific heat measurements. J.L. and J.H. contributed to resistivity and specific heat measurements. J.P. contributed to crystal growth in part. Neutron scattering measurements were carried out by M.Z., M.M. and X.K. Z.Q.M. supervised the project and co-wrote the manuscript with J.E.O. All authors reviewed and commented on the manuscript.
Supplementary Material
Supplementary Information
Acknowledgments
The work is supported by the NSF under grant DMR-1205469 and the LA-SiGMA program under award #EPS-1003897. X. K. acknowledges the financial support from the start-up funds at Michigan State University. Research at ORNL's High Flux Isotope Reactor was sponsored by DOE basic Energy Sciences, Scientific User Facilities Division. The authors are grateful to L. Zheng and X.S. Wu for informative discussions.
References
- Maeno Y. et al. Superconductivity in a layered perovskite without copper. Nature 372, 532–534 (1994). [Google Scholar]
- Ishida K. et al. Anisotropic pairing in superconducting Sr2RuO4: Ru NMR and NQR studies. Phys. Rev. B 56, R505–R508 (1997). [Google Scholar]
- Nishizaki S., Maeno Y., Farner S., Ikeda S. & Fujita T. Evidence for unconventional superconductivity of Sr2RuO4 from specific-heat measurements. J. Phys. Soc. Jpn. 67, 560–563 (1998). [Google Scholar]
- Mackenzie A. P. et al. Extremely strong dependence of superconductivity on disorder in Sr2RuO4. Phys. Rev. Lett. 80, 161–164 (1998). [Google Scholar]
- Jin R. et al. Observation of anomalous temperature dependence of the critical current in Pb/Sr2RuO4/Pb junctions. Phys. Rev. B 59, 4433–4438 (1999). [Google Scholar]
- Rice T. M. & Sigrist M. Sr2RuO4: an electronic analogue of 3He? J. Phys.: Condens. Matter 7, L643–L648 (1995). [Google Scholar]
- Luke G. M. et al. Time-reversal symmetry-breaking superconductivity in Sr2RuO4. Nature 394, 558–561 (1998). [Google Scholar]
- K. Ishida K. et al. Spin-triplet superconductivity in Sr2RuO4 identified by 17O Knight shift. Nature 396, 658–660 (1998). [Google Scholar]
- Nelson K. D., Mao Z. Q., Maeno Y. & Liu Y. Odd-parity superconductivity in Sr2RuO4. Science 306, 1151–1154 (2004). [DOI] [PubMed] [Google Scholar]
- Xia J., Maeno Y., Beyersdorf P. T., Fejer M. M. & Kapitulnik A. High resolution polar Kerr effect measurements of Sr2RuO4: evidence for broken time-reversal symmetry in the superconducting state. Phys. Rev. Lett. 97, 167002 (2006). [DOI] [PubMed] [Google Scholar]
- Kidwingira F., Strand J. D., Van Harlingen D. J. & Maeno Y. Dynamical superconducting order parameter domains in Sr2RuO4. Science 314, 1267–1271 (2006). [DOI] [PubMed] [Google Scholar]
- Jang J. et al. Observation of half-height magnetization steps in Sr2RuO4. Science 331, 186–188 (2011). [DOI] [PubMed] [Google Scholar]
- Mackenzie A. P. & Maeno Y. The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing. Rev. Mod. Phys. 75, 657–712 (2003). [Google Scholar]
- Maeno Y., Kittaka S., Nomura T., Yonezawa S. & Ishida K. Evaluation of spin-triplet superconductivity in Sr2RuO4. J. Phys. Soc. Jpn. 81, 011009 (2012). [Google Scholar]
- Vaknin D. et al. Antiferromagnetism in La2CuO4−y. Phys. Rev. Lett. 58, 2802–2805 (1987). [DOI] [PubMed] [Google Scholar]
- de la Cruz C. et al. Magnetic order close to superconductivity in the iron-based layered LaO1−xFxFeAs systems. Nature 453, 899–902 (2008). [DOI] [PubMed] [Google Scholar]
- Bauer E. et al. Heavy fermion superconductivity and magnetic order in noncentrosymmetric CePt3Si. Phys. Rev. Lett. 92, 027003 (2004). [DOI] [PubMed] [Google Scholar]
- Sidis Y. et al. Evidence for incommensurate spin fluctuations in Sr2RuO4. Phys. Rev. Lett. 83, 3320–3323 (1999). [Google Scholar]
- Mazin I. I. & Singh D. J. Competition in layered ruthenates: ferromagnetism versus antiferromagnetism and triplet versus singlet pairing. Phys. Rev. Lett. 82, 4324–4327 (1999). [Google Scholar]
- Minakata M. & Maeno Y. Magnetic ordering in Sr2RuO4 induced by nonmagnetic impurities. Phys. Rev. B 63, 180504(R) (2001). [Google Scholar]
- Braden M. et al. Incommensurate magnetic ordering in Sr2Ru1−xTixO4. Phys. Rev. Lett. 88, 197002 (2002). [DOI] [PubMed] [Google Scholar]
- Mazin I. I. & Singh D. J. Ferromagnetic spin fluctuation induced superconductivity in Sr2RuO4. Phys. Rev. Lett. 79, 733–736 (1997). [Google Scholar]
- Miyake K. & Narikiyo O. Model for unconventional superconductivity of Sr2RuO4: effect of impurity scattering on time-reversal breaking triplet pairing with a tiny gap. Phys. Rev. Lett. 83, 1423–1426 (1999). [Google Scholar]
- Fang Z. & Terakura K. Magnetic phase diagram of Ca2−xSrxRuO4 governed by structural distortions. Phys. Rev. B 64, 020509(R) (2001). [Google Scholar]
- Nomura T. & Yamada K. Roles of electron correlations in the spin-triplet superconductivity of Sr2RuO4. J. Phys. Soc. Jpn. 71, 1993–2004 (2002). [Google Scholar]
- Imai T., Hunt A. W., Turber K. R. & Chou F. C. 17O NMR evidence for orbital dependent ferromagnetic correlations in Sr2RuO4. Phys. Rev. Lett. 81, 3006–3009 (1998). [Google Scholar]
- Braden M. et al. Inelastic neutron scattering study of magnetic excitations in Sr2RuO4. Phys. Rev. B 66, 064522 (2002). [Google Scholar]
- Kikugawa N. et al. Rigid-band shift of the Fermi level in the strongly correlated metal: Sr2−yLayRuO4. Phys. Rev. B 70, 060508(R) (2004). [Google Scholar]
- Kikugawa N., Bergemann C., Mackenzie A. P. & Maeno Y. Band-selective modification of the magnetic fluctuations in Sr2RuO4: a study of substitution effects. Phys. Rev. B 70, 134520 (2004). [Google Scholar]
- Carlo J. P. et al. New magnetic phase diagram of (Sr,Ca)2RuO4. Nature Mater. 11, 323–328 (2012). [DOI] [PubMed] [Google Scholar]
- Nakatsuji S. et al. Heavy-mass fermi liquid near a ferromagnetic instability in layered ruthenates. Phys. Rev. Lett. 90, 137202 (2003). [DOI] [PubMed] [Google Scholar]
- Kanbayasi A. Magnetic properties of SrRuO3 single crystal. J. Phys. Soc. Jpn. 41, 1876–1878 (1976). [Google Scholar]
- Xia J., Siemons W., Koster G., Beasley M. R. & Kapitulnik A. Critical thickness for itinerant ferromagnetism in ultrathin films of SrRuO3. Phys. Rev. B 79, 140407(R) (2009). [Google Scholar]
- Agterberg D. F., Rice T. M. & Sigrist M. Orbital dependent superconductivity in Sr2RuO4. Phys. Rev. Lett. 78, 3374–3377 (1997). [Google Scholar]
- Deguchi K., Mao Z. Q., Yaguchi H. & Maeno Y. Gap structure of the spin-triplet superconductor Sr2RuO4 determined from the field-orientation dependence of the specific heat. Phys. Rev. Lett. 92, 047002 (2004). [DOI] [PubMed] [Google Scholar]
- Friedt O. et al. Structural and magnetic aspects of the metal-insulator transition in Ca2−xSrxRuO4. Phys. Rev. B 63, 174432 (2001). [Google Scholar]
- Bergemann C., Mackenzie A. P., Julian S. R., Forsythe D. & Ohmichi E. Quasi-two-dimensional Fermi liquid properties of the unconventional superconductor Sr2RuO4. Adv. Phys. 52, 639–725 (2003). [Google Scholar]
- Pucher K. et al. Transport, magnetic, thermodynamic, and optical properties in Ti-doped Sr2RuO4. Phys. Rev. B 65, 104523 (2002). [Google Scholar]
- Kikugawa N. & Maeno Y. Non-Fermi-liquid behavior in Sr2RuO4 with nonmagnetic impurities. Phys. Rev. Lett. 89, 117001 (2002). [DOI] [PubMed] [Google Scholar]
- Yamaji A., Yokoyama M., Nishihara Y., Narumi Y. & Kindo K. Specific-heat study for ferromagnetic and antiferromagnetic phases in SrRu1−xMnxO3. J. Phys.: Conf. Ser. 200, 012232 (2010). [Google Scholar]
- Maeno Y. et al. Two-dimensional Fermi liquid behavior of the superconductor Sr2RuO4. J. Phys. Soc. Jpn. 66, 1405–1408 (1997). [Google Scholar]
- Mao Z. Q., Maeno Y. & Fukazawa H. Crystal growth of Sr2RuO4. Mater. Res. Bull. 35, 1813–1824 (2000). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Information