Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2013 Sep 16;135(40):15144–15152. doi: 10.1021/ja407052t

Time-Resolved Magnetic Field Effects Distinguish Loose Ion Pairs from Exciplexes

Sabine Richert †, Arnulf Rosspeintner †, Stephan Landgraf ‡, Günter Grampp ‡, Eric Vauthey †, Daniel R Kattnig ‡,*
PMCID: PMC3797520  PMID: 24041160

Abstract

graphic file with name ja-2013-07052t_0011.jpg

We describe the experimental investigation of time-resolved magnetic field effects in exciplex-forming organic donor–acceptor systems. In these systems, the photoexcited acceptor state is predominantly deactivated by bimolecular electron transfer reactions (yielding radical ion pairs) or by direct exciplex formation. The delayed fluorescence emitted by the exciplex is magnetosensitive if the reaction pathway involves loose radical ion pair states. This magnetic field effect results from the coherent interconversion between the electronic singlet and triplet radical ion pair states as described by the radical pair mechanism. By monitoring the changes in the exciplex luminescence intensity when applying external magnetic fields, details of the reaction mechanism can be elucidated. In this work we present results obtained with the fluorophore-quencher pair 9,10-dimethylanthracene/N,N-dimethylaniline (DMA) in solvents of systematically varied permittivity. A simple theoretical model is introduced that allows discriminating the initial state of quenching, viz., the loose ion pair and the exciplex, based on the time-resolved magnetic field effect. The approach is validated by applying it to the isotopologous fluorophore-quencher pairs pyrene/DMA and pyrene-d10/DMA. We detect that both the exciplex and the radical ion pair are formed during the initial quenching stage. Upon increasing the solvent polarity, the relative importance of the distant electron transfer quenching increases. However, even in comparably polar media, the exciplex pathway remains remarkably significant. We discuss our results in relation to recent findings on the involvement of exciplexes in photoinduced electron transfer reactions.

I. Introduction

Electron transfer (ET) is one of the simplest and most ubiquitous reactions in nature. It has been extensively investigated and since the ground-breaking work by Marcus and successors is seemingly well-understood.1−10 However, some important details still remain unclear, in particular in the context of low solvent permittivity and whenever transient complexes play a role. Furthermore, the questions of whether ET proceeds as a contact or distant reaction or whether the loose or contact ion pair is initially formed remain a matter of debate.11−74 These questions are not easily answered, even using ultrafast spectroscopy, because the data analysis usually builds upon multiparametric models, which can give rise to ambiguous interpretations and quantification is difficult.15 In the case of photoinduced ET, the picture is getting even more complicated if exciplexes are involved.16 Exciplexes constitute important intermediates in many photochemical reactions in chemical or biological systems, and their contribution to ET quenching is debated even in polar media.11,17−23

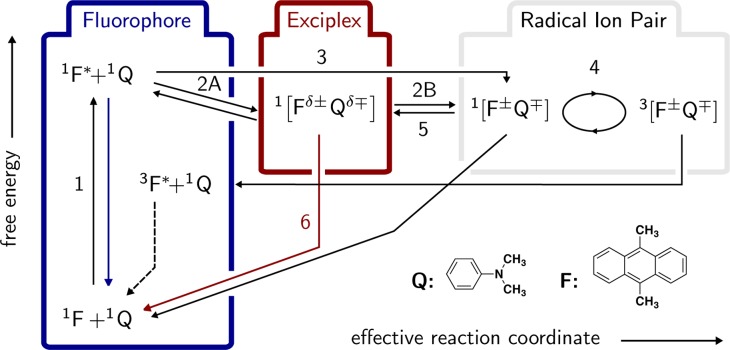
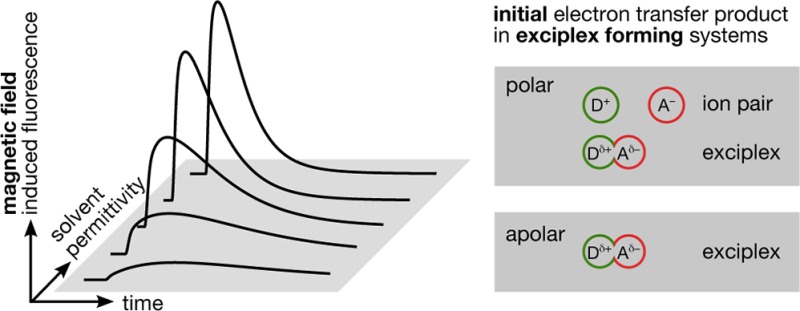
In general, exciplexes can be monitored by their emission. In addition, the exciplex population can react to weak external magnetic fields.24 This effect is brought about by the equilibration of the exciplex with the corresponding spin-correlated radical ion pair (RIP), which can undergo singlet–triplet transitions and subsequently recombines. The underlying process is described by the so-called radical pair mechanism.25,26 Figure 1 depicts a reaction scheme of the photoinduced ET processes in a typical exciplex forming donor–acceptor system. Here, the ordinate corresponds to free energy and the abscissa can be expressed as an effective reaction coordinate involving the distance between fluorophore (F) and quencher (Q) and the Marcus outer-sphere electron transfer reaction coordinate.27

Figure 1.

Figure 1

Open in a new tab

Species and reactions involved in the magnetic field effect of the exciplex. The ordinate corresponds to free energy; the abscissa is a projection of the two-dimensional reaction coordinate comprising the Marcus outer-sphere electron transfer reaction coordinate (i.e., solvent polarization) and the interparticle distance. Details can be found in ref (27). The blue and red arrows indicate the (radiative) decay processes of either the locally excited state or the exciplex that are observed in the experiment. The presented scheme is a unification of two reaction schemes suggested by Weller et al. in refs (28)–30.

Photoexcitation of the fluorophore (1) opens up two different pathways (numbers refer to Figure 1). Full ET may directly yield the RIP (3) or the exciplex may be generated by partial ET in a contact reaction (2A). If the charge transfer within the exciplex is complete, the term contact ion pair is more qualified. Clearly, in the latter case, with vanishing coupling the charge transfer emission also disappears. Note that often only one of these reaction pathways (2A or 3) is exclusively, and not seldomly arbitrarily, assumed. If the exciplex is the primary reaction product, the RIP can be formed in a secondary step by the dissociation of the exciplex (2B), with suitable solvent permittivities and viscosities taken for granted. In any case, the initial ET processes preserve the overall spin of the reactant pair, i.e., the RIP and the exciplex are formed in their singlet state.31 If the radical ion pair diffusively separates such that the exchange coupling becomes sufficiently weak, the electronic Zeeman and hyperfine interactions can coherently convert the electronic singlet state into an electronic triplet state (4). This process depends on the external magnetic field and, for the organic systems studied here, is less efficient if a magnetic field on the order of tens of millitesla is applied. (The low-field effect exhibits the opposite field dependence.32 However, here we focus on relatively “high” fields.) In the presence of such magnetic fields, the Zeeman-splitting of the triplet energy levels causes the intersystem crossing probability to diminish, since near-degeneracy can only be attained between the singlet state and one of the triplet states, whereas all of the three triplet states are involved in the interconversion process at low external magnetic fields. Experimentally, this translates into an increase of the observed exciplex luminescence. Note, that the singlet (S) and triplet (T) radical ion pairs can undergo charge recombination, yielding the ground state and the fluorophore in its triplet state, respectively. The singlet back electron transfer to the ground state is typically located in the Marcus inverted region and, hence, is slow.27,33−37 In addition, only the singlet ion pair can re-form the exciplex (5), and thus, its formation and emission (6) can be influenced by the external magnetic field. Note that magnetohydrodynamic effects and susceptibility differences do not play a role at the low magnetic field used here.38

In summary, the following elementary processes give rise to a magnetic field effect (MFE) on the exciplex emission: photoexcitation (1), exciplex formation and its dissociation into ions (2A, 2B), direct formation of the ions via distant ET (3), spin evolution accompanied by spin-selective charge recombination (4), re-formation of the exciplex (5), and exciplex emission (6). Note that all relevant species can be described in a unified picture as a function of interparticle distance and a solvent coordinate on a common free-energy hypersurface. This model was recently used to rationalize the exciplex emission using a Mulliken–Hush-like approach.27,39

In this work we will heavily rely on magnetic field effects and spin chemical ideas, which are now well-understood and the subject of comprehensive reviews.31,40−43 In fact, the radical pair mechanism44,45 is now again in the spotlight of current research, since it probably is the common denominator of the (adverse) effects of magnetic fields on biological systems46−49 or the cryptochrome-based magnetic compass of several migratory animals.50,51 It is even discussed in the context of spin-teleportation.52

The possibility of monitoring the magnetosensitive exciplex emission opens up the possibility of detecting radical pair dynamics with a much higher sensitivity than usually attained by making use of absorption spectroscopic techniques. Only recently could the sensitivity of the detection of time-resolved MFEs based on transient absorption be improved considerably using cavity ring-down detection.53 Yet, at the moment of writing, the time resolution so obtainable is lower than in the experiments presented herein. Recent studies that rely on the exciplex fluorescence as a probe of magnetic field effects comprise such diverse topics as degenerate electron transfer,54 the recombination function,55 radio- and microwave magnetic field effects,56 or excited state reversibility.57

Several attempts to detect the increased exciplex luminescence in a time-resolved manner have been realized. However, most of these studies were focused on intramolecular systems (chain linked donor–acceptor pairs). Staerk and co-workers, for example, investigated single photon timing traces of intramolecularly linked pyrene–N,N-dimethylaniline (Py–DMA).24,58 A proof of concept study has employed time-resolved measurements of the MFE on freely diffusing (intermolecular) exciplexes,59 but no systematic studies have been undertaken so far. Furthermore, time-resolved studies of the reaction products, i.e., ions, have frequently been employed, but the time resolution of these studies was rarely sufficient to observe the evolution of the geminate MFE in real time.60,61 The effect of microwave excitation on the time-resolved exciplex emission of a polymethylene-linked donor–acceptor system has also been studied.62

In most cases, the time-resolved data have been analyzed in a qualitative fashion. Systematic studies as well as detailed analyses of the results are generally missing. However, a more quantitative interpretation is desirable, since it could give further insight into the details of the reaction mechanism and the role of the exciplex in the magnetic field effect.

Only a single attempt has been made so far to simulate the experimental data theoretically. In ref (59) the authors made use of a simple analytical model. A reaction scheme according to which the RIP is formed initially and the exciplex recombination occurs irreversibly was used. Approximating the singlet probability by linear functions, the experimental data could be reproduced under the assumption that the singlet–triplet interconversion is slower than that predicted by a full Hamiltonian treatment. Unfortunately, no details about the mechanism as to the role of the exciplex could be extracted from the time-resolved data, since it was a priori assumed that the radical ion pair is the primary quenching product.

In the literature dealing with magnetic field effects it is generally assumed that the radical ion pair is initially generated by distant electron transfer and it later irreversibly combines to give the exciplex.29,30,54,55,58,63−65 In contrast to that, many studies focusing predominantly on photochemical aspects can be found, suggesting that the exciplex is the initial quenching product even at fairly high permittivities.28,57,66,67

In this paper, we would like to address these two opposing paradigms, in which either the exciplex or the radical ion pair is the initial quenching product in the above-mentioned reaction scheme. We will show that, by using time-resolved exciplex emission, we are able to identify the nature of the initial reaction product without introducing biasing assumptions but rather by direct observation of the MFE. Our simple idea relies on the fact that the exciplex dissociation is a comparably slow process. The ions resulting from the exciplex dissociation will be formed with delay with respect to those formed by direct electron transfer. As a consequence the MFE generated by the exciplex route will be delayed as well. In this way the time-resolved MFE allows discriminating both pathways (2 versus 3) and can effectively complement ultrafast observations.

The paper is structured as follows: In section II we commence by presenting photochemical properties of the donor–acceptor system 9,10-dimethylanthracene/DMA before we acquaint the reader with time-resolved MFE measurements and demonstrate how these measurements relate to steady-state results. Thereafter, in section III, three models will be discussed, two of which represent the current paradigm of irreversible exciplex formation (termed models 1a and 1b, sections III.I and III.II). In addition, we introduce model 2 (section III.III), which includes the reaction pathway of direct exciplex formation (2A), exciplex dissociation into a loose ion pair (2B), and reencounter (5). We continue by showing that only the latter model is suitable to explain the observed time-resolved MFEs. We then use this model in section IV to extract pertinent parameters of the exciplex kinetics, the most important parameter being the probability that the initial photoinduced ET reaction directly yields the exciplex. We show that even in comparably polar media the direct exciplex formation is found to be significant , and we close with a discussion and conclusions of these findings (sections IV and V).

II. Experimental Results

We have studied the time-dependent MFE on the 9,10-dimethylanthracene (F)/N,N-dimethylaniline (DMA, Q) system in propyl acetate (PA, εr = 6)/butyronitrile (BN, εr = 24) solvent mixtures. These mixtures allow for a systematic variation of the solvent permittivity, εr, in a range from 6 to 24 (at 295 K) while the viscosity and, thus, the diffusion coefficients are kept constant. In addition, the refractive index (nD = 1.3845) is amazingly invariant with the solvent composition, such that the Pekar factor [(1/n2) – (1/εr) = 0.459], which governs the outer-sphere electron transfer reorganization energy and, thus, the rate of ET processes,1,8 changes by less than ±6% for εr in the range from 11 to 24. At permittivities lower than εr = 11 the MFE of the investigated system decays strongly. At the lowest permittivity considered in this study (εr = 10), the deviation of the Pekar factor amounts to only −8%. Moreover, the zero–zero energy is practically constant in the used solvent mixture. Hence, the quenching and the back-ET reactions can to a good approximation be considered solvent-independent, and the changes of the MFE are predominantly brought about by the modulation of the radical pair interaction, i.e., the potential of mean force governing the diffusive excursion and the re-encounter probability of the RIP.

Figure 2 depicts the absorption and emission spectra of 9,10-dimethylanthracene in the absence and presence of DMA. The emission spectrum is decomposed into emission of the locally excited fluorophore and the exciplex emission. To separate the two contributions, the exciplex emission is modeled as a superposition of Franck–Condon weighted vibronic transitions.27,68 The spectrum of the pure fluorophore being known, linear least-squares fitting provides access to the spectrum of the exciplex.

Figure 2.

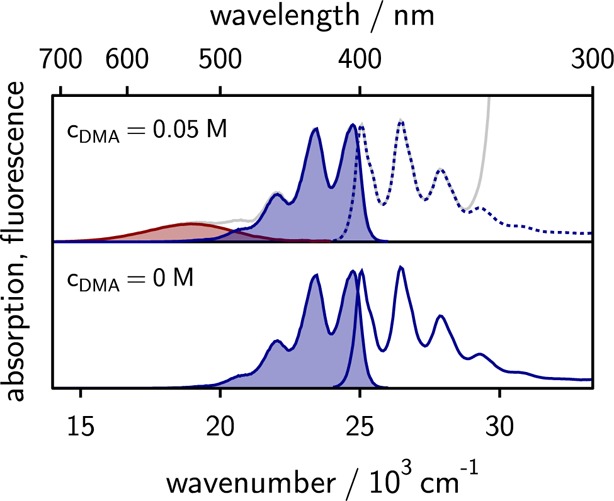
Figure 2

Open in a new tab

Absorption and emission spectra of 9,10-dimethylanthracene in the absence (bottom) and presence (top) of 0.05 M N,N-dimethylaniline. The solvent is a mixture of propyl acetate and butyronitrile of relative dielectric constant εr = 14 (43 wt % butyronitrile). The emissions of the exciplex and the locally excited fluorophore are shaded in red and blue, respectively.

When this donor–acceptor system is immersed in a magnetic field, the exciplex emission increases. This is expected on the basis of the radical pair mechanism, since the singlet–triplet degeneracy is lifted in the presence of an external magnetic field and the T± states no longer efficiently participate in the singlet–triplet conversion within the separated, yet spin-correlated, RIP. The extent of the MFE, χE, is quantified as the relative change of emission intensity by applying a saturating magnetic field of 150 mT. For the investigated system, the MFE goes through a maximum of approximately 11% for a dielectric constant of 19. It strongly depends on the permittivity, since εr balances the radical ion pair separation, which is necessary for efficient spin evolution and the (re)encounter of the pair. Note in this context that radical pair lifetimes on the order of nanoseconds are required for efficient singlet–triplet mixing by the hyperfine interaction in organic radicals. In addition to the exciplex, the locally excited fluorophore shows a feeble MFE brought about by excited state reversibility.57

The time-resolved data were measured using a custom-built time-correlated single photon counting apparatus with an excitation wavelength of 395 or 374 nm and a long-pass filter in front of the detection to ensure the observation of pure exciplex emission. A detailed description of the experimental procedure and the apparatuses used is given in the first three pages of the Supporting Information. Note that this technique employs very low light intensities and tiny fluorophore (and hence RIP) concentrations, such that no ions accumulate and bulk, i.e., bimolecular, processes are negligible next to the geminate processes. This is fundamentally different from the experimental conditions frequently employed in, for example, transient absorption experiments69 (if not making use of the recently introduced cavity ring-down detection53).

The exciplex time traces rise with a time constant of approximately 1.8 ns, which is within experimental error independent of the magnetic field. The decay kinetics is in general rather complex and includes the dissociation into free ions and recombination giving rise to delayed emission. When an external magnetic field is applied, the delayed fluorescence intensity increases, which can be seen in Figure 3 (lower panel). We have adjusted the time profiles by matching the intensities during the initial rise up to and including the maximum and formed the difference ΔI(t) = I(t,B0) – I(t,B=0) to obtain the time-resolved MFE, as also shown in Figure 3 (upper panel). Using an ultrafast setup we have verified that no significant MFE is detectable within the matching interval.

Figure 3.

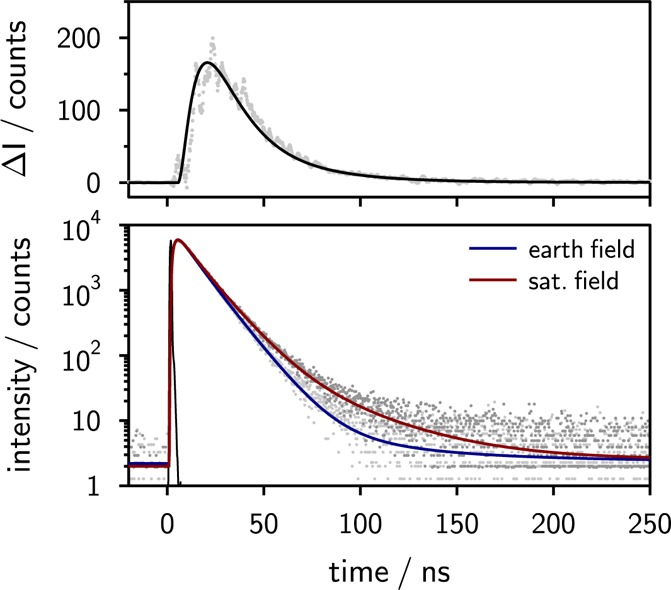
Figure 3

Open in a new tab

Lower panel: Exciplex emission decays of the 9,10-dimethylanthracene (10–5 M)/N,N-dimethylaniline (0.05 M) system in pure butyronitrile at εr = 24.3 in the presence and absence of an external magnetic field (ca. 150 mT) observed with a long-pass filter (>600 nm) after excitation at 395 nm. In the presence of an external magnetic field, the delayed fluorescence of the exciplex is enhanced. Upper panel: Time-resolved magnetic field effect ΔI obtained by taking the difference of the experimental single photon timing traces recorded in the presence and absence of an additional external magnetic field (gray) and the fit to the experimental data (black).

There is an intimate relation of ΔI and the total MFE observed in a steady-state experiment: Subsuming all time-resolved intensities the steady-state intensities can be calculated. (This holds true assuming that the time resolution of the experiment is sufficiently high to detect the entire decay kinetics, which is clearly fulfilled in the present case.)

II. 1

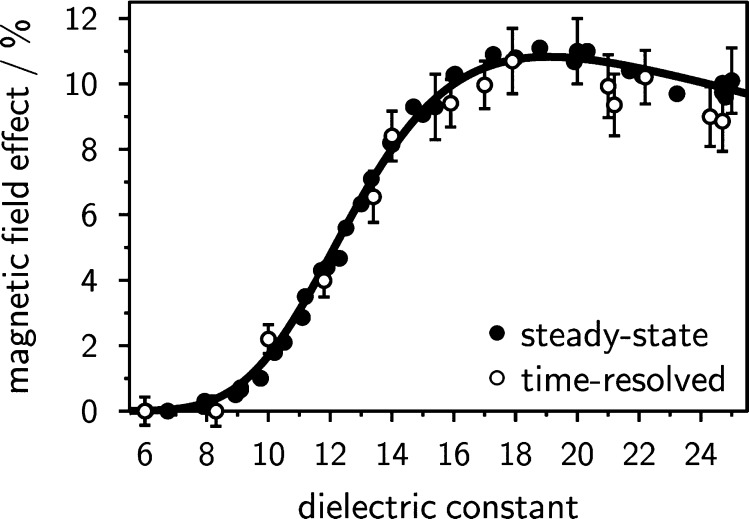
We have integrated the matched time traces for t < 400 ns to determine χE. The integrated MFEs are plotted in Figure 4 and compared to the steady-state results.57 The two sets of data apparently coincide, indicating that the entire MFE indeed occurs within the accessible time window (400 ns or significantly less at higher permittivities), under low light intensity and low concentration conditions. This applies to solutions of low and comparably high dielectric constants in the same manner. The agreement of the values for the absolute magnetic field effect obtained from steady state and time-resolved data suggests that no bulk processes contribute to the MFEs observed here. In particular, f-pairs, i.e., reencountering ions in the bulk, and processes involving triplet states of the fluorophore are negligible.41 This is corroborated by the fact that the time span of the MFE is reduced with increasing permittivity, even though the significance of processes stemming from diffusively separated ions is expected to increase.

Figure 4.

Figure 4

Open in a new tab

Solvent polarity dependence of the magnetic field effect of the 9,10-dimethylanthracene/N,N-dimethylaniline exciplex determined from steady-state (filled circles) and time-resolved (open circles with error bars) measurements. The dielectric constant is varied by altering the composition of the binary solvent mixture of propyl acetate and butyronitrile. Within experimental error, the steady-state and time-resolved magnetic field effects agree.

The time-resolved MFE for different permittivities is shown in Figure 5 together with simulations, to be discussed below. No MFE is detected within the first two nanoseconds of the experiment, which is expected in view of the slowness of the spin evolution. The maximum of the time-resolved MFE occurs in the range from 20 to 60 ns after excitation, with the larger values occurring at lower permittivities. In general, ΔI peaks at times where the delayed fluorescence is substantial and the primary fluorescence of the exciplex is low. Thereafter the effect decays and reaches the noise level of the experiment within a time window of 400 ns (or significantly earlier at higher permittivities).

Figure 5.

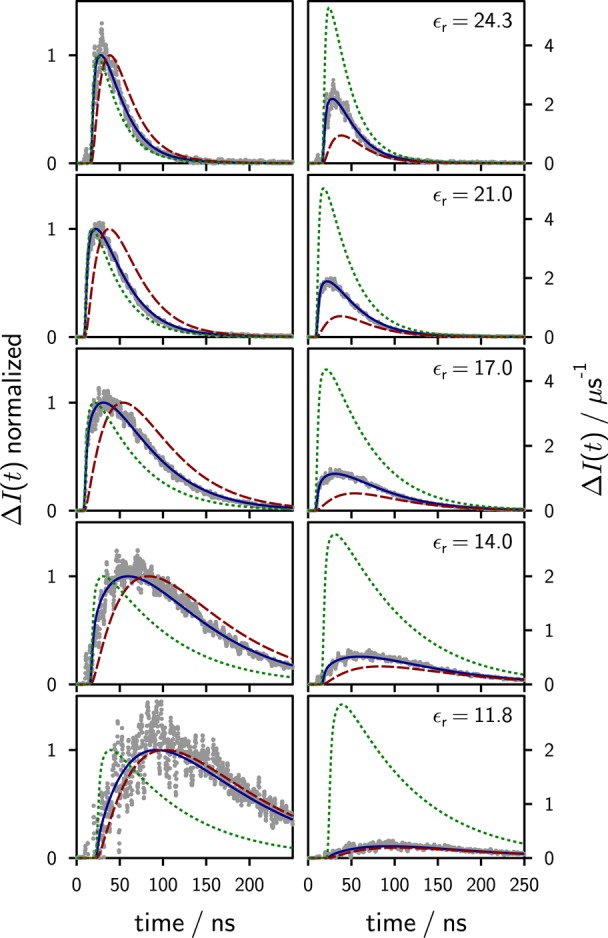
Figure 5

Open in a new tab

Experimental time-dependent magnetic field effects at different dielectric constants (as given in the figure) for the system 9,10-dimethylanthracene/N,N-dimethylaniline in propyl acetate/butyronitrile mixtures. The differences of the single photon timing traces in the presence and absence of an external magnetic field (150 mT) are shown in gray. The time traces have been amplitude-matched during the buildup of the exciplex (t < 2 ns after excitation). The green dotted lines are simulations of the data using model 2 with ϕI = 1 (ions are generated first), whereas the red dashed lines have been obtained using model 2 with ϕI = 0 (exciplex is generated first). The solid blue lines are simulations of the experimental data using model 2 and fitting ϕI; no scaling factor was used. The left-hand side shows the normalized data, which emphasizes the differences in the temporal evolution for ϕI = 0 and ϕI = 1. Note that only by using model 2 and a variable ϕI the shape and the amplitude of the experimental data can be reproduced without scaling.

III. Simulations

To model the time-resolved MFE data depicted in Figure 5 we started off using the commonly applied procedures found in the literature.

III.I. Model 1a—Irreversible Exciplex Formation from the Ions

Traditionally, the MFE on the exciplex has been modeled using59

III.I. 2

where pS(t,B0) is the probability that the RIP born in the singlet state is in its singlet state at time t,75 and f(t) is the recombination function, i.e., the probability that the RIP recombines at time t. τE is the intrinsic exciplex lifetime.76 Among these quantities, the only one depending on the external magnetic field, B0, is pS(t,B0). We shall refer to eq 2 as model 1a. Equation 2 results from a more general treatment based on the stochastic Liouville–von Neumann equation in the limit of low viscosities and/or not too low permittivities.54,55 In this low-viscosity approximation, distant and spin-selective recombination reactions as well as the exchange interaction can be neglected in the first order on account of the fact that the development of the MFE is a slow process and that trajectories yielding a large MFE predominantely involve diffusively separated particles.40 For these pairs, the details of the recombination and the exchange interaction are negligible during the majority of their lifetime.

Model 1a assumes that the initial quenching product is the singlet radical ion pair; i.e., it describes the irreversible pathway (3 → 4 → 5 → 6) in Figure 1. Despite its simplicity, the model has been very successfully used to describe the MFE on exciplexes57 and to model the dependence on solvent properties,59 degenerate electron exchange,54 and RIP recombination.55

Model 1a can easily be modified to account for initial exciplex formation by introducing a parameter ϕI describing the probability that the initial charge separation process yields the loose RIP (path 3 in Figure 1), thereby giving rise to model 1b.

III.II. Model 1b—Irreversible Exciplex Formation with ϕI ≠ 1

The irreversible model introducing the possibility of initial exciplex formation will be referred to as model 1b. The exciplex probability can in this case be calculated from

III.II. 3

Both models discussed so far rely on the assumption that the magnetic field effect only results from ions that irreversibly combine to the exciplex. When modeling experimental data using these models, the only adjustable parameter is the exciplex lifetime τE. Time-dependent magnetic field effect traces calculated with model 1b are shown in Figure 6.

Figure 6.

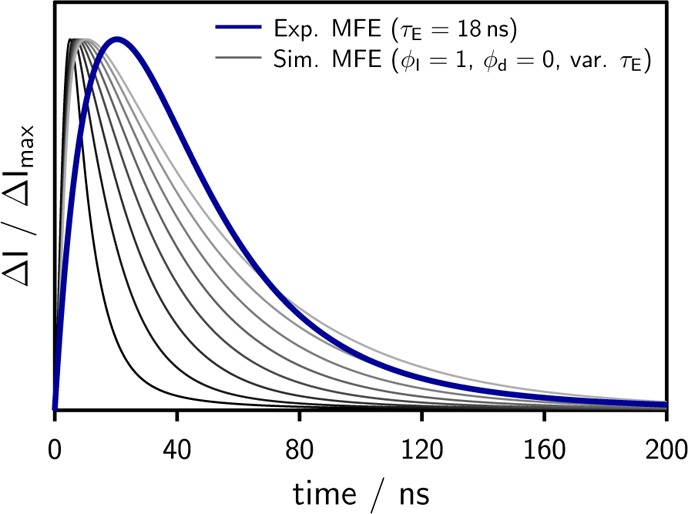
Figure 6

Open in a new tab

Normalized simulated time traces using the irreversible model 1b at different values of the only (artificially) variable parameter τE (from 5 to 30 ns) as opposed to a noise-free representation of the experimental data at τE = 18 ns, which was obtained by fitting a combination of exponential functions to the experimental time-dependent magnetic field effect. The experimental data was measured using the system 9,10-dimethylanthracene (10–5 M)/N,N-dimethylaniline (0.05 M) in a mixture of propyl acetate/butyronitrile at εr = 20 (75 wt % butyronitrile).

Note that variations of ϕI have predominantly the effect of changing the amplitude of the simulated trace, leaving its shape approximately unaltered. ϕI in model 1b has thus the role of a mere scaling factor, while the only parameter influencing the shape is τE. From Figure 6 it becomes clear that the data, obtained for an experimentally determined exciplex lifetime of 18 ns, cannot be described using this irreversible model. Even when artificially varying τE in the range from 5 to 30 ns as shown in Figure 6, the experimental data cannot be reproduced. In all cases, the experimental MFE rises significantly more slowly than predicted by model 1b. τE only increases the time span of the decay of the effect, but it does not lead to a significant shift in the peak position.

There are little doubts about the validity of the low-viscosity approximation and pS, which, in the same manner, do not only apply to exciplexes but also to pulse radiolysis studies, etc.54,55,57,70,71 In fact, the applicability of the low-viscosity limit has been thoroughly tested and found valid for exciplex systems in ref (55). We therefore propose that the discrepancy between model and experiments results from an incomplete description of the reaction scheme and that the exciplex dissociation must be taken into account.

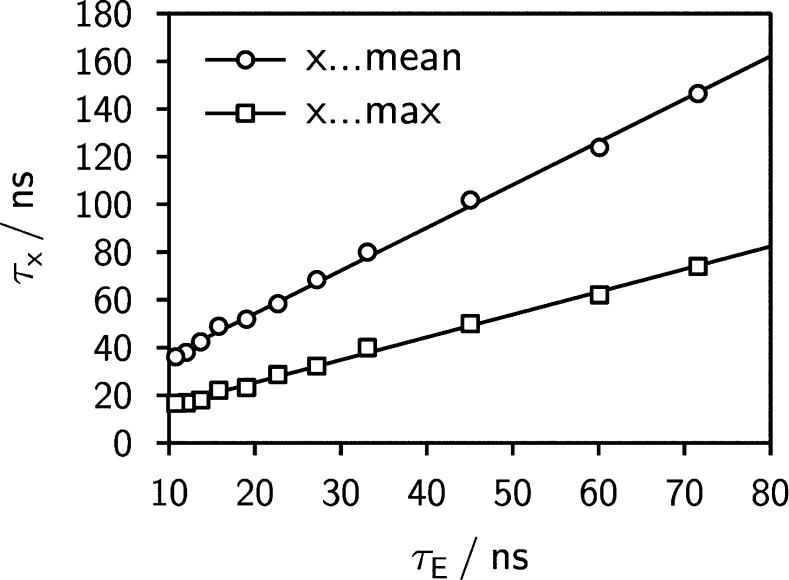
Additionally, we observe that the center of gravity and/or the position of the maximum of ΔI are linearly related to the lifetime of the exciplex, as is shown in Figure 7. As the lifetime of the exciplex relates to its initial decay, the observation of a linear relationship supports our proposition, since it suggests that the dissociation of the exciplex is the rate-limiting step for the MFE and needs to be taken into account for a proper description of the experimental data.

Figure 7.

Figure 7

Open in a new tab

Position of the maximum (or center of gravity) of the time-resolved magnetic field effect in time after excitation as a function of the exciplex lifetime. A linear correlation is observed.

III.III. Model 2—Including the Possibility of Exciplex Dissociation

We thus introduce model 2, which takes the dissociation of the exciplex into account. Equation 2 has to be extended by terms accounting for the initial quenching product and the exciplex kinetics. We propose evaluating the probability that the radical ion pair exists as exciplex, pE(t,B0), from

III.III. 4

where kd is the rate of exciplex dissociation and R(t,B0|rI) dt denotes the probability that the RIP formed at t = 0 at distance rI has recombined until t. rI is the formation distance of the loose ion pair by (distant) ET, and rE is the contact distance of donor and acceptor at which the transition of the loose ion pair to the exciplex (or contact ion pair) occurs, e.g., by assuming a favorable (relative and internal) orientation, giving rise to the possibility of assuming a stacked arrangement with large electronic coupling. Typically exciplex formation will eventually give rise to an interparticle distance smaller than rE. rE is also the interparticle distance to which the dissociation of the exciplex leads.

The different terms on the right-hand side of eq 4 can be understood as follows: The first summand, ϕE = 1 – ϕI, specifies the probability that the exciplex is formed initially (path 2A in Figure 1), while the second summand gives the probability that the initially formed RIP forms an exciplex until t. The third term gives the probability that the exciplex dissociates77 at time τ and is re-formed until t, and the last term describes the depopulation by dissociation or radiative/nonradiative decay. A graphic comparison of the discussed models is presented in Figure 8.

Figure 8.

Figure 8

Open in a new tab

Graphic visualization of the employed theoretical models for the irreversible case (radical ion pair is generated first, models 1a and 1b, left and center) and the reversible case (model 2, right).

Equation 4 is a Volterra integral equation of the second kind with convolution kernel.72 The equation has been solved numerically by discretizing the time axes on an equidistant grid and substituting the integral by the well-known quadrature expression based on repeated application of Simpson’s rule. Details of this approach can be found in ref (72). The singlet recombination probability R(t,B0|rI) depends on the singlet probability pS(t,B0), the mutual diffusion of the RIP, and the recombination rate ka in Figure 8. As a consequence, the time evolution of the MFE depends on the parameters of the diffusive motion via R(t,B0|rI), the exciplex lifetime, and its dissociation quantum yield, ϕdiss = kd τE, and parameters of the radical ion pair, in particular ϕI and the association constant, Ka= ka/kd, and the parameters governing the spin evolution (hyperfine coupling constants). The singlet probability also depends on the rate of degenerate electron exchange of the donors, and this effect has been fully taken into account (cf. Equation S5 in the Supporting Information). Most of these parameters are known from experiment or calculation. It turns out that there are only two parameters, namely, ϕI and Ka, which have a strong effect on the shape and the magnitude of the time-resolved MFE (cf. Figure S4 in the Supporting Information). These parameters can be extracted from the experimental data by least-squares fitting.

Figure 5 shows simulations of the time-resolved MFEs for several solvent permittivities using model 2. The simulation reproduces the experimental findings with respect to both shape (left panels) and magnitude (right panels in Figure 5). The exciplex lifetime, τE, was determined from the initial decay of the time-correlated single photon counting traces of the exciplex, and the dissociation quantum yield, ϕdiss, was estimated from the dependence of τE on permittivity assuming that for εr = 6 no dissociation occurs and that the radiative and nonradiative rates of the exciplex are constant (and/or small compared to the dissociation rate) within the polarity range studied here. The latter assumption is confirmed below.

IV. Discussion

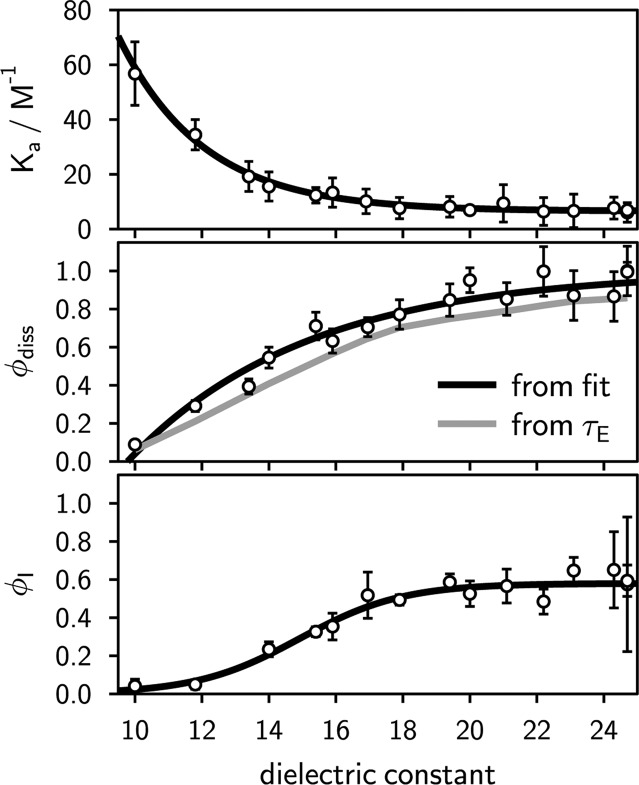
Figure 5 shows fits to the experimental MFEs for different solvent permittivities using model 2. The simulations obtained in the limit of no initial exciplex formation (ϕI = 1) and no initial ion formation (ϕI = 0) are also shown for comparison. As can be seen from the figure, the MFE always rises steeply for ϕI = 1, with the maximum occurring too early in time, as has been discussed before. From the fit of model 2 to the experimental data, values for ϕI and Ka are obtained as a function of permittivity and are shown in Figure 9.

Figure 9.

Figure 9

Open in a new tab

Solvent dependence of the association constant (Ka, top panel), the dissociation quantum yield of the exciplex (ϕdiss, center), and the fraction of excited fluorophore quencher pairs deactivating to solvent-separated ions (ϕI, bottom) as opposed to the exciplex. Trend lines have been added to guide the eye. The dissociation quantum yield has been evaluated from the exciplex lifetime under the assumption that for εr = 6 the exciplex does not dissociate and that its radiative and nonradiative rate constants do not change with solvent permittivity in the range accessible by the used solvent mixture (6 ≤ εr ≤ 25). Fitting the dissociation quantum yield ϕdiss did not give rise to significantly altered results for either Ka or ϕI.

The plot of ϕI as a function of permittivity shows, first, that direct exciplex formation contributes at all permittivities and, second, that the probability of distant electron transfer quenching increases with increasing polarity of the solution. For the investigated permittivity range, ϕI levels off at relative permittivities exceeding 20. Note, that the hypothesis of exciplexes contributing to the quenching in polar solution has been invoked several times to account for electron transfer quenching kinetics in polar solution, such as acetonitrile.11,12,17−23 In ref (19), for instance, the authors already recognized the importance of the two parallel channels, i.e., contact and loose ion pair formation were found to contribute simultaneously (based on a kinetic scheme and the determination of rate constants and ion yields, i.e., from indirect considerations). For 9,10-dicyanoanthracene/hexamethylbenzene in acetonitrile the efficiency of contact ion pair formation has been estimated to be around 0.7. Our experimental results seem to point in the same direction. However, here we are limited to moderate εr for which ample exciplex emission is detectable.

The dependence of the association constant Ka extracted from the least-squares fits (cf. Figure 9) indicates a weak exergonic association. Using Sutin’s approach,73 the free energies of association from the ion pair to the exciplex can be estimated (assuming a contact distance of 6.5 Å and a reaction zone of 0.8 Å width). Potential wells in the range from 5.3 kBT (low εr) to 3.2 kBT (high εr) are found in this way. In one analysis run, we have also adjusted ϕdiss, the quantum yield of exciplex dissociation, in a least-squares sense. The resulting values are also shown in Figure 9 and compared with the corresponding values estimated on the basis of τE, as discussed above. The dependences are nearly identical, suggesting that, for the permittivities giving rise to large MFEs, the exciplex lifetime is indeed mainly governed by separation into the ions. The delay of the maximum of the MFE with respect to the simplistic model 1a (eq 2) results from the fact that, first, the exciplex is formed directly and, second, that its dissociation into the ions is slow, the rate being given by ϕdissτE–1. The ions formed in this delayed manner will—via the radical pair mechanism—eventually give rise to a delayed MFE. This offers insight into the initial products of quenching, which is very difficult to obtain by different means.

The reliability of the proposed method can be tested using isotopologues. Substituting the protons in the fluorophore by deuterium has a huge impact on the singlet probability, pS(t,B0), since the hyperfine coupling constants of the deuteriums amount only to 15% of those of the protons and, in addition, the spin quantum numbers of the nuclei differ (ID = 1, IH = 1/2). The other parameters are not strongly affected.

In Figure 10, the experimental time traces are compared for perdeuterated pyrene, Py-d10, and pyrene of natural isotope composition, Py-h10, with DMA as quencher. No marked difference of the size of the MFE (χE,H = 8.3% and χE,D = 8.4%) as well as of its time dependence is observed. This is surprising at first view, since the singlet probabilities, calculated without taking degenerate electron exchange of the quencher DMA into account, differ markedly (cf. Figure S3 in the Supporting Information) and so do the calculated time curves. However, taking degenerate electron exchange into account, the differences in pS(t,B0) nearly disappear and the time-resolved MFE can indeed be modeled with one and the same set of parameters for Py-h10 and Py-d10 (cf. Figure 10). For this system, too, a significant amount of exciplex is directly formed from the excited fluorophore quencher pair (1 – ϕI = 0.45). Furthermore, this result emphasizes that it is mandatory to explicitly take degenerate electron exchange into account. The effect is particularly pronounced if the hyperfine contribution of the exchanging radical ion exceeds that of the radical ion originating from the fluorophore. With the weak hyperfine field of the deuterated pyrene, the singlet–triplet conversion is essentially governed by the DMA and thus the MFE is more sensitive to its degenerate electron exchange. For the system 9,10-dimethylanthracene/DMA of natural abundance the effect is not very pronounced.

Figure 10.

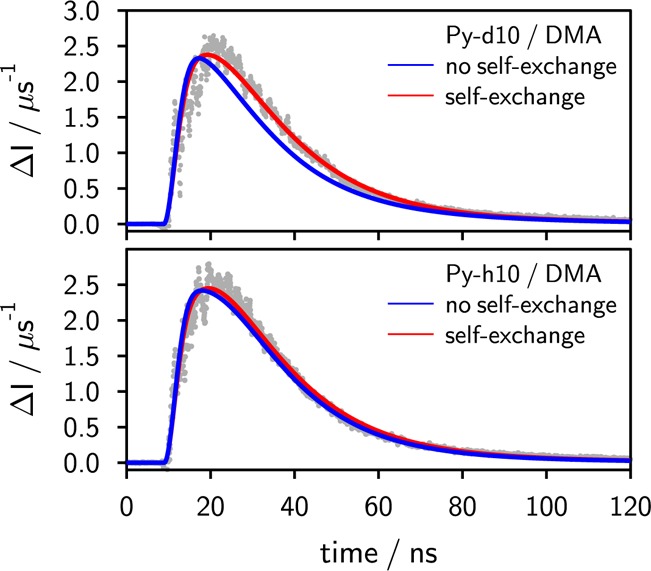
Figure 10

Open in a new tab

Time-resolved magnetic field effect of the exciplex of pyrene (Py-h10) (bottom panel) and perdeuterated pyrene (Py-d10) (top panel) with N,N-dimethylaniline in butyronitrile. For both fits the following identical set of parameters was used: ϕI = 0.55, Ka = 4.6 M–1, ϕdiss ≈ 1, τE = 8 ns. Only if the degenerate electron exchange of the N,N-dimethylaniline radical cation is taken into account does the model consistently, i.e., with a common set of parameters, describe both the pyrene and the pyrene-d10 system.

Note that model 2 introduced here reproduces the MFEs with respect to both shape and absolute value. In particular, the time-integral can be used to model the steady-state MFE depicted in Figure 4. Previously, we have modeled the steady-state data in terms of the recombination probability of a radical ion pair, i.e., in terms of a model that does not refer to properties of the exciplex.57 The long-time asymptote of Hong and Noolandi was utilized. The fact that this approach was successful despite neglecting essential details of the exciplex kinetics shows that the steady-state data are not suitable to discern these details. Only the time-resolved MFE technique can reveal the details of the exciplex kinetics and yield a comprehensive description of the MFE.

V. Conclusions

In this study we presented measurements of the time-resolved magnetic field effect on the exciplex kinetics in organic donor–acceptor systems. The integrated experimental data reproduces the steady-state data published earlier, demonstrating that bulk recombination of RIPs can be ruled out as a major contribution to the magnetic field effects observed here.

By systematically varying the solvent permittivity while leaving most parameters influencing electron transfer rates and the solvent viscosity constant, we could show that the irreversible model (model 1a or 1b), which is implicitly assumed in the commonly employed data treatment, is not able to reproduce the time-resolved experimental observations. Introducing a new model, we demonstrated that it is mandatory to take the dissociation equilibrium of the exciplex into account. Only then can a proper description of the shape and the magnitude of the time-resolved magnetic field effect be achieved. Although the proposed model may seem to introduce many additional free parameters, only two parameters, namely, the association constant, Ka, and the probability that the RIP is formed initially, ϕI, need to be fitted. All other parameters can be obtained experimentally from independent measurements or do not show a pronounced effect on the result. The exciplex lifetime in solvents of different permittivity was shown to provide a good estimate of the dissociation yield ϕdiss. The irreversible model commonly applied is contained in our model as the limiting case for ϕI = 1 and ϕdiss = 0.

The reliability of the model established on the basis of the results of the measurements on the donor/acceptor pair 9,10-dimethylanthracene/DMA was tested by applying the model to measurements on the classical model system Py/DMA. Results obtained with Py-h10 and its isotopologue Py-d10 showed that (1) our model is well-applicable for other systems as well and that (2) for a proper description of the experimental data degenerate electron exchange needs to be taken into account.

Finally, addressing the question whether the exciplex or the radical ion pair is the initial quenching product, we could show that, even at relatively high permittivities, the modeling of our time-resolved MFE data suggests that direct exciplex formation contributes significantly. This has already been postulated in the literature, but has so far not been considered in the context of magnetic field effects. We showed that the irreversible description of the magnetic field effect (ϕI = 1), which is commonly applied, fails to reproduce the time-resolved experimental findings and that it is mandatory to account for the exciplex kinetics. At low permittivities, electron transfer thus seems to be a contact reaction indicating that the exciplex is formed initially. At higher polarity, electron transfer becomes more distant, reflected in our model parameter ϕI, which increases slightly with increasing solvent permittivity (εr). All in all, we have successfully demonstrated that time-resolved magnetic field effect studies have the potential to provide new insights into the reaction dynamics of exciplexes and radical ion pairs that are difficult to obtain by other methods. Measurements on exciplex systems with a more exergonic forward ET are in progress.

Acknowledgments

Financial support from the FWF (Project P 21518-N19) and the Swiss National Science Foundation (Project No. 200020-147098) is gratefully acknowledged.

Supporting Information Available

Description of the applied experimental procedures and setups, as well as details on the computational methods and parameters used in the simulation of the data. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Supplementary Material

ja407052t_si_001.pdf (530.7KB, pdf)

References

  1. Marcus R. A. J. Chem. Phys. 1956, 24, 966–978. [Google Scholar]
  2. Marcus R. A. J. Chem. Phys. 1957, 26, 867–871. [Google Scholar]
  3. Marcus R. A. Annu. Rev. Phys. Chem. 1964, 15, 155–196. [Google Scholar]
  4. Efrima S.; Bixon M. Chem. Phys. Lett. 1974, 25, 34–37. [Google Scholar]
  5. Ulstrup J.; Jortner J. J. Chem. Phys. 1975, 63, 4358–4368. [Google Scholar]
  6. Zusman L. D. Chem. Phys. 1980, 49, 295–304. [Google Scholar]
  7. Siders P.; Marcus R. A. J. Am. Chem. Soc. 1981, 103, 748–752. [Google Scholar]
  8. Marcus R.; Sutin N. Biochim. Biophys. Acta, Rev. Bioenerg. 1985, 811, 265–322. [Google Scholar]
  9. Bixon M.; Jortner J. J. Phys. Chem. 1991, 95, 1941–1944. [Google Scholar]
  10. Tachiya M. J. Chem. Phys. 2008, 129, 066102–066102–2. [DOI] [PubMed] [Google Scholar]
  11. Kikuchi K.; Niwa T.; Takahashi Y.; Ikeda H.; Miyashi T.; Hoshi M. Chem. Phys. Lett. 1990, 173, 421–424. [Google Scholar]
  12. Kikuchi K. J. Photochem. Photobiol., A 1992, 65, 149–156. [Google Scholar]
  13. Inada T.; Kikuchi K.; Takahashi Y.; Ikeda H.; Miyashi T. J. Phys. Chem. A 2002, 106, 4345–4349. [Google Scholar]
  14. Mohammed O. F.; Adamczyk K.; Banerji N.; Dreyer J.; Lang B.; Nibbering E. T. J.; Vauthey E. Angew. Chem., Int. Ed. 2008, 47, 9044–9048. [DOI] [PubMed] [Google Scholar]
  15. In the literature, the terms loose ion pairs and solvent-separated ion pairs are encountered, which are employed to essentially name the same entity, namely, weakly coupled/noncoupled radical ion pairs with complete charge transfer. Since the weak coupling can originate from spatial separation of the radicals (by solvent molecules) as well as by attaining unfavorable relative orientations, etc., we will use the term loose ion pairs rather than solvent-separated ion pairs. In this study we will differentiate between exciplexes (partial charge transfer at contact), contact radical ion pairs (full charge transfer at the contact distance; the limiting case of an exciplex if the charge transfer is complete), and loose radical ion pairs (full charge transfer; the distance is larger than the contact distance).
  16. Kikuchi K.; Hoshi M.; Niwa T.; Takahashi Y.; Miyashi T. J. Phys. Chem. 1991, 95, 38–42. [Google Scholar]
  17. Gordon M., Ware W. R. (Eds.) The Exciplex; Academic Press: New York, 1975. [Google Scholar]
  18. Gould I. R.; Farid S. J. Phys. Chem. 1992, 96, 7635–7640. [Google Scholar]
  19. Kuzmin M. G.; Sadovskii N. A.; Weinstein J.; Kutsenok O. Proc. Indian Acad. Sci. (Chem. Sci.) 1993, 105, 637–649. [Google Scholar]
  20. Gould I. R.; Young R. H.; Mueller L. J.; Farid S. J. Am. Chem. Soc. 1994, 116, 8176–8187. [Google Scholar]
  21. Kuzmin M. G. J. Photochem. Photobiol. A: Chem. 1996, 102, 51–57. [Google Scholar]
  22. Vauthey E.; Högemann C.; Allonas X. J. Phys. Chem. A 1998, 102, 7362–7369. [Google Scholar]
  23. Muller P.-A.; Högemann C.; Allonas X.; Jacques P.; Vauthey E. Chem. Phys. Lett. 2000, 326, 321–327. [Google Scholar]
  24. Farid S.; Dinnocenzo J. P.; Merkel P. B.; Young R. H.; Shukla D.; Guirado G. J. Am. Chem. Soc. 2011, 133, 11580–11587. [DOI] [PubMed] [Google Scholar]
  25. Staerk H.; Kühnle W.; Treichel R.; Weller A. Chem. Phys. Lett. 1985, 118, 19–24. [Google Scholar]
  26. Kaptein R.; Oosterhoff L. J. Chem. Phys. Lett. 1969, 4, 195–197. [Google Scholar]
  27. Closs G. J. Am. Chem. Soc. 1969, 91, 4552–4554. [Google Scholar]
  28. Kattnig D. R.; Rosspeintner A.; Grampp G. Phys. Chem. Chem. Phys. 2011, 13, 3446–3460. [DOI] [PubMed] [Google Scholar]
  29. Weller A.; Staerk H.; Treichel R. Faraday Discuss. Chem. Soc. 1984, 78, 271–278. [Google Scholar]
  30. Leonhardt H.; Weller A. Z. Phys. Chem. 1961, 29, 277–281. [Google Scholar]
  31. Knibbe H.; Röllig K.; Schäfer F. P.; Weller A. J. Chem. Phys. 1967, 47, 1184–1185. [Google Scholar]
  32. Turro N. J.; Kräutler B. Acc. Chem. Res. 1980, 13, 369–377. [Google Scholar]
  33. Lukzen N. N.; Kattnig D. R.; Grampp G. Chem. Phys. Lett. 2005, 413, 118–122. [Google Scholar]
  34. Wasielewski M. R.; Niemczyk M. P.; Svec W. A.; Pewitt E. B. J. Am. Chem. Soc. 1985, 107, 1080–1082. [Google Scholar]
  35. Mataga N.; Kanda Y.; Okada T. J. Phys. Chem. 1986, 90, 3880–3882. [Google Scholar]
  36. Gould I. R.; Ege D.; Mattes S. L.; Farid S. J. Am. Chem. Soc. 1987, 109, 3794–3796. [Google Scholar]
  37. Mataga N.; Asahi T.; Kanda Y.; Okada T. Chem. Phys. 1988, 127, 249–261. [Google Scholar]
  38. Vauthey E. J. Phys. Chem. A 2001, 105, 340–348. [Google Scholar]
  39. Grant K. M.; Hemmert J. W.; White H. S. J. Am. Chem. Soc. 2002, 124, 462–467. [DOI] [PubMed] [Google Scholar]
  40. Murata S.; Tachiya M. J. Phys. Chem. A 2007, 111, 9240–9248. [DOI] [PubMed] [Google Scholar]
  41. Salikhov K. M., Molin Y. N., Sagdeev R. Z., Buchachenko A. L. (Eds.) Spin Polarization and Magnetic Effects in Radical Reactions; Elsevier: Amsterdam, 1984. [Google Scholar]
  42. Steiner U. E.; Ulrich T. Chem. Rev. 1989, 89, 51–147. [Google Scholar]
  43. Woodward J. R. Prog. React. Kinet. Mech. 2002, 27, 165–207. [Google Scholar]
  44. Hayashi H., Ed. Introduction to Dynamic Spin Chemistry; World Scientific Publishing: River Edge, NJ, 2004. [Google Scholar]
  45. Werner H.-J.; Schulten Z.; Schulten K. J. Chem. Phys. 1977, 67, 646–663. [Google Scholar]
  46. Schulten K.; Wolynes P. G. J. Chem. Phys. 1978, 68, 3292–3297. [Google Scholar]
  47. Grissom C. B. Chem. Rev. 1995, 95, 3–24. [Google Scholar]
  48. Buchachenko A. L.; Kuznetsov D. A. J. Am. Chem. Soc. 2008, 130, 12868–12869. [DOI] [PubMed] [Google Scholar]
  49. Hore P. J. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 1357–1358. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Solov’yov I. A.; Domratcheva T.; Moughal Shahi A. R.; Schulten K. J. Am. Chem. Soc. 2012, 134, 18046–18052. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Maeda K.; Henbest K. B.; Cintolesi F.; Kuprov I.; Rodgers C. T.; Liddell P. A.; Gust D.; Timmel C. R.; Hore P. J. Nature 2008, 453, 387–390. [DOI] [PubMed] [Google Scholar]
  52. Maeda K.; Robinson A. J.; Henbest K. B.; Hogben H. J.; Biskup T.; Ahmad M.; Schleicher E.; Weber S.; Timmel C. R.; Hore P. J. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 4774–4779. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Salikhov K. M.; Golbeck J. H.; Stehlik D. Appl. Magn. Reson. 2007, 31, 237–252. [Google Scholar]
  54. Maeda K.; Neil S. R. T.; Henbest K. B.; Weber S.; Schleicher E.; Hore P. J.; Mackenzie S. R.; Timmel C. R. J. Am. Chem. Soc. 2011, 133, 17807–17815. [DOI] [PubMed] [Google Scholar]
  55. Justinek M.; Grampp G.; Landgraf S.; Hore P. J.; Lukzen N. N. J. Am. Chem. Soc. 2004, 126, 5635–5646. [DOI] [PubMed] [Google Scholar]
  56. Rodgers C. T.; Norman S. A.; Henbest K. B.; Timmel C. R.; Hore P. J. J. Am. Chem. Soc. 2007, 129, 6746–6755. [DOI] [PubMed] [Google Scholar]
  57. Henbest K. B.; Kukura P.; Rodgers C. T.; Hore P. J.; Timmel C. R. J. Am. Chem. Soc. 2004, 126, 8102–8103. [DOI] [PubMed] [Google Scholar]
  58. Kattnig D. R.; Rosspeintner A.; Grampp G. Angew. Chem., Int. Ed. 2008, 47, 960–962. [DOI] [PubMed] [Google Scholar]
  59. Werner U.; Staerk H. J. Phys. Chem. 1995, 99, 248–254. [Google Scholar]
  60. Basu S.; Nath D. N.; Chowdhury M. Chem. Phys. Lett. 1989, 161, 449–454. [Google Scholar]
  61. Werner H.-J.; Staerk H.; Weller A. J. Chem. Phys. 1978, 68, 2419–2426. [Google Scholar]
  62. Goez M.; Henbest K. B.; Windham E. G.; Maeda K.; Timmel C. R. Chem., Eur. J. 2009, 15, 6058–6064. [DOI] [PubMed] [Google Scholar]
  63. Enjo K.; Maeda K.; Murai H.; Azumi T.; Tanimoto Y. Appl. Magn. Reson. 1997, 12, 423–430. [Google Scholar]
  64. Petrov N. K.; Borisenko V. N.; Starostin A. V.; Al’fimov M. V. J. Phys. Chem. 1992, 96, 2901–2903. [Google Scholar]
  65. Nath D. N.; Basu S.; Chowdhury M. J. Chem. Phys. 1989, 91, 5857–5859. [Google Scholar]
  66. Aich S.; Basu S. J. Phys. Chem. A 1998, 102, 722–729. [Google Scholar]
  67. Weller A. Z. Phys. Chem. N. F. 1982, 133, 93–98. [Google Scholar]
  68. Tanimoto Y.; Hasegawa K.; Okada N.; Itoh M.; Iwai K.; Sugioka K.; Takemura F.; Nakagaki R.; Nagakura S. J. Phys. Chem. 1989, 93, 3586–3594. [Google Scholar]
  69. Gould I. R.; Noukakis D.; Gomez-Jahn L.; Young R. H.; Goodman J. L.; Farid S. Chem. Phys. 1993, 176, 439–456. [Google Scholar]
  70. Iwasaki Y.; Maeda K.; Murai H. J. Phys. Chem. A 2001, 105, 2961–2966. [Google Scholar]
  71. Details on the calculation and time behavior of pS(t,B0) are given in the Supporting Information on page S5 and Figure S2.
  72. For steady-state studies addressing χE, the exciplex lifetime cancels out and the MFE depends on the integral of f(t) and pS(t,B0) only.
  73. Molin Y. N. Bull. Korean Chem. Soc. 1999, 20, 7–15. [Google Scholar]
  74. Brocklehurst B. Chem. Soc. Rev. 2002, 31, 301–311. [DOI] [PubMed] [Google Scholar]
  75. With probability kdpE(τ) dt.
  76. Press W. H.; Teukolsky S. A.; Vetterling W. T.; Flannery B. P.. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press, 2007. [Google Scholar]
  77. Strehlow H. (Ed.) Rapid Reactions in Solution; Wiley-VCH: Weinheim, Germany, 1992. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja407052t_si_001.pdf (530.7KB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES