Abstract
Biological organisms exist over a broad temperature range of −15°C to +120°C, where many molecular processes involving DNA depend on the nanoscale properties of the double helix. Here, we present results of extensive molecular dynamics simulations of DNA oligomers at different temperatures. We show that internal basepair conformations are strongly temperature-dependent, particularly in the stretch and opening degrees of freedom whose harmonic fluctuations can be considered the initial steps of the DNA melting pathway. The basepair step elasticity contains a weaker, but detectable, entropic contribution in the roll, tilt, and rise degrees of freedom. To extend the validity of our results to the temperature interval beyond the standard melting transition relevant to extremophiles, we estimate the effects of superhelical stress on the stability of the basepair steps, as computed from the Benham model. We predict that although the average twist decreases with temperature in vitro, the stabilizing external torque in vivo results in an increase of ∼1°/bp (or a superhelical density of ) in the interval 0–100°C. In the final step, we show that the experimentally observed apparent bending persistence length of torsionally unconstrained DNA can be calculated from a hybrid model that accounts for the softening of the double helix and the presence of transient denaturation bubbles. Although the latter dominate the behavior close to the melting transition, the inclusion of helix softening is important around standard physiological temperatures.
Introduction
DNA is the common substrate of genetic information in all living organisms. The mechanical properties of the DNA double helix play a crucial role in the molecular processes related to the replication and the regulated transcription of this information: examples include the tight wrapping of DNA around histone (1) and histonelike (2) proteins in prokaryotes, and sequence recognition by other molecules such as the TATA-box binding protein (3). With biological organisms living at very different temperatures (so-called extremophiles thrive over a temperature range of −15°C to +120°C (4,5)), the question arises of how the properties of DNA vary with temperature.
To discuss the basic ideas of this article regarding the temperature dependence of the DNA double-helix elasticity at different length scales, it is useful to briefly consider generic springlike degrees of freedom. In the simplest example of a harmonic spring, the excitation free energy has the form , where k is the spring stiffness. In a molecular mechanics force field, this functional form applies to bond lengths and suitable bond angles. Deformations lead to a purely energetic or enthalpic response. The stiffness of such springs is independent of temperature, , whereas the amplitude of the corresponding thermal fluctuations, , is directly proportional to the temperature. A first complication arises if the mechanical force field is anharmonic. In this case, the linear response of the system to external forces and torques described by a harmonic approximation becomes temperature-dependent. The opposite extreme from enthalpic springs is entropic springs, with and independent of temperature. Such springs represent the behavior of soft matter at much larger scales. The best-known examples are the entropic springs substituting random-walk-like polymer chains in the theory of rubber elasticity (6). In this case, as the entropy decreases with the extension of the polymer chain. As a result, a rubber band under a mechanical load contracts when its temperature is raised. The nanoscale elasticity of DNA combines all these complications. The double helix has a well defined average shape and its local behavior is not dominated by fluctuations. However, since the description results from integrating out more microscopic degrees of freedom, nanoscale force fields necessarily represent temperature-dependent deformation free energies. In the harmonic approximation and over a finite temperature range, the temperature dependence can always be written in the form and can be inferred from the amplitude of thermal fluctuations observed at different temperatures, . For , the results can, at least formally, be extrapolated to a temperature higher than those used to calibrate the harmonic model. If, as turns out to be the case, , the results cannot be extrapolated beyond a spinodal temperature , where the spring ceases to resist extension and thus becomes mechanically unstable. Consistency requires that the spinodal temperature be much higher than the actual melting temperature, , where the two DNA strands separate. In this case, the nanomechanical description of the double helix remains valid for , even though this state now only represents a metastable local free-energy minimum and no longer the global free-energy minimum. If DNA only undergoes partial melting, the mechanical properties of a given basepair step can be described by two-state spring models, which account for the different structures and elastic properties in the helix and coil sections of the molecule (7–9). For the calculation of suitable averages, the relative statistical weights of the two states need to be inferred from sequence-dependent models of DNA melting (10–13). Interestingly, external mechanical forces and torques may change the relative stability of the helix and coil states and hence modify the melting temperature (14).
In this article, we address the temperature-dependent properties of DNA over a wide span of length scales. We start from an atomistic model (15), with which we investigate DNA oligomers at different temperatures, thereby extending previous molecular dynamics (MD) results of the ABC consortium (16,17). The central part of our work deals with the nanoscale structure, elasticity, and stability of the double helix. In particular, we propose and parameterize a temperature-dependent generalization of the rigid-base and rigid-basepair models of DNA (18). Although our simulations were performed for torsionally unconstrained DNA, we estimate the effects of superhelical stress by introducing temperature-dependent torques estimated from the Benham model (14). Biological control of such a torque can serve to regulate spontaneous DNA opening at transcription start sites (19). In particular, the introduction of positive superhelical stress makes it possible to stabilize the double helix in a temperature interval beyond the standard melting transition (14), which is comparable to the conditions under which extremophiles exist. In the final step, we consider DNA on the wormlike chain level. We coarse-grain the nanoscale model to determine the temperature-dependent persistence length of the double helix (20) and reevaluate a recent kinked wormlike chain model (8) to account for the presence of transient denaturation bubbles (7) in the estimation of the apparent persistence length of DNA (9).
The article is organized as follows. The Models and Methods section describes the temperature-dependent rigid-base and rigid-basepair models, the MD simulations, the coupling with the Benham model, the coarse-graining to the wormlike chain model, and the inclusion of transient denaturation bubbles in the calculation of an apparent bending persistence length. Details of the analysis of the simulation data are described in the Supporting Material. In the Results section, we present our findings for the entropic contribution to the DNA nanoscale elasticity. This contribution is particularly strong for the internal basepair elasticity. At the basepair step level, the effect is weaker but detectable, and it results in a softening of the large-scale stiffness of the molecule. In the Discussion section, we address the temperature dependence of internal fluctuations of the double helix, the path to the melting transition, the effect of superhelical stress on the properties of the double helix in vivo, and the large-scale bending rigidity of DNA, including the temperature dependence of the apparent persistence length over the whole experimentally studied temperature interval. The article closes with a brief conclusion.
Models and Methods
DNA elasticity in the rigid-base and rigid-basepair models
We consider the fluctuations of the DNA double helix at two successive nanoscale levels, 1), inside the basepair (intra parameters), and 2), between adjacent basepairs (step parameters). In both cases, the conformation is described by a six-dimensional vector, , corresponding to the relative orientation and position of the relevant objects (bases or basepairs), in conventional notation: buckle, propel, opening, shear, stretch, and stagger in the first case, and tilt, roll, twist, shift, slide, and rise in the second (18).
In the harmonic approximation, the Gibbs free energy reduces to a quadratic form:
| (1) |
where T is the temperature, σ is the DNA sequence, and we have introduced the six-dimensional equilibrium conformation and the 6 × 6 stiffness matrix . The latter describes the couplings between the fluctuations of the different degrees of freedom and is proportional to the inverse of the covariance matrix,
| (2) |
For the rigid-base(pair) model of DNA, previous studies have extracted the sequence-dependent elastic parameters at room temperature, T0 = 300 K, from the analysis of DNA and DNA-protein crystallographic structures (21), from MD simulations of DNA oligomers (17,22), or from combinations of both approaches (23). Note that for an ensemble of crystal structures, the passage from the observed covariance matrix to the stiffness (Eq. 2) relies on the existence of an effective temperature governing the ensemble of experimentally observed conformations (22,23). This approach can therefore not be used to study the actual temperature dependence of the mechanical properties of DNA. Instead, we extend previous MD simulations of DNA oligomers (16,17) to a broad range of temperatures to study the sequence and temperature dependence of DNA structure and elasticity.
Inclusion of temperature effects
The knowledge of the elastic parameters at T0 gives no information on their temperature dependence around T0, which depends on the relative importance of the enthalpic and entropic contributions:
| (3) |
Here, H and S are quadratic forms:
| (4) |
| (5) |
From Eq. 3, the temperature-dependent elastic parameters and of Eq. 1 can be written in terms of enthalpic and entropic contributions. For the stiffness, the relation is simply
| (6) |
where and are the enthalpic and entropic contributions to the stiffness, and is the stiffness at room temperature.
Although the covariance matrix for the fluctuations (Eq. 2) takes the simple form , the equilibrium conformation has a more complex behavior, and in particular does not vary linearly with temperature:
To facilitate the estimation of the temperature-dependent contribution in the following numerical study, we consider the linear expansion of the latter expression around T0:
| (7) |
where is the equilibrium conformation at room temperature, and is the first-order coefficient.
The presence of two parameters in both Eqs. 6 and 7 signifies that the temperature-dependent elastic model involves twice as many parameters as the model at a single temperature, . In the following sections, we estimate these new parameters from MD simulations of DNA oligomers. For different temperatures and sequences, is estimated from the mean value of the conformational distribution, and is estimated by inverting the covariance matrix (Eq. 2). Because Eqs. 6 and 7 have a linear temperature dependence, the parameters can then be computed by linear regression.
Simulations of DNA oligomers
The protocol for the MD simulations was chosen to be as close as possible to that used by the ABC consortium (16,17). The oligomers used in the simulation were 18-mers built from tetranucleotide repeats: an oligomer termed xyzw has the sequence GCzw xyzw xyzw xyzw GC (uppercase letters are basepairs conserved in all oligomers). Thus, the oligomer AAAC has the sequence GCACAAACAAACAAACGC. To eliminate possible end effects, we excluded the four terminal basepairs at either end of the oligomers from our analysis.
We simulated four 18-mers of dsDNA (AAAC, AGAT, GCGC, GGGG) at five different temperatures (273 K, 283 K, 300 K, 325 K, and 350 K) for 50 ns each. This data set contains all unique dinucleotide sequences and includes the influence of different flanking sequences for a limited sample (see Table S1 in the Supporting Material). The two types of basepair (AT and GC) appear in nine different trinucleotides and are used for studying intra parameters. The 10 unique dinucleotides appear within single tetranucleotides, except for AA, which appears in two contexts (AAAC and CAAA, both in the oligomer AAAC). Our data set is therefore less comprehensive than the ABC study at room temperature but more varied than the previous generation of MD simulations (22).
Each oligomer was constructed in the B-DNA conformation and simulated in Amber (24) for 50 ns in 150 mM KCl. The parameters and protocol of the simulations can be found in Lavery et al. (17). In particular, the DNA force field includes the parmbsc0 backbone parameters (15). We assumed that these force fields remain valid for double-helical DNA in the temperature interval under consideration. Water was modeled with the TIP4P/Ew model (25), which was designed to reproduce the structural and dynamical properties of water in a broad temperature range (273–350 K), in contrast to the SPC/E model used in most ABC runs. The results obtained with both solvents were compared at room temperature and exhibited no significant difference (17).
The temperature and pressure, P = 1 atm, during the simulations were controlled with the Berendsen algorithm (26). The simulations were stable at all temperatures with the same time step, fs. Note that 350 K is beyond the experimental melting temperature of short oligomers; melting does not occur in the simulations, due to the limited sampling time and/or to limitations in the force fields.
Analysis of the trajectory
DNA conformations were analyzed with the program Curves+ (27), which uses commonly accepted conventions for the definitions of the helical parameters (18,28). From the distributions of the basepair and basepair-step parameters, we checked the validity of the harmonic approximation of the free energy (Eq. 1) at all sampled temperatures (see Figs. S2 and S3, and the detailed discussion in the Supporting Material). For all sequences, we then computed the mean values and covariance matrices, which were inverted to compute the stiffness matrices (Eq. 2). The entropic and enthalpic parameters were estimated by linear regression of 1), each element of the 6 × 6 stiffness matrix (Eq. 6) and 2), each degree of freedom of the equilibrium values (Eq. 7). We included a systematic estimation of statistical errors for the computed quantities by the block-averaging method (29). We used the weighted-least-squares fitting algorithm (30), which provides error estimates on the fitted model: the latter is therefore depicted by a shaded area corresponding to one standard-error deviation rather than a single line (see, for instance, Fig. 1 B). To discriminate the cases where the effect of temperature can be reliably estimated, we introduced a criterion based on the f-test (30), a statistical test that compares the accuracy of the two-parameter enthalpic + entropic model with that of a one-parameter enthalpic model. The different steps of this analysis procedure, as well as its validation on artificially generated data, are described in more detail in section II of the Supporting Material.
Figure 1.

Linear fitting of the stiffness (upper) and corresponding temperature dependence of the variance (lower) for two typical diagonal matrix elements. (A) Intrabasepair parameter shear (sequence AGA). (B) Step parameter roll (sequence GGGG). In both cases, the data points rule out a purely enthalpic model (dotted line). The temperature dependence of the distribution is compatible with a linear entropic contribution, within the statistical errors of the simulations (shaded area). This contribution is stronger within the basepair (A) than for the step parameters (B). Note that we plot the covariance divided by the temperature, which is constant for a purely enthalpic phenomenon. All quantities are expressed in reduced units, defined using the corresponding standard deviation (see Table 1).
Effects of superhelical stress in biological DNA
We augment a thermodynamic model that efficiently predicts the local opening properties of superhelical DNA (19) by adding the temperature and basepair step dependencies of torsional energetics, the computation of which is included in this article. Here, we briefly describe the model, and we refer the reader to a study by Jost and co-workers (19) for more details on the formalism.
Local opening of DNA basepairs can be described by the Benham model, a thermodynamic model of DNA under superhelical stress that couples the standard thermodynamic description of basepairing with the torsional stress energetics (31). In the limit of long sequences, this model, defined in a superhelical density-imposed ensemble, is equivalent to a similar model in the torque-imposed ensemble where the constant applied torque can be computed self-consistently for a given superhelical density (19,32). In this Ising-like model, the energy of a DNA configuration constrained by a torque, Γ, is given by
| (8) |
where is the Zimm-Bragg Hamiltonian describing the denaturation of unconstrained DNA (13), if the basepair step i is open and 0 if it is closed, and is the torsional stiffness of unpaired basepair steps. The sequence-dependent torsional stiffness, , of double-stranded steps and the natural helical twist, , given in Tables S9 and S10, are temperature-dependent and have been computed from Tables S5–S8. Computations of equilibrium properties for a given sequence (like the local opening probabilities ) are then performed using the transfer-matrix method (19).
Coarse-graining the nanoscale elasticity to the persistence length
Starting from the computed nanoscale stiffness parameters, we neglect the influence of the intrabasepair deformations on the large-scale elasticity and consider only the step fluctuations. In an ideal B-DNA helix, only the two bending angles (tilt, τ, and roll, ρ) contribute to the large-scale bending of the molecule:, where nm is the average rise. This relation is, however, not true for the real molecule, where all six step degrees of freedom contribute to this bending because of local distortions. We use a coarse-grain calculation (20) that takes these effects into account to compute the persistence length from the nanoscale parameters. The simpler tilt-roll relation is used to compute error bars. Note that because the deviations from the ideal B-DNA helix remain small, the discrepancy between the two methods is typically <5% (20).
From the sequence-dependent parameters obtained from the simulations, the sequence-neutral persistence length is computed by averaging the mean rise and the angle fluctuations (covariance matrix) over the 16 possible dinucleotides. The computed values are in the same order of magnitude as the experimental values, but significantly lower (∼40 nm instead of ∼50 nm, or 120 instead of 150 bp). Similar deviations have already been observed by Becker and Everaers (20), and it is unclear whether this effect is a consequence of the MD-estimated microscopic fluctuations or the calculation method. We assumed that this issue does not influence the computed temperature dependence and therefore rescaled them by their value at 278 K, following Theodorakopoulos and Peyrard (9).
Hybrid model
We construct a hybrid model by including the temperature dependence of the double-helical stiffness, computed in the previous paragraph, in a recently proposed model (9) that accounts for the reduction of the effective persistence length of DNA by transient denaturation bubbles. We describe here the main lines of the calculation; more detail can be found in Theodorakopoulos and Peyrard (9).
We model DNA polymer elasticity in terms of a heterogeneous Kratky-Porod (KP) (33) chain of N segments of length a with a configurational energy,
| (9) |
basepairs (considered as point monomers for simplicity), and contour length . is a unit vector joining the jth to the th basepair, and the local stiffness constants,
are weighted averages of hard (J) and soft (J′) couplings, according to the probability that the th basepair is in the unbound (open) state. The local melting fractions, , are computed in terms of the Peyrard-Bishop-Dauxois model (12,34), using only the sequence information and the molar ion concentration, c, with no further adjustable parameters (35,36).
The average end-to-end distance can be numerically computed for the heterogeneous KP model (9), because the correlation functions factorize. It is then possible to use it to extract an effective persistence length, λ, from the relationship which is valid in the continuum limit of the homogeneous KP chain (known as the wormlike chain), and should be quantitatively adequate as long as .
The above scheme was used in the Theodorakopoulos and Peyrard model (9), with , to compute the effective persistence length of the phage fragment studied in Geggier et al. (37). In this work, we incorporated the temperature dependence of the local stiffness constants arising from harmonic fluctuations, i.e.,
| (10) |
where is the temperature-dependent double-helical bending stiffness, as estimated from the MD simulations.
Results
We simulated four 18-mers of DNA of different sequences at temperatures of 273 K, 283 K, 300 K, 325 K, and 350 K at fixed pressure. The atomistic trajectories were analyzed with the conformational analysis software Curves+ (27), which provided distributions of intra (internal basepair) and step (basepair step) parameters. Our data set includes all unique mono- and dinucleotide sequences. However, basepairs and basepair steps can be influenced by the flanking sequences and in some cases (17) can lead to bimodal parameter distributions. We observe such effects (see Fig. S3) and deal with them by separately analyzing each trinucleotide or tetranucleotide sequence fragment (see Table S1). In this case, for the oligomers we studied, the distributions can indeed be approximated as single Gaussians, compatible with the harmonic approximation of the free energy. The covariance matrices are inverted to compute stiffness matrices, from which we estimate the entropic contribution according to Eq. 6. We include a systematic estimation of the statistical errors for the matrix elements, which are fitted independently of each other (see Models and Methods). Fig. 1 shows typical examples of such fits for diagonal matrix elements of intra (Fig. 1 A) and step (Fig. 1 B) parameters, where the entropic contribution is apparent.
Note that the different degrees of freedom cannot be analyzed separately. The passage between the stiffness and the covariance elements involves a matrix inversion, which couples the 6 × 6 degrees of freedom and their respective levels of statistical noise; an example of the complete fitting procedure is shown in Fig. S5. The good agreement between the fitted model and the data points in both representations is therefore nontrivial and validates the approximations used in our analysis. We now discuss separately the results obtained for the intra and step parameters.
Internal basepair flexibility
In this section, we describe the effect of temperature on internal basepair flexibility. As explained previously, we estimate the entropic contribution separately for each sequence fragment (here trinucleotides) where the harmonic approximation is valid. Fig. 2 shows the temperature evolution of the stretch and opening stiffnesses, averaged over the A-T (Fig. 2 A) and C-G (Fig. 2 B) basepairs. Note that we use reduced units, dividing all coordinates by their average standard deviations, , at T0 = 300 K (Table 1).
Figure 2.
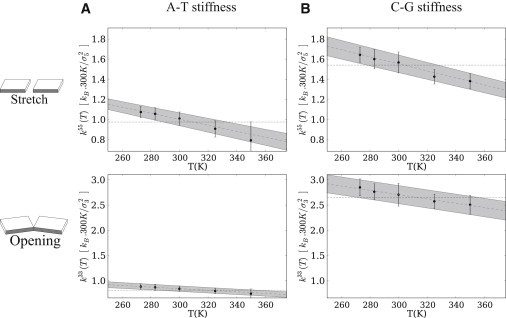
Temperature dependence of the stiffness for the stretch-stretch (upper) and opening-opening (lower) diagonal terms on the A-T (A) and C-G (B) basepairs. The reduced units are defined using the average standard deviation of each parameter, , given in Table 1. Here, the error bars partly reflect the structural heterogeneity due to the flanking sequences. The effect of temperature is strongest in these two degrees of freedom: at room temperature, the average stiffness has decreased by ∼45% and 30%, respectively, with respect to the values at 0 K (enthalpic stiffness).
Table 1.
Sequence-averaged standard deviations of the different degrees of freedom
| Buckle | Propel | Opening | Shear | Stretch | Stagger |
|---|---|---|---|---|---|
| 11.62° | 9.37° | 4.53° | 0.30 Å | 0.12 Å | 0.43 Å |
| Tilt | Roll | Twist | Shift | Slide | Rise |
| 4.46° | 7.10° | 6.76° | 0.71 Å | 0.71 Å | 0.35 Å |
All values given are at 300 K, . These reference values were used to express all covariance/stiffness elements in dimensionless units.
We were not surprised to find that the values depend strongly on the type of basepair, reflecting the different number of hydrogen bonds (three for C-G and two for A-T). The effect of temperature emerges in all cases as a regular linear decrease of the stiffness. We measure the strength of this entropic contribution by comparing it to the enthalpic part (Eq. 6). For stretch (Fig. 2, upper), this ratio is ∼0.5 at room temperature, i.e., the stiffness has already dropped to half its value at 0 K. For opening (Fig. 2, lower), the effect is weaker (∼0.3), and still more so for the other degrees of freedom.
Interestingly, the influence of base sequence is slightly different for these two parameters. For stretch, although the stiffness constant for the C-G basepair at T0 = 300 K is ∼50% larger than that for A-T, the entropic stiffness (slope) is of the same order: the relative entropic contribution is therefore stronger for A-T. For opening, on the other hand, the stiffness of the C-G basepair at room temperature is three times stronger than that of A-T, but here, the entropic contribution is also approximately three times higher, so that its relative weight is similar.
At this level, the error bars still partly reflect the structural heterogeneity due to the flanking sequences. We therefore look at the results obtained for the different trinucleotides, including the remaining degrees of freedom. These results are summarized in Fig. 3 A, which gives the relative entropic contribution (as described in the previous paragraph) plotted against the stiffness at room temperature. In this representation, the behavior noted previously for opening is reflected in the fact that the two groups of points are distant horizontally (different stiffness at T0) but have approximately the same values on the vertical axis.
Figure 3.
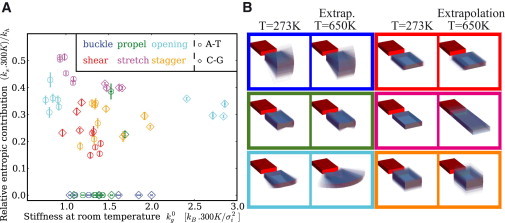
Entropic contribution to internal basepair elasticity: (A) Relative entropic contribution to the stiffness, compared to the enthalpic stiffness, for different sequences. Note that because the units are parameter-specific, the values of different parameters should not be compared. Although the stiffness of the A-T and C-G basepairs is very different in the opening direction, the relative entropic contribution is similar. (B) Illustration of the sequence-averaged range of fluctuations in the different degrees of freedom for T = 273 K and extrapolated to T = 650 K, i.e., close to the destabilization of the basepair (see text) to emphasize the temperature effect. Note that the colored rectangles in B correspond to the colors of the basepair parameters in A. In the directions most sensitive to temperature, stretch, and opening, the fluctuations become considerable.
We systematically determine which parameters present a detectable entropic contribution by applying a quantitative criterion, comparing the accuracy of the enthalpic + entropic model with that of a purely enthalpic one (see Models and Methods). An entropic contribution is detected for all sequences with respect to the opening angle and the three translational parameters stretch, shear, and stagger. The error bars are small enough to discriminate the individual (trinucleotide) sequences, confirming the influence of flanking sequences on basepairs. The contributions are strongest for stretch and opening, as noted previously; for shear and stagger, the relative entropic contribution is ∼0.25 at room temperature. In contrast, the two other angular parameters exhibit very little or no detectable entropic contribution (for details, see Table S2).
We then look at the equilibrium values, i.e., Eq. 7. The parameters for which temperature induces an average displacement are generally also those for which the stiffness changes; the average stretch increases, as does the average opening, but mainly for G-C. The other parameters do not exhibit a systematic effect.
Basepair step flexibility: parameterization of a T-dependent rigid-basepair model
We now focus on the step parameters. Our oligomers contain the 10 unique dinucleotides, each located within a single tetranucleotide except for AA, which is present in two sequence contexts (see Table S1).
The stiffness values for the step parameters are less uniform than those for the intra parameters, as is the effect of temperature. For most sequences, an entropic contribution is found for the two bending angles, tilt and roll, and for the translational-parameter rise. The relative weight of this contribution, defined in the previous section as ( × 300 K), spans the intervals 0.25–0.5, 0.15–0.35, and 0.25–0.4, respectively, depending on the sequence. As an example, Fig. 1 B shows the roll-roll diagonal elements of the GG dinucleotide: the entropic contribution clearly emerges from the statistical errors but is indeed smaller than for shear. More surprisingly, the twist and shift stiffnesses exhibit a very low sensitivity to temperature.
The temperature dependence of the equilibrium step parameters is a question of considerable interest: a modification of the spontaneous basepair stacking would be an evolutionary challenge to organisms living at high temperatures. Such a modification is not observed in the data. The only parameter where a clear and sequence-independent tendency emerges out of statistical noise is rise, which typically increases by 2–3% in the temperature interval considered. The equilibrium twist angle decreases by 1–2° for about half of the sequences (e.g., TA, GC, and GA) and remains approximately constant for the other ones, except in the case of CG, where it increases, yielding an average decrease of ∼0.5°. The relation between the living temperature of organisms and supercoiling is discussed in the next section.
These results show that the entropic effect on basepair step elasticity is detectable, but more limited than that on basepair elasticity. Note that this conclusion may also be affected by slower equilibration times, which would require a greater computational effort to resolve. Our analysis provides, to our knowledge, the first parameterization of a temperature-dependent rigid-basepair model of DNA where the entropic contributions are sequence-dependent. Altogether, the model includes 156 nonzero entropic parameters in addition to the 270 parameters required for describing the elasticity at a single temperature. It is also the first model, to our knowledge, that systematically includes confidence intervals for these parameters, which can be used to estimate error bars for the quantities computed at the coarse-grain level, as we show in the next paragraph. The model parameters are given in Tables S5 and S7. Note that for the AA dinucleotide, treated in two different sequence contexts, we arbitrarily chose the values computed for the CAAA data set, where the mean values are closer to those reported in crystallographic structures (21), and where we had more data points.
Discussion
Temperature dependence of soft vibration modes
Our results demonstrate that the basepair internal stiffness contains an important entropic contribution. This contribution is strongest for the stretch and opening degrees of freedom (Fig. 3 B). Although A-T and G-C basepairs differ by their enthalpic stiffness constants, they show similar ratios, (see also below). In an experimental setting, the corresponding temperature sensitivity of soft vibration modes might be accessible via Raman spectroscopy or neutron scattering.
Few studies have dealt with the temperature dependence of these spectra. Among those that have, the only one (to our knowledge) that focuses on the frequency shifts in the double helix is that of Grimm and Rupprecht (38). The neutron-scattering spectra in that study exhibit a mode at ∼1.1 THz (4.5 meV) at 193 K, which softens to ∼0.85 THz at 300 K, i.e., a relative softening of ∼20–25%, or, in our terms, a relative entropic weight at room temperature of ∼0.45, consistent with our results. These numbers must be treated with some caution, however, since the data only allow a qualitative estimation of this softening. Another problem is the indexing of the associated mode with respect to the base and basepair degrees of freedom. From the distributions in our simulations, we estimate that the internal basepair vibrations have frequencies between 0.6 THz (opening) and 2.4 THz (stretch); the latter value has been reported in Raman spectra (39). The step frequencies are generally lower, in the 0.3–0.6 THz range. This indexation thus requires further experimental support, but if the observed mode corresponds indeed to an intrabasepair eigenmode, it is in qualitative agreement with the entropic contribution observed in our simulations.
The path to the melting transition
Our harmonic model is the first-order approximation of the DNA double-helical free energy. For obvious reasons, these fluctuations have to be bounded for the model to be valid: the eigenvalues of the stiffness matrix have to be positive. Within our description of the temperature-dependent stiffness, , the double helix is thus predicted to become unstable at , known in the thermodynamics literature as the spinodal temperature (40). Depending on the sequence, this temperature is estimated to be between 550 and 660 K (Table S4). As a comparison, we note that the spinodal temperature of liquid water at atmospheric pressure, (41), is comparable to the value we estimate for the double helix.
These large values signify that our biologically relevant range of temperature (273–350 K) remains far below the limit of (meta)stability of the double helix, thus justifying the approximation of constant and values: the melting transition occurs before these values change significantly. Note that the double helix might still exist as a metastable state for temperatures .
The eigenvector associated with the decomposition of the basepair at reflects the directions for which the fluctuations are most sensitive to temperature. Fig. 3 B shows that the basepair is destabilized in the stretch direction, with a simultaneous partial opening. Qualitatively, these directions may also indicate the direction of the kinetic pathway toward melting.
With our MD simulations, sampling only double-helical states, we rely in the following on standard theories of DNA melting (11,13) to provide information on the relative stability of single-stranded DNA and the thermodynamics of bubble formation.
DNA in vivo: torque control of the local opening probability
How do our results apply to DNA in living cells, in particular for extremophiles living at temperatures close to or above 85°C, the typical melting temperature of unconstrained DNA (42)? In these organisms, many proteins bind to double-helical DNA (43), and the opening of a significant fraction of the molecule would probably be lethal. It has been suggested that the double helix could be stabilized by over-twisting (14). Maintaining DNA under superhelical stress by specific enzymes could thus be one of the strategies used by extremophiles to keep their DNA closed even beyond 85°C. In vivo, the double helix is therefore not free, as in our simulations, but in a constrained torsional state. Consequently, one may wonder if this constraint can affect the elastic and structural properties of the DNA double helix and therefore modify local physicochemical features like the binding constants of transcription enzymatic complexes.
To account for this effect, we use a recently proposed method that allows the efficient computation of DNA melting properties under superhelical stress imposed by an applied torque (19). Augmenting the Benham model to incorporate the temperature and basepair step dependencies of twisting energetics studied in this article (see Models and Methods), we evaluate the suitable torque needed to stabilize the double helix at high temperatures and combine this estimation with our previous results to estimate the elastic properties of the biologically relevant constrained helix.
As a function of the temperature, we compute the torque needed to maintain an open fraction of 1% for the genomic sequence of the extremophilic bacteria Thermus thermophilus. This fraction corresponds to the typical opening probability of Escherichia coli under standard physiological temperature and superhelical density (19). This propensity to open is mainly located at gene promoters and transcription start sites (19), enhancing gene expression by polymerase enzymes (44). The constraining torque increases with temperature (see Fig. S6), and as noticed in previous studies by Benham (14), the model predicts that the stability of the double helix can be maintained only up to a critical temperature, which depends on the sequence (data not shown). In Fig. 4, we plot the different contributions of the average basepair step stability. At high temperatures, thermal destabilization of pairing and stacking (gray dashed line) is prevented by the contribution of the average twist (dotted line) in the free energy of the constrained helix, maintaining an almost constant basepair-step opening penalty of 0.2 kcal/mol (black solid line). Above a certain temperature, the stabilization is limited by the strong twisting stiffness of double-stranded steps (dash-dotted line), and the double helix starts to melt. For T. Thermophilus, we find a critical temperature of 106°C, which is 15°C higher than the melting temperature in the absence of superhelical constraints. Interestingly, this value is close to the highest living temperatures of extremophilic organisms, suggesting that the stability of the double helix may indeed be the limiting condition for their existence.
Figure 4.
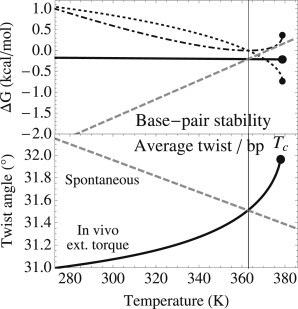
Stabilization of the DNA double helix in vivo by superhelical stress for temperatures between 273 K and 380 K, where extremophile organisms exist. Although unconstrained DNA (gray dashed line) is unstable at high temperatures, the contribution of the average twist in the free energy (dotted line) maintains the stability of the double helix (black solid line) for an additional 15 K, with an almost constant opening penalty of ∼0.2 kcal/mol. Above a critical temperature Tc ≈ 378 K (dots), the contribution from the twist stiffness of the double helix (dash-dotted line) prevents further stabilization. The superhelical stress opposes the spontaneous decrease of the average twist, and results in an ∼1°/bp increase in the considered interval.
At this limit, the stabilizing torque is surprisingly low . Although the resulting twist excess is important in 1% of open basepairs (∼33°/bp, close to the average twist of B-DNA; see Fig. S7), the action of the torque results only in a weak local twist excess for double-stranded regions, ranging from 0.8°/bp for stiff basepair steps to 2.5°/bp for soft ones. These values should be compared to the typical twist standard deviation at room temperature (∼6°/bp). For comparison, adding 1° to the spontaneous twist per basepair increases the superhelical density, , by ∼0.03. At the rigid-basepair level of description, the properties of the constrained helix can therefore be described in the regime of linear response, where the equilibrium conformation is displaced but the elasticity remains identical to that of the relaxed helix. The stiffness parameters extracted from our simulations, with their limited temperature dependence, are therefore relevant to biological DNA. Using these parameters, we compute the mean conformation at the critical temperature by relaxing the sequence-neutral helix under the suitable torque. The resulting twist modification is shown in Fig. 4: the external torque goes against the small spontaneous twist decrease and results in an average increase of ∼1° in the interval under consideration, between 0°C and the critical temperature.
Note that the computed values correspond to the base content of a specific organism and neglect the influence of other physicochemical parameters (ionic strength), as well as alternate structural transitions that may contribute to releasing the superhelical stress, in particular the B-Z transition (45). These contributions may therefore shift the computed critical temperature in an organism-dependent way (for instance, we estimate that for E. coli). However, since they are (at first order) purely enthalpic, they should not modify the basic mechanism.
Altogether, our results show (14) that under constraints, double-stranded DNA can exist above the typical DNA melting temperature. Our simulations make it possible to compute its elastic and structural properties, which remain close to those of unconstrained DNA at room temperature. These observations explain how similar molecular mechanisms of DNA-protein associations can exist for organisms living in the whole temperature range (43). Locally, the melting profiles may also be driven out of equilibrium by in vivo active processes, in particular transcription (46), which may induce a transient superhelical addition (or removal) in the same range of values computed here (47).
Large-scale flexibility of unconstrained DNA
As a final point, we address the (apparent) large-scale bending flexibility of DNA. At the wormlike-chain level, the details of the molecule are averaged out and the flexibility is described by the bending persistence length, , i.e., the bending correlation length of the polymer, which is related to the bending stiffness, , by the relation
| (11) |
where b is the length of a rigid element of the polymer. Within the rigid-basepair model, these parameters can be derived from the nanoscale structure and elasticity via a systematic coarse-graining procedure (20). We note that the three step parameters most influential in terms of large-scale bending are also the ones for which the effect of temperature is strongest. Not surprisingly, our estimate for the bending stiffness, , of the DNA double helix exhibits a weak, but noticeable, temperature dependence (Fig. 5, gray line; shaded area indicates the estimated error bar).
Figure 5.
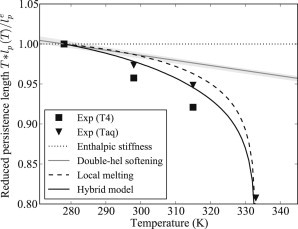
Persistence length of sequence-averaged DNA, multiplied by temperature and rescaled by its value at 278 K. In this representation, a purely enthalpic stiffness yields a temperature-independent value (dotted line). The markers ▾ and ■ are the experimental data points from Geggier et al. (37) obtained with two types of ligase enzymes. Gray solid line: MD-derived values of the persistence length, with the estimated error bars (shaded area), i.e., the contribution from the double-helical elasticity; dashed line: contribution predicted from the denaturation bubbles (9); black solid line: the hybrid model, including both contributions.
Recent measurements (37) have indeed ruled out a temperature-independent stiffness, (Fig. 5, dotted horizontal line). However, the data included in Fig. 5 show a temperature effect, which is considerably stronger than expected from our results for the DNA double helix. In addition to softening the double helix, the flexibility of DNA may also increase due to the presence of transient denaturation bubbles that generate local kinks (7,8). In a different study, two of the authors of the article presented here quantitatively implemented this idea and reproduced the dramatic decrease of the apparent stiffness in the premelting stage (Fig. 5, last datapoint) (9). However, at lower temperatures, the bubble formation is insufficient to reproduce the experimental slope if the stiffness of the double helix is assumed to be independent of T (Fig. 5, dashed line).
Here, we present the results from a hybrid model, which accounts for the temperature dependence of the double-helical stiffness, as well as for the effect of bubbles, and which is in good agreement with the experimental data (Fig. 5, solid line). At physiological temperatures, the two effects contribute equally strongly. Closer to the melting transition, the unharmonic effects dominate.
Conclusion
The nanoscale mechanical structure and elasticity of the DNA double helix can be inferred from the analysis of crystallographic data and MD simulations. To date, there is almost no information on how these properties vary with temperature. In this article, we present results from MD simulations of DNA oligomers at different temperatures. We show that entropy plays a significant role in double-helical elasticity, both inside the basepair and, to a lesser extent, between successive basepairs.
At the internal-basepair level, this entropic contribution is particularly strong in the stretch and opening degrees of freedom. With increasing temperature, it results in a significant broadening of the harmonic fluctuations in these directions of the basepair plane, which can be considered the initial step of the DNA melting pathway.
At the basepair step level, the entropic contribution is weaker but detectable. It is strongest in the roll, tilt, and rise degrees of freedom relevant to the large-scale bending rigidity. We include the resulting temperature dependence of the persistence length of the DNA double helix in a description of kinking in transient denaturation bubbles. Our predictions for the effective large-scale bending stiffness agree with the experimentally measured values for standard physiological conditions up to temperatures close to the melting temperature of DNA.
It is remarkable that living organisms thrive over an even broader temperature range. To describe DNA in vivo, we have assumed that biological organisms control the stability of the double helix by regulating superhelical stress. We have estimated the required values from the Benham model and included the effect in our description of the nanoscale properties. Overall, we find a remarkably small temperature dependence of the structure and flexibility of genomic DNA, compatible with conservation of protein-DNA binding mechanisms (43).
Acknowledgments
S.M. thanks K. Zakrzewska for her help with the simulation software. We acknowledge the Pole Scientifique de Modélisation Numérique for computing resources.
This work was supported by the Agence Nationale de la Recherche grants FSCF (ANR-12-BSV5-0009-01) (to R.E.) and Chrome (ANR-12-BSV5-0017-01) (to R.L.).
Footnotes
Sam Meyer’s present address is LIRIS, CNRS UMR 5205, INRIA, INSA Lyon, Université de Lyon, F-69621 Lyon, France.
Supporting Material
References
- 1.Davey C.A., Sargent D.F., Richmond T.J. Solvent mediated interactions in the structure of the nucleosome core particle at 1.9 Å resolution. J. Mol. Biol. 2002;319:1097–1113. doi: 10.1016/S0022-2836(02)00386-8. [DOI] [PubMed] [Google Scholar]
- 2.Dixon N.E., Kornberg A. Protein HU in the enzymatic replication of the chromosomal origin of Escherichia coli. Proc. Natl. Acad. Sci. USA. 1984;81:424–428. doi: 10.1073/pnas.81.2.424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kim Y., Geiger J.H., Sigler P.B. Crystal structure of a yeast TBP/TATA-box complex. Nature. 1993;365:512–520. doi: 10.1038/365512a0. [DOI] [PubMed] [Google Scholar]
- 4.Tansey M.R., Brock T.D. The upper temperature limit for eukaryotic organisms. Proc. Natl. Acad. Sci. USA. 1972;69:2426–2428. doi: 10.1073/pnas.69.9.2426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Takai K., Nakamura K., Horikoshi K. Cell proliferation at 122°C and isotopically heavy CH4 production by a hyperthermophilic methanogen under high-pressure cultivation. Proc. Natl. Acad. Sci. USA. 2008;105:10949–10954. doi: 10.1073/pnas.0712334105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rubinstein M., Colby R. Oxford University Press; Cary, NC: 2003. Polymer Physics (Chemistry) [Google Scholar]
- 7.Yan J., Marko J.F. Localized single-stranded bubble mechanism for cyclization of short double helix DNA. Phys. Rev. Lett. 2004;93:108108. doi: 10.1103/PhysRevLett.93.108108. [DOI] [PubMed] [Google Scholar]
- 8.Wiggins P.A., Phillips R., Nelson P.C. Exact theory of kinkable elastic polymers. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;71:021909. doi: 10.1103/PhysRevE.71.021909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Theodorakopoulos N., Peyrard M. Base pair openings and temperature dependence of DNA flexibility. Phys. Rev. Lett. 2012;108:078104. doi: 10.1103/PhysRevLett.108.078104. [DOI] [PubMed] [Google Scholar]
- 10.Zimm B.H., Bragg J. Theory of the phase transition between helix and random coil in polypeptide chains. J. Chem. Phys. 1959;31:526–535. [Google Scholar]
- 11.Poland D., Scheraga H.A. Phase transitions in one dimension and the helix-coil transition in polyamino acids. J. Chem. Phys. 1966;45:1456–1463. doi: 10.1063/1.1727785. [DOI] [PubMed] [Google Scholar]
- 12.Dauxois T., Peyrard M., Bishop A.R. Entropy-driven DNA denaturation. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1993;47:R44–R47. doi: 10.1103/physreve.47.r44. [DOI] [PubMed] [Google Scholar]
- 13.Jost D., Everaers R. Genome wide application of DNA melting analysis. J. Phys. Condens. Matter. 2009;21:034108. doi: 10.1088/0953-8984/21/3/034108. [DOI] [PubMed] [Google Scholar]
- 14.Benham C.J. Theoretical analysis of the helix-coil transition in positively superhelical DNA at high temperatures. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1996;53:2984–2987. doi: 10.1103/physreve.53.2984. [DOI] [PubMed] [Google Scholar]
- 15.Pérez A., Marchán I., Orozco M. Refinement of the AMBER force field for nucleic acids: improving the description of α/γ conformers. Biophys. J. 2007;92:3817–3829. doi: 10.1529/biophysj.106.097782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Beveridge D.L., Barreiro G., Young M.A. Molecular dynamics simulations of the 136 unique tetranucleotide sequences of DNA oligonucleotides. I. Research design and results on d(CpG) steps. Biophys. J. 2004;87:3799–3813. doi: 10.1529/biophysj.104.045252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lavery R., Zakrzewska K., Sponer J. A systematic molecular dynamics study of nearest-neighbor effects on base pair and base pair step conformations and fluctuations in B-DNA. Nucleic Acids Res. 2010;38:299–313. doi: 10.1093/nar/gkp834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dickerson R.E. Definitions and nomenclature of nucleic acid structure components. Nucleic Acids Res. 1989;17:1797–1803. doi: 10.1093/nar/17.5.1797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jost D., Zubair A., Everaers R. Bubble statistics and positioning in superhelically stressed DNA. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2011;84:031912. doi: 10.1103/PhysRevE.84.031912. [DOI] [PubMed] [Google Scholar]
- 20.Becker N.B., Everaers R. From rigid base pairs to semiflexible polymers: coarse-graining DNA. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007;76:021923. doi: 10.1103/PhysRevE.76.021923. [DOI] [PubMed] [Google Scholar]
- 21.Olson W.K., Gorin A.A., Zhurkin V.B. DNA sequence-dependent deformability deduced from protein-DNA crystal complexes. Proc. Natl. Acad. Sci. USA. 1998;95:11163–11168. doi: 10.1073/pnas.95.19.11163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lankas F., Sponer J., Cheatham T.E., 3rd DNA basepair step deformability inferred from molecular dynamics simulations. Biophys. J. 2003;85:2872–2883. doi: 10.1016/S0006-3495(03)74710-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Becker N.B., Wolff L., Everaers R. Indirect readout: detection of optimized subsequences and calculation of relative binding affinities using different DNA elastic potentials. Nucleic Acids Res. 2006;34:5638–5649. doi: 10.1093/nar/gkl683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pearlman D., Case D., Kollman P. Amber, a package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics and free energy calculations to simulate the structural and energetic properties of molecules. Comput. Phys. Commun. 1995;91:1–41. [Google Scholar]
- 25.Horn H.W., Swope W.C., Head-Gordon T. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 2004;120:9665–9678. doi: 10.1063/1.1683075. [DOI] [PubMed] [Google Scholar]
- 26.Berendsen H., Postma J., Haak J. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984;81:3684–3690. [Google Scholar]
- 27.Lavery R., Moakher M., Zakrzewska K. Conformational analysis of nucleic acids revisited: Curves+ Nucleic Acids Res. 2009;37:5917–5929. doi: 10.1093/nar/gkp608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Olson W.K., Bansal M., Berman H.M. A standard reference frame for the description of nucleic acid base-pair geometry. J. Mol. Biol. 2001;313:229–237. doi: 10.1006/jmbi.2001.4987. [DOI] [PubMed] [Google Scholar]
- 29.Flyvbjerg H., Petersen H. Error estimates on averages of correlated data. J. Chem. Phys. 1989;91:461–466. [Google Scholar]
- 30.Press W., Teukolsky S., Flannery B. 3rd ed. Cambridge University Press; New York: 2007. Numerical Recipes: The Art of Scientific Computing. [Google Scholar]
- 31.Fye R.M., Benham C.J. Exact method for numerically analyzing a model of local denaturation in superhelically stressed DNA. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1999;59:3408–3426. [Google Scholar]
- 32.Jost D. Twist-DNA: computing base-pair and bubble opening probabilities in genomic superhelical DNA. Bioinformatics. 2013 doi: 10.1093/bioinformatics/btt415. In press. [DOI] [PubMed] [Google Scholar]
- 33.Kratky O., Porod G. Röntgenuntersuchung gelöster fadenmoleküle. Recl. Trav. Chim. Pays-B. 1949;68:1106–1122. [Google Scholar]
- 34.Peyrard M., Bishop A.R. Statistical mechanics of a nonlinear model for DNA denaturation. Phys. Rev. Lett. 1989;62:2755–2758. doi: 10.1103/PhysRevLett.62.2755. [DOI] [PubMed] [Google Scholar]
- 35.Theodorakopoulos N. Melting of genomic DNA: predictive modeling by nonlinear lattice dynamics. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010;82:021905. doi: 10.1103/PhysRevE.82.021905. [DOI] [PubMed] [Google Scholar]
- 36.Theodorakopoulos N. Bubbles, clusters and denaturation in genomic DNA: modeling, parametrization, efficient computation. J. Nonlin. Math. Phys. 2011;18:429–447. [Google Scholar]
- 37.Geggier S., Kotlyar A., Vologodskii A. Temperature dependence of DNA persistence length. Nucleic Acids Res. 2011;39:1419–1426. doi: 10.1093/nar/gkq932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Grimm H., Rupprecht A. Low frequency dynamics of DNA. Phys. B Cond. Mat. 1997;234–236:183–187. [Google Scholar]
- 39.Urabe H., Tominaga Y. Low frequency raman spectra of DNA. J. Phys. Soc. Jpn. 1981;50:3543–3544. [Google Scholar]
- 40.Chandler D. Oxford University Press; Cary, NC: 1987. Introduction to Modern Statistical Mechanics. [Google Scholar]
- 41.Eberhart J., Pinks V., II The thermodynamic limit of superheat of water. J. Colloid Interface Sci. 1985;107:574–575. [Google Scholar]
- 42.Frank-Kamenetskii F. Simplification of the empirical relationship between melting temperature of DNA, its GC content and concentration of sodium ions in solution. Biopolymers. 1971;10:2623–2624. doi: 10.1002/bip.360101223. [DOI] [PubMed] [Google Scholar]
- 43.Grayling R.A., Sandman K., Reeve J.N. DNA stability and DNA binding proteins. Adv. Protein Chem. 1996;48:437–467. doi: 10.1016/s0065-3233(08)60368-x. [DOI] [PubMed] [Google Scholar]
- 44.Schneider R., Travers A., Muskhelishvili G. The expression of the Escherichia coli fis gene is strongly dependent on the superhelical density of DNA. Mol. Microbiol. 2000;38:167–175. doi: 10.1046/j.1365-2958.2000.02129.x. [DOI] [PubMed] [Google Scholar]
- 45.Zhabinskaya D., Benham C.J. Theoretical analysis of competing conformational transitions in superhelical DNA. PLOS Comput. Biol. 2012;8:e1002484. doi: 10.1371/journal.pcbi.1002484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Liu L.F., Wang J.C. Supercoiling of the DNA template during transcription. Proc. Natl. Acad. Sci. USA. 1987;84:7024–7027. doi: 10.1073/pnas.84.20.7024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Tsao Y.-P., Wu H.-Y., Liu L.F. Transcription-driven supercoiling of DNA: direct biochemical evidence from in vitro studies. Cell. 1989;56:111–118. doi: 10.1016/0092-8674(89)90989-6. [DOI] [PubMed] [Google Scholar]
- 48.Jones, E., T. Oliphant, and P. Peterson. 2001. Scipy: Open source scientific tools for python. http://www.scipy.org/.
- 49.Hunter J. Matplotlib: a 2d graphics environment. Comput. Sci. Eng. 2007;9:90–95. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


