Genetic topography of brain morphology

Significance

How diverse functional cortical regions develop is an important neuroscience question. Animal experiments show that regional differentiation is controlled by genes that express in a graded and regionalized pattern; however, such investigation in humans is scarce. Using noninvasive imaging techniques to acquire brain structure data of genetically related subjects (i.e., twins), we estimated the spatial pattern of genetic influences on cortical structure. We developed a genetic parcellation of cortical thickness to delineate the boundaries of cortical divisions that are—within each division—maximally under control of shared genetic influences. We also found differences in genetic influences on cortical surface area and thickness along two orthogonal axes. The concept of gradations is crucial for understanding the organization of the human brain.

Abstract

Animal data show that cortical development is initially patterned by genetic gradients largely along three orthogonal axes. We previously reported differences in genetic influences on cortical surface area along an anterior-posterior axis using neuroimaging data of adult human twins. Here, we demonstrate differences in genetic influences on cortical thickness along a dorsal-ventral axis in the same cohort. The phenomenon of orthogonal gradations in cortical organization evident in different structural and functional properties may originate from genetic gradients. Another emerging theme of cortical patterning is that patterns of genetic influences recapitulate the spatial topography of the cortex within hemispheres. The genetic patterning of both cortical thickness and surface area corresponds to cortical functional specializations. Intriguingly, in contrast to broad similarities in genetic patterning, two sets of analyses distinguish cortical thickness and surface area genetically. First, genetic contributions to cortical thickness and surface area are largely distinct; there is very little genetic correlation (i.e., shared genetic influences) between them. Second, organizing principles among genetically defined regions differ between thickness and surface area. Examining the structure of the genetic similarity matrix among clusters revealed that, whereas surface area clusters showed great genetic proximity with clusters from the same lobe, thickness clusters appear to have close genetic relatedness with clusters that have similar maturational timing. The discrepancies are in line with evidence that the two traits follow different mechanisms in neurodevelopment. Our findings highlight the complexity of genetic influences on cortical morphology and provide a glimpse into emerging principles of genetic organization of the cortex.

The cerebral cortex is a highly organized and complex structure that is divided into anatomically distinct and functionally specialized regions with a total surface area of ∼2,600 cm², and an average thickness of ∼2.5 mm (1, 2). The mechanisms that differentiate the cortical primordium into distinct regions have been elusive. However, animal experiments have demonstrated that the cortex is initially patterned by the combined action of secreted morphogens and related gradients of expression of transcription factors within cortical progenitors (3–7). These genetic gradients provide regional boundaries that confer positional information for initial formation of cortical areas that ultimately serve diverse cortical functions (8).

The direction of morphogenesis has three principal axes during embryonic development: anterior-posterior (A-P), dorsal-ventral (D-V), and medial-lateral (M-L) (9–13). Animal studies show that patterning centers that lie at the margins of the body tissue to be patterned are important in the formation of morphogenetic gradients (9, 13, 14). Patterning centers generate positional information by secreting morphogens to control the activation of transcription factors that determine areal fate and the expression of cell-surface molecules that control the topographic organization of synaptic inputs and outputs (15). Two major patterning centers in the mammalian cortex are an anterior patterning center (expressing fibroblast growth factors Fgf8 and Fgf17) and a dorsal/posterior patterning center [expressing Wnt signaling pathway and Bone Morphogenetic proteins (Bmps)] (9, 10). The gradients of transcription factors (e.g., Pax6 and Emx2) are set up by the patterning centers (9, 10). Before modern molecular biology, a “gradation hypothesis” was postulated based on cytoarchitectonic observations that gradation streams follow orthogonal axes and originate from the border regions of certain cortical regions (16, 17). With the advent of neuroimaging technology, diffusion magnetic resonance imaging (MRI) reported that the topography of fiber tracts follows the three orthogonal principal axes, creating a grid-like structure (18), and a review study of cognitive processing demonstrates an A-P functional gradient in the frontal cortex (19). Taken together, accumulating evidence indicates the presence of gradients in the cortex along principal axes at both genetic and phenotypic levels and across different cortical phenotypes.

Surface area and thickness are two anatomical properties that characterize the cortex, and findings from twin studies show that total surface area and average thickness are both highly heritable traits (heritability estimates: ∼90% and ∼80% respectively) (20). According to the radial unit hypothesis (21), these two traits reflect different mechanisms in cortical development. Cortical surface area is primarily driven by the number of radial columns perpendicular to the pial surface, and cortical thickness is largely determined by the horizontal layers in the cortical columns (including neurons and neuropil) (22). Thus, the human cortex is organized into columnar and laminar patterns with important functional implications. Cortical columns are thought to be functional units of the cortex, and the cortical layers are composed of diverse neuronal populations that organize cortical connectivity (22, 23). Consistent with this hypothesis, twin and family studies indicate that, to a large extent, global measures of surface area and thickness are influenced by distinct genetic contributions (20, 24), compatible with the notion of different developmental processes (25).

Little is known about how genetic influences on surface area and thickness are distributed across the human cortex (i.e., genetic patterning), including whether gradients of genetic influence can be seen for both measures and how these might be similar or different. Previously, we mapped the genetic patterning of surface area based on the MRI scans of over 400 adult twins (26, 27). Using the twin design, which compares monozygotic and dizygotic twins, we can estimate the relative influence of genes and the environment on variance of a phenotype. This method can be further extended to determine the magnitude of genetic and environmental covariance between phenotypes. In the present study, heritability represents the proportion of variance in any location on the cortical surface that is due to genes. Genetic correlations represent shared genetic influences on cortical structure between different points on the cortical surface. The estimated genetic effect is the aggregate effect of all genes as opposed to specific effects of a few individual genes. This approach is advantageous for estimating genetic influences on a complex trait like human brain structure, which probably involves large numbers of genes and possible gene–gene interactions (27). By examining shared genetic influences across the cortex, we demonstrated that maps of genetic patterning of surface area followed specific spatial features comparable with those demonstrated in mouse models, such as an A-P division and four basic cortical regions, which correspond to a mostly lobar pattern in the human cortex (10, 27). Additional partitions were nested within lobes that correspond to structurally and functionally meaningful regions, suggesting a central role of genetic control on regional differentiation. Of note, the genetic divisions were not the same as traditional regions that have been defined on the basis of structure or function.

Here, we adopt a similar analytic procedure in an examination of genetic patterning of cortical thickness in the normal adult human brain. Magnetic resonance (MR) images do not have sufficient spatial resolution to examine cortical thickness by each layer; instead, we measure the combined thickness across all cortical layers at each cortical location. We have previously explored the genetic patterning of cortical thickness based on three preselected cortical locations (seed points), and findings suggested that the genetic correlation pattern of cortical thickness differs from that of surface area, lacking the A-P or lobar divisions observed in the latter (28). This limited seed-point analysis made no attempt to define gradients or discover specific genetic boundaries, however. Here, we examine the entire cortex and apply a data-driven method to describe the topography in an unbiased manner. This approach permits generation of a genetically based parcellation of cortical thickness as we did for surface area.

Our analysis involves the following steps. First, we investigate the spatial distribution of genetic correlations of cortical thickness between different cortical locations on the entire cortical surface. Specifically, we use cluster analyses to identify the boundaries of cortical divisions that are maximally genetically correlated (i.e., under control of shared genetic influences on cortical thickness). The resulting cortical maps of cluster or seed-point analyses are referred to as the genetic patterning of cortical thickness, i.e., the spatial layout of the maps. It is worth clarifying at the outset that the term “patterning” is also used to refer to molecular or cellular differences between functional cortical areas as a result of a developmental process (9, 29). However, here we use genetic patterning to describe the spatial distribution of genetic correlation based on MRI data and modeling tools used in this study. Second, we explore the organization among the genetically based clusters, i.e., the genetic relationships among the clusters. In particular, we use a dendrogram based on the genetic similarity matrix among clusters to inspect the genetic proximity between clusters to search for underlying organizational principles related to genetic control over cortical thickness (e.g., whether clusters that are near to each other on the brain surface are more genetically related than those that are farther away). Third, we compare genetic influences on cortical thickness and surface area to see whether the spatial layout of the maps (i.e., the genetic patterning) looks the same and, independent of this result, whether the genetic relationships among the clusters (i.e., the genetic organization) are similar between the two brain phenotypes. Thickness and surface area could, for example, have similar spatial layouts (patterning) but the genetic correlations between parcels comprising that layout (organization) might be different. Finally, we examine the degree to which genetic influences on thickness and surface area within the identified genetic clusters are shared across the two measures to discover whether, within genetically meaningful boundaries, there are unique genetic influences on these two cortical dimensions.

Results

Genetic Influences on Cortical Thickness: Two-Cluster Solution.

When we constrained the number of clusters to be two, the solution identified a D-V division as the most distinct partition in the basic genetic patterning of cortical thickness. This division separated the motor/premotor, parietal, and occipital regions (the dorsal cluster) from prefrontal and temporal regions (the ventral cluster) (Fig. 1).

Fig. 1.

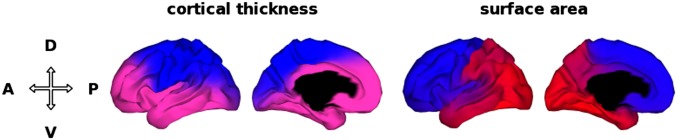
Two-cluster solution maps. When the number of clusters was constrained to be two, the solution identified a D-V division as the most distinct partition in the genetic patterning of cortical thickness, and an A-P division in the genetic patterning of surface area. D, dorsal; V, ventral; A, anterior; P, posterior.

We also performed seed-point analyses to map genetic correlations of cortical-thickness measures between selected seed regions and all other cortical locations after adjusting for mean thickness averaged across the entire cortex. The D-V division shown in the two-cluster solution was supported by a multiseed point analysis resulting in similar D-V patterns regardless of initial seed locations (Fig. S1).

Genetic Patterning of Cortical Thickness.

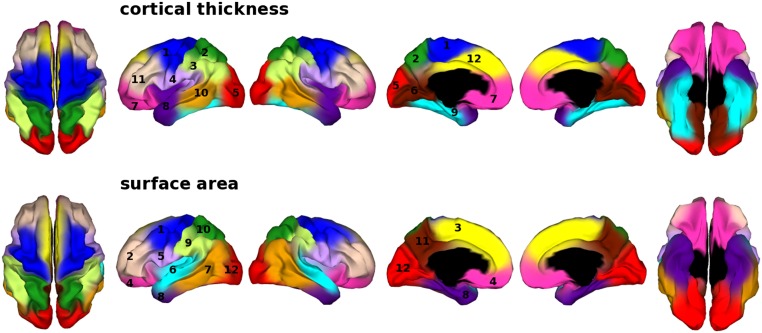
Here, we sought to determine the most appropriate number of clusters to explain patterns in the genetic correlation data based on several different clustering algorithms. These algorithms included spectral cluster analysis and the silhouette coefficients calculated from the results of fuzzy clustering. After testing the stability of the clustering using different approaches (Fig. S2), which all identified a similar range for the number of clusters being between 11 and 15 (SI Methods and Figs. S3 and S4), we focused on the cluster map of the 12-cluster solution based on the adjusted data (Fig. 2). We chose 12 clusters because (i) a lower number is more parsimonious, all other things being equal; and (ii) it enables a direct comparison with our previous report on the 12-cluster map of cortical surface-area measures (26). However, it is worth noting that whether we chose 11 or 12 clusters did not alter the interpretation of results in the present study.

Fig. 2.

Genetic clustering maps. Cortical thickness: 1, motor-premotor-supplementary motor area; 2, superior parietal cortex; 3, inferior parietal cortex; 4, perisylvian region; 5, occipital cortex; 6, ventromedial occipital cortex; 7, ventral frontal cortex; 8, temporal pole; 9, medial temporal cortex; 10 middle temporal cortex; 11, dorsolateral prefrontal cortex; 12, medial prefrontal cortex. Surface area: 1, motor-premotor cortex; 2, dorsolateral prefrontal cortex; 3, dorsomedial frontal cortex; 4, orbitofrontal cortex; 5, pars opercularis and subcentral region; 6, superior temporal cortex; 7, posterolateral temporal cortex; 8, anteromedial temporal cortex; 9, inferior parietal cortex; 10, superior parietal cortex; 11, precuneus; and 12: occipital cortex (26).

Organization Among Genetic Clusters.

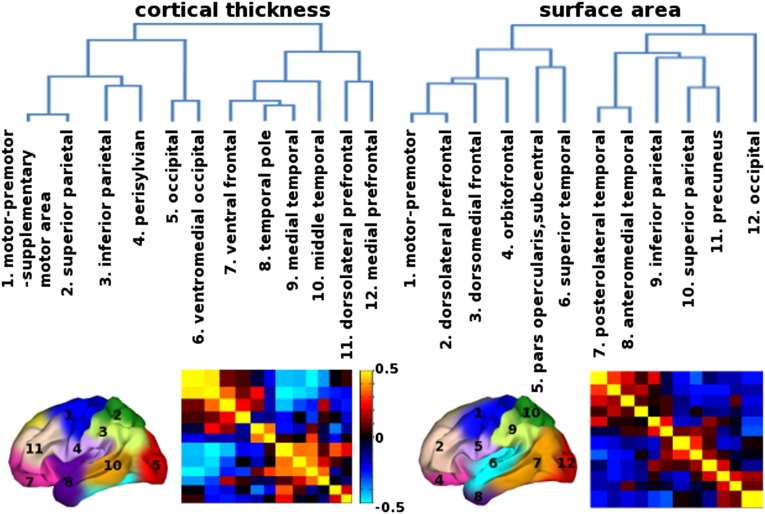
We calculated the genetic similarity matrix to determine the genetic relatedness between clusters and constructed a dendrogram, a tree-structured graph, derived from hierarchical clustering to summarize the genetic relations among them (Fig. 3). The most distinct genetic partitions located at the highest level of the hierarchy corresponded to the D-V division. The ventral division included the temporal and prefrontal clusters. The dorsal division included the occipital, parietal clusters, and motor/premotor clusters. Below that, there were four branches including (i) motor/somatosensory/parietal/perisylvian, (ii) occipital lobe, (iii) temporal/ventral frontal, and (iv) dorsal prefrontal regions. Finally, at the bottom of the dendrogram, there were clusters related to human functional specialization. These divisions can also be observed through the progression of cluster solutions, from 2 to 12 clusters (Fig. S5).

Fig. 3.

Organization among genetic clusters. (Upper) The dendrograms derived from hierarchical clustering based on genetic correlations among clusters. (Lower) The genetic clustering maps show anatomical locations of the clusters, and the heatmaps represent the weighted mean genetic correlations within and between clusters.

Comparisons Between Genetic Patterning of Cortical Thickness and Surface Area.

The genetic patterns of cortical thickness and surface area were similar, especially in the lateral aspect of the cortical surface; however, differences between the patterning were noted in the medial wall (Fig. 2). The spatial extent of clusters also differed. For example, cortical thickness clusters near the midline extended to both the lateral and medial parts of the hemispheres (e.g., the motor-premotor, superior parietal, and dorsomedial frontal clusters) whereas the most corresponding surface-area clusters were restrictively placed on either side of the hemispheres. We computed the Rand index to calculate the similarity between the clustering for cortical thickness and surface area. Despite the medial differences, it showed a considerable degree of similarity (Rand index = 0.91; adjusted Rand index = 0.44) (30, 31). The Rand index is a number between 0 and 1 that quantifies the degree of similarity between the two cluster solutions by computing the proportion of vertices that were given the same cluster label in both cluster solutions. It is possible for some vertices to have the same cluster label by chance, and this is accounted for in the adjusted Rand index.

Distinct Genetic Contributions to Cortical Thickness and Surface Area.

The cortical surface was divided into 12 cortical subregions for thickness and area separately using the corresponding genetically based cluster map of each trait. We calculated the weighted average cortical thickness and surface area for each cluster according to the partial memberships of all of the clusters assigned to each vertex. We then estimated genetic correlations between cortical thickness and surface area. The genetic correlation between cortical thickness and surface area for the dorsolateral prefrontal cluster was 0.01 [95% confidence interval (CI): −0.13∼0.16), and for the inferior parietal cluster it was 0.15 (95% CI: 0.01∼0.28]. These two clusters were selected because they showed the highest degree of similarity in boundaries between the two traits. Applying these comparisons to the same cortical regions showed an interesting contrast: namely, that the boundaries of genetic clusters can be very similar between the two traits but the genetic determinants underlying them appear quite distinct.

Discussion

Genetic Influences on Cortical Thickness Showed a Dorsal-Ventral Division (Two-Cluster Solution).

The most substantial genetic partition of cortical thickness corresponded to a D-V division. Although the boundary of the D-V division did not match any cortical folding patterns, it did correspond to a border characterized by cytoarchitectonic features, which separates the granular and agranular cortex in the frontal lobe (11). The granular cortex is defined by the presence of a granule cell layer IV (11). The prefrontal region is classified as the granular cortex whereas the motor-premotor region is classified as the agranular cortex (11). Thus, differences in cytoarchitecture might reflect the D-V genetic boundary of cortical thickness.

The genetic D-V division of cortical thickness may also be related to cortical connectivity patterns. For example, despite their lack of spatial contiguity, prefrontal and temporal regions’ cortical thickness had similar genetic influences. These regions are known to be structurally and functionally connected. This result is consistent with our previous report based on a limited seed-point analysis, which showed that the pattern of genetic correlations for cortical thickness partially correspond to neuroanatomical connectivity, with high genetic correlations between distal, noncontiguous regions (28). The cross-regional genetic patterning of cortical thickness may relate to underlying fiber tract structures (e.g., thalamocortical or intracortical connections).

We hypothesize that the D-V division of genetic influences on cortical thickness may relate to morphogenetic gradients along the D-V axis. The genetic divisions or gradients are in line with the cytoarchitectonic gradation. The gradation hypothesis describes gradations from the motor cortex toward the more rostrally located frontal regions with increasing granularity, and also suggests that the cytoarchitectonic changes are accompanied by myeloarchitectonic changes. Ample evidence on cortical gradients seen in genetic patterning, morphology, connectivity, and function provides a unique insight on the organization of the human brain (17, 19, 32).

The Genetic Patterning of Cortical Thickness Largely Corresponds to Functional Specializations (12-Cluster Solution).

Without any incorporation of anatomical knowledge in the clustering algorithm, the genetically based subdivisions corresponded closely to meaningful structural and functional regions (Fig. 2). Some cluster boundaries mapped onto traditionally parcellated regions, such as cytoarchitectural areas [e.g., Brodmann area (BA) 7] or gyral patterns, whereas others did not. Evidence of genetic expression domains recapitulating phenotypic boundaries has been observed in various body parts and diverse species (33–35). These findings partly address a challenging question about how genes shape initially homogeneous cells into different body parts (36). The close correspondence between genetic patterning and phenotypic boundaries is consistent with the idea that body patterning is blueprinted by genetic patterning (21, 37). We previously found such evidence in the genetic patterning of cortical surface area (26, 27), and here we see similar results for cortical thickness. Gene expression profiles between regions recapitulating the spatial topography of the cortex were also shown in an atlas of the adult human brain transcriptome (38). The genes included in that study coded proteins involved in many different aspects of structure and function other than cortical thickness and surface area, yet the genetic topography corresponded to the spatial topography of the brain.

All Genetic Divisions Were Bilaterally Located in Homologous Regions.

The genetic patterning of cortical thickness was predominantly bilaterally symmetrical. All clusters were bilaterally located in the homologous regions between hemispheres. Because the clustering algorithm is blind to location in space and the clustering was conducted on both hemispheres simultaneously, with no constraint for hemispheric symmetry, the results clearly indicate a predominantly bilaterally symmetrical feature. This characteristic is similar to that of the genetic patterning of cortical surface area, which also showed a predominantly symmetrical feature (26, 27).

Comparisons Between Genetic Patterning of Cortical Thickness and Surface Area.

The boundaries of genetic clusters of cortical thickness were most similar to those of surface area in the lateral part of the hemispheres, except for the temporal clusters (Fig. 2). Differences were most notable in the medial part of the hemispheres. At first glance, it may seem surprising to see similar genetic patterning between cortical thickness and surface area, given that they are very different measures along two orthogonal dimensions on the cortical ribbon. The observed similarity in genetic patterning between surface area and thickness might be explained by results showing that both genetically informed parcellations largely conform to functionally specialized domains of the human cortex.

It is also important to note that the genetic patterning of thickness and surface area was not identical. It remains unclear as to why genetic parcellations of these measures are most similar on the lateral surface, and least on the medial surface. Possibly, these differences in genetic patterning may be due to distinct genetic mechanisms controlling these two traits during development. Also possible are methodological limitations regarding low spatial resolution in MR measurements. There may be more genetic divisions than can be detected with our method. Our analysis can demarcate only the broad and prominent landscape of genetic patterning; thus, it is hard to predict how fine details that are missed in our analysis come into play in the observed discrepancies.

Similar Genetic Patterning but Distinct Genetic Organization and Contributions for Thickness and Surface Area.

Although the genetic patterns of the surface area and thickness 12-cluster solutions show a high degree of correspondence, the genetic organization among the clusters is fundamentally different (Fig. 3). We saw a D-V division as the most distinguished partition in the genetic patterning of cortical thickness, in contrast to the A-P division observed in the genetic patterning of cortical surface area. The dendrogram structure indicated that the genetic divisions of surface area are largely organized by four lobes such that the clusters that belong to the same lobes are genetically more similar to one another than to those from different lobes. However, the genetic divisions of thickness did not follow this organizing principle. Neither the A-P division nor the lobes were present in the dendrogram structure of cortical thickness. Clusters from different lobes showed close genetic proximity. For example, the motor and somatosensory clusters were first merged together in the dendrogram (see thickness cluster 1 and 2 in Fig. 3). Unlike the surface area clusters, spatially disconnected cortical-thickness clusters from different lobes also show close genetic relatedness such as anterior temporal and ventral prefrontal regions (see thickness cluster 7, 8, and 9 in Fig. 3). The organizational principles of thickness clusters appear to reflect maturation timing or primary vs. association cortex. Sensorimotor region and frontal pole, temporal, and occipital poles mature before higher-order association areas (12, 39). Interestingly, we indeed found that the genetic clusters in regions that mature early are grouped together (e.g., primary motor merged with somatosensory clusters, anterior temporal merged with ventral frontal including frontal pole, and two occipital clusters merged together).

The patterning of high cross-regional genetic correlations was a feature of the genetic organization of cortical thickness. In contrast, we have demonstrated predominantly spatially contiguous patterns of genetic correlations for cortical surface area (26, 27). From the sequential cluster analyses from 2- to 12-cluster solutions, the way that each additional cluster was “carved out from” or “fit into” the previous cluster solution differed greatly between surface area and thickness measures, even though the eventual 12-cluster solution was very similar in patterning (Fig. S5). This result is additional support for the conclusion of distinct organizational principles for genetic relations among clusters between surface area and thickness.

Furthermore, we found very little genetic overlap between measures of regional cortical thickness and surface area, i.e., very low genetic correlations between them, consistent with our previous report (20), as well as a report from an independent sample (24). In the current analysis, we calculated the genetic correlations using the genetic divisions defined by the cluster analyses. Even within largely spatially corresponding regions based on the genetic cluster maps, we failed to find evidence of common genetic influences between surface area and thickness. It is worth noting that minimal genetic overlap between cortical thickness and surface area is most evident for global measures. In our previous study, we did find evidence for nonzero genetic correlations between cortical thickness and surface area for some regional measures (e.g., lateral orbital frontal cortex) (20). It is therefore possible that there are common genes related to these traits locally in certain cortical regions or specific layers, which we could not detect with the present analysis. For example, rodent studies show that genes, controlling for area patterning, also regulate thickness in certain cortical layers (40–42). The molecular and cellular mechanisms in cortical development are complex and intricate and cannot be fully appreciated by MRI measures that focus on the examination of brain structure at the systems level.

Distinct organization among genetic clusters and few shared genetic influences between the two traits could be explained by separate underlying developmental trajectories. According to the radial-unit hypothesis, the overall expansion of surface area is largely determined by the number of radial cortical columns, starting from a layer of founder neural stem cells. The exponential growth of founder cells occurs before the onset of neurogenesis. After the onset of neurogenesis, the number of neurons increases linearly, derived from founder cells within each column that determine initial cortical thickness (43). Thus, our current knowledge suggests that different genetic mechanisms and time courses during neurodevelopment are involved in the features of cortical thickness and surface area.

Conclusion.

The human cortex is a complex structure with many cortical functional areas that are distinguishable by differences in gene expression, morphology, and connectivity (44–46). Despite the existence of a considerable degree of cortical plasticity, our study supports the concept of early genetic determination of cortical regionalization. We have examined the genetic patterning and organization of cortical morphology along two orthogonal dimensions, the tangential (horizontal) expansion of surface area and the radial (vertical) growth of cortical thickness. We showed that the genetic patternings of cortical thickness and surface area are largely similar to one another and consistent with functional specialization boundaries. However, the organizational principles among genetic clusters differ between the two traits. The genetic effects that influence cortical thickness and surface area were largely distinct, in line with previous findings. Further study of genetic patterning with different age groups is warranted to determine whether the pattern changes during development or aging. Our collective understanding of the genetic underpinnings of complex human traits is in its infancy. The current findings provide a glimpse into the genetic architecture of the human cortex and may facilitate future genomic investigation into diverse complex traits of the human brain.

Methods

Participants and Imaging Data.

The participants were 406 middle-aged men from the Vietnam Era Twin Study of Aging (VETSA) (47). There were 110 monozygotic and 93 dizygotic twin pairs. Based on demographic and health characteristics, the sample is representative of US men in their age range (47). T1-weighted MR images were acquired on Siemens 1.5 Tesla scanners at University of California, San Diego and Massachusetts General Hospital. The data were analyzed using the FreeSurfer software package to calculate cortical thickness measures (48, 49). In brief, the cortical surface was reconstructed to measure thickness at each surface location, or vertex. The resulting surface was covered with a polygonal tessellation. The boundary of the gray and white matter was identified and then deformed outwards to obtain a representation of the pial surface. Each subject’s cortical surface was aligned to an atlas space in a spherical surface-based coordinate system. The surface alignment method used is not anchored to specific anatomical landmarks (e.g., fundus of the central sulcus). Rather, it uses the entire pattern of surface curvature at every vertex across the cortex to register individual subjects to atlas space (50). The thickness of the gray matter can be computed at any point in the cortex as the shortest distance between the gray/white boundary and pial surfaces (2). See full method in SI Methods.

Twin Analysis.

We estimated genetic correlations of cortical-thickness measures between brain areas using Mx, a structural equation modeling software for genetically informative data (51). In brief, a standard bivariate twin (AE) model was used to estimate the proportion of phenotypic variance between vertices accounted for by additive genetic effects (A) and individual-specific environmental effects (E) for each measure (52). Before the model fitting, the cortical thickness data were adjusted for age and site effects, and then normalized to adjust for global effects (i.e., the average cortical thickness was subtracted from the vertex-wise data at each cortical location).

Cluster Analysis.

Clustering methods partition the dataset into clusters based on the pair-wise genetic correlations of thickness measures between every two vertices. The fuzzy clustering procedure was performed by the cluster package implemented in R (www.r-project.org/). A commonly used quantitative index called the silhouette coefficient was used to approximately determine the correct number of clusters. We also used an entirely different clustering algorithm called spectral clustering to validate the fuzzy clustering results (53, 54). See full method in SI Methods.