Probing the protein-folding mechanism using denaturant and temperature effects on rate constants

Significance

Analysis of effects of denaturants and temperature on folding and unfolding rate constants of 13 globular proteins yields the amount and composition of the surface buried in folding to and from the high–free-energy transition state (TS), and thereby provides information about folding mechanisms and early unstable folding intermediates. All 13 proteins preferentially bury amide surface in folding to TS; amounts of amide and hydrocarbon surface buried in folding to TS generally exceed those buried in forming the native secondary structure. From this, we conclude that most native secondary structure forms in early unstable folding intermediates and that conversion of these intermediates to TS involves nucleation of tertiary interactions, allowing preferential burial of hydrocarbon surface as TS folds.

Abstract

Protein folding has been extensively studied, but many questions remain regarding the mechanism. Characterizing early unstable intermediates and the high–free-energy transition state (TS) will help answer some of these. Here, we use effects of denaturants (urea, guanidinium chloride) and temperature on folding and unfolding rate constants and the overall equilibrium constant as probes of surface area changes in protein folding. We interpret denaturant kinetic m-values and activation heat capacity changes for 13 proteins to determine amounts of hydrocarbon and amide surface buried in folding to and from TS, and for complete folding. Predicted accessible surface area changes for complete folding agree in most cases with structurally determined values. We find that TS is advanced (50–90% of overall surface burial) and that the surface buried is disproportionately amide, demonstrating extensive formation of secondary structure in early intermediates. Models of possible pre-TS intermediates with all elements of the native secondary structure, created for several of these proteins, bury less amide and hydrocarbon surface than predicted for TS. Therefore, we propose that TS generally has both the native secondary structure and sufficient organization of other regions of the backbone to nucleate subsequent (post-TS) formation of tertiary interactions. The approach developed here provides proof of concept for the use of denaturants and other solutes as probes of amount and composition of the surface buried in coupled folding and other large conformational changes in TS and intermediates in protein processes.

Determination of the mechanism of protein folding [unfolded (U) → folded (F)] is a long-standing goal of biophysical research. Folding of a single domain globular protein is a very highly cooperative (thermodynamically two-state) process. From analysis of folding kinetic data for CI2 and barnase, Fersht et al. (1) concluded that proteins fold through a high–free-energy transition state (TS) with partially formed elements of native structure. Recently, Barrick and Sosnick (2) concluded that an ensemble of unstable, rapidly reversible intermediates form early in the folding mechanism, and that the most advanced and unstable of these undergoes a rate-determining conformational change with transition state TS. This transit step, slower than the reverse direction of previous rapidly reversible steps, is followed by rapid propagation of folding. Most proposals for the initial intermediates invoke unstable regions of α-helix and/or β-sheet; these are thought to coalesce and/or rearrange to form TS. Kay and coworkers (3) characterized a marginally stable early intermediate of Fyn SH3 domain and found that interactions of amide groups formed earlier in the folding pathway than interactions of methyl groups, indicating that 2° structure formed before the 3° fold. Recent hydrogen exchange pulse-labeling experiments analyzed with mass spectrometry by Englander, Marqusee, and collaborators (4) indicate that folding of RNase H occurs through a defined set of intermediates where each step of folding adds more native-like elements of 2° structure. Late intermediates in folding that contain most elements of native structure except side-chain close packing have been observed (5).

Mutational analyses of many proteins indicate that TS for protein folding are quite advanced (2). Here, we develop a different approach to characterize TS for noncovalent self-assembly processes like protein folding using solute effects and heat capacity changes as physical probes yielding amounts of hydrocarbon and amide surface buried in folding to and from TS, and apply it to characterize TS and infer properties of intermediates before TS for folding of 13 proteins. In addition to probing the character of TS in the protein-folding mechanism in a unique way, this research serves as a demonstration of the use of solutes as probes of conformational changes and interface formation in the steps of any protein process.

The vast majority of the accessible surface area (ASA) buried in folding an extended polypeptide into a globular protein is either hydrocarbon (H) (∼70%) or amide (A) (∼20%), with an average ratio ΔASA_H/ΔASA_A ∼ 3.5 for complete folding (6). [Structural values of ΔASA_H/ΔASA_A range from 2.7 to 3.9 for 12 of the proteins analyzed here; only one (FKBP) has a ratio outside this range (∼5).] Different folding mechanisms lead to very different predictions of the ΔASA_H/ΔASA_A ratio for folding from an extended chain to TS. Formation of isolated elements of 2° structure (particularly α-helix) buries proportionately less hydrocarbon surface and proportionately more amide surface than does overall folding. For example, ΔASA_H/ΔASA_A is 0.6 for formation of an (AEAAKA)_n α-helix (6) and 2.0 for formation of isolated α-helical elements present in phage 434 cro repressor (calculation described below), whereas for β-hairpin [Protein Data Bank (PDB) ID code 2EVQ] formation ΔASA_H/ΔASA_A ∼ 2.7. For hydrophobic collapse mechanisms, the ratio ΔASA_H/ΔASA_A for folding to TS is presumably as large or larger than the value for complete folding.

Denaturant Probes of Changes in Amide and Hydrocarbon Surface Area

Recently, the interactions of key denaturants, osmolytes, and Hofmeister salts with the functional groups of proteins and nucleic acid have been determined, allowing these solutes to be used as thermodynamic and kinetic–mechanistic probes of the amount and the composition of the surface buried or exposed in the steps of a noncovalent protein or nucleic acid process like helix formation, folding, or binding (6–14). For protein folding, urea and guanidinium chloride (GuHCl) thermodynamic m-values (derivatives of the standard free energy of folding with respect to denaturant concentration) are determined almost entirely by the preferential interactions of these denaturants with the hydrocarbon and amide surface buried in folding (6):

where α_H and α_A (Table 1) are interaction potentials quantifying the preferential interaction of urea or GuHCl per unit area with these two types of surface, obtained from analysis of thermodynamic data for the preferential interactions of urea and GuHCl with model compounds (6, 10). For GuHCl, α_A is 20-fold larger in magnitude than α_H (Table 1) (10). For overall protein folding (U → F), therefore, α_AΔASA_A is more than fivefold larger in magnitude than α_HΔASA_H, so GuHCl folding m-values are primarily determined by ΔASA_A. For urea, α_A is 3.7-fold larger than α_H (Table 1) (6), and therefore contributions from ΔASA_A and ΔASA_H to urea folding thermodynamic m-values are similar. For cases in which folding and unfolding kinetics are single-exponential (2, 14), Eq. 1 is also applicable to interpret kinetic m-values (obtained from derivatives of the logarithms of the folding and unfolding rate constants with respect to denaturant concentration), in which case ΔASA_H and ΔASA_A are the changes in water-accessible hydrocarbon and amide surface area in folding to or from TS (U → TS; TS → F).

Table 1.

α-Values for urea and GuHCl (Eq. 1) and ε-values (Eq. 2) for the composition of the amide and hydrocarbon surfaces buried in protein folding (SI Materials)

Property	Amide	Hydrocarbon
GuHCl α-value, cal⋅mol−1⋅m−1⋅Å−2	−2.2 ± 0.2	0.11 ± 0.05
Urea α-value, cal⋅mol−1⋅m−1⋅Å−2	−0.42 ± 0.01	−0.11 ± 0.03
ΔCp ε-value, cal⋅mol−1⋅K−1⋅Å−2	−0.14 ± 0.04	0.34 ± 0.02

Heat Capacity Probes of Changes in Hydrocarbon (and Amide) Surface Area

Neither denaturant is optimal as a probe of changes in hydrocarbon ASA (ΔASA_H), but the heat capacity change is. The overall (thermodynamic) heat capacity change for folding (ΔC_p°) is determined to a good approximation by the amounts of hydrocarbon and amide surface buried in folding (15–17):

where ε_H and ε_A are intrinsic values of ΔC_p° per unit area for these two types of surface, obtained from analysis of hydrocarbon and amide transfer thermodynamic data (Table 1). Whereas ε_H is only 2.4-fold larger in magnitude than ε_A, the contribution of ε_HΔASA_H to the overall ΔC_p° of protein folding is ∼9-fold larger in magnitude than ε_AΔASA_A. Eq. 2 (like Eq. 1) is also applicable to interpret activation heat capacity data obtained from the second derivatives of the unfolding and folding rate constants with respect to temperature.

Results and Discussion

Quantifying Amounts of Amide and Hydrocarbon Surface Buried in Folding to and from TS.

The kinetics of folding and unfolding of 13 single-domain globular proteins with known structures and ranging in size from 56 to 164 residues have been determined as a function of denaturant concentration and temperature (18–32). GuHCl or urea kinetic m-values and activation heat capacity changes for folding and unfolding are summarized in Table S1. Amounts of amide and hydrocarbon surface buried in folding to and from TS (i.e., U → TS and TS → F) and for overall folding (U → F), predicted from activation heat capacity change and denaturant kinetic m-values using Eq. S1, are reported in Table 2.

Table 2.

Predicted values of amide and hydrocarbon ΔASA for U → TS, TS → F, and U → F; comparison with structural values for U → F

Protein	PDB ID code	Predicted U → TS ΔASA		Predicted TS → F ΔASA		Predicted U → F ΔASA		U → F ΔASA from structure*
		Hydrocarbon, Å2	Amide, Å2	Hydrocarbon, Å2	Amide, Å2	Hydrocarbon, Å2	Amide, Å2	Hydrocarbon, Å2	Amide, Å2
NTL9	1CQU (51)	−1,282 ± 339	−471 ± 86	−958 ± 335	−328 ± 61	−2,241 ± 485	−799 ± 128	−2,726†	−729†
Bc-Csp	1C9O (52)	−1,800 ± 122	−801 ± 106	−908 ± 45	−133 ± 27	−2,708 ± 154	−934 ± 129	−3,436	−1213
Bs-Csp	1NMG (53)	−2,292 ± 238	−923 ± 238	−207 ± 266	−2 ± 71	−2,499 ± 358	−926 ± 256	−3,425	−1,054
FynSH3	1NYF (54)	−1,534 ± 94	−577 ± 75	−1,362 ± 66	−306 ± 48	−2,905 ± 152	−883 ± 122	−2,726	−691
434 Cro	2CRO (55)	−2,673 ± 469	−1,278 ± 333	−840 ± 506	−113 ± 147	−3,514 ± 698	−1,391 ± 400	−3,705†	−1,106†
PLB1	1HZ6 (56)	−1,231 ± 115	−703 ± 84	−686 ± 101	−308 ± 39	−1,916 ± 180	−1,011 ± 122	−3,259	−1,220
CI2	2CI2 (57)	−1,672 ± 95	−562 ± 75	−1,575 ± 93	−397 ± 59	−3,248 ± 174	−959 ± 134	−3,259	−834
HPr	1POH (58)	−2,629 ± 186	−890 ± 125	−2,370 ± 346	−542 ± 88	−4,999 ± 428	−1,431 ± 207	−4,656	−1,525
ACP	1APS (59)	−2,472 ± 256	−1,647 ± 344	−2,638 ± 166	94 ± 174	−5,110 ± 326	−1,554 ± 439	−5,391	−1,652
ACP-1	2VH7 (60)	−2,647 ± 346	−2,215 ± 455	−2,786 ± 266	−409 ± 207	−5,434 ± 491	−2,624 ± 608	−5,765	−1,818
RPS6	1RIS (61)	−3,026 ± 315	−909 ± 127	−3,065 ± 431	−494 ± 96	−6,091 ± 564	−1,402 ± 219	−5,796	−1,561
FKBP	1FKD (62)	−2,760 ± 271	−1,916 ± 396	−3,243 ± 253	−447 ± 242	−6,003 ± 437	−2,364 ± 588	−6,529†	−1,295†
T4L	1B6I (63)	−5,534 ± 570	−1,796 ± 255	−1,841 ± 189	−542 ± 79	−7,375 ± 643	−2,338 ± 328	−9,806	−2,606

^*ΔASA calculated for an extended model of the denatured state.

^†ΔASA values from Guinn et al. (6).

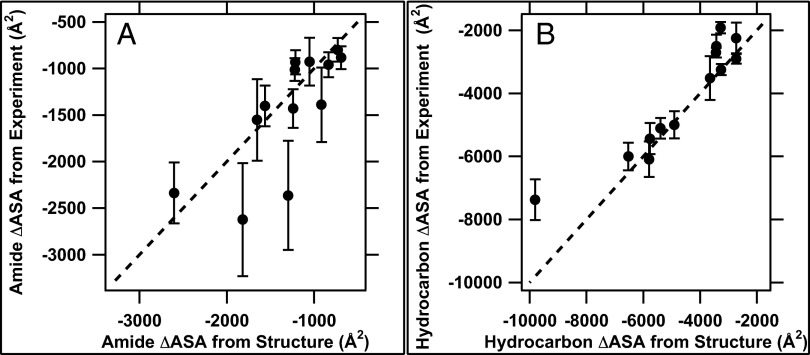
Thermodynamic m-values and ΔC_p° values for overall folding (U → F) are determined from differences between kinetic/activation quantities for folding and unfolding. To validate the use of kinetic m-values and activation ΔC_p° values as structural probes to determine amounts of amide and hydrocarbon ASA buried in folding to and from TS, we compared values of ΔASA_H and ΔASA_A for U → F predicted from the thermodynamic m-value and ΔC_p° with those calculated from structural data assuming the extended polypeptide model of the denatured state (6). Fig. 1 and Table 2 demonstrate the very good agreement obtained between predicted and structural values of ΔASA_H and ΔASA_A for most of the proteins in the dataset. Individual (Fig. 1) and summed (Fig. S1) values of ΔASA_H and ΔASA_A predicted from m-values and activation heat capacities agree within experimental uncertainty with those calculated from structural information for 9 of 13 proteins. (See SI Materials for discussion of uncertainties in ΔASA and of proteins deviating from the line in Fig. 1.) Fig. S1 shows that, in seven cases, the experimentally determined value of ΔASA_H plus ΔASA_A is equal to or slightly larger in magnitude than that calculated from the structural data, validating the use of the extended model of the unfolded chain for these calculations.

Fig. 1.

Comparison of amide (A) and hydrocarbon (B) ΔASA values for U → F from analysis of experimental data (using Eqs. 1 and 2) with values calculated from structural data for F and an extended-chain model for U (Table 2). The lines represent equality of experimental and structural values. Fig. S1 compares experimental and structural values for the sum of amide and hydrocarbon ΔASA for U → F.

To determine how advanced TS is on the folding pathway from U and F, the fraction θ of the overall the denaturant m-value or heat capacity change that occurs in formation of TS has been calculated. As noted by Plaxco et al. (33) for a subset of these proteins, the fraction θ_C^U→TS of the overall heat capacity change that occurs in folding to TS of these 13 proteins is less than the corresponding fraction θ_m^U→TS of the thermodynamic denaturant m-value for folding to TS (Table S2). Because burial of hydrocarbon surface largely determines the heat capacity change, and burial of amide surface is equally or more important for determining denaturant m-values as discussed above, the ranking θ_m^U→TS > θ_C^U→TS indicates that amide ASA is preferentially buried in folding to TS.

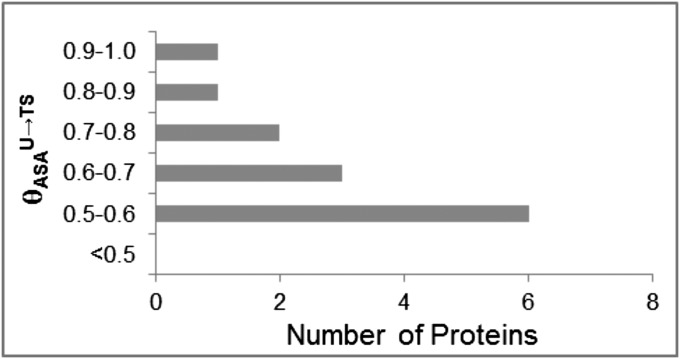
Values of the fraction θ_ASA^U→TS of total (hydrocarbon plus amide) ASA buried in folding (Eq. S2) ranges from 0.53 to 0.94, with 9 of the 13 proteins in the range 0.53–0.70 (Fig. 2 and Table S2). For all 13 proteins, more than one-half of the total (amide plus hydrocarbon) surface buried in folding is buried in folding to TS; the average for the dataset is 65 ± 10%. Mutational analyses and simulations have previously concluded that TS of many proteins is advanced as discussed below. For all 13 proteins, values of θ_ASA^U→TS are smaller than θ_m^U→TS and greater than θ_C^U→TS, as expected.

Fig. 2.

Distribution of θ_ASA^U→TS values quantifying the fraction of the total hydrocarbon plus amide ΔASA that is buried in folding to TS for 13 proteins (Table S2).

Several metrics can be used to quantify the extent to which amide or hydrocarbon ASA is preferentially buried in folding to TS and from TS to the globular protein. The simplest, applicable to each protein individually, compares hydrocarbon:amide ΔASA ratios r, defined as follows:

Values of r for U → TS, TS → F, and U → F are listed in Table S3. For all 10 proteins where values of r for TS → F can be accurately determined, Table S3 demonstrates that r_U→TS < r_TS→F, showing that folding to the TS preferentially buries amide ASA, whereas folding from the TS to the globular protein preferentially buries hydrocarbon ASA.

Because overall ratios r_U→F are different for different proteins, we normalize r_U→TS and r_TS→F by the thermodynamically determined r_U→F and define these ratios as Ω values as follows:

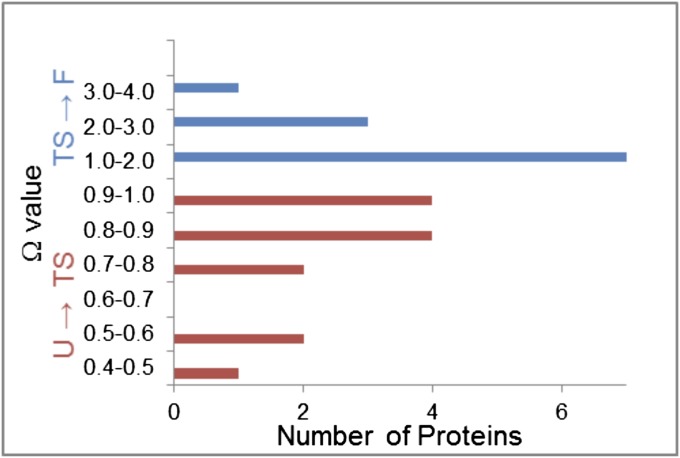
For all proteins Ω_U→TS ≤ 1 (13 examples) and Ω_TS→F ≥ 1 (10 examples), confirming the preferential burial of amide ASA in U → TS and of hydrocarbon ASA in TS → F (Fig. 3).

Fig. 3.

Distribution of Ω-values quantifying preferential burial of amide surface in folding to TS (Ω_U→TS ≤ 1) and preferential burial of hydrocarbon surface in folding from TS to F (Ω_TS→F ≥ 1) (Table S3).

Interpreting Amide ΔASA_A Values for Folding to TS; Comparison with Results of Other Methods.

Values of ΔASA_A for folding to TS determined from the analysis of kinetic m-values and activation heat capacities (Table 2) allow us to estimate the amount of secondary structure formed in folding to TS for each protein. Formation of (AEAAKA)_n α-helix (6) and β-hairpin (PDB ID code 2EVQ) buries ∼22 Ų and ∼12 Ų of backbone amide ASA per residue, respectively. Calculations of amide ASA (34) buried in formation of individual 2° structural elements of Bs-Csp, HPr, and phage 434 Cro protein (434 Cro) agree well with these values (Table S4). From the number of residues in α-helices or β-sheets in these folded proteins and the above per-residue values, we estimate the contribution to ΔASA_A from burial of the chain backbone in forming all of the native 2° structure in folding from U to F (Table S5) and compare with values of ΔASA_A determined from the experimental data for folding from U to TS (Table 2). For 11 of the 13 proteins investigated, the amount of amide ASA buried in folding from U to TS is either greater than (seven proteins) or approximately equal to (four proteins) the amount of backbone amide ASA buried in forming all of the native 2° structure (Table S5). Only for RPS6 and T4L is the amount of amide ASA buried in folding from U to TS less than the amount of backbone amide ASA buried in forming all of the native 2° structure (Table S5). This comparison indicates most simply that the 2° structural elements of these folded proteins are already present in TS. The additional amide ASA buried in seven of the TS investigated may result from reductions in side-chain amide ASA in 2° structure formation or interactions of 2° structures, or from organization of residues that are not involved in 2° structures formed in TS.

Analysis of All-2° and More Advanced Structural Models of Folding Intermediates and TS.

As a structural test of the interpretation that the native 2° structure is present in TS, models of putative folding intermediates (designated I_ss), which preserve the native 2° structure (abbreviated ss) but eliminate as much as possible of the native 3° structure, were made for proteins with α-helical (434 cro), β-sheet (Bs-Csp), and mixed (HPr) secondary structures. In these models, the native elements of α-helix and β-sheet structure are connected to the extent possible by extended chain segments like those in the model of U. Values of amide and hydrocarbon ΔASA for folding of U to form these proposed I_ss intermediates are summarized in Table S4, together with θ and r values calculated from these ΔASA values.

Table S4 reveals that I_ss models for all three proteins examined are significantly less advanced than TS in terms of the sum of amide and hydrocarbon ASA buried (θ_ASA^U→Iss << θ^U→TS). For all-α 434 Cro and all-β Bs-Csp, the amount of amide surface buried in forming all of the elements of native 2° structure is only 50–60% of that buried in folding to TS, whereas for HPr our I_ss model buries almost 100% of the amount of amide surface buried in folding to TS. To create more advanced models that may approximate the TS, we added native-like φ and ψ angles in the regions connecting 2° structure elements but avoided creating the contacts between these elements present in the native state. For all three proteins, we found more advanced models for which ΔASA^TS, θ_ASA^U→TS, and r values (Table S4) are more comparable to those predicted from ΔC_p and m-values and so designate these as TS. These structures for 434 Cro and Bs-Csp are shown on the activation free-energy diagrams of Fig. 4 using θ_ASA values for the fraction of total ASA buried in folding to the structure as the position on the reaction coordinate.

Fig. 4.

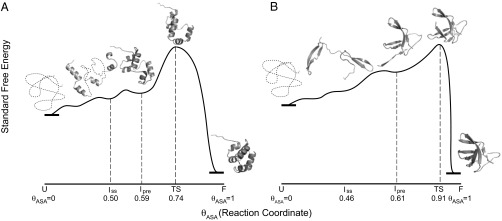
Proposed reaction progress diagrams for (A) 434 cro (all α-helix) and (B) Bs-Csp (all β-sheet). Models of the TS and of earlier folding intermediates, one with the native secondary structure (I_ss) and a more advanced intermediate in which tertiary structure formation is nucleated [a candidate for I_pre (2)], are placed along the reaction coordinate based on their θ_ASA-values (Table S5). Free energies are arbitrarily chosen; only the ASA scale is quantitative.

Comparison with Other Models of TS.

TS for several of the proteins studied here have been investigated previously by other methods. Relaxation dispersion NMR spectroscopy showed that a marginally stable intermediate in Fyn-SH3 (1NYF) folding contains the β-structure formed by the central portion of the polypeptide chain, but lacks the 2° structural elements nearer the N and C termini. The kinetic m-value/activation heat capacity analysis presented here predicts that ∼56% of the ΔASA of folding occurs in forming the high–free-energy Fyn-SH3 TS and that the amount of amide surface buried in forming TS is ∼1.5-fold greater than the backbone amide surface buried in forming the elements of Fyn-SH3 2° structure. Our results indicate that TS may be quite close on the reaction coordinate to the intermediate characterized by Kay and coworkers. Mutant ψ-value analysis, where metal ion binding sites are introduced to probe for contacts in TS, indicates that TS for protein L (1HZ6) contains the entire (28-residue) β-sheet network (35) (and some nonnative structure) but little if any of the native (21-residue) α-helical structure. Simulations and Φ-value analysis, where the effect of Ala substitutions on TS stability are observed, indicate that TS for chymotrypsin inhibitor (2CI2) contains the 14 residues of α-helix but not the 18 residues of β-sheet of the native protein (36). The kinetic m-value/activation heat capacity analysis presented here predicts that the amide ASA buried in forming TS is comparable to the amount of backbone amide surface predicted to be buried in forming all of the 2° structure of both these proteins (Table S5). Possibly there is extensive burial of side-chain amide surface in the TS of these proteins, or possibly the mutation analyses may underestimate the amount of 2° structure in TS. Additional experiments and structural analysis (like that performed here) will be needed to distinguish between these and other explanations.

Structural models of the proposed TS ensemble for six of the proteins investigated here have been predicted from unfolding or folding simulations. These included two small all-β cold shock proteins [Bc-Csp (37), Bs-Csp (38)] and four larger mixed α/β proteins [chymotrypsin inhibitor (39, 40), HPr (41), acylphosphatase (42), and ribosomal protein S6 (43)]. Properties like radius of gyration or numbers of native and nonnative contacts are reported for U, TS, and F states, but these characteristics are not directly related to ΔASA_H and ΔASA_A. Qualitatively, these simulated TS ensembles are quite advanced on the folding pathway, in agreement with the experimentally determined results in Fig. 2 and Table S2. However, simulations in many cases predict a relatively concerted formation (or disruption) of 2° and 3° structure in folding (or unfolding) to TS, whereas analysis of the experimental data indicates that most if not all of the 2° is formed before TS in folding. ASA calculations on predicted TS and intermediate complexes from simulations will permit more detailed comparisons.

Implications for the Protein-Folding Mechanism.

The amide and hydrocarbon ASA results and structural analysis presented here provide strong experimental support for a general mechanism of protein folding in which most if not all of the native elements of secondary structure form before TS, and begin to coalesce into more native-like structures in TS, as previously proposed (2, 4, 44–46). A rapidly equilibrating mixture of largely unfolded chains with various subsets of these elements of 2° structure comprises the ensemble of early folding intermediates. Nucleating each structural element is unfavorable and propagation in the observed range of element lengths is not sufficiently favorable to make them stable so formation of each is characterized by an equilibrium constant K_i < 1; the overall equilibrium constant for forming a species with all these elements present (the putative I_ss) is the product of these K_i (K_Iss = ΠK_i). Although I_ss should be very unstable, ASA analysis of I_ss and possible TS species for 434 Cro and Bs-Csp described above indicates that I_ss is significantly less advanced than TS in terms of ASA buried, and therefore that I_ss may not be the least stable on-pathway folding intermediate before TS (i.e., I_pre). Therefore, organization of these elements of 2° structure into native-like tertiary structure begins before the TS.

In the Barrick–Sosnick analysis (2), the folding rate constant k_f = K_Iprek_transit, where K_Ipre is the equilibrium constant for forming I_pre from U and k_transit is the rate constant for the rate-determining step with TS. We conclude that K_Iss ≥ K_Ipre and that the transit step with rate constant k_transit is either (i) organization of the backbone (and side chains) of one or more of the regions that are not part of the 2° structure in the most unstable on pathway intermediate, (ii) coalescence of one or more elements of structure, or (iii) both. TS models like those in Fig. 4 with sufficient backbone organization to nucleate formation of the native 3° structure from the isolated elements of 2° structure agree with the ASA characteristics of TS.

Conclusions

The analysis of kinetic m-values and activation heat capacity changes for protein folding and unfolding presented here quantifies the changes in amide and hydrocarbon surface area (ASA) in folding to and from the highest free energy TS; this information was not obtainable by other methods. We propose that changes in amide, hydrocarbon, and total ASA are the natural reaction coordinates of protein folding. From both the kinetic and structural analyses, we conclude that TS has both the elements of 2° structure of the native protein and the organization of other regions of the backbone required to nucleate the formation of 3° structure in subsequent folding from TS. The instability of TS is the result of the instability of the individual elements of 2° structure and of nucleation of 3° structure; subsequent propagation of 3° structure formation is of course highly favorable.

In addition to its contribution to our understanding of the protein-folding mechanism, this research provides proof of concept for the use of solute m-values and heat capacity changes to probe mechanisms, determine steps with coupled folding or other large conformational changes, and quantify the amount and composition of the surface buried or exposed in these intermediates or TS, information that is difficult or impossible to obtain by other methods. An example is the mechanism of open complex formation and stabilization in transcription initiation by Escherichia coli RNA polymerase (RNAP) at a DNA promoter (47). Here, information about interactions of solutes and noncoulombic (Hofmeister) interactions of salt ions with nucleic acid functional groups is also needed; this has been obtained for urea (11, 12), and research with other solutes and salts is in progress. The small effects of urea and Hofmeister salts on the rate and equilibrium constants for the step involving opening of 13 bp of duplex promoter DNA provide evidence that RNAP opens this region in the active site cleft (14, 48, 49). The large effects of urea, glycine betaine, and different Hofmeister salts on the subsequent step(s) that stabilize the initial open complex provide evidence for large-scale coupled folding and assembly of mobile elements of RNAP to form a clamp on the downstream duplex DNA (14, 48–50). Solutes are also excellent probes of intermediates and TS for RNA folding, because burial of base ASA is disfavored by all solutes whereas burial of backbone ASA is favored by some solutes (12, 13).