Abstract
Congenic strains continue to be a fundamental resource for dissecting the genetic basis of complex traits. Traditionally, genetic variants (QTLs) that account for phenotypic variation in a panel of congenic strains are sought first by comparing phenotypes for each strain to the host (reference) strain, and then by examining the results to identify a common chromosome segment that provides the best match between genotype and phenotype across the panel. However, this ‘‘common-segment’’ method has significant limitations, including the subjective nature of the genetic model and an inability to deal formally with strain phenotypes that do not fit the model. We propose an alternative that we call ‘‘sequential’’ analysis and that is based on a unique principle of QTL analysis where each strain, corresponding to a single genotype, is tested individually for QTL effects rather than testing the congenic panel collectively for common effects across heterogeneous backgrounds. A minimum spanning tree, based on principles of graph theory, is used to determine the optimal sequence of strain comparisons. For two traits in two panels of congenic strains in mice, we compared results for the sequential method with the common-segment method as well as with two standard methods of QTL analysis, namely, interval mapping and multiple linear regression. The general utility of the sequential method was demonstrated with analysis of five additional traits in congenic panels from mice and rats. Sequential analysis rigorously resolved phenotypic heterogeneity among strains in the congenic panels and found QTLs that other methods failed to detect.
Introduction
Both genetic variants and environmental factors contribute to the multifactorial origins of phenotypic variation and disease risk. Identifying these genetic variants, which are also known as quantitative trait loci (QTLs), is key to developing diagnostic markers and drug targets as well as to understanding the molecular foundations for systems properties and organismal biology. Typically, several tasks are involved in finding these QTLs in model organisms (Abiola et al. 2003; Glazier et al. 2002; Lander and Schork 1994; Nadeau et al. 2000), the first of which involves detecting and mapping them in crosses and genetically heterogeneous populations. Although mapping sometimes resolves the QTL to a single gene or other single structural, regulatory, or functional element (e.g., Cilila et al. 2001; Fridman et al. 2000; Huberle et al. 2009; Yamanouchi et al. 2007), more often additional genetic and functional studies are needed. Therefore, the next task frequently involves isolating the QTL in congenic strains. This is often challenging because sometimes QTLs that are identified in crosses are no longer evident in congenic strains and sometimes the locus is found to involve several closely linked genetic variants with related phenotypic effects (Lauwerys and Wakeland 2005; Legare and Frankel 2000; Legare et al. 2000; Morel et al. 2001; Shultz et al. 2003). The final step in QTL analysis involves functional studies to characterize the phenotype and genetically engineered models to prove gene discovery.
A congenic strain is made by transferring a chromosome segment from a donor strain to a host strain by repeated backcrossing and selection, a process that is continued until the integrity of the host strain background has been restored (Flaherty 1981; Silver 1995; Snell 1948, 1958, 1978). Marker-assisted selection can be used to reduce the number of backcross generations (Markel et al. 1997). More recently, chromosome substitution strains (CSSs) have been used as a resource to accelerate construction of congenic strains (Moreno et al. 2007; Shao et al. 2008; Youngren et al. 2003). For many of these genetic and functional studies, panels of congenic strains rather than single strains are being made and characterized (Moreno et al. 2007; Shultz et al. 2003; Youngren et al. 2003).
Traditionally, analysis of a panel of congenic strains has tested for a single locus that fully accounts for phenotypic variation. We call this the ‘‘common-segment’’ method. The hypothesis is that strains that are phenotypically similar share the same QTL. This method, which has been used since the introduction of congenic strains (Irwin 1939; Snell 1948, 1958, 1978), has led to many important discoveries and is the foundation for many aspects of genetic research (Flaherty 1981; Silver 1995; Snell 1948, 1958, 1978). Despite its wide use however, the common-segment method has several important but often overlooked limitations. The first is that the genetic model is inherently subjective, the second is that interpretation of strains with discordant phenotypes that do not fit a simple genetic model is difficult to resolve in a formal manner, and the third is that there is no formal method for dealing with closely linked QTLs. As a result, the genetic control of complex phenotypic traits can be ambiguous and sometimes underestimated.
We propose a formal method to systematically analyze complex traits in a panel of congenic strains. This method, called sequential analysis, readily detects multiple QTLs, regardless of whether they act in an additive or epistatic manner. The method objectively deals with strains that conflict with simple genetic models by systematically testing each strain (genotype) individually for QTLs in a way that is similar to the methods for analyzing chromosome substitution strains (Belknap 2003; Nadeau et al. 2000; Shao et al. 2008; Singer et al. 2004). We demonstrate the attributes of this method with results for five traits in panels of congenic strains for three chromosomes in mice and for two traits in a panel of congenic strains in rats. In particular, we compare results of sequential analysis with those of other methods of QTL analysis, including interval mapping, multiple linear regression, and common-segment. Although results of sequential analysis were recently reported in several cases (Millward et al. 2009; Shao et al. 2008), the analytical methods are reported here for the first time.
Analytical methods
Principles of the common-segment method
Typically, a sliding window is moved along the genetic map for the complete panel of strains to identify the best match between genotype for the genetic interval and phenotype for the strain. A statistical test such as Student’s t test is used at each marker to determine whether each congenic strain differs significantly from the B6 host strain, after Bonferroni correction (p = 0.05) for multiple testing. At this location, strains with phenotypes that differ significantly from the host strain should share a chromosome segment that is derived from the donor strain, whereas strains whose phenotype does not differ from the host strain should share a chromosome segment with the host strain. In the ideal case, a single interval will show a perfect match between genotype and phenotype. In practice, discordant strains are found that do not fit a simple genetic model. To resolve these ambiguities, some results are argued, in an ad hoc manner, to be false positives or false negatives, or additional QTLs are postulated.
Principles of the sequential method
We propose a method that is based on comparing phenotypes for sequential pairs of congenic strains, beginning with the strain with the shortest congenic segment and the host strain, and then in a stepwise fashion to strains with progressively longer, overlapping congenic segments. For each strain, the size of the congenic segment is calculated as the distance between the markers derived from the host strain that immediately flank the congenic segment. The location of these markers is usually based on the most recent consensus genome sequence, which for the present purposes was the consensus sequence of the mouse and the rat genomes (www.ensembl.org).
If the phenotypes for the strain with the shortest congenic segment and the host strain differ significantly, we conclude that at least one QTL maps to the congenic segment. By contrast, if the phenotypes for the congenic strain and the host strain do not differ significantly, we conclude that the congenic segment does not have a QTL with a significant phenotypic effect. Next, the congenic strain with the next-longer, overlapping segment is compared to the previous congenic strain. If the introduced segment does not have a single QTL with a significant effect, the phenotypes for the first and second strains will not differ. By contrast, if the introduced segment has a QTL, the phenotypes for the first and second congenic strains will differ significantly, thereby assigning a QTL to the chromosome segment that differs between the two congenic strains. This process is repeated until each strain in the panel has been tested once and only once. In this study, we used Bonferroni correction to control the false-positive rate, with 0.05 as the significance threshold. Given the limited number of congenic strains that are available for most panels, permutation tests are not meaningful (Doerge and Churchill 1996).
The main task is to optimize the sequence of pairwise comparisons, while at the same time limiting the total number of comparisons so as to minimize the penalty for multiple hypothesis testing. This can be described as an optimization problem: given a set of strains (Si) and genetic differences between strains (Di,j), find a set of comparisons to minimize ∑(Di,j) and use Si at least once but no more than twice. Graph theory provides a solution because the optimal sequence is analogous to the spanning tree problem. In our graph representation, nodes correspond to strains, and edges correspond to strain comparisons. The weight of an edge is defined as the physical difference in sequence or genetic length of the congenic segment for a pair of strains. Only connected nodes are compared, and a fully connected graph represents the case of exhaustive pairwise comparisons. Optimization involves finding a directed graph starting from the root, which is the host strain, such that the sum of edge weights is minimized and that each node is visited twice only (excluding the root node) and each strain is tested against the reference strain once only.
A Minimum Spanning Tree (MST) is a solution to optimizing the sequence of strain comparisons. In this study we used Kruskal’s algorithm to find the MST (Corman et al. 2003). The pseudocode is shown in Supplementary Table 1. With the MST, sequential comparisons are then conducted from root to leaves of the tree. An MST has two advantages: First, an MST guarantees that each node is visited at most twice, which in turn minimizes the total number of comparisons and hence the penalty for multiple testing. Second, an MST is usually unique because in most cases the physical or genetic distance between any pair of strains is different from the distances in other pairwise comparisons. As a result, edges in the graph usually have different weights, a property that typically yields a unique MST.
We note that the sequential method does not make assumptions about whether the genetic control of phenotypic variation is simple (monogenic) or complex (multigenic), or results from additive versus epistatic QTL effects. We also note that with the sequential method, congenic strains that do not differ from the host strain can nevertheless provide definitive evidence for a QTL.
Special considerations are needed when multiple consecutive nonsignificant effects act in the same phenotypic direction. In these cases, the last strain in the sequence differs substantially from the first, even though the phenotypic difference between each pair of strains in the sequence is not statistically significant. These trends result from the action of multiple QTLs, each of which has a modest effect acting in the same phenotypic direction. Although comparison of strains at the ends of the phenotype distribution can be used to test for directional effects, the genetic location of the QTLs nevertheless remains ambiguous.
Interval mapping
Interval mapping has been widely used to detect QTLs underlying quantitative traits (Lander and Botstein 1989). Maximum likelihood is used to estimate the phenotypic effect and LOD score at any given genetic location for a putative QTL. If a LOD score is greater than the score corresponding to the genome-wide significance level, a QTL is claimed. In the present study, the R/qtl package (Broman et al. 2003) was used for QTL detection. At any given genomic location, only two genotypes are possible, AA or BB, and therefore each congenic strain can be treated as a recombinant inbred (RI) strain. The recombinant inbred line (RIL) cross scheme in R/qtl therefore was adopted to analyze panels of congenic strains.
Multiple QTL mapping with a multiple linear regression model
We fit a multiple linear regression model to our data. Suppose we have M markers and N strains. Consider a regression Y = Xβ, where Y is the trait value, X represents markers with −1 as genotype A and +1 as genotype B. βm is the parameter we try to fit for marker m; it measures the contribution of m to the variation of the trait values, with each genetic marker treated as an independent variable (feature). Here, QTL mapping is viewed as a feature (model) selection problem. Given a data set, the problem is dissecting a subset of variable X (markers) so that they can reasonably explain the phenotypic variation across a set of congenic strains. Selected markers are considered QTLs. We used least angle regression (LAR) to fit the model (Efron et al. 2004) and the Cp statistic or cross validation was used to determine the number of selected markers.
The purpose of feature (model) selection with linear regression is to choose a linear model such that the chosen variables (markers) efficiently predict the trait values. The difficulty is to determine the tuning parameters of the objective function. For instance, in least shrinkage and selection operator (Lasso; Tibshirani 1996), the Lasso estimate (B) is subject to Σ B ≤ t, where t ≥ 0 is a tuning parameter. Although cross validation can be used for estimating t, a large number of observations are usually required. In LAR, at each step the algorithm adds one variable (marker); if it stops at step K, then K markers are selected, hence K QTLs are identified. A Cp-type statistic can be used to estimate the prediction error and select the subset of K markers. Cross validation can also be used to select K markers. As our results show, the MLR has uncertainty to select the optimal set of variables, thus QTL identification.
Congenic strains and phenotypes
Panels of congenic strains
For the mouse, a panel of 15 congenic strains was derived from the C57BL/6J-Chr6A/J/NaJ chromosome substitution strain (CSS-A6, Shao et al. 2008), a panel of 9 congenic strains was derived from the C57BL/6J-Chr10A/J/NaJ chromosome substitution strain (CSS-A10; Shao et al. 2008), and a panel of 7 congenic strains was derived from C57BL/6J-Chr13A/J/NaJ (CSS-A13; Nathan et al. 2006). Each panel collectively spans the length of the chromosome, and the congenic segments are bounded on one end by a telomere, except for the 6C15 and 13C25 strains. Details about the construction of the CSS-A6 and CSS-A10 panels can be found in a recent publication (Shao et al. 2008) and well as that for CSS-A13 (Fig. 1f, g, cf. Nathan et al. 2006). For the rat, the panel composed of 23 SS-13BN congenic strains was reported previously (Moreno et al. 2007).
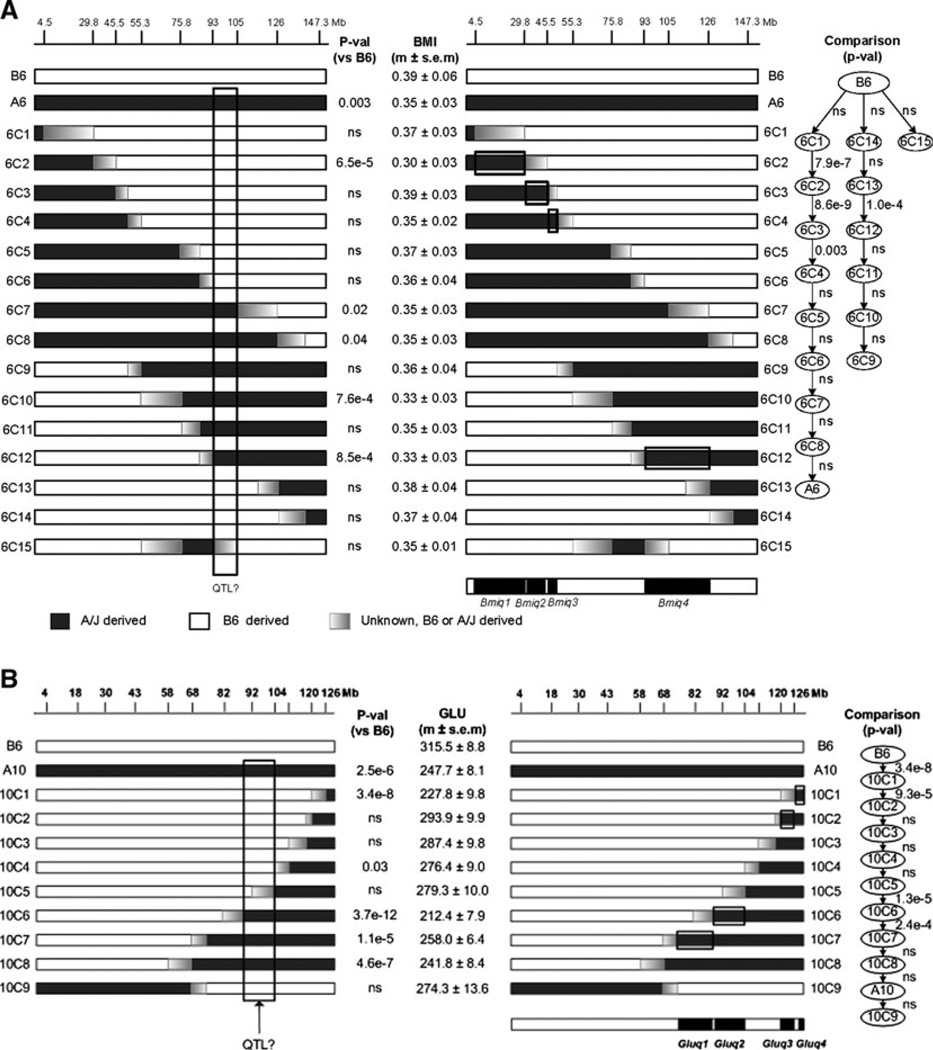
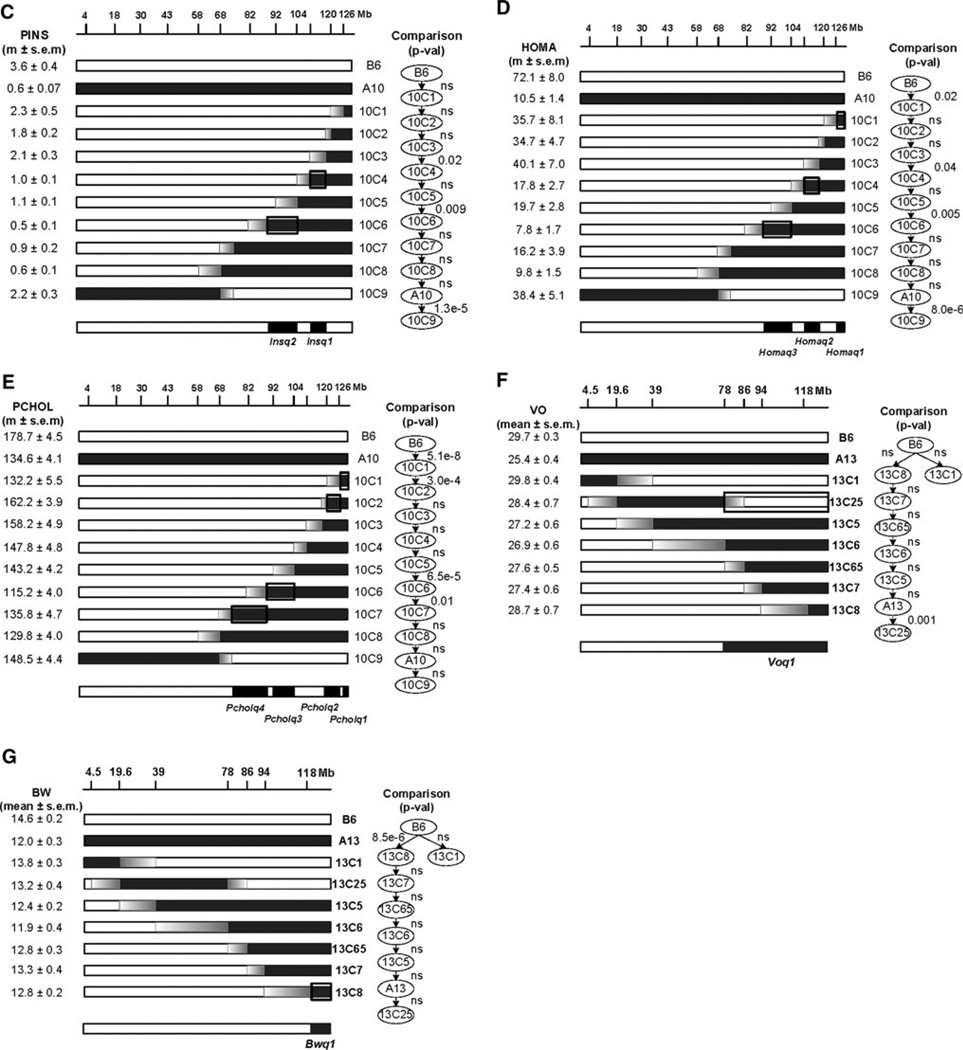
Fig. 1.
Comparison of congenic strain analysis with common-segment and sequential methods for traits related to diet-induced obesity. Results for each method are provided for each congenic panel and trait, with results for the common-segment provided on the left and that for the sequential method on the right. Sample sizes are provided in the Methods section. Selected genetic markers with their approximate locations in the DNA sequence (Mb coordinates) are provided above the map for each chromosome; the complete map of genetic markers is provided in the original publications for chromosomes 6 and 10 (Shao et al. 2008) and in Supplementary Table 2 for chromosome 13. The congenic strains are identified as #C# where the first number (#) refers to the chromosome number, C refers to congenic, and the second # refers to the unique congenic strain designation. The maps for the congenic strains are highlighted in white for segments that are derived from the host strain and in black from the donor strain. The intervals between the genetic markers that define the boundaries of the recombination breakpoints are graded from white to black to emphasize the uncertainty about the location of the crossover. Trait values (mean ± SEM) are listed between the two analyses. p values are also provided for each analysis, with p-val (vs. C57BL/6J) for the common-segment method and P-val for each strain comparison for the sequential method included with the Minimum Spanning Tree (MST). In all cases, studywide p values are reported after correction for multiple hypothesis testing. a Body mass index (Bmiq) in congenic strains from CSS-A6. b Blood glucose levels (Gluq) in congenic strains from CSS-A10. c Plasma insulin (Insq) for the CSS-A10 congenic panel. d HOMA (Homaq) for the CSS-A10 congenic panel. e Plasma cholesterol (Pcholq) for the CSS-A10 congenic panel. f Age (days) at vaginal opening (Voq) for the CSS-A13 congenic panel. g Body weight at vaginal opening (Bwvoq) for the CSS-A13 congenic panel
Sample sizes
Sample sizes for the chromosome 6 study: C57BL/6J (29), CSS-A6 (21), 6C1 (15), 6C2 (29), 6C3 (26), 6C4 (27), 6C5 (25), 6C6 (26), 6C7 (25), 6C8 (23), 6C9 (26), 6C10 (25), 6C11 (27), 6C12 (25), 6C13 (24), 6C14 (22), and 6C15 (39); sample sizes for the chromosome 10 study: C57BL/6J (40), CSS-A10 (40), 10A1 (40), 10A2 (39), 10A3 (40), 10A4 (40), 10A5 (40), 10A6 (40), 10A7 (39), 10A8 (40),and 10A9 (38); and samples sizes for the chromosome 13 study: 13C1 (27), 13C25 (16), 13C5 (23), 13C6 (15), 13C65 (20), 13C7 (18), and 13C8 (23).
Phenotype assays
Methods for plasma insulin, homeostatic model assessment (HOMA), and plasma cholesterol are described in Shao et al. (2008) and those for measuring mean arterial pressure are described in Moreno et al. (2007). Females were examined daily between 0800 and 1300 h, and the age (days) and weight (g) at vaginal opening were recorded (Nathan et al. 2006).
For the CSS-A6 and CSS-A10 congenic panels, we focused on five traits related to diet-induced obesity and metabolic disease. Males from the two congenic panels as well as the C57BL/6J (host) and A/J (donor) strains were weaned at 3 weeks of age. Then at 35 days of age they were placed on either a high-fat, simple-carbohydrate diet or a low-fat, complex-carbohydrate for approximately 100 days, at which point they were weighed and sacrificed and various metabolic traits measured (Shao et al. 2008). We focused on body mass index (BMI) for the CSS-A6 panel and blood glucose and insulin levels as well as HOMA for the CSS-A10 panel. Details about assay methods and phenotype results have been published (Shao et al. 2008).
We also studied timing of puberty (age at vaginal opening, VO) and body weight (BW) at VO for females from the CSS-A13 strain and the seven congenic strains in the CSS-A13 panel. Details about assay methods and about construction of the congenic strains can be found in Nathan et al. (2006).
Finally, in rats we examined mean arterial pressure (MAP) in a panel of congenic strains derived from the SS-13BNCSS (Moreno et al. 2007). The rats were raised on a purified AIN76 diet containing 0.4% NaCl (Dyets Inc., Allentown, PA). Experimental rats were switched to an 8.0% NaCl diet at 10 weeks of age, and 2 weeks after a microrenathane catheter was implanted in the left femoral artery for measurement of arterial blood pressure. After a 2-day recovery period, heart rate and systolic, diastolic, and mean arterial pressure were recorded for three consecutive days and averaged. A urine sample was collected for 24 h during the second day of recording for measurement of urine total protein and albumin excretion (Moreno et al. 2007).
Results
Comparing the four methods for two traits in two congenic panels
To assess the relative merits of the common-segment, interval mapping, multiple linear regression, and sequential methods, we focused on body mass index (BMI) in the CSS-A6 panel of congenic strains and glucose (GLU) in the CSS-A10 panel.
BMI in the CSS-A6 congenic panel
BMI differed significantly between C57BL/6J and CSS-A6 (Fig. 1a), demonstrating at least one QTL on the substituted chromosome. The 15 strains in the CSS-A6 panel were studied to establish the number and location of these BMI QTLs (Bmiq).
The common-segment method failed to identify a single interval that provided unambiguous evidence for a QTL that accounts for the phenotypic variation in BMI among C57BL/6J CSS-A6 and the congenic panel (Fig. 1a). To illustrate the difficulties, we highlight a candidate QTL location that provided the best match between genotype and phenotype (BMI). Although 12 of 15 strains fit a single-QTL model, three strains (6C2, 6C9, and 6C11) had discordant phenotypes. According to the candidate QTL location, the BMI for congenic strain 6C2 was significantly less than expected, whereas the BMI for strains 6C9 and 6C11 were significantly higher than expected. Similar discordances were found with alternative candidate locations for the QTL.
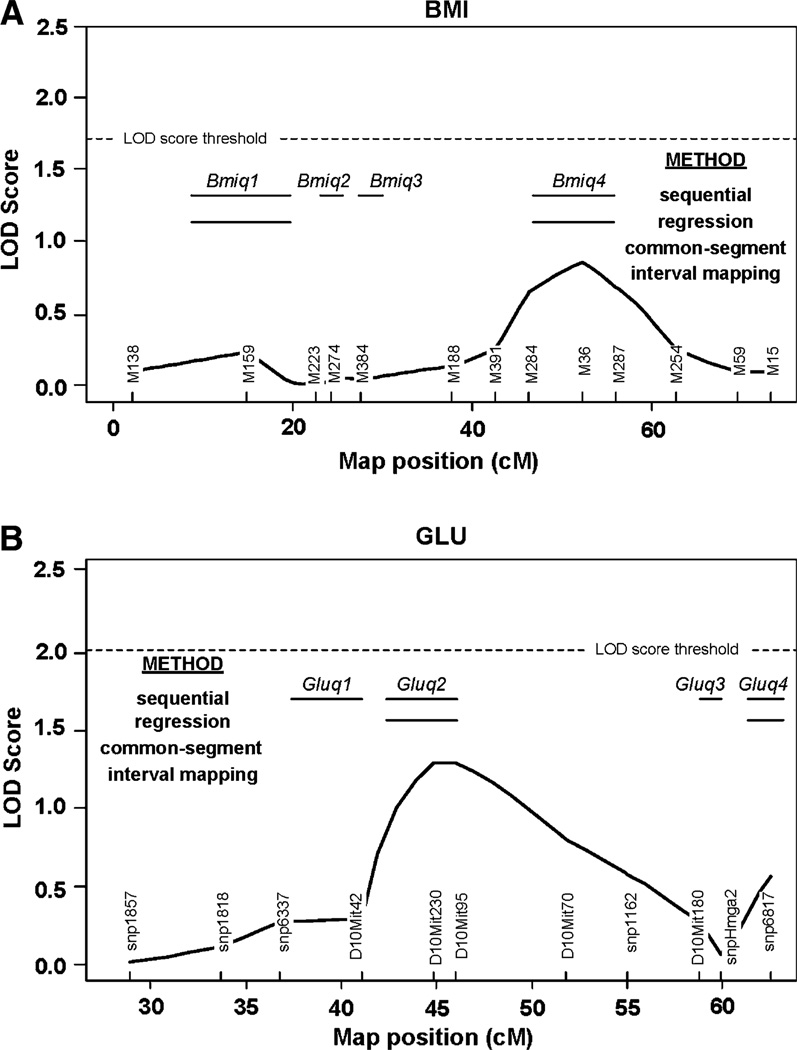
Interval mapping was then carried out with the R/qtl package. For each trait, the estimated significant LOD score threshold was based on 1000 permutation tests. The threshold was 1.71 for BMI and 2.07 for GLU. For BMI, the peak of the LOD curve was around marker M36 with a LOD score of 0.85 (Fig. 2a). Because it is less than the threshold value of 1.71, no QTL was detected by the interval mapping.
Fig. 2.
Comparison of QTL mapping results for BMI and GLU with common-segment, interval mapping, MLR, and sequential methods. Each method is aligned with the QTLs identified by that particular method. LOD score (y axis) is for interval mapping only. The dotted line represents the significance LOD score threshold in the interval mapping and the black line represents the LOD curve. The bars denote the location of QTLs based on sequential analysis of the congenic strains, with the short red bar showing the QTLs identified with the sequential method and the green bar the QTLs identified with MLR. Absence of a bar indicates that a QTL with a significant phenotypic effect was not found at that locus. a Body mass index (BMI) in congenic strains derived from CSS-A6. Additional details about methods and results can be found in the original publication (Shao et al. 2008). b Blood glucose levels (GLU) in congenic strains derived from CSS-A10. Additional details about methods and results can be found in the original publication (Shao et al. 2008)
Multiple linear regression (MLR) was implemented with the R/LARS package. Tenfold cross validation was used to determine K, the number of markers to select. Let Rss be the residual sum of squares and Rss_0 be the response values, then R2 = 1 – Rss/Rss_0 can be considered the proportion of variation explained by the selected markers. For BMI, MLR chose markers M36 and M159, with R2 = 0.22. Therefore, MLR identified two QTLs, near markers M36 and M159, which were also identified as Bmiq4 and Bmiq1 with the sequential method (see below). However, the R2 of 0.22 implied that these two QTLs explained only a small portion of BMI variation among these strains. Indeed, LAR missed QTLs Bmiq2 and Bmiq3. We also calculated the Cp statistic to determine the number of selected markers. The minimal Cp statistic occurred at step K = 12, indicating that all markers should be included; in other words, the entire chromosome is one QTL. Therefore the Cp statistic did not provide useful information to identify QTL locations.
The sequential method by contrast provided unambiguous evidence for four QTLs (Bmiq1–4) on chromosome 6 (Figs. 1A, 2A). The BMI for strain 6C2 was significantly less than that for 6C1, demonstrating that a QTL (Bmiq1) is located between the markers at 4.5 and 29.8 Mb in the congenic segment that differs between these two strains. Interestingly, the BMI for 6C3 was significantly greater than that for 6C2, indicating that a second QTL (Bmiq2) must be located in the interval between the markers at 29.8 and 45.5 Mb that is unique to 6C3. Comparing BMIs for 6C4 with 6C3 revealed a third QTL (Bmiq3) between markers at 45.5 and 55.3 Mb. Finally, the BMI for 6C12 was significantly less than that for 6C13, providing evidence for the fourth QTL (Bmiq4) between markers at 93 and 126 Mb. A unique attribute of the sequential method is that strains such as 6C3 and 6C4, which did not differ phenotypically from C57BL/6J, nevertheless provided unambiguous evidence for QTLs (Bmiq2 and Bmiq3) that were not detected with the other three methods, common-segment, interval mapping, and linear regression. Thus, the sequential method reliably resolved interpretation of each strain in the panel and in particular accounted for the seemingly exceptional phenotypes.
GLU in the CSS-A10 congenic panel
Glucose levels differed significantly between C57BL/6J and CSS-A10, indicating at least one QTL (Gluq) on the substituted chromosome 10 (Fig. 1b).
The common-segment method failed to provide an unambiguous location for this QTL (Fig. 1b). Although seven of the nine strains provided a strong candidate location, both congenic strains 10C1 and 10C4 had significantly lower than expected glucose levels according to a single-QTL model. The common-segment method does not have an easy explanation for these conflicting results.
The LOD curve from the interval mapping method peaked between D10Mit230 and D10Mit95, with a LOD score of 1.3 (Fig. 2b). Because this score was lower than the threshold value of 2.07, interval mapping did not detect a statistically significant effect on GLU.
MLR identified markers D10Mit230 and snp6817 with tenfold cross validation. These two markers corresponded to two of the QTLs identified with the sequential method, Gluq2 and Gluq4. The corresponding R2 was 0.45, which provided little evidence for a QTL.
The sequential method provided unambiguous evidence for four QTLs (Gluq1–4) on substituted chromosome 10 (Fig. 1b). The significant difference between 10C1 and C57BL/6J shows that a QTL (Gluq4) is located in the A/J-derived segment in the 10C1 strain. Similarly, the significantly elevated glucose level in 10C2 versus that in 10C1 demonstrates a QTL (Gluq3) in the congenic segment that is unique to the 10C2 strain, between markers at 120 and 126 Mb. The reduced glucose level in 10C6 versus 10C5 is evidence for a third QTL (Gluq2) between markers at 92 and 104 Mb. Finally, the elevated glucose level in 10C7 versus 10C6 demonstrates the fourth QTL (Gluq1) between markers at 68 and 92 Mb. Again, the sequential method detected two QTLs (Gluq1 and Gluq3) that were not detected with the other methods (Fig. 2b).
With these results we conclude that the sequential method performs better than the common-segment, interval mapping, and multiple linear regression methods. Reasons for these contrasting results are considered in the Discussion section.
Comparing results for the sequential method with published reports
The utility of the sequential method is highlighted with a reanalysis of MAP for females and males from a panel of 23 congenic strains involving chromosome 23 from the rat SS strain as host and the BN strains as donor (Moreno et al. 2007; see also Supplementary Table 2A and B for data and analysis, 2C for marker locations, and Supplementary Fig. 1 for the MST).
The common-segment method identified four QTLs for mean arterial pressure (MAP) in the SS-13BN panel of rat congenic strains with reasonable empirical support, but also with several ambiguities (Moreno et al. 2007).
For the sequential method, the complexity of this panel of strains is illustrated with its MST, with ten tips of the tree and the longest branch having six nodes (Supplementary Fig. 1A). For females, the sequential method identified three QTLs (Supplementary Table 2A). The first QTL coincided precisely with the QTL reported in the original study. This QTL is located telomeric to marker Rat111 and is responsible for the significant reduction in MAP in congenic strain B13C1 relative to the SS reference strain. The second QTL, which significantly reduces MAP in B13C5 relative to B13C6, was mapped to a similar but smaller interval as the QTL in the original study; the sequential method maps this QTL to the interval between markers Rat60 and Rat20 rather than between markers Rat60 and Rat 91. The third QTL, which significantly reduced MAP in B13C18 relative to B13C14, was mapped to a similar but smaller interval than was reported originally; the sequential method reduced the QTL from the interval between markers Rat77 and Rat83 to the interval between Rat61 and Rat197. The sequential method did not detect significant evidence for the fourth QTL that was reported in the original study between markers Rat88 and Rat127.
For males, the sequential method identified two QTLs (Supplementary Fig. 2B), one located between markers Rat60 and Rat20 and the second between markers Got45 and Rat19. Both QTLs significantly reduced MAP.
Analyzing five traits in two mouse congenic panels with sequential analysis
Insulin (INS) in the CSS-A10 congenic panel
The INS level in CSS-A10 was reduced sixfold compared to that in C57BL/6J (Fig. 1c), indicating that at least one INS QTL (Insq) is located on chromosome 10. The sequential method provided compelling evidence for two QTLs (Insq1 and Insq2) (Fig. 1c). The significant difference between 10C3 and 10C4 provides evidence for Insq1 between markers at 104 and 120 Mb. Similarly, the difference between the 10C5 and 10C6 shows that Insq2 is located in the segment between 92 and 104 Mb, which differs between these strains.
HOMA in the CSS-A10 congenic panel
The HOMA level in CSS-A10 was significantly reduced relative to that in C57BL/6J, suggesting at least one QTL (Homaq) on chromosome 10 (Fig. 1d). The sequential method showed strong evidence for three QTLs (Homaq1–3). The 10C1 versus C57BL/6J comparison shows that Homaq1 is located in the most telomeric interval, telomeric to the marker at 126 Mb. The significantly lower HOMA in 10C4 versus 10C3 shows that Homaq2 is located in the chromosome segment between markers at 104 and 118 Mb, which is unique between these two strains. The still lower HOMA in 10C6 versus 10C5 shows that Homaq3 is located in the unique chromosome segment in the 10C6 strain, between markers 82 and 103 Mb. Finally, CSS-A10 and 10C9 differed significantly, suggesting QTL effects distal to the marker at 68 Mb. The most parsimonious interpretation is that the combined action of the C57BL/6J-derived alleles of Homaq1–3 accounts for the significant increase in HOMA in 10C9 versus CSS-A10, although these combined effects do not appear to be additive.
Plasma cholesterol (Pchol) in the CSS-A10 panel
The plasma cholesterol levels in CSS-A10 and C57BL/6J differed significantly, indicating that at least one Pcholq QTL is located on chromosome 10 (Fig. 1e). The sequential method provided unambiguous evidence for four QTLs (Pcholq1–4). The significant difference between 10C1 and C57BL/6J shows that Pcholq1 is located in the segment distal to the marker at 126 Mb. The significantly higher plasma cholesterol level for 10C2 compared with that for 10C1 shows that a second QTL (Pcholq2) is located in the segment that is unique to the 10C2 strain between markers at 120 and 126 Mb. Evidence for the third QTL (Pcholq3, between markers at 82 and 103 Mb) is found in the significantly lower cholesterol level between the 10C5 and 10C6 strains. Finally, the difference between the 10C7 and 10C6 strains shows that the fourth QTL (Pcholq4), which significantly increases cholesterol level, is located between markers at 67 and 89 Mb. Together these four QTLs account for a considerable portion of the heterogeneity in cholesterol level among the panel of congenic strains for chromosome 10.
Vaginal opening (VO) in the CSS-A13 congenic panel
The age (in days) at vaginal opening in pubertal females differed significantly for the CSS-A13 and C57BL/6J strains, demonstrating at least one VO QTL (Voq) on chromosome 13. Only the 13C25 versus CSS-A13 comparison provided a statistically significant result, suggesting that Voq is located in the A/J-derived interval distal to the marker at 78 Mb (see Supplementary Table 3 for marker locations).
Body weight (BW) at VO in females from the CSS-A13 congenic panel
Body weight at VO also differed significantly between CSS-13 and C57BL/6J females, indicating at least one ‘‘BW at VO’’ QTL (Bwvoq) on chromosome 13 (Fig. 1g). Only one comparison was significant, 13C8 vs. C57BL/6J, which maps Bwvoq1 to the most telomeric interval distal to the marker at 118 Mb (Fig. 1g).
Discussion
An important challenge in genetics is discovering and characterizing the basis for phenotypic variation and common diseases. With new high-throughput genotyping and sequencing technologies, increasingly powerful analytical algorithms, and availability of phenotypically and clinically characterized populations, these studies are beginning to yield insights into disease genetics, protein functions, regulatory controls, and the associated systems networks and pathways (Altschuler et al. 2008; Hirschhorn 2009; Manolio et al. 2008; Zhu et al. 2008). Despite significant progress, however, genetic heterogeneity among populations and limited statistical power continue to challenge QTL discovery. As a result, the genetic architecture of complex traits tends to be inadequately understood (cf. Kruglyak 2008; Manolio et al. 2009; Shao et al. 2008).
For both gene discovery and functional analysis, model organisms continue to provide an important complement to studies in humans. Traditional strategies use standard crosses or small panels of recombinant inbred or recombinant congenic strains that in general have limited power and resolution. Several new and powerful strategies are now available for dissecting complex traits, including heterogeneous stocks and advanced intercrosses, large panels of recombinant inbred strains, complementation/ deletion strains, chromosome substitution strains, and panels of congenic strains (Churchill et al. 2004; Flint and Mott 2008; Iakoubova et al. 2001; Nadeau et al. 2000). Congenic strains are becoming increasingly important, in part because they can be readily constructed from the increasing number of chromosome substitution strains that are being made (Gregorová et al. 2008; Matin et al. 1999; Moreno et al. 2007; Singer et al. 2004; Takada et al. 2008). Subcongenic and sub-subcongenic strains derived from congenic strains that define the QTL will be a powerful way to rapidly and reliably identify genetic variants that are responsible for QTL effects. Therefore, robust methods are needed for QTL analysis of complex traits in congenic strains.
We began by comparing the attributes of four methods of QTL analysis in congenic strains, namely, interval mapping, multiple linear regression, common-segment, and sequential analysis. Probably because of the limited number of congenic strains in the two panels, interval mapping failed to find QTLs with statistically significant phenotypic effects. Multiple linear regression identified four QTLs but failed to identify four others. Common-segment identified strains that differed significantly from the C57BL/6J host (reference) strain but failed to find a shared chromosome interval with a perfect match between genotype and phenotype, with the exceptional strains leading to uncertainty about the proper explanation. By contrast, sequential analysis found a total of eight QTLs, including four QTLs, two for each trait, that were not found with any other analytical method. We propose that these QTLs were detected because sequential analysis tested each of the critical strains individually relative to the contrast strain, thereby revealing QTLs whose phenotypic effects were often dependent on the action of closely linked QTLs. Ongoing gene discovery studies clearly show that QTLs are indeed present at the locations identified with sequential analysis (Nadeau et al. unpublished).
Considerable phenotypic heterogeneity among congenic strains often leads to discordances with simple genetic models. Usual explanations for these exceptions include false-negative or false-positive assay results, undetected double crossovers, additional QTLs, or other unresolved genetic complexities. The common-segment method does not readily deal with discordant strains, largely because phenotypes for the congenic strains are interpreted relative to each other even though the statistical tests compare the congenic strains with reference strain. In addition, interval mapping and multiple linear regression focus on the panel of strains as a population rather than explicitly testing the attributes of individual strains. To resolve this dilemma, direct tests among congenic strains are needed, as is done with sequential analysis.
The nature of study populations together with their associated methods of QTL analysis provides contrasting insights into the genetics of complex traits. Interval mapping and marker regression, as well as common-segment, test for average effects across heterogeneous genetic backgrounds. The detected QTLs tend to have relatively strong, additive effects that are largely independent of genetic background. By contrast, sequential analysis tests individual genotypes for QTL effects. This approach shares important similarities with the ways that panels of CSSs are analyzed (Belknap 2003; Nadeau et al. 2000; Singer et al. 2004). CSSs enable adequately powered genome surveys in which genome segments (chromosomes) are independently tested for QTLs that affect the trait of interest on a defined and constant genetic background. In this way, statistically robust conclusions can be made about phenotypes associated with individual genotypes. Thus, congenic strains analyzed with the sequential method provide similar insights about individual, often context-dependent genetic effects, whereas segregating populations tested with conventional analytical methods estimate the magnitude of QTL effects that tend to be independent of genetic background.
Obtaining strong evidence for closely linked QTLs is a major challenge in complex trait analysis. Segregating populations sometimes provides evidence (e.g., Lauwerys and Wakeland 2005; Legare and Frankel 2000; Legare et al. 2000; Millward et al. 2009; Morel et al. 2001; Shao et al. 2008; Shultz et al. 2003), but more usually confidence intervals are wide and evidence for independent effects is weak. These difficulties arise in part because obtaining sufficient crossovers to distinguish individual QTL effects is logistically difficult, and in part because the phenotypic effects of one QTL may obscure the effects of others either because of epistasis or because the additive actions of one QTL obscure the actions of other closely linked QTLs (Matin et al. 1999; Youngren et al. 2003). As a result, the genetic complexity of traits can be underestimated. By contrast, as we demonstrate in this report (see also Shao et al. 2008), sequential analysis readily detects effects of closely linked QTLs in congenic panels, with Bmiq3 and Bmiq4 (Fig. 1a), Gluq1 and Gluq3 (Fig. 1b), Pcholq2 and Pcholq4 (Fig. 1e) as examples. By testing for context-dependent effects in individual congenic strains, these QTLs are readily detected and mapped in genetically defined strains that can in turn be used immediately to identify the underlying genetic variant.
With the growing focus on the genetic and functional characterizations of complex traits, dissecting QTLs effects and discovering their underlying genetic basis is an important task. However, the emerging picture of complex traits reveals a large number of closely linked QTLs that act in an additive or epistatic manner depending on genetic background (Brem and Kruglyak 2005; Fawcett et al. 2008; Kenney-Hunt et al. 2008; Kroymann and Mitchell-Olds 2005; Kruglyak 2008; Pomp et al. 2008; Shao et al. 2008; Sinha et al. 2008; Steinmetz et al. 2002; Youngren et al. 2003). Sequential analysis of panels of congenic strains is therefore a significant advance in complex trait analysis.
Supplementary Material
Acknowledgments
The authors thank Richard J. Roman, Andrew S. Greene, Mary L. Kaldunski, and Jozef Lazar for their contributions to the rat studies. This work was supported in part by NIH grants CA75056, CA116867, and RR12305 to JHN, grants HL54998 and HL82798 to AJC and HJJ, and grant HD048960 to MRP. DSS was supported by a fellowship from the Canadian Diabetes Association.
Footnotes
Electronic supplementary material The online version of this article (doi:10.1007/s00335-010-9267-5) contains supplementary material, which is available to authorized users.
Contributor Information
Haifeng Shao, Email: hxs61@case.edu, Department of Genetics, Case Western Reserve University School of Medicine, 10900 Euclid Avenue, Cleveland, OH 44106, USA.
David S. Sinasac, Department of Genetics, Case Western Reserve University School of Medicine, 10900 Euclid Avenue, Cleveland, OH 44106, USA
Lindsay C. Burrage, Department of Genetics, Case Western Reserve University School of Medicine, 10900 Euclid Avenue, Cleveland, OH 44106, USA
Craig A. Hodges, Department of Pediatrics, Rainbow Babies and Children’s Hospital and Case Western Reserve University School of Medicine, Cleveland, OH, USA
Pamela J. Supelak, Department of Pediatrics, Rainbow Babies and Children’s Hospital and Case Western Reserve University School of Medicine, Cleveland, OH, USA
Mark R. Palmert, Department of Pediatrics, Rainbow Babies and Children’s Hospital and Case Western Reserve University School of Medicine, Cleveland, OH, USA
Carol Moreno, Department of Physiology, Medical College of Wisconsin, Milwaukee, WI 53226, USA.
Allen W. Cowley, Jr., Department of Physiology, Medical College of Wisconsin, Milwaukee, WI 53226, USA
Howard J. Jacob, Department of Physiology, Medical College of Wisconsin, Milwaukee, WI 53226, USA
Joseph H. Nadeau, Email: jhn4@case.edu, Department of Genetics, Case Western Reserve University School of Medicine, 10900 Euclid Avenue, Cleveland, OH 44106, USA.
References
- Abiola O, Angel JM, Avner P, Bachmanov AA, Belknap JK, et al. The nature and identification of quantitative trait loci: a community’s view. Nat Rev Genet. 2003;4:911–916. doi: 10.1038/nrg1206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschuler D, Daly MJ, Lander ES. Genetic mapping in human disease. Science. 2008;322:881–888. doi: 10.1126/science.1156409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belknap JK. Chromosome substitution strains: some quantitative considerations for genome scans and fine mapping. Mamm Genome. 2003;14:723–732. doi: 10.1007/s00335-003-2264-1. [DOI] [PubMed] [Google Scholar]
- Brem RB, Kruglyak L. The landscape of genetic complexity across 5, 700 gene expression traits in yeast. Proc Natl Acad Sci U S A. 2005;102:1572–1577. doi: 10.1073/pnas.0408709102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broman KW, Wu H, Sen S, Churchill GA. R/qtl: QTL mapping in experimental crosses. Bioinformatics. 2003;19:889–890. doi: 10.1093/bioinformatics/btg112. [DOI] [PubMed] [Google Scholar]
- Churchill GA, Airey DC, Allayee H, Angel JM, Attie AD, et al. The collaborative cross, a community resource for the analysis of complex traits. Nat Genet. 2004;36:1133–1137. doi: 10.1038/ng1104-1133. [DOI] [PubMed] [Google Scholar]
- Cilila GT, Garrett MR, Lee SJ, Liu J, Rapp JP. High-resolution mapping of the blood pressure QTL on chromosome 7 using Dahl rat congenic strains. Genomics. 2001;72:51–60. doi: 10.1006/geno.2000.6442. [DOI] [PubMed] [Google Scholar]
- Corman T, Leiseson C, Rivest R, Stein C. Introduction to algorithms. 3rd edn. New York: McGraw-Hill; 2003. [Google Scholar]
- Doerge RW, Churchill GA. Permutation tests for multiple loci affecting a quantitative character. Genetics. 1996;142:285–294. doi: 10.1093/genetics/142.1.285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B, Hastie T, Johnstone I, Tibshirani R. Least angle regression. Ann Stats. 2004;32:407–499. [Google Scholar]
- Fawcett GL, Roseman CC, Jarvis JP, Wang B, Wolf JB, et al. Genetic architecture of adiposity and organ weight using combined generation QTL analysis. Obesity. 2008;16:1861–1868. doi: 10.1038/oby.2008.300. [DOI] [PubMed] [Google Scholar]
- Flaherty L. In: the mouse in biomedical research, Vol. 1. History, genetics, and wild mice. New York: Academic Press; 1981. Congenic strains; pp. 215–222. [Google Scholar]
- Flint J, Mott R. Applying mouse complex-trait resources to behavioural genetics. Nature. 2008;456:724–727. doi: 10.1038/nature07630. [DOI] [PubMed] [Google Scholar]
- Fridman E, Pleban T, Zamir D. A recombination hotspot delimits a wild-species quantitative trait locus for tomato sugar content to 484 bp within an invertase gene. Proc Natl Acad Sci U S A. 2000;97:4718–4723. doi: 10.1073/pnas.97.9.4718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glazier AM, Nadeau JH, Aitman TJ. Finding genes that underlie complex traits. Science. 2002;298:2345–2349. doi: 10.1126/science.1076641. [DOI] [PubMed] [Google Scholar]
- Gregorová S, Divina P, Storchova R, Trachtulec Z, Fotopulosova V, et al. Mouse consomic strains: exploiting genetic divergence between Mus m. musculus and Mus m. domesticus subspecies. Genome Res. 2008;18:509–515. doi: 10.1101/gr.7160508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirschhorn JN. Genomewide association studies—illuminating biologic pathways. N Engl J Med. 2009;360:1699–1701. doi: 10.1056/NEJMp0808934. [DOI] [PubMed] [Google Scholar]
- Huberle A, Beyeen AD, Ockinger J, Ayturan M, Jagodic M, et al. Advanced intercross line mapping suggests that ncf1 (ean6) regulates severity in an animal model of Guillain-Barre syndrome. J Immunol. 2009;182:4432–4438. doi: 10.4049/jimmunol.0803847. [DOI] [PubMed] [Google Scholar]
- Iakoubova OA, Olsson CL, Dains KM, Ross DA, Andalibi A, et al. Genome-tagged mice (GTM): two sets of genome-wide congenic strains. Genomics. 2001;74:89–104. doi: 10.1006/geno.2000.6497. [DOI] [PubMed] [Google Scholar]
- Irwin MR. A genetic analysis of species differences in Columbidae. Genetics. 1939;24:709–721. doi: 10.1093/genetics/24.5.709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kenney-Hunt JP, Wang B, Norgard EA, Fawcett G, Falk D, et al. Pleiotropic patterns of quantitative trait loci for seventy murine skeletal traits. Genetics. 2008;178:2275–2288. doi: 10.1534/genetics.107.084434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kroymann J, Mitchell-Olds T. Epistasis and balanced polymorphism influencing complex trait variation. Nature. 2005;435:95–98. doi: 10.1038/nature03480. [DOI] [PubMed] [Google Scholar]
- Kruglyak L. The road to genome-wide association studies. Nat Rev Genet. 2008;9:314–318. doi: 10.1038/nrg2316. [DOI] [PubMed] [Google Scholar]
- Lander ES, Botstein D. Mapping mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics. 1989;121:185–199. doi: 10.1093/genetics/121.1.185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lander ES, Schork NJ. Genetic dissection of complex traits. Science. 1994;30:2037–2048. doi: 10.1126/science.8091226. [DOI] [PubMed] [Google Scholar]
- Lauwerys BR, Wakeland EK. Genetics of lupus nephritis. Lupus. 2005;14:2–12. doi: 10.1191/0961203305lu2052oa. [DOI] [PubMed] [Google Scholar]
- Legare ME, Frankel WN. Multiple seizure susceptibility genes on chromosome 7 in SWXL-4 congenic mouse strains. Genomics. 2000;70:62–65. doi: 10.1006/geno.2000.6368. [DOI] [PubMed] [Google Scholar]
- Legare ME, Bartlett FS, Frankel WN. A major effect QTL determined by multiple genes in epileptic EL mice. Genome Res. 2000;10:42–48. [PMC free article] [PubMed] [Google Scholar]
- Manolio TA, Brooks LD, Collins FS. A HapMap harvest of insights into the genetics of common disease. J Clin Invest. 2008;118:1590–1605. doi: 10.1172/JCI34772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, et al. Finding the missing heritability of complex diseases. Nature. 2009;461:747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markel P, Shu P, Ebeling C, Carlson GA, Nagle DL, et al. Theoretical and empirical issues for marker-assisted breeding of congenic mouse strains. Nat Genet. 1997;17:280–284. doi: 10.1038/ng1197-280. [DOI] [PubMed] [Google Scholar]
- Matin A, Collin GB, Asada Y, Varnum D, Nadeau JH. Susceptibility to testicular germ-cell tumors in a 129.MOLF-Chr 19 chromosome substitution strain. Nat Genet. 1999;23:237–240. doi: 10.1038/13874. [DOI] [PubMed] [Google Scholar]
- Millward CA, Burrage LC, Shao H, Sinasac DS, Kawasoe JH, et al. Genetic factors for resistance to diet-induced obesity and associated metabolic traits on mouse chromosome 17. Mamm Genome. 2009;20:71–82. doi: 10.1007/s00335-008-9165-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morel L, Blenman KR, Croker BP, Wakeland EK. The major murine systemic lupus erythematosus susceptibility locus, Sle1, is a cluster of functionally related genes. Proc Natl Acad Sci U S A. 2001;98:1787–1792. doi: 10.1073/pnas.031336098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreno C, Kaldunski ML, Wang T, Roman RJ, Greene AS, et al. Multiple blood pressure loci on rat chromosome 13 attenuate development of hypertension in the Dahl S hypertensive rat. Physiol Genomics. 2007;31:228–235. doi: 10.1152/physiolgenomics.00280.2006. [DOI] [PubMed] [Google Scholar]
- Nadeau JH, Singer JB, Matin A, Lander ES. Analyzing complex genetic traits with chromosome substitution strains. Nat Genet. 2000;24:221–225. doi: 10.1038/73427. [DOI] [PubMed] [Google Scholar]
- Nathan BM, Hodges CA, Supelak PJ, Burrage LC, Nadeau JH, et al. A quantitative trait locus on chromosome 6 regulates the onset of puberty in mice. Endocrinology. 2006;147:5132–5138. doi: 10.1210/en.2006-0745. [DOI] [PubMed] [Google Scholar]
- Pomp D, Nehrenberg D, Estrada-Smith D. Complex genetics of obesity in mouse models. Annu Rev Nutr. 2008;28:331–435. doi: 10.1146/annurev.nutr.27.061406.093552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shao H, Burrage LC, Sinasac DS, Hill AE, Ernest SR, et al. Genetic architecture of complex traits: large phenotypic effects and pervasive epistasis. Proc Natl Acad Sci U S A. 2008;105:19910–19914. doi: 10.1073/pnas.0810388105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shultz KL, Donahue LR, Bouxsein ML, Baylink DJ, Rosen CJ, et al. Congenic strains of mice for verification and genetic decomposition of quantitative trait loci for femoral bone mineral density. J Bone Miner Res. 2003;18:175–185. doi: 10.1359/jbmr.2003.18.2.175. [DOI] [PubMed] [Google Scholar]
- Silver LM. Mouse genetics: concepts and applications. Oxford, UK: Oxford University Press; 1995. [Google Scholar]
- Singer JB, Hill AE, Burrage LC, Olszens KR, Song J, et al. Genetic dissection of complex traits with chromosome substitution strains of mice. Science. 2004;304:445–448. doi: 10.1126/science.1093139. [DOI] [PubMed] [Google Scholar]
- Sinha H, David L, Pascon RC, Clauder-Munster S, Krishnakumar S, et al. Sequential elimination of major-effect contributors identifies additional quantitative trait loci conditioning high-temperature growth in yeast. Genetics. 2008;180:1661–1670. doi: 10.1534/genetics.108.092932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snell GD. Methods for the study of histocompatibility genes. J Genet. 1948;49:87–108. doi: 10.1007/BF02986826. [DOI] [PubMed] [Google Scholar]
- Snell GD. Histocompatibility genes of the mouse. I. Demonstration of weak histocompatibility differences by immunization and controlled tumour dosage. J Natl Cancer Inst. 1958;20:787–824. [PubMed] [Google Scholar]
- Snell GS. Congenic resistant strains of mice. In: Morse HC, editor. Origins of inbred mice. New York: Academic Press; 1978. pp. 119–155. [Google Scholar]
- Steinmetz LM, Sinha H, Richards DR, Spiegelman JI, Oefner PJ, et al. Dissecting the architecture of a quantitative trait locus in yeast. Nature. 2002;416:326–330. doi: 10.1038/416326a. [DOI] [PubMed] [Google Scholar]
- Takada T, Mita A, Maeno A, Sakai T, Shitara H, et al. Mouse inter-subspecific consomic strains for genetic dissection of quantitative complex traits. Genome Res. 2008;18:500–508. doi: 10.1101/gr.7175308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. J R Stat Soc B. 1996;58:267–288. [Google Scholar]
- Yamanouchi J, Rainbow D, Serra P, Howlett S, Hunter K, et al. Interleukin-2 gene variation impairs regulatory T cell function and causes autoimmunity. Nat Genet. 2007;39:329–337. doi: 10.1038/ng1958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Youngren KK, Nadeau JH, Matin A. Testicular cancer susceptibility in the 129.MOLF-Chr19 mouse strain: additive effects, gene interactions and epigenetic modifications. Hum Mol Genet. 2003;12:389–398. doi: 10.1093/hmg/ddg036. [DOI] [PubMed] [Google Scholar]
- Zhu J, Zhang B, Schadt EE. A systems biology approach to drug discovery. Adv Genet. 2008;60:603–635. doi: 10.1016/S0065-2660(07)00421-X. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.