The Polarizable Atomic Multipole-based AMOEBA Force Field for Proteins

Abstract

Development of the AMOEBA (Atomic Multipole Optimized Energetics for Biomolecular Simulation) force field for proteins is presented. The current version (AMOEBA-2013) utilizes permanent electrostatic multipole moments through the quadrupole at each atom, and explicitly treats polarization effects in various chemical and physical environments. The atomic multipole electrostatic parameters for each amino acid residue type are derived from high-level gas phase quantum mechanical calculations via a consistent and extensible protocol. Molecular polarizability is modeled via a Thole-style damped interactive induction model based upon distributed atomic polarizabilities. Inter- and intramolecular polarization is treated in a consistent fashion via the Thole model. The intramolecular polarization model ensures transferability of electrostatic parameters among different conformations, as demonstrated by the agreement between QM and AMOEBA electrostatic potentials, and dipole moments of dipeptides. The backbone and side chain torsional parameters were determined by comparing to gas-phase QM (RI-TRIM MP2/CBS) conformational energies of dipeptides and to statistical distributions from the Protein Data Bank. Molecular dynamics simulations are reported for short peptides in explicit water to examine their conformational properties in solution. Overall the calculated conformational free energies and J-coupling constants are consistent with PDB statistics and experimental NMR results, respectively. In addition, the experimental crystal structures of a number of proteins are well maintained during molecular dynamics (MD) simulation. While further calculations are necessary to fully validate the force field, initial results suggest the AMOEBA polarizable multipole force field is able to describe the structure and energetics of peptides and proteins, in both gas-phase and solution environments.

INTRODUCTION

Proteins are a ubiquitous class of biopolymers whose functionalities depend on the details of their 3D structures, which are in turn encoded by their specific amino acid sequences. Computer modeling and simulations are widely utilized in the study of protein structure, function, dynamics, and interactions with other synthetic or biological molecules. In molecular mechanics (MM) approaches, interactions among atoms are described by classical empirical potentials often referred to as force fields. Unlike ab initio quantum mechanical (QM) methods, the classical MM models treat atoms as rigid particles with electronic degrees of freedom averaged out, thereby lowering the computational cost and allowing simulation of biological events for larger systems and longer time scales. On the other hand, high level ab initio theory is becoming more affordable and is now heavily utilized during the development of classic potentials for proteins such as Amber,¹ CFF,² CHARMM,³ GROMOS,⁴ MM3⁵ and OPLS-AA.⁶ This class of force field typically utilizes fixed atomic charges, point dispersion-repulsion, and simple empirical functions for valence interactions. The current generation of force field has enjoyed much success in many areas of biological and materials science; however, there remains significant room for future improvement.

Efforts to advance molecular mechanics force fields to the “next-generation” have largely focused on introducing explicit electronic polarization into the electrostatic model. A number of comprehensive reviews on the history and development of polarizable force fields have detailed the significance of polarization effects.^7-15 A wide range of studies on water,^16-18 organic molecules,^19-23 peptides,^24-25 protein-ligand binding,^26-33 ions,^34-38 and ion channels³⁹ using polarizable force fields have demonstrated various benefits of directly treating polarization effects. In addition to offering more accurate thermodynamic properties, a polarizable force field is more transferable, in principle, and can be more robustly parameterized by direct comparison with high-level ab initio quantum mechanical calculations in the gas phase.

Several different methods for incorporation of many-body effects have been explored. The fluctuating charge approach accounts for polarization by varying the magnitude of atomic charges based on electronegativity equalization.^40-47 It has been argued that fluctuating charge models fail for specific geometric situations, such as out of plane polarization and bifurcated hydrogen bonding, since charge flow is limited to bond directions.⁴⁸ Alternatively, the Drude oscillator or shell model, where a point charge moves about the nuclear position, has been applied to modeling of the induced dipole response in water and small molecule systems.^{17, 49-53} Compared to the classical induced dipole method,^{16, 19, 48, 54-57} these schemes involve less complex numerical algorithms since the point charge framework is retained. However, the interactive atomic induced dipole model ^58-59 is superior in terms of reproducing anisotropy and nonadditivity of molecular polarization response across many different types of compounds. Moreover, intramolecular polarization assumes a critical role upon moving from small molecules to larger peptides and proteins possessing alternative conformational states. The conformational dependence of electrostatics can be significant,^60-61 and has received attention in the design and development of both polarizable and nonpolarizable force fields.^{60, 62-64} As we have previously shown,²⁴ the interactive induction model used in AMOEBA can accurately reproduce this property.

In addition to polarization effects, we also want to stress the atomic partial charge-based representation of permanent electrostatics is itself inadequate. It has been shown that the error in a molecular electrostatic potential can be reduced by orders of magnitudes upon complementing atomic monopoles with dipole and quadrupole moments.^65-67 The incorporation of higher order atomic multipoles has been shown to greatly improve the quality of crystal structure predictions for simple organic molecules.^68-69 One may argue additional off-center charges are an alternative to point multipoles, as they can enable the same level of fidelity in description of electron density. For example, the use of charges at lone-pair sites of oxygen atoms can improve the ability of a water model to reproduce properties such as the density anomaly with temperature, and the dielectric constant.⁷⁰ Nevertheless, the determination of both position and magnitude of the charges at such extra sites is a nontrivial task, requiring fitting to the experimental density-temperature profile. In contrast, the distributed multipole analysis of Stone^71-72 provides relatively unambiguous sets of atomic multipoles directly from molecular orbital calculations.

In this work, we present the development of a protein potential based upon a polarizable atomic multipole representation of electrostatics. The intramolecular polarization scheme formulated previously allows us to obtain the permanent atomic multipoles, directly from ab initio calculations on blocked dipeptides. A new protocol is applied to combine Distributed Multipole Analysis (DMA) and electrostatic potential fitting to derive conformation-independent “permanent” multipoles. The valence and van der Waals parameters have been derived from liquid simulations of small organic molecules containing similar functional groups. Merging of inter- and intramolecular interactions at short separation, including electrostatics, vdW, and torsional contribution, is determined via comparison to gas phase QM data for di- and tetra-peptides. The resulting potential is examined and validated by dynamics simulation of a number of peptides and proteins in solution, and comparison with experimental data. Compared to the preliminary AMOEBA protein force field parameters described in a previous article,⁷³ the current paper reports a completely new protein AMOEBA-2013 force field that is systematically developed using a newly improved strategy to parameterize permanent electrostatics and torsions, coupled with substantial validation against experimental data.

POTENTIAL ENERGY MODEL

The potential energy model has been explained in detail in several previous publications^{18, 23}. Here we will briefly summarize the key features. The total energy of the system is given by

$$U=U_{\mathit{bond}}+U_{\mathit{angle}}+U_{\mathit{cross}}+U_{\mathit{oop}}+U_{\mathit{torsion}}+U_{\mathit{vdW}}+U_{\mathit{ele}}^{\mathit{perm}}+U_{\mathit{ele}}^{\mathit{ind}}.$$ (1)

The first five terms are the valence contributions corresponding to the bond, angle, bond-angle cross coupling, out-of-plane, and torsional energy, respectively. Common functional forms are used for these terms, and the detailed equations have been given previously.⁷³ Earlier versions of the AMOEBA protein force field included a torsion-torsion coupling term, implemented via a cMAP-style⁷⁴ two-dimensional bicubic spline. This term is essentially a grid-based correction to match the force field ϕ-ψ conformational energies to those of a target QM-based potential surface. In the current version, however, the “traditional” 3-term Fourier expansion function is used for all torsion angles, except for the backbone of glycine. The pairwise additive vdW interaction in AMOEBA is described by Halgren’s buffered 14-7 function.⁷⁵ The buffered 14-7 function yields a slightly “softer” repulsive region than the Lennard-Jones 6-12 function, but a steeper repulsive wall than typical Buckingham exp-6 formulations. For a hydrogen atom connected to a heavy atom X, the vdW site is placed along the HX bond such that the distance between the atom X and vdW site of H is a percentage of the full bond length, referred to as the “reduction factor”. This allows incorporation of some vdW anisotropy along the bond direction.

The permanent electrostatic energy in AMOBEA arises from atomic multipole-multipole interactions. Each atomic center consists of a point monopole (partial charge), a dipole vector and a quadrupole tensor. Note there are only five independent quadrupole components due to symmetry and use of traceless moments. The dipole and quadrupole are defined with respect to local reference frames formed by neighboring atoms. Examples of such local frames are illustrated in Figure 1. As the molecules rotate and diffuse over the course of a simulation, each atom’s atomic multipoles maintain a constant orientation with respect to their local frame. The equation for calculating interaction energies and gradients (forces and torques) between permanent multipoles, including a traditional Ewald summation method, was presented previously.¹⁸

Figure 1.

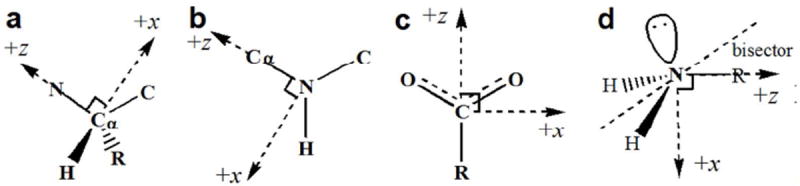
Local frame definitions for (a) a protein backbone Cα, (b) backbone amide N, (c) carboxylate carbon, and (d) amine nitrogen. The Cα and amide N use the “Z-then-X” convention, where a first neighboring atom is selected to define the Z-axis, and a second neighbor defines the ZX-plane and the positive X-direction. The carboxylate example uses the “Bisector” convention, where the bisector of two neighboring atoms defines Z-axis. This is typically used in structures with local 2-fold symmetry. The amine N is represented by the “Z-Bisector” convention, where the N-R bond defines the Z-axis, and the bisector between the two N-H bonds defines the ZX-plane. In all cases, the Y-axis is then defined according to the right hand rule.

Electronic polarization accounts for the majority of the many-body effects experienced in biomolecular systems although there are situations where many-body aspects of the dispersion and repulsion energies may be important as well.^76-77 AMOEBA utilizes an interactive atomic dipole induction scheme where the field produced by permanent multipoles and induced dipoles induces a dipole at each polarizable site, and each such induced dipole then further polarizes other atoms. As a result, anisotropic molecular polarizability can be effectively described by isotropic distributed atomic polarizabilities. Based on Thole’s model,⁵⁹ polarization at very short range is damped, yielding energies in better agreement with ab initio results and avoiding the so-called polarization catastrophe. The same polarization model is used for both intermolecular and intramolecular polarization. A group-based scheme, where permanent multipoles do not polarize other atoms within their group, but induced-induced mutual polarization occurs between all atoms, allow us to merge molecular fragments to represent a larger chain molecule such as a protein. We have previously described the procedure used to extract intramolecular polarization from ab initio quantum mechanical calculations, resulting in “true” permanent atomic multipoles.²⁴ The computation of the polarization energy and gradient in molecules containing multiple polarization groups is detailed in our previous report on the AMOEBA force field for general organic molecules.²³

The masking of short range intermolecular interactions is implemented by means of scale factors, which were determined by optimizing the transferability of conformational energies from alanine dipeptide to tetrapeptide, as discussed in the parameterization section. The final set of scale factors for interactions between permanent multipoles is 0.4 for the 1-4 interactions (separated by three bonds), 0.8 for 1-5 interactions, and zero (completely neglected) for any closer pair of atoms (1-2 and 1-3 interactions). The polarization energy between induced dipoles and permanent multipole moments is computed fully between atoms separated by three (1-4) or more bonds, and completely neglected for any closer separation. The analytical gradient of the polarization energy is nontrivial because the intramolecular “scaling” used in computing polarization interaction energies differs from the group-based scheme used during induced dipole generation. A derivation of the analytical polarization force resulting from the above masking scheme is detailed in the appendix our previous publication.²³

A particle-mesh Ewald (PME) treatment of polarizable multipole interactions has been developed⁷⁸ and implemented in TINKER,⁷³ Amber⁷⁹ and OpenMM⁸⁰ for AMOEBA calculations. The latest version of TINKER has OpenMP shared-memory parallelization of AMOEBA simulations, AMBER (PMEMD) has the MPI parallel capability, while OpenMM is accelerated for GPU-based calculations. For typical systems, roughly half of the computational expense of AMOEBA is due to iterative calculation of the induced dipoles. For highly charged systems, the relative cost of dipole iteration can be higher (e.g. containing divalent ions). Recently we have implemented a new induced dipole solver modified from a conjugated-gradient method,⁸¹ which significantly improves efficiency when tightly converged induced dipoles (< 10^-5 Debye RMS change) are required. In addition, we have introduced into TINKER a multiple time step (MTS) algorithm for AMOEBA molecular dynamics, in which nonbonded interactions including polarization are updated every 2-2.5 fs. This simple MTS algorithm allows use of longer MD time steps and yields improved computational throughput.

COMPUTATIONAL DETAILS

Ab initio calculations were performed using Gaussian 09⁸² and Q-Chem 4.0.⁸³ Geometry optimization was carried out at the MP2/6-31G* level, which is computationally efficient and gives reliable molecular geometries. Initial atomic multipoles for dipeptide model compounds were derived at the MP2/6-311G** level using Stone’s original DMA procedure.⁷¹ Basis sets containing diffuse functions are avoided in the initial DMA determination as they lead to spurious multipole values, especially for buried atoms.⁸⁴ Note the original DMA procedure can be achieved in the current version of the GDMA program (v2.0 and above)⁸⁵ by setting “switch” to 0, and the “radius factor” to 0.65 for all atom types. The resulting atomic multipole values were then optimized against MP2/aug-cc-pVTZ electrostatic potential values computed on a grid of points around each model compound. MP2/aug-cc-pVTZ was used because our previous studies indicate inclusion of diffuse basis functions is important for capturing intermolecular interactions and reproducing experimental hydration free energy.²³ Partial charge values (monopoles) are held fixed during the potential optimization. All single point conformational energies were obtained with complete basis set (CBS) extrapolation from RI-TRIM MP2/cc-pVTZ and cc-pVQZ results.⁸⁶ These CBS calculations provide highly accurate conformational energies while still being computationally affordable. The TINKER v6 and Amber v10 molecular modeling packages were used for all the molecular mechanics calculations. Particle-Mesh Ewald summation^{78, 87-88} was applied to treat electrostatic interactions, including polarization, with a real-space cutoff distance of 7.0 Å, a grid spacing of 0.8 Å, and 5^th-order B-splines. A cutoff with a switching window at 12 Å was applied to the vdW interactions. Induced dipoles were iterated to convergence, until the root mean square (RMS) change between interations fell below 0.01 Debye per atom. All molecular dynamics simulations were performed using a Velocity Verlet MTS integration algorithm⁸⁹ with a 2.5 fs time step. The system temperature was controlled via the Nose-Hoover chain thermostat method.⁹⁰

For alanine, glycine, proline and some terminal capping groups (Ala-COOH, Gly-COOH, Gly-COO^-), the minimum energy map of the dipeptide was calculated on a uniform 15° grid in ϕ-ψ space. At each of the 576 points, MP2/6-31G* geometry optimization with constrained ϕ and ψ values was performed prior to a single point energy calculation at the RI-TRIM/MP2 CBS level. For proline, fewer grid points were available for QM calculations due to the limited conformational freedom. For the chain terminal amino acids, a single point ab initio energy was also calculated for each optimized structure using the Polarizable Continuum Model (PCM) solvation model. The torsion parameters for model compounds were initially fit to gas-phase ab initio conformational energies, and then adjusted to agree with statistical populations sampled from the Protein Data Bank (PDB). For the residue side chain torsions, geometry optimization was performed at the MP2/6-31G* level with each torsional angle constrained at 30° increments from 0° to 360°, followed by single point RI-TRIM MP2/CBS energy calculations.

The potential of mean force (PMF) of a solvated alanine tripeptide, NH₃⁺-Ala-Ala-Ala-COO^-, with respect to ϕ and ψ angles of the central Ala residue was computed using the two-dimensional weighted histogram analysis method (2D WHAM).^91-93 A total of 576 independent molecular dynamics simulations of an alanine dipeptide and 206 water molecules in a 26.6 Å truncated octahedral box were carried out at 298K, using the same grid as for the gas phase map. In each simulation, the ϕ and ψ angles were restrained to a grid point on the Ramachandran map using weak harmonic potentials with a force constant of 0.01 kcal/mol-deg². The resulting conformer populations, sampled from the 576 × 70 ps production trajectories were utilized to construct the PMF and the relative free energy map via the 2D WHAM procedure.

An experimentally derived PMF was calculated from −ln(P) where P is the torsion distribution as sampled from PDB statistics.⁹⁴ For the alanine backbone, the PDB PMF was obtained by averaging the data for tripeptides with a central alanine and either the right- or left-neighboring residue being alanine (i.e., Ala-Ala-X or X-Ala-Ala, where X represents any residue type). For proline, PDB data with either a right- or left-neighbor residue being glycine (i.e., Gly-Pro-X or X-Pro-Gly) was averaged. Similarly, the glycine PMF was calculated by averaging the PDB data for Pro-Gly-X and X-Gly-Gly.

For peptide systems, including unblocked and protonated (Ala)₅, NH₃⁺-Gly-Pro-Gly-Gly-COO^-, and Ac-(Ala-Ala-Glu-Ala-Ala)₃–NH₂, replica exchange molecular dynamics (REMD)^95-96 simulations were performed using 36 replicas at temperatures between 278 K and 620 K. The (Ala)₅ peptide was unblocked, protonated at the N-terminus (-NH₃⁺) and neutral at the C-terminus (-COOH), corresponding to the experimental conditions of pH 2.^97-98 For each system, the peptide was placed in a truncated octahedral box with approximately 800 water molecules. REMD simulations were performed under the NVT ensemble for at least 30 ns/per replica, using the PMEMD program from Amber 10.⁷⁹ with snapshots saved every 0.5 ps for analysis.

Protein molecular dynamics simulations were performed using the Amber10 software package. The proteins simulated include: crambin (PDB:1EJG, 46 residues),⁹⁹ Trp cage (PDB:1L2Y, 20 residues),¹⁰⁰ villin headpiece (PDB:1VII, 35 residues),¹⁰¹ ubiquitin (PDB:1UBQ, 76 residues),¹⁰² GB3 domain (PDB:2OED, 56 residues),¹⁰³ RD1 antifreeze protein (PDB:1UCS, 64 residues),¹⁰⁴ SUMO-2 domain (PDB:1WM3, 72 residues),¹⁰³ BPTI (PDB:1BPI, 58 residues),¹⁰⁵ FK binding protein (PDB:2PPN, 107 residues),¹⁰⁶ and lysozyme (PDB:6LYT, 129 residues).¹⁰⁷ For each system, a single protein molecule was placed in a truncated octahedral water cell chosen to provide a minimum distance of 8 Å between protein and cell wall. Simulations were performed in the NPT ensemble at a temperature of 298K. Approximately 10 ns of MD trajectory were generated for each system. The initial 500 ps portion of each trajectory was discarded corresponding to equilibration, and structural information was saved every 0.5 ps during the subsequent production phase. Analysis of the dynamics trajectories, including computation of RMSD values and average structures, was performed via the Amber Ptraj module.⁷⁹

PARAMETER DERIVATION

Electrostatic Parameters

Permanent atomic multipoles for glycine, alanine and proline residues were derived from capped Ac-X-NMe dipeptides with X = Gly, Ala and Pro, with the goal of deriving conformationally independent electrostatic parameters for the central residue X from QM. A critical first step is definition of intramolecular direct polarization groups since the intramolecular polarization contribution needs to be extracted from the DMA multipole values as described in the Potential Energy Model section. Recall that an atom’s permanent atomic multipoles (PAMs) only polarize atoms outside its polarization group. Figure 2 shows the group definition for alanine. For side chains of other residues, the groups are chosen in the same spirit, i.e., no freely rotatable bonds within the group. For example, the -CH₂-, phenyl ring, and hydroxyl group are each classified as a single group for purposes of direct polarization. Next, the initial multipole parameters were derived by via DMA at the MP2/6-311G** level, and these parameters were then optimized against the MP2/aug-cc-pVTZ electrostatic potential computed on a set of grid points around the dipeptide compounds. Multiple grid layers were chosen at 0.35 Å intervals, beginning at a 1.0 Å distance from the vdW surface. Multipole parameters are iterated until the RMS difference from the target QM potential falls below 0.5 kcal/mol, and the RMS gradient is less than 0.5 kcal/mol/Å. Note the point charges are fixed at the original DMA values during the optimization process, while the dipole and quadrupole moments are allowed to relax. The point charges at the boundary between the middle and capping residues, and between the backbone and side chain atoms are then manually adjusted to ensure an integral net charge for each residue. This adjustment is usually very small and the ESP optimization process ensures that charge adjustments are compensated by dipole and quadrupole changes. The resulting PAMs for the central residue are the “conformation independent” PAMs included in the AMOEBA-2013 parameter file. When connected to other residues in proteins, intramolecular polarization due to the PAMs takes place according to the polarization group definition. For alanine, we selected five local minima (α_L, α’, C5, C7a and C7e conformers) and used all five conformers simultaneously in the above procedure. The multipoles from this multiple-structure potential fitting were used as the final set of permanent multipole parameters, and one additional conformer (β2) was used as validation by computing its electrostatic potential and dipole moments with the final parameters and comparing to QM results. PAMs for glycine and proline were obtained via an analogous protocol.

Figure 2.

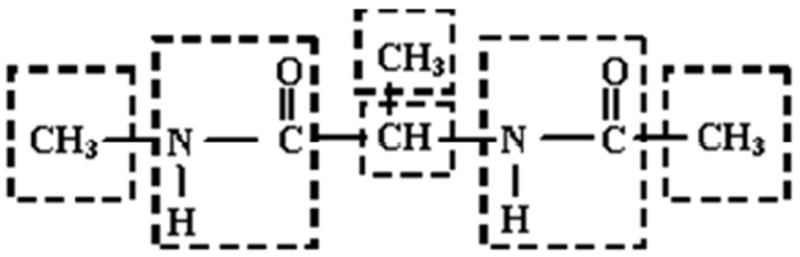
Illustration of the intramolecular polarization group definition. Each group consists of a functional group or cluster of atoms with limited conformational flexibility. The permanent multipole moments on each atom only polarize atoms of other groups, while induced dipoles on all atoms polarize all other atoms regardless of group membership.

For all other residues, capped (Ac-X-NMe) dipeptides were chosen as the model compounds. For each amino acid, three conformations were selected for use in permanent multipole (monopole, dipole and quadrupole) parameterization, and another three for validation. The conformers have either an extended backbone, or represent compact structures with internal hydrogen bonds corresponding to gas phase minima. The backbone atoms were constrained to have the same PAM values as alanine, while side chain PAMs were derived using the procedure outlined above. When the side chain parameters were merged with alanine backbone parameters, charge neutralization (typically on the order of one-hundredth of an electron) was performed at the C_β atom. Dipole and quadrupole moments were fit to MP2/aug-cc-pVTZ electrostatic potentials for the three conformers in the parameterization set, allowing only the side chain values to vary. ESP fitting and validation results are discussed in detail in the Simulation and Validation section. In addition to Ac (CH₃CO-) and NMe (-NHCH₃) terminal groups, other N-termini (-NH₃⁺ and -NH₂) and C-termini (-COOH and -COO^-) were also parameterized. Note glycine requires a separate parameterization for -NH₃⁺ and -COOH termini because of its use of a different C_α atom type. Due to the amount of data involved, most parameters, including the PAMs and direct polarization group definitions, are not given in the text, but are included in the AMOEBA-2013 parameter files, which are publicly available from the TINKER web site at http://dasher.wustl.edu/tinker/.

vdW and Valence Parameters

The van der Waals and valence parameters were transferred from the AMOEBA parameters for small organic molecules, as reported in a previous publication.²³ The parameterization for these terms follows essentially the approach used for water¹⁸ and ions,³⁴ where the vdW parameters were optimized to gas phase cluster structures and energetics as well as condensed-phase properties. A critical strategy in deriving the vdW parameters, due to their empirical nature, is to ensure chemical consistency among different elements. This was achieved by simultaneously parameterizing multiple compounds sharing the same vdW “classes” to improve transferability. The “atom classes” (super set of “atom types” used for electrostatics) in AMOEBA are subdivided beyond the simple chemical element types, largely to take into account different hybridizations such as sp² vs. sp³. A selection containing the most common vdW parameters is provided in Table. The valence parameters, including bond, angle, bond-angle cross term and out-of-plane parameters, were transferred from small organic molecules with minor modifications to improve agreement with ab initio (MP2/6-31G*) geometries and protein PDB structures.

Torsional Parameters

The valence parameters (bond stretching, angle bending, bond-angle cross terms, out-of-plane bending) were transferred from organic small molecules, which were derived by matching the QM geometry and vibrational frequency of small moelcules.¹⁰⁸ The last step was then to derive the torsional parameters by comparing AMOEBA (everything but the to-be-fit torsion) and ab initio conformational energy values. Note that the molecular mechanics conformational energy depends not only on the torsional energy term, but also on the treatment of nonbonded intramolecular interactions – in particular on the treatment of 1-4 interactions across each torsion. In this work the scaling factors for the intramolecular electrostatic and vdW interactions have been chosen in order to minimize the contribution of the explicit torsional terms and ensure maximal transferability of parameters between dipeptides and tetrapeptides.

The alanine dipeptide is used to parameterize backbone torsional terms for all amino acids, with the exception of glycine and proline. The ab initio (RI-TRIM MP2/CBS) energy of alanine dipeptide was systematically evaluated at different backbone torsion angles over a 24 × 24 grid (15° intervals in both ϕ and ψ) as described in the computational details. The AMOEBA energy without the ϕ/ψ torsional contribution was computed for the same conformation while enforcing torsion constraints. The difference between AMOEBA and RI-TRIM MP2/CBS energy is taken as the fitting target for the torsional parameters, using a standard three-term Fourier expansion. Subsequently 2D WHAM simulations of an Ala-Ala-Ala tripeptide in explicit water were performed to obtain the Ramachandran potential of mean force (PMF) for the middle residue. The backbone torsion parameters were further improved by comparing the AMOEBA PMF in solution to a statistically-derived alanine backbone PMF derived from the PDB database.⁹⁴ We note that the torsion parameters were not directly fit to the PDB PMF. Instead, the parameter refinement was achieved by assigning relatively higher weight factors to the QM energy of gas-phase conformers located in the polyproline II (PII), α-helical and β-sheet regions while still fitting to the whole QM gas phase energy map. Torsional parameters were manually refined over 3-4 iterations to balance the relative populations of solvated peptide in these minimum energy regions. The gas phase Ramachandran potential energy from RI-TRIM MP2/CBS and AMOEBA with the final torsion parameters are compared in Figure 3. The simulated solution phase AMOEBA PMF and the PDB-derived statistical PMF maps for the alanine backbone are shown in Figure 4a.

Figure 3.

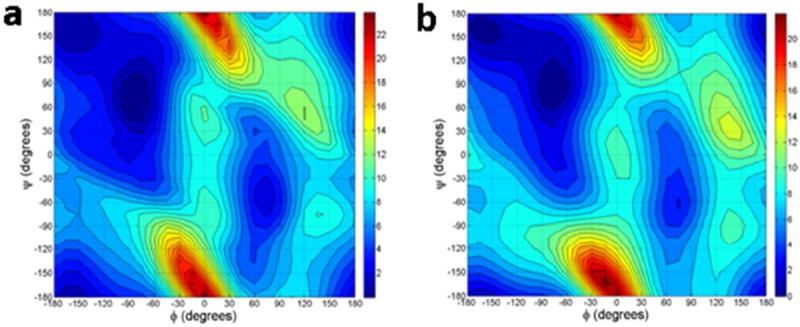
Gas-phase energy contours for alanine dipeptide from RI-TRIM MP2/CBS calculations (a) and the AMOEBA protein force field (b). The energies were computed on a 24 × 24 grid and then contoured.

Figure 4.

Comparison of Ramachandran map potentials of mean force for alanine. (a) Ala-2 residue of (Ala)3 as predicted by 2D-WHAM simulations. (b) Average of ala-2, ala-3, and ala-4 residues in replica exchange molecular dynamics simulation of the (Ala)5 peptide. The trajectory at 298 K was used. (c) The PDB data are ref 83.

The parameterization of proline backbone torsions followed essentially the same procedure as for alanine, except that fewer grid points were used due to the limited conformational freedom. For glycine, a torsion-torsion spline term is introduced in addition to the Fourier torsional terms for ϕ and ψ. After the Fourier torsional parameters were fit to the gas phase ab initio RI-TRIM MP2/CBS energy, the difference between the ab initio and AMOEBA energy was used to determine the torsion-torsion grid based correction table. (See Potential Energy Model for definition). These 2D values were fixed in the subsequent refinement of the Fourier torsional parameters. Use of the torsion-torsion term improves the fit to both ab initio data and solution phase properties. Similar to the parameterization of alanine backbone torsions, the torsional parameters for proline and glycine backbones were refined to match the statistical PMF for proline and glycine residues in the PDB database, respectively. REMD simulations were performed with a model tetrapeptide, GPGG (NH₃⁺-Gly-Pro-Gly-Gly-COO^-), to obtain the simulated backbone torsion angle distribution of proline and glycine. All other residues share the same backbone torsion parameters (together with valence, vdW and electrostatic parameters) as alanine. Parameterization of the -COOH C-terminal form of alanine (and other non-Gly/Pro residues), and the −COOH and -COO^- terminal forms of glycine were fit to RI-TRIM MP2/CBS energies on a 12 × 12 torsional grid. Since there are limited PDB data available for terminal residues, we optimized these parameters by matching AMOEBA energies in implicit solvent (based on Generalized Kirkwood model¹⁰⁹) with QM PCM energies at the MP2/6-311G(2d,2p) level.

In addition, conformation energies for a benchmark set of 27 alanine tetrapeptides¹¹⁰ have been assessed. This comparison was made to validate transferability and to adjust the scale factors for short-range intramolecular nonbonded interactions. The AMOEBA results are compared with those from MP2, LMP2, DFT and RI MP2 calculations in Table 3. All the ab initio calculations are single point energy evaluations at the same HF/6-31G** geometries. AMOEBA calculations were performed with both full geometry optimization, and with ϕ and ψ angles constrained to the HF geometry. All comparison is made against RI MP2/CBS results. While the AMOEBA-optimized structures deviate only slightly from those at HF/6-31G** (average SRMS = 0.47 Å), the RMS difference between AMOEBA and RI MP2/CBS energies is 1.15 kcal/mol, similar to those of LMP2/cc-pVTZ(-f) and MP2/6-311+G2d2p. Note that the relative conformational energies of the first two conformers (extended) vs. the third conformer (a compact structure) given by RI MP2/CBS lies between the canonical MP2 and LMP2 results, as do the AMOEBA results. The relative energy of extended and folded conformations is an important measure of the strength of intramolecular dispersion attraction is such systems.

Table 3.

Comparison of alanine tetrapeptide conformational energy (kcal/mol).

RI MP2 CBS	LMP2/cc-pVTZ(-f)	MP2/6-311+G2d2p	DFT B3LYP/6-31G*	AMOEBA	Struct. RMS (Å)	AMOEBA (ϕ/ψ restrained)
4.13	2.50	4.61	1.62	3.07	0.30	2.54
4.19	2.60	4.21	1.71	3.62	0.42	0.74
0.57	0.00	-0.70	-1.00	0.00	0.21	0.33
5.73	3.87	5.50	3.61	4.07	0.37	3.82
5.26	3.88	5.14	4.25	3.96	0.30	2.27
2.90	2.19	2.10	2.10	2.45	0.53	0.14
6.67	5.73	5.61	6.56	7.64	0.45	0.65
4.64	4.17	3.32	4.99	5.45	0.44	1.06
7.92	6.93	6.98	5.20	10.01	0.25	3.14
7.79	6.99	6.57	7.24	6.34	0.34	0.62
0.00	-0.19	-1.41	0.14	0.75	0.68	0.58
0.29	0.50	-1.07	1.73	0.75	0.91	0.22
3.66	1.77	3.20	1.14	3.56	0.62	0.02
4.68	3.68	4.14	3.89	4.66	0.71	0.00
2.19	2.07	0.65	3.47	2.28	0.59	0.08
3.55	2.83	2.33	3.31	2.93	0.48	0.24
3.42	2.78	2.02	2.00	2.32	0.28	1.09
1.91	0.52	1.15	-0.87	2.19	0.56	0.20
3.82	2.83	2.90	1.13	4.25	0.56	0.19
1.76	0.87	0.88	0.80	3.18	0.47	2.91
2.92	2.11	1.59	1.78	0.00	0.92	8.51
5.82	4.82	4.59	4.84	6.87	0.59	1.60
5.82	4.82	4.57	4.84	6.84	0.33	1.46
3.98	2.98	2.89	3.59	4.11	0.30	0.19
2.50	1.59	1.54	1.92	2.87	0.50	0.35
0.67	0.18	-0.41	1.40	1.60	0.37	1.51
4.02	3.18	3.04	3.53	6.26	0.38	5.57
RMS deviation	1.05	1.06	1.54	1.15	0.47	1.22

This set conformers were used in previous studies.^110,86 The RI MP2/CBS and other QM results are taken from taken from ref ⁸⁶. Two sets of AMOEBA results are listed. Both are from energy minimization of QM structures, one with backbone ϕ/ψ torsional angles restrained at QM optimal values and the other fully relaxed in the AMOEBA model. The RMSD was computed using RI MP2/CBS energies as the reference.

For the side chain torsions for all other residues, the parameters were obtained by fitting to the RI-TRIM MP2/CBS conformational energy of the corresponding dipeptides. To derive parameters independent of the backbone conformation and to verify the transferability of the backbone torsional parameters for alanine, two or more dipeptide conformations with backbone ϕ/ψ values fixed at α-helix and β-sheet values were used simultaneously to fit the parameters of side chain χ torsions. For each conformer, the side chain torsional angle of interest was rotated in increments of 30°. At each point, the dipeptide structure was optimized with ϕ, ψ and χ angles constrained to the same values in both ab initio level and AMOEBA calculations. Examples of conformational energy profiles for isoleucine and serine side chains are plotted in Figure 5. The former has an aliphatic side chain, and a single set of torsional parameters performs well across both conformers. The energy order of the local minima is also captured by AMOEBA. The situation for serine is a slightly worse due to the additional complication of intramolecular hydrogen bonding between the side chain and backbone. In both cases, the torsional energy contribution accounts for about 15% of the total conformational energy. In Table, the average RMS error from the conformational energy fitting for each residue is listed.

Figure 5.

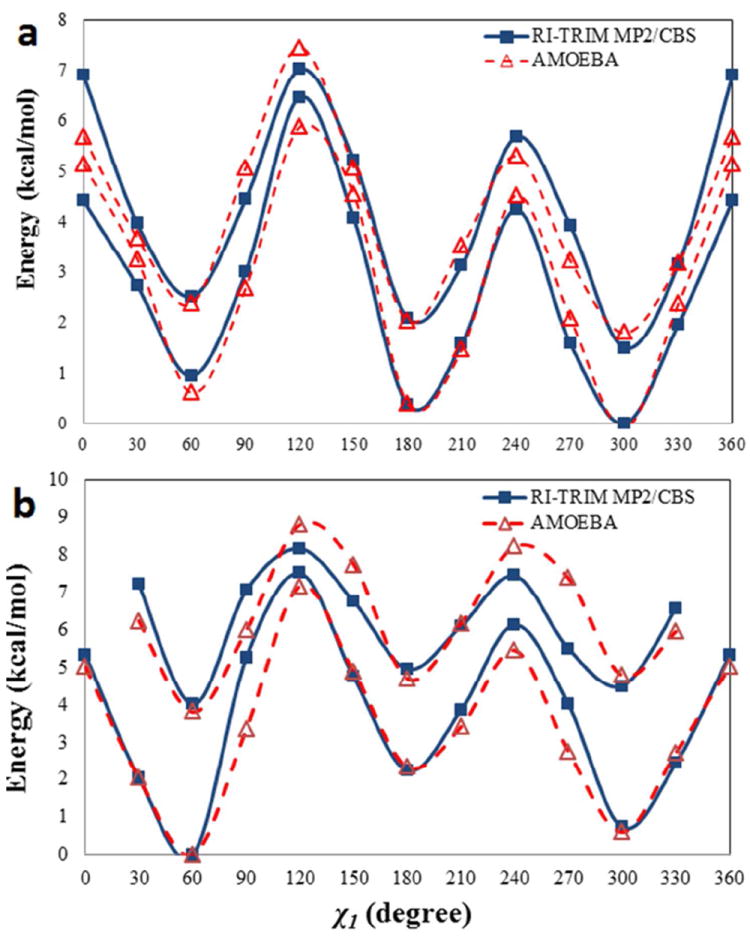
Comparison of (a) isoleucine and (b) serine conformational energy about χ1 angle. The solid lines are RI-TRIM MP2/CBS energy while the dashed lines are AMOEBA values. The AMOEBA curve is shifted to minimize the overall RMS difference between AMOEBA and QM. The top set of curves (with higher energy at 0 degree) corresponds to a backbone conformation of (-60.0, -45.0), and the other corresponds to (-140.0, 135.0).

SIMULATION AND VALIDATION

For small molecules, it is possible to systematically compare force field calculations over a range of ab initio data and experimental properties, which allows us to optimize the individual components in the potential energy model, such as the relative contributions from electrostatics and vdW interactions. For larger biomolecules, however, one can only compare detailed simulations with limited data such as database-derived statistical populations, NMR J coupling constants, and atomic structures of native proteins from X-ray or NMR experiments. Such comparison, while absolutely necessary, is most useful for inspecting the torsional parameters, and provides less feedback for other force field components (e.g. vdW or electrostatics). It will require more extensive investigation across a wide range of proteins research areas, such as protein folding, ligand binding, pKa shifts and mutant stability, to fully validate the different components and aspects of our proposed force field. Here we provide initial results through examination of the electrostatic parameters against QM for multiple conformations of each amino acid in the gas phase, and assessment of peptide conformational properties and protein structures in solution.

Electrostatic Properties in the Gas Phase

One of the important advantages of a polarizable force field is its transferability from gas phase to solution. Therefore, it is to our advantage that the gas phase electrostatic properties can be rigorously compared to QM ab initio results. It is especially important to ensure transferability of the alanine backbone electrostatic multipoles to other residues (except glycine and proline), as well as transferability among different conformations of each amino acid. We have validated the electrostatic properties of the AMOEBA protein model by computing the x-, y- and z-components of the dipole moment and the electrostatic potential of dipeptide model compound for each amino acid. For each amino acid dipeptide, three conformations were chosen as the validation set, and these structures were excluded from use in the parameterization process. In Figure 6, we compare the AMOEBA and QM molecular dipole moments of the dipeptide conformers in the validation set. The dipole moment xyz components of all the dipeptides are accurately reproduced, regardless of conformation and residue type, resulting in a correlation coefficient of 0.998. To the best of our knowledge, no other force field has demonstrated to be able to represent peptide electrostatic properties at different conformations with one set of electrostatic parameters to such accuracy. The comparison between ab initio and AMOEBA electrostatic potential for all dipeptide model compounds is detailed in the supporting information, for both the parameterization and validation sets. The average RMSE is 0.45 kcal/mol per unit charge on a grid surrounding the neutral amino acids, and only slightly higher (0.64) for charged dipeptides, with the absolute value of the potential for the latter being orders of magnitude higher. Thus, thanks to the intramolecular polarization model in AMOEBA, the transferability of backbone and side chain electrostatic multipoles of AMOEBA is quite satisfactory. We believe the test performed here, while not commonly used in force field development, is important and necessary for validating the electrostatics of a candidate force field model before other components such as the torsional parameters are empirically adjusted.

Figure 6.

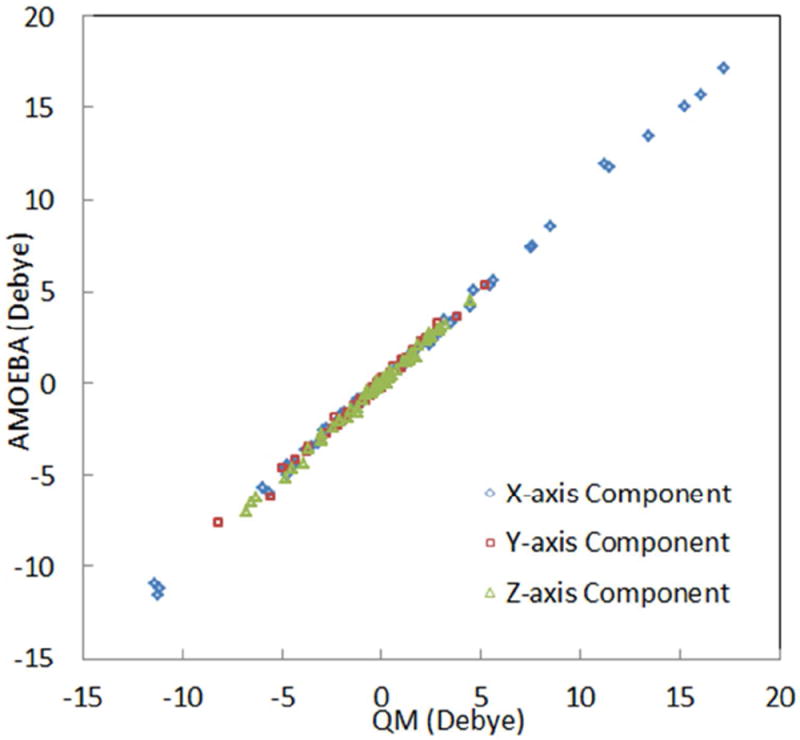
Comparison of amino acid molecular dipole moments predicted by AMOEBA and QM (MP2/aug-cc-pVTZ). The AMOEBA permanent atomic multipoles were derived from a set of dipeptides and validated on additional conformations (3 for each amino acid). Only the results for the validation sets are shown. The actual data can be found in the supporting information.

Polyalanine Conformational Free Energy in Solution

Several recent studies have used oligopeptide conformational properties in solution to calibrate force field torsional parameters.^{98, 111-117} Simulation results can be directly compared to experimental nuclear magnetic resonance (NMR) data for the corresponding peptides. Building on this prior work, we have performed a series of simulations on Ala/Gly/Pro-based peptides using the AMOEBA protein force field.

For alanine, we have first examined the solvation of the unblocked and protonated (Ala)₅ peptide using REMD. Conformational preference is presented as a potential of mean force with respect to ϕ and ψ angles in Figure 4b, which is calculated from the averaged torsional population distributions of Ala-2, Ala-3 and Ala-4 residues. A distinct global minimum is located around the PII conformation. Two other basins with energies approximately 0.5 kcal/mol higher in energy lie in the β-sheet and α-helix regions. The energy barriers separating the global basin from the two local minima are about 1~2 kcal/mol. Overall, the upper left region of the Ramachandran map is relatively flat compared to the rest of the conformational space. The distribution within this highly populated region of the map agrees well with the statistical PMF drawn from the PDB database (Figure 4c),⁹⁴ suggesting transferability of the overall model from (Ala)₃ to (Ala)₅.

The ϕ/ψ torsional angle distributions for (Ala)₅ have been probed experimentally by NMR.⁹⁸ The spin-spin coupling (J-coupling) constants reflect the ensemble character of the conformational distribution, and were compared with those calculated form REMD simulation trajectories of (Ala)₅ via Karplus relations.^{116, 118} In total, eight NMR J-coupling constants were reported: five for the backbone angle ϕ [³J(H_N,H_α), ³J(H_N,C’), ³J(H_α,C’), ³J(C,C’), ³J(H_N,C_β)], two for the backbone angle ψ [¹J(N,C_α), ²J(N,C_α)], and one value for both ϕ and ψ, [³J(H_N,C_α)].⁹⁸ The trajectory at 298K from REMD simulation of (Ala)₅ was extracted, and used to compute predicted J-coupling values. Twenty-seven predicted J-coupling values are compared to those measured by NMR in Table 4. The J-coupling constants involving the N- and C-termini were also included. The predicted values are in excellent agreement with those probed by experiment. The chi-square (χ²) difference between simulation and experiment, computed using the experimental uncertainties,⁹⁸ is about 0.994, while the overall RMS difference is 0.33 (Table 4). Note when using torsional parameters directly fit to the gas-phase QM energy of alanine dipeptide, the χ² is 3 or 4 times higher. Torsion refinement based on both QM (gas-phase) and the PDB PMF (in solution) thus plays a significant role in improving the calculated J-coupling constants. A notable consequence of the refinement is that the location of the α-helix population from simulations shifts lower and to the right, toward the average (φ, ψ) angles in the PDB distribution. In contrast, with torsional terms fit to QM gas-phase energies alone, the simulated α-helical population was broader than that from the PDB and centered at a more negative φ and less negative ψ value. A similar effect has recently been discussed for the CHAMRMM22/CMAP, CHARMM36-MP2 and CHARMM36 force fields, and it was suggested empirical correction to CMAP approach is important.^113-114 Improving agreement with PDB φ/ψ angle distribution in terms of shape and location, especially for residues not in actual helices, led to thermodynamic properties and helix-coil transition cooperativity more consistent with experimental data.

Table 4.

Comparison of J-coupling values (Hz) from AMOEBA simulations with experimental data for the (Ala)₅ peptide.

Rsidue index	J-coupling type	J-simulation	J-expt.98
Ala-2	1J(N,Cα)	11.066	11.36
Ala-3	1J(N,Cα)	10.923	11.26
Ala-4	1J(N,Cα)	10.922	11.25
Ala-2	2J(N,Cα)	8.448	9.20
Ala-3	2J(N,Cα)	8.170	8.55
Ala-4	2J(N,Cα)	8.232	8.40
Ala-5	2J(N,Cα)	8.250	8.27
Ala-2	3J(C’,C’)	0.866	0.19
Ala-2	3J(Hα,C’)	1.729	1.85
Ala-3	3J(Hα,C’)	1.705	1.86
Ala-4	3J(Hα,C’)	1.713	1.89
Ala-5	3J(Hα,C’)	1.929	2.19
Ala-2	3J(HN,C’)	1.087	1.13
Ala-4	3J(HN,C’)	1.315	1.15
Ala-5	3J(HN,C’)	1.216	1.16
Ala-2	3J(HN,Cβ)	1.819	2.30
Ala-3	3J(HN,Cβ)	1.833	2.24
Ala-4	3J(HN,Cβ)	1.743	2.14
Ala-5	3J(HN,Cβ)	1.584	1.96
Ala-2	3J(HN,Hα)	6.269	5.59
Ala-3	3J(HN,Hα)	5.988	5.74
Ala-4	3J(HN,Hα)	6.079	5.98
Ala-5	3J(HN,Hα)	6.607	6.54
Ala-2	3J(HN,Cα)	0.421	0.67
Ala-3	3J(HN,Cα)	0.614	0.68
Ala-4	3J(HN,Cα)	0.648	0.69
Ala-5	3J(HN,Cα)	0.663	0.73
χ2 = 0.994	RMS=0.33

The peptide was unblocked and protonated at both the N- and C-termini, corresponding to experimental conditions of pH=2. Replica exchange molecular dynamics (REMD) simulations were performed using 32 replicas at temperatures between 278 K and 620 K (30-ns of MD for each replica). The trajectory at 298 K was extracted and used for the J-coupling calculation.

Proline and Glycine Conformational Free Energies in Solution

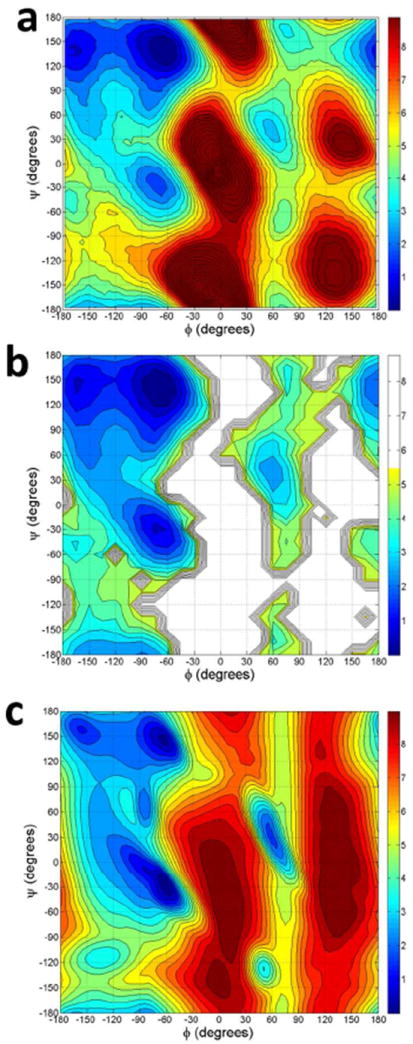
The ϕ/ψ torsional angle distributions for proline and glycine backbones were validated through REMD simulations of the GPGG tetrapeptide (NH₃⁺-Gly-Pro-Gly-Gly-COO^-). For both proline (Pro-2 residue) and glycine (Gly-3 residue), the simulated PMF maps with respect to the ϕ/ψ angles show good agreement with the PDB statistical PMF maps as shown in Figure 7. For Pro-2, the relative free energy of the α-helix and PII regions from the PDB data are well reproduced in our simulations, with the α-helical local minimum about 1 kcal/mole higher in energy than the global minimum in the PII region (Figure 7a). The simulated torsional distributions for the Gly-3 residue are also consistent with PDB data, with global minima located at the right- and left-handed α-helix regions. Two other local minima, about 1 kcal/mol higher in energy, are located at the PII structure and its mirror reflection (Figure 7c).

Figure 7.

Comparison of Ramachandran potential of mean force maps for proline and glycine. (a) Pro-2 residue of GPGG from AMOEBA simulations. (b) The PDB data for proline. (c) Gly-3 residue of GPGG from AMOEBA simulations. (d) PDB data for glycine. All PDB PMFs were computed using data from Dunbrack et al.83

Similar to alanine, the J-coupling constants were also calculated for the Pro-2 and Gly-3 residues. Three J-coupling constants, J(H_α,C’) for Pro-2, J(H_α,H_N) and J(H_α,C’) for Gly-3 were evaluated using the Karplus coefficients obtained from B972/EPR-III and B3LYP/EPR-III (methods for DFT investigations of electron paramagnetic resonance) level calculations.¹¹⁹ Table 5 compares the J-coupling values obtained from AMOEBA simulation and experiment for the GPGG tetrapeptide. The RMS difference between the calculated and experimental J-constants is 0.44 (with B972) and 0.39 (with B3LYP).

Table 5.

Comparison of J-coupling values (Hz) from AMOEBA simulations and NMR experimental data for the GPGG tetrapeptide.

Residue index	J-coupling type	J-simulation (B972 EPR-III)	J-simulation (B3LYP EPR-III)	J-expt.119
Pro-2	J(Hα,C’)	1.75	1.88	1.30
Gly-3	J(Hα,HN)	4.94	3.67	4.10
Gly-3	J(Hα,C’)	6.07	6.76	6.30
		RMS=0.44	RMS=0.39

Two sets of simulated J-coupling using different Karplus coefficients are shown. Replica exchange molecular dynamics (REMD) simulations were performed using 32 replicas at temperatures between 278 K and 620 K (30-ns of MD for each replica). The trajectory at 298 K was extracted and used for the J-coupling calculation.

Secondary Structure Distribution for the Ac-(AAQAA)₃-NH₂ Peptide

It is important for a protein force field to accurately reproduce ϕ/ψ structural distributions and correctly balance peptide secondary structure, as these metrics are directly related to phenomena such as folding, misfolding, aggregation and conformational change. The REMD simulation of the small peptide (Ala)₅, described above, provides the sensitive test of the “intrinsic” secondary structure preferences of the AMOEBA force field. However, the (Ala)₅ peptide is too short to form a stable α-helix, and a more extended PII backbone conformation is found more favorable than the helix in the Ramachandran free energy map.^{97-98, 116, 120-124} We have further simulated a longer helix-forming peptide, Ac-(AAQAA)₃-NH2,^125-126 to investigate the helix-coil transition. Because the helical population of Ac-(AAQAA)₃-NH2 has been determined from NMR chemical shift data,¹²⁷ we can directly compare the AMOEBA helical-fractions calculated from REMD simulations. We use the same definition of the helical state as a previous study,⁹⁷ namely φ in the range [-160°, -20°] and ψ in [-120°, 50°]. The fraction of helix was evaluated as the frequency of the individual residues existing in the helical states during the whole trajectory at 303 K. Figure 10 shows the fraction of helix, <h_i>, for each residue from our simulation and NMR chemical shift data. Reasonable agreement is seen between the simulated values and those obtained from NMR experiments at 303K, where both fluctuated between 10 to 30% for most residues. The error was estimated using block averages derived from six 5-ns simulation windows. In addition, the lower helical propensity trend at the C-terminus was well captured, while AMOEBA seems to underestimate the helix fraction for residues 3, 4 and 7.

Figure 10.

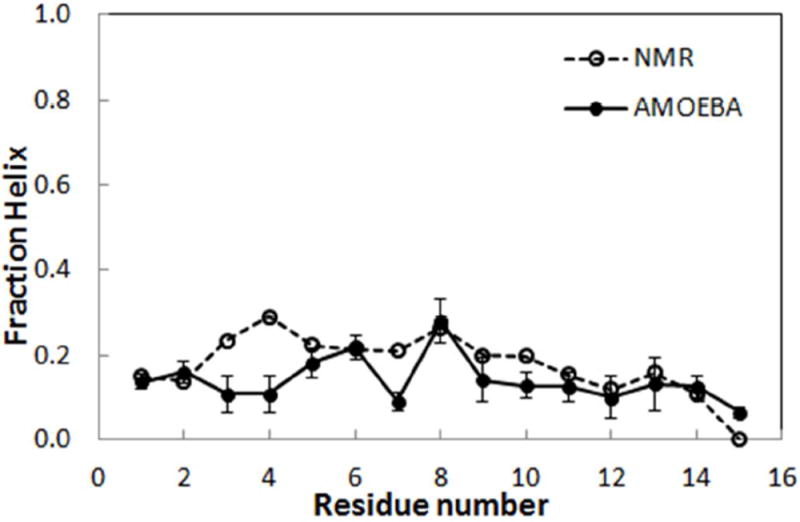
Fraction of helix 〈hi〉 for each residue in Ac-(AAQAA)3-NH2 from replica exchange MD simulations and NMR chemical shifts at 303 K.

Molecular Dynamics Simulations of Protein Systems

Ten well-studied proteins were chosen as the validation set to evaluate the new parameters. While limited, this set is representative of several different types of protein structures. For example, Trp cage (1L2Y) and villin headpiece (1VII) mainly consist of alpha helices; GB3 domain (2OED) and FK binding protein (2PPN) contain a significant proportion of beta sheet structure; crambin (1EJG) and lysozyme (6LYT) are disulfide bond-rich domains; the remaining proteins are mixtures of different motifs.

The stability of each protein was characterized by its backbone RMSD value relative to the PDB structure over 10 ns MD simulation, as summarized in Figure 8. The overall average RMSD of the ten simulated protein structures is 1.33 Å, and seven of them are close to 1.0 Å. The final MD trajectory snapshot for each protein is superposed on its PDB structure in Figure 9. We can see that helical and sheet motifs are well maintained, and do not significantly drift from the experiment structures. For many of the proteins, the large deviations arise from the terminal regions. For example, inspection of the PDB entry for ubiquitin shows the final five residues have significantly higher temperature factors than the rest of the molecule. Flexibility near the C-terminus is also observed in the MD results, particularly for the two glycine residues at positions 75 and 76. Elimination of just these two residues from the data analysis results in a backbone structural RMSD of 1.16 Å against the PDB structure.

Figure 8.

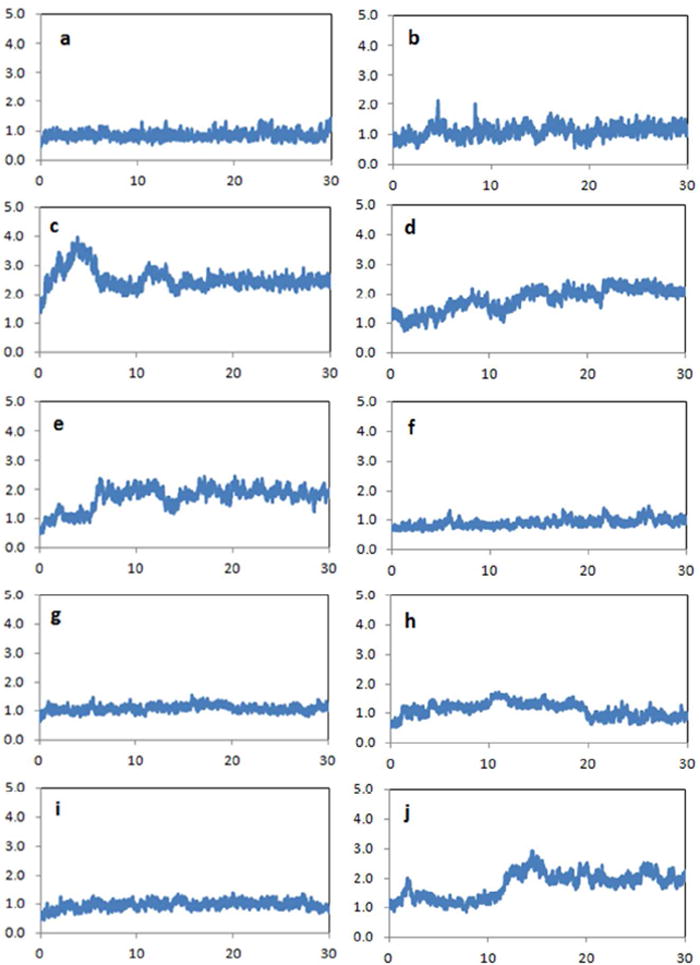
The time evolution of backbone RMSDs from the X-ray structures for ten simulated proteins. For each protein, 30 ns MD simulations were performed with the AMOEBA force field in explicit water. The X-axis represents time (ns) and the Y-axis is the RMSD values in Å. (a) crambin (PDB:1EJG), (b) Trp cage (PDB:1L2Y), (c) villin headpiece (PDB:1VII), (d) ubiquitin (PDB:1UBQ), (e) GB3 domain (PDB:2OED), (f) RD1 antifreeze protein (PDB:1UCS), (g) SUMO-2 domain (PDB:1WM3), (h) BPTI (PDB:1BPI), (i) FK binding protein (PDB:2PPN), (j) and lysozyme (PDB:6LYT).

Figure 9.

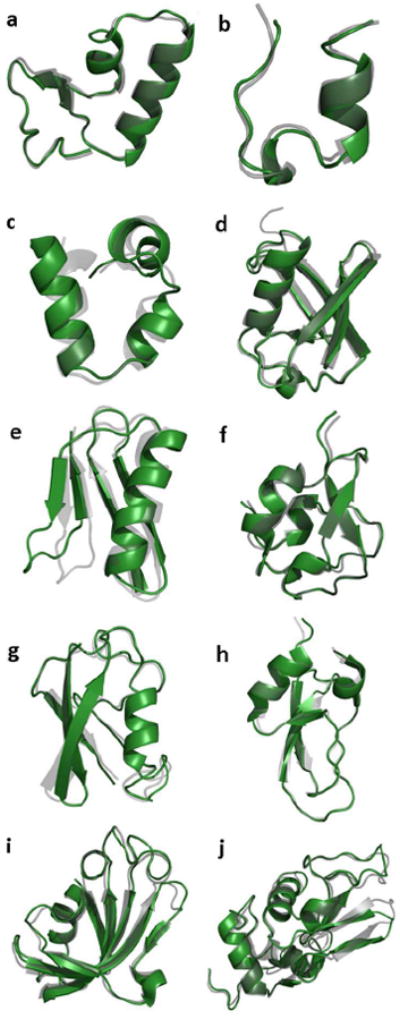
Superimposition of the final structures from AMOEBA simulations (green) and the experimental X-ray crystal structures (grey). (a) crambin (PDB:1EJG), (b) Trp cage (PDB:1L2Y), (c) villin headpiece (PDB:1VII), (d) ubiquitin (PDB:1UBQ), (e) GB3 domain (PDB:2OED), (f) RD1 antifreeze protein (PDB:1UCS), (g) SUMO-2 domain (PDB:1WM3), (h) BPTI (PDB:1BPI), (i) FK binding protein (PDB:2PPN), (j) and lysozyme(PDB:6LYT).

Calculation of NMR Order Parameters

The order parameter (S²) indicates the flexibility of each residue, with lower S² values corresponding to greater flexibility. We have compared simulated order parameters for ubiquitin and hen egg white lysozyme to NMR relaxation experiments^128-129 which measure the relaxation of amide ¹⁵N-¹H dipolar interaction.^130-131 Relaxation is caused by fluctuations of interaction energies as the internuclear interaction vectors are reoriented by thermal motion, and therefore allows the observation of anisotropic local residue motions.¹³² The isotropic reorientational eigenmode dynamics (iRED) matrix was extracted from the MD trajectories, and order parameters (S²) were then computed from the eigenvalues of this matrix.¹³³

Figure 11 compares of S² values computed from the 10 ns MD simulations with the corresponding NMR measurements. The calculated and experimental S² curves are generally well-correlated; the RMSDs between the two sets of values are 0.04 and 0.12 for ubiquitin and lysozyme, respectively. For ubiquitin, the high flexibility near turn 1 (residues 7-10), turn 3 (residues 37-40), turn 6 (residues 62-65), and the C-terminus was nicely reproduced. For lysozyme, flexibility at turn 1 (residues 46-49), long loop 2 (residues 61-78), loop 3 (residues 85-89), loop 4 (residues 100-107), loop 5 (residues 116-119) and the termini are in general agreement, although the computed values are somewhat higher than experiment. All the large deviations come from loop residues exposed to water. Specifically, the greater flexibility than what the experimental order parameters have indicated seems to suggest that the interactions between the 48D/61R and 101D/103N were underestimated by the model. However, the same types of residues give reasonable S2 values at other sites in lysozyme and ubiquitin. Additional evidence is necessary in order to decide whether we need to and how to improve the parameters for these residues. But overall, the AMOEBA force field appears able to reproduce protein structures and flexibilities.

Figure 11.

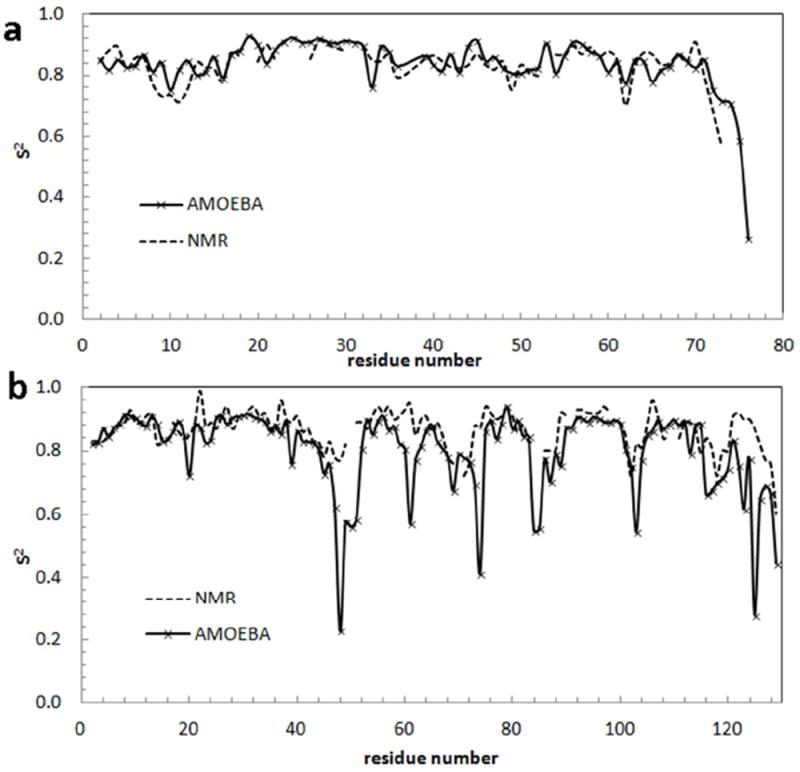
Order parameters (S2) derived from experimental NMR115, 116 (dash lines) and calculated from MD simulations in explicit water using AMOEBA. (a) Ubiquitin, (b) Lysozyme.

Calculation of Side Chain J-Couplings

Amino acid side chain distributions were evaluated by comparing the simulated side chain J-couplings to the experimental NMR values for four protein systems: BPTI, GB3 domain, ubiquitin and hen egg lysozyme.^{129, 134-137}

Table 6 shows the side-chain RMSD between the experimentally derived and simulation-based scalar couplings. Also listed for comparison are the RMSD values obtained from the Amber ff99SB force field and Amber ff99SB-ILDN,¹³⁸ which were refined against the side chain NMR data of the four proteins. Note the side chain parameters for AMOEBA were directly from fitting to QM energy profile and were not optimized against the experimental data. Overall, the performance of AMOEBA force field is comparable to Amber ff99SB-ILDN. Although a few outliers are evident for each protein system, most of the experimental scalar couplings are reasonably reproduced. The correlation between the calculated and experimental J-couplings of all the four protein systems is summarized in Figure 12. The overall R² correlation coefficient is 0.75. Details of the J-coupling values for each protein can be found in the Supporting Information. Within high scalar-coupling regions, AMOEBA failed to distinguish subtle differences observed in experiments. For example, most AMOEBA-predicted J-coupling values were ~10.8 Hz, while experimental data range from 8.0 to 15.0 Hz. We further subdivided the RMSD values by amino acid residue. The values ranged from ~0.7 to 3.3 (Figure 12). For residues with relatively high RMSDs, like Ile and Gln, we did not attempt force field modifications since the sample size for these residues is small in the four proteins studied. The side chain J-coupling data suggests the AMOEBA force field, derived from gas phase QM energy profiles, reasonably captures side chain conformational properties in solution. Further improvement would require additional reliable experimental data for individual residue types.

Table 6.

Comparison (RMSD) of J-coupling values (Hz) from AMOEBA simulations and experiments for BPTI, GB3, ubiquitin and lysozyme.

	BPTI	GB3	Ubiquitin	Lysozyme
AMOEBA	1.741	1.44	1.41	2.23
AMBER FF99SB138	1.779	1.48	1.89	2.60
AMBER FF99SB-ILDN138	1.448	0.89	1.43	2.12

Results from the Amber ff99SB force field, and the refined Amber ff99SB-ILDN force field are included for comparison.

Figure 12.

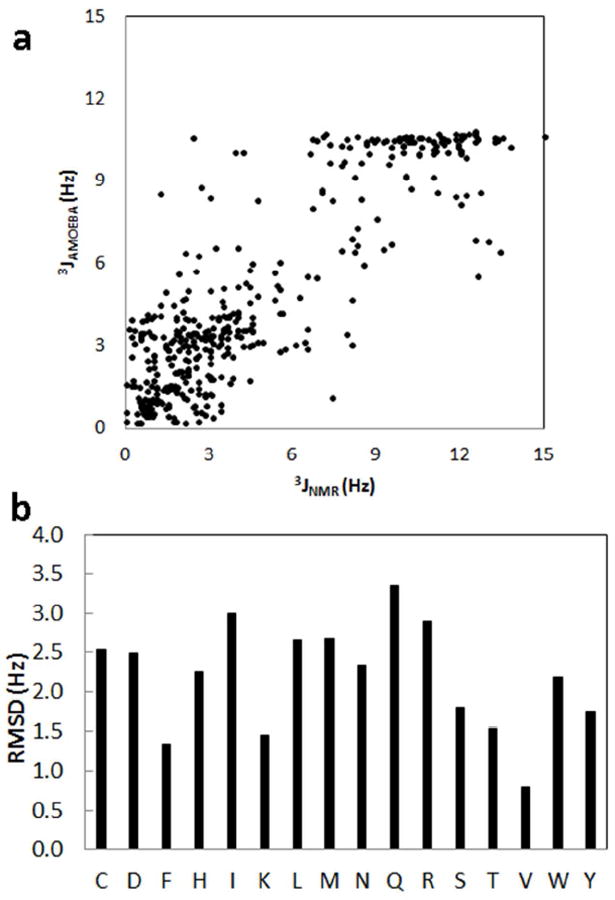
(a) Correlation of the experimental NMR J-couplings and the calculated J-coupling values from the MD simulations of BPTI, GB3 domain, ubiquitin and lysozyme. (b) The RMSDs between the experimental and AMOEBA calculated J-coupling constants for each residue.

CONCLUSIONS

The development and parameterization of the AMOEBA-2013 protein force field is been reported. A distinct feature of the force field is its use of atomic multipole-based electrostatics and explicit treatment of dipole polarization. A mutual induction model with Thole damping is applied to describe both intra- and intermolecular polarization in a consistent manner. The polarization among permanent multipoles is handled via a group-based scheme while induced-induced dipole polarization occurs amongst all polarizable sites. By extracting the intramolecular polarization as defined by the force field, we are able to derive conformation-independent electrostatic multipole parameters from high-level ab initio calculations using a combination of Distributed Multipole Analysis and electrostatic potential fitting. This rigorously derived electrostatic model will be important for accurate description of protein interactions with other biomolecules as well as electrostatic forces within protein molecules.

After determination of vdW parameters, largely obtained by transferred from liquid simulations of small organic molecules,²³ the AMOEBA model was applied to simulation of several peptides and proteins. In addition to the nonbonded electrostatic and vdW forces, the “torsional” energy also plays an important role in setting relative conformational energies. The torsion term is essentially an error function in most classical force fields, and yet it plays a crucial role in determining the detailed conformational properties of peptides and proteins. Recent improvements to the Amber ^{111, 138} and CHARMM force fields^113-114 have demonstrated that conformational populations of small peptides are extremely sensitive to subtle changes (involving fractions of a kcal/mol) in the torsional parameters. In developing the AMOEBA force field, we have resorted to both high-level ab initio (MP2/CBS) peptide energetics and PDB structural statistics in deriving the backbone torsion parameters. The resulting force field performs well in the reproduction of NMR J coupling constants and S² order parameters of several peptide and protein systems. Nonetheless, these are limited validations focusing on conformational properties and torsional parameters. Further extensive investigations involving more proteins and a broad range of thermodynamic properties will be necessary to fully explore various aspects of the potential energy model, and to determine the overall success and possible deficiencies of the force field.

As previously noted,^{113, 139} a CMAP-style splined 2D torsional potential allows a force field to reproduce gas-phase ab initio conformational energies exactly. Such CMAP terms may also exacerbate unphysical features in the rest of the force field and therefore are not transferable. For example, the QM and force field difference could result from an incorrect valence energy bin classical force field at extremely stressed conformations, an effect which has little to do with the “torsion” energy. We plan to revisit use of CMAP correction terms in the future. However, with the exception of Gly, we have removed such terms from the AMOEBA-2013 protein model. While we have strived to derive a balanced and physical force field, better understanding of the limitations of molecular mechanics force fields is essential for continued systematic improvement. Accurate modeling of short-range electrostatic and vdW components, as well as their coupling to valence interactions, will be the key to achieving still greater accuracy and transferability in a future protein force field that performs well in various physical and chemical environments.

Table 1.

The vdW parameters for protein backbone atoms.

Atom class	2r (Å)	ε (kcal/mol)	H-reduction factor
Cα	3.650	0.101
Hα	2.940	0.026	0.91
Cβ	3.820	0.101
Hβ	2.980	0.024	0.92
N (amide)	3.710	0.110
H (amide)	2.590	0.022	0.90
C (carbonyl)	3.820	0.106
O (carbonyl)	3.300	0.112
O- (in −COO-)	3.700	0.129
S	4.005	0.355
S-	4.200	0.355

AMOEBA uses “atom classes” to define vdW and valence parameters while more finely-grained “atom types” are used for electrostatic parameters. Several different atom types may belong to the same atom class. r is the atomic radius; ε is the potential well depth; H-reduction factor accounts for the distance reduction that moves H vdW sphere off its nuclear center toward the heavy atom (X) it attaches to. The number represents the percentage of H-X bond length where the H atom vdW sphere is located at. Note that 2r (diameter) is used here to be consistent with TINKER parameter format.

Table 2.

Comparison of side chain conformational energy (kcal/mol) as calculated by AMOEBA and QM (RI-TRIM MP2/CBS).

	Side chain torsion	RMSD		Side chain torsion	RMSD
Cys	χ1	0.67	Asn	χ1	1.35
	χ2	0.10		χ2	1.06
Met	χ1 same as Glu and Gln	0.40	Glu	χ1 from Met	0.79
	χ2	0.52		χ2 from Gln	1.86
	χ3	0.10		χ3 from Asp χ2	0.42
Ser	χ1	0.84	Leu	χ1	0.32
	χ2	0.22		χ2 averaged over Leu/ Ile	0.31
Thr	χ1 same as Ser and Val	0.96	Val	χ1	0.58
His	χ1	1.24	Phe	χ1	0.65
	χ2	1.31		χ2	0.54
Hid	χ1	0.83	Tyr	χ1 from Phe	0.55
	χ2	0.67		χ2	0.44
Hie	χ1	1.10	Trp	χ1	0.54
	χ2	1.00		χ2	0.55
Ile	χ1 from Val	0.53	Asph	χ1	1.39
	χ2 averaged over Leu/Ile	0.34		χ2	0.97
Arg	χ1 from Met	1.63	Lys	χ1 from Asn	0.74
	χ2 same as Lys	1.08		χ2	0.95
	χ3	1.76		χ3	0.96
	χ4	0.80		χ4	0.73
Asp	χ1 from Asph	1.22	Gln	χ1 from Met	0.79
	χ2	1.01		χ2	1.86
				χ3 from Asn χ2	0.42

The conformational energies were obtained by rotating each listed side chain torsion from 0 to 360° at 30° intervals. For all RMSD calculations, data from two backbone conformations, α-helical and β-sheet, were combined.