Abstract
In the context of observational longitudinal studies, we explored the values of the number of participants and the number of repeated measurements that maximize the power to detect the hypothesized effect, given the total cost of the study. We considered two different models, one that assumes a transient effect of exposure and one that assumes a cumulative effect. Results were derived for a continuous response variable, whose covariance structure was assumed to be damped exponential, and a binary time-varying exposure. Under certain assumptions, we derived simple formulas for the approximate solution to the problem in the particular case in which the response covariance structure is assumed to be compound symmetry. Results showed the importance of the exposure intraclass correlation in determining the optimal combination of the number of participants and the number of repeated measurements, and therefore the optimized power. Thus, incorrectly assuming a time-invariant exposure leads to inefficient designs. We also analyzed the sensitivity of results to dropout, mis-specification of the response correlation structure, allowing a time-varying exposure prevalence and potential confounding impact. We illustrated some of these results in a real study. In addition, we provide software to perform all the calculations required to explore the combination of the number of participants and the number of repeated measurements.
Keywords: optimal design, longitudinal study, sample size, intraclass correlation
1. Introduction
Sample size and power formulas in the context of longitudinal studies comparing two groups (e.g., exposed and unexposed) have been widely studied but mostly in the context of experiments. Hence, they assumed that the exposure is assigned by design and, in most cases, they considered that it is time-invariant, as in many clinical trials (e.g. placebo vs. treatment groups) [1–12]. Some studies have considered the case of exposures that vary over time but in a way that is controlled by the investigator, such as in crossover trials [13–15]. However, in observational longitudinal studies, exposure is not controlled by the investigator and often such studies involve time-varying exposures, which can imply both a large number of observed exposure patterns and a high variability in the number of exposed periods per participant. Two recently published papers showed that it is crucial to characterize the within-individual variation of the exposure in order to obtain correct calculations of power and sample size in that context [16, 17].
When neither the number of participants nor the number of repeated measurements are fixed a priori, it can be of interest to find their optimal combination in terms of maximizing the power or minimizing the cost of the study subject to a budget or power constraint, respectively. This is important for the efficient allocation of financial resources. Some authors have studied this problem but they did not consider a time-varying exposure [18–27]. As occurs in the unconstrained design problem, it is expected that the optimal design in the constrained problem will also be sensible to the degree of within-subject variation in exposure.
In this paper, we studied the combination of number of participants and number of repeated measurements in observational longitudinal studies such that the power to detect the hypothesized effect is maximized without exceeding a fixed budget, or the cost of the study is minimized while achieving a certain target power. We considered a multivariate normal response variable with a damped exponential covariance structure and a binary exposure that can be time-varying. We analyzed two response patterns under the alternative hypothesis, one assuming an acute and transient effect and the other a cumulative effect. We explored the influence of several parameters, including the dropout rate, on the design results. In addition, we also explored the potential impact of the presence of confounders in the study. We illustrate the new methodology with data from a study of the respiratory effects of cleaning products [28]. In addition, we provide a publicly available open source R package to perform all the design calculations described in the paper.
2. Parameterization and models
To design a longitudinal study with a fixed follow-up time, we need to find the combination of number of participants (N) and number of repeated measurements per participant (r, i.e., the total number of measurements per participant is r + 1). Without loss of generality, we defined the fixed duration of the study as the time unit. We assumed that all measurements for all participants are taken at the same set of time points, t = 0, 1/r, 2/r, … , 1, where 1/r is the elapsed time between two consecutives measurements. We also assumed a linear form for the mean, , where Yi and Xi are the multivariate normal response of interest and the covariate matrix for participant i, respectively, and B is the vector of unknown regression parameters; and Var(Yi|Xi) = Σ(i = 1, … , N), where Σ is the (r + 1) × (r + 1) residual covariance matrix assumed equal for all participants (i.e., we assumed homogeneity across the participants).
The constant mean difference (CMD) response pattern is defined as
| (1) |
where Yij and Eij ∈ {0, 1} are the response and the exposure state, respectively, for the i-th participant at the j-th measurement, and tj = j/r, j = 0, 1, … , r are the time points. The parameter of interest is β2, which can be interpreted as the expected difference in the mean of the response variable, at any time point, between exposed and non-exposed. The minimum value of r in model (1) is 0, which corresponds to a cross-sectional study.
The linearly divergent difference (LDD) response pattern is defined as
| (2) |
where is the cumulative exposure for the i-th individual in the j-th measurement, assuming for all participants. The parameter of interest is β3, which can be interpreted as the expected difference in the mean of the response variable at the end of the follow-up between the worst exposure pattern (i.e., those exposed at all measurements) and those not exposed for the entire follow-up. For a time-invariant exposure, model (2) is equivalent to a model with the main effects of time and exposure and their interaction. The minimum value of r in model (2) is 1, given that at least two measurements are needed to estimate the rate of change over time.
To characterize the covariance structure of the response, we considered a damped exponential structure (DEX) [29], whose covariance matrix has diagonal elements σ2 and off–diagonal [j, j’] elements, where ρ is the correlation between the first and the last response measurements and θ ∈ [0, 1] is the damping parameter. We focused especially on two well-known cases, compound symmetry (CS(σ, ρ)), when θ = 0, and first order autoregressive (AR(1)), when θ = 1.
We considered missing completely at random data by allowing a monotone dropout pattern, i.e. that losing one individual measurement implies losing all the subsequent measurements of that individual. We assumed that there is no missing data at the first measurement and that each subject that has not dropped out of the study at a given measurement time has a probability πm of dropout at the subsequent measurement, assuming a missing completely at random (MCAR) pattern. Thus, there are r + 1 possible dropout patterns. By representing the dropout patterns by a 0/1 string of length r + 1, the g-th pattern is () with probability
| (3) |
If r = 0, there is only one measurement and πm = 0.
For investigators performing study design calculations, it may be easier to provide a value for πM, the proportion of subjects lost at the end of follow-up. Its relation to πm is expressed as
The variance of the estimate of the regression coefficient of interest, β2 in model (1) and β3 in model (2), and hereinafter generically identified as β, is needed. We used the generalized least squares (GLS) estimator which takes into account the within-participant correlation. Since the covariate matrix Xi is unknown a priori, we used, following Whittemore [30] and Shieh [31], the asymptotic variance of the GLS estimate of B which is , where, after adapting for dropout following Yi [10],
| (4) |
πg is defined in (3), and can be fully specified by the first- and second-order moments of the covariate distribution because Σ is assumed independent of the covariates in our context [32].
We are interested in the [m, m]–th element of ΣB, where m is the position of β in the vector of regression coefficients B or, equivalently, the position of the column associated to the β parameter of interest in the design matrix, Xi,
| (5) |
For some covariance structures of Σ, such as CS, and under assumptions above, there is a simple formula for (5), while for others it must be computed numerically.
The prevalence vector of exposures pe = (pe0, … , per) is needed. We allow the prevalence to vary linearly from pe0 at the first measurement to per at the end of the follow-up. This linear trend of the exposure prevalence can thus be parameterized as
where is the mean of the exposure prevalence along the r + 1 measurements and is the relative change in the exposure prevalence between the first and the last measurements. When the exposure prevalence is constant, γ = 0.
In order to perform design calculations under models (1) and (2), the covariance of the exposure process, ΣE, must also be characterized. Once the intraclass correlation of exposure is known, the exact value of if the response covariance structure is CS and the response pattern is CMD is determined exactly (web-based supporting document, section A) or to good approximation otherwise [16, 17] without characterization of the full matrix ΣE. The intraclass correlation of exposure is defined as
where sum() and Tr() denote the sum of the elements and the trace of a matrix respectively [33]. ρe can be interpreted as a measure of within-participant variation of exposure. When ρe takes its maximum value of 1, each of the participants are either exposed or unexposed for the entire follow-up (i.e., the exposure is time-invariant). Conversely, when ρe takes its minimum value, the within-participant variation of exposure is greatest [33]. The upper bound of ρe is lower than 1 when the exposure prevalence is time-varying [16] and 1 otherwise. For binary variables, as here, the lower bound of ρe is
where frac(x) denotes the fractional (non-integer) part of x [34]. When the covariance structure of the exposure, ΣE, is CS and the exposure prevalence is constant, ρe becomes the common off-diagonal term of the exposure correlation matrix.
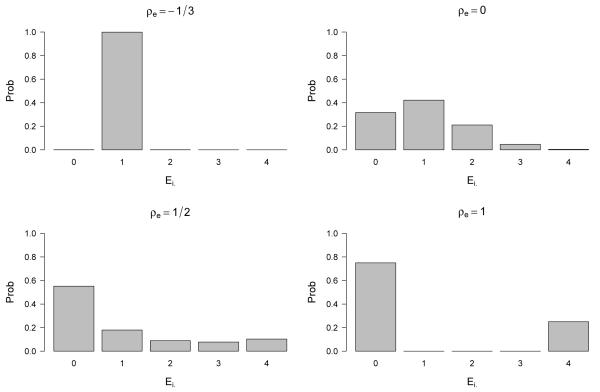
As a tool for deciding an appropriate value for ρe at the study design phase, it can be useful to explore the distribution of the number of exposed periods per participant, once the values of ρe, , and r have been fixed and ΣE is assumed to follow CS. For instance, Figure 1 shows this distribution for the case in which r = 3 and , for ρe = −1/3, 0, 1/2 and 1. Our R package can be used to build this kind of figures.
Figure 1.
Distribution of the number of exposed periods, Ei. for r = 3, and different values of ρe, assuming exposure covariance structure CS with correlation parameter ρe, and no dropout.
All parameters that need to be provided by the investigator to compute the optimal combination of number of participants and number of repeated measurements are described in Table 1.
Table 1.
Parameters needed to compute (ropt;Nopt).
| Parameter | Description |
|---|---|
| Pattern | Assumed pattern of the response Y (CMD or LDD) |
| σ 2 | Diagonal element of the DEX covariance structure matrix of the response Y |
| ρ | Correlation between the first and the last measurements of the response Y |
| θ | Damping parameter of the DEX covariance structure matrix of the response Y |
| ρ e | Intraclass correlation of the exposure E |
| p e0 | Prevalence of the exposure E at the first measurement (at time 0) |
| per | Prevalence of the exposure E at the last measurement (at the end of the follow-up) |
| π M | Proportion of subjects lost by the end of follow-up |
| κ | Ratio between the cost of the first measurement and each of the subsequent ones |
| c 1 | Cost of the first measurement (including recruitment) for one participant |
| Budget a | Total budget for the study, including recruitment and follow-up |
| Power b | Target power of the study |
| α b | Significance level |
| b | Effect size under the alternative hypothesis |
If interested in maximizing the power of the study without exceeding a fixed budget.
If interested in minimizing the total cost of the study while achieving a certain target power.
3. Optimal allocation
Let us call c1 the monetary cost of the first measurement of each participant and suppose it is κ times more expensive than each of the subsequent ones, i.e
This is justified by the incorporation of recruitment costs into the first measurement. Then, the total cost of recruitment and follow-up of N participants for a total of r + 1 measurements is
| (6) |
Asymptotically, the power of a study testing the significance of an individual regression coefficient, β, through a Wald test can be expressed as
| (7) |
where is the value of β under the alternative hyphotesis, is the standard error of , α is the significance level and zq and Φ(·) are the q–th quantile and the cumulative density of the standard normal distribution, respectively.
Our aim is to find the combination of N and r (Nopt, ropt) that maximizes the power of the study without exceeding a fixed budget, i.e.
It can be easily shown that the value of r that solves this problem is the same as the solution to the problem of minimizing the cost of a study while achieving a certain target power, i.e.
With the cost definition in (6), both problems are equivalent to solving the following unconstrained optimization problem,
| (8) |
whose solution provides the value of ropt. Then, the value of Nopt can be obtained from the constraint in the optimization problem as detailed below.
In the presence of missing data, the expression for the total cost of the study changes. The cost function (6) can be adapted by computing the expected cost over the r + 1 missing patterns (see web-based supporting document, section B), which results in
| (9) |
The function to minimize becomes then
| (10) |
which provides a solution for ropt.
The optimal number of participants Nopt, is obtained as follows. If the investigator is interested in fixing the maximum acceptable budget in order to maximize the power, then the total budget and c1 must be specified and Nopt is obtained from expression (9) as
| (11) |
and the floor function ⌊x⌋ denotes the greatest integer not greater than x.
If the investigator is interested in achieving a certain power while minimizing the cost, then the power and the expected effect under the alternative hypothesis, , are needed and Nopt is obtained from expression (7) as
| (12) |
where is the result of computing expression (5) for r = ropt and the ceiling function ⌈x⌉ denotes the smallest integer not smaller than x.
It should be made clear that the combination of N and r that solves problem (10) can be considered optimal in terms of maximizing the power or minimizing the cost, and under the assumptions implicity made in the problem as, for instance, the asymptotic approximation in both (4) and (7), the cost function and dropout structures assumed. In the next section, we first solve problem (10) for some basic scenarios in which we derived simple formulas for the solution, and subsequently explore numerically other more complex scenarios.
4. Results for the optimal number of repeated measurements
4.1. Basic scenarios results
In addition to assuming asymptotic regime, the basic scenarios for which we have obtained formulas for ropt are characterized by the following assumptions: 1) No dropout, i.e. πm = 0; 2) the correlation structure of the response is CS(σ, ρ), i.e. DEX with θ = 0; and 3) the exposure prevalence is constant, i.e. pej = pe, ∀j = 0, … , r. In addition, we make a fourth assumption when response pattern is LDD and the exposure is time-varying; in this case, the covariance structure of the exposure is assumed to be CS with correlation parameter ρe. Expressions for for these basic scenarios are given in Table 2 (web-based supporting document, section A). We then derived the expressions for the optimal total number of repeated measurements, ropt, and proved that ropt depends only on ρe, ρ and κ (web-based supporting document, sections C and D).
Table 2.
Expressions for under CMD and LDD patterns for the response assuming CS(σ, ρ) for the response covariance structure, no dropout (μm = 0) and a constant exposure prevalence (pej = pe; ∀j = 1, … , r + 1). Results for CMD are derived for any correlation structure for the exposure while results for LDD are derived under the assumption of CS correlation structure for the exposure.
For any correlation structure of exposure.
Assuming compound symmetry for the correlation structure of exposure.
For CMD under the basic scenario, the solution to the unconstrained problem (8) is
| (13) |
where
For a time-invariant exposure (ρe = 1), expression (13) becomes
| (14) |
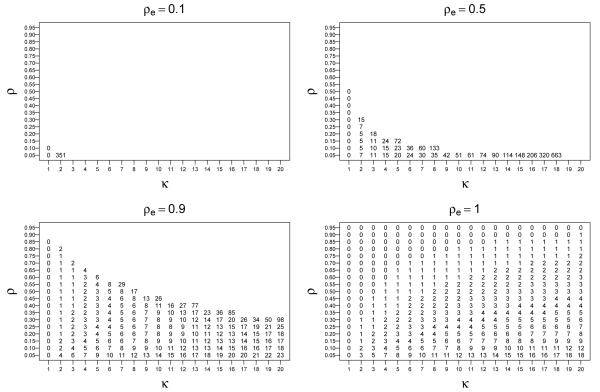
Result (14) has been given, in the particular context of cluster randomized trials, by Cochran [18] and Raudenbush [22]. According to (14), the optimal under CMD is to take only one measurement (i.e., no repeated measurements) if κ is not greater than the threshold , which increases as ρ increases. Otherwise, the optimal is to take a number of repeated measurements that increases as κ increases or ρ decreases. Overall, in the time-invariant case, values of κ and ρ close to 1 favor taking only one measurement, while the high cost of the first measurement relative to the following ones and the low correlation of the response become factors that favor more repeated measurements. When the solution is generalized to the context of a time-varying exposure (ρe < 1), the relationship between the optimal number of repeated measurements and the parameters ρe, ρ and κ is complex, as given by (13). Figure 2 illustrates more clearly this relationship. The intraclass correlation of exposure ρe strongly affects the optimal number of measurements. When comparing the value of ropt for a given combination of κ and ρ across different values of ρe in Figure 2, one can readily see that, in most cases, more repeated measurements are advisable as the within-subject variation in exposure increases (i.e. ρe decreases). In many instances, the optimal is to take as many repeated measurements as possible (corresponding to points without a label in the plot), a situation that becomes more common as κ or ρ increase. This behavior is pronounced as ρe decreases, to the point that if ρe = 0.1 then ropt = ∞ for any combination of κ ≥ 2 and ρ ≥ 0.1.
Figure 2.
Each number in the plot area indicates the optimal number of repeated measurements, ropt, under the CMD response pattern in the basic scenario, which assumes covariance structure CS(σ, θ) for the response (θ = 0), no dropout (πm = 0) and constant exposure prevalence (pej = pe, ∀j = 0, … , r). Points without label correspond to those cases in which we should make as many measurements as possible (mathematically, infinite). Results correspond to values of the ratio between the economic cost of the first measurement and one of the following ones, κ = 1, 2, … , 20, values of ρ = 0.05, 0.10, … 0.95 and values of the intraclass correlation ρe = 0.1, 0.5, 0.9 and the time-invariant exposure case, ρe = 1.
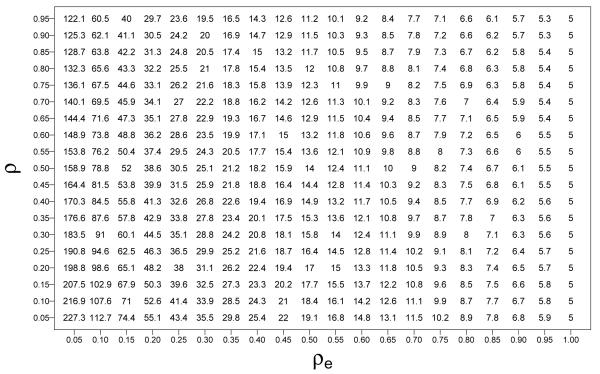
For LDD in the basic scenario, the optimal is to take only two measurements (i.e., only one repeated measurement) if the ratio of costs of the first to the subsequent measurements, κ, is not greater than and as many measurements as possible (mathematically, infinity) otherwise. The threshold κ*, which equals 5 for time-invariant exposure, increases as ρe or ρ decrease, as shown in Figure 3, where each number in the plot area represents the value of κ* for a specific combination of ρe and ρ. Thus, if κ is not greater than 5, the optimal number of repeated measurements is 1 independently of the values of ρe and ρ. Compared to the time-invariant case, when the exposure is time-varying it is harder to justify taking more than one repeated measurement, since the ratio of costs that justifies doing so, κ*, is higher.
Figure 3.
Threshold of the ratio of costs of the first measurement over the subsequent ones (κ*) above which it is advisable to take as many repeated measurements as possible in the LDD case under the basic scenario. Otherwise, if the ratio of costs is less than κ*, the optimal is to take ropt = 1. The basic scenario for the LDD response pattern assumes covariance structure CS(σ, ρ) for the response (θ = 0), no dropout (πm = 0), constant exposure prevalence (pej = pe, ∀j = 0, … , r) and CS(ρe) exposure correlation structure. The threshold takes the form . The column with constant value of κ* = 5 corresponds to a time-invariant exposure (ρe = 1).
Expressions (13) and (14) provide, in general, a non integer value for ropt. The effective value of ropt is that which, in combination with the value for Nopt given by (11) or (12), provides the maximum power or the minimum cost, respectively. The R package that we provide performs this correction.
4.2. Effect of varying the covariance stucture of the response
The results for the basic scenarios in the previous section were obtained assuming a CS(σ, ρ) covariance structure of the response, which is the particular case of DEX covariance structure with damping parameter θ = 0. There are many longitudinal situations where CS is not plausible and thus, in this section, we examine how the results change for θ > 0, in which case the minimization problem must be solved numerically. It can be easily shown that ropt does not depend on σ. Thus, one can evaluate the objective function for a specific combination of the parameters θ, ρe, ρ and κ and a range of values r = 0, 1, … , rmax and then find the minimum subject to ropt ≤ rmax. The value of rmax was fixed to 20 and 30 for CMD and LDD response pattern respectively. The maximum explored value of κ was 20.
For CMD response pattern, when varying θ from 0 (CS) to 1 (AR(1)), if the exposure is time-invariant (ρe = 1), differences in the result for ropt appear only for low values of ρ or high cost of the first measurement (κ ≥ 10). These differences were not greater than 3 units. For instance, for AR(1) covariance structure of the response, the optimal total number of repeated measurements varies only between 0 and 2 for κ ≤ 20 while for CS covariance structure of the response, it varies between 0 and 4. If the exposure is time-varying (ρe < 1), the effect of θ on ropt complexly depend on the combination of the values of the parameters ρe, ρ and κ.
For LDD response pattern, the exploration, constrained to rmax = 30 and κ ≤ 20, showed that positive values of θ break the dichotomy 1 vs. ∞ in the results for the optimal number of repeated measurements that was observed for CS (θ = 0). Still, the value 1 was obtained for most of the combinations of the parameters θ, ρe, ρ and κ, but higher values were obtained in a small portion of cases. Specifically, if θ ≥ 0.5, the optimal number of repeated measurements was 1 regardless of the value of the remaining parameters. The optimal number of repeated measurements was also 1 for any κ ≤ 9. Increasing ρe or κ, or decreasing ρ tends to increase ropt. As an illustration, Table 3 shows the approximate minimum value of κ, κ*, for which the optimal number of repeated measurements is greater than 1 and the corresponding maximum value of the optimal number of repeated measurements obtained in the exploration over ρ ∈ (0.05, 0.95). The exploration was restricted to κ ≤ 20 and the maximum value of ropt was reached systematically for the maximum explored value of κ and the minimum explored value of ρ.
Table 3.
Effect of θ in determining ropt for the LDD response pattern assuming no dropout, a constant exposure prevalence, CS(ρe) exposure covariance structure and DEX(θ, ρ) response covariance structure. Exploration was constrained to κ ≤ 20 and ρ ∈ (0:05; 0:95). Each pair represents (max(ropt); κmin) where κmin is an approximation to the minimum value of κ for which ropt is greater than 1 (over the range of ρ) and max(ropt) is the maximum value of ropt, which was always reached at the maximun explored value of κ (20) and the minimum explored value of ρ (0.05).
| Intraclass correlation of exposure (ρe) | |||||||
|---|---|---|---|---|---|---|---|
| θ | 0.1 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
| 0 (CS) | (∞, 60:5) | (∞, 11:2) | (∞, 9:2) | (∞, 7:7) | (∞, 6:6) | (∞, 5:7) | (∞, 5) |
| 0.10 | * | * | (18, 19) | (21, 14) | (23, 12) | (26, 10) | (30, 8) |
| 0.20 | * | * | * | * | (14, 16) | (15, 13) | (17, 10) |
| 0.25 | * | * | * | * | (11, 19) | (12, 15) | (14, 11) |
| 0.30 | * | * | * | * | * | (10, 17) | (12, 13) |
| 0.40 | * | * | * | * | * | * | ( 8, 16) |
| ≥ 0:50 | * | * | * | * | * | * | * |
ropt = 1 for any combination of κ ≤ 20, ρe ≥ 0:1 and ρ ∈ (0:05; 0:95).
4.3. Effect of dropout
We analyzed the effect of dropout on the results for the basic scenarios. To do so, we explored a grid of values for the proportion of losses at the end of follow-up, πM, between 0 (which corresponds to the basic scenarios) and 0.65. The exploration was constrained to r ≤ 30 with θ fixed at 0 (CS covariance structure of the response). For both the CMD and LDD response patterns, the results for ropt were the same as those obtained when πM = 0, except for a small percentage of combinations of values for ρe, κ and ρ. Specifically, for the CMD response pattern, increases of more than 3 units in ropt were observed in only 5% of explored scenarios corresponding to high values of πM (≥ 0.5). In few scenarios, characterized by a high value of ropt (24 to 30) and κ = 1, an slight decrease of ropt (1 to 3 units) was detected for high values of πM (0.6). For the LDD response pattern, an increase in πM favors ropt = 1 for high values of πM for a time-invariant exposure, while it favors increasing ropt for lower values of ρ and high values of κ for a time-varying exposure. In addition, very few changes were observed when θ was fixed to 1 (AR(1) covariance structure of the response).
According to (9), dropout can affect the value of Nopt even in those cases in which no changes were observed in ropt. For instance, Nopt increases as πM increases for a fixed value of ropt.
In addition, we performed a simulation study in order to explore the accuracy of our formulas and the potential impact of the violation of the MCAR structure assumed for the missing data in our methodology. Thus, we performed a simulation study (web-based supporting document, section E) assuming a missing at random (MAR) structure. In particular, we assumed that the probability of dropout of participant i at measurement j was π1 if the response at the measurement j – 1 was lower than its third quartile or π2 otherwise. We explored 9 scenarios, obtained from all combinations of the overall dropout fraction (0.1, 0.3 and 0.6) and the ratio π1/π2 (0.5, 0.8 and 1, the latter corresponding to MCAR), and fixing the values for the remaining parameters. In these scenarios, no significant differences were found when comparing the expected power according to our formulas (which was set at 0.8) with the empirical power obtained by simulation. Regarding the dropout pattern, these results provide some robustness to our formulas to departures from MCAR. However, the number of explored scenarios was very limited.
4.4. Effect of a time-varying exposure prevalence
To explore the effect of a time-varying exposure prevalence, we considered a grid of values for the average exposure prevalence, , between 0.05 and 0.95 and for γ between −0.95 (i.e. per = pe0/20) and 20 (i.e. per = 21pe0). The exploration was constrained to r ≤ 30, θ = 0 and κ ≤ 20.
For the CMD response pattern, our exploration revealed that increasing the difference between the prevalance at the beginning and the end of follow-up (i.e. the higher ∣γ∣) tends to increases the value of ropt. These changes, almost negligible in most cases, become meaningful for extreme changes in the exposure prevalence and high values of the mean prevalence (web-based supporting document, section F, Table F.1).
For the LDD response pattern, a time-varying exposure prevalence disrupts the dichotomy 1 vs. ∞ for ropt. As under the CMD response pattern, differences appeared only for large changes in the exposure prevalence between the first and the last measurements. For greatly time-increasing exposure prevalence, almost no changes were detected for values of κ ≤ 5 while for κ ≥ 8 and mean prevalence not higher than 0.3, the effect was to change ropt from ∞ to 1. For greatly time-decreasing exposure prevalence, essentially ropt tended to increase a few units (from 1 to 4) in those cases in which ropt was 1 under constant exposure prevalence (web-based supporting document, section F, Table F.2).
4.5. Confounding
In the context of observational studies, the confounding problem is unavoidable. The potential effect of confounding can not be addressed in a systematic way due to the wide range of possible scenarios, and some of the previously proposed methods are limited [35]. We performed a simulation study to explore the effect of confounding by assessing bounds for power, in line with Haneuse et al. [35]. We considered up to 6 confounders and 5 scenarios for strength of confounding, which were explored for different combinations of the values of ρe, N and r, resulting in a total of 840 scenarios with 1000 simulations per scenario (more details on the simulation design are available at the web-based supporting document, section G). In each scenario, we compared the empirical power, calculated after including the confounders in the model, with the expected power using our formulas, which do not take into account the effect of confounders. The scenarios were set so that the expected power was 0.9. Table 4 shows results under the CMD response pattern. As expected, it can be seen that, in general, the empirical power decays with both the strength of confounding and the number of confounders. The value of ρe seems to play a role in the confounding impact. Indeed, Table 4 shows that, in longitudinal studies with high values of ρe (0.8 in our explorations), the power after accounting for confounding was no lower than 0.8 (or 0.72 in scenarios with r = 1) when the target power was 0.9. For low values of ρe, occasional values lower than 0.8 were obtained for scenarios with several confounders with moderate to strong effect. Under the LDD response pattern, almost no impact of confounders was observed except in scenarios with ρe = 0.2 and r = 2. In these cases, the empirical power dropped to a minimum value of 0.82. The effect of confounding could be lower in the LDD case because when building the cumulative exposure variable the confounding effect simulated for (non-cumulative) exposure is diluted.
Table 4.
Estimated bounds of confounding impact on power under the CMD response pattern. In each confounding scenario and for any number of confounders from 0 to 6, the median, (minimum, maximum) values of the empirical power (%) were calculated across scenarios with common value of ρe and all combinations of the values of the parameters N = 50, 200, 500 and 2000; r = 1, 8 and 20. In all scenarios, the expected power according to our formulas, disregarding the potential confounding effect, was 0.9. The empirical power was calculated using 1000 simulations per scenario and including the confounders in the model. Further details on this simulation study are available in the web-based supporting document, section G.
| ρe = 0:2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Confounding scenario |
OR between Zm and E, ϕm |
Effect of Zm on Y, βZm † |
Number of confounders | ||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |||
| Constant strength | |||||||||
| 1. Weak | 1.5 | 0.5 | 90 (87, 91) | 88 (88, 89) | 89 (86, 91) | 88 (85, 89) | 88 (86, 90) | 87 (85, 88) | 86 (84, 88) |
| 2. Moderate | 2.0 | 1.0 | 90 (88, 92) | 87 (84, 90) | 87 (85, 88) | 84 (82, 86) | 84 (81, 86) | 81 (78, 83) | 79 (74, 83) |
| 3. Strong | 2.5 | 1.5 | 90 (88, 91) | 86 (84, 88) | 85 (83, 87) | 80 (76, 81) | 78 (74, 80) | 75 (70, 76) | 73 (70, 77) |
| Diminish strength | |||||||||
| 4. Moderate | 3.0 → 1.5 | 2.0 → 0.5 | 90 (89, 92) | 84 (81, 86) | 82 (80, 85) | 78 (75, 80) | 79 (77, 83) | 75 (72, 77) | 76 (73, 78) |
| 5. Strong | 4:0 → 1:5 | 3:0 → 0:5 | 90 (88, 91) | 79 (77, 82) | 78 (75, 82) | 72 (68, 75) | 70 (64, 72) | 69 (66, 72) | 68 (64, 72) |
| ρe = 0:8 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Confounding scenario |
OR between Zm and E, ϕm |
Effect of Zm on Y, βZm† |
Number of confounders | ||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |||
| Constant strength | |||||||||
| 1. Weak | 1.5 | 0.5 | 90 (89, 92) | 90 (88, 92) | 89 (87, 91) | 89 (88, 91) | 89 (86, 91) | 89 (87, 91) | 88 (86, 90) |
| 2. Moderate | 2.0 | 1.0 | 90 (89, 92) | 89 (87, 90) | 89 (87, 91) | 87 (84, 90) | 87 (84, 90) | 86 (81, 89) | 85 (80, 88) |
| 3. Strong | 2.5 | 1.5 | 91 (90, 92) | 88 (87, 90) | 88 (84, 90) | 86 (81, 89) | 85 (80, 89) | 83 (77, 88) | 83 (77, 88) |
| Diminish strength | |||||||||
| 4. Moderate | 3:0 → 1:5 | 2:0 → 0:5 | 90 (88, 92) | 88 (84, 90) | 86 (83, 89) | 85 (78, 87) | 85 (80, 89) | 83 (78, 87) | 84 (76, 88) |
| 5. Strong | 4:0 → 1:5 | 3:0 → 0:5 | 90 (89, 92) | 86 (80, 89) | 84 (78, 89) | 82 (73, 86) | 81 (75, 85) | 80 (72, 86) | 80 (72, 86) |
: In units of the β of interest.
In addition, we performed another simulation study (see web-based supporting document, section G) in order to explore how confounding affected the optimal combination of N and r. Under the CMD response pattern, discrepancies in the study design were observed exclusively for high values of ρe and κ. Similar results were obtained under the LDD response pattern.
Even taking into account that this exploration is not exhaustive, it appears that one can use conservative values of the target power (e.g. 0.9 when 0.8 is intended) to account for the effect of confounding when using our formulas. More detailed results on the simulations are presented in the web-based supporting document, section G.
5. Illustrative example
In this section, we used data from a study on cleaners and respiratory health to provide a design for a new hypothetical study on the same topic. Briefly, Medina-Ramón et al. [28] followed a group of N = 43 female domestic cleaners during r + 1 = 15 days. Each day, they provided measures of pulmonary function and annotated in a diary whether they performed certain cleaning tasks or used certain cleaning products. The study was observational and therefore the exposures were not assigned by design, rather, the cleaners performed the tasks and used the products that their work day required. All exposures showed day-to-day variations within-subjects. Here, we focus on the two exposures that had the highest and lowest value of ρe, namely vacuum cleaning and using air freshener sprays. The first one had ρe = 0.13 and an average prevalence of while the second had ρe = 0.60 and = 0.17. As expected, the prevalence of the exposures showed no trend so we assumed a constant prevalence of the exposures. Thirty-one participants in the original study provided complete data, so we set πM = 0.28. The residual variance and the response covariance damping parameter were taken from the study and set to σ2 = 0.43 and θ = 0.12, respectively. We used low (0.3) and high (0.7) values for ρ. Regarding the hypothesized effect, we fixed it at a difference of 10% in the expected mean value of the response between exposed and non exposed assuming the CMD response pattern. This results in = −0.39. The objective was to minimize the total cost of the study fixing a minimum required power of 0.9. The first measurement was assumed to be 2 times more expensive than each of the subsequent ones (i.e., κ = 2). We constrained the maximum number of repeated measurements to 20. All calculations were performed fixing a significance level α = 0.05.
Results, shown in Table 5, revealed a notable discrepancy in both the optimal number of repeated measurements and optimal number of participants between the assumptions of a time-invariant exposure (i.e., ρe = 1) and a time-varying exposure (using the observed value of ρe). When using the observed value of ρe, the optimal design was to take as many measurements as possible for both exposures, while assuming ρe = 1, the optimal was to perform a cross-sectional study (if ρ = 0.7) or a longitudinal study with only two measurements (if ρ = 0.3). As can be seen in Table 5, incorrectly using the design formulas for ρe = 1 when the exposure is actually time-varying can lead to discrepancies not only in ropt and Nopt, but also in the final cost of the study. For example, using the time-invariant exposure formulas leads to designs with an increase in cost of between 140% and 480% for using air freshener sprays, and of between 30% to 190% for vacuum cleaning. In some cases, the slope of the cost as a function of r attenuates as r increases and thus, the investigator could be interested in increasing the number of participants in exchange for reducing the number of repeated measurements without a significant increase of the cost (web-based supporting document, section H).
Table 5.
Optimal combination of number of repeated measurements and number of participants to achieve at least 90% power, and resulting cost of the study. The problem was constrained to ropt ≤ 20. Based on the data of the example, the following values for the parameters were used: For vacuum cleaning, ρe = 0:13 and = 0:37, and for using air freshener sprays ρe = 0:60 and = 0:17. Constant exposure prevalence was assumed. For all calculations, σ2 = 0:43, θ = 0:12, πM = 0:28, c1 = 1, κ = 2, α = 0:05. Calculations were performed to detect a difference of 10% between exposed and non-exposed under the CMD response pattern.
| Exposure | Response correlation |
Exposure covariance |
Optimum | Costa | |
|---|---|---|---|---|---|
| r opt | N opt | ||||
| Vacuuming | ρ = 0.3 | CS(ρe) | 18 | 6 | 51.6 |
| t.i.e.b | 1 | 92 | 125.1 | ||
| ρ = 0.7 | CS(ρe) | 15 | 3 | 22.0 | |
| t.i.e.b | 0 | 128 | 128.0 | ||
| Air freshener sprays | ρ = 0:3 | CS(ρe) | 20 | 17 | 160.7 |
| t.i.e.b | 1 | 152 | 206.7 | ||
| ρ = 0:7 | CS(ρe) | 19 | 8 | 72.2 | |
| t.i.e.b | 0 | 211 | 211.0 | ||
In units of the cost of the first measurement.
Using formulas assuming a time-invariant exposure (i.e. ρe = 1).
6. Discussion
In this work, we developed methods to explore, under certain assumptions, the optimal combination of number of participants and number of repeated measurements when there are cost or power constraints. We examined a variety of situations typical for observational longitudinal studies in which the exposure can vary over time within participants in a manner not controlled by the investigator. The degree of within-subject variation in exposure, as measured by the intraclass correlation of exposure, proved to be a key parameter for the optimal design. We provide an R package so that the optimal design can be calculated for specific studies, and also examined general patterns. In models studying acute exposure effects (CMD), results have already been presented for a time-invariant exposure, suggesting that when the repeated measurements are not much cheaper than the first, the optimal is to take one or just a few repeated measurements [18, 22]. If the exposure is time-varying, however, more repeated measurements may be advisable, and when the within-subject variation is high, the optimal design may be to take as many repeated measurements as possible. In models studying cumulative exposure effects (LDD), if the exposure is time-invariant, the optimal is to take just one repeated measure if the ratio of costs of the first measurement vs. the subsequent ones is less than 5, and to take as many measurements as possible otherwise. When the exposure is time-varying, the pattern is the same but the ratio of the costs threshold is higher than 5, thus increasing the number of situations where the optimal is to take just one repeated measure.
Our results extend the previous work on optimal allocation in longitudinal studies [18–26] to the case of a time-varying exposure, as often occurs in observational research. Previous work considered somewhat sligthly different settings, including different covariance structures, cost functions or missing data structure. The methodology described here can be easily adapted to those other settings. The general results described in the previous paragraph were found for a basic scenario in which the response had CS covariance, there was no dropout and the exposure prevalence was constant. We explored how the results changed when some of these assumptions were relaxed. Importantly, our explorations were performed by changing one assumption at a time, precluding general interpretations. If needed, the R package provided could be used to explore other combinations.
In terms of the covariance of the response, we explored variations following a DEX covariance structure. Others have studied covariances that resulted from mixed models with a random intercept and slope [8, 16], or covariances that mix a random intercept with autoregressive errors [26]. When the response follows DEX covariance instead of CS, under the acute exposure effect model, the optimal number of repeated measurements increases as the damping parameter θ increases. This amplifies the differences with the time-invariant exposure case. Under the cumulative exposure effects model, increasing the damping parameter breaks the dichotomy 1 vs. ∞ in the optimal number of repeated measurements observed when the response follows CS covariance. In general, high values of θ favor a smaller number of repeated measurements compared to the CS case.
Monotone dropout had almost no influence on ropt, except in a few combinations of the values of the study design parameters. Galbraith [25] also investigated the effect of missing data on the optimal combination (N, r) under the LDD response pattern in the context of a time-invariant exposure. They examined several dropout patterns and also found that the optimal allocation was in general not affected by the extent or kind of dropout. They suggested computing the sample size for 90 % power when 80 % power is intended, if the expected overall dropout is no more than 30%. In our case, the amount of dropout is directly used as an input parameter for the design calculation.
The exposure prevalence is a parameter that does not affect ropt when the exposure is time-invariant. However, it does play a role when the exposure is time-varying, and therefore we explored the effects of pe on ropt. Under the acute exposure effect model, the higher the variability of this prevalence the higher the optimal number of measurements. Under the cumulative exposure effect model, the effect depends on the sign of the time trend of the exposure prevalence. If the exposure prevalence is time-increasing, the optimal number of repeated measurements tends to decrease (changing always from ∞ to 1), while if the exposure prevalence is time-decreasing, the dichotomy 1 vs. ∞ is disrupted with no clear patterns with respect to the remaining parameters involved in the study design.
We performed a simulation study to explore the effect of confounding by assessing bounds for power, in line with Haneuse et al. We considered a variety of confounding scenarios. Results showed that the value of ρe plays an important role on the impact of confounding. In both CMD and LDD scenarios, we showed that in most cases one can account for the effect of confounding by using a conservative value of 0.9 when 0.8 power is intended.
Additional issues could affect our results. For example, it has been shown that the F-test using restricted maximum likelihood (REML) with Satterthwaite approximation for the degrees of freedom was found to provide better results than the Wald test for small samples [36]. In a simulation study, we found no significant differences in empirical power between the two tests in studies with more than about 30 participants while the Wald test resulted in overestimation of power for smaller values of N (web-based supporting document, section I). Another issue is that we assumed fixed measuring times but in real studies there might be participant variation around that schedule. Results from a simulation study suggest that this had minimal impact on our results (web-based supporting document, J).
Our methodology is easily adaptable for departures from several assumptions considered. For instance, different cost functions or more complex response covariance structures (such as those arising in mixed models with random intercept and slope). Also a continuous exposure can be considered. In this case, the first- and second-order moments of the exposure would be needed.
It should be noted that this study has limitations due to a number of approximations and assumptions. For instance, a linear time effect is assumed. This assumption made possible that the optimal is to take only 2 measurements in several scenarios. If an acceleration or higher order effect is expected or wants to be detected, such a design would not be appropriate. Results presented in this paper were obtained under asymptotic approximations, so one should be careful interpreting results for small samples. The scenarios explored in this paper are just a very small subset of simple cases, and much more complicated scenarios can be found in real studies. Furthermore, reasons other than power and cost can also favor other designs. For example, there might be design strategies that maximize the commitment of study participants. Thus, different aspects of the problem can be addressed in order to refine the methodology presented.
In summary, we have generalized, under certain assumptions, an algorithm for the search for the optimal combination of number of participants and number of repeated measurements in observational longitudinal studies to the case where the exposure is time-varying. We applied our methodology to an illustrative example whose results showed that assuming incorrectly a time-invariant exposure may produce an inefficient design. We provide an R package to perform all calculations. This package is available at http://www.creal.cat/xbasagana/software.html.
Supplementary Material
Acknowledgements
The authors wish to thank Dr Juan Ramón González and Dr Alejandro Cáceres for their help with the R package compilation as well as Dr Medina-Ramón, Dr Antó and Dr Zock for letting us use the EPIASLI data in our example.
Contract/grant sponsor: Research was supported, in part, by National Institutes of Health (grant number CA06516)
References
- 1.Schlesselman JJ. Planning a longitudinal study. II. Frequency of measurement and study duration. Journal of Chronic Diseases. 1973;26(9):561–570. doi: 10.1016/0021-9681(73)90061-1. DOI:10.1016/0021-9681(73)90061-1. [DOI] [PubMed] [Google Scholar]
- 2.Kirby AJ, Galai N, Muñoz A. Sample size estimation using repeated measurements on biomarkers as outcomes. Controlled Clinical Trials. 1994;15(3):165–172. doi: 10.1016/0197-2456(94)90054-x. DOI: 10.1016/0197-2456(94)90054-X. [DOI] [PubMed] [Google Scholar]
- 3.Frison LJ, Pocock SJ. Linearly divergent treatment effects in clinical trials with repeated measures: efficient analysis using summary statistics. Statistics in Medicine. 1997;16(24):2855–2872. doi: 10.1002/(sici)1097-0258(19971230)16:24<2855::aid-sim749>3.0.co;2-y. DOI: 10.1002/(SICI)1097-0258(19971230)16:24<2855::AID-SIM749>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 4.Dawson JD. Sample size calculations based on slopes and other summary statistics. Biometrics. 1998;54(1):323–330. DOI:10.2307/2534019. [PubMed] [Google Scholar]
- 5.Rochon J. Application of GEE procedures for sample size calculations in repeated measures experiments. Statistics in Medicine. 1998;17(14):1643–1658. doi: 10.1002/(sici)1097-0258(19980730)17:14<1643::aid-sim869>3.0.co;2-3. DOI:10.1002/(SICI)1097-0258(19980730)17:14<1643::AID-SIM869>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]
- 6.Hedeker D, Gibbons RD, Waternaux C. Sample size estimation for longitudinal designs with attrition: comparing time-related contrasts between two groups. Journal of Educational and Behavioral Statistics. 1999;24(1):70–93. DOI:10.2307/1165262. [Google Scholar]
- 7.Schouten HJ. Planning group sizes in clinical trials with a continuous outcome and repeated measures. Statistics in Medicine. 1999;18(3):255–264. doi: 10.1002/(sici)1097-0258(19990215)18:3<255::aid-sim16>3.0.co;2-k. DOI:10.1002/(SICI)1097-0258(19990215)18:3<255::AID-SIM16>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 8.Raudenbush SW, Xiao-Feng L. Effects of study duration, frequency of observation, and sample size on power in studies of group differences in polynomial change. Psychological Methods. 2001;6(4):387–401. DOI: 10.1037/1082-989X.6.4.387. [PubMed] [Google Scholar]
- 9.Diggle P, Heagerty P, Liang KY, Zeger S. Analysis of Longitudinal Data. 2nd edn vol. 25. Oxford University Press; Oxford, New York: 2002. (Oxford Statistical Science Series). [Google Scholar]
- 10.Yi Q, Panzarella T. Estimating sample size for tests on trends across repeated measurements with missing data based on the interaction term in a mixed model. Controlled Clinical Trials. 2002;23(5):481–496. doi: 10.1016/s0197-2456(02)00223-4. DOI:10.1016/S0197-2456(02)00223-4. [DOI] [PubMed] [Google Scholar]
- 11.Jung SH, Ahn C. Sample size estimation for GEE method for comparing slopes in repeated measurements data. Statistics in Medicine. 2003;22(8):1305–1315. doi: 10.1002/sim.1384. DOI:10.1002/sim.1384. [DOI] [PubMed] [Google Scholar]
- 12.Fitzmaurice GM, Laird NM, Ware JH. Applied Longitudinal Analysis. Wiley-Interscience; Hoboken, NJ: 2004. (Wiley Series in Probability and Statistics). [Google Scholar]
- 13.Jones B, Kenward MG. Design and Analysis of Cross-over Trials. 1st edn vol. 34. Chapman & Hall; London, New York: 1989. (Monographs on Statistics and Applied Probability). [Google Scholar]
- 14.Senn S. Cross-over trials in clinical research. 2nd edn John Wiley; Chichester, Eng., New York: 2002. [Google Scholar]
- 15.Julious SA. Sample sizes for clinical trials with normal data. Statistics in Medicine. 2004;23(12):1921–1986. doi: 10.1002/sim.1783. DOI:10.1002/sim.1783. [DOI] [PubMed] [Google Scholar]
- 16.Basagaña X, Spiegelman D. Power and sample size calculations for longitudinal studies comparing rates of change with a time-varying exposure. Statistics in Medicine. 2010;29(2):181–192. doi: 10.1002/sim.3772. DOI: 10.1002/sim.3772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Basagaña X, Liao X, Spiegelman D. Power and sample size calculations for longitudinal studies estimating a main effect of a time-varying exposure. Statistical Methods in Medical Research. 2011;20(5):471–487. doi: 10.1177/0962280210371563. DOI:10.1177/0962280210371563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cochran WG. Sampling techniques. 2nd edn Wiley; New York: 1977. [Google Scholar]
- 19.Bloch DA. Sample size requirements and the cost of a randomized clinical trial with repeated measurements. Statistics in Medicine. 1986;5(6):663–667. doi: 10.1002/sim.4780050613. DOI:10.1002/sim.4780050613. [DOI] [PubMed] [Google Scholar]
- 20.Snijders TAB, Bosker RJ. Standard errors and sample sizes for two-level research. Journal of Educational Statistics. 1993;18(3):237–259. DOI:10.2307/1165134. [Google Scholar]
- 21.Allison DB, Allison RL, Faith MS, Paultre F, Pi-Sunyer FX. Power and money: designing statistically powerful studies while minimizing financial costs. Psychological Methods. 1997;2(1):20–33. DOI:10.1037/1082-989X.2.1.20. [Google Scholar]
- 22.Raudenbush SW. Statistical analysis and optimal design for cluster randomized trials. Psychological Methods. 1997;2(2):173–185. doi: 10.1037/1082-989x.5.2.199. DOI:10.1037/1082-989X.2.2.173. [DOI] [PubMed] [Google Scholar]
- 23.Moerbeek M, Van Breukelen JP, Berger MPF. Design issues for experiments in multilevel populations. Journal of Educational and Behavioral Statistics. 2000;25(3):271–284. DOI:10.2307/1165206. [Google Scholar]
- 24.Moerbeek M, Van Breukelen JP, Berger MPF. Optimal experimental designs for multilevel models with covariates. Communications in Statistics - Theory and Methods. 2001;30(12):2683–2697. DOI:10.1081/STA-100108453. [Google Scholar]
- 25.Galbraith S, Marschner IC. Guidelines for the design of clinical trials with longitudinal outcomes. Controlled Clinical Trials. 2002;23(3):257–273. doi: 10.1016/s0197-2456(02)00205-2. DOI:10.1016/S0197-2456(02)00205-2. [DOI] [PubMed] [Google Scholar]
- 26.Winkens B, Schouten HJ, van Breukelen GJ, Berger MP. Optimal number of repeated measures and group sizes in clinical trials with linearly divergent treatment effects. Contemporary Clinical Trials. 2005;27(1):57–69. doi: 10.1016/j.cct.2005.09.005. DOI: 10.1016/j.cct.2005.09.005. [DOI] [PubMed] [Google Scholar]
- 27.Zhang S, Ahn C. Adding subjects or adding measurements in repeated measurement studies under financial constraints. Statistics in Biopharmaceutical Research. 2011;3(1):54–64. doi: 10.1198/sbr.2010.10022. DOI:10.1198/sbr.2010.10022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Medina-Ramón M, Zock JP, Kogevinas M, Sunyer J, Basagaña X, Schwartz J, Burge PS, Moore V, Antó JM. Short-term respiratory effects of cleaning exposures in female domestic cleaners. European Respiratory Journal. 2006;27(6):1196–1203. doi: 10.1183/09031936.06.00085405. DOI:10.1183/09031936.06.00085405. [DOI] [PubMed] [Google Scholar]
- 29.Muñoz A, Carey V, Schouten JP, Segal M, Rosner B. A parametric family of correlation structures for the analysis of longitudinal data. Biometrics. 1992;48(3):733–742. DOI:10.2307/2532340. [PubMed] [Google Scholar]
- 30.Whittemore AS. Sample size for logistic regression with small response probability. Journal of the American Statistical Association. 1981;76(373):27–32. DOI:10.2307/2287036. [Google Scholar]
- 31.Shieh G. On power and sample size calculations for likelihood ratio tests in generalized linear models. Biometrics. 2000;56(4):1192–1196. doi: 10.1111/j.0006-341x.2000.01192.x. DOI:10.1111/j.0006-341X.2000.01192.x. [DOI] [PubMed] [Google Scholar]
- 32.Tu XM, Kowalski J, Zhang J, Lynch KG, Crits-Christoph P. Power analyses for longitudinal trials and other clustered designs. Statistics in Medicine. 2004;23(18):2799–2815. doi: 10.1002/sim.1869. DOI:10.1002/sim.1869. [DOI] [PubMed] [Google Scholar]
- 33.Kistner EO, Muller KE. Exact distributions of intraclass correlation and Cronbach’s alpha with gaussian data and general covariance. Psychometrika. 2004;69(3):459–474. doi: 10.1007/BF02295646. DOI:10.1007/BF02295646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ridout MS, Demetrio CG, Firth D. Estimating intraclass correlation for binary data. Biometrics. 1999;55(1):137–148. doi: 10.1111/j.0006-341x.1999.00137.x. DOI:10.1111/j.0006-341X.1999.00137.x. [DOI] [PubMed] [Google Scholar]
- 35.Haneuse S, Schildcrout Gillen D. A two-stage strategy to accomodate general patterns of confounding in the design of observational studies. Biostatistics. 2012;13(2):274–288. doi: 10.1093/biostatistics/kxr044. DOI:10.1093/biostatistics/kxr044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Manor O, Zucker DM. Small sample inference for the fixed effects in the mixed linear model. Computational Statistics & Data Analysis. 2004;46(4):801–817. DOI: 10.1016/j.csda.2003.10.005. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.