The Horizontal Angular Vestibulo-Ocular Reflex: A Nonlinear Mechanism for Context-Dependent Responses

Abstract

Studies of the Vestibulo-ocular reflex have revealed that this type of involuntary eye movement is influenced by viewing distance. This paper presents a bilateral model for the horizontal angular vestibulo-ocular reflex (AVOR) in the dark based on realistic physiological mechanisms. It is shown that by assigning proper non-linear neural computations at the premotor level, the model is capable of replicating target-distance dependent VOR responses that are in agreement with geometrical requirements. Central premotor responses in the model are also shown to be consistent with experimental observations. Moreover, the model performance after simulated unilateral canal plugging also reproduces experimental observations, an emerging property. Such local nonlinear computations could similarly generate context dependent behaviors in other more complex motor systems.

I. INTRODUCTION

The vestibulo-ocular reflex (VOR) is a type of involuntary eye movement that stabilizes retinal images during head perturbations to maintain clear vision. As in any sensory-motor circuit, the VOR has three parts: i) a sensory device to drive the system; ii) a central processing stage that combines sensory and motor feedback signals to generate motor commands based on a specific goal; and iii) a neuromuscular plant that produces the desired output. The vestibular apparatus consists of the semicircular canals and the otolith organs which detect head movements during angular and translational motion, respectively. Circuits in the brainstem, including vestibular nuclei (VN) and prepositus hypoglossi (PH), act as the main system controller to integrate the sensory drive and eye position information and provide motor neurons with proper commands. Motor neurons in turn activate the extraocular muscles that apply torques on the eyeball and produce rotational eye movements. These three rather simple sensory-motor components constitute the main VOR path, the so-called three neuron arc [1].

The angular VOR (AVOR) is generally tested with passive whole-body rotation in the dark, while recording conjugate or monocular horizontal eye movements. The reflex consists of compensatory (slow phase) and reorienting (fast phase) segments. While the slow phases serve to stabilize gaze in space by moving the eyes in the opposite direction to the head, the fast phases redirect the gaze with very fast reorienting eye movements typically in the direction of the head velocity. These slow and fast intervals constitute VOR nystagmus. In clinical tests, the VOR is characterized by its gain defined as the ratio of peak eye velocity to peak head velocity during harmonic testing or short pulse perturbations.

Although the head movements sensed by the vestibular apparatus initiate this reflex, the response is also influenced by contextual factors such as viewing distance [2], [3]. It can be demonstrated geometrically that the magnitude of the ocular deviations required for compensating a translation of the eyes depends on the location of the fixation target relative to the observer. That is, the gain of the AVOR must increase as a function of decreasing fixation distance [2]. Holding gaze on a near target requires more ocular rotation than for a relatively far target during head movements since the eyes are not centered on the head.

There is little insight on the underlying mechanism that the neural system employs to achieve the context-dependent modulation of VOR gain. Experiments confirmed that the ability to maintain modulated VOR gain persists for many seconds in darkness and absence of visual targets [2]. Moreover, the short latency of VOR gain modulation compared to the latency of processing visual feedback, rejects the hypothesis that visual cues alone can trigger these changes [4]. The majority of models proposed to generate target-distance dependent VOR responses relate this property to i) an internal signal proportional to the inverse of target distance that scales VOR gain [2], [5], ii) projections from cortical computations [4] and/or iii) forcing parametric changes [6]. Zhou et. al. [7] suggested instead a multiplication of vestibular and eye position signals within the direct VOR pathway as the neural substrate that mediates VOR gain modulations. By using the concept of gain modulation [8], the theoretical work of Khojasteh and Galiana [9] suggested that imbedding an appropriate local nonlinearity in the response of bilateral VOR interneurons could generate context dependent responses. Their proposed mechanism uses monocular efferent copies of eye position that are known to converge on premotor cells in the medial VN as the signal to modulate VOR gain. However, a major shortcoming of their model was that the use of nonlinear gain in a loop also causes the dynamics of the system to vary as the VOR gain modulates. Moreover, it could not achieve VOR gains in complete agreement with the geometrical requirements for eccentric targets.

Gain modulation is defined as a change in the sensitivity of a neural response to one set of inputs that depends on the activity of a second set of inputs [10]. This has been observed mainly in cortical areas [11] and has come to be viewed as a major computation principle in nonlinear neural processing. The nonlinearities can be described as multiplicative or as nonlinear additions and can be seen at both the single neuron and network level [10].

The present study expands the concept of nonlinear neural computation in a simple bilateral model for slow phase horizontal AVOR in the dark, based on premotor anatomy and physiology. This model can replicate binocular responses for targets at different depths and eccentricities during short duration head velocity bumps. In this model it is postulated that nonlinear computations, appearing at the level of premotor cells in the VN, are a function of both monocular eye position and vergence angle estimates to generate target-distance dependent VOR gains for each eye. The model includes nonlinear semicircular canals [12] for a more realistic sensory system in the VOR. Simulation results are presented to evaluate the performance of the model under different viewing distance conditions. Moreover, the model is able to generate responses in cases of unilateral canal plugging that are consistent with published results [13], [14]. Such a model allows new interpretations about how the system operates and to make predictions about what should be observed in experiments. Moreover, this model can be used to make predictions about the behavior of the VOR response in the binocular responses of patients suffering from unilateral vestibular lesions.

The remainder of this article is organized as follows. Section II-A provides a brief review of the geometrical requirements for a distance dependent VOR. Section II-B proceeds to the analysis of the bilateral model. Simulation results are presented in section III followed by discussion and concluding remarks in section IV.

II. METHODS

A. Reference Coordinate

Reference coordinates in this model are selected such that for each eye, zero position is defined as looking straight ahead at optical infinity; temporal deviations are considered positive and nasal deviations, negative. Conjugate and vergence eye positions are thus defined as: $E_{\mathit{con}j}=\frac{1}{2}(E_R-E_L)$ and E_verg = −(E_R + E_L), where E_R and E_L refer to the right and left eye position, respectively.

According to geometrical requirements (Fig. 1-(a)), the ideal monocular VOR gains defined as the ratio of angular eye velocity to angular head velocity [2], for any target distance D (m) and eccentricity θ (rad), can be obtained as:

$$\{\begin{array}{l}\frac{\partial E_R}{\partial \varphi }=\frac{-D(D+r)(1+tan{\varphi }^2)}{D_R^2}\hfill \\ \frac{\partial E_L}{\partial \varphi }=\frac{D(D+r)(1+tan{\varphi }^2)}{D_L^2}\hfill \end{array}$$ (1)

where ϕ (rad) refers to head angular position, r (m) is the radius from the center of rotation to the eye and I (m) is the inter-ocular distance. D_R (m) and D_L (m) are distances of the target from the right and left eye, respectively. For a relatively large target distance compared to the interocular distance and small E_R (rad) and E_L (rad), Equ. (1) can be approximated with [6] (see Appendix. A for detail):

$$\{\begin{array}{l}\frac{\partial E_R}{\partial \varphi }\approx -1+\frac{r}{I}(E_R+E_L)cos{E}_R=-1+\frac{r}{I}{E}_{\mathit{verg}}cos{E}_R\hfill \\ \frac{\partial E_L}{\partial \varphi }\approx 1-\frac{r}{I}(E_R+E_L)cos{E}_L=1-\frac{r}{I}{E}_{\mathit{verg}}cos{E}_L\hfill \end{array}$$ (2)

Fig. 1.

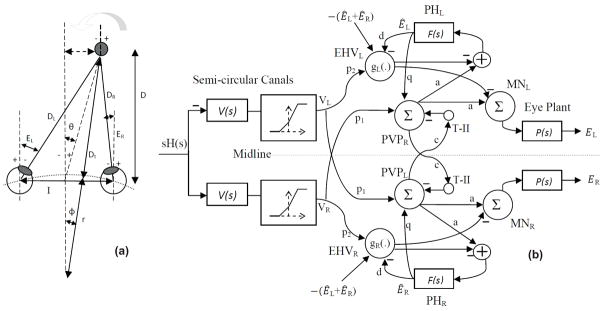
(a) Right and left eye positions for an eccentric target at a location given by (D, θ) during head rotation about radius r.(b) Bilateral model of horizontal AVOR in dark. (PVP cells are located on the opposite side to better view the connections crossing the midline). See Table I for projection weights that are shown on the connections. Projection weights that are not shown are assumed to be 1.

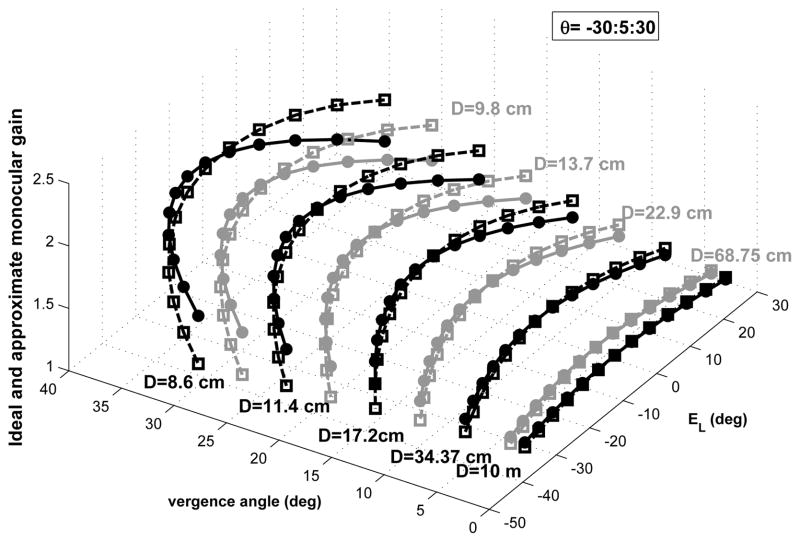
Equ. (2) implies that approximating the target location with respect to the eyes (for different depths and eccentricities) in the horizontal plane, requires an estimate of binocular angles, or a combination of them, e.g. monocular eye position and vergence state. In other words, there is no one-to-one mapping between the ideal monocular VOR gain and the associated monocular eye position - the latter is not sufficient to define target location in space. Fig. 2 shows the ideal and approximate gain for left eye velocity from Equ. (1) and (2) for different target distances and eccentricities with respect to the left eye position and the vergence angle for r = r_head = 8.8 cm and I = 6 cm. The gain is close to unity to hold gaze on a far target while looking at near targets requires higher gains. According to Fig. 2, the error of the approximation for ideal monocular gain is maximum for very near eccentric targets. This is expected since our assumption for obtaining the approximation was for target distances relatively larger than interocular distance. The mean squared error (MSE) for this approximation is 0.022 for the range of target distance D from 0.086m to 10m and the range of target eccentricity θ between ±30 deg. However, the MSE for the approximation of the ideal geometrical gain for conjugate VOR for the same range of target distance and eccentricity is much less (0.002). This small MSE is due to the cancellation of approximation errors in monocular gains when computing the conjugate (average binocular) gain.

Fig. 2.

Ideal monocular gain for the left eye velocity required by geometry from Equ. (1) (square marker-dashed line) and approximation from Equ. (2) (circle marker-solid line) for different target distances and ocular context: D = 8.9cm, …, 10m are lines of constant target distance, markers are located on these lines according to concurrent E_verg and left eye deviation, explored over range ±30 deg in 5 deg increments. In Equ. (2): r = r_head = 8.8 cm and I = 6 cm.

B. Model Description

Fig. 1-(b) presents our bilateral model for the AVOR in the dark. In this model, population responses of cells are considered and each element of the model represents the average behavior of a particular cell type rather than the response of any individual cell. Moreover, only firing modulation around a population resting rate is considered so biases due to resting rates are not included. Therefore, a negative firing rate refers to cell firing below the resting rate.

The input is head velocity, sH(s), sensed by semicircular canals. Normal physiological behavior involves high frequency head movements (≈ 0.1 − 10Hz). The geometric properties of the semicircular canals cause bending of the cupula approximately in phase with head velocity at rotational frequencies above ≈ 0.1 Hz that can be described as a high pass filter with a time constant of approximately 4–6 seconds [12]. Primary vestibular afferents carry sensory information from semicircular canals to VN. The mechano-neural transduction process has nonlinear properties causing asymmetric changes in firing rate on the primary afferents, sensitive to both the direction and speed of the head. Hence, the canals are modeled as high pass filters: $V(s)=\frac{{sT}_c}{{sT}_c+1}$ followed by a static nonlinearity [12]. The nonlinear block has asymmetric gains around zero (k_negative = 0.4 and k_positive = 0.6) and limits the primary afferent output V_R,L by saturation (+260 spikes/sec) and cut off levels (−90 spikes/sec), appropriate for primary vestibular afferents with 90 spikes/sec resting rate.

Different cell populations in the VN are distinguished in this model. Type I Position-Vestibular-Pause (PVP) neurons in the medial VN, which constitute the main intermediate leg of the VOR pathway, and receive monosynaptic projections from the ipsilateral semicircular canal. PVP cells increase their firing rate during contralaterally directed eye position and during ipsilaterally directed head velocity. A majority of these cells send excitatory projections to contralateral abducens nucleus and their discharge ceases during ipsilaterally directed saccades or VOR fast phases [15]. Note that PVP cells are placed on the graph (Fig. 1-(b)) opposite to the side of their brainstem location simply to aid in the visualization of the schematic. Contrary to PVP cells, Eye-Head-Velocity neurons (EHV) have eye and head velocity sensitivities in the same direction. They receive monosynaptic excitatory input from the canals and inhibit the ipsilateral abducens nucleus [16]. In this model, PVP and EHV cells receive semicircular canals and eye position information from canals and PH, respectively. T-II in our model refers to type II neurons in the medial VN [17] that receive projections from the contralateral VN. Here, we are assuming that contralateral VN projections are coming from PVP cells and form a feedback loop between the two sides of the VN [18]. These commissural pathways play an important role in the dynamics of the VOR system [19].

MN represents the net (summed) motoneuronal signals projecting to eye plants from ipsilateral oculomotor nuclei inhibition and contralateral abducens nuclei excitation. The eye plant is modeled with first order low pass dynamics, $P(s)=\frac{k_p}{Ts+1}$. The neural filters in PH generate internal estimates of eye position Ê with similar dynamics to the eye plant, $F(s)=\frac{k_f}{Ts+1}$. The output signal is eye position E . Subscripts R and L refer to locations in the right and left side of the brainstem or head.

The model structure and connections are similar to the one developed in [9] with linear summing junctions except for nonlinear canals and nonlinear EHV cells. It should be noted that some known connections, i.e. projections from PH to MN [20], or distinctions between type I and type II PVPs and EHVs are not considered in the model. First, as mentioned earlier in this section, we are modeling cell population responses with lumped Type I characteristics, and not individual cell responses. Second, we wish to represent the simplest model that can replicate general VOR characteristics - a minimalist approach. Third, adding more projections and loops between more elements in a bilateral model will only affect the current assigned projection weights and not the general characteristics of the bilateral model.

EHV cells are known to behave nonlinearly and also exhibit vergence dependent behavior [21], [5], [22]. In the former model [9], context dependency relied on a single nonlinearity applied after the sum of EHV afferent signals. Therefore, as different gains were generated with viewing context, the dynamics of the system also changed. Moreover, relying only on internal estimates of ipsilateral monocular eye position did not allow reaching ideal gain modulation.

In order to preserve stable dynamics with ideal gain modulations, the EHV cells in the new model only modulate the gain to the sensory inputs, V_R,L, according to the eye context information. We assume that there are two signals in the premotor circuit related to binocular eye positions that trigger the context-dependent gain modulation. Although there is evidence that the majority of premotor cells (saccadic Burst neurons, PVPs) encode monocular eye movements [23], [24], there are other neurons that encode binocular eye movements with ipsilateral preference or mixed sensitivities [24]. Thus an ipsilateral eye position efference copy is available from PH, while binocular information or at least contralateral eye position is also available to the EHV cells through commissural pathways and interneuron connections. Another source could be through projections from the so-called vergence neurons in the midbrain reticular formation that discharge proportionally to the vergence angle [25]; however, to date the exact anatomical projections of these neurons remain unknown [26]. Access to cells with such characteristics is essential to tune the nonlinear gain of EHV cells for different target distances and eccentricities. Therefore, we assume that ipsilateral monocular and vergence eye position inputs to the EHV cells define their sensitivities (gain) to vestibular signals in a nonlinear fashion; i.e. EHV_R,L = g_R,L(Ê_R,L, Ê_verg)p₂V_R,L, where g_R,L(.) is the nonlinear sensitivity of EHV cells to vestibular afferents. Given these assumptions, the equations for conjugate and vergence angles in the model are (see Appendix. B)

$$E_{\mathit{con}j}=\frac{k_p(c-1)(g_L{p}_2{V}_L-g_R{p}_2{V}_R)-{ak}_p{p}_1(V_L-V_R)}{2\left((c-1)(Ts+1)+{\mathit{adk}}_f\right)}$$ (3a)

$$E_{\mathit{verg}}=\frac{k_p(c+1)(g_L{p}_2{V}_L+g_R{p}_2{V}_R)-{ak}_p{p}_1(V_L+V_R)}{(c+1)(Ts+1)-{\mathit{adk}}_f}$$ (3b)

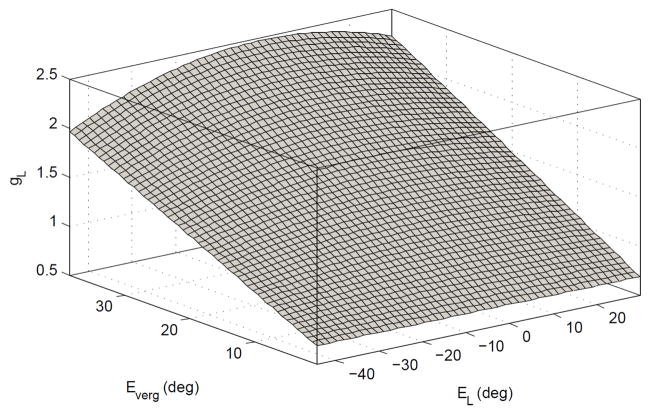
Modulation of g_R and g_L only changes the context gain but not the system dynamics (poles). The parameter set used provides system stability and approximates recorded time constants for version and vergence [6], (see Table I). The optimum values for g_R,L are computed so that the high frequency monocular VOR gains in the model match the ideals from Equ. (2) for different target depths and eccentricities with r = r_head = 8.8cm and I = 6cm. A surface fit optimization is performed to describe g_R,L as a 4th order polynomial function of Ê_R,L and 1st order polynomial of Ê_verg. Fig. 3 depicts this surface for g_L. The sum of squared error (SSE) was obtained as 5e-6, an excellent fit (see Appendix. C). Lower order polynomial selection results in a larger SSE (e.g. SSE=0.004 for a 3rd order polynomial function of Ê_R,L and 1st order polynomial of Ê_verg), which may still be satisfactory. The nonlinear functions are then assigned to the left and right EHV cell processes as mirror images.

TABLE I.

Numerical values of the model parameters

p1	p2	c	q	a	d	kf	kp	T	Tc
0.75	0.75	0.013	1.43	0.8	1	0.85	0.55	0.3	6

Fig. 3.

Nonlinear surface computed as the sensitivity of the left EHV in the model to vestibular afferent projections as a function of Ê_L and Ê_verg (Mirror image of surface for right EHV).

All simulations were performed using MATLAB Simulink (The MathWorks Inc., MA, USA). The solver used was the first order Euler approximation with a step size of 1 ms. The performance of the model under different conditions are provided next.

III. Results

The model simulates human AVOR responses during yaw rotations in darkness around a vertical axis though the center of the head. The performance of the nonlinear model was examined during brief high-velocity head perturbations in different binocular contexts. The firing rate modulation of model neurons with vergence is compared to experimental observations. We also replicated behavior after unilateral vestibular sensory loss from canal plugging. The simulation results are compared with published experimental data.

A. AVOR gain modulation with target depth and eccentricity

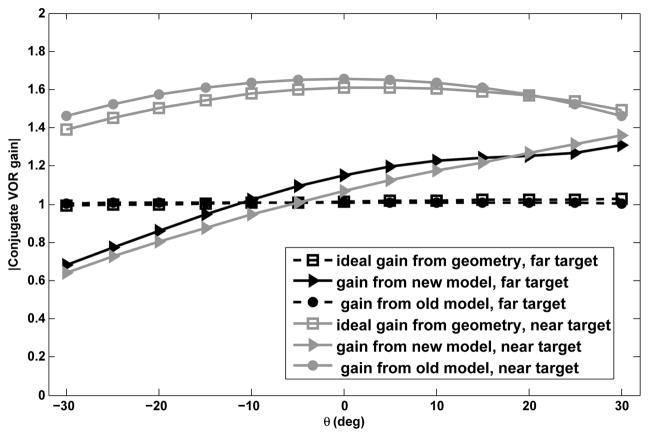
Fig. 4 shows absolute conjugate VOR gain plotted against target eccentricity for a far target (D = 10m) and a near target (D = 11cm) when head velocity is applied as a short duration (100 ms) pulse of amplitude 100°/s. In this figure the ideal gain from geometry refers to the gains obtained from Equ. (1). To test the VOR gain, target locations with respect to eyes are varied by setting specific initial conditions to both eye plants and the efference copies of each monocular eye position for the cases in Fig. 2. The gain here refers to the ratio of the peak conjugate eye velocity to the input head velocity peak as in clinical tests. According to the high-pass characteristics of the eye velocity system and slow dynamics of the conjugate system, when head velocity input frequency is higher than the break-frequency of the canals (f = 1/6 rad/sec) the ratio of peak eye velocity over head velocity is very close to the actual system high frequency gain. Therefore using a short duration pulse as the head velocity input, as commonly done to study VOR gain in experimental studies [13], [27], triggers the high frequency response of the system and the output/input peak-to peak ratio reflects the system gain (−1 in our model for far targets). Since in our model only the gain is modulated by target distance and the poles are fixed, low frequency VOR gains are also adjusted with target distance, but now proportional to the high-pass system gain at the specific frequency of the input.

Fig. 4.

Absolute conjugate gains vs. target eccentricity for a far target, D = 10 m, and a near target, D = 11 cm.

We also compared this to the performance of the prior nonlinear model [9] under the same conditions. The comparison is performed for the whole range of target distance and eccentricity shown in Fig. 2, i.e. target distance D from 0.086m to 10m and target eccentricity θ between ±30 deg. The new model is able to generate conjugate gains very close to the ideal ones required by geometry (SSE=0.102), much improved over [9], (SSE=15.3648). Since the latter model only relies on monocular eye position to modulate gain, it is not able to generate responses in complete agreement with geometrical requirements for different target eccentricities. However, by relying on both the efference copies of monocular eye and vergence angle, the improved model generates gains that are very close to the ones predicted from geometry and reported in monkeys [2].

B. Dependence of central neurons firing rate on vergence

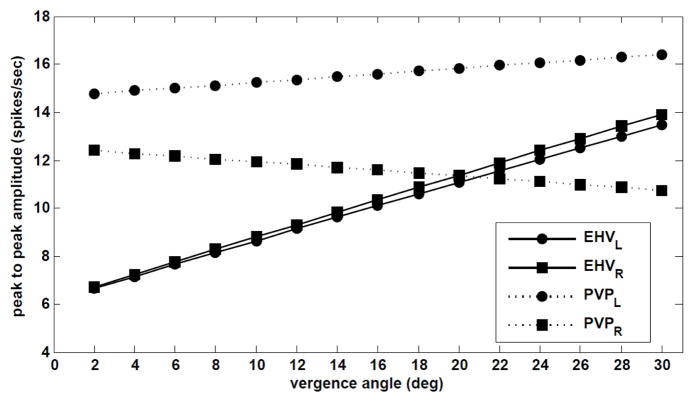
Single unit recordings from VOR premotor neurons show that distinct cell types modulate their firing rate according to vergence angle and eye position to generate compensatory VOR with respect to target location. These recording are done during low frequency horizontal rotations in the presence of visual feedback [5] or during combined semicircular canal and otolith stimulation [21]. Experiments by Meng et. al [22] included single unit recordings from PVPs and EHVs in macaque monkeys during both translational and rotational VOR in the dark. According to their observations during 4 Hz rotations in the dark and after extinguishing the target at different distances, the modulation depth on EHV and PVP firing rates was shown to relate linearly to vergence angle (see Fig. 4 in [22]). Moreover, EHV cells were more sensitive to the vergence angle (steeper slope) compared to type I PVP cells.

In order to quantify the dependence of EHV and PVP cells firing rates on vergence angle in our model, the same experiment (peak head velocity of 18 deg/s, 4 Hz) is simulated. Fig .5 shows the peak-to-peak amplitude of firing rate modulations during a rightward head rotation for EHV and PVP cells in our model with respect to vergence angle for central targets at different distances, i.e. θ = 0.

Fig. 5.

Dependence of PVP and EHV firing rates in the model on vergence during 4Hz rotation.

Despite assigning nonlinear computations only to EHV cells to modulate VOR gain, the depth of both EHV and PVP modulations varies linearly with vergence angle, consistent with experimental observations [22]. In fact, given central targets E_R = E_L, the non-linear surface embeds a line relating vergence with monocular angle (Fig .7), and the gain of EHV cells follows the line of E_verg = −2E_L on the nonlinear surface. Moreover, the slope of vergence dependence is larger for both right and left EHV cells compared to PVP cells. As in [22] where type I PVP cells show a negative vergence slope, right PVPs in our model have a negative slope while the left PVPs show little increase in their firing modulations with vergence.

Fig. 7.

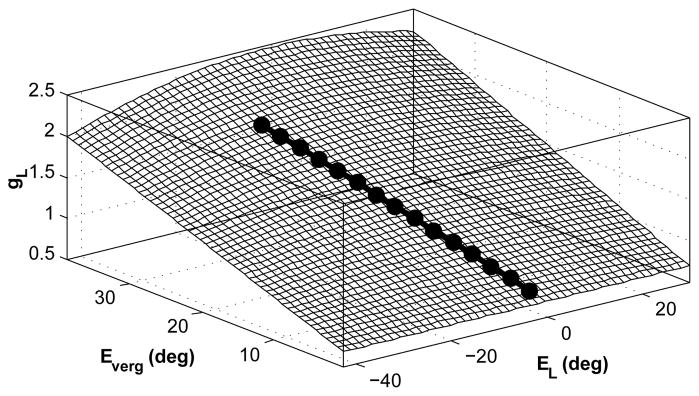
The linear line on the nonlinear surface assigned to EHV cells related to central targets for vergence angels in the range of 0 to 30 deg.

This suggests that despite assigning nonlinear computations in the premotor circuit of our bilateral model, the characteristics of the model neurons are similar to experimental results using the same conditions and analysis method.

It should be noted that although the reported results [22] are from experiments on monkeys, here we are comparing the general characteristics from the VN cells, that is, linear variation of the depth of modulations in EHV cells and PVP cells with vergence and positive or negative slope of such variations. These general characteristics will hold regardless of species-dependent interocular distance.

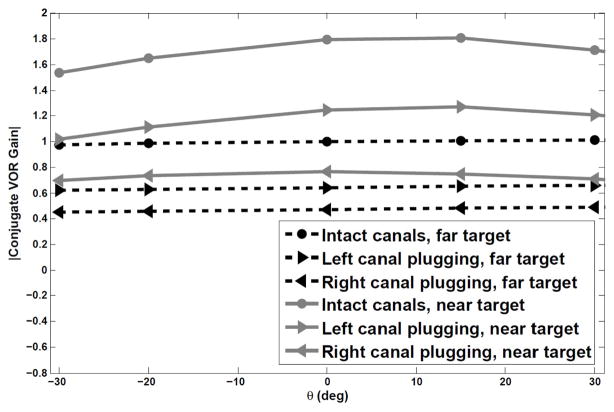
C. Target-distance dependent VOR gain with unilateral canal plugging

We studied the model performance assuming unilateral loss of sensory modulation (i.e. canal plugging). Canal plugging has been widely used as a treatment of certain vestibular disorders [28], [29]. Experimental results report that the gain of the horizontal AVOR evoked by high frequency, high acceleration head pulses in subjects with unilateral lesions show an asymmetry in the contralesional vs. ipsilesional rotations [13], [27]. The AVOR gain in squirrel monkeys during high frequency and high velocity steps of acceleration is reported as 0.9 ± 0.04 [30] in controls and after plugging, 0.61±0.14 for contralesional rotations and 0.33±0.03 for ipsilesional rotations after unilateral canal plugging [13]. Interestingly, Migliaccio et. al. [14] also reported that despite lower gains, the target-location dependent modulation of the human AVOR survives after canal plugging, though suboptimal. According to experiments on monkeys and toadfish, the VOR gain decreased after plugging to less than 0.1 for low frequency rotations (less than 2 Hz), while the gain increases to about 0.6 at high frequencies (≈ 15Hz). Moreover, while afferents innervating a plugged canal still increase their sensitivities with frequency [31], [32], they show a much reduced gain; this can be modeled as an increase in stiffness and a reduction in the dominant time constant and gain in their transfer function.

Thus, to study canal plugging effects, we change the lesioned canal dynamics according to [32], that is T_c = 0.03 s and gain reduction in V (s) to 30% for a plugged canal, rather than T_c = 6 s for an intact one. The model is then again stimulated with a rightward short duration (100 ms) head velocity pulse of amplitude 100 deg/s. All other model parameters including the nonlinear functions in the EHVs were left unchanged. Initial eye conditions were varied as before to test different initial target distance and eccentricities (Fig. 6). The model results confirm an asymmetry consistent with experiments. If the left sensor is plugged, the average generated absolute gain to a rightward contralateral head pulse is 0.67±0.02. In the case of a right canal plugging, the generated conjugate absolute gain is 0.45±0.02 for the same head pulse, now ipsilateral to the side of lesion. This is consistent with the observations of [13] - a larger gain for contralesional than ipsilesional head rotations. Despite the lesion, there is still an increase in the VOR gain for near targets, in accordance with the observations of [14] - gain modulation of the VOR survives canal plugging, though it may not be as optimal as before lesions.

Fig. 6.

Absolute conjugate gains vs. target eccentricity for a far target, D = 10 m, and a near target, D = 11 cm, in response to a rightward head pulse.

In order to explain the reason behind the asymmetric responses in lesion cases, Lasker et al. [13], [33], proposed that the VOR system incorporates two independent parallel linear and nonlinear pathways. Selective increases in the gain for these linear and nonlinear pathways can replicate the changes in VOR gains. In our model, this behavior is obtained by imbedding nonlinear sensors and nonlinear premotor cells in a bilateral circuit to both compensate for sensory limitations and provide context dependent VOR responses.

In order to test separately the effect of nonlinear EHV cells and nonlinear canals in the above results, we replaced the nonlinear surfaces of EHV cells in our model with a single linear gain, i.e. EHV_R,L = g × V_R,L with g = 0.7. In this case the high frequency VOR gain would be set to −1 for far central targets. We simulated this model with linear EHV and nonlinear canals under the same conditions as the previous case, i.e. far and near target with right or left canal plugged. The average generated absolute gain for contralesional head pulse of amplitude 100°/s is 0.72±0.06 for far target and 0.71±0.14 for a near target. For an ipsilesional head pulse, the average generated absolute gain is 0.58±0.06 for far target and 0.57±0.14 for near targets. This suggests that having nonlinear canals with asymmetric sensitivity to head movement direction contributes to the observed asymmetry in the contralesional vs. ipsilesional head pulses (note that the head pulse has not reached saturation or cut-off levels). However, the gain modulation of the VOR with respect to target distance does not exist with linear EHV cells as expected.

Note that the results from plugging were an emerging property. Model parameters were pre-set to satisfy response dynamics in normal cases.

D. Disconjugate eye movements in darkness - Vergence

In the presence of visual targets, eye movements contain both conjugate and vergence components and thus are disconjugate. However, in the absence of an imaginary or real target, it is generally believed that the AVOR is perfectly conjugate. Therefore, most experiments on AVOR in the dark record only conjugate or a single eye’s movements. The stimuli for vergence eye movements are considered to be visual cues such as retinal disparity or perception of depth and target size [34]. However, binocular recordings of AVOR, delivered in darkness, in both human and monkey [35], show a considerable vergence component that is modulated with head velocity. Khojasteh and Galiana [35] suggested that a possible source for vergence responses in the dark could be a secondary effect of nonlinearities that are needed for modulation with sensori-motor context.

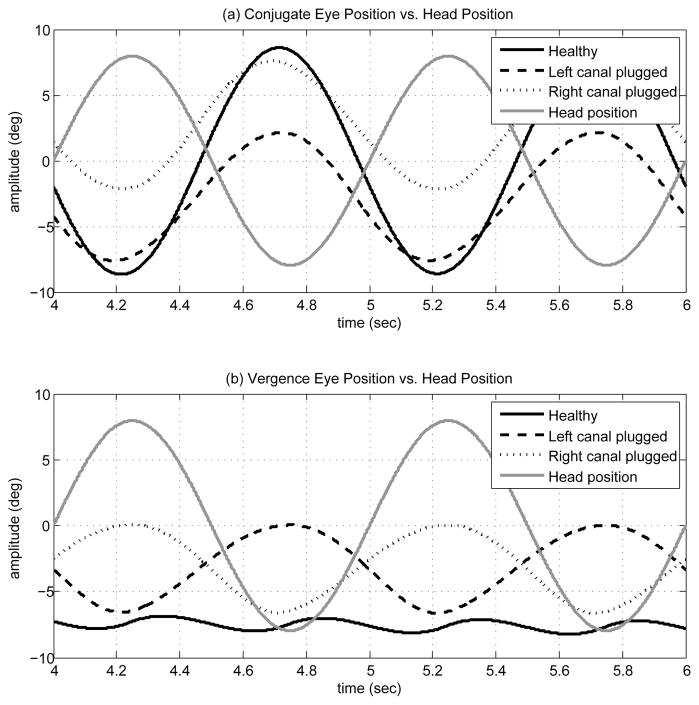
To the best of our knowledge, no study has explored the presence of vergence changes in unilateral vestibular dysfunctions. We have simulated pure VOR slow phase with our bilateral model in response to sinusoidal head rotations. The model is stimulated by 1Hz sinusoidal head velocity signal of 50 deg/s amplitude. It should be noted that high amplitude input signals in reality cause nystagmus, i.e. trigger VOR fast phases. Therefore, we use here a low-amplitude input to avoid eye position deviations beyond known physical limits. As in section III-C, the case of canal plugging is also studied below. First both canals are intact and healthy, and then either left or right canal transfer functions are replaced by a plugged canal model. Since all other parameters remain unchanged, this represents the acute state after a lesion.

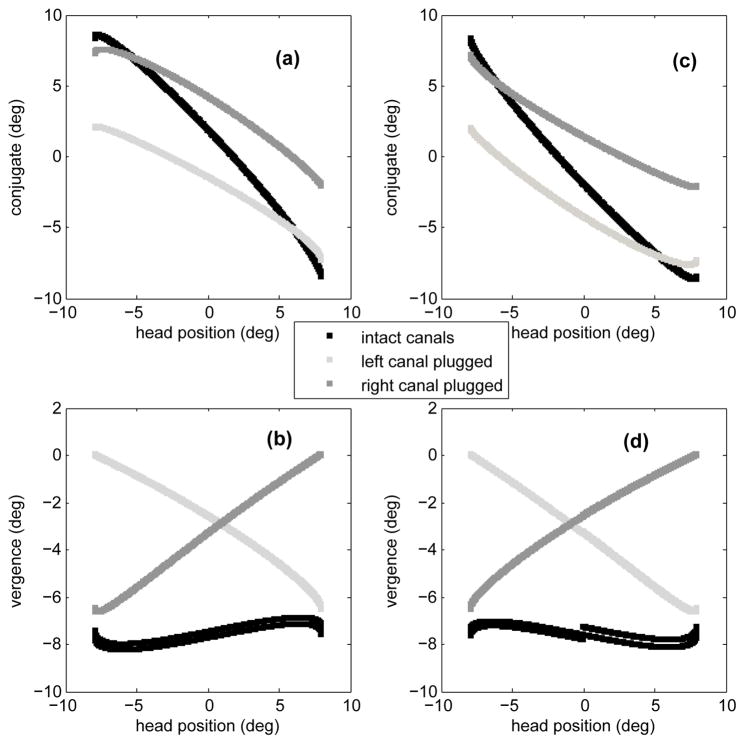
Fig. 8 shows the response of the bilateral model in these three cases. The conjugate eye position peak-to-peak amplitude decreases with a lesion, compared to the normal case. This is expected since the lesions involve considerable reduction in one sensor’s signal projections. However, compared to the case of intact canals, the model now predicts larger vergence modulation than in the healthy animal. In order to characterize the conjugate and vergence components of the slow phase eye movements in these cases, they are plotted as a function of head position for positive (a,b) and negative (c,d) head velocities during sinusoidal rotation (Fig. 9). In the case of intact canals (black trend), the eyes diverge for both positive (b) and negative (d) head velocities and the gain of vergence re. head position is small and negative for positive head velocities and positive for negative head velocities (small slope). This is consistent with the observations reported by [35] for control subjects. However, in the case of left canal plugging (light gray trend), the magnitude of vergence has increased and it’s gain re. head position is always negative. On the other hand, the gain of vergence re. head position remains positive in the case of a right canal plugging (dark gray trend). Therefore, not only are bigger vergence movements observed in the case of unilateral canal lesions, but vergence phase is expected to be correlated with the side of lesion.

Fig. 8.

(a) Conjugate eye position signal (deg) vs. head position (deg) in cases of intact canals, left canal plugged and right canal plugged. (b) Vergence eye position signal (deg) vs. head position (deg) in cases of intact canals, left canal plugged and right canal plugged.

Fig. 9.

Conjugate and vergence components of slow phase VOR vs. head position in cases of intact canals, left canal plugged and right canal plugged. In (a) and (b) head velocity is positive and in (c) and (d) head velocity is negative.

IV. Discussion

One of the factors that modulate the VOR is target distance. This work introduces an improved physiologically relevant model for the AVOR with nonlinear sensors and nonlinear computation in dominant classes of vestibular neurons to generate modulation of responses appropriate for target location.

Nonlinear computation in neural responses, so-called gain modulation, exists in many cortical and subcortical areas [8]. Different mechanisms such as recurrent neural networks [36], changes in the synchrony of inputs to a neuron [37] or varying the level of background synaptic input [38] have been proposed to explain such nonlinear neural responses. Here, it is postulated that the sensitivity of EHV cells to vestibular signals modulates nonlinearly with eye position and vergence state, enabling auto-adjustment of the VOR to the set point of both eyes. This could be mediated from projections within the brainstem, or from the cerebellum since floccular target neurons (FTN) in the VN and EHV cells have similar firing characteristics [39].

The response of the model in different contextual conditions is tested with simulations similar to reported experiments. By relying on binocular eye information, i.e. ipsilateral eye position and vergence angle, the model is able to provide near-ideal modulation of the AVOR, a great improvement over the initially proposed model that only used ipsilateral monocular signals. The model neurons modulate with vergence and are also shown to be consistent with experimental observations. Moreover, the new model replicates experimental data after acute unilateral canal plugging. The use of such gain modulation in the VN, perhaps at the same site, could also support geometrically required changes in the translational VOR, with target location.

The goal of modeling a sensory-motor system is unmasking potential control strategies used by the brain to gain insight for clinical applications. One prediction of our model is that vergence angle information (and likely vergence error with respect to target) plays a role in generating disconjugate VOR responses tuned for different target locations. Hence the first implication is a predicted projection from vergence cells to EHV cells or other premotor cells in the VN whose combined information can provide vergence. Moreover, another prediction is an increased vergence response with unilateral vestibular lesions, also associated with decreased conjugate gains. Due to central nonlinearities and nonlinear sensors, there is an increase in the VOR common mode response, E_verg, related to the sum of bilateral sensory signals (normally modulating in opposite directions). Hence, observing conjugate eye position alone is insufficient to evaluate VOR performance in the clinic. For a complete recovery after a lesion, both conjugate and vergence movements should be in the normal range. In a bilateral nonlinear circuit, we expect that unbalanced sensory inputs will result in larger vergence responses compared to the normal case. Such abnormal vergence responses could be a contributing factor to complaints of dizziness in vestibular patients even after compensation of conjugate eye movements. This needs to be verified with binocular VOR recordings in the clinic; if confirmed, new test protocols will follow for the evaluation of VOR performance and appropriate functional recovery in vestibular patients.

In summary, we have shown that VOR on-line gain modulation could rely on nonlinear functions that are dependent on concurrent monocular eye position and vergence angle efferent copies. The site of this gain modulation with target distance is proposed to be EHV cells in the VN that have firing characteristics similar to those reported for FTNs in the VN. The role of FTNs in long term adaptation of the VOR is already confirmed [39]. Moreover, [40] has suggested that subjects can learn to use vergence angle as the contextual cue that retrieves adaptive changes in the angular VOR. Therefore, the next step will be to extend the nonlinear computation hypothesis to account for long term adaptation or lesion compensation in the VOR. The goal will be to investigate whether long-term adaptive changes can result from simply shifting or reshaping the nonlinear functions in EHV processing thereby changing the selectivity of the premotor cells in VN.

Biographies

Mina Ranjbaran is currently a PhD candidate in biomedical engineering at McGill University, Montreal, Canada. She received her MASc degree in electrical engineering from Concordia University in 2010.

Her research interests include modeling and identification of biomedical systems and signals and sensory-motor mapping in physiological systems.

Ms. Ranjbaran has been an active member of IEEE since 2008 and served as the vice chair of women in engineering (WIE) affinity group, Montreal 2009–2011.

Henrieta L. Galiana received her Bachelors in Electrical Engineering (Honours) from McGill University in 1966, followed by a Masters Elect. Eng. (Biomedical) in 1968. After a few years working with Larry Young at MITs Man-Vehicle Lab, and a 7 year sabbatical to raise 2 kids, she returned to doctoral studies and received her PhD in Electrical Eng (Biomedical) from McGill in 1981. In 1983, she accepted a staff position in the new Department of Biomedical Eng, where she still serves as Full Professor and held the position of Chair from 2005–2012.

Dr. Galiana is a Fellow of the Engineering Institute of Canada and a Fellow of the IEEE, and a past President (2002) of the IEEE Engineering in Medicine and Biology Society. She has chaired the TAB Strategic Planning Committee and was a member of the TAB Society Review Committee. Her research interests focus on biosignal processing and the modelling of control strategies for the orientation of eyes and head, or segmented arms, and related issues of platform coordination and sensory fusion. Theoretical predictions are applied in the vestibular clinic for patient evaluation, and are ported to biomimetic robot systems to test novel control approaches.

Appendix

A. Geometrical Approximations

The geometrical relationship required for perfect retinal stabilization of a target at distance D (m) and eccentricity θ (rad) during head rotation about a given axis is illustrated in Fig. 1-(a). Ocular angels E_R,L (rad) are positive for temporal deviations and negative for nasal deviation and can be expressed according to:

$$\{\begin{array}{l}{E}_R={tan}^{-1}\left(\frac{(D+r)tan(-\varphi )-I/2}{D}\right)\hfill \\ E_L={tan}^{-1}\left(\frac{-(D+r)tan(-\varphi )-I/2}{D}\right)\hfill \end{array}$$ (4)

where r (m) is the radius of rotation and I (m) is the interocular distance. Target eccentricity, θ (rad), and rotation angle, ϕ (rad), are positive in the clockwise direction. For given values of D, θ, I and r, sensitivity of each ocular angle to a change in rotation angle is obtained by differentiating Equ. (4) with respect to ϕ:

$$\{\begin{array}{l}\frac{\partial E_R}{\partial \varphi }=\frac{-D(D+r)(1+tan{(\varphi )}^2)}{D_R^2}\hfill \\ \frac{\partial E_L}{\partial \varphi }=\frac{D(D+r)(1+tan{(\varphi )}^2)}{D_L^2}\hfill \end{array}$$ (5)

where $D_R^2$ and $D_L^2$ are the squared distances of the target from the right and left eye, respectively, given by:

$$\{\begin{array}{l}{D}_R^2=D^2+{((D+r)tan(-\varphi )-I/2)}^2\hfill \\ D_L^2=D^2+{(-(D+r)tan(-\varphi )-I/2)}^2\hfill \end{array}$$ (6)

For a relatively small ϕ and large target distance compared to interocular distance, the approximation (D ≈ D_R ≈ D_L) can be made and the term (1 + tan (ϕ)²) ≈ 1. Considering these approximations, the monocular gains in Equ. (5) simplify to:

$$\{\begin{array}{l}\frac{\partial E_R}{\partial \varphi }=-1-\frac{R}{D_R}\hfill \\ \frac{\partial E_L}{\partial \varphi }=1+\frac{R}{D_L}\hfill \end{array}$$ (7)

According to Fig. 1-(a), the following relations for ocular angles also hold according to target eccentricity θ and distance D:

$$\{\begin{array}{l}{E}_R={tan}^{-1}\left(\frac{Dtan(\theta )-I/2}{D}\right)\hfill \\ E_L={tan}^{-1}\left(\frac{-Dtan(\theta )-I/2}{D}\right)\hfill \end{array}$$ (8)

For small ocular angles tan(E_R,L) ≈ E_R,L (rad) and the following approximation is obtained from Equ. (8):

$$tan(E_R)+tan(E_L)=-\frac{1}{D}\approx E_R+E_L\Rightarrow D\approx \frac{I}{E_{\mathit{verg}}}$$ (9)

Using Equ. (9), expressions for D_R and D_L as a function of E_R and E_L are obtained as:

$$\{\begin{array}{l}{D}_R=\frac{D}{cos(E_R)}\approx \frac{-I}{(E_{\mathit{verg}})cos(E_R)}\hfill \\ D_L=\frac{D}{cos(E_L)}\approx \frac{-I}{(E_{\mathit{verg}})cos(E_L)}\hfill \end{array}$$ (10)

Substituting D_R and D_L into Equ. (7) the approximation of the ideal monocular VOR gains as a function of monocular eye position angle, vergence angle, interocular distance and radius of rotation are obtained as described in Equ. (2).

B. Bilateral Model Equations

In this section the equations to obtain the dynamic relations for conjugate and vergence components of the VOR in our bilateral model shown in Fig. 1-(b) are described. Subscripts R and L refer to the right and left side of the brainstem respectively. PVP and EHV here refer to the net output from these cell populations. The parameters a, p₁, p₂, d and q define the weight of the projections between cell types or brainstem centers according to Fig. 1-(b). Lower case letter s is the complex Laplace variable.

Signals from VN are added at MNs and then relayed to the eye plant $P(s)=\frac{k_p}{Ts+1}$ to generate ocular movements:

$$\{\begin{array}{l}{E}_R=({\mathit{aPVP}}_L-{\mathit{EHV}}_R)(\frac{k_p}{Ts+1})\hfill \\ E_L=({\mathit{aPVP}}_R-EH{V}_L)(\frac{k_p}{Ts+1})\hfill \end{array}$$ (11)

We are assuming that the eye position efference copies Ê_R,L are available through projections from PH with similar dynamics to the eye plant, $F(s)=\frac{k_f}{Ts+1}$; therefore,

$${\widehat{E}}_{R,L}=\frac{k_f}{k_p}{E}_{R,L}$$ (12)

EHVs are receiving ipsilateral canal projections V as well as efference copies of ipsilateral eye position and vergence angle. The net output however is a nonlinear gain that modulates the weight of canal projections according to the concurrent ocular angles; therefore,

$$\{\begin{array}{l}EH{V}_R=g_R({\widehat{E}}_R,{\widehat{E}}_{\mathit{verg}})p_2{V}_R\hfill \\ EH{V}_L=g_L({\widehat{E}}_L,{\widehat{E}}_{\mathit{verg}})p_2{V}_L\hfill \end{array}$$ (13)

PVPs are receiving projections from the ipsilateral canal V, contralateral PVPs and the PH; therefore,

$$\{\begin{array}{l}PV{P}_R=p_1{V}_R+{d\widehat{E}}_L-{\mathit{cPVP}}_L\hfill \\ PV{P}_L=p_1{V}_L+{d\widehat{E}}_R-{\mathit{cPVP}}_R\hfill \end{array}$$ (14)

The above equation can be rewritten as:

$$\{\begin{array}{l}PV{P}_R=\frac{1}{1-c^2}(p_1{V}_R-{cp}_1{V}_L+{d\widehat{E}}_L-{cd\widehat{E}}_R)\hfill \\ PV{P}_L=\frac{1}{1-c^2}(p_1{V}_L-{cp}_1{V}_R+{d\widehat{E}}_R-{cd\widehat{E}}_L)\hfill \end{array}$$ (15)

By substituting Equ. (12) in Equ. (13) and Equ. (15) and the results for PVPs and EHVs in Equ. (11), one can obtain the dynamic equations to describe conjugate and vergence VOR components as shown in Equ. (3a) and Equ. (3b), respectively.

C. Nonlinear Surface

The nonlinear surface assigned to the EHV cells, g_R,L, is obtained as a 4th order polynomial of x = Ê_R for the right EHV and x = Ê_L for the left EHV and a 1st order polynomial of y = Ê_verg according to the following equation:

$$g_{R,L}=m_0+m_{1}x+m_{2}y+m_3{x}^2+m_{4}xy+m_5{x}^3+m_6{x}^{2}y+m_7{x}^{3}y+m_8{x}^4$$ (16)

where m₀ = 0.7026, m₁ = −1.55e − 5, m₂ = 0.031, m₃ = −1.4e − 6, m₄ = 1.30e − 6, m₅ = 3.63e − 8, m₆ = −4.47e − 6, m₇ = − 3.55e − 9 and m₈ = − 3.56e − 9. The 95% confidence interval of the fit parameters m_i for i = 1, …, 9 does not include zero.