Comparison of diamine and Mg²⁺ interactions with RNA tertiary structures: similar vs. differential effects on the stabilities of diverse RNA folds

Abstract

Cations play a large role in stabilizing the native state of RNA in vivo. In addition to Mg²⁺, putrescine²⁺ is an abundant divalent cation in bacterial cells, but its effect on the folding of RNA tertiary structure has not been widely explored. In this study, we look at how the stability of four structured RNAs, each with a different degree of dependence on K⁺ and Mg²⁺, are affected by putrescine²⁺ relative to Mg²⁺. Through the use of thermal melts we observe that (i) at a given concentration, putrescine²⁺ is less effective than Mg²⁺ at stabilizing RNA; (ii) the stability imparted to RNA by various diamines is a function of charge density (average separation distance between charges) as well as flexibility of the counterion; and (iii) when Mg²⁺ is already present in a buffer, further addition of putrescine²⁺ may either destabilize or stabilize RNA structure, depending on whether the native RNA does or does not chelate Mg²⁺ ion, respectively. At ion concentrations likely to be found in vivo, the effect of putrescine²⁺ on the free energy of folding an RNA tertiary structure is probably quite small compared to that of Mg²⁺, but the ability of mixed Mg²⁺ - putrescine²⁺ environments to (in effect) discriminate between different RNA architectures suggests that, in some cells, the evolution of functional RNA structures may have been influenced by the presence of putrescine²⁺.

Introduction

The ionic composition of the cytoplasm plays a large part in dictating the stability of native RNA structure. In addition to the inorganic ions found in cells (predominantly K⁺ and Mg²⁺) organic cations such as putrescine²⁺ (1,4-diaminobutane) are found in concentrations high enough to warrant attention. (As putrescine is fully protonated near neutral pH, it will be referred to here as putrescine²⁺ when its cationic properties are being discussed.) Putrescine²⁺ is the third most abundant cation in bacterial cells with a total concentration that ranges between 10 and 60 mM in E. coli, depending on the growth medium (1). These levels are significant given that the most abundant divalent ion (Mg²⁺) in the cell has a total concentration of ∼100 mM (2). Despite the importance of understanding putrescine²⁺-RNA interactions, relatively few studies have focused on this subject (3-5).

In this study, we seek to understand the significance of putrescine²⁺ ion in regard to RNA tertiary structure stability in vivo. We compare the efficacy of putrescine²⁺ and Mg²⁺ at stabilizing the tertiary structure of four different RNAs, chosen to be representative of the diversity of RNA folds found within a bacterial cell. The results are consistent in that Mg²⁺ stabilizes the native state of all four RNAs to a greater degree than the same concentration of putrescine²⁺. In the presence of Mg²⁺, the change in thermal stability upon addition of putrescine²⁺ is found to either increase or decrease depending on the fold of the RNA. These findings can be attributed to the inability of putrescine²⁺ to occupy Mg²⁺ chelation sites as well as a difference in charge density among different divalent cations. The unexpected ability of mixed Mg²⁺ - putrescine²⁺ solutions to stabilize or destabilize RNAs of different native architectures suggests that, in some cells, RNA structures have adapted to the presence of putrescine.

Materials and Methods

Chemicals and RNA

All solutions were prepared using water at 18.3 MΩ resistivity. All buffers and salts were ≥ 99.5% purity. MOPS buffer was obtained from Sigma, and brought to pH 6.8 with KOH (K•MOPS). The standard buffer was 40 mM K•MOPS (with 13 mM K⁺) and 10 μM EDTA (Sigma). KCl (Fluka) was added to give the indicated total concentrations of K⁺, e.g. 37 mM KCl to give 50 mM K⁺. MgCl₂, and/or diamine were also added as indicated. (At pH 6.8, the diamines used in this study are all greater than 98% of the di-protonated species. . The relatively high concentration of K•MOPS was necessary to maintain pH 6.8 after additions of up to 10 mM of the HCl salts of the diamines used here.) Solutions of MgCl₂ (Fluka) were standardized by titration into an EDTA solution (pH 8.0) of known concentration, while monitoring absorbance at 230 nm (6).

The HCl salts of cis-1,4-diaminobutene and trans-1,4-diaminobutene were synthesized as described (7), and the products recrystallized twice from 1:1 methanol-ether. Cis and trans products were obtained in 70% and 58% yield, respectively and dried over phosphorus pentoxide. Proton NMR spectra recorded on a Bruker 400 confirmed the expected products; <1.5% of the total proton signal originated from unassigned peaks. The first acid dissociation constant (pK_a) of the 2HCl salts of putrescine, cis-1,4-diaminobutene and trans-1,4-diaminobutene were all determined by titration of the compound (at ∼ 20 mM in 12 ml H₂O) with a standardized 100 mM KOH solution (25°C) while monitoring the pH with a calibrated Thermo Scientific, Ross combination 8102BN electrode.

All RNAs were prepared by transcription of linearized plasmid DNA with a histidine-tagged bacteriophage T7 RNA polymerase (8), as described (9). Transcription products were purified by preparative electrophoresis on denaturing, 9-12% polyacrylamide gels. The desired product band was excised from the gel, from which the RNA was electroeluted in an Elutrap Electrophoresis Chamber (Schleicher & Schuell). Centricon filter units (Millipore) were used to equilibrate an RNA in the desired buffer.

Vapor Pressure Osmometry

The osmolalities of putrescine•2HCl solutions were assessed by vapor pressure osmometry (VPO), using a Wescor VAPRO 5520 (Logan, UT) at ambient temperature. Solutions were prepared gravimetrically from dried, crystalline putrescine•2HCl and water. Osmolalities were measured three times on each sample and repeated four times with fresh stocks. Data were fit to a second order polynomial using Kaleidagraph, and compared with literature values for MgCl₂ (Figure S4). Putrescine•2HCl clearly deviates more strongly from ideal behavior than does MgCl₂ at concentrations greater than ∼100 mmolal. The RNA stability measurements reported here use a mixture of divalent ion(s) and KCl/K•MOPS, the latter monovalent salts usually at a total of 50 mM and in excess over the concentration of Cl⁻ that accompanies the divalent ion. Under these conditions, the mean ionic activity coefficient of the divalent cation is largely determined by the concentration of the anion. A good approximation is that the MgCl₂ mean ionic activity coefficient in experiments with 50 mM KCl is approximately the same as that of a MgCl₂ solution of the same ionic strength (10). (At I = 50 mM, or ∼17 mM MgCl₂, γ ≈ 0.66 (11).) In this region of Figure S4, the MgCl₂ and putrescine•2HCl osmolalities are identical within experimental error, and the limiting slopes of the fitted osmolality curves are also approximately the same (2.53 and 2.58).

Although the slope of the osmolality vs. molality curve is related to the activity of the solute, it is necessary to carry out an integration to obtain the activity coefficient. The equation is ln γ₂ = (φ − 1) + ∫ [(ϕ − 1) /ϕ]dm₂, where m₂ is the solute concentration, ϕ is the practical osmotic coefficient (ϕ = Osm/m₂), γ₂ is the mean ionic activity coefficient, and the integration is carried out from 0 to the m₂ concentration of interest (12)(13). The (ϕ−1) term amplifies small errors at low molalities, and in addition the integrand approaches a non-zero value at zero solute concentrations. It is therefore necessary to have accurate measurements of osmolality at very low solute concentrations to obtain activities in the range of interest in these studies. VPO measurements are unable to quantify low solute osmolalities with sufficient accuracy, but we can estimate that about a three-fold lower osmolality for 25 mM putrescine•2HCl over 25 mM MgCl₂ would be necessary to generate even a factor of two difference in mean ionic activity coefficient. On this basis, we have compared the effectiveness of Mg²⁺ and putrescine²⁺ in stabilizing RNA in terms of their concentration, without introducing any correction for activity differences.

UV melting curves and melt data analysis

Thermal denaturation of RNA samples was carried out with either a Cary 400 spectrophotometer equipped with a six cell thermostatted cuvette holder or an Aviv model 14DS spectrophotometer with a five cell thermostatted cuvette holder. Each instrument was able to reproduce the results of the other within error. UV absorbance was variously monitored at 260, 280 and 295 nm. The temperature schedule for the experiments was as follows: heat from room temperature to 65°C, hold at 65°C for 5 minutes, cool to less than 10°C, then heat to 95°C. Temperature changes in the second and third stages was set between 0.5 and 0.66 °C/min. No significant hysteresis was observed between the cooling and second heating stages; we conclude that renaturation artifacts or RNA degradation has not biased the curves below 65 °C. Absorbance data were plotted as the derivative of absorbance with respect to temperature. The program Global Melt Fit was used to fit all resulting data and estimate errors by a bootstrap method (14). Global fitting of data collected at 260 and 280 nm was used to extract values for both T_m (melting temperature) and ΔH°. The fitted enthalpies of a tertiary unfolding transition did not vary more than 7% over all the conditions tested; the average value was used in calculating ΔG°_obs at temperature T₀ from the formula

$$\mathrm{\Delta }\mathrm{G}°({\mathrm{T}}_0)=\mathrm{\Delta }\mathrm{H}°({\mathrm{T}}_0)(1/{\mathrm{T}}_{\mathrm{m}}-1/{\mathrm{T}}_0)$$ (3)

where T₀, the reference temperature, is 25 °C.

Plots of ΔΔG°_obs, the difference between ΔG°_obs in the presence and absence of Mg²⁺ or putrescine, as a function of divalent ion concentration were fit to a Hill polynomial,

$$\mathrm{\Delta }{G}_{\mathit{obs}}^0=(\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{obs},\mathit{max}}^0)\frac{{([2+]/{[2+]}_0)}^n}{{(1+[2+]/{[2+]}_0)}^n}$$ (4)

where ΔΔG°_obs,max is the maximum ΔΔG°_obs at high divalent ion concentration, [2+] is the molar concentration of either Mg²⁺ or putrescine²⁺, [2+]₀ is the divalent ion concentration at the midpoint (half-maximal -ΔΔG°_obs) of the curve, and n is the Hill exponent. Note this y-axis is free energy, instead of the more familiar fraction folded. The number of excess divalent ions taken up in the folding transition is given by the Wyman linkage relation

$$\mathrm{\Delta }{\mathrm{\Gamma }}_{2+}=-\left(\frac{1}{\mathit{\text{RT}}}\right){\left(\frac{\partial (\mathrm{\Delta }\mathrm{\Delta }{G}^0)}{\partial ln[2+]}\right)}_{T,P,[\mathit{\text{KCl}}]}$$ (5)

where R is the gas constant and T the temperature. The value of this derivative at the midpoint of the ΔΔG°_obs curve is related to the exponent n by

$$\mathrm{\Delta }{\mathrm{\Gamma }}_{2+}=n\left(\frac{-\mathrm{\Delta }\mathrm{\Delta }{G}_{max}^0}{4\mathit{\text{RT}}}\right)$$ (6)

A similar equation is derived in ref. (15). We emphasize that ΔΓ₂₊ calculated from eq (6) applies only at the midpoint of the ΔΔG°_obs curve; ΔΓ₂₊ approaches zero at low and high divalent ion concentrations.

Results

RNA Selection

To survey the effects of putrescine on the stability of RNA tertiary structure, four RNAs that differ in their interactions with inorganic ions were selected for study (Figures 1 and S1). In this work, we distinguish “chelated” ions from all other cations interacting with an RNA, which we group together as the “ion atmosphere”. Chelated ions make at least two direct contacts with RNA electronegative groups, and are thus partially dehydrated; they are found in pockets of high negative electrostatic potential (16, 17). The ion atmosphere encompasses both fully hydrated ions at a distance from the RNA surface, and ions whose first-shell waters of hydration may be perturbed by the RNA surface (18).

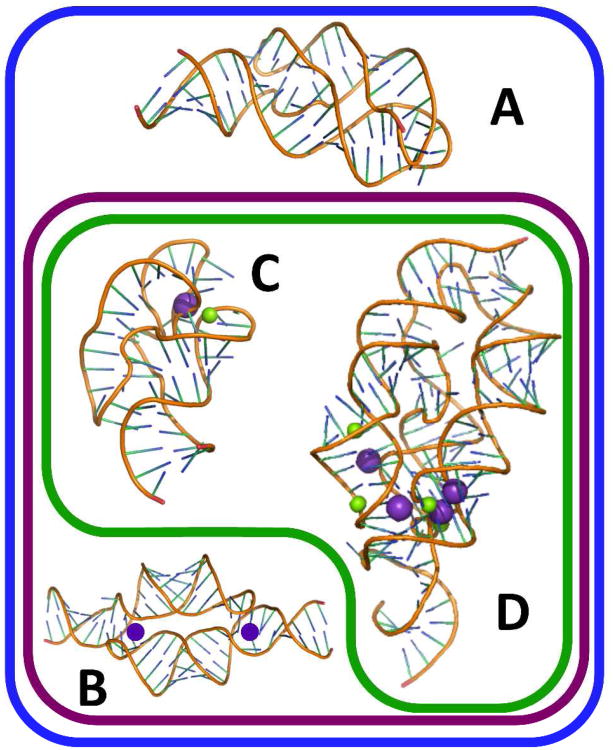
Figure 1.

Venn diagram depicting the RNA structures analyzed in this study and how they interact with cations. Blue outline contains population of RNAs stabilized by cations residing in the ion atmosphere. Purple outline contains RNAs that, in addition, have chelated K⁺ ions (purple spheres). RNAs within the green outline also have chelated Mg²⁺ ions (green spheres). A) A-riboswitch, PDB ID: 3G4M. B) TLR RNA, PDB ID:2I7E; (K⁺ ions have been added as discussed in text). C) 58mer rRNA, PDB ID: 1HC8. D) M-box riboswitch, PDB ID: 2QBZ. See Figure S1 for sequences used in this study.

The aptamer domain of the add adenine riboswitch (A-riboswitch, Figure S1A) was chosen as representative of a structured RNA exclusively stabilized by the ion atmosphere. The A-riboswitch folds into its native structure in the absence of divalent ions upon addition of adenine (or adenine derivatives) to the solution (19, 20). Although the RNA shows increased stability in the presence of Mg²⁺ (20, 21), crystallographic studies do not resolve any chelated Mg²⁺ or K⁺ ions (22, 23). In addition, studies on the monovalent ion dependence of A-riboswitch concluded that this RNA shows no monovalent ion selectivity that might suggest K⁺ chelation (9).

The homodimeric tetraloop receptor RNA (TLR RNA, Figure S1B) incorporates a motif first resolved in the Tetrahymena group I intron (24-26). This motif is known to chelate a K⁺ ion (27), and is more stable in the presence of K⁺ than other group I monovalent ions (9). When the TLR RNA dimerizes, two helical segments come into parallel alignment, a common arrangement in large RNAs. Because the negatively charged helices are brought fairly close together, there is a strong monovalent salt dependence to dimerization; however, Mg²⁺ is not essential for dimerization (9).

An rRNA fragment (58mer RNA, Figure S1C) and the aptamer domain of the M-box riboswitch (M-box RNA, Figure S1D) were chosen as examples of RNAs that chelate Mg²⁺. Structural studies of the 58mer RNA have concluded that both K⁺ and Mg²⁺ are chelated in close proximity within the native fold of the 58mer (28, 29). This RNA obtains maximum stability in the presence of K⁺ relative to other group I monovalent ions (30). In addition, electrostatic calculations concluded that a pocket of high negative potential on the RNA is capable of providing enough free energy to partially dehydrate and bind a Mg²⁺ ion (17). The M-box riboswitch is a sensor of the effective Mg²⁺ concentration in vivo(31). It is the largest of the RNAs used in this study (160 base pairs), and has a compact core that chelates at least three Mg²⁺ and three K⁺ ions.

The two Mg²⁺-chelating RNAs are distinct in their reliance on Mg²⁺ for folding to the native state. In the absence of a divalent ion, the 58mer requires 1.6 M NH₄Cl (32), and the M-box RNA does not fold even in 2.1 M NaCl (31). In the following sections, the two “Mg²⁺- chelator” RNAs will be discussed separately from the other two RNAs, which fold to their native structures in modest concentrations of KCl.

Comparison of A-riboswitch and TLR RNA stabilities with putrescine²⁺ vs. Mg²⁺

RNA stabilities were assessed using thermal melts monitored by UV absorbance (see Materials & Methods). Conditions are readily found under which both the A-riboswitch and TLR RNA fold to their native structures in the absence of divalent ions. The A-riboswitch folds in the presence of a tight-binding ligand (20 μM 2,6-diaminopurine, DAP) and 50 mM K⁺; a higher monovalent salt concentration (300 mM K⁺) is needed to observe the TLR RNA dimer. For the A-riboswitch, a distinctive unfolding transition is only observed in the presence of ligand and corresponds to the loss of tertiary structure (20). The transition shifts to higher T_m upon addition of either putrescine²⁺ or Mg²⁺ (Figure S2A). Dimerization of the TLR RNA is accompanied by a small but distinctive transition that is slightly hyperchromic at 260 nm and hypochromic at 280 nm; its T_m is also concentration-dependent as expected for a dimerization reaction (9). This transition also shifts to higher temperature in response to either Mg²⁺ or putrescine²⁺ (Figure S2B, S2C). Melting curves obtained under these buffer conditions can thus be analyzed to obtain standard free energies for tertiary structure folding, ΔG°_obs, in the presence or absence of divalent ion (see Materials and Methods).

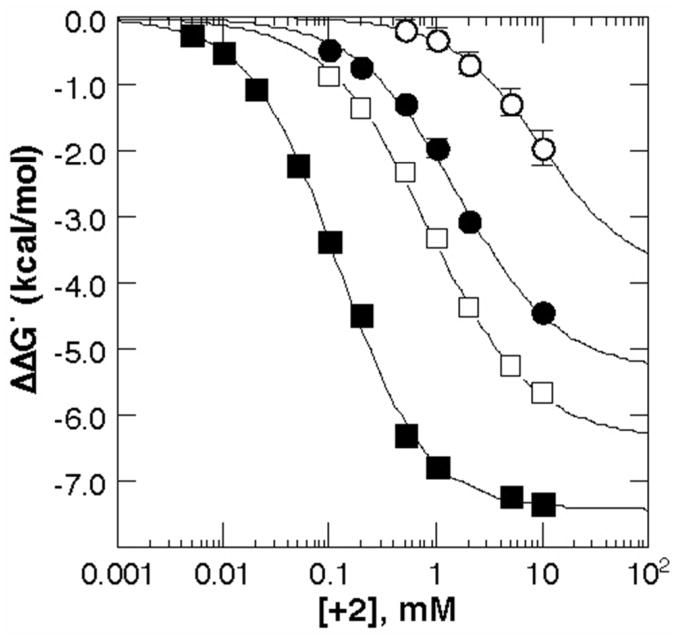
Figure 2 plots the increment in folding free energy due to the divalent ion:

Figure 2.

The increase in stability (ΔΔG°_obs, eq 1) upon titration of A-riboswitch (squares) or TLR RNA (circles) with chloride salts of Mg²⁺ (closed) or putrescine²⁺ (open). Tetraloop receptor data were collected in K•MOPS - EDTA buffer (see Materials and Methods) with 300 mM K⁺ while the A-riboswitch data were collected in the same buffer with 50 mM K⁺ and 20 μM DAP. Either MgCl₂ or putrescine•2HCl was added to the concentration indicated by the abscissa, [2+].

$$\mathrm{\Delta }\mathrm{\Delta }\mathrm{G}{°}_{obs}=\mathrm{\Delta }\mathrm{G}{°}_{obs,2+}-\mathrm{\Delta }\mathrm{G}{°}_{obs,\text{ref}}$$ (1)

where ΔG°_obs,ref is the folding free energy in the reference buffer with only monovalent ions, and ΔG°_obs,2+ the folding free energy with a given concentration of divalent ion. There is a striking difference in the effectiveness of the two ions; it takes 6 – 8 fold higher putrescine²⁺ concentration to achieve the same stability increase as with Mg²⁺.

To contrast the effectiveness of the two different ions in thermodynamic terms, the comparison should be made between RNA stabilities at the same ion activities, rather than ion concentrations. The activity of MgCl₂ over a range of concentrations is known (11, 33), and the mean ionic activity coefficient of millilmolar concentrations of Mg²⁺ in the presence of 50 mM KCl can be estimated as ∼0.66 (10). To our knowledge, there are no similar measurements of putrescine•2HCl activity. We carried out vapor pressure osmometry experiments to address this question (see Materials and Methods, Figure S4). Although it is difficult to measure putrescine osmolalities at low concentrations accurately, we argue from the data that MgCl₂ and putrescine•2HCl differ in activity by much less than a factor of two at the concentrations used in our experiments. We conclude that a difference in thermodynamic activity of Mg²⁺ and putrescine²⁺ cannot account for the large difference in concentrations needed to stabilize these two RNAs, and that it is reasonable to use a concentration scale when comparing RNA folding free energies measured with these two ions.

Besides the difference in the ability of the two divalent ions to stabilize RNA, another interesting feature of Figure 2 is the difference in uptake of divalent ion that accompanies the folding reaction. We express the number of “excess” divalent ions per RNA that are present in order to neutralize part of the RNA negative charge as Γ_Mg2+ (for Mg²⁺) or Γ_put2+ (for putrescine²⁺). Upon folding from a partially structured RNA to a more compact native conformation, Γ₂₊ invariably increases (20, 34). Under the conditions of excess K⁺ employed here, ΔΓ₂₊ evaluated at the divalent ion concentration required to fold half of the RNA molecules is identical to the Hill exponent n obtained by fitting the Hill equation to a plot of fraction RNA folded vs. ln[Mg²⁺] (20). In Figure 2, the slope d(ΔΔG°_obs)/d(ln[Mg²⁺], evaluated at the midpoint of the ΔΔG°_obs curve, is related to the same parameter (see Materials and Methods, eq 5). For both RNAs, ΔΓ_Mg2+ is larger than ΔΓ_put2+, though the large error in ΔΓ_put2+ for the TLR RNA means the difference is less significant. (The error is from uncertainty in the maximum value of -ΔΔG°obs; data cannot be collected at higher putrescine concentrations without biasing the measurement with a large excess of Cl⁻ ions (20).) ΔΓ₂₊ is not independent of divalent ion concentration, so a comparison between ΔΓ_Mg2+ and ΔΓ_put2+ could be misleading because of the large difference in ion concentrations at the midpoints of the two curves. The expectation is that ΔΓ₂₊ increases with the divalent ion concentration (20), but we find that the ion at higher concentration, putrescine²⁺, has the smaller value of ΔΓ₂₊. The difference in ion uptake therefore appears to be a real difference in the behaviors of the ions.

Finally, it appears that putrescine²⁺ does not stabilize either the A-riboswitch or TLR RNA to the same ΔΔG°_obs,max as Mg²⁺. As noted above, there is a large uncertainty in the maximum stability of the TLR RNA with putrescine²⁺, but the difference in the A-riboswitch stabilities with the two ions is significant (-1.06 ± 0.20 kcal/mol, see Table 1). Since ΔΓ_Mg2+ and ΔΓ_put2+ are different for this RNA, it is not surprising that ΔΔG°_obs,max is also different. Whether the difference stems from a stronger interaction of Mg²⁺ with the native state, a stronger interaction of putrescine²⁺ with partially unfolded RNA conformations, or both those factors, cannot be decided from the present experiments. Ideas about the relation between charge density of ions and their interactions with RNA are taken up in the Discussion.

Table 1. RNA stabilization by divalent ions^a.

RNA	divalent ion	pKab	[2+]0, mM	ΔΔG°obs, max, kcal/mol	ΔΓ2+, ions/RNA
A-riboswitch	Mg2+		0.104 ± 0.006	−7.30 ± 0.15	3.31 ± 0.20
A-riboswitch	putrescine	9.36 (9.35)	0.87 ± 0.57	−6.36 ± 0.14	2.39 ± 0.11
TLR RNA	Mg2+		0.1.62 ± 0.31	−5.33 ± 0.43	2.06 ± 0.30
TLR RNA	putrescine		9.80 ± 3.21	−3.88 ± 0.99	1.66 ± 0.47
A-riboswitch	cadaverine	(10.05)	1.30 ±0.15	−5.83 ±0.26	2.16 ± 0.17
A-riboswitch	1,3 diaminopropane	(8.6)	0.42 ± 0.2	−6.99 ± 0.12	2.58 ± 0.13
A-riboswitch	cis-1,4 diaminobutene	8.78	0.65 ± 0.06	−7.19 ± 0.26	2.41 ± 0.21
A-riboswitch	trans-1,4 diaminobutene	8.93	0.89 ±0.04	−7.09 ± 0.10	2.36 ± 0.07

^aΔΔG°_{obs, max} and [2+]₀ are for fits of eq (4) to data shown in Figures 2 and 3A. ΔΓ₂₊ was calculated by eq (5). All diamino compounds shown have a +2 charge at the pH of the experiments (6.8).

^bpK_a values are the observed macroscopic first acid dissociation constants for the diamino compounds. Values in parentheses were taken from the literature (49-51); other values were determined as described in Materials and Methods.

A-riboswitch stability with various diamines

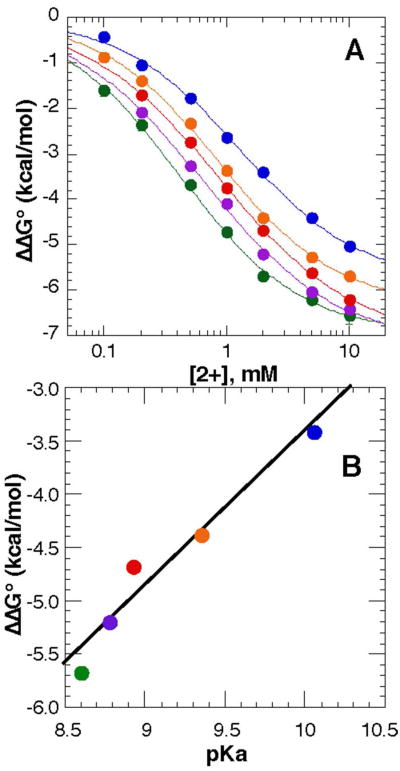
To better understand how putrescine²⁺ interacts with RNA, several diamines with different carbon linkers were used to ask whether RNA stability depends on either the average distance between amines or the rigidity of the linker. ΔΓ_put2+ weakly varies between ∼2.2 and 2.4 with different diamines, and is largest with the shortest alkyl linker (Table 1). The midpoint of the titration curve varies more significantly, by about a factor of three (Figure 3A). To ask whether stabilization free energy imparted by a given diamine is correlated with the average intramolecular distance between amine groups in solution, the first acid dissociation constant (pK_a) for each diamine was obtained (Table 1). Deprotonation of an amine is energetically less costly if a second positive charge is nearby. Based on Coulomb's law, the first pK_a is inversely proportional to the distance between the two charges. A plot of ΔΔG°_obs at a specific diamine concentration (2 mM) vs. the first pK_a of the cation results in an approximately linear trend (Figure 3B).

Figure 3.

Stability of the A-riboswitch in the presence of various diamines, as derived from thermal stability measurements. A, ΔΔG°_obs of the A-riboswitch vs. concentration of cadaverine (blue), putrescine (orange), trans-1,4-diaminobutene (red), cis-1,4-diaminobutene (purple) and 1,3-diaminopropane (green). B, stability of the A-riboswitch at 2 mM concentration of the diamines listed above vs the first acid dissociation constant (pK_a, Table 1) of the diamine. The slope of the least squares fit to all the data points (black line) is 1.45 kcal/mol (R=0.975).

A-riboswitch and TLR RNA stability in mixed Mg²⁺ - putrescine buffers

As shown in Figure 2, Mg²⁺ stabilizes the A-riboswitch and TLR RNA more effectively than putrescine²⁺. Under in vivo conditions, though, RNA is stabilized by a mixture of several different counter ions. In order to assess how mixtures of putrescine²⁺ and Mg²⁺ influence the stability of RNA, we conducted thermal melts on our set of four RNAs with varying concentrations of the two divalent ions. To help interpret the results, we note that an excess of cations and an exclusion of anions balance the charge of anionic phosphates on the RNA, as required by charge neutrality. Thus, any change in ΔΓ_put2+ (for instance) must be compensated by a change in the excess of other ionic species in solution (15, 34):

$$-2\mathrm{\Delta }{\mathrm{\Gamma }}_{\mathit{\text{put}}2+}=2\mathrm{\Delta }{\mathrm{\Gamma }}_{{\mathit{\text{Mg}}}^{2+}}+\mathrm{\Delta }{\mathrm{\Gamma }}_{K^{+}}-\mathrm{\Delta }{\mathrm{\Gamma }}_{{\mathit{\text{Cl}}}^{-}}$$ (2)

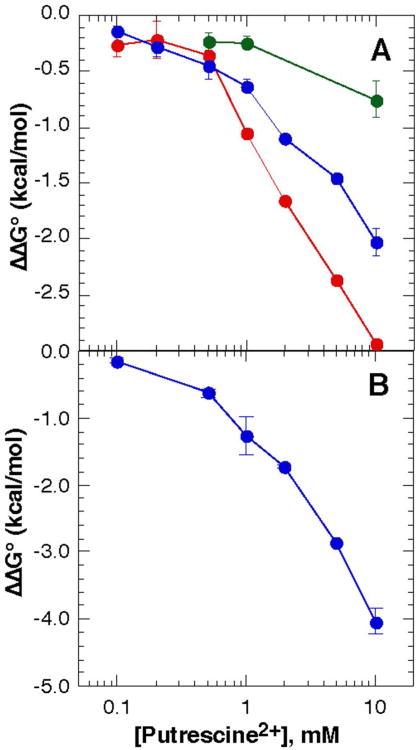
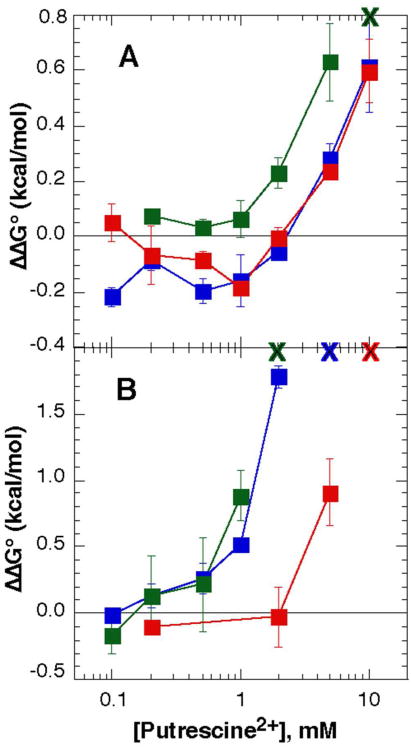
Figure 4A shows the change in A-riboswitch stability vs. concentration of putrescine²⁺, with the Mg²⁺ concentration kept constant at the indicated values. The negative slopes of these curves indicate a net uptake of putrescine²⁺ ions upon folding the RNA to its native state (see Materials and Methods, eq 5). As the Mg²⁺ concentration increases from 0. 1mM to 0.5 mM the resulting change in free energy upon addition of putrescine²⁺ becomes less negative, though the maximum uptake (ΔΓ_put2+ ≈ 1.4 ions/RNA at 2 mM putrescine²⁺ and 0.1 mM Mg²⁺, Figure 4A) and -ΔΔG°_obs at a given putrescine²⁺ concentration are never as great as seen with putrescine²⁺ alone (Figure 2). Thus, the uptake of putrescine²⁺ is opposed by increased Mg²⁺ concentrations, as might be expected on the basis of eq (2). The release of Mg²⁺ can be estimated from the dependence of ΔΔG°_obs on Mg²⁺ concentration at a constant putrescine²⁺ concentration (eq 1). At 2 mM putrescine and 0.1 mM Mg²⁺, ΔΓ₂₊ ≈ -1.4 (Figure 4A). Although it appears that ΔΓ_Mg2+ and ΔΓ_put2+ are equal and opposite, these estimates are not accurate enough to rule out small accompanying changes in ΔΓ_K+ and ΔΓ_Cl−.

Figure 4.

Effect of putrescine²⁺ on the stability of RNAs without Mg²⁺ chelation sites. ΔΔG°_obs for both RNAs was measured in K•MOPS - EDTA buffer with 50 mM K⁺ and 0.1 mM (red), 0.2 mM (blue) or 0.5 mM (green) MgCl₂. 20 μM DAP was included with the A-riboswitch. A, A-riboswitch; B, TLR RNA.

The TLR RNA also shows a net stabilization upon addition of putrescine²⁺ to a Mg²⁺-containing buffer (Figure 4B). The trend in ΔΔG°_obs is qualitatively similar to the A-riboswitch, although the magnitude of the stabilization is about twice as large for the TLR RNA. (In 0.2 mM MgCl₂ and 10 mM putrescine²⁺, the TLR RNA obtains a maximum stability of -4.03 kcal/mol ± 0.19 kcal/mol, versus −2.03 kcal/mol ± 0.12 kcal/mol for the A-riboswitch.)

Stability of Mg²⁺ -chelator RNAs in mixed Mg²⁺ - putrescine buffers

Melting curves of both Mg²⁺-chelator RNAs show the appearance of a new transition with a distinctive ratio of hyperchromicities at 260 and 280 nm when ∼1 mM MgCl₂ is included in the buffer, in addition to 50-60 mM KCl (35) (Figure 5 and S3 D-F). This transition is not observed when putrescine²⁺ is substituted for Mg²⁺ at concentrations up to 10 mM; apparently putrescine²⁺ cannot provide enough free energy of stabilization at the accessible concentrations. When the two Mg²⁺-chelating RNAs are first induced to fold by Mg²⁺ and then titrated with putrescine²⁺, the stability decreases (Figure 6 A, B). The 58mer RNA is destabilized only by putrescine²⁺ concentrations in excess of ∼2 mM (0.5 to 2.0 mM MgCl₂), but the M-box riboswitch is destabilized by >1.8 kcal/mol at 2 mM putrescine²⁺ and ≤ 1 mM Mg²⁺. Tertiary structure is undetectable in either RNA at a high enough ratio of putrescine²⁺ to Mg²⁺ ions. This behavior is the opposite from our observations with the A-riboswitch and TLR RNA in mixed Mg²⁺ - putrescine²⁺ buffers (Figure 4).

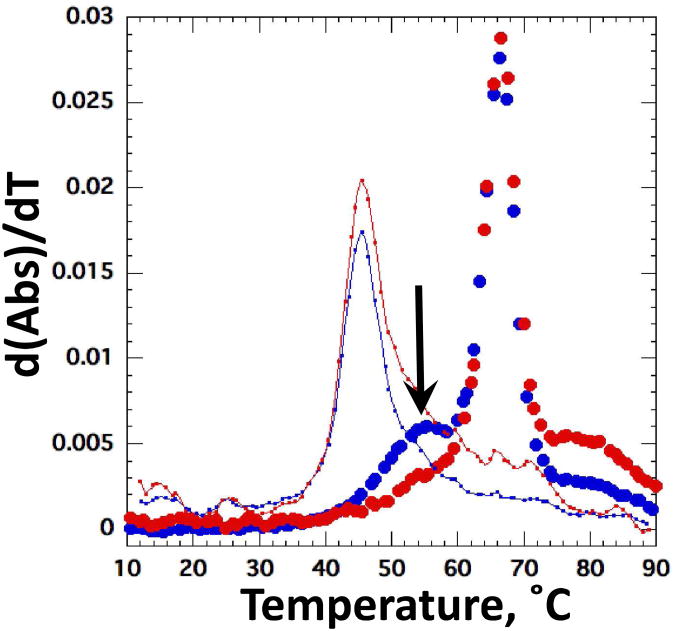
Figure 5.

Melting profile of the M-box riboswitch. Data are plotted as the derivative of absorbance with respect to temperature at 260 nm (blue) and 280 nm (red). Closed circles correspond to data collected in buffer with 50 mM K⁺, 1 mM putrescine²⁺ and 1 mM Mg²⁺, in K•MOPS – EDTA buffer. Solid lines correspond to data collected in the same buffer with 50 mM K⁺ and no divalent ions. Arrow indicates new transition that appears in the presence of Mg²⁺.

Figure 6.

Stability of the magnesium-chelating RNAs in varying concentrations of putrescine²⁺. A, stability of the 58mer rRNA fragment relative to stability in buffer with 50 mM K⁺ and 0.5 mM (green), 1.0 mM (blue), or 2.0 mM (red) MgCl₂. The green “X” at the top of the graph represents the concentration of putrescine²⁺ (with 0.5 mM Mg²⁺) at which the tertiary structure can no longer be detected in the melting curves. B, stability of the M-box RNA relative to buffer with 50 mM K⁺ and 0.75 mM (green), 1.0 mM (blue), or 2.0 mM (red) MgCl₂. An “X” at the top of graph represents the concentration of putrescine where the tertiary structure is no longer observed with 0.75 mM (green), 1 mM (blue), or 2 mM (red) Mg²⁺.

Discussion

In vivo relevance of putrescine to RNA folding

In vivo, the stability of an RNA structure may be affected by several different solution components, such as ions, osmolytes (36), and other macromolecules that act as crowding agents (37). Of the three most abundant cations in the bacterial cell, K⁺, Mg²⁺ and putrescine²⁺, relatively little is known about the effects of putrescine²⁺ on RNA stability. In this work, we try to gain some insight into the in vivo relevance of putrescine²⁺ to RNA folding by asking what change the ion causes in folding free energy (ΔΔG°_obs) and what degree of ion uptake is associated with structure formation (ΔΓ_put2+) for four different RNA tertiary structures.

The experiments reported here show that putrescine²⁺ is, in general, far less effective than Mg²⁺ at stabilizing RNA tertiary structure: two of the RNAs required more than five-fold higher concentrations of putrescine²⁺ than Mg²⁺ to reach the same stability (Figure 3), and two RNAs could not be induced to fold to the native structure in buffers with only putrescine²⁺ and monovalent ions. Putrescine²⁺ has also been found to be a very weak stabilizer of tRNA tertiary structure, compared to Mg²⁺ (4). The question of whether these weak effects may influence RNA stability in vivo is difficult to answer definitively. We first consider the range of ion activities that are likely to be found in bacteria in vivo, and then discuss the potential consequences for RNA tertiary folding.

The in vivo activity of Mg²⁺ is difficult to measure, but several kinds of measurements suggest it is equivalent to that of ∼1.0 mM Mg²⁺ in the presence of 150 mM KCl, (38-40). (The total cellular concentration of Mg²⁺ is about 100 fold higher (2), but because the ion interacts so strongly with cellular polynucleotides the effective concentration, or activity, is much lower.) The measurements in the present work were made in a background of 50 to 300 mM K⁺, with most of the anion as Cl⁻. At 50 mM KCl, the concentration of Mg²⁺ needed to reproduce the estimated in vivo activity is ∼0.30 mM. (This calculation is based on MgCl₂ and KCl activity coefficients and the principle that the mean ionic activity coefficient of a low concentration of Mg²⁺ in 50 mM KCl is the same as the mean ionic activity coefficient of Mg²⁺ in a MgCl₂ solution of the same ionic strength as 50 mM KCl, i.e. 17 mM MgCl₂(10).) These are rough estimates, but nevertheless, the four RNAs studied here are all significantly stabilized by submillimolar Mg²⁺ concentrations that are probably comparable to in vivo activities. The M-box RNA is in fact a regulatory switch that turns on or off expression of a Mg²⁺ transporter gene in response to changes in Mg²⁺ concentration in vivo, so this RNA might be expected to fold or unfold near physiological Mg²⁺ activity (31, 41).

We are not aware of any estimates of in vivo putrescine²⁺ activity. If we take the in vivo total concentration under standard growth conditions to be 60 mM (1), and the same ∼100:1 ratio of total to effective concentration as Mg²⁺, the activity would be the equivalent of ∼0.2 mM putrescine²⁺ in 50 mM KCl (or 0.6 mM at 150 mM KCl). However, the apparent affinity of putrescine²⁺ for helical DNA is 2-3 fold weaker than that of Mg²⁺ (3), and interactions with RNA may be even weaker, as suggested by the experiments reported here. The ratio of total to effective concentration may therefore be much smaller than 100:1, and the effective concentration in vivo somewhat higher than that of Mg²⁺. We consider 0.2 –1.0 mM putrescine²⁺ (50 mM KCl) a reasonable range for reproducing in vivo conditions.

Given the above considerations, it seems likely that, in the context of the bacterial cell, putrescine²⁺ makes a small but significant contribution to the overall stability of an RNA. For instance, 0.2 to 1.0 mM putrescine²⁺ stabilizes the A-riboswitch by -1.4 to -3.3 kcal/mol. Though these values drop by a factor of five in the presence of 0.2 mM Mg²⁺, even a –0.5 kcal/mol free energy gain over Mg²⁺ alone is enough to shift a folding equilibrium. The M-box RNA is a particularly interesting case, in which putrescine²⁺ destabilizes the RNA by nearly 2 kcal/mol when present at only twice the Mg²⁺ concentration (Figure 6B). For a sensor RNA that is tuned to respond to intracellular fluctuations in Mg²⁺ activity, this free energy change is quite significant. Noting that putrescine²⁺ concentrations may vary over at least an eight fold range as the osmolality of the growth medium changes (1), there is the intriguing possibility that the responses of the M-box RNA or other riboswitches are modulated to some extent by intracellular putrescine²⁺ activity.

A caveat about the distribution of putrescine in nature is necessary. Microorganisms such as bacteria and molds contain high concentrations of putrescine²⁺ (42), and E. coli requires polyamines for growth under anaerobic conditions (43). However, mammalian cells cells typically contain putrescine²⁺ in approximately 2-3 orders of magnitude lower concentration (42), which are unlikely to affect the folding or stability of any RNAs. The two riboswitches selected for this study are found exclusively in bacteria; consequently their structures may have evolved in response to the high bacterial levels of putrescine. The other two RNAs represent a motif and a structure that are found in all organisms, but it is still possible that their stability is modulated by putrescine in bacteria, and that the specific sequences utilized by the organism or other factors (such as a bound protein, (44)) compensate.

RNA stabilization by divalent ions of the “ion atmosphere”

A question raised by this and other studies of putrescine²⁺ with RNA (4, 5) is why putrescine²⁺ is less effective at stabilizing RNA, in comparison to Mg²⁺; this study additionally poses the question of why putrescine²⁺ destabilizes some RNAs when Mg²⁺ is present. For the purposes of the following discussion, it is convenient to use the distinction (see Results) between chelated ions that directly contact two or more RNA groups, and the ion atmosphere, defined here as the remaining cations that interact with an RNA at various distances from the RNA surface. Putrescine²⁺, or any other cation, is capable of favorable interaction with the RNA as a part of the ion atmosphere, but putrescine²⁺ is very unlikely to substitute for an inorganic ion at a chelation site. (We know of no RNA that specifically binds putrescine²⁺ in a way analogous to the chelation of an inorganic ion, though recognition of the amino-butyl side chain of lysine by the lysine riboswitch suggests such a site is feasible (45, 46).) We consider the ion atmosphere first and then discuss the possible effects of putrescine²⁺ on Mg²⁺ chelation sites.

Ion atmosphere

The A-riboswitch and TLR RNAs were selected as examples of RNAs for which Mg²⁺-induced stabilization is entirely by RNA interactions with the ion atmosphere; as detailed in Results, there is no evidence for Mg²⁺ chelation sites in either RNA. Our conclusions for these two RNAs are that (i) Mg²⁺ is always more stabilizing than putrescine²⁺ (Figure 2); (ii) ΔΓ₂₊ is perhaps slightly less for putrescine²⁺ than for Mg²⁺; and (iii) the stabilizing effect of Mg²⁺ and putrescine²⁺ together, while not additive, is always as least as strong as that of either of the ions alone (cf. Figures 2 and 4). Thus, with respect to the ion atmosphere, putrescine²⁺ apparently substitutes to some extent for Mg²⁺, but is not as effective. An argument has been made that ions with higher charge density (defined as charge divided by Van der Waals volume) are more effective stabilizers of native RNA structures because they may approach the RNA surface (and maximum negative electrostatic potential) more closely, and because of smaller excluded volume effects when ions accumulate in high concentration near the RNA (5). Our results with Mg²⁺ and putrescine²⁺ are consistent with this idea.

To further explore the way charge density might affect the interactions of organic ions with RNA, we compared the stability of the A-riboswitch with five different organic diamino compounds. The results (Figure 3 and Table 1) show distinct dependences on the length and saturation of the carbon chain separating the two charges. The first pK_a of these ions varies over a range of ∼1.5 pH units; it is a measure of the reciprocal distance between the two charges. To a good approximation, the stabilization imparted by the ion is proportional to a linear charge density, i.e. the charge divided by the average distance of separation (Figure 3B). However, an additional factor to consider is that the linear charge density of an organic ion may be influenced by its environment. In the diamino alkane compounds, the average distance of separation between two amino groups could decrease as the ion approaches the RNA surface, if the decrease in entropy is sufficiently compensated by the simultaneous placement of the two amines in a volume of high negative electrostatic potential. In fact, 1,4 trans-diaminobutene, which is locked in a more extended conformation than either putrescine or 1,4 cis-diaminobutene, imparts 0.45 kcal/mol less negative ΔΔG°_obs than expected based on the correlation between pK_a and ΔΔG°_obs for the diamino-alkanes. Thus, both the flexibility and length of carbon chains may be factors in determining how effectively organic ions (including spermine and spermidine) interact with compact RNAs.

Chelation sites

RNAs that contain Mg²⁺ chelation sites tend to be strongly dependent on Mg²⁺ to fold into their native structures, presumably because it is too costly to create the high electrostatic potential of an ion binding pocket if there is no cation capable of occupying the site (17, 47, 48). Steric constraints prevent putrescine²⁺ from replacing Mg²⁺ in a chelation site, so it is unsurprising that putrescine²⁺ (plus monovalent cation) are unable to stabilize the native state of either the 58mer or M-box RNAs. It is less obvious why addition of putrescine²⁺ should destabilize an RNA that has been driven into its native conformation by Mg²⁺ (Figure 6). The observation suggests that putrescine²⁺ weakens the affinity of Mg²⁺ for chelation sites, but there cannot be direct competition between the ions for occupancy of the site. To rationalize this observation, we turn to a calculation of the repulsive interactions between chelated Mg²⁺ and the ion atmosphere (17, 48). Occupancy of a chelation site by Mg²⁺ effectively neutralizes two negative charges of the RNA backbone and results, at high enough Mg²⁺ concentration, in the displacement of an approximately equivalent positive charge from among the divalent cations of the ion atmosphere. This displacement of favorably-interacting cations is an apparent repulsive (positive free energy) between site-bound Mg²⁺ and the ion atmosphere. As Mg²⁺ is titrated, the actual free energy (rather than the standard state free energy) of Mg²⁺-RNA interactions at the chelated site and in the ion atmosphere change in different ways (cf. Figure 2 of ref. (48)):

• The free energy of site-bound Mg²⁺, ΔG_site, decreases linearly (becomes more negative) with the logarithm of the Mg²⁺ activity;

• The repulsive interaction between the site-bound ion and the ion atmosphere, ΔG_IA-S, increases continuously with log[Mg²⁺].

For 1 mM Mg²⁺ interacting with the 58mer RNA (60 mM KCl), ΔG_site is estimated from experiments to be −4.5 kcal/mol, which is far larger than the calculated repulsive term (+1.2 kcal/mol under the same conditions (48)). We suggest that the contribution of putrescine²⁺ to a site-binding term must be nearly zero, as the ion cannot effectively take advantage of the small chelation site. However the second, repulsive term between Mg²⁺ in the chelation site and putrescine²⁺ in the ion atmosphere will persist and increase with increasing putrescine²⁺ concentration. It is this “repulsive” free energy that could reduce the free energy gain from Mg²⁺ chelation and cause a net destabilization of the RNA at high putrescine²⁺ concentrations.

Putrescine²⁺ vs. Mg²⁺ in vivo

In summary, in comparison to Mg²⁺, putrescine²⁺ is most likely a minor contributor to the overall stability of an RNA tertiary structure in vivo. However, putrescine²⁺ has the curious property of being able to tip the thermodynamic scales towards either folded or unfolded forms of an RNA, depending on the architecture of the specific RNA. This observation leads us to hypothesize that the evolution of functional RNA structures has been influenced by the presence of putrescine²⁺ in the cellular ionic environment.

Abbreviation

DAP

2,6 diamino-purine