A new statistic for identifying batch effects in high-throughput genomic data that uses guided principal component analysis

Abstract

Motivation: Batch effects are due to probe-specific systematic variation between groups of samples (batches) resulting from experimental features that are not of biological interest. Principal component analysis (PCA) is commonly used as a visual tool to determine whether batch effects exist after applying a global normalization method. However, PCA yields linear combinations of the variables that contribute maximum variance and thus will not necessarily detect batch effects if they are not the largest source of variability in the data.

Results: We present an extension of PCA to quantify the existence of batch effects, called guided PCA (gPCA). We describe a test statistic that uses gPCA to test whether a batch effect exists. We apply our proposed test statistic derived using gPCA to simulated data and to two copy number variation case studies: the first study consisted of 614 samples from a breast cancer family study using Illumina Human 660 bead-chip arrays, whereas the second case study consisted of 703 samples from a family blood pressure study that used Affymetrix SNP Array 6.0. We demonstrate that our statistic has good statistical properties and is able to identify significant batch effects in two copy number variation case studies.

Conclusion: We developed a new statistic that uses gPCA to identify whether batch effects exist in high-throughput genomic data. Although our examples pertain to copy number data, gPCA is general and can be used on other data types as well.

Availability and implementation: The gPCA R package (Available via CRAN) provides functionality and data to perform the methods in this article.

Contact: reesese@vcu.edu or eckel@mayo.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

1.1 Batch effects

Batch effects are defined to be systematic non-biological variation between groups of samples (or batches) due to experimental artifacts (Benito et al., 2004; Johnson et al., 2007; Luo et al., 2010). Many factors contribute to the generation of batch effects. Some of these include chip type, platform, laboratory, technician, storage and shipment conditions, protocols (sample, amplification, labeling and hybridization), cRNA/cDNA synthesis, wash conditions, etc (Luo et al., 2010).

Few methods have been developed to detect batch effects. For expression data, existing methods include principal component analysis (PCA) (Holmes et al., 2011; Yang et al., 2008) and unsupervised hierarchical clustering (Chow et al., 2012; Johnson et al., 2007; Konstantinopoulos et al., 2011). However, neither of these methods provides a statistical test for detecting whether batch effects are present.

A common method for visualizing the existence of batch effects is PCA. The first two principal components are plotted with each sample colored by the suspected batch, and separation of colors is taken as evidence of a batch effect. However, as pointed out by Benito et al. (2004), if the batch effect is not the greatest source of variation then PCA methods do not work well, as they look for the directions of greatest variation. Also, visual inspection of the first and second principal components is subjective. Methods that can detect batch effects are needed, as ignoring the potential for batch effects can have a serious effect on downstream analysis results. In this article, we propose a test statistic derived using both the traditional PCA method and guided PCA (gPCA) for detecting batch effects. We evaluate the performance of our test in extensive simulation studies. We also demonstrate the difference between PCA and gPCA using two copy number variation datasets; however, the methods are appropriate for any type of high-throughput genomic data.

2 METHODS

2.1 Statistical methods

2.1.1 Principal component analysis

PCA is used for data reduction and interpretation. It is used to explain the variance–covariance structure of a set of variables through linear combinations of the variables (Johnson and Wichern, 2002). PCA is a form of unsupervised learning that seeks to find the ‘combination of conditions that explain the greatest variation in the data’ (Yang et al., 2008). It is used in many types of analyses including neuroscience and computer graphics (Shlens, 2005), in addition to microarray data analyses (Holmes et al., 2011; Yang et al., 2008). The numerical workhorse of PCA is singular-value decomposition (SVD).

Singular-value decomposition Let X be a centered 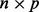matrix of real numbers where n denotes sample and p denotes genomic feature (e.g. probe). Then there exists an 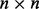orthogonal matrix U and a 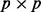orthogonal matrix V such that

where the 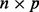matrix D has diagonal 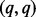entry 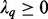for 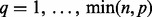where, by convention, and the other entries are 0. The positive constants 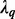are called the singular values of D (Johnson and Wichern, 2002).

Principal components are the length n column vectors (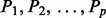) of

where X is an 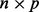matrix, V is the matrix of right singular vectors, 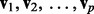, from the singular value decomposition and P is the 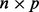principal component matrix.

The first principal component has the highest variance, and the second principal component has the next highest variance under the constraint that it is uncorrelated with the proceeding component. Typically, PCA is performed on X alone. Herein, we refer to this as ‘unguided’ PCA. As discussed in Section 1, unguided PCA is not effective for identifying batch effects if they are not the largest source of variation. In this case, it does not mean that batch effects do not exist in the data, but that alternate methods must be used to find them.

2.1.2 Guided PCA

For detecting batch effects, a more informative version of PCA is on 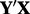, where Y is an 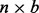indicator matrix where b denotes batch and n denotes sample.

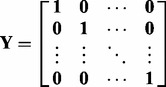where 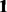and 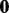are block matrices with

for 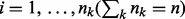and 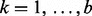. Performing SVD on 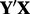results in a 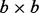matrix U that denotes the batch loadings and the 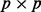matrix V that denotes the probe loadings. Large singular values imply that the batch is important for the corresponding principal component. gPCA guides the SVD to look for batch effects in the data based on the batch indicator matrix Y, which can be defined to indicate any type of potential batch effect.

Another commonly used method in this situation is Canonical Correlation Analysis, which finds the linear combination with maximum correlation; however, we are interested in variance, not correlation.

2.1.3 Proposed method: test statistic for testing whether batch effects exist

Our test statistic, δ, quantifies the proportion of variance owing to batch effects in experimental genomic data. The proportion of total variance owing to batch is the ratio of the variance of the first principal component from gPCA to the variance of the first principal component from unguided PCA.

where g indicates gPCA and u indicates unguided PCA. V is the matrix of probe loadings resulting from gPCA or PCA, respectively. Large values of δ (values near 1) imply that the batch effect is large.

To determine whether δ is significantly larger than would be obtained by chance, a P-value is estimated using a permutation distribution created by permuting the batch vector M = 1000 times so that 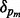is computed for 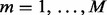where p indicates permutation. Here, 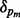is the proportion of the total variance due to the first principal component from the m^th permutation from gPCA to the total variance due to the first principal component from the m^th permutation from unguided PCA. A one-sided P-value is estimated as the proportion of times the observed δ was in the extreme tail of the permutation distribution.

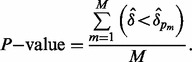Estimating percentage of total variation explained by batch. The percentage of total variation explained by batch is then calculated as

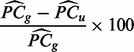where

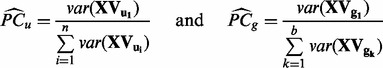where u and g represent unguided PCA and gPCA, respectively.

2.2 Simulation study

Most often investigators are interested in modeling their data in the presence of a known phenotype. Therefore, we simulated data to represent copy number data under three scenarios: (i) feature data (here, feature denotes probe) with no phenotypic effect; (ii) feature data with a phenotypic effect with high variance; and (iii) feature data with a phenotypic effect with low variance. The feature data were generated independently from a multivariate normal distribution with 1000 features and 90 observations. To study type I and II errors, for all three scenarios, the data were simulated in two ways: to include a true batch effect and without a true batch effect. When a batch effect was present, there were two batches with batch mean vectors of 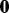and 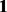. The variance associated with batch was 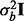, where 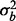was allowed to be 0.5 or 1. In the true phenotype scenarios, 10% of the features were affected by phenotype using mean vectors 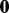and 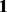and variance matrix 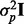where 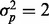for the high phenotypic variance scenario and 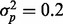for the low phenotypic variance scenario. The proportion of features affected by the phenotype was pprop = 0.1 or 0.05. In all scenarios with a phenotypic effect, the phenotype was generated independent from any batch effect. Each simulation scenario was repeated 500 times.

For the scenarios with no true batch effect, the resulting proportion of P-values 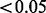formed our estimate of the type I error. The proportion of P-values 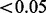for the scenarios with a true batch effect formed our estimate of the power. Here, phenotype can be thought of as any variable of interest, whether categorical (e.g. case versus control) or continuous (e.g. mammographic density).

2.3 Case studies

Our method was applied to two case studies. The U and V matrices are assumed to be orthogonal 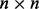(or 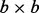for gPCA) and 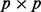matrices, respectively. To adjust for missing values, mean value imputation was performed on the centered data X before PCA.

2.3.1 Filtering

For unsupervised learning problems, non-informative features contribute random noise to distance calculations. The resulting effect is that non-informative features mask useful information provided by informative features. Therefore, non-informative features should be assigned a zero weight in the clustering algorithm (Kohane et al., 2003). The simplest implementation for assigning a non-zero weight in a cluster analysis is to exclude identified non-informative features. This filtering step is applied to genomic data to remove sources of obscuring variation before applying a clustering algorithm. In our simulation studies, we observed higher power when the proportion of features affected by batch increased; therefore, we filtered our data stringently to keep the most variable or informative features. A variance filter was applied to the data to remove noise and reduce the number of features. The standard deviation of each feature was calculated and the 1000 most variable features were retained (Causton et al., 2003; Dudoit et al., 2002; Inza et al., 2004). A sensitivity analysis was performed allowing the number of features retained by the variance filter to range between 10 and the full GENEMAM dataset. Further analysis implementing an analysis of variance filter was also investigated.

2.3.2 GENEMAM

The GENetic Epidemiology of MAMmogr-aphic Density (GENEMAM) study data included 614 samples from the Minnesota Breast Cancer family study (Sellers et al., 1995). These samples were genotyped using the Illumina Human 660 bead-chip array. Samples were processed over three time periods on eight plates. Forty-two samples failed quality-control checks from plates 1–4 because of an Illumina reagent problem, and these samples were replated on plate 5, along with six other samples. Samples on plates 6–8 were genotyped at a later date. This effectively yielded three batches corresponding to the three different runs. Data for all chromosomes were used. Illumina’s GenomeStudio software was used to obtain the Log₂ R ratio (LRR) values. LRR is a measure of relative intensity where R is the sum of the normalized allelic probe intensities produced by SNP assays and the ratio is of observed R divided by the expected value (Laurie et al., 2010).

2.3.3 GENOA

The Genetic Epidemiology Network of Arteriopathy (GENOA) data included 1418 of the non-Hispanic white adults enrolled in the GENOA study of the Family Blood Pressure Program, a study designed to identify germline genetic determinants of hypertension in multiple ethnic groups. These samples were genotyped on Affymetrix SNP Array 6.0 chips, and all samples had contrast QC values >0.4. The PennCNV-Affy Protocol (http://www.openbioinformatics.org/penncnv/penncnv_tutorial_affy_gw6.html) was followed to obtain the LRR values. The analysis focused on chromosome 22 data using the first 10 plates consisting of 703 samples.

3 RESULTS

3.1 Simulation study

The estimates for type I error for all scenarios are reported in Table 1. The proportion of features with a phenotypic effect is pprop = 0.1 for scenarios (b–c) and 0.05 for scenario (d). In all scenarios, the type I error is at or below the nominal 0.05 level. Figure 1 shows power of our test statistic as a function of the proportion of features with a true batch effect if there is no true phenotypic effect. If 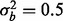, then our test statistic has 80% power if ∼0.3% of the features are affected by batch. If 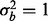, then ∼0.6% of features need to have a batch effect to achieve 80% power. If a phenotypic effect exists with high phenotypic variance, then ∼1.5 or 2% of the features need to have a batch effect to achieve 80% power for 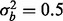and 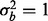, respectively (Fig. 2a). Similarly, if a phenotype exists with low phenotypic variance and 10% of features are affected by phenotype, then ∼1.5 or 1.2% of the features need to have a batch effect to achieve 80% power for 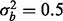and 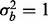, respectively, and if 5% of features are affected by phenotype, then ∼0.75% of the features need to have a batch effect to achieve 80% power for both 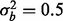and 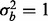(Fig. 2b).

Table 1.

Estimated type I error

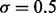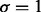(a) No phenotype	0.034	0.034
(b) High phenotype (pprop = 0.1)	0.014	0.014
(c) Low phenotype (pprop = 0.1)	0.000	0.002
(d) Low phenotype (pprop = 0.05)	0.010	0.046

Note: For all scenarios, there is no true batch effect. Scenario (a) has no phenotypic effect in the data; however, scenario (b) has a phenotypic effect with high variance included and scenarios (c and d) have phenotypic effects with low variance included in the analysis with phenotypic effect at pprop = 0.1 or 0.05, respectively.

Fig. 1.

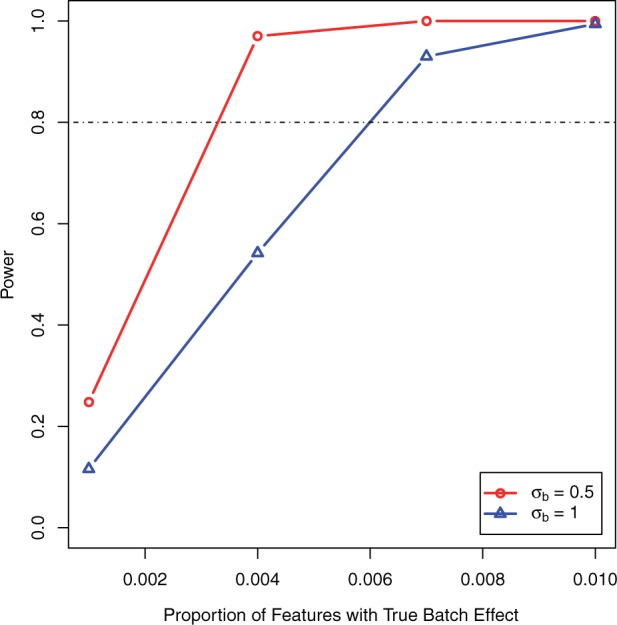
Power for detecting batch effect as a function of the proportion of features that are affected by batch when no true phenotype was included with batch proportion ranging from 0.1 to 1%

Fig. 2.

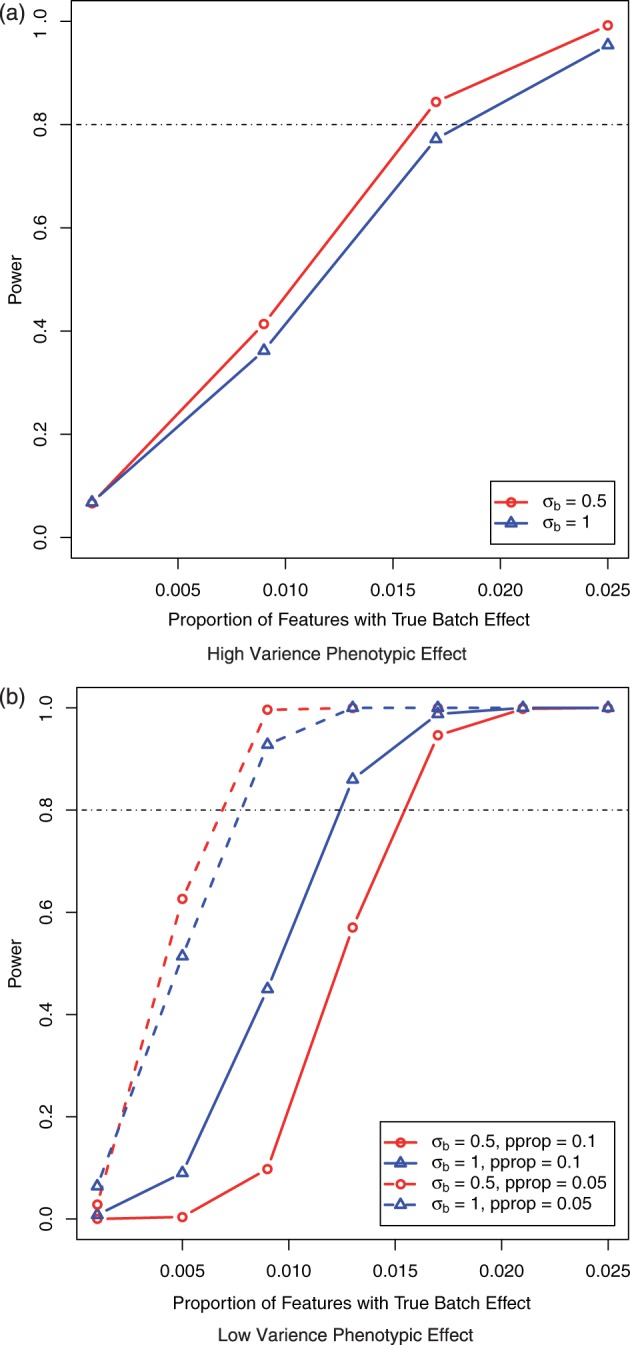
Power for detecting batch effect as a function of the proportion of features that are affected by batch when (a) phenotypic data with high variance were included in gPCA with batch proportion ranging from 0.1 to 2.5% and (b) phenotypic data with low variance were included in gPCA with batch proportion ranging from 0.1 to 2.5%

Power is also higher when the batch variance is smaller. Further simulations varying the batch variance, with the difference between batch means smaller than the difference between the phenotype means, and with high proportions of features affected by batch can be found in Supplementary Section 4. In the scenario where batch variance is varied and the batch mean difference is smaller than the phenotype mean difference, we found that as batch variance increased, so did the estimated power. The smaller the difference in the phenotypic means, the higher the power. In the no phenotype scenario, we found that power decreased as the batch variance increased. This is attributable to the first principal component from unguided PCA and gPCA being similar when no phenotype is affecting the feature data, which is unlikely in application datasets. In the scenario where a high proportion (between 50 and 90%) of features are affected by batch, we found that the estimated power was 100% (see Supplementary Table S5).

3.2 GENEMAM

The standard use of PCA is to look at the plot of the first principal component of the data (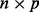 matrix X, where n denotes sample and p denotes probe) versus the second principal component (Fig. 3a). The GENEMAM data have an obvious batch effect, and the PCA plot of the first two principal components shows that this batch effect is due to the plate when colored by plate with three batches consisting of plates 1–4, 5 and 6–8. As is common with batch effects, this batch effect is due to the plates being run at different times.

Fig. 3.

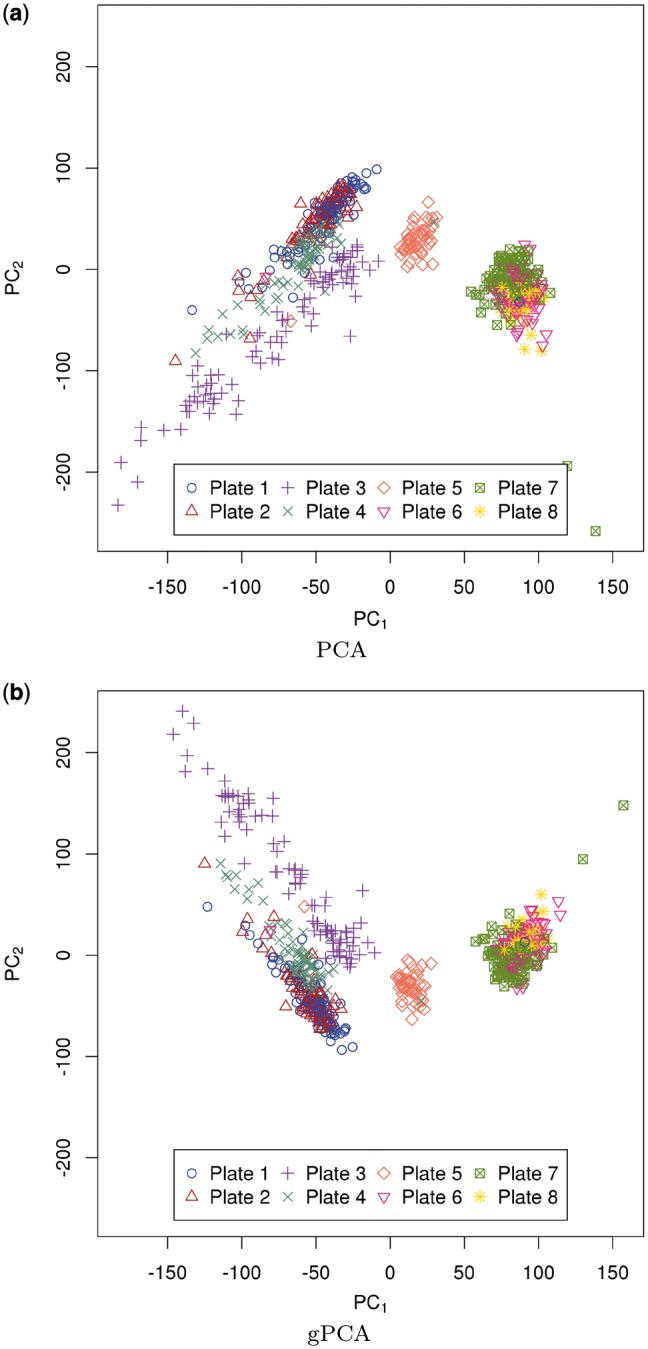
GENEMAM–(a) Unguided PCA of X and (b) gPCA of 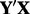. Samples for each plate are denoted by a different color (online version) and/or symbol

Next, we performed a gPCA with plate as the batch indicator. The gPCA plot of the first two principal components (Fig. 3b) shows greater separation in the batches, especially of plate 3 from plates 1, 2 and 4, than the unguided principal component plot (Fig. 3a). After filtering out all but the p = 1000 most variable features, our permutation test confirms that there is a significant batch effect separating the plates (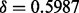; P-value < 0.001). Of the variance due to features in these data, 87.3% of the total variation is explained by batch.

We also performed a sensitivity analysis allowing the number of features retained by the variance filter to range between 10 and the full GENEMAM dataset. We found that our test statistic was not sensitive to filtering (for the application datasets and when no phenotypic effect was present in the simulation scenario). The test statistic applied to the simulated data was not affected by filtering provided that the number of features retained was 5% when there was a phenotype with high variance (a somewhat weak phenotypic effect) and ∼50% when there was a phenotype with low variance (i.e. a strong phenotypic effect), and thus filtering can be used as a method to reduce the analysis time required provided it is judiciously applied (Supplementary Table S1). We also implemented an analysis of variance filter to identify probes with a significant batch effect and found that even with stringent multiple comparison methods, the filtered datasets were still very large. A detailed discussion can be found in the Supplementary Section 1.

This case study is an example with an obvious batch effect and thus did not require specialized methods to detect, as batch was the largest source of variability.

3.3 GENOA

In this case study, batch is not so easily detected using unguided PCA. Unguided PCA was performed and Figure 4a shows the PCA plot of the first two principal components. Figure 4a shows that plates 7 and 8 might be slightly separated from the rest of the plates. A gPCA with batch defined by plate (Fig. 4b) shows that plates 7 and 8, along with plate 4, separate slightly from the other plates. It is not obvious from the unguided PCA that plate 4 is separate from the rest of the plates. However, gPCA shows a separation between plate 4 and the rest of the plates. After filtering out all but the 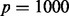most variable features, our permutation test shows that there is a significant batch effect separating the plates (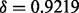; 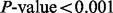). Of the variance due to features in these data, 71% of the total variation is explained by batch. gPCA identifies a batch (plate 4) that does not otherwise stand out in an unguided principal component plot.

Fig. 4.

GENOA–(a) Unguided PCA of and (b) gPCA of . Samples for each plate are denoted by a different color (online version) and/or symbol

3.4 Impact of identifying and correcting for batch effects

Although various methods exist for adjusting for batch effects, these methods do not incorporate a procedure for identifying whether a batch effect is truly present (Benito et al., 2004; Carvalho et al., 2010; Chow et al., 2012; Huang et al., 2012; Johnson et al., 2007; Konstantinopoulos et al., 2011; Leek and Storey, 2007, 2008; Leek et al., 2012; Marron and Todd, 2002; McCall et al., 2010; Sun et al., 2011). Using both simulated and real data (see Supplementary Section S3), we further assessed the effects of correcting for batch on the number of significant features. In our simulated dataset, there were 50 features with a phenotypic effect, 50 features with a batch effect and 100 features with both a phenotypic and a batch effect. After fitting a linear model using the lmFit() function with phenotype as the predictor, the number of significant features in simulated data was assessed using the eBayes() function in the limma package both before batch correction and after batch correction using the batch mean-centering method of Sims et al. (2008) and the FDR method of Benjamini and Hochberg (1995) for adjusting for multiple testing, letting 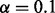. Forty-eight of the 150 features had a significant phenotypic effect before batch correction, whereas 148 of the 150 features were significant post-batch correction (Supplementary Table S4). This shows that batch correction allows features with a true phenotypic effect that is masked by batch to be identified as significant after batch correction.

3.5 Evaluating batch correction methods

Luo et al. (2010) observed the impact of batch effect removal on cross-batch prediction performance, and Lazar et al. (2012) and Chen et al. (2011) provided surveys of some of the many methods of batch effect removal. In Table 2, we report our test statistic 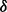and the corresponding 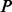-values when analyzing the raw uncorrected and batch mean-centering corrected data. Although there is a highly significant batch effect in the uncorrected data, the correction method successfully removed enough batch variation from all datasets. Therefore, our proposed test statistic is useful for identifying whether any batch adjustment methods should be applied before statistical analysis and for assessing the adequacy of the batch adjustment method applied.

Table 2.

Evaluating whether a batch correction method was successful: test statistic 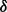and corresponding 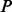-values before and after batch correction for the three simulated data scenarios (no phenotypic effect, high-variance phenotype and low-variance phenotype), and the two case study datasets, GENEMAM and GENOA

	Uncorrected		Corrected
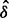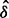No phenotype	0.902		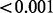0.060	1.000
High-variance phenotype	0.700		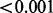0.030	1.000
Low-variance phenotype	0.572		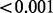0.020	1.000
GENEMAM (run time)	0.583		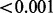0.044	1.000
GENEMAM (plate)	0.599		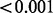0.050	1.000
GENOA (plate)	0.922		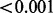0.017	1.000

Note: Batch mean-centering (Sims et al., 2008) was used for batch effect correction.

4 DISCUSSION

gPCA can be used to identify batch effects in large and messy data, such as expression, CNV, and methylation data, by computing the SVD while taking batch into account. Principal component plots are a standard method of looking for batch effects in high-throughput data. Here, we show how gPCA can be used both to visualize batch effects and to formally test whether batch effects are present in the data. From our simulation studies, the type I error of our statistic is close to nominal 0.05 level and power is reasonably good when an adequate proportion of the features are affected by batch. Additionally, when the proportion of features affected by batch is high (between 50 and 90%), the estimated power is 100% (Supplementary Table S5).

The matrix in the gPCA analysis can be formed by considering any combination of variables. We note that with the 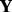matrix coding multiple variables, the variance ascribed to the first principal component of the gPCA may incorporate multiple sources, which would be difficult to disentangle. To estimate the variance attributed to multiple sources, gPCA could be used to examine each one by defining in separate analyses. Note that gPCA is dependent on knowing how to define potential batch effects. If this is not known, this statistic should not be used. If batch is misspecified by the investigator, provided the misspecified batch effect indicator matrix has no relationship to the experimental design, then the test will likely not reject the null hypothesis because type I error was close to the nominal 0.05 level.

In the case of microarray data, scaling of the batch identifier matrix 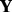is not in general useful for balanced experiments. However, when some batches have far more samples than others, scaling of is a useful tool to correct for the imbalance. In the case of the GENEMAM data, while plates 5 and 8 had half as many or fewer samples than the rest of the plates, the effect of scaling 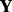was minimal, although it did have an effect. For microarray data, we do not want to scale the data matrix , as all the variables, probes in our case, are already on the same scale and scaling would only serve to adjust the variance. If the variances are smoothed, then we may miss an important difference between variables or batches.

gPCA can be used on other problems and types of data as well, including B-allele frequency data and expression data. Because pre-processing of microarrays is time-consuming, expensive and with abundant systematic errors, the ability to discover and adjust for these errors is important. Our test statistic that uses gPCA allows one to find the sources of systematic errors, or batch effects, in all types of microarray data and adjust for it during analysis.

In summary, herein we present a novel statistic to test for the presence of batch effects. The test is particularly useful to test whether batch effects exist after applying a global normalization procedure such as quantile or loess normalization. Although these global normalization procedures correct for batch effects that affect all probes similarly, they do not correct for probe-specific batch effects. Furthermore, our test statistic is useful for determining whether a batch-correction method has adequately removed observed batch effects.

Funding: National Institutes of Health research grants (R01 HL87660 to M.d.A.); (R01 CA128931 and CA140286 to C.M.V.); (T32 ES007334 S.E.R. and K.J.A.); Mayo Clinic Center for Individualized Medicine.

Conflict of Interest: none declared.