A-clustering: a novel method for the detection of co-regulated methylation regions, and regions associated with exposure

Abstract

Motivation: DNA methylation is a heritable modifiable chemical process that affects gene transcription and is associated with other molecular markers (e.g. gene expression) and biomarkers (e.g. cancer or other diseases). Current technology measures methylation in hundred of thousands, or millions of CpG sites throughout the genome. It is evident that neighboring CpG sites are often highly correlated with each other, and current literature suggests that clusters of adjacent CpG sites are co-regulated.

Results: We develop the Adjacent Site Clustering (A-clustering) algorithm to detect sets of neighboring CpG sites that are correlated with each other. To detect methylation regions associated with exposure, we propose an analysis pipeline for high-dimensional methylation data in which CpG sites within regions identified by A-clustering are modeled as multivariate responses to environmental exposure using a generalized estimating equation approach that assumes exposure equally affects all sites in the cluster. We develop a correlation preserving simulation scheme, and study the proposed methodology via simulations. We study the clusters detected by the algorithm on high dimensional dataset of peripheral blood methylation of pesticide applicators.

Availability: We provide the R package Aclust that efficiently implements the A-clustering and the analysis pipeline, and produces analysis reports. The package is found on http://www.hsph.harvard.edu/tamar-sofer/packages/

Contact: tsofer@hsph.harvard.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Methylation is a heritable and modifiable chemical process by which, most often, a methyl group attaches to a cytosine base that is followed by guanine on the same DNA strand (CpG dinucleotide, or CpG site). It is sensitive to environmental exposure, such as smoking, air pollution and chemicals (Anttila et al., 2003; Hou et al., 2012; Sofer et al., 2013). Modern array-based platforms measure methylation in hundreds of thousands of CpG sites, and sequencing methods measure methylation in millions of sites. Methylation is often measured as a continuous variable known as a β value, representing the proportion of methylated CpG sites out of the total in the measured tissue. Interestingly, sets of related-by-location CpG sites, whether associated with a gene or not, may be jointly affected by environmental exposure. It is of interest to identify such sets of CpG sites that are affected by an exposure in a computationally efficient and quick manner.

Methylation occurs throughout the genome, and it differs between tissues and cell types. Although it is known that methylation is associated with the control of genes, the mechanisms are still debated (Jones, 2012). The distribution of CpG sites varies across the genome. Areas densely populated with CpG sites are called CpG islands [CGIs; Gardiner-Garden et al. (1987)]. CGIs are often found in the promoter area of genes, and they exhibit low methylation. Higher CGI methylation is associated with gene silencing. Within gene bodies, CpG sites are usually hypermethylated, and are found in lower density. However, there are many exceptions to these general rules, such as CGIs within gene bodies or promoter areas without CGIs. There are other, predefined, regions associated with CGIs. In addition to the island itself, there are north and south shores and shelves, located up- and downstream from the island, respectively, and are defined according to their distance (in base pairs) from the island (Irizarry et al., 2009; Sandoval et al., 2011). Shores are up to 2 kb of the island, and shelves are within 2–4 kb of the islands. We term the collection of shelves, shores and island associated with a single CGI by a ‘resort’ to eliminate confusion. The definition of these regions is independent of any actual observed behavior of the sets of associated CpG sites. Further, Jacoby et al. (2012) report finding clusters of methylated CpG sites within specific cell types, these clusters are not related to CGIs. In other words, these regions do not necessarily correspond to regions that are co-regulated. Therefore, it is useful to employ computational tools for discovery of regions with CpG sites exhibiting common behavior that are not necessarily restricted to the known predefined methylation domains.

This article has three aspects: (i) automated identification of methylation regions based on the correlation between methylation sites, and independently of any exposure data; (ii) analysis of these regions to identify those affected by exposure; and (iii) development of a realistic correlation-preserving simulation scheme for methylation data. Jaffe et al. (2012) proposed a method to identify regions that are associated with exposure. Our proposed method differs from their work in that we perform general region detection, pose different modeling assumptions on the exposure effect on a region and, as a result, provide a simpler testing procedure. Others used the correlation for analysis of genetic data, more specifically, data from tiling arrays in which adjacent probes target overlapping sequences. For instance, Kuan et al. (2008) developed a software package to correct the P-values associated with a probe using the estimated correlation between the probe and neighboring probes. Pedersen et al. (2012) developed a software package, applying methods to combine adjacent correlated P-values and detect regions of low P-value. These methods identify differentially methylation regions (DMRs) after testing for the exposure effect on the methylation sites, while we first cluster sites, and then test for the exposure effect on the clusters. Wu et al. (2010) proposed a method to detect CGIs using a Hidden Markov Model. However, their work focuses on redefining CGIs to alleviate limitations of the traditional definition based on CpG content in an interval, rather than on identifying regions of common behavior of CpG sites. In terms of simulation, Jaffe et al. (2012) did perform some simulations, but our proposed simulation scheme better imitates the reality, by preserving the correlation structure and methylation patterns of a real dataset.

In what follows, we present an adjacent sites clustering method, dubbed A-clustering, to discover methylation regions by clustering together neighboring CpG sites according to their correlation, and under possible restrictions on their distance from each other on the DNA. The clustering can be preceded by a dbp-merge step, an algorithm that merges a set of methylation sites wedged between two highly correlated CpG sites, that are physically located close enough to each other along a chromosome. This combination of the dbp-merge and A-clustering detects regions of co-regulated CpG sites. We further provide a pipeline for analysis after normalization and batch correction are performed that first includes clustering CpG sites, and then tests the effect of exposure on each cluster. For testing, we assume that the exposure equally affects all CpG sites, while each site has its own baseline methylation level. We perform this analysis using generalized estimating equations (GEEs; Liang and Zeger, 1986) that are robust to the specification of data distribution. The clustering method and the following GEE analysis are implemented in the R package Aclust.

The article is organized as follows: in Section 2, we present the model at the basis of this work. Section 3 describes the A-clustering and dbp-merge algorithms, the proposed analysis pipeline and an abbreviated description of the correlation-preserving simulation scheme (complete details may be found in the Supplementary Material). In Section 4, we first study the performance of the proposed analysis pipeline for finding regions associated with the exposure, via an extensive simulation study with different implementations of the A-clustering algorithm and a subsequent sensitivity analysis. We then compare the analysis pipeline with the Bump Hunting method of Jaffe et al. (2012) as well as briefly review single-site analysis results. We then compare clustering results between two implementation options of the A-clustering and dbp-merge on a dataset of peripheral blood methylation of pesticide applicators. We conclude with discussion in Section 5.

2 MODEL

Suppose there are 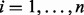subjects with 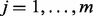sites with measured methylation. Denote the exposure measure of subject i by E_i, and the 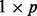vector of covariates of subject i by 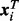. We model the methylation of a site j as a linear function of exposure and covariates, according to

where this is a general model that lets the jth site have a unique baseline methylation value 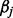, as well as unique exposure effect 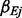and covariates’ effects 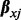on its methylation level. The vector of covariates 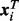includes biological covariates. Note that it can potentially include confounders and technical biases, such as variables derived using a Surrogate Variables Analysis (SVA) procedure (Leek and Storey, 2007), but in this article we limit the discussion to the clustering and association analysis and assume that technical biases were already removed from the data.

We assume that there are sets or regions of sites, i.e. clusters of methylation sites, such that their methylation values are correlated with each other. The correlation can be attributable to underlying unknown or unaccountable biological mechanisms, so that exposure effect of sites within these clusters is constant. For example, let 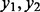and y₃ belong to the same cluster, or set of correlated sites. Then,

where 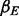is the common exposure effect on the methylation in the three sites, and 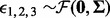for some mean zero distribution 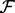with a 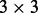covariance matrix .

3 METHODS

In this section, we describe the computational methods, the clustering algorithms and analysis pipeline and the correlation-preserving simulation scheme.

3.1 Computational methods

The proposed epigenome-wide analysis is composed of two steps. At the first step, we identify clusters of correlated methylation sites using the Adjacent sites algorithm (‘A-clustering’, or shortly ‘Aclust’), and at the second step, we test these clusters for association with exposure (or outcome) using GEEs. We expand here on each of these steps.

The first step is clustering of adjacent correlated CpG sites. The proposed clustering algorithm, Aclust, is similar to the agglomerative nesting clustering algorithm (Izenman, 2008). However, it is restricted so that only probes that are adjacent to each other (i.e. next to each other along the chromosome) could be clustered together, or, more generally, only neighboring clusters could be merged to form a larger single cluster. In general, the clustering is performed by cycling through the sites, ordered by location, and merging together neighboring clusters if the distance measure between them is smaller than a predefined threshold 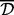. Here, the ‘distance measure’ is a similarity metric that depends on the actual methylation values observed in the sample. The distance measure between two clusters depends on the distances between probes in the cluster. The distance between two probes is defined by any general distance measure, where in our approach we recommend using the correlation-based distance measure:

where correlation could be Pearson or Spearman correlation, for instance. Then, the distance between two clusters could be defined as either the single, average or complete distance between sites in the corresponding two clusters. To merge two clusters, if the single distance type is used, then it suffices to have one site in each cluster, such that they are closer to each other by at least 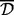. The average type requires the mean distance between all sites in the two clusters to be at most 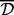, and the complete type requires the distance between every pair of sites in the two clusters to be at most 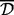. Note that for a fixed threshold 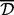, if the complete distance is used, then the clusters will be smaller than those created by using the average distance, which in turn will yield smaller clusters than the single distance. It is noteworthy that the clustering results are somewhat sensitive to the order of the clustering (e.g. starting from the first versus last location). In practice, these differences are expected to be minor. Pseudocode for the algorithm is given in Supplementary Material. Aclust potentially limits CpG sites from clustering, by specifying 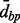, a maximal distance between two neighboring CpG sites to be clustered together. For instance, if 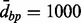, one may not allow for two CpG sites that are 1000 base pairs away that are without any other CpG site(s) in the middle to cluster together.

A-clustering is applied on an initial vector of cluster assignments (and a data matrix), so that only adjacent clusters can be merged at each step. An extension of this algorithm is motivated by the two following arguments. First, as was implied so far, these initial cluster assignments are the numbers 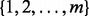where m is the number of sites, so that if the data from chromosome 4, say, consists of a measured methylation site on the 1000, 1200, 1500 and 3000 chromosomal base-pair locations, than these four sites are initially assigned with cluster 1, cluster 2, cluster 3 and cluster 4. Note that the physical distance between the measured sites is variable, and does not necessarily represent the complete set of sites in the stretch of chromosomal locations 1–3000 in chromosome 4, so that there may be additional, non-measured, methylation sites. Moreover, site 1 and site 3 are physically closer to each other than site 3 and site 4. Second, examinations of correlation plots (Fig. 1) reveal that some clusters are seemingly the composite of smaller clusters, close to each other, but with a few sites between these small clusters that evidently are not-highly correlated with their neighbors. For instance, looking at the correlation of a set of sites along a chromosome, one can see a pattern of [cluster of 5 probes, uncorrelated probe, cluster of 4 probes, many uncorrelated probes], where members of the 5-probe and 4-probe clusters are highly correlated with each other.

Fig. 1.

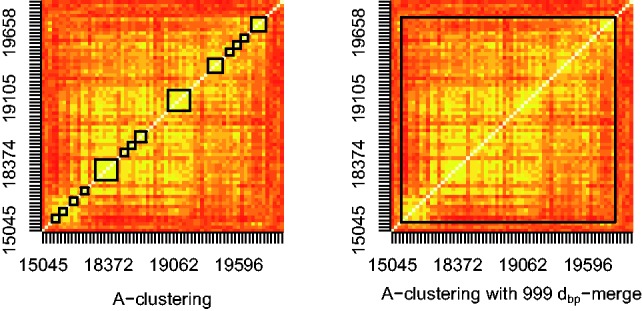
Spearman correlation heatmaps of a large cluster identified on chromosome 7, as detected by the A-clustering algorithm without (left) and with (right) 999 dbp-merge initialization. The algorithms were implemented using ‘Spearman’ as the distance measure, and single distance type. The axes’ labels represent the location on the chromosome 7, plus

Therefore, we extend the Aclust algorithm by adding a more flexible initiation step. We initialize with a ‘d-base-pair-merge’, or dbp-merge. The dbp-merge is an algorithm that can be performed before Aclust, in which all sites are scanned, and each is potentially merged into a cluster with another site 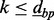base pairs away from it, and with all the sites wedged in between these two if the distance measure between them is small. For instance, set 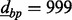, and consider CpG sites in locations 1000, 1200 and 1500, for sites 1–3, respectively, and the distance measure between them are 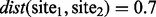, and 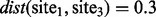. Then, for 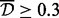, even though 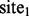and 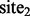are not similar to each other (as determined by the distance measure), because 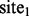and are similar to each other, and the base-pair distance between them is 500, which is smaller than 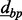, then the three CpG sites will be merged to a single cluster. Notice that this algorithm is aimed at merging sites rather than clusters. The dbp-merge step results in an initial clustering assignment, which is then complemented by the Aclust algorithm. The dbp-merge pseudocode is provided in the Supplementary Material.

After defining clusters of probes, whether with or without an initial dbp-merge step, a final step of the analysis, if desired, tests for the effect of exposure on the detected clusters of methylation sites, where one can choose the minimum cluster sizes, say two or three sites per cluster. We fit a GEE model assuming common exposure and covariate effects (including possible batch effects) on all sites within a cluster and an individual location effect for each site, as described in Section 2. Note that if batch effect was previously removed, such as with ComBat (Johnson et al., 2007), there is no need to further adjust for batch. The raw P-value is then the P-value of the exposure variable from the GEE model. We use the robust sandwich variance estimator in our computations. Note that GEEs are performed under less assumptions than regression or mixed model analyses, as only a marginal mean model is assumed. As such, a working covariance structure must be provided, but is allowed to be mis-specified. After producing raw P-values for each of the clusters, we correct for multiple testing using existing procedures, such as by control of the false-discovery rate (FDR) (Benjamini and Hochberg, 1995).

3.2 Simulating methylation data

We adapt the strategy of Gaile et al. (2007) to generate (spatial) correlation-preserved methylation data via sampling from a real methylation dataset. More specifically, we consider the comparison of methylation β values for two subgroups (e.g. low and high exposure). Simulated datasets consist of methylation assay β values for n = 40 samples from each subgroup, where assignment of methylation β values to the simulated samples is designed to preserve the true correlation structure within regional blocks of dense array coverage (described in greater detail below). The number of samples in each subgroup, and their definitions of high and low exposure groups, mimics the dataset we analyze (Section 4.2).

3.2.1 Description of data

The dataset on which the simulations were based consists of batch-corrected methylation β values for 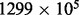breast invasive adenocarcinoma samples obtained from The Cancer Genome Atlas; specific dataset descriptions are provided in the Supplementary Material. These 539 samples were assayed with the Illumina 450 K array and provide estimates of 485 577 β methylation values located across the genome. We performed two simulation studies. First, we focused on chromosome 1, and simulated M = 5 differentially methylated clusters. We used this simulation to study different combinations of the Aclust parameters, and choose the most fitting parameters. Then, we conducted epigenome-wide association study (EWAS) simulations with M = 10 differentially methylated clusters, in which Aclust was implemented using the parameters settings selected in the chromosome 1 simulations.

3.2.2 Assigning samples to exposure groups

We conduct 100 simulations, where in each simulation we derive a simulated dataset from the original 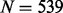samples. Consider first a single chromosome. A simulated dataset was constructed by preferentially resampling pre-specified ‘regional blocks’ (defined below) of the chromosome based on methylation values at the locations of M putative ‘targets’. The sites selected to serve as ‘targets’ satisfy three properties: (i) evidence of a substantial variability in methylation β values in the original 539 samples, (ii) evidence of substantial correlations with neighboring sites ( 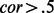for at least two neighbors) within the same regional block across the original 539 samples, and (iii) none of the M targets could be located within the same regional block. Note that although the preferential resampling to be described below focuses on single targets, owing to the correlation structure among neighboring sites, the entire correlated ‘cluster’ will be associated with exposure. For a whole epigenome simulation, a single dataset is composed of all simulated chromosomes, sampled independently of one another. Correlation heatmaps of the targets and associated clusters used in simulations are provided in the Supplementary Material.

We created regional blocks by partitioning each chromosome by defining breakpoints in areas of low array/site coverage. Specifically, breakpoints were formed between adjacent sites >10 K bp apart. For instance, in chromosome 1 there were 30 796 sites (after quality control) and 2861 regional blocks. Thus, contiguous portions of a chromosome that were densely assayed are grouped within the same regional block so that the any spatial correlation existing in these dense areas will be preserved during the resampling process.

To create each of the 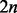samples within a simulated dataset, each of the regional blocks is sampled independently of each other, but the M regional blocks containing the targets are preferentially resampled to force differences in methylation between groups at the target and its associated cluster. Note that the regional block is sampled as a unit, so that all sites within a regional block sample travel together. Hence, in practice, we sample each regional block without replacement from the set of N ‘block samples’ for that particular region. Briefly, for each target, we assign n = 40 regional block samples containing the target (‘target block samples’, henceforth) to the high exposure group (group H) by sampling from the original 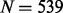target block samples, with the sampling probability of each target block sample as a function of its target’s ranked methylation level (rH) and a selection weight (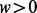) as 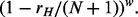From the remaining target block samples, we assign n = 40 target block samples with sampling probabilities 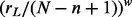to the low exposure group, group L, where rL is the rank of the target’s methylation value with respect to the remaining 499 target methylation values not assigned to group H. The weight w controls the magnitude of differential methylation between groups H and L. For example, if 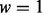, it is likely that the samples with the highest and lowest β values for the target will be assigned to different groups. As w decreases toward 0, the sampling becomes less biased, so that each group consists of target block samples with a mix of both high and low methylation β values at the target. For this simulation, the weight w was tuned such that the average value (across 1000 simulations) of single-site statistics matched typical ‘high signal’ sites. We specifically targeted Wald statistics such that the mean (across 1000 simulations) single-site (unadjusted) P-values were approximately 0.001.

Finally, each of the remaining regional blocks not containing a target need to be assigned to each of the 2n samples within the simulated dataset to ‘complete’ the chromosome. For each of these regional blocks, we randomly selected 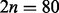block samples of the given region from the original N = 539 block samples of that region with equal probability, and assigned n to each exposure group. Thus, each sample within a simulated dataset is a composite of the N = 539 original samples, with regional blocks containing the target preferentially resampled so that the two groups are differentially methylated at the target. As a consequence of the locally preserved spatial correlation within regional blocks, the target’s neighboring sites will be differentially methylated, as well. The complete algorithm and more specific details are provided in the Supplementary Material.

4 RESULTS

4.1 Simulation results

We first performed simulations using 100 datasets sampled from chromosome 1 data. We simulated M = 5 differentially methylated clusters. We analyzed the data using a comprehensive set of parameter settings of Aclust and the ensuing GEE analysis, two implementations of Bump Hunting (using function dmrFind in R package charm; Aryee et al., 2011) and a more traditional single-site analysis. The goal in these simulations was 3-fold: compare the proposed pipeline to other analyses, study its robustness for parameter specification and identify optimal parameters settings to use in data analysis. Then, we carried out an EWAS simulations with M = 10 differentially methylated clusters and compared the proposed pipeline, with Aclust implemented using the parameters previously identified, and Bump Hunting. We first describe and report chromosome 1 results, and then the EWAS results.

4.1.1 Chromosome 1 simulation study

A major goal of these simulations was to study the appropriateness of the various Aclust parameters for an analysis that is focused on the identification of differentially methylated clusters, and find the ‘best’ parameters. Therefore, we analyzed each of the simulated datasets with all combinations of the following parameter specifications: Pearson or Spearman correlation, with or without 999-dbp-merge initiation, with and without 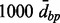distance restriction for merging, single, average or complete clustering type, and distance threshold 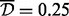. From these simulations we concluded that 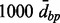distance restriction is beneficial, and that either average or complete clustering type is more appropriate than the single for the purpose of identification of DMRs. Note, however, that overall the results are robust for different specifications of the parameters, which is reassuring. The results of these simulations are provided in the Supplementary Material, including comparison to single-site analysis and to Bump Hunting.

Then, we performed a sensitivity analysis stage for these simulations. For each combination of Pearson and Spearman correlations, types average and complete and with and without 999-dbp-merge, we varied the value of 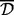as 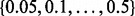and chose the most performant 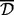for each setting. Table 1 reports the analysis results based on each of the above combinations with the matching (identified) 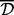, and compares them to the results of Bump Hunting. The complete sensitivity analysis results, parameter specifications used for Bump Hunting and correlation heatmaps for the neighborhoods around the targets are included in the Supplementary Material.

Table 1.

Clustering and association analysis results in chromosome 1 simulations

Method	Cluster	Memb1	TPR1	Memb2	TPR2	Memb3	TPR3	Memb4	TPR4	Memb5	TPR5	TPR	FP	Time
A-clustering
Pearson Correlation
Average
d+Aclust (0.15)	1068.86	5.41	0.61	7.00	0.73	5.89	0.70	6.76	0.80	3.95	0.76	0.26	0.31	143.98
Aclust (0.25)	1241.28	3.41	0.71	7.00	0.72	5.94	0.67	7.95	0.77	4.00	0.76	0.27	0.44	273.36
Complete
d+Aclust (0.15)	1068.67	5.41	0.61	7.00	0.73	5.89	0.70	6.76	0.80	3.95	0.76	0.26	0.31	137.10
Aclust (0.35)	1656.38	3.25	0.70	7.00	0.71	5.96	0.64	8.13	0.75	4.22	0.70	0.22	0.45	138.95
Spearman Correlation
Average
d+Aclust (0.20)	771.60	5.91	0.65	7.00	0.76	6.00	0.73	8.06	0.82	3.98	0.80	0.32	0.44	260.21
Aclust (0.30)	1018.20	3.79	0.67	7.00	0.73	5.95	0.69	8.78	0.77	4.00	0.78	0.24	0.60	132.14
Complete
d+Aclust (0.20)	771.21	5.89	0.65	7.00	0.76	5.92	0.73	8.06	0.82	3.98	0.80	0.32	0.44	299.06
Aclust (0.35)	1113.85	3.23	0.66	7.00	0.73	5.82	0.70	8.32	0.78	4.15	0.77	0.24	0.60	115.35
Bump Hunting	–	4.49	0.59	7.00	0.69	5.99	0.62	9.49	0.76	4.00	0.42	0.11	0.23	789.48

Note: Results of the proposed analysis pipeline based on different parameters of the Aclust algorithm, and the more performant implementation of Bump Hunting. Aclust and d+Aclust stand A-clustering without (Aclust) and with (d+Aclust) 999-dbp-merge initiation step. 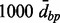restriction was always applied. The numbers in parentheses are the distance thresholds 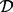used in each clustering implementation. These thresholds are the optimal ones for each settings, as determined by sensitivity analysis described in the Supplementary Material. Cluster provides the total number of detected clusters by Aclust. Memb m is the mean number of members in the mth cluster, and TPR m is the proportion of simulations in which the mth cluster was found to be significantly associated with the exposure after FDR correction. TPR is the proportion of simulations in which all five clusters were associated with exposure, and FP is the mean number of clusters that were falsely detected as associated with exposure. Time is the elapsed computation time (in seconds).

For each Aclust method, Table 1 provides the number of detected clusters of 3 or more members (not necessarily differentially methylated). For Bump Hunting, this measure is not provided because it searches DMRs, rather than performs clustering and then association analysis, as the proposed pipeline. For Aclust, we say that a cluster was detected if the Benjamini and Hochberg (BH)-adjusted (Benjamini and Hochberg, 1995) exposure effect P-value 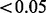from the GEE analysis. For Bump Hunting, a cluster was detected if its q-value was <0.05. The true-positive rate of target m (TPR m) is defined as the proportion of simulations in which a cluster containing target m was detected. The TPR is defined as the proportion of simulations in which clusters containing all M = 5 targets were detected. Finally, the false-positive (FP) rate is the mean number of non-target clusters detected across simulations. We also report the mean number of members in the mth cluster in each scenario (‘Memb m’) and the mean elapsed computation time (in seconds) for the analysis (Time).

Comparing TPRs across the different implementations of Aclust, the results are consistent, with the largest difference seen in cluster 1, with the lowest TPR1 being 0.61 and the highest 0.71. This difference is seen in the two implementations of Aclust using Pearson correlation and type average. Notice that specifically in this cluster, there was a relatively large fluctuation, of about 2, in the estimated number of members across Aclust specifications. Spearman correlation yielded overall larger TPRs, and also slightly larger FPs, but still the mean FPs are small, so that Spearman correlation seems to be more appropriate, especially when the dbp-merge initiation is used. When using both Pearson and Spearman correlations, and initiating with the dbp-merge, the average and complete clusterings gave almost identical results. Because the computation time of the average clustering is lower, this simulations study leads us to conclude that average clustering type is preferable.

As compared with the results from A-clustering, our implementation of Bump Hunting tended to detect less true differentially methylated clusters, slightly less FP and its computation time is longer. Interestingly, Bump Hunting performed well on large clusters, but less so on smaller clusters. Taken as a whole, the results of A-clustering tend to be robust to the implementation specifications that we considered, and are competitive with the Bump Hunting method.

We briefly summarize the single site comparisons here. Each of the sites along chromosome 1 was tested for differential methylation using Wald tests with robust standard error estimates. The resulting P-values were adjusted according to one of two methods: BH FDR (Benjamini and Hochberg, 1995) and Benjamini-Yekutieli FDR, which controls the FDR of sites under dependency (Benjamini and Yekutieli, 2001). A site was detected if its adjusted P-value <0.05. To make the results comparable with the clusters/DMRs-based analyses, define TPR m in the single site analysis as the proportion of simulations including at least one site detected within the cluster containing target m, and similarly TPR is the proportion of simulations in which at least one site was detected in all M target clusters. Define FPR as the proportion of simulations with detected sites not belonging to clusters containing any of the targets. The best TPR observed in the single-site analysis (i.e. across the different Aclust implementations) was 0.2, lower than any TPR reported in Table 1. The corresponding FPR was 0.7, higher than any of the clustering FPs in Table 1. We conclude that the single site analysis is less powerful then the clustering-based analysis; refer to the Supplementary Material for more details.

4.1.2 EWAS simulations results

In this set of simulations, we chose M = 10 ‘targets’, none of them overlapping with those used for chromosome 1 simulations, to allow for more scenarios. The correlation heatmaps for neighborhoods surrounding these targets are provided in the Supplementary Material. We compared the proposed pipeline, with the ‘best’ Aclust parameters settings from chromosome 1 simulations, with Bump Hunting. (The ‘best’ settings: Spearman correlation, average clustering type, 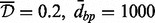and 999-dbp-merge initiation). As in the other simulations, the minimum cluster size was set to 3. Table 2 gives a brief summary of the simulations with three reported measures: the average number of true-positive detections across 100 simulations (here the maximum number is 10) and the average number of FP detections, or average number of clusters detected that are not in fact DMRs, and computation time (Time). More detailed results are reported in the Supplementary Material.

Table 2.

EWAS simulation results

	TP	FP	Time
d+Aclust	6.93	2.44	3774.75
Bump Hunting	4.52	1.48	8924.05

Note: Averaged EWAS simulations results, across 100 simulations. d+Aclust used Spearman correlation, 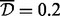, clustering type average, and maximum distance 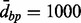. TP = average number of true-positive clusters; FP = average number of false-positive clusters. Time is computation time.

4.2 Data analysis

We applied the proposed clustering algorithm and analysis pipeline to data generated from a NIH-funded RC1 grant (1RC1ES018461-01) studying genome-wide methylation alterations in response to pesticide exposure using the Illumina Infimum 450 K beadchip. The data we used for our analysis in the present investigation were produced from 80 certified, white male US pesticide applicators. The exposure was defined as high versus low exposure to pesticides. There were 40 subjects in each exposure group. Before application of the A-clustering and subsequent analysis, the dataset was preprocessed by applying the pipeline proposed in Touleimat and Tost (2012). CpG sites in the proximity of Single Nucleotide Polymorphisms (SNPs) (up to 10 bp away) of minor allele frequency at least 0.05 were removed. The data were corrected for batch effect using empirical Bayes correction [ComBat, Johnson et al. (2007)].

We now describe the results of two clustering and analyses applied to the entire dataset. In the first analysis, we used the settings identified as optimal for the purpose of detection of DMRs in the simulations studies, and in the second analysis, we used less stringent distance criteria to both glean into the differences in the results, and also learn about the clustering outcomes themselves.

4.3 Clustering results

There were 460 337 CpG sites in the data used for analysis. We applied the A-clustering algorithm on the dataset twice. In the first analysis, we applied A-clustering with the settings identified in simulations as most appropriate to detect DMRs, i.e. Spearman correlation-based distance measure, average distance type, threshold distance for merging 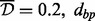-merge initiation (999 bp) and 1000 bp restriction on merging of adjacent CpG sites. Table 3 summarizes the results of this analysis. There were 7741 clusters with at least two CpG sites, with the largest cluster having 52 sites. Seventy percent of clusters were associated with a predefined CpG resort, and of these, 20% had sites from multiple resort regions (e.g. both island and north shore), suggesting that sites in different resort regions are in fact functionally associated. At the bottom part of Table 3, we provide characteristics of clusters with estimated exposure effect size larger than 0.02, and are also significant at the 0.05 level after FDR correction for multiple hypothesis testing. We restricted the effect size to be at least 0.02 because we cannot exclude the possibility that smaller effect sizes are due to changes in cell mixture composition (Houseman et al., 2012). There were 402 clusters with effect size 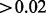, and four of them were significantly associated with exposure. Three of them had only two CpG sites, and the fourth had three. The sites were rather close to each other: two of the clusters had only 6 and 7 bp between extreme sites. One of these clusters contained 2 probes from a CGI, another cluster contained 3 probes from a north shore and another cluster contained 1 probe from an island and 1 probe from a north shore.

Table 3.

A-clustering results on the entire data, 999-dbp-merge initiation, 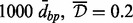, Spearman correlation, type average

Characteristics	Quality
Number of clusters (at least two sites)	4753
Number of CpG sites in clusters (min, median, max)	(2, 2, 52)
Base-pair distance between extremes (min, median, max)	(2, 115, 3611)
Clusters associated with a CpG resort (%)	3333 (70%)
w/CpGs from multiple resort regions (% of resort clusters)	659 (20%)
Restricted: clusters with exposure effect >0.02, and significant
Number of clusters with effect size >0.02	402
Number of significant clusters (FDR corrected)	4
Number of CpG sites in clusters (min, max)	(2, 3)
Base-pair distance between extremes (min, max)	(6, 725)
Clusters associated with a CpG resort	3
w/CpGs from multiple resort regions	1
w/CpGs from south shelf, shore, island, north shore, shelf	0, 0, 2, 2, 0

Note: Summary of the Aclust and analysis results on the 460 337 CpG sites. The first block in the table refers to the entire set of clusters. The second block refers to the set of clusters that had exposure effect size 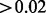, and significant at the 0.05 level after FDR correction. The minimum number of sites per cluster is 2.

In the second analysis (Table 4), we applied the A-clustering with less stringent distance criteria: this time the distance type was single, and 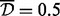. Other settings remained the same. Now, there were 17 515 clusters of at least two sites, with the largest cluster having 59 sites. Seventy-two percent of the clusters had at least one site from a resort and of these, 29% of sites from more than one region in a resort, a higher proportion than the equivalent number in the previous analysis (20% there). There were 641 clusters with estimated exposure effect size 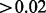. Applying FDR correction for multiple testing, seven of these clusters where significantly associated with the exposure at the 0.05 level. Four of these clusters had only two sites, and the others had 3, 4 and 7 sites. Four of these clusters had at least one CpG site from a CpG resort, while two of these had CpG sites from both an island and a north shore. Comparing the clusters identified as DMRs by the first analysis with those in the second analysis, the top three clusters detected in the first (average distance type, 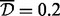) analysis where in the top five clusters identified in the second (distance type single, 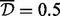) analysis. The fourth cluster was not identified as a DMR in the second analysis at all, and in fact, there it was part of a larger cluster of five sites, with a smaller effect size.

Table 4.

A-clustering results on the entire data, 999-dbp-merge initiation, 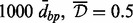, Spearman correlation, type single

Characteristics	quality
Number of clusters (at least two sites)	17 515
Number of CpG sites in clusters (min, median, max)	(2, 3, 59)
Base-pair distance between extremes (min, median, max)	(2, 193, 5338)
Clusters associated with a CpG resort (%),	12554 (72%)
w/CpGs from multiple resort regions (% of resort clusters)	3640 (29%)
Restricted: clusters with exposure effect >0.02, and significant
Number clusters with effect size >0.02	641
Number of significant clusters (FDR corrected)	7
Number of CpG sites in clusters (min, median, max)	(2, 2, 7)
Base-pair distance between extremes (min, median, max)	(6, 216, 725)
Clusters associated with a CpG resort	4
w/CpGs from multiple resort regions	2
w/CpGs from south shelf, shore, island, north shore, shelf	0, 0, 3, 3, 0

Note: Summary of the Aclust and analysis results on the 460 337 CpG sites. The first block in the table refers to the entire set of clusters. The second block refers to the set of clusters that had exposure effect size 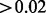, and significant at the 0.05 level after FDR correction. The minimum number of sites per cluster is 2.

We also performed the same analysis while restricting to three sites in a cluster, as in the simulations. In this case there was only one cluster, of three sites, identified as a DMR when average clustering and 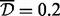were used, and four clusters, of 3–7 sites, were identified as DMRs when single and 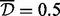were used.

Finally, we implemented the Bump Hunting algorithm to detect DMRs. In short, Bump Hunting, allowing for a minimum of two sites per DMR, and other settings used in the simulations suggested 452 potential DMR, but the lowest q-value was 0.18, i.e. none were determined as significantly associated with exposure. This is consistent with the simulations that showed that Bump Hunting performs well with large clusters, but does not easily detect small clusters.

5 DISCUSSION

We present the A-clustering algorithm that clusters together adjacent methylation sites according to their distance, usually derived from the correlation between them, and provide a pipeline for analysis of methylation data when they are treated as outcomes. The clustering is used both to detect regions of sites that are co-regulated, and also to reduce dimension, by forming a smaller set of analysis units. We demonstrated the use of the algorithm on a methylation dataset, in which methylation was measured using the Illumina Infimum 450 K beadchip. The proposed method is also appropriate for sequencing data, possibly even more so than for array data, which tend to be sparser. The clustering and analysis methods are efficient, and they do not require resampling methods to compute the P-values.

It is still an open question regarding what is the ‘right’ unit of analysis and for which purposes (e.g. CGIs, shores). Recent work by Jacoby et al. (2012) suggests that the unit of analysis differs by regions (e.g. in promoter or intragenic areas), and possibly by cell type as well. A-clustering is useful tool in studying such units of differentially methylated regions and loci. Clusters of methylation sites will often have higher P-values then individual methylation sites. For instance, the cluster will likely have a smaller effect estimate and a larger P-value than the site within the cluster with the largest effect. However, there is a considerable dimension reduction when clusters are considered, and further, we believe that the fact that multiple sites exhibit similar behavior increases our certainty that the effect is ‘real’, rather than a FP discovery, because the probability to detect multiple adjacent sites is lower than the probability of detecting at least one single site.

A-clustering uses correlation as the basis for clustering of CpG sites. This raises a few issues that are important to consider when analyzing data. First, the type of correlation to use. We explored the use of Pearson correlation, as well as the Spearman correlation, which is more robust to non-linearities in the association between two variables. In the dataset we used for data analysis, as well as the simulated data, we had 80 observations, a relatively low number, and, as was determined by simulations, Spearman correlation was slightly more appropriate for the detection of differentially methylated regions. When the number of observations is higher, it may be beneficial to use the Pearson correlation, especially because it reduces computation time compared with Spearman correlation. Second, one should consider redundant correlation due to covariates and batch effects. We recommend performing the entire analysis after normalization and batch effect removal, but one should also consider correcting for the effects of important covariates before A-clustering, by implementing Aclust on the partial residuals of the methylation measures, after regressing them on covariates. Note, however, that in our dataset, clustering results were nearly identical when we used the methylation values and when we used the partial residuals. Third, one can apply A-clustering based on a subset of the subjects. For instance, one can use only the high-exposure group to define the clusters, rather than all subjects. This would be useful if one expects that high exposure will ‘activate’ a region, say, so that the signal is completely driven by the high-exposure group. As another example, it may be advantageous to cluster methylation sites based on the controls in a case-control study, if one expects that cases will exhibit an aberrant methylation pattern.

We provide two options to extend and restrict the clustering algorithm. First, the dbp-merge that allows one to cluster a set of sites that are wedged between two correlated sites and are ‘close enough’ to each other, in terms of both correlation-based and physical distance. We also consider restricting adjacent CpG sites from clusters, if the base-pair distance between them (and without any CpG site measured between them) is smaller than a predetermined threshold. In the data analysis, we used 999 bp for the dbp merge and 1000 bp for the base-pair distance restriction. It is not entirely clear if these are the best numbers. The best distances would be such that the signal is maximized and yet not too much noise is added. More complex rules for merging and restrictions could also be devised, but that can lead to more complicated computation and less clear interpretation. Another possible extension to the clustering algorithm is the use of clustering indicators based on prior knowledge. For instance, one can decide that an island necessarily belongs to a certain cluster. Also, in validating the results of one study on a different dataset, one can use the clustering assignments from the first study.

Another tuning parameter is the type of distance between clusters to be used. In the simulations, mimicking the sample size and two exposure group’s design of our dataset, we found that the average distance is most appropriate for the goal of detecting differentially methylated regions.

We use GEEs for the analysis of clusters, as they use marginal mean models that are robust to mis-specification of correlation structure. We use exchangeable working correlation, but other types of correlation can be explored. Also, we assumed that the exposure effect is constant across all sites in the cluster. Although it is likely that the direction of exposure effect (increases/decrease methylation) is the same across the cluster, it is not clear that the constant effect is correct and therefore, it may not be the most advantageous assumption. For instance, it may be that even after allowing for single-site intercept (i.e. we allowed for a different baseline level of methylation for each site), some sites may be more quickly modified by exposure than others. It is a topic for future work to extend the method using other assumptions on the effect of exposure on methylation in sites (e.g. increasing as the site is closer to the transcriptional start site). A drawback of the proposed GEE-based analysis is limited detection of large clusters (e.g. 50 sites) when the sample size is small. Allowing for different intercept for each site in a cluster may yield high standard errors for the exposure effect. Thus, in the case of a large cluster and small sample size, it is possible that methods such as Bump Hunting, or analysis of the mean methylation measure of probes in the cluster, may be more powerful.