How do proteins locate specific targets in DNA?

Abstract

Many aspects of biology depend on the ability of DNA-binding proteins to locate specific binding sites within the genome. Interest in this target search problem has been reinvigorated through the recent development of microscopy-based technologies capable of tracking individual proteins in real-time as they search for binding sites. In this review we discuss how two different proteins, lac repressor and RNA polymerase, have solved the target search problem through seemingly different mechanisms, with an emphasis on how recent in vitro single-molecule studies have influenced our understanding of these reactions.

1. Introduction

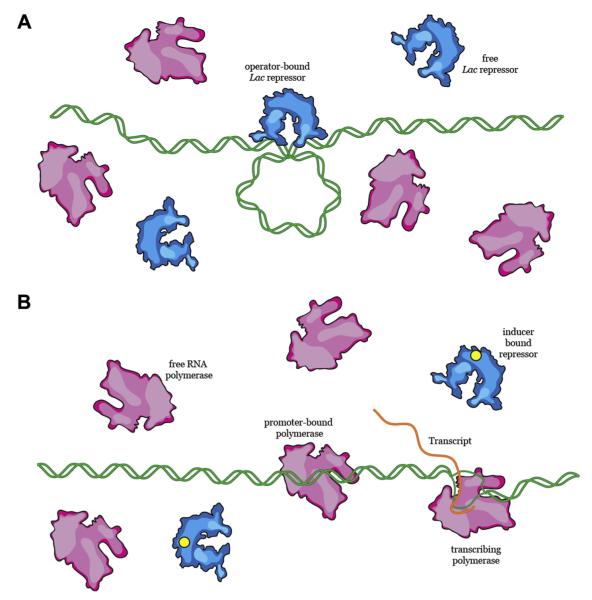
The flow of information between DNA, RNA, and proteins constitutes the fundamental basis of all biological regulation. A traditional example highlighting the dynamic interplay between proteins and DNA is metabolism of the disaccharide lactose in the bacterium Escherichia coli (Figure 1). Here, a region of the bacterial chromosome, termed the lac operon, comprises a set of genes that can be transformed into proteins required for the metabolism of lactose: the lacY gene encodes lactose permease, which allows lactose to enter the cytoplasm from the surrounding medium; the lacZ gene encodes β-galactosidase, which catalyzes the conversion of lactose into the monosaccharides glucose and galactose; and the lacI gene encodes the lac repressor, which turns off expression of the lac operon when lactose is unavailable [1–3]. Expression of the lacY, lacZ, and lacI genes requires another protein, RNA polymerase, which binds to a specific promoter sequence upstream of the lac operon and synthesizes the messenger RNA (mRNA) transcript that serves as a blueprint for the synthesis of these proteins by ribosomes [4]. This metabolic pathway must be carefully regulated in order to make efficient use of cellular resources. For example, in the absence of lactose, production of the lactose metabolizing proteins would expend valuable energy without benefiting the cell. To prevent this, the lac repressor binds to a set of three specific sites upstream of the lac genes, called lac operators; the binding of lac repressor to these sites prevents RNA polymerase from gaining access to the promoter (Figure 1) [1,2]. To prevent aberrant expression of the lac operon, the lac repressor must occupy the operator and preferentially outcompete polymerase; however, if the cell is provided with lactose as a carbon source, the lac repressor must dissociate from DNA thereby allowing RNA polymerase to bind the promoter (Figure 1) [1,2]. This transition is critical: if the lac repressor fails to dissociate from the operator site in the presence of lactose or if RNA polymerase fails to locate the promoter, then the cell will incur a competitive disadvantage relative to neighboring cells that are otherwise capable of faithfully regulating the lac operon. Conversely, if the lac repressor fails to bind the lac operator and the lac operon is therefore constitutively expressed, then the cell would waste energy producing lac proteins even in the absence of lactose, which would again place it at a competitive disadvantage.

Figure 1.

Regulation of the lac operon. (A) In the absence of lactose, the lac repressor protein binds to an operator sequence and prevents RNA polymerase from accessing its promoter. (B) When lactose is present, lac repressor dissociates from the DNA, allowing RNA polymerase to bind to its promoter and transcribe the genes necessary for lactose metabolism.

The simplified description provided above for the regulation of the lac operon helps illustrate how the interactions between proteins and DNA are essential in determining cellular fate, provides insight into the transmission and regulation of cellular information, and highlights contributions that site-specific DNA-binding proteins make to fundamental cellular processes. Importantly, in order to fulfill their respective biological roles, both lac repressor and RNA polymerase must be capable of efficiently locating and binding to their respective target sites, and they must also discriminate against non-specific targets. Here we will use these two classical model systems, lac repressor and RNA polymerase, as a framework for discussing how proteins search for and bind specific targets embedded within a vast excess of non-specific DNA.

2. Concepts governing specific and nonspecific DNA-binding

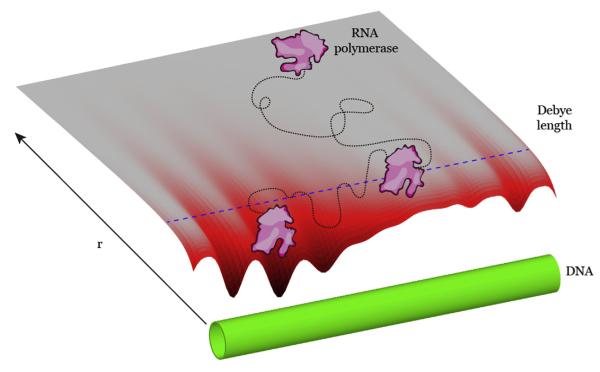
The binding of proteins to nucleic acid substrates is dominated by electrostatic and hydrogen bonding interactions, and can be thought of as the consequence of two potentials, both of which can be considered optimized when the protein in question is bound to a specific target (Figure 2) [5–9]. The first potential is entirely entropic and involves sequence-independent electrostatic interactions between the negatively charged phosphate backbone of DNA and positively charged amino acids present on the binding surface of the protein [5]. This potential is also influenced by charged ionic species (e.g. Mg²⁺, Na⁺, etc.), which affect the dielectric constant of the surrounding solution and set the functional length over which the electrostatic potential of the DNA permeates the local environment. Detailed calculations show that at modest distances (~1.0–1.5 nm from the DNA axis), the electrostatic potential of the DNA is purely radial. That is, it appears to a protein as a simple cylinder with an effective surface charge, U₀ [10]. Solutions of the Poisson–Boltzmann equation find this radially distributed potential has the form U_ns ≈ −U₀K₀(r/λ), where λ is the Debye screening length and K₀ is the modified Bessel function of the second kind [11]. The Debye screening length can be thought of as the fundamental length scale of a potential in a solution of given ionic strength, viz at one Debye length the potential drops to e⁻¹. Evidenced by the dependence on λ, the range of this potential is greatly affected by the ionic strength of the surrounding bath, which is an important consideration for experimental measurements involving non-specific DNA binding by proteins (see below).

Figure 2.

Specific and non-specific DNA binding. Schematic representation of a hypothetical three-dimensional surface plot showing the radial distance (r) dependence of the binding energy for a hypothetical protein (in magenta) and a DNA molecule (in green). The Debye length is shown as a dashed blue line. The minimum in the energy landscape would correspond to a specific binding site.

The second potential stems from unique sequence-specific DNA interactions and includes particular contacts between the protein and the DNA bases, interactions arising from the shape (either native or induced) of the DNA and the protein [8,12–14], contributions from dehydration of the resulting interface [15,16], as well as potential contributions arising from the displacement of polycations [16,17]. The net sum of these interactions can be imagined as a random potential, U(z), where z defines the position along the long axis of the DNA molecule. For illustrative purposes U(z) is presented statically, however an accurate profile would also incorporate the sundry potential orientations of the protein relative to the DNA. It is common to think of this potential as periodic in the regular spacing of base pairs [6,18]. However, even though this may not be necessarily true, there is likely some regularity due to the nature of sequence-specific binding. Within this framework, a landscape describing the radial-distance-dependent interaction between a hypothetical protein and DNA can be visualized as a three-dimensional potential energy surface plot (Figure 2). In this illustration, the energy minima reflect favorable sites of interaction along the DNA, which from a physical perspective might be considered specific binding targets.

In contrast to site-specific binding, non-specific binding is decidedly ephemeral, and is usually defined as when the protein is within some radial distance from the DNA axis, such that the electrostatic potential between the protein and DNA is not negligible. Practically, the cut off between non-specifically bound and freely diffusing through solution is defined as a discontinuous step transition, despite the continuum of non-specific binding energies, rather than a single defined non-specifically bound state, which is evident from the energy surface shown in Figure 2. One can gain an intuitive understanding for the difference between specific and non-specific interactions by considering the protein–DNA complex as a set of defined interactions, each of which can be scored according to a particular free energy contribution [6]. When the protein is correctly bound to its target, one expects that the free energy of this complex is substantially lower than if the same protein were to be placed on a random stretch of DNA. Now let one of these interactions be disrupted due to some change in the underlying DNA target sequence. The protein may retain substantial affinity for this region of DNA due to the remaining interactions, however the free energy will now likely be greater for this new complex, a fact borne out of the wealth of experimental investigations of target site mutations on binding energies. Allowing that all protein–DNA complexes can be realized by a continuous and sequential perturbation of this toy model leads to the conclusion that the affinity of a protein for any particular sequence of nonspecific DNA arises from its ability to interact specifically with its specific target site. Most importantly, while it is possible to have a protein that binds DNA non-specifically, but does not have a highly preferred specific target, the converse is not true: all site-specific DNA-binding proteins inherently possess some non-negligible affinity for non-specific DNA.

3. Target site association mechanisms

In addition to the fundamental physiochemical principles that underlie sequence-specific and non-specific interactions as described above, there exists a separation of specific and non-specific binding in terms of biological function. For site-specific DNA-binding proteins, the absolute distinction between specific and nonspecific binding must be one of biological relevance: these proteins perform a biological task while bound to a specific site. To fulfill their biological roles, all site-specific DNA-binding proteins must first locate the target sites at which they fulfill their biological functions. Importantly, the mechanism by which site-specific DNA-binding proteins begin the search for their respective target sites initiates identically across functionally diverse molecules. After maturation in the cytoplasm, the protein in question diffuses through the cellular milieu until encountering DNA. Specific binding sites are typically much more rare than non-specific sites. For example, there are only three lac operators in the entire E. coli genome (~6 × 10⁶ base pairs in length) [1,2], and although there are on the order of ~4000–5000 promoters in E. coli, they still only comprise <2% of the bacterial genome [19]. Therefore this initial journey likely leaves the protein bound to a random, non-specific sequence of DNA unrelated to the protein’s specific biological function. Hence the target search process must involve wading through the vast excesses of non-target DNA until the specific target is located. This raises the question of: how do proteins conduct this phase of the target search?

3.1. Facilitated target searches

The early work of Riggs et al. revealed that the lac repressor was capable of binding its target site in vitro at rates exceeding the 3D diffusion limit (~10⁸–10⁹ M⁻¹ s⁻¹) [20]. This remarkable finding in spired a large number of in vitro, in vivo, and in silico studies (e.g. [21–32]), resulting in a now generally accepted theory of protein association kinetics commonly referred to as ‘facilitated diffusion’[22,32–38].

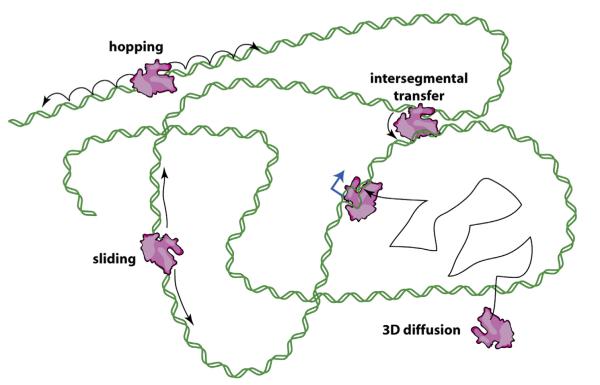
In the simplest of terms, a facilitated search process involves three protein states: (i) a free state, where the protein of interest is not associated with DNA; (ii) a non-specifically bound state, where the protein is bound to non-specific DNA; and (iii) a specifically bound state, where the protein has located and bound its cognate target site. The search process then consists of cycling through the non-specifically bound and free states until the protein locates the intended target. From the perspective of a single searching protein, this search process will be inherently slow, especially when the concentration of available non-specific sites vastly outnumbers specific sites. The ‘facilitation’ occurs due to two factors. First, the affinity of proteins for non-specific stretches of DNA localizes the protein to the DNA for extended periods of time, allowing for many successive rebinding events before complete dissociation into free solution; here we use the term into free solution to indicate that the protein has dissociated from the DNA and has equilibrated into the bulk solution (Figure 3). Second, if the protein scans along the DNA through diffusion-based mechanisms during its time in the non-specifically bound state, it can interrogate multiple sites during a single association event [22,34]. For example, before dissociating into free solution the protein can continue searching DNA by one-dimensional (1D) hopping, which involves a series of correlated dissociation and rebinding events, or by 1D sliding, where the protein diffuses continually along the DNA [22,34]. Proteins may also move from one site to another via a looped intermediate through a mechanism called intersegmental transfer [22,34], which for our purposes can effectively be considered an extension of hopping and/or sliding (Figure 3). Notably, intersegmental transfer requires more than one DNA-binding surface, but in principle this second surface could be comprised of even a single amino acid. Importantly, these different search mechanisms are not mutually exclusive, and it likely that different combinations contribute to site-specific targeting for any given DNA-binding protein. Search mechanisms that employ 1D hopping, sliding, or intersegmental transfer are collectively referred to as facilitated diffusion, because the effective reduction in dimensionality brought about by these mechanisms can, under certain conditions, increase target site association rates beyond the limits imposed by pure 3D diffusion (Figure 3) [21]. However, it is crucial to recognize that these same mechanisms can potential slow down target association rates, because the more time proteins spend bound to non-specific DNA the longer it will take them to find a specific target [32,35,37,39–41]. This problem will be considered in greater detail below.

Figure 3.

Mechanisms of facilitated diffusion. Diffusion-based models for how proteins might search for binding targets: random collision through 3D-diffusion (i.e. jumping); 1D-hopping, involving a series of microscopic dissociation and rebinding events; 1D-sliding, wherein the protein moves without dissociating from the DNA; and intersegmental transfer, involving movement from one distal location to another via a looped intermediate. These mechanisms are not mutually exclusive, and the latter three are categorized as facilitated diffusion because by reducing dimensionality they allow target association rates exceeding limits imposed by 3D-diffusion. DNA is green, the target site (promoter) is blue, and RNAP is magenta. Adapted with permission from reference [77].

3.2. All target searches are likely facilitated to some degree

The capacity of all DNA-binding proteins to bind non-specifically is the critical component of facilitated diffusion; however, the value of the so-called 3D limit (i.e. the target association rate in the absence of facilitation) is actually derived from calculations based on idealized systems where non-specific binding is ignored and specific binding is considered infinitely efficient [21,29,42,43]. As is now clear, neither of these conditions applies to biological macromolecules, a realization borne out of numerous experiments on a number of different proteins, including both lac repressor and RNA polymerase.

Interestingly, the mechanisms of facilitated diffusion arise entirely from the fact that proteins recognize specific regions of DNA. That is, the ability of a protein to bind specific DNA sequences implies its ability to bind DNA non-specifically, and this non-specific binding can account for the mechanisms of facilitation. Given the origins of non-specific binding described in Section 2, it is then straightforward to infer the molecular origins of both the hopping and sliding components of facilitated diffusion (Figure 3). Non-specific protein–DNA complexes must by definition have a binding lifetime, $k_d^{-1}$ related to the site-specific energy. Once a protein dissociates from DNA, its re-equilibration with the surrounding solution depends on the distance it travels away from the DNA and the geometry of both the DNA and the protein. This is a consequence of the redundant nature of passive thermal motion: the very existence of non-specific binding implies all search processes must contain an element of binding and dissociation from regions of non-specific DNA during which the protein cannot to equilibrate with the bulk solution. This process will lead to protein motion along the DNA that has previously been defined as ‘hopping’ (Figure 3) [34].

Furthermore, the idealized interaction profile shown in Figure 2 also gives rise to the 1D sliding. To illustrate this, consider the DNA as a linked series of non-specific binding sites, which are separated from one another by a local energetic barrier. We can then define a fundamental length scale, ϱ, which can be considered the diffusion ‘step size’ as the protein moves between the local potential wells along the DNA. Moreover, let E_j denote the depth of a particular energetic well, and E_ij express the height of the barrier between sites i and j. Then the transition rates along the DNA (i.e. along the energy landscape shown in Figure 2) can be expressed as Γ_i,j = Γ₀r−β(E_ij–E_j), where Γ is an attempt frequency. At any given site the eventual probability of a protein making a diffusive step to the left or right along the DNA axis before dissociation from the DNA (either into free solution or a shorter distance hop) is then given by:

$$P_{\pm }=\frac{{\Gamma }_{i\pm 1,i}}{{\Gamma }_{i\pm 1,i}+{\Gamma }_{i\mp 1,i}+k_d}$$

In the limit of k_d = ∞, the protein collides elastically with the DNA and the probability to slide along the DNA vanishes, which is, of course, the limit at which the calculated values for the 3D-diffusion limit are recovered. Alternatively, when k_d = ∞, the protein can never dissociate, and will continuously slide along the whole length of the genome. For a given process it may be convenient to assume a protein is effectively in one of these limits, however, neither limit is realistic for true biological macromolecules.

The above discussion centers around sliding and hopping as mechanisms of facilitated diffusion because of the relative ease with which one can quantitatively describe the underlying physical principles. Proteins can also utilize intersegmental transfer as a facilitated search mechanism, although this mechanism is more difficult to express mathematically because it necessarily involves a contribution of the DNA three-dimensional geometry, which is itself continuously changing in time. Nevertheless, in a very simplified sense, intersegmental transfer can be considered an extension of sliding and hopping in a scenario involving proteins with two or more DNA binding sites that can concurrently interact with different non-specific DNA sites.

3.3. Interpreting experimentally measured diffusion coefficients

The motion of a protein along the DNA axis in the idealized potential shown in Figure 2 can be quantified by a sliding diffusion coefficient, which we will call D_s, and can be expressed as:

$$D_s=\frac{{\varrho }^2}{N}\left[\sum _{i=1}^N{\Gamma }_{i+1},i\frac{e^{-\beta E_i}}{\frac{1}{N}\sum _{j=1}^N{e}^{-\beta E_j}}\right]$$

where i is an index over individual binding sites and N is the total number of binding sites [44]. In general, D_s can provide a direct readout of the binding energy, averaging the intrinsic transition rates normalized against thermal occupation factors. Furthermore, when measured experimentally, the diffusion coefficient will also average the energetic landscape to the resolution limits of the measurement. Notably, if the energy wells and barriers are all identical, the usual Einstein relation can be recovered. Therefore, the diffusion coefficient can potentially provide in-depth insights into the fundamental nature of protein–nucleic acid interactions. In addition, because the diffusion coefficient defines the speed at which proteins migrate away from their initial location, it seems reasonable to conclude that a large diffusion coefficient would correspond to a faster search process. However, an important implication of the above equation is that a fast search likely means that there is little preference for particular sites on the DNA because fast searches can only occur when the difference in potential energy between different sites is small (E_i±1 – E_i → zero), which implies that rapid diffusion will coincide with poor target)recognition efficiency [32,35,45].

The discussion above presents an idealized view of D_s, however one should recognize that this idealized view is at odds with what can be measured experimentally. In reality, there still exists a gulf between what diffusion coefficients can theoretically reveal about protein–DNA interactions, and what existing experimental measurements of diffusion actually mean regarding the underlying physical properties. This often misunderstood or ignored discrepancy remains a challenge for the field. Part of the problem lies in the fact that diffusion coefficients obtained from single-molecule data are unavoidably compromised by systematic error, arising largely from inaccuracies in particle localization and because the diffusion trajectories being measured are finite (typically no more than a few seconds) [46–54]. Therefore one does not measure D_s, but rather an experimentally observed ‘apparent’ diffusion coefficient, which we will define as D_1,obs. It is crucial to recognize that D_s≠D_1,obs. The idealized D_s assumes that all observed protein motion arises from sliding along the DNA while maintaining constant non-specific contacts. This assumption is not necessarily correct, but current instrument spatial and temporal resolution limits prevent any direct observation of short excursions away from the DNA (i.e. hops). Such ‘hops’ can be considered ‘sub-microscopic’ events because they cannot be detected by single-molecule imaging, and as a consequence all experimentally measured diffusion coefficients most likely represent a complex composite of both hopping and sliding components. At present it is not straightforward to rigorously disentangle the relative contributions of each of these two different modes of 1D diffusion through either experimental or theoretical analyses.

The above discussion begins to illuminate the important issue of how difficult it can be to differentiate the non-specifically bound state from the unbound state in single-molecule observations. The problem can be understood by considering that DNA has a diameter of just 2 nm, and both the protein and DNA are moving extremely fast; current of real-time imaging technologies lack the spatial and temporal resolution to definitively co-localize two small rapidly molecules with sufficient precision to fully resolve all of their interactions. Therefore even if a protein co-localizes with DNA in an image, it does not necessarily mean that the protein is actually bound to the DNA in that given instant. While the potential in Figure 2 becomes nearly featureless within a few Debye lengths from the DNA, the error on experimentally co-localizing the protein and DNA signals is much larger. To illustrate this point, take an experimentally observed dissociation event by the hypothetical protein shown in Figure 2 following a period of 1D diffusion along the DNA. In the 1D regime, the DNA-bound protein occupies the static landscape described above, however at the moment of sub-microscopic dissociation, the particle enters a volume around the DNA in which it diffuses three-dimensionally. The free energy landscape that the protein experiences while undergoing such hops is not the same free energy landscape it would experience if sliding along the DNA, nor is it the same free energy landscape that would be encountered during free diffusion in solution far away from the DNA. As a consequence of these uncertainties, it remains extremely challenging to interpret any experimentally measured value of D_1,obs in terms of detailed underlying physical interactions with the DNA.

While this review focuses on in vitro studies of target search mechanisms, a number of groups have also begun trying to analyze target searches in vivo using various forms of optical microscopy. As with the in vitro measurements, it also remains challenging to measure and understand the diffusion coefficient of proteins in living cells. This problem is again related to the spatial and temporal constraints of existing technologies, and is further compounded by nontrivial challenges in analysis of the resulting data and that fact that its not readily possible to determine when a protein is bound to DNA and when it is diffusing freely through solution. This can be illustrated by considering that DNA-binding proteins in vivo can access at least two diffusive modes: free diffusion in the cytoplasm and constrained diffusion near the DNA, as discussed above. Global diffusive motion in cases when the diffusion coefficient switches stochastically between well defined values results in motion that can be described by a single diffusion coefficient that is the result of a time-weighted average over the diffusion coefficient in each state:

$$\langle D_{\mathrm{obs}}\rangle =\sum _i{D}_i\frac{t_i}{t_T}$$

where i is an index of state, t_i and D_i are the time spent in and diffusion coefficient of each state, respectively, and t_T is the total time. This relation is commonly used to assess the motion of proteins in vivo [24,55]. However, one noteworthy problem with the above formulation is that when one diffusive state dominates, other states become masked, regardless of their possible importance to the overall search process. This insensitivity to t_i and D_i reveals the significant challenges one faces when trying to interpret in vivo diffusion data in terms of the molecular processes underlying target search mechanisms.

3.4. ‘Optimized’ target searches

One implication of the facilitated diffusion model is that interactions between a protein and DNA might be fine-tuned to minimize the time it takes for a protein to find its target site, and that the fastest possible search process should result from an optimized balance between diffusive motion along non-specific DNA and the non-specific residence time [29,35]. This balance yields an ‘ideal’ residence time on non-specific DNA, such that the protein minimizes the inherent redundancy in 1D diffusive searches while maximizing coverage of the genome through use of 3D diffusion, and theoretical studies have suggested that the ideal search process will involve roughly equivalent contributions of 1D and 3D search components [29,35].

But search optimization comes at a price. To bind a specific DNA target tightly, a protein must experience a deep energy well upon engaging the site. The energy landscape must be sufficiently smooth while surveying non-specific DNA, or the protein will spend excessive time bound to non-specific targets that are unrelated to the protein’s biological function [29,35]. This supposition indicates that there is a limit to the amount of ruggedness in the landscape, and that in order to support an optimized search, the dispersion in binding energies for non-specific sites must be ≤2 k_BT, while binding energies for specific targets should remain in excess of ≥5 k_BT to ensure high affinity [29,35]. To overcome this apparent paradox, Mirny and colleagues have suggested a two-state model wherein proteins remain in a low energy DNA-binding configuration while interrogating non-specific DNA for target sites, but then undergo a conformational change that may be coupled to target site association such that the protein remains tightly bound to its cognate target [35,50]. Indeed, the existence of conformational changes coupled to target binding has long been reported for a range of proteins based upon bulk biochemical and crystallo-graphic data [56,57]. There are now numerable instances of protein–DNA structures where the bound DNA deviates greatly from an ideal B-form double-helix, and/or where the DNA-bound protein conformation differs substantially from the apo protein, thus providing clear evidence of binding-induced structural changes[8,57,58]. These data indicate that conformational changes coupled to target recognition can apply to both protein as well as the bound DNA.

Recently we reported a set of single-molecule experiments that exemplifies this feature of protein–DNA dynamics [26,59]. In Saccharomyces cerevisiae, replication errors are recognized and marked for downstream repair by the protein complex MutSα [60–62]. We have elucidated a mechanism for this protein which involves an initial scanning step followed by recognition of a mis-paired base [59]. This initial target recognition step has a relatively low probability (<1%), suggesting that a conformational switch at the mismatch may indeed be coupled to recognition, and that this conformational change must occur on a time scale that is slower than the diffusive motion of the protein along the DNA. This finding is further supported by crystal structures showing the protein in complex with a highly kinked (~45–60°) mismatch-bearing DNA substrate [63–65]. Ensuing steps in the repair pathway require MutSα to be released from the mismatch upon binding ATP, and indeed, our experiments revealed that the protein undergoes another conformational switch after ATP-dependent mismatch release, as evidenced by a new diffusion coefficient and a change in target specificity [59]. Therefore, MutSα must experience a different energy landscape while sliding along the DNA before versus after mismatch recognition and subsequent release [59].

Several single-molecule florescence studies have shown other proteins diffusing while bound non-specifically to DNA, further supporting the above conception of the binding potential [46–52,66,67]. While interpretation of these results as evidence of energy minimization during the protein’s search process is over-reaching, these experiments still lend substantial insight into the nature of protein–nucleic acid interactions. Finally, it should be noted that in vivo results also suggest that the lac repressor is bound non-specifically to DNA 90% of the time during its search [24] as opposed to the 50% expected from theoretical calculations [35]. This result suggests that either the search by lac repressor is not optimized, or the assumptions underlying the calculations oversimplify the in vivo search scenario.

4. Are there different solutions to the target search problem?

The lac repressor and RNA polymerase have long served as model systems for studying protein–nucleic acid interactions, and lac repressor in particular has served as a model for the study of target search mechanisms [20–24,47]. Yet the story of target search mechanisms should not end with the lac repressor, because there remains crucial mechanistic information to be garnered from a broader examination of target search mechanisms used by other site-specific DNA-binding proteins. In addition, it is not at all clear that the results obtained from lac repressor studies can be applied to other DNA binding proteins [29,68].

4.1. Target searches by the lac repressor

Since the original work of Riggs et al. [20], both in vitro and in vivo experiments have been conducted to confirm that the target search mechanism used by the lac repressor involves facilitation (Figure 4)[23,24,47]. Single-molecule experiments have confirmed the fact that lac repressor can indeed slide for long distances on DNA, however, these single-molecule measurements required buffer conditions that strongly biased non-specific DNA interactions [24,47]. For example, non-specifically bound intermediates can only be observed within the existing temporal resolution limits of single-molecule imaging by lowering the ionic strength or raising the viscosity of the reaction buffer [24,47]. Similarly, the bulk biochemical measurements reporting search acceleration of lac repressor also utilized low ionic strength buffers, leading to the suggestion that the reduction in ionic strength was a major contributing factor to the observed search acceleration and that much more moderate effects would be expected in at physiological ionic strengths [68]. Lowering ionic strength increases overall affinity for non-specific DNA by strengthening the net electrostatic potential of the DNA, thereby increasing the basin of attraction, whereas increasing solution viscosity can promote interactions with non-specific DNA by dehydrating the protein–DNA interface as well as by restricting the ability of the protein to diffuse away from the DNA.

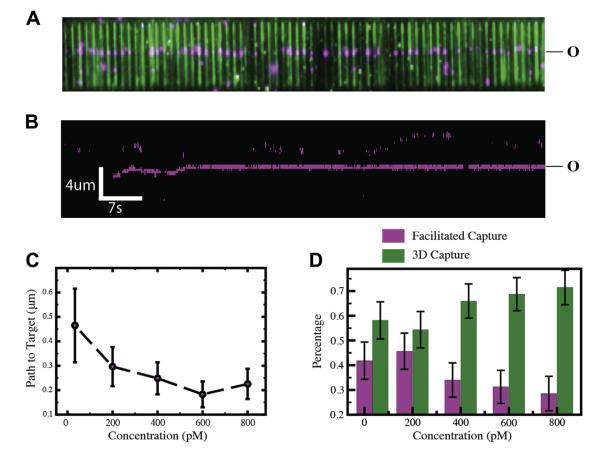
Figure 4.

Visualizing lac repressor at the single-molecule level. (A) Wide-field TIRF microscopy image of a DNA curtain [75,76] with quantum-dot tagged lac repressor bound to an idealized lac operator sequence (O). The DNA is stained with YOYO1 (green) and the proteins are shown in magenta. (B) Kymogram showing lac repressor (magenta) binding to DNA (unlabeled) and diffusing in 1D to the operator site. The mean 1D diffusion distance of lac repressor to the operator site as function of protein concentration. The relative distributions of operator binding events that occur through either facilitated search mechanisms or direct 3D binding as a function of protein concentration. Adapted with permission from reference [77].

Together, the collective results of work with lac repressor confirm that facilitated search mechanisms can play a role for the lac repressor on path to its target. Similar conclusions have also been made for a growing number of other DNA-binding proteins based upon both in vitro bulk biochemical and single-molecule studies, which has led to the commonly held view that all target search processes will be accelerated by facilitated search mechanisms involving a substantial 1D component. However, the validity of this broad generalization has not yet been established, and while it is certainly the case that facilitated diffusion can contribute to in vitro target searches for many different types of proteins, as will be discussed below, it is not yet completely clear whether or how these mechanisms work in vivo.

4.2. RNA polymerase and the influence of protein concentration

Insights into facilitated diffusion derived from experimental and theoretical work with lac repressor also motivated numerous studies with RNA polymerase to determine if it too used facilitated diffusion to locate promoter sequences. Accordingly, a number of bulk biochemical studies suggested that E. coli RNA polymerase could move along DNA by 1D sliding over distances up to ~13 kilo-bases (kb) [69,70], and early single-molecule studies also ~reported that RNA polymerase could slide on DNA [71–73]. Most notably, Kabata et al. observed the first single-molecule evidence of RNAP sliding using fluorescently labeled E. coli RNA polymerase, and reported that RNA polymerase could slide several micrometers along DNA in the presence of buffer flow [71]. However, long-distance diffusion was not detected in a later study by Harada et al., where only 2.6% of the observed RNAP polymerase molecules exhibited 1D diffusion detectable above instrumental resolution limits [73]. Nevertheless, these authors concluded that the RNA polymerase used a 1D diffusion-based mechanism to search for promoters, with mean sliding distance (l_sl) of 300 base pairs [73]. Similarly, Guthold et al. used atomic force microscopy (AFM) to image RNA polymerase bound to non-specific DNA adsorbed onto a mica surface and also reported that RNA polymerase could slide on DNA [72]. Based on these studies it had been largely accepted that RNA polymerase searches for promoters using facilitated diffusion involving a 1D scanning mechanism. However, no promoter association rate has ever been reported that is higher than the limit that would be imposed by 3D diffusion, suggesting that search mechanisms overall can be accounted for by simple 3D collisions with no need to invoke facilitated diffusion [74].

To help resolve the mechanism of the promoter search, we used in vitro single-molecule imaging of DNA curtains [75,76] to visualize fluorescently tagged molecules of E. coli RNA polymerase as they searched for promoters (Figure 5) [77]. Using this approach we could directly visualize the promoter search processes in real-time, allowing us to identify key intermediates in the transcription initiation pathway [77]. However, these experiments revealed no evidence for 1D sliding or hopping at a microscopically detectable scale, suggesting that facilitated search mechanisms might not contribute to promoter association [77]. However, these observations could not rule out the possibility that facilitated search mechanisms were occurring over short sub-microscopic distances below optical resolution limits.

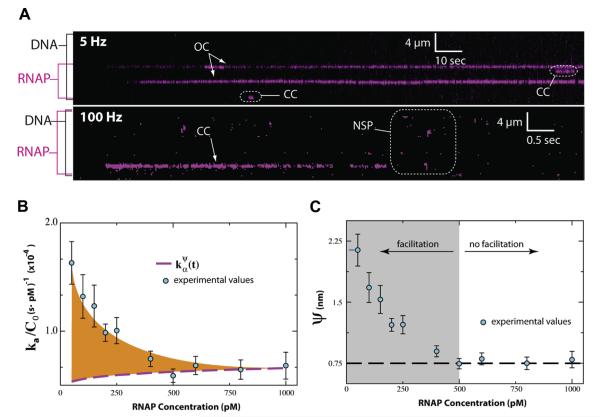
Figure 5.

Target search mechanism of RNA polymerase. (A) Kymograms of RNAP binding to λ-DNA showing kinetically distinct intermediates. DNA is unlabeled, and RNAP is magenta. NSP, CC, and OC, refer to non-specifically bound, closed complex, and open complex, respectively; note that CC could also represent another intermediate preceding the open complex. (B) Rate acceleration (k_a/C₀) versus RNAP concentration. The difference between the experimental values and ($\left(k_{\alpha }^{\left(\psi \right)}\right(t\left)\right)$) reflects facilitated diffusion, and the orange shaded region represents the maximum possible acceleration due 1D-sliding and/or hopping. (C) Effective target size (ψ) versus RNAP concentration. The dashed black line highlights the limiting value of ψ. Adapted with permission from reference [77].

We next investigated the promoter search at the sub-microscopic scale by experimentally measuring promoter association kinetics at varying protein concentrations to determine whether or not association rates exceeded expectations for 3D diffusion; the term ‘sub-microscopic’ is used to describe any events occurring below existing resolution limits. The flux of protein onto the promoters is the result of two components: (i) direct promoter binding in the absence of any search facilitation; and (ii) promoter binding after a facilitated search (i.e. hopping and/or sliding) [77]. To measure the magnitude of each of these fluxes, we built a custom flow-cell such that each term could be independently analytically solved. Importantly, because target association rates for any protein will become dominated by 3D diffusion as concentrations are increased [77], there is special significance on the rate of direct binding, which for our experimental system can be given as:

$$K_{\alpha }^{\psi }\left(t\right)=\frac{8}{\pi }\psi D_3{C}_0{\int }_0^{\infty }{e}^{-D_3{u}^{2}t}{\left[u\left(J_0^2\right(u\rho )+Y_0^2(u\rho \left)\right)\right]}^{-1}\mathit{du},$$

where C₀ is protein concentration, D₃ is the 3D diffusion coefficient of quantum-dot tagged RNA polymerase (QD-RNAP), ψ is the effective target size, ρ is the reaction radius, and J₀ and Y₀ are Bessel functions of the first and second kind, respectively. The effective target size ψ describes the size and orientation of the binding surface that transiently samples DNA during the promoter search, and can be recovered from the limiting value of the promoter associate rate obtained at high protein concentration [77]. Single-molecule experimental measurements of promoter association rates subsequently revealed that target search facilitation by either hopping or sliding provided a modest 3-fold enhancement in promoter association rates at 50 picomolar (pM) RNA polymerase, yielding an effective target size of just 2.23 nm (nm). However, evidence of promoter association rates exceeding the 3D diffusion limit were non-existent at protein concentrations above 500 pM, and corresponding calculations revealed that RNA polymerase would not recognize a promoter if it was more than 1.5-bp out of register upon initial binding [77].

These findings illustrate that sub-microscopic facilitated diffusion can in fact accelerate the promoter search by RNA polymerase, but that this acceleration is modest at best and only occurs at exceedingly low protein concentrations. Importantly, the in vivo concentration of RNA polymerase in bacteria (~2–3 μM) [78] vastly exceeds the concentration over which facilitated diffusion could beneficially accelerate the promoter search, arguing that facilitated diffusion mechanisms do not contribute to promoter targeting by E. coli RNA polymerase at physiologically relevant protein concentration regimes.

4.3. Lac repressor revisited

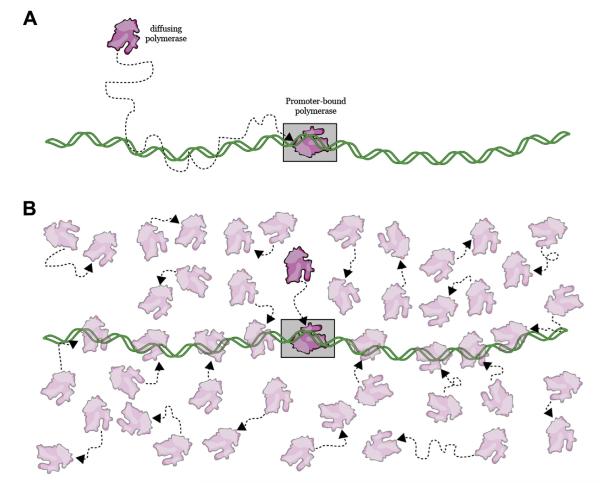
The mathematical formalism described above for analyzing the RNA polymerase promoter search problem also leads to a more general conclusion regarding target search mechanisms: the search process itself is strongly dependent upon protein concentration, and higher concentrations will always favor 3D search mechanisms over facilitated search mechanisms (Figure 6). This begs the question of whether a protein that is physically capable of diffusing in 1D along DNA would instead preferentially bind its target site through 3D diffusion if the concentration were raised. To address this issue, we visualized lac repressor as it searched for its operator over a range of protein concentrations in low ionic strength buffer that favored 1D sliding [77]; the use of low ionic strength conditions was essential to enhance non-specific DNA binding affinity, and interestingly we were unable to observe any search facilitation when the ionic strength was even moderately increased (S.R. unpublished observations). We then classified each successful search as having occurred through either facilitated diffusion or direct 3D binding, with the criteria being that a facilitated search was preceded by observable one-dimensional motion whereas a direct search lacked an observable 1D component (Figure 4). As expected, at the lowest concentration tested, many target binding events occurred through a facilitated search mechanism [77]. However, when the concentration of lac repressor was raised, there was a corresponding increase in the fraction of target binding events that occurred through 3D diffusion in the absence of any facilitation [77]. Importantly, even when the successful searches were dominated by 3D diffusion, other molecules of lac repressor still bound to and diffused along non-specific DNA; however, the searches being conducted by these other proteins had no chance for success once the lac operators was already bound by a protein that engaged it through 3D diffusion (Figure 4).

Figure 6.

Influence of protein concentration on target searches. (A) Facilitated diffusion will be favored at low protein concentrations because the initial encounter with the DNA will most often occur at non-specific sites. The protein can then diffuse along the DNA to its target site. (B) Higher protein concentrations favor 3D searches because the relative increase in protein abundance increases the probability of a direct collision with the target site. Facilitated diffusion related processes such as sliding/hopping can still occur at high protein concentrations, but those proteins undergoing such processes are less likely to reach the target site before those that collide directly with the target. An educational video illustrating these concepts can be found at: <http://www.youtube.com/watch?v=tIWv7rAe44M>.

These results highlight that the rate-accelerating effects of facilitated diffusion for proteins with short non-specific lifetimes can be easily overcome simply by increasing protein abundance, and also provide a cautionary note that must be taken into account when interpreting target search mechanisms. Namely, just because a protein is capable of hopping and/or sliding along DNA does not constitute proof that these processes will accelerate target binding because protein concentration can always dominate the overall search process. This work also highlights the need to reevaluate conclusions arising from past studies of target search mechanisms that may not have accounted for the influence of protein concentration.

4.4. What are the easiest means to ensure a rapid target search?

RNA polymerase and lac repressor must both find specific target sites among a vast excess of non-specific DNA, but they seem to have evolved different approaches to solve the search problem. This raises the questions of why they use different search mechanisms, and how generalizable is the concept of facilitated diffusion given that RNA polymerase seems to locate its target sites just fine in the absence of facilitation? One notable difference between lac repressor and RNA polymerase is the abundance of each protein in living cells: there are ~2000–3000 molecules of RNA polymerase in E. coli [78], and estimates suggest that ~20–50% of RNA polymerase may exist in the unbound state [55,78], whereas lac repressor is substantially less abundant, with fewer than 10 molecules present per cell [23,24]. RNA polymerase is highly abundant because it is necessary for all gene expression, whereas lac repressor is a non-essential protein that provides a growth advantage only in response to a very specific environmental condition that might be relatively rare outside of a laboratory setting. Interestingly, transcription factors (such as lac repressor) tend to be expressed at fairly low copy numbers, suggesting the possibility that this class of proteins may in fact frequently utilize facilitated search mechanisms involving a significant 1D component, whereas other DNA-binding proteins present in greater abundance may more prevalently utilize 3D searches; although we would add the cautionary note that this hypothesis is purely speculative. Nevertheless, one would predict that if the concentration of lac repressor (or any similar low copy number DNA-binding protein) were increased in vivo, then it too would be able to rapidly locate its target site with no need for facilitated diffusion.

Importantly, all possible routes of search facilitation involve interactions with non-specific DNA, and as indicated above site-specific binding cannot exist in the absence of non-specific binding. Therefore, any changes in a protein’s DNA binding surface will affect both specific and non-specific binding: mutations that increase target affinity will likely cause an increase in the affinity for non-specific DNA, whereas mutations that weaken non-specific interactions may also reduce target affinity. Thus there exists an intimate relationship between non-specific and specific DNA binding, and it seems likely that in most scenarios a mutation in the protein that increased affinity for specific targets might also increase the affinity for the non-specific DNA, and vice versa [79–82]. In contrast, changes in protein abundance can occur with no effect on the physical properties of the protein in question, thus cells may have the intrinsic ability to tune the speed of any target search process by controlling protein copy number. These considerations raise the interesting question of whether search facilitation has evolved to optimize target searches, or whether it is simply the unavoidable by-product of non-specific DNA binding activity.

5. Where do we go from here?

Until now, most single-molecule studies of protein–DNA interactions have utilized very simple single-component model systems, such as lac repressor, largely because these simple prokaryotic proteins are often amenable to experimental manipulation. In addition, with a few exceptions, most in vitro single-molecule work on the target searches of DNA-binding proteins have also focused on ‘frustrated’ searches, that is, searches that occur with DNA lacking a specific binding site for the protein of interest [26,46–52,83]. This focus on ‘frustrated’ searches has come about due to technical challenges inherent in engineering specific sites into the long DNA molecules that are amenable to single-molecule imaging. As a consequence, there remain many open questions with respect to actual target binding itself, such as whether proteins must repeatedly scan a target site before it is recognized as a specific target. Future observation of these search processes in the presence of DNA containing target and near-target sequences will aid in unraveling the subtleties of target recognition, which is likely the critical element of protein–DNA interaction kinetics. In addition, very few single-molecule studies of target search processes have addressed the role and importance of protein concentration on these reactions, which again arises in part from the technical difficulty inherent in this type of work. However, these challenges can be overcome in the relative short-term.

Another notable difficulty in interpreting the relationship between target searches and target recognition is the lack of structural information for non-specifically bound intermediates that are sampled during the search process. Crystal structures of nonspecific interactions remain exceptionally rare [84,85]. Even for existing structures there will always be the question of how well they reflect the transient non-specific states present during a target search because non-specifically bound protein–DNA complexes are highly dynamic, and it may not be reasonable to assume that they can be well-represented by a just one unique structural intermediate (Figure 2). This is an inherently challenging area of inquiry, however, newly developed NMR techniques offer great promise for probing the structural characteristics of transient search intermediates [86].

In the longer-term, the next generation of single-molecule experimentation on diffusion and target site searches must begin moving towards more physiologically relevant scenarios and should engage more complex biological problems. It will be critical to address how diffusion contributes to both initial target recognition as well as subsequent steps in the biological pathways, such as the assembly of multicomponent protein complexes at specific sites on DNA. Examples of protein–nucleic acid interactions that could benefit from such studies include: understanding how proteins assembly and function at origins of replication; studies of transcription that include both RNA polymerase and associated factors that promote promoter binding and/or other aspects of transcription initiation and RNA synthesis; and DNA repair reactions, which often involve the staged participation of multiple reaction components that encompass both initial DNA damage recognition and downstream repair steps. It will also be crucial to begin addressing what happens when these biological reactions occur within the context of chromatin and/or in the presence of other DNA binding proteins, in order to clarify how the 3D organization of the genome and molecular crowding affect these processes.

6. Summary

Diffusion is one of the most basic physical principles underlying the molecular basis of all of biology [87–89]. In recent years single-molecule imaging has played a key role in furthering our understanding of target searches because it enables direct visualization of the search process in real-time that before could only be inferred from ensemble measurements [67]. As such, the field has great potential for advancing our understanding of diffusion in biology. While this review has focused on the lac repressor and RNA polymerase as model systems for understanding how DNA-binding proteins search for specific targets through diffusion-based mechanisms, it is important to recognize that virtually all reactions involving biological macromolecules also require diffusion-based search processes. This includes processes related to nucleic acid metabolism, such as transcription, translation, DNA replication, and repair, and extends to any other processes involving bimolecular interactions (e.g. protein–protein interactions, enzymatic reactions requiring the binding of a substrate, 2D diffusion of molecules within cellular membranes, etc.). Nevertheless, the importance of diffusion in biological reactions is sometimes overlooked or ignored despite, or perhaps because of, its ubiquitous nature. However, in discussing lac repressor and RNA polymerase, one recognizes that even the simplest, most intensively studied systems still remain poorly understood, which can be most readily illustrated by considering that we still cannot rigorously interpret the physical meaning of the diffusion coefficients that are reported for these and other proteins that move along DNA. It is clear that the contributions of diffusion to biological reactions warrants further investigation, and that moving forward will require intensive interdisciplinary efforts, involving both biological experimentation and detailed theoretical analyses.

Biography

Sy Redding (right) received his BS in Physics from Texas State University in 2009, and entered the graduate program in Chemical Physics at Columbia University that same year. He is currently completing his PhD work using a combination of single-molecule imaging and theory to understand how proteins find targets in DNA.

Eric C. Greene (left) received his BS in Biochemistry from the University of Illinois, his PhD from Texas A&M University, and he conducted postdoctoral studies at the National Institute of Health. He joined the Department of Biochemistry and Molecular Biophysics at Columbia University in 2004 and was appointed as an Early Career Scientist with the Howard Hughes Medical Institute in 2009. Dr. Greene’s laboratory has developed novel technologies for studying protein–DNA interactions at the single-molecule level.