The partial independence of bioelectric and biomagnetic fields and its implications for encephalography and cardiography

Abstract

In this article, we clearly demonstrate that the electric potential and the magnetic field can contain different information about current sources in three-dimensional conducting media. Expressions for the magnetic fields of electric dipole and quadrupole current sources immersed in an infinite conducting medium are derived, and it is shown that two different point dipole distributions that are electrically equivalent have different magnetic fields. Although measurements of the electric potential are not sufficient to determine uniquely the characteristics of a quadrupolar source, the radial component of the magnetic field can supply the additional information needed to resolve these ambiguities and to determine uniquely the configuration of dipoles required to specify the electric quadrupoles. We demonstrate how the process can be extended to even higher order terms in an electrically silent series of magnetic multipoles. In the context of a spherical brain source model, it has been mathematically demonstrated that the part of the neuronal current generating the electric potential lives in the orthogonal complement of the part of the current generating the magnetic potential. This implies a mathematical relationship of complementarity between electroencephalography (EEG) and magnetoencephalography (MEG), although the theoretical result in question does not apply to the non-spherical case (Dassios (2008), Math Med Biol, vol. 25, p. 133). Our results have important practical applications in cases where electrically silent sources that generate measurable magnetic fields are of interest. Moreover, electrically silent, magnetically active moments of higher order can be useful when cancellation due to superposition of fields can occur, since this situation leads to a substantial reduction in the measurable amplitude of the signal. In this context, information derived from magnetic recordings of electrically silent, magnetically active multipoles can supplement electrical recordings for the purpose of studying the physiology of the brain. Magnetic fields of the electric multipole sources in a conducting medium surrounded by an insulating spherical shell are also presented and the relevance of this calculation to cardiographic and encephalographic experimentation is discussed.

I. INTRODUCTION

Increasing attention has been devoted in recent years to the theory of multipolar expansions of primary sources of bioelectric and biomagnetic activity [1, 10, 11]. Such expansions offer an improved parametric approach over simpler models and have the ability to adequately describe sources with significant spatial extent in the brain[16, 17, 23]. In magnetoencephalography (MEG) and electroencephalography (EEG), this can be essential for the realistic localization of cortical activity from inverse procedures [17, 22]. In magnetocardiography (MCG) and electrocardiography (ECG), quadrupolar sources are important for the magnetic field mapping of electrophysiological functions [20]. For example, the multipole model has been shown to be superior to the dipole modeling approach for the localization of ventricular preexcitation sites [30] and recently [29], an algebraic algorithm was developed for the reconstruction of dipole-quadrupole positions and moments based on boundary measurements of the electric potential, with potential applications to cardiography. Features of the magnetic field from stimulus and action currents in the isolated rabbit heart are not consistent with the simple current dipole model, because of the complicated electrical anisotropy of the tissue [3, 7, 14, 24]. The application of multipole modeling to magnetopneumography [8] has shown that multipolar expansions including dipolar, quadrupolar and octupolar moments are optimal for the characterization of magnetisable particle retention in the lung. In magnetogastrography, multipole models are important for the characterization of abnormal electrical activation patterns in the stomach due to gastroparesis and ischemia [15]. Several authors have addressed the information that is obtainable by inferring current dipole distributions from measurements of electric potential as opposed to measurement of the magnetic field of the heart or brain [18, 19, 35-37]. Two key advantages of multipolar modeling over dipolar models are that (1) multipole coefficients can be uniquely determined if they are used to model those source components that produce a non-vanishing field outside the volume conductor and (2) the multipolar approximation is mathematically close to the approximation of a few dipoles, but with the added benefit that the former can better describe extended sources [31]. It has been clearly established that fitting data from either electric or magnetic measurements to effective sources can lead to different source distributions. To illustrate these particular differences, we calculate the magnetic fields of current dipoles and quadrupoles and consider the fields from higher order sources. The magnetic fields of current sources in an infinite conducting medium are considered because the effects of inhomogeneities introduced by the bounding surfaces (the body surface) can be removed [36]. Corrections introduced by the presence of a spherical insulator enclosing the current sources are presented in the last section. Aside from the relevance such corrections have to MCG/ECG measurements, possible applications of these observations include MEG/EEG modeling.

The information content in measurements of electric potential versus that of magnetic field has been a controversy for some time. It is known that electric potential measurements do not supply information regarding magnetic dipole moments [16]. Proponents of the magnetic field method argue that unwanted secondary source contributions to the signal from conductivity inhomogeneities such as the skull-scalp interface distort the spatial frequency spectrum of the potential and increase the difficulty in obtaining an inverse image of the source current. On the other hand, electric potential advocates would say that the magnetic field detection is insensitive to dipolar sources oriented radially with respect to the external surface of the body. A corollary of that principle is the fact that magnetic field measurements are also insensitive to deep sources in approximately spherically shaped conductors since deep sources are necessarily more radial than shallow ones. In partial resolution of this controversy, many researchers believe that measurements of electric potential and magnetic field provide complementary information and both should be employed. The case we are presenting addresses this isssue.

Titomir and Kneppo [36] have discussed the differences in information content of electric and magnetic fields by examining a Helmholtz decomposition of the magnetic field. They note that the irrotational component of the magnetic field has the same radial component as the total field, and they present a spherical harmonic expansion of the radial field. We compare their expansion of B · r to our calculations of B to illustrate that the radial component contains the information needed to differentiate two quadrupole current distributions that are electrically equivalent but physically different. This may have important practical applications in cases where the existence of electrically silent sources that generate measurable magnetic fields has been shown to be possible. It has been demonstrated, for example, that the application of multipolar modeling within the framework of inverse algorithms can reveal important information regarding the activation of various cortex regions during the performance of auditive and visual tasks [13, 22, 27, 28].

II. SPHERICAL HARMONIC EXPANSION OF THE ELECTRIC POTENTIAL

The spherical harmonic expansion provides an elegant method for separating observation parameters from source paramenters in MEG [16]. We consider an impressed dipole current density J_i(r) that generates the current present in the medium. The total current density J(r) is the sum of the impressed current density and the Ohmic current

$$\mathbf{J}\left(\mathbf{r}\right)={\mathbf{J}}_i\left(r\right)+\sigma \mathbf{E}\left(r\right),$$ (1)

where σ is the conductivity of the medium. The quasistatic electric potential Φ(r) outside the region containing J(r) (to avoid confusion, V denotes a volume, not a potential) can be represented by the spherical harmonic expansion

$$\Phi \left(\mathbf{r}\right)=\frac{1}{4\pi \sigma }\underset{n=0}{\overset{\infty }{\Sigma }}\underset{m=0}{\overset{n}{\Sigma }}\frac{P_n^m}{r^{n+1}}(a_{nm}\cos m\theta +b_{nm}\sin m\theta ),$$ (2)

where a_nm and b_nm are the multipole moments of the dipole current density J_i(r) and the Legendre polynomials $P_n^m$ are functions of cosθ unless otherwise specified explicitly. They are expressed in terms of integration over J_i(r) in Table I.

TABLE I.

Spherical harmonic multipole moments in terms of dipole density J_i

Dipole

a10 = ∫ d3 r′ Jiz (r′)

a11 = ∫ d3 r′ Jix (r′)

a11 = ∫ d3 r′ Jiy (r′)

Quadrupole

a20 = ∫ d3 r′ [3z′ Jiz (r′) − r′ · Ji(r′)]

a21 = ∫ d3 r′ [x′ Jiz (r′) + z′ Jix(r′)]

b21 = ∫ d3 r′ [y′ Jiz (r′) + z′ Jiy(r′)]

2a22 = ∫ d3 r′ [x′ Jix (r′) − y′ Jiy(r′)]

2b22 = ∫ d3 r′ [x′ Jiy (r′) + y′ Jix(r′)]

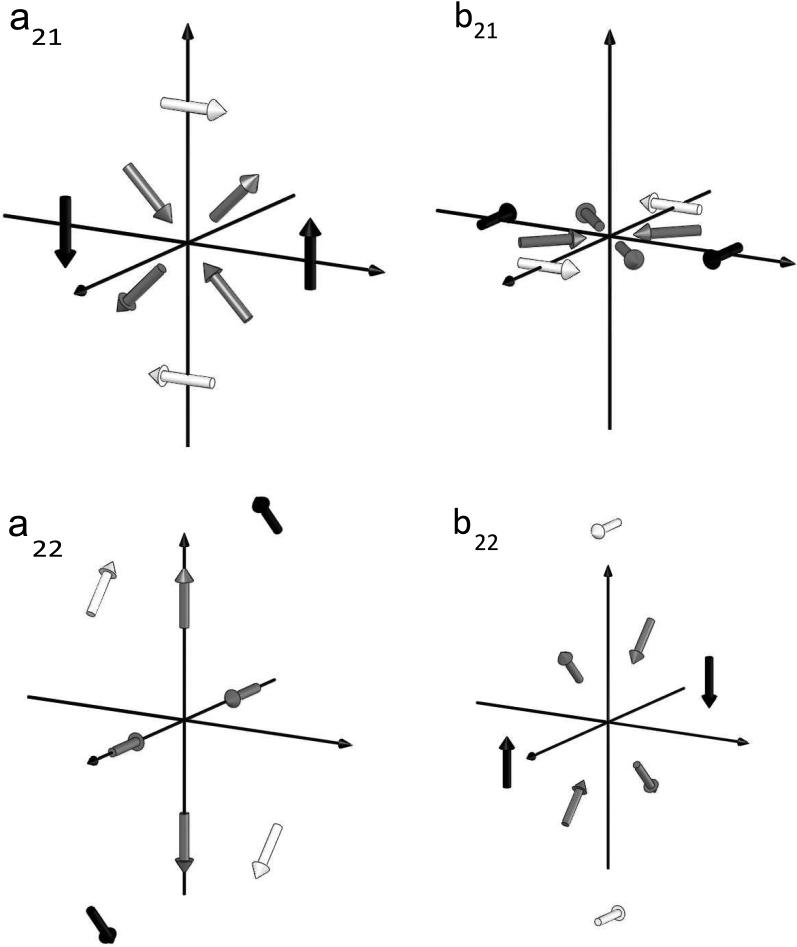
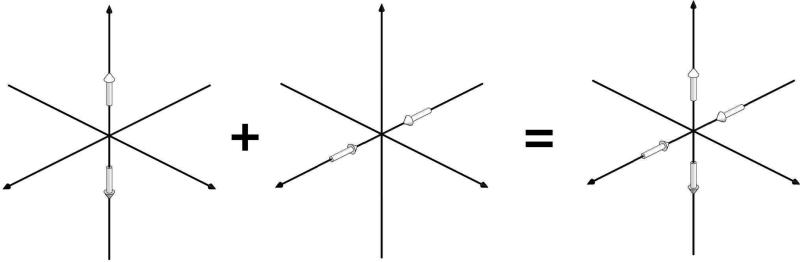
The electric multipoles can be understood as the limit of certain point dipole configurations, as the separation among these dipoles decreases while their strength increases proportionally. Pictures and tables of these configurations through the octupole moment are given in terms of point sources and sinks in [40]. The source-sink pairs can be replaced with dipoles that point from sink to source, shown in the figures of [40]. The representations are not unique, and Wikswo and Swinney [40] presented two configurations for each of the quadrupoles a₂₁, b₂₁, a₂₂ and b₂₂. These two and a third alternate configuration for each of these quadrupoles are shown in Fig. 1. The coordinate system used by Morse & Feshbach [26] (see the caption to FIG. 1) is also employed here to maintain consistency with our previous work [39, 40], which partly relies on [26]. In our figures, white arrows represent the first configuration of the multipole being depicted, black arrows represent the second one and gray arrows the third one. In the third representation, each of the quadrupoles, $a_{21}^3,b_{21}^3,a_{22}^3$ and $a_{22}^3$, is constructed from four radial dipoles, in contrast to the pair of tangential dipoles used in each of the first two representations. For example, Fig. 2 shows a₂₂ to be the combination of the axial quadrupoles c₂₀₂ and c₂₂₀; here we convert the source-sink pairs into dipoles before subtracting c₂₂₀ from c₂₀₂ to form $a_{22}^3$, and hence obtain two pairs of radial (axial) dipoles. In the same way, adding and subtracting c₂₀₀ from c₂₀₁ can be used with the appropriate pairing of sources and sinks to yield $a_{21}^3$. In this manner, we are exploiting degeneracies in the combination of the spherical harmonic (a_xx) and Taylor series (c_xxx) expansions of the potential to produce a third unique representation of the quadrupoles.

FIG. 1.

Three electrically equivalent dipole source representations for the four quadrupole terms a₂₁, b₂₁, a₂₂, b₂₂. Here and throughout, white arrows represent the first, black arrows the second and gray arrows the third configuration. Here and throughout, we use a right-handed coordinate system where the vertical axis is along x and where y and z point to the left and right, respectively (see text for explanation).

FIG. 2.

a₂₂ (third column) as the combination of the axial quadrupoles c₂₀₂ (first column) and c₂₂₀ (second column).

Since any quadrupole can be represented, with a suitable rotation, as a sum of the quadrupoles a₂₀ and a₂₂ [9], the three configurations in Fig. 1 for a₂₁, b₂₁, a₂₂ and b₂₂ are not unique, since any linear combination of representations for a particular quadrupole will also have all other moments zero. For example, the quadrupole

$$b_{22}^4=\frac{1}{2}(b_{22}^1+b_{22}^2)$$ (3)

has the same source-sink representation and hence the same electric field as the first three configurations. However, because the limits associated with converting sources and sinks into dipoles are taken in a different order for each configuration, each has a different dipole representation.

III. MAGNETIC FIELD CALCULATION

We now proceed to compute the magnetic field from the first three representations. It has been noted by several authors [18, 37, 40] that these representations can be added together to give a distribution which, in the limit, is electrically silent but magnetically active. The magnetic field B(r) of the current density given in Eq. 1 is calculated by the law of Biot and Savart

$$\mathbf{B}\left(\mathbf{r}\right)=\frac{1}{4\pi }{\int }_V{\mathbf{J}}_i\left({\mathbf{r}}^{\prime }\right)\times {\nabla }^{\prime }\frac{1}{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid }\mathrm{d}V,$$ (4)

where r is the field point and r^′ is the source point. Integration over the Ohmic component of J is zero because the medium is infinite, isotropic and homogeneous. We calculate the magnetic fields of the multipole moments represented in Fig. 1 by utilizing the Dirac delta functional expressions for J_i and taking the limit described earlier. The calculational details are more tractable if the Green function 1/|r − r′| is expanded in terms of the spherical harmonics

$$\frac{1}{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid }=\underset{n=0}{\overset{\infty }{\Sigma }}\underset{m=0}{\overset{n}{\Sigma }}(2-{\delta }_m^0)\frac{(n-m)!}{(n+m)!}\frac{{\left(r^{\prime }\right)}^n}{r^{n+1}}{P}_n^m\left(\cos {\theta }^{\prime }\right)P_n^m\left(\cos \theta \right)\cos \left[m(\varphi -{\varphi }^{\prime })\right],$$ (5)

where we have made use of the assumption that the field point r lies outside the region containing J_i. The gradient of Eq. 5 is

$$\begin{array}{cc}\hfill {\nabla }^{\prime }\frac{1}{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid }& =\widehat{\mathrm{x}}\left\{\frac{P_1^1\cos \varphi }{r^2}-\frac{P_2^0{x}^{\prime }}{r^3}+\frac{P_2^1{z}^{\prime }\cos \varphi }{r^3}+\frac{P_2^2}{2r^3}[x^{\prime }\cos \left(2\varphi \right)+y^{\prime }\cos \left(2\varphi \right)]\right\}\hfill \\ \hfill & +\widehat{\mathrm{y}}\left\{\frac{P_1^1\sin \varphi }{r^2}-\frac{P_2^0{y}^{\prime }}{r^3}+\frac{P_2^1{z}^{\prime }\sin \varphi }{r^3}+\frac{P_2^2}{2r^3}[-y^{\prime }\cos \left(2\varphi \right)+x^{\prime }\sin \left(2\varphi \right)]\right\}\hfill \\ \hfill & =\widehat{\mathrm{z}}\left\{\frac{P_1^0}{r^2}+\frac{2P_2^0}{r^3}{z}^{\prime }+\frac{P_2^1}{r^3}(x^{\prime }\cos \varphi +y^{\prime }\sin \varphi )\right\}\hfill \\ \hfill & {\nabla }^{\prime }\left\{\underset{n=3}{\overset{\infty }{\Sigma }}\underset{m=0}{\overset{\infty }{\Sigma }}(2-{\delta }_m^0)\frac{(n-m)!}{(n+m)!}\frac{r^{\prime n}}{r^{\prime n+1}}{P}_n^m\left(\cos \theta \right)P_n^m\left(\cos \theta \right)\cos \left[m(\varphi -{\varphi }^{\prime })\right]\right\},\hfill \end{array}$$ (6)

where the terms in the expansion for n = 0, 1 and 2 have been stated explicitly and the Legendre polynomials are functions of the cosine of θ. Eq. 6 is used with the delta functional expressions for the dipole and quadrupole sources. In the limit as dipole separation approaches zero with dipole strength increasing proportionally (the product of dipole separation and strength remains constant), all terms in Eq. 6 with n greater than 2 vanish. The magnetic fields calculated by this method are listed in Table II. Although are derivations are in spherical polar coordinates, we list the expressions for the magnetic fields in Table II in Cartesian coordinates. Tackling multipole expansion problems in the latter system is useful because the expressions for the dipolar and quadrupolar terms are elementary and because the translational invariance of the Cartesian system simplifies the construction of source models in MEG [16]. Comparison of Tables I and II shows that the magnetic fields reveal that the three different representations of the quadrupoles a₂₁, b₂₁, a₂₂ and b₂₂ are not the same.

TABLE II.

Magnetic fields of electric multipole moments immersed in an infinite medium of conductivity σ

Dipoles

$\mathbf{B}\left(a_{10}\right)=\frac{1}{4\pi }\frac{a_{10}}{r^3}(x\widehat{\mathbf{y}}-y\widehat{\mathbf{x}})$

$\mathbf{B}\left(a_{11}\right)=\frac{1}{4\pi }\frac{a_{11}}{r^3}(y\widehat{\mathbf{z}}-z\widehat{\mathbf{y}})$

$\mathbf{B}\left(b_{11}\right)=\frac{1}{4\pi }\frac{b_{11}}{r^3}(z\widehat{\mathbf{x}}-x\widehat{\mathbf{z}})$

Quadrupoles

$\mathbf{B}\left(a_{20}\right)=\frac{1}{4\pi }\frac{3a_{20}z}{2r^5}(x\widehat{\mathbf{y}}-y\widehat{\mathbf{x}})$

$\mathbf{B}\left(a_{21}^1\right)=\frac{1}{4\pi }\frac{a_{21}}{r^5}[-3xy\widehat{\mathbf{x}}+(3x^2-r^2)\widehat{\mathbf{y}}]$

$\mathbf{B}\left(a_{21}^2\right)=\frac{1}{4\pi }\frac{a_{21}}{r^5}[3yz\widehat{\mathbf{z}}-(3z^2-r^2)\widehat{\mathbf{y}}]$

$\mathbf{B}\left(a_{21}^3\right)=\frac{1}{4\pi }\frac{3a_{21}}{2r^5}[-xy\widehat{\mathbf{x}}+(x^2-z^2)\widehat{\mathbf{y}}+yz\widehat{\mathbf{z}}]$

$\mathbf{B}\left(b_{21}^1\right)=\frac{1}{4\pi }\frac{b_{21}}{r^5}[3xy\widehat{\mathbf{y}}-(3y^2-r^2)\widehat{\mathbf{x}}]$

$\mathbf{B}\left(b_{21}^2\right)=\frac{1}{4\pi }\frac{b_{21}}{r^5}[-3xz\widehat{\mathbf{z}}+(3z^2-r^2)\widehat{\mathbf{x}}]$

$\mathbf{B}\left(b_{21}^3\right)=\frac{1}{4\pi }\frac{3b_{21}}{r^5}[(z^2-y^2)\widehat{\mathbf{x}}+xy\widehat{\mathbf{y}}-xz\widehat{\mathbf{z}}]$

$\mathbf{B}\left(a_{22}^1\right)=\frac{1}{4\pi }\frac{a_{22}}{r^5}[(3{(x+y)}^2-2r^2)\widehat{\mathbf{z}}-3z(x+y)(\widehat{\mathbf{x}}+\widehat{\mathbf{y}})]$

$\mathbf{B}\left(a_{22}^2\right)=\frac{1}{4\pi }\frac{a_{22}}{r^5}[(2r^2-3{(x-y)}^2)\widehat{\mathbf{z}}+3z(x-y)(\widehat{\mathbf{x}}-\widehat{\mathbf{y}})]$

$\mathbf{B}\left(a_{22}^3\right)=\frac{1}{4\pi }\frac{3a_{22}}{r^5}[-yz\widehat{\mathbf{x}}-xz\widehat{\mathbf{y}}+2xy\widehat{\mathbf{z}}]$

$\mathbf{B}\left(b_{22}^1\right)=\frac{1}{4\pi }\frac{2b_{22}}{r^5}[3xz\widehat{\mathbf{x}}+(r^2-3x^2)\widehat{\mathbf{z}}]$

$\mathbf{B}\left(b_{22}^2\right)=\frac{1}{4\pi }\frac{2b_{22}}{r^5}[-(r^2-3y^2)\widehat{\mathbf{z}}-3yz\widehat{\mathbf{y}}]$

$\mathbf{B}\left(b_{22}^3\right)=\frac{3}{4\pi }\frac{b_{22}}{r^5}[zx\widehat{\mathbf{x}}-zx\widehat{\mathbf{y}}+(y^2-x^2)\widehat{\mathbf{z}}]$

The magnetic field of a localized impressed current source has been studied [35] by decomposing the total field into an irrotational component B⁽²⁾ and a component B⁽¹⁾ that results from the radial electric quadrupole so that

$$\mathbf{B}={\mathbf{B}}^{\left(1\right)}+{\mathbf{B}}^{\left(2\right)}.$$ (7)

In the reference frame where a₂₁, b₂₁ and b₂₂ are zero, the magnetic field is

$${\mathbf{B}}^{\left(1\right)}=\frac{1}{3}\mathbf{B}\left(a_{20}\right)+2\mathbf{B}\left(a_{22}^3\right).$$ (8)

The irrotational component B⁽²⁾ can be expressed as the gradient of a magnetic potential V_m, which in turn is represented by a spherical harmonic expansion

$${\Phi }_m=\frac{1}{4\pi }\underset{n=3}{\overset{\infty }{\Sigma }}\underset{m=0}{\overset{\infty }{\Sigma }}\frac{P_n^m}{r^{n+1}}[A_{nm}^M\cos \left(m\theta \right)+B_{nm}^M\sin \left(m\theta \right)]$$ (9)

Expressions for the magnetic moments are derived [35] by utilizing the condition that the radial component of B⁽²⁾ is also the radial component of B. There is only one non-zero magnetic dipole moment for each of the electric dipole representations of the electric quadrupoles. These are listed in Table III. Expressions in Table III are also the radial component of B derived by taking the vector dot product of r̂ with the fields of Table II.

TABLE III.

Radial component of magnetic field and magnetic dipole moments

Dipole
Br(a10) = 0
Br(a11) = 0
Br(b11) = 0
Quadrupoles	Non-zero magnetic moments
Br(a20) = 0	None
$B_r\left(a_{21}^1\right)=-\frac{a_{21}}{4\pi }\frac{y}{r^4}$	$B_{11}^m=a_{21}∕2$
$B_r\left(a_{21}^2\right)=-\frac{a_{21}}{4\pi }\frac{y}{r^4}$	$B_{11}^m=a_{21}∕2$
$B_r\left(a_{21}^3\right)=0$	None
$B_r\left(b_{21}^1\right)=-\frac{b_{21}}{4\pi }\frac{x}{r^4}$	$A_{11}^m=b_{21}∕2$
$B_r\left(b_{21}^2\right)=\frac{b_{21}}{4\pi }\frac{x}{r^4}$	$A_{11}^m=-b_{21}∕2$
$B_r\left(b_{21}^3\right)=0$	None
$B_r\left(a_{22}^1\right)=\frac{a_{22}}{4\pi }\frac{2z}{r^4}$	$A_{10}^m=a_{22}$
$B_r\left(a_{22}^2\right)=-\frac{a_{22}}{4\pi }\frac{2z}{r^4}$	$A_{10}^m=-a_{22}$
$B_r\left(a_{22}^3\right)=0$	none
$B_r\left(b_{22}^1\right)=\frac{b_{22}}{4\pi }\frac{2z}{r^4}$	$A_{10}^m=b_{22}$
$B_r\left(b_{22}^2\right)=-\frac{b_{22}}{4\pi }\frac{2z}{r^4}$	$A_{10}^m=b_{22}$
$B_r\left(b_{22}^3\right)=0$	None

IV. DETERMINATION OF THE CURRENT DIPOLE CONFIGURATION

Each electric dipole representation of a particular electric quadrupole has at most one non-zero magnetic dipole moment. It is the radially directed current dipoles with no radial magnetic field and no magnetic dipole moment from which Titomir and Kneppo [35] constructed B. Furthermore, the other two representations for each quadrupole have the same non-zero magnetic dipole moment with equal magnitude but opposite signs. For example, the configuration $a_{22}^1$ has magnetic moments $A_{11}^M$ and $B_{11}^M$ zero and $A_{10}^M$ equal to a₂₂. Configuration $a_{22}^2$ has $A_{10}^M$ equal to −a₂₂ and $A_{11}^M$ and $B_{11}^M$ are zero. Thus, if it is known that a quadrupole source has a non-zero a₂₂ moment, the magnetic moments (or radial components of the magnetic field) are required to discern the simplest dipole configuration which is representative of the source. This determination is not unique since the magnetic dipole moments are either zero or oppositely directed. For example, assume that we have a source, $a_{22}^4$, constructed by the linear combination of $a_{22}^1$ and $a_{22}^2$

$$a_{22}^4=\frac{1}{2}(a_{22}^1+a_{22}^2).$$ (10)

Then, $a_{22}^4$ has only the moment a₂₂ as non-zero and zero magnetic dipole moment. In the limit described earlier all other electric and magnetic moments are zero. However, $a_{22}^4$ is not the simplest dipole configuration with these properties. $a_{22}^3$ has the same electric and magnetic moments and is simpler. To discern such linear combinations of sources (i.e., when separations are not zero) the higher-order moments must be determined.

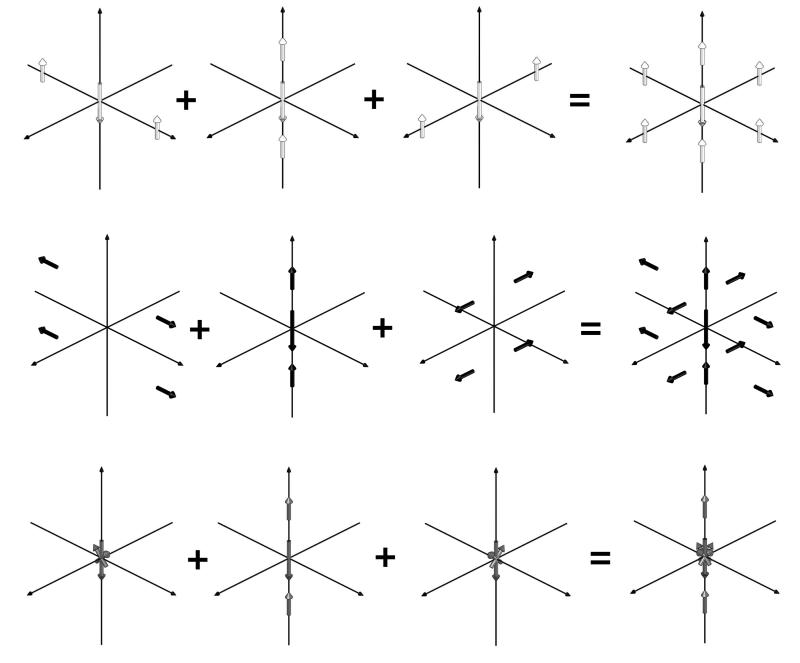
To replace two current dipole sources with a magnetic dipole source, the magnetic dipole is placed centrally between the current dipoles and oriented perpendicular to the plane containing the current dipole vector. Its direction is determined by treating the two current dipoles as a current loop and applying the right-hand rule. This example illustrates how the current dipole configurations are related to the magnetic dipole moment. This procedure can be applied to examine higher-order terms in what is an infinite series of electrically silent multipoles. For example, in Table V, three equivalent representations for an electrically silent, magnetically active octupole are presented. These representations can be obtained from superpositions of quadrupoles, in a manner analogous to that in Table IV, where the quadrupoles themselves were constructed using dipole representations (as shown in Fig. 1). Three equivalent representations for an electrically silent, magnetically active octupole based upon the three quadrupole terms in Table V are shown in FIG. 3.

TABLE V.

Coordinates of the dipole representations of quadrupoles for the three octupolar configurations in Fig. 3, where f ≡ a/2^1/3 and g ≡ a/(2 · 6^1/3). The strength is given in units of p.

			Dipole location coordinates			Dipole direction cosines
Moment	Strength	X	Y	Z	X	Y	Z
Configuration 1
c 301	+1	0	0	−f	+1	0	0
	+2	0	0	0	−1	0	0
	+1	0	0	+f	+1	0	0
c 303	+1	+2g	0	0	+1	0	0
	+2	0	0	0	−1	0	0
	+1	−2g	0	0	+1	0	0
c 321	+1	0	+f	0	+1	0	0
	+2	0	0	0	−1	0	0
	+1	0	−f	0	+1	0	0
Configuration 2
c 301	+1	+f/2	0	−f	0	0	−1
	+1	−f/2	0	−f	0	0	−1
	+1	+f/2	0	+f	0	0	+1
	+1	−f/2	0	+f	0	0	+1
c 303	+1	+2g	0	0	+1	0	0
	+2	0	0	0	−1	0	0
	+1	−2g	0	0	+1	0	0
c 321	+1	+f/2	+f/2	0	0	+1	0
	+1	−f/2	+f/2	0	0	+1	0
	+1	+f/2	−f/2	0	0	−1	0
	+1	−f/2	−f/2	0	0	−1	0
Configuration 3
c 301	+1	0	0	0	$+1∕\sqrt{2}$	0	$+1∕\sqrt{2}$
	+2	0	0	0	−1	0	0
	+1	0	0	0	$+1∕\sqrt{2}$	0	$-1∕\sqrt{2}$
c 303	+1	+2g	0	0	+1	0	0
	+2	0	0	0	−1	0	0
	+1	−2g	0	0	+1	0	0
c 321	+1	0	0	0	$+1∕\sqrt{2}$	$+1∕\sqrt{2}$	0
	+2	0	0	0	−1	0	0
	+1	0	0	0	$+1∕\sqrt{2}$	$-1∕\sqrt{2}$	0

TABLE IV.

Coordinates of the dipoles for the three configurations in Fig. 1, where $\mathrm{b}\equiv \mathrm{a}∕\sqrt{2}$ and $\mathrm{c}\equiv \mathrm{a}∕\left(2\sqrt{2}\right)$. The strength is given in units of p.

			Location coordinates			Direction cosines
Moment	Strength	X	Y	Z	X	Y	Z
Configuration 1
a 21	+1	−a/2	0	0	0	0	−1
	+1	+a/2	0	0	0	0	+1
b 21	+1	0	−a/2	0	0	0	−1
	+1	0	+a/2	0	0	0	+1
a 22	+1	−b	−b	0	$-1∕\sqrt{2}$	$+1∕\sqrt{2}$	0
	+1	+b	+b	0	$+1∕\sqrt{2}$	$-1∕\sqrt{2}$	0
b 22	+1	−a	0	0	0	−1	0
	+1	+a	0	0	0	+1	0
Configuration 2
a 21	+1	0	0	−a/2	−1	0	0
	+1	0	0	+a/2	+1	0	0
b 21	+1	0	0	−a/2	0	−1	0
	+1	0	0	+a/2	0	+1	0
a 22	+1	+b	−b	0	$+1∕\sqrt{2}$	$+1∕\sqrt{2}$	0
	+1	−b	+b	0	$-1∕\sqrt{2}$	$-1∕\sqrt{2}$	0
b 22	+1	0	−a	0	−1	0	0
	+1	0	+a	0	+1	0	0
Configuration 3
a 21	+1	+c/2	0	+c/2	$+1∕\sqrt{2}$	0	$+1∕\sqrt{2}$
	+1	−c/2	0	−c/2	$-1∕\sqrt{2}$	0	$-1∕\sqrt{2}$
	+1	+c/2	0	−c/2	$-1∕\sqrt{2}$	0	$+1∕\sqrt{2}$
	+1	−c/2	0	+c/2	$+1∕\sqrt{2}$	0	$-1∕\sqrt{2}$
b 21	+1	0	+c/2	+c/2	0	$+1∕\sqrt{2}$	$+1∕\sqrt{2}$
	+1	0	−c/2	−c/2	0	$-1∕\sqrt{2}$	$-1∕\sqrt{2}$
	+1	0	+c/2	−c/2	0	$-1∕\sqrt{2}$	$+1∕\sqrt{2}$
	+1	0	−c/2	+c/2	0	$+1∕\sqrt{2}$	$-1∕\sqrt{2}$
a 22	+1	+a/2	0	0	+1	0	0
	+1	−a/2	0	0	−1	0	0
	+1	0	−a/2	0	0	+1	0
	+1	0	+a/2	0	0	−1	0
b 22	+1	+c	+c	0	$+1∕\sqrt{2}$	$+1∕\sqrt{2}$	0
	+1	−c	−c	0	$-1∕\sqrt{2}$	$-1∕\sqrt{2}$	0
	+1	+c	−c	0	$-1∕\sqrt{2}$	$+1∕\sqrt{2}$	0
	+1	−c	+c	0	$+1∕\sqrt{2}$	$-1∕\sqrt{2}$	0

FIG. 3.

Three equivalent representations for an electrically silent, magnetically active octupole based upon the three quadrupole terms in Table V. The first configuration is in the first row, etc.

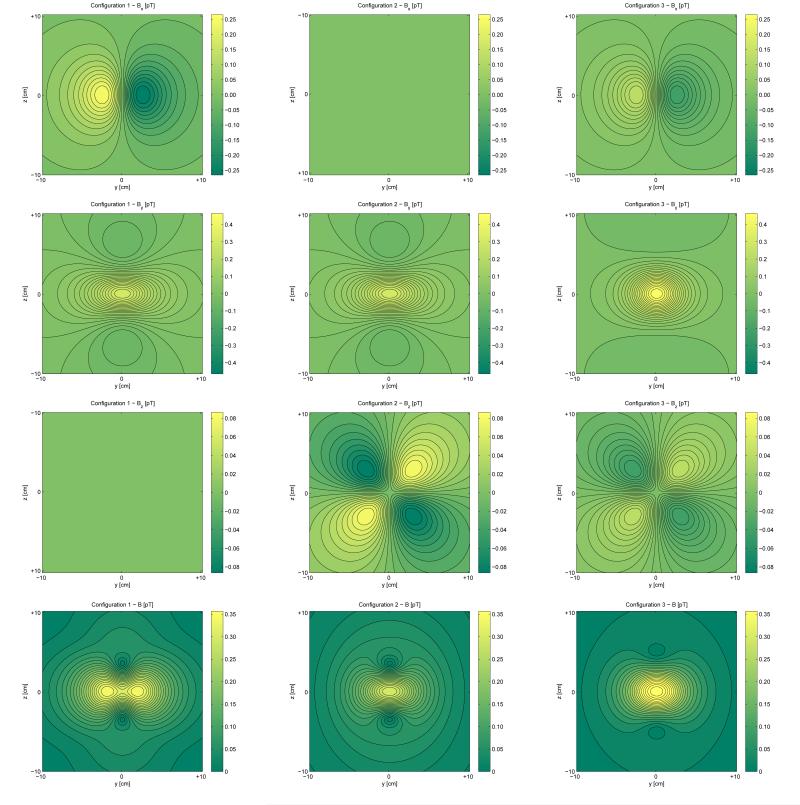
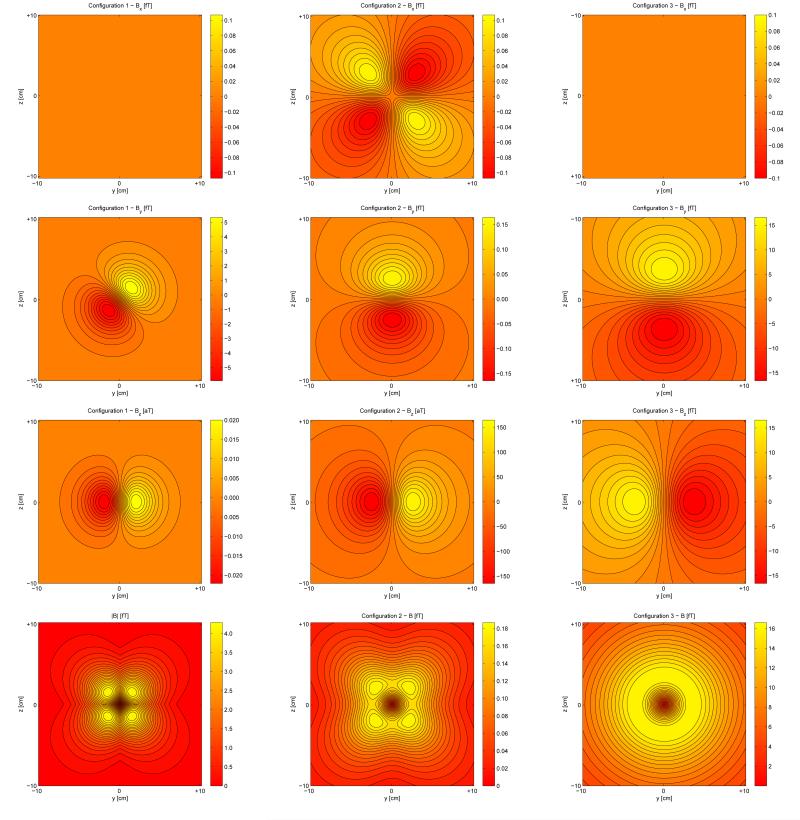
In FIG. 4, we depict the fields for three configurations of the electrically silent, magnetically active quadrupole a₂₁ shown in FIG. 1. Similarly, FIG. 5 shows the field components and magnitudes for the three octupolar configurations in FIG. 3. For convenience, we associate a distinct color scheme with the fields for the three types of multipoles (magenta to yellow for dipoles, green to yellow for quadrupoles and red to yellow for octupoles). The physical parameters selected to illustrate the fields were chosen to reflect a typical physiological measurement and are in good agreement with those selected in [31]. A source-to-sensor distance of 5 cm was chosen for calculating the fields (this distance is typical of field recordings from the brain or heart in MEG or MCG, respectively). Similarly, the current dipole strength (1 µA · m) and magnetic field magnitude are both physiologically plausible. Our illustrations qualitatively agree with other visual representations of multipolar patterns in other studies (see, for example, [16, 31, 32]), with the notable difference that our investigation deals with sources that are electrically silent. What is clear from our figures is that the three configurations produce distinct magnetic field patterns. In [31], Nolte & Curio show the magnetic field patterns of quadrupoles and octupoles due to electrically active sources located either in a sphere or in a homogeneous half-space. Our depictions in FIG. 5 (and especially that of configuration 3 in that figure) obviate a fact that has been pointed out by these two authors, namely that the octupole field might be difficult to detect experimentally because it shares structural features with the dipole field (this is particularly apparent upon comparison of configuration 3 in FIG. 5 to the dipolar pattern in the first row of FIG. 6). From a practical standpoint, the measurement of octupolar or higher-order terms is somewhat problematic in general because, although many SQUID systems for MEG/MCG research have the ability to measure even aT fields, their typical noise level of 𝒪(fT·Hz^1/2) raises SNR-related complications which are difficult to overcome. Nevertheless, the confirmed prediction that the magnetic field of a realistic electric octupole is of 𝒪(fT) [31], coupled with recent progress in SQUID technology [13] and with the fact that peak-to-peak noise levels of the same order are attainable in certain MEG experiments [5] are encouraging.

FIG. 4.

(Color online). Two-dimensional plots of the magnetic field components (B_x, B_y and B_z) and magnitude (|B|) due to the three alterative configurations of the electrically silent quadrupole a₂₁ in FIG. 1. The field components and magnitude for $a_{21}^1$ are in the first column (configuration 1 - white arrows in FIG. 1), those for $a_{21}^2$ are in the second column (configuration 2 - black arrows in FIG. 1), and those for $a_{21}^3$ are in the third column (configuration 3 - gray arrows in FIG. 1). Colormap scaling is symmetric for each plot in the sense that the minimum and maximum in each colormap have the same absolute value. Moreover, the colormap scaling is identical for each field component as well as field magnitude so that differences in amplitude between configurations can be more easily visualized. The origin of the coordinate system is located at (0, 0, 0) cm and the horizontal surface for which data are drawn is located at a height of x = 5 cm above the y − z plane. The unit of dipole strength q is equal to 1 μA · m. For configuration 1, because the resultant dipole vectors from which the multipoles are composed are directed along ẑ, the quantity B_z is identically equal to zero in the horizontal plane, though it is depicted for completeness. An analogous situation occurs in the case of the second configuration. For the third configuration, however, the constitutive dipoles (shown in gray in FIG. 1) are not aligned along any of the coordinate system axes, hence the analogy does not hold in this last case. The abbreviations used are pT (picoTesla = 10⁻¹² T), fT (femtoTesla = 10⁻¹⁵ T) and aT (attoTesla = 10⁻¹⁸ T).

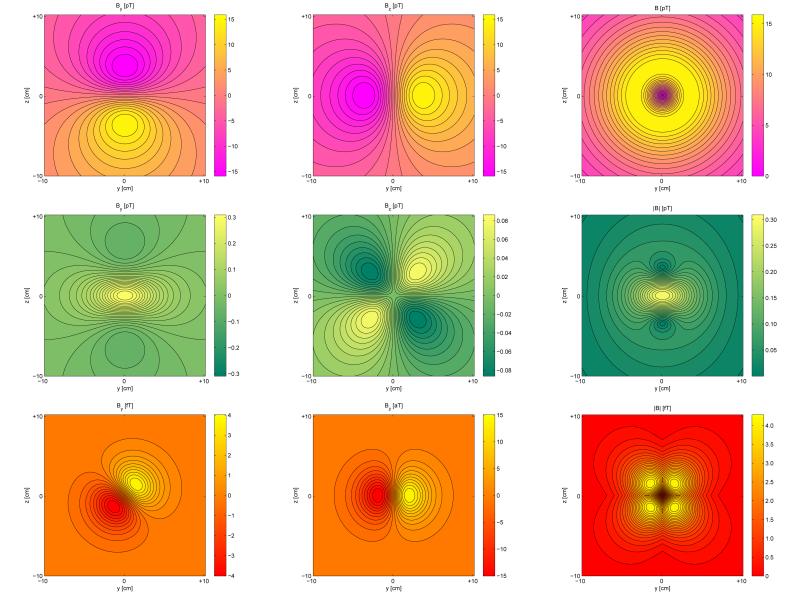
FIG. 5.

(Color online). Visual depictions of the magnetic field components and magnitude due to the three alterative configurations of the electrically silent octupoles in FIG. 3. As in FIG. 4, the field components and magnitudes for the first configuration (white arrows in FIG. 3) are in the first column, etc. One difference here is that, as opposed to FIG. 4, colormap limits are different for each plot due to the large field amplitude differences between plots.

FIG. 6.

(Color online). Comparison of the magnetic field components (B_y and B_z) and magnitude (|B|) due to an electrically active current dipole located at the origin and oriented along x̂ (first row), an electrically silent quadrupole ($a_{21}^2$, second row, see FIG. 1) and an electrically silent octupole (first configuration in FIG. 3, third row here). The physical parameters used are the same as in FIG. 4. Because the resultant dipole vectors from which the multipoles are composed are directed along x̂, the quantity B_x is identically equal to zero in the horizontal plane depicted and hence it is not displayed.

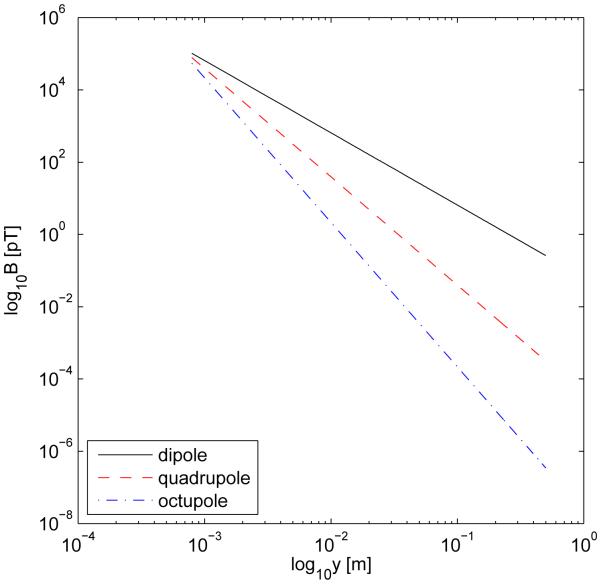
In FIG. 6, we compare examples of the magnetic fields due to three configurations: (1) an electrically-active current dipole oriented along the x axis, (2) the electrically-silent quadrupole $a_{21}^2$ (see FIG. 1) and (3) the electrically-silent octupole in the first configuration of FIG. 3. In the first row of FIG. 6, the field components and magnitude for a current dipole are shown. Since the current is along x and ∇ · B = 0, B_x vanishes. Both B_y, B_z and the magnitude B = |B| have values of the order of pT, which are realistic for physiological measurements. The second row of the figure displays the same quantities as in the first row, though this time for the electrically-silent quadrupole $a_{21}^2$, which is illustrated using black arrows in the top left plot of FIG. 1. Inspection of the equation for the magnetic field associated with this quadrupole (see Table II) and its visual representation in FIG. 1 both reveal that |B_y| is largest in the immediate vicinity of the dipoles from which the quadrupole representation is constructed. Comparison of the colorbars for B_y and B_z shows that B_y has a larger magnitude than B_z (as also predicted by the equation of the field for our problem of choice). Thus the plot for the magnitude of the quadrupolar field (second row, third column) essentially displays very similar information to that in the plot of B_y, with the appropriate difference that the absolute value of the field is shown. Perhaps the most interesting set of plots are associated with the octupolar field (third row). There, the line bisector for the minima and maxima of B_y is oriented at a 45-degree clockwise angle with respect to the y axis. From visual inspection of the figure, one would thus expect two of the maxima in the plot for |B| to occur at the locations of the two extreme values in the B_y plot, and this prediction is indeed confirmed (see plot of |B| in the third row, third column). The plot for the B_z component of the octupolar field is qualitatively similar to the corresponding one for the dipole configuration (top row, second column), which is not a surprise considering the underlying spherical harmonic formalism of the problem. What is at first sight curious about the octupolar field, however, is the fact that no maxima appear in the plot for |B| at the same points where extremas occur in the plot for B_z. This discrepancy can be explained by the fact that |B_y| in this case is about six orders of magnitude stronger than |B_z| (see axis units), which makes the latter’s contribution to |B| negligible. Thus, in the octupolar case again, the magnitude of the field is determined primarily by that of B_y for the particular parameters chosen for our illustration and it is possible that this is also the case for other higher-order terms in the expansion. For the dipole configuration, B_y and B_z have comparable magnitudes. In the case of the quadrupole, however, the absolute values of the extremas of B_y in the plane depicted are two orders of magnitude larger than those of B_z, while for the octupole the corresponding difference is of 𝜪(10⁶). From the formulas for B(a₁₁) and $\mathbf{B}\left(a_{21}^2\right)$ in Table II, it can be inferred that the reason for this behavior is that B_y and B_z have the same falloff rate (i.e. 1/r³), whereas for the octupole B_y ∝ 1/r³ and B_z ∝ 1/r⁵, and so on for terms of higher order. Finally, in FIG. 7, the falloff of the fields in FIG. 6 is shown as a function of distance from the source; this last figure summarizes some of the quantitative information in FIG. 6 and additionally provides the magnitude profile of the field as a function of source-to-sensor separation.

FIG. 7.

(Color online). Log-log plot for the fall-off of the dipolar, quadrupolar and octupolar magnetic fields displayed in FIG. 6 as a function of distance. The data shown are for a line segment along the x axis in the distance range 5 ≤ x ≤ 500 cm.

Electrically silent, magnetically active moments of higher order can be of interest when cancellation due to superposition of currents and/or fields can occur, since this situation leads to a substantial reduction in the measurable amplitude of the signal. In the context of a brain source model, for example, it has been rigorously demonstrated [6] that the part of the neuronal current generating the electric potential lives in the orthogonal complement of the part of the current generating the magnetic potential, which implies a clearly defined relationship of complementarity between EEG and MEG. In this context, information derived from magnetic recordings of electrically silent, magnetically active multipoles can supplement electrical recordings for the purpose of studying the physiology of the brain [12, 21]. In this respect, Jerbi et al. [16] showed that multipole expansion methods can accurately describe sources with significant spatial extent and arbitrary activation patterns and that multipole methods can be superior to equivalent current dipole models in providing source representations of extended regions of activity.

The set of physiological cases where electrically silent current multipoles may produce experimentally detectable magnetic fields is not restricted to the context of neurophysiology. For example, transverse tubules in skeletal muscle fibers, muscular tissue at the apex of the heart and helicoidal smooth muscle layers in the intestine are three distinct systems where it may be possible to measure magnetic fields in the absence of a recordable electric potential. The two essential characteristics shared by all these systems is that they have a helix-like anatomic structure and a spiral-like conductivity profile. In such conditions [33, 34], an impressed current can be written as a multipole expansion in which the antisymmetric part of the current multipole tensor can produce electrically silent magnetic fields.

V. MAGNETIC FIELDS OUTSIDE AN INSULATED SPHERE

Some authors [4, 25] have studied the electric activity of the heart by measuring the electric potential on the surface of a hollow spherical tank containing a beating animal heart immersed in a saline solution. Physical models of discrete dipole densities have been used to calibrate such tanks and the potential measurements on the tank surface are then used to infer the dipole current distribution model for the heart. It is possible to use these models to verify the multipolar calculations presented thus far if (1) magnetic field measurements are made outside the tank, and (2) the inhomogeneity introduced by the insulated sphere is taken into account before applying Table II. For this reason, we present the derivation of the corrections to Table II when the conducting medium is constrained to lie within an insulating spherical shell and the magnetic field measurement is made outside the sphere. The magnetic field can be calculated using the law of Biot and Savart

$$\begin{array}{cc}\hfill \mathbf{B}\left(r\right)& =\frac{1}{4\pi }{\int }_V{\mathbf{J}}_i\left({\mathbf{r}}^{\prime }\right)\times {\nabla }^{\prime }\frac{1}{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid }\mathrm{d}V\hfill \\ \hfill & -\frac{1}{4\pi }{\int }_S\widehat{\mathbf{n}}\times \frac{{\nabla }^{\prime }V\left({\mathbf{r}}^{\prime }\right)}{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid }\mathrm{d}{S}^{\prime }.\hfill \end{array}$$ (11)

The first term is the magnetic field if the conducting medium is infinite while the second one, involving an integration over the surface of the heart tank, is the correction that must be added to the infinite medium field, B_∞(r). We term this the spherical tank correction, and denote it by B_s(r)

$$\mathbf{B}\left(\mathbf{r}\right)={\mathbf{B}}_{\infty }\left(\mathbf{r}\right)+{\mathbf{B}}_s\left(\mathbf{r}\right).$$ (12)

The potential on the surface of the tank, expressed as a spherical harmonic expansion, is

$$\Phi \left(\mathbf{r}\right)=\frac{1}{4\pi \sigma }\underset{\stackrel{n=3}{m=0}}{\overset{\infty }{\Sigma }}\frac{2n+1}{n{R}^{n+1}}{P}_n^m(a_{nm}\cos m\varphi +b_{nm}\sin m\varphi )$$ (13)

where R is a vector from the origin at the center of the tank to the tank surface and a_nm and b_nm are as in Eq. 2. The spherical tank correction for a particular multipole a_nm or b_nm is calculated by assuming that all other moments are zero and using the potential from Eq. 13 to perform the integration in Eq. 12. The spherical tank correction calculated in this manner is

$$\mathbf{B}\left(\mathbf{r}\right)=\frac{1}{4\pi }\frac{a_{n0}}{r^2}{P}_1^1(\widehat{\mathrm{x}}\sin \theta -\widehat{\mathrm{y}}\cos \theta )$$ (14)

for m = 0 and

$$\mathbf{B}\left(\mathbf{r}\right)=\left(\begin{array}{c}\hfill a_{nm}\hfill \\ \hfill b_{nm}\hfill \end{array}\right)\frac{{\mathbf{A}}_{+}+[n(n+1)-m(m-1)]{\mathbf{A}}_{-}}{8\pi n{r}^{n+1}}$$ (15)

for m ≠ 0, where

$${\mathbf{A}}_{\pm }=P_n^{m\pm 1}\left(\begin{array}{c}\hfill +\widehat{\mathbf{x}}\sin (m\pm 1)\theta \mp \widehat{\mathbf{y}}\cos (m\pm 1)\theta \hfill \\ \hfill -\widehat{\mathbf{x}}\cos (m\pm 1)\theta \mp \widehat{\mathbf{y}}\sin (m\pm 1)\theta \hfill \end{array}\right).$$ (16)

The explicit expression for the dipoles (n = 1) and quadrupoles (n=2) is listed in Table VI. We point out that, since B_s(r) is a result of the potential on the surface of the sphere, the corrections for the two different representations of a₂₁, b₂₁, a₂₂ and b₂₂ are the same. This implies that the introduction of an inhomogeneity into the medium does not alter the ambiguity in determining the current distribution of an electrically silent multipole from measurements of potentials. This statement is supported by the work of Amir [2], who showed that two spatially distinct generators cannot create the same scalp potential map. In our situation, the locations of the sources and sinks composing the multipole configurations are identical (and hence their potential maps are identical, in agreement with Amir’s statement), which again justifies the fact that the corrections to the magnetic field for the quadrupoles named above are the same. However, as shown by our present work, the fact that the locations of the sources and sinks in question are identical does not exclude the possibility for spatially distinct current distributions due to identical configurations of sources and sinks to exist (as in the quadrupole and octupole cases discussed and visualized in the present article). In [2], such currents (which make the subject of our work) are described first as sources which share common points and then as “equivalent generators”. Furthermore, in Section III of [2], it is shown that “two [such] different but overlapping distributions create the same scalp potential”, a statement for which mathematical proof is provided by the author. In conclusion, Amir’s work (which does not address magnetic fields) fully justifies our previous statement regarding the ambiguity of determining the current distribution of such equivalent generators based solely on measurement of potentials. In conclusion, the essence of our argument can be most clearly captured in the context of [2], namely that distinct current distributions due to identical configurations of source-sink pairs can produce different magnetic fields, though not different electric potentials at the enclosing surface.

TABLE VI.

Spherical tank corrections to magnetic field of electric multipoles

Dipole

$B_s\left(a_{10}\right)=\frac{1}{4\pi }\frac{a_{10}}{2r^3}(y\widehat{\mathbf{x}}-x\widehat{\mathbf{y}})$

$B_s\left(a_{11}\right)=\frac{1}{4\pi }\frac{a_{11}}{2r^3}(-y\widehat{\mathbf{z}})$

$B_s\left(b_{11}\right)=\frac{1}{4\pi }\frac{b_{11}}{2r^3}\left(x\widehat{\mathbf{z}}\right)$

Quadrupoles

$B_s\left(a_{20}\right)=\frac{1}{4\pi }\frac{3a_{20}}{4r^5}z(y\widehat{\mathbf{x}}-x\widehat{\mathbf{y}})$

$B_s\left(a_{21}\right)=\frac{1}{4\pi }\frac{3a_{21}}{4r^5}[xy\widehat{\mathbf{x}}+(z^2-x^2)\widehat{\mathbf{y}})-yz\widehat{\mathbf{z}}]$

$B_s\left(b_{21}\right)=\frac{1}{4\pi }\frac{3b_{21}}{4r^5}[-(z^2-y^2)\widehat{\mathbf{x}}-xy\widehat{\mathbf{y}}+xz\widehat{\mathbf{z}}]$

$B_s\left(a_{22}\right)=\frac{1}{4\pi }\frac{3a_{22}}{2r^5}[yz\widehat{\mathbf{x}}+xz\widehat{\mathbf{y}}-2xy\widehat{\mathbf{z}}]$

$B_s\left(b_{22}\right)=\frac{1}{4\pi }\frac{3b_{22}}{2r^5}[-xz\widehat{\mathbf{x}}+yz\widehat{\mathbf{y}}+(x^2-y^2)\widehat{\mathbf{z}}]$

VI. SUMMARY

We have derived equations for the magnetic field of the electric multipole moments and demonstrated that measurements of the electric potential and the radial component of the magnetic field are sufficent to determine uniquely the configuration of dipoles required to specify the electric quadrupoles. We demonstrate how this can be extended to even higher order terms in an electrically silent series of magnetic multipoles. This is a clear demonstration that the electric potential and the magnetic field can contain different information about current sources in three-dimensional conducting media. In addition, we have provided equations useful when measuring magnetic fields outside of an insulated spherical tank.