Positive and Negative Design for Nonconsensus Protein-DNA Binding Affinity in the Vicinity of Functional Binding Sites

Abstract

Recent experiments provide an unprecedented view of protein-DNA binding in yeast and human genomes at single-nucleotide resolution. These measurements, performed over large cell populations, show quite generally that sequence-specific transcription regulators with well-defined protein-DNA consensus motifs bind only a fraction among all consensus motifs present in the genome. Alternatively, proteins in vivo often bind DNA regions lacking known consensus sequences. The rules determining whether a consensus motif is functional remain incompletely understood. Here we predict that genomic background surrounding specific protein-DNA binding motifs statistically modulates the binding of sequence-specific transcription regulators to these motifs. In particular, we show that nonconsensus protein-DNA binding in yeast is statistically enhanced, on average, around functional Reb1 motifs that are bound as compared to nonfunctional Reb1 motifs that are unbound. The landscape of nonconsensus protein-DNA binding around functional CTCF motifs in human demonstrates a more complex behavior. In particular, human genomic regions characterized by the highest CTCF occupancy, show statistically reduced level of nonconsensus protein-DNA binding. Our findings suggest that nonconsensus protein-DNA binding is fine-tuned around functional binding sites using a variety of design strategies.

Introduction

Genomewide measurements of protein-DNA association

Understanding the rules determining transcription-factor (TF) binding preferences toward genomic DNA is the key toward understanding design principles of transcriptional regulation (1–9). The answer to this fundamental question is hampered by the fact that DNA binding proteins recognize a wide variety of related sequences, and paradoxically, only a small fraction of specific motifs are usually bound in vivo (4,10). A specific consensus motif is a short DNA sequence, usually 6–20-bp long, possessing an enhanced binding affinity for a specific TF. For example, TTACCCG represents a specific consensus motif for a yeast transcription regulator, Reb1 (1). It has been recognized in a seminal work of Iyer and Struhl (3), performed in yeast, that genomic context surrounding factor-specific motifs significantly influences protein-DNA binding and gene expression. However, the general rules responsible for such influence remain unclear. Recent genomewide, in vivo measurements of protein-DNA binding preferences in yeast (2,11), Caenorhabditis elegans (12,13), Drosophila (14–16), mouse (17), and human (18) genomes demonstrate that hundreds of transcription regulators collectively bind low-complexity genomic regions, where few specific binding motifs are identified. The understanding of these striking findings is further complicated by the fact that several competing mechanisms, in addition to the direct protein-DNA sequence specific binding, are operational in vivo. These include histone-DNA binding leading to nucleosome and higher-order chromatin formation, ATP-dependent chromatin remodeling enzymes, and a variety of transcriptional cofactors influencing protein-DNA binding indirectly (19,20).

A recent ChIP-exo method developed by Rhee and Pugh (1,2) allowed genomewide measurements of protein-DNA binding preferences at the unprecedented singe-nucleotide resolution. These high-resolution, in vivo measurements performed for several sequence specific transcription regulators, such as Reb1 from yeast and CTCF from human, provide a genomewide snapshot of the eukaryotic cis-regulatory code (1). These measurements confirm that, surprisingly, a large fraction of specific binding motifs, even the Reb1 motifs located in the nucleosome-free promoter regions, remain unbound in vivo. This observation is remarkably interesting because Reb1 is known as being one of the most specific TFs, and it is often used as a benchmark for the experimental TF-DNA binding motif discovery (6).

Using an equilibrium statistical mechanics model without fitting parameters, in this work we suggest that genomic background surrounding specific consensus motifs statistically modulates the binding of sequence-specific TFs to such motifs. In particular, we suggest here that two quite different design strategies for nonconsensus protein-DNA binding might be operational in the genome:

The first design strategy (positive design) enhances the level of nonconsensus protein-DNA binding in the vicinity of binding sites. Such an enhancement might guide sequence-specific TFs toward their specific binding sites, greatly speeding up their diffusion (21,22). The existence of an optimal strength for nonspecific protein-DNA binding has been demonstrated theoretically in the past (23), and once such an optimal strength is exceeded, the diffusion of TFs slows down (23).

The second design strategy (negative design) is quite the opposite: it reduces the level of nonconsensus protein-DNA binding in the vicinity of binding sites. Such strategy might statistically reduce the competition of CTCF with other, nonspecific TFs, near specific CTCF binding sites, thus facilitating specific binding.

We now define, in detail, the notions of nonspecific and nonconsensus protein-DNA binding.

von Hippel-Berg definition of nonspecific protein-DNA binding

The notion of nonspecific protein-DNA binding was introduced and explored in seminal works of von Hippel and Berg et al. (21,22,24–27). Schematically, von Hippel and Berg (26) suggested splitting the definition of nonspecific protein-DNA binding into two related mechanisms:

The first mechanism is entirely DNA sequence-independent, and it assumes that DNA exerts an electrostatic attraction upon DNA-binding proteins, modulated by the overall DNA geometry (26). It has been suggested that DNA binding proteins use different conformations in specific and nonspecific binding modes (21–26).

The second mechanism assumes that imperfect (mutated) specific DNA consensus motifs retain some residual affinity for sequence specific TFs (26). Because the statistical probability of having such motifs in many genomic locations by random chance is high, nonspecific protein-DNA binding might become significant (26,28).

The significance of nonspecific protein-DNA binding has been experimentally demonstrated for a number of systems both in vivo (29,30) and in vitro (31–36). One of the key remaining questions: what is the functional significance of nonspecific protein-DNA binding in a living cell? The central working hypothesis, since the appearance of seminal works by von Hippel and Berg (21), Berg et al. (22), and von Hippel (27), is that such nonspecific binding speeds up the search process of TFs toward their specific binding sites. This hypothesis has been recently supported experimentally (30), and further developed and refined theoretically (23,37–43).

Definition of nonconsensus protein-DNA binding

We have recently suggested the mechanism of nonconsensus protein-DNA binding (44–47). Such nonconsensus protein-DNA binding represents an extension of the von Hippel-Berg’s mechanism of nonspecific binding as described in von Hippel and Berg (26). In particular, we showed quite generally that DNA sequence repeats possessing particular symmetries and length-scales of DNA sequence correlations exert an effective, statistical potential on all DNA binding proteins (44). This statistical potential can be attractive or repulsive, depending on the DNA sequence repeat symmetry. For example, repeated homo-oligonucleotide tracts, such as poly(A)/poly(C)/poly(T)/poly(G), lead to the strongest nonconsensus protein-DNA attraction. The longer the homo-oligonucleotide stretches, the stronger the predicted attraction (44). This is unlike DNA repeats where nucleotides of different types alternate (44).

We use the term “nonconsensus protein-DNA binding” to emphasize the fact that nonconsensus protein-DNA binding free energy is computed without any experimental knowledge of the high-affinity protein-DNA binding sites, known as “specific protein-DNA binding motifs” (44–46). The predicted nonconsensus effect is entropy-dominated, and it is nonlocal, meaning that the statistical protein-DNA binding free energy at any location along the DNA is influenced by the DNA sequence surrounding this location (44). We have demonstrated that such nonconsensus protein-DNA binding free energy is in excellent agreement with statistical, experimentally determined binding preferences of nearly 200 yeast transcription regulators (46), with nucleosome binding preferences (45), and with genomewide binding preferences of the yeast preinitiation complex (47). Below we explain in detail the procedure that we use to compute the nonconsensus protein-DNA binding free energy.

Synopsis of obtained results

Our article is organized as follows:

First, we analyze the strength of the nonconsensus protein-DNA binding within the genomic background surrounding the experimentally determined binding sites of the yeast transcription regulator Reb1 (1). In particular, we compute the free energy of nonconsensus protein-DNA binding for these DNA sequences, and we show that functional (i.e., bound) Reb1 specific motifs are surrounded by DNA sequences with statistically lower free energy of nonconsensus protein-DNA binding, as compared to nonfunctional (i.e., unbound) motifs (Figs. 1 and 2). The lower free energy represents the enhanced level of nonconsensus protein-DNA binding.

Figure 1.

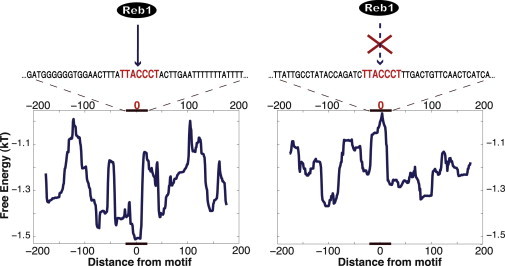
The example, from the ChIP-exo measurements of Reb1-DNA binding in Rhee and Pugh (1), illustrates the key hypothesis of this work. It was measured in Rhee and Pugh (1) that the transcription regulator Reb1 is bound to the specific Reb1 binding motif TTACCCT (red) (shown in the left panel), yet it is unbound to the identical specific motif (shown in the right panel). This result is obtained as the average in a cell population, and it is therefore highly statistically significant. Our key hypothesis here is that genomic background, surrounding the specific TF binding site, exerts the nonconsensus protein-DNA binding potential (free energy) that acts, statistically, on all DNA-binding proteins. The computed free energies of nonconsensus protein-DNA binding per bp (in units of k_BT), f = 〈F〉_TF/M, for two actual DNA sequences are shown in the bottom plots (note that the range where the free energy is shown, (−200,200) around the center of the binding motif, is much larger than the length of the shown sequences). The specific binding motif that was bound by Reb1 (left) is surrounded by the sequence with the lower free energy of nonconsensus binding, as compared to the case when Reb1 was unbound (right). We hypothesize, therefore, that the predicted nonconsensus protein-DNA binding modulates TF binding to specific (consensus) motifs along the genome, genomewide. To see this figure in color, go online.

Figure 2.

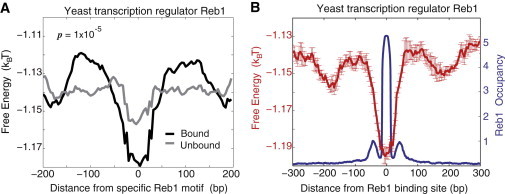
Specific, functional Reb1 binding sites are surrounded by the genomic background with enhanced nonconsensus protein-DNA binding free energy. (A) The computed average free energy per bp, 〈f〉 = 〈〈F〉_TF〉_seq/M, in the interval (−200,200) at ∼762 bound specific Reb1 motifs (black), as compared with the corresponding 〈f〉 for 1315 unbound specific Reb1 motifs (gray) genomewide, measured in Rhee and Pugh (1). The second averaging is performed over the sequences aligned with respect to the center of the specific Reb1 binding motif (TTACCCG/T); and M is the motif length. We used M = 8 and L = 50 in our calculations. The computed p-value is highly significant. (B) As experimentally measured in Rhee and Pugh (1), the cumulative Reb1 occupancy for 1029 bound sequences (blue), compared with the average free energy (red). To compute the error bars, we randomly divided the sequences into five subclusters, and computed 〈f〉 in each subcluster. The error bars are defined as one standard deviation of 〈f〉 between subclusters. To see this figure in color, go online.

Second, we perform a similar analysis for a human transcription regulator CTCF, and strikingly, we show that free energy of nonconsensus protein-DNA binding is increased around strongly bound CTCF binding sites (characterized by the high CTCF occupancy), as compared to weakly bound CTCF sites (Figs. 3 and 4). The higher free energy represents the reduced level of nonconsensus protein-DNA binding.

Figure 3.

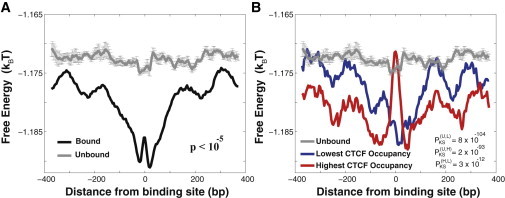
Specific, functional binding sites of human transcription regulator CTCF, are surrounded by the genomic DNA background with statistically modulated nonconsensus protein-DNA binding free energy. The genomewide ChIP-exo measurements of CTCF binding are taken from Rhee and Pugh (1). (A) The computed average free energy per bp, 〈f〉, in the interval (−400,400) around specific, experimentally bound CTCF motifs genomewide, as compared with the corresponding 〈f〉 computed around the control set of unbound motifs. In our calculations we used 5000 model TFs, M = 8 and L = 50. See Materials and Methods for the description of the control set of unbound motifs and for the calculation of the p value. To compute the error bars, we randomly divided the control set of sequences into five subclusters, and computed 〈f〉 in each subcluster. The error bars are defined as one standard deviation of 〈f〉 between subclusters. (B) The average free energy per bp, 〈f〉, for the 10% highest CTCF occupancy and the 10% lowest CTCF occupancy subgroups of sequences. The Kolmogorov-Smirnov p values are computed within the interval (−50,50). The notation, P_KS^(U,L), defines the Kolmogorov-Smirnov p value between the free energy distributions of the subgroup of unbound sequences and the subgroup of sequences with the lowest CTCF occupancy, respectively. The additional Kolmogorov-Smirnov p values are defined analogously. To see this figure in color, go online.

Figure 4.

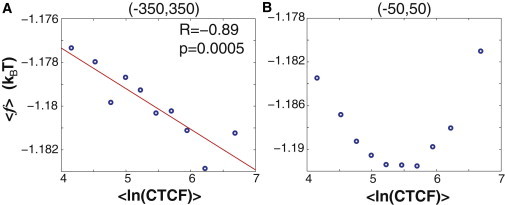
The free energy of nonconsensus protein-DNA binding correlates with the experimentally measured CTCF occupancy. Both positive and negative design strategies for nonconsensus protein-DNA binding are observed. Genomewide, on average, genomic regions with the enhanced CTCF-DNA binding occupancy are characterized by the statistically lower free energy of nonconsensus protein-DNA binding. However, in a narrower interval around the CTCF binding sites, genomic sequences characterized by the high CTCF occupancy show an opposite trend. (A) The correlation between the average value of the free energy of nonconsensus protein-DNA binding per bp, 〈f〉, in the interval (−350,350) around each experimentally determined CTCF binding site and the measured peak CTCF occupancy for the same binding site (1). The data are binned into 10 bins. (B) Similar to panel A, however, the average free energy per bp, 〈f〉, is computed in the interval (−50,50). To see this figure in color, go online.

Results

Calculation of the free energy of nonconsensus protein-DNA binding

We begin with the definition of nonconsensus protein-DNA binding free energy. To compute the free energy, we first compile a set of DNA sequences surrounding experimentally detected protein-DNA binding sites (Fig. 1). In particular, Rhee and Pugh (1) measured 762 binding sites of Reb1 in the entire yeast genome, where each binding site contains a specific Reb1 consensus-binding motif, TTACCCG/T. These measurements were performed at the unprecedented single-nucleotide resolution, using the ChIP-exo method (1). We therefore have a collection of 762 DNA sequences, such that for each sequence, we analyze the nonconsensus free energy in the interval (−200,200) around the center of the specific binding motif (Fig. 1).

To compute the free energy of nonconsensus protein-DNA binding at any given location along each DNA sequence, we position the center of the sliding window of width L = 50 bp in this location. We generate an ensemble of random DNA binders as a proxy for the phenomenon of nonconsensus protein-DNA binding in a crowded cellular environment (44). We do not use any experimentally predetermined protein-DNA binding preferences to model protein-DNA binding. The actual DNA sequence constitutes the only experimental input parameter for our model. In particular, we assume that a model protein makes contacts with M DNA basepairs, and the model protein-DNA interaction energy at each genomic position i is

$$U\left(i\right)=-\sum _{j=i}^{M+i-1}\sum _{\alpha =\left\{\text{A,T,C,G}\right\}}{K}_{\alpha }{s}_{\alpha }\left(j\right),$$ (1)

where s_α(j) represents the elements of a four-component vector of the type (δ_αA, δ_αT, δ_αC, δ_αG), with δ_αβ = 1 if α = β, or δ_αβ = 0 if α ≠ β. For example, if the A nucleotide is positioned at the coordinate j along the DNA, then this vector takes the form (1,0,0,0). To generate each model protein, we draw the values of K_A, K_T, K_C, and K_G from the Gaussian probability distributions, P(K_α), with the zero mean, 〈K_α〉 = 0, and the standard deviation, σ_α = 2 k_BT, where T is the temperature and k_B is the Boltzmann constant. We have previously demonstrated that the resulting free energy is qualitatively robust with respect to the choice of model parameters (44). An energy scale, 2 k_BT ≃ 1.2 kcal/mol, is chosen to represent a typical strength of one hydrogen bond, or one electrostatic bond that a protein makes with a DNA bp (24,26).

For each model protein, we define the partition function of protein-DNA binding within the chosen sliding window of width L = 50 bp,

$$Z=\sum _{i=1}^L\exp \left(\frac{-U\left(i\right)}{k_{\text{B}}T}\right),$$ (2)

and the corresponding free energy of protein-DNA binding in this sliding window as

$$F=-k_{\text{B}}T\ln Z.$$ (3)

We then assign the computed F to the sequence coordinate in the middle of the sliding window. For example, for the chosen sliding window size, L = 50 bp, 50 protein-DNA binding events contribute to the partition function (Eq. 2) in each sliding window, for each random binder. We move the sliding window along the DNA sequence and we compute F at each sequence location. This procedure allows us to assign the free energy of nonconsensus protein-DNA binding to each DNA bp within each DNA sequence.

Next, we repeat the described procedure for an ensemble of 250 model random binders (where each random binder is uniquely characterized by four random numbers, K_A, K_T, K_C, and K_G), and compute the average free energy, 〈F〉_TF, with respect to this ensemble, in each sequence location. Two examples of the resulting free energy landscapes, 〈F〉_TF, are shown in Fig. 1. The lower the 〈F〉_TF in a given sequence location, the stronger the statistical attraction that DNA-binding proteins experience (on average) toward this location. We note that the predicted effect is nonlocal, meaning that the magnitude of the free energy in each sequence location is influenced by the DNA sequence surrounding this location.

We stress the point that the resulting free energy is qualitatively robust with respect to the choice of the sliding window size, L, within a wide range of values (see Fig. S1 in the Supporting Material). The free energy profiles are also statistically robust with respect to a moderate variation of the value of M, within a typical range of the TF binding site size in yeast (see Fig. S1). The reason for a relative insensitivity of the predicted effect with respect to the choice of model parameters stems from the fact that DNA sequence symmetry is the key factor regulating the magnitude of the nonconsensus protein-DNA binding free energy (44). In particular, homo-oligonucleotide sequence repeats, such as repeated poly(A)/poly(C)/poly(T)/poly(G) tracts, universally lead to a wider spectrum of protein-DNA binding energies, P(U), as compared with DNA repeats, in which nucleotides of different types alternate.

Intuitively, the widening of the energy spectrum for the homo-oligonucleotide enriched DNA sequences can be understood in the following way: In each sequence location, for a given random TF binder, the protein-DNA binding energy, U, is simply the sum of M random numbers, K_α, where the nucleotide identities, L = 50, are uniquely determined by the DNA sequence. Despite the fact that all K_α come from the Gaussian distribution with zero mean and fixed standard deviation, σ, their sum will be a function of the DNA sequence. This sum will be sensitive to a variation of the local nucleotide composition in the window of width M, with homo-oligonucleotide tracts producing the strongest fluctuations of U. A wider energy spectrum universally results in a statistically lower average free energy, 〈F〉_TF (44,48). We use the term “sequence correlations” to describe the symmetry and the length-scale of DNA sequence repeats (44). We also note that the predicted nonconsensus protein-DNA binding free energy is entropy-dominated, and it is influenced exclusively by DNA sequence correlations, and not by the average nucleotide composition (see Fig. S2).

Free energy of nonconsensus protein-DNA binding is statistically reduced in the vicinity of functional Reb1 binding motifs in yeast

As a result of the procedure described above, we obtain the average profile of the nonconsensus protein-DNA binding free energy, 〈〈F〉_TF〉_seq, at ∼762 functional, specific motifs for Reb1 (Fig. 2 A), where the second average, 〈〉_seq, is performed at each sequence position with respect to the sequences aligned by the center of the specific motif. The observed minimum of the free energy around the location of the specific motif suggests that nonconsensus binding is statistically enhanced around functional, specific motifs genomewide in yeast. We use the term “positive design” to describe this design strategy.

To estimate the statistical significance of this effect, we also compiled a control set of nonfunctional sequences containing exactly the same specific motifs, TTACCCG/T. However, in all those control sequences Reb1 was not bound to the motifs (1). The average free energy of nonconsensus binding around functional motifs shows a more pronounced minimum compared with the control set of nonfunctional motifs (Fig. 2 A), with a highly statistically significant p-value, p ≃ 10⁻⁵ (see Materials and Methods). To further test the statistical significance of our results, we have restricted the sets of bound and unbound specific motifs to only those motifs, which are located in the vicinity of annotated Transcription Start Sites (TSSs) in yeast. The average free energies computed for those sets containing 415 bound and 271 unbound sequences, respectively, confirm that bound specific motifs are surrounded by sequences with the reduced free energy of nonconsensus protein-DNA binding, as compared with unbound motifs (see Fig. S3).

Fig. 2 B shows the comparison between the entire experimentally measured profile of Reb1 occupancy (1) and the computed average free energy of nonconsensus protein-DNA binding. This includes experimentally measured Reb1 occupancy for 1029 bound sequences, including sequences containing mutated Reb1 motifs (1). The sequences were aligned with respect to the center of the Reb1 binding site. The minimum of the free energy is positioned exactly at the maximum of the Reb1 occupancy (Fig. 2 B). We conclude therefore that nonconsensus protein-DNA binding is fine-tuned around functional, specific Reb1 motifs genomewide in yeast in a way that increases nonconsensus protein-DNA attraction in the immediate vicinity of these motifs.

Free energy of nonconsensus protein-DNA binding in the vicinity of functional CTCF binding motifs in human demonstrates alternative design strategies

The CTCF binding profiles measured using the ChIP-exo method in HeLa cells represent the first example obtained at the single-nucleotide resolution for the entire human genome (1). Although CTCF is known to be a sequence-specific DNA-binding transcription regulator, its consensus sequence is not well defined, and it is still a matter of dispute (1,49–52). Here we show that the predicted free energy of nonconsensus protein-DNA binding shows both positive and negative design strategies in the vicinity of experimentally detected CTCF binding sites (1).

We followed a procedure similar to the one described above. In particular, we collected DNA sequences at ∼35,000 experimentally detected CTCF binding sites. Strikingly, we observe that although the computed average nonconsensus free energy shows an overall minimum (Fig. 3 A), it shows a pronounced local maximum for a subgroup of the strongest bound sequences in the vicinity of binding sites (Fig. 3 B). To verify the statistical significance of the observed effect, we have also collected a controlled set of nonfunctional (unbound) sequences containing exactly the same binding motifs as functional (bound) CTCF sites, and we computed the free energy around such unbound CTCF motifs (see Materials and Methods). Because of this procedure, we confirmed that, overall, the average nonconsensus free energy is more significantly reduced in the vicinity of functional (bound) CTCF specific motifs as compared with unbound CTCF motifs (Fig. 3 A). However, for a subgroup of sequences characterized by the highest CTCF occupancy, the free energy is increased in the vicinity of binding sites (Fig. 3 B). We verified that the predicted effect stems from DNA sequence correlations and it is not affected by the overall nucleotide composition of DNA sequences (see Fig. S4). We also verified that the predicted effect is qualitatively robust with respect to the variation of the microscopic parameters of the model, such as the sliding window width, L, and the size of the TF binding site, M (Fig. S5).

The discussed case of genomewide binding preferences of the human transcription regulator CTCF represents a considerably more complex system than the yeast transcription regulator Reb1. In the case of CTCF, we observe that the nonconsensus protein-DNA binding landscape might be shaped by using quite different strategies (Fig. 3 B). One strategy (positive design) enhances the level of nonconsensus protein-DNA binding in the vicinity of the binding site. Such an enhancement might guide sequence-specific TFs toward their specific binding sites, greatly speeding up their diffusion (21,23). Yet, as the level of nonspecific binding becomes too high, the competition with other TFs might obstruct the specific binding, and slow down the diffusion (23). Another strategy (negative design) is quite the opposite: it reduces the level of nonconsensus protein-DNA binding in the vicinity of the binding site (Figs. 3 B and 4). Such strategy might statistically reduce the competition of CTCF with other, nonspecific TFs, in the vicinity of specific CTCF binding sites, thus facilitating specific binding. From our analysis it follows that the latter strategy is operational in the vicinity of CTCF binding sites characterized by the highest CTCF occupancy (Figs. 3 and 4 B). Our genomewide analysis suggests that the predicted positive and negative design strategies are quite general (Fig. 5), and most likely they represent the statistical law rather than the exception.

Figure 5.

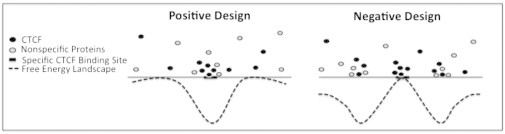
Schematic cartoon demonstrating the concept of positive and negative design strategies for nonconsensus protein-DNA binding free energy in the vicinity of functional protein-DNA binding sites. The first design strategy (positive design) enhances the level of nonconsensus protein-DNA binding in the vicinity of binding sites (i.e., reduced free energy in the vicinity of binding sites). Such an enhancement might guide sequence-specific TFs toward their specific binding sites, greatly speeding up their diffusion. The second design strategy (negative design) reduces the level of nonconsensus protein-DNA binding in the vicinity of binding sites (i.e., increased free energy in the vicinity of binding sites). Such strategy might statistically reduce the competition of CTCF with other, nonspecific TFs, in the vicinity of specific CTCF binding sites, thus facilitating specific binding.

Discussion and Conclusion

In this article, we attempted to rationalize design principles for nonconsensus protein-DNA binding in genomic regions surrounding specific transcription factor DNA binding sites. In both cases of Reb1 and CTCF, for our statistical analysis we used the genomewide binding preferences measured at the unprecedented single-nucleotide resolution (1). In particular, we showed that nonconsensus protein-DNA binding free energy is statistically reduced around functional specific motifs for the yeast transcription regulator Reb1 (Fig. 2). We use the term “functional specific motif” to describe those specific motifs that were experimentally detected in Rhee and Pugh (1) as being bound. This is in contrast to the case of nonfunctional specific motifs that were experimentally detected in Rhee and Pugh (1) as being unbound.

For the human transcription regulator CTCF, the landscape of the nonconsensus protein-DNA binding free energy is found to be more complex (Fig. 3). Whereas genomewide, on average, we observed that the nonconsensus free energy is statistically reduced around CTCF binding sites (Fig. 3 A), a subgroup of genomic sequences characterized by the highest CTCF occupancy demonstrated a different design principle (Fig. 3 B). In particular, the free energy is increased in the vicinity of such highly occupied binding sites (Fig. 3 B). This striking observation suggests that two quite-opposite design strategies for nonconsensus protein-DNA binding might be operational in the genome (Fig. 5). The first design strategy (positive design) enhances the level of nonconsensus protein-DNA binding in the vicinity of binding sites. Such an enhancement might guide sequence-specific TFs toward their specific binding sites, greatly speeding up their diffusion (21,23). It has been shown, theoretically, that there exists an optimal strength of nonspecific protein-DNA binding, and once such an optimal strength is exceeded, the diffusion of TFs slows down (23). The second design strategy (negative design) is quite different; it reduces the level of nonconsensus protein-DNA binding in the vicinity of binding sites. Such a strategy might statistically reduce the competition of CTCF with other, nonspecific TFs, in the vicinity of specific CTCF binding sites, thus facilitating specific binding. We suggested here that both of these design strategies might be operational in the human genome.

Despite the simplicity of our equilibrium biophysical model for protein-DNA binding, we suggest that the predicted design principles for nonconsensus protein-DNA binding are quite general. We expect that such principles should be operational in different eukaryotic organisms, for different transcription regulators. The functional significance of nonconsensus protein-DNA binding for transcriptional regulation remains an open question. Here, we suggested that such nonconsensus binding landscape provides a background surrounding specific DNA motifs, and possibly regulating the kinetics of transcription regulators in their search for such specific motifs (21,23,38). We suggest, therefore, that the predicted nonconsensus protein-DNA binding mechanism represents yet additional layer of transcriptional regulation operating in vivo, and it influences genomewide protein-DNA binding preferences in a eukaryotic cell.

It is important to note that the highly nonequilibrium nature of chromatin dynamics in vivo might significantly modify the predictions of our purely equilibrium, statistical mechanics model. One additional factor, critically important in vivo, is the competition between transcription factors and histones for nucleosome formation (45,53,54). To test the predictions of our model directly, one possibility would be to use a whole-cell, nucleosome-free extract, to remove the competition of TFs with histones for nonconsensus binding to DNA. It would be interesting to observe how genomewide TF binding preferences and gene expression vary in a nucleosome-free system upon insertion of low-complexity DNA sequences in different promoter regions.

Materials and Methods

p-value calculations

To compute the p value in Fig. 2 A, we compiled 10⁵ randomized pairs of datasets, each set containing 762 and 1315 sequences, respectively, where each sequence is drawn randomly from the actual, unified, and reshuffled sets of 762 bound and 1315 unbound sequences, respectively, as measured genomewide in Rhee and Pugh (1). Each sequence is in the interval (−200,200) around the specific Reb1 binding motif, TTACCCG/T. We then computed the average free energies of nonconsensus protein-DNA binding for each pair of these randomized sets, and we computed the average free energy difference (in the interval (−20,20) around the motif center) between the two sets within each pair. Finally, we defined the p value as the probability that the observed free energy difference in the randomized sets is equal to or larger than the actual free energy difference.

To compute the p value in Fig. 3 A, we searched the entire human genome sequence for specific CTCF binding motifs that were not bound by CTCF in the experiment (1). We then compiled the control dataset of sequences surrounding such not bound motifs, in the interval (−400,400) around the center of the motif. The average free energy of this dataset is also shown in Fig. 3 A. Next, we compiled 10⁵ pairs of randomized datasets, by randomly selecting the pairs of sequences from both bound and unbound datasets. Finally, we computed the probability that the average free energy difference in the interval (−100,100) between the randomized pairs of datasets is equal to or larger than the actual free energy difference. This probability is taken, then, as the p value. We defined specific motifs as 10-bp sequences, taken in the interval (−5,5) around the experimentally determined (at single-nucleotide resolution) CTCF-DNA binding peaks (1).