Automatic Magnetic Resonance Spinal Cord Segmentation with Topology Constraints for Variable Fields of View

Abstract

Spinal cord segmentation is an important step in the analysis of neurological diseases such as multiple sclerosis. Several studies have shown correlations between disease progression and metrics relating to spinal cord atrophy and shape changes. Current practices primarily involve segmenting the spinal cord manually or semi-automatically, which can be inconsistent and time-consuming for large datasets. An automatic method that segments the spinal cord and cerebrospinal fluid from magnetic resonance images is presented. The method uses a deformable atlas and topology constraints to produce results that are robust to noise and artifacts. The method is designed to be easily extended to new data with different modalities, resolutions, and fields of view. Validation was performed on two distinct datasets. The first consists of magnetization transfer-prepared T2*-weighted gradient-echo MRI centered only on the cervical vertebrae (C1-C5). The second consists of T1-weighted MRI that cover both the cervical and portions of the thoracic vertebrae (C1-T4). Results were found to be highly accurate in comparison to manual segmentations. A pilot study was carried out to demonstrate the potential utility of this new method for research and clinical studies of multiple sclerosis.

1. Introduction

The human spinal cord is a long thin cylindrical structure of the central nervous system (CNS) extending from the medulla oblongata to the lumbar vertebrae. It is the principal transmission pathway for neural signals between the brain and the rest of the body. The primary function of the spinal cord makes it of great importance in studying diseases that lead to deterioration in CNS function, such as multiple sclerosis (MS). In vivo magnetic resonance imaging (MRI) of the human spinal cord presents a unique diagnostic tool in studying the progression and characteristics of such neurological diseases.

The usefulness of MRI based analysis of the spinal cord can be traced as far back as Losseff et al. (1996) who demonstrated strong association between spinal cord area and disability as measured by Kurtzke’s Expanded Disability Status Scale (Kurtzke, 1983) (EDSS) (r = -0.7, P < 0.001). Since then, significant progress has been made in both the analysis and application of MRI in spinal cord imaging. Kalkers et al. (2002) proposed using MRI derived metrics to evaluate neuroprotective therapies. Studies from Lin et al. (2003, 2004) demonstrated that changes in edge detectability of the spinal cord boundary are related to changes in clinical disability. More recent work (Zackowski et al., 2009; Rocca et al., 2011) has shown the potential of using quantities derived from various imaging modalities as biomarkers to characterize patients with MS. Other studies (Freund et al., 2011) have shown that cross-sectional area of the spinal cord is well correlated with cortical activity.

A common requirement for these studies is a full or partial segmentation of the spinal cord (see Fig. 1) for each subject in the study. Such segmentations are currently performed manually or semi-automatically by human raters, which creates two immediate disadvantages. First, human raters are prone to unintended biases and inconsistency in their work. This is particularly common when segmenting small structures such as the spinal cord, and is evident when replicating a segmentation of the same image or comparing between two separate raters. Second, raters require extensive training and time to perform the task. This imposes a strict limitation on the scale of future studies and produces potentially long delays between acquiring the data and completing the analyses.

Figure 1.

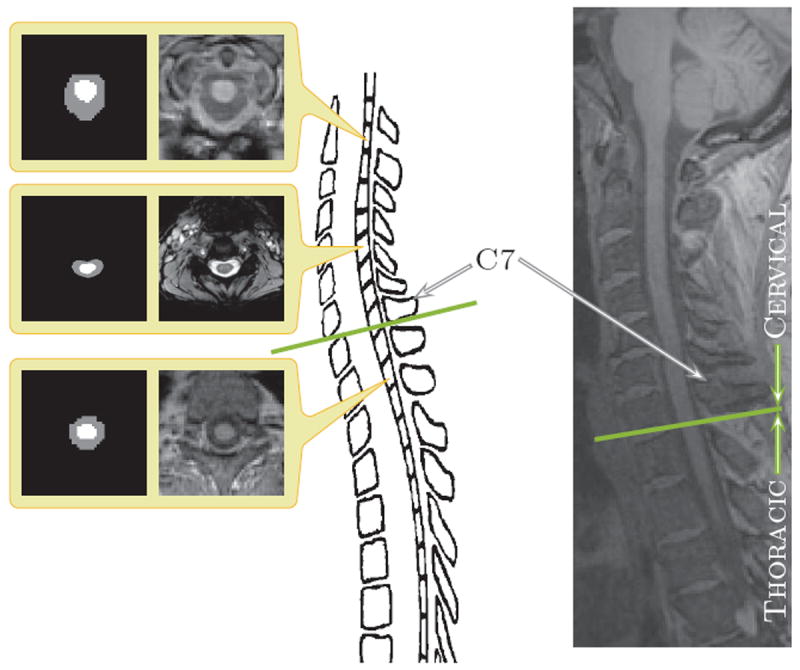
The center image is an illustration of a spinal cord. The left hand column shows (center) magnetization transfer-prepared T2*-weighted gradient-echo and (top and bottom) T1-weighted axial cross-sections of spinal cord MRIs and corresponding manual segmentations. The right-most column shows a sagittal slice of a T1-weighted MRI with a field of view covering the cervical and portions of the thoracic vertebrae. The green line in both the illustration and the sagittal slice on the right demarks the separation between the cervical and thoracic vertebrae.

There have been several attempts (Archip et al., 2002; Karangelis and Zimeras, 2002; Burnett et al., 2004; Nyúl et al., 2005) to automate the segmentation of the spinal cord in computed tomography (CT) imaging. However, such methods are limited by a lack of soft tissue contrast in CT, making it difficult to distinguish between the spinal cord itself and the surrounding cerebrospinal fluid (CSF). Most approaches are restricted to segmenting only the spinal canal, which is insufficient for analysis of spinal cord atrophy. This, in addition to concerns for patient safety, makes MRI a superior choice for imaging the spinal cord. However, MR imaging is not without its own difficulties. Inhomogeneities in receiver coil sensitivity can manifest as spatially distributed intensity biases. Susceptibility may create artifacts in the spinal cord proximal to the posterior fossa region (McGowan and Patel, 2000). Image quality is also degraded by truncation artifacts (Czervionke et al., 1988), ghosting artifacts from the heart and great vessels (Bronskill et al., 1988; Curtin et al., 1989; Hinks and Quencer, 1988; Levy et al., 1988) and contrast (Lycklama et al., 2003). Non-uniformity correction is particularly important for acquisitions from phased-array coils used to assess spinal cord atrophy (Lin et al., 2004).

These drawbacks have delayed the development of fully automated MR spinal segmentation tools. As such, the majority of the methods presented thus far to address this problem have been semi-automated in nature (Coulon et al., 2002; Van Uitert et al., 2005; Horsfield et al., 2010; Nieniewski and Serneels, 2002; McIntosh and Hamarneh, 2006). These approaches vary from the watershed based (Nieniewski and Serneels, 2002) to applications of deformable models (McIntosh and Hamarneh, 2006). To the best of our knowledge there are only three fully automatic methods in the literature for human MRI spinal cord segmentation (Koh et al., 2010, 2011; Mukherjee et al., 2010). Koh et al. (2010) developed a gradient vector flow (Xu and Prince, 1998) magnitude approach as part of a computer-aided diagnosis (CAD) system. Their algorithm estimates the spinal cord using the magnitude of the gradient vector flow edge map, followed by a connected component analysis to remove any holes in the segmentation. In Koh et al. (2011), the same group developed a different approach to the problem using active contour models (Kass et al., 1988) based on saliency maps. Mukherjee et al. (2010) also applied an active contour approach, but instead evolved an image gradient based, open-ended contour using dynamic programming-based energy-minimization. They initialize their method using an estimation of the vertebra bone contour in each 2D slice of the image, which is found using an optimal shortest path directed graph search based on gradient magnitude and gradient orientation. These 2D contours are then evolved under an active contour model that minimizes an energy based on the symmetry of the contour and the smoothness between successive contours (i.e., contours on adjoining 2D slices).

A common deficiency with current automated algorithms is their limitation to both a single MR-sequence and a particular field of view. The three existing methods mentioned above are designed to be used with T2 and T2*-weighted MRIs because it offers the best soft tissue contrast (Koh et al., 2010, 2011; Mukherjee et al., 2010). None of them provide an intuitive and easily generalized approach for addressing MR-sequences or fields of view outside of the particular dataset they were designed for. This is problematic in spinal cord MR imaging because data is generally only collected across specific subsections of the spinal cord, and the MR-sequence is rarely standardized between datasets. Addressing these limitations is one focus of our work.

There are various reasons why existing image segmentation technologies cannot be readily applied to spinal cord MRIs. For example, the structure of the spinal cord makes typical atlas-based registration highly inaccurate. This happens for two reasons; first, the long thin cylindrical nature of the spinal cord and its small size relative to the neck and torso leads to the spinal cord contributing only minimally to the overall cost function of a registration algorithm. This typically causes the registration algorithm to prioritize the alignment of other structures over the spinal cord during the optimization. Second, the spinal cord is a flexible non-rigid structure, which results in a large degree of variability in both the shape and curvature of the structure in MRIs (see Fig. 2). This variability removes rigid and affine registrations as viable choices for the transformation. Even for free-form deformable registration the accuracy is dramatically limited due to the large deformations often required to properly align the curvatures. This is particularly true for registration with strict regularization constraints on the deformation.

Figure 2.

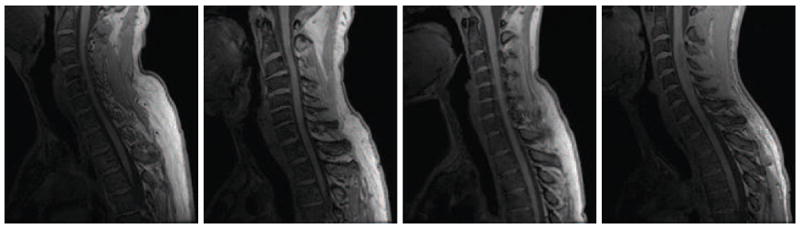
Sagittally acquired T1-weighted MR slices of the spinal cord from four different healthy subjects at approximately the same field of view. This demonstrates the wide variability in the shape and curvature of the spinal cord in the images.

Unsupervised intensity based segmentations encounter a different set of problems. They are prone to misclassification due to the partial voluming of nerve roots and the strong intensity inhomogeneities from the spine coils. The inhomogeneity from the surface coil is primarily a result of the MR signal dropping-off for tissues further away from the coils. However, the problem is exacerbated by the curvature of the spinal cord. Since the cord is not parallel to the coils, the anatomy interacts with the intensity inhomogeneity unevenly. As a result, intensity values along the spinal cord are inconsistent and depend on its curvature during acquisition. This effect is particularly evident for images covering large fields of view, where both the distance from the coil and the curvature of the spinal cord is larger. Fig. 3 shows an example of an axially acquired magnetization transfer-prepared T2*-weighted gradient-echo image and a sagittally acquired T1-weighted MRI of the spinal cord, each from separate subjects. Both images have been segmented with a fuzzy c-means (Bezdek, 1980) approach (Pham, 2001) which includes gain field correction and regularization. We see that the spinal cord could not be properly segmented in any of the cases, including those where the image was manually truncated to include only the spinal cord and CSF. The intensity drop-off seen in the examples could not be handled by the inhomogeneity correction built into the classification algorithm, nor by preprocessing with N3 (Sled et al., 1998), an intensity non-uniformity correction tool commonly used in whole head MRI.

Figure 3.

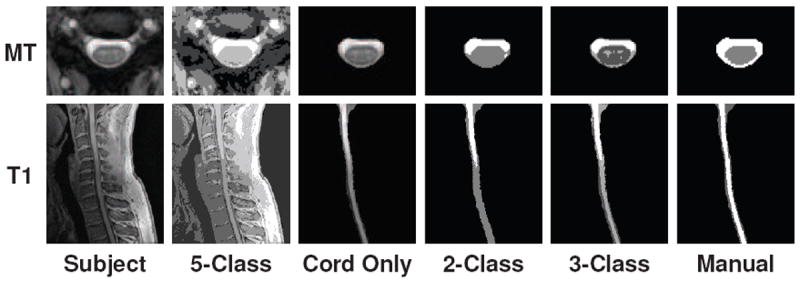
Examples of two, three, and five class segmentations using a standard tissue classification tool (Pham, 2001) on (top) axially acquired magnetization transfer-prepared T2*-weighted gradient-echo MRI and (bottom) sagittally acquired T1-weighted MRI of the spinal cord, each from separate healthy subjects. Results are shown for when the classification was performed on the full MRI (first two columns) and when the image was manually truncated to just the spinal cord and CSF (last four columns).

In this work we present a fully automated spinal cord segmentation algorithm that combines deformable registration with topology preserving intensity classification. Our approach is built upon a method by Bazin and Pham (2008), which uses a topological and statistical atlas in the fuzzy c-means model to classify tissues in the brain. We introduce a topological atlas that is appropriate for the spinal cord, and a statistical atlas that is dynamically adjusted to match its variability. In addition, we augment the framework with an intensity atlas that is used with deformable registration to allow the atlases to be properly initialized. Finally, we present a rapid approach for generating the necessary topology and statistical atlases from a single manual segmentation. This provides a quick and automatic procedure for adapting our method to better match datasets with very different fields of views and MR-sequences (e.g., T1-weighted, T2*-weighted, etc.). An early version of this work was presented in conference form (Chen et al., 2011), where we demonstrated its capabilities on a limited dataset with a fixed field of view. Our algorithm is freely available as part of the Java Integrated Science Toolkit (JIST) (Lucas et al., 2010), which can be downloaded at http://www.nitrc.org/projects/jist/.

2. Methods

The topology-preserving, anatomy-driven segmentation (TOADS) algorithm (Bazin and Pham, 2008) provides the main model for our segmentation approach. It is a fuzzy c-means (FCM) (Bezdek, 1980) based intensity classification algorithm that is capable of preserving the digital topology of the anatomy being segmented. The principal idea behind the model is to use prior knowledge about the target anatomy and its surrounding structures to constrain the topology of the final segmentation. This guarantees that the structures in the segmentation result are connected to each other (and themselves) in a fashion that respects what we know about the anatomy. The primary advantage of such constraints is that they allow the segmentation process to be highly resilient to noise and artifacts that would otherwise negatively affect the results. For example, if we know that the spinal cord in our images consists of a singular connected cylindrical structure, we can enforce this topologically by constraining the spinal cord in the segmentation to always be a single connected object. As a result, the segmentation becomes more robust to intensity drop-offs or artifacts in the middle of the image that might break the spinal cord segmentation into multiple objects.

In the following subsections we provide a brief summary of the TOADS algorithm. Then, we introduce several new elements to generalize the TOADS model for spinal cord segmentation in MRI. Specifically, we describe the constraints we use to construct the spinal cord topology atlas, and how deformable registration is incorporated into this framework to initialize the atlas such that it can account for the variability of the cord position in the image. This includes an explanation of our approach for maintaining the necessary digital topology of the atlas when applying large registration deformations. Finally, we present an approach for constructing the necessary topology and statistical atlases from a single manual segmentation of the spinal cord.

2.1. TOADS Overview

A brief overview of the TOADS algorithm is provided in this subsection. Complete details for the algorithm are available in Bazin and Pham (2008). The goal of the algorithm is to perform a FCM based intensity classification of an image, while maintaining digital topology constraints on the objects in the segmentation. This is achieved by starting the segmentation from a topology atlas that describes the desired topological configuration of relevant objects in the anatomy. The atlas is then evolved to match the target image through a series of homeomorphic growing and thinning steps that guarantee the digital topology between the objects is never broken. This thinning and growing is driven by the FCM centroid(s) and membership(s), with recalculation at each iteration as the segmentation is updated. Bazin and Pham (2008) describes the theory behind digital homeomorphism and how to augment the simple point criterion to evolve a segmentation while maintaining digital topology.

In addition to the topology atlas, TOADS also utilized a statistical atlas built from a collection of 18 manually generated segmentations of significant brain structures, derived from the IBSR dataset (Worth, 1996). The edge of each structure was smoothed, using a Gaussian kernel, to make a smooth probability map that approximates natural anatomical variations. This statistical atlas provides information for distinguishing adjoining structures with similar intensities.

Given an MR image, I, each iteration of TOADS consists of performing a fuzzy segmentation and then updating a topologically consistent segmentation using fast marching. The fuzzy segmentation is obtained by minimizing the energy function,

$$E\left(u_{\mathit{jk}}^q\right)=\sum _{\mathit{jk}}\frac{u_{\mathit{jk}}^q}{r_{\mathit{jk}}}{\Vert I_j-c_k\Vert }^2+\beta \sum _{l\in N_j,m\ne k}\frac{u_{\mathit{jk}}^q}{r_{\mathit{jk}}}{u}_{\mathit{lm}}^q+\gamma \sum _{m\ne k}\frac{u_{\mathit{jk}}^q}{r_{\mathit{jk}}}{w}_{\mathit{km}}{p}_{\mathit{jm}}^q,$$ (1)

with respect to a membership function, $u_{\mathit{jk}}^q$ for each voxel j in I, and each structure k being segmented. The parameter q controls the “hardness” or “fuzziness” of the membership functions and is usually set to be two (Pham, 2001).

The three terms on the right side of Eqn. 1 can be explained as follows. 1) The first term is a data term that compares the intensity I_j at each voxel against the intensity centroids c_k for each structure, where the differences are weighted by the membership functions for that voxel. 2) The second term enforces the smoothness of the membership functions. 3) The third term controls the influence of the statistical atlas, which provides the prior probability p_jk that a voxel j begins inside structure k. These atlas probabilities are weighted by w_km, which are distance measures between the centroids, c_k and c_m, of two classes; it is designed to be one when c_k = c_m and decays to zero as ∥c_k − c_m∥ → ∞. The variables β and γ in Eqn. 1 are weights on the relative importance of each term, while r_jk takes into account the global and local relationships between structures.

The digitally homeomorphic thinning and growing of the topology atlas is performed using a fast marching approach (Sethian, 1999). The thinning aims to remove errors from misalignment of the atlas to the image by only keeping high membership voxels. Then the growing step expands the skeletally thinned structures until all boundary voxels are in contact. In this manner, the segmentation captures more details of the structure boundaries at each iteration while retaining the topology of the atlas. The algorithm is assumed to converge when either the change in the energy function drops below a suitable threshold or a maximum number of iteration is reached.

2.2. Extending TOADS for the Spinal Cord

The flexibility of the TOADS algorithm allows the model to be adapted for the spinal cord; however, we must overcome several limitations in the existing framework. First, we must construct a set of topology and statistical atlases that are anatomically meaningful in the context of the spinal cord and have the flexibility to handle all possible fields of view. Unlike brain imaging where the whole brain is usually imaged, spinal cord MRIs tend to have limited fields of view that generally do not cover the entire cord. This results in possible artificial breaks in the topology when the image ends part way through the cord. This needs to be accounted for during both the construction and the initialization of the topology atlas. Second, TOADS assumes the brain images have been skull-stripped, e.g., via (Carass et al., 2011), prior to running the algorithm. The absence of non-brain tissue allows TOADS to rigidly register the topology atlas directly to the MRI for initialization. This is clearly not possible in our case, since our primary goal is to separate the spinal cord and CSF from the rest of the image. Hence, we must work with the surrounding tissue in the MRI, which makes registering the topology atlas (a segmentation image) to the MRI highly unreliable. In addition, the varied curvature of the spinal cord prevents a rigid, or even affine, transformation from providing an adequate initialization. The following sections will describe our solutions to these two problems.

2.3. Spinal Cord Topology and Statistical Atlases

The topology atlas serves as the topological rule set for the objects being segmented in our algorithm. In our model for the spinal cord, this atlas only contains three objects: 1) the spinal cord with spherical topology; 2) the CSF with a spherical shell topology; and 3) a “wrapper” object also with a spherical shell topology. The wrapper object serves as a catch-all object for any structures that immediately surround the spinal canal, including the vertebrae and surrounding muscles. Since it encompasses several tissue types, it covers a wide range of image intensities. Its primary purpose is to provide a boundary that prevents the CSF object from extending past the spinal canal. Everything outside the wrapper object is treated as background. We represent the topological relationships between these objects with just two basic assumptions:

1. The spinal cord is completely surrounded by the CSF.

2. The union of the CSF and spinal cord is completely surrounded by the wrapper object.

Fig. 4 shows examples of this atlas for a sagittally acquired T1-weighted MRI dataset. We note that in our atlas, the CSF forms a “cap” on the top and bottom of the spinal cord, which is not anatomically correct. This is done because the field of view of the MRI forces a cutoff at the superior and inferior edges of the images. Hence, we must completely cap the ends of the spinal cord object with the CSF object in order to prevent the background and wrapper objects from being connected to the spinal cord. Otherwise, those objects would be allowed to evolve in between the CSF and spinal cord, effectively separating the two objects, which we know should not happen. Similarly, the wrapper object completely surrounds the CSF object to enforce a similar topology. Both of these artificial caps are added outside the field of view and removed at the end of the algorithm. Thus, they do not interfere with the accuracy of the segmentation at the boundaries.

Figure 4.

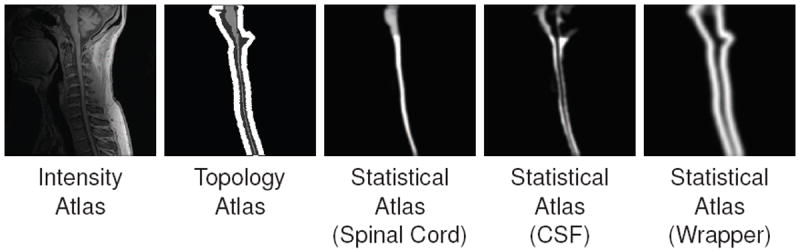
An example of the intensity, topology (spinal cord in light gray, CSF in dark gray, and wrapper in white) and statistical atlases constructed from a T1-weighted MRI.

In addition to the topology atlas, a statistical atlas is used to define probabilistic priors on the locations of objects in the topology atlas. This is created by taking multiple spinal cord MR images and deformably registering them to a common template. Manual segmentations of the structures in each MR image are then transformed using the same deformation. This provides an empirical calculation for the probability of each object occurring at each voxel in the template space. The resulting probabilities are Gaussian-smoothed to reduce discrete drop-offs in the atlas (Bazin and Pham, 2008). Fig. 4 shows a statistical atlas for the spinal cord, CSF and wrapper objects, constructed from five manual segmentations. In Section 2.6 we provide an automatic and more efficient approach for constructing both the topology and statistical atlases from only a single manual segmentation.

2.4. Incorporating Deformable Registration Into TOADS

Creating these two spinal cord specific atlases is still not sufficient to directly apply TOADS for spinal cord segmentation. We also need a new way to initialize the atlases, since the original TOADS relies on a rigid initialization, which cannot fully capture the variability of the spinal cord. To address this limitation, we replace the rigid alignment step with a deformable registration. Unfortunately, this replacement results in two new difficulties. First, deformable registration between a segmentation image (the topology atlas) and the MRI is highly unreliable. This is due to the segmentation image containing only a few structures, each with homogeneous intensity, while the MRI includes all the tissue surrounding the spinal cord, and contains noise and artifacts. This makes it extremely difficult to find the correct correspondences between these two types of images during registration. The small size of the spinal cord relative to the entire image also contributes to the difficulty.

Our solution to this is to introduce an intensity atlas into the TOADS framework. This atlas is directly associated with the objects in the topology atlas, and in most cases will be the underlying MRI that the topology atlas was constructed from. The goal is to use deformable registration to learn a mapping between the intensity atlas and the MRI being segmented. This learned deformation is then applied to the topology and statistical atlases to serve as their initialization in the algorithm. In this work, we evaluated two openly available, deformable registration algorithms to perform this task. The first is the adaptive bases algorithm (ABA) (Rohde et al., 2003) which models the deformation field using a summation of radial basis functions (RBFs). The algorithm attempts to maximize the normalized mutual information (NMI) (Studholme et al., 1999) between two images, a similarity metric commonly used for registration of MR images (Wells III et al., 1996). An adaptation of this algorithm is provided as part of the JIST package (Chen et al., 2010). The second is SyN, a fluid based registration method that maximizes cross-correlation in order to find symmetric diffeomorphic maps between images. It was ranked very highly among state of the art registration algorithms in recent evaluations (Klein et al., 2010), and is offered as part of the Advanced Normalization Tools (ANTS) package (Avants et al., 2011).

Fig. 5 shows examples of spinal cord MRI registrations between an intensity atlas and a subject image using these two registration algorithms. As expected, we see significant registration errors in parts of the spinal cord. However, they provide sufficient initialization for the TOADS algorithm, which is fairly robust to such errors in the initialization. In Section 4.1 we evaluate the effectiveness of both of these registrations algorithms in addition to their impact on our final segmentation.

Figure 5.

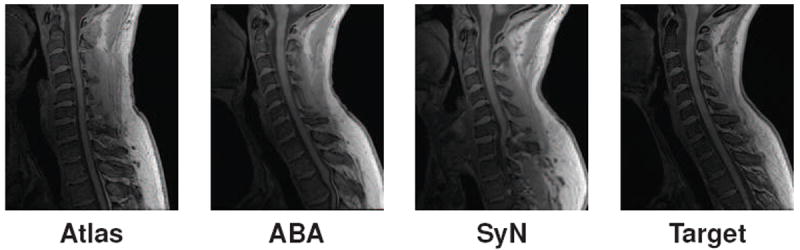
Example of registrations between an intensity atlas and a target image using ABA and SyN.

2.5. Topology Preserving Atlas Deformation

The second issue with including a deformable registration into the framework is that, in general, such registrations do not take into account the digital topology of the objects being deformed. The complexity of maintaining digital topology during registration is the primary reason why only a rigid alignment was used in the original TOADS algorithm, and even then, the transformation had to be applied carefully. Bazin and Pham (2008) showed that even simple rotations and/or scaling, which are purely homeomorphic in the continuous sense, are not necessarily homeomorphic in the digital domain. This demonstrates that simply having a homeomorphic (or diffeomorphic) transformation model is not sufficient to preserve digital topology. The only way to guarantee that a registration will produce a digitally homeomorphic transformation is to check the digital homeomorphism criterion at every step of the optimization. This is computationally expensive and becomes highly impractical for higher order registration that can generate complex deformations.

In Chen et al. (2011), this was addressed by using a technique, first presented in Bazin et al. (2007), that can generate a digitally homeomorphic approximation of a deformation field. The technique is applied after a deformation field is found between the intensity atlas and the target image. It starts by resetting the deformation field to zero and then slowly regrowing each deformation vector in the field back to its original value. This creates a series of incremental deformations that are applied to the topology atlas. At every step, the digital homeomorphism criterion is checked to make sure an increment does not break the topology of the atlas. If incrementing a particular deformation vector will cause a topology break, then that deformation is stopped from entirely growing back. This produces an approximation of the deformation field that can deform the topology atlas while maintaining its initial topology. Since this method is applied after the registration is completed, it also has the added advantage of being applicable to any registration algorithm.

In general, this digital homeomorphic approximation of the deformation field is very robust when the deformations are small or the atlas is simple. However, it can potentially introduce considerable segmentation errors when deforming complex topologies over large distances. This is a result of topology deadlocks that can occur, where a set of voxels are stuck in a configuration that prevents them from moving without breaking the object topology. The problem becomes more prominent when working with spinal cord MRI with large and varied fields of view, where the deformations produced by the registration are very large. An example of this is in the thoracic region of the spinal cord where the shape and distance can vary greatly between the atlas and target images. Fig. 6(b) shows an example of a topology deadlock that can be introduced when approximating such a deformation.

Figure 6.

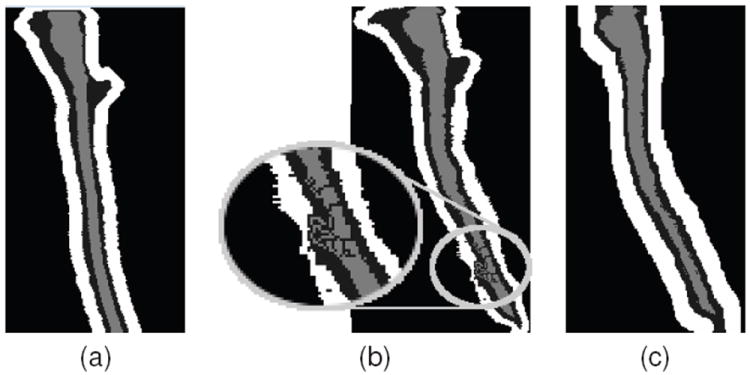
(a) Shows a topology atlas (spinal cord in light gray, CSF in dark gray, and wrapper in white) before initializing with a deformation learned from registration. (b) Shows an example of a topology deadlock that can occur when initializing the entire topology atlas by a digital homeomorphic approximation of the deformation. (c) Shows the result when only the spinal cord is initialized by the homeomorphic deformation, and the remaining topology atlas is rebuilt dynamically.

To prevent these errors, we introduce a dynamic approach for initializing the topology atlas. Instead of applying the learned deformation to all three objects in the atlas, we only apply it to the spinal cord object. After the spinal cord object has been deformed, the other two objects are then automatically added back to the atlas by following the topology rules listed in Sec 2.3. That is, the CSF object is added to the atlas as a dilation of the spinal cord label, and likewise the wrapper object is added as a dilation of the union of the spinal cord and CSF labels. Transforming and building the atlas on-the-fly in this manner greatly simplifies the homeomorphic deformation approximation, thereby allowing us to avoid topology deadlocks that can be introduced during the initial registration step. Fig. 6(c) shows how initializing the topology atlas in this manner can prevent the deadlock seen before.

We see from the example that initializing the topology atlas in this manner does alter the initial structure of the CSF and wrapper object in the atlas. However, it is important to remember that the role of the topology atlas is mainly to enforce our topology rule set. The initial structure of each object has little effect on the final segmentation, since all the objects are immediately thinned and then grown back to maximize their membership functions during the first iteration. It is more important that the atlas does not start with deadlocks that would prevent it from evolving in this manner.

2.6. Automated Atlas Construction

A major deficiency with existing methods for spinal cord segmentation is their inflexibility when facing very different datasets, particularly ones not used in the design of the algorithm. For example, in current methods that rely on deformable models (Koh et al., 2011; Mukherjee et al., 2010), the forces used in the algorithm are not immediately applicable for other datasets with different fields of view or MR-sequences. Redesigning such forces is time consuming and requires a certain level of expertise and familiarity with the algorithm.

Our introduction of deformable registration into the TOADS algorithm helps address this problem by allowing our atlas to be initialized on a wider variety of data. However, it is still possible for the target image to be so different from the atlas that a proper registration cannot be reasonably achieved. To overcome such situations, we describe an automatic process for generating the necessary topology and statistical atlases from a single manual segmentation of an image from the desired dataset. This is achieved by taking advantage of TOADS’s robustness to initialization errors, and the simple topology of the spinal cord.

2.6.1. Topology Atlas Construction

In Bazin and Pham (2008), the topology atlas was constructed by starting from an initial segmentation produced using the statistical atlas, and then manually editing the areas in the atlas that did not follow their assumptions about the topology. Constructing the topology atlas in this manner is not a trivial task. Small errors in the topology can easily be missed or obscured by the orientation the image is being viewed. In addition, the topology of every combination of objects in the image must be checked.

We follow a similar approach for our topology atlas construction by starting from a manual segmentation of our intensity atlas and fixing any topology errors that break our model. However, our task is greatly simplified due to the dynamic initialization approach introduced in Section 2.5. Since all the objects in our atlas are dynamically built from just the spinal cord object, we only need to correct the topology for that single object. In addition, since the spinal cord in our model has spherical topology, this correction can be performed automatically using a simple algorithm:

1. Find the largest connected component in the foreground.

2. Set all smaller connected components in the foreground to background.

3. Find the largest connected component in the background.

4. Set all smaller connected components in the background to foreground.

This allows the topology atlas for our method to be constructed quickly and automatically from a single segmentation.

2.6.2. Statistical Atlas Construction

Creating a true statistical atlas from a single manual segmentation is clearly not possible. By definition, such atlases require multiple subjects to empirically estimate the spatial variance of the anatomy. However, we make two observations. First, TOADS does not need a true statistical atlas to produce an accurate segmentation. The statistical prior only serves to provide a rough guideline for where a structure may lie in the image. Its primary purpose is to provide a prior for different tissues with similar intensities, which is not present in our problem. In our case, the underlying intensity provides the main driving force for the algorithm. Second, as we have shown in Fig. 5, deformable registration of the spinal cord is often inaccurate. As a result, statistical atlases constructed using such registrations are already fairly unreliable. Rather than representing the spatial variance of the spinal cord, they often just represent the variance of the registration error. This effect can be seen in Fig. 4, where the inferior ends of the spinal cords are not correctly aligned. Such registration variances are inconsistent across different images, and offer little value for the TOADS optimization. In certain cases, it may even degrade the segmentation result.

Given these considerations, we propose to approximate the statistical atlas by assuming a simple Gaussian distribution spatially around the single manual segmentation. This is equivalent to Gaussian smoothing each structure in the manual segmentation, and normalizing at each voxel. Fig. 7 shows a visual comparison between statistical priors constructed using the standard registration approach (with five segmentations) and our approximation of the atlas using Gaussian smoothing. In Section 4.2, we show that approximating the statistical atlas in this manner produces roughly the same accuracy as the standard atlas construction approach, and in certain cases can actually improve the overall accuracy of the final segmentation.

Figure 7.

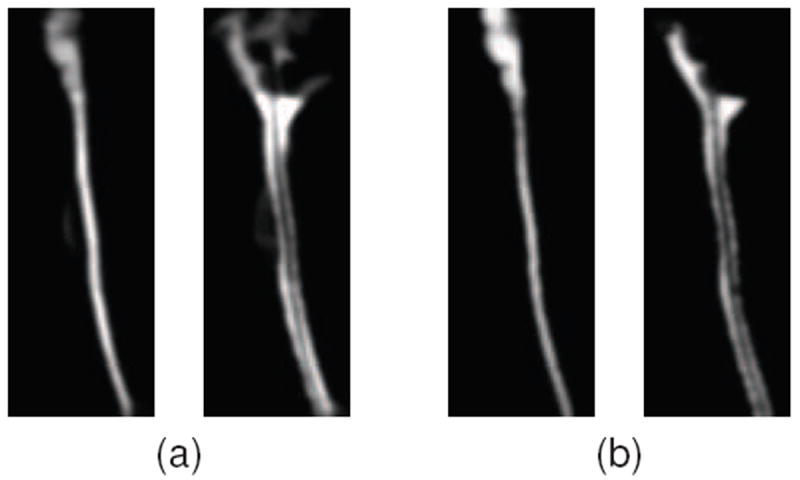
Comparison of statistical priors of the spinal cord and CSF constructed using (a) the standard registration approach (with five segmentations) and (b) a single manual segmentation Gaussian smoothed. A kernel size of σ = 1 was used in both cases. Further explanation and details are in Section 4.2.

3. Materials

Our algorithm was applied to two datasets having different population characteristics, MR protocols and scanners, and fields of view.

3.1. T1 Cohort

The first dataset used in our experiments consisted of MR images of the brain stem and spinal cord from the C1-T4 vertebrae acquired from seven patients diagnosed with multiple sclerosis (MS). Each image was acquired using a T1-weighted inversion recovery fast spoiled gradient recall (FSPGR) on a 3 Tesla GE Signa scanner (GE, Milwaukee WI) with the following parameters: TR=7.8ms, TE=2.98ms, TI=750ms, and flip angle=16°. The resolution of the acquired images was 1mm isotropic.

3.2. MT Cohort

The second dataset used in our experiments consisted of 238 MRIs of the cervical spinal cord, acquired from the C2-C6 vertebrae. The data were acquired from 18 healthy controls (HC) and 220 patients with multiple sclerosis (MS). The scans were performed with a 3 Tesla Philips Intera scanner (Philips Medical Systems, Best, The Netherlands) using body coil excitation and two-element phased array surface coil reception. The images were magnetization transfer (MT) prepared T2*-weighted gradient echoes, using an MT prepulse applied at 1.5 kHz off resonance (24 ms, five-lobed Sinc-Gauss pulse with maximum amplitude 9.5 mT), as described in (Smith et al., 2009). Other parameters: TR=110 ms, TE=13 ms, flip angle=9°, echo planar imaging factor 3, and SENSE acceleration factor 2. Each image had a through plane resolution of 2.25mm and an in-plane resolution of 0.6 × 0.6mm.

3.3. Manual Segmentations

All seven images in the T1 cohort were each manually segmented (labeling the spinal cord and the CSF) by two different raters. Twenty images (18 HC, 2 MS) in the MT cohort were similarly segmented by two different raters. Each rater labeled 10 and 14 subjects, respectively, with 4 images in common between the raters.

The image slice numbers corresponding to the C2 and C5 vertebrae were manually identified by a single rater in 146 images in the MT cohort. This subset was used in our statistical analysis in Section 4.4 and 4.5. Table 1 shows the detailed demographic information for this subset.

Table 1.

Detailed demographic description for the 146 subjects in the MT cohort with manual slice numbers for the C2 and C5 vertebrae (used in Section 4.4 and 4.5). Key: healthy controls (HC), clinically isolated syndrome (CIS), relapsing-remitting (RR), primary progressive (PP), and secondary progressive (SP).

	HC	CIS	RR	PP	SP
N (Male/Female)	15 (5/10)	5 (2/3)	76 (23/53)	16 (8/8)	34 (12/22)
Age (SD)	39.4 (9.1)	34.8 (9.6)	38.9 (10.5)	53.4 (6.7)	51.9 (7.3)

3.4. Metrics

We report the accuracy of our method in comparison to human raters by using the Dice coefficient (Dice, 1945),

$$\mathrm{Dice}(H,A)=\frac{2\left|H\cap A\right|}{\left|H\right|+\left|A\right|},$$

for a particular structure (e.g., cord or CSF), where H and A are the segmentations generated by the human rater and the algorithm, respectively. The Dice coefficient is a measure of set agreement and is commonly used as a volumetric measure for comparing the quality of automatic vs. manual segmentations. It has a range of [0.0, 1.0], where a value of 1.0 indicates perfect agreement between the algorithm and the manual result, while a score of 0.0 represents no overlap between the two.

4. Experimental Results

We perform several experiments to demonstrate the performance and applications of our spinal cord segmentation tool. Our first experiment evaluates the accuracy of our algorithm relative to human raters. It also considers the effect of our registration choice for initializing our atlases. We then evaluate the impact of our statistical atlas construction approach, and the size of the Gaussian smoothing kernel used in its construction. Lastly, we perform a large scale evaluation using the MT cohort to establish the robustness and potential clinical relevance of our algorithm.

4.1. Segmentation Comparison Against Manual Raters

We evaluated our automated segmentation results against the seven images from the T1 cohort and the twenty from the MT cohort that have corresponding manual segmentations. The Dice coefficient was calculated for the spinal cord, CSF, and the union of the two structures (i.e., the spinal canal). For each dataset, we evaluated using either ABA or SyN for initialization. Table 2 shows the mean and standard deviation of the Dice coefficient of our results against manual segmentations when initializing with each registration algorithm, and for each cohort.

Table 2.

Evaluation of the CSF, spinal cord (“Cord”), and combined (“CSF + Cord”) segmentation results against manual segmentations from two raters (R1 and R2) for the two cohorts (T1 and MT). Shown are the mean (standard deviation) of the Dice coefficient when using just the registration (ABA and SyN) for segmentation transfer, and the final segmentation result from the proposed method when using the registration for initialization.

T1	Registration Only			Final Segmentation
	CSF	Cord	CSF+Cord	CSF	Cord	CSF+Cord
ABA vs R1	0.67(0.10)	0.77(0.14)	0.70(0.12)	0.63(0.17)	0.82(0.18)	0.70(0.18)
ABA vs R2	0.65(0.09)	0.75(0.13)	0.68(0.10)	0.63(0.17)	0.77(0.15)	0.68(0.17)
SyN vs R1	0.13(0.11)	0.14(0.13)	0.13(0.11)	0.22(0.12)	0.28(0.18)	0.23(0.14)
SyN vs R2	0.12(0.09)	0.13(0.13)	0.12(0.10)	0.21(0.09)	0.26(0.17)	0.22(0.12)
R1 vs R2				0.81(0.03)	0.89(0.02)	0.84(0.02)
MT	Registration Only			Final Segmentation
	CSF	Cord	CSF+Cord	CSF	Cord	CSF+Cord
ABA vs R1	0.73(0.07)	0.83(0.07)	0.76(0.06)	0.85(0.03)	0.91(0.03)	0.88(0.02)
ABA vs R2	0.74(0.04)	0.87(0.01)	0.79(0.03)	0.84(0.02)	0.92(0.01)	0.87(0.01)
SyN vs R1	0.63(0.20)	0.73(0.25)	0.67(0.22)	0.72(0.28)	0.75(0.37)	0.74(0.31)
SyN vs R2	0.63(0.15)	0.70(0.21)	0.66(0.17)	0.82(0.05)	0.89(0.03)	0.85(0.04)
R1 vs R2				0.88(0.01)	0.93(0.01)	0.90(0.01)

In general, the algorithm performed better on the MT cohort than the T1 cohort, particularly for the CSF. This can be largely attributed to the better tissue contrast and smaller intensity inhomogeneities in the MT cohort images. These differences can be seen in Figs. 8 and 9, which show cropped examples of the original MRI, its manual segmentation, and our automatic segmentation results for each cohort. From the figures we see that the automatic results were very similar to the manual segmentations for both cases. However, the automatic results tended to be overall smoother due to the TOADS regularization. Comparing between the two figures, we see that the T1 cohort result had more areas where the CSF was mis-segmented as the spinal cord than in the MT cohort result. This is particularly noticeable in the inferior areas of the T1 image where the intensity inhomogeneity was very strong, and the contrast between the CSF and spinal cord was lower.

Figure 8.

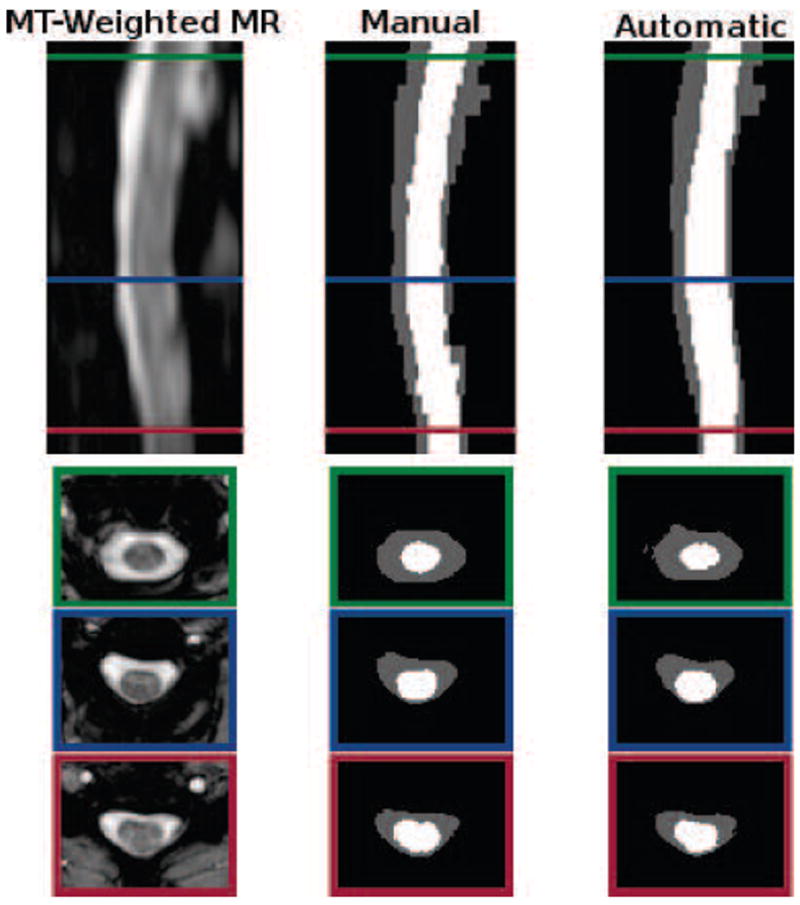
Cropped example of a MT-prepared T2*-weighted MRI segmentation by a human rater in comparison to the result from our algorithm. Shown are one sagittal and three axial views. The colored border around the axial slices denote the respective cross-section within the sagittal image. The Dice coefficient between the shown manual and automatic segmentations are 0.91 for the spinal cord (white) and 0.86 for the CSF (gray).

Figure 9.

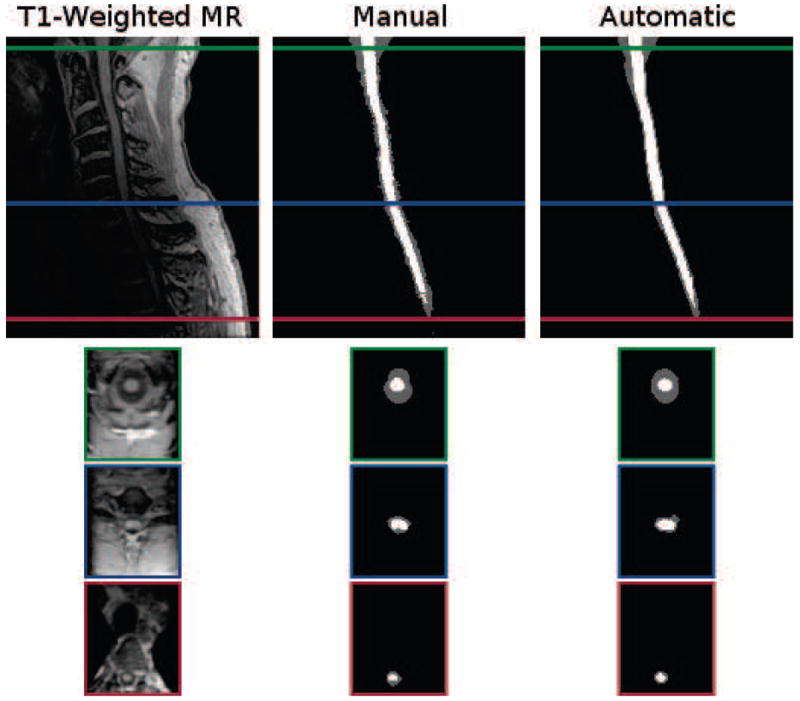
Cropped example of a T1-weighted MRI segmentation by a human rater in comparison to the result from our algorithm. Shown are one sagittal and three axial views. The colored border around the axial slices denote the respective cross-section within the sagittal image. The Dice coefficient between the shown manual and automatic segmentations are 0.87 for the spinal cord (white) and 0.73 for the CSF (gray).

The individual accuracy of each registration algorithm was also considered by looking at its ability to transfer the atlas segmentation to the target image through applying the learned deformation from the intensity atlas registration. Table 2 shows the Dice coefficient between the transferred segmentation from each registration algorithm and the manual segmentation for the target image. We see from these results that ABA generally performed much better than SyN for both datasets. Hence, it was the only registration algorithm considered in the remaining experiments.

4.2. Statistical Atlas Construction Parameters

The impact of the two statistical atlas construction approaches described in Secs. 2.3 and 2.6 was evaluated by repeating our algorithm on five images from each cohort, while using atlases from both approaches with increasing kernel sizes (σ) for the Gaussian smoothing. In general, σ can be seen as a parameter for controlling the capture range of the statistical atlas. A small value should be used if the initialization from the registration is believed to be very accurate and trustworthy. A large value can compensate for bad registrations, but may also cause the method to latch onto the wrong structure or artificially expand the segmentation size. Fig. 10 shows plots of the mean Dice coefficient between the manual segmentations and the automatic results, for each cohort, when using either the registration approach presented in Bazin and Pham (2008) or our single segmentation approach. For both cases, we ranged σ from one to five in increments of 0.5.

Figure 10.

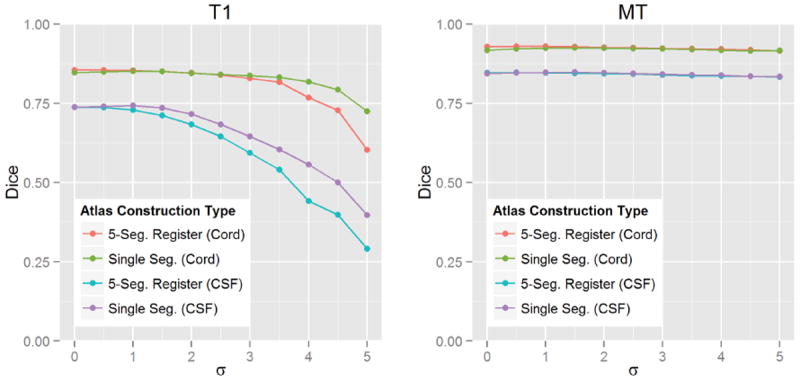
Average Dice coefficient between automatic and manual segmentations when using statistical atlases built from the standard registration based approach (using five segmentations) and our single segmentation approach, at different levels of Gaussian smoothing (σ). The left plot shows the average results for five T1-weighted images, and the right shows the average results for five MT-weighted images.

From the figure we see that, for the registration approach, the best performance was achieved without any smoothing (σ = 0). However, for our single segmentation approach, smoothing with σ = 1 was necessary to achieve the best performance. In addition, we see that the two approaches had roughly the same performance at their respective optimal configurations, with our single segmentation approach performing slightly better in the CSF for the T1 data. For these reasons, we chose to use our single segmentation approach (with σ = 1) for the experiments in the remaining sections.

4.3. Robustness in Large Scale Processing

To evaluate the robustness of our method, the entire MT cohort was processed using the proposed algorithm. The results were manually inspected for clear failures, which we designated as segmentations with roughly less than 75% spinal cord overlap (by visual inspection). Of the 238 images in the dataset, only eight failures were identified. Fig. 11 shows axial slices and their segmentation results for all eight failed cases. For reference, the figure also shows four successful cases from the processing.

Figure 11.

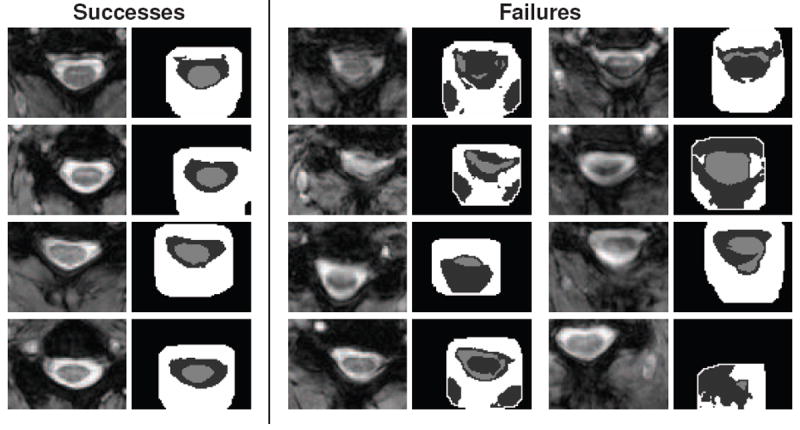
Shown are axial slices for four successful segmentations and the only eight failures found when processing the 238 images in the MT cohort with the proposed algorithm. For each pair of images, the left shows a crop of the original MRI, while the right shows the respective spinal cord (light gray), CSF (dark gray), and wrapper (white) segmentation results from the algorithm.

All eight failures were primarily due to strong artifacts present in each image. Seven of the cases were a result of motion artifacts that blurred the structures in the images. This caused the intensity for the spinal cord, CSF, and surrounding tissues to have similar means and high variances. This created segmentations where either the entire spinal canal was segmented as a single object, or the various tissues were classified interchangeably.

In the remaining failure, a strong intensity inhomogeneity was present that removed roughly a quarter of the image. This resulted in a very poor registration that translated the initial segmentation far from the spinal cord, which the algorithm could not recover from. We note that while the failures in Fig. 11 appear to be breaking the topology of the segmentation, it is actually a result of the 2D visualization of the images. In those cases where it appears that an object is in multiple pieces, the object is actually extending from above (or below) the slice.

4.4. Clinical Relevance

Statistical analysis was performed on the spinal cord volumes produced by our algorithm on the 146 images from the MT cohort that had manually selected slice numbers for the C2 and C5 vertebrae. For normalization, spinal cord volumes were divided by the length of distance between the C2 and C5 vertebrae, which produces normalized cross section areas (Healy et al., 2012).

Multivariate linear regression was used to perform age and sex adjusted Student’s t-tests between the healthy controls (HC) and patients with multiple sclerosis (MS). Pairwise group comparisons were also made between individual subgroups (healthy controls (HC), clinically isolated syndrome (CIS), relapsing-remitting (RR), primary progressive (PP), and secondary progressive (SP)). Table 3 shows the mean normalized cord area for each subgroup, and the significance of their difference after adjusting for age and sex. Significant differences were found when comparing healthy controls against the entire MS group (p-value = 0.042), however significant differences between healthy controls and individual MS subtypes could not be established. Within subtypes, significant differences were found when comparing secondary progressive patients against relapsing-remitting (p-value = 0.005) and primary progressive (p-value = 0.011) patients.

Table 3.

Pairwise group comparisons of normalized cord area (mm²) between healthy controls (HC) and patients with MS (ALL-MS) and the MS subtypes of clinically isolated syndrome (CIS), relapsing-remitting (RR), primary progressive (PP), and secondary progressive (SP). Shown are the mean and standard deviation of the normalized cord area for each group and the significance (p-values) of the cord area differences between each group pairing, after adjusting for age and sex.

Group Comparisons of Normalized Spinal Cord Area
	Area (mm2)	Pairwise p-Values
	Mean (SD)	CIS	RR	PP	SP	ALL-MS
HC	88.8 (14.5)	0.411	0.075	0.708	0.101	0.042
SP	68.7 (20.1)	0.826	0.005	0.011
PP	83.0 (19.2)	0.642	0.976
RR	81.2 (14.6)	0.779
CIS	83.1 (11.0)
ALL-MS	78.2 (17.4)

For the MS patients, semi-partial correlation was used to evaluate Pearson’s correlation coefficients between normalized cord area for both the Expanded Disability Status Scale (EDSS) and disease duration, while adjusting for age and sex. Further correlations were evaluated for the RR, PP, and SP subtypes. The CIS subtype was omitted due to the small number of subjects. Fig. 12 shows the relationship of normalized spinal cord area with EDSS (top plot) and disease duration (bottom plot), after adjusting the values for age and sex. In each case, the black line shows the relationship for the whole MS group, while colored lines indicate relationships for a particular MS subtype. Moderately weak, but significant relationships were found for normalized spinal cord area with both EDSS (r = −0.19, p-value = 0.03) and disease duration (r = −0.23, p-value = 0.01) when observing the whole MS group together. No relationship could be established when looking at each MS subtype group individually.

Figure 12.

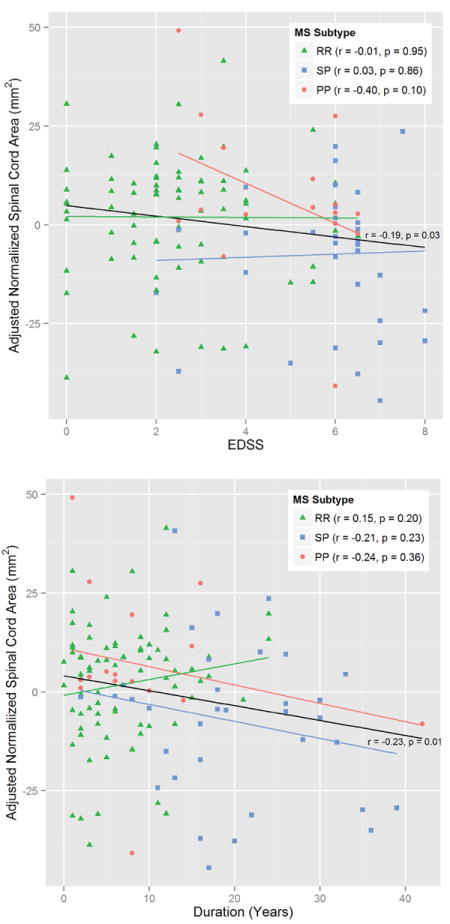
Correlation plots showing the relationship between normalized spinal cord area (age and sex adjusted) with EDSS (top) and disease duration (bottom) for MS patients. The black line shows the relationship for all MS patients grouped together. The colored lines indicate the relationship for the specific subtypes — relapsing remitting (RR) in green, secondary progressive (SP) in blue, and primary progressive (PP) in red. The correlation (r) and significance (p) are given for each line.

4.5. Exploratory Study of CSF Volumes

One advantage of our approach over existing methods is the ability to generate segmentations of cerebrospinal fluid (CSF) from the spinal cord image. To our knowledge, no study has been performed that observe the volume of spinal CSF with respect to multiple sclerosis. To demonstrate the potential of such analysis, we provide a basic exploratory study of such a measure. The data and methods used in this analysis is analogous to that used in 4.4 for the spinal cord volume. Since there are no clear guidelines for normalizing the CSF volume, we again normalize by the distance between the C2 to C5 vertebrae, producing a normalized CSF area.

Table 4 show the mean normalized CSF area for each MS subgroup, and the significance of their difference after adjusting for age and sex. No significant differences were found when comparing healthy controls against the entire MS group. However, several significant differences could be found when comparing against the progressive cases (SP and PP). The pairs where significant differences were found are SP vs. HC (p-value = 0.040), SP vs. RR (p-value < 0.001), and PP vs. RR (p-value = 0.003).

Table 4.

Pairwise group comparisons of normalized CSF area (mm²) between healthy controls (HC) and patients with MS (ALL-MS) and the MS subtypes of clinically isolated syndrome (CIS), relapsing-remitting (RR), primary progressive (PP), and secondary progressive (SP). Shown are the mean and standard deviation of the normalized CSF area for each group and the significance (p-values) of the CSF area differences between each group pairing, after adjusting for age and sex.

Group Comparisons of Normalized CSF Area
	Area (mm2)	Pairwise p-Values
	Mean (SD)	CIS	RR	PP	SP	ALL-MS
HC	128.3 (24.8)	0.850	0.304	0.472	0.040	0.141
SP	168.4 (45.5)	0.128	< 0.001	0.999
PP	173.7 (65.1)	0.990	0.003
RR	136.3 (28.3)	0.207
CIS	119.9 (33.5)
ALL-MS	148.6 (42.5)

5. Discussion

In this work we have presented a fully automatic approach for segmenting the spinal cord and cerebrospinal fluid from MRIs. Unlike existing methods, our approach is designed to be highly generalizable to spinal cord images of any field of view or MR contrast. The only criterion necessary for our algorithm is a reasonable registration between an atlas and the image being segmented. For data where such a registration is unreliable (i.e., if the images differs too greatly from the provided atlas), we have presented a fast and automatic approach for generating a suitable atlas using a single manual segmentation of an image from the desired dataset.

5.1. Accuracy and Robustness

Our evaluations show that the proposed method achieved high accuracy and robustness when compared against manual segmentations from two independent raters for two datasets with very different image characteristics. From Table 2, we see that on average our algorithm achieved a 0.91 Dice coefficient for the spinal cord and 0.85 Dice for the CSF when working with the MT-prepared T2*-weighted data. Such values are remarkably high, especially considering that the Dice coefficient is very sensitive to errors when the structures being compared are long and thin. In general, the overlap achieved by our algorithm on this data is on par with inter-rater accuracy for the spinal cord, and slightly lower for the CSF.

The T1-weighted data, which had a much larger field of view, proved to be more challenging. On average our algorithm achieved a 0.80 Dice coefficient for the spinal cord and 0.63 Dice for CSF when ran on this data. Overall, these values are still considered fairly high for Dice coefficients, particularly for the spinal cord. The lower CSF performance can be largely attributed to the strong field inhomogeneities in the image, making it difficult to distinguish it from surrounding tissues.

Our large scale evaluation on 238 images shows that the method is highly robust. Only eight failures were produced over the entire dataset, and all of them were a result of intense artifacts that rendered the images unusable. In the context of a clinical trial using the same MR-sequence, these example failures can provide a preliminary basis in the acquisition protocol for determining when an image contains too much artifact or distortion to be used with our algorithm. The overall quality and robustness of our results can be largely attributed to the topology constraint, which allows the algorithm to better handle the noise and artifacts that are prevalent in spinal cord MRIs.

5.2. Results Comparison Against Existing Literature

To our knowledge, none of the currently existing automatic MRI spinal cord segmentation algorithms (Koh et al., 2010, 2011; Mukherjee et al., 2010) nor the data used in their evaluation are openly available for download. This prevents a direct comparisons against their methods. However, compared against the Dice overlap reported in their work, on average our algorithm performed very favorably. Namely, Koh et al. (2010) achieved an average Dice of 0.70 when compared against two human raters on 52 images. In the alternative approach presented in Koh et al. (2011), they gained marginal improvements with an average Dice overlap of 0.71. In Mukherjee et al. (2010) a direct overlap validation was not performed, and instead only values for area correlation between manual raters was presented.

Our statistical results can be compared against several works studying the relationship between normalized spinal cord area and MS. The most relevant of these is the work presented by Horsfield et al. (2010) where a semi-automated approach was used to perform similar analysis as those we have presented in Section 4.4.

Our analysis when comparing normalized spinal cord volume between healthy control and MS patients produced several conclusions that are consistent with that reported by Horsfield et al. (2010). Namely, we showed significant differences between healthy controls and the entire MS group (p-value = 0.042), significant differences between relapsing-remitting and secondary progressive subtypes (p-value = 0.005), and a lack of significant difference between relapsing-remitting MS and healthy controls (p-value = 0.075). In addition, our correlation analysis with EDSS showed a moderate, but significant relationship between normalized spinal cord area for the whole MS group, but a lack of significant correlation when comparing against individual MS subtypes. Both of these results match those presented in Horsfield et al. (2010).

There are, however, two results that are distinct. Horsfield et al. (2010) found no significant relationship between normalized spinal cord volume and disease duration, while we found a small but significant correlation for the relationship. Horsfield et al. (2010) also found significant differences between HC and SP, while we did not (p-value = 0.101). This may be due, in part, to our control group being smaller and considerably younger than our SP group. Hence, first adjusting for age and sex might have removed any noticeable effect.

Finally, our analysis of CSF volume shows a capability that, to our knowledge, has not been expressed before. Our exploratory analysis on normalized CSF area showed a considerable trend of higher CSF in the progressive MS subtypes (SP and PP), with significant differences being found after adjusting for age and sex when compared against the RR subtype (p-value < 0.001 and p-value = 0.003, respectively), and between healthy controls and SP (p-value = 0.040).

5.3. Adapting to New Data

One major advantage of our algorithm is its ability to be quickly and automatically adapted for use with different spinal cord MRI data. We have designed a topology rule set that allows the topology atlas to be automatically constructed by correcting the topology of the spinal cord object and dynamically generating the remaining structures. We have also provided an alternative approach for approximating the statistical atlas, which does not require multiple manual segmentations to be registered to a common template. In Fig. 10 we show that if we Gaussian smooth a single manual segmentation, we can create an statistical atlas that provides roughly the same level of performance as an atlas generated through the standard registration approach. In addition, for the T1-weighted data, we see that this approach can actually be superior to the standard approach, particularly in the CSF. The main advantage, however, is that now only a single manual segmentation is necessary to construct all the atlases required for our algorithm to be entirely tailored to a specific dataset.

One important note regarding our algorithm’s adaptability is that the performance of the method is still heavily reliant on the data being used. As we see from the T1 and MT results, the performance is not guaranteed to be preserved when changing between MR-sequences. Our algorithm provides a rapid way to adapt to new datasets, which can be particularly useful if no existing method is available for such data. However, further evaluations are still necessary when applied to new MR-sequences and fields of view to ensure that the performance is preserved after the adaptation.

5.4. Conclusion

MRI of the spinal cord presents many challenges, such as noise and artifacts, which make automatic segmentation of the spinal cord and CSF a difficult task. We have presented a topology preserving approach for addressing this problem, and have shown its effectiveness for both accuracy and robustness. In addition, as spinal cord imaging rarely has a standard field of view or MR contrast, we assume that the atlases provided with our algorithm are not optimal for every type of spinal cord MRI data. Hence, we have gone to great length to allow our algorithm to be easily adaptable. This includes providing an automatic and reliable way to construct the necessary atlases from a single manual segmentation, and designing our framework so that it is not tied to a particular registration algorithm for initialization. This provides users with an option to use the registration algorithm that performs best on their particular given dataset.

Finally, our incorporation of deformable registration into TOADS has implications that extend beyond our application in the spinal cord. Allowing the atlas to be initialized deformably opens the model for segmentation in essentially any anatomy and image contrast where a successful registration can be achieved. Naturally, a topology and statistical atlas will have to be built for the specific anatomy, but our contribution has greatly generalized the framework for other applications. An implementation of the presented segmentation method and atlas construction approach can be freely downloaded as part of the Java Image Science Toolkit (JIST) software package at http://www.nitrc.org/projects/jist/.

Research Highlights.

• Fully automated topology preserving segmentation of the spinal cord.

• New capability of spinal cerebrospinal fluid segmentation.

• Capability to handle different fields of view.

• Evaluated on a cohort of more than two hundred subjects.