Correlation between Supercoiling and Conformational Motions of the Bacterial Flagellar Filament

Abstract

The bacterial flagellar filament is a very large macromolecular assembly of a single protein, flagellin. Various supercoiled states of the filament exist, which are formed by two structurally different conformations of flagellin in different ratios. We investigated the correlation between supercoiling of the protofilaments and molecular dynamics in the flagellar filament using quasielastic and elastic incoherent neutron scattering on the picosecond and nanosecond timescales. Thermal fluctuations in the straight L- and R-type filaments were measured and compared to the resting state of the wild-type filament. Amplitudes of motion on the picosecond timescale were found to be similar in the different conformational states. Mean-square displacements and protein resilience on the 0.1 ns timescale demonstrate that the L-type state is more flexible and less resilient than the R-type, whereas the wild-type state lies in between. Our results provide strong support that supercoiling of the protofilaments in the flagellar filament is determined by the strength of molecular forces in and between the flagellin subunits.

Introduction

Bacteria swim in aqueous medium by using their flagella, which act as true nanomachines (1). The bacterial flagellum consists of three parts: the basal body, the hook, and the filament. The basal body is included in the bacterial membrane and acts as a reversible rotary motor. It converts the flow of ion gradients across the membrane into mechanical work (2). The hook and the filament are located on the extracellular side. The filament acts as a propeller, and the flexible hook is the connection between the basal body and the filament. The filament reaches lengths up to 15 μm, but the diameter does not exceed 25 nm (1). The filament has a helical tubular structure made by polymerization of >20,000 copies of a single protein called flagellin. The filament can be described as a tubular structure made of 11 protofilaments or as a repeated helical assembly of 11 flagellin monomers (3). Both representations are equivalent. The wild-type filament has the ability to adopt different supercoiled forms depending on twisting torque and solution conditions such as pH and ionic strength (4–6). Theoretical predictions indicated that the filament could take 10 different supercoiled conformations, as well as two different straight forms (7–10). The extreme forms are the L- and R-type straight filaments, which consist of protofilaments with left-handed and right-handed helical symmetry, respectively (11). An illustration of the straight filament in the L-type and R-type conformations is shown in Fig. 1.

Figure 1.

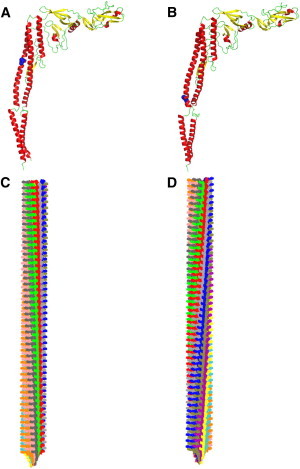
Structure of flagellin. (A and B) The L-type (A) and R-type (B) conformations (Protein Data Bank (PDB) structures 3A5X and 1UCU, respectively). The point mutations G426A and A449V, which induce the L- and R-type states, respectively, are drawn as blue spheres. (C and D) Models of the straight filament in the L-type (C) and R-type (D) conformations. The 11 protofilaments that compose the filament are drawn in different colors. Parameters of the filaments were taken from Yamashita et al. (12). To see this figure in color, go online.

The repeat distance between two molecules of flagellin along the protofilament in the L- and R-types was measured using x-ray fiber diffraction (12). The repeat distance was found to be 52.7 Å in the L-type, and slightly smaller, 51.9 Å, in the R-type. Between these two extreme states, 10 different supercoiled forms can be adopted by changing the ratio of the L- and R-type protofilaments (12,13). Packing interactions between the L- and R-type structures would therefore be responsible for the different conformations of the filament. The resting state of the wild-type supercoiled filament, for example, has a composition of two protofilaments in the R-type state and nine protofilaments in the L-type state (2R/9L) (12,13). The expression resting state refers here to the filament conformation in which the bacteria rest and do not swim. Interestingly, flagellin can be trapped either in the L-type or R-type state by single point mutations G426A and A449V, respectively. The structure of a flagellin fragment in the R-type form was first solved by x-ray crystallography (14). In consecutive works by Maki-Yonekura and colleagues, the atomic structures of the full-length flagellin in the R- and L-type filaments were determined by electron cryomicroscopy (15,16). The determination of atomistic structures allowed an accurate and detailed understanding of the key elements and molecular interactions of flagellin within the flagellar filament that are responsible for supercoiling of the protofilaments.

The structure of a protein determines its biological function. Conformational motions, however, play an equally important role. On one hand, molecular forces within proteins need to be sufficiently strong to keep the macromolecule in the folded conformation, whereas on the other hand, a certain flexibility of the protein structure is necessary to allow biological function. Static protein structures without any conformational mobility would not be biologically active. Concerning the flagellar filament, transitions between supercoiled states were investigated using coarse-grained (17) and molecular dynamics simulations (18) mainly with the aim of gaining information on the interactions between the different subunits. However, experimental evidence on molecular dynamics and forces of the different supercoiled states is still lacking.

Incoherent neutron scattering is a technique well-suited to the study of conformational motions within biological macromolecules. The incoherent scattering cross section of hydrogen is the largest of all elements that occur in biological matter, being also 40 times larger than that of its isotope deuterium (19). The scattering contribution of hydrogen atoms is therefore the dominating part in the incoherent scattering of concentrated protein solutions provided that they are performed using heavy water buffer (20). Hydrogen atoms are probes of average protein dynamics, as they are uniformly distributed within proteins. Neutron backscattering spectrometers offer a high-energy resolution, which allows detection of localized motions in proteins on the timescale of some nanoseconds and in the lengthscale of some Ångstroms. Mean-square displacements (MSDs) as a function of temperature can be determined from elastic incoherent neutron scattering (EINS) scans on backscattering spectrometers. On the other hand, neutron time-of-flight spectrometers access fast motions in proteins in the order of some picoseconds and in the lengthscale of some Ångstroms. Due to a high incident neutron flux on time-of-flight instruments, full quasielastic incoherent neutron scattering (QENS) measurements of proteins in solution are feasible within some days of beam time.

In this article, we report a comparative study on molecular dynamics in the flagellar filament in different conformational states. The aim of the study is to investigate whether protein dynamics on the picosecond to 0.1 ns timescale are modified by supercoiling of the protofilaments. Thermal fluctuations in the straight L- and R-type conformations were measured and compared to the wild-type state of the filament, which served as a reference. Amplitudes of motion on the picosecond timescale were explored using time-of-flight neutron spectroscopy. MSDs and protein resilience on the 0.1 ns timescale were measured using neutron backscattering spectroscopy.

Material and Methods

Sample preparation

Wild-type flagellin was expressed by the wild-type strain of Salmonella typhimurium, SJW1103. The R-type and L-types of flagellin with point mutations A449V and G426A were expressed by the mutated strains of S. typhimurium SJW1655 and SJW1660, respectively. The protein samples were polymerized by adding (NH₄)₂SO₄ to the monomeric flagellin solutions to a concentration of 1 M and stirred overnight. The filament solutions were centrifuged at 80,000 × g for ∼30 min. The pellet had gel-like properties and the residual buffer was removed. The pellet was dissolved in 10 ml of 1 M (NH₄)₂SO₄ D₂O (99.9 atom % D) buffer and stirred overnight. To remove the (NH₄)₂SO₄ and to exchange the H₂O with D₂O, the filament samples were repeatedly centrifuged, and the pellet was dissolved in D₂O buffer (0.1 M NaCl, 50 mM NaH₂PO₄, pD 7) until the (NH₄)₂SO4 concentration was ∼0.1 mM and the H₂O content ∼0.1%. The pellet was then spread on flat Al sample holders and sealed with indium wire. The beam paths of the Al sample holders were between 0.2 and 0.4 mm for the neutron experiments, depending on the amount of sample available. The amounts of pure protein measured on IN13 were 85 mg wild-type, 70 mg R-type, and 56 mg L-type. On TOFTOF the amounts of pure protein were 49 mg wild-type, 48 mg R-type, and 19 mg L-type. The hydration level, h = g D₂O/g protein, was determined by drying the samples, and it was found to be h = 4.4 for the wild-type and the R-type, and h = 4.2 for the L-type. The hydration levels are similar within the precision of the method. Protein concentrations, c = m/(V_D2O + mρ), and protein volume fractions, ϕ = ρc, were calculated from these values using D₂O bulk solvent volume, V_D2O, protein mass, m, and average protein partial specific volume, ρ = 0.71 mL/g (21). Protein concentrations were found to be c = 210 and 220 mg/mL, and volume fractions to be ϕ = 0.15 and 0.16, respectively.

Neutron scattering experiments

Neutron scattering was measured on the cold neutron time-of-flight spectrometer TOFTOF at the Forschungs-Neutronenquelle Heinz Maier-Leibnitz in Garching, Germany, and on the thermal high-resolution neutron backscattering spectrometer IN13 at the Institut Laue-Langevin in Grenoble, France.

On the TOFTOF spectrometer, the incident wavelength used was 5.1 Å, and the chopper speed and the chopper ratio were set to 12,000 rpm and 4, respectively. The setting yielded an energy resolution, ΔE, between 90 and 100 μeV (full width at half-maximum) depending on the scattering vector, and an accessible scattering vector range of 0.3 < q < 2.0 Å⁻¹. The energy resolution corresponds to observable motions up to $\Delta t=\hslash \text{/}\Delta E=7\text{ps}$ using the uncertainty relation. Alternatively, the measured instrumental resolution function was Fourier transformed into time space. The resolution function was found to decay to 10% at ∼30 ps, giving the maximum time during which relaxation functions typically can be determined. The protein samples and the D₂O buffer were measured at a temperature of 280 K. The intensities of the D₂O buffer were scaled according to the measured hydration levels and were subtracted from the data of the protein samples. The instrumental resolution function was measured with vanadium, and the detectors were calibrated with that measurement. The data were binned in steps of 0.01 meV and 0.1 Å⁻¹. Data were analyzed between −1.5 and 1.5 meV.

The instrument IN13 is characterized by a high energy resolution of ΔE = 8 μeV (full width at half-maximum), and a large accessible scattering vector range of 0.2 < q < 4.9 Å⁻¹. IN13 is sensitive to macromolecular motions in the space-time window of a few Ångstroms in some 0.1 ns. Neutron scattering of the samples was measured as a function of temperature. Measured data of the empty sample holder were subtracted from the samples. Neutron detectors were calibrated with a vanadium measurement.

The incoherent scattering contribution of D₂O buffer in the samples is ∼15% of the total incoherent-scattering cross section. On the timescale of the TOFTOF spectrometer, picosecond fluctuations of the D₂O molecules are seen and an accurate subtraction of the D₂O background is essential. D₂O buffer scatters predominantly incoherently up to ∼1.1 Å⁻¹, but coherent scattering starts to emerge at 1.2 Å⁻¹ (data not shown). During data analysis, the coherent contribution of the D₂O buffer could no longer be neglected above 1.5 Å⁻¹, and we limit our analysis of the data measured with the TOFTOF spectrometer to the region with q ≤ 1.5 Å⁻¹. On the timescale of IN13, motions of D₂O molecules are too fast and contribute only with a flat background to the measured data. No multiple scattering corrections were performed as the transmissions of all samples were >0.92.

Analysis of QENS data

QENS was interpreted with a scattering function, S(q,ω), consisting of a delta function for localized hydrogen motions and one Lorentzian for the quasielastic component:

$$S\left(q,\omega \right)=A_0\left(q\right)\times \delta \left(\omega \right)+\frac{1-A_0\left(q\right)}{\pi }\times \frac{\Gamma \left(q\right)}{{\omega }^2+\Gamma {\left(q\right)}^2}.$$ (1)

The factor A₀(q) is the so-called elastic incoherent structure factor (EISF), and Γ(q) are the half-widths at half-maximum of the Lorentzian. The q dependence of A₀(q) contains information on the amplitude of the localized motions. The complete theoretical scattering function, S_theo(q,ω), then consists of S(q,ω) multiplied by a Debye-Waller factor for fast thermal motions plus linear background, B(q):

$$S_{theo}\left(q,\omega \right)=\exp \left(-\langle u^2\rangle q^2/6\right)\times S\left(q,\omega \right)+B\left(q\right).$$ (2)

S_theo(q,ω) was convoluted with the instrumental resolution function and fitted to the measured QENS data using the software package DAVE (22).

Analysis of elastic neutron scattering data

Measured elastic intensities at sufficiently small q values are described by

$$I\left(q\right)\propto \exp \left(-\frac{<u^2>q^2}{6}\right),$$ (3)

which is termed Gaussian approximation.

MSD values were determined from the initial slope of the measured elastic intensities according to $<u^2>=-6\Delta \ln I\left(q\right)/\Delta q^2$. The <u²> were calculated in the range 0.6 < q² < 3.5 Å⁻² for IN13. For protein dynamics, the Gaussian approximation was found to be valid for <u²> × q² ∼ 8 (23). The <u²> values measured with IN13 in our study are in the range up to <u²> × q² < 8.1.

Becker and Smith (24) suggested an extension of the Gaussian approximation that accounts for 1), non-Gaussian single-atom scattering, and 2), dynamical heterogeneity in protein dynamics. The expression for non-Gaussian single-atom scattering reads

$$I\left(q\right)=e^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.q^2\langle u^2\rangle }\left(1+\sum _{m=2}^{\infty }{b}_m{\left(-q^2\right)}^m\right).$$ (4)

The correction for dynamical heterogeneity results in a sum of N exponentials, which can be approximated by

$$I\left(q\right)=e^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.q^2\langle u^2\rangle }\left[\frac{1}{N}\sum _{i=1}^N{e}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.q^2\left(\langle u_i^2\rangle -\langle u^2\rangle \right)}\right]=e^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.q^2\langle u^2\rangle }\left[\sum _{m=0}^{\infty }\frac{1}{m!}{\left(\frac{-q^2}{6}\right)}^m\mu \left(m\right)\right]\approx e^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.q^2\langle u^2\rangle }\left(1+\frac{q^4}{72}{\sigma }^2\right),$$ (5)

where μ(m) is the mth central moment of the distribution of <u²> and σ² is the variance of the <u²> distribution. Equations 4, with m = 2, and 5 have similar form and allow the description of the measured intensities up to larger q values. In this work, the q⁴ extension of Eq. 5 was used to fit the measured IN13 data from 0.2 < q² < 13 Å⁻² to determine both <u²> and σ².

Effective mean force constants, <k′>, that describe the resilience of the proteins were obtained from the slope of <u²> versus temperature, T, according to

$$<k^{\text{'}}>=\frac{0.00276}{\raisebox{1ex}{$\Delta <u^2>$}\!\left/ \!\raisebox{-1ex}{$\Delta T$}\right.}.$$ (6)

The units are chosen such that <k′> is in N m⁻¹ when <u²> is in Ų and T is in Kelvin (9,23).

Results and Discussion

Neutron scattering is a well-suited and established method for the study of molecular dynamics in biology and in soft condensed matter (25,26). Thermal motions in biological systems have been studied using incoherent neutron scattering mainly for globular (27–29) and membrane proteins (30,31), membranes (32–34), or in whole cells in vivo (35–38). Incoherent neutron scattering is not limited by size or molecular mass, and protein dynamics can be measured in very large protein assemblies such as the flagellar filament. In the following discussion, we present our experimental study on molecular dynamics in the straight L- and R-types of the flagellar filament and compare the results to the resting state of the wild-type supercoiled filament.

QENS

Fast protein motions in the picosecond time domain were measured using the TOFTOF neutron time-of-flight spectrometer. Typical measured QENS spectra and fits of Eq. 2 to the data for the wild-type and the L- and R-type conformations are shown in Fig. 2.

Figure 2.

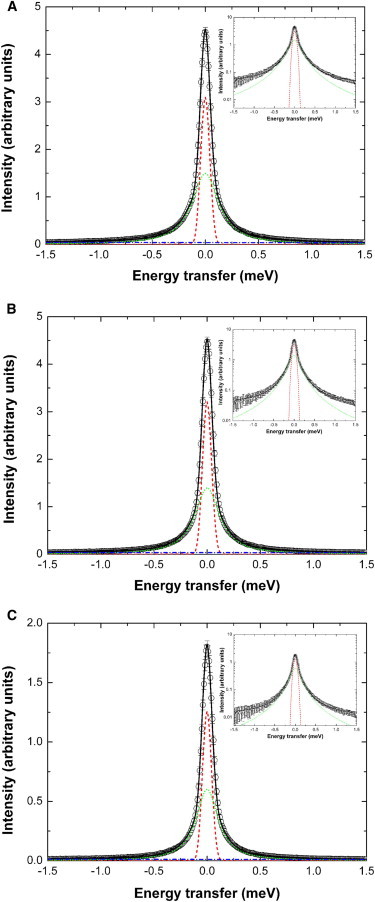
Measured quasielastic spectra. (A) Wild-type, (B) R-type, and (C) L-type states of the bacterial filament using the TOFTOF spectrometer at the scattering vector q = 1.5 Å⁻¹. The circles show measured data and the solid lines give the total fits (Eq. 2). The components correspond to the elastic fraction (dashed lines), the Lorentzian (dotted lines), and the linear background (dash-dotted lines). (Insets) The spectra on a logarithmic scale, illustrating the quality of the fits. To see this figure in color, go online.

The q dependence of the EISF was used to determine the amplitudes of motion. To be able to compare our results quantitatively with those of previous work, we used the Volino and Dianoux model for diffusion within a sphere (39). The equation for the diffusion-in-a-sphere model with radius a is $A_0\left(q\right)=A\times \left(1-p\right)\times {\left(3j_1\left(qa\right)/qa\right)}^2+p$, where A₀(q) is the EISF, p accounts for the fraction of immobile hydrogens, which are too slow and cannot be resolved by the instrument, (1 − p) is the fraction of hydrogens participating in the visible motions, and j₁(qa) is the first-order spherical Bessel function of the first kind. In an alternative approach, the EISF can also be interpreted using the Gaussian approximation according to $A_0\left(q\right)=A\times \left(1-p\right)\times e^{-\langle x^2\rangle \cdot q^2}+p$, where <x²> is the MSD in one direction around the average position. The prefactor A in both equations accounts for the fact that the EISF does not intercept unity at q → 0, which can be explained by a small contribution of multiple scattering (40). The measured EISF with the fits using the Gaussian approximation are shown in Fig. 3 A. To illustrate the quality of the fits, the residuals, defined as (data – fit)/error, are shown in Fig. 3 B. The obtained MSDs (<x²>), sphere radii (a), and immobile fractions (p) are summarized in Table 1. The immobile fractions of the Gaussian and the Volino-Dianoux model are identical. In general, the fits using the Gaussian approximation better describe the measured data, with a mean χ² of 1.02 compared to the Volino-Dianoux model, which gives a mean χ² of 1.98. On average, the sphere radii are larger by a factor of 1.35 than the <x²>.

Figure 3.

(Upper) EISFs of the different samples. The lines are fits to the data using the Gaussian approximation. (Lower) Residuals. To see this figure in color, go online.

Table 1.

Mean-square displacements, sphere radii, and immobile fractions determined from the experiment on the TOFTOF spectrometer

	<x2> (Å2)	a (Å)	p
Wild-type	2.2 ± 0.1	3.1 ± 0.1	0.32 ± 0.01
R-type	2.7 ± 0.1	3.4 ± 0.1	0.36 ± 0.01
L-type	2.3 ± 0.1	3.2 ± 0.1	0.36 ± 0.01

The main results from the EISF analysis are that on average, 35% of the nonexchangeable protons in the protein do not participate in the fast picosecond motions, and the amplitudes of motion of all three investigated conformational states of the flagellar filament are close to the average value of 2.4 Å² using the Gaussian approximation or 3.2 Å using the diffusion-in-a-sphere model. The amplitudes of motion of the R-type are slightly larger than those of the other mutants, whereas the immobile fraction of the wild-type is a bit smaller than those of the R- and L-types. The point mutations and different supercoiled conformations do not have a strong effect on the parameters deduced from the EISF on the picosecond timescale and do not allow unambiguous deduction about the differences between the mutants on the picosecond timescale. However, the absolute values of the amplitudes of motion using the diffusion-in-a-sphere model and the immobile fractions can be compared to those of previous studies that used neutron spectrometers with energy resolution similar to that used in this work and the same diffusion-in-a-sphere model. Jasnin and co-workers studied average macromolecular motions in whole Escherichia coli cells in vivo and observed amplitudes of motion of a = 3.1 Å with an immobile fraction of p = 0.61 at 280 K (35). Hemoglobin motions in whole red blood cells were classified with motional amplitudes of a = 2.0 Å and an immobile fraction of p = 0.35 at 288 K (36). Dynamics of hemoglobin in concentrated solution and in hydrated powder were found to have amplitudes of motion and immobile fractions of a = 2.3 Å and p = 0.38 at T = 290 K and a = 2.1 Å and p = 0.67 at T = 285 K, respectively (41). Experiments on dihydrofolate reductase yielded amplitudes of motion of a = 2.5 Å and p = 0.61 at T = 285 K (42). Thermophilic and mesophilic amylase were found to have amplitudes of motion and immobile fractions of a = 2.5 Å and p = 0.32, and a = 2.2 Å and p = 0.37, respectively, at 303 K (43). Note that in our experiment the sample temperature was set to 280 K, which is in the range of the temperatures in the cited studies. In a study that combined neutron scattering and computer simulations on hydrated C-phycocyanin, the simulated data were interpreted using the diffusion-in-a-sphere model (44). Side chains were found to have an average amplitude of motion of 2 Å, in the same range as the reported experimental values, whereas backbones were found to be significantly less mobile. Furthermore, the simulations demonstrated a strong radial dependence of the amplitudes of motion and relaxation times from the center of the protein toward the surface. On the experimentally accessible picosecond timescale, slow-moving side chains in the center of the protein or in the backbone would appear to belong to the immobile fraction. As a general experimental result, we found that compared with the set of proteins discussed above, flagellar filaments have the largest amplitudes of motion, comparable to those observed for whole E. coli cells. The fraction of hydrogens participating in the motion is similar to those in hemoglobin in solution, in red blood cells, and in thermophilic and mesophilic amylase in solution. Significantly more hydrogen atoms participate in the motions in the flagellar filament than in hydrated hemoglobin powder, dihydrofolate reductase, or E. coli. Thus, the large protein assembly of the flagellar filament is very flexible on the picosecond timescale when compared to other biological systems.

EINS

Slower internal motions in the flagellar filament on the 0.1 ns timescale were investigated using the neutron backscattering spectrometer IN13. Exemplary measured intensities, I(q), of the three samples are shown in Fig. 4.

Figure 4.

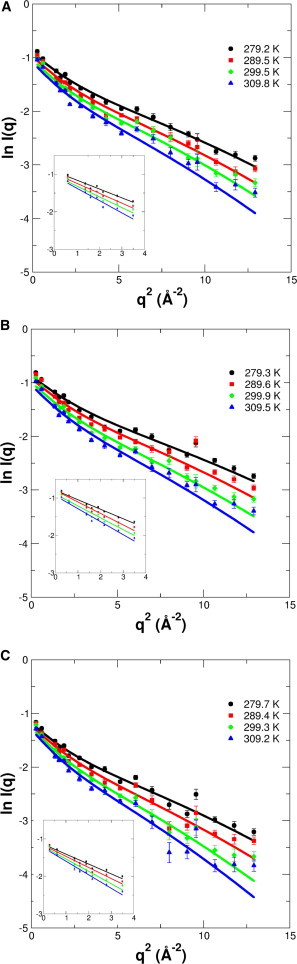
Measured elastic intensities. Experimental data obtained using the IN13 spectrometer of (A) the wild-type, (B) the R-type, and (C) the L-type bacterial filaments. The solid lines over the whole q² range are fits with the Gaussian model using the q⁴ extension. The straight lines in the insets are linear fits to lnI(q) versus q² using the Gaussian approximation in the initial slope. To see this figure in color, go online.

Neutron scattering could be detected down to ∼8% of the initial intensity over a large q² range from 0.04 to 12.9 Å⁻². Above that q² range the scattered signal of the protein is lost in the background noise. The concentrations of the filament samples were ∼200 mg/ml, and the center-of-mass diffusion of the monomeric flagellin with a molecular mass of 50 kDa would contribute to the <u²> on the 0.1 ns timescale. However, as the polymerized filament has an extremely large molecular mass, the contribution of center-of-mass diffusion to the <u²> on the 0.1 ns timescale can be safely neglected.

MSD values were calculated from the initial slope of lnI(q) versus q² using the classical Gaussian approximation. Examples of fits using the Gaussian approximation are given in the insets of Fig. 4, and the obtained <u²> values are shown in Fig. 5 A. Note here the relation <u²> = 6<x²>. Effective force constants, <k′>, were determined from the slope of the MSD versus temperature, and their values are reported in Table 2.

Figure 5.

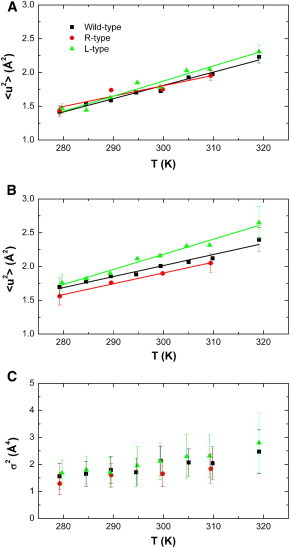
(A and B) MSDs of the bacterial filaments on the 0.1 ns timescale, determined by using the Gaussian approximation (A) and the Gaussian approximation with the q⁴ extension (B). (C) Variance, σ², determined by using the Gaussian approximation with the q⁴ extension. To see this figure in color, go online.

Table 2.

Force constants determined with IN13

	<k′> (N/m) from initial slope	<k′> (N/m) using q4 extension
Wild-type	0.14 ± 0.01	0.17 ± 0.01
R-type	0.18 ± 0.04	0.17 ± 0.01
L-type	0.12 ± 0.01	0.12 ± 0.01

Above q² = ∼5 Å⁻², the measured lnI(q) versus q² deviated from linear behavior, which was explained by either anharmonicity of the observed dynamics in proteins (27) or a distribution of harmonic motions with different amplitudes of motion (dynamical heterogeneity) (45). Becker and Smith suggested a modified version of the Gaussian approximation (24), which accounts for both anharmonicity and dynamical heterogeneity. The authors introduced an additional q⁴σ² term, where q⁴ is the scattering vector to the fourth power and σ² is the variance of the distribution of the MSD, which is independent of the actual shape of the distribution (see the Materials and Methods section for details). The Gaussian model with the q⁴ extension was fitted to the measured intensities over the whole q² range (Fig. 4). The obtained <u²> and σ² values using the Gaussian model with the q⁴ extension are given in Fig. 5, B and C, respectively. The Gaussian model with the q⁴ extension gives a good description of the measured data over the whole q² range. Including the next term, q⁶, does not improve the quality of the fits. In contrast, during the fitting process, the prefactor of the q⁶ term converges toward zero, and the same results are obtained as with the q⁴ term only. Effective force constants were also determined from the MSD as a function of temperature and are given in Table 2.

The MSD of the flagellar filament on the 0.1 ns timescale determined by using the Gaussian approximation are rather similar between the wild-type, the R-state, and the L-state at low temperatures, which is in agreement with the result that the amplitudes of motion are similar on the picosecond timescale at low temperature. The <u²> values of the L-state filament are slightly larger than those of the wild-type and the R-type at higher temperatures. Extrapolating the <u²> of the R-state to higher temperatures indicates a reduced flexibility of the R-state compared to the wild-type and the L-state. The Gaussian model including the q⁴ extension reveals differences in the MSD of the different conformational states more clearly. Using the q⁴ extension, the L-state was found to have the largest flexibility, whereas the R-state is significantly less flexible. The flexibility of the wild-type state lies between that of the two mutated states, being closer to the R-type. In that sense, the results of the Gaussian approximation and the model with the q⁴ extension are in agreement. The distribution of the <u²> of the different conformational states was found to be rather similar within the errors of all samples and increases slightly as a function of temperature (see Fig. 5 C). Effective force constants were calculated from the MSD values to investigate the influence of the point mutations on protein stiffness, also called protein resilience in the literature. A large resilience value indicates strong internal forces, whereas a small resilience value demonstrates that forces within the protein are weak. Independent of whether the Gaussian approximation or the q⁴ extension is used, the L-type conformation is softer than the R-type conformation. The resilience of the wild-type state was found to lie between that of the two mutations, and was more similar to the R-type than to the L-type conformation. Using the Gaussian approximation, the resilience of the wild-type state was found to lie between that of the L- and R-types, and using the model with the q⁴ extension, the resilience of the wild-type state was, within error, identical to that of the R-type.

A priori MSD values and effective force constants are independent properties of the biological macromolecules, and the general assumption that a flexible protein is always less resilient (softer) than a protein with lower flexibility is not always valid (28,46). For the flagellar filament, however, an inverse correlation between protein flexibility and resilience was found. The L-type conformation, which has the largest flexibility, was found to have the smallest resilience, whereas the R-type filament, which was found to have smaller flexibility, is more resilient. In the following discussion, we compare the absolute values of internal forces within the flagellar filament with those of other proteins studied using the IN13 spectrometer: In a previous study, the effect of heme binding on the dynamics of myoglobin was investigated (47), and values of <k′> were 0.10 N/m for wild-type myoglobin and 0.18 N/m for myoglobin without a heme group (apomyoglobin). The correlation between thermal stability, body temperature, and internal forces of hemoglobin from different species was studied. Effective force constants of 0.11 N/m for platypus hemoglobin (Hb), 0.15 N/m for human Hb, 0.18 N/m for crocodile Hb, and 0.23 N/m for chicken Hb were determined (28). In whole extremophilic bacteria in vivo, effective average force constants of macromolecules were determined to be 0.21, 0.42, 0.39, 0.67, and 0.60 N/m for the psychrophilic Aquaspirillum arcticum, the mesophilic E. coli and Proteus mirabilis, the thermophilic Thermus thermophilus, and the hyperthermophilic Aquifex pyrofilus cells, respectively (37). Therefore, the flagellar filament in the L-type conformation, with an effective force constant of 0.12 N/m, is a rather soft protein, whereas the R-type conformation and the wild-type state, with effective force constants of 0.18 (0.17) N/m and 0.14 (0.17) N/m, respectively, using the Gaussian approximation (q⁴ extension) would be classified as macromolecules with intermediate resilience. Finally, remembering that the resting state of the wild-type flagellar filament can be described as a combination of two R-type protofilaments and nine L-type protofilaments (12,13), one would expect, in theory, a resilience of the wild-type state of 0.13 N/m when taking the weighted <k′> values from the R-type and L-type straight filament using the Gaussian approximation. The experimental result for the wild-type, with an effective force constant of 0.14 ± 0.01 N/m using the Gaussian approximation, is close to that value, which would indicate that the resilience of the R-/L-type protofilaments in the wild-type state is similar to that in the R-/L-type straight filaments.

Conclusion

In this experimental study, we investigated the correlation between molecular dynamics and supercoiling of the protofilaments in the bacterial flagellar filament. Amplitudes of motion and the fraction of hydrogen atoms participating in the fast dynamics on the picosecond timescale were found to be independent of filament conformation. MSD values on the 0.1 ns timescale demonstrate that the L-type state is more flexible than the R-type, whereas the wild-type state has an intermediate flexibility. Protein resilience was found to be smaller in the L-type than in the R-type state. Previous studies using x-ray fiber diffraction reported that the repeat distance in the L-type filament is larger than that in the R-type (12). Structural comparison between the L-type and R-type filaments by electron cryomicroscopy showed that a cluster of hydrophobic residues in domain D1 of flagellin, which is responsible for determining the protofilament conformation, is stably formed in the R-type but not in the L-type (15). Our results provide strong support for the observation that local interactions within and between subunits are weaker in the L-type filament than in the R-type. Molecular forces in and between the flagellin subunits seem to be correlated with the packing interactions, the intersubunit spacing, and also the quaternary structure of the subunits.