Abstract
Time delay is an inevitable factor in neural networks due to the finite propagation velocity and switching speed. Neural system may lose its stability even for very small delay. In this paper, a two-neural network system with the different types of delays involved in self- and neighbor- connection has been investigated. The local asymptotic stability of the equilibrium point is studied by analyzing the corresponding characteristic equation. It is found that the multiple delays can lead the system dynamic behavior to exhibit stability switches. The delay-dependent stability regions are illustrated in the delay-parameter plane, followed which the double Hopf bifurcation points can be obtained from the intersection points of the first and second Hopf bifurcation, i.e., the corresponding characteristic equation has two pairs of imaginary eigenvalues. Taking the delays as the bifurcation parameters, the classification and bifurcation sets are obtained in terms of the central manifold reduction and normal form method. The dynamical behavior of system may exhibit the quasi-periodic solutions due to the Neimark- Sacker bifurcation. Finally, numerical simulations are made to verify the theoretical results.
Keywords: Neural network, Multiple delays, Stability switches, Double Hopf bifurcation, Quasi-periodic behavior
Introduction
Time delay is an inevitable factor in the signal transmission between biological neurons or electronic-model-neurons due to the finite propagation velocity and switching speed (Campbell 2007; Sun et al. 2010). The neural network with time delays can be described by a class of infinite-dimensional delayed differential equations. To study the effect of time delay on neural systems, Marcus and Westervelt (1989) improved the Hopfield neural network by introducing delay-coupling into the nonlinear activation function. Due to the existence of time delay, some complex dynamic phenomena can be easily obtained near the equilibrium point of neural system.
It is well known that neural system may lose its stability by making the equilibrium point unstable even for very small delays. However, effect of time delay is an interesting problem. For example, in field of machine tool industry, the disturbance of the pure regeneration (one single delay) by e.g. variable angle distribution between milling edges, time variation of the delay can increase the stability of the cutting process (Budak 2003; Zatarain et al. 2008). A small delay is sufficient to destabilize a system, but a large delay may stabilize a system (Liao and Lu 2011; Ye and Cui 2012). This implies that time delays can induce system to exhibit the multi-stable regions, which is called the delay-dependent stability regions. The system behavior switches from being stable to unstable and then back to stable as delay increases. As early as 1980s, Cooke and Grossman (1982) constructed a delayed system with at least N times switching. Hale and Huang (1993) investigated a linear differential equation and obtained some global geometrical characteristics of the stability regions located in two-delayed plane. For the general linear delayed systems consisting of multiple delays, the stability regions have been shown in two-delayed plane (Gu et al. 2005, 2007) and three-delayed space (Sipahi and Delice 2009; Gu and Naghnaeian 2011; Sipahi et al. 2011). Multiple delays can induce the stability switching of linear dynamical systems.
Bifurcation is one of the most important dynamical phenomena for the nonlinear neural systems (Jia et al. 2012; Liebovitch et al. 2011). Different bifurcations can lead to different kinds of dynamic behaviors. For example, Hopf bifurcation gives rise to the periodical activity, while double Hopf bifurcation results in two types of oscillations with different frequencies and a quasi-periodic behavior. Hopf bifurcation and periodical activity for neural network models with one single delay have been investigated extensively, see, e.g., Liao et al. (2007), Yuan and Li (2010), Guo and Huang (2003), Yan (2006) and the references cited therein. Due to the complexity of multiple delays, the analysis of stability and Hopf bifurcation for the multi-delayed differential equations is far from complete. Many researchers tried to fill in some “piece of the puzzle” for the multiple delays problem (Li et al. 1999). Considered the average/sum of time delays as the variable parameter and used the time-scale transformation, some multiple-delayed neural network systems with simple architecture can be transformed to the equivalent models with one single delay (Cao and Xiao 2007; Mao and Hu 2008; Wei and Zhang 2008).
In order to get a deep and clear understanding for multiple delays on dynamical behaviors, many researchers focused on the neural network systems with two delays, which are relatively simple. The stability and Hopf bifurcation for some special system with two delays have been investigated, such as neural system (Xu et al. 2006; Xu 2008), Lotka-Volterra predator–prey system (Nakaoka et al. 2006; Song et al. 2004), epidemic model (Cooke et al. 1996), tumor growth (Shi et al. 2011; Xu 2009), plastic deformation instability (Hilout et al. 2010), Mackey–Glass system (Li and Jiang 2011; Wan and Wei 2009), and so on. In 1994, Bélair and Campbell (1994) considered a simple motor control system with two negative delayed feedback loops. The stability regions of the equilibrium point are analyzed in the parameter 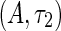 plane for the fixed delay τ1. In addition, the criticality of the Hopf bifurcation was considered in detail in terms of some numerical simulations. The result shows that the first order differential equation containing two delays can exhibit the double Hopf bifurcation. Similar analysis for the neural network with multiple delays can be referred in (Shayer and Campbell 2000; Yuan and Campbell 2004; Campbell et al. 2006). This approach can obtain a “piecewise global” perception for the bifurcation diagram in the multi-delayed system. However, to the best of our knowledge, in the existing relative literatures, there are few researchers chosen the multiple delays as the independent parameters for the dynamics analysis. The mutual effect of multiple delays on system dynamical behavior has been not considered yet. It is our research motivation in the present paper. In terms of the stability analysis of the corresponding linear part, the bifurcation points with high co-dimensional singularity and the bifurcation diagram are presented in the two-delayed plane for the neural network system.
plane for the fixed delay τ1. In addition, the criticality of the Hopf bifurcation was considered in detail in terms of some numerical simulations. The result shows that the first order differential equation containing two delays can exhibit the double Hopf bifurcation. Similar analysis for the neural network with multiple delays can be referred in (Shayer and Campbell 2000; Yuan and Campbell 2004; Campbell et al. 2006). This approach can obtain a “piecewise global” perception for the bifurcation diagram in the multi-delayed system. However, to the best of our knowledge, in the existing relative literatures, there are few researchers chosen the multiple delays as the independent parameters for the dynamics analysis. The mutual effect of multiple delays on system dynamical behavior has been not considered yet. It is our research motivation in the present paper. In terms of the stability analysis of the corresponding linear part, the bifurcation points with high co-dimensional singularity and the bifurcation diagram are presented in the two-delayed plane for the neural network system.
To study the two-delayed effects on neural system in detail, in this paper, a codimension-two singularity, namely the double Hopf bifurcation, is analyzed employing the multiple delays as the bifurcation parameters. Various dynamical behaviors are classified in the neighborhood of the singularity point. The bifurcation sets consisting of the oscillation behaviors with the different frequencies and quasi-periodic state are obtained in the delay parameter plane in terms of the central manifold reduction and normal form method (Orosz and Stepan 2004; Dombovari et al. 2008), which was introduced firstly by Faria and Magalhaes (1995a, b). The double Hopf bifurcation analysis for the differential equation with one single delay can be found in some existing works, such as (Yu et al. 2002; Xu et al. 2007; Xu and Pei 2008). This approach provides a convenient tool to compute a relatively simple form of the original differential equation, which can be used to analyze the system dynamic behaviors.
Neural system considered in this paper is described by the following differential equation:
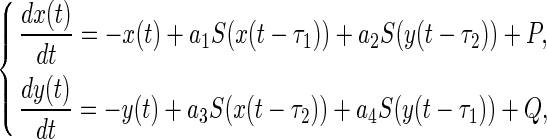 |
1 |
where x(t) and y(t) represent the neural behaviors at time t, a1, a2, a3 and a4 denote the coupled weights, τ1 and τ2 are the signal transmission delays for the self- and neighbor-connection, respectively, P and Q are the external inputs, the neuron activation function in S(u) is given by 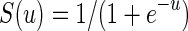 .
.
For neural network (1), when the self-connection delay τ1 = 0, our previous works have illustrated that system exhibits the complex dynamical behaviors for the different values of time delay and external input (Song and Xu 2009). The types of equilibrium points are studied analytically in details in terms of the characteristic equation and static bifurcation. The central manifold reduction and normal form method are employed to determine the Hopf bifurcation and its stability. In addition, time delay can affect the existence of the Bogdanov-Takens bifurcation (refer to Song and Xu 2012a). For some delayed interval, system may exhibit the saddle-node homoclinic bifurcation. Furthermore, when the variation slope ratio is proposed to the sigmoid activation function S, the dynamical behaviors of system (1) with τ1 = τ2 = τ may exhibit the chaotic behavior (Song and Xu 2012b).
The paper is organized as follows. Firstly, the local asymptotic stability of equilibrium point for system (1) is investigated by analyzing the corresponding characteristic equation of the linearized system. General stability criteria involving the time delays are obtained. The results show that stability switches may occur for some interval of delay τ1 when τ2 increases. In section “Existence of double Hopf bifurcation”, the stability regions and Hopf bifurcation curves are illustrated in the delay (τ1, τ2) parameter plane. The double Hopf bifurcation points can be obtained from the intersection points of the first and second Hopf bifurcation, i.e., the characteristic equation has double imaginary eigenvalue with multiplicity two. In section “Central manifold reduction”, regarding two delays as the bifurcation parameters, the typical dynamic behaviors near the double Hopf bifurcation are investigated in detail in terms of the central manifold reduction and normal form method. The system may exhibit the quasi-periodic solutions due to the Neimark-Sacker bifurcation. Finally, numerical simulations are made to verify the theoretical results. Conclusions are given in the last section.
Linear stability switches
The equilibrium point (x0, y0) for system (1) is the solution of the following equations:
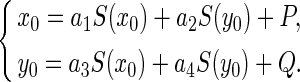 |
2 |
To translate (x0, y0) to the trivial equilibrium point, letting x → x−x0 nd y → y−y0 one has the linearized equation of system (1) given by
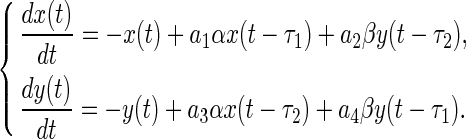 |
3 |
where 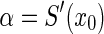 ,
, 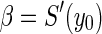 . The corresponding characteristic equation of system (3) is
. The corresponding characteristic equation of system (3) is
 |
4 |
namely
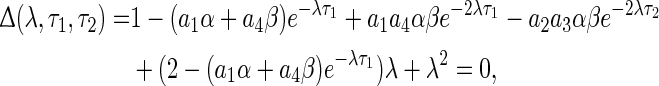 |
5 |
It is well known that the equilibrium point is locally asymptotically stable if and only if each of eigenvalues has negative real parts. It follows that the boundary of the stability region can be determined by equations λ = 0 and λ = iω (ω > 0). However, from the dynamical bifurcation theory, the typical static bifurcation is exhibited as the parameters varying near λ = 0. That is to say, system exhibits the different number of equilibrium point when the eigenvalue passes through the imaginary axis along the real axis (Song and Xu 2012a, b). However, in this paper, we just investigate the stability switches induced by multiple delays. Since time delay can not change the number of the equilibrium point, in the following section, the purely imaginary eigenvalues λ = iω (ω > 0) for the characteristic equation (5) are only studied. For simplify, the investigation begins with the case τ2 = 0 in (5) as follows
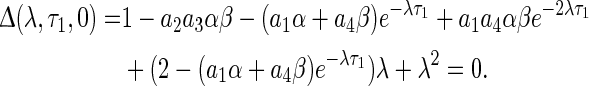 |
6 |
Without loss of generality, letting τ1 = 0 in (6) implies
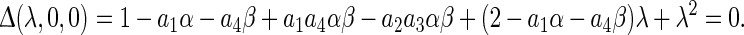 |
7 |
It follows from the Routh-Hurwitz criterion that the necessary and sufficient conditions for all roots of (7) having negative real parts is given by
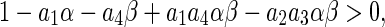 |
8 |
and
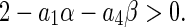 |
9 |
This implies that the equilibrium point (x0, y0) is locally asymptotically stable if the parameters are satisfied with the conditions of (8) and (9). With the time delay τ1 varying, system (1) will lose the stability. To obtain such critical values of time delay, supposing λ = iv (v > 0) is a pair of purely imaginary roots of (6), one has
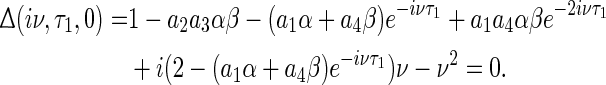 |
10 |
Separating (10) into the real and imaginary parts yields
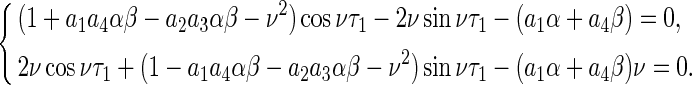 |
11 |
Taking the square, adding the equations and performing some simplification processes, we have
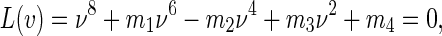 |
12 |
where
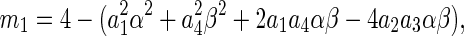 |
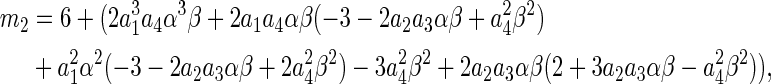 |
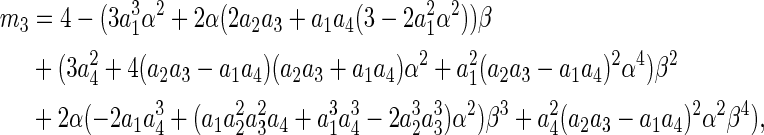 |
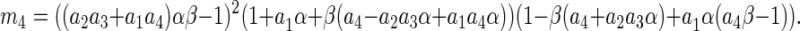 |
Without loss of generality, letting (12) has a number of positive and simple roots vi = 1, 2, …, one has the following critical delays
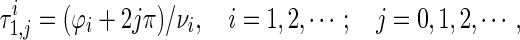 |
13 |
where 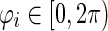 and satisfied with
and satisfied with
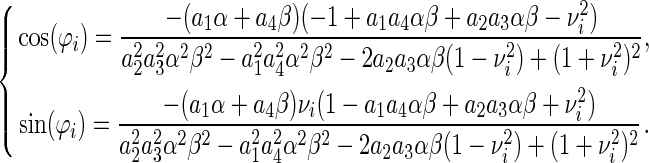 |
14 |
In order to determine whether the real part of eigenvalue increases or decreases when delay τ1 crosses the critical values 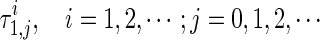 .
.
Differentiating λ with respect to τ1 in (10) reaches
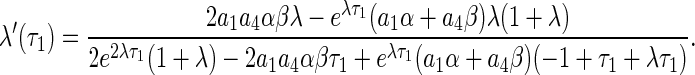 |
15 |
Moreover, as shown in Hu and Wang (2002), one obtains
 |
16 |
Therefore, based on the conditions of (8) and (9), one obtains the effect of delay τ1 on the eigenvalue of characteristic equation (6) by using the transversality condition (16) and the Hopf bifurcation theorem of functional differential equation. When the polynomial L(v) has no positive real root, all eigenvalues of the characteristic equation (6) have negative real parts for the arbitrary τ1. If L(v) has only one positive and simple root (not multiple root) v0 satisfied with 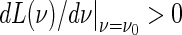 , there exists the critical delayed value
, there exists the critical delayed value 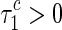 such that all the eigenvalues of the characteristic equation (6) have negative real parts for
such that all the eigenvalues of the characteristic equation (6) have negative real parts for 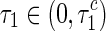 and at least one root has a positive real part for
and at least one root has a positive real part for 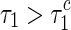 . Furthermore, if L(v) has two positive and simple roots 0 < v1 < v2 satisfied with
. Furthermore, if L(v) has two positive and simple roots 0 < v1 < v2 satisfied with 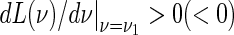 and
and 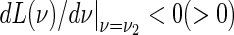 , there exist a finite number of the delayed τ1 intervals in which all eigenvalues of the characteristic equation (6) have negative real parts. However, when L(v) has at least three positive and simple roots 0 < v1 < v2 < v3 < …, the distribution of eigenvalues in the complex plane is very complexity.
, there exist a finite number of the delayed τ1 intervals in which all eigenvalues of the characteristic equation (6) have negative real parts. However, when L(v) has at least three positive and simple roots 0 < v1 < v2 < v3 < …, the distribution of eigenvalues in the complex plane is very complexity.
In order to investigate the effect of multiple delays on the local stability of equilibrium point, we regard τ2 as the varying parameter for any fixed delay τ1. Letting λ = iω (ω > 0) is the simple root of characteristic equation (5), one obtains
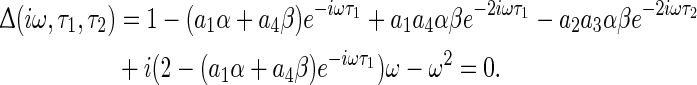 |
Separating the real and imaginary parts gives
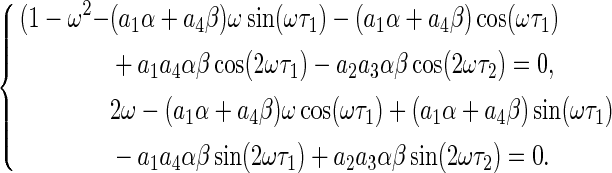 |
17 |
Eliminating τ2 from (17), one has
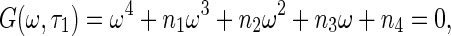 |
18 |
where
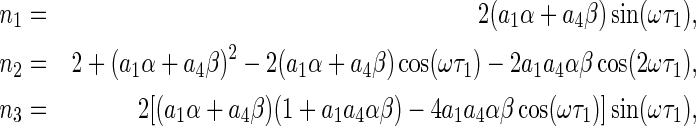 |
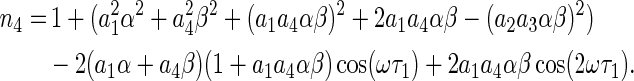 |
If (18) has a number of positive and simple roots ωi, i = 1, 2, …, then (5) has a series of critical delays
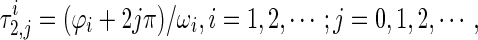 |
19 |
where 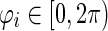 and satisfied with
and satisfied with
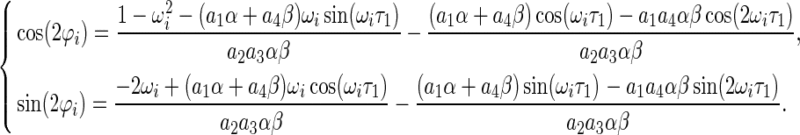 |
20 |
To make sure the occurrence of the Hopf bifurcation, it is needed to check the transversality condition. Without loss of generality, the time delay τ2 is chosen as the bifurcation parameter. The necessary condition for the existence of the Hopf bifurcation is that the critical eigenvalues cross the imaginary axis with non-zero velocity. Differentiating λ with respect to τ2 in (5), one reaches
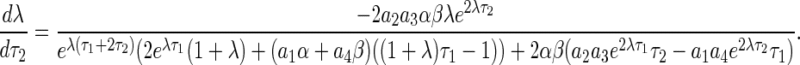 |
21 |
It follows that
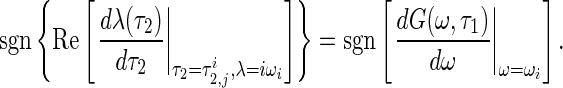 |
22 |
Based on the transversality condition (22) and the Hopf bifurcation theorem, one has the following assertions when each eigenvalue of the characteristic equation (6) has negative real part. If (18) has no positive root, the equilibrium point of system (1) is locally asymptotically stable for the arbitrary delay τ2, which is called the delay-independent stability. On the other hand, if (18) has one simple positive root ω0 satisfied with 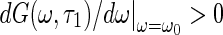 , there exists only a critical delay value denoted by τc. All eigenvalues of system (1) have strictly negative real parts for
, there exists only a critical delay value denoted by τc. All eigenvalues of system (1) have strictly negative real parts for 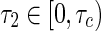 , while at least one of eigenvalues with positive real part for
, while at least one of eigenvalues with positive real part for 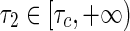 . The equilibrium point of system loses its stability via a Hopf bifurcation. The direction and stability of the Hopf bifurcation can be studied by means of the central manifold reduction and normal form method (Song and Xu 2012c). Furthermore, if G(ω, τ1) has two positive and simple roots 0 < ω1 < ω2 satisfied with
. The equilibrium point of system loses its stability via a Hopf bifurcation. The direction and stability of the Hopf bifurcation can be studied by means of the central manifold reduction and normal form method (Song and Xu 2012c). Furthermore, if G(ω, τ1) has two positive and simple roots 0 < ω1 < ω2 satisfied with 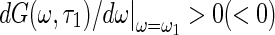 and
and 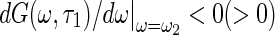 , there exist a finite number of the delayed τ2 intervals in which all eigenvalues of the characteristic equation (5) have negative real parts. It implies that there exist a finite number of delayed intervals. If time delay is fixed into these intervals, the equilibrium point is locally asymptotically stable, while instable for the outside of the delayed ranges. That is to say, the system dynamic switches from stable to unstable, and then back to stable when delay increases and crosses the critical delayed values.
, there exist a finite number of the delayed τ2 intervals in which all eigenvalues of the characteristic equation (5) have negative real parts. It implies that there exist a finite number of delayed intervals. If time delay is fixed into these intervals, the equilibrium point is locally asymptotically stable, while instable for the outside of the delayed ranges. That is to say, the system dynamic switches from stable to unstable, and then back to stable when delay increases and crosses the critical delayed values.
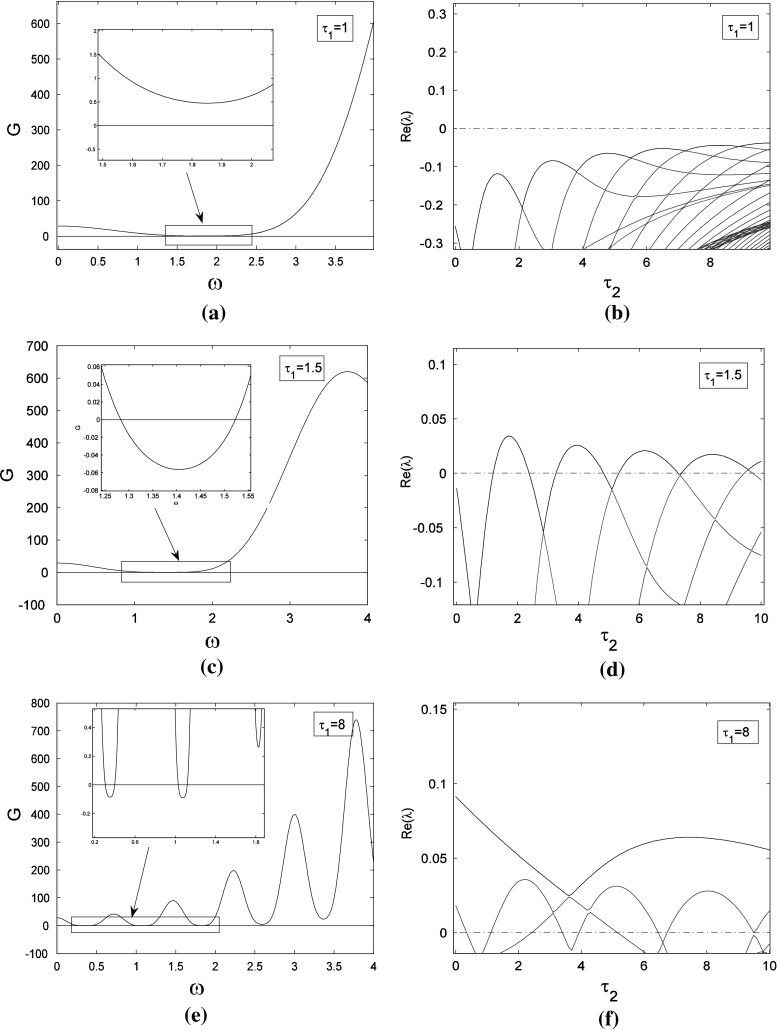
For example, we choose the coupled weights and external inputs as a1 = −6, a2 = 2.5, a3 = 2.5, a4 = −6, P = 0.4 and Q = 0.4, respectively. The time delays of self- and neighbor-connection, namely τ1 and τ2 are considered as the variable parameters. The figures of function G (18) and eigenvalue real parts of (5) are displayed in Fig. 1 for the different self-connection delay τ1, where the eigenvalue real parts are obtained with the aid of the numerical tool DDE BIFTOOL (Engelborghs et al. 2002). Figure 1a shows that the curve determined by function G and the line G = 0 have not intersection point when ω > 0 holds. It implies that function G (18) exhibits no positive real root for the fixed delay τ1 = 1. The real parts of all eigenvalues have the negative part, as shown in Fig. 1b. The equilibrium point of system (1) is locally asymptotically stable for the arbitrary delay τ2. With the self-connection delay τ1 increasing to 1.5, the curve determined by function G moves down and crosses the line G = 0. Function G (18) has two positive roots 1.2827 and 1.523, as shown in Fig. 1c. It follows from Fig. 1d that there exist the delay τ2 intervals in which the eigenvalues have the negative parts. The system dynamics switch from stable to unstable, and then back to stable state with delay τ2 increasing. It implies that if self-connection delay τ1 is fixed, we can adjust the neighbor-connection delay τ2 into the stability regions to suppress system vibration. When delay τ1 is increased to 8, function G has two pairs of positive roots, as shown in Fig. 1e. However, at this time, the maximum eigenvalue of (5) for the fixed delay τ1 = 0, i.e. the characteristic equation (6) has positive real part 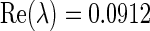 . The equilibrium point of system (1) is unstable for any delay τ2, as shown in Fig. 1f.
. The equilibrium point of system (1) is unstable for any delay τ2, as shown in Fig. 1f.
Fig. 1.
Roofs of function G (left column) and eigenvalue real parts with τ 2 varying (right column) for the fixed self-connection delay a–b
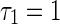 , c–d
, c–d
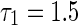 and e–f
and e–f
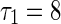 , respectively. The other parameters are chosen as a
1 = −6, a
2 = 2.5, a
3 = 2.5, a
4 = −6, P = 0.4, Q = 0.4
, respectively. The other parameters are chosen as a
1 = −6, a
2 = 2.5, a
3 = 2.5, a
4 = −6, P = 0.4, Q = 0.4
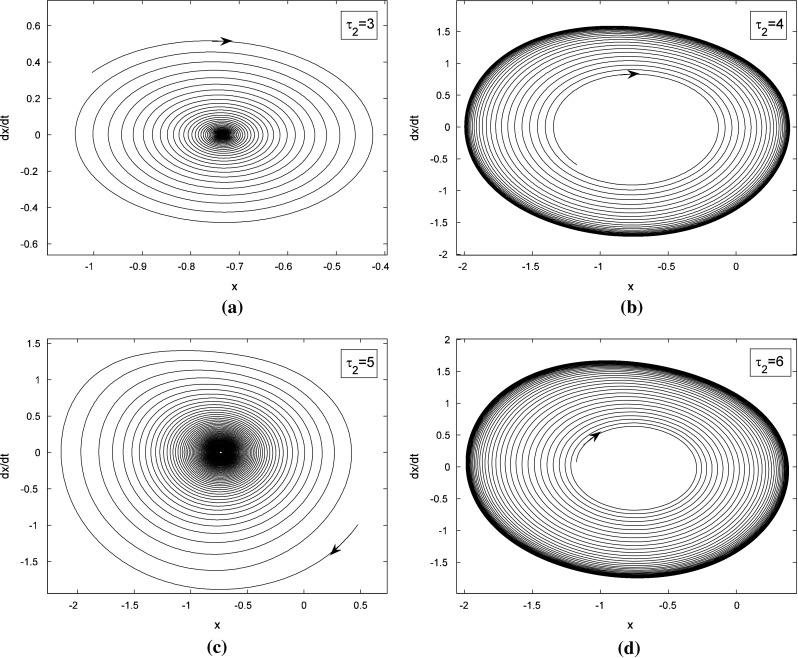
To get a deep investigation for the stability switches of equilibrium point, we fix the self-connection delay τ1 = 1.5. The partial eigenvalues and phase portraits are shown in Figs. 2 and 3 respectively for the different delay τ2. Figure 2a shows the maximum eigenvalues are a conjugate pair with negative part given by −0.0295 ± 1.5705i, where the neighbor-connection delay is fixed as τ2 = 3. It implies that the equilibrium point of system (1) is locally asymptotically stable, as shown in Fig. 3a. Letting τ1 = 1.5 and varying τ2 yield that the conjugate pair start to pass through the imaginary axis and go into the right-half in the complex plane. For τ2 = 4, the pair become to be 0.0256 ± 1.4012i shown in Fig. 2b, which suggests that the equilibrium point loses its stability (Fig. 3b). Continuing to increase τ2, the conjugate pair return and pass through the imaginary axis again. The maximum eigenvalues with negative real parts occurs in the left-hand of complex plane. Figure 2c shows the eigenvalues are −0.00936 ± 1.2591i for the fixed delay τ2 = 5. The equilibrium point of system is stabilized again by the neighbor-connection delay τ2, as shown in Fig. 3c. If the delay τ2 is fixed as τ2 = 6, the maximum eigenvalues are conjugate pair with positive part 0.0199 ± 1.4311i, as shown in Fig. 2d. The equilibrium point loses its stability again (Fig. 3d). In a word, time delay can lead system to exhibit multi-stable regions. The dynamics of equilibrium point can multi-switch from stable to unstable, and then back to stable state.
Fig. 2.
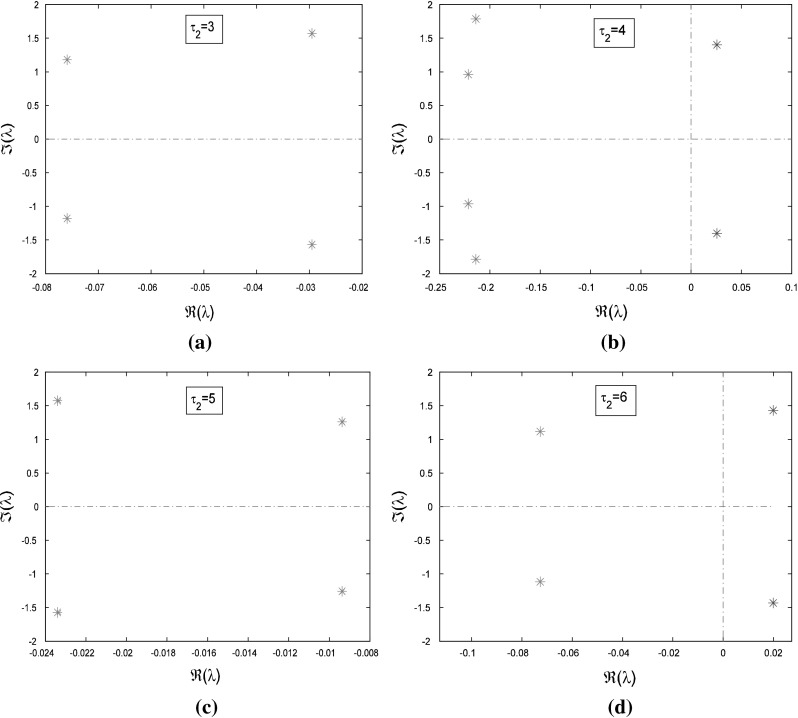
Distribution of eigenvalues with time delay τ
2 varying a
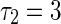 , b
, b
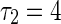 , c
, c
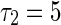 and d
and d
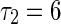 for the fixed parameters a
1 = −6, a
2 = 2.5, a
3 = 2.5, a
4 = −6, P = 0.4, Q = 0.4,
for the fixed parameters a
1 = −6, a
2 = 2.5, a
3 = 2.5, a
4 = −6, P = 0.4, Q = 0.4, 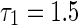 , where the asterisk in green represents the eigenvalues with negative real part and one with positive real part is in red color
, where the asterisk in green represents the eigenvalues with negative real part and one with positive real part is in red color
Fig. 3.
Phase portraits with time delay τ
2 varying a
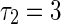 , b
, b
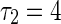 , c
, c
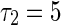 and d
and d
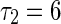 for the fixed parameters a
1 = −6, a
2 = 2.5, a
3 = 2.5, a
4 = −6, P = 0.4, Q = 0.4,
for the fixed parameters a
1 = −6, a
2 = 2.5, a
3 = 2.5, a
4 = −6, P = 0.4, Q = 0.4, 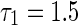
Existence of double Hopf bifurcation
It follows from above section that the multiple roots of equation (18) can lead system (1) exhibit the phenomenon of stability switches. The dynamical behavior of equilibrium point undergoes the multiple transitions between stability and instability when delays increase and cross the critical delayed values. In this section, we will illustrate these critical values and find the stability regions located in the delayed plane. To this end, the Hopf bifurcation curves represented by delay parameters are investigated. The coordinate values of the intersection points of these curves are presented, which are the points of the double Hopf bifurcation.
As mentioned above, two pairs of purely imaginary solutions of equation (5) are denoted by  , with ω2 > ω1 > 0. Then two series of the critical delays corresponding to such pairs of purely imaginary eigenvalues are given by
, with ω2 > ω1 > 0. Then two series of the critical delays corresponding to such pairs of purely imaginary eigenvalues are given by
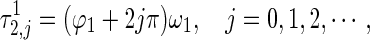 |
23 |
where 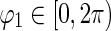 ,
,
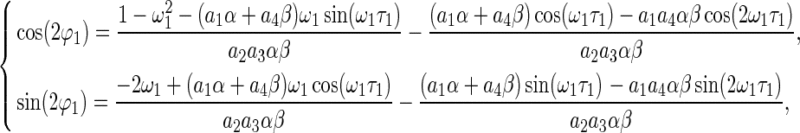 |
and
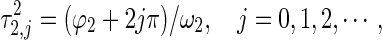 |
24 |
where 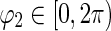 ,
,
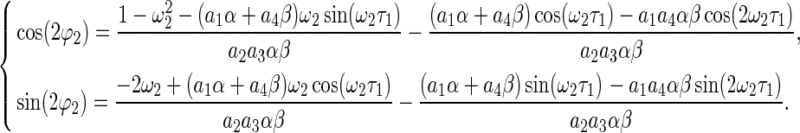 |
It follows from (21) that the sign of  at
at  ,
, 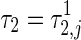 and
and 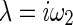 ,
, 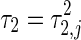 is difficult to determine analytically in terms of the expression of ω1,2. But it can be easily computed numerically. In fact, numerical results show that the quantity of
is difficult to determine analytically in terms of the expression of ω1,2. But it can be easily computed numerically. In fact, numerical results show that the quantity of 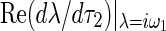 is negative and
is negative and 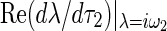 is positive. This implies that the crossing of the imaginary axis is from left to right as τ2 increases to a certain critical value
is positive. This implies that the crossing of the imaginary axis is from left to right as τ2 increases to a certain critical value 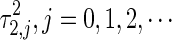 corresponding to ω2, and crossing from right to left occurs at a certain values
corresponding to ω2, and crossing from right to left occurs at a certain values 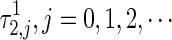 corresponding to ω2.
corresponding to ω2.
For instance, if 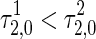 holds for some certain intervals of τ1, then the unstable equilibrium point becomes stable as τ2 is increased to cross the critical value
holds for some certain intervals of τ1, then the unstable equilibrium point becomes stable as τ2 is increased to cross the critical value 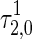 . When τ2 is further increased to pass through the critical value
. When τ2 is further increased to pass through the critical value 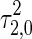 , the equilibrium point loses its stability again, where a pair of eigenvalues cross the imaginary axis and arrive to the right half plane. The occurrence and termination of stability switches for the equilibrium point are located at the points of the first and second Hopf bifurcation corresponding ω1 and ω2 frequencies, respectively. Similarly, higher order stability regions may be located by
, the equilibrium point loses its stability again, where a pair of eigenvalues cross the imaginary axis and arrive to the right half plane. The occurrence and termination of stability switches for the equilibrium point are located at the points of the first and second Hopf bifurcation corresponding ω1 and ω2 frequencies, respectively. Similarly, higher order stability regions may be located by 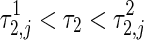 for 1, 2, …, resulting in a possibility of multiple stability regions.
for 1, 2, …, resulting in a possibility of multiple stability regions.
Furthermore, the double Hopf bifurcation may occur when the two critical delays are identical, which correspond to the different frequencies ω1 and ω2. Geometrically, the double Hopf bifurcation points are the intersections of the first and second Hopf bifurcation curves. Owing to the multiple delays of system (1) considered in the present paper, more complicated expressions have been derived for the critical delays. The possible points of the intersection for the Hopf bifurcation curves cannot be given in a theoretical form. But for a given set of the system parameters, the double Hopf bifurcation points can be solved by the numerical procedure.
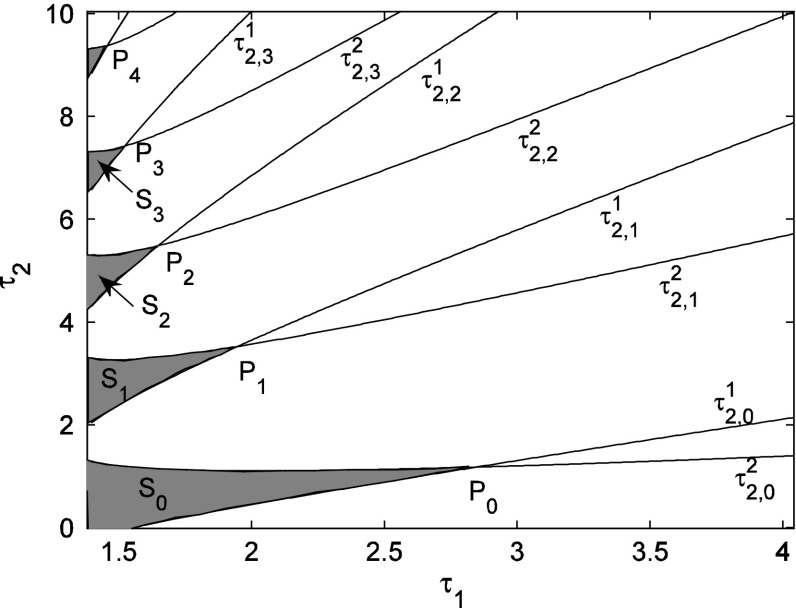
As an illustrative example, consider a specific system with the fixed parameters a1 = −6, a2 = 2.5, a3 = 2.5, a4 = −6, P = 0.4 and Q = 0.4, which are analyzed in section “Linear stability switches”. The delays τ1 and τ2 are taken as the variable parameters. It follows from (2) that system (1) has only unique equilibrium point given by 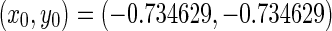 . The frequencies of the first and second Hopf bifurcation can be obtained in terms of (18) for each fixed value of delay τ1. For example, chosen time delay as τ1 = 1.8, one has the frequencies
. The frequencies of the first and second Hopf bifurcation can be obtained in terms of (18) for each fixed value of delay τ1. For example, chosen time delay as τ1 = 1.8, one has the frequencies 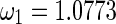 and
and 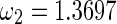 , respectively. The equilibrium point switches to stable state τ2 when increases to
, respectively. The equilibrium point switches to stable state τ2 when increases to 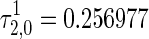 corresponding to the first Hopf bifurcation, and remains its stability until τ2 reaches
corresponding to the first Hopf bifurcation, and remains its stability until τ2 reaches 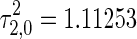 relating to the second Hopf bifurcation. Similarly, the equilibrium point is locally asymptotically stable if the delay is fixed into the range of
relating to the second Hopf bifurcation. Similarly, the equilibrium point is locally asymptotically stable if the delay is fixed into the range of 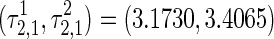 , which is the second order stability region. In such a way, the equilibrium point switches its stability and instability a finite number of times. For each fixed delay τ1, based on (23) and (24), a series of critical curves of the stability regions can be exhibited in the (τ1, τ2) parameter plane, as shown in Fig. 4. These curves divide the parameter plane into several stable and unstable regions. The stability regions are indicated by
, which is the second order stability region. In such a way, the equilibrium point switches its stability and instability a finite number of times. For each fixed delay τ1, based on (23) and (24), a series of critical curves of the stability regions can be exhibited in the (τ1, τ2) parameter plane, as shown in Fig. 4. These curves divide the parameter plane into several stable and unstable regions. The stability regions are indicated by 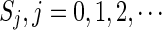 , where j stands for the order of the stability regions.
, where j stands for the order of the stability regions.
Fig. 4.
Variation of the critical delay values τ
2 with τ
1 in the (τ
1, τ
2) parameter plane for the fixed parameters as a
1 = −6, a
2 = 2.5, a
3 = 2.5, a
4 = −6, P = 0.4 and Q = 0.4, respectively, where 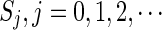 denote the stability regions of equilibrium point (x
0, y
0) and Pj, j = 0, 1, 2, … are the double Hopf bifurcation points
denote the stability regions of equilibrium point (x
0, y
0) and Pj, j = 0, 1, 2, … are the double Hopf bifurcation points
It follows from Fig. 4 that the curves of the first and second Hopf bifurcation intersect at the point 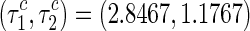 . The frequencies corresponding to the Hopf bifurcation are respectively
. The frequencies corresponding to the Hopf bifurcation are respectively 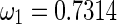 and
and 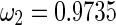 , as shown in Fig. 5. It implies that the intersection point is a non-resonate double Hopf bifurcation, which is usually referred as the codimension-two bifurcation. This singularity point is a source of more complicated dynamics, such as the stable quasi-periodic behavior and unstable solution. Similarly, the higher order double Hopf bifurcation points and the corresponding frequencies can be obtained in the (τ1, τ2) parameter plane, which are shown in Fig. 4 and Table 1.
, as shown in Fig. 5. It implies that the intersection point is a non-resonate double Hopf bifurcation, which is usually referred as the codimension-two bifurcation. This singularity point is a source of more complicated dynamics, such as the stable quasi-periodic behavior and unstable solution. Similarly, the higher order double Hopf bifurcation points and the corresponding frequencies can be obtained in the (τ1, τ2) parameter plane, which are shown in Fig. 4 and Table 1.
Fig. 5.
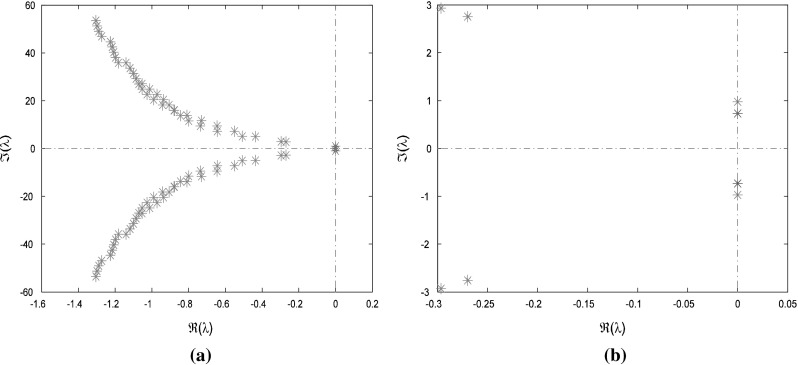
a Roots of the characteristic equation in the complex plane for 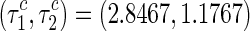 and b enlargement near (0, 0) corresponding to a, where the other parameters are fixed as a
1 = −6, a
2 = 2.5, a
3 = 2.5, a
4 = −6, P = 0.4, Q = 0.4
and b enlargement near (0, 0) corresponding to a, where the other parameters are fixed as a
1 = −6, a
2 = 2.5, a
3 = 2.5, a
4 = −6, P = 0.4, Q = 0.4
Table 1.
Coordinate values of the double Hopf bifurcation points and the corresponding frequencies
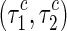
|
ω 1 | ω 2 |
|---|---|---|
| (2.8467, 1.1767) | 0.7314 | 0.9735 |
| (1.9473, 3.5226) | 1.0052 | 1.2985 |
| (1.6481, 5.4804) | 1.1682 | 1.4474 |
| (1.5225, 7.4198) | 1.2630 | 1.5121 |
| (1.4584, 9.3768) | 1.3222 | 1.5422 |
Central manifold reduction
It follows from the previous section that multiple delays of system (1) induce two different values of frequencies corresponding to the first and second Hopf bifurcation. The existence of a double Hopf bifurcation can be detected by the local stability analysis. The intersections of these Hopf bifurcation curves are the double Hopf bifurcation points. In this section, we represent the typical dynamical behaviors and the bifurcation sets in the neighborhood of the double Hopf bifurcation point by means of the central manifold reduction and normal form method (Buono and Belair 2003; Faria and Magalhaes 1995a, b). The periodic solutions corresponding to the different frequencies and the stable quasi-periodic solutions resulting from the double Hopf bifurcations point are investigated in the system under consideration. Introducing the transformation 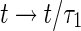 yields that system (1) becomes
yields that system (1) becomes
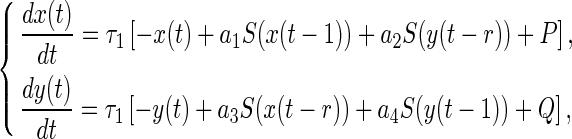 |
25 |
where 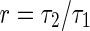 . For the rescale system defined by system (25), the two Hopf bifurcation frequencies, namely
. For the rescale system defined by system (25), the two Hopf bifurcation frequencies, namely 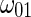 and
and 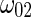 , are now given by
, are now given by 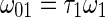 and
and 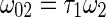 , respectively. Setting
, respectively. Setting 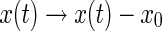 and
and 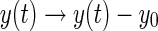 yields that system (25) can be rewritten as system (26).
yields that system (25) can be rewritten as system (26).
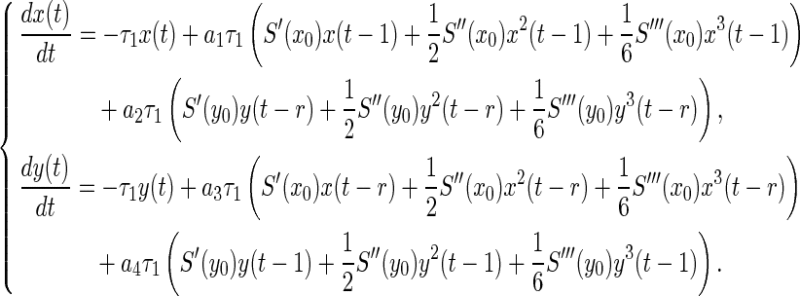 |
26 |
Regarding the time delays τ1 and r as the bifurcation parameters, we let
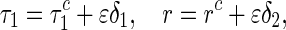 |
where 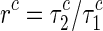 and
and 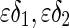 are the unfolding parameters. It follows that
are the unfolding parameters. It follows that
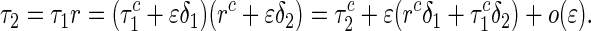 |
27 |
Then system (25) becomes
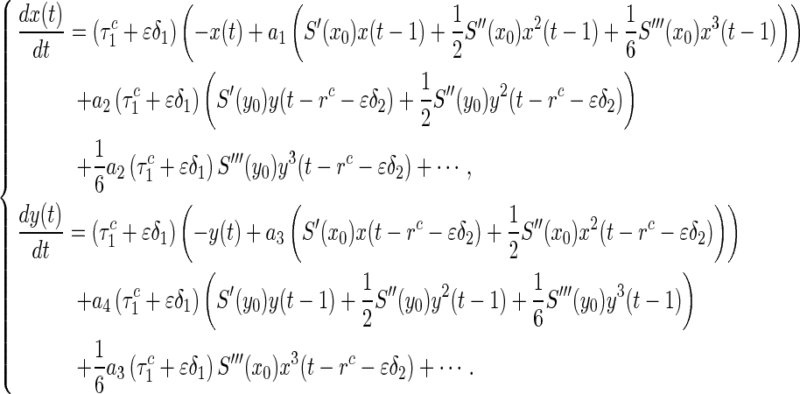 |
28 |
To apply the central manifold reduction, it is necessary to changes system (28) into a functional differential equation (Hale 1977). Let 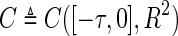 as the Banach space of continuous functions from
as the Banach space of continuous functions from 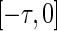 to R2 with the supremum norm, where
to R2 with the supremum norm, where 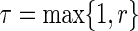 . For any
. For any 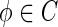 , we define
, we define
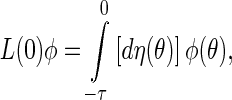 |
29 |
where 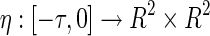 is a real-valued function of bounded variation in
is a real-valued function of bounded variation in 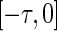 with
with
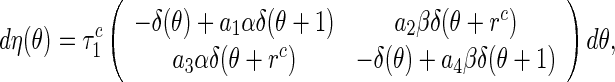 |
30 |
where 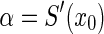 ,
, 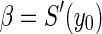 , and δ(θ) is Dirac function. Further, we define
, and δ(θ) is Dirac function. Further, we define
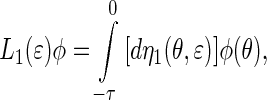 |
31 |
where
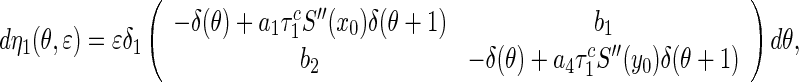 |
32 |
and
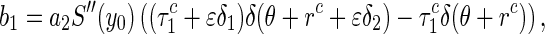 |
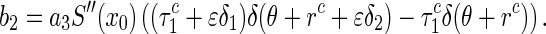 |
For 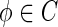 , the linear operator defined by system (28) generates an infinitesimal generator of the semi-flow of bounded linear operators with
, the linear operator defined by system (28) generates an infinitesimal generator of the semi-flow of bounded linear operators with
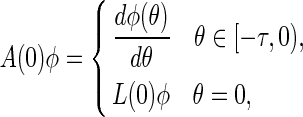 |
33 |
and
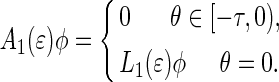 |
34 |
Set
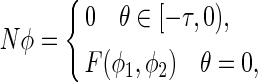 |
35 |
where
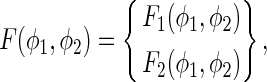 |
36 |
and
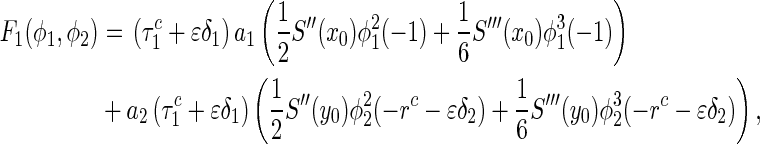 |
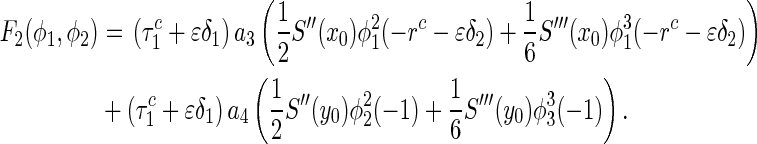 |
Thus, system (28) becomes
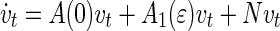 |
37 |
where 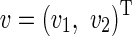 ,
,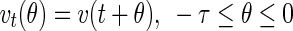 . For
. For 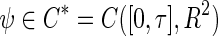 , the adjoint operators
, the adjoint operators 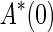 and
and 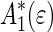 of
of 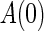 and
and 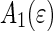 , respectively, are given by
, respectively, are given by
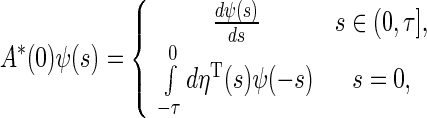 |
38 |
and
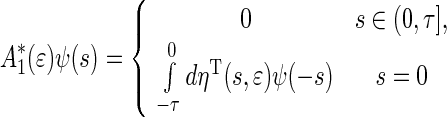 |
39 |
For 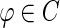 and
and 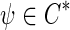 , we introduce the bilinear form
, we introduce the bilinear form
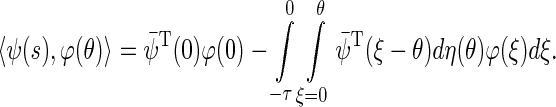 |
40 |
From the above discussion, we know that system (25) has two pairs of purely imaginary eigenvalues 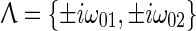 and the other eigenvalues with negative real parts at the double Hopf bifurcation point. Therefore, the Banach space C can be split into two subspaces as
and the other eigenvalues with negative real parts at the double Hopf bifurcation point. Therefore, the Banach space C can be split into two subspaces as 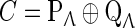 , where
, where 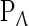 is the four-dimensional center subspace spanned by the basic vectors of the linear operator
is the four-dimensional center subspace spanned by the basic vectors of the linear operator 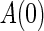 associated with the imaginary characteristic roots, and
associated with the imaginary characteristic roots, and 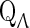 is the complement subspace of
is the complement subspace of 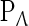 (Faria and Magalhaes 1995a, b). Now, We suppose
(Faria and Magalhaes 1995a, b). Now, We suppose 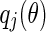 and
and 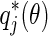 are the eigenvectors of
are the eigenvectors of 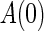 and
and 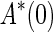 , respectively, corresponding to eigenvalue
, respectively, corresponding to eigenvalue 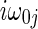 and
and 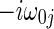 ,
, 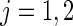 , i.e.
, i.e. 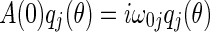 , and
, and 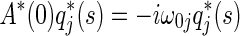 . By the direct computation, we have
. By the direct computation, we have
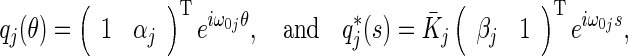 |
where
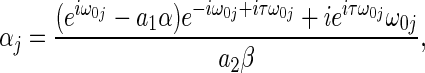 |
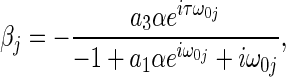 |
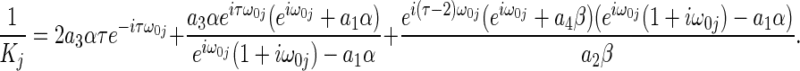 |
Furthermore, it follows that the real bases for 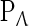 and its dual space can be expressed as (Chen and Yu 2006)
and its dual space can be expressed as (Chen and Yu 2006)
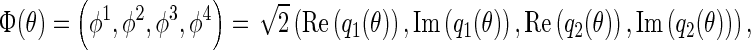 |
41 |
and
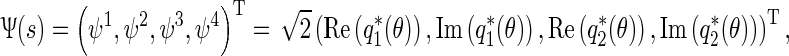 |
42 |
respectively. Note that the factor 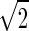 is required for normalizing the linear part of transformed equation. It is easily verified that
is required for normalizing the linear part of transformed equation. It is easily verified that 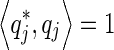 and
and 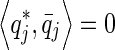 , where
, where  and
and
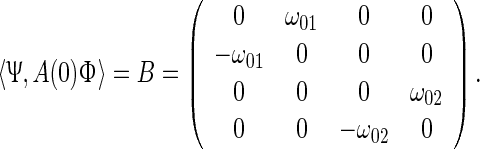 |
43 |
Define
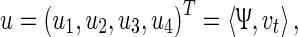 |
44 |
which actually represents the local coordinate system on the four-dimensional center manifold, induced by the basis Ψ. It follows (41) and (42) that one can decompose vi into two parts given by
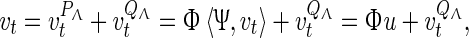 |
45 |
which implies that Φu is the projection of vi on the center manifold. Substituting (45) into (37) and applying the bilinear operator (37) with Ψ given by (37) to the resulting equation yields
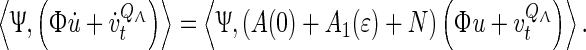 |
46 |
With the aid of (45), one obtains
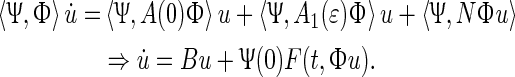 |
47 |
where B is determined by (43). It should be noted that 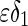 and
and 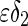 are very small in the neighborhood of
are very small in the neighborhood of 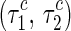 . This implies that
. This implies that
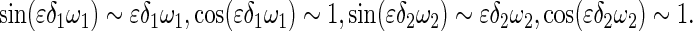 |
Executing the standard normalization technique as (Xu and Pei 2008; Buono and Belair 2003), one obtains the amplitude equation coming from the polar normal form of the central manifold system given by (Guckhenheimerm and Holmes 1983)
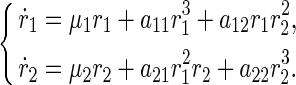 |
48 |
As mentioned above, chosen the system parameters as 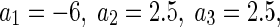
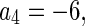
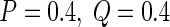 , the double Hopf bifurcation points are illustrated in Fig. 4 and Table 1. For convenience, we only investigate the first order critical delayed value of the double Hopf bifurcation given by
, the double Hopf bifurcation points are illustrated in Fig. 4 and Table 1. For convenience, we only investigate the first order critical delayed value of the double Hopf bifurcation given by 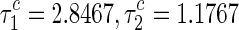 . The same procedure can be applied to the other points. Substituting the parameter values into system (48), one obtains the corresponding coefficients given by
. The same procedure can be applied to the other points. Substituting the parameter values into system (48), one obtains the corresponding coefficients given by 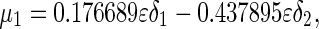
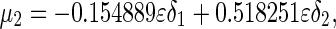
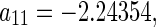
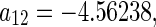
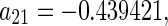
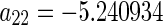 , respectively. From the dynamical theory (Guckhenheimerm and Holmes 1983), the curves of the secondary bifurcation are represented as
, respectively. From the dynamical theory (Guckhenheimerm and Holmes 1983), the curves of the secondary bifurcation are represented as 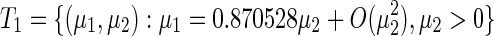 and
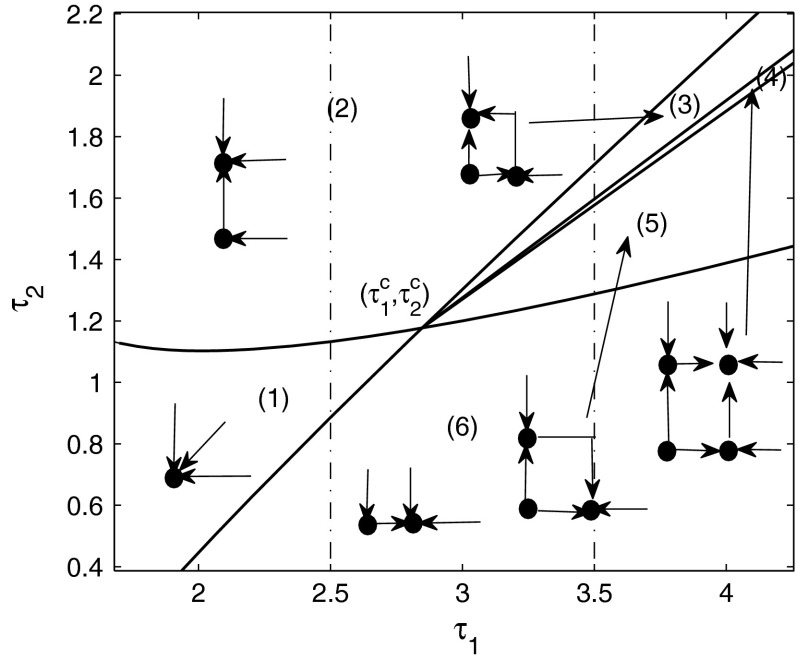
and 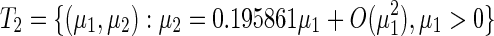 in the (μ1, μ2) plane. To analyze the dynamical behaviors of system (1) in parameter (τ1, τ2) plane, the bifurcation curves in terms of τ1 and τ2 can be obtained by virtue of (27). The dynamical classification near the first order point of double Hopf bifurcation is shown in Fig. 6, which is called the two-parameter bifurcation diagram. It should be noticed that the fixed point with r1 = r2 = 0 in system (48) corresponds to the equilibrium point of the origin system. Possible fixed point in the invariant coordinate axes for (48) with r1 = 0 or r2 = 0 correspond to limit cycle of the origin system, while a nontrivial fixed point with r1 > 0 and r2 > 0 generates a two-dimensional tours (quasi-periodic solution with two incommensurate frequencies). The stability of all these solutions in the original system is clearly detectable from that of the corresponding object in (48), as shown in Fig. 6.
in the (μ1, μ2) plane. To analyze the dynamical behaviors of system (1) in parameter (τ1, τ2) plane, the bifurcation curves in terms of τ1 and τ2 can be obtained by virtue of (27). The dynamical classification near the first order point of double Hopf bifurcation is shown in Fig. 6, which is called the two-parameter bifurcation diagram. It should be noticed that the fixed point with r1 = r2 = 0 in system (48) corresponds to the equilibrium point of the origin system. Possible fixed point in the invariant coordinate axes for (48) with r1 = 0 or r2 = 0 correspond to limit cycle of the origin system, while a nontrivial fixed point with r1 > 0 and r2 > 0 generates a two-dimensional tours (quasi-periodic solution with two incommensurate frequencies). The stability of all these solutions in the original system is clearly detectable from that of the corresponding object in (48), as shown in Fig. 6.
Fig. 6.
Classification and bifurcation sets for system (1) near the first order point of the double Hopf bifurcations 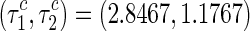 in the parameter (τ
1, τ
2) plane. The other parameters are chosen at the same as those in Fig. 4
in the parameter (τ
1, τ
2) plane. The other parameters are chosen at the same as those in Fig. 4
Numerical simulations
To illustrate the theoretical works of determining the double Hopf bifurcation properties, in this section, we present some numerical simulation to verify the system solutions. As mentioned above, we kept on choosing the parameters as a1 = −6, a2 = 2.5, a3 = 2.5, a4 = −6, P = 0.4 and Q = 0.4, respectively. The time delays τ1 and τ2 are considered as the variable parameters. Fig. 7 shows the one-parameter bifurcation diagrams with varying delay τ2 for fixed delay τ1. Phase portraits of the typical behaviors near the double Hopf bifurcation point are illustrated in Fig. 8, respectively.
Fig. 7.
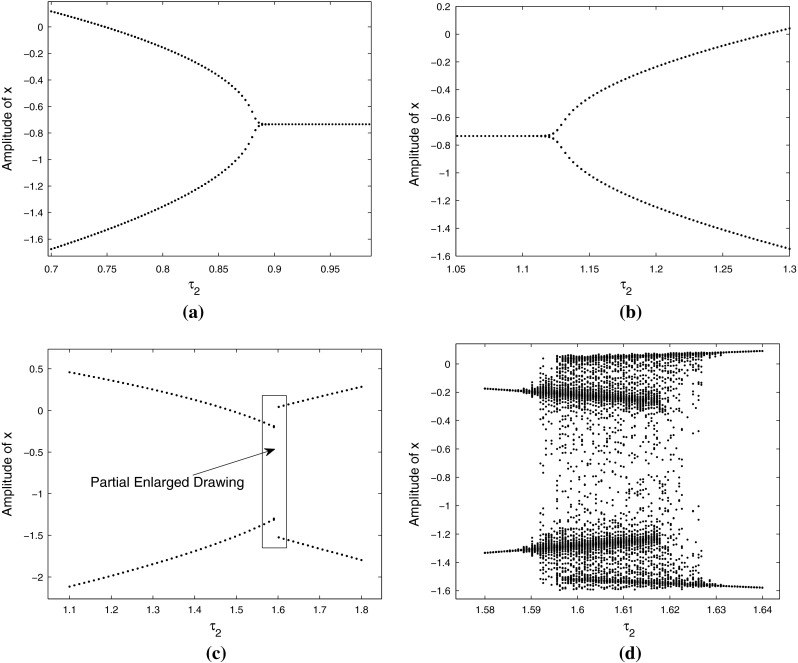
One-parameter bifurcation diagram with varying the delay τ 2 for a τ 1 = 2.5, τ 2 ∈ [0.7,1], b τ 1 = 2.5, τ 2 ∈ [1.05, 1.3], c τ 1 = 3.5, τ 2 ∈ [1.1, 1.8], and d the partial enlargement of the c box, respectively. The other parameters are chosen at the same as those in Fig. 4
Fig. 8.
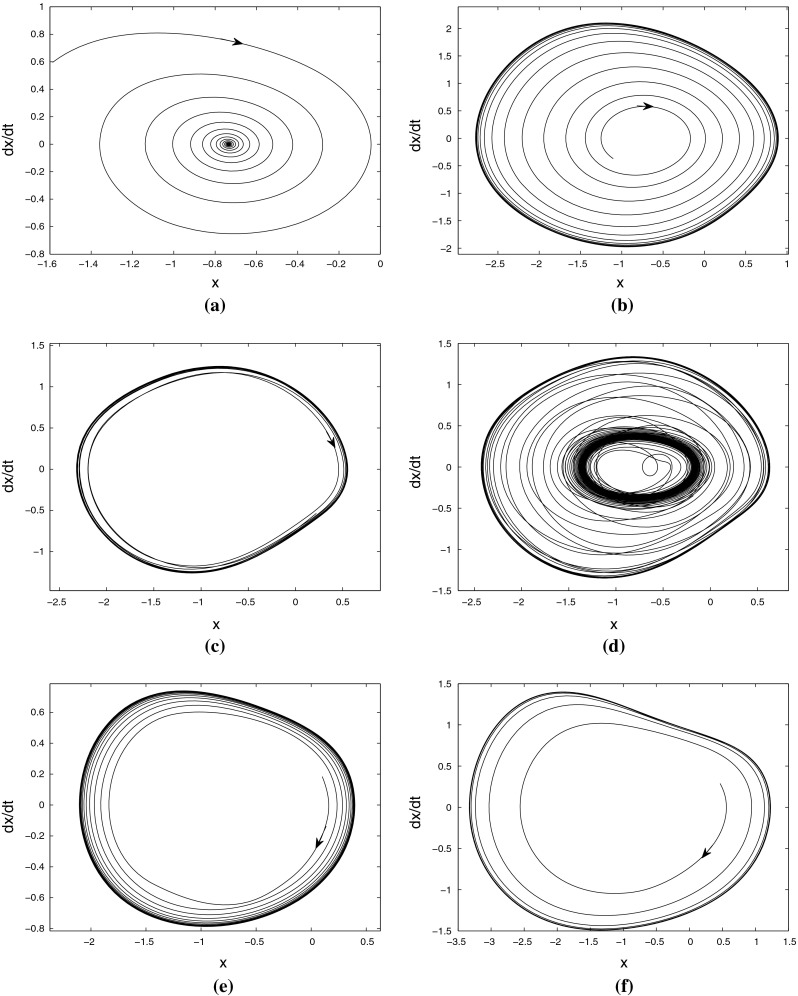
Phase portraits of the numerical simulation for the dynamical behavior in system (1) near the first order point of the double Hopf bifurcation, where (τ 1, τ 2) is fixed as a (2.0, 0.8), b (2.5, 1.6), c (3.5, 1.6), d (3.5, 1.64), e (3.5, 1.4), and f (3.5, 0.8), respectively. The other parameters are chosen at the same as those in Fig. 4
Firstly, two delays are fixed as 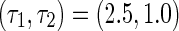 located in region 1 of Fig. 6. The numerical solution of system (1) is shown in Fig. 8a. The trajectory asymptotically converges to the equilibrium point
located in region 1 of Fig. 6. The numerical solution of system (1) is shown in Fig. 8a. The trajectory asymptotically converges to the equilibrium point 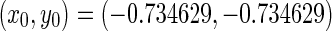 . It implies the point is locally asymptotically stable. With the increasing of delay τ2, the equilibrium point loses its stability in term of the supercritical Hopf bifurcation, where the parameters encounter the second Hopf bifurcation curve and enter region 2 of Fig. 6. The system periodically oscillates with the second frequency, as shown in Fig. 8b. The one-parameter bifurcation diagram with increasing τ2 is shown in Fig. 7b. The oscillation amplitude of system is increasing with delay τ2 varying. However, when delay τ2 is decreased from region 1 of Fig. 6, the parameters will encounter the first Hopf bifurcation curve related to ω1 frequency. This implies that the equilibrium point loses its stability through a reverse Hopf bifurcation, as shown in Fig. 7a. It follows that this bifurcation is also supercritical Hopf bifurcation. The system is exhibited the oscillation solution with ω1 frequency as it enters into region 6, as shown in Fig. 8f.
. It implies the point is locally asymptotically stable. With the increasing of delay τ2, the equilibrium point loses its stability in term of the supercritical Hopf bifurcation, where the parameters encounter the second Hopf bifurcation curve and enter region 2 of Fig. 6. The system periodically oscillates with the second frequency, as shown in Fig. 8b. The one-parameter bifurcation diagram with increasing τ2 is shown in Fig. 7b. The oscillation amplitude of system is increasing with delay τ2 varying. However, when delay τ2 is decreased from region 1 of Fig. 6, the parameters will encounter the first Hopf bifurcation curve related to ω1 frequency. This implies that the equilibrium point loses its stability through a reverse Hopf bifurcation, as shown in Fig. 7a. It follows that this bifurcation is also supercritical Hopf bifurcation. The system is exhibited the oscillation solution with ω1 frequency as it enters into region 6, as shown in Fig. 8f.
Furthermore, when we choose delay 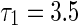 , the one-parameter bifurcation diagram with varying τ2 is shown in Fig. 7c, where Fig. 7d is the partial enlargement of the box in Fig. 7c. Figure 8c and e respectively show the stable state of periodical solutions with the different frequencies. With delay τ2 varying from region 3–4, the stable periodic solution loses its stability through the Neimark-Sacker bifurcation. It suggests that the system behavior moves to a two-frequency quasi-periodic state, as shown in Fig. 8d. The phase portrait clearly shows the modulation of the peak intensities, which is also called as 2-torus. Keeping delay τ2 vary, when parameters encounter and cross the other secondary bifurcation, the system behavior transforms into the periodic activity again from the 2-torus solution. The analytical predictions of system solutions are good representatives of the numerical results.
, the one-parameter bifurcation diagram with varying τ2 is shown in Fig. 7c, where Fig. 7d is the partial enlargement of the box in Fig. 7c. Figure 8c and e respectively show the stable state of periodical solutions with the different frequencies. With delay τ2 varying from region 3–4, the stable periodic solution loses its stability through the Neimark-Sacker bifurcation. It suggests that the system behavior moves to a two-frequency quasi-periodic state, as shown in Fig. 8d. The phase portrait clearly shows the modulation of the peak intensities, which is also called as 2-torus. Keeping delay τ2 vary, when parameters encounter and cross the other secondary bifurcation, the system behavior transforms into the periodic activity again from the 2-torus solution. The analytical predictions of system solutions are good representatives of the numerical results.
Conclusion
In neural system, action potential plays a crucial role in many information communications. To understand the information representation, many mathematical models are proposed and the mechanism of information processing is investigated by using the analytical method of nonlinear dynamics. The quiescent state, periodic spiking, quasi-periodic behavior and bursting activity are all the important biological behavior with the different neuro-computational properties (Song and Xu 2012a; 2012b). The action potential exhibits the quasi-periodic behavior when the number of incommensurable frequencies is finite, which is called the multi-frequency rhythmic activity. Their power spectra are discrete with peaks corresponding to the composed frequencies (Izhikevich 1999). In fact, EEG recordings of brain can demonstrate the rhythmic activity with a few pronounced frequencies. For example, the most prominent are gamma (30–100 Hz) oscillations in the cortex and theta (4–8 Hz) oscillations in the hippocampus (Llinas 1988). Recently, Marichal et al. (2010) considered the dynamic behavior of a quasi-periodic orbit obtained by the Neimark-Sacker bifurcation in a simple discrete recurrent neural network model.
It is well known that time delay is an inevitable factor in the signal transmission between biological neurons or electronic-model-neurons. Neural systems with time delays have very rich dynamical behaviors. In this paper, a neural network with two different types of delays involved in self- and neighbor-connection has been studied. The occurrence of the multiple delays greatly complicates the analysis of stability and bifurcation. The stability regions are strongly relied on time delays. For the different values of delays, the system may exhibit the different parameter regions involved in the delay-independence stability and delay-dependence stability. In special, when the characteristic equation of the system has multiple roots, there exists the delay window, where the equilibrium point is either locally asymptotically stable. To illustrate these critical values and find the stability regions, the Hopf bifurcation curves are illustrated. The multiple stability regions are obtained in the delayed parameter plane. The transverse direction of the imaginary eigenvalues located at the critical values is determined by means of the numerical computation.
Furthermore, the system exhibits the double Hopf bifurcation points due to the two pairs of imaginary eigenvalues appearing on the margin of stability regions simultaneously. Considering the multiple delays as the bifurcation parameters, the classification of the various dynamic behaviors in the neighborhood of the double Hopf bifurcation point is obtained in detail in term of the central manifold reduction and normal form method. The system may exhibit the equilibrium solution, periodic solutions with the different frequencies of the first and second Hopf bifurcations, and quasi-periodic solutions. In addition, the quasi-periodic solution is obtained by the Neimark- Sacker bifurcation of the periodic solutions. Numerical results are given to illustrate that the double Hopf bifurcation is an interaction of the supercritical–supercritical Hopf bifurcations. Finally, the one-parameter bifurcation diagrams and phase portraits verify the agreement between the theoretical analysis and numerical simulations.
Acknowledgments
This research is supported by the State Key Program of National Natural Science of China under Grant No. 11032009, Shanghai Leading Academic Discipline Project in No. B302, the PhD Start-up Fund of Shanghai Ocean University in No. A-2400-11-0214 and Young Teacher Training Program of Colleges and Universities in Shanghai under Grant No. ZZhy12030.
Contributor Information
Zi-Gen Song, Email: zigensong@163.com.
Jian Xu, Phone: +86-216-5983395, FAX: +86-216-5983267, Email: xujian@tongji.edu.cn.
References
- Bélair J, Campbell SA. Stability and bifurcations of equilibrium in multiple-delayed differential equation. SIAM J Appl Math. 1994;54(5):1402–1424. doi: 10.1137/S0036139993248853. [DOI] [Google Scholar]
- Budak E. An analytical design method for milling cutters with nonconstant pitch to increase stability, part I: theory. ASME J Manuf Sci Eng. 2003;125(1):29–35. doi: 10.1115/1.1536655. [DOI] [Google Scholar]
- Buono PL, Belair J. Restrictions and unfolding of double Hopf bifurcation in functional differential equations. J Differ Equ. 2003;189(1):234–266. doi: 10.1016/S0022-0396(02)00179-1. [DOI] [Google Scholar]
- Campbell SA. Time delays in neural systems. In: McIntosh AR, Jirsa VK, editors. Handbook of brain connectivity. Berlin: Springer; 2007. p. 65. [Google Scholar]
- Campbell SA, Ncube I, Wu J. Multistability and stable asynchronous periodic oscillations in a multiple-delayed neural system. Physica D. 2006;214(2):101–119. doi: 10.1016/j.physd.2005.12.008. [DOI] [Google Scholar]
- Cao J, Xiao M. Stability and Hopf bifurcation in a simplified BAM neural network with two time delays. IEEE Trans Neural Netw. 2007;18(2):416–430. doi: 10.1109/TNN.2006.886358. [DOI] [PubMed] [Google Scholar]
- Chen YP, Yu P. Double-Hopf bifurcation in an oscillator with external forcing and time-delayed feedback control. Int J Bifurcation Chaos. 2006;16(12):3523–3537. doi: 10.1142/S0218127406016963. [DOI] [Google Scholar]
- Cooke KL, Grossman Z. Discrete delay, distributed delay and stability switches. J Math Anal Appl. 1982;86(2):592–627. doi: 10.1016/0022-247X(82)90243-8. [DOI] [Google Scholar]
- Cooke KL, van den Driessche P. Analysis of an SEIRS epidemic model with two delays. J Math Biol. 1996;35(2):240–260. doi: 10.1007/s002850050051. [DOI] [PubMed] [Google Scholar]
- Dombovari Z, Wilson R, Stepan G. Estimates of the bistable region in metal cutting. Proc R Soc A-Math Phy Eng Sci. 2008;464(2100):3255–3271. doi: 10.1098/rspa.2008.0156. [DOI] [Google Scholar]
- Engelborghs K, Luzyanina T, Roose D. Numerical bifurcation analysis of delay differential equations using DDE-BIFTOOL. ACM Trans Math Softw. 2002;28(1):1–21. doi: 10.1145/513001.513002. [DOI] [Google Scholar]
- Faria T, Magalhaes LT. Normal forms for retarded functional differential equations with parameters and applications to Hopf bifurcation. J Differ Equ. 1995;122(2):181–200. doi: 10.1006/jdeq.1995.1144. [DOI] [Google Scholar]
- Faria T, Magalhaes LT. Normal form for retarded functional differential equations and applications to Bogdanov-Takens singularity. J Differ Equ. 1995;122(2):201–224. doi: 10.1006/jdeq.1995.1145. [DOI] [Google Scholar]
- Gu K, Naghnaeian M. Stability crossing set for systems with three delays. IEEE Trans Autom Control. 2011;56(1):11–26. doi: 10.1109/TAC.2010.2050162. [DOI] [Google Scholar]
- Gu K, Niculescu S-I, Chen J. On stability crossing curves for general systems with two delays. J Math Anal Appl. 2005;311(1):231–253. doi: 10.1016/j.jmaa.2005.02.034. [DOI] [Google Scholar]
- Gu K, Niculescu S-I, Chen J. Computing maximum delay deviation allowed to retain stability in systems with two delays. In: Chiasson J, Loiseau JJ, editors. Applications of time delay systems. Lecture notes in control and information sciences. Berlin: Springer; 2007. p. 157. [Google Scholar]
- Guckhenheimerm J, Holmes P. Nonlinear oscillations, dynamical systems and bifurcations of vector fields. Berlin: Springer; 1983. [Google Scholar]
- Guo S, Huang L. Periodic solutions in an inhibitory two-neuron network. J Comput Appl Math. 2003;161(1):217–229. doi: 10.1016/j.cam.2003.08.002. [DOI] [Google Scholar]
- Hale JK. Theory of functional differential equations. New York: Springer; 1977. [Google Scholar]
- Hale JK, Huang W. Global geometry of the stable regions for two delay differential equations. J Math Anal Appl. 1993;178(2):344–362. doi: 10.1006/jmaa.1993.1312. [DOI] [Google Scholar]
- Hilout S, Boutat M, Laadnani I, et al. Mathematical modelling of plastic deformation instabilities with two delays. Appl Math Model. 2010;34(9):2484–2492. doi: 10.1016/j.apm.2009.11.013. [DOI] [Google Scholar]
- Hu HY, Wang ZH. Dynamics of controlled mechanical systems with delayed feedback. Heidelberg: Springer; 2002. [Google Scholar]
- Izhikevich EM. Weakly connected quasi-periodic oscillators, FM interactions, and multiplexing in the brain. SIAM J Appl Math. 1999;59:2193–2223. doi: 10.1137/S0036139997330623. [DOI] [Google Scholar]
- Jia B, Gu H, Li Li, et al. Dynamics of period-doubling bifurcation to chaos in the spontaneous neural firing patterns. Cogn Neurodyn. 2012;6:89–106. doi: 10.1007/s11571-011-9184-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Jiang W. Global existence of periodic solutions in the linearly coupled Mackey- Glass system. Int J Bifurcation Chaos. 2011;21(3):711–724. doi: 10.1142/S0218127411028726. [DOI] [Google Scholar]
- Li X, Ruan S, Wei J. Stability and bifurcation in delay-differential equations with two delays. J Math Anal Appl. 1999;236(2):254–280. doi: 10.1006/jmaa.1999.6418. [DOI] [Google Scholar]
- Liao C-W, Lu C-Y. Design of delay-dependent state estimator for discrete-time recurrent neural networks with interval discrete and infinite-distributed time-varying delays. Cogn Neurodyn. 2011;5:133–143. doi: 10.1007/s11571-010-9135-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao X, Guo S, Li C. Stability and bifurcation analysis in tri-neuron model with time delay. Nonlinear Dyn. 2007;49(1):319–345. doi: 10.1007/s11071-006-9137-6. [DOI] [Google Scholar]
- Liebovitch LS, Peluso PR, Norman MD, et al. Mathematical model of the dynamics of psychotherapy. Cogn Neurodyn. 2011;5:265–275. doi: 10.1007/s11571-011-9157-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llinas RR. The intrinsic electrophysiological properties of mammalian neurons: a new insight into CNS function. Science. 1988;242:1654–1664. doi: 10.1126/science.3059497. [DOI] [PubMed] [Google Scholar]
- Mao X, Hu H. Stability and Hopf bifurcation of a delayed network of four neurons with short-cut connection. Int J Bifurcation Chaos. 2008;18(10):3053–3072. doi: 10.1142/S021812740802224X. [DOI] [Google Scholar]
- Marcus CM, Westervelt RM. Stability of analog neural network with delay. Phys Rev A. 1989;39(1):347–359. doi: 10.1103/PhysRevA.39.347. [DOI] [PubMed] [Google Scholar]
- Marichal RL, Piñeiro JD, González EJ, et al. Stability of quasi-periodic orbits in recurrent neural networks. Neural Process Lett. 2010;31:269–281. doi: 10.1007/s11063-010-9138-9. [DOI] [Google Scholar]
- Nakaoka S, Saito Y, Takeuchi Y. Stability, delay, and chaotic behavior in a Lotka- Volterra predator-prey system. Math Biosci Eng. 2006;3:173–187. doi: 10.3934/mbe.2006.3.173. [DOI] [PubMed] [Google Scholar]
- Orosz G, Stepan G. Hopf bifurcation calculations in delayed systems with translational symmetry. J Nonlin Sci. 2004;14:505–528. doi: 10.1007/s00332-004-0625-4. [DOI] [Google Scholar]
- Shayer PL, Campbell SA. Stability, bifurcation, and multistability in a system of two coupled neurons with multiple time delays. SIAM J Appl Math. 2000;61(2):673–700. doi: 10.1137/S0036139998344015. [DOI] [Google Scholar]
- Shi B, Zhang F, Xu S (2011) Hopf bifurcation of a mathematical model for growth of tumors with an action of inhibitor and two time delays. Abstract Appl Anal. doi:10.1155/2011/980686
- Sipahi R, Delice II. Extraction of 3D stability switching hypersurfaces of a time delay system with multiple fixed delays. Automatica. 2009;45(6):1449–1454. doi: 10.1016/j.automatica.2009.01.017. [DOI] [Google Scholar]
- Sipahi R, Niculescu S, Abdallah CT, et al. Stability and stabilization of systems with time delay. IEEE Control Syst. 2011;31(1):38–65. doi: 10.1109/MCS.2010.939135. [DOI] [Google Scholar]
- Song Z, Xu J. Bursting near Bautin bifurcation in a neural network with delay coupling. Int J Neural Syst. 2009;19(5):359–373. doi: 10.1142/S0129065709002087. [DOI] [PubMed] [Google Scholar]
- Song Z, Xu J. Codimension-two bursting analysis in the delayed neural system with external stimulations. Nonlinear Dyn. 2012;67(1):309–328. doi: 10.1007/s11071-011-9979-4. [DOI] [Google Scholar]
- Song Z, Xu J. Bifurcation and chaos analysis for a delayed two-neural network with a variation slope ratio in the activation function. Int J Bifurcation Chaos. 2012;22(5):1250105. doi: 10.1142/S0218127412501052. [DOI] [Google Scholar]
- Song Z, Xu J. Stability switches and multistability coexistence in a delay-coupled neural oscillators system. J Theor Biol. 2012;313(21):98–114. doi: 10.1016/j.jtbi.2012.08.011. [DOI] [PubMed] [Google Scholar]
- Song Y, Han M, Peng Y. Stability and Hopf bifurcations in a competitive Lotka-Volterra system with two delays. Chaos, Solitons Fractals. 2004;22(5):1139–1148. doi: 10.1016/j.chaos.2004.03.026. [DOI] [Google Scholar]
- Sun W, Wang R, Wang W, et al. Analyzing inner and outer synchronization between two coupled discrete-time networks with time delays. Cogn Neurodyn. 2010;4:225–231. doi: 10.1007/s11571-010-9118-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wan A, Wei J. Bifurcation analysis of Mackey-Glass electronic circuits model with delayed feedback. Nonlinear Dyn. 2009;57(1):85–96. doi: 10.1007/s11071-008-9422-7. [DOI] [Google Scholar]
- Wei J, Zhang C. Bifurcation analysis of a class of neural networks with delays. Nonlinear Anal-Real World Appl. 2008;9(5):2234–2252. doi: 10.1016/j.nonrwa.2007.08.008. [DOI] [Google Scholar]
- Xu X. Local and global Hopf bifurcation in a two-neuron network with multiple delays. Int J Bifurcation Chaos. 2008;18(4):1015–1028. doi: 10.1142/S0218127408020811. [DOI] [Google Scholar]
- Xu S. Hopf bifurcation of a free boundary problem modeling tumor growth with two time delays. Chaos, Solitons Fractals. 2009;41(5):2491–2494. doi: 10.1016/j.chaos.2008.09.029. [DOI] [Google Scholar]
- Xu J, Pei L. The nonresonant double Hopf bifurcation in delayed neural network. Int J Comput Math. 2008;85(6):925–935. doi: 10.1080/00207160701405469. [DOI] [Google Scholar]
- Xu X, Hu H, Wang H. Stability switches, Hopf bifurcation and chaos of a neuron model with delay-dependent parameters. Phys Lett A. 2006;354(1):126–136. doi: 10.1016/j.physleta.2006.01.034. [DOI] [Google Scholar]
- Xu J, Chung KW, Chan CL. An efficient method for studying weak resonant double Hopf bifurcation in nonlinear systems with delayed feedbacks. SIAM J Appl Dyn Syst. 2007;6(1):29–60. doi: 10.1137/040614207. [DOI] [Google Scholar]
- Yan X-P. Hopf bifurcation and stability for a delayed tri-neuron network model. J Comput Appl Math. 2006;196(2):579–595. doi: 10.1016/j.cam.2005.10.012. [DOI] [Google Scholar]
- Ye Q, Cui B (2012) Mean square exponential and robust stability of stochastic discrete-time genetic regulatory networks with uncertainties. Cogn Neurodyn. doi:10.1007/s11571-012-9200-6 [DOI] [PMC free article] [PubMed]
- Yu P, Yuan Y, Xu J. Study of double Hopf bifurcation and chaos for an oscillator with time delayed feedback. Commun Nonlinear Sci Numer Simul. 2002;7(1):69–91. doi: 10.1016/S1007-5704(02)00007-2. [DOI] [Google Scholar]
- Yuan Y, Campbell SA. Stability and synchronization of a ring of identical cells with delayed coupling. J Dyn Differ Equ. 2004;16(3):709–744. doi: 10.1007/s10884-004-6114-y. [DOI] [Google Scholar]
- Yuan S, Li P. Stability and direction of Hopf bifurcations in a pair of identical tri-neuron network loops. Nonlinear Dyn. 2010;61(3):569–578. doi: 10.1007/s11071-010-9671-0. [DOI] [Google Scholar]
- Zatarain M, Bediaga I, Muñoa J, et al. Stability of milling processes with continuous spindle speed variation: analysis in the frequency and time domains, and experimental correlation. CIRP Ann Manuf Techn. 2008;57(1):379–384. doi: 10.1016/j.cirp.2008.03.067. [DOI] [Google Scholar]