Abstract
One hundred and thirty composite soil samples were collected from Hamedan county, Iran to characterize the spatial distribution and trace the sources of heavy metals including As, Cd, Co, Cr, Cu, Ni, Pb, V, Zn, and Fe. The multivariate gap statistical analysis was used; for interrelation of spatial patterns of pollution, the disjunctive kriging and geoenrichment factor (EFG) techniques were applied. Heavy metals and soil properties were grouped using agglomerative hierarchical clustering and gap statistic. Principal component analysis was used for identification of the source of metals in a set of data. Geostatistics was used for the geospatial data processing. Based on the comparison between the original data and background values of the ten metals, the disjunctive kriging and EFG techniques were used to quantify their geospatial patterns and assess the contamination levels of the heavy metals. The spatial distribution map combined with the statistical analysis showed that the main source of Cr, Co, Ni, Zn, Pb, and V in group A land use (agriculture, rocky, and urban) was geogenic; the origin of As, Cd, and Cu was industrial and agricultural activities (anthropogenic sources). In group B land use (rangeland and orchards), the origin of metals (Cr, Co, Ni, Zn, and V) was mainly controlled by natural factors and As, Cd, Cu, and Pb had been added by organic factors. In group C land use (water), the origin of most heavy metals is natural without anthropogenic sources. The Cd and As pollution was relatively more serious in different land use. The EFG technique used confirmed the anthropogenic influence of heavy metal pollution. All metals showed concentrations substantially higher than their background values, suggesting anthropogenic pollution.
Keywords: Heavy metals, Spatial variability, Land use patterns, Geostatistics, Multivariate statistics, Gap statistical analysis
Introduction
Heavy metal accumulation in soils caused by industrialization has attracted wide attention. Soil contamination by metals has become a serious widespread problem in many parts of the world especially in developing countries. Heavy metals in soil may come from agricultural activities (Huang and Jin 2008), urbanization, industrialization, and mining activities (Zhong et al. 2012). Among these intensive agricultural and industrial activities are considered as two of the most damaging anthropogenic activities in the world. According to numerous studies, heavy metals pollution in the environment are mainly derived from anthropogenic sources (Acosta et al. 2011; Gu et al. 2012; Bini et al. 2011; Li and Feng 2012b; Chabukdhara and Nema 2012; Cai et al. 2012; Guo et al. 2012; Zhang et al. 2009). Pollutions (e.g., fertilizers, pesticides, heavy metals, and salts) produced by human activities (e.g., agriculture, industry, and urban) affect the quality of soil and water drastically. In fact, these activities lead to heavy metals accumulation in soils. These result in changes in landscape, contamination of soil and water, and degradation of land resources. Therefore, the protection of soil quality is very important and vital.
The spatial distribution of heavy metals in soils is of primary significance in assessing soil quality and locating pollution sources (Gu et al. 2012). However, a variety of monitoring programs have generated numerous intricate datasets that are difficult to interpret because of the interactive influences. Thus, multivariate geostatistical and geographic information system (GIS) methods have been widely employed as powerful tools to extract the majority of meaningful information from datasets without losing useful information (Gu et al. 2012; Acosta et al. 2011; Li and Feng 2012b; Lin et al. 2010; Yang et al. 2011; Chabukdhara and Nema 2012; Cai et al. 2012; Bini et al. 2011; Lu et al. 2012; Guo et al. 2012).
Multivariate analysis offers techniques for classifying relationships among measured variables. The two most common multivariate analyses are principal components analysis and cluster analysis. Notable examples of their recent use in assessment of soil pollution by heavy metals are found in the following reports (Li and Feng 2012b; Acosta et al. 2011; Gu et al. 2012; Lu et al. 2012; Cai et al. 2012; Zhong et al. 2012; Chabukdhara and Nema 2012; Yang et al. 2011).
Principal component analysis, a statistical technique, linearly transforms an original set of variables into a substantially smaller set of uncorrelated new variables that represent most of the information of the original dataset (Chabukdhara and Nema 2012). A small set of uncorrelated variables is much easier to understand and use in further analysis than a larger set of correlated variables. The purpose of cluster analysis is to identify groups or clusters of similar sites on the basis of similarities within a class and dissimilarities between different classes. Agglomerative hierarchical clustering (AHC) examines distances between samples. The most similar points are grouped forming one cluster and the process is repeated until all points belong to a cluster. The results obtained are presented in a two-dimensional plot called a dendrogram (Irpino and Verde 2006; Ward 1963; Everitt et al. 2001).
Geostatistical techniques are based on the theory of a regionalized variable (Matheron 1963), which is distributed in space (with spatial coordinates) and shows spatial autocorrelation such that samples close together in space are more alike than those that are further apart. A geostatistical technique measures the spatial variability and provides for spatial interpolation (Webster and Oliver 2007; Shi et al. 2007).
Hamedan county is one of the most developed areas in Iran. This region in terms of agriculture is one of the centers of excellence in terms of Iran’s economic growth. In recent decades, the development of industry and overuse of fertilizers in agricultural activities have consequently increased the risk of pollution by metallic elements. There were no previous studies on heavy metals pollution in this area, and thus in 2010, the Hamedan Department of Environment (Hamedan-DoE) began a collaborative research program to identify the presence of Cr, Co, Zn, V, Cu, Pb, Ni, Fe, As, and Cd in soils. The results of this project are presented in this article.
The study involved factor analysis of 130 sampling sites in Iran’s Hamedan county to characterize the patterns of ten heavy metals in the soil (Cr, Co, Zn, V, Cu, Pb, Ni, Fe, As, and Cd). A new integration statistical method, enrichment factors to assess metal enrichments in soil under different geological structures and land uses, were determined to interpret the background concentration of metals, examine spatial dependency and variation mechanisms of the metals, and evaluate spatial distribution patterns and delineation of polluted areas. Correlations between the factor patterns and the physical soil parameters were analyzed to elucidate the characteristics of the heavy metal pollution of the soils at these 130 sampling sites. Agglomerative hierarchical clustering and gap statistics were also applied to group the metals and physical parameters, and thereby delineate the interrelationships between metals and anthropogenic activities.
Materials and methods
Study area
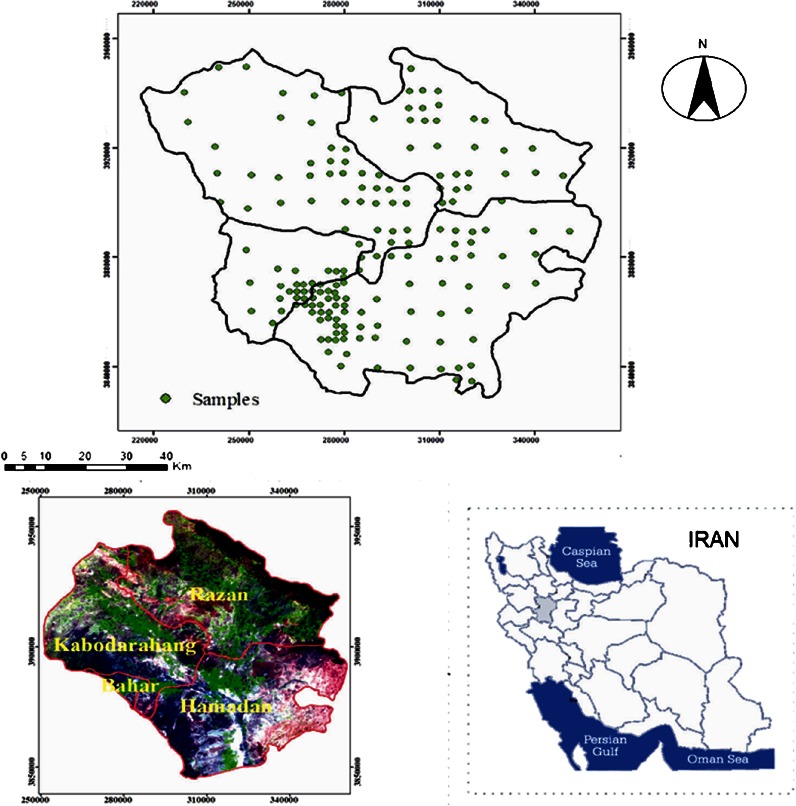
The study area includes four adjacent townships (Kaboudarahang, Razan, Hamedan, and Bahar) located in Hamedan county in the west of Iran comprising a total area of 118,577.2 ha, including 63,316.55 ha (53.4 %) of agricultural land (latitudes 33°59′ and 35°48′ and longitudes 47°34′ and 49°36′; Fig. 1). The predominant crops in these areas are wheat, barley, alfalfa, potato, garden crops, and orchards. Hamedan province, in terms of agriculture, is one of the centers of excellence in terms of Iran’s economic growth. This is a semi-arid region with a mean annual rainfall of 400 mm which varies within the year.
Fig. 1.
Study area and sampling sites
Spatial data
The geology map with a scale of 1:100,000 was acquired from the National Cartographic Center sites in the network formation. Preparation of land use maps began with field studies in March 2010 using multitemporal satellite IRS-P6 AWiFS data (6 March, 3 April, 27 April, and 18 July) and digital topographic maps (of scale 1:50,000).
Image processing and ground step’s data were integrated with satellite data. The first image correction was carried out and the images were used as the georeference. The best false color images of Optimal Index Factor (OIF) were used to identify the best bands with the minimum correlation and maximum variance, and the function is expressed as:
| 1 |
where is standard deviation of three bands, and is a sum of absolute correlation between two of three bands.
Hybrid image classification was carried out for the preparation of land use maps using ERDAS EMAGINE 9.1 software. In order to assess thematic accuracy, a stratified random sampling design was used to select a total of 360 pixels for the land use map. The accuracy of the land use map was checked using GPS points obtained during the March and July 2010 fieldwork as reference. Classified and reference information were cross-tabulated in an error matrix. Errors of commission (user’s accuracy), omission (producer’s accuracy), and the overall accuracies were calculated. The map location of industries and mines was prepared using GPS data obtained during the fieldwork.
Soil sampling
In accordance with soil types and the uniformity of sampling distribution in the study area, in April 2010, the area was divided into 5 × 5 km grids using random systematic method and 130 composite soil samples were collected (0–20 cm depth). The distribution of sampling points is presented in Fig. 1. The coordinates of the sample points were detected using GPS and were plotted on a topographic map with a scale of 1/50,000. The samples were air dried. Gravel, coarse organic matter, and plant root residues were removed. Soil samples were dried in an oven at 105 °C for 24 h. The dried samples were passed through a 2-mm plastic sieve and stored in 1-kg plastic bags prior to chemical analysis.
Chemical analysis
Selected soil properties relevant to mobility and bioavailability of heavy metals were analyzed for the general characterization of soils. Particle size distribution was measured by the hydrometric method to determine the sand, silt, and clay percentages. Soil pH (soil, H2O ratio = 1:2) was measured using a pH meter with a glass electrode (Shi et al. 2007). Electrical conductivity was determined on the saturation paste extract (Micó et al. 2006). Organic matter concentration was determined by the Walkley–Black method. A 0.5 g of milled soil sample was digested with 8 ml of HNO3 (65 %), 5 ml of HCl (37 %), and 1.5 ml of HF (40 %) in a Milestone Microwave (Milestone Ethos 900 plus Mod. 44062) in accordance with the ISO 11466 procedure (International Organization for Standardization, 1995). Metal contents were analyzed by inductively coupled plasma atomic emission spectrometry for Cr, Co, Zn, V, Cu, Pb, Ni, Fe, and Cd, and by hydride generation atomic fluorescence spectrometry for As (Fu et al. 2008).
Quality assurance and quality control
The reagent blanks were monitored throughout the analysis and were used as required to correct the analytical results. All analyses were performed at the Iran Mineral Processing Research Center. All samples were analyzed in triplicate, with the analytical process monitored using certified reference standards.
Background concentration of metals
Background of the status of heavy metals was prepared by using soil samples from virgin regions, e.g., pristine rangelands and regions, which were far from human activities. The mean of each metal was calculated and these virgin points were overlayed on to geological maps to produce the background concentration of each metal.
Statistical analysis using computer software
Multivariate analysis
Prior to statistical analysis, the datasets were evaluated using Kolmogorov–Smirnov method; and when the distribution was not normal, the data were log-transformed (Shi et al. 2007) before statistical treatment. The outliers can result in discrete data that breach the geostatistical theories. Box plots were then used to assess and correct the outliers in the study. Data higher than ± 3 SD were replaced with maximum or minimum of row datasets which were lower than ± 3 SD. Pekey (2006) and Inácio et. al. (2008) had also used this method to assess and correct the outliers in their studies.
All statistical analyses were thus made based on data in normal distribution. Descriptive statistics (mean, standard deviation, range, and coefficient of variation) of metals and soil properties were derived applying the SPSS®16.0 for Windows. The t test was used to determine the existence of significant differences among soil properties and metals. Multivariate analysis was performed using SPSS® software, with XlStat an add-in package of Microsoft Excel 2010. AHC and gap statistic (Gs) were used to identify differences between the classes and clustering the samples with similar metal content and soil properties. AHC was undertaken according to the Ward algorithmic method. Results are presented in a dendrogram where steps in the hierarchical clustering solution and values of distances between clusters (squared Euclidean distance) are represented (Chabukdhara and Nema 2012). Gap statistic is an important tool for estimating the number of clusters (groups) in a set of data (Tibshirani et al. 2001). The function of gap statistic is expressed as (Dudoit and Fridlyand 2002):
| 2 |
Varying the total number of clusters from k = 1…K, giving within cluster point scatters W k. Generate B reference datasets from a uniform distribution over the range of the observed data, and cluster each one giving within cluster point scatters W *kb, b = 1…B, k = 1…K. The gap statistic is computed as follows:
| 3 |
The standard deviation of the B replicates log (W k *) is computed as:
| 4 |
| 5 |
The number of clusters was chosen via,
= the smallest k such that gap (k) G(k + 1) − sdk + 1 (Tibshirani et al. 2001).
Principal component analysis (PCA) with Varimax normalized rotation was used for interpreting relationships and the hypothetical source of metals (lithogenic or anthropogenic). Varimax rotation was applied because the orthogonal rotation minimizes the number of variables with a high loading on each component and facilitates the interpretation of results (Acosta et al. 2011; Bini et al. 2011; Zhong et al. 2012; Li and Feng 2012a; Cai et al. 2012; Guo et al. 2012; Yang et al. 2011).
Geostatistical methods
Geostatistics was used to describe the geospatial distribution of the ten heavy metals at the regional scale. The geospatial data were compiled, merged, loaded, and spatial interpolation was performed with geostatistic extension. Geostatistic extension uses the technique of semivariogram (or variogram) to measure the spatial variability of a regionalized variable and provides the input parameters for spatial interpolation of kriging (Webster and Oliver 2007). Kriging is an interpolation method applied widely to elucidate spatial distribution of many parameters including metallic elements. Kriging interpolation refers to a group of spatial interpolation methods for assigning a value of a random field to an unsampled location based on the measured values in random fields at nearby locations (Xie et al. 2011). The semivariogram model was fitted before a kriging operation can be performed. The process of semivariogram model fitting was conducted using ILWIS 3.6® and the spatial distribution was achieved using disjunctive kriging. Semivariogram calculations were conducted and experimental semivariograms of soil heavy metal concentrations could be fitted with the available spherical, exponential, Gaussian, wave, rational quadratic, circular, and power models (Hendrikse 2000). Semivariograms were used in the study to analyze discrete soil samples. The function is expressed as:
| 6 |
where: is the semivariogram value of points that have a certain distance (h) towards each other; Z i is the value of point i, Z i + h is the value of a point at distance h from point i, ∑(Z i − Z i + h)2 the sum of the squared differences between point values of all point pairs within a certain distance class, and n is the number of point pairs within a distance class.
The function of semivariogram models are expressed as follows;
Spherical model:
for 0 < h < = a
| 7 |
for h > a
| 8 |
Exponential model:
| 9 |
Gaussian model:
| 10 |
Wave model:
| 11 |
Rational quadratic model:
| 12 |
Circular model:
for 0 < h < = a
| 13 |
for h > a
| 14 |
Power model:
| 15 |
where, h is the distance, C 0 is the nugget variance, C 0 + C is the sill, a is the range, k linear slope for the power function, m power exponent (0 < m < 2).
In developing a spatial distribution map for the pollution areas the spherical, exponential, Gaussian, wave, rational quadratic, circular, and power semivariogram models were used in order to determine the best model for fitting the probability of the true values of soil heavy metals at unsampled points. The best output map based on R 2 for each metal was selected for delineation of heavy metal pollution by geoenrichment index.
Interpretation of heavy metal pollution by geo-enrichment factor
Geoenrichment factor (EFG) is a geochemical index based on the assumption that under natural soil conditions, there is a linear relationship between a reference element and other elements. The metallic elements which are most often used as reference elements are Fe (Kartal et al. 2006), Al, Li, and TOC (Zhang et al. 2007; Gu et al. 2012; Li and Feng 2012a). In this study, we did not analyze that Al, Li, and TOC concentrations in the soils. We used Fe as a conservative tracer to differentiate natural from anthropogenic components (Kartal et al. 2006). In fact, several authors have successfully used Fe to normalize heavy metal contaminants (Bhuiyan et al. 2011; Esen et al. 2010; Gu et al. 2012). The EFG is defined as follows:
| 16 |
where (Me/Fe)sample map is the map of metals to Fe map ratio in the samples of interest; (Me/Fe)background map is the map of geochemical background value of metals to Fe map ratio.
Result and discussion
Descriptive statistics
A summary of the basic statistics of the investigated heavy metals and soil properties is presented in Table 1. It was noted that the K–S test for soil properties showed normal distribution, with the exception of Cd, V, EC, and OM, and thus the raw datasets were logarithmically transformed before performing geostatistical analysis. Logarithmic transformation resulted in reduced skewness and kurtosis values of Cd, V, EC, and OM, and the transformed datasets passed the log-normal tests. The geomean values of the heavy metal contents arranged in decreasing order were: Cr > Zn > Ni > Cu > Pb > Co > As > V > Fe > Cd (Table 1). The micronutrients such as Fe were present at the lowest levels in soils, whereas Cr and Zn were present at higher values. The coefficients of variations of EC, OM, Cd, As, clay, and sand were higher than 50 %, which implies that those metals had greater variation among the soil samples and thus were possibly influenced by extrinsic factors such as human activity. The average soil pH of 7.78 indicated that the soil in the study area was alkaline.
Table 1.
Descriptive statistics of soil properties and heavy metals
| Variable | Symbol | Unit | Descriptive statistics | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Range | G. Mean | SD | CV (%) | Kurtosis | Skewness | K–S test | |||
| Arsenic | As | mg kg−1 | 1.00–37.35 | 6.53 | 5.63 | 86.22 | 4.49 | 1.53 | 0.055 |
| Cadmium | Cd | mg kg−1 | 0.40–2.60 | 0.81 | 0.716 | 88.40 | −1.19 | 0.60 | 0.015 |
| Logarithm of Cd | −0.92–0.96 | 0.64 | 0.711 | 111.09 | −1.7 | 0.27 | 0.057 | ||
| Cobalt | Co | mg kg−1 | 8.10–27 | 17.27 | 3.56 | 20.61 | 0.19 | 0.013 | 0.394 |
| Chromium | Cr | mg kg−1 | 30–140 | 83.95 | 22.90 | 27.28 | −0.38 | −0.012 | 0.58 |
| Copper | Cu | mg kg−1 | 13.50–57 | 32.91 | 9.16 | 27.83 | −0.38 | 0.15 | 0.9 |
| Iron | Fe | mg kg−1 | 1.80–5.10 | 3.66 | 0.66 | 18.03 | 0.11 | −0.41 | 0.7 |
| Nickel | Ni | mg kg−1 | 26–110 | 60.97 | 17.73 | 29.08 | −0.25 | 0.22 | 0.95 |
| Lead | Pb | mg kg−1 | 13–57 | 23.93 | 5.34 | 22.32 | 9.96 | 1.88 | 0.094 |
| Vanadium | V | mg kg−1 | 50–150 | 101.6 | 21.11 | 20.78 | .138 | −0.28 | 0.019 |
| Logarithm of V | 3.91–5.01 | 4.61 | 0.22 | 4.77 | 1.37 | −1.0 | 0.064 | ||
| Zinc | Zn | mg kg−1 | 35–150 | 74.78 | 17.48 | 23.38 | 1.69 | 0.69 | 0.674 |
| pH | pH | – | 7.23–8.37 | 7.78 | 0.22 | 2.83 | 0.20 | 0.10 | 0.53 |
| Electrical conductivity | EC | dS m−1 | 0.48–38.80 | 1.27 | 3.54 | 278.74 | 92.97 | 9.04 | 0.00 |
| Logarithm of EC | −0.73–3.66 | 0.33 | 0.67 | 203.03 | 4.64 | 1.68 | 0.072 | ||
| Organic matter | OM | % | 0.03–2.69 | 0.45 | 0.50 | 111.11 | 4.27 | 1.89 | 0.023 |
| Logarithm of OM | −3.51–0.99 | 0.63 | 0.93 | 147.62 | 1.34 | −0.98 | 0.23 | ||
| Clay content | Clay | % | 1.46–66.63 | 26.88 | 13.49 | 50.19 | −0.48 | 0.26 | 0.611 |
| Sand content | Sand | % | 2.99–66.92 | 23.86 | 9.96 | 41.74 | 1.42 | −0.59 | 0.723 |
| Silt content | Silt | % | 12.65–54.15 | 42.38 | 8.41 | 19.84 | 0.087 | 0.45 | 0.574 |
SD standard deviation, G. Mean geometric means (geometric means were used to describe the central trend of data), CV coefficient of variation, K–S test Kolmogorov–Smirnov test (K–S > 0.05 data is normal)
Multivariate analyses
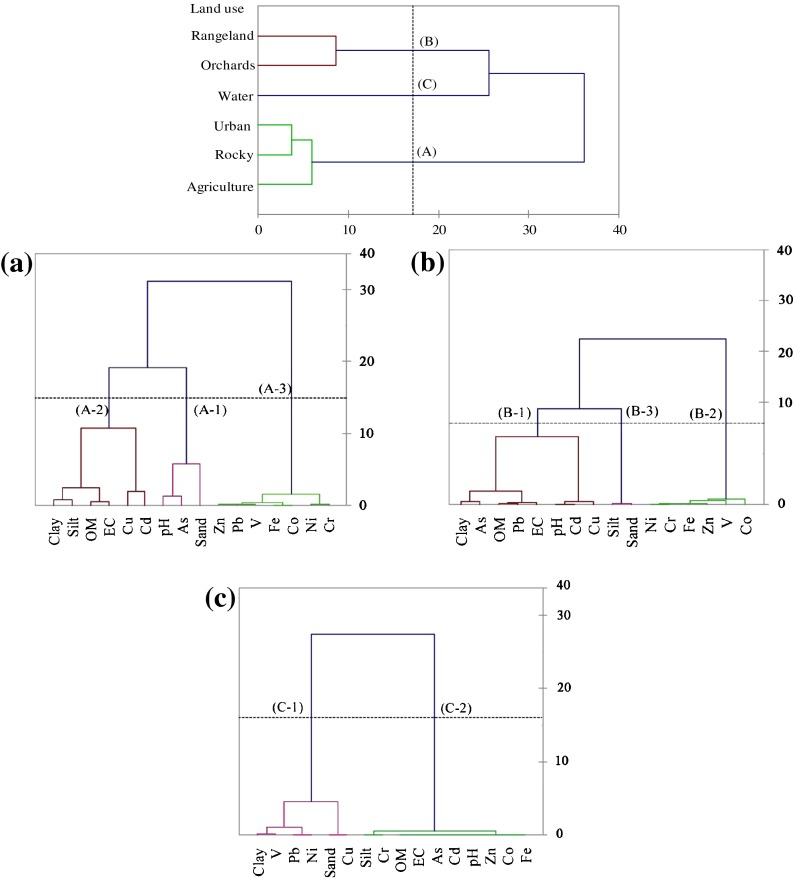
Heavy metals, soil properties, and land use grouping using AHC and Gs
AHC and Gs was used on both datasets of variables and land use sites, in order to identify clusters of land use, soil properties, and metals. AHC and Gs as an iterative classification method enabled the identification of three main groups (Fig. 2a), which included: group A (agriculture, rocky, and urban), group B (rangeland and orchards), and group C (water). The integration of AHC and Gs were performed on heavy metals and soil properties based on these three major groups obtained through AHC and Gs performed earlier (Fig. 2a). Results of AHC performed on groups A, B, and C are depicted in Fig. 2b–d. The dendrogram representing group A displayed three clusters (Fig. 2b). In the first cluster, As, pH, and sand were very well associated with each other (A-1 in Fig. 2a). The second cluster comprised of Cd which was also linked with Cu, EC, and OM. Soil properties (silt and clay) were associated in the second cluster. In the third cluster Co, Cr, Ni, Pb, V, Zn, and Fe were very well linked with each other. Heavy metals (As, Cd, and Cu) in the first and second cluster appear to be associated with anthropogenic origin. Fe is usually present in soils in relatively high concentration under natural condition. Co, Cr, Ni, Pb, V, and Zn may represent mixed origins (anthropogenic and lithogenic). In the group B sites, As, Cd, Cu, Pb, pH, EC, OM, and clay are grouped together, while Fe, Co, Cr, Ni, V, and Zn, and sand and silt formed subgroups B-2 and B-3, respectively. In group C, As, Cd, Co, Cr, Zn, Fe, pH, EC, and OM formed a separate group, although also linked with Cu, Ni, Pb, V, and soil properties (sand, silt, and clay).
Fig. 2.
Dendrogram showing clustering of a land use, b heavy metals and soil properties in group A, c group B, and d group C land use
Discriminating natural and anthropogenic sources using PCA
PCA (VARIMAX rotation mode) was performed separately for the three different groups (A, B, and C), as delineated by AHC and Gs techniques, to compare the compositional pattern between analyzed soil properties, metal samples and identify the factors influencing each one. PCA of the three datasets yielded three PCs for group A sites and three PCs for group B and two PCs for the group C sites with eigenvalues >1, explaining 63.6, 65.6, and 96.8 % of the cumulative variance, respectively (Table 2). In order to have a clear visualization of the data trends and the relationship between variables, PCA was depicted with loadings and score plots were derived. For datasets related to group A sites, PC1 elucidated 36.24 % of total variance and had strong positive loadings on Co, Cr, Ni, Pb, V, Zn, and Fe (Table 2). There were significant relationships between Co, Cr, Ni, Pb, V, Zn, and Fe. The geological structure of the area suggests lithogenic sources of these heavy metals. Mico et al. (2006) assessed heavy metal sources in soils of the European Mediterranean area, and observed that the metals Co, Cr, Zn, and Fe were in PC1 with maximum variance. These components were considered as lithogenic components and the variability of these metals is determined by the parent rocks.
Table 2.
Principal component matrix with eigenvalues, variability, and cumulative spatial variations of variables and factors
| Variables | Group A | Group B | Group C | |||||
|---|---|---|---|---|---|---|---|---|
| PC1 | PC2 | PC3 | PC1 | PC2 | PC3 | PC1 | PC2 | |
| As | 0.228 | −0.346 | −0.415 b | 0.403 | 0.659 a | 0.062 | −0.814 a | −0.157 |
| Cd | −0.273 | 0.155 | 0.885 a | −0.349 | −0.112 | 0.767 a | −0.927 a | 0.150 |
| Co | 0.956 a | −0.0001 | 0.056 | 0.958 a | 0.162 | 0.005 | −0.399 b | −0.043 |
| Cr | 0.863 a | 0.199 | −0.034 | 0.813 a | −0.046 | −0.002 | 1.066 a | −1.345 |
| Cu | 0.355 | 0.186 | 0.849 a | 0.283 | −0.137 | 0.870 a | 0.056 | −0.577 b |
| Ni | 0.806 a | 0.287 | 0.096 | 0.838 a | −0.119 | 0.100 | −0.374 | 1.536 a |
| Pb | 0.766 a | −0.073 | −0.133 | 0.478 b | 0.180 | −0.262 | 0.393 | −1.362 a |
| V | 0.918 a | −0.189 | −0.048 | 0.760 a | 0.468 | 0.040 | 1.125 a | 2.989 |
| Zn | 0.864 a | −0.057 | −0.035 | 0.793 a | 0.285 | 0.065 | 2.930 a | −0.158 |
| Fe | 0.941 a | −0.094 | 0.108 | 0.877 a | 0.053 | −0.009 | −0.718 a | −0.204 |
| pH | −0.036 | 0.062 | −0.266 b | 0.251 | 0.056 | 0.731 a | −0.723 a | 0.049 |
| EC | −0.086 | 0.210 b | 0.098 | −0.180 b | −0.130 | 0.154 | −0.916 a | 0.172 |
| OM | −0.268 | 0.465 b | 0.019 | −0.371 | −0.213 | 0.415 b | −0.948 a | 0.177 |
| Sand | −0.207 | −0.954 a | −0.008 | −0.132 | 0.937 a | −0.178 | 0.032 | −0.279 b |
| Silt | 0.099 | 0.739 a | −0.171 | −0.229 | −0.879 a | 0.241 | 0.450 b | −0.477 |
| Clay | 0.212 | 0.653 a | 0.211 | 0.538 b | −0.493 | −0.004 | −0.233 b | −0.471 |
| Eigenvalue | 5.81 | 2.76 | 1.59 | 5.74 | 2.99 | 1.76 | 1.79 | 0.20 |
| Variability | 36.24 | 15.62 | 11.74 | 34.01 | 17.51 | 14.08 | 89.95 | 6.85 |
| Cumulative | 36.24 | 51.87 | 63.61 | 34.01 | 51.52 | 65.60 | 89.95 | 96.80 |
Italicized values with the same letter are not significantly different at p<0.01a or p<0.05b
PC2, which explained 15.62 % of the total variance, had strong positive loading for EC, OM, silt, and clay, and a strong negative loading for sand. This component, accounted for soil organic matter and electrical conductivity. PC3, which explained 11.7 % of total variance, had strong positive loadings for Cd and Cu, a strong negative loading for As, and a moderate loading for pH (Table 2). Main anthropogenic sources of these heavy metals (Cd, Cu, and As) are direct discharges from local point sources, such as industrial and urban discharges carrying metal contaminants. Industrial sources include chemical, petrochemical, and agricultural fertilizer industries, several mining (iron, copper, arsenic, cadmium, stone, etc.) activities, and agricultural activities involving the use of chemical fertilizers and municipal waste. In the group B dataset, PC1 was dominated by Co, Cr, Ni, Pb, V, Zn, Fe, EC, and clay, which accounted for 34.01 % of the total variance. The possible sources could be similar to those mentioned earlier. PC2, which explained 17.5 % of total variance had strong positive loadings on As and sand, and a strong negative loading on silt. PC3, which explained 14.08 % of total variance, was dominated by Cd, Cu, soil organic matter, and electrical conductivity (Table 2). PC1 metal loadings are attributed to natural sources. In group C, PC1 which explained 89.95 % of the total variance had strong positive loadings for Cr, V, Zn, and silt, and strong negative loadings for As, Cd, Co, Fe, pH, EC, OM. and clay. PC2, which explained 6.85 % of the total variance showed strong loadings for Cu, Ni, Pb, and sand.
PC1 components may be controlled by natural factors, while PC2 components (Cu, Ni, and Pb) as mentioned earlier may have different sources of origin. It was also evident that the results of PCA support the findings of the AHC and correlation analysis.
Spatial data
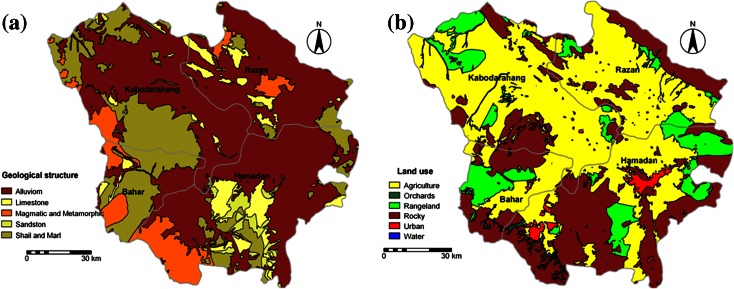
The geology of the area is characterized by quaternary alluvium, orbitalin lime, shale, and marls. The soils of this region were shallow and semi-deep, with gravel and lime. The texture of these soils was light to medium (Fig. 3a). Background concentration of heavy metals in virgin areas showed that the mean concentration of V and Cr was naturally high in all parent rocks and the lowest concentration in bedrocks was for Cd (Table 3).
Fig. 3.
Geology (a) and land use (b) maps of the study area
Table 3.
Background concentration of metals in parent rocks of study region (mg kg-1)
| Metal | parent rocks | ||||
|---|---|---|---|---|---|
| Alluvium | Limestone | Magmatic and metamorphic rocks | Sandstone | Shale and marl | |
| As | 8.22 | 8.8 | 9.41 | 7.03 | 7.60 |
| Cd | 0.83 | 1.59 | 1.11 | 0.90 | 1.73 |
| Co | 15.94 | 19.05 | 21.05 | 18.34 | 19.25 |
| Cr | 83.90 | 106.68 | 101.36 | 99.66 | 100.26 |
| Cu | 30.45 | 36.62 | 33.04 | 40.70 | 37.72 |
| Fe | 4.37 | 5.24 | 5.66 | 5.01 | 5.27 |
| Ni | 58.07 | 72.76 | 70.04 | 74.47 | 71.75 |
| Pb | 23.53 | 23.28 | 25.98 | 24.98 | 25.13 |
| V | 93.87 | 113.51 | 122.03 | 111.91 | 115.11 |
| Zn | 67.21 | 75.61 | 86.62 | 82.02 | 78.42 |
A total of six land use classes (agriculture, orchards, rangeland, rocky, urban, and water) were recognized (Fig. 3b). Results of accuracy assessment of land use maps are summarized in Table 4. It presents the errors of commission (user’s accuracy), omission (producer’s accuracy), and overall accuracy. The error of omission is the proportion that is incorrectly identified as belonging to a particular class. The overall accuracy gives the proportion of correctly classified areas relative to the total validation area. The overall accuracy was found to be 89.5 %. When interpreting this number, one has to bear in mind the classification process and the six different types that were distinguished. Highest accuracies were obtained for agriculture (92 %), rocky land (87.6 %), and rangeland (86.6 %), while moderate accuracies of more than 70 % were obtained for orchards, urban areas, and water. Most of the classification error was associated with water and urban areas. Only 70.3 % of water classes were correctly classified, while 13.2 % were misclassified as being agriculture. Urban was misclassified as rangeland or agriculture.
Table 4.
Error Matrix for individual classifications of land use (errors of commission: user’s accuracy, omission, producer’s accuracy and overall accuracy)
| Land use | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Reference data | Agriculture | Orchards | Rangeland | Rocky | Urban | Water | Area in ha | Correctly classified area in ha | Errors of omission (ha,%) | |
| Agriculture | 92 | 1.6 | 3.7 | 1.2 | 0.8 | 0.7 | 63,316.55 | 58,251.2 | 5,065.3 8.70 | |
| Orchards | 82 | 15 | 3 | 1,455.19 | 1,193.3 | 261.9 22.0 | ||||
| Rangeland | 10.1 | 86.6 | 1.8 | 1.1 | 0.4 | 14,328 | 12,408.0 | 1,920.0 15.50 | ||
| Rocky | 5.8 | 87.6 | 6.4 | 0.2 | 37,307.27 | 32,681.2 | 4,626.1 14.2 | |||
| Urban | 10.3 | 10.6 | 1.2 | 73 | 4.9 | 2,090.38 | 1,526.0 | 564.4 37.0 | ||
| Water | 13.2 | 4.1 | 11.5 | 0.9 | 70.3 | 79.81 | 56.1 | 23.70 42.20 | ||
| Area in ha | 63,316.55 | 1,455.19 | 14,328 | 37,307.27 | 2,090.38 | 79.81 | ∑118,577.2a | 10,6115.8 | ||
| Correctly classified area in ha | 58,251.2 | 1,193.3 | 12,408.0 | 32,681.2 | 1,526.0 | 56.1 | 106,115.8 | Overall accuracy 89.5 % | ||
| Errors of commission (ha, %) | 5,065.3 | 261.9 | 1,920.0 | 4,626.1 | 564.40 | 23.70 | ||||
| 8.7 | 22.0 | 15.50 | 14.20 | 37.0 | 42.20 | |||||
aOverall validation area
Geostatistical analysis
Spatial distribution patterns
The range of the semivariograms for Ni, Cr, and As were much greater than those for V, Pb, and Fe (Table 5). The smallest range of the semivariogram was presented by V and was 20.74 km. This confirmed the rational for the sampling density chosen, which was with 5-km intervals for the precise environmental survey of the heavy metals tested in this study.
Table 5.
Best-fitted semivariogram models of heavy metals and their parameters
| Soil attributes | Model | C 0 | C + C 0 | C 0/C + C 0 | Range (km) | R 2 |
|---|---|---|---|---|---|---|
| As | Exponential | 0.536 | 0.976 | 0.55 | 58.86 | 0.78 |
| Cd | Spherical | 0.666 | 1.316 | 0.51 | 48.90 | 0.87 |
| Co | Exponential | 5.938 | 12.845 | 0.46 | 38.01 | 0.72 |
| Cr | Exponential | 0.039 | 0.077 | 0.51 | 60.84 | 0.86 |
| Cu | Circular | 0.054 | 0.088 | 0.61 | 44.19 | 0.75 |
| Ni | Circular | 0.055 | 0.141 | 0.39 | 86.12 | 0.95 |
| Pb | Spherical | 0.48 | 0.994 | 0.48 | 21.22 | 0.68 |
| V | Circular | 0.016 | 0.08 | 0.20 | 20.74 | 0.64 |
| Zn | Rational quadratic | 0.026 | 0.058 | 0.45 | 54.38 | 0.76 |
| Fe | Exponential | 0.011 | 0.048 | 0.23 | 32.47 | 0.70 |
C 0 nugget variance, C structural variance, C + C 0 sill variance
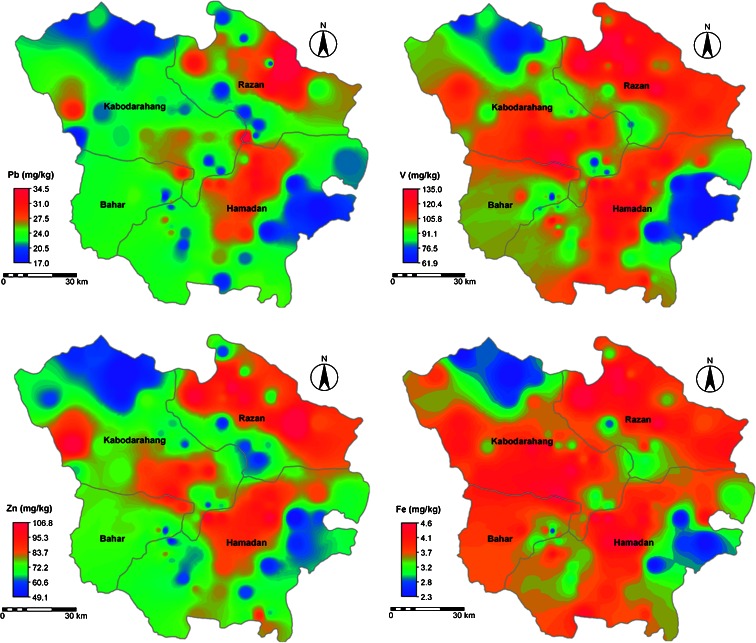
The spatial correlation between the available data with disjunctive kriging technique was used to map the metal contents and delineation of polluted areas. The experimental semivariograms of the heavy metals with the fitted models are presented in Table 5. The results showed that soil Zn data was fitted well with the rational quadratic model; Cd and Pb were fitted with the spherical model; Cu, Ni, and V were fitted with the circular model; and the other four heavy metals were all best fitted with the exponential model. The attributes of the semivariograms for each heavy metal are also summarized in Table 5. All of the Nug/Sill ratios for the ten metals were less than 0.72. In theory, the Nug/Sill ratio in geostatistics is regarded as the criterion to classify spatial dependence of soil attributes. The ratios of 0.25 and 0.75 are two thresholds for the relative strength index of spatial correlations. The variable with a ratio of less than 0.25 is strongly spatial dependent, while the variable with the ratio of between 0.25 and 0.75 is moderately spatial dependent; whereas the variable with the ratio greater than 0.75 is only weakly spatial dependent (Shi et al. 2007).
The Nug/Sill ratios of both V and Fe were less than 0.25, showing strong spatial dependence due to the effects of natural factors such as parent material, topography, and soil type (Table 5). The corresponding ratios for As, Cd, Co, Cr, Cu, Ni, Pb, and Zn were however, between 0.25 and 0.75, which belonged to the scope of moderate spatial dependence, revealing that anthropogenic factors such as industrial production, fertilization, and other soil management practices had changed their spatial correlation after a long process of utilization.
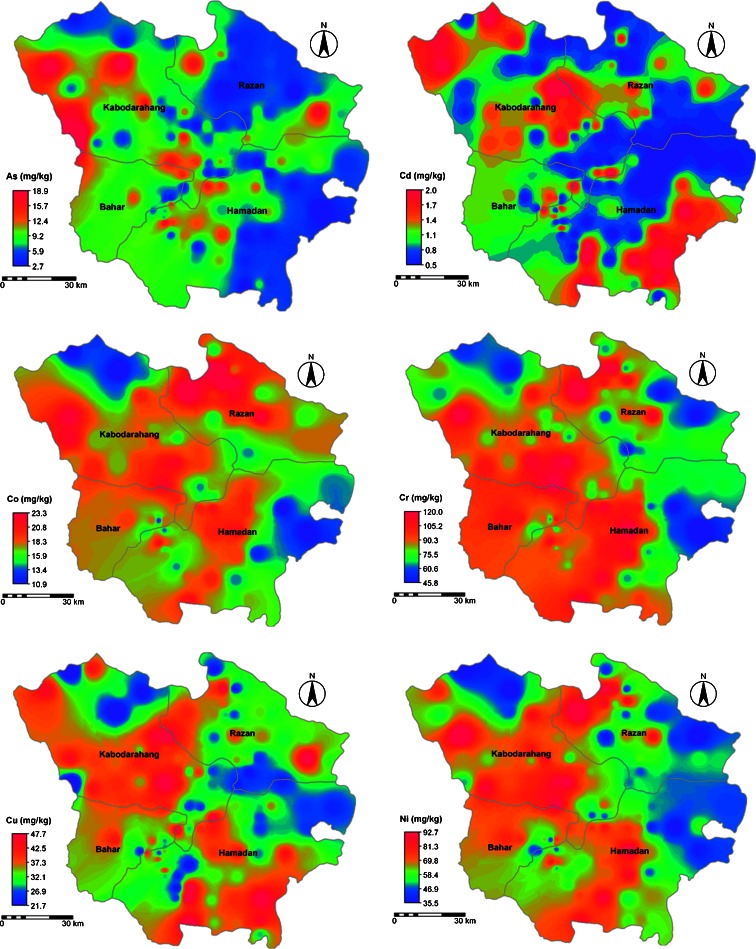
The spatial patterns of the ten heavy metals generated from their semivariograms showed that all metals had distinct geographical distributions (Fig. 4). The spatial distribution maps showed dissimilar geographical trends, with high contents both in the northeast and southern areas.
Fig. 4.
Spatial concentration maps of soil As, Cd, Co, Cr, Cu, Ni, Pb, V, Zn, and Fe produced by disjunctive Kriging
Geoenrichment factor and pollutant assessment
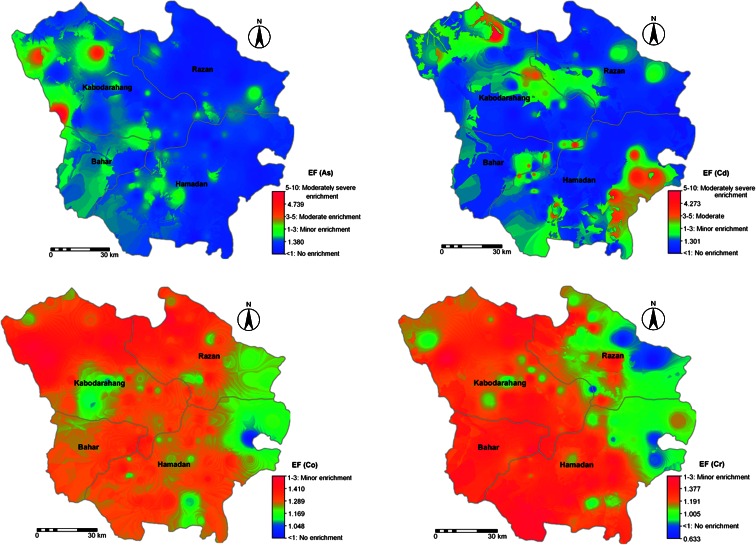
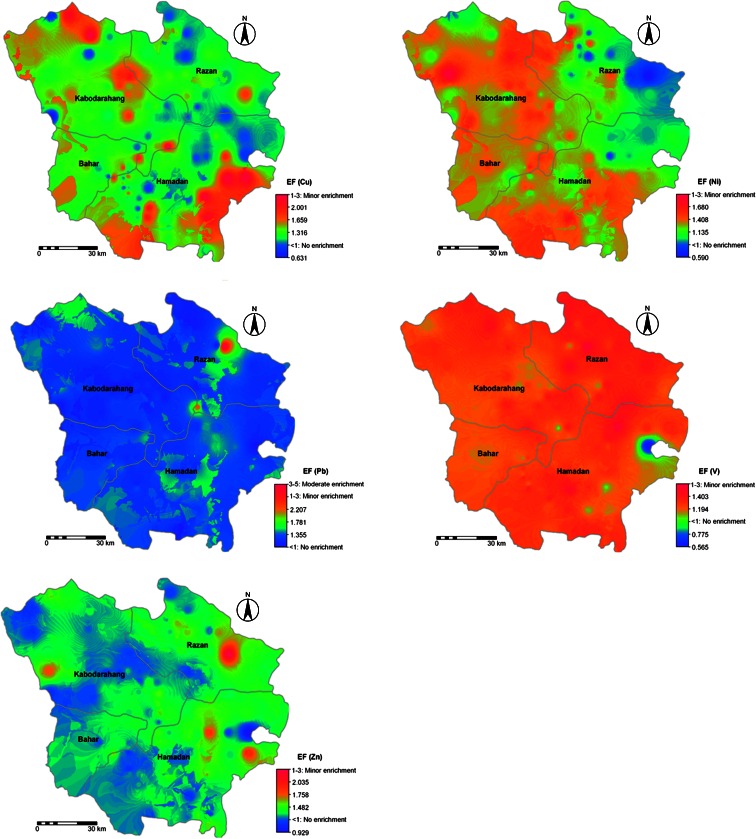
Unlike the application of multivariate techniques to the three major groups (A, B, and C), geoenrichment indices were calculated separately for all six land use classes, to delineate the polluted areas. The EFG values were interpreted in terms of heavy metal pollution as suggested by Birth (2003) and later adapted by Chabukdhara and Nema (2012). Birth proposed seven classes of enrichment (Table 6). Soils in the six land use classes in Hamedan showed a wide range of metal enrichment. In general, the mean predominant values showed moderate enrichment for As and Cd, and minor enrichment for Co, Cr, Cu, Ni, Pb, V, and Zn. Overall, the EF values of these metals followed the sequence Cd > As > Pb > Cu > Zn > Ni > Cr > V > Co. Similarly, Ghrefat et al. (2011) and Chabukdhara and Nema (2012) had reported EF of Cd to be the highest among the metals in the sediments of Kafrain Dam, Jordan and in the Hindon River, India. From the pollution point of view, agriculture and orchard lands were highly polluted and showed moderately severe enrichment for As and Cd, but with minor enrichment for Co, Cr, Cu, Ni, Pb, V, and Zn. The order of land use in terms of metal enrichment was: agriculture > orchards > rocky > rangeland > urban > water. None of the land use was absolutely free from anthropogenic enrichment.
Table 6.
Enrichment factor (EFG) of metallic elements in soils under different land use
| Enrichment factor (EFG) | Grade standards for EF (birth, 2003) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Land use | As | Cd | Co | Cr | Cu | Ni | Pb | V | Zn | Value | Enrichment status |
| Agriculture | 5.85 a | 5.26 | 1.53 | 1.56 | 2.34 | 1.95 | 3.05 | 1.61 | 2.31 | <1 | No enrichment |
| Orchards | 5.06 | 5.26 | 1.52 | 1.52 | 2.28 | 1.72 | 3.05 | 1.43 | 1.66 | 1–3 | Minor enrichment |
| Rangeland | 3.62 | 4.22 | 1.52 | 1.51 | 2.30 | 1.70 | 3.02 | 1.46 | 1.94 | 3–5 | Moderate enrichment |
| Rocky | 5.85 | 5.26 | 1.51 | 1.53 | 2.31 | 1.73 | 2.45 | 1.57 | 1.92 | 5–10 | Moderately severe enrichment |
| Urban | 3.47 | 3.90 | 1.51 | 1.49 | 2.17 | 1.69 | 3.05 | 1.51 | 1.86 | 10–25 | Severe enrichment |
| Water | 1.73 | 3.17 | 1.34 | 1.50 | 1.66 | 1.55 | 1.99 | 1.40 | 2.31 | 25–50 | Very severe enrichment |
| Min. | 1.73 | 3.17 | 1.34 | 1.49 | 1.66 | 1.55 | 1.99 | 1.40 | 1.66 | >50 | Extremely severe enrichment |
| Max. | 5.85 | 5.26 | 1.53 | 1.56 | 2.34 | 1.95 | 3.05 | 1.61 | 2.31 | ||
| Mean | 4.27 | 4.51 | 1.49 | 1.52 | 2.18 | 1.72 | 2.77 | 1.50 | 2.00 | ||
| SD | 1.62 | 0.88 | 0.07 | 0.02 | 0.25 | 0.12 | 0.44 | 0.08 | 0.25 | ||
aItalicized values indicate anthropogenic influences
The heavy metal pollution maps plotted based on reference values in Table 6, showed that As and Cd exhibited moderately severe pollution risk. The pollution patches developed from EFG are presented in Fig. 5. For soil As, the northeast of Kabodarahang was the area with moderate to severe pollution, with levels reaching 3.06–5.85 mg kg−1. Overlaying As contamination and land use maps revealed that agricultural lands with the geological structure containing magmatic and metamorphic rocks, shale, and marl had high contamination. The areas with high concentrations of As in red patches are illustrated in Fig. 5. Soil Cd in general exibited moderate to moderately severe pollution, with similar pollution patches, but was more serious than that of As, and covered the wider southeast region of Hamedan. Besides Hamedan, the highest risk (of minor pollution) with Co pollution was distributed in the north and northwest of the studied region (Kabodarahang and Razan town). The EFG values for Cr, Cu, Ni, V, and Zn were greater than 1 over a wide range of the study area, indicating minor pollution largely from human activities. The EFG values for Pb was higher than 1 in a major portion of the study area, revealing significant Pb contamination. Thus, areas with high heavy metal contamination would contribute to the environmental pollution and ultimately threaten the health of humans and other living organisms.
Fig. 5.
Spatial distribution map of heavy metals pollution (As, Cd, Co, Cr, Cu, Ni, Pb, V, and Zn)
Critical values of soil pollution by Cd, As, Cu, and Ni have been reported by Kabata-Pendias (2004). In the most parts of the study area, the soil concentrations of these metals were higher than critical levels, but the presence of lime in the soil will decrease the solubility and bioavailability of the metals. Elsewhere in the region, the low levels of metal contamination indicate that these areas can be regarded as safe areas.
Conclusion
The article is an original contribution as a case study, as it is a study of the Hamedan county (Iran) where the soils contamination situation has not been previously studied. The present study was conducted to: (1) determine the spatial patterns of heavy metals in soil under different geological structures and land uses collected from Hamedan county; (2) identify their natural or anthropogenic sources by integration multivariate, gap statistics, and GIS; and (3) assess the level of heavy metal contamination in the topsoil based on EFG. The methods followed in order to reach the aims of the study were basic statistical parameters calculation, agglomerative hierarchical clustering, gap statistic, correlations matrix, principal components analysis, to characterize the spatial distribution, and trace the sources of metallic element and finally an integrated GIS for interrelation spatial patterns of pollution patches. Based on the increases in their variation rates in soil, heavy metals can be listed as Cd, As, Ni, Cu, Cr, Zn, Pb, V, Co, and Fe. The results of the present study using multivariate and gap statistical analysis suggest antrhropic origin of As, Cd, and Cu, and lithogenic origin of Co, Cr, Ni, Pb, V, Zn, and Fe. The results of the geostatistical approach confirmed the severity of pollution and its anthropogenic influence based on spatial variation in the level of contamination. Comparing the spatial distribution of geo-enrichment indices to auxiliary GIS layers (geology, land use, industrial, mines, and background concentration of metals) suggests that Cd, As, and Cu far exceeded the safe limit in most of the land use classes. Both natural factors (e.g., the high soil shale, sandstone, limestone, and metamorphic parent rocks and background values) and anthropogenic factors (e.g., the discharge of industrial wastes, the exploitation of mines special mineral ores, and the high and unmanaged uses of fertilizers; 500–700 kg ha−1 year−1 urine, 200–330 kg ha−1 year−1 potassium, and 300–558 kg ha−1 year−1 phosphorus fertilizers) had contributed to the genesis of the pollution process. Although almost all the monitored land use classes suffered from heavy metal contamination, agricultural lands was the most polluted. This information will be helpful to land use planners and environmental risk managers who seek to encourage responsible, environmentally friendly economic development strategies.
References
- Acosta J, Faz A, Martinez-Martinez S, Zornoza R, Carmona D, Kabas S. Multivariate statistical and GIS-based approach to evaluate heavy metals behaviour in mine sites for future reclamation. Journal of Geochemical Exploration. 2011;109(1–3):8–17. doi: 10.1016/j.gexplo.2011.01.004. [DOI] [Google Scholar]
- Bhuiyan MAH, Suruvi NI, Dampare SB, Islam M, Quraishi SB, Ganyaglo S, Suzuki S. Investigation of the possible sources of heavy metal contamination in lagoon and canal water in the tannery industrial area in Dhaka, Bangladesh. Environmental Monitoring and Assessment. 2011;175(1–4):633–649. doi: 10.1007/s10661-010-1557-6. [DOI] [PubMed] [Google Scholar]
- Bini C, Sartori G, Wahsha M, Fontana S. Background levels of trace elements and soil geochemistry at regional level in NE Italy. Journal of Geochemical Exploration. 2011;109(1–3):125–133. doi: 10.1016/j.gexplo.2010.07.008. [DOI] [Google Scholar]
- Cai L, Xu Z, Ren M, Guo Q, Hu X, Hu G, Wan H, Peng P. Source identification of eight hazardous heavy metals in agricultural soils of Huizhou, Guangdong Province, China. Ecotoxicology and Environmental Safety. 2012;78:2–8. doi: 10.1016/j.ecoenv.2011.07.004. [DOI] [PubMed] [Google Scholar]
- Chabukdhara M, Nema AK. Assessment of heavy metal contamination in Hindon River sediments: a chemometric and geochemical approach. Chemosphere. 2012;87(8):945–953. doi: 10.1016/j.chemosphere.2012.01.055. [DOI] [PubMed] [Google Scholar]
- Dudoit S, Fridlyand J. A prediction-based resampling method for estimating the number of clusters in a dataset. Genome biology. 2002 doi: 10.1186/gb-2002-3-7-research0036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esen E, Kucuksezgin F, Uluturhan E. Assessment of trace metal pollution in surface sediments of Nemrut Bay, Aegean Sea. Environmental Monitoring and Assessment. 2010;160(1–4):257–266. doi: 10.1007/s10661-008-0692-9. [DOI] [PubMed] [Google Scholar]
- Everitt, B., Landau, S., & Leese, M. (2001) Cluster analysis (4th edition). London: Edward Arnold Publishers Ltd.
- Fu J, Zhou Q, Liu J, Liu W, Wang T, Zhang Q, Jiang G. High levels of heavy metals in rice (Oryzasativa L.) from a typical E-waste recycling area in southeast China and its potential risk to human health. Chemosphere. 2008;71(7):1269–1275. doi: 10.1016/j.chemosphere.2007.11.065. [DOI] [PubMed] [Google Scholar]
- Ghrefat HA, Abu-Rukah Y, Rosen MA. Application of geoaccumulation index and enrichment factor for assessing metal contamination in the sediments of Kafrain Dam, Jordan. Environmental Monitoring and Assessment. 2011;178(1–4):95–109. doi: 10.1007/s10661-010-1675-1. [DOI] [PubMed] [Google Scholar]
- Gu YG, Wang ZH, Lu SH, Jiang SJ, Mu DH, Shu YH. Multivariate statistical and GIS-based approach to identify source of anthropogenic impacts on metallic elements in sediments from the mid Guangdong coasts, China. Environmental Pollution. 2012;163:248–255. doi: 10.1016/j.envpol.2011.12.041. [DOI] [PubMed] [Google Scholar]
- Guo G, Wu F, Xie F, Zhang R. Spatial distribution and pollution assessment of heavy metals in urban soils from southwest China. Journal of Environmental Sciences. 2012;24(3):410–418. doi: 10.1016/S1001-0742(11)60762-6. [DOI] [PubMed] [Google Scholar]
- Hendrikse J (2000) Geostatistics in ILWIS. International Archives of Photogrammetry and Remote Sensing 33 (B4/1; PART 4):365–375
- Huang S-W, Jin J-Y. Status of heavy metals in agricultural soils as affected by different patterns of land use. Environmental Monitoring and Assessment. 2008;139(1–3):317–327. doi: 10.1007/s10661-007-9838-4. [DOI] [PubMed] [Google Scholar]
- Inácio M, Pereira V, Pinto M. The soil geochemical atlas of Portugal: overview and applications. Journal of Geochemical Exploration. 2008;98(1–2):22–33. doi: 10.1016/j.gexplo.2007.10.004. [DOI] [Google Scholar]
- Irpino, A., Verde, R. (2006) A new Wasserstein based distance for the hierarchical clustering of histogram symbolic data. In: Batagelj, V., Bock, H. H., Ferligoj, A., & Ziberna, A. (Eds.) Data Science and Classification, vol Part IV. (pp 185-192). Berlin-Heidelberg: Springer-Verlag. doi:10.1007/3-540-34416-0_20.
- Kabata-Pendias A. Soil–plant transfer of trace elements—an environmental issue. Geoderma. 2004;122(2):143–149. doi: 10.1016/j.geoderma.2004.01.004. [DOI] [Google Scholar]
- Kartal Ş, Aydın Z, Tokalıoğlu Ş. Fractionation of metals in street sediment samples by using the BCR sequential extraction procedure and multivariate statistical elucidation of the data. Journal of Hazardous Materials. 2006;132(1):80–89. doi: 10.1016/j.jhazmat.2005.11.091. [DOI] [PubMed] [Google Scholar]
- Li X, Feng L. Geostatistical analyses and fractionation of heavy metals in urban soil from industrial district in Weinan, NW China. Environmental Earth Sciences. 2012 [Google Scholar]
- Li X, Feng L. Multivariate and geostatistical analyzes of metals in urban soil of Weinan industrial areas, Northwest of China. Atmospheric Environment. 2012;47:58–65. doi: 10.1016/j.atmosenv.2011.11.041. [DOI] [Google Scholar]
- Lin YP, Cheng BY, Shyu GS, Chang TK. Combining a finite mixture distribution model with indicator kriging to delineate and map the spatial patterns of soil heavy metal pollution in Chunghua County, central Taiwan. Environmental Pollution. 2010;158(1):235–244. doi: 10.1016/j.envpol.2009.07.015. [DOI] [PubMed] [Google Scholar]
- Lu A, Wang J, Qin X, Wang K, Han P, Zhang S. Multivariate and geostatistical analyses of the spatial distribution and origin of heavy metals in the agricultural soils in Shunyi, Beijing, China. Science of the Total Environment. 2012;425:66–74. doi: 10.1016/j.scitotenv.2012.03.003. [DOI] [PubMed] [Google Scholar]
- Matheron G. Principles of geostatistics. Economic Geology. 1963;58(8):1246–1266. doi: 10.2113/gsecongeo.58.8.1246. [DOI] [Google Scholar]
- Micó C, Recatalá L, Peris M, Sánchez J. Assessing heavy metal sources in agricultural soils of an European Mediterranean area by multivariate analysis. Chemosphere. 2006;65(5):863–872. doi: 10.1016/j.chemosphere.2006.03.016. [DOI] [PubMed] [Google Scholar]
- Pekey H. The distribution and sources of heavy metals in Izmit Bay surface sediments affected by a polluted stream. Marine Pollution Bulletin. 2006;52(10):1197–1208. doi: 10.1016/j.marpolbul.2006.02.012. [DOI] [PubMed] [Google Scholar]
- Shi J, Wang H, Xu J, Wu J, Liu X, Zhu H, Yu C. Spatial distribution of heavy metals in soils: a case study of Changxing, China. Environmental Geology. 2007;52(1):1–10. doi: 10.1007/s00254-006-0443-6. [DOI] [Google Scholar]
- Tibshirani R, Walther G, Hastie T. Estimating the number of clusters in a data set via the gap statistic. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2001;63(2):411–423. doi: 10.1111/1467-9868.00293. [DOI] [Google Scholar]
- Ward, J. (1963) Hierarchical grouping to optimize an objective function. Journal of the American Statistical Association, 58(301), 236–244. doi:10.1080/01621459.1963.10500845.
- Webster R, Oliver MA. Geostatistics for environmental scientists. John Wiley & Sons Inc: Second Edition edn; 2007. [Google Scholar]
- Xie Y, Chen T, Lei M, Yang J, Guo Q, Song B, Zhou X. Spatial distribution of soil heavy metal pollution estimated by different interpolation methods: Accuracy and uncertainty analysis. Chemosphere. 2011;82(3):468–476. doi: 10.1016/j.chemosphere.2010.09.053. [DOI] [PubMed] [Google Scholar]
- Yang Z, Lu W, Long Y, Bao X, Yang Q. Assessment of heavy metals contamination in urban topsoil from Changchun City, China. Journal of Geochemical Exploration. 2011;108(1):27–38. doi: 10.1016/j.gexplo.2010.09.006. [DOI] [Google Scholar]
- Zhang L, Ye X, Feng H, Jing Y, Ouyang T, Yu X, Liang R, Gao C, Chen W. Heavy metal contamination in western Xiamen Bay sediments and its vicinity, China. Marine Pollution Bulletin. 2007;54(7):974–982. doi: 10.1016/j.marpolbul.2007.02.010. [DOI] [PubMed] [Google Scholar]
- Zhang X, Lin F, Wong MT, Feng X, Wang K. Identification of soil heavy metal sources from anthropogenic activities and pollution assessment of Fuyang County, China. Environmental Monitoring and Assessment. 2009;154(1):439–449. doi: 10.1007/s10661-008-0410-7. [DOI] [PubMed] [Google Scholar]
- Zhong L, Liu L, Yang J (2012) Characterization of heavy metal pollution in the paddy soils of Xiangyin County, Dongting lake drainage basin, central south China. Environmental Earth Sciences: 1–8. doi:10.1007/s12665-012-1671-6