Reproductive competition between females in the matrilineal Mosuo of southwestern China

Abstract

The matrilineal Mosuo of southwestern China live in communal households where brothers and sisters of three generations live together (duolocal residence), and men visit their wives, who reside elsewhere, only at night in ‘visiting’ marriages. Here we show that these communally breeding sisters are in reproductive conflict, in the sense that they share the resources needed to reproduce. We analyse determinants of reproductive success in females and males, and show that co-resident female kin are in competition; the more female kin reside in the household, the more reproductive success is reduced. Male reproductive success, however, is not determined by the kin in his natal household; duolocal males are not in reproductive conflict with their siblings. Competition with female cousins can be worse than that between sisters. We also find that female work on the farm (which is the main communal resource) is not equal. We use a ‘tug-of-war’ model of reproductive skew generated by incomplete control, to model the patterns of effort put into competition between sisters and cousins. The model predicts that more dominant (older) sisters will put less effort into reproductive conflict than will less dominant (younger) sisters; but younger sisters will also have lower reproductive success because they are less efficient at gaining access to the shared resource. Both predictions are consistent with our data. Younger sisters work less in the fields than do older sisters, which may represent a form of conflict or may be because their average relatedness to the household is lower than that of their more fertile older sisters.

1. Introduction

Human families are very diverse, showing a wide range of residence patterns; although females usually but not always disperse at marriage [1,2], a significant minority of human societies have matrilocal residence, in which males disperse [3]. In a few societies, neither sex disperse (known as duolocal residence), as is the case of the Mosuo of southwestern China (and a very small number of other Asian matrilineal peasant societies). Here we examine this rare case in which males and females usually stay in their maternal household throughout their life; they do marry, but males are not co-residents with their spouses and offspring. We seek evidence for reproductive conflict between household members, and model how we would expect such reproductive competition to influence household work patterns. Our data support models of reproductive conflict owing to ‘incomplete control’, where older, more dominant sisters have higher reproductive success, but also expend less effort on competing for communal resources in the household.

The Mosuo (also known as the Na [4]) inhabit strips of farmland around the shores of Lugu Lake in southwestern China, which covers a geographically constrained habitat surrounded by steep and forested hills that are not suitable for farming. Diets used to be supplemented by fishing and hunting, but wildlife resources are now depleted. The group is related to Tibetans and Naxi and speak a Tibeto-Burman language. Land is farmed by matrilineal family groups, although it is technically on lease from the Chinese government, and prior to the revolution was under the ultimate control of an aristocracy. Mosuo families live in large matrilineal households of three generations of brothers and sisters and the matrilineal offspring. There are several co-resident breeding women (mean of 2.14 breeding-age females per household [5]), who co-operate with child care, domestic and farm labour, and share all the household resources [5,6]. Mosuo houses are large structures, traditionally built around a courtyard. The grandmother is usually the head of the household, and the house is centred around a large grandmother's room, where the children also sleep and guests are received at a central fireplace. The grandmother plays a key role running the household, helping with child care as well as continuing to help with farming and feeding the family. Sisters and adult daughters have their own rooms, where their husbands visit them at night, but husbands do not eat in their wife's household (except in rare circumstances, for example if the husband is helping the family with his labour during the planting season). Males eat in their natal household but are expected either to visit their wives at night or share another room in the house with the unmarried men and boys. Senior men may get their own room in larger houses. Men are more likely to help with agricultural labour at planting and harvest and are rarely seen in the fields at other times [7]. Domestic labour (with the exception of building work) is almost exclusively done by females. Thus Mosuo females are working hard, cooperating in both the domestic arena, including child care and cooking, as well as doing the majority of the agricultural labour [5]. Men generally do more market trading and historically many may have gone to live and worship in monasteries, but there was general agreement among all our informants with our observation that females work harder than males in both the domestic and agricultural spheres. Under the duolocal system, Mosuo mothers and sisters appear willing to feed their sons and brothers throughout life while making relatively low demands on their labour [5]. All available farmland is in use, and this farmland is passed down to all matrilineal offspring who farm it communally (although individuals can now make a claim to the government to separate off their own farmland—a trend that is unpopular with families as it potentially causes conflict). Communal breeding is associated with saturated habitat and limited opportunities to disperse in mammals and birds [8,9]. The large, costly houses and the saturated farming habitat appear to be limiting resources, because when these restrictions are removed by the introduction of new economic opportunities now available through investing in tourism, especially by building tourist hotels, then the communal living and duolocal marriage system quickly breaks down in favour of nuclear neolocal households [10]. However, duolocal group households were still a common form of residence in Lugu Lake in 2008 [5].

In contrast to some suggestions from earlier ethnographic accounts [4,11], we find that reproductive marriage is now reported as being relatively monogamous; although this may have been influenced by the current government favouring monogamy and restricting family size to no more than three children, and thus it is likely that rates of polygyny and polyandry were higher in the past. We have argued elsewhere that it is the communal breeding of sisters and other closely related matrilineal kin, rather than paternity uncertainty, that underpins the matrilocal bias in male work patterns and duolocal residence [5].

Here, we examine the working patterns and fitness consequences of communal breeding by females. We conducted a demographic survey of a large Mosuo population, combined with data on household resources and working patterns. Hence, we can identify patterns of competition and co-operation within the family that arise in this matrilineal duolocal system. We apply a model of optimal effort on competition versus co-operative activity in females sharing common resources that maximizes the reproductive success of both sisters (or cousins) in reproductive conflict with each other in an attempt to explain these patterns.

2. Data and methods

In 2007, we conducted a demographic census of 7034 people in five Mosuo villages in Lugu Lake Town on the shores of Lugu Lake in the Tibetan borderlands of Sichuan province, China. Lugu Lake Town is about 283 km², and the total population is about 10 000. Most of the inhabitants are Mosuo, and others are Yi, Han, Pumi and a few Tibetan people. In the planting season of 2011 and 2012, we also conducted spot observations on who was working on the land from a random sample of 159 farms in three villages, recording all the personal information of each individual seen working on a field, including name, gender, ethnic group, age, animal sign of the year of birth and relationship with the owner of the land.

For each household, one adult representative was interviewed about the personal information of all male and female family members as well as household information, which included name, ethnic group, gender, year of birth, animal sign, education, parents' name, marriage status, spouses’ name, children's name, children's year of birth, children's gender, and place of residence, GPS location, land size, number of livestock and number of hotels and businesses.

We analyse the relationship between reproductive success (RS; number of surviving children), age at first birth and age, education, number of co-resident kin, size of land per adult, number of livestock and tourist income for Mosuo ‘visiting marriage’ males and females. Poisson regression is used to model determinants of RS (number of surviving children) and age at first birth is modelled with a linear regression for Mosuo duolocal males and females over the age at which 95% of them would be expected to have given birth.

We use a model selection approach [12,13] to investigate the determinants of the fertility (surviving children) and age at first birth of adult Mosuo women and men in duolocal households and mixed households (mixed household is a household in which parents are co-residents and all children are in duolocal marriages, co-resident parents are excluded from the calculation). Tables S1 and S2 in the electronic supplementary material show statistics of samples used and variables analysed in the model selection approach. Because the number of surviving children is count data and there is no evidence of overdispersion, we conduct generalized linear regression with a Poisson distribution. Age at first birth is modelled with linear regression, only using data from duolocal women who are older than 33 (n = 434) and men who are older than 35 (n = 266), which is the time when most duolocal women and men have already had their first birth.

For each analysis, we considered a set of a priori candidate models that explain reproductive success (in terms of the number of surviving children controlling for age, or age at first birth); candidate models included a null model, a control model of just age (or cohort) and education, and further models adding either number of co-resident female kin, co-resident male kin or sources of income entered in all possible combinations. The full set of candidate models can be found in tables S3 and S4 in the electronic supplementary material. The information theoretic approach compares the fit and complexity of each model; model rankings were calculated based on the Akaike information criterion (AIC), and Akaike weights were calculated by AIC difference among candidate models [12,13]. We present only those models that collectively account for 95% of the available model weight (tables 1–8). These are the models that contain only those variables that are most likely to explain the data. Parameter estimates were obtained by weighted-support model averaging from the entire set of candidate models; this means that the estimates and measures of precision (standard error and confidence intervals) were presented as standardized average estimators allowing better precision and reduced bias compared with the estimator of that parameter only for the best selected model. Analyses were carried out using the AICcmodavg package [14] in R software (R Development Core Team, v. 2.15.1) [15].

Table 1.

Best models of determinants of fertility in adult Mosuo females in duolocal and mixed households as a function of age, co-resident kin and household wealth (n = 824). Controlling for age and education, we find that the most informative model contains co-resident female kin, male kin, sources of wealth and interaction terms between age and co-resident kin. All co-resident kin are negatively associated with fertility, with the number of sisters and maternal cousins having the biggest negative effect. Livestock and tourism income have positive effects. The interaction between age and co-resident kin predicts that negative effects of siblings and cousins on fertility were higher in older generations. Control model includes age + age² + the years of education; female kin represents co-resident number of sisters + number of female cousins + number of female elders; male kin represents number of brothers + number of male cousins + number of male elders; wealth represents number of livestock + averaged size of land + tourist income (0 represents the household has no tourism income and 1 represents the household has tourism income); K, no. of parameters in the model; ΔAIC, deviation in AIC; ω_i, Akaike weight; LL, log-likelihood.

models	K	AIC	ΔAIC	ωi	LL
control + female kin + male kin + wealth + age × female kin + age × male kin	19	2351.41	0	1	−1156. 70

Table 2.

Parameter estimates in best-fitted candidate models of determinants of fertility in adult Mosuo females in duolocal and mixed households as a function of age, co-resident kin and household wealth (n=824). Significant effects are in bold.

variables	model-averaged estimate	unconditional s.e.	95% unconditional CI
age	0.0922	0.0105	0.0716	0.1128
age2	−8×10−4	1×10−4	−0.001	−5×10−4
years of education	−0.0742	0.0146	−0.1029	−0.0455
no. sisters	−0.0482	0.0225	−0.0923	−0.0042
no. female cousins	−0.163	0.1049	−0.3685	0.0426
no. female elders	−0.0685	0.0515	−0.1693	0.0324
no. brothers	−0.0147	0.0213	−0.0565	0.027
no. male cousins	−0.1583	0.0745	−0.3043	−0.0123
no. male elders	−0.036	0.044	−0.1222	0.0502
no. livestock	0.0064	0.0027	0.0011	0.0118
averaged size of land	0.0053	0.0132	−0.0206	0.0311
tourist income	0.0562	0.0529	−0.0475	0.1598
age×sisters	−0.0048	0.0019	−0.0084	−0.0011
age×female cousins	−0.007	0.008	−0.0226	0.0086
age×female elders	0.0061	0.0048	−0.0032	0.0155
age×brothers	−0.0056	0.0016	−0.0088	−0.0024
age×male cousins	−0.0044	0.007	−0.0181	0.0094
age×male elders	0.0061	0.0042	−0.0021	0.0143

Table 3.

Best models of determinants of fertility in adult Mosuo males in duolocal and mixed households as a function of age, co-resident kin and household wealth (n = 809). The Akaike weight of best-fit model is only 0.34. The second best-fit model is simply the control model (age and education), which shows that the no. co-resident kin and wealth are only weakly associated with male fertility, if at all. Control model includes age + age² + the years of education; female kin represents no. sisters + no. female cousins + no. female elders; male kin represents no. brothers + no. male cousins + no. male elders; wealth represents no. livestock + averaged size of land + tourist income (0 represents the household has no tourism income; and 1 represents the household has tourism income); K, no. of parameters in the model; ΔAIC, deviation in AIC; ω_i, Akaike weight; LL, log-likelihood.

models	K	AIC	ΔAIC	ωi	LL
control + female kin + male kin + wealth + age × female kin + age × male kin	19	1964.27	0	0.34	−963.14
control	4	1965.15	0.88	0.22	−978.58
control + male kin	7	1965.64	1.37	0.17	−975.82
control + wealth	7	1966.98	2.71	0.09	−976.49
control + male kin + wealth	10	1967.29	3.02	0.07	−973.65
control + female kin	7	1967.62	3.34	0.06	−976.81

Table 4.

Parameter estimates in best-fitted candidate models of determinants of fertility in adult Mosuo males in duolocal and mixed households as a function of age, co-resident kin and household wealth (n = 809). Significant effects are in bold.

variables	model-averaged estimate	unconditional s.e.	95% unconditional CI
age	0.2383	0.0153	0.2084	0.2683
age2	−0.002	2×10−4	−0.0024	−0.0015
years of education	−0.0033	0.0092	−0.0214	0.0147
no. sisters	0.0301	0.0264	−0.0216	0.0818
no. female cousins	−0.0269	0.0733	−0.1705	0.1168
no. female elders	−0.0415	0.0589	−0.1569	0.074
no. brothers	0.038	0.0259	−0.0127	0.0887
no. male cousins	−0.102	0.0721	−0.2433	0.0393
no. male elders	−0.0079	0.0566	−0.1187	0.103
no. livestock	−0.001	0.0036	−0.0081	0.0062
averaged size of land	−0.0219	0.0167	−0.0546	0.0108
tourist income	0.1022	0.0659	−0.0269	0.2313
age×sisters	−0.0032	0.0023	−0.0077	0.0013
age×female cousins	0.0031	0.006	−0.0086	0.0148
age×female elders	−0.0012	0.0057	−0.0124	0.01
age×brothers	−0.0032	0.0026	−0.0082	0.0018
age×male cousins	0.0038	0.0062	−0.0084	0.016
age×male elders	0.0167	0.0061	0.0047	0.0286

Table 5.

Best models of determinants of age at first birth in adult Mosuo females in duolocal and mixed households as a function of education, co-resident kin and household wealth (n = 434, age from 33 to 90). The most informative model contains female kin, male kin, wealth and interactions between cohort and kin. Control model includes age cohort + the years of education; female kin represents co-resident number of sisters + number of female cousins + number of female elders; male kin represents number of brothers + number of male cousins + number of male elders; wealth represents number of livestock + averaged size of land + tourist income (0 represents the household has no tourism income; and 1 represents the household has tourism income); K, no. of parameters in the model; ΔAIC, deviation in AIC; ω_i, Akaike weight; LL, log-likelihood.

models	K	AIC	ΔAIC	ωi	LL
control + female kin + male kin + wealth + cohort × female kin + cohort × male kin	19	2422.84	0	0.89	−1192.42
control + female kin + wealth	10	2427.83	4.99	0.07	−1203.92

Table 6.

Parameter estimates in best-fitted candidate models of determinants of age at first birth in adult Mosuo females in duolocal and mixed households as a function of education, co-resident kin and household wealth (n = 434). All co-resident kin are associated with a delay in age at first birth, with the number of female cousins and female elders having the most significant negative effect. Livestock and tourism income are associated with females having earlier first births. Significant interaction between cohort and female cousins predicts the negative effect of female cousins is higher in older generations, but the effect in delaying age at first birth by female elders is lower in older generations. Significant effects are in bold.

variables	model-averaged estimate	unconditional s.e.	95% unconditional CI
cohort	0.7092	0.1897	0.3374	1.081
years of education	−0.0696	0.1302	−0.3248	0.1856
no. sisters	0.2238	0.1713	−0.112	0.5596
no. female cousins	1.8392	0.754	0.3615	3.317
no. female elders	0.7793	0.3804	0.0337	1.5248
no. brothers	0.1269	0.1619	−0.1904	0.4442
no. male cousins	0.7191	0.6759	−0.6056	2.0438
no. male elders	0.2409	0.3936	−0.5305	1.0123
no. livestock	−0.0468	0.0208	−0.0877	−0.006
averaged size of land	0.0317	0.096	−0.1564	0.2199
tourist income	−0.7933	0.3971	−1.5715	−0.0151
cohort×sisters	−0.0903	0.1584	−0.4009	0.2202
cohort×female cousins	2.4644	0.9489	0.6046	4.3241
cohort×female elders	−1.3584	0.4877	−2.3144	−0.4025
cohort×brothers	−0.1734	0.1309	−0.43	0.0832
cohort×male cousins	−0.5422	0.8835	−2.2738	1.1893
cohort×male elders	−0.1692	0.5663	−1.2792	0.9407
income×sisters	−0.2155	0.3182	−0.8393	0.4082
income×female cousins	−0.4801	1.8285	−4.0639	3.1038
income×female elders	−1.001	0.7293	−2.4303	0.4284
income×brothers	−0.1734	0.1309	−0.43	0.0832
income×male cousins	−0.5422	0.8835	−2.2738	1.1893
income×male elders	−0.1692	0.5663	−1.2792	0.9407

Table 7.

Best models of determinants of age at first birth in adult Mosuo males in duolocal and mixed households as a function of education, co-resident kin and household wealth (n = 266). Controlling for cohort and education, the most informative models contain income variables. Control model includes age cohort + years of education; female kin represents number of sisters + number of female cousins + number of female elders; male kin represents number of brothers + number of male cousins + number of male elders; wealth represents number of livestock + averaged size of land + tourist income (0 represents the household has no tourism income; and 1 represents the household has tourism income); K, no. of parameters in the model; ΔAIC, deviation in AIC; ω_i, Akaike weight; LL, log-likelihood.

models	K	AIC	ΔAIC	ωi	LL
control + female kin + wealth	10	1510.70	0	0.35	−745.35
control + wealth	7	1510.89	0.19	0.32	−748.45
control + female kin + male kin + wealth + income × female kin + income × male kin	19	1513.26	2.56	0.10	−737.63
control + female kin + male kin + wealth	13	1513.64	2.94	0.08	−743.82
control	4	1513.83	3.13	0.07	−752.92
control + female kin	7	1514.97	4.27	0.04	−750.49

Table 8.

Parameter estimates in best-fitted candidate models of determinants of age at first birth in adult Mosuo males in duolocal and mixed households as a function of education, co-resident kin and household wealth (n = 266). Tourism income is associated with males having the first child earlier. Significant effects are in bold.

variables	model-averaged estimate	unconditional SE	95% unconditional CI
cohort	1.1504	0.2784	0.6049	1.696
years of education	−0.0426	0.0724	−0.1845	0.0993
no. sisters	0.2891	0.2145	−0.1313	0.7096
no. female cousins	1.087	0.6459	−0.179	2.353
no. female elders	0.3762	0.5101	−0.6235	1.3759
no. older brothers	0.1456	0.2083	−0.2627	0.5538
no. male cousins	−1.05	1.0111	−3.0317	0.9318
no. male elders	−0.0612	0.5153	−1.0712	0.9487
no. livestock	−0.016	0.0272	−0.0693	0.0372
averaged size of land	−0.0403	0.149	−0.3323	0.2517
tourist income	−1.5532	0.5296	−2.5912	−0.5151
cohort×sisters	−0.059	0.2195	−0.4892	0.3711
cohort×female cousins	0.0578	0.5972	−1.1126	1.2282
cohort×female elders	−0.1298	0.614	−1.3333	1.0736
cohort×brothers	−0.28	0.2345	−0.7395	0.1796
cohort×male cousins	−0.7526	0.9076	−2.5314	1.0262
cohort×male elders	−0.2636	0.7733	−1.7793	1.2522
income×sisters	−0.059	0.2195	−0.4892	0.3711
income×female cousins	0.0578	0.5972	−1.1126	1.2282
income×female elders	−0.1298	0.614	−1.3333	1.0736
income×brothers	−0.28	0.2345	−0.7395	0.1796
income×male cousins	−0.7526	0.9076	−2.5314	1.0262
income×male elders	−0.2636	0.7733	−1.7793	1.2522

Other statistical analysis and all figures were done using SPSS v. 18.0. (SPSS, Inc., Chicago, IL, USA). Models and graphics from models use Maple 15 and full details of the modelling procedures are given below.

3. Results

(a). Determinants of reproductive success in duolocal households

Tables 1–8 show factors that determine the reproductive success of Mosuo males and females in ‘visiting marriages’ in duolocal and mixed households, measured both by number of living children and by age at first birth. Mortality is low, so the number of living children closely approximates to fertility (D. Yu 2010, unpublished data). The number of children of each Mosuo couple is currently limited to three (since the 1980s) by the government's family planning policy, but fertility appears to have been quite low for some time prior to that policy [16]; the number of children per woman averaged 2.66 ± 1.41 in our census (n = 1411 women). Those who had more than three children after 1980 either paid a heavy fine or had the children before the policy came into force. In view of the fact that total fertility is now being constrained by government policy, we also examine variation in age at first birth. We examine how characteristics of the household and the individual are associated with measures of reproductive success of males and of females separately.

Variation in both reproductive success and age at first birth is apparent in both sexes even after controlling for cohort effects. Variables relating to income (particularly tourist income) are the more important determinants of male reproductive success (tables 7 and 8). It should be noted that variation in land owned has been minimized by government policies to redistribute land according to need in 1956, causing its effects to be complex and not obviously related to reproductive success. For females, farm income is associated with higher reproductive success, but the most striking determinants of reproductive success are the negative effects of all co-resident kin (tables 1 and 5). While all co-resident kin have some negative association with female fertility and age at first birth, the most important effects are that of sisters, who are associated with significantly suppressed fertility, and co-resident female cousins who are significantly associated with later first birth (tables 2 and 6). Interactions with age suggest a more negative effect on siblings and cousins in older age groups, suggesting that the effect of kin competition on female fertility may have been stronger in the older generations, when family sizes were larger. Thus, reproductive competition between co-resident breeding-age females keeps fertility low. By contrast, sisters are either irrelevant to or have a positive influence on male reproductive success, and brothers do not compete with each other much, if at all (tables 4 and 8); one brother may even be helpful to a male, perhaps diluting the male workload (figure 1). The overall effect of competition with same- and different-sex siblings is shown in figure 1a,b, and how this is influenced for males and females by birth order with same-sex siblings is shown in figure 1c. The number of older generation females in the household appears in all the best fitting models of female reproductive success associated with slightly reduced fertility (tables 2 and 6), but their effects are not significant for males (tables 4 and 8); this suggests some competitive effects between cousins in households with several older generation sisters, and/or negative effects of older generation females even if the older females are after the age of menopause. But the largest effect remains the competition between reproductive females of the same generation. Income appears to reduce this competition for everyone, having beneficial effects on all reproductive measures for females and brings forward age at first reproduction for males.

Figure 1.

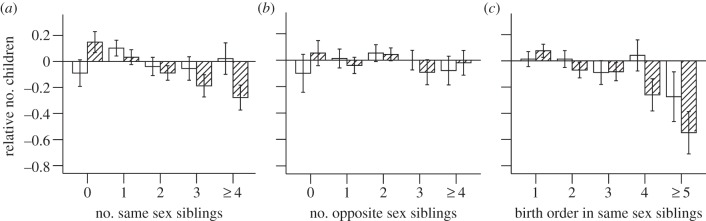
Relative number of children in relation to the number of (a) same-sex, (b) opposite-sex siblings and (c) to birth order in same-sex siblings (579 males and 875 females), for duolocal Mosuo. y-Axis indicates residuals from the Poisson regression line of the number of surviving children against age and age square. (Hatched bars denote females; open bars, males.)

(b). Work patterns of Mosuo women

Table 9 shows the work patterns of Mosuo women, collected during the planting season, which is a period of high workload where almost everyone is likely to be seen working on the fields at some time. Farm produce is shared by all household residents, as farm ownership and labour is communal. Data were recorded by spot observations, recording who was in the working party on each field, and then moving on to the next field. Owing to the cooperative nature of farming during periods of labour-intensive farming, workers could be found on their own household's field or helping out a neighbour or kin [5]. The work involves weeding, ploughing, planting, watering and covering with plastic sheets to retain water—with only the water pumping being partly mechanized and the rest being done by hand or, in the case of ploughing, with the help of oxen; it is generally done in groups of between 2 and 30 people. In table 9, we report the number of times a woman is seen working in the fields as a function of her family size and sororal birth order (we show only data of those individuals who have at least one sister). The data show that for all observed family sizes, there are almost always more observations of older sisters working in the fields than younger ones. While it is probable that the younger sister was also working on another communal task elsewhere, such as cooking or child care, there was general agreement that these tasks were less arduous than working the fields. Thus it seems that, while older sisters are winning the reproductive conflict, so having higher reproductive success, they are putting in more communal (co-operative) efforts than are younger sisters.

Table 9.

Number of females of different birth orders working on farms during the planting season, out of 346 Mosuo females who have at least one sister, mean age is 40.87 (s.d. = 10.68). Binomial test between all combinations of two sisters (older versus younger): p = 0.0328.

total no. sisters in a household	birth orders of females						total
	1	2	3	4	5	6
2	88	61	—	—	—	—	149
3	41	41	37	—	—	—	119
4	24	16	14	7	—	—	61
5	0	0	4	0	0	—	4
6	3	1	2	2	2	2	12
8	1	0	0	0	0	0	1
total	157	119	57	9	2	2	346

4. A game theoretical analysis of inclusive fitness for reproductive conflict between sisters, when females do not disperse

To provide a possible theoretical framework to understand the evolutionary significance of Mosuo residence and reproductive patterns, we developed a simple game theoretical model based on inclusive fitness to investigate the reproductive conflict when males breed outside the group. The model follows the ‘tug-of-war’ game originally developed by Reeve et al. [17,18]. We focus this model on reproductive conflicts between sisters and between co-resident female cousins.

Following the model developed by Cant and Johnstone [18], we develop a model for the reproductive conflict between older and young sisters in a Mosuo household under male-biased dispersal or males breeding elsewhere. We let x and y be the competitive effort of the older and younger sisters, and assume that the increase of selfish competitive effort (x + y) will reduce the total reproductive success in the household. The share of reproductive success obtained by the older sister is x/(x + y), and that by the younger sister is by/(x + by), where the parameter b is a positive constant that represents the relative competitive ability of the younger sister. Obviously, if the older sister is behaviourally dominant (that is making her more efficient in the competition for reproductive success; i.e. b < 1), then she will be favoured by the consequence of the competition. Conversely, if the situation with b > 1 is possible, then the younger sister will be favoured by the consequence of the competition. In its application to animal behaviour, competition could be fighting or infanticide but in the case of the Mosuo no overt conflict is apparent and there are no records that we know of infanticide.

We call these two sisters S₁ and S₂, and x is the effort of S₁, y is the effort of S₂ and b the relative competitive ability of S₂. So, the inclusive fitness of S₁ and of S₂, denoted by 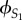and 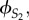respectively, are given by

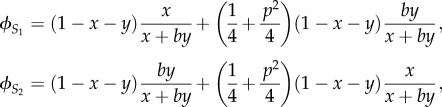4.1

where the parameter p (paternity certainty) represents the probability that a female's offspring is fathered by her husband [19], (1/4 + p²/4) is the expected relatedness between a female and her sister, and when multiplied by the term 

represents the contribution of the younger sister's reproductive success to the older sister's inclusive fitness, and the term

represents the contribution of the older sister's reproductive success to the younger sister's inclusive fitness.

For all possible b and p, the stable levels of x and y, denoted by x* and y*, are the numerical solutions of equations

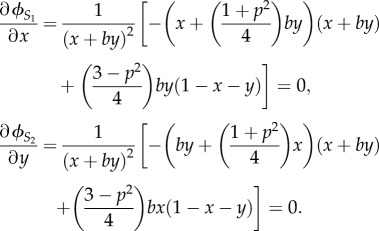4.2

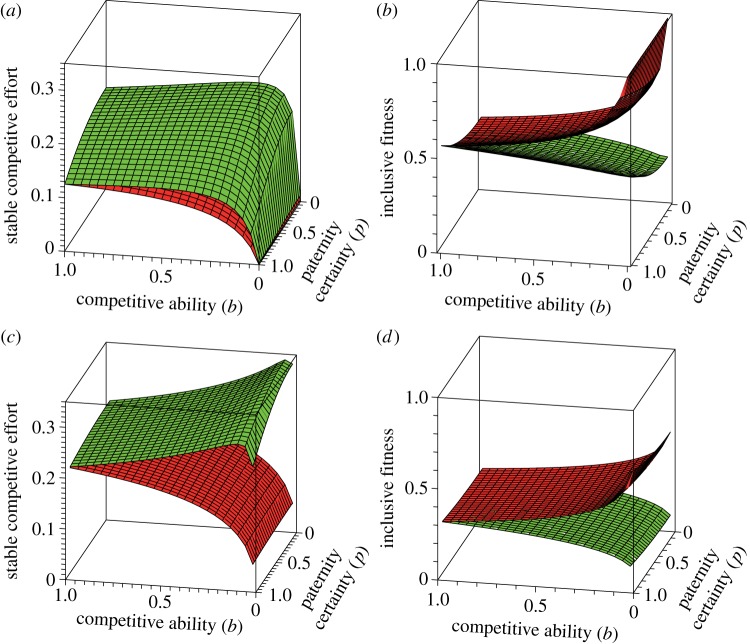
So, x* maximizes the inclusive fitness of the older sister given the effort of the younger sister and, similarly, y* maximizes the inclusive fitness of the younger sister given the older sister's effort. The numerical solutions of equation (4.2), for all possible b and p, are plotted in figure 2a, where the red surface denotes x* and the green surface y*. These numerical solutions show that for all 0 < b < 1 and 0 < p < 1, we have x* < y*. In the special case of b = 1, then we have x* = y* = (3 − p²)/16. For all (x*, y*) (which correspond to all possible b and p), ϕ_S1 (x*, y*) and ϕ_S2 (x*, y*) are plotted in figure 2b, where the red surface denotes ϕ_S1 (x*, y*) and the green surface denotes ϕ_S2 (x*, y*), and for all (x*, y*), ϕ_S1 (x*, y*)>ϕ_Ss (x*, y*) if b < 1.

Figure 2.

(a) The optimal allocation of competitive effort by each sister to maximize inclusive fitness, i.e. numerical solutions of for all possible b (dominance) and p (paternity certainty). The red surface represents x* (optimal competitive effort by older sister) and green surface denotes y* (optimal competitive effort by younger sister). (b) The inclusive fitness of S₁ and S₂ for all (x*, y*). The red surface denotes ϕ_S1 (x*, y*) and the green surface denotes ϕ_S2 (x*, y*). The older sister always has higher fitness, because she needs to exert less competitive effort, for all values where b < 1. (c) The optimal allocation of competitive effort by each female cousin to maximize inclusive fitness, i.e. numerical solutions of The red surface represents x* (optimal competitive effort by older female cousin) and green surface y* (optimal competitive effort by younger female cousin). (d) The inclusive fitness of C₁ and C₂ for all (x*, y*). The red surface denotes ϕ_C1 (x*, y*) and the green surface ϕ_C2 (x*, y*).

Similarly, we also model the reproductive conflict between older and younger female cousins (that is co-resident females whose mothers are sisters) in a Mosuo household. These two female cousins are called C₁ and C₂; x is the effort of C₁, and y is the effort of C₂ and b the relative competitive ability of C₂. So, the inclusive fitness of C₁ and C₂, denoted by and , respectively, are given by

4.3

For all possible b and p, the stable levels of x and y, denoted by x* and y*, are the numerical solutions of equations

4.4

The numerical solutions of equation (4.4), for all possible b and p, are plotted in figure 2c, where the red surface denotes x* and the green surface denotes y*. These numerical solutions show that, for all 0 < b < 1 and 0 < p < 1, we have x* < y*. In the special case of b = 1, we have x* = y*. For all (x*, y*) (which correspond to all possible b and p), ϕ_C1 (x*, y*) and ϕ_C2 (x*, y*) are plotted in figure 2d, where the red surface denotes ϕ_C1 (x*, y*) and the green surface denotes ϕ_C2 (x*, y*), and for all (x*, y*), ϕ_C1 (x*, y*)>ϕ_C2 (x*, y*) if b < 1.

This model thus predicts that the optimal allocation of effort that maximizes fitness for both sisters is for the younger sisters to put more effort into competitive activity, but the older sisters will have more offspring than younger sisters, as long as their dominance enables them to use the resources more efficiently (b < 1); therefore, younger sisters have less to put into their own reproductive success. Figure 2c,d shows that reproductive conflict between co-resident female cousins is even stronger than that between sisters. Both female cousins spend more effort in selfish activities, and thus all have reduced fitness. Paternity uncertainty increases reproductive conflict but only slightly; a far greater effect on reproductive differences is the relative dominance of the sisters or cousins (b). Dominant cousins appear even more detrimental to fitness than dominant sisters.

5. Discussion

Communal breeding is fraught with potential reproductive conflict in any species, including humans, if family members all need the same resources to breed. Reproductive skew between sisters has been observed in communally breeding mammals [20]. In humans, it is less common for female kin of reproductive age to co-reside, but in matrilineal societies they do live in close proximity, often in neighbouring houses within the same compound, or in the same house as here in the case of the Mosuo. This is why we see matrilineal co-resident kin having a negative effect on each other's fitness. A negative effect of female kin has also been observed in matrilineal Chewa in Malawi [21]. Patrilocal residence generates groupings of unrelated females (although they often cook and eat in separate household units and have separate sources of food). Patrilocality is more common, but reproductive overlap between mother-in-law and daughter-in-law are rather rare in such systems, owing to menopause and late male marriage; and while mother/daughter reproductive overlap is more common, it usually involves the daughter living elsewhere owing to cultural residence rules [18,22,23]. Here, we show an unusual case where related human females do breed communally at the same time in the same household, and we show that they are in reproductive conflict. Older sisters appear to win that conflict through achieving or inheriting dominance over younger sisters, and thus reproduce more than do younger sisters, but also then put more effort into the communal farming that supports all the family.

Our interpretation of b in the Mosuo context is that we assume b is a product of cultural norms that favour elders over youngers in terms of who is obedient to whom. In Mosuo culture, marriages were normally arranged by elders in the past and to some extent even now (although there are conflicting ethnographic accounts on this). The cultural norm that assumes age as a form of dominance within each sex is widespread across human cultures (although it can be subverted when certain younger individuals have particular skills or older individuals become incapable). It is possible that the dominance of older persons over younger ones may originally have been enforced by physical fights, which older individuals might be more likely to win, but later a dominance hierarchy became codified into cultural norms, in part to avoid fights. Birth order frequently predicts the order of marriage and hence often reproductive success, and elders find themselves in a position to control the marriage rate of younger kin if they control family resources [24]. This may approximate to a fitness optimizing strategy when resources are not sufficient for large numbers of siblings using the same household resource to all marry and reproduce. In such cases, if children are married as they become mature, then younger children may have such a low chance of marriage that they do not enhance reproductive success [25]. Thus families may not support the production of too many offspring within the communal household, and younger sisters may find themselves facing harsher competition (or reproductive suppression) from the family when their elder sisters or co-resident female cousins have reproduced ahead of them, and the household is not eager to feed more mouths. However, it may not be beneficial for older sisters or mothers to completely prevent younger sisters from reproducing if they are to be part of the communal farming effort, and of course their offspring contribute inclusive fitness to family members. The balance of reproductive skew will thus depend on the costs and benefits of conflict to individuals, largely determined by b (relative competitive ability).

The modelling suggests that paternity uncertainty is having only a small effect on the optimal behaviours of women, as has been shown previously [17]. Elsewhere we use a modelling approach to show that paternity uncertainty is making a relatively small contribution towards favouring a male working on his sister's (which is also his own) family farm in this system; we show that it is the communal breeding of matrilineal females that is promoting duolocal residence and the ‘visiting marriage’ situation, where males mate outside the group but are fed in and contribute most of their labour to their natal household [5]. As breeding opportunities are constrained by competition for household resources among females, but not males, mothers should preferentially invest in male offspring who breed elsewhere, as noted by Johnstone and Cant in the case of killer whales, which also do not disperse and mate outside the group [26]. The effects that family members have on each other's reproductive success here in the Mosuo may explain why mothers are willing to feed their male offspring, who are not competing for breeding opportunities with any of their other offspring, while females do compete with each other for household resources. While land inheritance could be considered daughter-biased investment, because only daughters can make use of it to raise offspring [27], other investments are male biased if males have relatively light workloads compared with females [5]. Hypotheses for the evolution of menopause are that it reduces reproductive conflict and increases cooperation between generations of human females [18,22,23,28–30]. However, our results suggest that elder females are also associated with reduced fertility in co-resident younger females. This could in part be because of several female elders being associated with increased competition with cousins co-residing, and reduced relatedness between breeding females, although cousins are controlled for in the analysis. It could also be because elder females are dominant and continue supporting their sons’ mating effort, even after they themselves have stopped reproducing. Household resources in part generated by sisters are used to feed brothers, as we have shown that brothers can be a cost to their sisters. Interestingly, in killer whales, mothers are thought to support sons for this reason and sons have been observed to die at a much higher rate once their mothers are gone [26,31] (perhaps because sisters have less reproductive interest in their brother's fitness than do their mothers). It remains to be seen whether Mosuo males do worse after their mother dies, but we did note that older males do sometimes leave their natal residence to join their wives' households later in life [5].

The Mosuo attach great importance to family harmony, and generally family relations appear peaceful. This approach to reproductive conflict shows how closely co-operation and conflict are related to each other. Sisters and female cousins are in competition, mainly with each other, but also to a lesser extent with their brothers and even their mothers and aunts. However, rather than waste too much effort on conflict against relatives, the stable strategy is to maximize inclusive fitness by helping with the communal farming effort even if sisters take unequal shares of the family resources for their own reproduction. This approach successfully predicts patterns of reproduction and may predict patterns of work in the communal household. We have addressed the lower work rate of males elsewhere [5]. The reduced labour by younger sisters may reflect an expression of greater conflict in the ‘tug-of-war’, or may represent a decision as a result of reproductive skew to invest less in the household simply owing to having lower inclusive fitness benefits from the household.

All procedures described were reviewed and approved by the ethical committee of the Institute of Zoology, Chinese Academy of Sciences.

Data accessibility

The demographic database collected is not currently openly available, in line with ethics protocols agreed with CAS and UCL. For enquiries regarding access to the abridged data used in this paper, email Ting Ji (jiting@ioz.ac.cn) or Jia-Jia Wu (jiajiawu01@gmail.com).

Funding statement

This research was supported by ‘Hundred Talents Program’ of the Chinese Academy of Sciences (grant no. NSFC 31270439) and the British Academy and the European Research Council (grant no. AdG 249347).