Ultrafast folding kinetics and cooperativity of villin headpiece in single-molecule force spectroscopy

Significance

Proteins are amazing nanomachines that achieve their functionality through a complex three-dimensional folding process. Some proteins can fold within microseconds. Only a few experimental techniques are available for studying folding on this timescale. In this paper, we expanded the use of single-molecule force spectroscopy toward ultrafast folding proteins. Using this technique, we demonstrate that rapid folding transitions of a single villin headpiece (HP35) can be experimentally monitored and analyzed using distribution moment analysis and autocorrelation functions. We show differences in the folding dynamics and cooperativity between wild-type HP35 and a stable mutant. Brownian dynamics simulations reproduce all key features of our experiments.

Abstract

In this study we expand the accessible dynamic range of single-molecule force spectroscopy by optical tweezers to the microsecond range by fast sampling. We are able to investigate a single molecule for up to 15 min and with 300-kHz bandwidth as the protein undergoes tens of millions of folding/unfolding transitions. Using equilibrium analysis and autocorrelation analysis of the time traces, the full energetics as well as real-time kinetics of the ultrafast folding of villin headpiece 35 and a stable asparagine 68 alanine/lysine 70 methionine variant can be measured directly. We also performed Brownian dynamics simulations of the response of the bead-DNA system to protein-folding fluctuations. All key features of the force-dependent deflection fluctuations could be reproduced: SD, skewness, and autocorrelation function. Our measurements reveal a difference in folding pathway and cooperativity between wild-type and stable variant of headpiece 35. Autocorrelation force spectroscopy pushes the time resolution of single-molecule force spectroscopy to ∼10 µs thus approaching the timescales accessible for all atom molecular dynamics simulations.

Protein folding is a spontaneous process where a linear polypeptide chain acquires a functional and highly complex 3D structure. Conformational folding can occur on timescales ranging from hours down to microseconds (1, 2). The study of small fast-folding proteins has provided key information for understanding fundamental aspects of protein-folding mechanisms. Recently, it has even become possible to simulate folding trajectories of small proteins in full atomic detail using molecular dynamics simulations up to the millisecond time range (3, 4). However, direct time-resolved experimental measurements of such ultrafast processes have largely been limited to a few ensemble methods like temperature-jump, continuous-flow experiments, and triplet-lifetime measurements.

The C-terminal subdomain of the actin-binding protein villin (villin headpiece, HP35) has been used as a model system in a number of both experimental and simulation studies of protein folding at the speed limit (5–19). The folding kinetics of HP35 has been studied extensively mostly by T-jump and by triplet-lifetime experiments (6–8, 11, 12, 16). Folding of the wild-type HP35 at 30 °C occurs at 348 × 10³ s⁻¹, and unfolding at 7.4 × 10³ s⁻¹, which in combination yields a free energy of folding of ∼4 k_BT (6). Before crossing the major folding barrier, HP35 undergoes a rapid local rearrangement on the nanosecond timescale, which results in stable contacts of tertiary structure. Triplet-triplet-energy transfer (TTET) measurements have reported a native-state heterogeneity and an additional high-energy intermediate on the native-state side of the major unfolding barrier (16). A detailed structural picture of the locking–unlocking reaction of the native states as observed in TTET data were given by recent all-atom molecular dynamics simulations (5). Along this line, a variety of native conformations was found consistently by 2D IR vibrational spectroscopy (20) and time-resolved fluorescence (21) using cyano-substituted phenylalanine.

In the last few years, single-molecule methods, such as FRET and single-molecule force spectroscopy, have provided important insight into protein-folding mechanisms due to their capability to follow individual molecules on their way from the unfolded to the folded state (22–25). Single-molecule optical-tweezers assays have provided real-time recordings of multistate protein-folding networks (24, 26, 27) with sensitivity for states populated as little as 0.01% (28). So far, the fastest directly detectable kinetics of mechanical assays has been limited to the millisecond range and, hence, the realm of ultrafast conformational kinetics in proteins has not been directly accessible to those techniques. Extracting kinetics from single-molecule hopping traces has so far been generally achieved by state assignment through models such as hidden Markov models. However, if the folding kinetics becomes too fast to be clearly separated from the diffusive motion of the beads, such models must fail.

In the current paper, we use fast force spectroscopy by optical tweezers to show that a model-free autocorrelation analysis of folding time traces allows the direct measurement of ultrafast protein-folding kinetics under load. We find differences both in folding-rate constants and cooperativity between wild-type HP35 and a stable mutational variant. The comparison between wild types and mutant gives important insight into the folding pathway of one of the most prominent and yet not fully understood model systems for protein folding.

Results

Equilibrium Folding/Unfolding of Villin Headpiece.

To study the mechanics of villin headpiece under load, we designed a single-chain construct with villin headpiece flanked by two ubiquitin domains at each terminus (refs. 28, 29; Fig. 1A). The ubiquitin domains served as hubs to link the protein to the double-stranded DNA handles that were subsequently attached to 1-µm glass beads (27). To prevent interference of the terminal ubiquitin domains with the folding of villin, we inserted glycine/serine-rich peptide linkers (SI Appendix). The presence of ubiquitin had an additional beneficial effect on the expression and yield of the protein construct. We also prepared pure DNA tethers (hereafter referred to as DNA construct) by dimerizing thiol containing oligonucleotides in the absence of protein as a control.

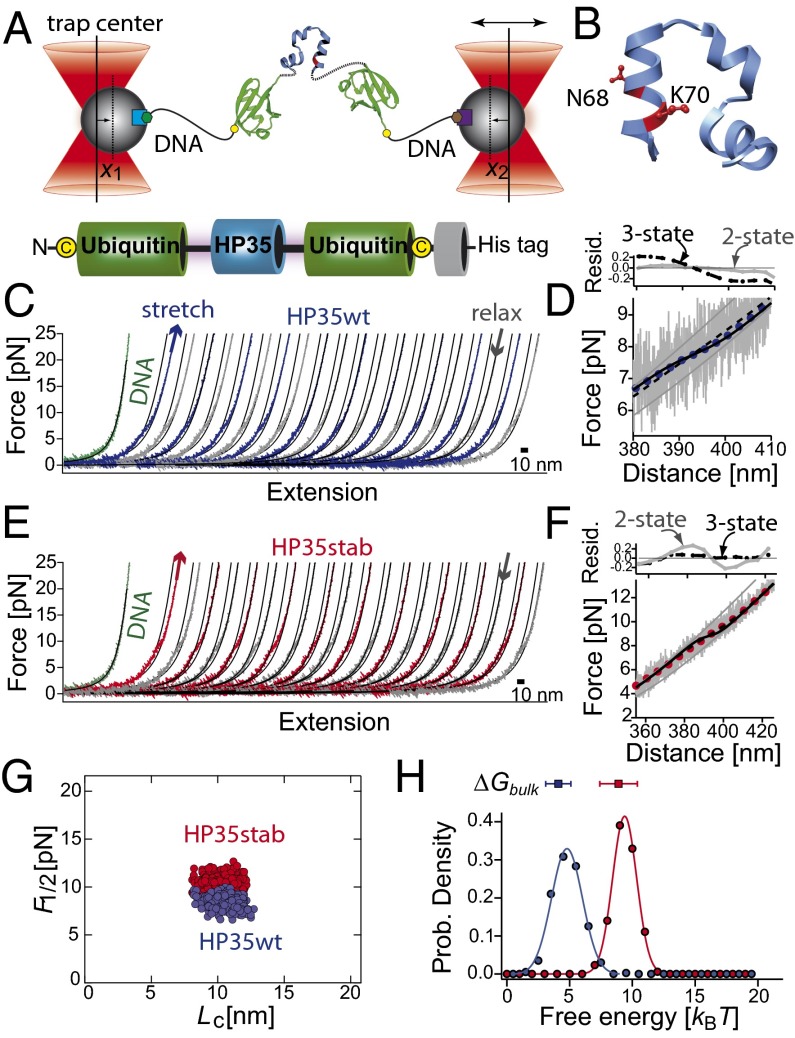
Fig. 1.

(A) Sketch of the experimental setup with the HP35 protein (blue) embedded within two copies of ubiquitin (green) and connected to DNA (black, biotin: green hexagon, digoxygenin: brown hexagon) handles attached to functionalized silica beads (beads gray, α-digoxygenin: purple square, streptavidin: light blue square). The terminal cysteine residues are shown as yellow dots. Total bead deflection is x(t) = x₁(t) + x₂(t). (B) Three-dimensional structure of the C-terminal subdomain HP35 as extracted from villin headpiece HP67 (PDB code 1yu5) (29). The residues N68 and K70 are shown in ball-and-stick representation. They are replaced by alanine and methionine in HP35stab. (C and E) Force-extension traces of consecutive stretch (blue) and relax (gray) cycles of HP35WT and of HP35stab (red–gray). The curves were filtered to 1 kHz. Solid lines are curve fits of a wormlike chain model to the data (SI Appendix). For comparison, stretching of the tethered DNA is shown as a green curve. (D and F) Force-distance trace of HP35WT at 20 kHz (gray lines) and filtered to 100 Hz (blue dots) and of HP35stab (gray–red). The solid gray lines are fits of the folded and unfolded states to an extensible wormlike chain model. Black solid lines are curve fits as obtained from an equilibrium unfolding model assuming a two-state model (SI Appendix). The dashed black line is a fit with a three-state model assuming unfolding of the protein in two steps with equal length and folding free energy (SI Appendix, Table S1). Residual plots for a two-state model (gray circles, gray solid line) and for a three-state model (black circles, black dashed line) are shown in Upper. (G) Scatterplot of the transition midpoint forces for HP35WT (blue dots, n = 445, < F_1/2 ≥ 8.4 ± 0.6 pN) and HP35stab (red dots, n = 437, <F_1/2 ≥ 10.3 ± 0.7 pN) versus contour-length increase (L_c). Data were obtained from force-extension curves of several single molecules and fits of an equilibrium folding model (SI Appendix, Eq. S9) to the data. (H) Distributions of the folding free energies for HP35WT (blue circles) and HP35stab (red circles). The solid curves passing through the points are fits to a Gaussian distribution function to guide the eye. The free energies from the chemical unfolding experiments are shown at the top of the graphs (SI Appendix, Table S1).

We investigated both the wild-type protein (HP35WT) and the N68A/K70M variant of the villin headpiece subdomain (30). The wild-type protein has been intensively investigated and the stability and folding kinetics are well known. In contrast, although it is known that the equilibrium stability for N68A/K70M (HP35stab) variant is significantly higher than for HP35WT (30), kinetic information does not exist.

To directly compare mechanical equilibrium results with ensemble equilibrium free energies, we measured guanidinium chloride–induced unfolding transitions using the single-tryptophan residue present in HP35. We used identical protein constructs and buffer conditions both in bulk and mechanical unfolding experiments, including the terminal ubiquitin domains. Hence unfolding of ubiquitin and HP35 could be monitored independently from each other (SI Appendix). We found that the bulk unfolding transitions of HP35WT and HP35stab are fully cooperative and well described by a two-state model yielding a free energy of unfolding, ΔG(H₂O, 303 K), of ∼4.1 k_BT and ∼8.9 k_BT, respectively (SI Appendix, Fig. S1 and Table S1 and S2). The stabilities and transition cooperativities of HP35WT and HP35stab as well as ubiquitin in the fusion constructs are similar as reported earlier for the isolated proteins (30–32). This indicates that the presence of the terminal ubiquitin in our constructs does not affect HP35 stability significantly.

We then recorded force vs. extension curves of both HP35WT and HP35stab (Fig. 1 C and E). In the traces shown in Fig. 1 filtered to 1-kHz bandwidth, a continuous humplike equilibrium transitions can be observed at around 8.3 pN for HP35WT and 10.4 pN for HP35stab. The shape of the transition remained unchanged at all pulling velocities used (10–5,000 nm/s). This clearly demonstrates that the system is at equilibrium at our experimental conditions. Wormlike chain fits using a serial combination of DNA and polypeptide elasticity (SI Appendix) yielded a contour length increase from the folded to the stretched conformation of the HP35 protein of 11 nm, consistent with the 35 amino acid residues contained in HP35 unfolding in the transition (Fig. 1G). To extract equilibrium free energies of folding/unfolding and measure the degree of cooperativity of the mechanical unfolding transition we applied an equilibrium folding/unfolding model to the data (SI Appendix). We find that only a two-state model with full cooperativity of the unfolding protein fits the HP35WT data (black solid line in Fig. 1D). The equilibrium model yields the folding free energy at zero load for the protein constructs. We find an average folding free energy of 4.9 ± 1 k_BT for HP35WT (blue histogram in Fig.1H, n = 445). A three-state model, assuming unfolding of the protein in two steps with equal length and folding free energy (dashed line, folding intermediate with L_c of ∼5.5 nm and folding free energy of 2.5 k_BT), reproduces the data poorly. In the mechanical assay, folding of HP35stab appears to have lower cooperativity than expected from a two-state model. We found that a three-state folding/unfolding model describes the data better than an equilibrium model with all-or-none folding cooperativity (Fig. 1F). We find an average folding free energy of 9.8 ± 1 k_BT for HP35stab (red histogram in Fig. 1H, n = 437). The fit parameters and equations are summarized in SI Appendix, Table S1.

The robust equilibrium nature of mechanical HP35 unfolding indicates that the underlying folding/unfolding kinetics is very fast. Can we detect this fast kinetics directly in single-molecule force experiments? A magnification of the transition region of two stretch (red) relax (black) cycles of HP35stab collected at an increased bandwidth of 30 kHz is shown in Fig. 2A. At this bandwidth, enhanced thermal fluctuations can be observed in the transition region. Thus, it is apparent that the traces contain direct information about the folding/unfolding kinetics under load.

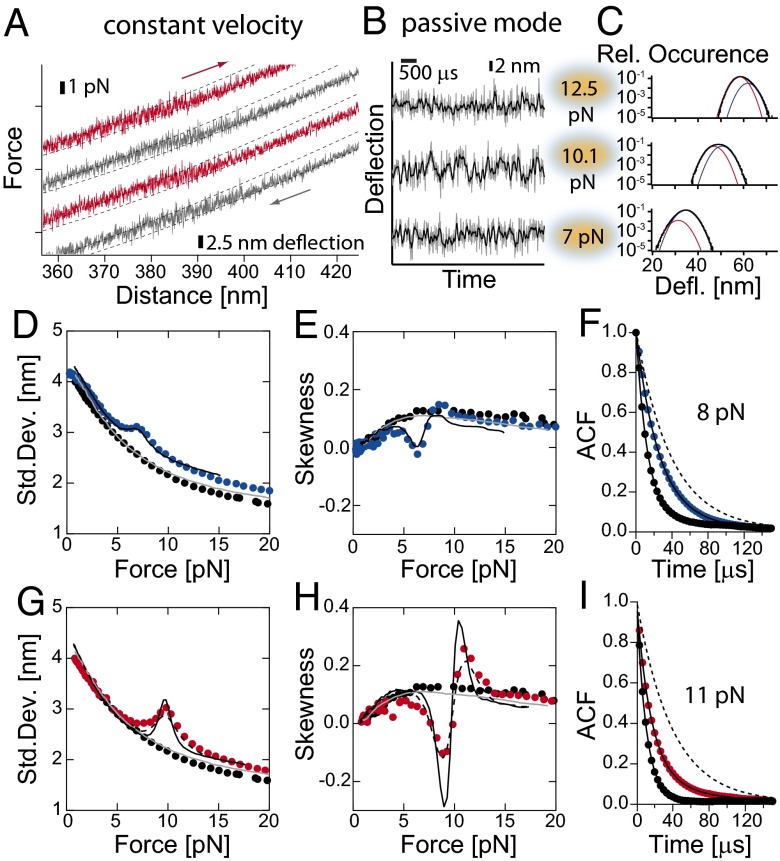
Fig. 2.

(A) Force-distance traces for HP35stab at 30 kHz. Red traces are stretch cycles and the gray traces are relax cycles. For kinetic analysis, the positions of both traps were fixed and set at different forces. (B) Time trace of deflection fluctuations of HP35stab at 12.5, 10.1, and 7 pN as measured at 300 kHz (gray lines) and at 30 kHz (black lines), and (C) corresponding histograms of deflections. Histograms were fitted by assuming two skewed Gaussian distributions: for folded state (blue line) and for unfolded state (red line) and the sum of the both Gaussian curves (black line). From the distribution, we extracted describing parameters such as SD and skewness. (D, E, G, and H) Continuous lines are results from Brownian dynamics simulations (SI Appendix). The solid gray line is obtained from a simulation describing the bead-DNA-bead system assuming linker parameters as obtained from experiments. The black solid line is the result of a simulation of the bead-DNA-protein-DNA-bead system assuming linker parameters as obtained from experiments. The protein folding/unfolding transitions were modeled as a two-state system or a three-state system in the case of HP35stab (black dashed line) with Markov chain properties (Table 1 and SI Appendix, Figs. S5 and S4). (D and G) SD of fluctuations in bead deflection as function of mean force. Shown are DNA construct (black circles), HP35WT (blue circles), and HP35stab (red circles). (E and H) Skewness of fluctuations in bead deflection as function of mean force. Shown are data for a DNA construct (black circles), HP35WT (blue circles) and HP35stab (red circles). (F) Autocorrelation function of the deflection signal of DNA (black circles) and HP35WT at 8.0 pN (red circles). For comparison, we also show the autocorrelation function for untethered beads (dashed line). The solid lines are curve fits to a single- or double-exponential decay function. Analysis gave time constant for untethered beads of τ₀ = 56 µs, for a DNA-only tether τ₀ =13 µs and for an HP35WT tether τ₀ = 13 µs and τ₁ = 32 µs, respectively. (I) Autocorrelation function of the deflection signal of DNA (black circles) and HP35stab at 11.0 pN (red circles). For comparison, the autocorrelation function for untethered beads is also shown (dashed line). The solid lines are curve fits of a single- or double-exponential equation to the data. Analysis resulted in a time constant of τ₀ = 56 µs for untethered beads, for DNA τ₀ = 11 µs, and for HP35stab τ₀ = 14 µs and τ₁ = 30 µs with τ₀ as a free fitting parameter.

Single-Molecule Kinetics of Villin Folding Under Load.

For a kinetic analysis, the beads were held at constant trap separations at different forces (Fig. 2B). To ensure that as much kinetic information as possible is captured, we increased the sampling frequency to 300 kHz (with a 150-kHz eight-pole Butterworth hardware filter). As shown below, this frequency is well above the corner frequencies of the combined bead-DNA–protein-system at all forces applied. Fig. 2C shows distributions of the bead position signal (deflection) at three different forces. The position histograms show a clear asymmetry (skewness) reflecting the sum of two Gaussian distributions the amplitudes of which shift with force. Apparently, the population equilibrium of folded and unfolded states shifts with force (Fig. 2C). A model-free analysis of the force dependence of the key features of the equilibrium distributions can be achieved by calculating their second and third moments i.e., the SD (Fig. 2 D and G) and the skewness (Fig. 2 E and H; for details, see SI Appendix). Around the midpoint forces, a clear increase in SD as well as a sign switch in the skewness can be observed for both HP35WT (Fig. 2 D and E) and HP35stab (Fig. 2 G and H). For comparison, a construct containing only the DNA linkers of same length shows a monotonic dependence as expected for this system stiffening at higher forces (black dots in Fig. 2 D and G) (33).

To investigate whether kinetic information is presented in the data, applied a quantitative analysis to extract folding- and unfolding-rate constants. Kinetic information from folding/unfolding transitions at equilibrium has so far been obtained from hidden Markov models or from pair-correlation analysis (34, 35). However, these methods become unreliable if the levels of folded and unfolded states exchange too quickly and lifetimes become comparable to the timescales of the beads motions and, hence, cannot be clearly separated from each other. A time trace of HP35stab fluctuations recorded around the transition midpoint (Fig. 2B and SI Appendix, Fig. S2) illustrates this problem. Folded and unfolded states cannot be clearly assigned anymore (Fig. 2C).

To assess the kinetics of HP35 folding in a more fundamental way, we computed autocorrelation functions of the time traces at varying forces. Autocorrelation analysis has found numerous applications in fluorescence correlation spectroscopy, although it has not been used for the kinetic analysis of equilibrium fluctuations in single-molecule force spectroscopy (36, 37). Autocorrelation signals for time traces recorded with and without HP35WT at 8 pN are shown in Fig. 2F. The bottom curve (black) is the autocorrelation of a pure DNA tether with no protein attached. Here we find a single exponential with a time constant τ₀ of 13 µs (black solid line). This time constant comes from the Brownian diffusion of the beads linked by the stiff DNA tether and marks a lower limit for the time constants that we will be able to pick up from a protein at this force. It is interesting to note that the application of force and hence the stretching of the DNA tethers increases the response time of our experiments. For comparison, the top curve (gray dashed line) marks the autocorrelation of the differential signal of untethered beads (τ₀ = 56 µs).

The blue circles show the autocorrelation of a time trace recorded at 8.0 pN for HP35WT. Here, the autocorrelation function is double exponential (SI Appendix, Eq. S15) with a fast time constant of τ₀ = λ₀⁻¹ = 13 µs and a slow time constant around τ₁ = λ₁⁻¹ = 32 µs (black solid line). Apparently the fast intrinsic time constant τ₀ of the DNA tethered beads is preserved and protein fluctuations add the slow component τ₁. This analysis now allows us to quantify directly the protein folding/unfolding kinetics of HP35WT under load. The microscopic folding and unfolding rate constants for a simple two-state reaction are related to τ₁ according to: τ₁ = λ₁⁻¹ and λ₁ = k_f + k_u (36). Hence τ₁ = 32 µs means a combined rate of k_f + k_u = 3.1 × 10⁴ s⁻¹. The same analysis was performed on HP35stab (Fig. 2I) and the combined rate we find at 11 pN is k_f + k_u = 3.3 × 10⁴ s⁻¹. To obtain the force-dependent folding/unfolding rate constants, we now performed this analysis for both HP35WT and HP35stab over the full range of accessible forces.

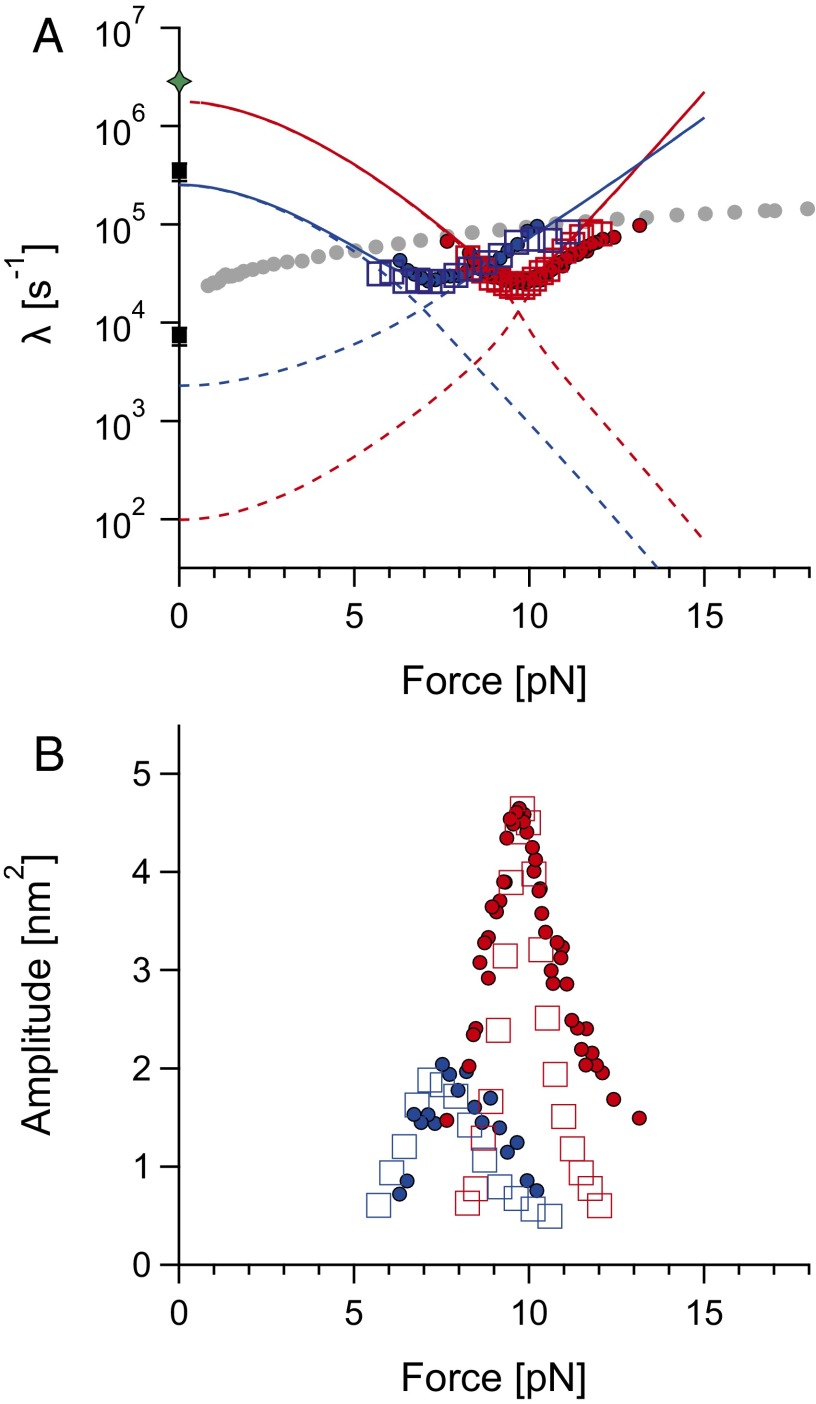
For the DNA-only construct we found that the minimal response time (1/λ₀) decreases monotonically with force. Hence, λ₀ (gray circles in Fig. 3A) marks the resolution limit for rates measured in our force assay. The dependence of the combined rate (λ₁) on force yields a chevronlike plot well known from bulk kinetic protein-folding experiments (38) (Fig. 3A) (HP35stab: red circles, HP35WT: blue circles in Fig. 3). To increase the robustness of the double exponential fits, we fixed λ₀ to values obtained from the DNA-tether measurements and thus used them as input in our analysis (gray circles). The dashed lines are fits to a folding/unfolding model satisfying detailed balance (SI Appendix). For HP35WT and HP35stab, using this model we extrapolate zero-force folding rates of 251 × 10³ s⁻¹ and 1,200 × 10³ s⁻¹ and unfolding rates of 2.3 × 10³ s⁻¹ and 0.09 × 10³ s⁻¹, respectively (Table 1). We should note that all rates are extrapolated over a large range of forces, which likely negatively affects the precision of the zero-force rate estimate. Moreover, the unfolding limb of the HP35stab chevron plot systematically deviates from the cooperative two-state fit. It is also important to note that the autocorrelation analysis is only robust in a force range where the amplitudes associated with λ₁ are greater than 10%, which is about 6–11 pN for HP35WT and 8–13 pN for HP35stab (see Fig. 3B and SI Appendix, Fig. S3 for the amplitudes of the fast component). Because many of the values lie close to the detection limit of the response time of the DNA-bead tethers (gray dots, Fig. 3A), we had to ensure the robustness of our analysis using Brownian dynamics simulations.

Fig. 3.

(A) Chevron plot for HP35WT (in blue) and HP35stab (in red) and (B) corresponding amplitudes. Experimental data (closed circles) and rates calculated from Brownian dynamics simulations (empty squares) for HP35WT (in blue) and HP35stab (in red) are shown. Dashed lines correspond to microscopic rate constants; they are listed in Table 1 (for the force dependence, see SI Appendix). Thick solid lines are effective rates (λ₁ = k_u + k_f) used for kinetic Brownian dynamics simulations. Black squares at zero force are rate constants obtained from T-jump experiments (40). The green star at value of 2.85 × 10⁶ s⁻¹ indicates the theoretical speed limit for the 35-residue villin headpiece as calculated from N/100 µs, where N is number of residues (1). Methods and the fit parameters describing extrapolations are listed in SI Appendix, Table S2.

Table 1.

Folding/unfolding rates for HP35 variants at 30 °C

Method	HP35WT	HP35stab
T-jump,* s−1
kf	(348 ± 70) × 103	No data
ku	(7.4 ± 1.5) × 103	No data
Force spectroscopy, s−1
kf	(251 ± 100) × 103	(1,200 ± 200)† × 103
ku	(2.3 ± 1.0) × 103	(0.09 ± 0.07)† × 103

^*Data were taken from reference (40).

^†Under assumption of a two-state mechanism (see Results, Validation of Autocorrelation Analysis of Villin Headpiece–Folding Rate Constants).

Brownian Dynamics Simulation of the Bead-DNA–Protein System.

We modeled the bead-DNA–protein system in a Brownian dynamics simulation where the hydrodynamics of the beads was included using Stokes drag. The elasticity of DNA and unfolded protein was modeled according to the wormlike chain model of polymer elasticity (33), and protein folding and unfolding was included as an instantaneous two-state transition changing the length of unfolded polypeptide. At each time step, the Langevin equation was solved numerically, taking into account the effects of a random thermal force (39). To include the effects that arise from finite sampling bandwidth, we also included filtering procedures analogous to experimental procedures (for details, see SI Appendix). The model does not contain any free parameters but is based on values published in the literature (viscosity, persistence length, bead size, and length of unfolded polypeptide protein) and values obtained in independent experiments (mechanical properties of DNA linker molecule and thermodynamic stability of protein).

Simulations of a DNA tether with no attached protein adequately reproduced the distributions of bead deflection values that were determined experimentally, as judged by SD (gray line in Fig. 2 C and F) and skewness (gray line in Fig. 2 D and G). The simulations reproduce the experimentally measured load-dependent autocorrelation times of the tethered bead-DNA-bead system within a factor of 2.

Validation of Autocorrelation Analysis of Villin Headpiece–Folding Rate Constants.

We now used the Brownian dynamics simulations to test the accuracy and robustness of the autocorrelation analysis used to extract the chevron plot in Fig. 3A. Brownian simulations were performed using the force-dependent folding kinetics of the solid lines in Fig. 3A, and analyzed the obtained traces in the same way as described above for the experimental data with double exponential fits to the autocorrelation functions yielding the open square symbols of Fig. 3A. The fact that we are able to precisely extract known kinetic information from simulated traces using autocorrelation analysis gives us confidence in our method of analysis.

The simulations were used to assess the robustness of the kinetic data obtained from autocorrelation analysis. To this end, we repeated the simulations with slightly accelerated and decelerated folding/unfolding rates (SI Appendix, Fig. S4). Although the simulation results with our best-fit folding rates agree with the experimental data, those with rates that are off by a factor of about 3 do not. We conclude that we are able to unambiguously discern differences in kinetics using autocorrelation analysis that differ by a factor of less than 3.

For HP35WT, simulations using a two-state fully cooperative folding model with folding and unfolding rates as determined experimentally (Table 1) agree with the experimental data (40). SD, as well as skewness of the simulated system, is in good agreement with experimental values over a wide range of forces (black lines in Fig. 2 D and E).

In the case of HP35stab, the simulations best describe the experimental results with a three-state model where an intermediate is partially populated. Although a two-state system captures the general aspects of the SD, skewness, and autocorrelation analysis (black continuous lines in Fig. 2 G and H), we find that at least a simple three-state model is necessary to adequately reproduce experimental data (black dashed lines in Fig. 2 G and H). For a comparison between the outcomes of a two-state and a three-state model, see SI Appendix, Fig. S5. Unfortunately, response times of the beads constrain the resolution of the additional kinetic phases and our data cannot yield quantitative information at this point. Therefore, effective rates are listed in Table 1 assuming a two-state model.

Discussion

Time Resolution in Single-Molecule Force Experiments.

Despite its role as the arguably most important model system for the all atom simulation of protein folding (5, 9, 10, 13, 15), studying the folding kinetics of villin headpiece is accessible to only a few experimental techniques. Because, under all conditions, HP35 folding occurs faster than 100 µs, it is beyond reach of standard mixing techniques such as stopped flow. Most of the experimental data on HP35 has been collected in temperature-jump and triplet-lifetime experiments (6–8, 11, 12, 16, 17). Single-molecule force spectroscopy has always been strong in observing single molecules over long time spans up to hours (28); however, kinetics faster than milliseconds could not be observed due to the limited response time of the sensors. At first glance, it may appear that the cutoff frequency (f_3dB) of the noise spectrum of the differential signal at zero force (in our case, ca. 3.5 kHz) in the optical trap limits the time resolution for the observable kinetics. However, two important aspects make it possible to observe kinetics as fast as 10 µs in a two-bead optical trap setup using differential detection. First, it is important to note that not the cutoff frequency but rather the autocorrelation time τ₀ = 1/(2πf_3dB) of the relative bead motion sets the detection limit for the observable kinetics. Second, with increasing applied force, τ₀ drops from 56 µs at F = 0 pN down to 5 µs at F = 20 pN (Fig. 3, gray circles λ₀ = 1/τ₀). This consideration calls for significantly higher sampling frequencies than the previously applied frequencies, which ranged from 1 to 50 kHz (26, 28). The effect of sampling speed and measurement bandwidth on the captured dynamics is illustrated in Fig. 2B and SI Appendix, Fig. S6. The relatively slow roll-off of the frequency response of our bead-DNA dumbbell, which acts a single-pole filter, causes a considerable loss of dynamics if the sampling frequency is not chosen well above the corner frequency f_3dB. Hence, the combination of autocorrelation analysis and high sampling speeds explains the more than one order of magnitude increase in the observable rates that we report here.

Because the measured kinetics are at the upper limit of what a single-molecule optical trap assay can measure, it was key to check all used analysis methods with simulations capturing the translational Brownian dynamics of the dumbbell system. The autocorrelation analysis was able to reliably recover the protein-folding kinetics used in the Brownian dynamics simulation as long as the relative amplitude of the autocorrelation signal exceeded 10% (Fig. 3 and SI Appendix, Fig. S4).

Kinetics of HP35 Folding/Unfolding.

For HP35stab as well as HP35WT we find rapid folding kinetics of ca. 30,000 s⁻¹ at the midpoint force of the transition (Fig. 3A). These are by far the fastest kinetics that have been reported so far in single-molecule mechanics measurements. We extrapolate the folding- and unfolding-rate constants for HP35WT using a model incorporating detailed balance (SI Appendix) match reported values from T-jump experiments very well (see black squares in Fig. 3A) (40). The extrapolation to zero force of the data for HP35stab yields an unfolding rate constant of 90 s⁻¹ and a folding rate of 1.2 10⁶ s⁻¹. This folding rate constant is close to the assumed “speed limit” of protein folding (1) (see green star in Fig. 3A).

Villin Stability and Folding Cooperativity Can Be Modulated by Helix 3.

An important aspect of our mechanical kinetic–folding data concerns the cooperativity of the folding/unfolding transition of HP35. A recent paper studying forced unfolding of HP35WT using atomic force microscopy interpreted the absence of a well-defined unfolding signal as evidence for low cooperativity of HP35 folding (41). However, in the AFM assay used in that study, the force resolution did not allow to measure forces lower than 20 pN, which is far above the forces at which HP35WT unfolds. In contrast, the direct observation of folding/unfolding kinetics possible in our optical-tweezers assay clearly shows a well-defined, robust, and fully cooperative folding transition, in accord with earlier solution measurements and simulations.

Based on several experimental techniques, it was suggested that energy basin of HP35 consists of diverse rapidly exchanging conformations differing in the geometry and helicity of the C-terminal helix (helix 3) (20, 21). The two stabilizing residues introduced in HP35stab target this dynamic helix. These two mutations act as local stabilizers, which likely explains the deviation from a two-state model and hence the lower cooperativity we find for this variant compared with the wild type. In accord with this interpretation, the ΔN peptide fragments with these two replacements show high helical content, whereas the wild-type background is largely unfolded (SI Appendix, Fig. S1). The estimated helical content in the fragment peptide ΔN HP35stab suggests that possibly the complete helix 3 is in helical conformation. Thus, the replacements within the helix do not only stabilize the helix locally but they also propagate along the rest of the C-terminal helix.

The increased stability of HP35stab compared with HP35WT seems to affect both folding (fivefold increase) and unfolding rates (25-fold decrease). This has interesting consequences for the folding pathways. First, the involvement of helix 3 in the early steps of the folding manifests itself in an acceleration of the folding rate. Second, significant helicity of the N-terminal helices indicates that like in the wild type, in the case of HP35stab, the folding can also proceed from the N-terminal helix. Lei et al. predicted such a competition of pathways in all-atom MD simulations with the wild-type protein of HP35 (42, 43). In our experiments, however, we cannot distinguish between a model involving two parallel pathways starting from either N or C termini and a model where both helices form simultaneously before reaching the transition state. In later folding steps, after engaging and locking of the termini, the two mutations within helix 3 contribute an additional ∼3 k_BT leading to the 25-fold decrease in the unfolding rate constant.

Methods

The gene for the C-terminal subdomain of headpiece villin (headpiece numbering: 42–76) was synthesized by GenScript, Inc. The fragment was cloned into pET28a using SacI and KpnI restriction sites, which were placed between the two copies of ubiquitin with C-terminal His-tag and separated by the Gly-Ser–rich linker. For the full protein sequence see SI Appendix. The proteins were expressed in Escherichia coli BL21 (DE3) and purified by a Ni-NTA affinity column followed by gel filtration chromatography (HPLC System; Jasco Germany, GmbH) using Superdex S200 (10/300 GL, GE Healthcare) and YMC diol-120 columns (YMC Europe, GmbH) for protein–oligonucleotide purification. Protein and peptide concentration was calculated from the absorbance at 280 nm using an extinction coefficient of 5,500 M⁻¹⋅cm⁻¹ (44). Attachment of oligonucleotides and purification optical trap assays were performed as described previously (27, 28). The experiments were performed in 0.1 sodium phosphate, 0.65% glucose, 0.15 M NaCl, 2% (vol/vol) glycerol at pH 7.2, and the pulling velocity was 500 nm/s. The experimental setup used for optical trapping is a custom-built high-resolution dual-trap optical tweezers with back-focal plane detection as described previously (45). The quadrant photodiode were used because they show an improved temporal response compared with the previously used detectors (46).