Abstract
A primary goal of evolutionary genetics is to discover and explain the genetic basis of fitness-related traits and how this genetic basis evolves within natural populations. Unprecedented technological advances have fueled the discovery of genetic variants associated with ecologically relevant phenotypes in many different life forms, as well as the ability to scan genomes for deviations from selectively neutral models of evolution. Theoretically, the degree of overlap between lists of genomic regions identified using each approach is related to the genetic architecture of fitness-related traits and the strength and type of natural selection molding variation at these traits within natural populations. Here we address for the first time in a plant the degree of overlap between these lists, using patterns of nucleotide diversity and divergence for >7000 unique amplicons described from the extensive expressed sequence tag libraries generated for loblolly pine (Pinus taeda L.) in combination with the >1000 published genetic associations. We show that loci associated with phenotypic traits are distinct with regard to neutral expectations. Phenotypes measured at the whole plant level (e.g., disease resistance) exhibit an approximately twofold increase in the proportion of adaptive nonsynonymous substitutions over the genome-wide average. As expected for polygenic traits, these signals were apparent only when loci were considered at the level of functional sets. The ramifications of this result are discussed in light of the continued efforts to dissect the genetic basis of quantitative traits.
Keywords: association mapping, complex traits, Pinus taeda, natural selection, population genomics
A primary goal of population and quantitative genetics is to understand the genetic architecture of ecologically relevant traits (Stinchcombe and Hoekstra 2008; Barrett and Hoekstra 2011; Neale and Kremer 2011). A primary step on the path to this goal is to link genetic with phenotypic variation, either through linkage mapping of quantitative trait loci using pedigrees or through linkage disequilibrium mapping in natural populations (Lander and Schork 1994), with the latter currently being the most utilized. A multitude of studies ranging across a diverse set of taxa have discovered myriad genotype–phenotype correlations (Hindorff et al. 2009; Ingvarsson and Street 2011; Neale and Kremer 2011). Each discovered variant, however, often explains only a small fraction of the heritable phenotypic variance, thus being consistent with a polygenic model for the genetic architecture of complex traits (Lynch and Walsh 1998). Concomitant with the discovery of these associations are population genomic scans documenting deviations from expectations derived using the neutral theory (Nielsen 2005). Such scans have also discovered large numbers of loci putatively underlying phenotypic traits in many different taxa (e.g., Pollinger et al. 2005; Pritchard et al. 2010; Hufford et al. 2012), but in this case the link between genotype and phenotype is not explicit. A natural question thus arises about how much overlap exists between the lists generated using each approach.
Nonneutral signals of evolution at loci underlying polygenic, quantitative traits are expected to differ from those of selective sweeps due to directional selection (Maynard Smith and Haigh 1974; Bürger and Gimelfarb 1999; Pritchard et al. 2010; Pavlidis et al. 2012), with classic selective sweeps at these loci expected to be very rare (Chevin and Hospital 2008). Loci with small phenotypic effects are thus expected to rarely have advantageous alleles reach fixation, but rather are expected to have a polymorphic equilibrium reached (Pavlidis et al. 2012). As shown repeatedly, these loci are largely indistinguishable with regard to their patterns of nucleotide diversity and linkage disequilibrium from neutral loci (e.g., Chevin and Hospital 2008, Pritchard et al. 2010), yet depending on a number of parameters (e.g., the function relating phenotypic values to fitness) recently reached polymorphic equilibria may resemble incomplete sweeps (see Pavlidis et al. 2012). The ability to detect this, however, is expected to be rare, as the timing of sampling must coincide with the attainment of the equilibrium. A simple expectation is thus that the overlap between lists of genes correlated with phenotypic traits and lists of genes identified as outliers in genomic scans should be minimal.
In contrast to this expectation, genetic associations often involve SNPs located in distinctive portions of genomes (e.g., Orozco et al. 2009; Chan et al. 2010a,b), with large effect genes often clearly displaying signals of selection (e.g., Pollinger et al. 2005). For example, Casto and Feldman (2011) examined 1300 single-nucleotide polymorphisms (SNPs) identified as associated with a variety of human phenotypes and showed that those associated with certain phenotypes were located in genomic regions that would have been outliers with regard to measures such as FST. In an examination of the genetic associations with 292 primary metabolites for loblolly pine (Pinus taeda L.), however, a similar pattern was not found, as loci with elevated values of FST were not enriched in genetic associations (Eckert et al. 2012). In this case, genetic associations were enriched for rare alleles, both at the level of SNPs and at the level of the genes containing these SNPs, which could be indicative of synthetic associations (see Goldstein 2011) or some form of linked selection. A generalization of the expected pattern that should emerge from these types of studies is hampered by the uncertainty about the predominant type of natural selection that affects the phenotypic traits commonly investigated in combination with the underlying genetic architecture of those traits (Barton and Keightley 2002; Mitchell-Olds et al. 2008).
Both of the aforementioned uncertainties are intertwined, as, for example, the type of natural selection, as well as the patterning of the intensity of selection pressures across the range of a species, acting on a phenotypic trait will affect its underlying genetic architecture (Orr 1998; Barton and Keightley 2002; Mitchell-Olds et al. 2008; Eyre-Walker 2010). Knowledge of the type of selection acting on a phenotypic trait, however, requires information about the factors affecting fitness within natural populations (i.e., the ecological context, see Endler 1986). Species of forest trees have a long history of ecological genetic investigation that is coupled with an even more developed history of quantitative genetic experimentation (White et al. 2007), so that these species of plants are optimal targets for examining the genetic architecture of ecologically relevant traits (Neale and Kremer 2011). This extensive research has identified the importance of locally adapted phenotypes to standing levels of genetic diversity across geographical ranges of many different tree species. As such, it is expected that conditional on appropriate sampling, many of the signals of selection and links between genotypes and phenotypes should reflect local adaptation.
Linkage disequilibrium mapping has been successively carried out for numerous forest tree species with a variety of phenotypes (reviewed by Neale and Ingvarsson 2008; González-Martínez et al. 2011; Ingvarsson and Street 2011). This success is due largely to the life history characteristics of many tree species (Neale and Savolainen 2004). For example, >1000 genetic associations for loblolly pine, each of small effect on the phenotype, have been discovered for a range of phenotypic traits that span the spectrum of trait complexity: expression profiles of genes related to lignin biosynthesis (Palle et al. 2011, 2013), primary metabolite concentrations (Eckert et al. 2012), drought tolerance and growth (González-Martínez et al. 2008; Cumbie et al. 2011), disease resistance (Quesada et al. 2010), and wood quality (González-Martínez et al. 2006a). In addition, much is known about the ecological context of the natural populations from which the trees used for the aforementioned studies were sampled, so that a set of complementary environmental associations has also been described (Eckert et al. 2010a,b). The set of associations in loblolly pine, therefore, is comprehensive with regard to phenotypic trait diversity. This includes both explicitly and implicitly measured phenotypic traits, as environmental associations are expected to reflect unmeasured phenotypic traits since phenotypic traits are selected upon in natural populations (see Eckert et al. 2009a for an example).
Loblolly pine is an ecologically and economically important tree species of southeastern North America. Its range extends from eastern Texas throughout the southeastern United States and north into Delaware and thus is distributed across diverse environmental gradients (Figure 1). As described previously, loblolly pine is one of the most intensively studied tree species with regard to the genetic architecture of phenotypic traits. The aforementioned phenotypic traits were measured from the same set of clonally replicated materials and correlated with the same set of SNPs (see Cumbie et al. 2011 for materials and Eckert et al. 2010a for SNPs). This study system thus offers an unparalleled chance to examine the degree of overlap between signals documented using linkage disequilibrium mapping and those discovered using population genomic scans. Here we address this question, using >7000 unique amplicons described from the extensive expressed sequence tag (EST) libraries generated for this species. Prior to addressing this question, we describe the current knowledge of the structure and diversity of the gene space of loblolly pine based upon these 7000 amplicons. We use these descriptions subsequently to examine patterns of neutrality, or the lack thereof, for individual genes, as well as sets of genes based upon their associations with phenotypes, and show that loci associated with phenotypic traits and environmental variables are indeed unique with regard to neutral expectations. The ramifications of this result are discussed in light of the continued efforts to dissect the genetic basis of quantitative traits in tree species as well as the evolutionary genetic ramifications of these studies (sensu Barton and Keightley 2002).
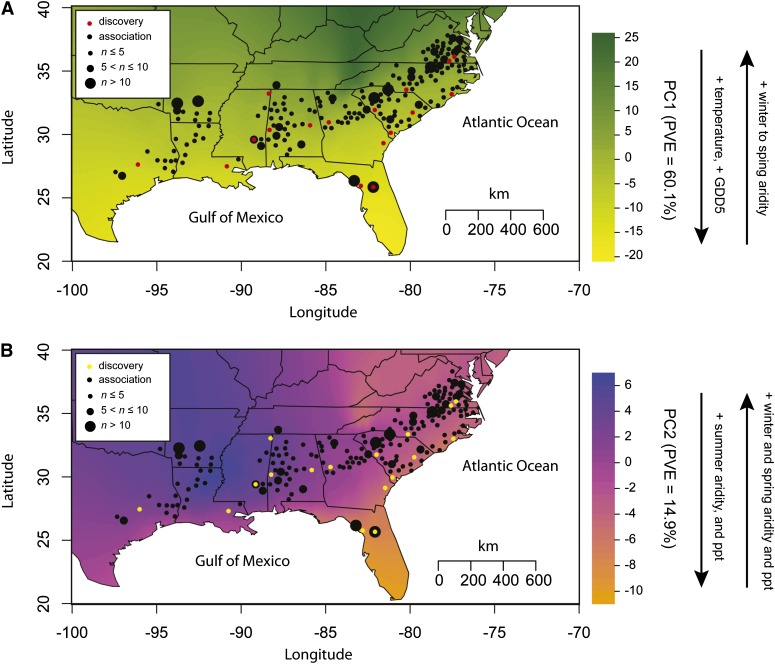
Figure 1.
Sampling localities for loblolly pine for the samples used to discover single-nucleotide polymorphisms (SNPs) and to associate SNP genotypes with phenotypes. (A) Sample localities with respect to the first climatic principal component (PC), which largely represents temperature-related variables and seasonal aridity. (B) Sample localities with respect to the second climatic PC, which largely represents precipitation-related variables. PVE, percentage of variance explained.
Materials and Methods
The results presented here are derived from data generated previously and thus represent a mixture of previously published results and novel population genetic analyses. In general, the following results were published previously: SNP genotypes based on a high-density SNP genotyping array (Eckert et al. 2010a,b, 2012; Quesada et al. 2010; Cumbie et al. 2011; Palle et al. 2013), the linkage map (Eckert et al. 2010a,b), and the association results (Quesada et al. 2010; Cumbie et al. 2011; Eckert et al. 2012; Palle et al. 2013). Results novel to this study are those related to nucleotide diversity, nucleotide divergence, linkage disequilibrium, and inferences of deviations from neutral models. We note in each subsection of Materials and Methods whether data or results are novel to this study.
Population sampling
SNP discovery panel:
A total of 18 trees covering the natural range of loblolly pine were selected for resequencing (Figure 1). Multiple seeds were obtained from each sampled tree for which haploid megagametophyte tissue was manually excised. Megagametophyte tissue proliferates directly from one of the meiotic daughter cells (i.e., the megaspore), which also produces the female gamete, and thus the haploid genotype of the megagametophyte is that of the maternal contribution to the seed (see Pichot and El Maataoui 1997 for exceptions). Megagametophytes were grouped into 96-well plates, one per well, for DNA extraction. Total genomic DNA was extracted subsequently, using 96-well DNeasy Plant Mini Kits (QIAGEN, Valencia, CA), following the manufacturer’s protocol. All tissue excision and DNA extractions were performed by the staff at the National Forest Genetics Electrophoresis Laboratory (U.S. Department of Agriculture Forest Service, Placerville, CA). A set of 7216 SNPs discovered using these samples was published previously and formed the basis for all inferences of genotype–phenotype associations (Quesada et al. 2010; Cumbie et al. 2011; Eckert et al. 2012; Palle et al. 2013).
Linkage-mapping panel:
Two three-generation, outbred pedigrees have been used extensively for linkage mapping in loblolly pine (Devey et al. 1999). Parents for each pedigree were derived from crosses of outbred grandparents and were each crossed twice to produce two sets of full-sib progeny—the discovery set (n = 95–172 per pedigree) and the validation set (n = 500 per pedigree). We randomly selected 93 offspring from the discovery set from each pedigree to genotype with the newly designed SNP genotyping arrays. Data derived from this population were published previously (Eckert et al. 2010a,b).
Association mapping panel:
A set of 498 largely unrelated genotypes has been used extensively for association mapping in loblolly pine (Figure 1). These genotypes were established from seeds collected from natural stands and form parts of the North Carolina State University Cooperative Tree Improvement and Western Gulf Forest Tree Improvement Programs. Germinated seedlings were grown for 1 year and then hedged for stem cuttings following standard protocols (Lebude et al. 2004), after which rooted cuttings were planted in replicates of two to four per genotype at three common garden localities: Texas A&M University (TAMU), North Carolina State University (NCSU), and the University of Florida (UF). Data and results from this population were published previously (Quesada et al. 2010; Cumbie et al. 2011; Eckert et al. 2012; Palle et al. 2013).
Development and application of genetic markers
Construction of EST clusters:
A set of 40,000 EST sequences from loblolly pine was extracted from NCBI’s dbEST repository and clustered using custom internal scripts (Beckman Coulter Genomics, Danvers, MA) into 20,500 unique EST contigs. Approximately 7900 high-quality amplicons were passed subsequently to the production pipeline from these 20,500 unique EST contigs (Supporting Information, File S1). The resulting 7900 amplicons were annotated functionally, using a comparative sequence analysis pipeline. These amplicons are synonymous with respect to the term loci (i.e., we annotated 7900 loci). NCBI BLAST searches were performed against the curated, nonredundant RefSeq plant protein database (Release 43). Sequences without initial hits were compared against the NR database of GenBank (NCBI Release 192). All BLAST searches were subject to an e-value cutoff of 0.5 and 1e-05, respectively. Given putative functional annotations, coding regions were subsequently annotated using output from the SIBSim4 package (Florea et al. 1998). ESTs were trimmed based on matching to the PCR-generated amplicons, using matches to the amplification primer sequences. These ESTs were then aligned against the most common haplotype from the resequenced genomic alignments. Introns were subsequently annotated from the amplicon sequences based on the SIBSim4 predictions.
Resequencing and SNP discovery:
A customized PCR and sequencing pipeline was established at Agencourt Biosciences (now Beckman Coulter Genomics) to resequence 7900 unique EST clusters for 18 loblolly pine trees via bidirectional Sanger sequencing (see File S1). A customized pipeline, PineSAP (Wegrzyn et al. 2009), which employs PHRED/PHRAP (Ewing et al. 1998; Ewing and Green 1998), CONSED (Gordon et al. 1998), POLYBAYES (Marth et al. 1999), POLYPHRED (Nickerson et al. 1997), and machine-learning tools, was used to generate sequence alignments and identify polymorphisms for these data. All reported polymorphisms were those detected after masking bases at a PHRED score of 30.
SNP genotyping:
A total of 7216 SNPs from the set of those discovered as described previously were chosen for further analysis based on quality scores derived from the original sequence data and not on functional or site annotations. This ensured thorough coverage of the available EST cluster sequences for loblolly pine. Genotyping of SNPs utilizing the Infinium platform (Illumina, San Diego) was carried out at the University of California, Davis Genome Center DNA Technologies Core Facility (http://dnatech.genomecenter.ucdavis.edu/) for each of the genotypes that were established at the NCSU common garden and the 93 offspring from of each of the discovery linkage-mapping populations. These data were published previously (Eckert et al. 2010a,b, 2012; Quesada et al. 2010; Cumbie et al. 2011; Palle et al. 2013). Further information is given in File S1.
Phenotypic trait analysis
Phenotypic traits in four general categories, expression levels for lignin and cellulose-related genes (expression), primary metabolite concentrations (metabolite), drought tolerance and growth (drought), and disease resistance (disease), were evaluated in the same set of clonally replicated materials established at NCSU, TAMU, and UF, and the results from phenotypic analyses were published previously in a series of articles linking SNP genotypes to phenotypic traits, using association mapping (Quesada et al. 2010; Cumbie et al. 2011; Palle et al. 2011; Eckert et al. 2012; Palle et al. 2013), or to specific environments (Eckert et al. 2010a,b). More details about each phenotypic trait are given in File S1, as well as in the original publications.
Statistical analysis
Generation of linkage maps:
We utilized a maximum-likelihood method that allows for genotyping errors (Cartwright et al. 2007) to create linkage maps composed of SNPs and restriction fragment length polymorphism (RFLP) framework markers (see Eckert et al. 2009b and references therein), following a double pseudotestcross strategy (Grattapaglia and Sederoff 1994). Additional information is provided in the original publications (Eckert et al. 2010a,b) and in File S1.
Identification of phenotypic associations:
Methodologies used to discover genotype–phenotype and genotype–environment associations are described fully in the original publications (Eckert et al. 2010a,b, 2012; Quesada et al. 2010; Cumbie et al. 2011; Palle et al. 2013) and are summarized in File S1.
Estimation of nucleotide diversity and divergence:
Standard estimates of nucleotide diversity [θW (Watterson 1975) and θπ (Tajima 1983)], haplotype diversity [number of haplotypes, k, and haplotype diversity, Hd (see Nei 1987)], and nucleotide divergence [Dxy (Nei 1987)] were made from each alignment. Nucleotide divergence was estimated relative to P. radiata [∼15–20 MY divergent or less (Gernandt et al. 2008)] and P. lambertiana [∼72–87 MY divergent (Gernandt et al. 2008)]. Estimates were made for different categories of sites (i.e., all, nonsynonymous, synonymous, and noncoding sites) for all statistics by calculating all statistics for each class of sites for each amplicon. When multiple mutations were segregating within a single codon and the pathways could not be unambiguously assigned as silent or replacement, we assumed a pathway requiring the fewest changes. We further assumed an infinite-sites model for all polymorphism calculations, and, thus, sites violating this model or with missing data were dropped prior to estimation. Alignment gaps consistent with insertion–deletion events (indels) were considered separately and were visually validated. Variation in coverage (i.e., base counts at a PHRED score ≥30 at an aligned site across all sampled individuals and targeted base pair positions) was primarily concentrated among alignments, so that sites within alignments for a single amplicon with gaps were ignored and a weighting scheme was used to account for variation among amplicons. The resulting estimates from each alignment were combined into average estimates for groups of amplicons, such as genome-wide, categorical (i.e., sets of genes), and genomic windows along the consensus linkage map, using weighted averages following the logic of Begun et al. (2007). The weights for each alignment were the maximal coverage class attained for the majority of the aligned sites. Genomic windows along the linkage map were defined in 5-cM bins with a step size of 2 cM. All calculations were conducted using DnaSAM (Eckert et al. 2010c) and the libsequence, analysis, and gestimator C++ libraries (Thornton 2003). The latter C++ library uses the method of Comeron (1995) to calculate nonsynonymous (Ka) and synonymous (Ks) divergences, with the average across pairwise comparisons between ingroup and outgroup sequences being presented for each statistic when multiple sequences were available from the outgroup. For different categories of sites, genome-wide estimates were averaged across amplicons, using the aforementioned weighting scheme. All results derived from these methodologies are novel to this study.
Linkage disequilibrium:
Linkage disequilibrium within genes was investigated using the ZnS statistic (Kelly 1997), which is the average r2 among all possible pairwise comparisons of SNPs within an amplicon. Nonlinear regression was used to fit the expected decay of r2 with physical distance (base pairs) following Remington et al. (2001), using R (R Development Core Team 2010). Separate analyses were conducted for each coverage class. All results derived from these methodologies are novel to this study.
Site-frequency spectrum and tests of neutrality:
Folded and unfolded site-frequency spectra were estimated for alignments placed in each coverage class (i.e., the weights used in the weighted averages described previously). Unfolded site-frequency spectra were determined separately for each outgroup comparison. Genome-wide and categorical estimates were made using the method implemented in SoFoS (http://www.scit.us/sofos/) (see Hufford et al. 2012, especially the supplemental information). Standard statistics based on the site-frequency spectrum [D (Tajima 1989) and H (Fay and Wu 2000)] were also estimated for each coverage class, using DnaSAM. Estimates of H were made separately for each outgroup, although we concentrate on those using radiata pine as the outgroup due to the much larger number of amplicons.
Fit of the data to the standard neutral model (SNM) was assessed using two types of tests that are sensitive to deviations from the SNM at different temporal scales. First, outlier tests for D and H were conducted per locus, using coalescent simulations (n = 100,000) conditional on the observed value of θπ and assuming no recombination. A liberal threshold of P = 0.05 was used to assess significance of deviations from the SNM. We also incorporated an aspect of historical demography for these coalescent simulations by using the three-epoch model (TEM) given by Ersöz et al. (2010), which was parameterized based upon a set of 42 disease-resistance candidate genes resequenced for loblolly pine. In brief, this model describes a single lineage experiencing a bottleneck in the recent past, so that the three epochs refer to prebottleneck, bottleneck, and postbottleneck (see Ersöz et al. 2010). Simulations were performed and outliers were assessed and summarized by coverage classes for each model separately. All results derived from these methodologies are novel to this study.
Second, polymorphism and divergence at nonsynonymous and synonymous sites were contrasted using an extension of the McDonald–Kreitman approach (Welch 2006; Obbard et al. 2009). Forty-eight different models, based on whether parameters were fixed or allowed to vary across sets of amplicons (Table S10), were explored in this framework and the best model was chosen using the Akaike information criterion corrected for finite sample sizes (AICc) (see Burnham and Anderson 2004). Parameters of each model were estimated from four observations that were generated for each amplicon: the number of nonsynonymous polymorphisms (PN), the number of synonymous polymorphisms (PS), divergence at nonsynonymous sites (DN), and divergence at synonymous sites (DS). These values were also used to estimate the direction of selection (DoS) statistic for each amplicon (Stoletzki and Eyre-Walker 2011). The main parameter of interest of all models was the proportion of adaptive substitutions (α). Positive values of α represent the proportion of nonsynonymous substitutions driven to fixation by positive selection, while negative values result from the segregation of slightly deleterious variation and sampling error. The effect of the segregation of slightly deleterious variation on estimates of α was assessed by eliminating low-frequency variants from the data set at multiple thresholds (5% and 10%). All analysis was conducted using the MKtest-2.0 software (available at http://sitka.gen.cam.ac.uk/research/welch/GroupPage/Software.html), and all results derived from these methodologies are novel to this study.
Patterns among categories of alignments:
Genome-wide levels of nucleotide diversity were assessed for constancy across amplicons, using a multilocus likelihood-ratio test (Hudson 1990, as used by Brown et al. 2004) (see https://github.com/RILAB/ThetaCurve for the Perl script; Ross-Ibarra, J., personal communication). Average levels of diversity were also assessed for differences across categories of amplicons defined by their putative functions, ability to be placed on the linkage map, linkage groups, whether or not SNPs were genotyped, presence or absence of indels, or presence or absence of genotype–phenotype associations. Gene Ontology (GO) categories (Ashburner et al. 2000) were assigned primarily through molecular function and were standardized to the same level in the GO hierarchy, to allow for appropriate comparisons. Following standardization, some categories were combined or split where appropriate to represent relevant high-level gene families (e.g., heat shock, transcription factors, ATPases). Categories for genotype–phenotype associations were defined in numerous ways, ranging from a binary categorization (associated to unassociated) to a multistate categorization (unassociated, metabolite associations, expression associations, disease associations, and drought associations). For completeness, the environmental associations from Eckert et al. (2010a,b) were also included. Permutation tests (n = 10,000 permutations) were used to assess differences among averages or to validate inferences from statistical tests (e.g., Kruskal–Wallis rank sum tests). Permutation tests were carried out by randomizing amplicons between (e.g., for t-tests) or among (e.g., for Kruskal–Wallis rank sum tests) categories and calculating the relevant test statistic 10,000 times to form a null distribution. Bootstrapping of amplicons (n = 10,000 replicates with replacement) within categories was also used to construct confidence intervals for categorical averages (Efron 1985). All results derived from these methodologies are novel to this study.
Results
Resequencing data summary
The number of amplicons passing design thresholds decreased from ∼7900 to 7413 after requiring both forward (F) and reverse (R) reads to be present for each sample, which was followed by a further decrease to 6669 amplicons after screening for amplification primers in both reads. A total of 5773 amplicons passed our final quality thresholds, which also included screens for organellar contamination. A total of 22,621 SNPs were detected across the 5773 amplicons. Of these 22,621 SNPs, 10,591 could be annotated as nonsynonymous (n = 2915), synonymous (n = 3233), and noncoding (n = 4443). Detailed information is located in File S1 (see also Table 1, Table S1, Table S2, Table S3, Figure S1, Figure S2, Figure S3, Figure S4, and Figure S5). All sequence data used in the downstream analyses have been deposited at GenBank (accession numbers: File S2).
Table 1. Summary of sequence data generated for loblolly pine (Pinus taeda L.).
| Catagories | All | Not genotyped | Mapped | Unassociated | Associated |
|---|---|---|---|---|---|
| No. ampliconsa | |||||
| Total | 5,773 | 3,154 | 1,306 | 1,930 | 689 |
| Annotated | 2,626 | 1,453 | 562 | 864 | 309 |
| Not annotated | 3,147 | 1,701 | 744 | 1,066 | 380 |
| Sample size (n)a | |||||
| Total | 12 ± 6 | 11 ± 6 | 12 ± 5 | 13 ± 5 | 13 ± 5 |
| Annotated | 12 ± 6 | 11 ± 6 | 13 ± 5 | 13 ± 5 | 13 ± 5 |
| Not annotated | 12 ± 6 | 11 ± 6 | 12 ± 5 | 13 ± 5 | 12 ± 5 |
| Length (bp)a | |||||
| All | 2,135,607 (370 ± 126) | 1,107,387 (351 ± 120) | 520,300 (398 ± 129 | 745,025 (390 ± 130) | 283,195 (400 ± 131) |
| NS | 583,159 (235 ± 83) | 308,837 (230 ± 82) | 132,704 (244 ± 84) | 197,612 (238 ± 83) | 76,710 (249 ± 84) |
| SY | 160,814 (65 ± 24) | 84,829 (63 ± 23) | 36,439 (67 ± 24) | 54,677 (66 ± 24) | 21,308 (69 ± 24) |
| NC | 417,915 (132 ± 153) | 197,736 (114 ± 142) | 110,076 (158 ± 165) | 163,867 (156 ± 162) | 56,312 (149 ± 161) |
| No. SNPsa | |||||
| All | 22,621 (4 ± 5) | 11,064 (4 ± 6) | 6,079 (5 ± 5) | 8,485 (4 ± 4) | 3,072 (4 ± 4) |
| NS | 2,915 (1 ± 2) | 1,568 (1 ± 2) | 709 (1 ± 2) | 898 (1 ± 2) | 449 (1 ± 2) |
| SY | 3,233 (1 ± 2) | 1,490 (1 ± 2) | 897 (2 ± 2) | 1,265 (1 ± 2) | 478 (2 ± 2) |
| NC | 4,443 (1 ± 3) | 1,660 (1 ± 2) | 1,462 (2 ± 3) | 2,159 (2 ± 4) | 624 (2 ± 3) |
NC, noncoding; NS, nonsynonymous; SY, synonymous.
Numbers are either total counts or arithmetic averages ± one standard deviation. Decimal remainders for averages and standard deviations were rounded to whole numbers according to >0.0–0.5 round down and >0.5–1.0 round up.
Nucleotide diversity and insertion–deletion events
Genome-wide patterns:
Nucleotide diversity (per site), as measured by θπ and θW, varied significantly among sample coverage classes (Kruskal–Wallis rank sum tests: P < 1.0e-9, Pperm < 1.0e-4). Thus, weighted estimates for averages and variances were used to construct genome-wide estimates. The overall weighted average (±1 SD) for each estimator was 0.0033 (±0.0048) and 0.0038 (±0.0049), respectively. These values are similar to those published previously for loblolly pine, using sets of candidate genes (Brown et al. 2004; González-Martínez et al. 2006a; Ersöz et al. 2010). Analysis by categories of sites also revealed similarity to previous estimates, with synonymous site diversity being the largest and nonsynonymous site diversity being the smallest (Figure S5 and Figure S6). Average estimates of diversity were also similar to those obtained using a multilocus maximum-likelihood method (Hudson 1990). Likelihood-ratio tests, however, rejected equality of nucleotide diversity across amplicons for all, nonsynonymous, synonymous, and noncoding sites (Table S4).
A total of 1572 indels occurred in 1080 of the 5773 amplicons, with sizes ranging from 1 to 352 bp. Indels accounted for 15,286 of the 2,139,768 aligned sites (0.71%). Most of the indels were ≤10 bp in size (79.45%), with a weighted average size of 10 bp, where the weights were the sample frequencies for each unique indel length. The majority of amplicons with indels contained only a single indel (Figure S7), yet 16 amplicons contained ≥5 indels, with indel lengths ranging in size from 1 to 316 bp. A total of 547 of the 1572 indels were located in 393 amplicons with annotations. Indels were primarily located in the noncoding regions of these amplicons (86.76%), with 190 and 305 located in introns and UTRs, respectively. The 52 remaining indels were within coding regions and, as required during validation of the annotations, did not result in frameshift mutations. Indels occurred across coverage classes (n = 2–18), in approximately the same proportion as expected given the distribution of amplicons across coverage classes (Wilcoxon signed rank test: P = 0.059, Pperm = 0.087).
The number of indels within amplicons also affected diversity, divergence, and the shape of the site-frequency spectrum (Figure S8, Table S5; see also Results, Departures from neutrality). Conditional on an indel being present, the number of indels was positively correlated with average number of SNPs (Spearman’s ρ = 0.83), average nucleotide diversity (Spearman’s ρ = 0.77), average Tajima’s D (Spearman’s ρ = 0.82), the number of haplotypes (Spearman’s ρ = 0.63), and haplotype diversity (Spearman’s ρ = 0.83). These patterns could result from mutation rate variation introducing an autocorrelation. If this is true, then the trend with nucleotide diversity should disappear if diversity is scaled by divergence. This does not happen when using radiata pine (t = −4.577, d.f. = 1077.045, P = 5.257e-06, Pperm = 0.0001) or sugar pine (t = −4.238, d.f. = 145.239, P = 3.994e-05, Pperm = 0.0009) as outgroups, although the relative difference for the averages is reduced (i.e., the average diversity is 2.6-fold greater in amplicons with indels, while the average diversity scaled by divergence is only 1.2- to 1.5-fold greater, depending on the outgroup comparison; see Figure S8). No differences in these patterns were apparent across sets of amplicons based on phenotypic categories or based on any other categorization (Wilcoxon signed rank or Kruskal–Wallis rank sum tests: P < 1.45e-05, Pperm < 0.0001).
Comparisons across categories of amplicons:
Nucleotide diversity varied across sets of amplicons (Table 2; Figure 2). The consensus linkage map for loblolly pine included a total of 1268 amplicons with more than one sampled allele. These amplicons had average levels of nucleotide diversity that were larger than those of the entire set of 5773 amplicons, with θπ and θW being 1.2- and 1.1-fold larger, respectively. Nucleotide diversity varied across linkage groups for loblolly pine, ranging from 0.00323 (θπ) and 0.00320 (θW) for linkage group 1 to 0.00458 (θπ) and 0.00473 (θW) for linkage group 10 (Figure S9 and Figure S10; Table S6). These differences, however, were not significant for diversity at all, nonsynonymous, synonymous, or noncoding sites (Kruskal–Wallis rank sum tests: P > 0.20, Pperm > 0.10), yet were significantly correlated with linkage group length for synonymous sites (Spearman’s ρ = 0.420, Pperm = 0.0052). Nucleotide diversity also varied among categories of amplicons based on those that were annotated vs. those that were not annotated, those that were associated to at least one type of phenotypic trait, and those associated with each of the four phenotypic trait categories (Table 2). Most differences, however, were not significant (Kruskal–Wallis rank sum tests: P > 0.30, Pperm > 0.20). The only significant difference observed was for nonsynonymous and noncoding diversities (Kruskal–Wallis rank sum tests: P < 0.001, Pperm < 0.005), with amplicons containing SNPs related to expression and metabolite phenotypes having higher nonsynonymous diversities and lower noncoding diversities. Total nucleotide diversity, however, did differ significantly among functional categories of amplicons (Kruskal–Wallis rank sum tests: P < 0.001, Pperm < 0.005; Figure 2), with the highest levels of diversity being in amplicons whose gene products were associated with disease resistance and the lowest levels of diversity being in amplicons whose gene products were classified as isomerases. Similar patterns were observed for divergence at different categories of sites.
Table 2. Nucleotide diversity across the loblolly pine (Pinus taeda L.) genome.
| Nucleotide diversity (θπ) | Nucleotide diversity (θW) | |||||||
|---|---|---|---|---|---|---|---|---|
| Amplicons | All: | NS: | SY: | NC: | All: | NS: | SY: | NC: |
| (L = all/annotated) | 95% C.I.a | 95% C.I.a | 95% C.I.a | 95% C.I.a | 95% C.I.a | 95% C.I.a | 95% C.I.a | 95% C.I.a |
| All | 0.0033 | 0.0013 | 0.0059 | 0.0021 | 0.0038 | 0.0015 | 0.0067 | 0.0024 |
| (L = 5773/2626) | 0.0032–0.0034 | 0.0012–0.0014 | 0.0056–0.0062 | 0.0019–0.0023 | 0.0037–0.0039 | 0.0014–0.0016 | 0.0064–0.0071 | 0.0023–0.0025 |
| Not genotyped | 0.0030 | 0.0012 | 0.0050 | 0.0016 | 0.0035 | 0.0015 | 0.0059 | 0.0019 |
| (L = 3154/1453) | 0.0027–0.0033 | 0.0011–0.0013 | 0.0045–0.0055 | 0.0014–0.0018 | 0.0033–0.0037 | 0.0014–0.0016 | 0.0054–0.0063 | 0.0017–0.0021 |
| Mappedb | 0.0040 | 0.0016 | 0.0081 | 0.0031 | 0.0042 | 0.0017 | 0.0083 | 0.0032 |
| (L = 1306/562) | 0.0038–0.0042 | 0.0014–0.0018 | 0.0074–0.0088 | 0.0027–0.0034 | 0.0040–0.0044 | 0.0015–0.0019 | 0.0076–0.0090 | 0.0029–0.0035 |
| Unassociated | 0.0037 | 0.0013 | 0.0070 | 0.0028 | 0.0041 | 0.0015 | 0.0078 | 0.0031 |
| (L = 1930/864) | 0.0035–0.0039 | 0.0012–0.0014 | 0.0064–0.0076 | 0.0026–0.0030 | 0.0039–0.0042 | 0.0013–0.0016 | 0.0072–0.0084 | 0.0029–0.0034 |
| Associated | 0.0034 | 0.0014 | 0.0065 | 0.0022 | 0.0039 | 0.0017 | 0.0073 | 0.0024 |
| (L = 689/309) | 0.0031–0.0037 | 0.0012–0.0016 | 0.0057–0.0075 | 0.0018–0.0025 | 0.0036–0.0041 | 0.0015–0.0019 | 0.0065–0.0081 | 0.0021–0.0028 |
| Expression | 0.0033 | 0.0017 | 0.0077 | 0.0016 | 0.0042 | 0.0023 | 0.0084 | 0.0022 |
| (L = 76/39) | 0.0028–0.0038 | 0.0013–0.0021 | 0.0049–0.0102 | 0.0009–0.0022 | 0.0037–0.0047 | 0.0018–0.0028 | 0.0057–0.0110 | 0.0014–0.0029 |
| Metabolite | 0.0033 | 0.0014 | 0.0067 | 0.0021 | 0.0038 | 0.0017 | 0.0075 | 0.0024 |
| (L = 576/257) | 0.0031–0.0035 | 0.0012–0.0016 | 0.0060–0.0074 | 0.0018–0.0024 | 0.0036–0.0040 | 0.0015–0.0019 | 0.0068–0.0082 | 0.0021–0.0027 |
| Drought | 0.0017 | 0.0006 | 0.0084 | 0.0007 | 0.0020 | 0.0009 | 0.0090 | 0.0012 |
| (L = 12/6) | 0.0012–0.0022 | 0.0001–0.0012 | 0.0017–0.0130 | 0.0001–0.0012 | 0.0014-0.0025 | 0.0001–0.0017 | 0.0032–0.0132 | 0.0001–0.0024 |
| Disease | 0.0037 | 0.0006 | 0.0029 | 0.0029 | 0.0044 | 0.0009 | 0.0033 | 0.0037 |
| (L = 9/5) | 0.0020–0.0051 | 0.0001–0.0014 | 0.0013–0.0046 | 0.0008–0.0057 | 0.0026-0.0060 | 0.0001–0.0021 | 0.0011–0.0057 | 0.0015–0.0074 |
C.I., confidence interval; L, number of amplicons; NC, noncoding; NS, nonsynonymous; SY, synonymous.
Nonparametric bootstrapping (n = 1000 replicates) across amplicons was used to estimate 95% C.I.’s.
Estimates per linkage group are given in Table S6.
Figure 2.
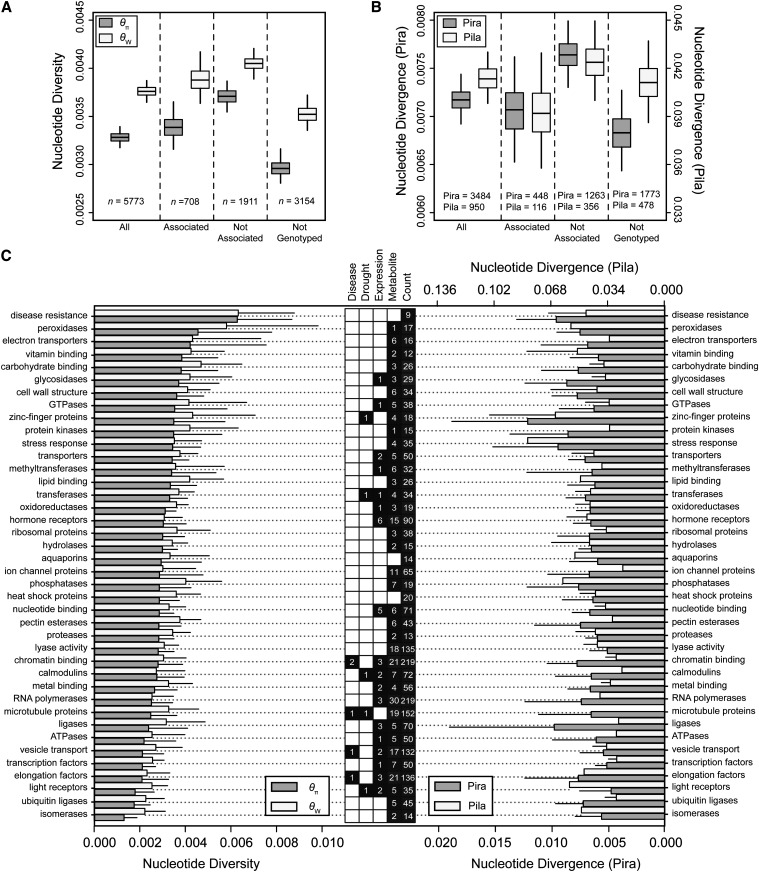
Nucleotide diversity and divergence across categories of amplicons for loblolly pine. (A) Average levels of total nucleotide diversity by category of amplicons. Whiskers represent 95% confidence intervals generated via bootstrapping across amplicons. (B) Average levels of total nucleotide divergence by category of amplicons and outgroup (Pira, P. radiata; Pila, P. lambertiana). Whiskers represent 95% confidence intervals generated via bootstrapping across amplicons. (C) Average levels of total nucleotide diversity (left) and divergence (right) by functional categories in relation to categories of phenotypic associations (center). Numbers in the center box represent numbers of amplicons for each functional category (Count) and the number of phenotypic associations (solid, associated; open, no association). Error bars represent 95% confidence intervals generated via bootstrapping across amplicons.
Nucleotide divergence
Genome-wide patterns:
Nucleotide divergence as measured by Dxy relative to radiata and sugar pines varied significantly among sample coverage classes (Kruskal–Wallis rank sum tests: P < 1.00e-9, Pperm < 1.00e-4). Nucleotide divergence was ∼2–12 times the level of nucleotide diversity, depending upon choice of outgroup (Table 3), and, as with nucleotide diversity, was affected by the presence or absence of an indel (Table S5). On average (±1 SD), sequences from loblolly pine differed with respect to radiata pine at 0.72% (±0.79%) of sites, while for sugar pine they differed at 4.1% (±2.3%) of sites. As with nucleotide diversity, nucleotide divergence was largest at synonymous sites (radiata pine, 1.2 ± 1.6%; sugar pine, 8.7 ± 6.1%) and lowest at nonsynonymous sites (radiata pine, 0.28 ± 0.58%; sugar pine, 1.9 ± 1.8%; Table 3, Figure S10). The average Ka/Ks ratio (±1 SD) thus varied from 0.59 (±1.68) to 0.27 (±0.30) for radiata and sugar pines, respectively.
Table 3. Nucleotide divergence across the loblolly pine (Pinus taeda L.) genome.
| Nucleotide divergence (Dxy: Pira) | Nucleotide divergence (Dxy: Pila) | |||||||
|---|---|---|---|---|---|---|---|---|
| Amplicons | All: | NS: | SY: | NC: | All: | NS: | SY: | NC: |
| (L = all/annotated) | 95% C.I.a | 95% C.I.a | 95% C.I.a | 95% C.I.a | 95% C.I.a | 95% C.I.a | 95% C.I.a | 95% C.I.a |
| All | 0.0072 | 0.0028 | 0.0117 | 0.0080 | 0.0410 | 0.0186 | 0.0871 | 0.0492 |
| (Pira: 3484/1659) | 0.0069–0.0075 | 0.0025–0.0031 | 0.0109–0.0126 | 0.0074–0.0085 | 0.0396–0.0426 | 0.0171–0.0204 | 0.0825–0.0928 | 0.0461–0.0526 |
| (Pila: 950/497) | ||||||||
| Not genotyped | 0.0068 | 0.0028 | 0.0115 | 0.0074 | 0.0408 | 0.0191 | 0.0907 | 0.0464 |
| (Pira: 1773/857) | 0.0064–0.0072 | 0.0024–0.0033 | 0.0102–0.0127 | 0.0065–0.0083 | 0.0382–0.0432 | 0.0169–0.0215 | 0.0826–0.0987 | 0.0408–0.0518 |
| (Pila: 478/255) | ||||||||
| Mappedb | 0.0078 | 0.0032 | 0.0129 | 0.0081 | 0.0429 | 0.0198 | 0.0864 | 0.0503 |
| (Pira: 836/365) | 0.0073–0.0082 | 0.0027–0.0037 | 0.0112–0.0147 | 0.0071–0.0091 | 0.0396–0.0464 | 0.0156–0.0248 | 0.0749–0.0986 | 0.0446–0.0561 |
| (Pila: 212/111) | ||||||||
| Unassociated | 0.0076 | 0.0028 | 0.0120 | 0.0086 | 0.0420 | 0.0174 | 0.0849 | 0.0515 |
| (Pira: 1263/588) | 0.0073–0.0080 | 0.0025–0.0032 | 0.0109–0.0131 | 0.0079–0.0095 | 0.0396–0.0444 | 0.0152–0.0199 | 0.0768–0.0938 | 0.0473–0.0561 |
| (Pila: 356/208) | ||||||||
| Associated | 0.0071 | 0.0029 | 0.0117 | 0.0082 | 0.0391 | 0.0206 | 0.0787 | 0.0521 |
| (Pira: 448/214) | 0.0065–0.0076 | 0.0023–0.0035 | 0.0101–0.0133 | 0.0068–0.0098 | 0.0360–0.0422 | 0.0163–0.0255 | 0.0662–0.0918 | 0.0425–0.0611 |
| (Pila: 116/62) | ||||||||
| Expression | 0.0071 | 0.0027 | 0.0155 | 0.0072 | 0.0370 | 0.0205 | 0.0696 | 0.0510 |
| (Pira: 44/23) | 0.0061–0.0085 | 0.0016–0.0038 | 0.0110–0.0203 | 0.0044–0.0101 | 0.0319–0.0431 | 0.0145–0.0282 | 0.0536–0.0918 | 0.0356–0.0578 |
| (Pila: 17/9) | ||||||||
| Metabolite | 0.0070 | 0.0028 | 0.0115 | 0.0085 | 0.0390 | 0.0203 | 0.0814 | 0.0517 |
| (Pira: 373/180) | 0.0066–0.0075 | 0.0023–0.0032 | 0.0010–0.0130 | 0.0071–0.0098 | 0.0364–0.0415 | 0.0164–0.0240 | 0.0704–0.0919 | 0.0435–0.0598 |
| (Pila: 92/49) | ||||||||
| Drought | 0.0036 | 0.0022 | 0.0143 | 0.0031 | 0.0878 | 0.0499 | 0.1496 | 0.1025 |
| (Pira: 7/4) | 0.0031–0.0070 | — | — | — | — | — | — | — |
| (Pila: 2/1) | ||||||||
| Disease | 0.0105 | 0.0074 | 0.0111 | 0.0065 | 0.0463 | 0.0581 | 0.0734 | — |
| (Pira: 6/3) | 0.0062–0.0147 | — | — | — | — | — | — | — |
| (Pila: 2/1) | ||||||||
C.I., confidence interval; L, number of amplicons; NC, noncoding; NS, nonsynonymous; Pila, Pinus lambertiana; Pira, P. radiata; SY, synonymous.
Nonparametric bootstrapping (n = 1000 replicates) across amplicons was used to estimate 95% C.I.’s.
Estimates per linkage group are given in Table S7.
Comparisons across categories of amplicons:
Nucleotide divergence across all sites relative to radiata pine varied across sets of amplicons (Table 3; Figure 2, Figure S11, and Figure S12) as defined by their presence or absence on the consensus linkage map (Wilcoxon signed rank test: P = 7.56e-08, Pperm < 0.001), their being annotated or not (Wilcoxon signed rank test: P < 2.20e-16, Pperm < 0.001), their being associated or unassociated with at least one phenotypic trait (Wilcoxon signed rank test: P = 0.048, Pperm = 0.032), their being associated to different phenotypic categories (Kruskal–Wallis rank sum test: P = 6.75e-09, Pperm < 0.0001), and their classification into functional categories (Kruskal–Wallis rank sum test: P = 5.53e-07, Pperm < 0.0001). On average, nucleotide divergence at all sites relative to radiata pine was lower for amplicons that were mapped, those that were annotated, those associated to at least one phenotypic trait, and those that encoded light receptors or ion channels (Figure 2). For those amplicons that were mapped, differences among linkage groups (see Table S7) were significant (Kruskal–Wallis rank sum test: P = 0.0197, Pperm = 0.009). Among phenotypic trait categories, amplicons associated with disease resistance had the largest nucleotide divergence, while those associated with drought had the lowest (Table 3). Nucleotide divergence was largely similar for different categories of sites across different categories of amplicons. For example, nucleotide divergence at nonsynonymous, synonymous, and noncoding sites was not significantly different for amplicons associated with at least one phenotypic trait vs. those that were unassociated (Wilcoxon signed rank tests: P > 0.40, Pperm > 0.50). This contradiction with respect to nucleotide divergence for all sites can be explained by the fact that annotated amplicons had a lower level of nucleotide divergence relative to amplicons that were not annotated, so that the previously reported difference for overall nucleotide divergence differing between sets of amplicons associated vs. unassociated to at least one phenotypic trait was driven by amplicons that were not annotated. With regard to amplicons associated with specific phenotypic categories, the average (±1 SD) Ka/Ks was largest for amplicons associated with disease phenotypes (0.67 ± 0.89), while it was smallest for amplicons related to drought phenotypes (0.15 ± 0.22). Similar numerical patterns were noted across categories of amplicons when using sugar pine as the outgroup. These differences, however, were not statistically significant (Wilcoxon signed rank tests and Kruskal–Wallis rank sum tests: P > 0.15, Pperm > 0.20).
Linkage disequilibrium
Genome-wide patterns:
Levels of intragenic linkage disequilibrium varied across amplicons, but were within the range of those previously published for conifers (e.g., Neale and Savolainen 2004; Namroud et al. 2010; Pyhäjärvi et al. 2011). For example, the weighted average (±1 SD) value of Kelly’s ZnS statistic across amplicons with two or more polymorphic sites was 0.311 (±0.288). The expected rapid decay with physical distance, however, was apparent only when including singletons in the analysis (Table S8, Figure S13, and Figure S14). When singletons were included, the expected value of r2 decayed to half its initial value in 102–496 bp, depending upon coverage class, indicating that recombination events were ∼1.4- to 9.1-fold more likely than mutation events. When excluding singletons, the decay of linkage disequilibrium with physical distance was much reduced to nonexistent, with only three coverage classes experiencing any decay (Table 4). For these analyses, recombination events were ∼1.2- to 4.8-fold less likely than mutation events, so that r2 would decay to half its initial value in 1279–4633 bp. These patterns are related to the relatively short physical distances for most amplicons (i.e., <500 bp; see Results, Resequencing data summary). Further descriptions of linkage disequilibrium, including those for categories of amplicons, can be found in File S1.
Table 4. Estimates for the intralocus, per site crossing-over rate (C = 4Ner) for coverage classes where a decay of r2 was observed over physical distance (bp).
| Coverage class | Amplicons | C | LD-half (bp) | ZnS | C/θπ |
|---|---|---|---|---|---|
| 18 | 898 | 0.0021 (0.0006–0.0044) | 1,279 (629–4,477) | 0.266 (0.243–0.288) | 0.868 (0.253–1.831) |
| 17 | 755 | 0.0016 (0.0004–0.0031) | 1,706 (881–6,824) | 0.270 (0.247–0.292) | 0.555 (0.151–1.057) |
| 15 | 374 | 0.0006 (0.0001–0.0025) | 4,633 (1,112–27,800) | 0.286 (0.253–0.320) | 0.208 (0.034–0.902) |
Decay of r2 with physical distance was not observed for amplicons in all other coverage classes. In these cases, the regression-based estimate of C was approximately zero or negative. Table S8 gives estimates when singletons were included for coverage classes ranging from 11 to 18. Values in parentheses are 95% nonparametric bootstrap (n = 10,000 replicates) confidence intervals based on resampling of amplicons with replacement. LD-half represents the distance in base pairs required for r2 to decrease to half its initial value. Values of θπ represent arithmetic averages across amplicons within each coverage class.
Departures from neutrality
Genome-wide patterns:
The folded site-frequency spectrum for all sites deviated strongly from the SNM (Figure S15). This was also apparent for different categories of sites (data not shown), with deviations most apparent for categories corresponding to low-frequency variants. Similar patterns were observed for the unfolded site-frequency spectrum, but deviations were observed for low- and high-frequency derived variants. This pattern was consistent across unfolded site-frequency spectra based on each outgroup (Figure S16 and Figure S17). Summarizing site-frequency spectra by locus using Tajima’s D gave genome-wide weighted averages (±1 SD) of −0.474 (±0.951), −0.465 (±0.925), −0.354 (±0.984), and −0.417 (±0.961) for all, nonsynonymous, synonymous, and noncoding sites, respectively. Genome-wide estimates of Fay and Wu’s H were similarly negative, with weighted averages (±1 SD) of −0.223 (±0.987), −0.268 (±1.052), −0.198 (±0.945), and −0.247 (±0.967) for all, nonsynonymous, synonymous, and noncoding sites, respectively.
Comparison of amplicon-specific values by coverage class of Tajima’s D to the distribution predicted under a strict neutral model revealed that 3.9–8.0% of amplicons were outliers (n = 260 amplicons total) at a significance level of P = 0.05 (Figure S18A). None of these survived corrections for multiple tests, using a false-discovery rate (FDR) correction (Storey and Tibshirani 2003). Incorporation of a simple TEM of demography from Ersöz et al. (2010), however, removed the vast majority of these outliers (Figure S18B), so that only 52 of the previously described 260 outliers remained as outliers at a significance level of P = 0.05 after incorporation of the TEM. These amplicons tended to be in either tail (i.e., the extreme positive or extreme negative tail) of the genome-wide distribution for Tajima’s D conditional on coverage class. This was expected as the TEM fitted the data better than the SNM (Table S9), even though the formulation of the TEM by Ersöz et al. (2010) was based on samples collected only from the eastern portion of the range of loblolly pine and disease-related candidate genes (but see Figure S19). In addition, none of the significant amplicons survived corrections for multiple tests, using a FDR approach.
Analysis using Fay and Wu’s H produced a similar trend for the SNM, but with the number of significant outliers increasing from 178 to 692 when the TEM was incorporated into the null model. This resulted in 21.3–38.9% of the observed values of Fay and Wu’s H being outliers across coverage classes at a significance threshold of P = 0.05, which exceeds the expected number of false positives by approximately fivefold. As with Tajima’s D, these amplicons were in the tails of the genome-wide distributions for Fay and Wu’s H conditional on coverage class (Figure S20). Using a FDR correction for the TEM resulted in 57 amplicons remaining significant, using a threshold of Q = 0.05. Part of this difference relative to Tajima’s D is due to the poor predictive ability of the TEM for the variance across amplicons for Fay and Wu’s H [i.e., the observed value for the weighted variance of H across amplicons is in the upper 0.01% tail of the simulated distribution (n = 1.0 × 105 simulations) under the TEM].
Joint consideration of Tajima’s D and Fay and Wu’s H under the TEM identified 31 amplicons with D and H both significant at P = 0.05 (Table S10). All 31 amplicons had negative values for D and H that were ∼3.8- (D) to 22.3-fold (H) more negative than the average across amplicons. These 31 amplicons spanned the spectrum of putative gene functions ranging from heat-shock proteins (e.g., 0_10631_01) and universal stress protein family proteins (e.g., 0_12117_01) to protein kinases (e.g., CL2463Contig1_03), with 15 of these 31 amplicons, however, not being annotated with respect to putative gene function or categories of sites. Although not a formal multidimensional test (see Zeng et al. 2007), this list gives the most extreme outliers with respect to D and H when considered jointly. When compared with the list of amplicons associated with phenotypic traits, there was no enrichment for associated amplicons to be in the lower tail of the distributions of D and H (permutation tests: P > 0.20).
Comparisons of polymorphism and divergence at multiple classes of sites using an extension of the McDonald–Kreitman test revealed that the loblolly pine genome contains significant signatures of past positive selection (Figure 3). Using levels of nucleotide diversity and divergence at nonsynonymous and synonymous sites suggested that on average 29% [95% confidence interval (C.I.): 22–37%] of new nonsynonymous substitutions have been fixed by positive, directional selection within the loblolly pine genome. This estimate is derived from a model of polymorphism and divergence where each amplicon has a unique value of θ = 4Neu (see Table S11) and a fixed level of divergence (ut = 0.0083, 95% C.I.: 0.0078–0.0089), selective constraint (f = 0.22, 95% C.I.: 0.15–0.29), and α. Of the 48 models tested, where these parameters were set to zero, fixed, or allowed to vary across amplicons (see Table S11), this model was one of the best and, when fixing α across amplicons, it was the best (AICc: 18,936.13 vs. next best model AICc: 19,383.60, so ΔAICc = 447.47). Modifying the data to exclude segregating variation below a frequency threshold of 10% did not change this estimate dramatically (α = 25%, 95% C.I.: 19–35%), which suggests that the segregation of slightly deleterious mutations is not driving this result.
Figure 3.
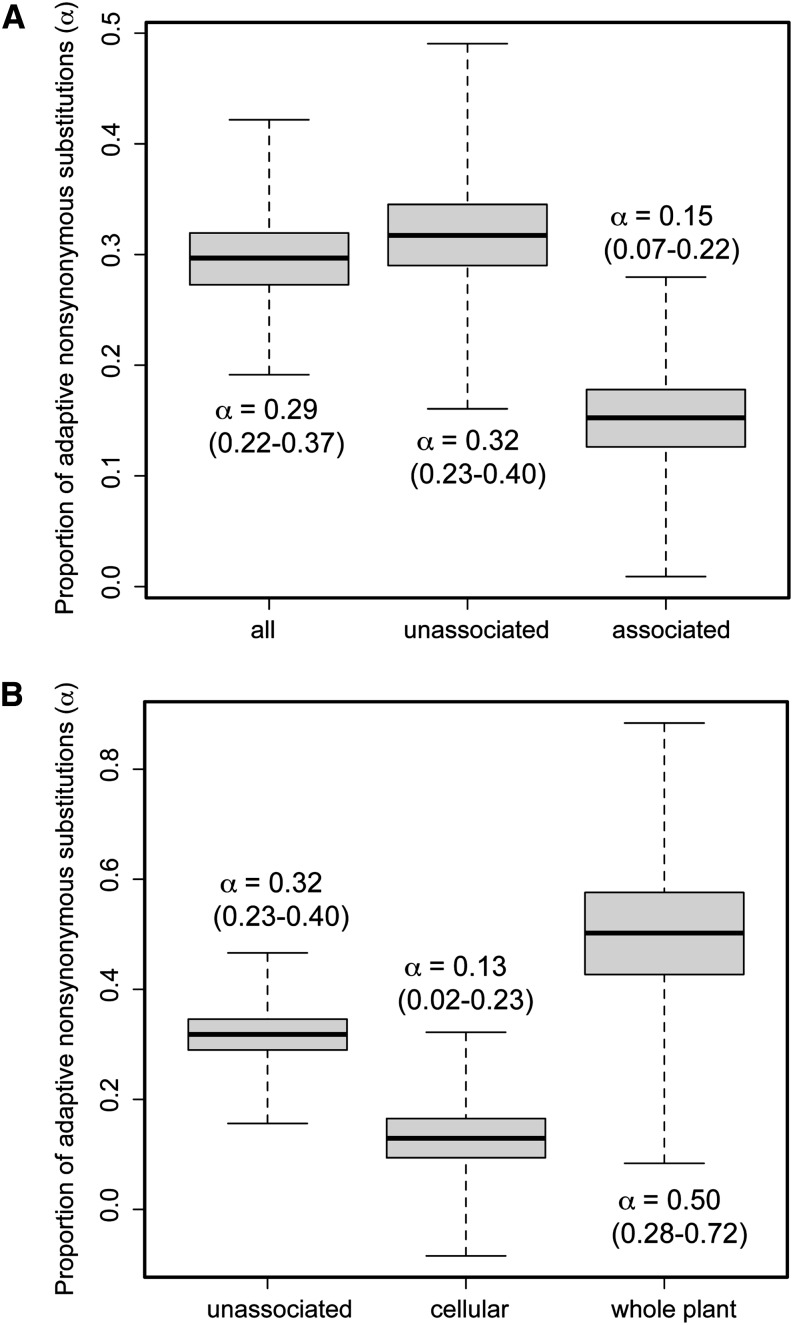
The proportion of adaptive nonsynonymous substitutions (α) is significantly different from zero for the loblolly pine genome and varies across classes of amplicons. Numbers in parentheses give 95% bootstrap confidence intervals (n = 10,000 replicates) for α in both panels. (A) Whereas α is significantly larger than zero for all classes of amplicons, it is highest for the set of amplicons without associations to any of the phenotypes. (B) The patterns observed in A, however, are driven by amplicons associated to one of the cellular phenotypes (expression and metabolites), where the point estimate of α is 3.8 times lower than the point estimate for whole plant phenotypes (drought, disease, environmental associations).
Comparisons across categories of amplicons:
As noted previously, nucleotide diversity differed significantly between amplicons associated with at least one phenotypic trait relative to those that were not (see Results, Nucleotide diversity and insertion–deletion events, Figure 2, and Figure S21). This translated into significant differences for Tajima’s D (Figure S21) and Fay and Wu’s H (Wilcox rank sum tests: all, P = 0.254, Pperm = 0.196; nonsynonymous, P < 2.2e-16, Pperm < 0.001; synonymous, P = 0.137, Pperm = 0.098; noncoding, P = 0.051, Pperm = 0.048) between these classes. The strongest differences occurred for nonsynonymous sites, which exhibited significantly more negative values for D and H for amplicons associated with phenotypic traits relative to amplicons not associated with a phenotypic trait for both statistics.
With respect to polymorphism and divergence, the best model of those examined allowed α and θ to vary and for the strength of selective constraint and divergence to be constant across amplicons (AICc = 18,884.98). The estimate for the average value of α across amplicons in this model (average α = 0.32, 95% C.I.: 0.19–0.45) was similar to that for fixed α. This result, however, established that α varied across amplicons. To investigate this variation further, we utilized classes of amplicons based on whether or not they were associated with a phenotypic trait and fitted a model where α was allowed to vary between classes of amplicons. This model fitted the data almost as well as the best-fit model with variable α drawn from a β-distribution (AICc = 18,953.98, so ΔAICc = 69.00), which suggests that much of the variability of α across amplicons is driven by differences between these classes of amplicons. Estimates of α for each class in this model illustrate a twofold higher value for amplicons unassociated with a phenotype (α = 0.32) compared to amplicons associated with a phenotype (α = 0.15; Figure 3A). If we again divide amplicons from the class entitled “associated with a phenotypic trait” into two categories, whole plant phenotypic traits and cellular phenotypic traits, and fit a model with three classes of amplicons, the fit of the resulting model is again almost as good as that of the best-fit model (AICc = 18,960.11, so ΔAICc = 75.13). In this case, the estimate of α for amplicons unassociated with a phenotypic trait does not change, but the estimates for α for the two classes of amplicons associated with a phenotypic trait were significantly different (Figure 3B). The whole plant phenotypic traits were associated with amplicons with abundant signals of positive, directional selection (α = 0.50, 95% C.I.: 0.28–0.72), while the cellular phenotypic traits were associated with amplicons displaying marginal signals of positive, directional selection (α = 0.13, 95% C.I.: 0.02–0.23). In accordance with α varying between these classes, so did the level of selective constraint, with cellular phenotypic traits being associated to amplicons with much higher levels of selective constraint (f = 0.305, 95% C.I.: 0.256–0.354) than those associated with whole plant phenotypic traits (f = 0.106, 95% C.I.: 0.053–0.148).
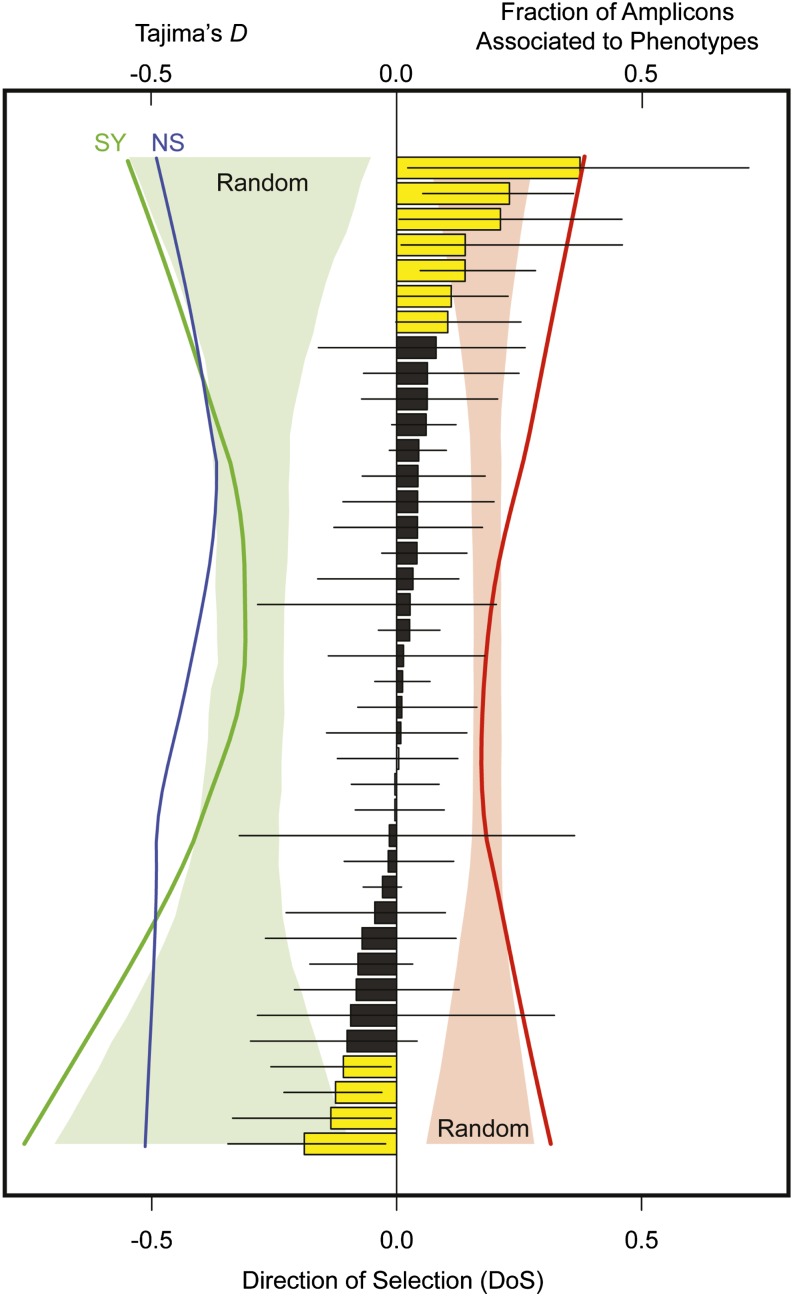
Similar trends were apparent when amplicons containing a SNP associated to at least one phenotypic trait were clustered into categories based on putative gene functions (Table S12, Figure 4). In general, the higher the fraction of amplicons associated to a phenotypic trait, the more extreme were deviations from neutrality based on the site-frequency spectrum (Figure 4, left) and polymorphism and divergence (Figure 4, right). The site-frequency spectrum was most skewed, as measured using the weighted average of Tajima’s D, for synonymous sites, with many of the functional categories, especially those at extreme values of the DoS statistic, being significantly more skewed than expected by chance. For polymorphism and divergence, 11 functional categories had 95% bootstrap confidence intervals for the DoS statistic excluding zero (7 with significantly positive values of DoS and 4 with significantly negative values of DoS), and those tended to be categories with more amplicons associated to at least one phenotypic trait and those with more skewed site-frequency spectra (see Table S12). These categories contained genes encoding proteins such as microtubules (+DoS), ferredoxins (+DoS), metal-binding proteins (+DoS), ligases (+DoS), phosphatases (+DoS), protein kinases (+DoS), glyoxyl oxidases (+DoS), zinc-finger proteins (−DoS), isomerases (−DoS), ATPases (−DoS), and vitamin-binding proteins (−DoS).
Figure 4.
Nonneutral evolution was apparent by functional categories of amplicons, so that as the fraction of amplicons associated to at least one phenotype increased within a functional category, so did patterns of divergence and polymorphism at nonsynonymous (NS) and synonymous (SY) sites as well as the skew in the site-frequency spectrum at synonymous sites. The bar plot gives the weighted average of the direction of selection (DoS) statistic for amplicons within the 40 functional categories. All amplicons within one category (methyltransferases) did not have outgroup data available, so that DoS was undefined. Error bars are 95% bootstrap confidence intervals (n = 10,000 replicates over amplicons). Yellow bars have 95% confidence intervals excluding zero, while black bars do not (see Table S11). The bottom x-axis is for the DoS statistic, while the top x-axis is split between Tajima’s D (left) and the fraction of amplicons associated with at least one phenotype (right). The red colored area to the right gives the 95% confidence interval for the null distribution, based on 10,000 permutations of amplicons among categories, for the fraction of amplicons associated to at least one phenotype across functional categories. Similarly, the green area on the left does the same for the weighted average value of Tajima’s D at SY sites. Lines give observed values (green, Tajima’s D at SY sites; blue, Tajima’s D at NS sites; red, fraction of amplicons associated to at least one phenotype). All lines were loess smoothed, including those comprising the null distributions. The null distribution for the weighted average of Tajima’s D at NS sites was similar to that for synonymous sites, so was omitted for clarity.
Discussion
Understanding the genetic basis of ecologically relevant traits is a primary focus of evolutionary genetics, with ramifications for the basic understanding of genetic diversity, including the origin and maintenance of this diversity (reviewed by Barton and Turelli 1989; Barton and Keightley 2002), as well as the conservation and management of this diversity in natural populations (González-Martínez et al. 2006b; Neale 2007; Neale and Kremer 2011). Here we have shown that the genetic variation correlated with a wide range of different phenotypic traits for loblolly pine appears to be nonneutral, but also that the magnitude of the skew from neutral expectations by this genetic variation depends upon the type of phenotypic trait under investigation.
Nucleotide diversity, nucleotide divergence, and linkage disequilibrium
Genome-wide patterns of nucleotide diversity were similar to those reported previously for loblolly pine (Brown et al. 2004; González-Martínez et al. 2006a; Ersöz et al. 2010), as well as for conifers in general (Savolainen and Pyhäjärvi 2007). Novel to this study, however, is the observation that indel-associated mutations or a combination of indel-associated mutations and variation in selective constraint likely drive associations between indels and nucleotide diversity (see Table S5; Tian et al. 2008; Hollister et al. 2010). Inspection of a large number of amplicons (n = 5773), moreover, allowed for the dissection of this pattern by types of amplicon. As noted by Ersöz et al. (2010) and as illustrated here (see Figure 2 and Figure S21), nucleotide diversity varied by amplicon category, with this being true for functional categories and for categories based on whether amplicons were associated with a phenotypic trait. With respect to the latter, this was observed for both noncoding and nonsynonymous sites (see Figure S21). For amplicons associated with a phenotypic trait, nucleotide diversity, as measured with θW, was significantly higher at nonsynonymous sites, while for noncoding sites it was significantly lower. This is indicative of an increase in the level of rare segregating variation at nonsynonymous sites for amplicons associated with a phenotypic trait. This pattern could reflect either an increase in segregating deleterious variation for these amplicons or the action of linked, positive selection where the targeted SNP was not typed (e.g., another nonsynonymous variant not seen in the sample).
Teasing apart segregating deleterious variation from linked, positive selection, however, depends, at least partly, on the patterns of linkage disequilibrium within conifer genomes. As shown repeatedly, linkage disequilibrium decays over physical distance quickly within coding regions (Neale and Savolainen 2004; but see Namroud et al. 2010; Pyhäjärvi et al. 2011), yet conifers appear to have extremely low recombination rates (Jaramillo-Correa et al. 2010) and effective population sizes as estimated from estimates of Θ are moderate (Savolainen and Pyhäjärvi 2007). The same pattern was observed here, as linkage disequilibrium decayed quite often within 500 bp to half its initial value. This pattern, however, was apparent only when including singletons in the analysis and removal of these types of polymorphisms resulted in fairly strong linkage disequilibrium being detected. Inspection of values less sensitive to sample size (e.g., D′, data not shown), moreover, showed little decay with physical distance, so that linkage disequilibrium may be more prominent in some regions than thought previously within conifer genomes (e.g., Moritsuka et al. 2012). The observation that average levels of linkage disequilibrium varied across sets of amplicons defined as being associated with certain phenotypic traits is consistent with this conclusion (File S1), as is the observation that autocorrelation in values of nucleotide diversity and divergence occurred at the centimorgan scale (Figure S9; autocorrelation >0 extended upward of 3 cM for each measure, results not shown). Further studies on a genome-wide scale with larger samples, however, are needed to resolve the issue fully with regard to patterns of linkage disequilibrium and recombination (see Mackay et al. 2012).
Genome-wide levels of nucleotide divergence were also as expected given recent estimates of the divergence times among pine species (Gernandt et al. 2008; Parks et al. 2009). For example, the per site divergence of loblolly relative to radiata pine was 0.72%, and although severalfold greater than nucleotide diversity, was relatively low. This was also reflected in the low number of fixed differences observed between these two species, which is likely a function of their recent divergence time (∼ ≤20 MY). When broken down by categories of sites, the largest divergence was seen at synonymous sites and the lowest was observed at nonsynonymous sites, which supports the ubiquitous nature of purifying selection (average Ka/Ks << 1, Stephan 2010; Charlesworth 2013). With regard to categories of amplicons, however, several categories exhibited average Ka/Ks ratios that were severalfold larger than the genome-wide average (e.g., disease-associated amplicons). Such ratios have been used as evidence of selection previously in species of Pinus (e.g., Palmé et al. 2008) and are also consistent with previous studies that documented strong signals of positive selection in genes related to disease resistance for loblolly pine (Ersöz et al. 2010). When sugar pine was used as an outgroup, however, these quantitative patterns largely disappeared. This is likely a function of the decreased number of amplicons available for analysis (3484 vs. 950), as well as the bias imposed by use of PCR primers from diverged taxa (Kern 2009; Eckert et al. 2013).
Evolutionary genetics of gene regions underlying phenotypic traits
Genome-wide patterns of diversity and divergence were used to infer that ∼29% of new nonsynonymous substitutions on average were fixed due to the action of positive directional selection. This is the first report of this quantity on a genome-wide scale for a conifer (but see Eckert et al. 2013), which will add to the emerging literature of adaptive amino acid evolution estimates for plant species (Gossmann et al. 2010; Slotte et al. 2010; Strasburg et al. 2011). In addition, a suite of 31 outliers with respect to summaries of the site-frequency spectrum was also identified after accounting for a simple demographic null model (see Table S10). As such, this represents one of the first comprehensive scans of a conifer genome for deviations from neutrality (see also Pavy et al. 2013), with the conclusion that signals of positive directional selection are apparent and moderately abundant.
The central question addressed here, however, is how amplicons identified using population genomic scans relate to those identified using linkage disequilibrium mapping. The genetic architecture of phenotypic traits amenable to linkage disequilibrium mapping is likely composed of mostly additive genetic variance (Hill et al. 2008; but see Hansen 2013). As such, marginal signals of selection for the amplicons comprising the underlying genetic architecture of these phenotypic traits are expected to be minimal (Hermisson and Pennings 2005; Chevin and Hospital 2008; Pavlidis et al. 2012). This was supported by the results presented here, as the individual amplicons themselves did not emerge from scans of summary statistics such as Tajima’s D or Fay and Wu’s H. The joint effects of multiple amplicons grouped together because of their associations with phenotypic traits, however, do emerge as different from those of amplicons not associated with phenotypic traits. This implies that it is the multilocus attributes that are important when considering the links between phenotypic traits, genetic associations, and scans for positive selection (Bürger and Gimelfarb 1999; Bürger 2000; Pritchard et al. 2010). This pattern emerged on several levels of analysis: summaries of nucleotide diversity and divergence, average summary statistics based on the site-frequency spectrum, and results from a MacDonald–Kreitman-type analysis. Moreover, as the fraction of amplicons associated with a phenotypic trait increased within functional categories, so did signals deviating from neutrality (Figure 4). In general, the differences were consistent with deviations from neutrality supporting the presence of positive, directional selection, but also in many instances that of purifying selection.
While this lends credence to the methods employed previously for linkage disequilibrium mapping, as signals in these studies appear to be driven by biological indicators, it does not explain fully the type, magnitude, and dynamics of natural selection that could be driving the results. Specifically, we have not addressed the role of population structure, both neutral patterns due to phylogeographic history and adaptive divergence due to local selection pressures, as influencing the observed patterns. As mentioned previously, forest trees, and specifically loblolly pine, display clear patterns of local adaptation (Neale and Kremer 2011). These patterns likely drive the environmental associations detected previously (e.g., Eckert et al. 2010a,b), as well as many of the genotype–phenotype associations (Quesada et al. 2010; Cumbie et al. 2011; Palle et al. 2011, 2013; Eckert et al. 2012). This may thus explain the disconnect between summaries of the site-frequency spectrum for individual amplicons and their frequency of being associated with a phenotype. In this case, our sample design does not likely have the power to detect the effects of local selection pressures (Städler et al. 2009), as this power depends on sampling intensity and pattern with respect to the largely unknown important selective gradients (see discussion in Sork et al. 2013).
Population structure, however, is unlikely to explain the observed patterns for α. Depending on the method used to estimate α, population structure would need to be pronounced, the sampling relatively even across diverged populations, and magnitudes of population structure would need to differ between categories of amplicons due to demographic history (see Eckert et al. 2013). Further work based on population-level sampling, however, would be needed to quantify any effects of population structure on our inferences.
It is clear from the data and analysis presented here that long-term signals of positive selection were apparent for amplicons associated with phenotypic traits, while those for recent selective sweeps (in terms of 4Ne generations) were only marginally different from genome-wide estimates. This implies that the amplicons underlying these phenotypic traits have experienced fixation of adaptive alleles over the divergence time separating loblolly and radiata pines. As such, segregating variants within these amplicons are subject to this historical context, so that an interesting question arises with regard to whether these variants, which are correlated with phenotypic traits, represent the segregation of slightly deleterious variants (i.e., new deleterious mutations deviating from the adaptive fixed allele) or indeed reflect positively selected alleles (i.e., some form of recurrent selection). For example, the putatively synthetic associations documented by Eckert et al. (2012) for the loblolly pine primary metabolome could reflect linked selection upon rare deleterious mutations, but also could reflect complex patterns of recent positive selection. Both processes would affect standing patterns of linkage disequilibrium, so that answering this question without a truly genomic resource is difficult, especially since the landscape of linkage disequilibrium, despite the data presented here, remains largely unknown for this species (see Goldstein and Weale 2001; but see also Moritsuka et al. 2012). One tempting glimpse into the answer of this question, however, is found by comparing estimates of long-term selection, as measured by α, across different phenotypic trait categories.
As the genome-wide estimate of α was significantly greater than zero, it is not surprising that amplicons associated with phenotypic traits were estimated to have statistically significant signals of long-term positive selection. This similarity also carried over to the distribution of fitness effects for newly arising nonsynonymous mutations. Using method 2 of Eyre-Walker and Keightley (2009), as implemented in the DoFE software ver. 3 (see http://www.lifesci.sussex.ac.uk/home/Adam_Eyre-Walker/Website/Software.html and Eckert et al. 2013 for a description of how DoFE was implemented), this distribution was estimated to be similar regardless of whether the data were from amplicons associated with a phenotype or not, with most new nonsynonymous variants being highly (Nes > 100, ∼65% for both associated and unassociated amplicons) or slightly (Nes < 1, ∼20% for both associated and unassociated amplicons) deleterious. One of the most striking results, however, is that phenotypic trait class was differentiated with respect to estimates of α relative to the genome-wide average. For example, whole plant phenotypes (including the environmental associations) were almost twofold greater than the genome-wide average, while cellular phenotypes were almost twofold less than the genome-wide average. Differences of this magnitude, moreover, were unable to be replicated by randomly permuting the full data set among category labels (Pperm < 0.001) so that it is unlikely these patterns are statistical artifacts. This implies that the strength, type, and dynamics of natural selection for amplicons within these classes differ (see Casto and Feldman 2011 for a similar case for humans), as was shown, for example, by the larger estimate of selective constraint for amplicons associated with cellular phenotypes.
The implication would then be that genetic associations discovered for cellular phenotypes represent the segregation of slightly deleterious mutations, whereas this would not likely be the case for whole plant phenotypes. This is consistent with the lower estimates of α, the significant enrichment for rare alleles in genetic associations, and the increased estimates of selective constraint for amplicons associated with cellular phenotypes (Park et al. 2010). In addition, an analysis using method 2 of Eyre-Walker and Keightley (2009) shows that the distribution of newly arising nonsynonymous mutations is skewed toward an increase of slightly deleterious mutations (i.e., Nes in the range 0–1) for amplicons associated with cellular phenotypes (i.e., this proportion was 0.32 with a 95% confidence interval of 0.27–0.37) compared to those associated with whole plant phenotypes (this proportion was 0.16 with a 95% confidence interval of 0.09–0.23). With respect to α, however, the lower estimate for amplicons may instead just reflect an increased abundance of segregating slightly deleterious variants that is independent from the discovered genetic associations (i.e., these are not driving the discovery of the genetic associations), so that estimates for α are downwardly biased. The segregation of slightly deleterious mutations will produce this effect (Charlesworth and Eyre-Walker 2008). Successive removal of low-frequency variants (i.e., singletons) for just the amplicons associated with cellular phenotypes, however, did not increase the estimate for α beyond 0.15 (95% C.I.: 0.08–0.25). In addition, estimates of α using method 2 of Eyre-Walker and Keightley (2009), which models the segregation of deleterious variants explicitly, were similar to those reported here (i.e., changes of <20% of the point estimates shown in Figure 3 with all estimates of α still significantly >0), so that it is unlikely that segregating deleterious variation is solely driving the observed patterns. Cellular phenotypes thus appear to be different with regard to their genetic architecture and patterns of selection compared with whole plant phenotypes.
Limitations and conclusions
The analysis presented here is limited with respect to sample design and power. The disconnect between results from population genomic scans and those from linkage disequilibrium mapping with regard to amplicons identified by each approach may thus be an artifact. For example, only 18 trees were sampled for the population genomic scan utilized here. While much of the underlying information about a sample genealogy can be obtained from a relatively small sample size, sample size does have a direct effect on estimates of the summary statistics used to test neutrality and on inferences of linkage disequilibrium (Nielsen 2005). As such, estimates were stratified by sample size and weighted averages were used (Begun et al. 2007). Caution is thus needed when interpreting the results presented here, especially since sample coverage affected most statistics (see Table S3). This effect, moreover, is likely related to standing levels of population structure, our conservative sequence analysis pipeline, and inclusion of small coverage classes (i.e., n = 2–5). We have also used a recently diverged outgroup, and only a single sequence from this outgroup for analysis, that may in fact not be reciprocally monophyletic (Syring et al. 2007). As such, estimates of divergence may be biased and thus by extension so would estimates of long-term positive selection. With that said, however, the genome-wide estimate of α using sugar pine as the outgroup remained significantly positive (α = 0.10, 95% C.I.: 0.01–0.20), with the difference likely attributed to the increase of conserved amplicons in this set (Kern 2009; Eckert et al. 2013). A more thorough analysis, however, was not performed, as only 950 amplicons were available, and many of the amplicons associated with phenotypes were not in this set. Finally, the models considered during the estimation of α did not explicitly account for the segregation of slightly deleterious mutations. The same quantitative patterns, however, emerge as those presented in Figure 3 as rare mutations are excluded from the data set (data not shown for singletons and doubletons removed) and when using a method that specifically models the segregation of deleterious mutations. In these cases, estimates of α change by <15–20%.
The continued application of linkage disequilibrium mapping will help to uncover the identity of genes putatively composing the genetic architecture of complex traits for populations of forest trees. As shown here, the amplicons identified by these studies appear to be nonneutral with respect to patterns of nucleotide diversity and divergence, yet further work will be needed to make general statements across groups of taxa. This nonneutrality, moreover, appears to be detectable most clearly over long periods of time (e.g., since the divergence with the outgroup). As noted by Hahn (2008), the most interesting steps forward, once truly genome-wide data are available, will not be to reject neutrality, but to determine why this null model was rejected.
Supplementary Material
Acknowledgments
The authors thank the staff at Agencourt Biosciences (now Beckman Coulter Genomics) for help in sequencing and the initial bioinformatics. Comments from the associate editor and two anonymous reviewers greatly improved this manuscript. Funding for this project was made available from the National Science Foundation (NSF) Integrative Organismal Systems (IOS) Plant Genome Research Program (PGRP) (NSF-IOS-PGRP: 0501763).
Footnotes
Communicating editor: S. I. Wright
Literature Cited
- Ashburner M., Ball C. A., Blake J. A., Botstein D., Butler H., et al. , 2000. Gene ontology: tool for the unification of biology. The Gene Ontology Consortium. Nat. Genet. 25: 25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett R. D. H., Hoekstra H. E., 2011. Molecular spandrels: tests of adaptation at the genetic level. Nat. Rev. Genet. 12: 767–780. [DOI] [PubMed] [Google Scholar]
- Barton N. H., Keightley P. D., 2002. Understanding quantitative genetic variation. Nat. Rev. Genet. 3: 11–21. [DOI] [PubMed] [Google Scholar]
- Barton N. H., Turelli M., 1989. Evolutionary quantitative genetics: How little do we know? Annu. Rev. Genet. 23: 337–370. [DOI] [PubMed] [Google Scholar]
- Begun D. J., Holloway A. K., Stevens K., Hillier L. W., Poh Y.-P., et al. , 2007. Population genomics: Whole-genome analysis of polymorphism and divergence in Drosophila simulans. PLoS Biol. 5: e310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown G. R., Gill G. P., Kuntz R. J., Langley C. H., Neale D. B., 2004. Nucleotide diversity and linkage disequilibrium in loblolly pine. Proc. Natl. Acad. Sci. USA 101: 15255–15260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bürger R., 2000. The Mathematical Theory of Selection, Recombination, and Mutation. John Wiley & Sons, West Sussex, UK. [Google Scholar]
- Bürger R., Gimelfarb A., 1999. Genetic variation maintained in multilocus models of additive quantitative traits under stabilizing selection. Genetics 152: 807–820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burnham K. P., Anderson D. R., 2004. Model Selection and Multimodal Inference: A Practical Information-Theoretic Approach, Ed. 2 Springer-Verlag, New York. [Google Scholar]
- Cartwright D. A., Troggio M., Velasco R., Gutin A., 2007. Genetic mapping in the presence of genotyping errors. Genetics 176: 2521–2527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casto A. M., Feldman M. W., 2011. Genome-wide association study SNPs in the human genome diversity project populations: Does selection affect unlinked SNPs with shared trait associations? PLoS Genet. 7: e1001266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan E. K. F., Rowe H. C., Kliebenstein D. J., 2010a Understanding the evolution of defense metabolites in Arabidopsis thaliana using genome-wide association mapping. Genetics 185: 991–1007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan E. K. F., Rowe H. C., Hansen B. G., Kliebenstein D. J., 2010b The complex genetic architecture of the metabolome. PLoS Genet. 6: e1001198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B., 2013. Background selection 20 years on – The Wilhelmine E. Key 2012 Invitational Lecture. J. Hered. 104: 161–171. [DOI] [PubMed] [Google Scholar]
- Charlesworth J., Eyre-Walker A., 2008. The McDonald-Kreitman test and slightly deleterious mutations. Mol. Biol. Evol. 25: 1007–1015. [DOI] [PubMed] [Google Scholar]
- Chevin L.-M., Hospital F., 2008. Selective sweep at a quantitative trait locus in the presence of background genetic variation. Genetics 180: 1645–1660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comeron J., 1995. A method for estimating the numbers of synonymous and nonsynonymous substitutions per site. J. Mol. Evol. 41: 1152–1159. [DOI] [PubMed] [Google Scholar]
- Cumbie W. P., Eckert A. J., Wegrzyn J. L., Whetten R., Neale D. B., et al. , 2011. Association genetics of carbon isotope discrimination, height, and foliar nitrogen in a natural population of Pinus taeda L. Heredity 107: 105–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devey M. E., Sewell M. M., Uren T. L., Neale D. B., 1999. Comparative mapping in loblolly and radiata pine using RFLP and microsatellite markers. Theor. Appl. Genet. 99: 656–662. [DOI] [PubMed] [Google Scholar]
- Eckert A. J., Bower A. D., Pande B., Jermstad K. D., Krutovsky K. V., et al. , 2009a Association genetics of coastal Douglas fir (Pseudotsuga menziesii var. menziesii, Pinaceae). I. Cold-hardiness related traits. Genetics 182: 1289–1302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckert A. J., Pande B., Ersöz E. S., Wright M. H., Rashbrook V. K., et al. , 2009b High-throughput genotyping and mapping of single nucleotide polymorphisms in loblolly pine (Pinus taeda L.). Tree Genet. Genomes 5: 225–234. [Google Scholar]
- Eckert A. J., van Heerwaarden J., Wegrzyn J. L., Nelson C. D., Ross-Ibarra J., et al. , 2010a Patterns of population structure and environmental associations to aridity across the range of loblolly pine (Pinus taeda L., Pinaceae). Genetics 185: 969–982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckert A. J., Bower A. D., González-Martínez S. C., Wegrzyn J. L., Coop G., et al. , 2010b Back to nature: ecological genomics of loblolly pine (Pinus taeda, Pinaceae). Mol. Ecol. 19: 3789–3805. [DOI] [PubMed] [Google Scholar]
- Eckert A. J., Liechty J. D., Tearse B. R., Pande B., Neale D. B., 2010c DnaSAM: software to perform neutrality testing for large datasets with complex null models. Mol. Ecol. Res. 10: 542–545. [DOI] [PubMed] [Google Scholar]
- Eckert A. J., Wegrzyn J. L., Cumbie W. P., Goldfarb B., Huber D. A., et al. , 2012. Association genetics of the loblolly pine (Pinus taeda, Pinaceae) metabolome. New Phytol. 193: 890–902. [DOI] [PubMed] [Google Scholar]
- Eckert A. J., Bower A. D., Jermstad K. D., Wegrzyn J. L., Knauss B. J., et al. , 2013. Multilocus analyses reveal little evidence for lineage wide adaptive evolution within major clades of soft pines (Pinus subgenus Strobus). Mol. Ecol. DOI: 10.1111/mec.12514. [DOI] [PubMed] [Google Scholar]
- Efron B., 1985. Bootstrap confidence intervals for a class of parametric problems. Biometrika 72: 45–58. [Google Scholar]
- Endler J. A., 1986. Natural Selection In the Wild. Princeton University Press, Princeton, NJ. [Google Scholar]
- Ersöz E. S., Wright M. H., González-Martínez S. C., Langley C. H., Neale D. B., 2010. Evolution of disease response genes in loblolly pine: insights from candidate genes. PLoS ONE 5: e14234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewing B., Green P., 1998. Base-calling of automated sequencer traces using PHRED. II. Error probabilities. Genome Res. 8: 186–194. [PubMed] [Google Scholar]
- Ewing B., Hillier L., Wendl M. C., Green P., 1998. Base-calling of automated sequencer traces using PHRED. I. Accuracy assessment. Genome Res. 8: 175–185. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A., 2010. Genetic architecture of a complex trait and its implications for fitness and genome-wide association studies. Proc. Natl. Acad. Sci. USA 107: 1752–1756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eyre-Walker A., Keightley P. D., 2009. Estimating the rate of adaptive molecular evolution in the presence of slightly deleterious mutations and population size change. Mol. Biol. Evol. 26: 2097–2108. [DOI] [PubMed] [Google Scholar]
- Fay J. C., Wu C.-I., 2000. Hitchhiking under positive Darwinian selection. Genetics 155: 1405–1413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Florea L., Hartzell G., Zhang Z., Rubin G. M., Miller W., 1998. A computer program for aligning a cDNA sequence with a genomic DNA sequence. Genome Res. 8: 967–974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gernandt D. S., Magallon S., Lopez G. G., Flores O. Z., Willyard A., et al. , 2008. Use of simultaneous analyses to guide fossil-based calibrations of Pinaceae phylogeny. Int. J. Plant Sci. 169: 1086–1099. [Google Scholar]
- Goldstein D. B., 2011. The importance of synthetic associations will only be resolved empirically. PLoS Biol. 9: e1001008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldstein D. B., Weale M. E., 2001. Population genomics: linkage disequilibrium holds the key. Curr. Biol. 11: R576–R579. [DOI] [PubMed] [Google Scholar]
- González-Martínez S. C., Ersöz E., Brown G. R., Wheeler N. C., Neale D. B., 2006a DNA sequence variation and selection of tag SNPs at candidate genes for drought-stress response in Pinus taeda. Genetics 172: 1915–1926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- González-Martínez S. C., Krutovsky K. V., Neale D. B., 2006b Forest tree population genomics and adaptive evolution. New Phytol. 170: 227–238. [DOI] [PubMed] [Google Scholar]
- González-Martínez, S. C., D. Huber, E. Ersoz, J. M. Davis, and D. B. Neale, 2008 Association genetics in Pinus taeda L. II. Water Use Efficiency. Heredity 101: 19–26. [DOI] [PubMed] [Google Scholar]
- González-Martínez, S. C., S. Dillon, P. Garnier-Géré, K. Krutovsky, R. Alía et al., 2011 Patterns of nucleotide diversity and association mapping, pp. 239–275 in Genetics, Genomics, and Breeding of Conifers (Series on Genomics of Industrial Crops), edited by C. Plomion and J. Bousquet. Science Publishers, Enfield, New Hampshire. [Google Scholar]
- Gordon D., Abajian C., Green P., 1998. Consed: a graphical tool for sequence finishing. Genome Res. 8: 195–202. [DOI] [PubMed] [Google Scholar]
- Gossmann T. I., Song B.-H., Windsor A. J., Mitchell-Olds T., Dixon C. J., et al. , 2010. Genome wide analyses reveal little evidence for adaptive evolution in many plant species. Mol. Biol. Evol. 27: 1822–1832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grattapaglia D., Sederoff R., 1994. Genetic linkage maps of Eucalyptus grandis and E. urophylla using a pseudo-testcross mapping strategy and RAPD markers. Genetics 137: 1121–1137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly J., 1997. A test of neutrality based on interlocus associations. Genetics 146: 1197–1206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kern A. D., 2009. Correcting the site frequency spectrum for divergence-based ascertainment. PLoS ONE 4: e5152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hahn M. W., 2008. Toward a selection theory of molecular evolution. Evolution 62: 255–265. [DOI] [PubMed] [Google Scholar]
- Hansen T. F., 2013. Why epistasis is important for selection and adaptation. Evolution DOI: 10.1111/evo.12214. [DOI] [PubMed] [Google Scholar]
- Hermisson J., Pennings P. S., 2005. Soft sweeps: molecular population genetics of adaptation from standing genetic variation. Genetics 169: 2335–2352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill W. G., Goddard M. E., Visscher P. M., 2008. Data and theory point to mainly additive genetic variance for complex traits. PLoS Genet. 4: e1000008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hindorff L. A., Sethupathy P., Junkins H. A., Ramos E. M., Mehta J. P., et al. , 2009. Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc. Natl. Acad. Sci. USA 106: 9362–9367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollister J. D., Ross-Ibarra J., Gaut B. S., 2010. Indel-associated mutation rate varies with mating system in flowering plants. Mol. Biol. Evol. 27: 409–416. [DOI] [PubMed] [Google Scholar]
- Hudson R. R., 1990. Gene genealogies and the coalescent process. Oxf. Surv. Evol. Biol. 7: 1–44. [Google Scholar]
- Hufford M. B., Xun X., van Heerwaarden J., Pyhäjärvi T., Chia J.-M., et al. , 2012. Comparative population genomics of maize domestication and improvement. Nat. Genet. 44: 808–811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingvarsson P. K., Street N. R., 2011. Association genetics of complex traits in plants. New Phytol. 189: 909–922. [DOI] [PubMed] [Google Scholar]
- Jaramillo-Correa J. P., Verdu M., Gonzalez-Martinez S. C., 2010. The contribution of recombination to heterozygosity differs among plant evolutionary lineages and life-forms. BMC Evol. Biol. 10: 22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lander E. S., Schork N. J., 1994. Genetic dissection of complex traits. Science 265: 2037–2048. [DOI] [PubMed] [Google Scholar]
- Lebude A. V., Goldfarb B., Blazich F. A., Frampton J., Wise F. C., 2004. Mist, substrate water potential, and cutting water potential influence rooting of stem cuttings of loblolly pine. Tree Physiol. 24: 823–831. [DOI] [PubMed] [Google Scholar]
- Lynch M., Walsh B., 1998. Genetics and Analysis of Quantitative Traits. Sinauer Associates, Sunderland, MA. [Google Scholar]
- Mackay J., Dean J. F., Plomion C., Peterson D. G., Canovas F. M., et al. , 2012. Towards decoding the conifer giga-genome. Plant Mol. Biol. 80: 555–569. [DOI] [PubMed] [Google Scholar]
- Marth G. T., Korf I., Yandell M. D., Yeh R. T., Gu Z., et al. , 1999. A general approach to single nucleotide polymorphism discovery. Nat. Genet. 23: 452–456. [DOI] [PubMed] [Google Scholar]
- Maynard Smith J., Haigh J., 1974. The hitch-hiking effect of a favorable gene. Genet. Res. 23: 23–35. [PubMed] [Google Scholar]
- Mitchell-Olds T., Feder M., Wray G., 2008. Evolutionary and ecological functional genomics. Heredity 100: 101–102. [DOI] [PubMed] [Google Scholar]
- Moritsuka E., Hisataka Y., Tamura M., Uchiyama K., Watanabe A., et al. , 2012. Extended linkage disequilibrium in noncoding regions in a conifer, Cryptomeria japonica. Genetics 190: 1145–1148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Namroud M.-C., Guillet-Claude C., Mackay J., Isabel N., Bousquet J., 2010. Molecular evolution of regulatory genes in spruces from different species and continents: heterogeneous patterns of linkage disequilibrium and selected but correlated recent demographic changes. J. Mol. Evol. 70: 371–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neale D. B., 2007. Genomics to tree breeding and forest health. Curr. Opin. Genet. Dev. 17: 539–544. [DOI] [PubMed] [Google Scholar]
- Neale D. B., Ingvarsson P. K., 2008. Population, quantitative and comparative genomics of adaptation in forest trees. Curr. Opin. Plant Biol. 11: 149–155. [DOI] [PubMed] [Google Scholar]
- Neale D. B., Kremer A., 2011. Forest tree genomics: growing resources and applications. Nat. Rev. Genet. 12: 111–122. [DOI] [PubMed] [Google Scholar]
- Neale D. B., Savolainen O., 2004. Association genetics of complex traits in conifers. Trends Plant Sci. 9: 325–330. [DOI] [PubMed] [Google Scholar]
- Nei M., 1987. Molecular Evolutionary Genetics. Columbia University Press, New York. [Google Scholar]
- Nickerson D. A., Tobe V. O., Taylor S. L., 1997. PolyPHRED: automating the detection and genotyping of single nucleotide substitutions using fluorescence-based re-sequencing. Nucleic Acids Res. 25: 2745–2751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R., 2005. Molecular signatures of natural selection. Annu. Rev. Genet. 39: 197–218. [DOI] [PubMed] [Google Scholar]
- Obbard D. J., Welch J., Kim K. W., Jiggins F. M., 2009. Quantifying adaptive evolution in the Drosophila immune system. PLoS Genet. 5: e1000698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orozco L. D., Cokus S. J., Ghazalpour A., Ingram-Drake L., Wang S., et al. , 2009. Copy number variation influences gene expression and metabolic traits in mice. Hum. Mol. Genet. 18: 4118–4129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr H. A., 1998. The population genetics of adaptation: the distribution of factors fixed during adaptive evolution. Evolution 52: 935–949. [DOI] [PubMed] [Google Scholar]
- Palle S. R., Seeve C. M., Eckert A. J., Cumbie W. P., Goldfarb B., et al. , 2011. Natural variation in expression of genes involved in xylem development in loblolly pine (Pinus taeda L.). Tree Genet. Genomes 7: 193–206. [Google Scholar]
- Palle S. R., Seeve C. M., Eckert A. J., Wegrzyn J. L., Neale D. B., et al. , 2013. Association of loblolly pine xylem development gene expression with single nucleotide polymorphisms. Tree Physiol. 33: 763–774. [DOI] [PubMed] [Google Scholar]
- Palmé A. E., Wright M., Savolainen O., 2008. Patterns of divergence among conifer ESTs and polymorphism in Pinus sylvestris identify putative selective sweeps. Mol. Biol. Evol. 25: 2567–2577. [DOI] [PubMed] [Google Scholar]
- Park J.-H., Gail M. H., Weinberg C. R., Carroll R. J., Chung C. C., et al. , 2010. Distribution of allele frequencies and effect sizes and their interrelationships for common genetic susceptibility variants. Proc. Natl. Acad. Sci. USA 108: 18026–18031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parks M., Cronn R., Liston A., 2009. Increasing phylogenetic resolution at low taxonomic levels using massively parallel sequencing of chloroplast genomes. BMC Biol. 7: 84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlidis P., Metzler D., Stephan W., 2012. Selective sweeps in multilocus models of quantitative traits. Genetics 192: 225–239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavy N., Deschenes A., Blais S., Lavigne P., Beaulieu J., et al. , 2013. The landscape of nucleotide polymorphism among 13,500 genes of the conifer Picea glauca, relationships with functions and comparison with Medicago trunculata. Genome Biol. Evol. 5: 1910–1925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pichot C., El Maataoui M., 1997. Flow cytometric evidence for multiple ploidy levels in the endosperm of some gymnosperm species. Theor. Appl. Genet. 94: 865–870. [Google Scholar]
- Pollinger J. P., Bustamante C. D., Fledel-Alon A., Schmutz S., Gray M. M., et al. , 2005. Selective sweep mapping of genes with large phenotypic effects. Genome Res. 15: 1809–1819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard J. K., Pickrell J. K., Coop G., 2010. The genetics of human adaptation: hard sweeps, soft sweeps, and polygenic adaptation. Curr. Biol. 20: R208–R215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pyhäjärvi T., Kujala S. T., Savolainen O., 2011. Revisiting protein heterozygosity in plants – nucleotide diversity in allozyme coding genes of conifer Pinus sylvestris. Tree Genet. Genomes 7: 385–397. [Google Scholar]
- Quesada T., Gopal V., Cumbie W. P., Eckert A. J., Wegrzyn J. L., et al. , 2010. Association mapping of quantitative disease resistance in a natural population of loblolly pine (Pinus taeda L.). Genetics 186: 677–686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team, 2010 R: A Language and Environment for Statistical Computing R Foundation for Statistical Computing, Vienna. Available at: http://www.R-project.org.
- Remington D. L., Thornsberry J. M., Matsuoka Y., Wilson L. M., Whitt S. R., et al. , 2001. Structure of linkage disequilibrium and phenotypic associations in the maize genome. Proc. Natl. Acad. Sci. USA 98: 11479–11484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savolainen O., Pyhäjärvi T., 2007. Genomic diversity in forest trees. Curr. Opin. Plant Biol. 10: 162–167. [DOI] [PubMed] [Google Scholar]
- Slotte T., Foxe J. P., Hazzouri K. M., Wright S. I., 2010. Genome-wide evidence for efficient positive and purifying selection in Capsella grandiflora, a plant species with a large effective population size. Mol. Biol. Evol. 27: 1813–1821. [DOI] [PubMed] [Google Scholar]
- Sork V. L., Aitken S. N., Dyer R. J., Eckert A. J., Legendre P., et al. , 2013. Putting the landscape into the genomics of forest trees: approaches for understanding local adaptation and population responses to a changing climate. Tree Genet. Genomes 9: 901–911. [Google Scholar]
- Städler T., Haubold B., Merino C., Stephen W., Pfaffelhuber P., 2009. The impact of sampling schemes on the site-frequency spectrum in nonequilibrium subdivided populations. Genetics 182: 205–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephan W., 2010. Genetic hitchhiking vs. background selection: the controversy and its implications. Philos. Trans. R. Soc. B 365: 1245–1253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stinchcombe J. R., Hoekstra H. E., 2008. Combining population genomics and quantitative genetics: finding the genes underlying ecologically important traits. Heredity 100: 158–170. [DOI] [PubMed] [Google Scholar]
- Stoletzki N., Eyre-Walker A., 2011. Estimation of the neutrality index. Mol. Biol. Evol. 28: 63–70. [DOI] [PubMed] [Google Scholar]
- Storey J. D., Tibshirani R., 2003. Statistical significance for genome-wide studies. Proc. Natl. Acad. Sci. USA 100: 9440–9445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strasburg J. L., Kane N. C., Raduski A. R., Bonin A., Michelmore R., et al. , 2011. Effective population size is positively correlated with levels of adaptive divergence among annual sunflowers. Mol. Biol. Evol. 28: 1569–1580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Syring J., Farrell K., Businsky R., Cronn R., Liston A., 2007. Widespread genealogical nonmonophyly in species of Pinus subgenus Strobus. Syst. Biol. 56: 163–181. [DOI] [PubMed] [Google Scholar]
- Tajima F., 1983. Evolutionary relationship of DNA sequences in finite populations. Genetics 105: 437–460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tajima F., 1989. Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 123: 585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton K., 2003. libsequence: a C++ class library for evolutionary genetic analysis. Bioinformatics 19: 2325–2327. [DOI] [PubMed] [Google Scholar]
- Tian D., Wang Q., Zhang P., Araki H., Yang S., et al. , 2008. Single-nucleotide mutation rate increases close to insertions/deletions in eukaryotes. Nature 455: 105–108. [DOI] [PubMed] [Google Scholar]
- Watterson G. A., 1975. On the number of segregating sites in genetic models without recombination. Theor. Popul. Biol. 7: 256–276. [DOI] [PubMed] [Google Scholar]
- Wegrzyn J. L., Lee J. M., Liechty J. D., Neale D. B., 2009. PineSAP - Pine alignment and SNP Identification Pipeline. Bioinformatics 25: 2609–2610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welch J. J., 2006. Estimating the genomewide rate of adaptive protein evolution in Drosophila. Genetics 173: 821–837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White T. L., Adams W. T., Neale D. B., 2007. Forest Genetics. CABI Publishing, Cambridge, MA. [Google Scholar]
- Zeng K., Shi S., Wu C.-I., 2007. Compound tests for the detection of hitchhiking under positive selection. Mol. Biol. Evol. 24: 1898–1908. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.