Regulatory Potential Scores From Genome-Wide Three-Way Alignments of Human, Mouse, and Rat

Abstract

We generalize the computation of the Regulatory Potential (RP) score from two-way alignments of human and mouse to three-way alignments of human, mouse, and rat. This requires overcoming technical challenges that arise because the complexity of the models underlying the score increases exponentially with the number of species. Despite the close evolutionary proximity of rat to mouse, we find that adding the rat sequence increases our ability to predict genomic sites that regulate gene transcription. A variant of the RP scoring scheme that accounts for local variation in neutral mutational patterns further improves our predictions.

Several computational methods have been developed for predicting, within a given genomic sequence, the location of signals that regulate gene expression. A search for clustered consensus-binding motifs can guide experimental studies when gene regulation is accomplished by cooperative binding of characterized transcription factors (e.g., Berman et al. 2002; Hannenhalli and Levy 2002). For uncharacterized regulatory mechanisms that are conserved among two or more species, conserved noncoding segments are strong candidates for experimental verification (e.g., Hardison et al. 1997a; Loots et al. 2000). On the other hand, sequence conservation by itself may not differentiate between regulatory segments and other functional regions, such as non-translated RNA genes.

We recently proposed a computational approach for identifying regulatory regions within two-way DNA alignments of human and mouse (Elnitski et al. 2003), which uses statistical models based on frequencies of short alignment patterns in regulatory regions and neutral DNA. The resulting regulatory potential (RP) score is effective in locating previously identified erythroid regulatory elements. It has been used in combination with conserved transcription-factor binding sites to predict candidate regulatory regions, which frequently show effects on gene expression when tested experimentally (Hardison et al. 2003b).

Theoretical analyses indicate that simultaneous comparison of three sequences, rather than two, increases the statistical power to distinguish significant matches from regions that match purely by chance (Altschul and Lipman 1990). More generally, multispecies comparisons are expected to add information, as they frequently reveal phylogenetic footprints that are not discernable with only two sequences (e.g., Gumucio et al. 1992; Hardison et al. 1997b). However, this provides no assurance that adding a particular species will improve performance of a particular method that leverages sequence conservation for a particular goal.

In this spirit, we have extended our RP score to human-mouse-rat alignments to verify whether the newly available rat genome sequence can improve prediction accuracy for regulatory signals in the human genome sequence, notwithstanding the close physiological and phylogenetic similarity between rat and mouse. Beyond the specific scope of this analysis, the RP approach can be applied to discriminate between any two sets of alignments, and the extension we present here can be adapted to any multispecies comparison, provided that sequenced genomes and adequate training data exist.

Extension of the RP score to three sequences presents serious technical challenges, because the complexity of the models underlying the score can increase exponentially with the number of species. Thus, we need to use more sophisticated approaches than in our previous study, to select informative models and limit complexity.

This study also describes and verifies a separate avenue to improve the performance of RP scores, which can be used with comparisons of any number of species. Instead of estimating a single genome-wide model for alignments in neutrally evolving regions, we produce local estimates in a sliding window of the genome. This accounts for local variation in neutral evolutionary rates (International Mouse Genome Sequencing Consortium 2002; Hardison et al. 2003a).

RESULTS

Basic Strategy

In the original implementation of the RP score, we first reduced each two-way alignment of human and mouse to a string of symbols in an appropriate alphabet. For example, we used a collapsed five-symbol alphabet to describe two-way alignment columns as follows: (1) match involving A or T; (2) match involving G or C; (3) transition; (4) transversion, and (5) column containing a gap. Then, for a fixed word-size, say k, we used statistical models to classify each alignment depending on whether the words (k-mers) in its symbol string are more characteristic of regulatory regions or of neutral DNA. Parameters of the statistical models are estimated using training data from alignments of experimentally confirmed regulatory elements and aligned ancestral interspersed repeats. We use the latter as a template for neutral behavior, as most appear to be under no selective pressure (International Mouse Genome Sequencing Consortium 2002). In more detail, the RP score is derived from a log-ratio comparison between transition probabilities of two Markov models, estimated on the two training sets. The order of the Markov models (i.e., the number of preceding positions upon which the current position depends) is determined by the word-size, t = k - 1. In our implementation, we measured the frequency of hexamers in the alignments, thus estimating transition probabilities for 5th order Markov models.

Extension of RP scores to three sequences presents serious technical challenges because of a combinatorial increase in the number of possible individual alignment columns and short alignment patterns when comparing multiple sequences. For two-way alignments, the number of possible alignment columns composed by A,C,G,T,-, minus the {-,-} pair, amounts to 5² - 1 = 24. For three-way alignments, the number of possible alignment columns composed by A,C,G,T,-, minus the {-,-,-} triplet, amounts to 5³ - 1 = 124. When turning to short alignment patterns, these numbers are further raised to a power linked to the pattern's length (see below). Moreover, the available regulatory training data decreased by ∼25% with respect to our previous study, at least in part because the rat genome sequence is currently incomplete.

Thus, here we use more sophisticated approaches to collapsing the alphabet (state space) and selecting the order of the Markov models. This fine-tuning is necessary to make efficient use of the available data, and avoid overfitting and deterioration in estimate accuracy associated with large alphabets and high orders.

Training Sets

Our analyses use training data for known regulatory elements and ancestral repeats (i.e., repeats predating the split between human and rodent lineages). We extract three-way alignments corresponding to trimmed regulatory elements (REG) available at http://bio.cse.psu.edu/mousegroup/Reg_annotations. These alignments comprise a total of 26,721 alignment columns, and are parsed into a collection of 273 contiguous nonoverlapping segments of length approximately W = 100 bp (median = 100, 1^st quartile = 92, 3^rd quartile = 101). In the following, we indicate this collection as C(W)_REG and the number of segments it contains as N_REG = 273. The parsing is implemented for score evaluation purposes, and has almost no effect on the training of the score (see Methods for more details; W = 100 bp is also the window size we later adopt in computing the score genome-wide). Next, we consider three-way alignments of ancestral repeats (AR). We sample at random from these alignments to produce a training set comparable to that for regulatory elements. The sampled alignments comprise a total of 27,327 alignment columns, which are parsed into a collection of 260 nonoverlapping segments of approximate length W = 100 bp (median = 100.5, 1^st quartile = 92.25, 3^rd quartile = 116.75). The short-hand notations for this collection and its size are C(W)_AR and N_AR = 260.

Collapsed Alphabet, Order Selection, and Calculation of the Three-Way RP Score

The regulatory potential score of a generic three-way alignment segment of fixed length is given by

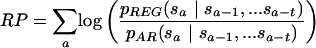1

where a ranges over the positions in the segment, the s's indicate symbols in a state space, that is, an alphabet of three-way alignment columns, and the p_REG's and p_AR's transition probabilities for two Markov models of order t estimated on C(W)_REG and C(W)_AR, respectively. Considering the full state space of 124 three-way alignment columns:

would entail estimation of 124^t × (124 - 1) plus 124^t × (124 - 1) free parameters (each row of a transition probability matrix is subject to the constraint of adding up to 1). Therefore, to make efficient use of the limited REG (and matching AR) training data currently available, we need to fine-tune the complexity of our models through appropriate state space collapsing and order selection. We want to allow for enough complexity as to capture systematic signals with discriminatory content, while avoiding overfitting and deterioration in estimate accuracy associated with large model sizes. Our computation involves several modules, as described below.

State collapsing is implemented through a hierarchical agglomeration algorithm on the basis of a figure of merit expressing separation between the RP scores of segments in C(W)_REG and C(W)_AR. The algorithm considers a range of possible orders through a mixing mechanism, so as not to skew state collapsing toward specific orders (see Methods). If applied directly to the 124 states in S, this algorithm would proceed essentially at random through early iterations. As long as the number of states is very large, overfitting would make most of the possible agglomerations equivalent in terms of the figure of merit, as they will all allow nearly perfect separation between REG and AR scores. This may, in turn, lock the procedure as a whole into markedly sub-optimal solutions. To overcome this problem, we perform a precollapse that groups together symbols that are very rare in our training collections, and symbols whose frequency profiles across the N_REG + N_AR segments in C(W)_REG and C(W)_AR are very similar (see Methods)—note that the precollapse does not target discrimination between REG and AR, and does not make use of a Markov structure, it simply aggregates at the outset symbols with highly correlated individual occurrence behavior. The resulting alphabet S₀ is then further collapsed on the basis of discrimination, producing a sequence of nested alphabets of progressively smaller size, eventually reducing to an alphabet of one symbol. As the agglomeration proceeds, we follow the relative loss in the figure of merit (see Methods). This relative loss remains fairly constant for nested alphabets of size >10, acquires an increasing trend for nested alphabets ranging in size between 10 and 5, and finally spikes when agglomerating from 5 to 4 symbols. Thus, among the smallest alphabets produced by the agglomeration, those of sizes 10 to 5 are natural candidates for more careful investigation.

Next, we use cross-validation to choose among these candidate alphabets, and select an order as to parsimoniously fit the data once translated into them. For each candidate alphabet, and each order t ranging from 0 (independent positions) to T = 5 (which would capture hexamer structures associated with binding sites), we compute cross-validation misclassification rates. The final choices of collapsed alphabet S^* and order t^* are determined on the basis of these rates (see Table 1 and Methods). The largest of the candidate alphabets (10 symbols) and order t^* = 2 provide the best results. The cross-validation scheme we use is a leave-one-out, in which segments in the training sets are withheld from training and then classified one at a time (see Methods).

Table 1.

Rates From Leave-One-Out Cross-Validation for Selected Nested Alphabets and Orders

	REG alignment segments			AR alignment segments
Alphabets and orders	Correct (TP)	Unclassified	Wrong (FN)	Correct (TN)	Unclassified	Wrong (FP)
10 symbols
order 1	0.758242	0.000000	0.241758	0.865385	0.000000	0.134615
order 2	0.805861	0.000000	0.194139	0.850000	0.000000	0.150000
order 3	0.637363	0.000000	0.362637	0.907692	0.000000	0.092308
order 4	0.065934	0.919414	0.014652	0.042308	0.957692	0.000000
9 symbols
order 1	0.743590	0.000000	0.256410	0.873077	0.000000	0.126923
order 2	0.761905	0.000000	0.238095	0.876923	0.000000	0.123077
order 3	0.703297	0.000000	0.296703	0.773077	0.000000	0.226923
order 4	0.069597	0.919414	0.010989	0.088462	0.911538	0.000000
8 symbols
order 1	0.761905	0.000000	0.238095	0.846154	0.000000	0.153846
order 2	0.809524	0.000000	0.190476	0.800000	0.000000	0.200000
order 3	0.706960	0.000000	0.293040	0.773077	0.000000	0.226923
order 4	0.161172	0.835165	0.003663	0.046154	0.953846	0.000000
7 symbols
order 1	0.750916	0.000000	0.249084	0.846154	0.000000	0.153846
order 2	0.791209	0.000000	0.208791	0.834615	0.000000	0.165385
order 3	0.758242	0.000000	0.241758	0.800000	0.000000	0.200000
order 4	0.293040	0.695971	0.010989	0.123077	0.869231	0.007692
6 symbols
order 1	0.747253	0.000000	0.252747	0.846154	0.000000	0.153846
order 2	0.743590	0.000000	0.256410	0.853846	0.000000	0.146154
order 3	0.783883	0.000000	0.216117	0.765385	0.000000	0.234615
order 4	0.498168	0.421245	0.080586	0.384615	0.546154	0.069231
5 symbols
order 1	0.732601	0.000000	0.267399	0.873077	0.000000	0.126923
order 2	0.725275	0.000000	0.274725	0.861538	0.000000	0.138462
order 3	0.681319	0.000000	0.318681	0.838462	0.000000	0.000000
order 4	0.633700	0.000000	0.366300	0.792308	0.000000	0.207692
order 5	0.340659	0.351648	0.307692	0.584615	0.361538	0.053846

Thinking of REG as the category to be recognized, the Correct and Wrong columns are also labeled as TP (true positive) FN (false negative) for REG, and TN (true negative) and FP (false positive) for AR. When an order is reached that gives high rates of unclassified elements—over-fitting—larger orders, for which such rates become even higher, are not listed. The 10-symbol alphabet and order 2 (in bold) are the ones used for the 3-way RP and 3-way LRP scores.

Table 2 summarizes S^*. Symbols #1 and #3 both aggregate a very large number of triplets (51 and 35, respectively). Symbol #1 is almost entirely composed by highly diverged triplets (three mismatching species, two mismatching species and one gap, one species and two gaps). In fact, it contains all “very seldom” triplets identified in the precollapse stage. Roughly half of the triplets in Symbol #3 are again highly diverged, although slightly more frequent in our training data—they were not labeled as rare in the precollapse. The other half of the triplets in Symbol #3 are ones that contradict phylogenetic distance, with human matching one of the rodents, and the second rodent mismatching or gapped. Interestingly, 14 of 32 of these triplets, as well as 9 of 12 triplets with one species and two gaps, escape the two populous symbols. They can be found in the remaining, smaller groups, along with 12 of 14 triplets with the two rodents matching and human mismatching or gapped (two of these, GTT and TCC, are actually in Symbol #1), and the four triplets of perfect matches. Also, if we consider transversions and transitions among triplets with human matching one of the rodents, and the second rodent mismatching, we see that none of the transversions escapes the two populous symbols, whereas six of eight transitions do, and can be found mostly in Symbols #4 and #5. If we consider transversions and transitions among triplets with rodents matching, and the human mismatching, we see that transversions can be found mostly in Symbols #9 and #10, and transitions again mostly in Symbols #4 and #5. In summary, although with exceptions, Symbols #9 and #10 concentrate transversions between human and rodents, whereas Symbols #4 and #5 concentrate both transitions between human and rodents and transitions in one of the two rodents, where the other keeps matching human. Finally, the four triplets of perfect matches all occupy a symbol of their own (#2, #6, #7, and #8, which actually sees -CC lumped with TTT), indicating that when reading perfectly conserved strings of the three-way alignments, spelling bases does matter for the purpose of discriminating between regulatory and neutral locations.

Table 2.

Summary of the Final Collapsed Alphabet S^* (10 Symbols)

In the triplets, first, second, and third positions correspond, respectively, to human, mouse, and rat. (Underlined) one species and two gaps. (Black) very rare triplets; two mismatching species and one gap, or three mismatching species. (Green) more triplets with two mismatching species and one gap, or three mismatching species. (Brown) triplets with human matching one of the rodents, and the second rodent mismatching or gapped. (Blue) triplets with rodents matching, and human mismatching or gapped. (Red) matches of all three species. (tv and ts) Near triplets in Symbols #4, #5, #9, and #10 indicate transversions and transitions, respectively.

Another important point is whether our collapsed S^* is capable of conveying discriminatory information that comes from having the rat sequence in addition to mouse. Corresponding to each of the 24 possible human-mouse pairs, there are five (four in the case of the {-,-} pair) human-mouse-rat triplets. Using Table 2, we can observe where these triplets fall in terms of symbols in S^*. For instance, triplets corresponding to the CC pair fall in four different symbols; CCT in symbol 1, CCA and CCG in symbol 2, CC- in symbol 4, and the three-way match CCC in symbol 6. In general, triplets corresponding to the same human-mouse pair do not tend to cluster together in the collapsed alphabet; most are spread across three clusters, some across two, and some across four. Thus, S^* can convey information carried by the rat sequence.

Ability of Three-Way and Two-Way RP Scores to Distinguish Alignments in Regulatory Regions From Alignments of Neutral DNA

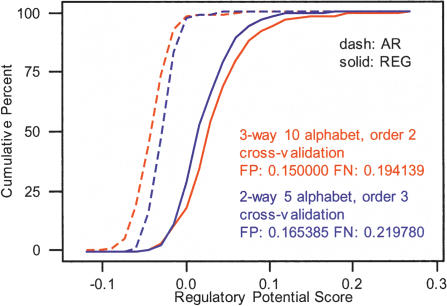
The red curves in Figure 1 represent cumulative distribution functions for the scores of three-way alignment segments in C(W)_REG and C(W)_AR, obtained through equation 1 using estimated transition probabilities (see Methods) for the final models. Also in the figure are misclassification rates from cross-validation (false positives 15%, false negatives ∼19.41%). On the basis of these results, the RP score from three-way alignments of human, mouse, and rat provides good discrimination between regulatory and neutral DNA, especially considering the limited amount of data on which the score is trained.

Figure 1.

Cumulative distributions for two-way (blue) and three-way (red) RP scores on C(W)_REG and C(W)_AR. The text box contains the corresponding misclassification rates from leave-one-out cross-validation. Scores are all length normalized to correct for the slightly different sizes of the training segments (all around W = 100 bp).

To verify the effectiveness of extending our scoring scheme to multiple alignments, and assess the informational contribution of the rat sequence, we compare the performance of the three-way RP score with that of the RP score computed on the basis of two-way human-mouse alignments only (Elnitski et al. 2003). For comparability, we use here only human-mouse alignments extracted from the three-way alignments of regulatory regions and ancestral repeats used for the three-way score. As a consequence, we are using only 26,721 two-way alignment columns from regulatory elements, whereas 35,206 were used in our previous study. On these data, the 24 original states in

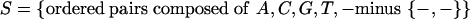are collapsed in the 5-symbol alphabet from Elnitski et al. 2003 (matches of A's and T's, matches of G's and C's, transitions, transversions, and pairs containing one gap). The order t^* = 3 (smaller than the one used previously) is again selected on the basis of cross-validation, and as to give a modeling complexity comparable to that underlying the three-way score.

The blue curves in Figure 1 are the cumulative distribution functions for the resulting two-way RP scores of human-mouse alignment segments extracted from the C(W)_REG and C(W)_AR collections, with the accompanying misclassification rates (false positive ∼16.54%, false negatives ∼21.98%). Comparing these curves and rates to those relative to the three-way score, we see a clear increase in separation, as well as a small improvement in cross-validation outcomes. Thus, a modest, but robust improvement can be attributed to information carried by the rat.

Adjusting for Variation in Local Evolutionary Rates: The Localized RP Score

Motivated by the abundant evidence of local variation in neutral evolutionary patterns (International Mouse Genome Sequencing Consortium 2002; Hardison et al. 2003a), we also implement an alternative version of the three-way score, in which AR transition probabilities are estimated locally. This is possible in terms of data availability because, unlike alignments from known regulatory regions, alignments of ancestral repeats needed for this estimation are abundant.

First, we partition the genome-wide three-way alignments into nonoverlapping windows u, each containing 10,000 AR alignment columns. These windows have different lengths, depending on the local AR density (in terms of human sequence, median = 440,200 bp, 1^st quartile = 307,500 bp, 3^rd quartile = 622,700 bp).

Next, for each window u, we consider the AR content of the window itself, the one preceding it, and the one following it, for a total of 30,000 alignment columns, which form a local collection C(W)_AR,u (see Methods). This way, each local collection matches approximately in size our previous C(W)_AR and C(W)_REG. Considering the same 10-symbol alphabet S^* and order t^* = 2, we then calculate local estimates of the transition probabilities (p_AR,u's) using the data in each C(W)_AR,u. The localized RP score of a generic three-way alignment segment of fixed length is thus given by

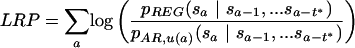2

where u(a) indicates the window in which position a falls, and again a ranges over the positions in the segment.

Local estimation of the denominator terms in this log-odds equation allows us to incorporate varying composition and short pattern features of neutral DNA, as observed in ancestral repeats. Localization results in an increased score for 106 of the N_REG = 273 segments in C(W)_REG, circa 39% of the REG training set. Also, the relative increase (LRP-RP)/RP exceeds 0.10 (i.e., 10%) for 97 segments, circa 36% of the REG training set. This demonstrates how reference to a localized neutral background can sharpen our discriminatory signals. However, for many of the regulatory elements in our training set, the LRP score is approximately the same, or lower, than the RP score. A preliminary screening suggests that in regions of low-repeat density, the windows defining the local collection C(W)_AR,u extend very broadly (in terms of human sequence, the largest window reaches 48,610,000 bp), which, in turn, may result in an increased resemblance between short alignment patterns in C(W)_AR,u and the randomly sampled collection C(W)_AR. For these regions, differences between local and overall neutral background are minor. A second interesting possibility, which warrants a more detailed future investigation, is that ancestral repeats in some regions may have a tendency to resemble functional sequences.

Examples of RP Scores in Regions Containing Known Regulatory Elements

Equations 1 and 2 can also be used to construct genome-wide regulatory potential tracks. Using the human sequence as reference, we move along the genome-wide three-way alignment of human, mouse, and rat with a sliding window of size W = 100 bp, and calculate our scores at a given spacing frequency (every r = 5th position). More precisely, counting positions from the start of the alignment, we consider each window centered at a position that is an even multiple of r, score the window according to our equations, and associate the resulting score values to the center position. Here, we provide two instances of these calculations. The three-way RP, the two-way RP as recomputed for the current analysis, and the three-way LRP are plotted along two ∼10-kb human regions, one surrounding the cardiac α-actin (ACTC) locus on chromosome 15 (Fig. 2A), and the other surrounding the CCAAT enhancer-binding protein α (C/EBPα) locus on chromosome 19 (Fig. 2B). Both of these loci are part of our regulatory training data.

Figure 2.

Plots of two-way RP, three-way RP, and three-way LRP scores superimposed to annotations from the UCSC human genome browser along two selected genomic regions. (A) Approximately 10 kb around the cardiac α actin locus on human chromosome 15. (B) Approximately 10 kb around the C/EBPα locus on human chromosome 19. Scores are all length normalized to the fixed size W = 100 bp of the sliding windows on which they are calculated.

Cardiac α-actin, or acidic actin, is a highly conserved protein in mammals (Biesiada et al. 1999). It is involved in the development of skeletal and cardiac muscles, serving as a major structural constituent in thin filaments. Tissue-specific expression of ACTC gene requires simultaneous interaction of MyoD1, serum response factor (SRF or a related protein), and Sp1 (Sartorelli et al. 1990), whose binding sites are found within a 100-bp region upstream of the transcription start site. The RP scores for this promoter are higher than for any other DNA segments in the locus, including the exons (Fig. 2A). The three-way RP is higher than the two-way RP in the promoter, and the three-way LRP is even higher. This provides an example of the improved discriminatory power provided by three-way alignments and local adjustment. The promoter is also a strong peak for the human-mouse conservation track, but the latter does not distinguish the promoter from the exons.

C/EBPα is an intronless gene whose expression is regulated during liver development, adipocyte differentiation, and liver regeneration. It also plays a role in maintaining highly differentiated hapatocytes and adipocytes. Despite similarities in the promoters of humans and mice, the human gene is autoregulated by interaction of C/EBPα with a bound USF protein (Timechenko et al. 1995). In mice, autoregulation occurs when C/EBPα binds directly to the promoter region. This locus shows several peaks of high RP score, two of which overlap with the promoter (Fig. 2B). The three-way RP is higher than the two-way RP, and again sharpens discrimination between the promoter and other segments. However, the effect of adjusting the three-way RP scores for variation in local evolutionary rates is minor. As a possible explanation, the localization window containing C/EBPα, is 452,182 bp in length, whereas that containing cardiac α-actin is 335,969, indicating that the surroundings of C/EBPα are poorer in ARs. The annotation of other coding exons in this region is not extensive, and some of the peaks in RP scores could be from unannotated exons.

Tracks for two-way and three-way RP scores are available at UCSC Human Genome Browser, and more information and resources on RP scores can be gathered at the site of the Center for Comparative Genomics and Bioinformatics (http://www.bx.psu.edu).

DISCUSSION

Many groups have tackled the job of identifying and annotating protein-coding regions in sequenced mammalian genomes. Fewer efforts (e.g., Dieterich et al. 2003) have begun to annotate confirmed or predicted functional noncoding elements genome-wide, and much work remains to be done in this area. RP scores provide one means to annotate entire mammalian genome sequences with predictive information about sites that may regulate gene transcription. In this study, we also provide evidence supporting the hypothesis that the addition of the rat sequence to those of human and mouse allows for better discrimination of regulatory sites.

Some existing computational approaches for predicting the location of regulatory sites use criteria based purely on interspecies sequence conservation. For example, Loots et al. (2000) searched for regions of at least 100 bp, having at least 70% identity between human and mouse. When homologous sequences from more than two species are available, blocks of strongly conserved sequences, or phylogenetic footprints, can effectively predict binding sites for transcription factors (Gumucio et al. 1992; Hardison et al. 1997b). Numerous plausible ways have been explored to characterize well conserved regions within multiple alignments (e.g., Schneider et al. 1986; Stojanovic et al. 1999).

Another approach is to look for the occurrence of short motifs of nucleotides that are characteristic of the binding sites for known transcription factors (e.g., Hughes et al. 2000). Experiments have suggested that a combination of conservation and motifs is superior to either approach in isolation (Levy and Hannenhalli 2002), and web resources exist to help users apply both approaches (Jegga et al. 2002; Loots et al. 2002; Sharan et al. 2003).

The Markov modeling underlying our RP scores places both interspecies conservation and occurrence of nucleotide motifs under one umbrella. Extreme cases of the model correspond to pure conservation (e.g., where a symbol depends only on the number of matching pairs of nucleotides in a column of the alignment) at one end of the spectrum, or pure nucleotide content (e.g., the alphabet that simply records the nucleotide in the first species) at the other. Our procedure for model selection (collapsing of the original alignment column alphabet, choice of order) uses the available training data to determine how to mix criteria to maximize discriminatory power.

Our approach makes no a priori assumptions about the physical mechanisms behind gene regulation. Although many examples of cis-regulatory modules are known that function by proteins binding to genomic segments of around 6 bp in length, this is not taken as an assumption in our modeling. The approach is not inherently tied to prediction of regulatory sites; we train a score to distinguish between two sets of genomic segments. Consequently, the same computational strategy can be adapted for prediction of any class of genomic DNA for which adequate training data are available. For example, one could compute a score to distinguish between CpG islands that are methylated in the germ line and those that are not.

Our comparison of two-way and three-way RP scores demonstrates that computational tools for prediction of gene regulatory sequences can be effectively generalized to take advantage of multiple species alignments. Interestingly, the rat sequence, when added to human and mouse, does contribute to the discriminatory power of the RP score, notwithstanding its proximity to one of the sequences already in use. This suggests that other mammalian genome sequences at a larger phylogenetic distance will allow for yet larger gains in the resolution of functional from nonfunctional sequences. The examination of many vertebrate genome sequences demonstrates that more sequences can improve the identification of sequences likely under selection (Thomas et al. 2003).

The exploration of computational methods to predict functional noncoding regions, or even just signals that regulate gene transcription, is still in its infancy. Statistical methods that combine sequence conservation with a search for DNA motifs seem very promising, and we anticipate the development of multiple worthwhile approaches in the bioinformatics community.

METHODS

Training Data Preparation

We use whole-genome three-way human, mouse, and rat alignments as described in Blanchette et al. (2004). These were created from human genome release hg15 (build 33, 2003-04-10), mouse genome mm3 (2003-07-17), and rat genome rn3.1 (2003-06-08) using the new RepeatMasking (version 2003-06-23). They are available in the downloads section of the genome.ucsc.edu site.

The three-way alignments corresponding to the trimmed known regulatory elements available at http://bio.cse.psu.edu/mousegroup/Reg_annotations are parsed into N_REG = 273 contiguous nonoverlapping segments of approximate length W = 100 bp (median 100, q1 = 92, q3 = 101), forming a collection C(W)_REG, which comprises a total of 26,721 bp. In detail, alignments with length ≥75 and <150 are retained as they are, those with length ≥150 and ≤250 are split in half, and contiguous segments of 100 bp are progressively cut from alignments with length >250, until the reminder has length ≤250. For the purpose of training the score, which requires counting occurrences of short strings of symbols in these alignments, the parsing is immaterial—it only causes us to lose a small number of strings at the boundaries of the segments.

An analogous collection C(W)_AR is formed randomly sampling three-way alignments of ancestral repeats. These are located via the four-way alignments with repeat consensus sequences. Alignments are again parsed as to produce N_AR = 260 nonoverlapping segments of approximate length W = 100 bp (median 100.5, q1 = 92.25, q3 = 116.75), for a total of 27,327 bp. The local collections C(W)_AR,u are formed in the same fashion, except that ancestral repeats are not randomly sampled, but gathered through a partition of the genome-wide three-way alignment, as described in the Results. For first and last window in the partition for each human chromosome, the local collections are formed using first, second, and third window, and second to last, next to last, and last window, respectively—thus, the local collections for first and second window coincide, as do those for next to last and last window.

State Space Precollapse

Using the segments in C(W)_REG and C(W)_AR, we compute frequency vectors for the 124 symbols in the initial state space S—a frequency vector is a (N_REG + N_AR)-vector containing frequencies of a symbol in each segment in the training collections. For each symbol, we compute the average frequency across all segments in C(W)_REG, and across all segments in C(W)_AR. Symbols for which the maximum between these is <0.001 are lumped together (they occur on average less than once in every 1000 bp of REG training data, and of AR training data). Hierarchical clustering (with Euclidean distance and Complete linkage, see for instance Hartigan 1975) of frequency vectors is then used to agglomerate the remaining symbols. This does not pursue discrimination between REGs and ARs; it allows us to identify, if they exist, groups of symbols whose frequency profiles across training segments (of whichever type) are very similar. We interrupt agglomeration at 95% similarity level. This precollapse leads to a space S₀ containing one symbol for seldom triplets, and one symbol for each cluster of triplets.

State Space Agglomeration

S₀ is further collapsed by hierarchical agglomeration, this time according to a figure of merit (see below) that targets discrimination between REGs and ARs. Let S(j) = {s(j,i), i = 1,...I(j)} and M(j) be, respectively, the state space and the corresponding figure of merit at agglomeration stage j. Also, let S(j; i = h) be the space obtained merging s(j,i) and s(j,h), and M(j; i = h) the corresponding figure of merit. To pass to agglomeration stage j + 1, select i^* and h^* such that

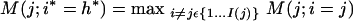and merge these two states, setting S(j + 1) = S(j; i^* = h^*). Correspondingly M(j + 1) = M(j; i^* = h^*). We record the series M(j), j = 0,1,2..., and compute the relative loss in merit at agglomeration stage j = 1,2,... as

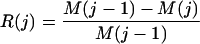Following this quantity along agglomeration stages allows us to identify a small number of nested candidate alphabets to be investigated, together with appropriate orders, through cross-validation (see below).

Figure of Merit

At each agglomeration stage j, the figure of merit is built considering a range of orders t = 0 (iid case) to t = T(j). We use the alignment columns in C(W)_REG and C(W)_AR to produce individual symbol and string (overall) frequencies

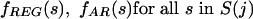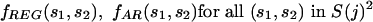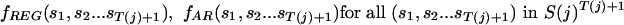Next, we estimate transition probability matrices for REG, one for each order. For any given t, we compute the frequency ratios

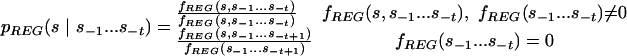3

If for at least one (but not all) s we have f_REG(s, s_-1... s_-t) = 0, we use Laplace's rule (Durbin et al. 1998), that is, increment each count by 1. These quantities form a I(j)^t by I(j) matrix, which is augmented replicating each row I(j)^(T(j)-t) times, to produce a I(j)^T(j) by I(j) matrix P_REG(t,j). The matrices P_REG(t,j), t = 0... T(j) are then combined using weights:

(we use uniform weights). After proceeding similarly for AR, we use the two combined matrices to score all elements in C(W)_REG and C(W)_AR using the function

where a ranges along the positions in a segment. A figure of merit could then be defined through simple or cross-validation misclassification rates associated with this score function. However, notwithstanding the precollapse, in the initial agglomeration stages overfitting may cause little if any overlap between the REG and AR distributions, and a cross-validation scheme, repeating the above calculations iteratively withholding training data, would constitute a computationally intensive iteration within the agglomeration iteration itself. As an alternative, we consider q_AR = (100 - q)% quantile of the score distribution for segments in C(W)_AR and q_REG = q% quantile of the score distribution for segments in C(W)_REG, and define the figure of merit as

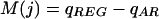(we use q = 10). This is negative when the overlap between the two distributions goes past the chosen quantile value, and becomes positive and increases as the two distributions separate.

The maximal order T(j) used at each agglomeration stage changes depending on the number of states I(j). This induces a marked nonmonotonicity in M(j). To maintain the procedure computationally feasible, we restrict ourselves to T(j) = 2 for I(j) larger than 15, T(j) = 3 for I(j) between 15 and 11, T(j) = 4 for I(j) between 10 and 6, and T(j) = 5 for I(j) equal to or smaller than 5. Note T = 5 would capture hexamer structures associated with binding sites, and is the order used previously in Elnitski et al. (2003).

Cross-Validation

Although we do not use cross-validation to define the figure of merit, we do sustain the computational burden of a leave-one-out cross-validation scheme to choose among a set of nested candidate alphabets suggested by the agglomeration and select orders. For each candidate alphabet, and orders t ranging from 0 to T = 5, we proceed as follows:

1. Withhold an individual training segment, either from C(W)_REG or from C(W)_AR.

2. Estimate the REG and AR transition probabilities on the remaining data.

3. Score the segments used in training using equation 1; if the two distributions overlap, define one threshold as the value H that minimizes (%REG scores<H) + (%AR scores>H); if the two distributions do not overlap, define two thresholds as H_AR = max of AR scores and H_REG = min of REG scores.

4. Score the withheld segment using equation 1. Assume it is a REG; count it as correctly classified if its score is on the right of H (H_REG), as incorrectly classified if its score is on the left of H (H_AR), and as unclassifiable in case the two distributions do not overlap and its score is between H_AR and H_REG— conversely, if the segment is an AR.

Repeating 1-4, above for each segment in the training collections produces counts of correctly classified, incorrectly classified, and unclassifiable REGs (ARs), which can then be turned into rates dividing by N_REG (N_AR).

The final S^* and t^* are selected on the basis of these rates. In particular, we seek to maximize %true positives + %true negatives (i.e., %correctly classified REGs + %correctly classified ARs), because low %false negatives + %false positives (i.e., %incorrectly classified REGs + %incorrectly classified ARs) may occur in coincidence with high percentages of unclassifiable REGs and/or ARs in case of overfitting. Table 1 contains rates for selected candidate alphabets and order combinations, and Table 2 summarizes our final alphabet S^*.

Estimation

The transition probabilities' estimates

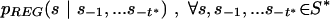to be used in equations 1 and 2 to compute RP and LRP scores, are simply obtained as ratios of string frequencies from C(W)_REG, C(W)_AR, and C(W)_AR,u. With proper changes of subscripts, the formulae are the same as in equation array 3, above.