A comprehensive experimental and detailed chemical kinetic modelling study of 2,5-dimethylfuran pyrolysis and oxidation

Abstract

The pyrolytic and oxidative behaviour of the biofuel 2,5-dimethylfuran (25DMF) has been studied in a range of experimental facilities in order to investigate the relatively unexplored combustion chemistry of the title species and to provide combustor relevant experimental data. The pyrolysis of 25DMF has been re-investigated in a shock tube using the single-pulse method for mixtures of 3% 25DMF in argon, at temperatures from 1200–1350 K, pressures from 2–2.5 atm and residence times of approximately 2 ms.

Ignition delay times for mixtures of 0.75% 25DMF in argon have been measured at atmospheric pressure, temperatures of 1350–1800 K at equivalence ratios (ϕ) of 0.5, 1.0 and 2.0 along with auto-ignition measurements for stoichiometric fuel in air mixtures of 25DMF at 20 and 80 bar, from 820–1210 K.

This is supplemented with an oxidative speciation study of 25DMF in a jet-stirred reactor (JSR) from 770–1220 K, at 10.0 atm, residence times of 0.7 s and at ϕ = 0.5, 1.0 and 2.0.

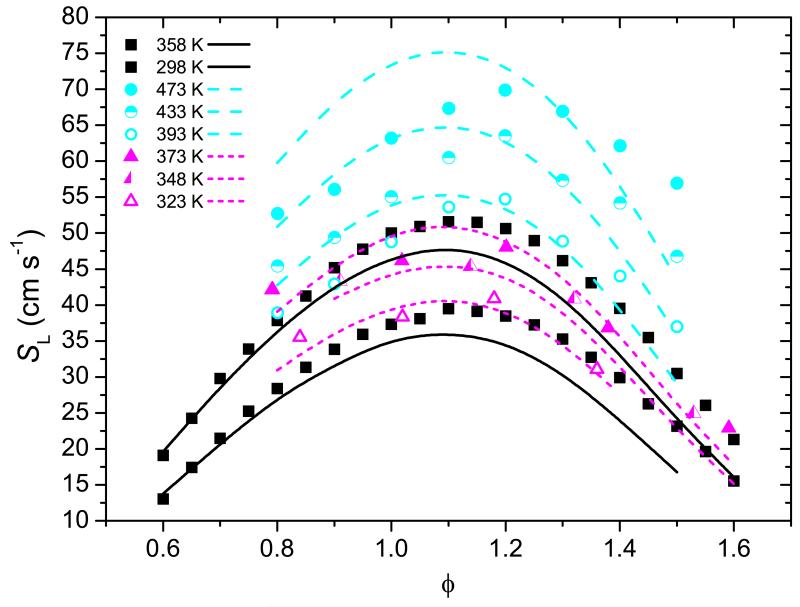
Laminar burning velocities for 25DMF-air mixtures have been measured using the heat-flux method at unburnt gas temperatures of 298 and 358 K, at atmospheric pressure from ϕ = 0.6–1.6. These laminar burning velocity measurements highlight inconsistencies in the current literature data and provide a validation target for kinetic mechanisms.

A detailed chemical kinetic mechanism containing 2768 reactions and 545 species has been simultaneously developed to describe the combustion of 25DMF under the experimental conditions described above. Numerical modelling results based on the mechanism can accurately reproduce the majority of experimental data. At high temperatures, a hydrogen atom transfer reaction is found to be the dominant unimolecular decomposition pathway of 25DMF. The reactions of hydrogen atom with the fuel are also found to be important in predicting pyrolysis and ignition delay time experiments.

Numerous proposals are made on the mechanism and kinetics of the previously unexplored intermediate temperature combustion pathways of 25DMF. Hydroxyl radical addition to the furan ring is highlighted as an important fuel consuming reaction, leading to the formation of methyl vinyl ketone and acetyl radical. The chemically activated recombination of HȮ₂ or CH₃Ȯ₂ with the 5-methyl-2-furanylmethyl radical, forming a 5-methyl-2-furylmethanoxy radical and ȮH or CH₃Ȯ radical is also found to exhibit significant control over ignition delay times, as well as being important reactions in the prediction of species profiles in a JSR. Kinetics for the abstraction of a hydrogen atom from the alkyl side-chain of the fuel by molecular oxygen and HȮ₂ radical are found to be sensitive in the estimation of ignition delay times for fuel-air mixtures from temperatures of 820–1200 K.

At intermediate temperatures, the resonantly stabilised 5-methyl-2-furanylmethyl radical is found to predominantly undergo bimolecular reactions, and as a result sub-mechanisms for 5-methyl-2-formylfuran and 5-methyl-2-ethylfuran, and their derivatives, have also been developed with consumption pathways proposed. This study is the first to attempt to simulate the combustion of these species in any detail, although future refinements are likely necessary.

The current study illustrates both quantitatively and qualitatively the complex chemical behavior of what is a high potential biofuel. Whilst the current work is the most comprehensive study on the oxidation of 25DMF in the literature to date, the mechanism cannot accurately reproduce laminar burning velocity measurements over a suitable range of unburnt gas temperatures, pressures and equivalence ratios, although discrepancies in the experimental literature data are highlighted. Resolving this issue should remain a focus of future work.

1 Introduction

Depletion of fossil energy reserves and increasing concerns over climate change are key incentives for the development of energy technologies which are sustainable from social, economical and environmental perspectives. Biofuels, liquid or gaseous fuels derived from biological sources, are considered as a natural successor to the petroleum derived products which are the dominant energy carriers for the transportation sector.

Ethanol is presently the most abundantly produced biofuel globally, with 86.1 billion litres manufactured in 2011 derived largely via fermentation of sugar cane and corn [1]. Yet despite its status as the leading renewable energy source in the transportation sector, problems with its use are now well founded in the literature.

Production feedstocks are in direct competition with food crops and agricultural land [2,3], combustion in unmodified direct-injection spark-ignition engines is only possible when blended with fossil fuels, its energy density is much lower than that of gasoline and its volatility and complete miscibility with water make it difficult to transport and store. Nevertheless, its ability to reduce emissions, CO, CO₂, NO_x and unburnt hydrocarbon (HC), when blended with gasoline and diesel illustrate the environmental benefits which the use of oxygenated biofuels can achieve.

Next-generation production methods have recently been developed [4-10] capable of converting inedible waste biomass, into the platform chemical 5-hydroxymethyl-2-furaldehyde, with subsequent conversion into the novel biofuel, 2,5-dimethylfuran (25DMF). The literature highlights the energy density of 25DMF (30 MJ L⁻¹) as a notable improvement over that of ethanol (21.3 MJ L⁻¹) with its higher boiling point (366 K) and lower aqueous solubility also making it preferable to the alcohol in terms of transportation and storage [7]. Other considerations such as atmospheric lifetimes and ecological and toxicological aspects are covered in a recent review by Simmie and Würmel [11].

Since the development of these production methods, combustion studies have ensued. 25DMF performed wholly similar to commercial gasoline in research engine tests [12, 13], the authors concluding that no major modifications to engine design would be necessary to achieve equivalent emissions and performance levels to gasoline. Daniel et al. [14] recently found that total carbonyl emissions from a direct-injection spark-ignition engine fueled with 25DMF were lower than those of methanol, ethanol, n-butanol and gasoline, in particular formaldehyde emissions, which may bear on its suitability as a biofuel. 1,3-cyclopentadiene, methyl vinyl ketone and 2-methylfuran (2MF) were also found in the exhaust gas, with unburnt fuel dominating the characterised emissions.

Wu et al. [15] determined laminar burning velocities of 25DMF-O₂-N₂/CO₂ mixtures as a function of equivalence ratio (ϕ) and dilution ratio at unburnt gas temperatures (T_i) of 393 K and atmospheric pressure. Laminar burning velocity was found to decrease linearly as a function of increased N₂/CO₂ concentrations, with peak burning velocities occuring for ϕ = 1.1–1.2. They complemented this work with studies on the laminar burning velocities of atmospheric pressure 25DMF-air mixtures over a range of equivalance ratios as a function of T_i (393–473 K) [16] and as a function of pressure (0.1–0.75 MPa) [17] for T_i = 393 K.

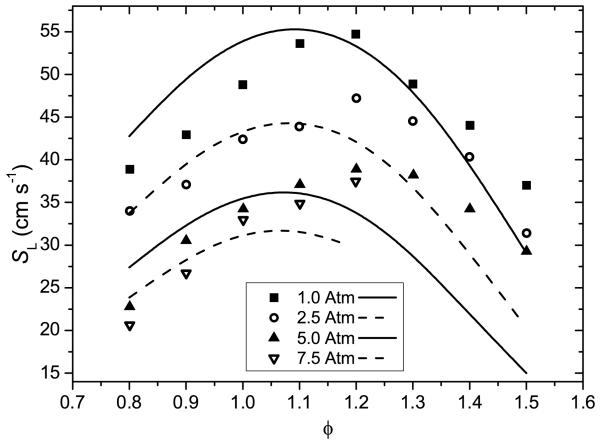
Tian et al. [18] determined laminar burning velocities of 25DMF, ethanol and gasoline as a function of ϕ and T_i (323–373 K) under atmospheric pressure in a combustion bomb. The laminar burning velocities of 25DMF were found to be the slowest of all three fuels studied, but were within 10% of gasoline between equivalence ratios of 0.9–1.1. Unfortunately, no measurements were made under directly comparable conditions to those of Wu and co-workers [15-17]. These laminar premixed flame burning velocity measurements will form a portion of the kinetic mechanism validation described in this work, along with experimental laminar burning velocities measured as part of this work using the heat-flux method.

Experimental work to isolate the chemical pathways of 25DMF combustion have also ensued of late, but other than early works by Grela et al. [20] in 1985 and Lifshitz et al. [21] in 1998 the literature remained sparse until very recently. Grela et al. [20] pyrolysed 25DMF in a heated tubular reactor at very low pressures (1 mTorr) from 1050–1270 K, analysing the product mixtures via on-line mass spectrometry. They detected water, CO, C₅H₆ and C₆H₆ in their effluent stream and hypothesised their formation from 25DMF by isomerisation to 2,4-dimethylfuran through a cyclopropenylcarbonyl intermediate – 25DMF or 2,4-dimethylfuran could then decompose via biradical intermediates through simple C-O bond fission. Lifshitz et al. [21] studied the thermal decomposition of 25DMF behind reflected shock waves in the temperature range 1070–1370 K, at pressures of 2–3 atm. They analysed the post-shock mixtures via gas chromatography, quantifying the concentrations of 19 intermediate species and reporting a rate constant (pseudo-first order) for the decomposition of 25DMF of 10^15.81exp(−75.1×10³/RT) where R is in units of cal K⁻¹ mol⁻¹. A chemical kinetic mechanism consisting of 50 species and 180 elementary reactions was developed to account for the product distributions.

However, it would appear that the mechanistic proposals of Grela et al. [20] and Lifshitz et al. [21] are erroneous, in light of recent theoretical work on the furans, and in particular the quantum chemical calculations by Liu et al. [22,23] and Sendt et al. [24], which went some way to disproving the long held belief that furan decomposition was routed through biradical intermediates [25-27]. The authors showed that the unimolecular decomposition of furan was initiated through singlet carbene intermediates formed from hydrogen atom transfer reactions, with Sendt et al. [24] constructing a kinetic scheme capable of reproducing laboratory pyrolysis experiments, thus validating their kinetic and mechanistic proposals.

More recently, Simmie and Curran [28] applied quantum chemical methods (CBS-QB3, CBS-APNO and G3) and developed isodesmic working reactions to calculate enthalpies of formation for a range of substituted furans and their corresponding furfuryl radicals, thus determining bond dissociation energies. They noted that for alkylfurans, the ring–H bonds are extremely strong, in excess of 500 kJ mol⁻¹, but that radicals formed from the alkyl side chains of a range of 2/3-methyl and 2/3/4/5-dimethyl furans, are considerably weak, all in the region of 357–380 kJ mol⁻¹. The important consequence of their findings is that the alkyl side chains of these species are a plausible source of radical initiators within a combustion environment, and that hydrogen atom abstraction by free radicals is likely to occur exclusively at the alkyl side chain.

Simmie and Metcalfe [29] used electronic structure methods and canonical transition state theory to study the initial steps in the thermal decomposition of 25DMF. They provided high pressure limiting kinetics and thermodynamic parameters for the carbene-mediated decomposition of the reactant, reactions of hydrogen atom and hydroxyl radical with the fuel and reactions which open the furan ring once furan-derived radicals are formed. They concluded that hydrogen atom addition to the double bonds of the furan ring is dominant up to temperatures of 2000 K.

Friese et al. [30,31] used time-resolved resonance absorption spectrometry to detect hydrogen as a product in the thermal decomposition of 25DMF from 1280–1520 K, and as a reactant with 25DMF between 980–1250 K, at 1.6 and 4.7 bar. Rate coefficients for the reactions 25DMF → Ḣ + product and 25DMF + Ḣ → products were derived from concentration-time profiles. Statistical rate theory, including a master equation (ME) to describe the thermally and chemically activated processes, was applied to rationalise their results, with accurate prediction of the experimentally derived rate constants found. The total rate constant for the reaction of Ḣ atom with 25DMF was found to exhibit only a weak dependence on pressure both theoretically and experimentally.

Sirjean and Fournet [32] added to the above work with a full exploration of the unimolecular decomposition pathways of 25DMF, including Rice-Ramsperger-Kassel-Marcus (RRKM) and ME analysis on the carbene and biradical mediated decomposition pathways of the reactant, with rate constants estimated for simple fission processes. They found that a 3-2 hydrogen atom transfer forming 3,4-hexadiene-2-one was the dominant decomposition pathway and direct ring opening reactions to form biradical intermediates are of little significance, as in the case of furan [22-24]. The same authors carried out an extensive exploration of the potential energy surface (CBS-QB3) upon hydrogen atom addition to the furan ring of 25DMF coupled with RRKM/ME modelling of collisional energy transfer within the chemically activated pathways involved [33]. They found that hydrogen atom addition at carbon atoms remote from the oxygen atom of the furan ring could be neglected based on the endothermicity and barrier heights of the subsequent ring-opening reactions. Hydrogen atom addition at carbon atoms adjacent to the oxygen atom of the furan ring would result in the formation of 2-methylfuran (2MF) predominantly, with lesser yields of 1,3-butadiene and acetyl radical. Only above temperatures of 1300 K would hydrogen atom abstraction by hydrogen atom become dominant. The total rate constant for the reaction of hydrogen atom with 25DMF was found to be nearly pressure independent and within a factor of two of the experiments of Friese et al. [30,31].

In a recent study, Sirjean and Fournet [34] also investigated the thermal reactions of the 5-methyl-2-furanylmethyl radical, formed from C–H fission or hydrogen atom abstraction from 25DMF. Through CBS-QB3 calculations and RRKM/ME modelling of the detailed, and complex, potential energy surfaces they found that the resonantly stabilised radical predominantly undergoes ring opening, followed by a hydrogen atom transfer reaction and ring enlargement to cyclohexenone radicals. Linear and cyclic unsaturated C₅ species could also be produced with CO in lesser quantities. The cyclohexenone radicals could decompose to form hydrogen atom and stable cyclohexadienone isomers which could undergo keto-enol tautomerisation to form phenol, through a well established mechanism [35-37]. Pressure and temperature dependent rate constants were provided from 10⁻²–10 bar and 1000–2000 K.

Phenol is therefore a likely intermediate in the combustion of 25DMF, with plausible pathways to its formation now recognised. It was recently detected in a low pressure premixed laminar 25DMF-O₂-Ar flame by Xu et al. [38] on the basis of its ionization energy, along with 2MF, furan and 1,3-butadiene for which credible formation channels are now well characterised based on the above work.

Djokic et al. [39] recently used a 1.475 m long heated flow reactor to pyrolyse 25DMF using GC × GC-FID(TOF-MS) to quantify the decomposition of the fuel and formation of intermediates from 873–1098 K, at 1.7 bar and at heating times of 300–400 ms. They were able to quantify species which are important indicators of the fuel decomposition such as phenol, 2MF, 1,3-butadiene and 1,3-cyclopentadiene, along with a host of small hydrocarbon species and mono- and poly-aromatic species up to C₁₇.

Recently, Sirjean and co-workers [40] described a chemical kinetic model for the high temperature combustion of 25DMF. They validated their mechanism against ignition delay time measurements from 1300–1831 K, at 1 and 4 bar, for mixtures of 25DMF in argon at ϕ = 0.5, 1.0 and 1.5, and the experimental data of Lifshitz et al. [21]. They identify reactions important in predicting their experimental targets, although no comparison was made with literature flame speeds. Together with the kinetic model described by Somers et al. [41] for 2MF which could accurately describe ignition delay times and laminar burning velocities, only two detailed mechanisms to describe the combustion of alkylfurans currently exist in the literature.

Here we aim to remedy this deficit by providing a detailed chemical mechanism to describe the combustion of 25DMF based on the theoretical and experimental works described above, along with experiments detailed in the following sections, thus providing the most comprehensive experimental and modelling analysis of its combustion to date.

2 Experimental

Experiments have been carried out in five separate facilities in order to gather data relevant to both practical combustors and to the validation of a detailed chemical kinetic mechanism, including:

• A single pulse shock tube to investigate the pyrolysis of 25DMF

• A low pressure shock tube to measure ignition delay times of dilute 25DMF/O₂/Ar mixtures

• A high pressure shock tube to measure ignition delay times of non-dilute 25DMF/O₂/N₂ mixtures, representing “fuel in air”

• A jet-stirred reactor to quantify mole fractions of reactants and products for the oxidation of dilute 25DMF/O₂/N₂ mixtures

• A flat-flame burner (heat-flux method) to determine laminar burning velocities of atmospheric pressure 25DMF/O₂/N₂ mixtures as a function of equivalence ratio and unburnt gas temperature.

Table 1 summarises the experimental conditions studied.

Table 1.

Summary of experimental work carried out as part of this study. SP = single pulse, ST = shock tube, IDT = ignition delay time, JSR = jet-stirred reactor, S_L = laminar burning velocity.

T / K	p / atm	[25DMF]	[O2]	[Ar]	[N2]	φ	Measurement	Reactor
1191–1328	2.28 ± 0.16	3.00	-	97.00	-	-	Speciation	SPST
1343–1628	1.12 ± 0.06	0.75	11.25	88.00	-	0.5
1404–1808	1.01 ± 0.04	0.75	5.63	93.63	-	1.0
1494–1941	1.06 ± 0.04	0.75	2.81	96.44	-	2.0	IDT	ST
852–1207	19.2 ± 1.4	2.66	19.95	-	77.39	1.0
820–1097	75.9 ± 6.4	2.66	19.95	-	77.39	1.0
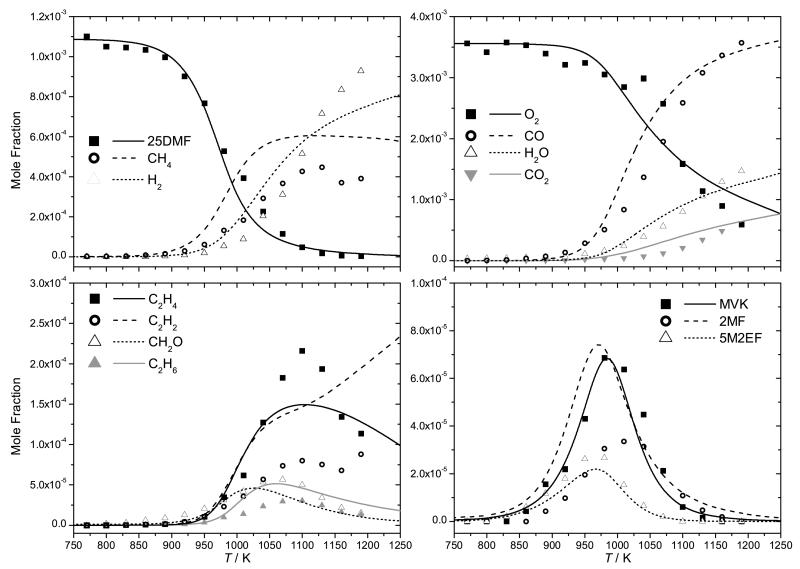
770–1100	10 ± 0.1	0.10	1.50	-	98.40	0.5
530–1160	10 ± 0.1	0.10	0.75	-	99.15	1	Speciation	JSR
770–1190	10 ± 0.1	0.10	0.38	-	99.53	2
298, 358	1	Synthetic air (O2:N2 = 21:79)				0.6–1.6	SL	Heat-flux

2.1 Shock tube studies

2.1.1 Pyrolysis

The single-pulse magic-hole type shock tube used to study the thermal decomposition of 25DMF has been described in detail by Hidaka et al. [42-45]. The reacted gas mixtures, quenched using the single-pulse method, were extracted into a preevacuated vessel (50 cm³) through a valve near the end plate. The gas mixtures were then analyzed using three serially connected gas chromatographs equipped with thermal conductivity detectors (TCD) [44,45].

25DMF concentrations were determined using a Shimadzu GC-8APT with 2 m column packed with Sebaconitrile and heated to 348 K. A Shimadzu GC-8APT with 2 m column packed with Porapak Q connected to a 2 m column packed with Unibeads 1S was used to determine the concentrations of C₂H₆, C₂H₄, C₂H₂ and C₃H₆ where a temperature gradient of 3 K per minute from 323 to 403 K was employed. A Shimadzu GC-8APT with 2 m column packed with Molecular Sieve 5A at 323 K was used to determine the concentrations of methane and CO in post-shock mixtures. Helium was used as a carrier gas. The output signals from each gas chromatograph were fed to Shimadzu Chromatopac C-R8A data processors.

An effective reaction time (t_e), defined as the time between heating of the mixture by the reflected shock wave and the time reflected shock pressure had fallen by 20%, was determined using the method described previously [43, 44]. Assuming the adiabatic expansion of a non-reactive mixture, the temperature drops by ≈ 8.5% from its initial value at t_e. Given that the single-pulse shock tube has cooling rates of 6.6 × 10⁵ K s⁻¹ [42], it can be assumed that the reaction was frozen at t_e. The validity of the effective heating time and cooling rate was previously tested for N₂O pyrolysis [42]. The uncertainties in the measured concentrations of small hydrocarbons in the post-shock mixtures are less than 2% except for 25DMF (Kanto Kagaku, 99% purity) where the estimated uncertainty of the post-shock concentration is less than 30%. The argon (99.9999%) was supplied by Iwatani.

The uncertainty in reaction time is 5% and in the reflected shock temperature ± 1%. Uncertainties in the reflected shock pressure are ± 0.15 atm based on the standard deviation (1σ) of our experiments.

2.1.2 Ignition delay times

Atmospheric pressure ignition delay times have been measured using a low pressure shock tube facility as described by Smith et al. [46] and briefly reiterated here. The tube is constructed from stainless steel with a short (62 cm) barrel shaped driver section and a 52 cm diameter coupled to a 622 cm long test section of 10.24 cm internal diameter. Shock waves are generated by piercing a polycarbonate diaphragm using a cross shaped blade. In the final 50 cm of the test section, four pressure transducers are mounted, (three in the sidewall, one at the endwall) in order to determine the shock velocity of the incident shock, with extrapolation to the endwall to account for attenuation of the shock wave. The GasEq application [47] was used to determine the reflected shock parameters from the known initial pressure, temperature and shock velocity via the usual one-dimensional gas equations.

We estimate an uncertainty of ±0.06 atmospheres in the reflected shock pressure based on the standard deviation (1σ) of our experiments. Uncertainties of 1% are present in the reflected shock temperature. An uncertainty of 20% is estimated in the ignition delay time of each experiment due to uncertainties in the conditions behind the reflected shock wave. Uncertainties in the mole fractions of reactants are minimal (< 5%) as high accuracy digital pressure gauges were used in the preparation of mixtures.

A photo-diode array (PDA) mounted in the sidewall with a 430 nm filter was used in order to determine light emission by excited CH⋆ upon ignition through a quartz window. The ignition delay time was defined as the time from arrival of the incident shock wave at the endwall, measured by a Kistler 603B transducer, and the maximum rate of change of light emission measured using the PDA. The maximum rate of change of CH⋆ concentrations has also been taken as the ignition delay time definition in our modelling of these experiments. Ignition delay times for mixtures of 0.75% 25DMF (Sigma Aldrich, > 99%) in 2.81%, 5.625% and 11.25% O₂ (BOC, > 99.99%) were measured using the above method in the high temperature regime (> 1300 K). Argon (BOC, > 99.99%) was used as the diluent gas and helium (BOC, > 99.99%) as the driver gas.

High pressure (20 and 80 bar) ignition delay time measurements for 25DMF in synthetic air at stoichiometric equivalence ratios were carried out in a shock tube facility at RWTH Aachen in the intermediate to high-temperature regime (820–1210 K). All experiments were performed behind reflected shock waves in a helium/air driven, stainless steel, high-purity shock tube with an inner diameter of 14 cm and an 11 m long driven section [48,49].

The driver and driven sections were separated by a double-diaphragm chamber, which houses two stainless steel or aluminium diaphragms, depending upon the desired test pressure. The facility was heated up to 383 K to keep the fuel vaporized and to avoid condensation prior to the experiment. The 25DMF-synthetic air mixtures were prepared directly in the driven section of the shock tube. The 25DMF (Sigma Aldrich, 99%) was injected into the evacuated driven section. After evaporation, the synthetic air (Westfalen, 20.5% O₂ and 79.5% N₂) was added manometrically, and test mixtures were allowed to mix for 1 hour to ensure homogeneity and consistency.

The incident shock velocity was measured using six piezoelectric pressure transducers (Kistler 603B, 601H and 6005), located over the last 2.5 m of the driven section. Pressure-time profile measurements were made with the piezoelectric pressure transducer located 10 mm from the endwall. All piezoelectric pressure gauges were shielded with a thin coating of silicone rubber to dampen the heat flux transfer from the hot gas to the pressure probe [48]. Light emission from CH⋆ at a wavelength of 430 nm was also measured using a photomultiplier (Hamamatsu, R212UH) through a narrow band pass filter (LOT 430FS10, FWHM 10 ± 2 nm) at an observation window located at the same axial location as the sidewall pressure transducer.

The ignition delay time was defined as the time difference between the arrival of the reflected shock wave at the endwall of the shock tube and the ignition event recorded by an abrupt pressure rise at the sidewall observation location (10 mm from the endwall), which is coincident (within 3%) with the CH⋆ emission rise signal, Figure 1.

Fig. 1.

Typical pressure and CH⋆-emission time profiles for ignition delay measurement and definition for 2.66% 25DMF, 19.95% O₂ and 77.39% N₂ at 1009 K and 81.9 bar. 1 – arrival of incident shock wave at sidewall pressure transducer, 2 – arrival of incident shock wave at endwall and corresponding transition to reflected shock conditions (T₅, p₅, t = 0.0), 3 – arrival of reflected shock wave at sidewall pressure transducer.

The pre-shock test mixture pressure (p₁), temperature (T₁) and the incident shock velocity were used to determine initial conditions (p₅ and T₅) behind the reflected shock wave using the KASIMIR [50] software package. The uncertainty of T₅ has been calculated from the uncertainties in the measured shock velocity (±0.3%), T₁ and the filling pressure, and is close to ± 10 K [48-50]. Uncertainties in reactant mole fractions are estimated to be < 3%.

2.2 Oxidation in a jet-stirred reactor

A fused-silica spherical jet-stirred reactor (JSR) similar to that used previously [51] and operating up to 10 atm was used to determine reactant (25DMF/O₂) and intermediate species profiles. It was located inside a regulated electrical resistance oven of 1.5 kW, which was surrounded by insulating ceramic wool and a stainless steel pressure-resistant jacket.

The liquid fuel (Sigma Aldrich, > 99% purity) was pumped, using a micro piston HPLC pump (Shimadzu LC-120 ADvp) with an on-line degasser (Shimadzu DGU-20 A3). The fuel was sent to an in-house stainless steel atomizer-vaporizer assembly maintained at 448 K, with a 50 L/h flow of nitrogen used for the atomization. The oxygen (99.995% purity) flow was diluted by a separate flow of nitrogen (< 50 ppm of O₂; < 1000 ppm of Ar; < 5 ppm of H₂). The O₂-N₂ flow was mixed with the fuel-N₂ flow just before the entrance of the injectors, after pre-heating. All the gases were regulated by thermal mass-flow controllers (Brooks 5850E).

Residence time distribution studies showed that under the conditions of the present study the reactor is operating under macro-mixing conditions [51]. As in previous work [51,52], thermocouple measurements were made using 0.1 mm diameter Pt/Pt-Rh 10% wires located inside a thin-wall fused-silica tube to prevent catalytic reactions on the wires. These measurements showed good thermal homogeneity along the vertical axis of the reactor. Typical temperature gradients of approximately 2 K/cm were measured.

Since the experiments were performed under high dilution, the temperature rise due to fuel oxidation was generally ≤ 30 K. Low pressure samples of the reacting mixtures were taken by sonic probe sampling and collected in 1 liter Pyrex bulbs at 40 mbar for immediate GC analysis, as in previous work [52-54].

For the measurements of hydrocarbons and oxygenates, capillary columns of 0.32 mm i.d. (DB-624, 50 m and Al₂O₃/KCl, 50 m) were used with a flame ionization detector (FID) using helium as the carrier gas. Hydrogen and oxygen were measured using a 0.53 mm internal diameter capillary column (Carboplot, 25 m) fitted to a thermal conductivity detector (TCD). Nitrogen was used as the carrier gas. Online Fourier transform infra-red (FTIR) analyses of the reacting gases were also carried out by connecting the sampling probe to a temperature controlled gas cell maintained at 413 K, via a Teflon heated line kept at 483 K.

The sample pressure in the 10 m path length cell was 0.2 bar and a 0.5 cm⁻¹ resolution was used for the data acquisition. This analytical equipment allowed for measurements of the reactants (oxygen and 25DMF), and products: H₂, H₂O, CO, CH₂O, CO₂, CH₄, C₂H₆, C₂H₄, C₂H₂, CH₃CHO, 2-propenal, acetone, propyne, allene, 2-methyl furan, 5-ethyl-2-methylfuran, 5-methyl-2-formylfuran, methyl vinyl ketone, 3-penten-2-one, C₃H₆, 1-C₄H₈, 2-C₄H₈, 1,3-C₄H₆, 1,3-cyclopentadiene, 4-methylene cyclopentene, 1-methyl 1,3-cyclopentadiene and benzene. As previously noted [53, 54], good agreement between the GC and FTIR analyses was observed for the compounds measured using both techniques.

Uncertainties in reactant mole fractions are typically <10%, in residence time <5%, in pressure <0.1 atmosphere and in measured species concentrations < 15% based on carbon balance.

2.3 Laminar Burning Velocities

The heat-flux method for determining the adiabatic burning velocity of laminar flames was first proposed by de Goey et al. [19] in 1993. When compared with combustion bombs or counter-flow flame burners for example, the ability to forego post-experimental correction of data for the influences of stretch make the heat-flux method an efficient and accurate way of determining the laminar burning velocity of a fuel-oxidiser mixture. The apparatus at the LRGP in the Université de Lorraine and experimental method have been described recently by Dirrenberger et al. [55], where the validity of the apparatus was also verified through comparison with literature experimental data for alkanes from methane to propane. The apparatus has also been used recently to validate kinetic mechanisms for liquid fuels including diethyl ether [56] and 2-methylfuran [41]. Only essential points on the apparatus will be noted here.

The heat-flux method relies on measurement of the radial temperature distribution on the surface of the burner plate upon which the flame is to be stabilised. In this instance, eight type K thermocouples (TC S.A. Dardilly, France) of 0.5 mm diameter are soldered onto the plate in order to measure the temperature distribution. When the radial temperature distribution is uniform, the heat loss from the flame to the burner plate is in equilibrium with the heat flux from the burner plate to the fresh gases and consequently, no net heat flux is observed. By adjusting the flow rate of the unburnt gases, in this case using Bronkhorst High-Tech Mass Flow Controllers, the adiabatic flame burning velocity can be determined. When the temperature distribution of the plate is homogeneous, the mass flow rate of the unburnt gases equals the laminar burning velocity of the specific mixture.

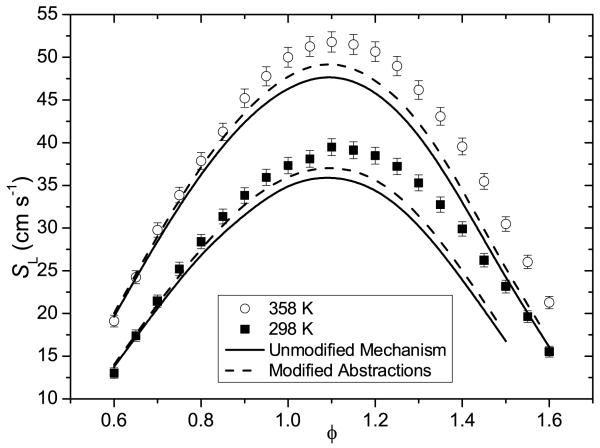
Laminar burning velocities for 25DMF-synthetic air mixtures have been measured at atmospheric pressure, initial temperatures of 298 and 358 K and ϕ = 0.60–1.60 based on this principle. Uncertainties in determination of the burning velocity are due to uncertainties in:

• mass flow measurements, with a maximum uncertainty of 0.5% per mass-flow controller, as given by the manufacturer, Bronkhorst, which result in a maximum global uncertainty in laminar burning velocity of 1.5%.

• the thermocouples, with an uncertainty of 0.2 cm s⁻¹ in the laminar flame velocity. This uncertainty was measured by changing the gas flow rate by small amounts that did not affect the uniform temperature profile of the flame on the burner plate noticeably.

• flame distortions, for example edge effects, with an uncertainty of 0.2 cm s⁻¹ in the laminar flame velocity in the range of equivalence ratios studied. This uncertainty was measured similar to the uncertainty in the thermocouples.

Based on these uncertainties discussed above, the final uncertainty (σ, cm s⁻¹) in the measured laminar burning velocity (S_L) is computed via:

$$\sigma =(S_L\times 0.015)+0.4$$

Uncertainties of around 1% were also present when determining the equivalence ratio due to mass flow effects, as given by Bronkhorst. The temperature of the unburnt gas mixture before and after it flowed through the plenum chamber was measured with a thermocouple. An uncertainty of 2 K was estimated. Uncertainties in gas and liquid fuel purity were not significant as high purity compounds (25DMF, 98% purity, Alfa Aeser; O₂ and N₂, 99.995% purity, Messer) were used.

2.4 Computational methods

Modelling of experiments was carried out using the Chemkin-Pro [57] application. The Aurora module under constant volume conditions is utilised for the simulation of low pressure shock tube ignition delay times and speciation data and JSR profiles. The Aurora module under constant pressure conditions was also used to simulate the flow reactor experiments of Djokic et al. [39].

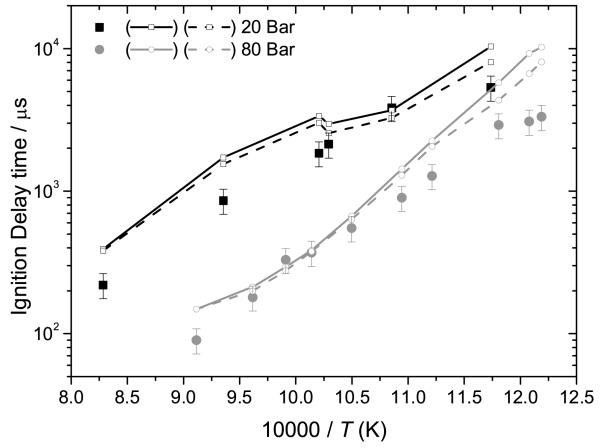
Simulations of high pressure ignition delay time experiments are carried out through inclusion of a volume-time profile, which is created from the experimental pressuretime profile, knowing the functional relationship between the volume and pressure of a gaseous mixture undergoing isentropic compression/expansion. Every experimental data point therefore receives individual simulation under the reflected shock temperatures and pressures of interest. For 20 bar experiments the % pressure rise used in simulation was of the order of 5.51 ± 0.38% per millisecond and at 80 bar, 3.52 ± 0.94% per millisecond. This approach is necessary to adequately describe facility effects given the extended test times of our experiments (> 1 ms). We also compare this approach with constant volume-constant internal energy simulations, which are known to adequately describe shock tube experiments of dilute mixtures which undergo ignition on shorter time scales, such as those used in the simulation of our low pressure shock tube measurements. Experimental pressure-time profiles, and corresponding volume-time profiles are included in the supplementary material.

Burning velocity simulations have been carried out using the Premix module. All flame speed simulations were carried out to a GRAD and CURV of 0.1 and include thermal diffusion effects. Converged simulations typically contained on the order of 300 grid points. For the simulation of laminar burning velocities, the mechanism was reduced in order to consistently achieve convergence to this criteria, given the size of the current mechanism. Reactions of all species larger than toluene are therefore removed for simulation of laminar burning velocity, as well as pathways relevant to the low temperature oxidation of species in the C₀–C₄ sub-mechanism. The final mechanism used for laminar burning velocity calculations consisted of 432 species and 2143 reactions. The mixture-average transport approximation was also used to reduce the computational burden.

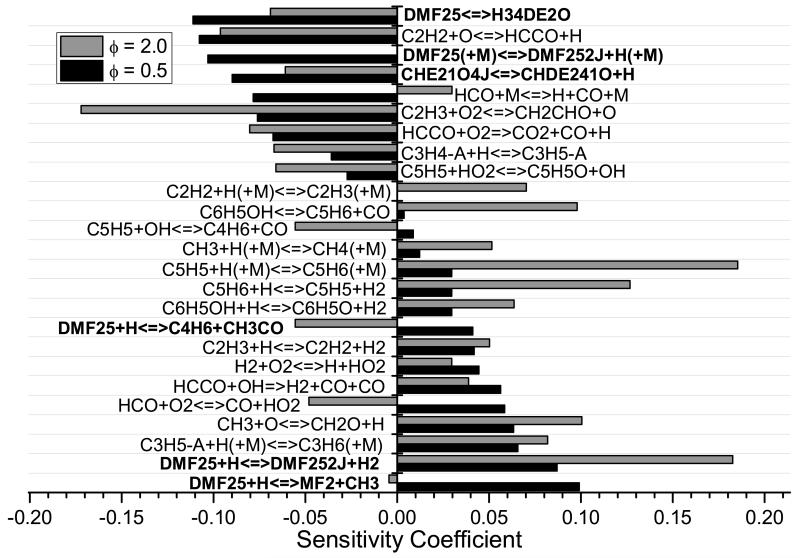
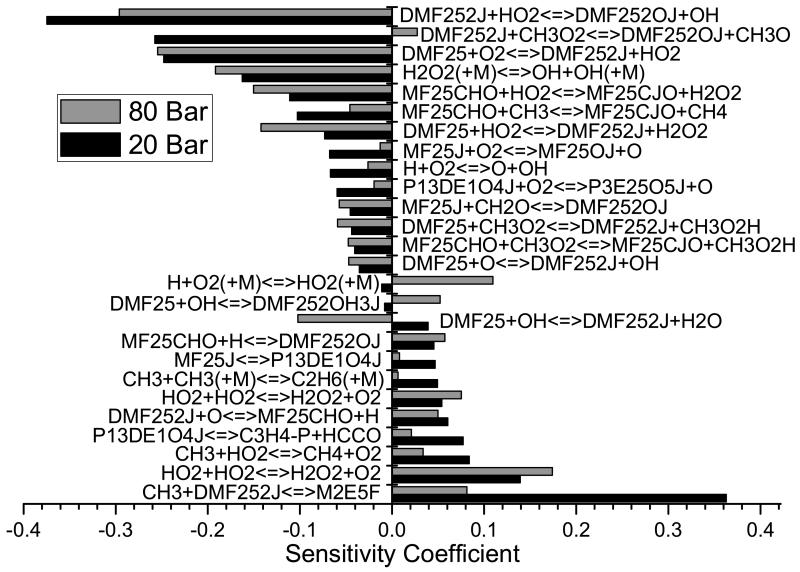
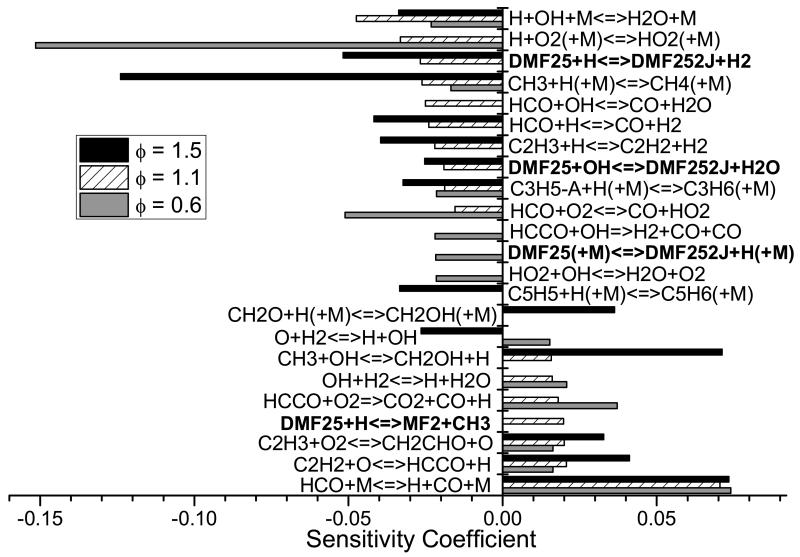
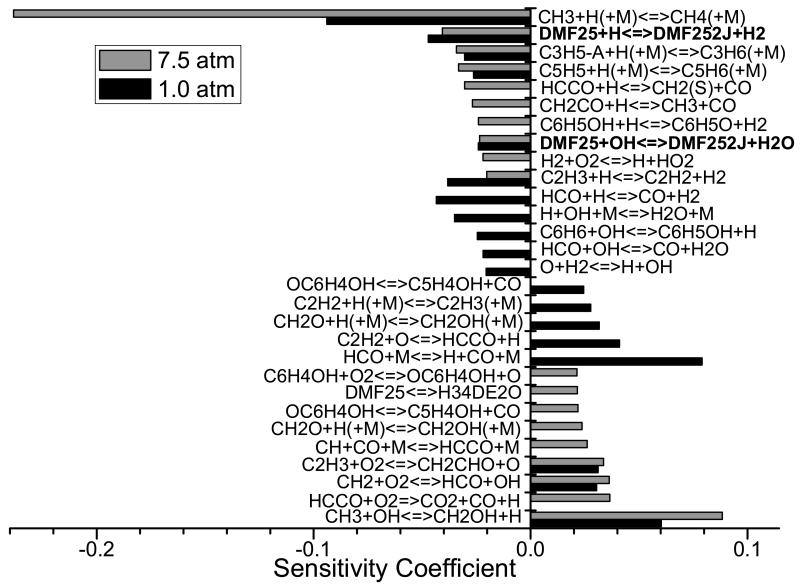
Sensitivity analyses were carried out in order to identify the key reactions which control ignition delay time calculations. For each reaction in the current mechanism, rate constants are multiplied by two, divided by two and the respective ignition delay times calculated in a “brute force” approach. Sensitivity coefficients (S_i) are then calculated via:

$$S_i={\log }_{10}\left\{\right({\tau }_{k\times 2}∕{\tau }_{k∕2})∕{\log }_{10}(2∕0.5\left)\right\}$$

with a negative sensitivity coefficient indicative of a reaction which promotes reactivity and vice versa. The first order sensitivity coefficient of the mass flow rate to the A-factor of each rate constant was used to identify kinetic parameters controlling the calculated laminar burning velocities. This approach was implemented using the “ASEN” keyword of the Chemkin-Pro software package.

Specific rate constant calculations have been carried out where analogy with a similar system is not possible. The CBS-QB3 [58], CBS-APNO [59] and G3 [60] levels of theory were used to calculate optimised geometries, frequencies and single point energies for reactants and transition states with the Gaussian 03 and 09 packages [61]. Transition states were connected to products and reactants with intrinsic reaction co-ordinate (IRC) calculations. Relaxed potential energy surface scans are carried out where low-frequency torsional modes exist to determine potential energy and rotational constants as a function of dihedral angle as part of a 1-D hindered rotor treatment. High pressure limiting rate constants and thermochemical parameters are determined using transition state theory and statistical thermodynamics respectively, via the Thermo module of the Multiwell program [62].

3 Kinetic Model Development

3.1 Unimolecular decomposition

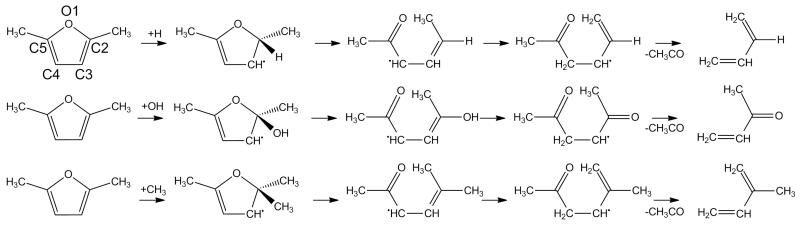
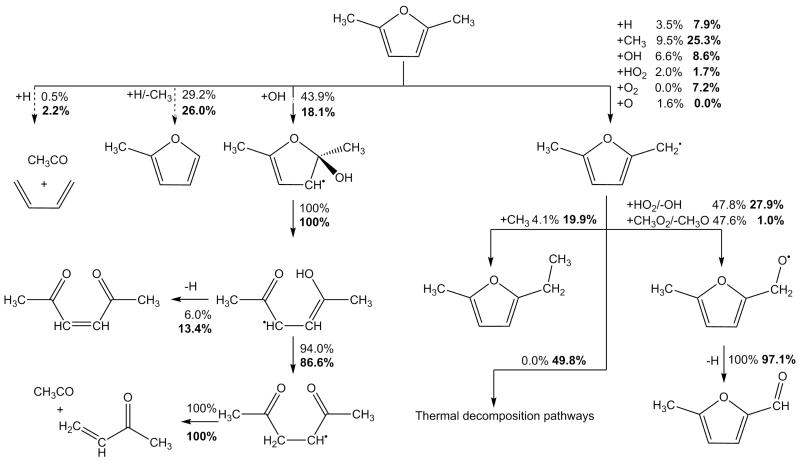
The unimolecular decomposition pathways of 25DMF have been studied by Simmie and Metcalfe [29] previously, and more recently in detail by Sirjean and Fournet [32]. Both works concluded that the thermal decomposition of 25DMF should proceed with competition between simple C–H bond fission from the alkyl side chain of the fuel, and carbene formation and consumption via hydrogen atom transfer reactions. Simmie and Metcalfe [29] calculated a high pressure limit rate constant of 9.48 × 10¹³ exp(−35230/T) s⁻¹ for a 3-2 hydrogen atom transfer reaction forming a β-carbene, in good accord with the analogous reaction in furan [24]. For the same process Sirjean and Fournet [32] report an almost identical rate constant of 4.93 × 10¹¹T^0.659 exp(−34577/T) s⁻¹.

Both sets of authors also found that the β-carbene intermediate, formed from a 3-2 hydrogen atom transfer reaction, undergoes ring opening readily to form 3,4-hexadiene-2-one, in a reaction with virtually no barrier. Sirjean and Fournet [32] carried out RRKM/ME calculations on this multiple-well system, reporting pressure dependent rate constants for the carbenic decomposition pathway which we adopt in this study, as well as further unimolecular decomposition reactions of 3,4-hexadiene-2-one. The primary decomposition pathway of 3,4-hexadiene-2-one was found to be a simple fission reaction forming CH₃—Ċ=O and CH≡C—ĊH—CH₃, which in turn could decompose to form ĊH₃ radical and CO, or CH≡C—CH=CH₂ and Ḣ atom respectively. Kinetics from the study of Sirjean and Fournet are adopted [32] in the current work.

For the homolytic fission of the alkyl C–H bonds in 25DMF, two estimates currently exist in the literature for the process. Lifshitz et al. [21] recommended a rate constant of 1.60 × 10¹⁶ exp(−43276/T) s⁻¹, which is an empirical estimate derived from fitting to a complex mechanism. Friese et al. [30] measured Ḣ atom concentrations upon shock heating of dilute 25DMF/argon mixtures and recommended a high pressure limiting rate constant of 3.5 × 10¹⁶ exp(−42817/T) s⁻¹ for the simple fission reaction. However, the rate constant estimated by Friese et al. [30] is a global measurement of Ḣ atom production from the thermal decomposition of 25DMF, and does not account for the formation of Ḣ from the β-carbene pathway described above.

Somers et al. [41] recently used a recombination rate constant of 1×10¹⁴ cm³ mol⁻¹ s⁻¹ as an estimate for the recombination of hydrogen atom with the 2-furanylmethyl radical in the case of 2MF, thus implying a decomposition rate constant of 2.52 × 10¹²T^0.9 exp(−42974/T) s⁻¹ from microscopic reversibility. Likewise, Sirjean and Fournet [32] assumed a similar rate constant for the recombination of hydrogen atom with the 5-methyl-2-furanyl-methyl radical, 6.55 × 10¹³T^0.07 exp(+25.9/T) cm³ mol⁻¹ s⁻¹, based on analogy with the recombination of hydrogen atom with benzyl radical. A unimolecular decomposition rate constant for the simple fission reaction of 4.75 × 10¹⁵T^0.07 exp(−43125/T) s⁻¹ was implied from microscopic reversibility, in good agreement with the estimate of Somers et al. [41] for the 2MF system accounting for reaction path degeneracy, and within a factor of 2 of that estimated by Lifshitz et al. [21]. Kinetics from the study of Sirjean and Fournet are adopted.

3.2 Fuel-radical reactions

Kinetic studies on the reactions of Ḣ with 25DMF are perhaps the most thoroughly investigated pathways on the combustion reactions of 25DMF to date. Simmie and Metcalfe [29] investigated numerous abstraction pathways from 25DMF in their theoretical work, recommending a rate constant of 3.86 × 10⁵T^2.68 exp(−2683/T) cm³ mol⁻¹ s⁻¹ for hydrogen atom abstraction by Ḣ atom from the alkyl side chain of the molecule. Their computed rate constant of 7.78 × 10⁷T^2.00 exp(−10156/T) cm³ mol⁻¹ s⁻¹ for the same process from the ring carbon bonds clearly illustrated that for abstraction reactions, the dominant pathways are from the alkyl side chain.

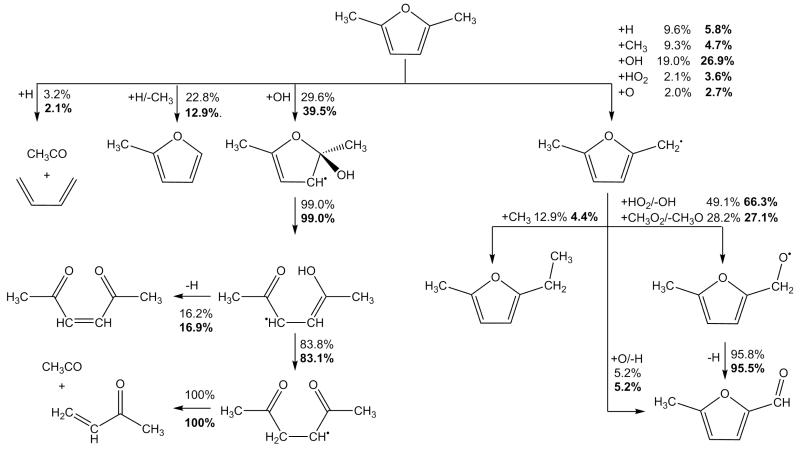
However, they found that Ḣ atom addition reactions are dominant up to 2000 K, with a high pressure limiting rate constant of 8.84 × 10⁸T^1.50 exp(−782.7/T) cm³ mol⁻¹ s⁻¹ reported for addition to C2 of the furan ring (see Figure 2 for atomic notation). Subsequent demethylation of the adduct was reported to occur with a rate constant of 1.974 × 10⁵ exp(−16469/T) cm³ mol⁻¹ s⁻¹, thus elucidating the formation of 2MF from 25DMF.

Fig. 2.

Radical addition pathways to 2,5-dimethylfuran included in the current mechanism along with numbering scheme of furan ring.

More recently, Sirjean and Fournet [33] carried out CBS-QB3 calculations to explore the reactions of hydrogen atom with 25DMF. They found addition to C2, followed by ring opening of the nascent radical was competitive with the demethylation process. RRKM/ME calculations on their potential energy surface showed that 2MF and ĊH₃ radical, and 1,3-butadiene and CH₃—Ċ=O radical were the dominant products upon the chemically activated addition of hydrogen to 25DMF. Their reported rate constant for the reaction of hydrogen atom with 25DMF is within a factor of two of experimental measurements [31]. They report rate constants for the reaction of 25DMF+Ḣ to form bimolecular products and radical intermediates (Figure 2) at pressures of 1–10 bar, which we utilize in this work.

For the reactions of ȮH radical with 25DMF, both abstraction and addition pathways are included in the current kinetic mechanism. The rate constant for abstraction from the methyl group is based on a theoretical determination by Simmie and Metcalfe [29] of 1.016 × 10⁴T^3.133 exp(−1085/T) cm³ mol⁻¹ s⁻¹. For ȮH radical addition to the furan ring we include only addition to C2, as remote addition tends to lead to less stable radical intermediates as exhibited in the case of Ḣ atom addition. A rate constant has been calculated as part of this work based on CBS-APNO and G3 calculations of the reactants and transition state. The transition state for the addition process is found to lie 27.59 kJ mol⁻¹ and 24.13 kJ mol⁻¹ below the reactants at these two levels of theory respectively, in substantially good agreement with one another.

A rate constant of 2.21 × 10⁴T^2.45 exp(+3649/T) cm³ mol⁻¹ s⁻¹ is computed in the temperature range 600-2000 K, the reaction displaying a negative activation energy. A pre-reaction complex is found based on IRC analysis, but its influences are not accounted for in the present rate constant calculations as it is likely to be unimportant in the temperature ranges of this study. The computed rate constant is in good agreement with CCSD(full)/6-11+G(3df,2p) RRKM calculations for the reaction of ȮH radical with furan computed recently by Mousavipour et al. [63]. They also concluded that ȮH radical addition to C3 of furan, or abstraction of any of the ring–H bonds, was unimportant in comparison with this addition process. We estimate an uncertainty of a factor of 3 in the high pressure limiting rate constant for the addition process therefore.

The product of ȮH radical addition can undergo ring opening by β-scission of the C–O bond of the furan ring, Figure 2. The pre-exponential factor of the rate constant is estimated from the similar ring opening process after hydrogen atom addition to C2 of 25DMF. A reduction in the activation energy of 4.2 kJ mol⁻¹ is included to account for the electron withdrawing effect of the oxygen atom adjacent to the breaking ring C–O bond. The ring opening product, 3-hexene-2-one-5-hydroxyl-3-yl, is a heavily functionalised resonantly stabilised radical. A hydrogen atom transfer reaction from the hydroxyl group to the radical site at C3 of the hydrocarbon chain to form 2,5-hexadione-3-yl is computed to have a rate constant of 4.27 × 10⁷T^1.49 exp(−14668/T) s⁻¹. 2,5-hexadione-3-yl can in turn undergo β-scission to form methyl vinyl ketone (3-butene-2-one) and CH₃—Ċ=O radical, the rate constant for which is estimated in the reverse addition direction, based on analogy with external CH₃—Ċ=O radical addition to 1,3-butadiene [33].

A second plausible reaction for the product of hydroxyl radical addition is a demethylation reaction to form 5-methyl-2-furanol. We estimate the rate constant for the process in the exothermic radical addition direction based on the addition of ĊH₃ radical to 2-methylfuran [33], with a rate constant of 2.99 × 10⁴T^2.34 exp(−3478/T) cm³ mol⁻¹ s⁻¹.

For the reactions of ĊH₃ radical with 25DMF, both hydrogen atom abstraction and ĊH₃ radical addition reactions are considered. Abstraction from the alkyl side chain is computed to have a rate constant of 1.26×10³T^3.02 exp(−3734/T) cm³ mol⁻¹ s⁻¹. For the addition process we again use an analogy with reaction of ĊH₃ radical with 2-methylfuran [33]. This estimate is based on the closest analogy possible, and an uncertainty in this rate constant as small as 2–3 is reasonable. Based on these estimates, hydrogen atom abstraction is found to be the dominant pathway, the rate constant being a factor of 2.85 times greater than addition at 800 K and 6.48 times greater at 2000 K. This is somewhat reinforced by past studies [21, 38] and the current study in which the product of this ĊH₃ radical addition pathway (Figure 2), 2-methyl-1,3-butadiene, has not been detected.

Abstraction by HȮ₂ radical from the alkyl side chain is computed to have a barrier at 0 K of 40.81 kJ mol⁻¹ at the CBS-QB3 level of theory, with G3 calculations differing substantially with a computed barrier of 57.23 kJ mol⁻¹. Based on B3LYP/CBSB7 partition functions and a 1-D hindered rotor treatment of low frequency torsional modes, a pre-exponential factor of 1.98T^3.78 cm³ mol⁻¹ s⁻¹ is computed for the reaction. The Boltzmann factor can assume values of exp(−6207/T) or exp(−4234/T) based on G3 or CBS-QB3 energetics respectively. Ultimately, the rate constant used in the current mechanism is based on G3 energetics, as use of the CBS-QB3 results was found to have a deleterious impact on JSR predictions. Use of the G3 results leads to positive predictions of JSR profiles however, and an uncertainty of 4–5 in this rate constant is a reasonable assignment. For hydrogen atom abstraction by CH₃Ȯ₂ radical from the same site, we simply reduce the frequency factor for abstraction by HȮ₂ radical by a factor of three.

For the reactions of 25DMF with molecular oxygen, an abstraction pathway is included based on an Evans-Polanyi relationship to determine the activation energy. Activation energies and enthalpies of reaction for this relationship are based on the kinetic and thermodynamic parameters contained within the C₀–C₄ sub-mechanism detailed in Section 3.4 below. The activation energy was found to relate to the heat of reaction via:

$$E_a=1.055{\Delta }_{r}H-9.44$$

with units of kJ mol⁻¹. The correlation showed good linearity with R² = 0.94. Given an enthalpy of reaction of 149.1 kJ mol⁻¹ for the abstraction reaction in question, an activation energy of 147.5 kJ mol⁻¹ follows. To determine the pre-exponential factor of this rate constant, we analyse the frequency factors of those reactions utilised in the above Evans-Polanyi relationship on a per hydrogen atom basis. Values range from a lower limit of 7 × 10¹¹ cm³ mol⁻¹ s⁻¹ to an upper limit of 3 × 10¹³ cm³ mol⁻¹ s⁻¹. Here we find abstraction by O₂ to be a sensitive parameter in terms of the current mechanism performance against ignition delay times measurements in the intermediate temperature regime, with a pre-exponential factor of 1.25×10¹³ cm³ mol⁻¹ s⁻¹ assumed in order to replicate these experiments and preliminary rapid compression machine experiments to be discussed in detail in the future. We believe an uncertainty of a factor of 4–5 still exists in this rate constant based on the method of estimation used, and the rate coefficient we adopt may represent an upper limit for this process.

Abstraction of a hydrogen atom by atomic oxygen showed little sensitivity to any of the current validation targets, so we assume it to equal the rate of hydrogen atom abstraction of a benzylic-type hydrogen from toluene [68] with a two-fold increase in the pre-exponential factor to account for reaction path degeneracy.

3.3 Unimolecular and bimolecular consumption reactions of 5-methyl-2-furanylmethyl radical

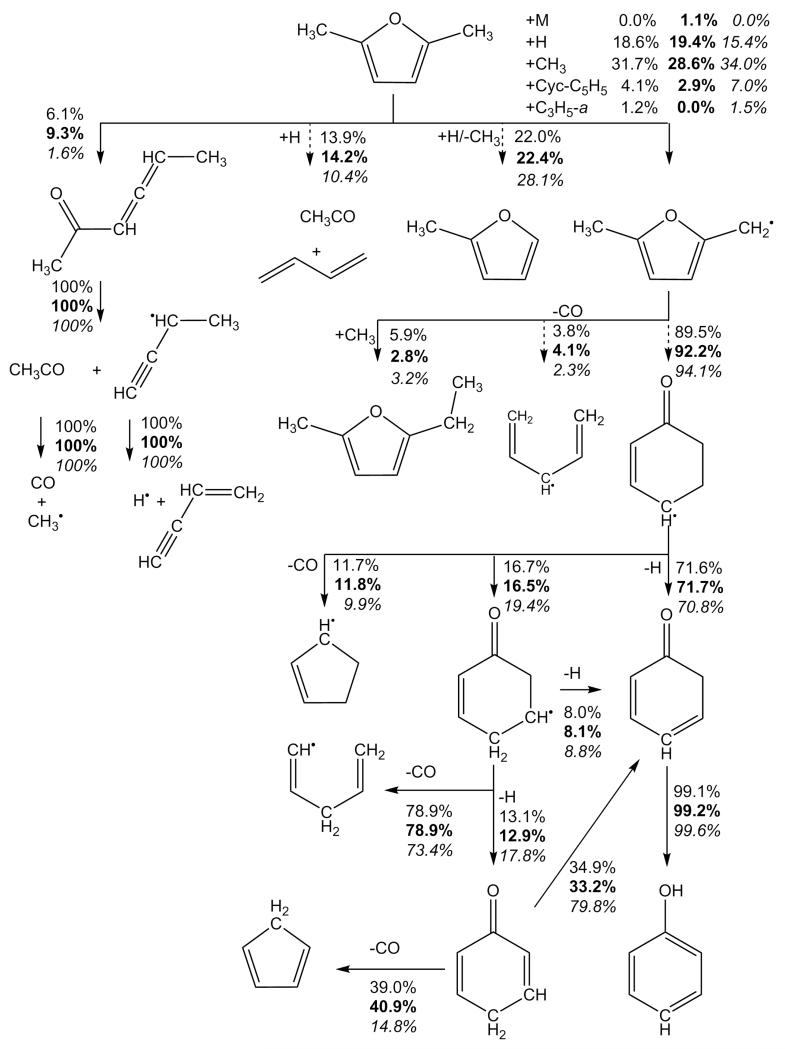
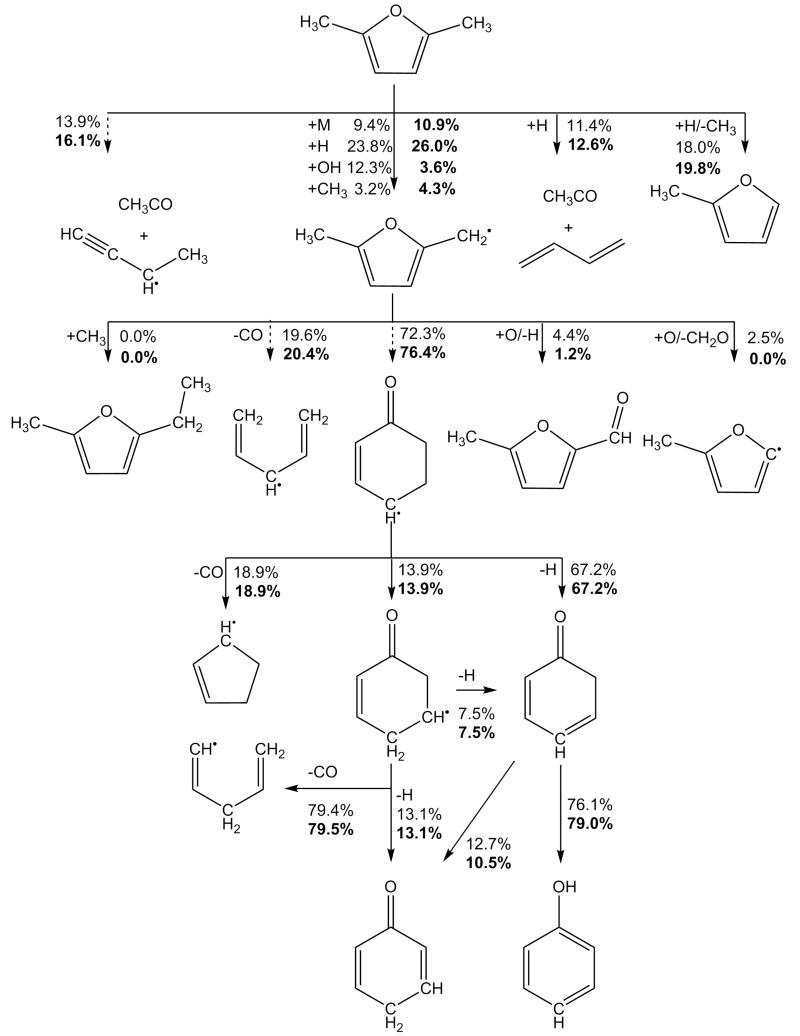
The 5-methyl-2-furanylmethyl radical, 25DMF2R henceforth, is the primary product of hydrogen atom abstraction reactions from 25DMF and a discussion on its fate under combustion conditions is relevant. The kinetics of the thermal decomposition of the 25DMF2R radical have recently been studied in detail using CBS-QB3 calculations and RRKM/ME modelling [34]. The important consumption pathways will be briefly re-iterated and can be seen in Figure 3. The reaction was found to proceed primarily via ring opening, to produce an acyclic ketone, 4,5-hexadiene-2-one-3-yl, which can isomerize via hydrogen atom transfer to form, 3,5-hexadiene-2-one-1-yl. 3,5-hexadiene-2-one-1-yl can in turn undergo a 6-membered ring closing reaction to form a 2-cyclohexene-1-one-4-yl which can decompose to form 2,4-cyclohexadiene-1-one and a Ḣ atom. Other possible pathways could lead to the formation of 2,5-dimethylene furan and a Ḣ atom, 2,5-cyclohexadiene-1-one and a Ḣ atom or carbon monoxide and a range of linear and cyclic Ċ₅H₇ radicals closely related to 1,3-pentadiene and 1,3-cyclopentadiene. Thermodynamics parameters for all Ċ_6H7O species involved in these pathways are taken from Sirjean and Fournet [34].

Fig. 3.

Primary thermal decomposition pathway of 5-methyl-2-furanylmethyl radical [34] showing key intermediates with IUPAC names.

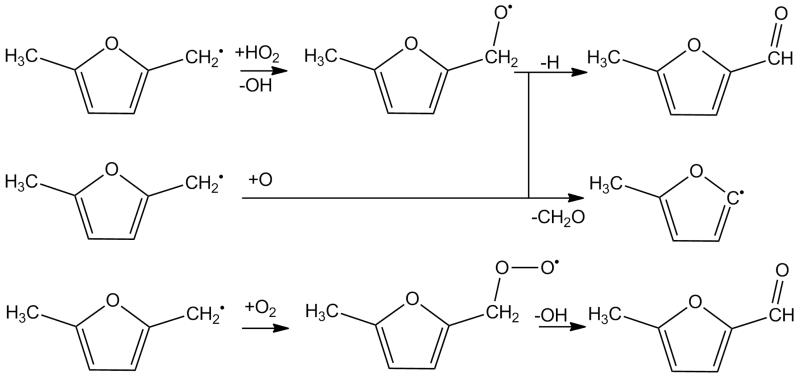
The reactions of resonantly stabilised radicals with HȮ₂ radical are known to be important in the intermediate temperature combustion regime and at high pressures for reactants such as propene and toluene, but no discussion on this reaction class exists in the literature for 25DMF. Franklin Goldsmith and co-workers [64] recently studied the reaction of allyl with HȮ₂ using high-level ab initio calculations and RRKM/ME methods to compute temperature and pressure dependent rate constants and product branching ratios. They determined that the reaction of CH₂=CH—ĊH₂ + HȮ₂ proceeds primarily to CH₂=CH—CH₂—Ȯ + ȮH via chemical activation. Using similar methods, da Silva and Bozzelli [65] showed that the reaction of the resonantly stabilised benzyl radical with HȮ₂ radical proceeds via chemical activation to form benzoxyl radical and ȮH radical. At atmospheric pressure and from 800–2000 K they recommend a rate constant of 1.19 × 10⁹T^1.03 exp(+1132/T) cm³ mol⁻¹ s⁻¹ for this chemically activated process, with the rate constant having an average value of 4.78 × 10¹² cm³ mol⁻¹ s⁻¹ in this regime. In a similar work, da Silva and co-workers [66] also showed that the chemically activated recombination of a Ḣ atom with benzylperoxy radical proceeds almost exclusively to benzoxyl and ȮH radicals over a wide range of temperatures and pressures.

Based on the work of da Silva and Bozzelli [65], here we assume a temperature and pressure independent rate constant of 5.0 × 10¹² cm³ mol⁻¹ s⁻¹ for the reaction of 25DMF2R + HȮ₂ → 5-methyl-2-furylmethanoxy radical + ȮH, with the intermediate peroxide species omitted in our scheme, Figure 4. For the reaction of a CH₃Ȯ₂ radical with 25DMF2R to form 5-methyl-2-furylmethanoxy radical and CH₃Ȯ radical, we assume the same pressure and temperature independent rate constant. We believe an uncertainty of 2–3 exists in these estimated rate constants.

Fig. 4.

Oxidation pathways of 5-methyl-2-furanylmethyl radical included in the current mechanism.

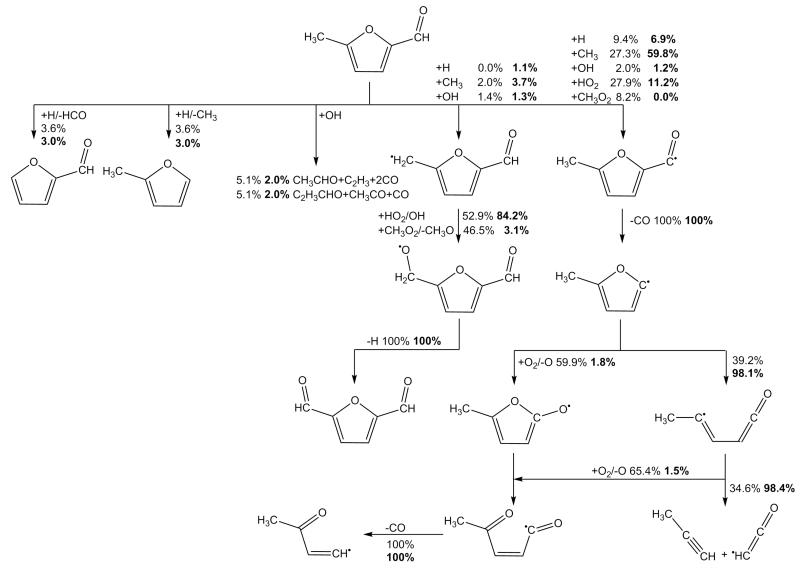
The 5-methyl-2-furylmethanoxy radical can in turn undergo β-scission to form 5-methyl-2-formyl furan and a Ḣ atom or 2-methyl-5-furanyl radical and CH₂O. For these reactions, we have drawn analogy with the decomposition of the benzoxyl radical to benzaldehyde and a Ḣ atom and/or phenyl radical and CH₂O. For the decomposition to 5-methyl-2-formylfuran and Ḣ atom, we assume a rate constant of 1.13 × 10¹²T^0.22 exp(−1702/T) cm³ mol⁻¹ s⁻¹ for the addition reaction, which is derived from the rate constant provided for the decomposition of benzoxyl to a Ḣ atom and benzaldehyde from Sakai et al. [67]. The thermochemical parameters used for computation of the equilibrium constant are those supplied in the kinetic modelling study of Metcalfe and co-workers [68]. The rate constant for the decomposition of the 5-methyl-2-furylmethanoxy radical to formalydehyde and 2-methyl-5-furanyl radical is similarly derived. In turn unimolecular decomposition rates for the 5-methyl-2-furylmethanoxy radical to these respective products are given as 7.72 × 10¹²T^0.04 exp(−8397/T) s⁻¹ and 1.48 × 10¹²T^0.77 exp(−14746/T) s⁻¹, thus implying that the channel forming 5-methyl-2-formylfuran and a Ḣ atom is dominant throughout the temperature range of interest in this work, as expected given the instability of the vinylic 2-methyl-5-furanyl radical which is produced with formaldehyde.

The above product set can also be plausibly formed from the reaction of atomic oxygen with 25DMF2R. Here we estimate rate constants for 25DMF2R + Ö → 5-methyl-2-formylfuran + Ḣ or 2-methyl-5-furanyl + CH₂O based directly on those used in recent kinetic modelling studies of toluene oxidation [67,68] in the case of benzyl + Ö.

Reaction with molecular oxygen is another plausible consumption pathway for 25DMF2R radical, Figure 4. The initial formation of the RȮ₂ adduct is found to be exothermic by some −66.7 ± 3.61 kJ mol⁻¹ (0 K) based on CBS-QB3, CBS-APNO and G3 calculations. The analogous reaction in the case of the allyl radical was recently found to be exothermic by −75.6 ± 2.3 kJ mol⁻¹ [70]. In the case of the reaction of benzyl radical with O₂, Murakami and co-workers [71] found the adduct to have a well depth of 93.3 kJ mol⁻¹ at the CBS-QB3 level of theory.

From a kinetic perspective, Murakami et al. [71] carried out temperature and pressure dependent computations of the product branching ratios concluding that back-dissociation to benzyl and O₂ was the dominant reaction pathway by some orders of magnitude, followed by the formation of benzaldehyde and ȮH radical. Here we assume the high pressure limiting rate constant for the reaction of 25DMF2R with O₂ is equal to the high pressure limiting rate constant for the reaction of benzyl with O₂ at 6.58 × 10³¹T^−6.38 exp(−3346/T) cm³ mol⁻¹ s⁻¹. A rate constant of 8.50×10³⁶T^−7.61 exp(−11770/T) s⁻¹ for the dissociation of the adduct to 25DMF2R and O₂ follows from microscopic reversibility. In terms of the RȮ₂ decomposition, a hydrogen atom transfer reaction with concerted elimination of ȮH radical to form 5-methyl-2-formylfuran was computed by Simmie and Metcalfe [29] to have a rate constant of 1.46 × 10¹³ exp(−24192/T) s⁻¹, which we also adopt. Based on the branching ratios for the consumption of the furanic RȮ₂ species, back dissociation to radical and O₂ is dominant throughout the temperature range of this work.

The recombination of methyl radical with 25DMF2R forming 5-methyl-2-ethylfuran has also been considered as part of this work. A temperature independent recombination rate constant of 2.50 × 10¹³ cm³ mol⁻¹ s⁻¹ is assumed for the process. The kinetics of these substituted furans are further discussed below.

3.4 Sub-mechanisms

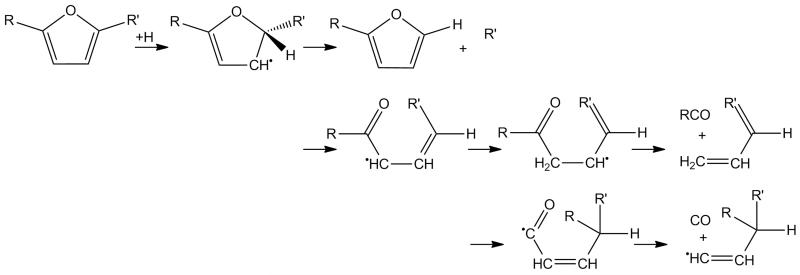
A discussion on the kinetics applied to various furan derivatives is worthwhile given that the mechanism presented in this work is the first to include detailed mechanistic and kinetic proposals on their combustion. For the unimolecular decomposition of substituted furans such as formylfurans, ethylfurans, vinylfurans and furanols a generic reaction scheme for carbene-mediated decomposition is presented in Figure 5 for a di-substituted furan with substituents R and R′. We assume that the formation of β-carbene intermediates and subsequent ring opening to isomeric species is of the same order as that computed in the case of 25DMF [32], with corrections for symmetry. The ring opening product can undergo unimolecular decomposition by simple fission or, where R is a hydrogen atom (e.g. a mono-substituted furan), concerted elimination reactions forming CO and an alkyne. Rate constants for the simple fission process forming two radical products are estimated in the reverse addition direction, with a recombination rate constant of 2 × 10¹³ cm³ mol⁻¹ s⁻¹. For hydrogen atom transfer with CO elimination and formation of an alkyne, we apply a rate constant of 4.15 × 10¹¹T^0.48 exp(−22192/T) s⁻¹ based on the computation of Somers et al. [41] for the decomposition of 2,3-pentadiene-1-one to CO and 1-butyne.

Fig. 5.

Reaction scheme applied to mono- and disubstituted furans for their thermal decomposition via hydrogen atom transfer and β-carbene intermediates.

Simple fission reactions from the side chain functional group of these species forming a Ḣ atom and a substituted furan radical are estimated in the reverse recombination direction, with a temperature independent rate constant of 1 × 10¹⁴ cm³ mol⁻¹ s⁻¹ [72], with the forward rate determined from the known equilibrium constant for the reaction (see Section 3.5). For formylfurans, a hydrogen transfer reaction with concomitant elimination of CO was thought plausible. For the formation of furan and CO from 2-formylfuran, we have computed a rate constant of 3.77 × 10¹²T^0.87 exp(−44381/T) s⁻¹ at the CBS-QB3 level of theory. This rate constant is applied to all formylfurans in the current mechanism for decomposition to a furan derivative and CO. The reaction was found unlikely to be competitive with carbene-mediated decomposition in the temperature range of this work based on these computations however.

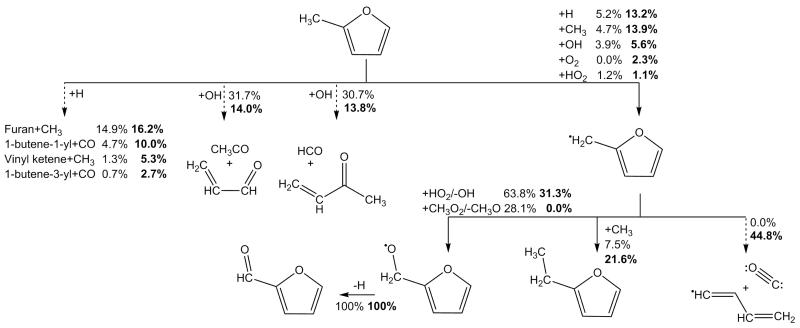
For Ḣ atom addition reactions, a generic reaction scheme which is based on Ḣ atom addition to 25DMF is shown in Figure 6. The scheme allows for the ipsosubstitution at C2 of the furan ring as well as opening of the furan ring followed by hydrogen atom transfer and subsequent decomposition to bimolecular products. In order to simplify the kinetic parameters, we do not include thermochemical and kinetic parameters for all intermediate steps in the current kinetic mechanism. Instead we take the high pressure limiting rate constant for Ḣ atom addition to 25DMF [33] as the total rate of Ḣ atom addition to the ring of a given furan derivative. This is a safe assumption given that the total rate constant for hydrogen atom addition to 25DMF was found to show little dependence on pressures [30, 31, 33]. We then take the branching ratio between the formation of 2-methylfuran and ĊH₃ radical and 1,3-butadiene and acetyl radical as used for 25DMF [33] for the formations of “cyclic” and “acyclic” products respectively for each substituted furan within the mechanism.

Fig. 6.

Reaction scheme applied to mono- and disubstituted furans for hydrogen atom addition reactions.

For methyl-substituted furans, abstraction rate constants are taken to be equal to half of those applied to 25DMF as described previously. For abstraction from the secondary allylic site of ethylfurans, first we scale the rate constants applied to 25DMF on a per hydrogen atom basis, the frequency factor is then scaled with the ratio of primary hydrogen atom abstraction to secondary atom abstraction in a normal alkane. The secondary allylic sites therefore have a higher selectivity than the primary sites for hydrogen atom abstraction reactions, as one would expect. For the primary alkyl sites on the ethyl side chain of ethylfurans, abstraction rate constants are taken as equal to those of primary alkanes. The rate constants for abstraction of a primary/secondary hydrogen atom in an n-alkane are based on those for n-butane found in the C₀–C₄ sub-mechanism of this work described below.

We assume that for radicals formed at the secondary allylic sites and primary ethyl sites of these ethylfurans, β-scission reactions can occur forming Ḣ atom and a vinylfuran. The rate constants for these β-scission reactions are estimated in the reverse addition direction and are assumed to be of the same order as hydrogen atom addition to propene [69]. At intermediate temperatures, the resonantly stabilised primary and secondary radicals can react with HȮ₂ and CH₃Ȯ₂ radicals by analogy with those reactions applied to 25DMF, as described above. Kinetics and thermodynamics for the thermal decomposition of these species via ring opening have been estimated by analogy with those for the 25DMF2R radical as computed by Sirjean and Fournet [34].

For abstraction from formylfurans (monoformyl-, methylformyl- and diformylfuran), we scale the rate constant for hydrogen atom abstraction from 25DMF by the ratio of the rate constants applied by Metcalfe and co-workers [68] in the case of hydrogen atom abstraction by various radicals in the benzaldehyde/toluene systems. The likely fate of the formyl radicals formed from these abstraction reactions is via α-scission reactions forming a vinylic furan radical and CO. The rate constant is taken directly from the decarbonylation of the similar benzaldehyde radical [68]. Where abstraction from 5-methyl-2-formylfuran occurs from the alkyl side chain, the allylic radical formed can react with HȮ₂ radical forming an alkoxy radical and ȮH radical, the alkoxy radical in turn decomposing to form 2,5-diformylfuran and Ḣ. The kinetics are by analogy to the similar reaction class applied to 25DMF.

For abstraction from the hydroxyl group of furanols, we simply adopt the kinetics of abstraction from phenol [68], as these species are of less importance compared to formyl-, ethyl- and vinyl furans in the current kinetic scheme. The furanyloxy radical formed from fission of the O–H bond in 2-furanol has recently been shown to be extremely stable, with bond dissociation energies of approximately 279 kJ mol⁻¹ [73], finding a suitable analogy for estimation of abstraction rate constants thus proves difficult.

2,4-cyclohexadien-1-one is the primary product of hydrogen atom abstraction and homolytic fission at the alkyl side chain of 25DMF. Its keto-enol tautomerisation to phenol is well known [35-37]. Here we adopt pressure dependent rate constants for its decomposition which were recently computed by Sirjean and Fournet [40]. The kinetics and thermodynamic parameters of 2-methylfuran oxidation are taken directly from the kinetic modelling study of Somers et al. [41]. Minor updates have been made to the hydroxyl radical addition pathways for this species, in line with those described above for 25DMF. The mechanism of Tian et al. [74] has been used to describe the oxidation of furan. For the combustion of phenol and related aromatic species (C₆H₆, toluene, 1,3-cyclopentadiene) we incorporate the kinetic mechanism of Metcalfe et al. [68].

Methyl vinyl ketone is an important intermediate formed from hydroxyl radical addition to 25DMF. Unimolecular decomposition, hydrogen atom abstraction and radical addition reactions are all included in the current scheme to account for its oxidation. Unimolecular decomposition reactions are estimated in the reverse addition direction, with rate constants of 2 × 10¹³ cm³ mol⁻¹ s⁻¹ assumed for all recombinations involving hydrocarbon radicals, and 1 × 10¹⁴ cm³ mol⁻¹ s⁻¹ for hydrogen atom recombination with its derived radicals. For abstraction from the acetonyl site, abstraction rate constants are assumed as half of those applied to acetone within the C₀–C₄ sub-mechanism. Rate constants for abstraction of the secondary hydrogen atom are assumed equal to those for abstraction from the secondary site of 1,3-butadiene on a per hydrogen atom basis and abstraction of a hydrogen from the primary vinylic site are similarly adopted from propene, as described in the C₀–C₄ sub-mechanism.

The sub-mechanism for C₀–C₄ species is based on a previously published mechanism [75-79]. Relevant updates are described in the work of Kochar and co-workers [80] and in a recent comprehensive validation study of C₁–C₂ hydrocarbon and oxygenated fuels from Metcalfe et al. [81]. The H₂/O₂ base mechanism is described in the work of Kéromnés et al. [82,83].

3.5 Thermochemistry and transport properties

Where possible the thermochemical parameters have been taken directly from several recent computational studies on the kinetics of 25DMF combustion [29, 32-34, 40]. Elsewhere, a set of group additivity rules have been developed as part of this study in order to estimate reliable thermochemistry for a range of mono- and di-substituted furans and their radicals. We base these rules on a number of recent quantum chemical studies which explored the thermochemistry of alkyl- [28, 84] and polyoxygenated- [85] furan derivatives.

For linear species, where specific quantum chemical calculations are not carried out, we apply a set of group additivity rules developed in house for hydrocarbons and oxygenated species. Transport properties for all furanic species are assumed equal to those for 25DMF used by Sirjean and Fournet in their theoretical study [33]. For acyclic species, the Transport Data Estimator package of the Reaction Mechanism Generator software of Green and co-workers [86] has been used to provide relevant transport properties.

The Chemkin-Pro format kinetic mechanism, thermodynamic and transport files and group additivity rules are available as part of Electronic Supplementary Data with a complete list of species chemical structures. Kinetic mechanisms compatible with previous versions of the Chemkin code, which cannot incorporate the PLOG description of pressure dependent reactions which are used in this work, can be obtained from the corresponding author.

4 Results and Discussion

4.1 Shock tube studies

4.1.1 Pyrolysis

The pyrolysis of 25DMF has been studied previously by Lifshitz et al. [21] for mixtures of 0.5% fuel in argon bath gas from 1070–1370 K, at residence times ≈ 2 ms and at pressures of ≈ 2–3 atm. Small quantities (0.1%) of 1,1,1-trifluoroethane (1,1,1-TFE) were added to the reaction mixtures to act as a chemical thermometer and the reflected shock temperatures determined from the relationship:

$$T=(E∕R)∕\left[\ln \left\{-\frac{\ln (1-\chi )}{A\tau }\right\}\right]$$

where τ is the reaction dwell time, and χ is defined as:

$$\chi ={[{\mathrm{CH}}_2={\mathrm{CF}}_2]}_t∕({[{\mathrm{CH}}_2={\mathrm{CF}}_2]}_t+{[{\mathrm{CH}}_3-{\mathrm{CF}}_3]}_t)$$

The parameters E and A are the activation energy and pre-exponential factor taken from the first order rate constant assumed by the authors for the molecular elimination reaction CH₃—CF₃ → HF + CH₂=CF₂ of 6.31 × 10¹⁴ exp(−37238/T) s⁻¹. However, early in the development of our mechanism, the temperatures of 25DMF decomposition were under-predicted by up to 90 K by our kinetic mechanism when compared with the experiments of Lifshitz et al. This led us to undertake a study of the pyrolysis of 25DMF where reflected shock parameters are determined independent of a chemical thermometer for mixtures of 3% 25DMF in argon, under conditions similar to those of the Lifshitz study.

Recently, Sirjean and co-workers [40] highlighted the same issue, which led to a reevaluation of the thermal decomposition rate constant of 1,1,1-TFE via CBS-QB3 computations and RRKM/ME modelling. Their reported rate constant is up to a factor of 3.8 times slower than that used in the Lifshitz study at 2.5 bar and leads to an increase in the temperature profile of the Lifshitz et al. experimental data, which they subsequently corrected [40] via the relationship:

$$T_{corr}=1.14\times T_{exp}-110$$

where temperatures are defined in Kelvin.

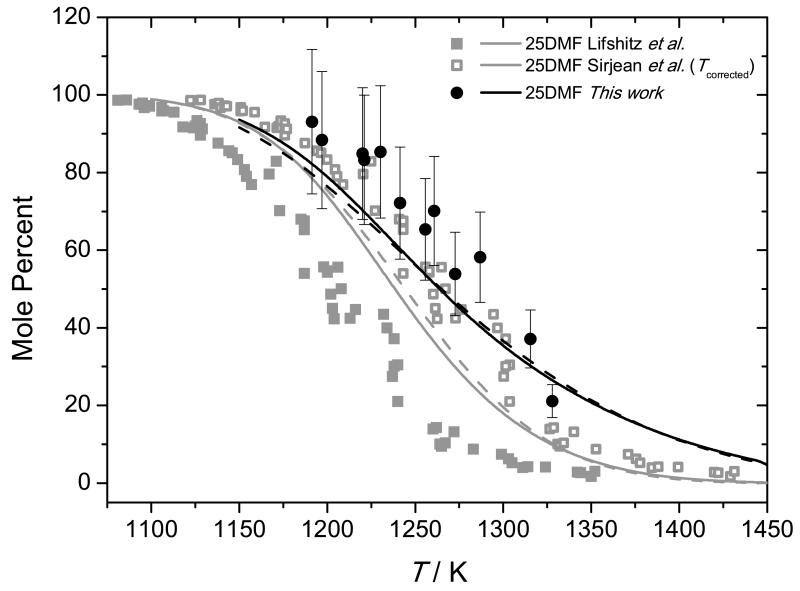
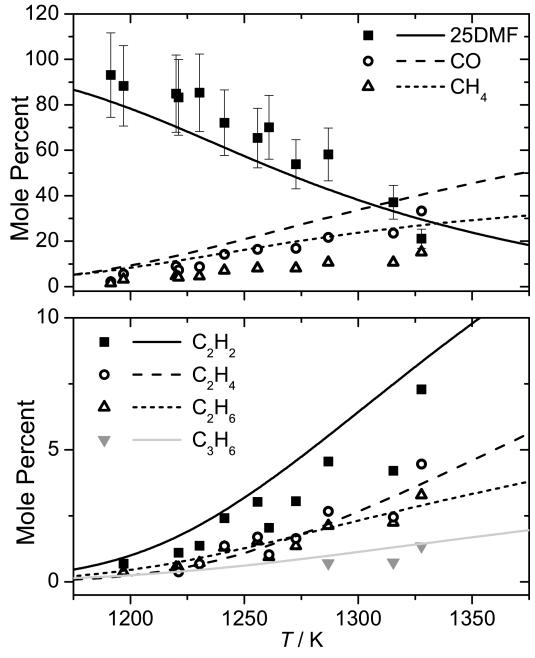
Experimental data and current modelling predictions for the decomposition of 25DMF can be seen in Figure 7, with intermediate profiles in Figures 8 and 9. The results of the current study show that 25DMF undergoes decomposition at temperatures ≈ 90 K greater than those determined in the study of Lifshitz et al. and temperatures approximately 25 K greater than the theoretical temperature correction proposed by Sirjean and Fournet [40]. Adsorption of the reactant was found to be a plausible source of error in determining concentrations of 25DMF in the post shock mixtures, with an error of up to 30% possible. Given this uncertainty, the temperature corrected data of Lifshitz et al. and that of the current study are in reasonable agreement.

Fig. 7.

Shock tube decomposition profile for 0.5% 2,5-dimethylfuran in argon from Lifshitz et al. (closed squares) [21] and temperature corrected measurements of Lifshitz et al. from Sirjean et al. (open squares) [40]. Thermal decomposition measurements from the current study (3.0% 2,5-dimethylfuran in argon) are presented with 20% uncertainty bars (closed circles). Lines are modelling calculations; — (current study), − − (Sirjean et al. [40])

Fig. 8.

Single pulse shock tube profiles (symbols) and simulations (lines) for the pyrolysis of 3% 2,5-dimethylfuran in argon from 2–2.5 atm and τ ≈ 2 ms

Fig. 9.

Temperature corrected pyrolysis experiments of Lifshitz et al. (0.5% 2,5-dimethylfuran in argon from 2–3 atm and τ ≈ 2 ms, symbols) [21, 40] with current modelling predictions (lines).

Current modelling predictions show that the total decomposition rate of 25DMF is over-predicted by the current model when compared with both sets of data. However, given the uncertainty in both sets of experiment the current modelling predictions are not unreasonable. Rate of production analyses corresponding to 20% fuel consumption have been carried out for our experiments and those of Lifshitz et al. and are shown in Figure 11. Under our experimental conditions, abstraction by methyl radical is the largest fuel consuming reaction at 31.7%. Reactions with hydrogen atom consume a total of 54.5% of the fuel, with 13.9% forming 1,3-butadiene and acetyl radical, 22.0% consumed through the ipso addition forming 2-methylfuran and methyl radical and 18.5% consumed via abstraction from the alkyl group.

Fig. 11.

Rate of production analysis carried out at 20% fuel conversion under the pyrolysis conditions studied as part of this work, the conditions of Lifshitz et al. [21] (bold font), and the conditions of the Djokic et al. [39] flow reactor study (italic font). Dashed lines represent the product(s) of a series of reactions within the current mechanism.

With reactions of hydrogen atom with the fuel of such importance under these conditions, the source of these atoms is of interest. 58.4% of hydrogen atom is produced through the β-scission reaction of 2-cyclohexene-1-one-4-yl to 2,4-cyclohexadien-1-one and hydrogen atom. 10.4% is produced from the decomposition of CH≡C—ĊH—CH₃ to vinylacetylene and hydrogen atom, with effectively all (97.2%) of the CH≡C—ĊH—CH₃ being produced from the hydrogen atom transfer reaction forming 3,4-hexadiene-2-one, which consumes 6.5% of the fuel. 12.1% of the hydrogen atom in the system is produced from the decomposition of 1,4-pentadiene-3-yl (CH₂=CH—ĊH—CH=CH₂) to 1,3-cyclopentadiene and hydrogen atom.

Predictions of small hydrocarbons are in good agreement with the experiment data of this work (Figure 8) however, the carbon monoxide profile is currently over-predicted when compared with the experimental data of this work, as is that of methane by up to 100%. 52.9% of carbon monoxide is found in rate of production analyses to be produced from the decomposition reaction CH₃—Ċ=O → ĊH₃+ CO. 65.1% of the acetyl radical in the system is produced via hydrogen atom addition to the reactant, also forming 1,3-butadiene, with 29.7% formed from the decomposition of 3,4-hexadiene-2-one. These pathways producing carbon monoxide also tend to produce methyl radical in a 1:1 ratio, with abstraction by methyl radical being an important fuel consuming reaction. The overproduction of both carbon monoxide and methane may therefore be linked through these pathways, along with the over-prediction of the reactivity of 25DMF.

The current mechanism accurately predicts effectively all intermediates detected in the experiments of Lifshitz et al., although 2-methylfuran and methane yields are both slightly over-predicted. The former is produced from an important 25DMF consuming hydrogen atom addition reaction, the latter is primarily formed by abstraction by methyl radical.

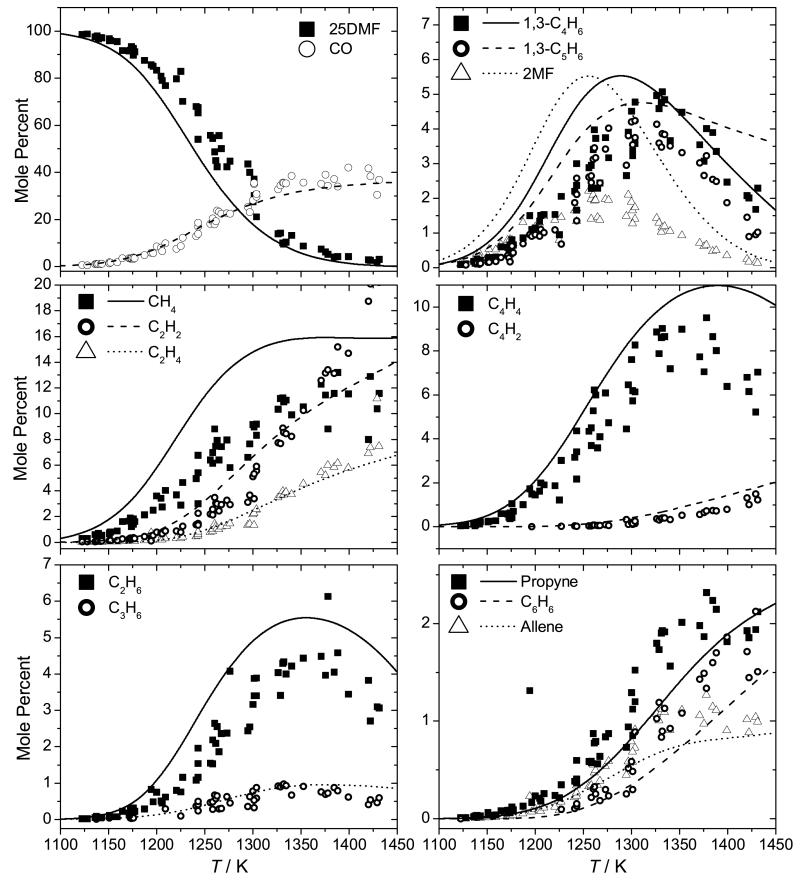
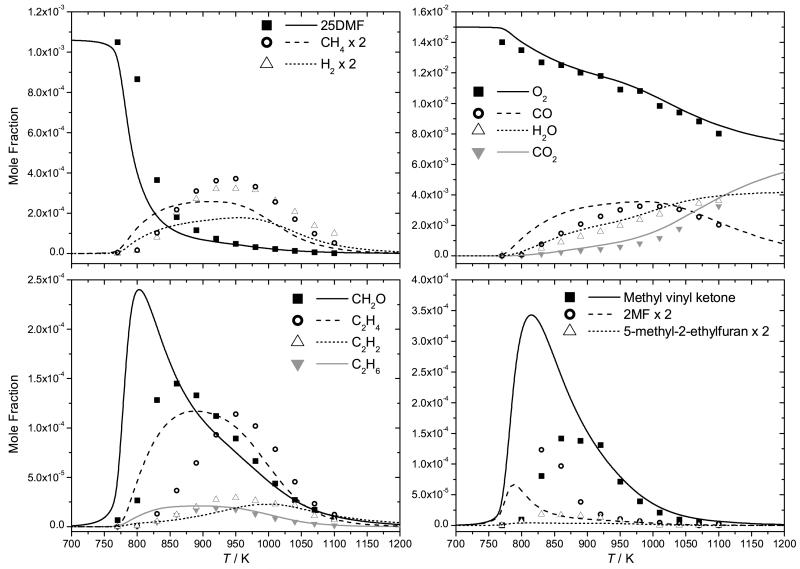
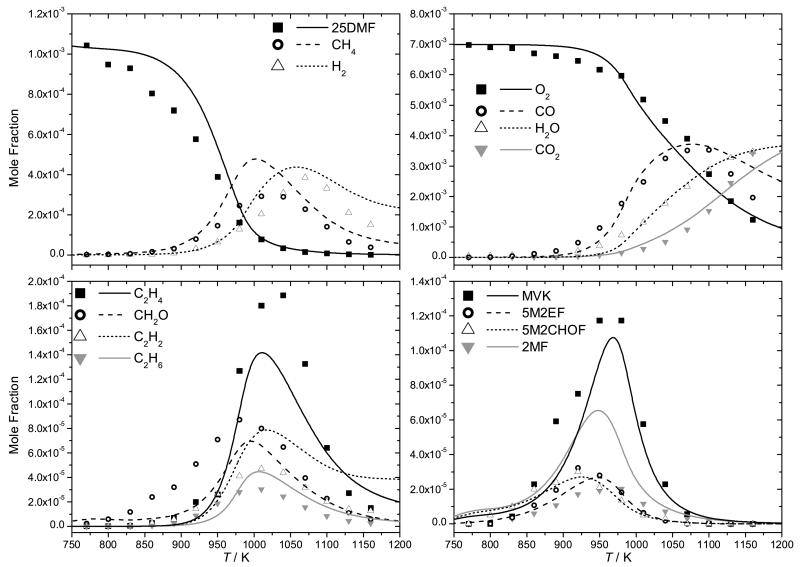
Although not a shock tube study, the pyrolysis of 25DMF in a flow reactor has been studied recently by Djokic et al. [39] from 873–1098 K, at 1.7 bar and τ = 300–400 ms and the current mechanism is also compared with this data, Figure 10. The flow reactor data is significantly more reactive than the current mechanism estimates, a finding which is in conflict with the shock tube measurements discussed above, where modelling work slightly over-predicts the measurements of 25DMF decomposition.

Fig. 10.

Experimental data (symbols) [39] for the pyrolysis of 25DMF-N₂ in a flow reactor at 1.7 bar with modelling predictions (lines).

A rate of production analysis was performed under the conditions of this flow reactor work (Figure 11) at 1023 K and τ = 0.32 s, corresponding to 20% fuel consumption. The analysis shows that the reactions governing the consumption of 25DMF are largely the same as those seen in the shock tube studies. Discounting the discrepancy in the temperature range of conversion of 25DMF, yields of phenol, which is the primary product of the 25DMF2R radical decomposition, are grossly over-predicted compared to the flow reactor data. Peak concentrations of 2-methylfuran and 1,3-butadiene are also slightly over-predicted, with peak concentrations of 1,3-cyclopentadiene being perhaps the best predicted of all four of these important intermediates.

In the temperature range of the flow reactor study, a radical mechanism must be the dominant consumption route of 25DMF, yet the kinetics of the reactions of hydrogen atom [30, 31, 33] and methyl radical with the fuel are not so uncertain as to provide realistic optimisation targets for resolving the discrepancy with respect to predictions of 25DMF concentrations. It is difficult within the current kinetic scheme to resolve these differences without significant performance loss against the shock tube experimental data, where predictions of 25DMF, CO, 2-methylfuran, 1,3-butadiene and 1,3-cyclopentadiene are all in good agreement with experiment. It is well known that surface catalysed reactions can perturb the interpretation of batch and flow reactor results. In this case, the authors [39] have shown that doubling the surface to volume ratio of their reactor has negligible effect on reactant conversion and product selectivities. This is not a definitive test however as detailed by Rice and Herzfeld [87], who described instances whereby changing the surface to volume ratio had no influence on the rate of a heterogeneous reaction in cases where chain reactions were both initiated and terminated at the walls of the reactor. Further analysis may be required to reconcile these experiments with other measurements and the kinetic model of this work.

4.1.2 Low pressure ignition delay times

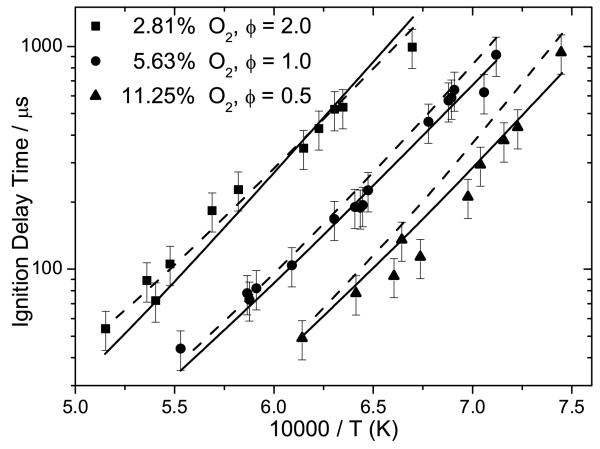
Atmospheric pressure ignition delay times are detailed in Figure 12, along with current numerical modelling results. The kinetic mechanism can accurately reproduce the experimental data under all conditions, capturing the reduction in ignition delay times with increasing oxygen concentrations and temperature. The kinetic mechanism of Sirjean et al. [40] is also simulated under these conditions and largely replicates the experiments within their assigned uncertainty. At ϕ = 0.5 and the lowest temperatures studied (1350 K), the mechanism of Sirjean et al. calculates ignition delay times notably longer (≈ 50%) than those of this work.

Fig. 12.

Experimental ignition delay times from the current study (symbols) for 0.75% 2,5-dimethylfuran in argon at 1 atm pressure with 20% uncertainty bars. Lines are modelling calculations from the current study (—) and Sirjean et al. (− −) [40].

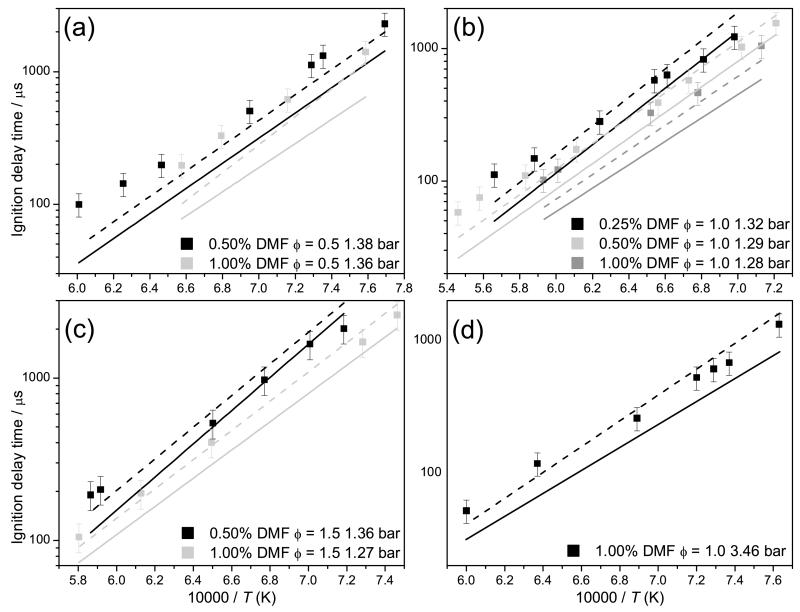
Numerical predictions of shock tube experiments from Sirjean et al. [40] have been carried out using the mechanism developed as part of this work, and that developed by Sirjean et al., Figure 13. The ignition delay times were measured at pressures close to 1 and 4 bar, for temperatures of 1300–1831 K, for equivalence ratios of 0.5–1.5, for varying concentrations of fuel, oxygen and diluent. A comparison of experiments from this work and from Sirjean et al. at equivalent fuel oxygen ratios are presented in supplementary material. The measurements of this work consistently show shorter ignition delay times for 25DMF/O₂/Ar mixtures at ϕ = 0.5, although ignition delay times are of a similar order at stoichiometric equivalence ratios.

Fig. 13.

Experimental ignition delay times from Sirjean et al. [40] with 20% uncertainty bars. Lines are modelling calculations from the current study (—) and Sirjean et al. (− −) [40].

Both mechanisms tend to estimate shorter ignition delay times for ϕ = 0.5 and ϕ = 1.0 mixtures of 25DMF/O₂/Ar, particularly measurements containing 1% fuel, Figures 13 (a) and (b). Under these conditions, the mechanism of Sirjean et al. is within 20% of experiment in the best instances, and 50% of experiment in the worst instances. The mechanism of this work is considerably faster than these experiments, deviating from experiment by 40% at the lowest temperatures studied, but deviating further with increasing temperature, where numerical work estimates ignition delay times 60% shorter than those measured.

Under fuel rich conditions, Figure 13 (c), the agreement of both mechanisms with experiment improves. The simulations of Sirjean et al. are found to be within experimental error, and simulations using the mechanism of this work are within 20–30% of experiment. Estimations of ignition delay times for ϕ = 1.0 mixtures at 3.46 bar, Figure 13 (d), also show good agreement with experiment, with the results of Sirjean et al. within the 20% error assigned to experiment. Our mechanism reproduces ignition delay times within 30–40% of experiment in this case.

The mechanism of this work is found to consistently calculate shorter ignition delay times than those produced by the mechanism of Sirjean et al.. Possible reasons for this have been investigated. However it should be noted that the core pyrolytic chemistry of 25DMF is effectively the same in both mechanisms, as shown in Section 4.1.1.

Rate constants for hydrogen atom abstraction from the alkyl side chain of 25DMF by methyl, hydroxyl and hydroperoxy radicals are in excellent agreement between both mechanisms. Sirjean et al. did increase a theoretical rate constant [33] for abstraction from this site by hydrogen atom by a factor of two as part of their modelling work. The source of this rate constant is common in both mechanisms although and the influence of increasing this rate constant by a factor of two has been investigated (see supplementary material). For 1.3 bar simulations reductions in ignition delay time of up to 9% were observed at ϕ = 0.5, up to 15% at ϕ = 1.0 and up to 17% at ϕ = 1.5. At 3.5 bar and ϕ = 1.0, the greatest reduction in reactivity was found to be ≈ 12%. Altering this rate constant has a more pronounced influence under stoichiometric and rich conditions, where calculated ignition delay times are perhaps in best agreement with the experiments of Sirjean et al.. Adopting this change will therefore not result in dramatically increased agreement between our mechanism and the experimental or numerical ignition delay times of Sirjean et al..

We have also found that our estimate of the rate constant for hydrogen atom abstraction by O₂ is a factor of 5.4–4.6 times faster than that chosen by Sirjean et al. in the temperature range (1300–1800 K) of their shock tube experiments. Adoption of their rate constant was tested (see supplementary material), but the kinetics of this reaction show little sensitivity under these conditions, with a maximum increase in ignition delay times of 6% observed. It is worth noting that the rate constant estimated for this process in this work is reinforced by high pressure-intermediate temperature shock tube experiments to be described in the latter part of this section, where it is found to be particularly sensitive in predicting ignition delay times.

It is difficult to reconcile the ignition delay times calculated by our mechanism, with those determined experimentally and numerically by Sirjean et al.. Both mechanisms show similar trends when compared with two sets of shock tube experiments; neither mechanism can replicate the experiments of Sirjean et al. under fuel lean conditions, although better agreement is observed with experiment as a function of increasing fuel-oxygen equivalence ratio and pressure. Both mechanisms predict a greater dependency of ignition delay time on fuel and oxygen concentrations than is observed experimentally by Sirjean et al. Conversely, absolute predictions of our shock tube ignition delay times, and the accompanying dependency of ignition delay times on oxygen concentrations, are well predicted by both mechanisms.

Sensitivity and rate of production analyses based on the mechanism of this work are shown in Figures 14 and 15 respectively and provide insight into the key reactions which govern the prediction of our ignition delay times.

Fig. 14.

Rate of production analysis carried out at 20% fuel consumption under shock tube conditions at 1 atm, 1600 K at ϕ = 0.5 and ϕ = 2.0 (bold font). Dashed lines represent the product(s) of a series of reactions within the current mechanism.

Fig. 15.

Ignition delay time sensitivity coefficients for mixtures of 0.75% 2,5-dimethylfuran in argon at 1 atm, ϕ = 0.5 and 1600 K (black bars) and at ϕ = 2.0 and 1600 K (grey bars). Negative coefficients indicate a reaction which reduces the computed ignition delay time and vice versa. The reaction Ḣ + O₂ → Ö + ȮH has been omitted for clarity. Chemical “nicknames” above correspond to assignments in the Chemkin format kinetic mechanism.

A rate of production analysis at 20% fuel consumption shows that 53.2% of the fuel is consumed by reactions with Ḣ atom under fuel lean conditions, and 58.4% under rich conditions. Abstraction by Ḣ atom from the alkyl site is the most dominant of these 25DMF + Ḣ reactions, consuming 23.8% of the fuel under lean conditions, with Ḣ atom addition forming 1,3-butadiene and acetyl radical and 2-methylfuran and ĊH₃ radical consuming 11.4% and 12.6% of the fuel respectively. Sensitivity analyses highlight all three reactions as being important in the prediction of ignition delay times, with all three reactions inhibiting reactivity under fuel lean conditions, which stems from their competition with the chain branching reaction Ḣ + O₂ → Ö + ȮH.

Under rich conditions, hydrogen atom addition reactions forming 2MF and methyl radical and 1,3-butadiene and acetyl radical have a promoting influence on the predicted ignition delay times, whereas hydrogen atom abstraction by hydrogen atom becomes increasingly inhibiting. The reversal in the sensitivity coefficient for hydrogen atom addition reactions is likely due to further reactions of 2MF and 1,3-butadiene generating vinyl radical, whose reactions are seen to reduce ignition delay times under rich conditions. The reaction of vinyl with molecular oxygen for instance is the second most promoting reaction under rich conditions, after the reaction Ḣ + O₂ → Ö + ȮH.

Abstraction of a hydrogen atom from the fuel and simple fission of the alkyl C–H bonds leads largely to the formation of phenol and radical derivatives of 1,3-cyclopentadiene and 1,3-pentadiene through the decomposition of 25DMF2R. The resonantly stabilised/aromatic products of this reaction sequence could also be responsible for the inhibiting influence of hydrogen atom abstraction by Ḣ atoms, particularly under fuel rich conditions. For instance, the chain termination reaction of Ḣ atom with cyclopentadienyl is the most inhibiting reaction found in the sensitivity analysis under fuel rich conditions, followed closely by hydrogen atom abstraction from 1,3-cyclopentadiene by Ḣ atom and the decomposition of phenol to 1,3-cyclopentadiene.

On the other hand, the reaction of cyclopentadienyl radical with HȮ₂ radical forming a resonantly stabilised cyclopentadienol radical and ȮH is seen to promote reactivity under rich conditions, as it prevents the chain termination of hydrogen atom with this species, whilst also providing a source of reactive hydroxyl radicals. It is clear therefore, that the predictions of ignition delay times are dependent on the subsequent reactions of the aromatic species and their derivatives, which are formed largely from hydrogen atom abstraction reactions from the alkyl side chain of 25DMF.

The decomposition of 2-cyclohexene-1-one-4-yl to 2,4-cyclohexadien-1-one and Ḣ atom is seen to promote reactivity, as it offers 29.9% of all Ḣ atoms in the system under fuel lean conditions according to the rate of production analysis. Abstraction by ĊH₃ and ȮH radicals consumes 3.2% and 12.3% of the fuel respectively under fuel lean conditions, the kinetics of neither reaction are overly sensitive in terms of the prediction of ignition delay times.

Unimolecular decomposition of the fuel via a β-carbene intermediate consumes 13.9% of the fuel under lean conditions and is seen to reduce the computed ignition delay times under these conditions, as it results in the formation of Ḣ atoms through the subsequent decomposition of 3,4-hexadiene-2-one. This reaction accounts for 18.4% of the Ḣ atoms within the system at fuel lean conditions. Simple fission forming 25DMF2R radical and Ḣ atom consumes 9.4% of the fuel and produces 11.9% of the hydrogen atom within the system and is of lesser importance in predicting ignition delay times than the carbene mediated decomposition pathways, as evidenced in the sensitivity analyses.

4.1.3 High pressure ignition delay times

Ignition delay times for stoichiometric fuel-air mixtures at 20 and 80 bar for temperatures in the range 820–1210 K are shown in Figure 16, along with current model calculations. Although the mechanism tends to under estimate the ignition delay times observed experimentally at 20 bar, at 80 bar better agreement is obtained.

Fig. 16.

Experimental ignition delay time measurements for stoichiometric mixtures of 2.66% 2,5-dimethylfuran/O₂/N₂ at elevated pressures with 20% uncertainty bars. Lines with symbols are modelling calculations; constant volume batch reactor (—), facility effects (− −, see Section 2.4).

At these extended test times, there is a clear need to include facility effects in the computation of ignition delay times as the constant volume-constant internal energy assumption regularly used for numerically modelling shock tube experiments is not applicable in these instances. There is clear evidence of pre-ignition pressure rise in some experiments; these effects are illustrated in supplementary material where example pressure profiles at approximately 20 and 80 bar are shown. Chaos and Dryer [88] highlight the need for careful interpretation of shock tube measurements for non-dilute fuel-air mixtures undergoing ignition at extended test times (> 1 ms). They conclude that ignition delay data under these conditions do not always represent purely chemical kinetic observations, but can be perturbed by numerous, sometimes complex, sources. Our modelling approaches here are line with those recommended by Chaos and Dryer [88]; inclusion of facility effects as described in Section 2.4 leads to improved agreement with experiments.

Rate of production analyses at 950 K and simulation times corresponding to 20% fuel consumption were performed to identify important fuel consuming reactions under these experimental conditions, Figure 17, along with sensitivity analysis, Figure 18. These analyses illustrate the important intermediate temperature oxidation pathways of 25DMF, in contrast with the atmospheric pressure and high temperature experiments described previously.

Fig. 17.

Rate of production analysis carried out at 20% fuel consumption under shock tube conditions at 950 K, 20 bar and 80 bar (bold font) for stoichiometric 2,5-dimethylfuran-air mixtures.

Fig. 18.

Ignition delay time sensitivity coefficients for stoichiometric 2,5-dimethylfuran-air mixtures at 950 K, 20 bar (open bars) and 80 bar (filled bars). Negative coefficients indicate a reaction which decreases the computed ignition delay time and vice versa. Chemical “nicknames” above correspond to assignments in the Chemkin format kinetic mechanism.

25DMF is primarily consumed by ȮH radical addition reactions at both 20 and 80 bar, with 29.6% and 39.5% of the fuel consumed by this pathway at these respective pressures. The primary product of this pathway is methyl vinyl ketone, although smaller quantities of 3-hexene-2,5-dione are also produced. The reaction kinetics of neither of these stable species is highlighted as important in sensitivity analyses. Abstraction reactions consume 42.0% and 43.7% of the fuel with increasing pressure, with abstraction by ȮH radical the largest contributer to the total flux at 19.0% and 26.9% respectively.

Despite ȮH radical addition and abstraction reactions being the largest consumers of the fuel in the above rate of production analysis, the kinetics of these reactions do not appear to be sensitive variables in the calculation of ignition delay times under these conditions. The hydroxyl radical addition reaction has a slight inhibiting influence on reactivity at 80 bar and a slight promoting influence at 20 bar. Bimolecular initiation by molecular oxygen forming 25DMF2R and HȮ₂ radical is found to be amongst the most promoting reactions in our mechanism at both 20 and 80 bar. This reaction exhibits little sensitivity to the prediction of the previously described atmospheric pressure ignition delay time experiments. However, it does exhibit significant control over the predicted ignition delay times under these conditions.

The reaction of 25DMF2R + HȮ₂ → 5-methyl-2-furylmethanoxy radical + ȮH consumes 49.1–66.3%% of the 25DMF2R radical at intermediate temperatures, and it is found to have a highly promoting influence on the predicted ignition delay times — it is the most sensitive reaction at both 20 and 80 bar. This is due to the conversion of two relatively unreactive species into a reactive ȮH radical with the subsequent generation of a hydrogen atom from the decomposition of 5-methyl-2-furylmethanoxy radical to 5-methyl-2-formylfuran. effectively all hydrogen atom abstraction reactions from the fuel are found to reduce ignition delay times, as a result of this important oxidation reaction of the allylic 25DMF2R radical. Abstraction of a hydrogen atom by HȮ₂ radical from both 25DMF and 5-methyl-2-formylfuran are found to reduce the predicted ignition delay times, as the subsequent decomposition of H₂O₂ generates two hydroxyl radicals which can further react with 25DMF.

The chain branching nature of the 25DMF2R radical oxidation pathways is in competition with the chain termination reaction of 25DMF2R with ĊH₃ radical forming 5-methyl-2-ethylfuran, which is found to be the most inhibiting reaction at 20 bar, despite consuming only 12.9% of the 25DMF2R radical. At 80 bar, the sensitivity of the predicted ignition delay times to this rate constant diminishes as this reaction consumes less of the 25DMF2R radical (4.4%), which is a result of increased HȮ₂ and CH₃Ȯ₂ radical concentrations at elevated pressures.

The subsequent reactions of 5-methyl-2-ethylfuran show little sensitivity in the prediction of ignition delay times, unlike 5-methyl-2-formylfuran, with hydrogen atom abstraction reactions from the formyl site of this species exhibiting sensitivity coefficients on a par with the abstraction reactions of 25DMF. The combustion chemistry of formylfurans may therefore be worthy of further exploration, both theoretically and experimentally, along with studies of their atmospheric chemistry and toxicological properties. They have been detected in recent engine studies as products of 25DMF combustion [14] and here and in Section 4.2 we show that they are important intermediates in the oxidation of 25DMF, yet literature discussion on the combustion of these aldehydes is scarce at best. The subsequent reactions of 5-methyl-2-ethylfuran show little sensitivity in the prediction of ignition delay times, unlike 5-methyl-2-formylfuran, with hydrogen atom abstraction reactions from the formyl site of this species exhibiting sensitivity coefficients on a par with the abstraction reactions of 25DMF. The combustion chemistry of formylfurans may therefore be worthy of further exploration, both theoretically and experimentally, along with studies of their atmospheric chemistry and toxicological properties. They have been detected in recent engine studies as products of 25DMF combustion [14] and here and in Section 4.2 we show that they are important intermediates in the oxidation of 25DMF, yet literature discussion on the combustion of these aldehydes is scarce at best.

4.2 Jet-stirred reactor species profiles

Experimental profiles of key species detected in the current JSR study are shown in Figures 19, 20 and 21 along with current modelling predictions. Due to the temperature range of these experiments, these data complement the high pressure ignition delay time data presented previously. Fuel and O₂ concentrations, which offer good tests of global reactivity are well predicted under all equivalence ratios, although the mechanism slightly over-predicts the fuel reactivity under fuel lean conditions. Rate of production analyses are used to identify those reactions contributing to the consumption of the fuel, Figure 22.

Fig. 19.

Experimental jet-stirred reactor profiles (symbols) and current modelling predictions (lines) for the oxidation of 2,5-dimethylfuran at ϕ= 0.5, 10 atm and τ = 0.7 s. 2MF = 2-methylfuran.

Fig. 20.

Experimental jet-stirred reactor profiles (symbols) and current modelling predictions (lines) for the oxidation of 2,5-dimethylfuran at ϕ= 1.0, 10 atm and τ = 0.7 s. MVK = methyl vinyl ketone, 5M2EF = 5-methyl-2-ethylfuran, 5M2CHOF = 5-methyl-2-formylfuran, 2MF = 2-methylfuran.

Fig. 21.

Experimental jet-stirred reactor profiles (symbols) and current modelling predictions (lines) for the oxidation of 2,5-dimethylfuran at ϕ= 2.0, 10 atm and τ = 0.7 s. MVK = methyl vinyl ketone, 5M2EF = 5-methyl-2-ethylfuran, 2MF = 2-methylfuran.

Fig. 22.

Rate of production analysis for 2,5-dimethylfuran in a jet-stirred reactor at 10 atm and τ = 0.7s, at ϕ = 0.5 (775 K) and ϕ = 2.0 (930 K and bold font) corresponding to approximately 20% fuel consumption. Dashed lines represent the product(s) of a series of reactions within the current mechanism.

Under fuel lean conditions at 775 K and τ = 0.7 s, 25DMF is consumed largely (43.9%) by an ȮH radical addition reaction ultimately forming stable methyl vinyl ketone, and acetyl radicals. Concentrations of methyl vinyl ketone are over-predicted under lean conditions, although under stoichiometric and rich conditions the computed yields are in excellent agreement with experiment. Under lean conditions this overproduction may be linked to an overproduction of ȮH radical or perhaps a competitive pathway absent from the exploratory ab initio calculations of the reactions of ȮH radical with 25DMF which were carried out as part of this work. For instance, a Waddington type reaction mechanism, whereby molecular oxygen could add to a precursor of methyl vinyl ketone thus competing with its production, is plausible. Detailed quantum chemical explorations of such hypothetical pathways are beyond the scope of this study however but could perhaps be investigated as part of future refinements of the current mechanism.

The addition and abstraction reactions of hydrogen atom with the fuel account for approximately 33.2% of total fuel consumption. Yields of hydrogen gas are well predicted under stoichiometric and rich conditions (900–1200 K), but are under-predicted under lean conditions (750–1100 K). Stable products of hydrogen atom addition reactions, 2MF in particular, are over-predicted under all conditions studied.

As expected under rich conditions at 930 K, the hydroxyl radical addition pathway consumes less fuel (18.1%), with abstraction by methyl radical becoming an important fuel consuming reaction at 25.3%, having increased from 9.5% under lean conditions. Methane yields are slightly over-predicted at all equivalence ratios studied, in line with pyrolysis data discussed previously. Hydrogen atom addition pathways consume 28.2% of the fuel under rich conditions, with abstraction by hydrogen atom of less importance (7.9%).

Under fuel lean conditions, the 25DMF2R radical is primarily consumed by reaction with HȮ₂ radical (47.8%) and CH₃Ȯ₂ radical (47.6%) forming 5-methyl-2-furylmethanoxy radical and ȮH or CH₃Ȯ respectively, although its significance decreases from fuel lean to fuel rich conditions, with thermal decomposition pathways of 25DMF2R becoming important at higher temperatures and reduced oxygen concentrations. 5-methyl-2-formylfuran, the stable intermediate of these pathways, was quantified at stoichiometric conditions and its concentrations are very well reproduced by the mechanism. Recombination of 25DMF2R with a ĊH₃ radical to form 5-methyl-2-ethylfuran accounts for 4.1% of the consumption of this species under lean conditions, assuming much greater importance with reduced oxygen concentrations, accounting for 19.9% of the consumption of 25DMF2R under rich conditions. Yields of 5-methyl-2-ethylfuran are also well predicted at all equivalence ratios.

The branching ratio between the bimolecular recombination of HȮ₂ radical and ĊH₃ radical with 25DMF2R is therefore an important one in terms of the prediction of intermediate profiles and ignition delay times seen previously, as the former tends to promote reactivity due to their chain branching nature, with the latter chain termination reaction inhibiting reactivity. Our predictions of these furanic species give credence to the rate constants applied in the current study. Unimolecular decomposition of 25DMF2R consumes 49.8% of this species under rich conditions (930 K), and is of lesser significance in the intermediate temperature regime than bimolecular consumption of this species. The primary products of these thermal decomposition pathways are in line with those discussed in our shock tube studies and include hydrogen atom and phenol or CO and Ċ_5H7 radicals. Phenol was not quantified because the online sampling system used was not appropriate. However, it was identified by GC/MS in the products.

A range of stable furan derivatives are seen to be important products of the oxidation of 25DMF under the experimental conditions studied in the JSR. Rate of production analyses for 2-methylfuran and 2-methyl-5-formylfuran have therefore been carried out under the same conditions as those for 25DMF to further explore the chemistry of these intermediates, Figures 23 and 24.

Fig. 23.

Rate of production analysis for 5-methyl-2-formylfuran in a JSR at 10 atm and τ = 0.7s, at ϕ = 0.5 (775 K) and ϕ = 2.0 (930 K and bold font).

Fig. 24.

Rate of production analysis for 2-methylfuran in a JSR at 10 atm and τ = 0.7s, at ϕ = 0.5 (775 K) and ϕ = 2.0 (930 K and bold font). Dashed lines represent the product(s) of a series of reactions within the current mechanism.

For 5-methyl-2-formylfuran, abstraction from the formyl group constitutes the largest consuming reactions, in particular by methyl and hydroperoxy radicals. Both reactions were highlighted as sensitive in predicting ignition delay times. The formylfuran radical is consumed completely by a decarbonylation reaction forming the vinylic 2-methyl-5-furanyl radical. The 2-methyl-5-furanyl radical can undergo ring opening to form an acyclic vinylic ketene radical which can subsequently decompose to form ketene and propyne by β-scission, or react with molecular oxygen to form a dione radical which can undergo α-scission to form a methyl vinyl ketone radical and carbon monoxide. 2-methyl-5-furanyl radical can also react directly with molecular oxygen to form a furanol radical, which can undergo ring opening and subsequent decarbonylation to form methyl vinyl ketone radical and carbon monoxide.

Hydrogen atom abstraction from the methyl group of 5-methyl-2-formylfuran leads to a resonantly stabilised radical similar to the 25DMF2R radical, and like 25DMF2R radical, it is consumed largely by reaction with HȮ₂ and CH₃Ȯ₂ radicals forming furanic alkoxy radical and ȮH or CH₃Ȯ radicals respectively. The alkoxy radical decomposes to hydrogen atom and 2,5-diformylfuran, which was not detected experimentally, reflecting on the dominant pathways for 5-methyl-2-formylfuran oxidation occuring at the formyl site. Hydrogen atom addition pathways consume less than 10% of this species, notably forming 2-formylfuran and 2-methylfuran via ipso-addition reactions.

2-methylfuran like 25DMF, is consumed under lean conditions primarily by hydroxyl radical addition reactions (62.4%). The products of these pathways are likely to be methyl vinyl ketone and formyl radical and acrolein and acetyl radical based on the analogous pathway we described above for 25DMF. Hydrogen atom addition reactions constitute 21.6% of 2-methylfuran consumption under lean conditions and 34.2% under rich conditions, with abstraction from the alkyl group consuming 15% and 36.1% of this species under lean and rich conditions respectively. The primary 2-methylfuran radical (2MF2R) is consumed via oxidation by HȮ₂ and CH₃Ȯ₂ radicals under lean conditions, ultimately forming 2-formylfuran as a stable intermediate. Recombination with methyl radical forming 2-ethylfuran becomes more important under rich conditions, consuming 21.6% of the 2MF2R radical as HȮ₂ and CH₃Ȯ₂ radical concentrations decrease. Like the 25DMF2R radical, ring opening with ultimate formation of n-butadienyl radical and carbon monoxide also becomes important under richer conditions and increasing temperatures, accounting for 44.8% of 2MF2R radical consumption under these conditions. No JSR data currently exists for 2-methylfuran, though it is clear that a study under similar conditions to the current study would provide a good test of our mechanistic and kinetic proposals for 25DMF, as both species should undergo similar reactions, mechanistically and kinetically.

4.3 Laminar burning velocities

4.3.1 Experimental

Experimental laminar burning velocities at atmospheric pressure are shown in Figure 25 along with mechanism calculations. A brief analysis of the experimental data is worthwhile given the wide range of conditions for which experimental laminar burning velocities for 25DMF-air mixtures have been determined.

Fig. 25.

Experimental laminar burning velocities for 2,5-dimethylfuran-air mixtures as a function of unburnt gas temperature and equivalence ratio from this work (closed squares), Wu et al. [15,16] (open and closed circles) and Tian et al. [18] (open and closed triangles). Lines represent model calculations. The reader is referred to the web version of this article for interpretation of colour in this figure.

Tian et al. [18] used a constant volume vessel to determine the laminar burning velocities of 25DMF-air mixtures at 0.1 MPa pressure and at initial temperatures (T_i) of 323, 348 and 378 K. Similarly Wu et al. [15,16] used a constant volume cylindrical combustion chamber to determine the laminar burning velocity of 25DMF-air mixtures at 0.1 MPa initial pressure and T_i of 393, 433 and 473 K. In all three studies the un-stretched laminar burning velocity was calculated from the experimentally measured stretched flame speed, stretch rate and Markstein length, along with a calculated ratio of burnt to unburnt gas densities. Linear stretch extrapolation was used in all three studies. To negate the influence of ignition energy and pressure rise on their final measurements, the observation range was confined to flame front radii of 6–18 mm in the case of Tian et al. [18], and 6–25 mm in the case of Wu et al. [15,16].

When comparing our experiments with those of Tian et al. at similar T_i, (358 K this study, 348 K Tian et al.), those measured by Tian et al. are slower than those of this study. At 358 K, the peak burning velocity of 51.8 cm s⁻¹ is determined at ϕ = 1.10 in this study, which contrasts with the peak velocity of ≈ 45 cm s⁻¹ determined by Tian et al. at ϕ = 1.15. The experimental burning velocities of Tian et al. measured at 373 K are also slower than our 358 K measurements for equivalence ratios of 1.0–1.2 and their measurements at 323 K are not dissimilar to our 298 K measurements in the same range of ϕ. The measurements of Tian et al. are therefore found to be consistently slower than those of this study, in the region where peak flame speed can be anticipated. Both sets of studies do agree well in terms of the equivalence ratio at which peak flame speed is observed.

Comparison of our measurements with those of Wu et al. [15,16] show their data at 393 K is of a similar order to both our 358 K measurements and the 373 K measurements of Tian et al. for equivalence ratios up to ϕ = 1.1. This seems inconsistent and one might expect this data to show a greater laminar burning velocity than the other measurements given the greater T_i of their experiments. Above ϕ = 1.1 the experiments of Wu et al. range from 3–6.5 cm s⁻¹ faster than our 358 K measurements which is more reasonable. Peak laminar burning velocities for Wu et al. are observed at ϕ = 1.2, although they are typically observed at ϕ = 1.1 in this study, and in that of Tian et al.

Although the experimental data of Tian et al. [18] and Wu et al. [15, 16] appear consistent within the confines of their own studies, comparisons with each other and with the current study show inconsistencies. This is possibly due to the linear stretch extrapolations necessary to determine the laminar burning velocity of spherically expanding flames analysed using combustion bombs and vessels.

Kelley and Law [89] have recently noted that linear extrapolation of the stretched flame propagation speed may lead to inaccurate determination of the unstretched laminar burning velocity. For example, linear extrapolation may be perturbed by ignition energy and the presence of electrodes in the early stages of flame propagation and confinement and chamber effects in the latter stages. Deviations from linearity may arise due to high stretch rates, mixture non-equidiffusion and small diffusivity of larger fuels. One should note that these corrections are not necessary with the heat-flux method used in this study.

Wu et al. [17] also measured laminar burning velocities at various initial pressures up to 0.75 MPa for a T_i of 393 K as an extension of their atmospheric work discussed above, Figure 26. Maximum laminar burning velocities were measured at ϕ = 1.2 at all pressures studied, with a decrease in burning velocity observed with increasing pressure – a result of the increased free-stream density and influence of pressure-dependent radical chain termination reactions. At pressures above 0.5 MPa, wrinkling of the flame was observed with flame instabilities observed at 0.75 MPa for ϕ ≥ 1.2.

Fig. 26.

Experimental laminar burning velocities for 2,5-dimethylfuran-air mixtures as a function of pressure and equivalence ratio at unburnt gas temperatures of 393 K [17]. Lines represent model predictions.

4.3.2 Modelling

Current modelling calculations of atmospheric pressure laminar burning velocities (Figure 25) show that peak burning velocity for a given T_i is consistently predicted to occur at ϕ = 1.1. Indeed a highly linear increase (R² = 0.99) in peak laminar burning velocity is predicted by the mechanism for the eight unburnt gas temperatures studied. This linear relationship between the computed laminar burning velocity and T_i at a given ϕ can be expected, given the corresponding linear increase in the adiabatic flame temperature with T_i. Somers et al. [41] found experimentally (heatflux method) that the peak burning velocity for closely related 2-methylfuran-air mixtures increased linearly with T_i. The same is expected for 25DMF-air mixtures, yet this trend is not observed experimentally when all data is considered and the current analysis is important in highlighting discrepancies in the presently available experimental data for 25DMF. It is extremely unlikely therefore that a single kinetic mechanism will accurately predict all experimental data in the literature, with the experimental data of Wu et al. [15,16] seemingly deviating most from our numerical predictions and other literature data both qualitatively and quantitatively.

At a T_i of 298 and 358 K, the burning velocities calculated using our mechanism are 3–4 cm s⁻¹ (≈ 8%) lower than our experimental data at ϕ = 1.1, with a consistent underestimation of the laminar burning velocity under rich conditions, showing deviations as large as 6 cm s⁻¹ (≈ 27%) from experiment. From ϕ = 0.6–1.2 the mechanism is within 10% of all experiment data, even in the worst instances. The mechanism therefore seems to deviate most from experiment under fuel rich conditions.

When compared with the experiments of Tian et al. [18], our kinetic mechanism is in good agreement with the experimental laminar burning velocities from 323–373 K, allowing for some scatter in the reported measurements. Deviations at 323 K are at most ≈ 7%, deviations at 343 K are ≈ 18.6% at ϕ = 1.5 but are within ≈ 9% for the other three measurements, and deviations at 373 K are ≈ 19% at ϕ = 1.6, but calculations are within ≈ 9% of experiment for all other measurements. As with the heat-flux method measurements described above, the mechanism estimations differ most from experiment under fuel rich conditions.

When compared with the experiments of Wu et al. [15,16], our mechanism consistently over-predicts the laminar burning velocity under lean conditions (for ϕ = 0.8; ≈ 9.9% at 373 K, ≈ 12% at 433 K, ≈ 14% at 473 K) and vice-versa under rich conditions (for ϕ = 1.5; ≈ 22% at 373 K, ≈ 23% at 433 K, ≈ 24% at 473 K). At peak experimental burning velocity (ϕ = 1.2), the mechanism agrees with experiment within 2% at 373 K, 1% at 393 K and 6% at 473 K.

The predictions of our mechanism therefore agree best with the literature data of Tian et al., within their limited range of ϕ, and measurements from this work under lean to stoichiometric equivalence ratios. Although the peak flame speed of Wu et al. is well estimated by our mechanism, the experimental dependency of laminar burning velocity on equivalence ratio is not in agreement with numerical modelling, and it would also seem that this data may be inconsistent with respect to the measurements of this work and those of those of Tian et al..

For laminar burning velocities as a function of pressure, Figure 26, our kinetic mechanism does predict the general trend of decreasing burning velocity with increasing initial pressures, but deviates more from the experimental measurements with increasing equivalence ratio and pressure. Considering that the atmospheric pressure data of Wu et al. [15,16] appears inconsistent in light of other experimental and modelling work, it is not surprising that modelling predictions of laminar burning velocity at elevated pressures by the same authors are in poor agreement. Re-determination of the laminar burning velocities of 25DMF-air mixtures at elevated pressures may therefore be of interest for future studies.

Sensitivity analyses were carried out to identify the kinetic parameters which control our predictions of laminar burning velocity over a range of conditions, Figures 27 and 29. In particular we focus on the kinetics of reactions of 25DMF or its related intermediates which can serve as optimization targets to improve agreement with the experimental data, particularly under fuel rich conditions. However, it is quite apparent from the sensitivity analyses that it is the kinetics of smaller hydrocarbon species and the reactions of hydrogen atom which exert most control of the predicted burning velocity.

Fig. 27.

First order sensitivity analysis of computed laminar burning velocities for 2,5-dimethylfuran-air mixtures at 1.0 atm and T_i = 298 K, as a function of equivalence ratio. A negative coefficient corresponds to a reaction which reduces the computed laminar burning velocity and vice versa. The reaction Ḣ + O₂ → Ö + ȮH and CO + ȮH → CO₂ + Ḣ have been omitted for clarity. Chemical “nicknames” above correspond to assignments in the Chemkin format kinetic mechanism.

Fig. 29.

First order sensitivity analysis of computed laminar burning velocities for 2,5-dimethylfuran-air mixtures ϕ = 1.5 and T_i = 393 K, as a function of pressure. A negative coefficient corresponds to a reaction which reduces the computed laminar burning velocity and vice versa. The reaction Ḣ + O₂→ Ö + ȮH has been omitted for clarity. Where no bars are visible for a given condition, the corresponding reaction was not found to be amongst the top 30 most sensitive reactions. Chemical “nicknames” above correspond to assignments in the Chemkin format kinetic mechanism.

At ϕ = 1.1 and 1.5, hydrogen atom abstraction from the alkyl side chain by Ḣ atom and ȮH radical are found to inhibit reactivity. Ḣ atom addition forming 2-methylfuran and ĊH₃ radical is seen to promote laminar burning velocities at ϕ = 1.1 but shows little sensitivity under other conditions. We find that hydrogen atom abstraction reactions from the methyl group lead to the formation of 2,4-cyclohexadien-1-one, which in turn isomerises to phenol or forms a range of cyclopentadiene and 1,3-pentadiene radicals as seen during high temperature ignition delay and pyrolysis studies previously. These species tend to form resonantly stabilised free radicals, which may persist in a flame and act as a sink for Ḣ atom, whose kinetics are particularly sensitive to the accurate prediction of the laminar burning velocity of effectively all hydrocarbon fuels.

In contrast, hydrogen atom addition reactions lead to formation of 2-methylfuran and methyl radical, and 1,3-butadiene and acetyl radical. 2-methylfuran can be consumed by abstraction reactions, which ultimately leads to the formation of n-butadienyl radical and CO, with n-butadienyl capable of decomposing to a vinyl radical and ethylene, as described by Somers et al. [41] in their 2-methylfuran modelling work. This reaction sequence can lead to chain branching in the flame from the reaction of vinyl radical with molecular oxygen, which is seen to promote reactivity in sensitivity analysis. Similarly, 1,3-butadiene can undergo hydrogen atom addition to form vinyl radical and ethylene. The contrasting products of free radical abstraction and addition reactions provide some insight into why the former inhibits the computed burning velocity, and the latter has a slight promoting effect.

As a test, simulations were carried out under the conditions of our burning velocity experiments to assess how a variation in some of the kinetics relevant to 25DMF impacts the computed laminar burning velocity. Figure 28 shows the result of simultaneously reducing the pre-exponential factor of the rate constants for hydrogen atom abstraction by Ḣ atom and ȮH radical by a factor of two. As before, the modified mechanism matches the laminar burning velocities measured as part of this work under fuel lean conditions, with an increase in peak flame speed of approximately 1–1.5 cm s⁻¹ at both 298 and 358 K observed. Laminar burning velocities remain under-predicted by up to 2 cm s⁻¹ (≈ 5%) at peak experimental flame speed, however predictions under rich conditions show a modest improvement and remain under-estimated (ϕ = 1.6, 24% at 298 K, 18% at 358 K). The influence which altering these rate constants has on elevated pressure laminar burning velocity calculations is similar, and is shown in supplementary material.

Fig. 28.

Experimental laminar burning velocities for 2,5-dimethylfuran-air mixtures from this work with modelling predictions showing variation in predicted laminar burning velocities with modification of hydrogen atom abstraction reactions (see text).

This test illustrates the small influence which altering these parameters has on the the computed laminar burning velocities. It is therefore difficult to resolve the discrepancies between our mechanism and our heat-flux method experiments under fuel rich conditions, by the sole alteration of kinetic parameters unique to the 25DMF mechanism, given that those highlighted in sensitivity analyses stem from computational studies [29,33] where uncertainties in the rate constants are probably of the order of a factor of 2–3 for hydrogen atom abstraction pathways.

At elevated pressures and rich conditions, hydrogen atom termination reactions show an increased sensitivity also, Figure 29. In particular, the reaction of Ḣ + ĊH₃ → CH₄ clearly reduces the computed laminar burning velocity and an alteration to this, albeit extensively studied, rate constant is likely to have more influence on our prediction of the elevated pressure data of Wu et al. [17] than would an alteration of the kinetics of 25DMF and its related species. The recombination of Ḣ atom with resonantly stabilised allyl and cyclopentadienyl radicals forming propene and 1,3-cyclopentadienyl respectively is also seen to inhibit laminar burning velocity, but to a much smaller extent than the previous reaction. Quantitative flame speciation measurements, which do not currently exist in the literature for 25DMF, may provide further insight into the flame chemistry of this species, thus complementing the global measurements presented herein and allowing a future resolution to the outstanding discrepancies between modelling and experimental work.

5 Conclusions

This paper presents novel experiments on the pyrolysis and oxidation of 2,5-dimethylfuran. We also describe the development of a detailed kinetic mechanism which is based on a combination of literature theoretical studies, newly presented ab initio calculations and by analogy with similar chemical systems. The mechanism is compared with our new experiments and relevant literature data with rate of production and sensitivity analyses used to identify important reaction pathways and kinetic parameters.

Shock tube experiments on the pyrolysis of 2,5-dimethylfuran have been carried out based on indications [40] that a previous determination [21] of the temperature of at which 25DMF decomposes was in error, or at least, in doubt. Our experiments, coupled with numerical modelling results, support the findings of Sirjean et al. [40], who proposed that the chemical thermometer used by Lifshitz et al. [21] to determine the temperature behind their reflected shock waves was probably at fault. Two kinetic mechanisms, one from this work, the second from Sirjean et al. [40], are now in good agreement with shock tube decomposition profiles of 25DMF from 1200–1340 K, at 2–3 atm and residence times of 2 ms. The results support the validity of both mechanisms under pyrolysis conditions.

Previous experiments on the pyrolysis of 25DMF in a bench scale flow reactor [39] from 873–1098 K, 1.7 bar and 300–400 ms have also been numerically investigated for the first time. Modelling results show that the consumption mechanism of 25DMF under these conditions is largely the same as under the shock tube conditions described above — unimolecular decomposition through a 3–2 hydrogen atom transfer acts as the primary chain initiator, with subsequent radical attack on the fuel, predominantly by hydrogen atom and methyl radical, further propagating the chain reaction. Despite some initial resolutions on the pyrolysis behavior of 2,5-dimethylfuran as described above, our kinetic mechanism under-predicts the conversion range of the fuel under flow reactor conditions. There remains an unresolved discord between our mechanism/higher temperature pyrolysis experiments and these flow reactor results.

We have measured ignition delay times in a shock tube for mixtures of 0.75% 25DMF, 2.8/5.63/11.25% O₂ in argon from 1350–1800 K at atmospheric pressure. Typical Arrhenius behavior is observed as a function of temperature, and a clear trend showing a reduction in ignition delay time with increasing O₂ concentrations is found. Our mechanism reproduces these trends within the 20% uncertainty of experiment. The kinetic mechanism developed by Sirjean et al. [40] is also used to model these experiments, where good agreement is observed under all conditions. However, comparison of both mechanisms with shock tube ignition delay times measured by Sirjean et al. [40] show that neither mechanism can replicate their experiments within 20% uncertainty under fuel lean conditions. The mechanism of this work shows poorer agreement with these measurements than the mechanism proposed by Sirjean et al., although the high temperature kinetics and mechanism highlighted as sensitive for 25DMF oxidation appear to be in good agreement for the two mechanisms.

Shock tube ignition delay times for stoichiometric mixtures of 2.66% 25DMF in synthetic air are presented at 20 and 80 bar for temperatures of 820–1200 K, at measuring times up to 5 ms. Numerical predictions of these experiments shows satisfactory agreement at 80 bar, but ignition delay times are over-predicted at 20 bar and are not within experimental uncertainty. The influence of facility effects are discussed and inclusion of volume-time profiles in numerical modelling leads to an improved agreement with experiment. Rapid compression machine experiments are underway to supplement these measurements and refine the kinetic mechanism in this temperature and pressure regime.

Profiles of reactants, intermediates and products of 25DMF oxidation in a jet-stirred reactor are quantified from 770–1220 K, at 10 atm, τ = 0.7 s and ϕ = 0.5–2.0, and complement our high pressure shock tube measurements. Computed yields of 25DMF and O₂ are in good agreement with experiment. Newly described reaction pathways and kinetics for the formation of methyl vinyl ketone, 5-methyl-2-formylfuran and 5-methyl-2-ethylfuran lead to acceptable prediction of these species which are experimentally found to be important intermediates in the oxidation of 25DMF.

The kinetics of the reactions:

$$\begin{array}{c}\hfill 25\mathrm{DMF}+{\mathrm{O}}_2\to 5-\mathrm{methyl}-2-\mathrm{furanylmethyl}+\mathrm{H}{\stackrel{.}{\mathrm{O}}}_2\hfill \\ \hfill 25\mathrm{DMF}+\mathrm{H}{\stackrel{.}{\mathrm{O}}}_2\to 5-\mathrm{methyl}-2-\mathrm{furanylmethyl}+{\mathrm{H}}_2{\mathrm{O}}_2\hfill \\ \hfill 5-\mathrm{methyl}-2-\mathrm{furanylmethyl}+\mathrm{H}{\stackrel{.}{\mathrm{O}}}_2\to 5-\mathrm{methyl}-2-\mathrm{furylmethanoxy}+\stackrel{.}{\mathrm{O}}\mathrm{H}\hfill \\ \hfill 5-\mathrm{methyl}-2-\mathrm{furanylmethyl}+{\mathrm{CH}}_3{\stackrel{.}{\mathrm{O}}}_2\to 5-\mathrm{methyl}-2-\mathrm{furylmethanoxy}+{\mathrm{CH}}_3\stackrel{.}{\mathrm{O}}\hfill \end{array}$$

are highlighted as important variables in the prediction of high pressure ignition delay times and jet-stirred reactor profiles. ȮH radical addition to the 25DMF is also found to be an important fuel consuming reaction in the intermediate temperature regime. Further theoretical and experimental studies on these pathways may be of interest to reduce uncertainty in the rate coefficients assigned to these reaction channels. Studies on the combustion behavior of ethyl- and formyl- furans may also be worthwhile as we now propose they are important intermediates in the oxidation of 25DMF, yet experimental and theoretical work is lacking.

The laminar burning velocities (S_L) of 25DMF-synthetic air mixtures have been measured using the heat flux method at unburnt gas temperatures of 298 and 358 K, at atmospheric pressure, for ϕ = 0.6–1.6. The new experiments are compared with available literature data [15,16,18] measured using combustion vessels at similar initial temperatures and equivalent pressures. When measurements from different apparatus are compared, inconsistencies are evident in terms of the magnitude of the peak laminar burning velocities and the dependency of S_L on fuel-oxygen equivalence ratio. Possible reasons for the disagreement are discussed.

Numerical modelling of these 25DMF-air laminar burning velocities have also been carried out for the first time. Predictions are within 8% of our experiments from ϕ = 0.6–1.1. At greater equivalence ratios, modelling results deviate further from our experiments, underestimating S_L by ≈ 27% in the worst instances. Predictions of the experiments of Tian et al. [18] show similar trends, with the best agreement observed (within ≈ 9%) for lean to stoichiometric mixtures, with modelling results again deviating substantially from experiment (up to 20%) under fuel rich conditions. Our mechanism does not predict the experiments observed by Wu and co-workers [15,16] with any degree of accuracy.

Although numerical predictions of our experiments and those of Tian et al. are in less than satisfactory agreement, it would appear that the results of Wu [15,16] are inconsistent when considered in light of the other experimental measurements and our modelling work. Predictions of laminar burning velocities at elevated pressures, also from Wu et al. [17], are in poor agreement with experiment. Sensitivity analysis do not identify a clear route to resolving the predictions of burning velocities under fuel rich conditions. Further experiments coupled with future refinements of the current mechanism are therefore necessary for a better understanding of the laminar burning velocities of 25DMF-air mixtures.

In summary, the work presented herein represents the most comprehensive and wide ranging experimental and kinetic modelling study on the combustion of 2,5-dimethylfuran to date. The kinetic mechanism developed as part of this work can adequately describe a wide range of experimental measurements and contributes to our fundamental understanding of the combustion of furanic biofuels. However, further experimental and theoretical work are required to improve our knowledge of the very interesting chemistry that lies at the root of the reactivity of 2,5-dimethylfuran under the conditions outlined above. In particular, studies on elementary reaction steps are advised to refine estimated kinetic parameters, to validate proposed reaction pathways more rigorously and to support the numerous global reactivity measurements which now exist in the literature. This study provides a platform for this future work.