Abstract
An increasing number of studies have reported computations of the absolute binding free energy of small ligands to proteins using molecular dynamics (MD) simulations with results that are in good agreement with experiments. This encouraging progress suggests that physics-based approaches hold the promise of making important contributions to the process of drug discovery and optimization in the near future. Two types of approaches are principally used to compute binding free energies with MD simulations. The most widely known are based on alchemical free energy methods, in which the interaction of the ligand with its surrounding are progressively switched off. An alternative method is to use a potential of mean force (PMF), in which the ligand is physically separated from the protein receptor. For both of these computational approaches, restraining potentials affecting the translational, rotational and conformational freedom of the ligand and protein may be activated and released during the simulations to aid convergence and improve the sampling. Such restraining potentials add bias to the simulations, but their effects can be rigorously removed to yield a binding free energy that is properly unbiased with respect to the standard state. A review of recent results is presented. Examples of computations with T4-lysozyme mutants, FKBP12, SH2 domain, and cytochrome P450 are discussed and compared. Differences in computational methods are discussed and remaining difficulties and challenges are highlighted.
I. INTRODUCTION
In recent years, a number of studies have reported computations of the absolute binding free energy of small ligands to proteins using molecular dynamics (MD) simulations with explicit solvent molecules. In many ways, the results are in good agreement with experiments. The progress is encouraging and suggests that physics-based approaches hold the promise of becoming an important predictive tool for drug discovery and optimization in the near future. The goal of this article is to review the recent progress in computations of absolute binding free energies, contrast the different methodologies that are available, and highlight the remaining challenges for the future.
Issues of molecular recognition, involving the non-covalent association of small ligands to large macromolecules with high affinity and specificity, plays a crucial role in biology and medicinal chemistry.1–3 Computational studies can help elucidate the fundamental principles governing those issues at the molecular level. Moreover, improving our ability to screen large databases of compounds in silico to identify potential lead drug molecules with accurate prediction of binding affinities could have a great impact on structure-based drug design. So far, however, computational screening methods have had only a mixed success rate. In the language of molecular modeling, ligand screening can be separated into two well-defined steps, “docking” and “scoring”.4 The docking step aims at predicting the preferred orientation of the ligand molecule bound to the protein receptor (the “pose”), and the scoring step aims at predicting the binding affinity of the ligand for a given ligand pose. While docking can proceed successfully via heuristic simplifications, the worse shortcomings of ligand screening approaches stem from the approximate scoring functions.
The fundamental principles controlling ligand binding are relatively well understood5,6, but scoring often relies on extremely simplified approximations in order to achieve the computational efficiency needed to handle large databases.7 To have any predictive and practical value, scoring must reflect the binding free energies with sufficient accuracy. Arguably, physics-based approaches such as free energy perturbation molecular dynamics (FEP/MD) simulations represent the most accurate approach to quantitatively characterize the binding free energy of small ligand with macromolecules. FEP/MD simulations can naturally handle the influence of solvent and dynamic flexibility,6 and previous studies indicate that the method is more reliable than simpler scoring schemes.8,9
Calculation of free energies are among the most important applications of biomolecular simulations.10–13 Initial applications of FEP/MD to biomolecular systems such as, for example, the calculations of hydration free energies14,15 and of binding free energies.16–20 go back the 1980’s. The early work was obviously burdened by the limited sampling from short simulations, though the potential of FEP methods was recognized. Considerable progress has been made since then, in part due to the increased availability of powerful computers. Moreover, the theoretical framework for carrying out various free energy computations has been greatly clarified.13 In recent years, free energy simulations have been used to characterize solvation properties of a wide range of molecules and have now become integral tools to test, validate, and refine biomocular force fields.21–24 Absolute hydration free energy were calculated for the amino acids sidechains25,26 and for a wide range of small molecules,27–30 water-cyclohexane transfer free energies of amino acids have been determined.31 Decomposition of free energies into contributions by the core repulsion, van der Waals dispersion, and electrostatic interactions helps clarify the intermolecular forces underlying solvation.26 Free energy simulations are arguably the most powerful and promising approaches to estimate the binding free energy of ligands to macromolecules. While FEP/MD remains too demanding computationally for screening extremely large databases of compounds, the recent success is indicative that these methods are going to play an increasingly important role in drug discovery and optimization in the near future.
In the following section, we review briefly the statistical thermodynamics formulation of molecular association, and describe the main approaches to compute binding free energies from MD simulations. There are the methods based on alchemical perturbation, in which the interaction of the ligand with its surrounding are progressively witched off, and there are methods based on the potential of mean force (PMF), in which the ligand is physically separated from the receptor. For both of these computational strategies, restraining potentials may be activated and released during the simulation to sample more efficiently the changes in translational, rotational and conformational freedom of the ligand and protein upon binding. A review of recent results is then presented, and differences in computational methods are discussed. A particular attention is given to studies of ligand binding to T4-lysozyme mutants,32–37 and FKBP12.38–42 Our focus is mainly on studies based on free energy simulation methods with explicit solvent. The wide range of scoring methods that are available for virtual screening are not covered here, as they have been the object of recent reviews (e.g., see 43–45). The review is concluded with a discussion highlighting the remaining challenges with an outlook to the future.
II. THEORY AND METHODS
A. Statistical Mechanics and Equilibrium Binding Constant
To calculate a standard binding free energy with computer simulations, a relation has to be established between macroscopic observables and microscopic variables. For the sake of concreteness, let us consider a protein macromolecule (P) in thermodynamic equilibrium with a dilute solution containing ligand molecules (L). The equilibrium constant Kb of the binding reaction L + P ⇌ LP is defined as Kb = [LP]/([L][P]), where [L], [P], and [LP], are the equilibrium concentrations of the unbound ligand, unbound protein, and bound complex, respectively. The standard binding free energy is defined from the equilibrium constant by , where C° is a standard concentration, kB is the Boltzmann constant and T is the absolute temperature.
To obtain an expression for Kb it is useful to consider the occupancy operator H equal to 1 when the ligand is in the binding site of the protein, and 0 otherwise. The probability to find one protein with one ligand bound is , the probability to find a protein with no ligand bound is , and the ratio of these occupancy probabilities is directly related to the equilibrium constant, . This ratio is independent of the concentration of the protein, as long as the solution is relatively dilute. Following classical statistical mechanics, it can be shown that the equilibrium constant can be expressed as34,46–48
| (1) |
where U is the total potential energy of the system, β ≡ 1/kBT, L and X represent respectively the coordinates of the ligand and all remaining atoms (solvent and protein), rL is the position of the center of mass of the ligand, and r* is some arbitrary position far away in the bulk region relative to the protein.34,46,49 This derivation in terms of ⟨H⟩, which be traced back to Bjerrum,50 is more direct than the traditional treatments based on chemical potentials.47,48,51 One may note that Kb has the dimension of volume, hence the need to multiply by the standard concentration C° (1 mol/L = 1/1660 Å3), to define the dimensionless quantity KbC° and a meaningful binding free energy .
Based on Eq. (1), one may picture the binding process as the ligand leaving the bulk region (in the denominator) and moving into the binding site (in the numerator). In principle the binding free energy could be determined directly from the average population of the bound state ⟨H⟩, via an unbiased trajectory. However, while this has been done previously (e.g., see ref 52), it is generally more advantageous to introduce a sequence of intermediate states between the bound and unbound “end-points” states in order to enable practical computations. The most popular approaches rely on alchemical free energy thermodynamic perturbation techniques in which the intermediates are chosen to progressively switch “off” the interactions of the ligand with its surrounding.20,34,40,46,47,53,54 Alternatively, convenient intermediates may be chosen to control the physical separation between the ligand and the protein without alchemical decoupling. In this approach, the binding constant is computed via a protein-ligand potential of mean force (PMF).41,49,55,56 One may refer to this PMF-based approach as the “pulling” method.41 At a practical level, any number of restraining potentials may be activated and then released at different stages during the PMF calculations to improve convergence. As long as the total reversible work between the end-points is properly calculated, the final result is independent of the intermediate states.
B. Standard Binding Free Energy from Alchemical Perturbation
The alchemical method compute the reversible thermodynamic work for decoupling the ligand from its surrounding (protein and bulk solvent). As an illustration, let us first consider the free energy associated with decoupling the ligand in the bulk solvent,
| (2) |
where U0 represents the total potential energy of the system with a non-interacting (decoupled) ligand. The thermodynamic decoupling in Eq. (2), which corresponds to the transfer of the ligand to the gas phase, is often referred to as an “annihilation” process. This should not be misconstrued since the ligand is only decoupled from its environment. The solvation free energy in Eq. (2) can be computed using alchemical free energy perturbation (FEP) or thermodynamic integration (TI) (see 57, 11 and 58 for reviews on methodology).
Applying directly the decoupling scheme of Eq. (2) for the ligand in the binding site can be attempted,53 though this is often impractical. The non-interacting (decoupled) ligand should in principle drift away from the binding site and wander anywhere in the volume of the simulation box. This increases the difficulty to obtain a statistically converged and reversible free energy from standard methods (see the discussion in 54). A proper free energy calculation must be reversible, i.e., the change in free energy for introducing the ligand molecule into a system should be equal, but of opposite sign, to the free energy for removing the ligand. Nevertheless, if one assumes that the ligand has explored the entire simulation box and the free energy calculation is converged, then the equilibrium constant follows from Eq. (1),
| (3) |
where Vpbc is the volume of the box for the periodic boundary conditions (PBC) used in the MD simulation to calculate is the solvation free energy calculated from a simulation with the ligand in a pure solvent box defined in Eq. (2). The relation to the standard state expressed in Eq. (3) presumes that the unrestrained alchemical decoupling state is fully converged, which would need to be monitored with attention. Furthermore, using the above expression assumes implicitly that the ligand binds tightly to the protein and that the concentration of ligand in the MD box is large compared to 1/Kb (i.e., all contributions to are dominated by the bound state).
Such difficulties are easily avoided by introducing a restraining potential, ut, at an intermediate step to control the translation of the ligand relative to the protein binding site. This strategy, introduced by Hermans and Subramaniam,20 has been progressively enriched over the years by a number of additional developments and variants.32–35,46,54 The restraining potential is introduced at one end-point to “confine” the uncoupled ligand within the binding site, and is then “released” at the other end-point, where this step can be carried out analytically.20,46,54 Gilson et al.47 called free energy calculations in which there is no translational restraint the “double annihilation method” (DAM), and calculations in which there is a translational restraint the “double decoupling method” (DDM).
In subsequent developments, restraining potentials have been introduced to control the ligand rotation32,34,35,54 conformation,34,40,49 and protein sidechain conformation.36 The potential restraining the translation, rotation, and conformation, denoted ut, ur, and uc, respectively, are sometimes called “virtual molecular tweezers”32 or “virtual bonds”.54 The reversible work for the entire association/dissociation process is then carried out as a series of sequential steps, during which the interaction of the ligand with its surrounding (protein and solvent) as well as the various restraining potentials are switched on and off.40
The standard binding free energy obtained from the step-by-step procedure can be expressed as,34,40
| (4) |
where and and are the free energy cost associated with applying the conformational restraint on the ligand and protein in the binding site and bulk solvent, Ft and Fr are the factors associated with applying restraints on ligand rotation and translation when it is decoupled, and are the free energy associated with applying restraints in the binding site, is the free energy associated with switching on ligand interaction in the binding site with all restraint potentials applied, is the free energy associated with switching on ligand interaction in bulk solvent with conformational restraint potential. In practice, the potential uc for restraining the conformation of the ligand has been written as a quadratic form kξ2, where ξ is the root mean standard deviation (RMSD) of the ligand relative to its bound conformation.34,40,49 Simple dihedral torsion potentials have also been used to confine the conformation of the protein by restraining the orientation of protein sidechains.36
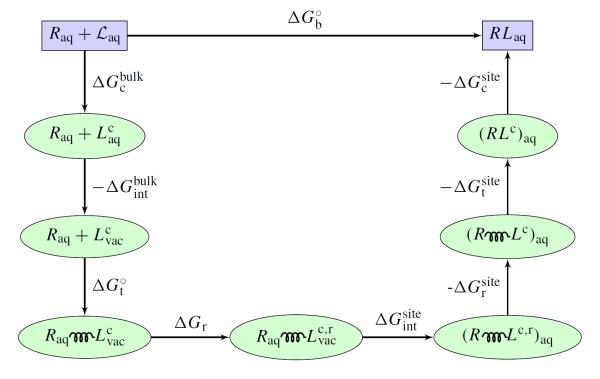
Eq. (4) provides a decomposition of the dominant factors affecting the binding free energy.32,34,40 Normally, the interaction component, ΔΔGint, is highly favorable but is strongly opposed by unfavorable contributions from the ligand translation, , rotation/orientation, ΔΔGr, and conformation, ΔΔGc. The decomposition can also be used to clarify the significance of end-point approximations, such as the explicit/implicit solvent MM/PB-SA13,59,60 and the linear interaction energy (LIE).61,62 The value of the various contributions depends on the details of the restraint potential, but the total standard binding free energy is independent of those factors. The complete DDM procedure is illustrated schematically in Figure 1.
Figure 1.
Shown in the figure is path for the free energy computation accordinng to the alchemical DDM with restraining potentials. denotes the configuration restricted ligand in bulk solvent. denotes the non-interacting ligand with configurational restraint. denotes the non-interacting ligand with both configurational and rotational restraints. The spring represents the translational restraint potential. See reference 34 for a complete theoretical formulation.
There is sometimes the misperception that computations based on DAM yield more meaningful (unbiased) results because they do not involve restraining potentials. This is incorrect. Judiciously chosen restraining potential actually enhance sampling efficiency.40,49,63,64 The various restraining potentials serve as a “guide” to prevent large excursions of the configurations of the molecular system, thus helping to reduce the size of the configurational space that needs to be sampled between the end-points of a free energy calculation. Spatial confinement via biasing potentials is a general noise-reduction technique to aid the convergence of simulations (see ref 65). While the convergence and reversibly in standard DAM poses a real problem, restraining potentials may be activated and then released at different stages during a DDM calculation, as long as their free energy contributions are properly accounted for.
Any restraining potential that is activated (confine step) must be deactivated before the end-state (release step) in order to yield properly unbiased results. The effects of switching any restraining potential on and off may be calculated via standard TI or FEP, or combined with umbrella sampling66 to achieve a higher precision.34,40,63 Typically, the free energy associated with ut and ur have been computed directly with FEP or TI.32–35,40,49 In this case, unbiased simulations are assumed to be able to achieve conformational sampling. A more powerful approach is often needed to treat slow varying degree of freedom involving the conformation of the ligand or the protein. For example, the free energy cost and associated with restraining the conformation of the ligand in the bulk or in the binding site by the potential uc have been calculated as
| (5) |
and
| (6) |
where and are PMFs of the ligand in the bulk and in the binding site, respectively.34,40,49 They must be calculated with biased simulations according via umbrella sampling. A similar umbrella sampling technique has been utilized by Dill and co-workers to treat the effect of sidechain configurations on ligand binding in T4 Lysozyme.36 The above procedure with Eqs. (5) and (6) constitute the basis of what one might call a “deliberate” sampling strategy: a PMF along some clearly identified degree of freedom is first calculated with biased simulations, and then unbiased averages are extracted via an explicit numerical integration of the probability distributions involving the Boltzmann factor of the unbiased PMF. The free energy difference , corresponds to the reversible work for switching on a conformational restraint in one end-point state and switching it off in the other. This reversible process has been referred to a “confine-and-release cycle”.36
C. Nonpolar and Electrostatics Interactions
A deeper insight into the microscopic factors driving ligand binding can be achieved by further dissecting the interaction components and according to the character of intermolecular forces.26 Intermolecular forces are dominated by short-range harsh repulsive interactions, arising from Pauli’s exclusion principle, and long-range van der Waals attraction and electrostatic interactions, arising respectively from quantum mechanical dispersion and the non-uniform molecular charge distribution. In standard biomolecular potential functions, the nonpolar forces are modeled with Lennard-Jones (LJ) 6-12 potentials, while electrostatics forces are represented on the basis of coulomb interactions between partial charges.21–24 For example, the Lennard-Jones 6-12 potential can be separated into purely repulsive and attractive parts according to the Weeks-Chandler-Anderson (WCA) scheme.26,67 Assuming that the repulsive, dispersive and electrostatic components of the interactions are switched on sequentially, in a step-by-step process, the decoupling free energy may be written as,26
| (7) |
where , and . The separation of intermolecular forces in Eq. (7) provides a useful framework for decomposing the interaction free energy of a molecular ligand with its surrounding into distinct contributions with a clear and well-defined physical meaning.
D. Binding Free Energy from a PMF
The equilibrium association constant and binding free energy may also be calculated using a PMF,68,69 without resorting to the alchemical decoupling steps as in DDM. In simple cases, a strategy based on the one-dimensional (1D) radial PMF may work,55
| (8) |
where r* is a reference position far away in the bulk. However, the considerable complexity of biological systems often hinders the utilization of a straightforward approach. For example, the conformational freedom of the ligand may vary considerably between the bound and free state, which may be difficult to sample with unbiased simulations. To improve convergence in calculating the PMF, it may be advantageous to introduce various restraining potentials to limit the fluctuations of the conformation and orientation of the ligand, and to confine its translation along a well-defined axis “a” relative to the binding site. According to this restrained-PMF approach, the equilibrium binding constant is expressed in terms of a 1D integral,49
| (9) |
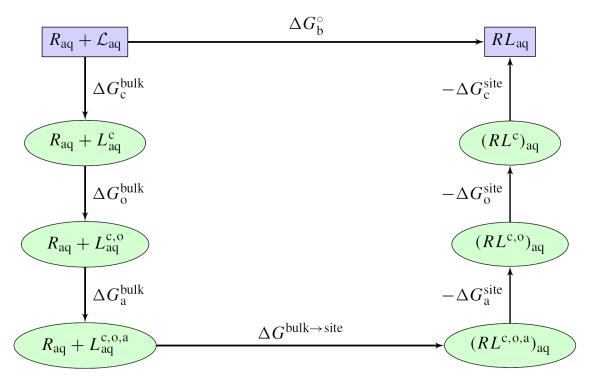
where w(r) is the 1D-PMF calculated in the presence of the configurational and orientational restraints. The quantity S* corresponds to the effective cross-sectional area swept by the ligand restrained along the axis “a” when it is at a distance r* from the protein. represents the free energy for restraining the bound ligand along the 1D axis. The additional factors ΔΔGc and ΔΔGr represent the loss of conformational and rotational freedom of the bound ligand relative to the unbound ligand and have the same meaning as in Eq. (4). As with the alchemical methods described above, restraining potentials of different shape may be introduced to carry out a calculation, as long as their contributions are correctly accounted for in the final equilibrium binding constant.70 The PMF-based method is illustrated schematically in Figure 2.
Figure 2.
Shown in the figure is path for the free energy computation using a PMF-based method with restraining potentials. denotes the configuration restricted ligand in bulk solvent. denotes the ligand with both configuration and orientation restraints. denotes the ligand in the bulk with all configurational, orientational and axial restraint potentials. is related to S* in Eq (9). ΔGbulk→site is related to I* in Eq (9). See reference 49 for a complete theoretical formulation.
E. Molecular System and Solvation
It is possible to carry detailed FEP molecular dynamics (MD) simulations to calculate the standard (absolute) binding free energy of a ligand to a receptor with the theoretical framework presented above. For meaningful results, one must simulate accurately the thermal fluctuations and the environment-mediated interactions arising in diverse and complex systems (i.e., the bulk solution and the protein binding site). Computational approaches at different level of complexity and sophistication have been used to describe the influence of solvent on biomolecular systems.71 Those range from MD simulations based on all-atom models with PBC, in which the solvent is treated explicitly, to continuum electrostatic models in which the influence of the solvent is incorporated implicitly. Conducting all-atom FEP/MD simulations is, however, often prohibitive and it is important to seek ways to reduce the computational cost of the calculations. An intermediate approach combines some aspects of both explicit and implicit solvent treatments.72–74 It consists in simulating a nonperiodic system with a small number of explicit solvent molecules in the vicinity of a region of interest, while representing the influence of the surrounding solvent with an effective “solvent boundary potential”. Many of our own free energy studies26,34,40 have used reduced atomic systems were simulated using the spherical solvent boundary potential (SSBP)73 for the bulk solvent, and the generalized solvent boundary potential (GSBP) for the binding site.74 The SSBP and GSBP are mixed discrete/continuum models. A detailed atomic model of the ligand and its nearest neighbors is simulated while the influence of the rest of the system is incorporated implicitly via a mean-field continuum electrostatic approximation. SSBP includes the reaction field from the dielectric response of the solvent acting on the atoms of the simulation region, while GSBP includes the reaction field for a solvent region of arbitrary geometry, as well as the solvent-shielded static field from the distant atoms of the protein receptor. Simulations of a reduced system embedded into a continuum mean-field environment offer an attractive strategy to decrease the computational cost of MD/FEP computations. Computationally this can be advantageous because binding specificity is often dominated by local interactions in the vicinity of the ligand while the remote regions of the receptor contribute only in an average manner. Nevertheless, one must be cautious with these approaches when the protein macromolecule undergoes a large conformational change upon ligand binding.
III. OVERVIEW OF RECENT RESULTS
A number of well-characterized ligand-binding protein systems have been the object of intense scrutiny, including mutants of T4-Lysozyme (T4L),75,76 the FK506 binding protein (FKBP12),38–42 cytochrome P450,77,78 and SH2 domains.79–81 While current studies ultimately are aimed at clarifying the fundamental principles driving molecular association, they also serve in large part as “testing grounds” to highlight and address critical issues with the various computational methodologies.
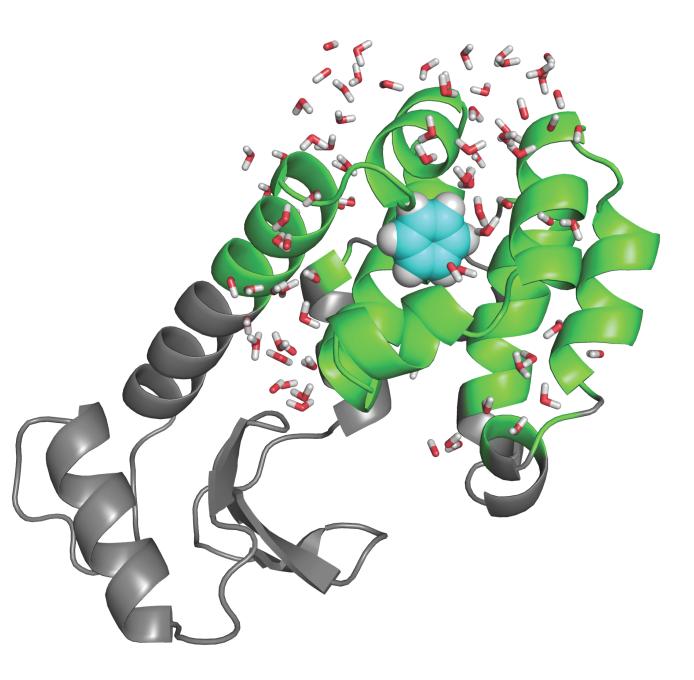
Some the most interesting and useful model systems to investigate noncovalent binding have been provided by Mutants of T4-Lysozyme (T4L) in which artificial cavities were engineered.75,76 A hydrophobic cavity, created by the mutation L99A in T4L, has been found to bind nonpolar aromatic molecules such as benzene and indole.75,82 Polar derivatives of benzene like phenol do not bind to this nonpolar pocket.75 The double mutation M102Q-L99A provides a hydrogen bond partner for the ligand, thus making the cavity able to bind more polar ligands.76 T4L/L99A with bound benzene is illustrated in Figure 3. The T4L systems have been the object of several computational studies.32–37 By virtue of their simplicity, these systems are particularly attractive for computational studies. The binding sites are buried inside the protein and not directly accessible to the bulk solvent. In addition, the cavities are believed to be essentially “dry” in the holo state, i.e., no solvent molecules are displaced upon ligand binding.
Figure 3.
T4 lysozyme L99A mutant with benzene bound in the cavity. The grey parts are treated as a mean field approximation with generalized solvent boundary potential.74 See reference 34 for computational details.
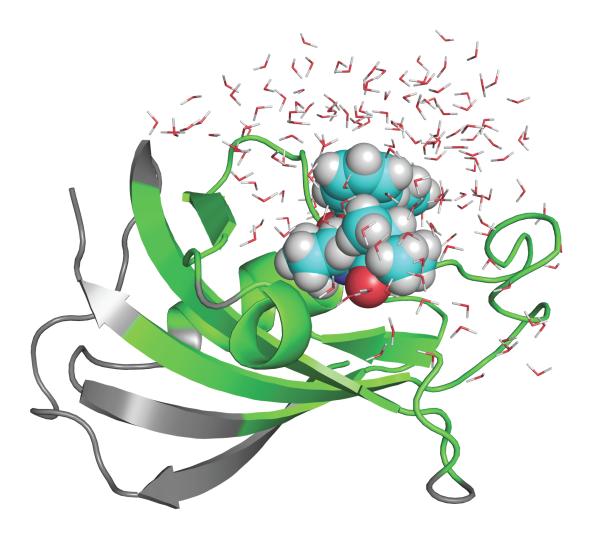
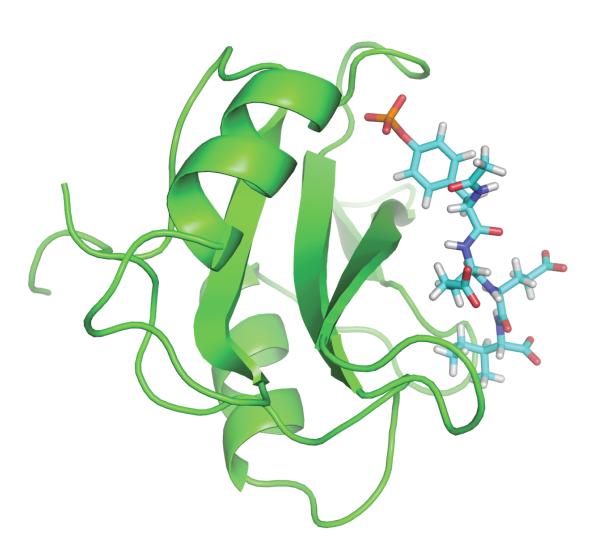
Another system that has been extensively studied is the FK506 binding protein (FKBP12).38–42 There is a vast collection of ligands, which are real drug molecules displaying considerable flexibility. Furthermore, the binding site is exposed to the bulk and solvent molecules must be displaced upon ligand binding. The FKBP12 system is also of extreme importance for immunosuppression because the binding of the drug FK506 to FKBP12 forms a complex that inhibits calcineurin and blocks the signal transduction pathway for T-cell activation.83,84 One the ligand included in a previous study40 is shown in Figure 4. Although FKBP12 is a small rigid protein, which does not undergo very large fluctuations, this system is considerably more complex than the simple pockets engineered in T4L.
Figure 4.
FKBP12 bound with ligand #8 studied previously.38,40 The grey parts are treated as a mean field approximation with generalized solvent boundary potential.74 See reference 40 for computational details.
A. Computational Methodologies
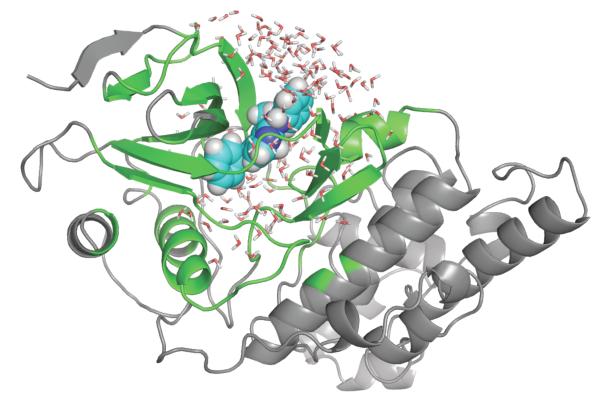
Relatively few studies have been based on PMF-based approaches. Those include the original study of amide association by Jorgensen,55 the binding of K+ into the gramicidin A channel56 the binding of the peptides to signaling modules,79,81 and ligands of FKBP12.41 The greatest advantage of a PMF approach is to avoid the alchemical decoupling of the ligand with its surrounding. In that sense, the PMF method imitates roughly the binding process whereby the ligand moves along a reaction path from the binding site to the bulk solution, though for meaningful results it is essential to unbias properly the effect of any restraining potential (see ref56). A PMF-based approach is particularly useful if a ligand is charged and its solvation free energy is very large.49,56,81 The issue is well illustrated by the calculation of the binding free energy of a phosphotyrosyl peptide, Ace-pYEEI, to the Src homology 2 (SH2) domain of Lck kinase.49 Figure 5 shows the SH2 domain with bound phosphotyrosyl peptide. An alchemical FEP strategy is essentially impractical in this case because the solvation free energy of the ligand is on the order of −800 kcal/mol.49 Even if the statistical uncertainty of a DDM calculation was only about 1 percent of the total solvation free energy, that would still translate into an error that is of the same order of magnitude as the quantity of interest itself. Using a restrained PMF approach, the computed standard binding free energy is −8.8 kcal/mol, in good accord with the experimental value of −7.1 kcal/mol.49
Figure 5.
SH2 domain with bound peptide pYEEI. The system was simulated with PBC and water is not shown for clarity. See reference 49 for computational details.
PMF-based approaches become less practical if the binding site is deeply buried and a simple path for ligand association cannot be found. In this case, alchemical decoupling free energy techniques are more effective. For this reason, the majority of binding free energy calculations has been carried out using alchemical decoupling approaches. A large number of computations on a wide range of systems based on DAM have been reported. However, with a few exceptions, the significance of those results is unclear due to unresolved issues of convergence and reversibility. The study of FKPB12 ligands by Fujitani and coworkers based on DAM is of particular interest because extensive efforts were made to achieve convergence and reversibility in the calculations.39 The connection to the standard state expressed in Eq. (3) was not specified and the calculated binding free energies were empirically shifted by an offset constant for comparison with experiments. In a study of the same system, Pande and co-workers used an approach with some similarities to both DAM and DDM.42 The simulation sampled a full decoupled state with the ligand wandering anywhere in the box, but only the configurations with the ligand within a small sub-volume near the binding site was included in the free energy. This analysis made it possible to specify the connection with the standard state. Generally, however, DDM with translational restraints appears to be more advantageous than DAM in terms of its ability to yield well-converged and reversible results that can be related unambiguously to the standard state. Computations based on DDM have been used to characterize water occupancy in protein cavities,46,85,86 and examine the binding of ligands to the T4L mutants,32–37 FKBP12,38–42 and cytochrome P450.77,78 The latter system has been used to test a method combining DDM with a grand canonical Monte Carlo (GCMC) algorithm to account for the change in water occupancy in the buried cavity.78
B. Salient Contributions to the Binding Free Energy
While there is definitely room for improvement, it is fair to say that the results from the many of the computational studies are in good agreement with experiments. It is clear that current computational approaches are sufficiently accurate to yield meaningful observations about the microscopic factors governing ligand binding. In the following, we review the most important conclusions drawn from the different computational studies.
1. Ligand-receptor interactions
One advantage of the alchemical approach based on DDM is the possibility to dissect the non-bonded interaction of the ligand with its surrounding (protein or solvent). Computing the reversible work in a step-by-step procedure makes it possible to separate the interaction free energy into repulsive, dispersive and electrostatic components based on Eq.(7). The decomposition provides important insight into the microscopic forces driving ligand binding.
As an illustration, Table IV and Table IV show the results for the T4L cavities and FKBP12, respectively, taken from our previous studies.34,40 The free energy decomposition indicates that both the LJ-core repulsion and dispersion contribute favorably to the binding free energy. In the case of nonpolar ligand binding to T4L/L99A, the favorable contribution from the core repulsion is consistent with the idea that the protein provides an empty cavity that is preformed for ligand binding. Essentially, no reversible work is needed to insert the repulsive core of the ligand into the protein binding site. In the case of FKBP12, the repulsive component is still favorable but much smaller (Table IV). The main difference with T4L can be understood by the location of the binding site. The binding pocket of FKBP12 is at the protein surface, whereas the binding site in T4L mutants is located deep inside the protein core. For FKBP12, there is no preformed empty cavity to bind the ligand and the repulsive interaction does not make a strong contribution to the free energy.
Interestingly, van der Waals dispersive interaction makes a systematically favorable contribution to the binding free energy, both in the case of T4L and FKBP12, i.e., dispersion is more favorable when the ligand is in the binding site than when it is in the bulk solvent. The origin of the difference can be directly traced back to the number density of van der Waals interaction centers per unit volume surrounding the ligand. The density is invariably larger in a protein environment than in bulk water. A similar observation was made by Levy and co-workers in developing implicit solvent models.87 The large dispersive contribution is correlated with the number of nonhydrogen atoms in the ligand. This observation agrees with the empirical observation that, barring large shape change, binding increased by adding heavy atoms to a ligand.88 Furthermore, one may note that the contribution from the van der Waals dispersion to the binding free energy is almost equal to the average van der Waals dispersion of the ligand with its surrounding in the bound state minus the average van der Waals dispersion of the unbound ligand with the bulk solvent. This clarifies the circumstances for which the difference in simple end-point averages may be a useful indicator for assessing the relative affinity of series of ligands with a similar shape.
Ligand specificity is strongly affected by the polarity of the cavity.37,76 This is well illustrated by contrasting the affinity of benzene and phenol for the T4L cavities engineered in the L99A and the M102QL99A mutants. As shown in Table IV, the free energy calculation is able to identify phenol as a binder of T4L/M102Q-L99A and as a nonbinder of T4L/L99A. In contrast, benzene binds to both the T4L/L99A and T4L/M102Q-L99A cavities. As the free energy decomposition shows, the nonpolar contribution for phenol is comparable to that of similar sized binding ligands, and it is only the high desolvation penalty from electrostatics that lowers its affinity for the L99A cavity. The M102Q-L99A double mutant provides a polar group that helps stabilize phenol electrostatically. This shows why phenol binds to the M102Q-L99A double mutant of T4L but not to the single mutant L99A.
2. Restriction of ligand motion
The loss of motional freedom of the ligand is intuitively associated with the concept of entropy. However, estimating changes in entropy accurately from simulations is very difficult,27,89 and schemes to partition the entropy into particular motions involves further approximations.90 Alternatively, the reversible work associated with the activation and release of restraining potentials can be utilized to estimate directly the loss of free energy associated with the loss of motional freedom upon binding. While such estimates depend on the specific pathway for decoupling the ligand, they can provide useful insight on the various contributions to the binding free energy.32,34 Based on an analysis with the restraining potential, the loss of translational freedom yields a free energy , where ΔV is an effective accessible volume for the center-of-mass of the ligand in the binding site. The microscopic volume ΔV is normally on the order of ~ 1 Å3, which yields the well-known standard state offset factor −kBT ln(C°ΔV ) of 4.4 kcal/mol. Thus, the reduction in translational freedom of the ligand almost invariably makes an unfavorable contribution to the binding free energy. Based on a similar analysis with the restraining potential, the loss of rotational freedom translates into a free energy ΔΔGr = −kBT ln(ΔΩ/8π2), where ΔΩ is the magnitude of the orientational fluctuations of the ligand. Because the factor ΔΩ/8π2 is typically much smaller than 1, the reduction in rotational freedom of the ligand always makes a considerable unfavorable contribution to binding free energy. Therefore, reduction in both translational and orientational freedom yields unfavorable contributions to the binding free energy. Interestingly, ΔV and ΔΩ can be related to the dynamical fluctuations of the bound ligand. This can be exploited to clarify the significance of end-point approximations, in which the translational and orientational contributions are often estimated using a quasi-harmonic approximation.47,59,60 For the T4L systems, roughly 5 to 9 kcal/mol arises from the loss of translational and rotational freedom of the ligand.34 For the FKBP12 ligands, the loss of translation corresponds roughly to 3.5 kcal/mol and the loss of rotation corresponds roughly to 4.5 to 5.5 kcal/mol.40
Except for small and rigid ligands, one expects a reduction of internal ligand flexibility upon binding. The free energy associated with the loss of conformational freedom of the ligand, ΔΔGc is the reversible work first to confine the ligand near its bound (reference) conformation with the restraining potential when it is in the bulk solvent , and then release it freely when it is in the binding site .34,40,49 The conformational restraining potential was written in terms of the RMSD of the ligand relative to its bound conformation and the calculation proceeded via the PMF of the ligand in the bulk and in the binding site, see Eqs. (5) and (6). Upon binding to the SH2 domain, there is a loss of conformational freedom of the phosphotyrosyl-peptide ligand which gives rise to an unfavorable free energy of about 2 kcal/mol.49 In the case of the flexible FK506-related ligands, the conformational free energy of the ligand varies from 1 to 7 kcal/mol;40 it is 6.9 kcal/mol for ligand 8, see Table IV). The utilization of a PMF to control the conformation of the ligand is useful to obtain more accurate estimates of the solvation free energy of the ligand, in cases when a direct decoupling scheme without conformational restraints may fail due to incomplete sampling.
In summary, the loss of motional freedom plays a key role in the resulting binding free energy. As a result, a large fraction of the total (favorable) contribution from the ligand-protein interaction is opposed by the (unfavorable) contribution arising from the loss of translational, orientational and conformational freedom of the ligand. In the case of benzene shown in Table IV, about half of the total interaction free energy (−11.52 kcal/mol) is canceled by the loss of motional freedom upon binding (5.42 kcal/mol). In the case of the FK506-related ligand shown in Table IV the interaction free energy of almost −26 kcal/mol is opposed by +15.7+ kcal/mol of unfavorable contributions from the translational, orientational and conformational loss, yielding a net binding free energy of only −10.3 kcal/mol. Even though FKBP12 itself is relatively rigid, about 60 percent of all the favorable interaction free energy of −26 kcal/mol is actually opposed by unfavorable contributions that are often ignored or discarded in simple scoring schemes. This has important implications for end-point methods47,59,60 and for the parameterization of empirical scoring functions that are adjusted to estimate the binding free energy from one fixed configuration.4
3. Conformation of the protein
Large conformational changes in the protein are expected to be an important component of the binding free energy. However, even seemingly minor conformational changes can have a considerable impact on the calculated binding free energy. A case in point is the orientation of the Val111 side-chain in the T4L/L99A system. In the bound complexes with small ligands (e.g., benzene, toluene, benzofurane, indole), the protein structure is almost unaffected and the side-chain of Val111 adopts the same conformation as in the apo structure. The calculated binding free energies for the small nonpolar ligands are generally in excellent agreement with experiments.34,37 Difficulties arise in the case of larger ligands (e.g., indene, n-butylbenzene, isobutylbenzene, o-xylene, p-xylene). The side-chain of Val111, which is in direct contact with the bound ligand, changes its rotameric states from a t conformation (χ1 = 180°) for the ligand-free or bound state with small ligands, to a g− conformation (χ1 = −60°) for the bound state with large ligands. The energy barrier around the χ1 torsion is sufficient to prevent the Val111 side-chain from rotating on the timescale of typical simulations, and the free energy for decoupling the ligand starting from the holo conformation is not correctly account for. As a result, calculated absolute binding free energies are too favorable by 2-3 kcal/mol when the DDM calculations are initiated directly from the ligand-bound structure of the protein.34 Additional problems were also noted in the case of indene, for which there is an erroneous sidechain rotamer of Val111 in the crystallographic X-ray structure of the bound complex (PDB 183L).34 While the problems with Val111 were resolved by adopting a deliberate sampling strategy involving the calculation of the PMF for the χ1 dihedral angle of the side-chain via umbrella sampling,37 the quantitative impact of a single protein sidechain on the calculated binding free energies is truly sobering. Whether a sidechain rotameric state is incorrect in the X-ray structure34 or insufficiently sampled in free energy simulations,37 the consequences can amount to an error of several kcal/mol. This highlights the importance of having accurate structural models for the calculations, and the importance of sampling all the relevant degrees of freedom.
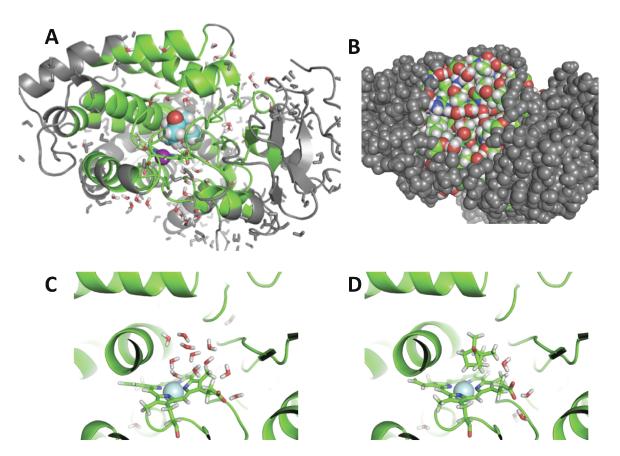
4. Binding site hydration
While the solvent configurations are generated spontaneously by MD when the binding site is exposed to the bulk phase, sampling difficulties become particularly acute when a binding site is deeply buried and inaccessible. In this case, the exchange of water molecules with the bulk region may be very slow, and the accuracy of free energy perturbation (FEP) calculations based on unbiased MD trajectories is severely compromised. Several theoretical studies have specifically examined the thermodynamics stability of water molecules in buried protein cavities46,85,86,91–93 and their impact on the thermodynamics of ligand binding.94–96 Ligand binding often disrupts the hydration of the binding site.97–99 A particularly challenging example is provided by cytochrome P450, a monooxygenase that oxidizes endogenous and xenobiotic substrates.77,78 Simulation studies have shown that some conformational change is required to open up a channel allowing exchange between the cavity and the bulk phase,100–102 and about five water molecules must be expelled from the deeply buried cavity upon the binding of camphor. Such a change in hydration state must be captured in free energy calculations to yield accurate and meaningful results. In a previous study, Wade and co-workers designed an alchemical transformation combining the annihilation of five water molecules together with insertion of the ligand in the cavity.77 While the strategy can produce accurate results, it requires an estimate of the number of water molecules to annihilate in the cavity. Figure 6 shows the buried binding site in p450, and the impact on water occupancy upon camphor binding. The binding of camphor to cytochrome P450 was studied using a free energy method combining MD with a grand canonical Monte Carlo (GCMC) algorithm79,103,104 to account for the change in water occupancy in the buried cavity during the alchemical free energy calculation.78 In this context, the reversible free energy work to alchemically decouple the bound ligand can be expressed in terms of standard TI,78
| (10) |
where denotes the probability of n solvent molecules occupying the binding pocket, the bracket ⟨⋯⟩λn means a constrained average with fixed number of solvent molecules in the binding pocket. The calculated binding free energy for camphor to P450 is −8.25 kcal/mol, in good agreement with the experimental value of −7.75 kcal/mol.77 In contrast, fixed water calculation with both the holo and apo water configuration give results with huge errors. When the calculation is carried out with the water molecules of the apo state, then the ligand has to push its way into the cavity and the resulting free energy is +12.60 kcal/mol, which is incorrect by almost 20 kcal/mol. On the other hand, when the calculation is carried out with the water molecules of the holo state, then there is a preformed empty cavity to receive the ligand and the resulting free energy is −14.25 kcal/mol, which is now too favorable by about 6 kcal/mol.
Figure 6.
The binding site of cytochrome p450 binding site. In A is an overview of the simulation system with the burried binding site. In B, the binding site is not visible with a space-filling representation. In C, the site with no camphor isoccupied by water, in D camphor is bound. See reference 78 for theoretical formulation and computational details.
C. Putting Binding Free Energy Calculations To The Test
While many of the recent studies demonstrate that free energy simulations provide a satisfying physics-base perspective of ligand binding,32,34–42,54,78,79 it is important to ascertain the accuracy and predictive power that can be achieved with current methods. One particularly nice study recently combined both computations and experiments to examine the binding of a large number of ligands to the nonpolar L99A cavity of T4L.37 In retrospective tests, computed absolute binding free energies for 13 ligands had an RMS error of about 1.9 kcal/mol relative to previously determined experimental values. In blind prospective tests, binding orientations and affinities were predicted for a set of 5 uncharacterized compounds identified by docking as putative binders. The calculations discriminated between several true binders and decoys, recognized the one nonbinder, accurately predicted ligand-bound orientations, correctly ranked the ligand binding affinities, and quantitatively predicted binding free energies. The main conclusions from this extensive effort are that alchemical free energy methods are more accurate than docking, are able to distinguish binders from nonbinders, and can make successful predictions of bound orientations and binding affinities.37 The authors also noted that accounting for protein conformational change via deliberate sampling of the rotameric state of the sidechain of Val111 was important for accuracy.
There have been also some extensive studies of the ligand binding FKPB12.38–40 This system is more difficult to manipulate than T4L, but it has the virtue of being representative of a real pharmaceutical target that binds drug-like compounds. Computed binding free energies for a series of 8 FK506-related ligands display an average RMS error of about 2 to 2.5 kcal/mol relative to previously determined experimental values.38–40 Recent results on the same series with extensive sampling show some improvement, with an RMS error of about 1.4 kcal/mol.42 Therefore, the results of retrospective tests on FKBP12 are now approaching an accuracy similar to that of T4L. It is worth noting that some of the results have been obtained from simulations of a fully solvated protein with PBC,38,39,42 and some were based on a reduced system embedded in a GSBP mean-field surrounding.40
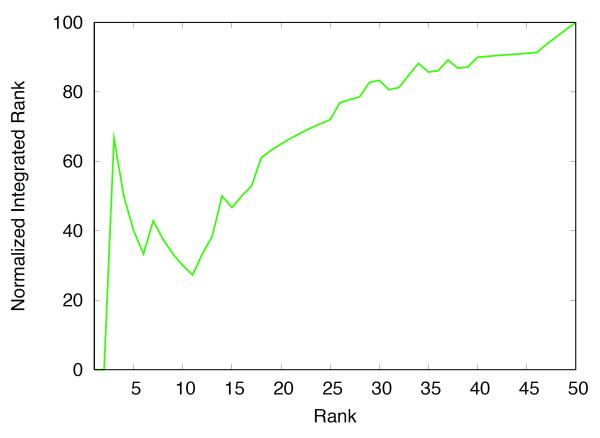
Recently, we have used free energy methods to participate to the OpenEye statistical assessment of the modeling of proteins and ligands (SAMPL) challenge.105 In a blind test, the binding free energies of 50 neutral compounds to the JNK kinase were computed from provided coordinates. Figure 7 shows the jnk kinase bound in complex with ligand 19. Most of the calculations were setup and submitted via automated scripts, trying to minimize human intervention as much as possible. Details about the computations are given in the caption. Among the 50 compounds, the free energy computations correctly predicted two of the top five binders, as well as six of the ten worst binders. Five out of nine non-active compounds were correctly identified. Figure 8 shows the enrichment plot. Though there are clearly some false positives and false negatives, it shows a good separation of the binding and non-binding compounds. Nonetheless, the error in many case is considerable, e.g., the computed binding free energy for ligand 10 is −15.7 kcal/mol whereas the experimental value is −8.7 kcal/mol (ranked at the top experimentally and third computationally). The computed binding free energies range from −16 to −3 kcal/mol while the experimental values range from −8.6 to −5.5 kcal/mol. Thus, the binding affinity is strongly overestimated for a number of ligands. Based on the lessons from T4L, it is likely that this is caused by an inadequate sampling of the conformational changes in the protein.34,37
Figure 7.
The jnk kinase bound with ligand 19 from the OpenEye statistical assessment of the modeling of proteins and ligands (SAMPL) challenge.105 The grey parts are treated as a mean field approximation with generalized solvent boundary potential. The computations were carried out according to the same protocol presented in previous studies.34,40,78
Figure 8.
The cumulative experimental rank (vertical axis) is plotted as a function of the calculated (horizontal axis). The top five ligands from the computations are: 40, 27, 10, 47, 8 ; the experimental top five are: 10, 1, 27, 11, 38. The worse ten ligands from the computations are: 9, 43, 51, 6, 5, 21, 23, 56, 31, 17; the experimental worst ten are: 51, 4, 5, 6, 17, 23, 29, 30, 36, 43.
IV. OUTLOOK
The theoretical foundations are clearly established and one can broadly choose between alchemical free energy perturbation methods, in which the ligand is decoupled progressively from its surrounding, and PMF-based methods, in which the ligand pulled away from the binding site. The former befit computations for ligands bound to buried sites and cavities, while the latter are advantageous for charged ligands that bind to the surface of a protein. For both of these computational approaches, various restraining potentials may be activated and released during the simulation to enhance and aid configurational sampling. While there is ample room for improvement, recent studies demonstrate that absolute binding free energy computations are applicable to increasingly challenging problems.
The treatment of very large conformational changes in the receptor induced by ligand binding remain one of the biggest challenge in calculations of absolute binding free energies. Striking examples are provided by the HIV protease,106–108 or ligand-activated membrane receptors such as the ionotropic glutamate receptor (iGluR).109,110 In principle, an adequate sampling of conformational changes could be achieved via exceedingly long unbiased MD simulations, though this approach rapidly becomes computationally prohibitive in practice. At the present time, one must rely on a deliberate sampling strategy of the relevant degrees of freedom,34,36,37,40,79,81 and thus, some prior identification of those degrees of freedom. In practice, this requires calculating a PMF along some chosen order parameter with biased simulations. In some cases, the order parameter may be relatively simple, such as the dihedral torsion used to control the rotameric state of Val111 in the T4L/L99A system,36 or could be relatively complicated, such as the combination of inter-domain distances used to control the large conformational change induced by the binding of glutamate to iGluR.110 The RMSD relative to a reference conformation is a useful order parameter to control a flexible ligand.34,40,49 Extending the RMSD to a protein macromolecule is possible111,112 but limited. A general approach for mapping arbitrarily complex conformational changes onto a simple order parameter is lacking at present. This is currently an outstanding problem in computational biophysics.113 It may be possible to make progress with the advance of methods aimed at finding the reaction path between the conformations of a macromolecular system.113–116 The treatment of large protein conformation remains an outstanding issue in binding free energy calculations.
Apart from issues of conformational sampling, it is important to recall that the accuracy of computations is determined ultimately by the underlying atomic force field. Because they depend on a free energy difference between the bound and unbound states, computations can benefit from a cancellation of errors. For example, the absolute binding free energy will remain roughly correct even if the van der Waals interaction of a ligand with the solvent and with the protein deviate systematically from the correct values. But this can only be valid up to a point. Dependable results in the future will require that that the force field represents the ligand, the protein, and the solvent, as accurately as possible. Current biomolecular force fields with effective fixed partial charges, such as CHARMM,21 AMBER,22 OPLS,23 and GAFF24 with AM1-BCC charge model,117,118 provide atomic models able to yield solvation free energies that are in reasonably good agreement with experiments for amino acids and a wide range of small molecules.25,26,28–30 Nonetheless, it is clear that the effect of induced electronic polarizability need to be taking into account in order to achieve reliable results of high accuracy.119 Additional complexities somewhat related to the force field, including among other factors, changes in protonation states120 and the existence of tautomers,121 will require a special attention. In considering the accuracy of various force field in the future, it will be helpful to draw more clearly the distinction between extremely rapid automatic assignment of force field parameters for an arbitrary ligand aimed at large database screening,24,117 and more computationally intensive physics-based approaches aimed at generating models of high accuracy.122
Computations of absolute binding free energies methodologies are now approaching the point where making accurate prediction and addressing issues of molecular recognition will be achievable. While there is still much to be done, the methods are already bearing fruits and the path toward progress is very clear.
Table I.
Binding Free Energy for the T4L cavities
| Ligand | Δ Δ G rep | Δ Δ G dis | Δ Δ G elec | Exp | ||
|---|---|---|---|---|---|---|
|
| ||||||
| L99A nonpolar site | ||||||
| benzene | −4.73 | −7.43 | 0.69 | 5.42 | −5.96 | −5.19 |
| phenol | −4.58 | −8.19 | 4.35 | 7.55 | −0.88 | – |
|
| ||||||
| L99A/M102Q polar site | ||||||
| benzene | −4.37 | −8.53 | 0.51 | 6.78 | −5.61 | – |
| phenol | −4.06 | −9.74 | −0.32 | 8.52 | −5.64 | −5.55 |
Table II.
Binding Free Energy for ligand 8 of FKBP12
| Δ Δ G rep | Δ Δ G dis | Δ Δ G elec | Δ Δ G t | Δ Δ G r | Exp | ||
|---|---|---|---|---|---|---|---|
| −1.1 | −21.1 | −3.7 | 6.9 | 3.4 | 5.4 | −10.2 | −10.9 |
| −25.9 | 15.7 | ||||||
Acknowledgments
We would like thank Hideaki Fujitani, Vijay Pande, Michael Shirts, David Mobley, Ken Dill, Devleena Shivakumar, Hyung-Jun Woo, and Jiayao Wang for their help. This work was supported by the National Science Foundation through the grant MCB-0415784.
Contributor Information
Yuqing Deng, Biosciences Division, Argonne National Laboratory.
Benoît Roux, Gordon Center for Integrative Science, University of Chicago.
References
- 1.Vindigni A. Energetic dissection of specificity in serine proteases. Comb. Chem. High Throughput Screen. 1999;2:139–153. [PubMed] [Google Scholar]
- 2.Cheng AC, Calabro V, Frankel AD. Design of rna-binding proteins and ligands. Curr. Opin. Struct. Biol. 2001;11(4):478–484. doi: 10.1016/s0959-440x(00)00236-0. [DOI] [PubMed] [Google Scholar]
- 3.Garvie CW, Wolberger C. Recognition of specific dna sequences. Mol. Cell. 2001;8(5):937–946. doi: 10.1016/s1097-2765(01)00392-6. [DOI] [PubMed] [Google Scholar]
- 4.Shoichet B. Virtual screening of chemical libraries. Nature. 2004;432:862–865. doi: 10.1038/nature03197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shoichet B, Leach A, Kuntz I. Ligand solvation in molecular docking. Proteins. 1999;34:4–16. doi: 10.1002/(sici)1097-0134(19990101)34:1<4::aid-prot2>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- 6.Carlson H, Masukawa K, Rubins K, Bushman F, Jorgensen W, Lins R, Briggs J, McCammon J. Developing a dynamic pharmacophore model for HIV-1 integrase. J Med Chem. 2000;43:2100–2114. doi: 10.1021/jm990322h. [DOI] [PubMed] [Google Scholar]
- 7.Schneider G, Bohm HJ. Virtual screening and fast automated docking methods. Drug Discov. Today. 2002;7(1):64–70. doi: 10.1016/s1359-6446(01)02091-8. [DOI] [PubMed] [Google Scholar]
- 8.Price D, Jorgensen W. Computational binding studies of human pp60c-src SH2 domain with a series of non-peptide, phosphophenyl-containing ligands. Bioorg Med Chem Lett. 2000;10:2067–2070. doi: 10.1016/s0960-894x(00)00401-7. [DOI] [PubMed] [Google Scholar]
- 9.Wesolowski S, Jorgensen W. Estimation of binding affinities for celecoxib analogues with COX-2 via Monte Carlo-extended linear response. Bioorg Med Chem Lett. 2002;12:267–270. doi: 10.1016/s0960-894x(01)00825-3. [DOI] [PubMed] [Google Scholar]
- 10.Beveridge DL, Dicapua FM. Free energy via molecular simulation - applications to chemical and biomolecular systems. Annu. Rev. Biophys. Bio. 1989;18:431–492. doi: 10.1146/annurev.bb.18.060189.002243. [DOI] [PubMed] [Google Scholar]
- 11.Straatsma T, McCammon J. Computational alchemy. Annu. Rev. Phys. Chem. 1992;43:407–435. [Google Scholar]
- 12.Kollman P. Free Energy Calculations: Applications to Chemical and Biochemical Phenomena. Chem. Rev. 1993;93:2395–2417. [Google Scholar]
- 13.Simonson T, Archontis G, Karplus M. Free energy simulations come of age: Protein-ligand recognition. Acc. Chem. Res. 2002;35:430–437. doi: 10.1021/ar010030m. [DOI] [PubMed] [Google Scholar]
- 14.Postma J, Berendsen H. Thermodynamics of cavity formation in water - a molecular-dynamics study. Symp. Chem. Soc. 1982;17:55–67. [Google Scholar]
- 15.Jorgensen W, Ravimohan C. Monte-carlo simulation of differences in free-energies of hydration. J. Chem. Phys. 1985;83:3050–3054. [Google Scholar]
- 16.Warshel A. Dynamics of reactions in polar-solvents - Semi-classical trajectory studies of electron-transfer and proton-transfer reactions. J. Phys. Chem. 1982;86:2218–2224. [Google Scholar]
- 17.Tember B, McCammon A. Ligand receptor interactions. Comp. Chem. 1984;8:281–283. [Google Scholar]
- 18.Warshel A. Simulating the Energetics and Dynamics of Enzymatic Reactions. Pontificiae Academiae Scientiarum Scripta VariA. 1982;55:59–81. [Google Scholar]
- 19.Lybrand T, McCammon A, Wipff G. Theoretical calculation of relative binding-affinity in host guest systems. Proc. Nat. Acad. Sci. USA. 1986;83:833–835. doi: 10.1073/pnas.83.4.833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hermans J, Subramaniam S. The free energy of xenon binding to myoglobin from molecular dynamics simulation. Isr. J. Chem. 1986;27:225–227. [Google Scholar]
- 21.MacKerell AD, Jr, Bashford D, Bellott M, Dumbrack RL, Jr, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, III, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiórkiewicz-Kuczera J, Yin D, Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 22.Cornell WD, Cieplak P, Bayly CL, Gould IR, Merz KM, Jr, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
- 23.Jorgensen WL, Maxwell DS, Tirado-Rives J. Development and testing of the OPLS all-atom froce field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996;118:11225–11236. [Google Scholar]
- 24.Wang J, Wolf RM, Caldwell JW, Kollman PA, Case DA. Development and testing of a general amber force field. J. Comput. Chem. 2004;25:1157–1174. doi: 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- 25.Shirts MR, Pitera JW, Swope WC, Pande VS. Extremely precise free energy calculations of amino acid side chain analogs: Comparison of common molecular mechanics force fields for proteins. J. Chem. Phys. 2003;119:5740–5761. [Google Scholar]
- 26.Deng Y, Roux B. Hydration of amino acid side chains: Nonpolar and electrostatic contributions calculated from staged molecular dynamics free energy simulations with explicit water molecules. J. Phys. Chem. B. 2004;108:16567–16576. [Google Scholar]
- 27.Wan S, Stote RH, Karplus M. Calculation of the aqueous solvation energy and entropy, as well as free energy, of simple polar solutes. J. Chem. Phys. 2004;121:9539–9548. doi: 10.1063/1.1789935. [DOI] [PubMed] [Google Scholar]
- 28.Mobley D, Dumont E, Chodera J, Dill K. Comparison of charge models for fixed-charge force fields: Small-molecule hydration free energies in explicit solvent. J. Phys. Chem. B. 2007;111:2242–2254. doi: 10.1021/jp0667442. [DOI] [PubMed] [Google Scholar]
- 29.Mobley DL, Baylyâ CI, Cooper MD, Shirts MR, Dill KA. Small molecule hydration free energies in explicit solvent: An extensive test of fixed-charge atomistic simulations. J. Phys. Chem. B. 2008 doi: 10.1021/ct800409d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Shivakumar D, Deng Y, Roux B. Calculation of absolute solvation free energies of small molecules using explicit and implicit solvent model. J. Phys. Chem. B. 2008 doi: 10.1021/ct800445x. [DOI] [PubMed] [Google Scholar]
- 31.Maccallum JL, Tieleman DP. Calculation of the water-cyclohexane transfer free energies of neutral amino acid side-chain analogs using the OPLS all-atom force field. J. Comput. Chem. 2003;24:1930–1935. doi: 10.1002/jcc.10328. [DOI] [PubMed] [Google Scholar]
- 32.Hermans J, Wang L. Inclusion of loss of translational and rotational freedom in theoretical estimates of free energies of binding. application to a complex of benzene and mutant T4 lysozyme. J. Am. Chem. Soc. 1997;119:2707–2714. [Google Scholar]
- 33.Mann G, Hermans J. Modeling protein-small molecule interactions: Structure and thermodynamics of noble gases binding in a cavity in mutant phage T4 lysozyme L99A. J. Mol. Biol. 2000;302:979–989. doi: 10.1006/jmbi.2000.4064. [DOI] [PubMed] [Google Scholar]
- 34.Deng Y, Roux B. Calculation of standard binding free energies: Aromatic molecules in the T4 lysozyme L99A mutant. J. Chem. Theory Comput. 2006;2:1255–1273. doi: 10.1021/ct060037v. [DOI] [PubMed] [Google Scholar]
- 35.Mobley DL, Chodera JD, Dill KA. On the use of orientational restraint and symmetry corrections in alchemical free energy calculations. J. Chem. Phys. 2006;125:084902. doi: 10.1063/1.2221683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Mobley DL, Chodera JD, Dill KA. Confine-and-release method: Obtaining correct binding free energies in the presence of protein conformational change. J. Chem. Theory Comput. 2007;3:1231–1235. doi: 10.1021/ct700032n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mobley DL, Graves AP, Chodera JD, McReynolds AC, Shoichet BK, Dill KA. Predicting absolute ligand binding free energies to a simple model site. J. Mol. Biol. 2007;371:1118–1134. doi: 10.1016/j.jmb.2007.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Shirts MR. Ph.D. thesis. Stanford University; 2005. Calculating precise and accurate free energies in biomolecular systems. [Google Scholar]
- 39.Fujitani H, Tanida Y, Ito M, Jayachandran G, Snow CD, Shirts MR, Sorin EJ, Pande VS. Direct calculation of the binding free energies of FKBP ligands. J. Chem. Phys. 2005;123:084108. doi: 10.1063/1.1999637. [DOI] [PubMed] [Google Scholar]
- 40.Wang J, Deng Y, Roux B. Absolute binding free energy calculations using molecular dynamics simulations with restraint potentials. Biophys. J. 2006;91:2798–2814. doi: 10.1529/biophysj.106.084301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lee MS, Olson MA. Calculation of absolute portein-ligand binding affinity using path and endpoint approaches. Biophys. J. 2006;90:864–877. doi: 10.1529/biophysj.105.071589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Jayachandran G, Shirts MR, Park S, Pande VS. Parallelized-over-parts computation of absolute binding free energy with docking and molecular dynamics. J. Chem. Phys. 2006;125:084901. doi: 10.1063/1.2221680. [DOI] [PubMed] [Google Scholar]
- 43.Rajamani R, Good AC. Ranking poses in structure-based lead discovery and optimization: current trends in scoring function development. Curr Opin Drug Discov Devel. 2007;10:308–15. [PubMed] [Google Scholar]
- 44.Seifert MHJ, Kraus J, Kramer B. Virtual high-throughput screening of molecular databases. Curr Opin Drug Discov Devel. 2007;10:298–307. [PubMed] [Google Scholar]
- 45.Kontoyianni M, Madhav P, Suchanek E, Seibel W. Theoretical and practical considerations in virtual screening: a beaten field? Curr Med Chem. 2008;15:107–16. doi: 10.2174/092986708783330566. [DOI] [PubMed] [Google Scholar]
- 46.Roux B, Nina M, Pomès R, Smith JC. Thermodynamic stability of water molecules in the bacteriorhodopsin proton channel: A molecular dynamics free energy perturbation study. Biophys. J. 1996;71:670–681. doi: 10.1016/S0006-3495(96)79267-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Gilson MK, Given JA, Bush BL, Andrew McCammon J. The statistical-thermaldynamic basis for computation of binding affinities: A critical review. Biophys. J. 1997;72:1047–1069. doi: 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Luo H, Sharp K. On the calculation of absolute macromolecular binding free energies. Proc. Nat. Acad. Sci. USA. 2002;99:10399–10404. doi: 10.1073/pnas.162365999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Woo H-J, Roux B. Calculation of absolute protein-ligand binding free energy from computer simulations. Proc. Nat. Acad. Sci. USA. 2005;102:6825–6830. doi: 10.1073/pnas.0409005102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bjerrum N. Untersuchungen über Ionenassoziation. I. der Einfluss der Ionenassoziation auf die Akativität der Ionen bei Mittleren Assoziationsgraden. Kgl. Danske Videns. Selsk. Mat.-fys. Medd. 1926;7:1–48. [Google Scholar]
- 51.Mihailescu M, Gilson MK. On the theory of noncovalent binding. Biophys. J. 2004;87:23–36. doi: 10.1529/biophysj.103.031682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Hunenberger P, van Gunsteren WF. Experimental and theoretical approach to hydrogen-bonded diastereomeric interactions in a model complex. J. Am. Chem. Soc. 1997;119:7533–7544. [Google Scholar]
- 53.Jorgensen WL. Free energy calculations: a breakthrough for modeling organic chemistry in solution. Acc. Chem. Res. 1989;22:184–189. [Google Scholar]
- 54.Boresch S, Tettinger F, Leitgeb M, Karplus M. Absolute binding free energies: A quantitative approach for their calculation. J. Phys. Chem. B. 2003;107:9535–9551. [Google Scholar]
- 55.Jorgensen WL. Interactions between amides in solution and the thermodynamics of weak binding. J. Am. Chem. Soc. 1989;111:3770–3771. [Google Scholar]
- 56.Allen TW, Andersen OS, Roux B. Energetics of ion conduction through the gramicidin channel. Proc. Nat. Acad. Sci. USA. 2004;101:117–122. doi: 10.1073/pnas.2635314100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Beveridge DL, DiCapua FM. Free energy via molecular simulation: Applications to chemical and biomolecular systems. Annu. Rev. biophys. Biomol. Struct. 1989;18:431–492. doi: 10.1146/annurev.bb.18.060189.002243. [DOI] [PubMed] [Google Scholar]
- 58.Kollman P. Free energy calculations: Applications to chemical and biochemical phenomena. Chem. Rev. 1993;93:2395–2417. [Google Scholar]
- 59.Kollman PA, Massova I, Reyes C, Kuhn B, Huo S, Chong L, Lee M, Lee T, Duan Y, Wang W, Donini O, Cieplak P, Srinivasan J, Case DA, Cheatham TE., III Calculating structures and free energies of complex molecules: Combining molecular mechanics and continuum models. Acc. Chem. Res. 2000;33:889–897. doi: 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- 60.Swanson JMJ, Henchman RH, McCammon JA. Revisiting free energy calculations: A theoretical connection to MM/PBSA and direct calculation of the association free energy. Biophys. J. 2004;86:67–74. doi: 10.1016/S0006-3495(04)74084-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Åqvist J, Luzhkov VB, Brandsdal BO. Ligand binding affinities from MD simulations. Acc. Chem. Res. 2002;35:358–365. doi: 10.1021/ar010014p. [DOI] [PubMed] [Google Scholar]
- 62.Sham YY, Chu ZT, Tao H, Warshel A. Examining methods for calculations of binding free energies: LRA, LIE, PDLD-LRA, and PDLD/S-LRA calculations of ligands binding to an HIV protease. Proteins: Struct. Funct. Genet. 2000;39:393–407. [PubMed] [Google Scholar]
- 63.Souaille M, Roux B. Extension to the weighted histogram analysis method: Combining umbrella sampling with free energy calculations. Computer Phys. Comm. 2001;135:40–57. [Google Scholar]
- 64.Axelsen P, Li D. Improved convergence in dual-topology free energy calculations through use of harmonic restraints. J. Comput. Chem. 1998;19:1278–1283. [Google Scholar]
- 65.van Duijneveldt S, Frenkel D. Computer-simulation study of free-energy barriers in crystal nucleation. J. Chem. Phys. 1992;96:4655–4668. [Google Scholar]
- 66.Patey GN, Valleau JP. A Monte Carlo method for obtaining the interionic potential of mean force in ionic solution. J. Chem. Phys. 1975;63:2334–2339. [Google Scholar]
- 67.Weeks JD, Chandler D, Andersen HC. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971;54:5237–5247. [Google Scholar]
- 68.Chandler D, Pratt L. Statistical-mechanics of chemical-equilibria and intramolecular structures of nonrigid molecules in condensed phases. J. Chem. Phys. 1976;65:2925–2940. [Google Scholar]
- 69.Roux B, Simonson T. Implicit solvent models. Biophys. Chem. 1999;78:1–20. doi: 10.1016/s0301-4622(98)00226-9. [DOI] [PubMed] [Google Scholar]
- 70.Roux B, Andersen O, Allen T. Comment on “Free energy simulations of single and double ion occupancy in gramicidin A”. J Chem Phys. 2008;128:227101. doi: 10.1063/1.2931568. [J. Chem. Phys. 126, 105103 (2007)] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Roux B, Simonson T. Implicit solvent models. Biophys. Chem. 1999;78:1–20. doi: 10.1016/s0301-4622(98)00226-9. [DOI] [PubMed] [Google Scholar]
- 72.King G, Lee F, Warshel A. Microscopic simulation of macroscopic dielectric constants of solvated proteins. J. Chem. Phys. 1991;95:4365–4377. [Google Scholar]
- 73.Beglov D, Roux B. Finite representation of an infinite bulk system: Solvent boundary potential for computer simulations. J. Chem. Phys. 1994;100:9050–9063. [Google Scholar]
- 74.Im W, Bernèche S, Roux B. Generalized solvent boundary potential for computer simulations. J. Chem. Phys. 2000;114:2924–2937. [Google Scholar]
- 75.Morton A, Baase WA, Matthews BW. Energetic origins of specificity of ligand binding in an interior nonpolar cavity of T4 lysozyme. Biochemistry. 1995;34:8564–8575. doi: 10.1021/bi00027a006. [DOI] [PubMed] [Google Scholar]
- 76.Wei BQ, Baase WA, Weaver LH, Matthews BW, Shoichet BK. A model binding site for testing scoring functions in molecular docking. J. Mol. Biol. 2002;322:339–355. doi: 10.1016/s0022-2836(02)00777-5. [DOI] [PubMed] [Google Scholar]
- 77.Helms V, Wade RC. Computational alchemy to calculate absolute protein-ligand binding free energy. J. Am. Chem. Soc. 1998;120:2710–2713. [Google Scholar]
- 78.Deng Y, Roux B. Computation of binding free energy with molecular dynamics and grand canonical Monte Carlo simulations. J. Chem. Phys. 2008;128:115103. doi: 10.1063/1.2842080. [DOI] [PubMed] [Google Scholar]
- 79.Woo H-J, Dinner AR, Roux B. Grand canonical Monte Carlo simulation of water in protein environments. J. Chem. Phys. 2004;121:6392–6400. doi: 10.1063/1.1784436. [DOI] [PubMed] [Google Scholar]
- 80.Chipot C, Rozanska X, Dixit S. Can free energy calculations be fast and accurate at the same time? Binding of low-affinity, non-peptide inhibitors to the SH2 domain of the src protein. J. Comput. Aided Mol. Des. 2005;19:765–770. doi: 10.1007/s10822-005-9021-3. [DOI] [PubMed] [Google Scholar]
- 81.Gan W, Roux B. Binding specificity of SH2 domains: Insight from free energy simulations. PROT. 2008 doi: 10.1002/prot.22209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Morton A, Matthews BW. Specificity of ligand binding in a buried nonpolar cavity of T4 lysozyme: Linkage of dynamics and structural plasticity. Biochemistry. 1995;34:8576–8588. doi: 10.1021/bi00027a007. [DOI] [PubMed] [Google Scholar]
- 83.Kissinger CR, Parge HE, Knighton DR, Lewis CT, Pelletier LA, Tempczyk A, Kalish VJ, Tucker KD, Showalter RE, Moomaw EW, Gastinel LN, Habuka N, Chen X, Maldonado F, Barker JE, Bacquet R, Villafranca JE. Crystal structures of human calcineurin and the human FKBP12-FK506-calcineurin complex. Nature. 1995;378:641–644. doi: 10.1038/378641a0. [DOI] [PubMed] [Google Scholar]
- 84.Griffith JP, Kim JL, Kim EE, Sintchak MD, Thomson JA, Fitzgibbon MJ, Fleming MA, Caron PR, Hsiao K, Navia MA. X-ray structure of calcineurin inhibited by the immunophilin-immunosuppressant FKBP12-FK506 complex. Cell. 1995;82:507–522. doi: 10.1016/0092-8674(95)90439-5. [DOI] [PubMed] [Google Scholar]
- 85.Hamelberg D, McCammon JA. Standard free energy of releasing a localized water molecule from the binding pockets of proteins: Double-decoupling method. J. Am. Chem. Soc. 2004;126:7683–7689. doi: 10.1021/ja0377908. [DOI] [PubMed] [Google Scholar]
- 86.Olano LR, Rick SW. Hydration free energies and entropies for water in protein interiors. J. Am. Chem. Soc. 2004;126:7991–8000. doi: 10.1021/ja049701c. [DOI] [PubMed] [Google Scholar]
- 87.Levy RM, Zhang LY, Gallicchio E, Felts AK. On the nonpolar hydration free energy of proteins: Surface area and continuum solvent models for the solute-solvent interaction energy. J. Am. Chem. Soc. 2003;125:9523–9530. doi: 10.1021/ja029833a. [DOI] [PubMed] [Google Scholar]
- 88.Kuntz ID, Chen K, Sharp KA, Kollman PA. The maximal affinity of ligands. Proc. Nat. Acad. Sci. USA. 1999;96:9997–10002. doi: 10.1073/pnas.96.18.9997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Meirovitch H. Recent developments in methodologies for calculating the entropy and free energy of biological systems by computer simulation. Curr. Opin. Struct. Biol. 2007;17:181–186. doi: 10.1016/j.sbi.2007.03.016. [DOI] [PubMed] [Google Scholar]
- 90.Chang CA, Chen W, Gilson MK. Ligand configurational entropy and protein binding. Proc. Nat. Acad. Sci. USA. 2007;104:1534–1539. doi: 10.1073/pnas.0610494104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Hummer G, Szabo A. Free energy surfaces from single-molecule force spectroscopy. Acc. Chem. Res. 2005;38:504–513. doi: 10.1021/ar040148d. [DOI] [PubMed] [Google Scholar]
- 92.Collins MD, Hummer G, Quillin ML, Matthews BW, Gruner SM. Cooperative water filling of a nonpolar protein cavity observed by high-pressure crystallography and simulation. Proc. Nat. Acad. Sci. USA. 2005;102:16668–16671. doi: 10.1073/pnas.0508224102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Yin H, Hummer G, Rasaiah JC. Metastable water clusters in the nonpolar cavities of the thermostable protein tetrabrachion. J. Am. Chem. Soc. 2007;129:7369–7377. doi: 10.1021/ja070456h. [DOI] [PubMed] [Google Scholar]
- 94.Li Z, Lazaridis T. The effect of water displacement on binding thermodynamics: Concanavalin A. J. Phys. Chem. B. 2005;109:662–670. doi: 10.1021/jp0477912. [DOI] [PubMed] [Google Scholar]
- 95.Lu Y, Yang C-Y, Wang S. Binding free energy contribution of interfacial waters in HIV-1 protease/inhibitor complexes. J. Am. Chem. Soc. 2006;128:11830–11839. doi: 10.1021/ja058042g. [DOI] [PubMed] [Google Scholar]
- 96.Li Z, Lazaridis T. Water at biomolecular binding interfaces. Phys. Chem. Chem. Phys. 2007;9:573–581. doi: 10.1039/b612449f. [DOI] [PubMed] [Google Scholar]
- 97.Helms V, Wade RC. Hydration energy landscape of the active site cavity in cytochrome P450cam. Proteins: Struct. Funct. Genet. 1998;32:381–396. [PubMed] [Google Scholar]
- 98.Barillari C, Taylor J, Viner R, Essex JW. Classification of water molecules in protein binding sites. J. Am. Chem. Soc. 2007;129:2577–2587. doi: 10.1021/ja066980q. [DOI] [PubMed] [Google Scholar]
- 99.Mancera RL. Molecular modeling of hydration in drug design. Curr. Opin. Drug Discov. Devel. 2007;10:275–280. [PubMed] [Google Scholar]
- 100.Oprea TI, Hummer G, García AE. Identification of a functional water channel in cytochrome P450 enzymes. Proc. Nat. Acad. Sci. USA. 1997;94:2133–2138. doi: 10.1073/pnas.94.6.2133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Cojocaru V, Winn PJ, Wade RC. The ins and outs of cytochrome P450s. Biochim. Biophys. Acta. 2007;1770:390–401. doi: 10.1016/j.bbagen.2006.07.005. [DOI] [PubMed] [Google Scholar]
- 102.García AE, Hummer G. Water penetration and escape in proteins. Proteins: Struct. Funct. Genet. 2000;38:261–272. [PubMed] [Google Scholar]
- 103.Resat H, Mezei M. Grand canonical ensemble Monte Carlo simulation of the dCpG/proflavine crystal hydrate. Biophys. J. 1996;71:1179–1190. doi: 10.1016/S0006-3495(96)79322-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Clark M, Guarnieri F, Shkurko I, Wiseman J. Grand canonical Monte Carlo simulation of ligand-protein binding. J. Chem. Inf. Model. 2006;46:231–242. doi: 10.1021/ci050268f. [DOI] [PubMed] [Google Scholar]
- 105. http://sampl.eyesopen.com/
- 106.Hornak V, Okur A, Rizzo R, Simmerling C. HIV-1 protease flaps spontaneously open and reclose in molecular dynamics simulations. Proc. Natl. Acad. Sci. U.S.A. 2006;103:915–920. doi: 10.1073/pnas.0508452103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Hornak V, Okur A, Rizzo R, Simmerling C. HIV-1 protease flaps spontaneously close to the correct structure in simulations following manual placement of an inhibitor into the open state. J. Am. Chem. Soc. 2006;128:2812–2813. doi: 10.1021/ja058211x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Hornak V, Simmerling C. Targeting structural flexibility in HIV-1 protease inhibitor binding. Drug Discov. Today. 2007;12:132–138. doi: 10.1016/j.drudis.2006.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Armstrong N, Mayer M, Gouaux E. Tuning activation of the AMPA-sensitive GluR2 ion channel by genetic adjustment of agonist-induced conformational changes. Proc. Natl. Acad. Sci. U.S.A. 2003;100:5736–5741. doi: 10.1073/pnas.1037393100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Lau A, Roux B. The free energy landscapes governing conformational changes in a glutamate receptor ligand-binding domain. Structure. 2007;15:1203–1214. doi: 10.1016/j.str.2007.07.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Banavali N, Roux B. Free energy landscape of A-DNA to B-DNA conversion in aqueous solution. J. Am. Chem. Soc. 2005;127:6866–6876. doi: 10.1021/ja050482k. [DOI] [PubMed] [Google Scholar]
- 112.Banavali N, Roux B. The N-terminal end of the catalytic domain of SRC kinase Hck is a conformational switch implicated in long-range allosteric regulation. Structure. 2005;13:1715–1723. doi: 10.1016/j.str.2005.09.005. [DOI] [PubMed] [Google Scholar]
- 113.Elber R. Long-timescale simulation methods. Curr. Opin. Struct. Biol. 2005;15:151–156. doi: 10.1016/j.sbi.2005.02.004. [DOI] [PubMed] [Google Scholar]
- 114.Maragliano L, Fischer A, Vanden-Eijnden E, Ciccotti G. String method in collective variables: minimum free energy paths and isocommittor surfaces. J Chem Phys. 2006;125:24106. doi: 10.1063/1.2212942. [DOI] [PubMed] [Google Scholar]
- 115.Christen M, van Gunsteren WF. On searching in, sampling of, and dynamically moving through conformational space of biomolecular systems: A review. J. Comput. Chem. 2008;29:157–166. doi: 10.1002/jcc.20725. [DOI] [PubMed] [Google Scholar]
- 116.Pan A, Sezer D, Roux B. Finding transition pathways using the string method with swarms of trajectories. J Phys Chem B. 2008;112:3432–3440. doi: 10.1021/jp0777059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Jakalian A, Bush BL, Jack DB, Bayly CI. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: I. Method. J. Comput. Chem. 2000;21:132–146. doi: 10.1002/jcc.10128. [DOI] [PubMed] [Google Scholar]
- 118.Jakalian A, Jack DB, Bayly CI. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and Validation. J. Comput. Chem. 2002;23:1623–1641. doi: 10.1002/jcc.10128. [DOI] [PubMed] [Google Scholar]
- 119.Jiao D, Golubkov P, Darden T, Ren P. Calculation of protein-ligand binding free energy by using a polarizable potential. Proc. Natl. Acad. Sci. U.S.A. 2008;105:6290–6295. doi: 10.1073/pnas.0711686105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Gohlke H, Klebe G. Approaches to the description and prediction of the binding affinity of small-molecule ligand to macromolecular receptors. Angew. Chem. Int. Ed. 2002;41:2644–2676. doi: 10.1002/1521-3773(20020802)41:15<2644::AID-ANIE2644>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- 121.Pospisil P, Ballmer P, Scapozza L, Folkers G. Tautomerism in computer-aided drug design. J. Recept. Signal Transduct. Res. 2003;23:361–371. doi: 10.1081/rrs-120026975. [DOI] [PubMed] [Google Scholar]
- 122.Anisimov V, Lamoureux G, Vorobyov I, Huang N, Roux B, MacKerell A. Determination of electrostatic parameters for a polarizable force field based on the classical Drude oscillator. J. Chem. Theo. Comput. 2005;1:153–168. doi: 10.1021/ct049930p. [DOI] [PubMed] [Google Scholar]